PROGRAM STOKASTIK
2.1 Pengertian Program Stokastik
Banyak persoalan keputusan yang dapat dimodelkan dengan menggunakan program matematika yang bertujuan menentukan nilai maksimum atau minimum. Keputusan yang dihasilkan akan bergantung kepada kendala yang dibatasi oleh sumber dana, persyaratan minimum dan lain-lain. Keputusan yang dinyatakan oleh variabel dapat berupa bilangan cacah atau nonnegatif. Tujuan dan kendala adalah fungsi dari variabel, dan persoalan data. Sebagai contoh dari persoal-an data termasuk biaya perunit, rata-rata produksi, penjualpersoal-an atau kapasitas. Andaikan keputusan dinyatakan oleh variabel x1 +x2 +x3 +...+xn. Sebagai contoh xi menyatakan produksi ke−i dari n produk. Bentuk umum program matematikanya adalah : min f(x1, x2, x3 · · ·,xn) Kendala: g1(x1, x2, x3 · · · , xn)≤0 g2(x1, x2, x3 · · · , xn)≤0 (2.1.1) ...≤... gm(x1, x2, x3 · · · , xn)≤0 x1, x2, x3, . . . , xn∈X. dimana X adalah himpunan bilangan real non negatif.
Stokastik programming adalah sebuah nama yang menyatakan program ma-tematika yang dapat berupa linear, cacah, cacah campuran, non linear tetapi de-ngan menampilkan elemen stokastik pada data. Oleh karena itu dapat dinyatakan bahwa:
a. Pada program matematika deterministik, data koefisien adalah bilangan-bilangan yang diketahui (tertentu).
b. Pada program stokastik, data (koefisien) merupakan bilangan yang tidak diketahui (tidak pasti) yang disajikan sebagai distribusi peluang.
Program stokastik merupakan program matematika dengan situasi (yang mengandung) ketidakpastian. Program stokastik adalah merupakan program ma-tematika, dimana beberapa data yang termuat pada tujuan atau kendala meng-andung ketidakpastian, ketidakpastian biasanya dicirikan oleh distribusi peluang pada parameter. Walaupun ketidakpastian didefinisikan dengan tepat tetapi pa-da prakteknya diberikan beberapa skenario (hasil yang mungkin pa-dari pa-data) yang spesifik dan distribusi peluang gabungan yang cepat. Hasil-hasil secara umum di-gambarkan pada elemen w∈ W. Ketika beberapa data acak, maka penyelesaian dan nilai tujuan optimal untuk masalah optimisasi juga acak.
Ada dua tipe permasalahan program stokastik, yaitu : 1. Recourse Models (Model Rekursif)
2. Probabilistically Constrained Models (model Kendala Berpeluang)
Suatu cara logis yang diperlukan dalam persoalan adalah membuat sebuah ke-putusan sekarang dan meminimumkan biaya rata-rata harapan (yang digunakan) sebagai konsekwensi dari keputusan. Paradigma ini dikenal sebagai model Reco-urse. Andaikanxadalah vektor keputusan yang diambil, dan y(ω) adalah sebuah vektor keputusan yang menyatakan aksi terbaru atau konsekwensi dari x. Him-punan berbeda yang berisi y akan dipilih dari tiap-tiap hasil yang mungkin dari ω. Formulasi dua tahapnya adalah
min f1(x) + nilaiharapan[f2(y(ω), ω)]
Kendala: g1(x),· · · , gm(x)≤0 h1(x, y(w))≤0, ∀ω ∈W (2.1.2) ... ≤ ... hk(x, y(w))≤0, ∀ω ∈W x∈X, y(ω)∈Y.
Himpunan kendala h1, h2,· · · , hk, menggambarkan hubungan antara keputusan tahap pertamaxdan keputusan tahap keduay(ω). Di catat bahwa dipersyaratkan (diharuskan) tiap-tiap kendala dipenuhi dengan peluang 1, atau untuk setiap ω ∈W yang mungkin.Fungsif2 merupakan penyelesaian yang sering muncul dari persoalan matematika. Tidak dibutuhkan untuk membuat korelasi yang berubah-ubah (recourse) untuk keputusan tahap pertama, perlu untuk dibuat korelasi yang terbaik.
Model Recourse dapat diperluas dengan banyak cara. Untuk persoalan ta-hap ganda, pengaruh keputusan sekarang akan ditunggu untuk beberapa keti-dakpastian yang diselesaikan kembali (direalisasikan), sehingga pembuatan ke-putusan yang lain didasarkan pada apa yang terjadi. Tujuannya adalah untuk meminimumkan biaya yang diharapkan dari semua keputusan yang diambil.
Pada beberapa kasus, dapat digunakan suatu metode yang lebih tepat untuk mencoba menentukan sebuah keputusan, yang mana keputusan tersebut dijamin oleh himpunan kendala yang akan dipenuhi oleh sebuah peluang tertentu. Model umum dengan kendala berpeluang disebut sebagai probabilistically constrained models yang dirumuskan sebagai berikut :
min f(x1, x2, x3 · · · , xn) Kendala: P r[g1(x1, x2, x3 · · · , xn)≤0,· · · , gm(x1, x2, x3 · · · , xn)≤0]≥α ...≤... (2.1.3) h1(x1, x2, x3 · · · , xn)≤0 h2(x1, x2, x3 · · · , xn)≤0 x1, x2, x3, . . . , xn∈X
2.2 Jalur Terpendek Pada jaringan acak
Persoalan yang ada pada jalur terpendek yaitu merupakan suatu persoal-an dimpersoal-ana bilpersoal-angpersoal-an acak digunakpersoal-an sebagai koefisien (data)dalam menentukpersoal-an panjang busur Steele (1995), Martin (1965). Membicarakan persoalan bilangan
acak pada panjang jalur ataupun lintasan, tidak akan terlepas dari persoalan sto-kastik. Hal-hal yang akan dibahas bagaimana menyajikan suatu tehnik untuk menghitung fungsi distribusi dari panjang jalur sumber ke panjang jalur tujuan. Dapat digunakan untuk menghitung jalur terpendek, yang diarahkan ke suatu jaringan acyclic yang panjang busurnya memiliki jangkauan terbatas. Bereanu (1966)merumuskan masalah program linear stokastik dengan fungsi objective se-bagai koefisien acak. Studi ini memberikan penyelesaian yang memerlukan pe-ngetahuan tentang dasar probabilitas yang optimal. Grimmett dan Welsh (1982), mempetimbangkan aliran maksimum dalam jaringan dengan kapasitas distribusi yang independent (bebas) dan identik. Dan juga menemukan Teorema limit untuk kasus-kasus dimana jaringan graph lengkap dan cabang pohon. Frieze, Grimmett, dan Andretta(1985) bersama teman-temannya dengan pendekatan masing-masing memeriksa situasi dimana panjang busur adalah variabel acak, dan jalur dengan probabilitas maksimum yang terpendek adalah tetap.
2.3 Jaringan Tak Lengkap
Ketika menganalisa lintasan terpendek antara node sumber s ke node tu-juan t didalam suatu jaringan lengkap dengan masing-masing panjang busur, se-lama perhitungan pada himpunan bagian node tengah dapat digunakan mulai dari sumber s ke tujuan,t, himpunan bagian panjang jalur dapat dihitung secara hukum probabilitas. Sehingga suatu lintasan dibangun dengan memberikan ma-salah secara instan, dan barisan node didefinisikan sebagai lintasan yang hanya boleh dilalui node. Analisis lintasan apriori yang diharapkan sebagai panjang minimum, dapat didefinisikan sebagai persoalan lintasan terpendek probabilistik. Jaillet (1992). Ketika suatu parameter dari jaringan tidak lengkap dipilih sebagai variable acak, kemudian hasilnya diketahui sebagai jaringan stokastik tidak leng-kap, dan persoalan ini ditemukan sebagai lintasan minimum, maka diharapkan panjang yang diketahui bisa dipilih sebagai persoalan lintasan terpendek jaringan stokastik tidak lengkap. Sebagian literature ada yang mengatasi ketidak jelas-an ini untuk persoaljelas-an jelas-analisis dengjelas-an asumsi jarak acak dijelas-antara node pada jaringan stokastik tidak lengkap, Kulkarni (1986), Martin (1965), Frank (1969. Sebagai hasilnya dibutuhkan suatu pengenalan metodologi (formula model)untuk menghitung panjang minimal dan diharapkan distribusi dari node sumber s ke node tujuantdalam jaringan stokastik tidak lengkap, sebagai satu komponen dari
panjang busur (travel time or speed) antara node dipilih sebagai variable acak,
2.4 Program Stokastik Dua Tahap
Banyak persoalan perencanaan dan manajemen yang mengandung resiko dan ketidakpastian dibahas dan diselesaikan dengan program stokastik dua ta-hap. Persoalan stokastik dengan kompensasi dari divergensi pada sistem dengan kendala mempunyai aplikasi yang lebih banyak dari pada model program yang lain. Penyelesaian persoalan program stokastik dua tahap berisi vektor acak dan vektor deterministik. Pada tahap pertama, penyelesaian persoalan rencana awal deterministik akan dibuat. Pembentukan rencana awal deterministik dilakuk-an sebelum kondisi acak dari persoaldilakuk-an ditentukdilakuk-an. Sebuah vektor acak pada penyelesaian persoalan yang sesuai digunakan untuk merencanakan kompensasi divergensi, spesifikasi parameter dari persoalan akan muncul pada tahap kedua. Tujuan dari manager pada persoalan di atas adalah meminimum nilai rata-rata biaya, yang mana tidak hanya termasuk pengeluaran pada tahap perencanaan pendahuluan tetapi juga pada tahap kedua yang diperlukan untuk mengkompen-sasi pada divergensi di dalam sistem kendala persoalan. Jika persoalan program stokastik dengan model dua tahap dapat diselesaikan maka pemilihan dari ren-cana awal deterministik akan menjamin keberadaan (eksistensi) vektor acak di dalam kompensasi untuk sistem yang divergen.
Andaikan terdapat persoalan berikut :
min(C, X) (2.4.1) A0X =B0 (2.4.2) AX =B (2.4.3) X ≥0 (2.4.4) dimana: C ={cij}, j = 1,2,3· · ·m B = (bi), i= 1,2,3· · ·m B0 = (b0k), k = 1,2,3· · ·m A0 = a0kj , k= 1,2,3· · ·m, j = 1,2,3· · ·m A =kakjk, k= 1,2,3· · ·m, j = 1,2,3· · ·m.
Andaikan elemen dari matiks A = A(ω), vektor B = B(ω) dan C = C(ω) ber-nilai acak. Maka untuk proses acak penyelesaian dari persoalan (2.4.1)–(2.4.4) akan dibagi menjadi dua tahapan, sebelum pengamatan dari parameter acak pa-da kondisi pa-dari tahap pertama dipilih rencana non-negatif deterministik X0 yang memenuhi kondisi (2.4.2). Pada tahap kedua ditentukan spesikasi ω0 dari setiap kejadian acak yang bersamaan (sesuai)dengan nilai A(ω0) dan B(ω0). Hitung divergensi B(ω0) = A(ω0)X0 yang muncul pada kondisi (2.4.3) setelah realisa-si ω0 ∈ Ω. definisikan vektor konpensasi Y ≥ 0 yang sesuai dengan hubungan berikut:
D(ω0Y(ω0) = B(ω0)−A(ω0)X0, (2.4.5) dimanaD=kdijk,i= 1,2,3, . . . , nadalah matriks kompensasi yang berisi elemen acak. Sehingga diasumsikan bahwa realisasi acak ω yang diamati pada tahap kedua tidak bergntung pada pemilihan rencana pendahuluan X0.
Perhatikan persoalan program matematika berikut: Tentukan vektorX ber-dimensi n dan vektor Y(ω) berdimensi n1, ω ∈Ω yang menghasilkan;
min X Eω n C(ω), X) + min Y (H, Y(ω)) o (2.4.6) Kendala: A0X =B0 (2.4.7) A(ω)X+D(ω)Y(ω) = B(ω), ω ∈Ω (2.4.8) X≥0, Y(ω)≥0. (2.4.9)
H adalah vektor penalti yang bergantung pada nilai kompoinen dari vektor Y(ω) yang mana merupakan kompensasi divergensi. E adalah notasi ekspekstasi mate-matika setelah ditentukan rencana awalX0, kita pilih komponen vektorY(ω) de-ngan cara menjamin penalti minimum untuk kompensasi divergensi pada kondisi dari persoalan. Dengan kata lain, setelah ditentukan vektor X0, perlu menyele-saikan persoalan; n min Y (H, Y(ω))|D(ω)Y(ω) =B(ω)−A(ω)X 0, Y(ω) ≥0o (2.4.10)
Persoalan (2.4.10) akan mempunyai banyak rencana, vektor Y(ω) tidak dapat ditentukan pada tiap ω ∈ W yang menjamin penemuhan kondisi (2.4.8). perso-alan (2.4.6)–(2.4.9) dikenal sebagai persoperso-alan program stokastik dua tahap dan persoalan (2.4.10) adalah persoalan tahap kedua.
Model dan pendekatan dari penyelesaian persoalan program stokastik (dina-mik) dua tahap dapat digunakan untuk perspektitif perencanaan dan operasional manajemen, karena selalu terdapat keacakan yang mempengaruhi yang sudah di-rencanakan dan sistem manajemen (pelaksanaan). Model dua tahap juga kurang sensintif terhadap perubahan pada parameter dari kondisi persoalan, yang me-nyebabkan lebih stabil. Akibatnya vektor dapat diterima untuk rencana tahap pertama yang diperlukan untuk setiapω ∈W, terdapat vektorY ≥0 sedemikian hingga,
D(ω)Y(ω) =B(ω)−A(ω)X (2.4.11) Andaikan kendala tambahan yang disebutkan secara implisit pada (2.4.11) muncul pada tahap kedua dari persoalan yang dihasilkan; dan andaikan kondisi yang ditentukan pada vektor non-negatif X dari persamaan (2.4.7) sudah diten-tukan.
Andaikan himpunanK1 ={X :A0 =B0, X ≥0}didefinisikan oleh kendala yang sudah ditentukan tetapi
K2 ={X :∀ω∈Ω,∃Y ≥0, A(ω)X =B(ω)−D(ω)Y(ω)}
didefinisikan oleh kendala yang dihasilkan. Maka himpunan K =K1∩K2 adalah himpunan vektor X yang layak/memenuhi persoalan (2.4.6)–(2.4.9).
Jika X ∈ K, maka vektor X memenuhi kendala yang sudah ditentukan A0X = B, X ≥0 dan disamping itu, persoalan tahap kedua (2.4.3) akan memiliki banyak rencana.
Untuk perhitungan lanjutan diperlukan hasil berikut :
Teorema 2.1 . HimpunanK dengan vektorX pada persoalan program stokastik dua tahap adalah konveks.
Bukti. K =K1∩K2 tetapi K1 ={X :A0 =B0, X ≥0}adalah konveks. Defini-sikan untuk ω ∈Ω tertentu (yang ditentukan) himpunan K2ω ={X|∃Y(ω)≥ 0}
sedemikian hingga A(ω)X = B(ω)−D(ω)Y(ω) adalah konveks. Hal ini menya-takan bahwa K2 =∩ω∈ΩK2ω danK =K1∩K2 adalah himpunan konveks sebagai pertolongan himpunan konveks.
2.5 Analisis Persoalan Program Stokastik Dua Tahap
Himpunan K dari rencana pendahuluan untuk persoalan program stokas-tik dua tahap secara implisit telah ditentukan. Pada kasus generalisasi tidak diketahui bagaimana untuk mengkonstruksi himpunan K2. Untuk beberapa ka-sus parsial, dimana sangat penting untuk banyak aplikasi, himpunan K2 mirip dengan Rn. Diasumsikan bahwa rank dari matriks D adalah sama dengan m, kecuali (2.4.8) dapat disubstitusikan untuk relasi ekivalen padap baris, sehingga:
OY =B −AX,
dimana O adalah vektor berisi nol berdimensi m dan p adalah banyaknya baris bergantung padaD. Asumsikan bahwa rank dari matrikDyang berdimensimxn adalah sama dengan m dan m kolom pertama adalah linier independen.
Andaikan bahwa untuk setiap v ∈Rn terdapat Y ≥0 sedemikian hingga :
DY =v. (2.5.1)
Lema 2.1 (Kall, 1994) Jika asumsi di atas dipenuhi, maka D mempunyai pa-ling sedikit (m+ 1) kolom, yaitu : n ≥(m+ 1).
Teorema 2.2 (Kall, 1994) Karena sistem persamaan DY =v mempunyai pe-nyelesaian non-negatif untuk setiap v ∈ Rn, maka hal ini cukup menunjukkan
bahwa terdapat penyelesaian non-negatif untuk sistem homogen dari persamaan linier :
Dπ = 0 (2.5.2)
π lebih besar dari pada 0 untukj = 1,2, ..., m
Bukti. Sistem persamaan DY =v selalu mempunyai penyelesaian. Mula-mula, andaikan ˆYj 6= 0 untuk j = 1,2, ..., mtetapi yang lainnya sama dengan nol.
Selanjutnya hubungan α(Dπ) +DYˆ = υ akan dipenuhi untuk sembarang α, jika diambil α yang cukup besar akan diperoleh penyelesaian non-negatif pada
persamaan (2.5.1). Kondisi (2.5.2) sulit dibuktikan dengan ekspektasi beberapa kasus parsial.
Andaikannmenjadi sama denganm = 1, maka kondisi cukup akan menjadi: m+1
X
j=1
πjDj = 0,
karena jika πm+1 = 0 akan diperoleh dependen linier darim kolom pertama Dj, yang mana akan kontradiksi dengan fakta bahwa matriks D mempunyai rankm. Konsekwensinya adalah πm+1 >0, sehingga diperoleh :
−Dm+1 = m X j=1 πjDj, πj = πjˆ ˆ πj
Sistem di atas adalah persamaan linier yang hanya mempunyai satu penyelesaian. Jika positif maka K2 =Rn.
Kondisi Teorema 2.2 tidak cukup tetapi perlu, sedemikian hingga DY = v mempunyai penyelesaian cukup untuk keperluan pemecahan non-negatif dari DY = vtidak untuk setiap v ∈ Rm tetapi hanya untuk v = B −AX dengan setiap X ∈ K1ω ∈ W dan setiap ω ∈ W sehingga v jauh dari memenuhi untuk semua Rm.
Persoalan (2.4.1)–(2.4.4) dapat diinterpretasi sebagai perencanaan produksi, dimana A adalah matriks untuk metode teknologi dasar dan D adalah matriks untuk metode teknologi secara kebetulan pada penentuan varian yang mungkin untuk kompensasi pada divergensi di dalam sistem yang dikondisikan. Pada kasus kondisi dari Teorema 2.2 dapat diinterpretasikan dengan cara berikut. Sehingga untuk sembarang divergensi v ∈ Rm, kompensasi Y dapat diterima temuannya, yang dicukupkan oleh metode teknologi kebetulan menyatakan sebuah sistem ter-tutup, karena itu terdapat intensitas tidak nol, yang mana semua hasilnya dieks-ploitasikan oleh metode produksi tertentu dapat dikonsumsi oleh yang lainnya. Sebagai contoh : penjualan dan pembelian dipisahkan dengan baik.
Teorema 2.3 Karena persoalan (2.4.10) mempunyai penyelesaian yang berhing-ga, maka hal ini perlu dan cukup menunjukkan bahwa sistem pertidaksamaan
mempunyai penyelesaian
Pembuktian teorema diatas dapat dilihat dengan jelas pada teorema dua-litas program linier yang diajukan oleh Dantzig (1959). Jika persoalan (2.4.10) dapat diselesaikan dan mempunyai penyelesaian optimal maka dualnya jiga da-pat diselesaikan dan begitu juga sebaliknya. Kendala dari persoalan dual untuk (2.4.10) adalah kondisi (2.5.3)
Kondisi dari Teorema 2.3 memiliki kegunaan secara ekonomi. Sehingga bi-aya pada eksploitasi pada metode teknologi kebetulan dilikuidasi dari divergensi yang berhingga, karena itu cukup dan perlu terdapat sistem estimasi Z untuk menghasilkan metode teknologi kebetulan. Biaya produksi yang disebabkan oleh estimasi output pada metode teknologi yang ke-i tidak lebih tinggi pada eksplo-itasi dengan singular intensity dari pada pengeluaran pada eksploeksplo-itasi dengan singular intensity.
Teorema 2.4 (Judin (1974)) Andaikan matriks D mempunyai m + 1 kolom dan memenuhi kondisi Teorema 2.2 yaitu :
−Dm+1 = m
X
j+1
πjDj, πj >0, j = 1,2,3,· · ·m
maka untuk pemenuhan kondisi Teorema 2.3 adalah syarat perlu dan cukup bahwa digantikan relasi (hubungan) berikut
m
X
j=1
πjhj +hm+1 ≥0, , , j = 1,2,3,· · · (2.5.3)
Bukti. Syarat perlu. Andaikan persoalan tahap kedua (2.4.10) dapat diselesaik-an, maka kumpulan rencana dari masalah dual menjadi tidak kosong. Andaikan vektor Z0 memenuhi kondisi (2.5.3) persoalan dual yaitu :
Z0Dj ≤hj, j = 1,2, ..., m+ 1, (2.5.4) karena itu, denganπj >0
m X j=1 πjZ0Dj ≤ m X j=1 πjhj;Z0Dm+1 =− m X j Z0πjDj (2.5.5)
disamping itu, kita dapatkan Z0Dm+1 =− m X j=1 Z0πjDj ≤hm+1 (2.5.6)
Dari kondisi (2.5.5) dan (2.5.6) diperoleh hasil (2.5.3) syarat cukup.
Andaikan (2.5.3) digantikan oleh fungsi tujuan pada persoalan tahap kedua (2.4.10) yang tidak berkendala pada himpunan rencana, maka himpunan rencana persoalan dual untuk persoalan tahap kedua adalah kosong.
Z|ZD≤H =∅ (2.5.7)
Dari linear independen vektor-vektorD1, D2, ..., Dm jika mengikuti sistem ; ZDj =hj, j = 1,2, ..., m, (2.5.8) hanya mempunyai penyelesaian Z0, karena persamaan (2.5.7) diperoleh
Z0Dm+1 > hm+1, (2.5.9) Dari kondisi teorema dan persamaan (2.5.8), (2.5.9) diperoleh
Z0Dm+1 =− m X j=1 Z0πjDj =− m X j=1 πjhj > hm+1
yang mana kontradiksi dengan kondisi (2.5.3) sehingga teorema dipenuhi.
Kondisi (2.5.3) menguntungkan secara ekonomi pada persoalan penjadwal-an. Andaikan metode teknologi berbentuk sistem tertutup, maka biaya dari explo-itasi metode accindetal output yang bertujuan kompensasi divergensi akan ber-hingga, jika tidak mungkin mendapatkan keuntungan dari rezim yang tidak jalan dari pekerjaan (jika persamaan (2.5.2) dapat dipenuhi). Dalam pekerjaan yang diajukan oleh Kall (1964) ditunjukan bahwa kondisi analog yang hilang dari ke-untungan juga tergantikan dalam kasus ketikan > m+ 1, tetapi kondisi ini hanya syarat perlu.
Perhatikan sebuah deterministik ekivalen untuk persoalan program stokastik dua tahap pada (2.4.6)–(2.4.9) dan tunjukkan bahwa persoalan (2.4.6)–(2.4.9) adalah persoalan program konveks. Dual untuk persoalan tahap kedua (2.4.10) adalah ;
(Z, B −AX)→max (2.5.10)
Andaikan penyelesaian persoalan (2.4.10) ada dan berhingga, maka terdapat pe-nyelesaian berhingga untuk persoalan (2.5.10)–(2.5.11) dan nilai optimal untuk keduanya telah dikerjakan oleh Dantzig (1956). Definisikan nilai fungsi sebagai . Dapat diperoleh bahwa (X, A, B) menjadi titik maksimum (2.5.10) yang di-capai dengan kondisi (2.5.11) untuk X, A, B yang ditetapkan. Sehingga untuk sembarang X1 dan X2 nilai ekstrimum fungsi tujuan (2.5.10) adalah berhingga, diperoleh ;
Z(αX1+ (1−α)X2, B)(B−A(αX1+ (1−α)X2) = Z(αX1+ (1−α)X2, A, B)[α(B−AX1) + (1−α)(B−AX2)]≤
αZ(X1, A, B)(B−AX1) + (1−α)Z(X2, A, B)(B−AX2)
Andaikan∅adalah fungsi tujuan dari persoalan deterministik ekivalen, maka ada-lah fungsi konveks, karena kombinasi non-negatif fungsi konveks adaada-lah fungsi konveks. Dari konveksitas fungsi tujuan mengikuti kontinuitas pada setiap titik dalam dari himpunan konveks K. Oleh karena itu dibuktikan oleh pernyataan berikut.
Teorema 2.5 Deterministik ekivalen untuk persoalan program stokastik dua-tahap
(2.4.6)–(2.4.9) adalah persoalan program konveks. Pernyataan selanjutnya mem-berikan dasar teori untuk mengkonstruksi pendekatan numerik pada penyelesaian persoalan dua-tahap. Perhatikan metode untuk menyelesaikan persoalan dua ta-hap diperlukan penggunaan hubungan (persamaan) fungsi dasar untuk ∅(X) dan menyediakan kondisi differensiabel ∅(X). Pada bagian ini akan digunakan fungsi dasar untuk fungsi konveks F(µ) pada titik µ0 ∈ M, untuk fungsi linear L, jika F(µ)−F(µ0 ≥ (L, µ,−µ0) untuk setiapµ∈ M. Hal ini dapat dilihat pada Judin
(1974) dan Kall (1994). Teorema 2.6 Fungsi E{C−Z∗(A, B, X0)A}= Z Ω{ C(ω)−Z∗[A(ω), B(ω), X0]A(ω)}dp
adalah dasar untuk fungsi tujuan dari persoalan deterministik ekivalen pada titik
X0 ∈K.
Di dalam pembahasan yang dikerjakan oleh Kall (1994) telah didemonstra-sikan bahwa jika ukuran peluang pada ruang A, B kontinu absolut relatif terha-dap ukuran lebesque pada ruang A, B dan kondisi tertentu dipenuhi maka fungsi
tujuan ∅(X) yang merupakan persoalan deterministik ekivalen adalah kontinu differensiabel setiap tempat pada himpunan K.
Untuk investigasi kondisi optimalitas rencanaX pada persoalan tahap per-tama, dibutuhkan vektor CX =E[C−Z∗(A, B, X)A] dan bentuk linear
Lx = (Cx1, X) =E[C−Z∗(A, B, X)A]. Judin (1974) mengajukan formulasi
kon-disi perlu untuk optimalitas pada rencanaXdi dalam persoalan program stokastik dua tahap.
Teorema 2.7 Jika X∗ adalah rencana deterministik untuk persoalan dua tahap
maka untuk sembarang X ∈K,
LX(X∗)≤LX(X). (2.5.12)
Bukti. Andaikan X∗ adalah rencana optimal tetapi X rencana yang diterima
untuk persoalan dua tahap. Dapat diperoleh : ∅(X∗)≤ ∅(X)
E(CX∗+Z∗(A, B, X∗)(B−AX∗))≤E(CX +Z∗(A, B, X)(B−AX)) (2.5.13) E(Z∗(A, B, X∗)(B −AX∗))≥E(Z∗(A, B, X)(B−AX)). (2.5.14) Kurangkan (2.5.14) dari (2.5.13), dan diambil Z∗(A, B, X∗) sebagai rencana
op-timal untuk masalah dual dan diperoleh hasil (2.5.12).
Melalui pekerjaan yang diajukan oleh Efimov (1970) dan Judin (1974) dipe-roleh bahwa kemungkinan untuk membuat kegunaan secara ekonomi pada kondisi (2.5.12). VektorZ∗(A, B < X) adalah penyelesaian masalah dual untuk persoalan
dua tahap dan merupakan vektor estimasi untuk produk jarang (kurang) atau ber-lebihan pada intensitasX dari metode teknologi setelah matriks teknologiA dan vektor permintaan B yang di realisasikan. Estimasi ini mendefinisikan pengaruh dari nilai divergensi pada pengeluaran untuk likuidasi ekonomi dari divergensi. Nilai
m
X
i=1
aijZi∗(A, B, X)−Cj
menunjukkan keuntungan dari eksploitasi pada metode teknologi dengan intensi-tas singular, dengan perkiraan parameter persoalan direalisasikan sebagai elemen matriksA dan komponen vektorB danC, tetapi estimasi produk dihitung untuk
kasus di dalam eksploitasi metode teknologi yang dikerjakan dengan intensitas X. Jika vektor X∗ mendefinisikan rencana awal optimal untuk persoalan program
dua tahap, rekaptulasi keuntungan rata-rata pada intensitas X∗ selama
penggu-naan metode produksi teknologi dihitung pada optimasi optimal yang tidak lebih kecil dari rekapitulasi keuntungan rata-rata yang dihitung pada estimasi optimal untuk sembarang rencana lain X yang dibolehkan.
Akan diformulasi tanpa pembuktian teorema pada kondisi cukup dan perlu dari optimalitas untuk rencana persoalan program stokastik dua tahap.
Teorema 2.8 AndaikanX∗ titik internal (dala) dari himpunanK, tetapi sebuah
fungsi objektif (X) pada persoalan deterministik ekivalen terhadap persoalan dua tahap yang diferensiabel di dalam neighbourhood dari titik X∗. Maka persoalan
dual Z∗(A, B, X∗) sedemikian hingga
C∗
X =E[C−Z∗(A, B, X∗)A] = 0 (2.5.15)
Jika dan hanya jika X∗ adalah penyelesaian persoalan dua tahap (Judin, 1974).
2.6 Program Stokastik Tahap Ganda
Persoalan program stokastik dinamik digeneralisasi oleh kasus dua tahap. Ba-nyak persoalan praktis yang berupa perencanaan, perancangan dan manajemen tidak dapa digambarkan dengan bantuan model statis. Perencanaan dengan per-iode waktu yang panjang berkembang pada sistem ekonomi, kontrol operasional pada peralatan militer, regulasi pada proses teknologi dan persoalan lain yang termasuk pada parameter acak dan mengharuskan deskripsi untuk penggunaan model probabilistik dinamik. Untuk model bertujuan, metode program stokastik tahap ganda seringkali digunakan. Model program stokastik tahap ganda dan metode untuk realisasi secukupnya bergantung pada informasi mengenai nilai pa-rameter di dalam kondisi persoalan, yang mana memiliki waktu untuk membuat keputusan selanjutnya. Terdapat persoalan dinamik yang mana tiap-tiap tahap berurutan disyaratkan untuk melengkapi kompensasi divergensi yang dikondisik-an oleh kondisi realisasi persoaldikondisik-an ddikondisik-an oleh pembuatdikondisik-an keputusdikondisik-an tercepat (tahap sebelumnya). Pada masalah yang lain disyaratkan bahwa tiap-tiap tahap peluang yang memenuhi kendala tidak melebih nilai tertentu yang diberikan sebelumnya
atas ekspektasi matematika pada fungsi dari divergensi di dalam kondisi yang dibatasi oleh bilangan yang diberikan atau nilai dari fungsi pada parameter acak yang direalisasikan pada tahap sebelumnya.
Kebergantungan (keadaan) pada bermacam-macam proses aktual yang da-pat dimodelkan, menyebabkan persoalan dinamik akan memiliki salah satu ben-tuk berikut yaitu : tidak dapat dikondisikan, kondisi probabilistik atau kendala statistik. Untuk persoalan dinamik dengan kendala tidak dapat dikondisikan, karakteristik keputusan adalah membuat pada basis informasi mengenai distri-busi yang dikombinasikan oleh parameter acak dari kondisi pada semua tahapan. Pada persoalan dinamik dengan kondisi dua kasus kendala dapat dibedakan men-jadi : (a) jika oleh momen pembuatan keputusan hanya realisasi dari parameter acak pada tahap sebelumnya yang diperkirakan diketahui dan (b) jika oleh mo-men pembuatan keputusan melengkapi informasi yang tersedia mo-mengenai realisasi parameter acak (termasuk kondisi) yang dinyatakan tahapan, tetapi nilai dari pa-rameter acak pada tahapan berurutan tidak diketahui. Terdapat relasi tertentu antara persoalan tahap ganda dengan yang tidak dapat dikondisikan dan kon-disi kendala. Penyelesaian optimal untuk persoalan program stokastik dinamik dapat diperoleh dengan strategi murni atau campuran. Pada komponen kasus akhir pada penyelesaian atau karakteristik statistik dari distribusi yang membe-rikan penyelesaian akan bergantung pada nilai parameter acak di dalam kondisi persoalan, yang direalisasikan oleh momen pembuatan keputuan
Konstruksi model probabilistik dinamik dan melaksanakan metode untuk realisasi yang ditampilkan akan sangat sulit. Pada bagian ini akan diberikan beberapa persoalan yang berisi model matematika untuk persoalan tahap ganda dan prosedur untuk mengkonstruksi penyelesaiannya.
Untuk perhitungan selanjutnya dan analisis persoalan program stokastik tahap ganda, didefinisikan konsep yang diberikan berikut ini. Andaikan terda-pat tahap ke-i yaitu Ωi, i = 0,1, ..., n untuk beberapa ruang kejadian elementer ωi, dimana Ω0 berisi satu elemen ω0. Andaikan Ωk adalah descartian produ-ct Ωi, i = 1,2, ..., k;ωk = (ω1, ..., ωk),Ωn = Ω dan andaikan pada Ω diberik-an ukurdiberik-an probabilistik p yang didefinisikan dengan cara : jika A ⊂ Ωk maka pk(A) =p(AxΩk+1x...xΩn). Diperkenalkan ruang probabilistik (Ω,P
, P) dengan
P
probabi-listik pada Ωk
Pk(A|ωk−1 ∈B) =
Pk(AxB) Pk(ΩkxB) Untuk sembarang A⊂Ωk, B ⊂Ωk−1.
VariabelXkdinyatakan sebagai descartian product Xi, i= 1,2, . . . , k;Xk = (x1, . . . , xk) ∈ Xk, Xn ≡ X dimanaX0,X1, . . . ,Xn adalah barisan himpunan dari struktur sembarangXk ∈Xk, k= 0,1, . . . , ndan himpunanXtermasuk satu titik X0.
Andaikan mk diberikan sebagai fungsi vektor pada ϕk(ωkXk) berdimensi untuk setiap ωk ∈ Ωk, Xk ∈ Xk, k = 1, ..., n dan juga untuk setiap ω ∈ Ω pa-da himpunan X fungsi ϕ0(ωnXn). Masukkan himpunan acak G0k = G0k(ωk) dan bk(ωk−1)mk fungsi vektor. Bk berdimensi acak dari ωk−1 (dibatasi dan terukur) dinyatakan sebagai ruang Banach yang termasuk pada fungsi vektor berdimen-si bk(ωk−1)Pk
i=1mi. Akhirnya, Ewk(U(ωk)|ωk−1) menyatakan kondisi ekspektasi matematika U(ωk) dibawah perkiraan realisasi ωk−1 yang diketahui.
Andaikan dibahas model berbeda pada persoalan program stokastik tahap ganda dengan menggunakan notasi yang diperkenalkan di atas. Andaikan terda-pat persoalan program stokastik tahap ganda :
Eϕ0 = (ωn, Xn)→inf, (2.6.1) Eϕk = (ωk, Xk)≥bk, (2.6.2) Xk ∈G
k, k= 1,2, ..., n. (2.6.3) Untuk memformulasi persoalan secara lengkap, diperlukan titik luar apakah ken-dalah yang tidak dapat dikondisikan atau kondisional, apakah penyelesaian per-soalan ditentukan dengan strategi murni atau strategi campuran, dan di dalam kelas fungsi yang terukur atau distribusi yang akan mendapatkan penyelesaian. Persoalan praktisnya akan bergantung pada makna isi, penyelesaian pada tiap-tiap tahap dapat dihitung sebagai vektor deterministik atau sebagai rule-function pada penyelesaian dari realisasi dan parameter acak yang diobservasi dari kondisi, atau sebagai distribusi menentukan distribusi kontinu Xk dengan perkiraan infor-masi yang diperlukan mengenai nilai yang direalisasikan data initial acak yang diperoleh model konkrit untuk persoalan dan struktur informasinya ditentukan
oleh keputusan selanjutnya. Di dalam syarat-syarat yang diajukan oleh Ermolyev (1970), hasil-hasil persoalan stokastik tahap ganda dari rangkaian tipe - pengamatan keputusan pengapengamatan ... keputusan Keputusan pengapengamatan -keputusan - ... - -keputusan Andaikan dibahas bermacam-macam model persoalan program stokastik tahap ganda yang menggunakan klasifikasi yang diberikan oleh Judin (1972). Persoalan stokastik tahap ganda dengan kendala yang tidak dapat dikondisikan adalah Z Ωn xXn ϕ0(ωn, Xn)dFωn ,Xn →inf, (2.6.4) Z Ωk xXk ϕk(ωk, Xk)dFωk ,Xk, (2.6.5) Xk∈Gk, k= 1,2, ..., n. (2.6.6)
Pemilihan beberapa kelas yang paling menarik untuk aplikasi dari sejumlah struk-tur informasi yang merupakan persyaratan persoalan program tahap ganda de-ngan kendala kondisional. Model kongkrit dari (2.6.1) –(2.6.3) pada kasus perso-alan dengan kendala kondisional, diselesaikan dengan strategi campuran adalah : Z Ωn xXn ϕ0(ωn, Xn)dFωn,Xn →inf, (2.6.7) Z ΩkxXk ϕk(ωk, Xk)dFωk |ωdFωk |ωk−1 ≥bk(ωk−1), (2.6.8) Xk ∈Gk(ωk), k = 1,2, ..., n. (2.6.9)
Penyelesaian persoalan akan menjadi himpunan fungsi distribusi .Biasanya untuk mengatakan persoalan diselesaikan dengan distribusi yang ditentukan ke-mudian jika didefinisikan setelah realisasi dan pengamatan parameter acak k, distribusi yang ditentukan kemudian bergantung pada Xk−1 dan k. Dikatakan bahwa persoalan yang diselesaikan dengan distribusi yang ditentukan sebelumnya, jika didefinisikan setelah realisasi dan pengamatan k−1 tetapi sebelum penga-matan k, distribusi yang ditentukan sebelumnya bergantung pada Xk − 1 dan k−1.
Jika persoalan tahap ganda dengan kendala kondisional diselesaikan dengan strategi murni, model konkrit (3.30) - (3.32) akan menjadi :
Z Ωn ×Xn ϕ0(ωn, Xn)dFωn →inf, (2.6.10) Z Ωk ×Xk ϕk(ωk, Xk)dFωk |ωk−1 ≥bk(ωk−1), (2.6.11) Xk∈Gk(ωk), k= 1,2, ..., n. (2.6.12) Fungsi Xk dari parameter acak yang direalisasikan dan diamati pada kondisi dari persoalan merupakan penyelesaian. Persoalan diselesaikan dengan aturan yang ditentukan kemudian jika keputusan dibuat setelah realisasi dan pengamatan k; aturan-aturan yang ditentukan kemudian untuk penyelesaian sedemikian hingga Xk=Xk(k). Dikatakan bahwa persoalan diselesaikan dengan aturan yang diten-tukan sebelumnya jika keputusan dibuat setelah realisasi dan pengamatan k−1, tetapi sebelum pengamatan k. Pada kasus aturan sebelumnya :
Xk=Xk(k−1)
Biasanya, persoalan (2.6.7) –(2.6.9) atau (2.6.10)–(2.6.12) dikenal sebagai perso-alan stokastik tahap ganda dengan rigid model, jika kondisi (2.6.8) atau (2.6.11) tidak dihadirkan, keputusan tiap-tiap tahap dibuat setelah observasi kondisi dan keputusan pada tahap sebelumnya.
Relasi tertentu yang dimiliki antara determinasi domain untuk persoalan de-ngan kendala yang tidak dapat dikondisikan dan kendala yang dapat dikondisikan. Pernyataan berikut akan menggeneralisasi hasil yang diperoleh, yang telah diker-jakan oleh Eismer (1971) untuk persoalan stokastik tahap ganda parsial linear. Pernyataan yang berikut diambil dari Judin (1974).
AndaikanU adalah himpunan penyelesaian yang layak untuk persoalan sto-kastik tahap ganda dengan kendala yang tidak dapat dikondisikan
U ={Xk∈Gi×...×Gn|Eϕk(ωk, Xk)} ≥bk, k= 1,2, ..., n
dan V[bn(ωn−1)] adalah himpunan penyelesaian (aturan penyelesaian, distribusi sebelum atau sesudah penyelesaian) pada persoalan dengan kendala kondisional.
Teorema 2.9 Teorema 3.9. Himpunan U dan V adalah terhubung oleh relasi
Bukti. V˜ = {Xn ∈ V[˜bn(ωn−1)]|E˜bk(ωk−1)} = bk, k = 1,2, ..., n. Andaikan Xn ∈V˜. Yang menyatakan bahwa
Eωkϕk(ωk, Xk) =Eωk−1{Eωkϕk(ωk, Xk)|ωk−1}
≥Eωk−1˜bk(ωk−1) = bk;k= 1,2, ..., n
karena Xn ∈U. Andaikan Xn∈U, didefinisikan ˜
bk(ωk−1) =Eωk{ϕk(ωk, Xk)|ωk−1}+{bk−E
ωkϕk(ωk, Xk)}
≤Eωk{ϕk(ωk, Xk)|ωk−1}, k = 1,2, ..., n
Dengan definisi ˜bk(ωn−1) didapatkan E
ωk−1˜bk(ωk−1) = bk. Sehingga Xn∈V˜. Akibat. Dengan fungsi samaϕk(ωk, Xk) dan himpunanGk,k= 1,2, ..., n, domain penyelesaian layak dari persoalan (2.6.4)–(2.6.6) dan (2.6.7)–(2.6.9) atau (2.6.10)– (2.6.12) (bergantung pada persoalan yang diselesaikan dengan strategi campuran atau strategi murni) bersamaan bentuknya jika dan hanya jika Ebk(ωk−1) =bk.
Pernyataan diatas menyebabkan kemungkinan untuk memformulasi ulang hasil kualitatif dan seringkali juga menghitung metode yang dikerjakan untuk persoalan dengan kelas tertentu dan untuk investigasi konstruktif pada persoalan kelas lain.
Relasi antara distribusi penyelesaian dan aturan penyelesaian sangat mena-rik. Jika fungsiϕ0 adalah konveks dan komponen fungsi vektor ϕk adalah konkaf pada X dengan tiap-tiap ω, maka nilai optimal dari fungsi objektif yang dica-pai pada distribusi penyelesaian dapat dicadica-pai juga dengan aturan penyelesaian. Konveksitas dari ϕ0 dan −ϕk tidak menghabiskan kondisi dengan strategi opti-mal murni dan strategi campuran yang didefinisikan menyatu dan nilai sama dari fungsi tujuan.
Nilai fungsi tujuan untuk aturan optimal sebelumnya pada persoalan sto-kastik tahap ganda didalam rigid model dengan nilai fungsi tujuan distribusi pe-nyelesaian optimal sebelumnya.
Pernyataan lebih tegas untuk aturan penyelesaian sesudahnya dan distribusi penyelesaian diberikan berikut.
Teorema 2.10 (a) Andaikan ukuran probabilistik Fω didalam Ω ≡ Ωn adalah
kontinu (b) Andaikan terdapat fungsi positif g0(ω) dan gk(ωk) berkendala atas
menurut moduleϕ0(ωn, Xn)dan semua komponenϕk(ωk, Xk). Maka penyelesaian
aturan optimal sesudahnya untuk persoalan stokastik tahap ganda didefinisikan oleh nilai yang sama pada fungsi tujuan sebagai distribusi penyelesaian optimal sesudahnya.
Bukti: Untuk persoalan stokastik satu tahap diberikan oleh Judin (1972).
Bukti. Untuk persoalan stokastik satu tahap diberikan oleh Judin (1972). Persoalan program stokastik tahap ganda dengan kendala kondisional dapat disubstitusikan untuk sistem persamaan yang memenuhi pemisahan tahapan. An-daikan akan dibahas persoalan (2.6.10)–(2.6.12) yang diselesaikan dengan strategi murni (dengan penyelesaian sebelum aturan penyelesaian sesudahnya).
Untuk definisi domain pada persoalan tahap ke-i bekaitan dengan himpunan: Ki ={Xi ∈G0|∃{yi+1 ∈G0i+1, ..., yn∈G0n}; Eωi[ϕi(ωi, Xi)|ωi−1]≥bi(ωi−1), Eωi+s[ϕi(ωi+s, xi, yi+1, ..., yi+s)|ωi+s−1] (2.6.13) ≥bi+s(ωi+s−1), jika ∀ωi+s−1, ..., ωn−1, s= 1,2, ..., n−1} G0
i menyatakan proyeksi Gi terhadap hyper-plane dari kordinat yang didefini-sikan oleh komponen vektor Xi. Persyaratan keberadaan dari vektor yi+s, s = 1,2, ..., n−iyang memenuhi kondisi (2.6.13) adalah ekivalen terhadap keberadaan kendala didalam persoalan dua tahap. Kondisi cukup dan perlu untuk menyele-saikan persoalan (2.6.10)–(2.6.12) adalah kondisiK1 6= Φ (fungsi objektif (2.6.10) dengan asumsi berkendala). Jika disamping K1 6= Φ, Ki 6= Φ, i= 2,3, ..., n.
Fungsi tujuan dari persoalan Qi(Xi) pada tahap ke-i mengatakan kondi-sional ekspektasi matematika ϕ0(ωn, Xn) pada asumsi semua tahapan sebelum tahap ke-i, himpunan ωi−1 merupakan parameter yang direalisasikan dengan kon-disi persoalan dan komponen keputusan himpunan Xi−1, dan sesudah tahap ke-i keputusan optimal berikutnya: X∗
i+1, ..., Xn∗:
Qi(Xi) = Eωn|ωi−1(ωn, Xi−1, Xi, Xi+1, ..., X∗
Sejauh ini, definisi penyelesaian aturan optimal pada tahap ke-i dari per-soalan stokastik tahap ganda direduksi untuk menyelesaikan perper-soalan program matematika berikut
inf Xi∈Xi
Qi(Xi) (2.6.15)
Aturan sesudahnya untuk penyelesaian adalah: Xi = Xi(ωi), yi
+s = yi+s(ωi+s); s= 1,2, ..., n−i, dan aturan sebelumnya untuk penyelesaian adalah:
Xi =Xi(ωi−1);yi+s =yi+s(ωi+s−1);s= 1,2, ..., n−i.
Jika fungsi tujuan dapat dipisahkan, yaitu ϕ0(ωn, Xn) = n X j=1 ϕ0j(ωj, Xj) kita mempunyai Qi(Xi) =Eωi |ωi−1{ϕ0(ωi, Xi) +Q∗ i+1(ωi, Xi)}. dimana Q∗ i(ωi−1, Xi−1) = inf Xi∈KiEω i |ωi−1{ϕ0(ωi, Xi) +Q∗i+1(ωi, Xi)}, i= 1,2, ..., n−1, dengan i=n Q∗n(ωn−1, Xn−1) = inf Xi∈Ki Eωi |ωi−1ϕ0n(ωn, Xn).
Analog dengan persoalan pemisahan tahapan untuk persoalan stokastik tahap ganda dengan strategi campuran yang dikonstruksikan.
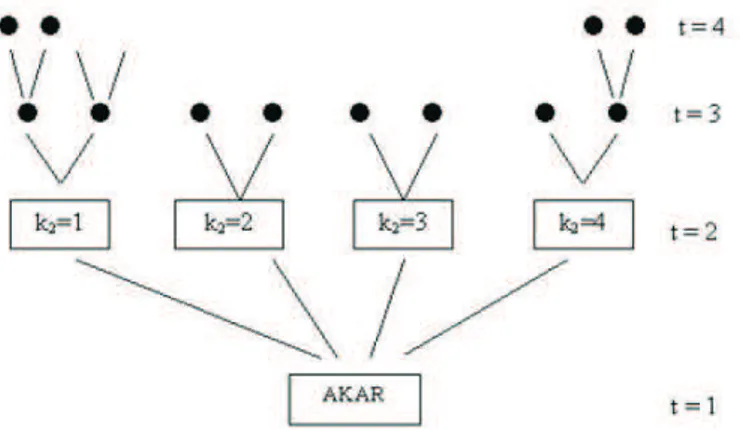
2.7 Pengertian pembentukan pohon skenario
alam banyak aplikasi, sebaran peubah acak tidak diketahui atau walaupun diketahui, terlalu mahal untuk memperhatikan sebaran diskrit dengan banyak hasil yang mungkin atau menangani sebaran kontinu dengan integrasi numerik. Merupakan hal yang umum untuk memilih himpunan hasil representatif yang relatif kecil yang disebut skenario untuk menyajikan kejadian acak. Skenario dapat merupakan kuartil dari sebaran yang diketahui atau data historis, prediksi dan beberapa pohon atau dibangun dengan simulasi. Setiap skenario diberikan nilai probabilitas untuk merefleksikan kemungkinan kejadiannya. Untuk model tahap ganda, informasi skenario dapat diorganisasikan kedalam struktur pohon. Gambar 1, memberikan contoh pohon skenario untuk persoalan 4 tahap. Buhul AKAR menyatakan waktu sekarang atau bagian dari data yang diketahui. Pada
Gambar 2.1 : Gambar.1 Pohon Skenario
tahap 2, terdapat 4 kemungkinan berbeda dan setiap daripadanya mempunyai berbagai hasil berbeda yang mungkin di tahap 3 dan seterusnya. Suatu skenario terdiri dari lintasan lengkap dari buhul akar ke satu buhul daun, mendefinisikan realisasi tunggal dari himpunan peubah acak.
Ambil jumlah tahap T dan jumlah hasil yang mungkin dalam setiap tahap dapat dilabel secara berurutan oleh Kt, untuk t = 1, ...T. Buhul disetiap tahap dapat dilabel secara berurutan dengan kt = 1, ..., Kt untuk semua t. Dt(k) me-nyatakan turunan langsung dalam waktu t dari buhul k. Misalnya dalam pohon skenario di Gambar 2.1 . D3(1) memperlihatkan turunan langsung dari buhul 1 yang merupakan dua buhul paling kiri dalam waktu 3. Untuk setiap buhul daun k dalam tahap T, andaikan Pk
t merupakan probabilitas terkait dari keterjadian skenario. Untuk t =T−1,− − − −1, pk t diberikan oleh pkt+1 = X lǫDt+1 plt+1 dengan pl = 1
Pohon keputusan memberikan kelenturan kepada pemodel untuk memilih skenario yang diperlukan untuk diperhatikan dan kepentingannya. Begitupun tidaklah praktis untuk memperhatikan terlalu banyak skenario. Ini terutama terjadi untuk persoalan dimana banyak mengandung faktor acak.
Untuk mengoperasikan model program stokastik, pembentukan skenario dan pohon kejadian sangatlah penting. Dibawah ini diuraikan secara singkat metode pembentukan tersebut.
a. Bootstrap Data Historis
b. Pemodelan statistika dengan pendekatan ”value at risk” c. Model vektor Autoregressi
a. Bootstrap Data Historis
Pendekatan paling sederhana untuk membangun skenario hanya memakai data yang ada tanpa pemodelan matematika. Setiap skenario merupakan sampel dari perolehan aset yang diperoleh dengan mensampling perolehan yang diamati di masa lalu. Waktu dari catatan historis yang tersedia dipilih secara acak dan untuk setiap waktu dalam sampel dibawa perolehan dari semua kelas tersebut. Ini merupakan skenario perolehan bulanan. Jika ingin dibangun skenario perolehan untuk horizon waktu panjang misalnya 1 tahun, disampel perolehan 12 bulan dari titik waktu yang berbeda. Susunan perolehan dari deretan yang disampel merupakan perolehan 1 tahun. Dengan pendekatan ini korelasi diantara kelas aset dipertahankan.
b. Model Statistika dari Konsep Value-at-Risk
Analisis deret waktu dari data historis dapat dipakai untuk mengestimasi perubahan dari matriks korelasi antara kelas aset. Matriks korelasi ini dipakai untuk mengukur resiko dengan metode Value-at-Risk (VaR).
Nyatakan peubah acak dengan vektor acak k−dimensi w. Dimensi w sama dengan jumlah faktor resiko yang ingin dimodelkan. Dengan mengandaikan bah-wa peubah acak secara gabungan bersebaran normal dapat didefinisikan fungsi kepadatan peluang dari w sebagai.
f(w) = (2π)−p/2|Q|−1/2exp − 1 2(w−w)¯ ′Q−1(w−w)¯
disiniwadalah ekspektasi dariwdanY matriks kovarian dan dapat dihitung dari data historis.
Setelah parameter dari sebaran normal multivariat diestimasi kita dapat me-makainya dalam simulasi Monte Carlo dengan menggunakan pendekatan faktori-sasi Cholesky atau prosedur pembentukan skenario yang didasarkan pada analisis komponen utama yang diajukan oleh Jamshidian dan Zhu (1997).
Simulasi dapat diterapkan secara berulang pada status berbeda dari pohon kejadian. Segitupun, mungkin saja ingin dipersyaratkan nilai acak yang dibangun pada nilai-nilai yang diperoleh oleh beberapa peubah acak.
Sampling bersyarat dari peubah normal multivariat dilakukan seperti beri-kut. Peubahwdipartisi menjadi 2 subvektorw1 danw2denganw1 vektor dimensi K, dari peubah acak untuk nama beberapa informasi tambahan tersedia dan w2 adalah vektor dimensiK2−K−K1 dari peubah sisa. Vektor nilai ekspektasi dan matriks kovarian dipartisi secara analog sebagai
¯ w=h w¯1 ¯ w2 i dan Q=h Q11 Q12 Q21 Q22 i
Fungsi kepadatan peluang marginal dari w2 dengan diketahui w1 = w∗1 di-berikan oleh f(w|w1 =w∗1) = (2π)−P2/2|Q22.1|−1/2exp − 1 2(w2−w¯2.1) ′Q−1 22.1(w2−w¯2.1)
dimana nilai ekspektasi bersyarat dan matriks kovarian diberikan oleh ¯
w2.1(w1∗) = ( ¯w2−Q21Q11−1µ1) +Q21Q−111w∗1
dan
Q22.1 =Q22−Q21Q−111Q12
Skenariow2 untuk periode t dipersyaratkan pada nilaiw1 diberikan oleh w1t dapat dibangun dari peubah normal multivariat melalui pernyataan
w2ti =w02iexp[σi√tw2i]
denganwt
2i nilai hari ini danσi adalah perubahan periode tunggal dari komponen ke ipeubah acak w2.
c. Model Vektor Autoregressi
Model vektor Autoregressi dapat dipakai untuk membentuk skenario. Da-lam hal ini diambil ilustrasi tentang sistem simulasi Asset Liahlity Management (ALM) untuk dana pensiun. Karena cakupan dari sistem ini selalu dibatasi pada keputusan strategis jangka panjang model investasi hanya mempraktekkan kum-pulan kecil dari kelas aset yang besar yaitu deposito, bond, real estate dan saham.
Terpisah dari perolehan atas aset-aset ini, setiap skenario harus mengandung in-formasi tentang pertumbuhan gaji masa datang untuk menghitung nilai masa datang pensiun.
Model vektor autoregressi untuk membentuk skenario perolehan aset dan pertumbuhan gaji adalah
Rt=c+V ht−1+ǫt, ǫt∈N(0, Q), t= 1,2, ..., T Rit = ln(1 +πit), i= 1,2, ..., T
Denganmjumlah deret waktu aset,πit laju perubahan diskrit dari peubahi ditahun t, Rt vektor dimensi-m dari laju majemuk, cvektor koefisien berdimensi m, V adalah matriks koefisien m×m, ǫt vektor dimensi m dari pencilan dan Q matriks kovariansi m×m.
Spesifikasi model vektor autoregressi harus dipilih secara hati-hati, wala-upun beberapa hubungan inter-temporal diantara perolehan mungkin signifikan lemah yang didasarkan pada data historis, tidak berakibat bahwa hubungan ini juga bermanfaat untuk membentuk skenario.