Sylvain Béal
*On s’intéresse à un aspect de la rationalité des joueurs dans le cadre de la théo-rie des jeux répétés. L’hypothèse centrale est que le choix des joueurs est limité aux stratégies calculables par un modèle de calcul (ou machine). Nous considérons deux modèles de calcul : l’automate fini et le perceptron. Les capacités d’un modèle de calcul sont associées à celles du joueur qui utilise ce modèle. Plusieurs critères de mesure de la complexité d’une machine sont envisageables. L’objectif de cet article est de présenter les principaux résultats liés à l’étude de la complexité des stratégies pour la classe des jeux de machines.
BOUNDED RATIONALITY AND MACHINE GAME
We study one aspect of the rationality of players in repeated games. The central assumption is that player’s choice is limited to strategies that can be computed by a model of computation (or machine). We investigate two of such models : the finite automaton and the perceptron. Each model of computation gives its own abilities to the player that uses it. We consider several possible measures for the complexity of a machine. We survey in this article the most important results on the complexity of strategies for the class of machine games.
Classification JEL : C72
INTRODUCTION
Dans un jeu non coopératif, la rationalité d’un joueur peut être scindée en
ratio-nalité cognitive et en ratioratio-nalité instrumentale. Selon Walliser [1989], la première
exprime la capacité de l’individu à utiliser l’information de son environnement afin de construire ses anticipations. Lorsqu’un joueur possède une rationalité cogni-tive parfaite, il est capable de former des anticipations parfaites. La deuxième traduit la capacité de l’individu à utiliser les moyens dont il dispose pour atteindre ses objectifs. Lorsqu’un joueur possède une rationalité instrumentale parfaite, il se comporte en agent maximisateur. Lorsque les rationalités cognitive et instrumen-tale d’un joueur sont parfaites, il parvient instantanément à la solution d’un problème. Dans ce contexte, l’analyse d’un jeu peut se résumer à la démonstration
*CREUSET, Université de Saint-Étienne, 6, rue Basse des Rives, 42023 Saint-Étienne, France. Courriel : sylvain.beal@univ-st-etienne.fr
d’un théorème d’existence d’une solution. Cependant, montrer l’existence d’une solution et exhiber cette solution sont deux exercices différents. Dans l’esprit de Simon [1987], un joueur dont la rationalité est limitée met en place une procédure qui calcule une solution au problème. Si l’on s’accorde à dire qu’un modèle de calcul est une extension de la rationalité du joueur, alors ce type de procédure sera implémentée par le modèle de calcul en question. Notre objectif, dans cet article, est d’étudier ces procédures de calcul pour la classe des jeux répétés et ses appli-cations en économie. La particularité de cette classe de jeux est que l’espace des stratégies des joueurs augmente exponentiellement avec le nombre de périodes de jeu. Il est donc peu probable qu’un joueur dont la rationalité est limitée puisse, en pratique, considérer autant de comportements différents. C’est pour cette raison qu’il semble raisonnable de faire l’hypothèse que l’ensemble des choix du joueur se réduise aux stratégies implémentables par un modèle de calcul. D’une manière générale, on peut se poser plusieurs questions liées à la rationalité des joueurs. Nous les abordons successivement à travers les trois situations suivantes.
Considérons tout d’abord une situation dans laquelle le joueur sait que le problème auquel il fait face possède une solution. Ce joueur doit s’efforcer de trouver une procédure constructive lui permettant d’exhiber une solution. C’est à cet effet que nous utilisons la théorie de la décidabilité, laquelle détermine s’il existe une procédure constructive susceptible de répondre à la question de l’exis-tence de solution d’un problème. Cette procédure de calcul de la solution doit être implémentable par le modèle de calcul qui matérialise la rationalité du joueur. On dit alors qu’un problème est décidable si l’exécution d’une procédure constructive implémentée par le modèle de la machine de Turing s’arrête et répond à la question de l’existence d’une solution au problème considéré. Ceci signifie que la rationalité des joueurs est limitée dans sa dimension cognitive par les capacités de fonctionnement du modèle de la machine de Turing. En revanche, la rationalité instrumentale du joueur reste parfaite car il cherche une solution optimale au problème en utilisant au mieux ses capacités. Cette question a été étudiée en théorie des jeux par Rabin [1957] et Sofronidis [2004], et en économie par Velupillai [2000]. Notons que, si le problème considéré n’est pas décidable, le joueur est incapable d’identifier une solution même si les propriétés mathématiques du problème en garantissent l’existence.
Si le problème considéré est décidable, cela ne signifie pas automatiquement que la procédure calcule une solution en temps raisonnable. La théorie de la
complexité algorithmique examine cette question du temps de calcul de la
solu-tion d’un problème. On dit qu’une solusolu-tion est calculée efficacement par une machine de Turing (le problème est dit « facile ») si le temps d’exécution de la procédure de calcul est un polynôme de la taille du problème1. Cette appréciation de la complexité du fonctionnement d’un modèle de calcul constitue une première mesure possible de la complexité d’une solution d’un jeu non coopé-ratif. Ici, les limites de la rationalité cognitive des joueurs sont celles du modèle de la machine de Turing. La rationalité instrumentale des joueurs est limitée dans la mesure où la recherche de la solution optimale prend du temps. Une liste de problèmes « faciles » et « difficiles » a été établie en théorie des jeux sous l’impulsion des travaux de Sahni [1974] et Gilboa et Zemel [1989].
Considérons enfin une situation dans laquelle le joueur s’intéresse aux straté-gies calculables lui permettant d’atteindre une solution du jeu. La théorie de la
complexité des stratégies étudie cette question. Dans cette situation, nous
consi-dérons la complexité propre du modèle de calcul. Aumann [1981] et Abreu et Rubinstein [1988] proposent, par exemple, d’évaluer la complexité d’une stra-tégie par le nombre d’états du plus petit automate fini capable de la mettre en œuvre. Dans ce cas, la rationalité cognitive du joueur correspond aux capacités du modèle de calcul. En revanche, compte tenu de ses moyens d’actions, le joueur recherche toujours une solution optimale au problème auquel il fait face. En ce sens, sa rationalité instrumentale est parfaite. L’utilisation d’un modèle de calcul rend de facto décidable le problème de calcul de la solution, mais n’assure pas que le temps nécessaire au calcul d’une solution soit raisonnable1. L’examen de la complexité des stratégies se présente donc comme une démarche complé-mentaire aux deux précédentes.
Dans cet article, nous présentons de manière détaillée cette dernière classe de modèles. La section 2 rappelle les notions nécessaires de théorie des jeux. Nous introduisons le jeu répété du dilemme du prisonnier qui nous servira à illustrer les concepts essentiels et à donner l’intuition des principaux résultats. Dans la section 3, nous reviendrons en détail sur le fonctionnement du modèle de l’auto-mate fini et nous présenterons un deuxième modèle de calcul, le modèle du
perceptron. Nous verrons que les modèles de calcul confèrent des aptitudes
diffé-rentes aux joueurs, que ce soit dans leurs capacités à mémoriser de l’information ou à construire des anticipations sophistiquées. La section 4 est consacrée à la présentation des principaux résultats liés à l’étude de la rationalité limitée dans la classe des jeux répétés. Nous envisagerons plusieurs paramètres permettant d’évaluer la complexité d’un modèle de calcul. Nous verrons également qu’il existe, pour chaque modèle de calcul, deux types d’approche de la complexité d’implémentation des stratégies. On peut introduire un coût de complexité dont les joueurs tiennent compte dans leurs préférences. Cela permet de sélectionner un sous-ensemble des équilibres d’un jeu répété. On peut aussi borner la taille des machines que peuvent choisir les joueurs. Dans le jeu du dilemme du prisonnier répété sur un horizon fini, cette deuxième approche peut engendrer des équilibres de Nash dans lesquels les joueurs coopèrent à chaque période. Plusieurs modèles d’applications économiques viendront enrichir cette section. Dans la section 5, trois exemples serviront de points de comparaison entre les modèles de l’auto-mate et du perceptron. Nous conclurons par quelques remarques.
PRÉLIMINAIRES
Jeu sous forme normale
Pour faciliter la lecture de l’article, les définitions et résultats sont donnés pour le cas 2 joueurs et il sera précisé lorsque le résultat est valable pour un nombre
de joueurs. Un jeu fini sous forme normale G, appelé jeu de base, est défini par les éléments suivants :
1. Un ensemble fini de joueurs. Le symbole – i désigne l’adversaire du joueur i ;
2. Un ensemble fini d’actions pour chaque joueur i. Sur un profil d’actions du jeu de base G, désigne l’action du joueur i. L’ensemble des profils d’actions est noté ;
3. Pour chaque joueur une fonction de gain : qui associe à chaque profil d’actions un gain .
Le gain minmax du joueur
reflète le gain de sécurité que le joueur i peut se garantir contre toutes les actions de l’opposant. La paire de gains minmax est notée .
Un profil d’actions est un équilibre de Nash de
si pour tout , et tout ,
Jeu répété
Un jeu répété est la répétition du jeu de base G aux périodes . Lorsque (respectivement ), on parle de jeu répété à horizon infini (respectivement à horizon fini) noté (respectivement ). Nous donnons la suite des définitions pour mais il est facile de les adapter à .
Une histoire du jeu répété à la période t est la succession des profils d’actions joués de la période 1 à la période . On note
l’ensemble des histoires possibles à la période t et
l’ensemble de toutes les histoires possibles de .
Une stratégie pure du joueur i dans le jeu répété est une suite de fonc-tions . Pour chaque période t⭓1, la fonction : associe une action à chaque histoire . On note un profil en straté-gies pures, l’ensemble des stratéstraté-gies pures du joueur , et l’ensemble des profils en stratégies pures du jeu répété.
Chaque profil induit une unique suite de profils d’actions . Nous considérons deux formulations distinctes du gain du joueur i dans 1:
1. Le gain moyen défini par
2. Le gain moyen actualisé au taux défini par
1. On considère la limite inférieure car le gain moyen peut ne pas converger.
Dans la première formulation, les joueurs sont infiniment patients. Ainsi, une perte de gain sur un nombre fini de périodes n’a pas d’incidence sur le gain moyen total du joueur. Ce n’est pas le cas dans la seconde formulation, puisque les joueurs accordent davantage d’importance aux gains qu’ils obtiennent dans les premières périodes.
Un profil en stratégies pures est un équilibre de Nash de si pour
tout , et tout ,1
« Folk » théorème
Dans un jeu répété, on dit qu’une paire de gains est
strictement individuellement rationnelle si , c’est-à-dire pour tout .
THÉORÈME1 (« folk » théorème – gain moyen non actualisé). Dans un jeu
à deux joueurs, pour toute paire réalisable, il existe un équilibre de Nash qui garantit une paire de gains aux joueurs.
THÉORÈME2 (« folk » théorème – gain moyen actualisé). Dans un jeu à
deux joueurs, pour toute paire réalisable, tel que, si , il existe un équilibre de Nash qui garantit une paire de gains aux joueurs.
Les deux théorèmes sont aussi valables pour joueurs2. Nous intro-duisons l’exemple du jeu répété du dilemme du prisonnier qui nous permettra par la suite d’illustrer plusieurs résultats.
Exemple 1. Dans le jeu du dilemme du prisonnier à deux joueurs, chaque joueur
a le choix entre une action C de coopération et une action D de défection. La matrice des gains du jeu de base est la suivante :
Le profil d’actions est le seul équilibre de Nash du jeu mais la paire de gains obtenue du profil d’actions (le gain coopératif) domine au sens de Pareto. Lorsque ce jeu de base est répété sur un horizon infini, on peut repré-senter graphiquement la zone des gains intertemporels des deux joueurs dans un
1. La définition est semblable lorsque les joueurs actualisent leurs gains futurs. 2. Voir, par exemple, Fundenberg et Maskin [1986].
joueur 2
(1)
C D
joueur 1 C 3,3 0,4
D 4,0 1,1
s*∈ G∞
i = 1 2, si∈Si\ s{ }i* π˜i( )s* ⭓π˜
i(si,s–*i).
π˜ s( ) = (π˜1( ) πs , ˜2( )s ) π˜ s( )>v π˜i( )s >vi i = 1 2,
G∞
v>v
s* π˜ s( )* = v
G∞
v>v ∃δ<1 δ< <δ 1
s* πˆ s( )* = v
n>2
D D,
( )
C C,
plan en deux dimensions, ici , où le point est la paire de gains minmax. La zone grisée représente l’ensemble des gains atteignables à l’équilibre (Théorème 1). Maintenant, nous allons présenter deux stratégies du jeu répété du dilemme du prisonnier auxquelles nous ferons régulièrement appel. Ces stratégies sont définies, pour , par , et, pour , par :
1.TIT-FOR-TAT:
2.GRIMTRIGGER:
Figure 1. Gains moyens d’équilibre du jeu répété du dilemme du prisonnier
Un joueur i, qui utilise la stratégie TIT-FOR-TAT, débute en jouant une action coopérative et joue ensuite, à la période t, l’action jouée par son adversaire à la période . Le joueur i pardonne à son adversaire : lorsque ce dernier dévie de l’action coopérative, le joueur i le punit mais lui laisse la possibilité de revenir sur le chemin de coopération s’il joue à nouveau l’action coopérative
C. Par contre, le joueur i, qui met en œuvre la stratégie GRIM TRIGGER, ne pardonne aucune erreur. Il joue l’action C à la première période et continue à jouer l’action C tant que son opposant joue également l’action C. En revanche, dès que son adversaire choisit l’action D, le joueur i déclenche des représailles
définitives. 䊐
Lorsqu’un joueur met en œuvre une de ces stratégies, il laisse la possibilité à l’opposant, s’il coopère, de générer une histoire complète de profils d’actions coopératifs. En ce sens, lorsque deux stratégies produisent une suite de T profils d’actions , on dit indifféremment que ce sont deux stratégies coopératives, qu’elles génèrent une histoire coopérative, ou qu’elles procurent aux joueurs un gain moyen coopératif. TIT-FOR-TAT et GRIM TRIGGER sont deux stratégies coopératives.
π˜1( ) πs ,˜2( )s
( ) (D D, )
t = 1 si1( )∅ = C t>1 sit( )ht C si a–i
t–1 = C D si a–t–i1 = D.
=
sit( )ht
C si a–τi = C∀τ = 1 … t, , –1
D sinon.
=
(C, D)
(C, C)
(D, C) (D, D)
~ π2(s)
~ π1(s)
1 3 4
1 3 4
0
t–1
C C,
IMPLÉMENTATION DES STRATÉGIES
PAR UN MODÈLE DE CALCUL
Modèle de calcul
La procédure de décision d’un joueur comprend les étapes suivantes : le joueur emmagasine de l’information factuelle, puis il traite cette information afin de prendre ses décisions. Cette procédure peut être vue comme un processus d’entrée/sortie au cours duquel l’individu effectue la tâche de traitement de l’information. Aumann [1981] suggère d’utiliser les outils de l’informatique théorique afin de modéliser ce processus par un modèle de calcul ou machine. Dans le cadre de la théorie des jeux répétés, une machine est un mécanisme qui reçoit en entrée de l’information sur l’histoire du jeu, traite cette information et, ensuite, associe en sortie une action à chaque histoire du jeu. Le fonctionnement de la machine dans son ensemble correspond au calcul d’une stratégie. On parle alors de jeu de machines pour décrire un jeu répété dans lequel les joueurs sont amenés à choisir une machine à laquelle ils délèguent la tâche de jouer le jeu. On mesure la complexité d’une machine par un paramètre lié à sa taille. De cette manière, nous nous intéressons à un aspect de la rationalité des joueurs dans la mesure où ils considèrent la complexité de leurs stratégies. Lorsqu’un coût est associé à la complexité d’une stratégie, ils auront une incitation à mettre en œuvre des stratégies simples.
Rationalité et machines
À ce stade, il faut préciser quel type de rationalité intervient lorsqu’on étudie un jeu de machines, ce qui revient à spécifier les capacités des joueurs.
Avant chaque exécution, une machine finie se trouve dans une configuration particulière. Par hypothèse, à partir d’une entrée donnée, le nombre de configu-rations atteignables par la machine est fini. Lorsque le jeu est répété indéfini-ment, le fonctionnement dynamique de la machine finit nécessairement par décrire un cycle de configurations de longueur l⭓1. Par conséquent, un modèle de calcul peut implémenter uniquement un sous-ensemble des stratégies d’un jeu répété à horizon infini. Autrement dit, chaque joueur doit s’accommoder des capacités de la machine sélectionnée pour implémenter sa stratégie. Un joueur ne peut pas engager une stratégie que sa machine ne peut pas calculer. Pour chaque modèle de calcul examiné, nous verrons qu’une machine implémente bien une stratégie pure d’un jeu répété. Ainsi, nous pourrons utiliser le terme de machine pure ou simplement de machine pour signifier qu’elle implémente une stratégie pure.
À chaque période t d’un jeu répété, l’action choisie par un joueur dépend
(i) du comportement passé observé de l’opposant, (ii) du comportement futur anticipé de l’opposant.
du jeu. Dans le cadre des jeux de machines, nous verrons, dans l’exemple 8, que certaines machines sont parfois incapables de mémoriser l’intégralité ou même un sous-ensemble des actions jouées par l’opposant.
Le point (ii) fait référence à la capacité d’anticipation du joueur. Lorsque la rationalité cognitive d’un joueur est parfaite, il peut anticiper exactement le comportement futur de son adversaire, pour toutes les périodes de jeu à venir. Une machine n’est pas forcément capable de réaliser une telle tâche.
Par exemple, l’automate d’un joueur ne peut anticiper les actions de son oppo-sant que pour un nombre fini de périodes lorsque celui-ci utilise une stratégie qui ne cycle pas. Cette contrainte n’existe pas lorsque deux machines aux capacités identiques s’affrontent. Cependant, lorsqu’un joueur rencontre un adversaire dont la rationalité est parfaite, ce n’est plus le cas. Il est possible de construire un exemple dans lequel le joueur i, dont la rationalité est parfaite, met en œuvre une stratégie que la machine du joueur – i ne peut pas reconnaître. La rationalité cognitive du joueur – i est dite limitée dans la mesure où il est incapable d’anti-ciper les choix futurs de son opposant face à ses propres actions. Nous illustre-rons ce point à l’aide de l’exemple 3.
Par contre, dans un jeu de machines, les joueurs possèdent une rationalité instrumentale parfaite. Ils utilisent tous les moyens dont ils disposent pour atteindre leurs objectifs. Ils calculent la solution d’un problème d’optimisation dynamique. Il est vrai que l’utilisation d’un modèle de calcul réduit l’espace des stratégies des joueurs à l’espace des stratégies implémentables par le modèle de calcul en question, mais cette limitation des stratégies intervient comme une contrainte dans le programme d’optimisation. Ce sont les limites de la rationalité cognitive des joueurs qui définissent la contrainte que doit satisfaire le programme d’optimisation. Précisément, la rationalité cognitive d’un joueur est ici indissociable de sa rationalité instrumentale. La rationalité cognitive définit une contrainte sur le programme d’optimisation du joueur mais elle n’a pas d’effet sur le degré de perfection de la rationalité instrumentale.
Nous allons maintenant définir les trois principaux modèles utilisés pour rendre compte de certains aspects de la rationalité limitée des joueurs.
Automates
Un automate pour le joueur i est un quadruplet où : 1. est l’ensemble fini des états de la machine avec un élément typique de ;
2. est l’état initial ;
3. : est la fonction de sortie qui associe une action à chaque état de l’automate. Le résultat indique au joueur i l’action à jouer chaque fois que l’automate se trouve dans l’état ;
4. : est la fonction de transition. À la période t, si l’automate est dans l’état et que le joueur adverse a joué l’action , alors l’automate transite vers l’état .
Dans un modèle de théorie des jeux répétés, un automate correctement défini doit spécifier une transition pour chaque joueur et pour chaque paire
Mi Qi qi0 λ i µi
, , ,
( )
=
Qi mi Mi qi
Qi
qi0 Q i ∈
λi Qi→Ai λi( )qi ∈Ai
qi∈Qi λi( )qi
qi µi Qi×A–i→Qi
Mi qi∈Qi a–i∈A–i
µi(qi,a–i)
1. Dans la paire , est l’automate choisit par le joueur . L’ensemble des paires d’automates finis est noté ᏹ. On note l’ensemble des automates du joueur i dont le nombre d’états est au plus m.
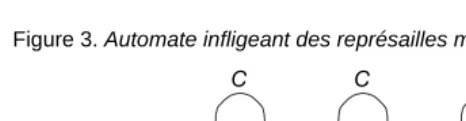
Considérons le jeu répété du dilemme du prisonnier. Les plus petits automates M1 et M2 capables d’implémenter les stratégies TIT-FOR-TAT et GRIMTRIGGER sont décrits par la figure 2. Ils comportent deux états. Lorsqu’on représente graphiquement un automate, un cercle correspond à un état. Ici, nous identifions un état par le symbole inscrit à l’intérieur de cet état indiquant l’action jouée dans cet état. Une flèche correspond à une transition et le symbole inscrit au dessus de cette flèche indique l’action jouée par l’adversaire et observée par le joueur. L’état initial est signalé par la flèche ne possédant pas d’état prédécesseur.
Figure 2. Automates implémentant deux stratégies du dilemme du prisonnier
Une mesure possible de la complexité d’une stratégie est le nombre d’états du plus petit automate capable de l’implémenter. Les stratégies GRIM TRIGGER et TIT-FOR-TAT ont donc une complexité de 2. À chaque période, le fonctionnement de l’automate dépend de l’état dans lequel il se trouve et de l’action jouée par l’opposant. Une histoire du jeu s’exprime à travers une suite de transitions. Chaque transition conduit à un nouvel état de l’automate qui indique au joueur i l’action à jouer. À toute histoire du jeu, un automate associe une action. Un auto-mate implémente bien une stratégie.
Nous introduisons deux exemples mettant en évidence les limites de la ratio-nalité cognitive d’un joueur. L’exemple 2 identifie les limites de la ratioratio-nalité d’un joueur dont le choix de stratégies est restreint aux automates d’une certaine taille, alors que son adversaire peut sélectionner des automates d’une taille supé-rieure. L’exemple 3 souligne les limites de la rationalité d’un joueur dont le choix de machines est réduit au modèle de l’automate alors que son adversaire n’est pas limité dans le choix de ses stratégies.
Exemple 2. Considérons le jeu de machines du dilemme du prisonnier répété sur
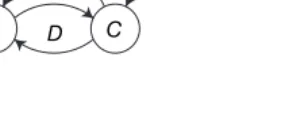
un horizon infini et dans lequel les joueurs considèrent le gain actualisé moyen. Les choix de stratégies des joueurs 1 et 2 sont limités aux automates de taille 2 et 4 respectivement. Supposons que le joueur 2 emploie la stratégie suivante : jouer l’action C tant que le joueur 1 n’a pas joué l’action D plus de deux fois, sinon jouer l’action D. L’automate M3 implémente cette stratégie.
1. Lorsqu’un automate est doté d’une fonction de sortie λi, on le qualifie de machine de Moore. Dans le cadre des jeux répétés, l’évidente utilité de sa fonction de sortie plaide en faveur de l’usage de la machine de Moore.
qi,a–i
( )∈Qi×A–i M = (M1,M2) Mi
i = 1 2, ᏹim
D C
C D
D C
D
C
C C, D
D
Figure 3. Automate infligeant des représailles minmax après trois défections
Face à cette stratégie, lorsque , la meilleure réponse possible consiste à coopérer à toutes les périodes, excepté aux deux premières. Or, cette stratégie n’est pas implémentable par un automate à deux états. Mettre en œuvre une telle stratégie requiert un état dans lequel est jouée l’action D (aux périodes ) puis un autre état dans lequel est jouée l’action C (pour toute autre période). Cependant, il est impossible de construire un tel automate jouant l’action C à toutes les périodes . La rationalité cognitive du joueur 1 est limitée dans la mesure où sa machine est incapable d’anticiper que son adversaire le punira s’il
dévie trois fois de l’action C. 䊐
Exemple 3. Considérons le jeu du dilemme du prisonnier répété indéfiniment. Dans cet
exemple, le joueur 1 doit choisir un automate d’une taille quelconque, alors que le choix de stratégies du joueur 2 n’est pas limité. La stratégie du joueur 2 est la suivante. Il construit une suite de Fibonacci dont les deux premiers termes sont et et de récurrence indépendante de l’indice t des périodes du jeu. Le joueur 2 joue l’action C si les deux conditions suivantes sont vérifiées : 1. soit , soit il n’existe pas d’entier n tel que , c’est-à-dire chaque fois que l’indice de la période de jeu n’est pas un terme de la suite de Fibonacci ;
2. , c’est-à-dire que le joueur 1 a exécuté à chaque
période passée la même action que le joueur 2 (parfait mimétisme).
Dans les autres cas, le joueur 2 joue l’action D. Autrement dit, le joueur 1 doit coordonner ses choix d’actions avec ceux de son adversaire, sinon celui-ci lui inflige des représailles minmax définitives. Si le joueur 1 coopère, la fréquence d’apparition du profil d’actions dans l’histoire du jeu augmente au fil du temps si bien que le gain moyen obtenu par chaque joueur tend vers 3. Néan-moins, par définition de la suite de Fibonacci, la stratégie du joueur 2 ne comporte pas de cycle sur le chemin d’une telle coordination. L’automate du joueur 1 est donc incapable de coordonner ses choix d’actions avec ceux de l’opposant, exception faite d’une suite infinie d’actions D. En effet, à chaque période t, il lui faudrait au moins t états pour déterminer si t appartient à l’ensemble des valeurs de la suite de Fibonacci. Comme l’horizon de jeu n’est pas borné, un nombre infini d’états serait nécessaire alors que par définition l’automate du joueur est fini. Le joueur 1 ne peut donc pas anticiper correctement
les actions futures de son adversaire. 䊐
Dans la section suivante, nous allons présenter un modèle de calcul dont le fonctionnement est complètement différent de celui du modèle de l’automate. Le modèle du perceptron amène le joueur à choisir ses actions sur la base d’un résumé statistique de l’histoire du jeu.
Perceptrons
Dans le cadre d’un jeu répété à deux joueurs et deux actions , un perceptron pour le joueur est le triplet où
C C
D D
C, D
C C
D
D
C C
M3 :
δ>1 3⁄
t = 1 2,
t>2
s2
u1 = 1
u2 = 1 un+2 = un+1+un
t = 1 un+2 = t
a1τ = a2τ ∀τ = 1 … t, , –1 τ<t
C C,
( )
C D,
{ }
1. Une fonction résumée f : définie par
associe à chaque profil d’actions sa fréquence d’apparition dans l’histoire
. Par définition, pour tout ;
2. Une collection finie de classificateurs. Un classificateur est défini par le triplet
où la fonction : associe un réel à chaque profil d’actions du jeu de base. Le classificateur agrège les informations issues de l’histoire du jeu et résu-mées par la fonction f en les pondérant par les poids de la fonction . On obtient une valeur réelle que le classificateur compare à un seuil, souvent fixé à 0. Préci-sément, la valeur du classificateur au début de la période t ⭓1 est :
où exprime la valeur initiale du classificateur. Finalement, l’unité de décision est la fonction à seuil : définie comme suit :
3. La règle de comportement à la période t du perceptron ψ du joueur i est une
fonction r : qui associe une action à tout vecteur
. Elle indique au joueur i l’action à jouer à la période t en fonction des valeurs prises par l’ensemble des classificateurs.
Grâce à son unité de décision, chaque classificateur donne une valeur 0 ou 1 à l’information factuelle enregistrée jusqu’ici selon le seuil fixé. Ensuite, le perceptron agrège les valeurs des classificateurs, et la règle de comportement les classe en deux zones ; l’une où est jouée l’action C, l’autre où est jouée l’action
D. Nous décrirons ce processus au cours de la section 4.
Par la suite, désignera l’action choisie par le perceptron ψ suite à une histoire . Pour une histoire du jeu à la période t, un perceptron muni de classificateurs peut être représenté par le schéma suivant :
Notons, d’ores et déjà, que lorsque le nombre d’unités de décision augmente, la classification devient plus fine. De cette manière, la règle de comportement gagne en précision lorsque augmente. Nous utiliserons le nombre de classi-ficateurs comme une mesure de la complexité du perceptron.
Exemple 4. Dans le cadre du jeu répété du dilemme du prisonnier, pour le joueur 1,
les stratégies TIT-FOR-TAT et GRIMTRIGGER sont implémentées par les perceptrons et munis chacun d’un seul classificateur et définis de la manière suivante :
et une unité de décision identique, :
Pour chaque t, la fonction r fait correspondre l’action C à 1 et l’action D à 0. Examinons plus en détail le perceptron qui implémente TIT-FOR-TAT. La valeur initiale du perceptron est positive, ce qui amène le perceptron à jouer l’action
C à la première période conformément à la définition de l’unité de décision. Si le
joueur adverse joue aussi initialement l’action C, alors la valeur du classificateur reste positive et le perceptron joue à nouveau l’action C. Tant que le joueur adverse joue l’action C, ce processus se reproduit. Par contre, une déviation de l’opposant est évaluée à un poids par le perceptron et fait passer la valeur du classificateur en dessous du seuil 0. Le perceptron joue alors l’action
D en représailles. Tant que le joueur adverse continue de jouer l’action D,
le poids associé au profil d’actions (D, D) maintient et le perceptron joue l’action D. En revanche, si l’opposant coopérère à nouveau, un poids entre dans le calcul de la valeur du classificateur qui repasse au dessus du seuil 0. Le perceptron répond à ce basculement en jouant l’action C à la période suivante. Le fonctionnement d’un tel perceptron implémente bien la stra-tégie TIT-FOR-TAT. Pour le joueur 2, la construction de ces deux stratégies est
similaire. 䊐
Chaque classificateur kl résume une histoire du jeu en une simple valeur via la fonction . L’unité de décision puis la règle de comportement associent ensuite une action à toute histoire du jeu. Le modèle du perceptron implémente donc une stratégie.
COMPLEXITÉ D’IMPLÉMENTATION DES STRATÉGIES
Dans cette section, nous présentons les principaux résultats liés à l’étude des jeux de machines. Quel que soit le modèle utilisé, il est possible de regrouper l’ensemble des travaux en deux grandes catégories :
: :
κ
k1 k2
k1 α1(C C, ) = 0 k2 α2(C C, ) = 0
α1(C D, ) = – 2 α2(C D, ) = – 2
α1(D C, ) = + 2 α2(D C, ) = 0
α1(D D, ) = 0 α2(D D, ) = –2
V11 = 1 V
21 = 1
l
∀ = 1 2,
d1 1 si Vl t ⭓0 0 si Vlt<0.
=
V11
k1
α1(C D, ) = –2
V1t <0
α1(D C, ) = + 2
1. Complexité endogène. Le coût de complexité d’une stratégie est assimilé à la taille de la machine qui l’implémente. Les préférences des joueurs tiennent compte de ce coût. On examine les conséquences de cette modification sur l’ensemble des équilibres du jeu de machines. Dans ce type de modèle, les joueurs prennent des décisions avec des limites computationnelles (contrainte coût/taille de la machine) bien que la taille de leurs machines puisse être arbitrai-rement grande.
2. Complexité exogène. On opère une restriction supplémentaire sur l’espace des stratégies en bornant la taille des machines que peuvent sélectionner les joueurs. Dans un jeu répété sur un horizon fini, on cherche à obtenir des équilibres coopé-ratifs. Il est également possible d’étudier une situation de complexité
asymé-trique dans laquelle la rationalité des deux joueurs est soumise à des bornes
diffé-rentes. Dans ce type de modèle, la taille de la machine des joueurs est fixée. Les stratégies des joueurs sont donc computationnellement limitées (les anticipations sont bornées) mais la rationalité instrumentale des joueurs reste parfaite sous cette contrainte.
Jeux d’automates
Complexité endogène
Nous abordons deux mesures distinctes de la complexité d’un automate. Nous considérons tout d’abord le nombre d’états de l’automate, puis le nombre d’états et de transitions de l’automate.
Mesure de la complexité par le nombre d’états
Rubinstein [1986] et Abreu et Rubinstein [1988] étudient la classe des jeux de machines à deux joueurs dans lesquels le choix des joueurs est limité aux stratégies implémentables par le modèle de l’automate. Le modèle repose essentiellement sur la prise en compte du coût de complexité des stratégies. Ce coût est mesuré par le nombre d’états de l’automate qui implémente la stratégie en question et entre de manière lexicographique dans la fonction de préférence du joueur. Dans un premier temps, le joueur maximise son gain moyen sans escompte en fonction de la stratégie adverse anticipée. Ensuite, il cherche à minimiser le coût de sa stratégie, c’est-à-dire la taille de son automate. Lorsque deux stratégies lui procurent le même gain, le joueur opte pour la stratégie la moins complexe.
Précisons la définition d’un cycle. Le nombre d’états d’un automate étant fini, il existe forcément une paire d’états qui apparaît une deuxième fois dans l’histoire du jeu, disons à la période . Notons la période à laquelle cette paire d’états est apparue pour la première fois. La suite de paires d’états décrit un cycle de longueur . Puisque le jeu est répété indéfiniment, le gain moyen de chaque joueur est le gain moyen qu’il obtient au cours du cycle.
Abreu et Rubinstein [1988] montrent que tout équilibre de Nash de leur jeu de machines possède les propriétés suivantes.
PROPOSITION 1 (Abreu et Rubinstein [1988]). (i) Toute histoire du jeu se
décompose en une phase 1 d’introduction qui comprend des états tous distincts visités une seule fois et n’étant ensuite jamais réutilisés ; une phase 2
q = (q1,q2)
tc2 tc1
qtc1,… q, tc2–1
( ) tc2–tc1
M1,M2
de transition au cours de laquelle les états du cycle sont utilisés mais pas de manière coordonnée ; une phase 3 de cycle se répétant indéfiniment et composée d’états tous distincts.
(ii) , les deux automates ont la même taille. Ils possèdent également le même nombre d’états cycliques et non cycliques.
(iii) Lors de la phase 3, les deux joueurs coordonnent parfaitement leurs actions, c’est-à-dire que pour tout tel que et pour tout t,
si et seulement si .
La suite d’états générée par chaque automate Mi finit inévitablement par cycler à partir de la période . Par définition, les états visités entre la première période et la période ne peuvent pas faire partie du cycle. Les états de la phase 1 apparaissent donc une unique fois. À l’équilibre, l’existence de la phase 2 provient du fait que deux machines possédant une structure de fonctionnement identique n’ont pas forcément le même état de début de cycle. La coordination des actions n’est pas immédiate et la phase 2 sert de période d’ajustement. Ensuite, la phase 3 débute. Notons que les phases 1 et 2 peuvent être vides. L’exemple 5 illustre le rôle de la phase 2.
Exemple 5. Considérons le jeu de base à deux joueurs dont la matrice des gains
est la suivante :
Ce jeu est doublement symétrique et possède deux équilibres de Nash stricts en stratégies pures, (C, D) et (D, C), qui procurent la même paire de gains aux joueurs. Notons que le gain moyen que chaque joueur obtient sur chaque équi-libre de Nash est le gain maximum du jeu. Supposons que les joueurs 1 et 2 choi-sissent les automates et respectivement :
Figure 5. Deux automates illustrant la phase 2
Ces deux automates débutent chacun par l’action C, alors que chaque joueur a intérêt à choisir l’action alternative à celle sélectionnée par l’adversaire. Ensuite, les deux automates décrivent un cycle (C, D), (D, C) :
La phase 2 permet d’ajuster la dynamique de fonctionnement des automates pour que la phase 3 de cycle puisse débuter. À chaque période du cycle, les deux joueurs reçoivent le gain maximum du jeu. De plus, si le joueur i choisit la machine , son opposant ne peut pas obtenir le même gain moyen en optant pour un automate muni d’un seul état1. Les joueurs n’ont pas intérêt à dévier de leurs stratégies. La paire est donc un équilibre de Nash.
Une fois la phase de cycle initiée, chaque joueur connaît exactement l’état dans lequel se trouve l’automate adverse. Les joueurs se coordonnent parfaite-ment dans leurs choix d’actions (condition (iii)).
Lorsqu’on considère le gain moyen non actualisé, la phase 2 n’a pas d’influence sur le gain moyen du joueur puisque seul compte le gain obtenu en moyenne lors du cycle. Par contre, lorsqu’on considère le gain actualisé moyen, la présence d’une phase d’ajustement a une répercution négative sur le gain moyen des joueurs. Dans cette situation, la phase 2 est vide à l’équilibre. Par exemple, le joueur 2 a intérêt à choisir une machine dont la seule différence avec est que l’état initial est l’état jouant l’action D. Avec la paire ,
la phase de cycle (C, D), (D, C) débute immédiatement. 䊐
La condition (ii) s’explique par le fait qu’il suffit d’un automate à m états pour obtenir une meilleure réponse face à un autre automate à m états. On peut montrer que si un automate comporte un état non utilisé, cet état peut être supprimé sans entraîner une perte de gain. À l’équilibre, tous les états de l’auto-mate sont utilisés.
Pour la classe des jeux de machines , la proposition 1 implique que les gains à l’équilibre sont nécessairement des combinaisons linéaires des gains obtenus des profils d’actions inscrits dans les diagonales de la représentation matricielle du jeu. Pour le jeu de machines du dilemme du prisonnier, tout équi-libre de Nash est une combinaison linéaire des profils d’actions (C, C) et (D, D) ou des profils d’actions (C, D) et (D, C). La zone des gains moyens rationnels du théorème 1 est réduite à la « croix » représentée par la figure 6.
Figure 6. La « croix » dans le jeu répété du dilemme du prisonnier
1. Les deux joueurs peuvent néanmoins parvenir au même résultat avec une paire d’automates à un état.
Mi4
M14 M 25 ,
( )
M25′
M25 M
14,M25′
( )
Mi M–i
2×2
(C, D)
(C, C)
(D, C) (D, D)
~ π2(s)
~ π1(s)
1 3 4
1 3 4
Les stratégies GRIMTRIGGER et TIT-FOR-TAT ne sont pas des stratégies du jeu de machines à l’équilibre. Les deux automates de la figure 2 qui implémentent ces stratégies comportent chacun un état utilisé dans l’unique but de punir le joueur adverse lorsqu’il dévie de l’action coopérative. Cet état sert de menace et, par conséquent, n’est jamais visité sur le chemin d’équilibre. Lorsque cet état est supprimé, l’automate est moins coûteux pour le joueur alors que son gain reste inchangé. Dans ce jeu de machines, les menaces hors du chemin d’équilibre n’existent pas. Par contre, l’exemple suivant montre que la phase 1 d’introduc-tion peut jouer le rôle de menace.
Exemple 6. Considérons le jeu de machines du dilemme du prisonnier répété
indéfiniment et supposons que le joueur 1 utilise l’automate suivant :
Figure 7. Automate comportant une menace sur le chemin d’équilibre
Face à la stratégie employée par le joueur 1, la meilleure réponse du joueur 2 consiste à jouer une fois l’action D puis à coopérer afin d’obtenir en moyenne le gain coopératif. Cette meilleure réponse est implémentée par la machine . La paire produit l’histoire du jeu suivante :
La phase 1 d’introduction comporte un seul état. Ensuite, la phase 3 commence et chaque automate cycle sur l’état C. Si l’opposant dévie, il est possible de revenir à l’état de la phase 1. Cela signifie que la période initiale joue le rôle de la menace dans la mesure où elle inflige clairement le châtiment que le joueur adverse recevra en cas de déviation. De plus, cet état impose également une contrainte sur le choix de machines du joueur adverse. En effet, s’il veut entrer dans la phase cyclique de coopération, l’automate de l’opposant doit jouer une fois l’action D. Cet automate contient donc au moins deux états. Grâce à l’état dans lequel est jouée l’action D, toute déviation est punie par l’emploi de l’action D et aucun automate de taille inférieure ne permet au joueur d’obtenir le gain moyen coopératif face à . La paire est donc un équilibre de
Nash du jeu de machines. 䊐
Mesure par le nombre d’états et la complexité de transition
Banks et Sundaram [1990] proposent une mesure de la complexité d’un auto-mate plus contraignante. Cette mesure tient compte à la fois du nombre d’états de l’automate et de la complexité des transitions. Par complexité de transition, Banks et Sundaram [1990] entendent l’information nécessaire à l’état d’un
mate pour transiter. Par exemple, l’automate à deux états implémentant la stratégie GRIMTRIGGER n’a plus besoin d’information pour fonctionner une fois que le joueur adverse a dévié (l’automate joue l’action D quelle que soit la stra-tégie de l’adversaire). En revanche, l’automate à deux états implémentant la stratégie TIT-FOR-TAT doit, pour toute période t, mémoriser l’action choisie par le joueur adverse à la période précédente. L’automate TIT-FOR-TAT est considéré comme plus complexe que l’automate GRIMTRIGGER. Dans ce jeu de machines, l’utilité des joueurs est croissante en fonction du gain moyen mais décroissante en fonction des deux critères mesurant la complexité de l’automate. Le reste du modèle est similaire à celui d’Abreu et Rubinstein [1988].
Dans ce modèle, chaque transition étant coûteuse, un automate à l’équilibre ne comporte aucune transition inutilisée. Précisément, pour chaque état , il existe une unique transition , ce qui signifie que les transitions du joueur i sont indépendantes du choix d’action du joueur . Le joueur i à intérêt à jouer, à chaque période t, une action qui est meilleure réponse du jeu de base face à l’action anticipée. Banks et Sundaram [1990] montrent que tout équilibre de Nash de leur jeu de machines est forcément constitué, à chaque période, par un profil d’actions qui est un équi-libre de Nash du jeu de base1. Par conséquent, l’ensemble des gains atteignables à l’équilibre est une combinaison linéaire des gains obtenus sur les équilibres de Nash du jeu de base. Lorsque le jeu de base est un duopole de Cournot, le profil d’action , où est la quantité de Cournot-Nash pour la firme , est le seul équilibre de Nash. Compte tenu des contraintes de complexité, une paire d’automates à un état telle que chaque firme fixe la quantité de Cournot-Nash à chaque période est le seul équilibre de Nash du modèle de Banks et Sundaram [1990]. De même, pour le jeu de machines du dilemme du prisonnier, le seul équi-libre de Nash est alors une paire d’automates à un état jouant l’action D.
Les remarques formulées sur le modèle d’Abreu et Rubinstein [1988] s’éten-dent à la complexité des transitions. Puisque toute transition inutilisée doit être supprimée, les transitions se trouvant hors du chemin d’équilibre ne peuvent pas faire partie d’un automate d’équilibre. À la lumière de cette remarque, le couple d’automates de l’exemple 6 n’est pas un équilibre de Nash du modèle de Banks et Sundaram [1990] puisque, pour chaque , les transitions et ne sont pas utilisées à l’équilibre. Dans le jeu de machines de Banks et Sundaram [1990], il n’est donc pas possible de mettre en place une menace sur le chemin d’équilibre (au cours de la phase 1). L’absence totale de menaces renforce l’intuition du résultat selon lequel seules les meilleures réponses du jeu de base sont jouées à l’équilibre.
Complexité exogène
Nous nous sommes jusqu’à présent concentré exclusivement sur une approche en termes de coût de complexité des stratégies. Dans cette section, nous nous intéressons à une classe de modèles dont la complexité est un paramètre exogène.
1. Piccione et Rubinstein [1993] obtiennent le même résultat en considérant la forme extensive du jeu de base et en mesurant la complexité d’un automate seulement par son nombre d’états.
M2
M1
qi∈Qi,∀a–i∈A–i µi(qi,a–i) i
– ait
a–t i
q1c q 2 c ,
( ) qic i = 1 2,
Coopération à horizon fini
Neyman [1985] étudie le jeu du dilemme du prisonnier répété sur un horizon fini. En plus des limites cognitives imposées par le modèle de l’automate sur la rationalité des joueurs, l’auteur ajoute une contrainte supplémentaire sur la taille des machines que peuvent sélectionner les deux joueurs. La rationalité cognitive des joueurs est ainsi encore plus réduite. Lorsque l’horizon de jeu est fini, les joueurs suivent un raisonnement par rétroduction qui les conduit inévitablement à jouer l’action D à chaque période. Mais ce résultat suppose certaines aptitudes de la part des joueurs dans la capacité de leurs machines à identifier la dernière période du jeu. Neyman [1985] montre que des joueurs dont la rationalité cogni-tive est suffisamment limitée peuvent coopérer à chaque période.
Neyman s’intéresse également à la situation dans laquelle les joueurs effec-tuent des choix probabilistes sur leur ensemble de stratégies. Une stratégie mixte du jeu de machines pour le joueur est une loterie sur l’ensemble des automates de taille au plus que peut choisir le joueur. On la note
où représente la probabilité que le joueur i choisisse l’automate . L’ensemble des stratégies mixtes du joueur i est noté :
La fonction de gain espéré : associe un gain espéré
à chaque profil en stratégies mixtes
. Lorsque le jeu du dilemme du prisonnier décrit par (1) est répété T fois, Neyman [1985] montre que :
PROPOSITION 2 (Neyman [1985]) (i) Si pour tout ,
alors il existe un équilibre de Nash en stratégies pures qui, à chaque période, procure le gain coopératif aux joueurs.
(ii) S’il existe tel que , alors le seul équilibre en stratégies pures est celui dans lequel les deux joueurs jouent l’action D à chaque période. (iii) Pour tout entier , il existe un entier tel que pour tout et , il existe un équilibre de Nash en stratégies mixtes
qui garantit un gain espéré à chaque joueur .
Le point (i) s’explique par le fait qu’en utilisant un automate dont le nombre d’états est inférieur au nombre T de périodes, les machines des joueurs ne sont pas capables de compter jusqu’à T. Le raisonnement par rétroduction ne peut donc pas avoir lieu puisque les machines ne savent pas quand s’arrête le jeu. Chaque joueur anticipe que son adversaire peut dévier de l’action coopérative pour toute période . Face à une stratégie coopérative, le gain moyen qu’un joueur i peut obtenir d’une stratégie dans laquelle il dévie à une période est strictement inférieur au gain moyen que lui procure une stratégie coopérative. Du point de vue des machines, le jeu se déroule comme si l’horizon était infini. L’intérêt de la machine du joueur i est alors de jouer l’action
coopérative à chaque période et de punir toute déviation en jouant l’action D de manière définitive. La rationalité cognitive bornée des joueurs permet d’obtenir un meilleur résultat que celui obtenu dans le jeu répété standard1. Illustrons les points (i) et (ii) de la proposition 2 par un exemple.
Exemple 7. Considérons le jeu du dilemme du prisonnier répété sur quatre
périodes. D’après la proposition 2, lorsque les deux joueurs utilisent des auto-mates possédant deux ou trois états, ils peuvent recevoir le gain coopératif lors des quatre périodes de jeu. Supposons, par exemple, que le joueur 1 choisisse l’auto-mate à deux états de la figure 2 qui implémente la stratégie GRIMTRIGGER.
Face à cette stratégie, le joueur 2 aurait intérêt à coopérer les trois premières périodes et à dévier la dernière période. Si le joueur 1 anticipe ce comportement, il choisit alors l’action D lors de la dernière période. Le joueur 2 anticipe lui aussi le comportement de son adversaire et a intérêt à dévier lors de la période , et ainsi de suite. Le raisonnement par rétroduction conduirait alors les deux joueurs à jouer l’action D lors de chaque période. Dans ce jeu de machines, un telle démarche n’est pas possible. En étant limité aux automates composés de deux ou trois états, le joueur 2 ne possède pas les capacités suffisantes pour mettre en œuvre une stratégie capable de dévier après trois périodes de coopéra-tion. En effet, il n’existe pas d’automate doté de deux ou trois états qui repère à la période 4 que l’on joue la dernière période du jeu. L’automate qui consiste à jouer l’action D à chaque période, comme tout autre automate consistant à choisir l’action D au moins une fois, n’est pas une meilleure réponse face à la stratégie GRIM TRIGGER2. Lorsque le joueur 2 emploie une stratégie dans laquelle il dévie à une période , il obtient le gain moyen suivant :
,
qui est clairement inférieur au gain moyen qu’il se procure en coopérant lors des quatre périodes de jeu. La meilleure réponse du joueur 2 consiste à coopérer à chaque période en menaçant de représailles toute déviation adverse. Le profil de stratégies est donc un équilibre de Nash du jeu de machines de Neyman [1985] dans lequel les joueurs obtiennent le gain coopératif pour toute période . Notons qu’en l’absence d’un coût à la Abreu et Rubinstein [1988], il est possible de mettre en place une menace située en dehors du chemin d’équilibre. En revanche, dès que les machines des joueurs possèdent quatre états ou plus, ce raisonnement ne tient plus. Le joueur 1 anticipe que le joueur 2 possède un automate d’une taille suffisante pour savoir que 4 est l’indice de la dernière période. Le joueur 1 conclut que le joueur 2 est capable de choisir l’action D lors de cette dernière période. Par symétrie, le joueur 2 analyse la
1. Gilboa et Samet [1989] s’intéressent à une situation de complexité asymétrique dans laquelle le choix d’un seul joueur est limité aux stratégies implémentables par le modèle de l’automate. Lorsque le jeu est répété indéfiniment et que le nombre de périodes de représailles faisant suite à une déviation est fini, les auteurs montrent que le joueur dont la rationalité est limitée peut se comporter en dictateur et obtenir quasiment son gain moyen maximum. Ben-Porath [1993] obtient des résultats comparables pour la classe des jeux à somme nulle.
2. Par contre, la paire d’automates qui jouent chacun l’action D systématiquement est un équi-libre de Nash de ce jeu de machines.
M2
T–1
M2D
t<4 π˜ M2( 12,M2D)
t–1
( )×π2(C C, )+π2(C D, )+(4–t)×π2(D D, ) 4
---<3 =
M12 M 2 2 ,
( )
t = 1 … 4, ,
situation de la même manière. Le raisonnement par rétroduction amène les
joueurs à dévier à chaque période . 䊐
Le point (iii) indique que le gain coopératif peut être approché bien que les joueurs puissent choisir des automates d’une taille raisonnablement supérieure à T1. Il s’agit d’imposer à chaque automate à l’équilibre d’avoir à répondre par une action précise à de petites séquences de l’histoire du jeu, ou autrement des repré-sailles consistant à jouer l’action D définitivement sont mises en œuvre (voir exemple 3). Lors des autres périodes, l’automate choisit l’action coopérative. La mémoire de l’automate est ainsi utilisée de telle sorte qu’il ne reste pas suffisam-ment d’états disponibles pour compter le nombre de périodes.
Application économique au comportement de marché
Dans un contexte de marchés multiples répété indéfiniment, Fershtman et Kalai [1993] étudient le comportement de deux firmes dont les capacités à implémenter des stratégies de production sont restreintes aux automates d’une taille bornée . À chaque période, chaque firme i reçoit le signal
lui indiquant la nature haute (h) ou basse (b) de la demande sur le marché . La fonction de transition de l’automate d’une firme à la période tient compte à la fois du niveau de production de l’opposant en et du signal de demande au début de la période t. À chaque période, il existe configu-rations de demandes possibles sur l’ensemble des marchés. Si , la firme i peut implémenter une stratégie de production qui répond parfaitement aux signaux reçus en affectant des niveaux de production optimaux ou , , à chaque configuration de demandes. Une telle stratégie requiert au moins états et est donc trop complexe pour être implémentée lorsque . Dans ce cas, la firme sera contrainte, sur certains marchés, de fixer une quantité qui maximise son profit sur le marché k sans tenir compte du signal de demande.
Notons
l’accroisse-ment de profit de la firme i sur le marché k lorsqu’elle répond parfaitel’accroisse-ment au signal de demande avec et les fonctions de profits de la firme i dans le marché k lorsque la demande est haute et basse respectivement. Un marché est qualifié de peu profitable (PP) lorsque , c’est-à-dire que la firme i y subit des pertes lorsque son choix de production ne tient pas compte du signal de demande. Deux situations sont étudiées.
Dans la première, une firme est en situation de monopole sur K marchés et . Supposons que la firme 1 ait l’opportunité d’entrer sur un ième marché. Produire en plus sur un ième marché requiert une fraction des ressources de l’automate et diminue de fait la qualité de réponse face aux signaux dans les K autres marchés. Lorsque , , et le marché 2 est PP, la firme 1 a intérêt à ne pas produire sur le marché 2 car ce qu’elle y gagnerait
1. Zemel [1989] obtient également un équilibre de Nash coopératif dans le jeu répété du dilemme du prisonnier à horizon fini. La preuve est obtenue en dotant l’automate d’une capacité à communi-quer des messages. Papadimitriou et Yannakakis [1994] retrouvent le résultat de Neyman [1985] et montrent qu’il suffit que l’automate d’un des deux joueurs comporte un nombre d’états sub-expo-nentiel en fonction du nombre de périodes pour tendre à l’équilibre vers le gain moyen coopératif. Enfin, Neyman [1998] généralise ce résultat pour tout jeu répété à deux joueurs.
ne compenserait pas la perte de profit due à la baisse de qualité de réponse face au signal sur l’autre marché.
Dans la seconde, la firme 1 opère sur deux marchés et la firme 2 peut entrer sur le marché 1 de type PP. Lorsque deux firmes sont présentes sur le même marché, elles peuvent fixer la quantité de Cournot-Nash auquel cas elles obtiennent le profit . Fershtman et Kalai [1993] montrent que l’implémentation d’une stra-tégie de Cournot-Nash requiert deux états. Les deux firmes peuvent également se comporter de manière collusive auquel cas elles obtiennent chacune une moitié du profit de monopole . Il faut par contre un automate avec au moins trois états pour implémenter une telle stratégie. Trois effets économiques sont possibles :
– Concentration. Supposons , et le marché 2 est du type PP.
Lorsque et , la firme 1 a intérêt à sortir du marché 2
en réponse à une entrée de la firme 2 sur le marché 1. La firme 1 concentre son activité sur le marché 1 et utilise entièrement son automate pour s’y comporter de manière collusive avec l’entrant.
– Spécialisation. Supposons à nouveau , et le marché 2 est du type PP. Lorsque et , l’intérêt de la firme 1 est de sortir de marché 1 en réponse à une entrée de la firme 2 sur ce marché. La firme 1 se spécialise dans la production du marché 2 et chaque firme se retrouve alors en situation de monopole sur un marché.
– Barrière à l’entrée. Supposons que la firme 2 n’a intérêt à entrer sur le marché 1 que lorsque la firme 1 s’y comporte de manière collusive suite à cette entrée. Lorsque et , la firme 1 ne coopérera pas avec la firme 2 si celle-ci entre sur le marché en raison de ses capacités restreintes à répondre au signal de demande. La rationalité limitée de la firme 1 rend crédible cette menace qui constitue une barrière à l’entrée.
Jeux de perceptrons
Nous nous plaçons maintenant dans une situation dans laquelle les stratégies des joueurs sont implémentées par le modèle du perceptron. Comme pour le modèle de l’automate, les joueurs choisissent un perceptron pour jouer à leur place dans un jeu de machines répété indéfiniment. Dans les deux premiers para-graphes, nous présentons deux modèles de complexité exogène. Ensuite, nous considérons un modèle de complexité endogène dans lequel la complexité d’un perceptron est évaluée par son nombre de classificateurs.
Perceptrons et « folk » théorème
Cho [1995] examine le jeu de machines du dilemme du prisonnier dans lequel les deux joueurs choisissent des perceptrons. Il utilise l’équilibre de Nash Parfait
pour ses Sous-Jeux (ENPS) comme concept solution. Dans un jeu répété indéfini-ment , chaque répétition du jeu de base qui fait suite à une histoire est la racine d’un sous-jeu noté . Un profil est un ENPS si, pour tout t et tout sous-jeu
, induit un équilibre de Nash. Cho [1995] prouve le résultat suivant1.
1. Cho [1996b] étend son analyse du jeu de perceptrons à tout jeu répété à deux joueurs sans restriction sur le nombre d’actions à la disposition des joueurs.
qc πik c,
πik m 2, ⁄
m1 = 4 Λ1>Λ2 π11 m 2, ⁄ >π11 c, +π12 π11 c, >0
m1 = 4 Λ1>Λ2 π11 c, ⭐0 π11 m 2, ⁄ <π12
k⭐4 π
11 m 2, ⁄ –π11 c, <Λi1
G∞ ht∈Ht
Gt∞ s*
PROPOSITION 3 (Cho [1995]). Pour toute paire de gains , il existe une paire de perceptrons , munis chacun d’un unique classifi-cateur, qui induit un ENPS du jeu et pour lequel .
Bien que l’espace des stratégies soit restreint aux stratégies implémentables par le modèle du perceptron, Cho [1995] utilise une paire de perceptrons de complexité réduite (munis d’un seul classificateur ) pour obtenir l’ensemble des gains moyens du « folk » théorème 1. Pour chaque joueur , la fonc-tion est construite comme la différence entre le gain moyen désiré par le joueur adverse et le gain du jeu de base que ce dernier obtient . La valeur mesure la somme de ces différences aux périodes .
Pour résumer, en fixant ,1
et .
La règle de comportement est alors intuitive : tant que , c’est-à-dire tant que le joueur adverse reçoit en moyenne un gain plus élevé que , le joueur i le punit en jouant l’action D ; dès que , il le récompense en jouant l’action C. Par conséquent, le gain moyen de l’opposant converge vers , et il n’est pas nécessaire de définir de représailles particulières en cas de déviation. Une paire de perceptrons construite de cette manière induit un ENPS du jeu de machines.
Dans ce jeu de machines, c’est la fonction à seuil du classificateur (ou plus généralement la règle de comportement pour un perceptron composé de plusieurs classificateurs) qui incorpore une menace. Chaque valeur en dessous du seuil est perçue comme une déviation et entraîne une sanction sous la forme de l’utilisation de l’action D par le joueur i. De plus, ici, la durée des représailles est proportionnelle à l’ampleur de la déviation puisque le retour à une situation de coopération ne s’effectue qu’une fois que est de nouveau supérieure au seuil. Un couple de perceptrons implémentant la stratégie TIT-FOR -TAT (exemple 4) constitue également un équilibre de Nash de ce jeu de machines. La menace de représailles y est similaire. Enfin, à l’équilibre, dans le cadre d’une paire de perceptrons GRIM TRIGGER, chaque joueur menace son opposant de représailles définitives. Ainsi, tous les types de menaces sont réalisables dans ce jeu de perceptrons. Comme nous l’avons déjà souligné, une telle variété de menaces n’est pas possible dans les jeux d’automates d’Abreu et Rubinstein [1988] et de Banks et Sundaram [1990].
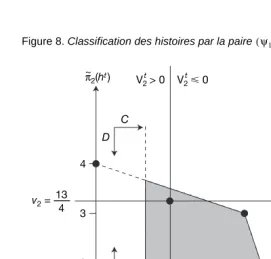
Illustrons le rôle de classification des histoires des perceptrons . Fixons une paire de gains individuellement rationnels et . Notons le gain moyen du joueur à la période t. La figure 8 réper-torie les quatre situations auxquelles font face les perceptrons et .
Pour chaque période t, les droites d’équations , , séparent le plan en quatre zones dans chacune desquelles la paire de perceptrons joue une paire d’actions. Les doubles flèches présentes dans chacune des zones indiquent le sens de déplacement de la paire de gains moyens entre et . Par exemple, lorsque le joueur 1 reçoit
1. Notons que ce résultat est valable pour toute valeur initiale du classificateur .
à la période t un gain moyen supérieur à (c’est-à-dire ), l’histoire est rangée du coté droit de la droite de séparation et le perceptron du joueur 2 punit alors le joueur 1 en employant l’action . Par symétrie, le perceptron du joueur 1 procède de la même manière. Le graphique souligne bien que le gain moyen de chaque joueur converge forcément vers .
Figure 8. Classification des histoires par la paire pour et .
Application économique aux relations d’agence
Cho [1996a] applique cette modélisation à un jeu principal/agent répété1 dont le jeu de base est le suivant. L’agent a une aversion pour le risque et est engagé dans Z projets . Si le projet z réussit, , sinon, . Le succès du projet z est entièrement déterminé par l’effort que produit l’agent :
Prob
Le principal, neutre au risque, ignore l’effort fourni par l’agent. Il rémunère l’agent en fonction du résultat de chaque projet. Autrement dit, le principal utilise le résultat de chaque projet comme estimateur des niveaux d’efforts de l’agent. Comme dans le jeu de perceptrons précédent, le principal considère le nombre de succès dans chaque projet ainsi que la rémunération
1. Le lecteur est aussi renvoyé à Rubinstein [1993] pour une utilisation des perceptrons à l’analyse d’informations sur les prix dans un modèle de ventes.
moyenne qu’il a versée à l’agent. Le perceptron du principal pondère ces informations, les agrège en un réel, puis le compare au seuil 0. Le fonctionne-ment du perceptron de l’agent est comparable.
Cho [1996a] montre que, pour toute paire d’utilités non efficiente au sens de Pareto, il existe une paire de perceptrons qui constitue un équi-libre de Nash du jeu principal/agent répété pour lequel et . La paire de stratégies est de nature comparable à celle de la proposition 3. Elle est basée sur les vecteurs d’efforts et de rémunérations qui permettent aux acteurs d’obtenir, à chaque période, les gains et . Précisément, les perceptrons d’équilibres spécifient pour l’agent de produire les efforts si le principal obtient en moyenne moins que son gain cible et 0 sinon, et pour le principal, de verser la rémunération si l’estimation du gain de l’agent est inférieure à son gain cible et 0 sinon. Pour le cas Z = 1, l’intui-tion géométrique est similaire à celle de la figure 8.
Perceptrons et coût de complexité
Cho et Li [1999] examinent un jeu répété à deux joueurs dans lequel chaque joueur choisit un perceptron d’une taille quelconque pour implémenter sa stra-tégie. Comme dans le modèle de Rubinstein [1986], les auteurs introduisent un coût de complexité défini par le nombre de classificateurs du perceptron. Les préférences sont lexicographiques : un joueur maximise d’abord son gain moyen puis minimise la taille (la complexité) de son perceptron. Cette procédure se traduit en termes de complexité par le fait qu’un joueur peut supprimer tout clas-sificateur qui ne permet pas de procéder à une séparation plus fine du plan dans
sans subir une perte de gain.
Une autre hypothèse du modèle de Cho et Li [1999] est que les joueurs envi-sagent la possibilité que des perturbations interviennent dans le déroulement du jeu. Le perceptron de chaque joueur commet des erreurs d’implémentation qui entraînent la dynamique du jeu hors du chemin d’équilibre. Il est peu probable qu’un joueur dont la rationalité est limitée puisse anticiper toutes les histoires futures engendrées par ces perturbations. Chaque joueur est conscient des limites de sa machine et de celle de son opposant et a donc intérêt à choisir un perceptron qui lui procure le gain moyen d’équilibre compte tenu de ces perturbations. Cette hypothèse permet à Cho et Li [1999] d’introduire le concept solution d’équilibre
de Nash localement stable. Pour chaque profil d’actions et toute paire de perceptrons , les auteurs font l’hypothèse qu’il existe une fonction
L’ensemble désigne le voisinage de rayon de la fonction résumée f, et est défini par :
.
Un équilibre de Nash est localement stable si tel que
, et tels que et , les deux
conditions suivantes sont vérifiées :