BAHAN AJAR I
SESI/PERKULIAHAN KE : 1
TPU : Setelah mengikuti matakuliah Teori Statistika I, mahasiswa dapat memahami konsep dasar teori statistika
TPK : Pada akhir pertemuan ini mahasiswa diharapkan dapat mengingat kembali dasar-dasar kalkulus
Pokok Bahasan : Dasar-Dasar Kalkulus
Deskripsi Singkat : Dalam Pertemuan ini Anda akan diingkatkan kembali mengenai dasar-dasar kalkulus yang akan sangat berguna saat memahami Teori Statistika I
I. Bahan Bacaan Wajib (BW)
1. Casella, G & Berger, R.L. 2002. Statistical Inference. Second Edition. Duxbury.
2. Hog and Craig, 1978. Introduction to Mathematical Statistics Callier Macmillon Publisher, London
3. Mendenhall at. All, 1989. Mathematical Statistics With Applications, University of Florida. Boston.
4. Mursita, D. 2007. Matematika Dasar Untuk Perguruan Tinggi. Bandung : Rekayasa Sains. Purcell, E.J & Varberg, D.1989. Kalkulus dan Geometri Analitis. Edisi Bahasa Indonesia. Jakarta : Erlangga
5. Tobing, H (Alm), & Siregar, P. Pengantar Statistika Matematis. Jurusan Statistika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Padjadjaran Bandung.
II. Pertanyaan Kunci
Ketika anda membaca bahan bacaan berikut, gunakanlah pertanyaan-pertanyaan berikut ini untuk memandu anda :
2. Turunan
3. Rungsi Transenden 4. Teknik Pengintegralan 5. Barisan dan Deret
TINJAUAN MATA KULIAH
Pendahuluan
Dalam memahami teori statistika I, sangat penting bagi mahasiswa untuk mengingat kembali pelajaran Kalkulus I dan II yang meliputi fungsi real, turunan, rungsi transenden, teknik pengintegralan, barisan dan deret.
1.1 Fungsi Real Sistem Bilangan Real
Bilangan real, dinotasikan dengan memainkan peranan yang sangat penting dalam kalkulus. Sifat-sifat yang dimiliki bilangan real adalah sifat TRIKOTOMI, yaitu bila ada dua bilangan real a dan b, maka hanya berlaku salah satu dari tiga sifat berikkut :
1. a = b atau 2. a < b atau 3. a > b
Definisi I- 1
Misalkan a dan b bilangan real, maka
1. a < b berarti b - a merupakan bilangan real positif 2. a b berarti bahwa a < b atau a = b
3. a b beratti bahwa a > b atau a = b
Berikut sifat pertidaksamaan dari bilangan real yang sangat fundamental dan sering digunakan :
1. Bila a < b dan b < c maka a<c
-a b
3. Bila a < b dan c < d maka a + c < b + d 4. Bila a < b dan c > 0 maka ac < bc 5. Bila a < b dan c < 0 maka ac > bc
6. Bila a dan b keduanya bilangan real positif atau negatif dan a < b maka
1 1
a b
Secara geometri, bilangan real dapat digambarkan sebagai garis bilangan dengan notasi interval diberikan dengan R =(-,). Sedangkan himpunan bagian dari bilangan real (garis bilangan) berupa segmen garis atau interaval yang dapat dieklompokkn menjadi :
1. Interval tutup, dinotasikan dengan […,...] 2. Interval buka, dinotasikan dengan (….,…)
3. Interval setengah buka/setengah tutup dinotasikan dengan [….,…) atau (…,…]
Selengkapnya kemungkinan interval yang ada pada sebuah garis bilangan bila diberikan dua buah bilangan sembarang a dan b dinyatakan sebagai berikut :
Gambar I- 1 : Bilangan dan Himpunan
[ a, b ] = { x | a x b } ( a, b ) = { x | a < x < b } [ a, b ) = { x | a x < b } ( a, b ] = { x | a < x b } ( b, ) = { x | x > b } [ b, ) = { x | x b } ( -, a ) = { x | x < a } ( -, a ] = { x | x a }
Pertidaksamaan
Permasalahan matematika yang berkaitan dengan interval terletak pada pertidaksamaan aljabar. Himpunan jawab atau solusi dari pertidaksamaan alajabar merupakan salah satu dari bentuk interval di atas. Adapun penjelasannya diberikan berikut :
-a b c
(+) (-) (+) (-)
( ) ( ) ( ) ( ) A x C x B x D x
Dengan A(x), B(x), C(x), dan D(x) : suku banyak (tanda < dapat digantikan oleh , , >)
Sebagai gambaran diberikan perdiksamaan
2 3
1 1
x x
x x
. Maka pertidaksamaan terdiri dari suku banyak A(x) = x -2; B(x) = x -1; C(x) = x + 3 dan D(x) = x + 1 Himpunan bilangan real x yang memenuhi pertidaksamaan disebut himpunan penyelesaian atau solusi pertidaksamaan.
Cara mencari solusi pertidaksamaan aljabar dilakukan sebagai berikut :
1. Nyatakan pertidaksamaan sehingga didapat salah satu ruasnya menjadi nol. Misalkan ruas kanan di buat menjadi nol maka didapat
( ) ( ) 0 ( ) ( ) A x C x B x D x
2. Sederhanakan bentuk ruas kiri menjadi satu suku misalkan ( )
0 ( ) P x Q x
3. Cari dan gambarkan pada garis bilangan semua pembuat nol dari P(x) dan Q(x)
4. Tentukan setiap tanda ( + atau - ) pada setiap intervalyang terjadi dari garis bilangan di atas. Misalkan pembuat nol dari P(x) dan Q(x) berturut-turut dari kecil ke besar adalah a, b, dan c, maka interval pada garis bilangan digambarkan berikut :
Gambar I- 2 : Bilangan Untuk Pertidaksamaan 5. Interval dengan tanda (-) merupakan solusi pertidaksamaan
Contoh I- 1
Misalkan diketahui pertidaksamaan sebagai berikut :
2 3
1 1
x x
x x
--1 1/3 1
(+) (-) (+) (-)
Penyelesaian
2 2
2 3 2 3 ( 2)( 1) ( 3)( 1)
0 0
1 1 1 1 ( 1)( 1)
2 2 ( 3 3) 3 1
0 0
( 1)( 1) ( 1)( 1)
x x x x x x x x
x x x x x x
x x x x x x x
x x x x
� � �
�
Pembuat nol dari pembilang dan penyebut adalah -1, 1/3 dan 1. Pada garis bialgan didapatkan nilai pada setiap selang, yaitu :
Gambar I- 3 : Bilangan Untuk Pertidaksamaan Contoh I-1 Himpunan penyelesaian (solusi) pertidaksamaan adalah (-, -1) (1/3, 1)
Pertidaksamaan dengan Nilai Mutlak
Secara geometris, nilai multak atau nilai absolute dari bilangan real x didefinisikan sebagai jarak dari x terhadap 0, sehingga nilai mutlak dari setiap bilangan selalu bernilai positif. Notasi yang digunakan adalah :
; 0
| |
; 0
x x x
x x
� �
�
�
Bila diberikan bentuk nilai mutlak | x -2 | maka dapat dituliskan menjadi :
( 2) ; 2
| 2 |
2 ; 2
x x
x
x x
�
�
�
�
Sehingga bentuk nilai mutlak dapat diperumum menjadi
; /
| | ; 0
; /
ax b x b a
ax b a
ax b x b a
�
�
� �
�
Sifat-sifat nilai mutlak
1. | |x x2
2. | |x a� a x a
a b c d
1 2 3 4
a b c d
1 2 3 4
A B
f
A B
f 4. |x y | | | | |�x y (ketidaksamaan segitiga)
5. |xy| | || | x y
6.
| | | | x x y y
7. | | | |x y � x2 y2
Fungsi dan Grafik
Pembahasan menganai fungsi tidak bisa dilepaskan dari masalah pemetaan atau pengaitan. Suatu pengaitan f dari himpunan A ke himpunan B disebut fungsi bila mengaitkan setiap anggota dari himpunan A dengan tepat satu anggota dari himpunan B. Hal ini diperlihatkan seperti gambar 1.4 di bawah ini :
Gambar I- 4 : Fungsi
Himpunan A disebut domain atau daerah asal dari fungsi f dinotasikan dengan Df,
sedangkan himpunan B disebut kodomain dari fungsi f. Bila semua elemen dari himpunan B yang merupakan pasangan dari elemen dari himpunan A dihimpun maka akan didapatkan himpunan yang merupakan sub himpunan atau humpunan bagian dari himpunan B yang dinamakan Range atau daerah hasil dari fungsi f. Notasi untuk range dari fungsi adalah Rf
a b c d
1 2 3 4
a b c d
1 2 3 4
A B
g
A B
h
X Y
Gambar I- 5 : Bukan Fungsi
Misalkan himpunan A dan B merupakan sub himpunan dari himpunan bilangan real (A dan B ). Maka fungsi f yang memetakan dari himpunan A ke himpunan B dapat dinyatakan dengan
f : A B x | f(x) = y
Daerah hasil atau range dari fungsi f dinyatakan dengan Rf = {y|f(x) = y, x A}.
Nampak bahwa setiap anggota range dari fungsi f(x) juga merupakan anggota dari B sehingga Rf B
Fungsi Bernilai Mutlak
Bentuk fungsi bernilai mutlak dinyatakan oleh f(x) = |x|. Grafik fungsi f(x) simetris terhadap sumbu Y dan terletak di atas dan atau pada sumbu X seperti terlihat pada Gambar 1.6
Hal ini menunjukkan bahwa f(x) 0 untuk setiap xDf, sehingga domain dari f(x)
adalah Rf=[0,)
Secara umum fungsi bernilai multak dapat dinyatakan oleh ( ) ;
( ) | ( ) | ;
( ) ;
c f
c g x x A
f x g x D A A
g x x A
� �
� �
�
�
Yang dapat disimpulkan dari fungsi bernilai mutlak adalah selalu memunya Range [0,)
Contoh I- 2
Tentukan nilai x agar fungsi f(x) = |x2 + 1| terletak di bawah garis y=2
Penyelesaian
Dicari nilai x yang memenuhi pertidaksamaan , f(x) = |x2+1|< 2. Menggunakan
sifat pertidaksamaan nilai multak
2 2 2 2 2
|x 1| 2�(x 1) 4�(x 3)(x 1) 0.
Dikarenakan (x2 + 3) definit positif atau selalu bernilai positif untuk setiap
bilangan real x maka x2 – 1 < 0. Sehingga nilai x yang memenuhi adalah -1< x < 1
atau |x| < 1
Fungsi Genap dan Fungsi Ganjil
Fungsi f(x) disebut fungsi genap bilai f(x) = f(-x) untuk setiap x di domain f(x) ( grafik f(x) simetris terhadap sumbu y).
Fungsi f(x) disebut fungsi ganjil bila f(x) = -f(-x) untuk setiap x di domain f(x) ( Grafik f(x) simetris terhadap titik pusat atau pusat sumbu).
Bila suatu fungsi bukan merupakan fungsi genap, belum tentu merupakan fungsi ganjil.
Tabel I- 1 : Sifat Fungsi Gendap dan Ganjil
f(x) g(x) f(x)g(x) f(x)/g(x)
Genap Genap Genap Genap
Genap Ganjil Ganjil Ganjil
y=f(x)
a L=K
X Y
Ganjil Ganjil Genap Genap
Limit dan Kekontinuan
Pengertian dan notasi dari limit suatu fungsi, f(x) di suatu nilai x = a diberikan secara intuitif menggunakan bantuan gambar berikut :
Gambar I- 7 : Limit
Bila nilai f(x) mendekati L untuk nilai x mendekati a dari arah kanan maka dikatakan bahwa limit fungsi f(x) untuk x mendekati a dari kana (x a+) sama
dengan L dan dinotasikan lim ( )
x a� f x L (1.1)
Bila nilai f(x) mendekati K untuk nilai x mendekati a dari arah kiri maka dikatakan bahwa limit fungsi f(x) untuk x mendekati a dari arah kiri (x a-) sama
dengan K dan dinotasikan lim ( )
x a� f x K (1.2)
Bila L = K maka dikatakan bahwa limit fungsi f(x) untuk x mendekati a (x a) sama dengan L (nilai limit dari f(x) di x = a ada dan sama dengan L dan dinotasikan
lim ( )
x a� f x L (1.3)
y=f(x)
a L=K
f(a)
dikatakan ada bila nilai limit sepihaknya sama atau nilai limit kana (1.1) sama dengan nilai limit kiri (1.2). Dari keberadaan limit fungsi, nilai limit fungsi f(x) di x = a tidak selamanya sama dengan fungsi f(x) di x = a atau f(a). Gambar 1.8 berikut menunjukkan nilai limit dari fungsi f(x) di x = a ada namun tidak sama dengan f(a)
lim ( ) ( )
x a� f x L�f a
Gambar I- 8 : Limit
Ketidakberadaan limit fungsi f(x) di titik x =a sebab nilai limit kana dari f(x) di x = a tisak sama dengan nilai limit kiri dari f(x) di x =a, diperlihatkan pada Gambar 1.9 berikut :
Gambar I- 9 : Limit
y = f(x)
a K
L = f(a)
Gambar I-9 memperlihatkan nilai limit dari f(x) di x mendekati a dari arah kiri
sama dengan nilai fungsi f(x) di x = a, x alim ( )� f x f a( )
Gambar I- 10 : Limit
Gambar I-10 memperlihatkan nilai limit dari f(x) di x mendekati a dari arah kanan
sama dengan nilai fungsi f(x) di x = a, x alim ( )� f x f a( )
Gambar I- 11 : Limit
y = f(x)
a L
f(a) =K
y = f(x) a
L f(a)
K
X Y
Y
Gambar I-11 memperlihatkan bahwa nilai limit kanan maupun nilai limit kiri tidak sama dengan nilai fungsi f(x) di x = a
Kesimpulan yang dapat diambil dari penjelasan tentang lmit di atas adalah 1. Nilai limit sebuah fungsi di suatu titik bisa ada dan tidak ada
2. Bila nilai limit sebuah fungsi ada maka ada dua kemungkinan yaitu nilai limit sama dengan nilai fungsi dan nilai limit tidak sama dengan nilai fungsi
Dalam perhitungan limit dari fungsi f(x) di x = a dilakukan dengan mensubstitusikan nilai x =a terhadap fungsi f(x) namun sebetulnya nilai yang dimaksud adalah nilai pendekatan.
Sifat –sifat limit
Misalkan lim ( )x�a f x Ldan lim ( )x a� g x G, maka 1. lim[ ( )x a� f x g x( )] L G
2. lim[ ( )x a� f x g x( )] L G 3. lim[ ( ) ( )]x a� f x g x L G
4. lim[ ( ) / ( )]x a� f x g x L G bila G/ , �0 5. lim ( ) lim ( )
n
n n
x a� f x x a� f x L untuk L > 0 bila n genap
Kekontinuan Fungsi
Fungsi f(x) dikatakan kontinu pada suatu titik x = a bila nilai limit f(x) pada x mendekati a sama dengan nilai fungsi di x = a atau f(a). Seara lebih jelas, f(x) dikatakan kontinu di x =a bila berlaku :
1. f(a) terdefinisi atau f(a)
y
b P
Q y = f(x) Y
Bila minimal salah satu dari persyaratan di atas tidak dipenuhi maka f(x) dikatakan tidak kontinu atau diskontinu di x =a dan titik x = a disebut titik diskontinu. Secara geometris, grafik fungsi kontinu tidak ada loncatan atau tidak terputus. Bilamana kita menggambarkan suatu fungsi grafik fungsi sembarang dengan menggerakkan pensi kita di atas kertas dan tanpa pernah mengangkat pensil tersebut sebelum selesai maka akan kita dapatkan fungsi kontinu.
Contoh I- 3
Selidiki apakah fungsi
2
2 1 ; 1
( )
2 3
; 1
1
x x
f x
x x
x x
�
� �
� �
�
�
�
Penyelesaian
Untuk menentukan nilai fungsi di x = -1 maka digunakan rumus fungsi f(x) = 2x-1 sehingga nilai fungsi f(x) di x = -1 yaitu f(-1) = -3. Kemudian limit sepihak ditentukan sebagai berikut :
2
1 1 1 1
2 3 ( 1)( 3)
lim ( ) lim lim lim ( 3) 4
1 1
x x x x
x x x x
f x x
x x
� � � �
dan
xlim ( )�1 f x xlim (2�1 x 1) 3
Sebab nilai limit kanan tidak sama dengan nilai limit kiri maka nilai limit fungsi f(x) di x = -1 tidak ada. Jadi fungsi tidak kontinu (diskontinu) di x = -1 atau dapat dikatakan bahwa x = -1 merupakan tidak diskontinu dari f(x)
1.2 Turunan Fungsi
Gambar I- 12 : Turunan Fungsi Gradien garis PQ dapat dinyatakan dengan :
( ) ( ) PQ
y b f x f a m
x a x a
Bila titik Q digerakkan sehingga berimpi dengan P maka x akan mendekati a ( x – a 0) dan f(x) mendekati f(a) ( f(x) – f(a) 0) serta garis PQ akan merupakan garis singgung kurva f(x) di titik P. Adapun gradient garis sehinggung PQ dinyatakan dengan :
( ) ( ) lim
x a
f x f a m
x a �
Definisi I- 2 Turunan
Turunan dari fungsi f(x) di titik x =a didefinisikan sebagai gradien dari garis singgung kurva f(x) di x = a dan diberikan :
( ) ( ) '( ) lim
x a
f x f a f a
x a �
Bila nilai limit ada maka f(x) dikatakan deferensiabel atau dapat diturunkan di x=a Misal h = x – a, maka turunan f(x) di x = a dapat dituliskan :
0
( ) ( )
'( ) lim h
f a h f a f a
h �
Notasi lain
( ) ( )
'( ) df a dy a '( )
f a y a
dx dx
( ) ( ) dV a A a
dx
Teorema I- 1
Bila y = f(x) diferensiabel di x = a maka y = f(x) kontinyu di x = a.
Teorema tersebut tidak berlaku sebaliknya, yaitu ada fungsi yang kontinu tetapi tidak diferensiabel.
Hal ini ditunjukkan oleh contoh berikut :
Contoh I- 4
Tunjukkan bahwa f(x) kontinu di x = 0 tetapai tidak diferensiabel di x = 0 Penyelesaian
Fungsi f(x) kontinu di x = 0, sebab f(0) lim ( ) 0x�0 f x
Turunan f(x) di x = 0 dicari menggunakan rumus berikut :
0 0
(0 ) (0) ( )
'(0) lim lim
h h
f h f f h
f
h h
� �
Karena 0 0
| | | |
1 lim lim 1
h h
h h
h h
� �
�
maka f(x) = |x| tidak diferensiabel di x = 0 Seperti bagaimana pengertian dari keberadaan limit fungsi ( limit kiri =limit kanan) dan kekontinuan fungsi (kontinu kana dan kontinu kiri) , dapat juga diturunkan suatu pengertian diferensiabel kanan dan diferensiabel kiri.
Definisi I- 3
Misalkan fungsi f(x) diferensiabel di x = a, dapat didefinisikan :
Diferensiabel kanan
'
0
( ) ( )
( ) lim h
f a h f a f a
h
�
, dan
Diferensiabel kiri
'
0
( ) ( )
( ) lim h
f a h f a f a
h
�
Kekontinuan suatu fungsi merupakan syarat perlu dari suatu fungsi yang diferensiabel. Artinya untuk menunjukkan bahwa suatu fungsi diferensiabel di suatu titik maka fungsi tersebut harus kontinu di titik tersebut. Selanjutnya diperiksa apakah nilai diferensiabel kanan sama dengan diferensiabel kiri. Jadi syarat yang harus dipenuhi agar fungsi f(x) diferensiabel di x = a adalah
Fungsi f(x) kontinu di x = a, yaitu f a( ) lim ( )x a� f x
Turunan kiri di x = a sama dengan turunan kana di x =a, yaitu
'( ) '( )
f a f a
Penjelasan di atas dinyatakan dalam teorema berikut : Teorema I- 2
Misalkan fungsi f(x) kontinu di x – a dan kedua limit berikut ada,
0
( ) ( )
lim h
f a h f a h
�
dan 0
( ) ( )
lim h
f a h f a h
�
. Fungsi f(x) diferensiabel di x = a jika dan hanya jika nilai kedua limit ada. Selanjutnya nilai turunan dari fungsi f(x)
di x =a dinyatakan dengan 0 0
( ) ( ) ( ) ( )
'( ) lim lim
h h
f a h f a f a h f a f a h h � � Rumus Turunan
Untuk menentukan turunan suatu fungsi sangat sulit bilamana harus digunakan definisi formal di atas, namun akan lebih mudah digunakan rumus –rumus berikut:
1.
1
( )r r d x rx dx
; x
2.
[ ( ) ( )] [ ( )] [ ( )] d f x g x d f x d g x
dx dx dx
3.
[ ( ) ( )] [ ( )] [ ( )]
( ) ( )
d f x g x d f x d g x
g x f x
dx dx dx
4. 2
[ ( ) / ( )] ( ) [ ( )] ( ) [ ( )] ( )
d f x g x g x d f x f x d g x
dx g x
Teorema I- 3 Rantai
Untuk mendapatkan turunan fungsi kompoisi dapat dilakukan dengan cara mencari bentuk eksplisit dari hasil koposisi fungsi. Namun dapat juga dicari dengan cara langsung mengunakan metode atau aturan rantai.
Misalkan diberikan fungsi komposisi y = f(u(x)), maka turunan pertama terhadap x yaitu
[ ( )]
[ ( )]'[ ( )] '( ) ( )
d f u x
dy d u x
f u x u x dx du x dx
Bila y = f(u) dengan u = v(x) maka rurunan pertama y terhadap x dicari
( )
( ( )) ( ( ))'( ) '( ) '( ) d f u
dy d u v d v x
f u u v v x dx du dv dx
Metode penurunan di atas dikenal dengan teorema rantai.
Contoh I- 5
Carilah turunan pertama dari y = (2x – 3)10
Penyelesaian
10
9 9
(2 3) (2 3)
10(2 3) (2) 20(2 3) (2 3)
d x
dy d x
x x
dx d x dx
Turunan Tinggkat Tinggi
Turunan kedua dari fungsi f(x) didapatkan dengan menurunkan sekali lagi bentuk turunan pertama. Demikian seterusnya untuk turunan ke-n di dapatkan dari penurunan bentuk turunan ke-(n-1)
Turunan pertama
( ) '( ) d x f x
dx
Turunan kedua
2 2
( ) "( ) d x f x
Y
X y = f(x) f(b)
f(c) f(d)
d c
a b O
g
e Turunan ke-n
( )n ( ) n( ) n d x f x
dx
Kemonotonan dan Kecekungan Kurva
perhatikan Gambar I-13, diperlihatkan bahwa grafik y = f(x) monoton naik pada selang / interval (a, b) atau (c, d), sedangkan grafik fungsi y = f(x) monoton turun pada selang / interval (b,c).
Gambar I- 13 : Turunan Fungsi
Definisi I- 4
Misalkan diberikan kurva y = f(x) dan selang/ interval l yang terletak pada domain y = f(x) maka,
Grafik fungsi f(x) dikatakan Monoton Naik pada selang l bila f(x1) > f(x2)
f(x2) f(x1)
x1 x2
f(x2) f(x1)
x1 x2
Grafik fungsi f(x) dikatakan Monoton Turun pada selang l bila f(x1) < f(x2)
untuk x1 < x2 ; x1,x2 l
a. Fungsi Naik b. Fungsi Turun f(x1) < f(x2) bila x1 < x2 f(x1) > f(x2) bila x1 < x2
Gambar I- 14 : Fungsi Naik dan Fungsi Turun Definisi I- 5
Misalkan diberikan fungsi y = f(x) dan selang / interval l yang memuat x =a, maka
Nilai f(a) disebut nilai (esktrim) maksimum pada selang / interval l bila f(a) > f(x) untuk setiap x l. Titik dengan koordinat (a, f(a)) dinamakan titik maksimum dari fungsi y = f(x)
Nilai f(a) disebut nilai (esktrim) minimum pada selang / interval l bila f(a) < f(x) untuk setiap x l. Titik dengan koordinat (a, f(a)) dinamakan titik minimum dari fungsi y = f(x)
Untuk menentukan jenis nilai esktrim (maksimum atau minimum( dari fungsi dapat dilakukan dengan uji turunan kedua sebagai berikut :
1. Tentukan turunan pertama dan kedua, f’(x) dan f’’(x)
2. Tentukan titik stasioner yaitu pembuat nol dari turunan pertama (f’(x) = 0), misalkan nilai statisioner x =a
Titik Belok
Misalkan diberikan fungsi y = f(x) maka syarat perlu x = b merupakan absis dari titik belok bila berlaku :
1. f’’(b) = 0
2. f(x) tidak diferensiabel dua kali di x = b
Definisi I- 6 Titik Belok
b
a X
Y
y = f(x)
( )
kf X
k
X
Xk Xk-11.3 Integral
Integral Tak Tentu
Fungsi F(x) disebut anti turunan dari f(x) pada selang l bila F’(x) = f(x) untuk setiap x l. Bila x merupakan titik ujing dari selang l maka F’(x) cukup turunan sepihak (turunan kana atau turunan kiri). Prosesa mencari anti turunan disebut integrasi (integral). Notasi yang digunakan untuk menyatakan integral
( ) ( )
f x dx F x C
�
. Bentuk integral ini disebut integral tak tentu.Integral Tentu
Pandang suatu fungsi f(x) yang didefinisikan pada suatu selang tutup [a, b]. pada
Gambar I- 15 : Konsep Integral Tentu
Pandang suatu partisi P pada selang [a, b] yang dibagi menjadi n sub selang (dalam hal ini diambil yang panjangnya sama walaupun hal ini tidaklah mutlak), misalnya a = x0 < x1 < … < xn = b dan xk x xk xk1. Pada setiap sub selang
1
[xk , ]xk kita ambil suatu titik xk ( titik sembarang namun untuk memudahkan
dipilih titik tengah sub selang) yaitu
1
2 k k k
Partisi yang terbentuk merupakan segiempat dengan ukuran x dan f x( )k sebagai panjang lebarnya, sehingga luas setiap partisi adalah f x( )k x. Oleh
karena itu didapat jumlah luas partisi pada selang [ a, b] yaitu 1
( ) n
k k
f x x
�
. Jumlah tersebut dinamakan jumlah Riemann untuk f(x) yang bersesuaian dengan partisi P. Maka luas daerah yang dibatasi oleh y = f(x), garis x =a, garis x = b dan sumbu X akan didekati oleh Jumlah Riemann di atas bila diambil n . Dari sini dapat didefinisikan suatu Integral Tentu yaitu integral f(x) pada suatu selang [a,b] berikut.
Definisi I- 7 Titik Belok
Misalkan fungsi f(x) kontinu pada selang [a, b], k
b a
x x
n
, lebar partisi
dari [a, b], a = x0, b = xn,
1
2 k k k
x x x
, maka integral dari f(x) atas [a, b] didefinisikan sebagai limit jumlah Riemann yaitu :
0 1 1
( ) lim ( ) lim ( )
b n n
k k
x k n k
a
f x dx f x x f x x
� ��
�
�
�
Bila limit ada maka fungsi f(x) dikatakan itegrabel (dapat diintegralkan) pada [ a, b ]. Integral ini disebut integral Riemann atau integral Tentu.
Teorema I- 4
1. Misalkan fungsi f(x) terbatas pada selang [a,b] (yaitu terdapat M sehingga |f(x)| M untuk setiap x [a, b]) dan fungsi f(x) kontinu kecuali pada sejumlah hingga titik pada [a, b]. Maka fungsi f(x) integrabel pada [a,b]
Teorema I- 5 Teorema Dasar Kalkulus I
Misalkan f(x) kontinu pada [a,b] dan fungsi F(x) adalah anti turunan dari fungsi
f(x), maka berlaku
( ) ( ) ( )
b
a
f x dx F b F a
�
Teorema I- 6 Teorema Dasar Kalkulus II
Misal fungsi f(x) kontinu pada [a, b], maka terdapat c (a, b) sehingga berlaku
( ) ( )( )
b
a
f x dx f c b a
�
Teorema ini disebut juga teorema nilai rata-rata integral dengan f(c) merupakan nilai rata-rata integral dari fungsi f(x)
Contoh I- 6
Tentukan nilai rata-rata fungsi f x( )x 2x21 pada selang [0, 2]
Penyelesaian
Misalkan u = 2x2 + 1, maka du = 4 dx. Bila x = 0 da x = 2 maka berturut-turut u =
1 dan u = 9 jadi
Rata-rata =
9
2 9
2
1
0 1
1 1 1 9 1 13
( ) 2 1
2 8 12 4 12 6
f x
�
x x dx�
udu u u Sehingga kalo dihitung nilai dari
2 2 0
13 13
2 1 (2 0)
6 3
x x dx
�
Sifat-sifat Intergral Tentu :
1.
[ ( ) ( )] ( ) ( )
b b b
a a a
pf x qg x dx pf x dx qg x dx
�
�
�
2. Misal fungsi f(x) kontinu pada [a, b] dan f(x) 0 untuk x [a, b], maka
berlaku
( ) 0
b
a
3. Misalkan fungsi f(x) kontinu pada [a,b] dan f(x) 0 untuk x [a,b], maka
( ) ( )
b b
a a
pf x dx� qg x dx
�
�
(sifat perbandingan)
4. Misalkan fungsi f(x) integrabel pada [a,b] dan berlaku m f(x) M
untuk x [a,b], maka m(b-a)
( ) ( )
b
a
f x dx M b a�
�
5.
( ) ( ) ( )
c b c
a a b
f x dx f x dx f x dx
�
�
�
6.
( ) 0 dan ( ) ( )
a b a
a a b
f x dx f x dx f x dx
�
�
�
7. Bila fungsi ganjil maka
( ) 0
a
a
f x dx
�
8. Bila fungsi genap maka 0
( ) 2 ( )
a a
a
f x dx f x dx
�
�
9. Bila fungsi periodic dengan periode p maka
( ) ( )
b p b
a p a
f x dx f x dx
�
�
10.
( )( )
( ) '( ) ( )
g b b
a g a
f g x g x dx f u du
�
�
Integral Bagian (Parsial)
Misalkan f(x) dan g(x) merupakan fungsi yang dapat diturunkan, maka dengan teorema rantai dapat diperoleh turunan dari hasil kali kedua fungsi yaitu,
( )
( )
[ ( ) ( )] ( )d g x ( )d f x d
f x g x f x g x
dx dx dx
( ) ( )
[ ( ) ( )] ( ) ( )
( ) ( )
( ) ( ) ( ) ( )
d g x d f x
d
f x g x dx f x dx g x dx
dx dx dx
d g x d f x
f x g x C f x dx g x dx
dx dx
�
�
�
�
�
Atau
( ) '( ) ( ) ( ) ( ) '( ) f x g x f x g x g x f x C
�
�
Karena integral pada kedua ruas akan meghasilkan konstanta C, maka dapat dituliskan sebagai berikut :
( ) '( ) ( ) ( ) ( ) '( ) f x g x f x g x g x f x
�
�
Misal
u = f(x) du = f’(x) dx v = g(x) dv = g’(x) dx
Substitusikan ke dalam rumus integral di atas didapatkan rumus integral bagian untuk integral tak tentu adalah :
udv uv vdu
�
�
Bila f(x) dan g(x) integrabel pada [a,b] maka rumus integral bilangan untuk integral tentu dapat dituliskan
b b
b a
a a
udv uv vdu
�
�
Contoh I- 7
Hitunglah integral berikut : a.
x xe dx
�
b. 1
ln e
dx
�
Penyelesaian a.
x xe dx
Dengan memisalkan u = x dan dv = ex dax maka didapatkan du = dx dan v
= ex sehingga penyelesaian integral tak tentu dengan metode integral
bagian sebagai berikut : ( )
x x x x x x
xe dx xd e xe e dx xe e C
�
�
�
b. 1 ln e dx�
Dengan memisalkan u = ln x, 1 du dx
x
dan dv = dx, v = x maka diperoleh solusi integral tak tentu
lnxdx x lnx dx x lnx x
�
�
Penyelesaian integral tertentu diperoleh sebagai berikut :
11
ln ln 1
e
e xdx x x x
�
Integral Tak Wajar
Bentuk integral ( ) b
a
f x dx
�
disebut Integral Tak Wajar , jika 1. Paling sedikit satu batas integrasinya tak berhingga atau
a.
( ) lim ( )
b b
a a
f x dx f x dx � � �
�
�
b.( ) lim ( ) b
b
a a
f x dx f x dx �
��
�
�
c.
( ) lim ( ) lim ( )
p b
a b
a p
f x dx f x dx f x dx � � � �� �
�
�
�
Bila limit pada ruas kana nada dan bernilai hingga, maka integral tak wajar disebut Konvergen ke nilai limit tersebut. Bila limit tidak ada atau nilainya menunju tak hingga maka integral tak wajar disebut Divergen.
1.4 Fungsi Logaritma dan Eksponen
Fungsi logaritma dan fungsi eksponen merupakan dua fungsi yang saling invers dan dinyatakan sebagai berikut :
y = blog x x = by ; x , b > 0
Sifat-sifat logaritma 1. blog 1 = 0
2. blog b = 1
3. blog ac = blog a+ blog c
4. blog a/c = blog a - blog c
5. blog ar = r blog a
6. blog a = clog a / clog b
Bilangan Natural
Bilangan natural dinotasikan dengan e dan didefinisikan sebagai
1/
0 0
lim(1 ) x lim(1 1/ )x 2,718...
x x
e x x
� �
Fungsi logaritma natural didefinisikan sebagai
1
1
ln ; 0
x
x dt x t
�
ln x = elog xTurunan fungsi logaritma natural :Dx[ ln x] = 1/x
Jadi secara umum :
1 1
[ln ] ln
x
du
D u du u C
u dx u
�
�
Eskponen Natural
Fungsi eksponen natural didefinisikan sebagai inverse dari logaritma natural dan dinotasikan sebagai berikut :
y = ex x = ln y
Sifat yang dapat diturunkan langsung dari definisi adalah 1. eln y = y , untuk setiap y > 0
Y
X 1
1
y = ln x y = ex
Turunan dan integral dari eskponen natural :
( )u u u u
x
du
D e e e du e C
dx
�
�
Misalkan a > 0 dan x . Didefinisikan : ax = ex ln a , maka
(i) ( ) (ln )
u u
x
du
D a a a
dx
(ii)
1 ln
u u
a du a C a
�
Misal y = alog x =
ln log
ln
a x
y x
a
Maka
1 ( log )
ln a
x
D x
x a
Jadi secara umum
1 ( log )
ln a
x
du
D u
u a dx
Grafik fungsi eksponen dan logarima natural diberikan sebagai berikut :
Gambar I- 16 : Fungsi Eksponen dan Logaritma Natural
Contoh I- 8
Carilah turunan dari
2 2 1
( ) x
f x e
Misalkan u = 2x2 – 1, maka f(x) = eu dan u’ = 4x. Jadi turunan pertama 2
2 1
4 x
df df du xe dx du dx
1.5 Barisan dan Deret Barisan Bilangan
Barisan bilangan tak hingga dedefinisikan sebagai fungsi dengan domain merupakan bilangan positif. Notasi yang biasanya digunakan adalah :
a : n
an n 1 a a1, ,....2 n B�
�
an merupakan suku barisan ke –n dan tiga buah titik setelah suku kedua
menunjukkan bahwa suku-suku barisan tersebut sampai tak hingga. Barisan bilangan tak hingga
an n 1�
disebut barisan konvergen ke L bila
lim n
n��a L, sedangkan bila limit tidak ada atau nilainya tak hingga maka barisan bilangan tak hingga
an n 1�
disebut barisan divergen.
Definisi I- 8 Barisan Monoton Barisan bilangan tak hingga
an n 1�
disebut :
(i) Monoton Naik bila an an+1
(ii) Monoton Turun bila an an+1
Deret Tak Hingga
Bentuk deret tak hingga dinyatakan dengan notasi sigma sebagai beriktu :
1 2
1
... ...
k k
k
a a a a
�
ak disebut suku-suku deret
Jumlah Deret
Misalkan Sn menyatakan jumlah parsial n suku pertama deret 1
k k a �
�
, maka dapat dinyatakan sebagai berikut :
S1 = a1
S2 = a1 + a2
………..
Sn = a1+a2+…+an = 1
n k k a
�
Barisan
Sn n 1�
disebut barisan jumlah parsial deret 1
k k a �
�
Misalkan
Sn n 1�
merupakan barisan jumlah parsial deret 1
k k a �
�
dikatakan deretkonvergen ke S dan S disebut jumlah dari derat k 1 k
a �
�
, dinotasikan dengan
1
k k S �a
�
. Sedangkan bila barisan
Sn n 1�
divergen maka 1
k k a �
�
dikatakan deret divergen dan tidak ada jumlahDeret Geometri
Bentuk deret geometri yaitu :
1 1 k k ar �
�
= a + ar + …+ark-1 + …. dengan a 0 dan r
merupakan rasio. Pandang jumlah parsial n suku petama deret geometri berikut : Sn = a + ar+…+arn-1
rSn = ar + ..+arn-1 +arn
1
1 n n a r S r Bila r = 1 maka Sn tidak terdefinisi. Sedang untuk | r| > 1 maka
lim n n��r �,
sehingga limn��Sn � atau barisan
Sn n 1�
divergen. Oleh karena itu, deret
1 1 k k ar �
�
divergen. Untuk | r| < 1 maka lim 0 n
n��r sehingga limn n 1 a S
r �� atau
barisan
Sn n 1�
konvergen ke 1 ;( 0) a
a
r �
. Jadi
1 1 k k ar �
�
konvergen ke
;( 0) 1
a a
r �
atau
1 1 k k ar �
�
= 1 ;( 0) a
a
r �
Deret Taylor dan Mac Laurin
Misalkan fungsi f(x) dapat diturunkan sampai k kali pada x = b, maka fungsi f(x) dapat diperderetkan menjadi menjadi deret kuasa dalam bentuk :
( ) 2 0 ( ) ''( ) ( ) ( ) ( ) '( )( ) ( ) ... ! 2! k k k
f b f b
f x x b f b f b x b x b
k �
�
Deret di atas disebut Deret Taylor dengan pusat x = b atau disebut deret polynomial Taylor pada x = b. Bila b = 0 maka disebut Deret Mac Laurin, yaitu berbentuk :
( )
2 0
(0) ''(0)
( ) (0) '(0) ...
! 2!
k k k
f f
f x x f f x x
k �
�
Contoh I- 9
Perderetkan fungsi f(x) = ex ke dalam deret Mac Laurin
Bila f(x) = ex maka turunan fungsi ke-n diberikan oleh f(n)(x) = ex dan nilai turunan
di x = 0 adalah f(n)(0) = 1. Oleh karena itu, deret Mac Laurin dari f(x) = ex yaitu :
2 3
0 0 0
0 2 3
2 3
0
'(0) ''(0) ''(0)
(0) ...
1! 2! 3!
....
1! 2! 3!
1 .... 2! 3! ! x k k
f f f
e f x x x
e e e
e x x x
x x x x k �
�
1.6 Latihan Soal
1.1 Selidiki apakah fungsi
2 ; 1
( ) 1
; 1
x x
f x diferensiabel di x x x � � � � � �
1.2 Carilah turunan
a. 1 ( ) f x x
b. f x( ) (2 x1) x
c. 2 1 ( ) 1 x f x x d. 2 1 1 x y x � � � � � �
1.3 Selesaikan integral berikut a.
2
(1 2 )10 x x x dx
�
b.
2 2
(x1)ex xdx
�
1.4 Penderetkan fungsi berikut ke dalam deret Mac Laurin
BAHAN AJAR II
SESI/PERKULIAHAN KE : 2-3
TPU : Setelah mengikuti matakuliah Teori Statistika I, mahasiswa dapat memahami konsep dasar teori statistika
TPK : Pada akhir pertemuan ini mahasiswa diharapkan dapat memahami konsep-konsep peluang dengan benar
Pokok Bahasan : Dasar-Dasar Peluang
Deskripsi Singkat : Dalam Pertemuan ini Anda akan diingkatkan kembali mengenai dasar-dasar peluang akan sangat berguna saat memahami Teori Statistika I
I. Bahan Bacaan Wajib (BW)
1. Casella, G & Berger, R.L. 2002. Statistical Inference. Second Edition. Duxbury.
2. Hog and Craig, 1978. Introduction to Mathematical Statistics Callier Macmillon Publisher, London
3. Mendenhall at. All, 1989. Mathematical Statistics With Applications, University of Florida. Boston.
4. Mursita, D. 2007. Matematika Dasar Untuk Perguruan Tinggi. Bandung : Rekayasa Sains. Purcell, E.J & Varberg, D.1989. Kalkulus dan Geometri Analitis. Edisi Bahasa Indonesia. Jakarta : Erlangga
II. Pertanyaan Kunci
Ketika anda membaca bahan bacaan berikut, gunakanlah pertanyaan-pertanyaan berikut ini untuk memandu anda :
Apa yang anda pahami menganai : 1. Peluang
A B
S S
A B
S
A B
TINJAUAN MATA KULIAH
P E L U A N G
2.1 Himpunan
Hipunan merupakan gabungan dari unsur-unsur yang bisa berupa apa saja baik benda, manusia ataupun bilangan. Unsur biasanya dituliskan dalam hurup kecil Yunani, himpunan biasanya dilambangkan dengan huruf besar latin, dan himpunan semesta dilambangkan dengan S. Himpunan biasanya ditulikan dalam kurung kurawal { }.
Kita akan mengunakan huruf besarA, B, C,…, untuk menyatakan himpunan titik. Jika di dalam himpunan A ada a, b, c, atau dengan notasi aA, bA, cA, kita dapat menulis A={a,b,c}. Selanjutnya a,b,c disebut unsur atau elemen himpunan.
Ambil S menyatakan himpunan semua unsur yang menjadi perhatian, yang disebut himpunan semesta.
Untuk setiap dua himpunan A dan B kita sebut bahwa A himpunan bagian dari B, atau A dikandung dalam B (dinotasikan AB ), jika setiap unsur di A juga merupakan unsur di B. Himpunan konsong dinotasikan dengan adalah himpunan yang tidak mengandung titik. Himpunan dan hubunan antara dua himpunan dapat digambarkan dengan menggunakan diagram Venn.
A B A B A B Gambar II- 1 Diagram Venn
Gabungan dari A dan B dinyatakan oleh A B, adalah himpunan semua titik dalam A atau B atau kedua-duannya. Yaitu, gabungan A dan B memuat semua titik yang ada di dalam paling sedikit satu dari himpunan tersebut.
Dengan notasi : A B={x|xA atau xB}
Irisan dari A dan B dinyatakan oleh A B, adalah himpunan semua titik dalam kedua-duanya A dan B.
Dengan notasi A B={x|xA dan xB}
Jika AS, maka komplemen A dinyatakan oleh A, adalah himpunan titik yang ada di S tetapi tidak di A.
Dengan notasi : A={x|xA dan xS}
A : Komplemen dari A A B Gambar II- 2 Diagram Venn Untuk A dan A B
Dua himpunan A dan B dikatakan lepas atau saling eksklusif jika AB= yaitu himpunan saing eksklusif, tetapi tidak mempunyai titik persekutuan. Perhatikan pelantuan sebuah dadu. Di sini S={1,2,3,4,5,6}.
Misalkan A={1,2}, B={1,3}, dan C={2,4,6} Maka AB={1,2,3}, AB={1}, dan A={3,4,5,6} Juga perhatikan bahwa BC= sedangkan AC
Ada dua kesamaan yang sungguh penting, ialah hukum distributif diberikan oleh: A ( B C ) = ( A B ) ( A C )
A ( B C ) = ( A B ) ( A C ) Contoh Operasi Himpunan
A = { 1, 2, 3 , 4, 5, 6, 7, 8, 9, 10 } S
A
A
S
B = { 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20 } C = { 15, 16, 17, …, 40 }
A B = { 1, 2, 3, …,10, 11, ….., 20 } A C = { 1, 2, 3, …, 10, 15, 16, …, 40 } A B = { 8, 9, 10 }
A C = { } = AC = { 11, 12, 13, ….}
Teorema II- 1
Misalkan A, B, C merupakan kejadian-kejadian dalam ruang contoh S : a. Komutatif AB = BA = A+B {x;xA atau xB}
AB = BA = A*B {x;xA dan xB} b. Asosiatif A(BC) = (AB)C = A+B+C
A(BC) = (AB)C = A*B*C
c. Distributif A(BC) = (AB)(AC) = (A+B)*(A+C) A(BC) = (AB)(AC) = A*B+A*C d. DeMorgan’s (AB)C = (ACBC) = AC* BC
(AB)C = (ACBC) = AC+ BC
Definisi II- 1
A dan B disebut terputus (disjoint or mutually exclusive) jika AB = . Kejadian A1, A2, …, Ai, … disebut himpunan saling terputus/saling asing (pairwise
disjoint) jika AiAj = untuk semua i ≠ j ; i = 1, 2, 3, …. dan j = 1, 2, 3, ….
Definisi II- 2
A1, A2, … , Ai,….. disebut sekatan (partition) dari himpunan
semesta S jika i=¿1
n
Ai=S
dan AiAj = semua i ≠ j dengan n
dapat mencapai nilai tak hingga ( n →)
Peluang sering dikatakan sebagai harapan terjadinya suatu kejadian dari hasil suatu tindakan. Peluang meliputi ruang contoh terbilang dan tidak terbilang. Di
A1
A2
bawah ini diperlihatkan kesepadanan antara Aljabar Himpunan dengan Peluang (Aljabar Kejadian )
HIMPUNAN PELUANG
(Aljabar Kejadian) Tindakan (Trial)/
Eksperimen Unsur (Element)/
Unit Pengamatan
(x) Peristiwa (Outcome)
Himpunan (Set) / Gabungan dari Unsur
(A) Kejadian (Event)
Himpunan Semesta
(Universum )/Himpunan meliputi semua unsur yang diperhatikan
“Ada Pembatasan”
(S) Ruang Contoh (Sample Space) / Himpunan hasil yang mungkin dari percobaan
Himpunan Kosong (Empty Set)/ Himpunan yang tidak ada anggotanya
() Kejadian Mustahil
(Impossible Event)
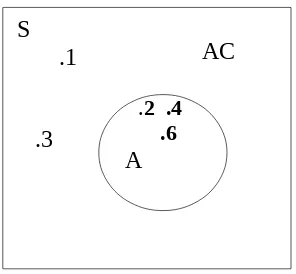
Contoh II- 1
Eksperimen : Pelantunan Sebuah Dadu
Tindakan : Pelembaran Sebuah Dadu bersisi 6 Peristiwa : Munculnya satu sisi dari hasil pelantunan Kejadian : Muncul sisi genap
A : Muncul sisi genap A={ 2, 4, 6 } AC: Muncul selain sis genap AC = { 1, 3, 5 }
Ruang Sampel : Semua peristiwa yang mungkin tejadi dari hasil tindakan S = { 1, 2, 3, 4, 5, 6 }
S .1
.3 .5
.2 .4 .6 A
[image:39.595.234.382.173.310.2]AC Diagram Venn kasus di atas.
Gambar II- 3 Diagram Venn Untuk A dan A Himpunan Bagian (Subset)
Jika setiap peristiwa dalam kejadian A adalah juga peristiwa dalam kejadian B, maka dikatakan A bagian dari B (A subset B). Operasi himpunan bagian biasanya dilambangkan dengan “ “ namun banyak buku yang melambangkan dengan “ “. Untuk lambang pertama “ “, misalkan A himpunan bagian B dapat ditulis A B. Dalam kasus ini unsur A < B. Sedangkan untuk lambang kedua misalkan A himpunan bagian B. Dalam kasus ini unsur A ≤ B, atau dengan kata lain A bisa lebih kecil dari B atau A sama dengan B.
2.2 Konsep Dasar Teori Peluang
Ketika eksperimen telah dilakukan, hasil dari percobaan menyatakan ruang sampel (sample space). Jika eksperimen dilakukan berulang-ulang kali, perbedaan hasil akan mungkin terjadi. Frekuensi dari kejadian tersebut akan dikaitkan dengan nilai peluang.
Untuk setiap kejadian A dalam ruang sampel kita ingin mengaitkan A dengan nilai antara 0 dan 1 yang akan kita kenal dengan nilai peluang dari A yang dinotasikan dengan P(A).
(B) (Sigma Algebra). Nilai yang diberikan pada kejadian mencerminkan harapan kita pada munculnya satu kejadian.
Definisi II- 3 Medan Borel (B)
Kumpulan subset (elemen) dari S disebut sebagai sigma algebra (Borel filed), dinotsikan dengan B jika memenuhi syarat berikut :
1. B
2. Jika kejadian A B maka AC B (B bersifat tertutup terhadap
komplementasi)
3. Jika A1, A2, …, An B maka 1
i i A
�
� �
� �
�U � B (B bersifat tertutup terhadap
operasi gabungan)
Himpunan kosong merupakan bagian dari semua himpunan sehingga S. Ini menyebabkan selalu anggota B ( B). Sebagai akibat dari (1) B
dan (2) C B dengan C = S maka S selalu anggota B (S B). Sebagai
tambahan, dengan Hukum DeMorgan’s dapat ditunjukkan bahwa B bersifat tertutup terhadap komplementasi. Jika A1, A2,… Bmaka 1, 2,...
c c
A A B dengan
menggunakan sifat (2), sehingga 1
c i i A
�
U
B. Dengan menggunakan hukum
DeMorgan’s diperoleh
1 1
c c
i i
i i
A A
� �
� �
� �
�
U
�I
Dengan menggunakan sifat (2) maka 1
i i
A �
I
B
Medan Borel (B) paling sederhana adalah Medan Borel yang hanya memuat kejadian mustahil dan himpunan semesta S
B = { , S }
Ruang Contoh (S) : Semua hasil yang mungkin dari pelantunan
S = { 1, 2, 3, 4, 5, 6 } Kejadian :
A: Muncul Sisi Genap A = { 2, 4, 6}
B : Muncul Sisi Ganjil B = { 1, 3, 5 }
: Kejadian Mustahil
Perhatikan himpunan B = { , A, B, S }
Jika himpunan B = { , A, B, S } memenuhi syarat Medan Borel (1), (2), (3) berarti himpunan B = { , A, B, S } dapat dikatakan sebagai Medan Borel (B).
Pengujian : Syarat 1 :
Himpunan B = { , A, B, S } memuat kejadian mustahil () dimana (
B) Terpenuhi Syarat 2 :
Bersifat tertutut terhadap komplementasi :
C = S. Terlihat S B
AC = B. Terlihat B B
B C = A. Terlihat A B
SC = . Terlihat B
Semua komplemen dari subset dalam himpunan B = { , A, B, S } masuk dalam himpunan B sehingga syarat 2 Terpenuhi
Syarat 3
Bersifat tertutup terhadap operasi gabunganA = A. Terlihat AB
B = B. Terlihat BB
AB = S. Terlihat SB
AB = S. Terlihat SB
ABS = S. Terlihat SB
Semua operasi union (penggabungan) masuk dalam himpunan B sehingga syarat 3 terpenuhi.
Contoh II- 3 (Himpunan Tidak Masuk Dalam Syarat Medan Borel)
Misalkan dalam Contoh II-2 di atas ditambah satu kejadian lagi yaitu kejadian C : Muncul Sisi Bernomor 5 atau lebih
C = { 5, 6 }
Apakah B *= {, A, B,C, S } merupakan Medan Borel ?
Pengujian : Syarat 1 :
Himpunan B*= {, A, B,C, S } memuat kejadian mustahil () dimana ( B*) Terpenuhi
Syarat 2 :
Bersifat tertutut terhadap komplementasi Misalkan CC = D.
C = S. Terlihat S B *
AC = B. Terlihat B B *
BC = A. Terlihat A B *
CC = D. Terlihat D B * atau CC B*
S C = . Terlihat B*
Terlihat bahwa dalam himpunan B* tidak memuat komplemen C yaitu D sehingga Syarat (2) tidak terpenuhi. Dapat disimpulkan B* bukan merupakan Medan Borel (B)
1. Jika S memiliki n anggota maka akan ada sebanyak 2n himpunan dalam
Medan Borel. Ini berakibat semua himpunan kejadian (2n) dimasukkan
dalam himpunan akan memenuhi syarat Medan Borel.
2. Memberikan nilai pada kejadian dan kejadian harus dalam ruang lingkup pembicaraan (memiliki batasan yang jelas) atau memenuhi ketiga syarat Medan Borel (B). Definisi ini memberikan gambaran bahwa untuk dapat menentukan nilai peluang suatu kejadian maka kejadian tersebut harus dalam ruang lingkup himpunan semesta S dan merupakan anggota Medan Borel (B) yang memenuhi ketiga syarat Medan Borel. Sehingga akibatnya jika kita mengetahui nilai pelungan kejadian A (P(A)) maka kita juga akan dapat mengetahui nilai pelung komplemen A (P(AC)).
2.3 Model Peluang Untuk Satu Percobaan Kasus Diskrit
Definisi II- 4 (Percobaan)
Suatu percobaan adalah proses yang mana suatu pengamatan dilakukan.
Contoh percobaan, antara lain, pelantunan mata uang dan dadu, mengukur skor IQ untuk suatu individu, atau penentuan jumlah bakteri per cm kubik dalam bagian pengolahan makanan. Apabila suatu percobaan dibentuk, percobaan itu dapat menghasilkan suatu atau lebih hasil yang disebut kejadian. Jika percobaan terdiri atas menghitung banyaknya bakteri dalam bagian makanan, beberapa kejadian diinginkan dapat dibuat antara lain :
A: Ada 40 bakteri
B: Ada lebih dari 200 bakteri
C: Banyak bakteri antara 100 dan 300
Definisi II- 5 (Kejadian Sederhana)
Suatu kejadian sederhana ialah suatu kejadian yang tidak dapat dipecah. Setiap kejaidan sederhana perbadanan dengan satu dan hanya satu titik sampel. Kejadian sederhana dalam pelantunan dadu satu kali.
E2: hasil angka 2
E3: hasil angka 3
E4: hasil angka 4
E5: hasil angka 5
E6: hasil angka 6
Definisi II- 6 (Ruang Sampel)
Ruang sampel yang dihubungkan dengan percobaan adalah himpunan yang terdiri atas semua titik sampel yang mungkin. Suatu ruang sampel akan dinotasikan dengan S
Dalam pelantunan sebuah dadu satu kali S={1,2,3,4,5,6}
Definisi II- 7 (Ruang Sampel Diskrit)
Ruang sampel diskrit adalah ruang sampel yang mengandung berhingga atau terhitung banyaknya titik sampel.
Untuk percobaan dengan ruang sampel diskrit, kejadian majemuk dapat dipandang sebagai himpunan titik sampel atau ekuivalen sebagai gabungan himpunan sederhana. Misalnya, pelantunan dadu kejadian A (pengamatan angka ganjil) akan terjadi jika dan hanya jika kejadian seerhana E1, E3 atau E5 terjadi.
Berarti A={ E1, E3, E5} atau A= E1 E3 E5
Sama halnya, B (pengamatan angka kurang dari 5) dapat ditulis sebagai B={E1,
E2, E3, E4} atau B=E1 E2 E3 E4
Kejadian sederhana Ei dimasukkan dalam kejadian A jika dan hanya jika A terjadi
bilamana Ei terjadi.
Definisi II- 8
Model peluang untuk percobaan dengan ruang sampel diskrit dapat dibentuk dengan menetapkan peluang terhadap setiap kejadian sederhana dalam ruang sampel S. Dalam melakukan demikian, kita akan memilih bilangan, suatu ukuran kepercayaan kita, dalam kemunculannya pada tindakan (ulangan) percobaan tunggal, sehingga hal itu akan konsisten dengan konsep frekuensi relatif untuk peluang. Meskipun frekuensi relatif tidak memetakan definisi yang tetap untuk peluang, suatu definisi yang dapat dipakai untuk dunia nyata setuju dengan faham intuisi kita, akan sifat dari frekuensi relatif kejadian.
Pada analisis konsep frekuensi untuk peluang, kita lihat bahwa tiga syarat harus dipenuhi, yaitu :
1. Frekuensi relatif akan kemunculan suatu kejadian harus lebih besar atau sama dengan nol (fr (Ai) 0)
2. Frekuensi relatif dari ruang sampel keseluruhan S harus menjadi satu. Karena setiap kemungkinan muncul dari percobaan adalah titk dalam S, titik itu menyertai bahwa S harus muncul setiap waktu percobaan
dibentuk.( 1
( ) 1 n
r i i
f A
�
)
3. Jika dua kejadian saling eksklusif, frekuensi relatif gabungan sama dengan jumlah frekuensi relatif masing-masing (fr (Ai Aj ) = fr (Ai) + fr (Aj) ; ij
Definisi II- 9
Andaikan percobaan telah dihubungkan dengan ruang sampel S. Terhadap setiap kejadian A di S (AS) kita menetapkan suatu bilangan P(A) disebut peluang A, sehingga aksioma berikut dipenuhi :
Aksioma 1 : P(A) 0 Aksioma 2 : P(S) =1
Aksioma 3 : jika A1, A2, A3,….. membentuk barisan kejadian yang saling eksklusif
berpasangan (AiAj = , ij) di S maka P(A1 A2 A3 …..) = P(A1) + P(A2)
+ P(A3) +…
Peluang suatu kejadian dalam ruang contoh S adalah suatu fungsi dengan Domain Medan Borel B yang memenuhi Aksioma/aturan peluang berikut :
1. Peluang kejadian A , P(A) 0 untuk A B
2. Peluang ruang semesta S, P(S) = 1 untuk S B
3. Jika A1, A2, …, An B dan Ai Aj = (tidak berpotongan/disjoint) untuk
setiap i j maka 1 1
( ) n
i i
i i
P A P A
�
� �
� �
�
U
��
Teorema II- 2
Jika P adalah fungsi peluang dengan domain Medan Borel B : a) P() = 0, dengan adalah himpunan kosong
b) P(A) ≤ 1, c) P(AC) = 1- P(A)
Bukti
a) P() = 0
( S) = S ( S) =
Aturan (3) karena S = P( S) = P() +P(S) P(S) = P() + P(S)
1 = P() + 1 (Aksioma 2) Sehingga P() haruslah sama dengan 0
b) AAC = S
A AC =
Aksioma (3) AAC =
P(AAC) = P(A) + P(AC)
S
A
B
ABC AB BAC
1 = P(A) + P(AC) (Aksioma 2)
Sehingga P(AC) = 1- P(A)
c) 0 ≤ P(A) ≤1
(AB)=S
Aksioma (3) karena A B = P(AB) = P(A) + P (B) P(S) = P (A) + P (B)
1 = P (A) + P (B) (Aksioma 2)
Karena P (A) 0 dan P (B) 0 dan P (A) ≤ 1 dan P (B) ≤1 sehingga akibatnya 0 ≤ P(A) ≤1
atau :
P(A) = 1 – P(AC)
P(AC) 0 Aksioma (1)
Sehingga P(A) ≤ 0 Akibatnya : 0≤ P(A) ≤ 1
Teorema II- 3
AB , BB dan P adalah “fungsi peluang” dengan domain Medan Borel B maka: a) P(BAC) = P(B) – P(AB)
b) P(AB) = P(A) + P(B)-P(AB) c) Jika AB maka P(A) ≤ P(B)
Bukti
a) P(BAC) = P(B) – P(AB)
B = (AB)( BAC)
Karena (AB)( BAC)= (Aksioma 3)
Maka :
P(B) = P(AB) + P(BAC)
P( BAC) = P(B) - P(AB)
S
A
B
ABC AB BAC
S
BAC
A
B
b) P(AB) = P(A) + P(B)-P(AB)
(AB) = A( BAC)
Karena A( BAC) = (Aksioma 3)
Maka
P(AB) = P(A) + P( BAC)
Dari (a) P( BAC) = P(B) - P(AB)
Sehingga :
P(AB) = P(A)+P(B)-P(AB)
c) Jika AB maka P(A) ≤ P(B) AB
B = A(BAC)
Karena A(BAC) = (Aksioma 3)
Maka :
P(B) = P(A) + P(BAC)
P(BAC) 0 Sehingga :
P(A) ≤ P(B)
Catatan :
P(AB) = P(A) + P(B) – P(AB) Terdapat dua Kasus :
Kasus I :
AB = P(AB) = 0
Aksioma (3) P(AB) = P(A) + P(B) Kasus II :
A = (ABC)(AB)
Aksioma (3) (ABC) (AB)=
P(A) = P(ABC)+P(AB)
P(ABC)= P(A)- P(AB) (*)
AB = B(ABC)
Aksioma (3) B (ABC)=
P(AB) = P(B)+P(ABC) (**)
Substitusi (*) ke (**)
P(AB) = P(B) + P(A)- P(AB)
Teorema II- 4
Jika P adalah fungsi peluang maka :
a)
P
(
A
)=
∑
i=1
∞
P
(
A
∩
C
i)
untuk setiap C1, C2 ....
b)
P
(
¿
i=1
∞
A
i)≤
∑
i=1
∞
P
(
A
i)
untuk setiap himpunan A1, A2, ...
(Ketaksamaan Booie)
Bukti :
a)
P
(
A
)=
∑
i=1
∞
P
(
A
∩
C
i)
untuk setiap C1, C2 ....
Karena C1, C2, ... adalah suatu bentuk partisi/sekatan maka Ci Cj =
untuk semua i j dan
S
=
i=¿
1∞
C
i. Sehingga
A
=
A
∩
S
=
A
∩
(
¿
i=1
∞
C
i)
=
¿
i=1
∞
(
A
∩
C
i)
. Karena Ci disjoint maka ACi
juga disjoint maka
P
(
A
)=
P
(
¿
i=1
∞
A
∩
C
i)=
∑
i=1
∞
b)
P
(
¿
i=1
∞
A
i)≤
∑
i=1
∞
P
(
A
i)
untuk setiap himpunan A1, A2, ...
Misalkan : B1 = A1
B2 = A1A1C
. . .
Bi = Ai
(
¿
j=1
i−1
A
j)
C¿
i=1
∞
A
i=
¿
i=1
∞
B
idan B1, B2, B3, ... kejadian-kejadian saling asing maka :
P
(
¿
i=1
∞
A
i)
=
P
(
¿
i=1
∞
B
i)
=
∑
i=1
∞
P
(
B
i)
Karena Bi Ai , maka P(Bi) ≤ P(Ai) sehingga :
P
(
¿
i=1
∞
A
i)
=
P
(
¿
i=1
∞
B
i)
=
∑
i=1
∞
P
(
B
i)≤
∑
i=1
∞
P
(
A
i)
Jadi :
P
(
¿
i=1
∞
A
i)
≤
∑
i=1
∞
P
(
A
i)
Akibat : P
(
¿i=1
n
A
iC
)
≤∑
i=1 n <