Untuk SMA MA Jilid I

(1)

Februari

2010

Muhammad Hajarul Aswad A, S.Pd.,M.Si

Februari 2010

Kendari - Sulawesi Tenggara

MATEMATIKA

Untuk SMA / MA Jilid I

(2)

www.aswhat82.blogspot.com

2 | Matematika_untuk_SMA/MA_Jilid I

Kata Pengantar

Bismillahirrahmanirrahim

Ide dari tulisan ini yakni menampilkan secara sederhana materi matematika yang ditemukan di jenjang Sekolah Menengah Atas. Hal ini dilakukan tentu saja tanpa bermaksud mengurangi hirarki penurunan rumus dari setiap bentuk rumus yang ada. Pokok bahasan yang dimuat dalam Matematika Untuk SMA/MA Jilid I ini adalah: Eksponen (pangkat) dan Bentuk Akar, Logaritma, Persamaan dan Fungsi Kuadrat, Logika Matematika, Trigonometri, Dimensi Tiga, Fungsi Komposisi dan Fungsi Invers, Limit Fungsi, Diferensial (Turunan), dan Lingkaran.

Dalam tulisan ini, penyusun hanya menampilkan bagian terpenting saja dari setiap pokok bahasan, mengingat sasaran yang ingin dituju penyusun adalah pembaca bisa mengetahui garis-garis besar dari setiap pokok bahasan yang ingin dipelajari terlebih dahulu, baru kemudian mengembangkannya untuk kasus-kasus terntentu. Dengan alasan itu pula, tulisan ini tidak dapat berdiri sendiri tanpa adanya buku matematika lainnya. Disamping itu pula, penyusun berasumsi bahwa paling tidak pembaca telah memiliki dasar berhitung dalam matematika.

Tentu saja hal tersebut menjadi kekurangan dari tulisan ini dan akan segera diperbaiki untuk penyempurnaan tulisan-tulisan selanjutnya. Untuk itu, dengan senang hati penyusun bersedia menerima segala bentuk kritik dan saran yang dianggap perlu untuk menyempurnakan tulisan ini dikemudian hari. Kritik dan saran bisa dialamatkan ke

as_wad82@yahoo.co.id

atau bisa melalui website penyusun di

www.aswhat82.blogspot.com atau www.aswhat.multiply.com

.

Akhir kata, selamat membaca semoga tulisan ini bisa memberikan masukan dan inspirasi dalam ber-matematika.

Penyusun

(3)

Daftar Isi

Halaman

Halaman Sampul ... 1

Kata Pengantar ... 2

Daftar Pustaka ... 3

Eksponen (pangkat) dan Bentuk Akar ... 4

Logaritma ... 9

Persamaan dan Fungsi Kuadrat ... 12

Logika Matematika ... 17

Trigonometri ... 22

Dimensi Tiga ... 32

Fungsi Komposisi dan Fungsi Invers ... 36

Limit Fungsi ... 39

Diferensial (Turunan) ... 44

Lingkaran ... 50

Daftar Pustaka ... 54

(4)

www.aswhat82.blogspot.com

Eksponen (Pangkat) dan Bentuk Akar

1. Bentuk Eksponen

Misalkan a adalah bilangan real dan n merupakan bilangan bulat positif, maka bentuk an (a pangkat n) menyatakan perkalian n faktor yang setiap faktornya adalah a. Secara umum dapat ditulis:

...

n

sebanyak n faktor

a a x a x a x a x x a 

Dalam mengoperasikan bilangan berpangkat, perlu diperhatikan sifat-sifat bilangan berpangkat berikut:

 Pangkat Bulat Positif

Misalkan a, b, ∈ℝ dan m, n adalah bilangan bulat positif 1) am x an = am+n

2) am : an = am-n 3) (am)n = amn 4) (a x b)n = an x bn

5) , 0

n n

n

a a

b b b

   

   

 Pangkat Nol dan Bulat Negatif

Perhatikan kembali sifat bilangan berpangkat yang ke (b), (am : an = am-n). Jika diambil m = n maka diperoleh

am : an = am-n

⟺ an : an = an-n ⟺ 1 = a0

(5)

www.aswhat82.blogspot.com

Selanjutnya, jika diambil m = 0 maka diperoleh am : an = a0-n

⟺ a0 : an = a-n ⟺ 1 : an = a-n ⟺ 1_n

a = a

-n

Jadi 1 n n a

a



 atau 1 n

n a

a  , untuk a ≠ 0

 Pangkat Rasional

Bilangan pangkat rasional (disebut juga pecahan) adalah bilangan yang dapat dinyatakan dalam bentuk m/n dengan ketentuan m,n adalah bilangan bulat, n ≠ 0. Dengan kata lain, bilangan berpangkat rasional adalah bilangan yang berpangkat bilangan pecahan.

m

n m n

a  a

2. Bentuk Akar

Bilangan irrasional adalah bilangan real yang tidak dapat dinyatakan dalam bentuk p/q, dengan p dan q adalah bilangan bulat, dan q ≠ 0. Bilangan-bilangan

3

2, 5, 4 termasuk dalam bentuk bilangan irrasional karena hasil akar dari bilangan-bilangan tersebut bukan merupakan bilangan-bilangan rasional. Sedangkan _{4, 2, 25, 27 bukan}3 merupakan bilangan irrasional.

Ada beberapa sifat yang perlu diperhatikan dalam menyelesaikan / menyederhanakan bentuk akar.

Untuk a, b ∈ℝ, dan c, d ∈ bilangan rasional non negatif. 1) n _axb  n _{a x b}n

(6)

www.aswhat82.blogspot.com

5) a a

b

b  , dengan b ≠ 0

Satu hal yang juga menarik adalah ketika kita menjumpai permasalahan yang berkaitan dengan merasionalkan bentuk akar. Perhatikan contoh berikut

 4

5 3

 2

5 24

Mudah bagi kita untuk menyederhanakan bentuk yang terdapat pada contoh yang pertama yaitu dengan mengalikan bentuk sekawan dari 5 3, sehingga diperoleh 2



5 3



. Tetapi, cara tersebut kurang tepat jika diterapkan untuk contoh yang kedua. Sebelum kita menjawab itu, terlebih dahulu perhatikan hal berikut,

Untuk bentuk



ab



2 a b. , dapat diubah menjadi bentuk



a  b



dengan syarat a,b ∈

ℝ dan a > b. Bukti:





2





2 . 2

a b  a a b b ab  ab





2

a b  ab  ab

Jadi



ab



2 ab  a  b

Dengan demikian, untuk menyelesaikan contoh yang kedua, terlebih dahulu kita mengkonversi

bentuknya ke dalam bentuk



ab



2 a b. , sehingga diperoleh





2 2 2 2

3 2

5 24 5 2 6 3 2 2 3 2x

  



   

(7)

www.aswhat82.blogspot.com

3. Persamaan Eksponen

Persamaan eksponen dalam varibel x merupakan suatu persamaan yang eksponennya paling sedikit memuat suatu fungsi. Berikut beberapa hal yang perlu diperhatikan dalam menyelesaiakn soal dalam bentuk persamaan eksponen.

1) Jika af(x) = ap(a > 0 dan a ≠ 1), maka f(x) = p 2) Jika af(x) = ag(x) (a > 0 dan a ≠ 1), maka f(x) = g(x)

3) Jika af(x) = bf(x)(a > 0, a ≠ 1, b > 0, b ≠ 0, dan a ≠ b), maka f(x) = 0. 4) Jika h(x)f(x) = h(x)g(x), maka kemumngkinannya adalah

a. f(x) = g(x) b. h(x) = 1

c. h(x) = 0, asalkan f(x) dan g(x) keduanya positif.

d. h(x) = -1, asalkan f(x) dan g(x) keduanya ganjil atau f(x) dan g(x) keduanya genap. 5) Jika f(x)h(x) = g(x)h(x), maka kemumngkinannya adalah

a. f(x) = g(x)

b. h(x) = 0, asalkan f(x) dan g(x) keduanya ≠ 0.

4. Fungsi Eksponen

Fungsi eksponen adalah fungsi yang memetakan setiap bilangan Real x menjadi ax. Bentuk umum fungsi eksponen adalah sebagai berikut:

f(x) = ax, dengan a > 0, a ≠ 0, dan x ∈ℝ

(8)

www.aswhat82.blogspot.com

Berikut grafik fungsi eksponen untuk y = ax dan y = (1/a)x.

Berdasarkan gambar di atas terlihat bahwa kurva y = ax dan y = (1/a)x simetri terhadap sumbu Y dan berpotongan di titik (0,1).

5. Pertidaksamaan Eksponen

Secara umum, dalam menyelesaikan soal pertidaksamaan, terlebih dahulu tanda

ketaksamaan (<, >, ≤, ≥, dan ≠) dirubah menjadi kesamaan (=). Selanjutnya ditemukan

variabelnya. Dan yang terakhir adalah yang paling penting, yaitu menguji varibel yang ditemukan dengan menggunakan garis bilangan, apakah sudah menyebabkan pertidaksamaan yang dimaksud menjadi suatu kalimat matematika yang bernilai benar.

Untuk pertidaksamaan eksponen, jika af(x) > ag(x) maka 1. f(x) > g(x), untuk a > 1

2. f(x) < g(x), untuk 0 < a < 1. y = 1

x

a    

(9)

www.aswhat82.blogspot.com

Logaritma

Logaritma merupakan invers dari bilangan berpangkat atau eksponen, sehingga antara eksponen dan logaritma mempunyai hubungan seperti berikut

ax = b ⟺ alog b, untuk b > 0, a > 0, dan a≠ 1 dengan a disebut bilangan pokok

b disebut numerus x disebut hasil logaritma

Untuk menyelesaikan soal yang berkaitan dengan logaritma, tidak ada acara lain selain menguasai terlebih dahulu sifat-sifat yang berlaku pada logaritma.

1. log a.b = log a + log b 2. loga loga logb

b  

3. alog b . blog c = alog c 4. log an = n. log a 5.

1 1

log log log

n a n a

a b b b

n

 

6. nlog k k alog

a b b

n 

7. alogb

a b

8. log log 1

log log

a

b

b b

a a

 

9. alog1 0

sebab a0 = 1 10. alog 1

a sebab a1 = a.

 Persamaan Logaritma

(10)

www.aswhat82.blogspot.com

Sifat-sifat yang berlaku pada persamaan logaritma 1. Jika alog f(x) = alog p, maka f(x) = p, untuk f(x) > 0. 2. Jika alog f(x) = blog f(x), dengan (a≠ b), maka f(x) = 1.

3. Jika alog f(x) = alog g(x), maka f(x) = g(x), untuk f(x) dan g(x) keduanya bernilai positif.

4. Jika h(x)log f(x) = h(x)log g(x), maka f(x) = g(x), untuk f(x) dan g(x) keduanya bernilai positif serta h(x) > 0 dan h(x) ≠ 1.

5. Jika f(x)log h(x) = g(x)log h(x), maka kemungkinannya adalah:

a. f(x) = g(x) untuk h(x) = 1, f(x) > 0, f(x) ≠ 1, g(x) > 0 dan g(x) ≠ 1. b. f(x) = g(x) untuk h(x) ≠ 1, dan h(x) > 0.

 Grafik Fungsi Logaritma

Fungsi logaritma merupakan fungsi invers dari fungsi eksponen. Jika x > 0, a > 0, dan a≠ 1, maka

y = alog x ⟺ x = ay fungsi logaritma dengan bilangan pokok a dapat ditulis dalam bentuk

f : x⟶alog x atau y = f(x) = alog x

 Grafik fungsi logaritma dengan bilangan pokok a > 1

(11)

www.aswhat82.blogspot.com

 Grafik fungsi logaritma dengan bilangan pokok 0 < a < 1.

Fungsi logaritma y = f(x) = alog x dengan 0 < a < 1 merupakan fungsi monoton turun, sebab untuk x2 > x1 maka alog x2 < alog x1.

Cara Smart

Ada beberapa cara cepat yang bisa dilakukan untuk menyelesaikan soal dalam bentuk bilangan berpangkat. Tetapi, perlu berhati-hati dalam penggunaannya karena cara ini tidak berlaku untuk semua kasus. Melainkan untuk kasus-kasus tertentu yang memiliki bentuk/model yang sama dengan cara cepat yang akan diterapkan.

Berikut beberapa bentuk cara cepat yang bisa diterapkan

 Jika a. (px)2–b.px + c = 0, maka ₁ ₂ plogc

x x

a

 

 Jika a. plog2x + b. plog x + c = 0, maka ₁. ₂

b a

x x p





 Jika a.Q + x + a.P - x = K maka x1 + x2 = P–Q

 Jika a.Q + nx + a.P - nx = K maka x₁ x₂ P Q n 

 

 Jika a.x–a-x = p maka (ax)2– (a-x)2 = p2 + 2 Selain itu pula, hafalkan nilai logaritma berikut

 Log 1 = 0

 Log 2 = 0,3010

 Log 3 = 0,4771

 Log 5 = 0,6989

 Log 7 = 0.8451

(12)

www.aswhat82.blogspot.com

Persamaan dan Fungsi Kuadrat

Persamaan Kuadrat

Persamaan kuadrat merupakan suatu persamaan yang pangkat tertinggi variabelnya bernilai 2. Bentuk umum persamaan kuadrat adalah

ax2 + bx + c = 0, untuk a≠ 0, dan a, b, c∈ℝ. Dengan x merupakan variabel dari persamaan kuadrat

a merupakan koefisien x2 b merupakan koefisien x c merupakan konstanta

1. Cara Penyelesaian Persamaan Kuadrat

 Memfaktorkan

Bentuk ax2 + bx + c = 0 diuraikan menjadi (x – x1) (x – x2) = 0, dengan x1 dan x2

merupakan akar-akar persamaan kuadrat yang dimaksud.

Pemfaktoran persamaan kuadrat untuk a = 1 dapat dilakukan dengan cara mencari dua buah angka yang jika dikalikan hasilnya adalah c, dan jika dijumlahkan hasilnya adalah b. Sementara untuk nilai a yang lain, dapat dilakukan coba-coba.

 Menggunakan Rumus ABC

Cara ini umumnya digunakan jika mengalami kesulitan dalam menerapkan pemfaktoran. Adapun rumus ABC yang dimaksud adalah

2

1,2

4 2

b b ac x

a

  

 , dengan a ≠ 0.

Nilai b2– 4ac disebut dengan diskriminan, ditulis D.

Jika D > 0, maka persamaan kuadrat memiliki dua akar real yang berlainan (x1≠ x1)

Jika D = 0, maka persamaan kuadrat memiliki dua akar real yang sama (x1 = x1).

(13)

www.aswhat82.blogspot.com

13 | Matematika_untuk_SMA/MA_Jilid I  Melengkapkan Kuadrat Sempurna

Cara lain dalam menyelesaikan bentuk persamaan kuadrat adalah dengan melengkapkan kuadrat sempurna. Cara ini umumnya kurang populer dibandingkan dengan pemfaktoran dan menggunakan rumus ABC, karena hanya dapat digunakan pada bentuk kuadrat dengan nilai a tertentu. Bentuk umum dari persamaan kuadrat yang berbentuk kuadrat sempurna adalah

(x + p)2 = q, dengan q > 0

2. Jumlah dan Hasil Kali Akar-Akar Persamaan Kuadrat

Untuk menghitung jumlah dan hasil kali akar-akar persaman kuadrat ax2 + bx + c = 0 dengan a≠ 0, dapat dicari tanpa terlebih dahulu menemukan akar-akarnya.

1 2 b

x x

a 

  x₁ . x₂ c

a 

Fungsi Kuadrat

Fungsi kuadrat adalah suatu fungsi yang pangkat variabel tertingginya adalah dua. Bentuk umumnya adalah

y = ax2 + bx + c, a≠ 0, dan a, b, c∈ℝ.

1. Grafik Fungsi Kuadrat

Grafik fungsi kuadrat berupa parabola. Jika a > 0, maka parabola terbuka ke atas. Sedangkan jika a < 0, maka parabola terbuka ke bawah.

(14)

www.aswhat82.blogspot.com

A adalah titik potong kurva terhadap sumbu-y B dan C adalah titik potong kurva terhadap sumbu-x.

P adalah titik puncak. L adalah sumbu sinetri.

Berikut dibarikan ciri-ciri fungsi kuadrat dan grafiknya.

 Sumbu simetri 2

b x

a  

 Puncak , ,

2 4 2 2

b D b b

f

a a a a

    

 _  

 _    

    

 a > 0, grafik terbuka ke atas a < 0, grafik terbuka ke bawah

 Tanda b dikaitkan dengan tanda a.

Jika tanda b sama dengan tanda a, puncak di sebelah kiri sumbu y. Jika tanda b berbeda dengan tanda a, puncak di sebelah kanan sumbu y.

 c > 0 jika grafik memotong sumbu y positif c < 0 jika grafik memotong sumbu y negatif c = 0 jika grafik melalui titik (0,0)

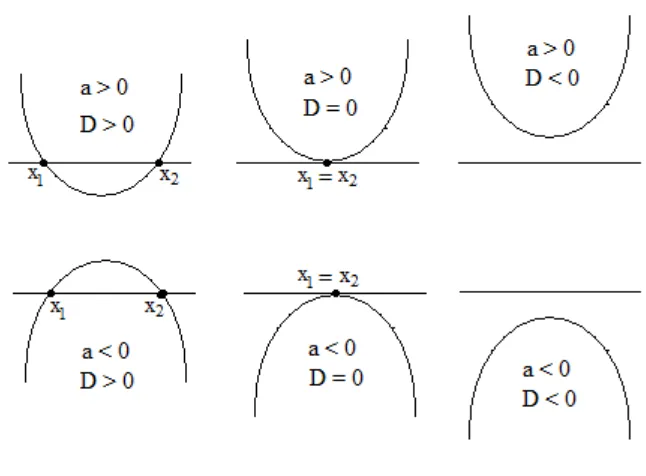
 D > 0, grafik memotong sumbu x di dua titik yang berbeda. D = 0, grafik menyinggung sumbu x.

D < 0, grafik tidak memotong sumbu x.

2. Titik-Titik Potong terhadap Sumbu-Sumbu Koordinat

Titik potong terhadapa sumbu-x; Grafik fungsi kuadrat memotong sumbu-x jika y = 0. Sehingga koordinat titik potongnya adalah (x1, 0) dan (x2, 0). Titik potong terhadap

(15)

www.aswhat82.blogspot.com

3. Titik Puncak / Titik Balik dan Sumbu Simetri

Bentuk y = ax2 + bx + c dapat ditulis menjadi

2 ₂ 4

2 4

b b ac y a x

a a



 

 _  _ 



  .

x disebut sumbu simetri (penyebab ekstrim), sedangkan y disebut nilai ekstrim. Jika a > 0, maka yeks = ymin

Jika a < 0, maka yeks = ymax

Titik puncak parabola adalah

2 4 ,

2 4

b b ac

a a

  

 _ 

 

Jika a > 0, maka titik puncak adalah titik balik minimum dan parabola terbuka ke atas. Jika a < 0, maka titik puncak adalah titik balik maksimum dan parabola terbuka ke bawah.

4. Kegunaan Diskriminan pada Fungsi Kuadrat

Letak grafik terhadap sumbu-x dapat dilihat dari nilai diskriminannya. Perhatikan grafik berikut

(16)

www.aswhat82.blogspot.com

5. Menentukan Persamaan Kurva dari Fungsi Kuadrat

Untuk menentukan persamaan (rumus) fungsi kuadrat dapat menggunakan rumus berikut:

 f(x) = ax2 + bx + c bila minimal tiga titik yang dilalui diketahui.

 f(x) = a(x– x1)(x – x2) bila x1 dan x2 absis titik potong dengan sumbu x dan satu titik

lain diketahui.

(17)

www.aswhat82.blogspot.com

Logika Matematika

1. Pernyataan (Kalimat Tertutup) dan Kalimat Terbuka

 Pernyataan atau kalimat tertutup adalah suatu kalimat yang dapat dinilai dan bernilai benar saja atau salah saja. Suatu pernyataan biasanya disimbolkan dengan sebuah huruf kecil, misalnya p, q, r, dan sebagainya.

Misalnya:

p : hari ini matahari bersinar terang

 Kalimat terbuka adalah suatu kalimat yang belum dapat ditentukan nilai kebenarannya karena mengandung variabel. Suatu alimat terbuka dengan variabel x dilambangkan dengan p(x), q(x), atau yang lainnya.

Misalnya:

p(x) : 2x + 1 = 5, untuk x ∈ℝ.

Apabila x diganti dengan 2, maka kalimat terbuka tersebut menjadi pernyataan yangbernilai benar. Sedangkan jika diganti dengan tidak selain 2, maka kalimatterbuka tersebut menjadi pernyataan yang bernilai salah.

 Ingkaran atau negasi dari suatu pernyataan adalah suatu pernyataan yang diperoleh dari pernyataan semula sedemikian sehingga jika pernyataan semula bernilai benar, maka ingkarannya bernilai salah, demikian sebaliknya. Ingkaran dari pernyataan p

diseimbolkan dengan “~p”.

2. Pernyataan Berkuantor

(18)

www.aswhat82.blogspot.com

Kuantor universal disimbolkan dengan “∀” yang artinya untuk setiap atau semua.

Sedangka kuantor eksistensial disimbolkan dengan “∃”, yang artinya ada, beberapa, terdapat, atau sekurang-kurangnya satu.

Ingkaran pernyataan berkuantor adalah sebagai berikut

 Ingkaran dari pernyataan berkuantor universal

Ingkaran dari pernyataan berkuantor semua p adalah ada / terdapat / beberapa ~p. Misalkan

p : Semua orang asing berkulit putih

~p : tidak benar bahwa semua orang asing berkulit putih. atau ~p : ada orang asing tidak berkulit putih. atau

~p : beberapa orang asing tidak berkulit putih

 Ingkaran dari pernyataan berkuantor eksistensial

Ingkaran dari pernyataan berkuantor ada / terdapat / beberapa p adalah semua ~p. Misalkan

p : Ada laki-laki yang tidak berkumis

~p : tidak benar bahwa ada laki-laki yang tidak berkumis. atau ~p : semua laki-laki berkumis

3. Pernyataan Majemuk, Bentuk Ekuivalen, dan Ingkarannya

Peryataan majemuk adalah pernyataan yang dibentuk dari beberapa pernyataan tunggal dengan menggunakan kata penghubung dan, atau, jika...maka..., jika dan hanya jika.

Kata Hubung Logika Lambang Istilah

... dan ... ∧ Konjungsi

... atau ... ∨ Disjungsi

Jika ... maka ... ⇒ Implikasi

... jika dan hanya jika ... ⟺ Biimplikasi

(19)

www.aswhat82.blogspot.com

p q p ∧ q p ∨ q p ⇒ q p ⟺ q

B B B B B B

B S S B S S

S B S B B S

S S S S B B

4. Tautologi, Kontradiksi, dan Bentuk Ekuivalen Pernyataan Majemuk

Tautologi adalah pernyataan majemuk yang selalu benar untuk semua kemungkinan nilai kebenaran dari komponen-komponen pernyataannya.

Kontradiksi adalah pernyataan majemuk yang selalu salah untuk semua kemungkinan nilai kebenaran dari komponen-komponen pernyataannya.

Dua pernytaan majemuk dikatakan ekuivalen jika kedua pernyataan majemuk itu mempunyai nilai kebenaran yang sama. Ekuivalen dua pernyataan majemuk dinotasikan

dengan “≡”.

Perhatikan tabel berikut

p q ~p ~q ~p ∧ q ~p ∨ q p ⟹ q p ∨ (~p ∨ q) p ∧ (~p ∧ q)

B B S S S B B B S

B S S B S S S B S

S B B S B B B B S

S S B B S B B B S

Ekuivalen

↓

tautologi

↓

Kontradiksi

5. Ingkaran Suatu Pernyataan Majemuk

 ~( p ∧q ) ≡ ~p ∨ ~q

 ~( p ∨q ) ≡ ~p ∧ ~q

 ~( p ⟹q ) ≡ p ∧ ~q

 ~( p ⟺q ) ≡ (p ∧ ~q) ∨ (q ∧ ~p)

(20)

www.aswhat82.blogspot.com

Dari suatu implikasi, dapat dibentuk suatu implikasi lain yaitu konvers, invers,dan kontraposisi.

Misalkan, Implikasi : p ⟹ q

Maka Konvers : q ⟹ q

Invers : ~p ⟹ ~q Kontraposisi : ~q ⟹ ~p

7. Penarikan Kesimpulan

Dalam penarikan suatu kesimpulan / konklusi, diperlukan beberapa pernyataan (premis). Apabila premis-premisnya bernilai benar, maka kesimpulan / konklusinya juga bernilai benar (sah). Atau dengan kata lain, penarikan kesimpulan dari beberapa pernyataan dikatakan sah atau valid jika pernyataan yang dimaksud bersifat tautologi.

P1 : (B) Premis 1

P2 : (B) Premis 2

...

Pk : (B) Premis-k

∴ Kesimpulan (B) Kesimpulan / konklusi

Ada tiga pola penarikan kesimpulan yang selalu digunakan. 1. Modus Ponens

P1 : p ⟹ q (B) Premis 1

P2 : p (B) Premis 2

∴ q (B) Kesimpulan / konklusi

2. Modus Tollens

P2 : ~q (B) Premis 2

(21)

www.aswhat82.blogspot.com

3. Silogisme

P2 : q ⟹ r (B) Premis 2

(22)

Trigonometri

Trigonometri berasal dari dua kata Yunani yaitu Trigonos yang berarti segitiga dan Metron yang berarti ukuran.

1. Perbandingan Trigonometri

 Perbandingan Trigonometri pada Segitiga Siku-Siku Perhatikan gambar segitiga siku-siku ABC berikut

Berdasarkan segitiga ABC tersebut, maka diperoleh perbandingan trigonometri sudut A

= α0

sebagai berikut:

0 0

sin cos

cos sec

tan cot

a c

ec

c a

b c

c b

a b

an

b a

 

 

Nilai perbandingan trigonometri untuk sudut-sudut istimewa adalah sebagai berikut

 Perbandingan Trigonometri Sudut Berelasi

(23)

www.aswhat82.blogspot.com

 Perbandingan Trigonometri Sudut di Kuadran Pertama (90 –α)0 sin (90 –α)0= cos α0 cotan (90 –α)0= tan α0

cos (90 –α)0= sin α0 sec (90 –α)0= cosec α0 tan (90 –α)0= cotan α0 cosec (90 –α)0= sec α0

 Perbandingan Trigonometri Sudut di Kuadran Kedua (180 –α)0 sin (180 –α)0= sin α0 cosec (180 –α)0= cosec α0 cos (180 –α)0 = - cos α0 sec (180 –α)0 = - sec α0 tan (180 –α)0 = - tan α0 cotan (180 –α)0 = - cotan α0

 Perbandingan Trigonometri Sudut di Kuadran Ketiga (180 + α)0

sin (180 + α)0

= - sin α0 cosec (180 + α)0 = - cosec α0

cos (180 + α)0_{= -}_{cos α}0 _{sec (180 + α)}0_{= -}_{sec α}0 tan (180 + α)0_{= tan α}0

cotan (180 + α)0= cotan α0

 Perbandingan Trigonometri Sudut di Kuadran Keempat (360 –α)0 atau (- α)0 sin (360 –α)0 = - sin α0 cosec (360 –α)0 = - cosec α0

cos (360 –α)0= cos α0 sec (360 –α)0= sec α0 tan (360 –α)0 = - tan α0 cotan (360 –α)0 = - cotan α0 atau

sin (- α)0 = - sin α0 cosec (- α)0 = - cosec α0 cos (- α)0= cos α0 sec (- α)0= sec α0 tan (- α)0 = - tan α0 cotan (- α)0 = - cotan α0

 Perbandingan Trigonometri untuk Sudut yang Lebih dari 3600.

(24)

www.aswhat82.blogspot.com

Cara smart  Sudut relasi

 Hafalkan nilai dari sudut-sudut istimewa berikut

0 30 45 60 90

Sin ∝ 0 1

2 1 2 2 1 3 2 1

Cos ∝ 1 1

3 2 1 2 2 1 2 0

Tan ∝ 0 1

3

1 ₃ Tak

terdefinisi

Untuk menentukan sudut yang lain, gunakan aturan sudut relasi.

 Hubungan Perbandingan Trigonometri

 Hubungan Antara Perbandingan-Perbandingan Trigonometri 0 0 0 0 0 0 0 0 0 0 0 0 1 sin sin tan cos cos 1 cos cos cot sec sin 1 tan cot ec an an                  f(n.90 ±∝)

n genap

Fungsi tetap: sin → sin, cos → cos, tan → tan

tanda (+) atau (-) sesuai dengan kuadran fungsi awal

n ganjil

Fungsi berubah: sin → cos, cos → sin, tan →

cotan

(25)

www.aswhat82.blogspot.com

25 | Matematika_untuk_SMA/MA_Jilid I  Identitas Trigonometri

cos2α + sin2α = 1 1 + tan2α = sec2α 1 + cotan2α = cosec2α

2. Satuan Ukuran Sudut

Terdapat beberapa istilah yang digunakan dalam satuan sudut. Namun yang biasa digunakan adalah derajat dan radian.

Sudut 1 putaran = 3600= 2π radian Sudut 1/2 putaran = 1800= π radian

3. Koordinat Kutub (Polar)

Letak suatu titik pada bidang X-Y dapat disajikan dalam koordinat cartesius, yaitu (x,y), atau dalam koordinat kutub yaitu (r, α0). Perhatikan gambar berikut:

Letak suatu titik P dalam koordinat Cartesius dapat diubah ke dalam koordinat kutub atau sebaliknya sebagaimana penjelasan berikut:

 Dari titik P(x,y) menjadi P(r, α0

) 2 2

r  x y

2 y x  

 Dari titik P(r, α0_{) menjadi P(x,y)} x = r cos α0

(26)

www.aswhat82.blogspot.com

4. Rumus-Rumus Segitiga Dalam Trigonometri

 Aturan Sinus dan Aturan Cosinus

Pada segitiga ABC sebarang berlaku aturan sinus dan cosinus sebagai berikut

 Aturan Sinus

sin sin sin

a b c

A  B  C

 Aturan Cosinus

a2 = b2 + c2– 2bc cos A b2 = a2 + c2– 2ac cos B c2 = a2 + b2– 2ab cos C

 Luas Segitiga

 Luas segitiga jika diketahui dua sisi dan satu sudut apit (sisi-sudut-sisi) 1

sin 2

L ab C

1 sin 2

L ac B

1 sin 2

L bc A

 Luas segitiga jika diketahui dua sudut dan satu sisi 2

sin sin 2sin

a B C

L A  2 sin sin 2sin

b A C

L B  2 sin sin 2sin

c A B

L

C 

 Luas segitiga jika diketahui panjang ketiga sisinya







L s sa sb sc

dengan 1





2

(27)

www.aswhat82.blogspot.com

 Luas segi banyak (segi-n) beraturan

Segi empat beraturan Segi lima beraturan Segi enam beraturan

2

1 360

sin 2

o segi n

L n R

n

   

 

dengan : n = banyaknya sisi pada segi banyak beraturan

R = panjang kaki segitiga sama kaki pembentuk segi-n beraturan

 Lingkaran Dalam, Lingkaran Luar, dan Lingkaran Singgung Segitiga

 Lingkaran Dalam Segitiga

Jari-jari lingkaran dalam (rd) ∆ ABC yang sisi-sisinya a, b, c dapat ditentukan dengan menggunakan rumus

 r_d L



s a



s b



s c



s s

  

 

atau







tan1 2

d

r  sa A







tan1 2

d

r  sb B







tan1 2

d

(28)

www.aswhat82.blogspot.com

28 | Matematika_untuk_SMA/MA_Jilid I  Lingkaran Luar Segitiga

Jari-jari lingkaran luar (rl) ∆ ABC yang sisi -sisinya a, b, c dapat ditentukan dengan menggunakan rumus



2sin 2sin 2sin

l

a b c

r

A B C

   atau 







4 ₄ l abc abc r

L _{s s} _a _s _{b s} _c

 

  

 Lingkaran Singgung Segitiga

Jari-jari lingkaran singgung ∆ ABC yang panjang sisi-sisinya a, b, c dapat ditentukan dengan menggunakan rumus

 tan1 2

a

r s A

 r_a L s s



a



s b



s c



s a s a

  

 

 

 tan1 2

b

r s B

 r_b L s s



a



s b



s c



s b s b

  

 

 

 tan1 2

c

r s C

 r_c L s s



a



s b



s c



s c s c

  

 

(29)

www.aswhat82.blogspot.com

dengan 1





2

s a b c

5. Rumus-Rumus Trignometri

 Rumus Trgigonometri untuk Jumlah Dua Sudut dan Selisih Dua Sudut

cos (α ± β) = cos α cos β ∓sin α sin β sin (α ± β) = sin α cos β ± cos α sin β





tan tan

tan

1 tan tan

         





tan tan

tan

1 tan tan

         

 Rumus Trigonometri untuk Sudut Rangkap

sin 2α = 2 sin α cos α cos 2α = cos2_{α –}

sin2α = 2 cos2α – 1

= 1 - 2 sin2α

2 2 tan tan 2 1 tan     

sin 3α = 3 sin α – 4 sin3α

cos 3α = 4 cos3_{α –}_{3 cos α}

 Rumus Perkalian Sinus dan Kosinus













1

sin cos sin sin

2

       













1

cos sin sin sin

2

       













1

cos cos cos cos

2

       













1

sin sin cos cos

2

(30)

www.aswhat82.blogspot.com

 Rumus Penjumlahan dan Pengurangan Sinus dan Kosinus









1 1

sin sin 2sin cos

2 2

      









1 1

sin sin 2cos sin

2 2

      









1 1

cos cos 2cos cos

2 2

      









1 1

cos cos 2sin sin

2 2

       

6. Fungsi Trignometri

 Grafik Fungsi Sinus

Ciri-ciri grafik fungsi y = sin x

 Nilai maksimum = 1, dan minimum =-1

 Amplitudo = ½ (nilai maks-nilai min) = 1

 Periode sebesar 2π radian

 Periodisitas fungsi sin (x + k.2π) = sin

x, dengan k ∈ bil. bulat

 Grafik Fungsi Cosinus

Ciri-ciri grafik fungsi y = cos x

 Nilai maksimum = 1, dan minimum =-1

 Amplitudo = ½ (nilai maks-nilai min) = 1

 Periode sebesar 2π radian

 Periodisitas fungsi cos (x + k.2π) = cos

(31)

www.aswhat82.blogspot.com

31 | Matematika_untuk_SMA/MA_Jilid I  Grafik Fungsi Tangens

Ciri-ciri grafik fungsi y = tan x

 Nilai maksimum = +~, dan minimum = -~

 Periode sebesar π radian

 Periodisitas fungsi tan (x + k. π) = tan

x, dengan k ∈ bil. bulat

7. Persamaan dan Pertidaksamaan Trigonometri

Rumus-rumus dasar persamaan trigonometri adalah sebagai berikut

 sin x = sin α

x1= α + k . 360o atau x2 = (180o–α) + k . 360o

 cos x = cos α x = ±α + k . 360o

 tan x = tan α x = α + k . 180o

(32)

www.aswhat82.blogspot.com

Dimensi Tiga

1. Bangun Ruang

Bangun dimensi tiga yang akan dibahas dalam bab ini adalah bangun dimensi tiga berbentuk Kubus, Balok, Limas, Kerucut, dan Bola. Untuk selanjutnya, bangun dimensi tiga disebut bangun ruang.

 Kubus

Misalkan kubus ABCD.EFGH di samping memiliki panjang rusuk a. maka

 Panjang diagonal bidang = a 2

 Panjang diagonal ruang = a 3  Volume kubus = a3

 Luas permukaan kubus = 6 x luas ABCD = 6a2

 Balok

Balok ABCD.EFGH di samping memiliki panjang p, lebar l, dan tinggi t. Maka

 Volume balok = p x l x t

(33)

www.aswhat82.blogspot.com

33 | Matematika_untuk_SMA/MA_Jilid I  Limas

Limas segi-3 Limas segi-4 Limas segi-5

Volume limas = 1

3 x Luas alas x tinggi

Luas permukaan limas = Luas alas + luas bidang/sisi tegak

 Kerucut

Kerucut di samping mempunyai jari-jari r, tinggi t, dan panjang garis pelukis s.

 s2 = r2 + t2

 Volume kerucut = 1 2

3r t

(34)

www.aswhat82.blogspot.com

34 | Matematika_untuk_SMA/MA_Jilid I  Bola

Bola di samping mempunyai jari-jari r.

 Volume bola = 4 3

3r

 Luas permukaan bola = 4π r2

2. Jarak pada Bangun Ruang

 Jarak Antara Dua Titik

Jarak titik A ke titik B sama dengan panjang ruas garis AB yang ditentukan dengan menggunakan teorema Pythagoras

2 2

AB x y

 Jarak Titik ke Garis

(35)

www.aswhat82.blogspot.com

Titik A terletak di luar bidang ∝.

Jarak titik A terhadap garis g yang tidak terletak pada satu bidang adalah sama dengan jarak garis AC, dimana AB tegak lurus terhadap bidang ∝, dan BC tegak lurus terhadap garis g.

 Jarak Antara Dua Titik

(36)

Fungsi Komposisi dan Fungsi Invers

Fungsi atau pemetaan dari himpuan A ke himpunan B merupakan relasi khusus yang memasangkan setiap anggota A dengan tepat satu anggota B. Misalkan f adalah suatu fungsi atau pemetaan dari himpunan A ke himpunan B, maka fungsi f dinotasikan dengan :

f : A → B

pada fungsi f : A → B, himpuan A disebut daerah asal (domain) fungsi f yang dinotasikan dengan Df, himpuan B disebut daerah kawan (kodomain) fungsi f yang dinotasikan dengan

Kf, dan himpuan semua pemetaan A pada B disebut daerah hasil (range) fungsi f yang

dinotasikan dengan Rf.

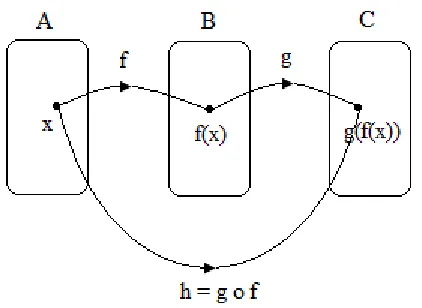
1. Fungsi Komposisi

Apabila f suatu fungsi dari A ke B (f : A → B) dan g suatu fungsi dari C ke D (g :

C → D), maka terdapat h yang merupakan fungsi dari A ke C (h : A → C) yang disebut

fungsi komposisi yang iasa dinyatakn dengan h = g o f (dibaca g bundaran f). Perhatikan gambar berikut

(37)

www.aswhat82.blogspot.com

2. Fungsi Invers

Apabila f adalah suatu fungsi dari himpunan A ke himpunan B, maka invers fungsi f adalah suatu relasi dari himpunan B ke himpunan A. Hal ini berarti invers suatu fungsi tidak selalu merupakan fungsi. Jika invers suatu fungsi merupakan fungsi, maka invers tersebut dinamakan fungsi invers dari fungsi semula. Fungsi f mempunyai fungsi invers f-1 jika dan hanya jika f merupakan fungsi korespondensi satu-satu.

Beberapa cara cepat yang bisa diterapkan untuk memperoleh invers dari suatu fungsi adalah sebagai berikut

 Jika f x( )axb maka f 1

 

x x b a

 _ 

 Jika 2

( )

f x ax bxc maka 1

 

1

4 2

D b

f x x

a a a

 _{ }  _ _

 

 

 Jika ( )f x ax b

cx d

 

 maka

 

1 dx b

f x

cx a

 _  



 Jika ( ) bx

f x a maka

 

1 1 a_log _b

f x  x

3. Tinjauan Grafik

Fungsi yang mempunyai fungsi invers adalah fungsi bijektif (korespondensi satu-satu). Dalam bentuk kurva, fungsi bijektif dapat diketahui dengan cara menarik garis-garis yang sejajar dengan sumbu-x dan sumbu-y. Apabila kedua garis itu hanya memotong kurva di satu titik, maka fungsi dari kurva tersebut mempunyai invers. Apabila kedua garis itu memotong kurva di dua titik atau lebih, maka fungsi kurva tersebut tidak mempunyai invers. Perhatikan gambar berikut

(38)

www.aswhat82.blogspot.com

4. Fungsi Invers dari Fungsi Komposisi

Rumus fungsi invers dari fungsi komposisi yang lain adalah (g o f)-1 = f-1 o g-1

(39)

Limit Fungsi

Secara intuisi, lim

 

xa f x L berarti bahwa jika x mendekati a dengan x≠ a, maka

f(x) mendekati L.

1. Limit fungsi f(x) untuk x→ a, (a≠ 0)

Perhitungan limit fungsi f(x) untuk x → a, (a ≠ 0) dapat dilakukan melalui tiga cara yaitu subtitusi langsung, pemfaktoran, dan rasionalisasi bentuk akar.

Jika dengan subtitusi langsung dihasilkan bentuk tak tentu 0 0    

  maka perhitungan limit dilakukan dengan cara pemfaktoran atau rasionalisasi bentuk akar.

2. Limit fungsi f(x) untuk x→ 0

Perhitungan limit fungsi f(x) untuk x → 0 sama halnya dengan perhitungan limit fungsi f(x) untuk x→ a, (a≠ 0).

3. Limit fungsi f(x) untuk x→ ~

Cara subtitusi langsung tidak dapat diterapkan pada perhitungan limit fungsi f(x) untuk x → ~ yang berbentuk

 

~ lim

x

f x g x

 Karena jika disubtitusi langsung, akan

menghasilkan bentuk tak tentu  _{ }  



 . Untuk itu, perhitungannya dilakukan dengan cara

membagi pembilang f(x) dan penyebut g(x) dengan xn dimana n adalah pangkat tertinggi dari g(x).

Sementara untuk limit fungsi yang berbentuk



 



~

lim

x f x  g x jika

(40)

www.aswhat82.blogspot.com

perhitungannya dilakukan dengan cara mengalikan dengan faktor lawan, yaitu

 

f x g x



 .

4. Teorema Limit

Terdapat beberapa teorema limit yang harus diperhatikan diantaranya :

 Jika f(x) = k maka lim

 

xa f x k, (untuk setiap k konstan, dan a bilangan real)

 Jika f(x) = x maka lim

 

xa f x a, untuk f(x) = k. (untuk setiap a bilangan real)

 lim



 



lim

 

lim

 

xa f x g x  xa f x xag x .

 lim .

 

.lim

 

xak f x k xa f x , untuk k konstan.

 lim



   

.



lim

 

. lim

 

xa f x g x  xa f x xag x



 

lim lim lim x a x a x a f x f x

g x g x

 



 , dengan lim

 

0

xag x 

 lim



 





lim

 



n n

xa f x  xa f x

 limn

 

_nlim

 

xa f x  xa f x , dengan limxa f x

 

0

atau

 







 



1 1

lim n lim n

xa f x  xa f x

5. Limit Fungsi Trigonometri

Secara umum, rumus-rumus limit fungsi trigonometri yang sering digunakan adalah



0 0 0

sin sin

lim lim lim

sin sin

x x x

ax ax ax a

bx bx bx b

     



0 0 0

tan tan

lim lim lim

tan tan

x x x

ax ax ax a

bx bx bx b

(41)

www.aswhat82.blogspot.com

41 | Matematika_untuk_SMA/MA_Jilid I  0 0 sin tan lim lim tan sin x x

ax ax a

bx bx b

   

Rumus-rumus trigonometri yang sering digunakan untuk merubah fungsi pada limit fungsi trigonometri adalah

 cos x = sin (900–x)

 cos2ax + sin2ax = 1

 sin 2sin 1 cos 1

2 2

ax ax ax

 _cos _{1 2sin}2 1 2

ax  ax

2

2 2

1

2 cos 1

2 1 1 cos sin 2 2 ax ax ax    

6. Teorema L’Hospital

Dalam menentukan nilai

 

lim

x a

f x g x

 yang menghasilkan bentuk tak tentu

0 0      ,

dapat digunakan teorema L’Hospital yaitu

 

'

lim lim

'

x a x a

f x f x

g x g x

  

Apabila

 

' lim ' x a f x g x

 juga menghasilkan bentuk tak tentu

0 0    

 , maka nilai

 

lim x a f x g x

 dapat

ditentukan dari turunan kedua, yaitu

 

"

lim lim

"

x a x a

f x f x

g x g x

(42)

www.aswhat82.blogspot.com

Cara Smart

Beberapa cara smart yang bisa diterapkan untuk bentuk-bentuk limit tertentu diantaranya:

 Misalkan 1 1 ~ ... lim ... m m n n x ax bx L px qx      _  

Jika m < n, maka L = 0 Jika m = n, maka L a p 

Jika m > n, maka ~ untuk 0 ~ untuk 0

a L a    _ _ 

 Misalkan



2 2



~ lim

x ax bx c px qxr L

Jika a < p, maka L = - ~ Jika a = p, maka

2 b q L a  

Jika a > p, maka L = ~

 Untuk menyelesaikan soal dalam bentuk limit, gunakan aturan L’Hospital.

 Perhatikan contoh berikut

i.

2

0

1 .2

1 2 cos 2 ₂ 2

lim

5 tan 5.1 5

x

x x



 _ _

ii.





2

2 2

0

1 5. .6

sin 5 1 cos 6 ₂ 10

lim

7

7 tan 3 7.3

x x x x x    

Yang perlu diperhatikan dalam menyelesaikan bentuk limit dengan cara ini adalah bahwa setiap bentuk f(x) dan g(x) dari

 

0 lim x f x f x

 harus dalam bentuk operasi perkalian

atau dalam bentuk f(x) pada contoh i. Jika tidak maka bentuk yang ada, terlebih dahulu dikonversi ke dalam bentuk perkalian atau sebagaimana yang terlihat pada contoh i dan ii. Rumus trigonometri yang biasa digunakan adalah

 2 2

sin xcos x1

 2

1 cos 2 x2sin x

 cos cos 2cos1





cos1





2 2

(43)

www.aswhat82.blogspot.com

























1 1

cos cos 2sin sin

2 2

1 1

sin sin 2sin cos

2 2

1 1

sin sin 2 cos sin

2 2

x y x y x y

    

   

(44)

Diferensial (Turunan)

1. Pendahuluan

Suatu f(x) dikatakan diferensiable pada x = a jika

 





 

0

' lim

h

f a h f a

f a

h



 



Perhatikan gambar berikut

2. Turunan Fungsi Aljabar

Rumus-rumus turunan fungsi aljabar adalah sebagai berikut

 Jika f(x) = k maka f '(x) = 0

 Jika f(x) = k.u(x) maka f '(x) = k . u'(x), untuk k konstan

 Jika f(x) = xn maka f '(x) = n xn-1

 Jika f(x) = u(x) ± v(x) maka f '(x) = u'(x) ± v'(x)

 Jika f(x) = u(x) . v(x) maka f '(x) = u'(x) v(x) + u(x) v'(x)

 Jika f(x) = {u(x)}n maka f '(x) = n [u(x)]n-1 . u'(x)

 Jika

 

   

, 0

u x

f x v x

v x

  maka

 

       

 





2

' . . '

' u x v x u x v x

f x

(45)

www.aswhat82.blogspot.com

3. Turunan Fungsi Trigonometri

Rumus-rumus turunan fungsi trigonometri adalah sebagai berikut

 Jika f(x) = sin x maka f '(x) = cos x

 Jika f(x) = cos x maka f '(x) = - sin x

 Jika f(x) = tan x maka f '(x) = sec2x = 1₂ cos x

4. Turunan Fungsi Logaritma dan Eksponensial

Rumus-rumus turunan fungsi logaritma dan eksponensial adalah sebagai berikut

 Jika f(x) = ln x maka f '(x) = 1. 'x x

 Jika f(x) = alog x maka f '(x) = 1 . ' ln x

x a

 Jika f(x) = ex maka f '(x) = ex . x'

 Jika f(x) = ax maka f '(x) = ax ln a. x' 5. Persamaan Garis Singgung pada Kurva

suatu titik P(x1, y1) terletak pada kurva y = f(x), maka persamaan garis yang melalui titik

tersebut adalah

(46)

www.aswhat82.blogspot.com

dengan gradien garis singgung m1 = f '(x1) atau 1

1 dy

m

x x

dx

 

  _ _ _ . Garis yang tegak lurus

garis singgung dan melalui titik P(x1, y1) disebut garis normal. Garis normal juga tegak

lurus terhadap kurva y = f(x).

Karena garis normal tegak lurus terhadap garis singgung (sarat dua garis yang tegak lurus adalah: m1 . m2 = -1, sedagkan sarat dua garis sejajar adalah: m1 = m2), maka persamaan

garis normal yang melalui titik P(x1, y1) dengan gradien m2 adalah

y – y1 = m2 (x – x1)

=



₁



1 1

x x

m

 

6. Fungsi Naik dan Fungsi Turun

Misalkan grafik suatu fungsi y = f(x) seperti terlihat pada gambar tersebut di atas. Maka dapat dikatakan bahwa:

 Fungsi y = f(x) merupakan fungsi naik untuk nilai-nilai x dalam interval x > a, sebab dalam interval x > a,untuk nilai x yang semakin besar maka fungsi f(x) juga semakin besar.

 Fungsi y = f(x) merupakan fungsi turun untuk nilai-nilai x dalam interval x < a, sebab dalam interval x < a,untuk nilai x yang semakin besar maka fungsi f(x) semakin kecil. Berdasarkan hal tersebut, maka dapat didefinisikan sebagai berikut

Misalkan fungsi f(x) tersefinisi dalam interval I.

Fungsi f(x) dikatakan fungsi naik dalam interval I jika untuk setiap bilangan x1 dan x2

dalam interval I dengan x1 < x2, berlaku hubungan f(x1) < f(x2), atau ditulis

(47)

www.aswhat82.blogspot.com

Fungsi f(x) dikatakan fungsi turun dalam interval I jika untuk setiap bilangan x1 dan x2

dalam interval I dengan x1 < x2, berlaku hubungan f(x1) > f(x2), atau ditulis

x1 < x2 ⟹ f(x1) > f(x2)

misalkan fungsi f kontinu dalam interval I dan diferensiabel di setiap titik dalam interval tersebut, maka

 Jika f '(x) > 0 untuk x∈ I, maka fungsi f(x) naik pada I.

 Jika f '(x) < 0 untuk x∈ I, maka fungsi f(x) turun pada I.

 Jika f '(x) = 0 untuk x∈ I, maka fungsi f(x) stasioner pada I.

7. Titik Stasioner dan Jenis-Jenis Nilai Stasioner

Jika fungsi y = f(x) diferensiabel di x = a dengan f '(a) = 0, maka f(a) adalah titik stasioner dari fungsi f(x) di x = a.

Berdasarkan gambar tersebut di atas, dapat dikatakan bahwa

 Nilai x yang menyebabkan f(x) mempunyai nilai stasioner, dapat ditentukan dari syarat f '(x) = 0

 Titik (a, f(a)) yang terletak pada grafik y = f(x) disebut sebagai titik stasioner.

(48)

www.aswhat82.blogspot.com

Terdapat 3 jenis nilai stasioner yaitu a. Nilai balik masksimum

Fungsi y = f(x) mencapai nilai balik maksimum pada x = a atau f(a) merupakan nilai balik maksimum jika f '(a -) > 0; f '(a) = 0; dan f '(a +) < 0. Atau jika f '(a) = 0 dan f ''(a) < 0.

b. Nilai balik masksimum

Fungsi y = f(x) mencapai nilai balik minimum pada x = a atau f(a) merupakan nilai balik minimum jika f '(a -) < 0; f '(a) = 0; dan f '(a +) > 0. Atau jika f '(a) = 0 dan f ''(a) > 0.

c. Titik belok

Fungsi y = f(x) mempunyai titik belok pada x = a atau f(a) merupakan titik belok jika f '(a -) < 0; f '(a) = 0; dan f '(a +) < 0, atau f '(a -) > 0; f '(a) = 0; dan f '(a +) > 0, atau jika f '(a) = 0 dan f ''(a) = 0.

Perhatikan grafik dari ketiga jenis nilai stasioner tersebut

Grafik fungsi dengan nilai maksimum

x a- a a+

f '(x) + 0 -

Grafik fungsi dengan nilai minimum

x a- a a+

(49)

www.aswhat82.blogspot.com

Grafik fungsi dengan titik belok

x a- a a+

f '(x) - 0 -

x a- a a+

(50)

LINGKARAN

Lingkaran merupakan tempat kedudukan titik-titik yang berjarak sama terhadap sebuah titik tertentu. Jarak yang sama itu disebut jari-jari (r) dan titik tertentu itu disebut pusat lingkaran.

1. Persamaan Lingkaran

 Persamaan Lingkaran ynag Berpusat di titik (0,0)

Persamaan lingkaran yang berpusat di titik O(0, 0) dan berjari-jari r dengan titik P(x,y) terletak pada lingkaran adalah

OP = r



 

2



2

0 0

x  y = r x2 + y2 = r2

 Persamaan Lingkaran ynag Berpusat di titik (a,b)

Persamaan lingkaran yang berpusat di titik P(a,b) dan berjari-jari r dengan titik P(x,y) terletak pada lingkaran adalah

OP = r



 

2



2

(51)

www.aswhat82.blogspot.com

Jika kita menjabarkan kembali persamaan (x–a)2 + (y–b) 2 = r2

Maka akan diperoleh

x2 + y2 + Ax + By + C = 0

dengan A = -2a → 1

2

a  A

B = -2b → 1

2

b  B

C = a2 + b2–r2 → 1 2 1 2

4 4

r  A  B C

Sehingga, secara umum dapat dikatakan bahwa persamaan lingkaran x2 + y2 + Ax + By + C = 0 merupakan persamaan lingkaran yang berpusat di 1 , 1

2A 2B

_ _ 

 

 , dengan

jari-jari 1 2 1 2

4 4

r  A  B C.

2. Perpotongan Garis dan Lingkaran

Pandang lingkaran dengan persamaan x2 + y2 + Ax + By + C = 0 dan sebuah garis h dengan persamaan y = mx + n. Jika y = mx + n disubtitusikan ke persamaan lingkaran tersebut, maka diperoleh suatu bentuk persamaan kuadrat baru sebagai berikut

(1 + m2)x2 + (2mn + A + Bm)x + (n2 + Bn + C) = 0 Diskriminan dari persamaan kuadrat tersebut adalah

D = (2mn + A + Bm)2– 4(1 + m2) (n2 + Bn + C)

Sehingga, terdapat tiga kemungkinan hubungan antara garis dengan lingkaran, yaitu

Garis h tidak memotong dan tidak menyinggung lingakaran jika D < 0

Garis h menyinggung lingakaran jika D = 0

(52)

www.aswhat82.blogspot.com

3. Persamaan garis Singgung Lingkaran

 Garis Singgung Lingkaran yang Melalui Sebuah Titik pada Lingkaran

Persamaan garis singgung melalui titik P(x1, y1) pada lingkaran x2 + y2 = r2

ditentukan dengan menggunakan rumus berikut x1 . x + y1 . y = r2

Persamaan garis singgung melalui titik P(x1, y1) pada lingkaran (x–a)2 + (y–b) 2 = r2

ditentukan dengan menggunakan rumus berikut

(x – a) (x1– a) + (y – b) (y1– b) = r2

Persamaan garis singgung melalui titik P(x1, y1) pada lingkaran x2 + y2 + Ax + By + C

= 0 ditentukan dengan menggunakan rumus berikut









1 1 1 1

1 1

0

2 2

x xy y A xx  B yy  C

 Garis Singgung dengan Gradien yang Diketahui

 Jika garis y = mx + n menyinggung lingkaran x2 + y2 = r2 maka persamaan garis singgungnya adalah

2 1 ymxr m 

 Jika garis y = mx + n menyinggung lingkaran (x – a)2 + (y – b) 2 = r2 maka persamaan garis singgungnya adalah









2

1 yb m xa r m 

 Garis Singgung Melalui Sebuah Titik di Luar Lingkaran

(53)

www.aswhat82.blogspot.com

Persamaan umum garis singgung lingkaran melalui sebuah titik P(x1, y1) yang terletak

di luar lingkaran adalah

y – y1 = m(x – x1)

Nilai m ditentukan dengan cara sebagai berikut:

 Subtitusikan persamaan y – y1 = m(x – x1) ke persamaan lingkaran sehingga

diperoleh suatu persamaan kuadrat.

(54)

www.aswhat82.blogspot.com

Daftar Pustaka

Boediono dan Koster, wayan., 2004. Teori dan Aplikasi Statistika dan Probabilitas. PT Remaja Rosdakarya, Bandung.

Cunayah, Cucun, dkk., 2006. 1700 Bank Soal Bimbingan Pemantapan Matematika: untuk SMA/MA, Penerbit Yrama Widya, Bandung.

Gunawan T.,2000. Matematika SMU Jilid I, II, dan III. Delta Teknik Jakarta, Jakarta. Juliartawan, I Wayan., 2005. Matematika; Contoh Soal dan Penyelesaiannya. Penerbit

Andi Yogyakarta, Yogyakarta.

(55)

www.aswhat82.blogspot.com

PROFIL PENYUSUN

Muhammad Hajarul Aswad A, S.Pd., M.Si, lahir di Bau-Bau pada 3 November 1982. Merupakan anak kedua dari enam bersaudara dari pasangan Drs. Achmad Mustari dan Andi Hasirah.