BAB I
DEFINISI – DEFINISI DAN PENGGUNAANNYA DIDALAM PEMBUKTIAN
Mendifinisikan suatu kata adalah penting, sebab (1) definisi-definisi tersebut dibentuk untuk keperluan manusia dalam kaitannya dengan diskusi, dan (2) setiap definisi yang telah ditetapkan, tidak dapat diubah oleh sembarang salah satu unsurnya yang tidak memperhitungkan yang lain dalam kelompoknya.
Sifat-sifat definisi yang harus ada sebagai berikut.
(1) Kata yang didefinisikan harus ditempatkan dalam kelasnya; pertama-tama kelas yang menunjukkan kumpulan (koleksi) dan memiliki kesamaan sifat.
(2) Perlu menunjukkannya bilamana kata yang didefinisikan tersebut berbeda dari yang lain didalam kelasnya; hal ini dapat dilakukan dengan menambahkan frase (phrase).
(3) kata-kata didalam definisi harus sesederhana mungkin, daripada yang didefinisikan.
(4) Suatu definisi harus dapat dibalikkan.
Menurut jenisnya, definisi terbagi atas definisi demonstratif dan konotatif.. Sedangkan untuk kata yang lebih sederhana, selanjutnya tidak didefinisikan seluruhnya. Kata yang dimaksud seperti kata pertama, istilah primitif, atau unsur dasar istilah, lebih sederhana disebut istilah yang tidak didefinisikan.
Pengertian Pangkal (Undefined Terms)
Terdapat 5 pengertian pangkal dalam geometri sebagai dasar untuk mendefinisikan semua geometri lainnya dalam geometri Euclid, yaitu:
(1) Titik (Point) (2) Garis (Line)
(3) Terletak pada (Lie on); misalnya dua titik terletak pada sebuah garis (4) Diantara (Between); misalnya C diantara titik-titik A dan B
Istilah titik tidak didefinisikan. Meskipun kita tidak mungkin untuk mendefinisikan, tetapi dapat dicoba untuk membuat arti atau penjelasannya. Hal ini dapat dikerjakan dengan mendaftar beberapa sifat atau ciri-cirinya dengan tanpa melakukan klasifikasi. Suatu kata yang tidak dapat didefinisikan, kata tersebut dapat dijelaskan. Perbedaan menjelaskan (deskripsi) dengan mendefinisikan, dapat diterangkan sebagai berikut.
(1) Bila suatu kata tersebut didefinisikan, berarti mengklasifikasikan.
(2) Bila suatu kata tersebut dijelaskan, sifat-sifat kata itu diketahui tanpa mengklasifikasikan.
Beberapa ide tentang sifat-sifat titik yang dipilih, dicoba untuk menggambarkan titik dengan suatu ujung jarum. Hasilnya kita dapatkan bahwa: titik tidak mempunyai panjang atau lebar tetapi menunjukkan letak. Istilah garis tidak didefinisikan. Sifat-sifat garis dapat disebutkan sebagai: garis tidak mempunyai lebar tetapi dapat diperpanjang sejauh yang dikehendaki pada kedua ujungnya. Istilah himpunan (set) tidak didefinisikan. Namun jika dicoba untuk menjelaskan, artinya antara lain sebagai berikut: himpunan adalah sesuatu yang diartikan (well defied) sebagai kumpulan (collection).
Penekanan kata diartikan (well defied), menerangkan sebagai berikut. (1) Jika unsur-unsur himpunan tersebut diketahui, kita dapat menerangkan
bagaimana mendapatkannya.
(2) Dengan diketahui unsur – unsur himpunan tersebut, dapat didaftar anggota-anggotanya.
Istilah diantaranya (betweenness) tidak didefinisikan. Hal ini dapat digambarkan sebagai berikut.
A B C
Pada garis ini, B diantara A dan C. Urutan tidak menjadikan masalah; misalkan dapat diurutkan sebagai A,B,C atau C,B,A. Jika ketiga titik tersebut tidak segaris, B tidak
A,B,C A,C,B B,A,C
Setiap struktur geometri memiliki pembatasan-pembatasan. Misalnya dalam geometri Euclid “setiap dua titik yang berbeda dapat dilukis satu dan hanya satu garis”; sehingga dalam geometri Euclid tidak bisa diterima bahwa melalui dua titik dapat dilukis dua buah garis, sebagaimana Gambar 1.1 berikut ini.
Gambar 1.1
Empat Postulat Pertama Euclid’s
Postulat Euclid-1. Untuk setiap titik P dan setiap titik Q yang tidak sama
P Q
terdapat secara unik sebuah garis yang melalui P dan Q.Secara informal postulat ini dapat dinyatakan dengan “dua buah titik menentukan secara unik sebuah garis”. Selanjutnya garis yang melalui titik-titik P dan Q dinotasikan dengan PQ. Untuk memulai postulat kedua, dapat dibuat definisi pertama
Definisi 1. Diberikan dua buah titik, yaitu A dan B. Segmen AB adalah himpunan titik A, titik B, dan titik-titik yang terletak pada garis AB dan diantara A dan B (Gambar 1.2). Titik A dan titik B dikatakan titik-titik akhir (endpoints) dari segmen AB. Selanjutnya notasi AB digunakan untuk “segmen AB”.
Gambar 1.2
Postulat Euclid-2. Untuk setiap segmen AB dan untuk setiap segmen CD terdapat secara unik titik E sehingga B diantara A dan E, dan segmen CD kongruen dengan segmen BE (Gambar 1.3).
P Q
A C B
Segmen AB
Gambar 1.3 CD BE
Postulat ini kadang-kadang secara informal dapat dikatakah bahwa: “Sembarang segmen AB dapat diperluas oleh sebuah segmen BE yang kongruen dengan segmen CD yang diberikan”. Dalam postulat ini telah digunakan pengertian pangkal tentang “kongruen”. Selanjutnya notasi CD BE digunakan untuk mengungkapkan CD kongruen dengan BE. Untuk melanjutkan ke postulat 3, diawali dulu mengenalkan definisi yang lain sebagai berikut.
Definisi 2. Diberikan dua titik O dan A. Himpunan dari semua titik P sehingga segmen OP kongruen dengan segmen OA disebut lingkaran dengan O sebagai pusat, dan setiap segmen OP disebut dengan jari-jari lingkaran. Diduga bahwa pada pembicaraan sebelumnya disebutkan bahwa OA OA, sehingga A adalah juga titik yang tepat pada lingkaran yang terdefinisi.
Postulat Euclid-3. Untuk setiap titik O dan setiap titik A (O A), terdapat sebuah lingkaran dengan pusat O dan jari-jari OA (Gambar 1.4).
Gambar 1.4 Lingkaran dengan pusat O dan jari-jari OA
Definisi 3. Sinar AB adalah himpunan titik pada garis AB : titik-titik yang dimiliki segmen AB dan semua titik C pada garis AB sehingga B diantara A dan C. Sinar AB
A B E D C P A O
dikatakan memancar dari titik vertek A(emanate from the vertek A) yang merupakan bagian dari garis AB (Gambar 1.5).
Gambar 1.5 Sinar AB
Definisi 4. Sinar AB dan AC bertolak belakang jika keduanya sinar berbeda, memancar dari titik A yang sama, dan keduanya bagian dari garis yang sama
AC
AB (Gambar 1.6).
Gambar 1.6 Sinar Berlawanan
Definisi 4. Sebuah sudut dengan vertek A adalah sebuah titik A dengan dua sinar berbeda dan tidak berlawanan yakni AB dan AC (sisi dari sudut) yang memancar dari A (Gambar 1.7).
Gambar 1.7 Sudut dengan vertek A Untuk sudut di atas, dinotasikan dengan A,BAC,atau CAB.
A B C B A C B A C
Definisi 5. Jika BADdan CAD memiliki sisi bersama yakni sinar AD dan sisi-sisi
lainnya AB dan AC merupakan dua sinar berlawanan, maka sudut yang satu suplemen dari sudut lainnya, atau dua sudut yang saling bersuplemen (Gambar 1.8).
Gambar 1.8 Sudut saling bersuplemen
Definisi 6. Sebuah sudut BAD adalah sudut siku-siku jika memiliki sebuah sudut yang bersuplemen yang kongruen (Gambar 1.9).
Gambar 1.9 Sudut siku-siku BADCAD
Postulat Euclid-4. Untuk semua sudut siku-siku kongruen satu sama lain.
Soal-soal
1. Dari definisi-definisi berikut, manakah yang merupakan definisi yang tidak lengkap ?.
a. Bangku ialah sesuatu yang digunakan untuk landasan menulis. b. Buku sejarah adalah buku yang berisi sejarah.
c. Jika persegi panjang merupakan bujur sangkar, maka keempat sisinya sama. 2. Tulislah definisi no. 1 tersebut, sehingga memenuhi sifat definisi.
3. Definisikan istilsh-istilah berikut :
a. sepatu lari. b. biografi. c. kertas tulis.
4. Apakah mungkin dalam anda mempelajari geomerti akan mendefinisikan istilah B
D
A C
B A C
5. A
5 1 2 2 4 3 B C D
a. Namakan suatu garis pada 1, dengan 2 cara berbeda. b. Namakan suatu garis pada 3, dengan 2 cara berbeda c. Namakan suatu garis pada 4, dengan 6 cara berbeda d. Namakan suatu garis pada 5, dengan 6 cara berbeda e. Namakan suatu garis pada 1, dengan 2 cara berbeda f. Namakan suatu garis pada 2, dengan 2 cara berbeda
6.
a. Namakan suatu sudut pada 1 , dengan 2 cara berbeda . b. Namakan suatu sudut pada 2 , dengan 2 cara berbeda c. Namakan suatu sudut pada 3 , dengan 4 cara berbeda d. Namakan suatu sudut dengan sisi-sisi AB dan AC . e. Namakan suatu sudut dengan sisi-sisi CB dan CA . f. Namakan dua sisi pada <ACB , <ACD , <BCD.
7 Dengan menggunakan sifat-sifat definisi konotatif , terangkan mengapa suatu garis tidak dapat didefinisikan sebagai “ garis adalah himpunan titik-titik “ .
4 A B C 3 2 D 1
8. Pada diagram dibawah ini , bagaimanakah mungkin untuk dapatnya menjelaskan bahwa AB dalam batas-batas AC dan BD , :
D A B C
9. Ilustrasikan bagaimana mungkin dua sinar garis yang mempunyai sebuah titik potong, tetapi gabungannya tidak berupa suatu sudut.
10. Bilamanakah suatu definisi itu berbeda dengan diskripsi.
11. a adalah himpunan titik-titik sebuah garis , b himpunan titik-titik garis kedua , dan c himpunan titik-titik garis ketiga ;
a. gambarlah diagram yang menunjukkan bahwa perpotongan a da b adalah suatu elemen pada c
gambarlah diagaram yang menunjukkan bahwa perpotongan b dan c adalah tiga unsur yang berbeda.
Tes Formatif 1. Perhatikan illustrasi 1. 0 50 ) 1 ( m . Find: a. m(4),m(3) b. m(1)m(2)m(3) c. m(2)m(4) 2. Perhatikan ilustrasi 2
segmenAB dan CDberpotongan,
0 180 ) 4 ( ) 3 ( ) 1 ( m m m and ), 4 ( ) 3 ( m m m(4)m(5).Tentukan ) 6 ( ), 3 ( ), 2 ( ), 1 ( m m m m 3. Perhatikan ilustrasi 3, ) 2 ( and ) 1 ( m m berkomplemen. Buktikan dan ) 3 ( m m(4) berkomplemen. 1 4 2 D 6 5 100 2 1 A 4 C B Ilustrasi 2 4 3 2 1 Ilustrasi 1
4. Perhatikan ilustrasi 4. Manakah pernyataan berikut yang benar. Bila salah, jelaskan alasannya.
a. Sinar GF Memiliki titik pangkal di G.
b. Segmen garis AGtidak memiliki titik akhir.
c. Garis CDmemiliki 3 titik akhir. d. EFtegak lurus AB.
e. AGCFGC
f. GEgaris bagi AGB
5. Perhatikan ilustrasi 5. ABadalah sebuah garis.
a. Sebutkan sudut siku-siku. b. Sebutkan sudut-sudut lancip.
c. Sebutkan pasangan sudut-sudut yang bersisian.
d. Jelaskan mengapa sudut 3 bukan sudut bertolak belakang dengan sudut 1 pada ilustrasi 5.
6. Perhatikan ilustrasi 6. Jika AB ACdan
AE AD , buktikan BD CE. Illustration 5 C A 400 B D 4 E 1 2 3 Ilustrasi 6 E C B D A Ilustrasi 4 900 600 300 900 600 300 E G C D B F A
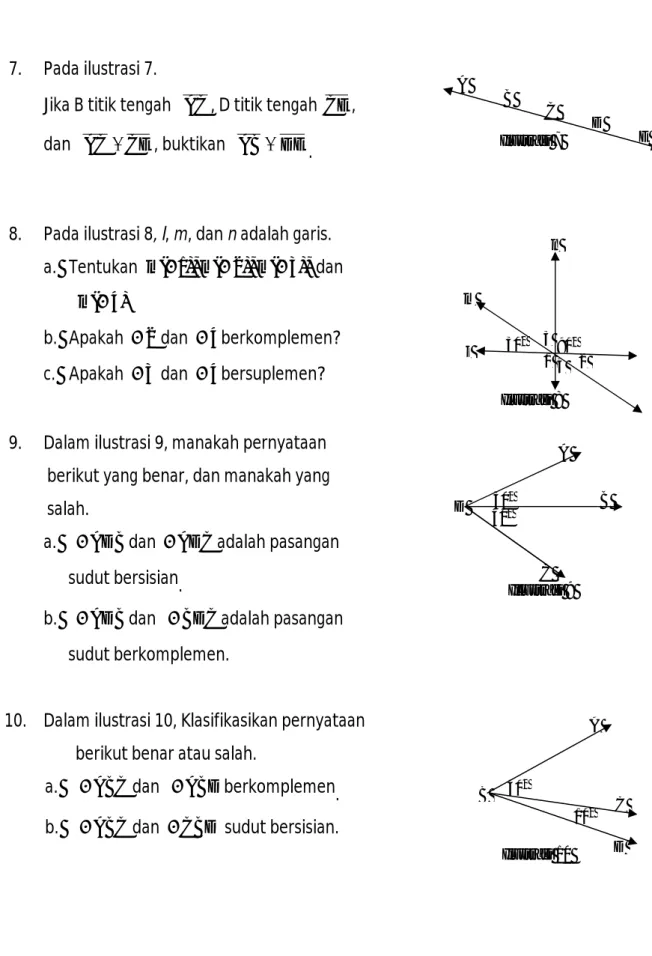
7. Pada ilustrasi 7.
Jika B titik tengah AC, D titik tengah CE, dan AC CE, buktikan AB DE.
8. Pada ilustrasi 8, l, m, dan n adalah garis. a. Tentukan m(1),m(2),m(3), dan
) 4 ( m
b. Apakah 2 dan 4berkomplemen? c. Apakah 3 dan 4bersuplemen?
9. Dalam ilustrasi 9, manakah pernyataan berikut yang benar, dan manakah yang salah.
a. ADBdan ADCadalah pasangan sudut bersisian.
b. ADBdan BDCadalah pasangan sudut berkomplemen.
10. Dalam ilustrasi 10, Klasifikasikan pernyataan berikut benar atau salah.
a. ABCdan ABDberkomplemen.
b. ABCdan CBD sudut bersisian.
Ilustrasi 10 A B 40 0 100 D C Illustrasi 9 A B 300 D 400 C Ilustrasi 8 3 900 2 300 n 1 4 m l Ilustrasi 7 A B C D E
BAB II
DEFINISI – DEFINISI PADA PERISTILAHAN GEOMETRI
DEFINISI 1 : Ruas garis AB adalah himpunan titik-titik dari garis yang memuat titik A dan titik B dan semua titik diantara titik A dan titik B.
A B
Pada titik A, B, dan titik-titik diantaranya, dikatakan meliputi segmen AB. Titik A dan B keduanya disebut titik akhir dari segmen AB. Segmen AB diberi tanda AB , sedangkan garisnya diberi tanda AB
DEFINISI 2 : sinar adalah himpunan titik – titik yang merupakan gabungan dari titik pangkal sinar garis dan semua titik pada sisi yang sama terhadap titik pangkalnya.
Gambar disamping menggambarkan sinar AB dan dinota-
A B sikan AB .
DEFINISI 3 : sinar – sinar yang berlawanan adalah dua sinar berlainan pada garis yang sama dan mempunyai titik pangkal yang sama.
C E A B F Pada gambar disamping, AB dan AC
dua sinar yang berlawanan, yaitu keduanya berlainan sinar, pada garis yang sama ( EF ) dan masing-masing mempunyai titik pangkal A.
DEFINISI 4 : sudut adalah himpunan titik-titik yang merupakan gabungan dua sinar dan kedua titik pangkalnya berserikat.
B
C disebut verteks (titik sudut; pada gambar dapat dituliskan sudut-sudutnya < ACB atau < BCA.
Karena yang dipelajari disini berorientasi pada himpunan (set), maka yang dimaksud AB = CD merupakan persamaan dua himpunan, yaitu masing-masing unsurnya sama dan hanya nama saja yang berbeda. Selanjutnya yang dimaksud ukuran dua garis AB = CD yang ditulis : u AB = u CD berarti menyatakan kesamaan bilangan panjangnya.
Ukuran suatu sudut dapat dijelaskan sebagai berikut :
Pada gambar, titik-titik di setengah lingkaran berkorespondensi 1-1 dengan bilangan real 0-180; sehingga RVA dikatakan sudut 50 derajat (500 ). Derajat merupakan satuan untuk ukuran sudut.
DEFINISI 5: Titik tengah dari luas garis adalah suatu titik ada ruas garis itu sedemikian membentuk dua ruas garis yang sama ukurannya.
• • • U AB = U CB karena C titik tengah AB . B C A R 50 0 B V A 180
DEFINISI 6: Garis bagi ( disektor) dari luas garis adalah garis yang memotong ruas garis pada titik tengahnya.
AB bisektor CD , maka B titik tengah CD , karena B titik tengah CD , maka u CB = u BD .
DEFINISI 7-12 :
7. Sudut siku-siku adalah suatu sudut dari 900. 8 Sudut lurus adalah suatu sudut dari 1800.
9. Sudut lancip adalah suatu sudut yang ukurannya lebih besar 0 dan lebih kecil 90. 10. Sudut tumpul adalah suatu sudut yang ukurannya lebih besar 90 dan lebih kecil
180.
11. Dua sudut saling berkomplemenadalah suatu sudut yang jumlah ukurannya 90. 12. Dua sudut saling bersuplemen adalah dua sudut yang jumlah ukurannya 180.
DEFINISI 13 : Dua garis saling tegak lurus adalah dua garis yang saling berpotongan membentuk sudut siku-siku.
DEFINISI 14 : Garis bagi suatu sudut adalah suatu sinar sedemikian hingga titik pangkalnya titik sudut itu dan membentuk dua sudut yang sama ukurannya dengan kaki sudut itu.
D B
C
Tes Formatif
1. Didasarkan atas sifat suatu garis, terangkan mengapa suatu garis tidak mungkin memiliki titik tengah.
2. Jika pada diagram berikut : U BC = U CD = U DE , maka C dan D disebut “titik-titik triseksi “ BE . Coba anda definisikan tentang “ “titik-titik-“titik-titik ttriseksi suatu segmen garis “.
3. Dari diagram soal no. 2 ; jika U BC = U CD = U DE , maka AC dan AD disebut “ trisektor-trisektor “ BE . Coba anda definisikan tentang “trisektor-trisektor suatu segmen garis “.
4. a. Apakah kkomplemen dari sebarang sudut :
150 , 480 , 10 , 5 1/20 , X0
b. Apakah suplemen dari sebarang sudut yang berukuran : 126 , 57 , 38 , 129 , A +B
5. Dari diagram soal no .2 ; jika u<BAC =u CAD = u<DAC , maka AC dan AD adalah trisektor-trisektor <BAE . Coba anda definisikan tentang “trisektor-trisektor suatu sudut “.
6. a. Apa arti dari ukuran suatu garis ?
b. Mungkinkah untuk segmen garis yang sama akan mempunyai ukuran yang berbeda
jelaskan jawaban anda.
7. Jika VR dan VS adalah subset RS . maka dua kemungkinan apakah yang terjadi , mengenai ukuran <RVS ?.
8. Jika <ABC adalah lancip , apa yang dapat dikatakan mengenai ukuran E
D C
B
9. a. Jika AB BC , implikasinya bahwa B titik tengah AC . Jelaskan jawaban anda
b. Jika <ABC <CBD , implikasinya bahwa BC merupakan bisektor <ABD . Jelaskan jawaban anda !.
10. Pada keadaan yang khusus yang mungkin , daapatkah dituliskan suatu kesamaan AB
= CD ? .
11 a. Berapakah ukuran sudut yang lima kallinya sama besarnya dengan komplemennya
b. Ukuran suatu sudut adalah 15 lebih besar dari dua kali suplemennya . Bilamanakah ukuran sudut tersebut .
12. Definisi sutu sudut refleks adalah “ suatu sudut refleks adalah suatu sudut yang ukurannya lebih besar 180 dan lebih kecil 360 “.
a. Apakah kebalikan definisi tersebut ?
b. Terangkan mengapa sudut refleks tidak dimasukkan / dibicarakan dalam geometri bidang ?.
c. Bilamanakah sudut refleks tersebut diklasifikasikan .
d. Bilamanakah sudut refleks dibedakan dari anggota-anggota yang lain pada kelasnya ? .
BAB III
ASUMSI-ASUMSI DAN PENGGUNAANNYA DIDALAM PEMBUKTIAN
POSTULAT GEOMETRI 1-4 :
1. Sebuah garis dapat diperpanjang sejauh-jauhnya dari kedua ujungnya. 2. Untuk setiap dua titik pada garis, ada titik ketiga yang terletak diantaranya. 3. Ada korespondensi 1-1 antara titik-titik pada garis dengan bilangan-bilangan
real.
4. Ada satu dan hanya satu garis yang melalui dua titik.
POSTULAT 5-11 :
5. Jika a=b dan c=d , maka a+c = b+d. 6. Jika a=b dan c=d , maka a-c = b-d. 7. Jika a=b dan c=d , maka a.c = b.d 8. Jika a=b dan c=d , maka a/c = b/d 9. a=a ; sifat refleksif.
10. Jika a=b , maka b=a ; sifat simetri.
11. Jika a=b dan b=c , maka a=c ; sifat transitif.
DEFINISI 15 : ruas-ruas garis yang kongruen adalah ruas-ruas garis yang mempunyai ukuran sama.
DEFINISI 16 : sudut-sudut yang kongruen adalah sudut-sudut yang mempunyai ukuran sama.
Notasi kongruensi adalah “ “. Perlu diingat bahwa jika u AB = u CD , maka AB CD. Tetapi jika AB CD , belum tentu AB = CD ; yaitu dua ruas garis yang berlainan tetapi ukurannya sama.
DEFINISI 17 : Jumlah dari dua ruas garis AB dan BC adalah AC jika dan hanya jika B diantara A dan C; dapat dilambangkan AB + BC = AC .
DEFINISI 18 : AC terletak diantara ruas garis AB dan BC yang berlainan jika dan hanya jika C diantara A dan B; dilambangkan : AB - BC = AC
DEFINISI 19 : sinar PB terletak diantara sinar PA dan PC berarti u<APB + u<BPC =u< APC.
Agar berlaku konsep terletak diantara, ditegaskan bahwa ukuran sembarang sudut haruslah : 180.
DEFINISI 20 : Jumlah dari dua sudut , < ABC dan < DBC, adalah < ABD jika dan hanya jika BC diantara BA dan BD ; dapat dilambangkan : < ABC + < DBC = < ABD.
DEFINISI 21 : < CBD terletak diantara dua sudut, < ABD dan < ABC jika dan hanya jika BC diantara BA dan BD ; dapat dilambangkan : < ABD - < ABC = < CBD.
Tes Formatif
1 . Dengan cara apakah suatu postulat terbedakan dari kepercayaan ? .
2. Jika titik-titik A , B dan C unsur-unsur RS , maka kondisi apakah sehingga AC + CB = AB ? .
3 Jika AB dan CD berpotongan pada X dan Y , maka kesimpulan apakah yang dapat ditarik dari hal tersebut ? .
4 Jawablah masing-masing pertanyaan dibawah ini dalam batas gambar yang ada. Jika jawabannya tidak mungkin, cukup tuliskan tak terjawab, (setelah berupa soal bilangan).
EEe a. AD + DB = ? b. CE + ED = ? c AE + ED = ? d. BC - FC = ? e AC - AE = ? f. <AEF = <DEF = ? g <BCD + <BCA = ? h. <AEF = <DEF = ? 5. Suatu ukuran sudut APB = 60 dan u <BPC = 20 .
a. Jika PB diantara PA dan PC , maka u <APC = ? b. “ PC “ PA dan PB , “ u <APC = ? E B F C D A
BAB IV
TEOREMA – TEOREMA SEDERHANA
POSTULAT 12 :
pernyataan kondisional : jika P, maka q
dan menyatakan kebenaran P : diketahui P ( antesenden ) berakibat benarnya q : jadi q ( konsekuen ). Contoh : jika AB CD , maka <1 dan <2 masing – masing sudut siku – siku.
Diketahui : AB CD .
Jadi <1 dan <2 masing – masing sudut siku – siku.
TEOREMA 1 : Jika dua sudut siku – siku, maka keduanya kongruen. Cara pembuktian :
Diketahui : < A sudut siku -siku.
< B sudut siku -siku.
Buktikan : < A < B Bukti : Pernyataan Alasan 1. < A siku-siku 2. u < A = 90 3. < B siku-siku 4. u < B = 90 5. u < A = u < B 6. < A < B 1. Diketahui
2. Def. sudut siku-siku 3. Diketahui
4. Sama no. 2
5. Sifat transitif dari kasamaan 6. Def. kongruensi
Catatan : sudut dapat dinamakan dengan sebuah huruf saja; yaitu dengan titik sudutnya.
B A
TEOREMA 2 : jika dua sudut adalah sudut lurus, maka keduanya kongruen. (Bukti seperti Teorema 1).
TEOREMA 3 : jika dua sudut saling bersuplemen pada sudut yang sama, maka keduanya kongruen. Pembuktian : Diketahui : < B suplemen pada < A < C suplemen pada < A Buktikan : < B < C Bukti : Pernyataan Alasan
1. < B suplemen dari <A 2. u < B + u < A = 180 3. u < B = 180 – u < A 4. < C suplemen dari < A 5. u < C + u < A = 180 6. u < C 180 – u < A 7. u < B – u < C 8. < B < C 1. Diketahui
2. Def. dua sudut yang bersuplemen 3. Postulat pengurangan dari kesamaan 4. Diketahui
5. Sama No. 2 6. Sama No. 2 7. Sifat Transitif
8. Def. Kongruensi sudut
TEOREMA 4 : Jika dua sudut saling berkomplemen pada sudut yang sama, maka kedua sudut itu kongruen. (Bukti seperti teorema 3).
C
Pembuktian : Diketahui :
< ABD bersuplemen terhadap < 1. < EFH bersuplemen terhadap < 2. < 1 < 2.
Buktikan : < ABD < EFH.
Bukti :
Pernyataan Alasan
1. < ABD bersuplemen terhadap < 1 2. < ABC sudut lurus
3. < EFH bersuplemen terhadap < 2 4. < EFG adalah sudut lurus
5. < ABC < EFG 6. < 1 < 2 7. < ABD < EFH
(isilah kolom ini sebagai latihan)
TEOREMA 6 : jika dua sudut berkomplemen terhadap dua sudut yang kongruen, maka keduanya kongruen (Bukti seperti Teorema 5).
DEFINISI 22 : dua sudut bertolak belakang adalah dua sudut sedemikian rupa hingga kaki – kaki dari dutu itu yang satu merupakan sinar yang berlawanan dengan kaki- kaki sudut yang lain.
A B C D 1 E F G H 2
TEOREMA 7 : jika dua sudut saling bertolak belakang, maka keduanya kongruen. (Bukti sebagai latihan).
TEOREMA 8 : jika a = x dan b = y sedangkan x = y, maka a = b. (Bukti sebagai latihan).
TEOREMA 8a : jika dua ruas garis kongruen dengan dua ruas garis yang kongruen, maka keduanya kongruen. (Bukti sebagai latihan).
TEOREMA 8b : jika dua sudut kongruen dengan dua sudut yang kongruen. (Bukti sebagai latihan).
Tes Formatif
Pada masing-masing soal berikut , pernyataan yang dilengkapi alasan adalah benar atau tidak benar. Jelaskan jawaban anda untuk setiap kejadian ini :
1. Jika hujan , kita tidak pergi ke dansa. Sekarang tidak hujan .
Jadi kita pergi ke dansa.
2. Jika AB CD , maka <1 dan <2 sudut siku-siku.
Diketahui AB CD .
Jadi <1 dan <2 adalah sudut siku-siku.
3. Jika suatu sinar adalah bisektor sebuah sudut , maka terbertuk dua sudut yang kongruen .
Diketahui BA bisektor <B.
Jadi dua sudut kongruen terbenuk. 4. Jika a = b daan c = d , maka a+c = b+d.
a b dan c d . jadi a+c b+d
Apakah benar ?. jika tidak , benarkah alasannya , nyatakan mengapa hal tersebut perlu diberikan.
5. Jika suatu substansi adalah asam , mengubah litmus biru kertas merah. Subtstansi mengubah limus biru kertas merah ,
6. Jika x = -2 , maka x2 =4. Tetapi x2 =4
7. jika sustu sudut adalah kongruen terhadap sudut yang sama, maka mempunyai ukuran-ukuran yang sama.
<A dan <B tidak kongruen terhadap sudut yang sama.
8. AB BC , jika B adalah titik tengah BC . B adalah titik tengah AC 9. <1 bukan sudut siku-siku , jika AB tidak tegak lurus terhadap CD
AB tegak lurus CD.
10. Dua sudut adalah bersuplemen, jika jumlah ukuran-ukurannya adalah 180. u <A + u < B = 180.
11. x adalah unsur B, jika x adalah unsur A. x adalah unsur B.
13. Jika perpotongan AB dan CD adalah himpunan kosong, maka AB dan CD bukan himpunan yang kosong.
BAB V
KONGRUENSI SEGITIGA
DEFINISI 23 : Poligon adalah gabungan himpunan titik-titik P1, P2, P3, . . . P n - 1, Pn
dengan ruas-ruas garis : P1 P2,P2 P3, . . . . P n - 1 Pn , Pn P1. sedemikian rupa hingga jika
dua sebarang dari ruas garis berpotongan, bertitik potong salah satu dari titik P1, P2,
P3, . . . ,
P n - 1, Pn dan tidak ada titik lain.
P1, P2, P3, . . . P n - 1, Pn disebut titik-titik
sudut
Poligon, sedangkan P1 P2,P2 P3, . . . . P n - 1 Pn disebut sisi- sisi poligon.
Suatu poligon dinamakan dengan titik-titik sudutnya secara berurutan dengan cara searah
jarum jam, atau berlawan arah jarum jam.
Contoh : EDCBA, atau ABCDE, dan
sebagainya.
DEFINISI 24 : korespodensi sudut-sudut dari dua poligon adalah dua sudut dengan titik sudut dengan titik sudutnya berpasangan, yang merupakan korespondensi unsur-unsur yang bersesuaian diantara titik sudut-titik sudut dua poligon.
DEFINISI 25 : korespodensi sisi-sisi dari dua poligon adalah dua sisi dengan titik ujung-titik ujungnya berpasangan yang merupakan korespodensi unsur-unsur yang
E D C B A P1 P2 P3 P4 P5 Pn-1 Pn
DEFINISI 26 : dua poligon adalah kongruen, jika ada korespodensi 1-1 diantara titik-titiknya sedemikian rupa hingga: (1) semua sisi yang korespondensi kongruen, dan (2) semua sudut yang korespondensi kongruen.
DEFINISI 27 : segitiga adalah poligon yang bersisi tiga.
POSTULAT 13 : dua segitiga adalah kongruen, jika ada suatu korespondensi diantara titik sudut-titik sudutnya sedemikianrupa hingga dua sisi dan sudut apitnya dari sebuah segitiga kongruen terhadap bagian-bagian yang berkorespondensi segitiga kedua. ( sd – s – sd ).
ABC DEF
POSTULAT 14 : dua segitiga adalah kongruen, jika ada suatu korespondensi diantara titik sudut-titik sudutnya sedemikianrupa hingga dua sudut dan sisi apitnya dari sebuah segitiga kongruen terhadap bagian-bagian yang berkorespondensi segitiga yang kedua. ( sd – s – sd ). ABC DEF F N E D C A B B F D C E A
Contoh : Diketahui : AB DC ; DE AC BC CE Buktikan : DC AC Bukti : Pernyataan Alasan 1. AB DC
2. < ABC sudut siku-siku 3. DE AC
4. < DEC sudut siku-siku 5. < ABC < DEC 6. BC CE 7. < C < C 8. CDE ABC 9. DC AC 1. Diketahui
2. Def. 2 garis saling
3. Diketahui 4. Sama No. 2 5. Def. 6. Diketahui 7. Sifat refleksif 8. ( sd – s – sd )
9. Akibat dari kongruensi dua segitiga
Spesifikasi segitiga :
1. Berdasarkan sisinya : Sebutan/Nama : a. 3 sisinya kongruen segitiga sama sisi b. 2 sisinya kongruen segitiga sama kaki c. tidak ada sisinya yangg kongruen segitiga sembarang
2. Berdasarkan sudutnya : Sebutan/Nama : a. 3 sudutnya sama segitiga sama sudut b. 1 sudutnya siku – siku segitiga siku- siku c. 1 sudut tumpul segitiga tumpul
E D
C B
DEFINISI 28 – 31 tentang : segitiga sama sudut, segitiga siku-siku, segitiga sama sisi, dan segitiga sama kaki. (sebagai latihan).
ABC sama kaki : BC alas segitiga, < B dan < C sudut – sudut alas segitiga, AB dan AC kaki-kaki segitiga. <A dibentuk oleh sisi-sisi yang kongruen, yang disebut : sudut verteks.
DEFINISI 32 A : Interior dari sebuah sudut adalajh suatu himpunan titik-titik
sedemikian rupa hingga jika sebuah sinar yang titik pangkalnya adalah verteks sudut tersebut, ditarik melalui sembarang sebuah titik pada himpunan titik-titik itu, sinar akan terletak diantara sisi-sisi sudut tersebut.
DEFINISI 32 B : Interior pada suatu segitiga adalah himpunan titik-titik yang merupakan persekutuan sembarang dua interior-interior sudut segitiga tersebut.
POSTULAT 15 ( AKSIOMA PASCH ) : suatu garis berinteraksi dengan salah satu sisi segitiga dan masuk pada daerah interiornya, pasti berinteraksi dengan sisi yang kedua dari segitiga tersebut.
POSTULAT 16 : setiap sudut mempunyai bisektor.
TEOREMA 9 : jika dua sisi suatu segitiga adalah kongruen, maka sudut-sudut dihadapan kedua sisi tersebut kongruen. (Bukti sebagai latihan).
TEOREMA 10 : jika dua sudut suatu segitiga adalah kongruen, maka sisi-sisinya dihadapan kedua sudut tersebut kongruen.
C B
Diketahui : < B < C. Buktikan : AB AC Bukti : Pernyataan Alasan 1. < B < C
2. BP dan CQ masing – masing bisektor < ABC dan < ACB
3. BP dan CQ pasti memotong sisi AB dan AC masing – masing pada E dan D 4. < EBC < DBC 5. BC BC 6. EBC DCB 7. BE CD 8. < BDC < BEC 9. < ADC < AEB 10. < ABE < ACD 11. ABC ACD 12. AB AC 1. Diketahui
2. Setiap sudut mempunyai bisektor
3. Aksioma Pasch
4. kongruensi sudut – sudut yang kongruen 5. Sifat reflektif.
6. ( sd – s – sd )
7. Def. kongruensi poligon 8. Def. kongruensi poligon
9. Dua sudut bersuplemen dengan dua sudut yang kongruen.
10. Sama No. 4 11. ( sd – s – sd ) 12. Sama No.7 Q P E D C B A
DEFINISI 33 : garis tinggi pada suatu segitiga adalah suatu segmen yang ditarik dari sembarang verteks ( titik sudut ), tegak lurus terhadap sisi dihadapannya (dapat diperpanjang, jika diperlukan) pada segitiga tersebut.
DEFINISI 34 : garis berat pada suatu segitiga adalah suatu segmen yang ditarik dari sembarang verteks ke titik tengah sisi dihadapan sudut tadi .
DEFINISI 35 : garis bagi pada suatu segitiga adalah suatu segmen yang membagi dua sama ukurannya sembarang sudut pada segitiga dan berujung pada sisi hadapannya.
TEOREMA 11 : jika dua segitiga adalah kongruen terhadap segitiga yang sama, maka kedua saling kongruen, ( Buktikan dengan memakai postulat s – sd – s ).
POSTULAT 17A : jika suatu titik P terletak pada suatu garis yang diketahui, adalah mungkin untuk mendapatkan titik yang kedua Q pada garis tersebut sedemikian rupa sehingga PQ akan kongruen pada sembarang segmen garis AB yang diketahui.
POSTULAT 17B : jika suatu titik diketahui terletak pada suatu garis, ada suatu sudut yang titik sudutnya adalah titik tadi dan satu pada sisinya terhadap garis tadi adalah suatu sinar sedemikianrupa hingga sudut tersebut kongruen dengan sembarang sudut yang diketahui.
Penjelasan :
Dengan garis l yang diketahui dan titik P pada l, adalah mungkin untuk mendapatkan titik kedua Q pada l, sehingga PQ kongruen dengan segmen AB yang diketahui.
P Q l
B A
Titik P pada garis PQ adalah mungkin untuk mendapattkan suatu sudut (misalnya ) RPQ sedemikinrupa hingga kongruen dengan ABC yang diketahui.
TEOREMA 12 : dua segitiga adalah kongruen jika ada suatu korespondensi diantara titik sudut-titik sudutnya, ketiga sisi pada sebuah segitiga adalah kongruen terhadap sisi-sisi yang korespondensi pada segitiga yang lain. ( s – s – s ) I. II. Q P R C B A F E D C B A S E F D C B A R
Diketahui : AB DE BC EF AC DF Buktikan : ABC DEF Bukti : Pernyataan Alasan
1. Titik B pada BC, terdapat < SBC < DEF 2. Memperluas BS sehingga RB DE 3. RC garis yang melalui titik R dan C 4. RA garis yang melalui titik R dan A 5. BC EF 6. DEF RBC 7. RC DF 8. AC DF 9. Jadi AC RC 10. <CAR < CRA 11. AB DE 12. RB DE 13. Jadi AB RB 14. <BAR < BRA 15. <BAC < BRC 16. DEF RBC 17. ABC DEF 1. Postulat 17 2. Postulat garis 3. Postulat garis 4. Idem 5. Diketahui 6. (s-sd-s)
7. Def .kongruensi poligon 8. Diketahui
9. Sifat transitif kongruensi 10. Teorema segitiga sama kaki 11. Diketahui 12. Sama no. 2 13. Sama no. 9 14. Sama no. 10 15. Postulat (+) 16. ( s – ds – s ) 17. Teorema 11
DEFINISI 36 : suatu lingkaran adalah suatu himpunan titik sedemikian rupa hingga segmen garis-segmen garis yang ditarik dari masing-masing titik pada himpunan tersebut ke titik tetap adalah kongruen.
Catatan : notasi lingkaran sebagai O, dan titik tetap
Lingkaran disebut titik pusat.
Menurut gambar, segmen-segmen :
AB, AC, AD kongruen dengan AE , maka gambar
tersebut lingkaran.
DEFINISI 37 : jari-jari suatu lingkaran adalah segmen garis yang ditarik dari sebarang titik pada lingkaran tersebut ke pusat lingkaran.
TEOREMA 13 : semua jari-jari pada suatu lingkaran adalah kongruen. (bukti sebagai latihan).
TEOREMA 14 : dua segitiga siku-siku kongruen, jika ada suatu korespondensi diantara titik sudut-titik suduttnya, hipotenosa dan satu kaki siku-siku segitiga yang satu kongruen dengan yang berkorespondensi pada segi tiga yang lain. (bukti seperti teorema 12).
Dapatkah anda membuktikan bahwa dalam segitiga ABC dengan AB AC , maka <ABC <ACB ?.
Diketahui : ABC AB AC , BD CE.
Buktikan : <ABC <ACB A B C D E A D E
Soal-soal
1. Jika <A <B, <C <F dan <E <D, maka tulislah korespondensi poligon-poligon ACE dan BDF, dan bahwa korespondensi sudut-sudutnya kongruen.
2. Jika RS WY , ST YX dan TR XW , maka tulislah korespondensi diantara poligon-poligon RST dan XYW, dengan korespondensi sisi –sisinya kongruen. Apakah komentar anda selanjutnya ?.
a. Gambarlah suatu diagram untuk poligon-poligon RST dan XYW, dengan korespondensi sisi-sisinya kongruen.
b. Gambarlah poligon untuk ACE dan BDF dari soal no. 1, sudut – sudutnya adalah kongruen. Apakah korespondensi sisi-sisinya juga kongruen ?. Jika sudut yang berkorespondensi kongruen, dapatkah poligon tersebut digambarkan bahwa korespondensi sisi-sisinya tidak kongruen ?.
3. Pada poligon berikut, tulislah suatu korespondensi sisi-sisinya yang kongruen, sebagai tertanda diagram.
a. Apakah sudut-sudut korespondensinya dalam korespondensi juga kongruen ?.
b. Jika sisi-sisi korespondensinya dalam berkorespondensi diantra dua poligon adalah kongruen, maka sudut-sudut korespondensinya juga kongruen ?. A D E H
B C F G
4. Suatu korespondensi ABCD RSTW merupakan kongruensi korespondensi diantara titik sudut-titik sudut poligon ABCD dan RSTW. Apakah akibat dari pernyataan tersebut ?.
5. Dalam hal apakah sehingga mungkin dua segitiga kongruen menurut dua perbedaan kongruensi-kongruensi ?.
6. Jika ada suatu korespondensi diantra titik sudut-titk sudut dua segitiga siku-siku sedemikian hingga sebuah kaki dan sudut lancip dengan titik sudutnya,
merupakan suatu titik ujung kaki dalam segitiga suku-siku yang satu adalah kongruen terhadap bagian-bagian yang berkorespondensi segitiga siku-siku yang lain; mungkinkah kedua segitiga tersebut kongruen ?, jelaskan jawabannya !. 7. Jiak definisi kongruensi poligon-poligon digunakan untuk membuktikan dua
segitiga menjadi kongruen, apakah dapat ditunjukkan kebenarannya ?.
8. Kongklusi apakah yang dapat ditarik, jika garis berat dan garis tinggi terhadap suatu sisi segitiga, merupakan suatu segmen garis yang sama ?.
9. Jika segitiga ABC kongruen dengan segitiga EFG, maka <A <E. Kerjakan implikasi ini, jika ABC EFG, maka maka <A <E .
10. Dengan memakai metode yang sama terhadap hal yang diketahui pada soal no.5, buktikan suatu teorema bahwa : Jika dua sudut suatu segitiga kongruen, maka sisi-sisi dihadapan sudut tersebut adalah kongruen.
Tes Formatif
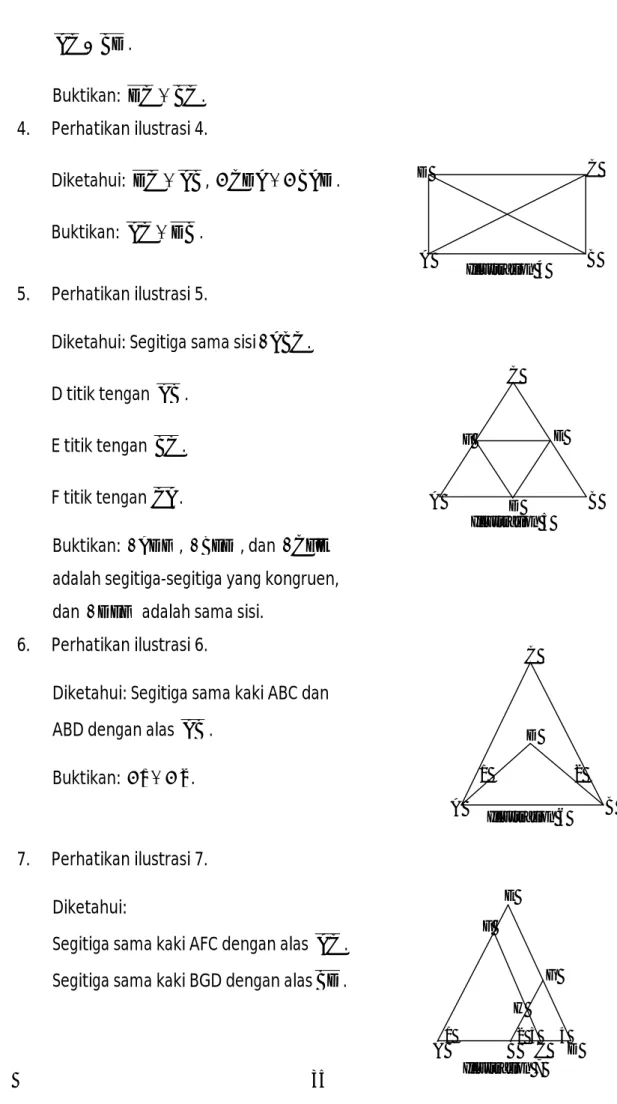
1. Perhatikan ilustrasi 1.
Diketahui: CA DB, CB DA.
Buktikan: ABC BAD.
2. Perhatikan ilustrasi 1.
Diketahui: AD AC, AB AE.
Buktikan: ADBACE.
3. Perhatikan ilustrasi 3. C A E B D Illustration 1 D E B A Illustration 2 F C D C
BD AC .
Buktikan: DC BC. 4. Perhatikan ilustrasi 4.
Diketahui: DC AB, CDABAD.
Buktikan: AC DB.
5. Perhatikan ilustrasi 5.
Diketahui: Segitiga sama sisi ABC . D titik tengan AB.
E titik tengan BC . F titik tengan CA .
Buktikan: ADF , BED , dan CFE adalah segitiga-segitiga yang kongruen, dan DEF adalah sama sisi.
6. Perhatikan ilustrasi 6.
Diketahui: Segitiga sama kaki ABC dan ABD dengan alas AB.
Buktikan: 12.
7. Perhatikan ilustrasi 7. Diketahui:
Segitiga sama kaki AFC dengan alas AC . Segitiga sama kaki BGD dengan alasBD.
Illustration 4 D C B A Illustration 5 F E D C B A Illustration 6 2 1 C D B A H G F E
Segitiga sama kaki BHC dengan alas BC . Buktikan: AED adalah sama kaki.
8. Perhatikan ilustrasi 8.
Diketahui: Titik-titik A, B, dan C segaris. AE
CA , 2 A.
Buktikan: BCF sama kaki.
9. Perhatikan ilustrasi 9.
Diketahui: ABC sama kaki dengan alas
AB. BD AC . BC AE . 2 1 . Buktikan: 34. 10. Perhatikan ilustrasi 10.
Diketahui: ABC sama kaki dengan alas
AB. ) ( ) ( ) (AD m DF m DC m . Illustration 8 G F E D C B A 1 2 A Illustration 9 E D C B 1 3 2 4 F C B 3 4
DC AD
BAB VI KETEGAKLURUSAN
POSTULAT 18 : Jika dua bilangan adalah sama, suatu sibsutitusi pada yang satu ke yang lain diperbolehkan.
DEFINISI 38 : Sinar PB terletak diantara sinar-sinar PA dan PC berarti bahwa u <APB + <BPC = u <APC. (Seperti definisi 19).
DEFINISI 39 : Sudut-sudut ABC dan <DBC berserikat, adalah dus sudut sedemikian hingga keduanya mempunyai titik sudut persekutuan B dan sisi persekutuan BC
yang terletak diantara BA dan BD .
Pada gambar I : B adalah titik sudut serikatnya dan BC sisi serikat yang terletak diantara BA dan BD . Pada gambar II : B adalah titik sudut serikatnya. < ABC merupakan sudut tumpul dan <CBD merupakan sudut lancip, sedemikian
D C B A II D C B A I B C P A
diantara BA dan BD . Cobalah jika <ABC dan <CBD masing-masing sudut tumpul, apa kesimpulan yang anda peroleh untuk selanjutnya ?. (Lihat definisi 19)
TEOREMA 15: Jika dua garis berpotongan membentuk sudut sudut bersisihan yang kongruen, maka dua garis tersebut adalah tegak lurus. (Bukti anda coba).
DEFINISI 40: Jarak antara dua bangun geometri adalah ukuran garis hubung yang terpendek diantaranya.
POSTULAT 19: Garis hubung diantara dua titik adalah segmen garis adalah yang dibentuk oleh dua titik tersebut.
TEOREMA 16 : Jika dua titik masing-masing berjarak sama dari titik ujung-titik ujung suatu segmen garis, maka perpotongan garis persekutuannya merupakan bisektor tegak lurus segmen garis tadi. (Bukti anda coba).
TEOREMA 17 : Jika suatu titik terletak pada bisektor tegak lurus segmen garis, maka titik tersebut berjarak sama dari titik ujung- titik ujung segmen garis. (Bukti sebagai latihan, dan ujilah konversnya)
POSTULAT 20 : Setiap segmen memiliki sebuah titik tengah.
TEOREMA 18 : Jika sebuah titik berjarak sama dari titik ujung-titik ujung sebuah segmen garis, maka titik tersebut terletak pada bisektor tegak lurus segmen garis tersebut. (Bukti anda coba).
Tes Formatif
Pada masing-masing soal ini gambarlah diagramnya, kemudian tulislah yang diketahui dan kesimpulannya, dan lengkapi buktinya :
1. Diketahui : segitiga sama kaki dengan bisektor sudut pada titik sudutnya. Buktikan : bisektor sudut pada titik sudutnya adalah tegak lurus terhadap alas. 2. Diketahui : segitiga samakaki dengan dua garis berat terhadap kaki-kaki.
Buktikan : garis yang ditarik dari titik sudut terhadap titik potong dua garis berat akan tegak lurus terhadap alas.
3. Diketahui : Dua lingkaran berpotongan , sebua ssegmen garis persekutuan dengan titik persekutuannya , dan sebuah garis ditarik dari sebuah lingkkaran ke titik tengah segmen tersebut.
Buktikan : garis tersebut akan melalui pusat lingkaran yang lain.
Pada masing-masing proposisi berikut , gambarlah diagramnya dan tulislah diketahui , buktikan , dan bukti.
4. Jika pada poligon bersisi empat sisi-sisi berhadapannya kongruen , maka garis persekutuan titik sudut-titik sudut yang berhadapan membagi poligon kedalam dua segitiga kongruen.
5. Jika suatu titik berjarak sama dari titik sudut-titik sudut suatu sudut alas segitiga samakaki , maka titik tersebut terletak pada bisektor sudut segitiga.
BAB VII
BUKTI TIDAK LANGSUNG DAN KESEJAJARAN
POSTULAT 21 : jika a, b dan c adalah bilangan-bilangan positif dengan a = b + c, maka a > b dan a > c.
Contoh :
1. Jika 5 = 2 + 3, maka 5 > 2 dan 5 > 3
2. Diketahui: A B C , u AC didefinisikan sebagai u AC = u AB + BC .
Konsekuensi dari postulat tersebut, berarti u AC > u AB dan u AC + u BC .
POSTULAT 22 : keseluruhan adalah lebih besar dari sembarang bagian- bagiannya.
DEFINISI 46 : sudut eksterior (luar) pada suatu poligon adalah suatu sudut yang bersisihan dan bersuplemen terhadap suatu poligon tersebut.
Sudut 4,5,6,7 disebut sudut eksterior ( luar ) pada segitiga ABC dan sudut 1,2,3 adalah sudut interior ( dalam ) segitiga ABC. Sudut 4,5 disebut sudut eksterior tidak bersisihan terhadap sudut 2 dan 3
TEOREMA 22 :ukuran suatu sudut eksterior segitiga adalah lebih besar dari ukuran sudut- sudut interiornya yang tidak bersisihan.
C B A 7 6 5 4
Penjelasannya : karena sudut interior yang tidak bersisihan dari sebuah eksterior segitiga sejumlah dua, maka yang dibuktikan dari hubungan tersebut, haruslah sebanyak dua.
Diketahui: segitiga ABC, ACD sudut eksterior. Buktikan : (1) u ACD u A. (dibuktikan) (3) u ACD u B. (bukti sebagai latihan) Bukti:
Pernyataan Alasan
1. M titik tengah AC
2. BM garis yang ditarik melalui B dan M 3. Perpanjangan BM terdapat P sedemikian
hingga MP BM
4. PC adalah garis yang melalui P dan C 5. AM CM 6. AMB CMP 7. AMB CMP 8. A C1 9. uA = uC1 10. uACD uC1 11. Jadi uACD uA
1. Setiap segmen mempunyai titik tengah 2. Postulat: sebarang 2 titik menentukan garis
3. Sebarang garis dapat diperpanjang sekehendak dari kedua ujung 4. ?
5. Definisi titik tengah 6. ?
7. ?
8. Definisi: kongruensi dari poligon 9. ? 10. ? 11. ? 1 M P D C B A
POSTULAT 23 : Salah satu p atau –p adalah benar, tidak ada kemungkinan lain (Hukum penyisihan jalan tengah).
POSTULAT 24 : p dan –p kedua-duanya tidak dapat benar pada saat yang sama (Hukum kontradiksi).
Eksistensi p dan –p, kedua-duanya dalam suatu pembuktian dikatakan “tidak konsistennya sifat kelogisan” (logical inconsistency), dan untuk hukum kontradiksi kedua-duanya tidak dapat benar pada saat yang sama. Sehingga dalam pembuktian perlu adanya eleminasi.
Dasar kerja dari pembuktian dengan eleminasi, dapat diterangkan sebagai berikut.
1. Ujilah konklusi yang ditanyakan tersebut, selanjutnya untuk dibuktikan. 2. Bentuklah pernyataan yang merupakan kontradiksi dari konklusinya.
3. Setelah menerima pernyataan dari (2), dapatkan pernyataan-pernyataan baru yang mengarah pada adanya kontradiksi terhadap salah satu menurut: (a) adanya data yang diketahui, (b) asumsi, (c) definisi, atau (d) teorema.
4. Konklusi selanjutnya dapat dibenarkan setelah mengeleminasi satu dari dua kemungkinan yang ada, dan satu sisanya pastilah benar. Pembuktian ini disebut “Bukti tidak langsung”. Sedangkan penggunaan pembuktian ini, contohnya dapat dipelajari seperti dibawah ini.
a. Diketahui: F E D C B A
DF AC EF BC DE AB , , Buktikan : BE
Bukti: Misal E B, maka dengan diketahuinya AB DE dan BC EF berakibat ABC DEF. Sehingga AC DF (menurut definisi kongruensi dua poligon). Hal ini bertentangan dengan yang diketahui bahwa
DF tidak
AC . Kesimpulannya pemisalan bahwa B E mengarah pada adanya “tidak konsistennya sifat kelogisan”, yaitu AC DF
dan AC tidak DF. Menurut hukum kontradiksi, keduanya tidak
daapat dibenarkan pada saat yang sama. Jika AC tidak DF harus
benar (menurut data yang diketahui), maka AC DF pastilah salah dan juga lebih salah lagi E B. Jadi B tidak Eyang harus benar dari satu-satunya pilihan yang mungkin.
b. Suatu segitiga tidak dapat mempunyai lebih dari satu sudut tumpul.
Diketahui: Segitiga ABC
Buktikan : ACB dan ABC tidak keduanya sudut tumpul.
D C
B
Bukti:
Misal diterima kemungkinan bahwa ACB dan ABC keduanya sudut tumpul.
ACB dan ACD adalah sudut-sudut yang bersuplemen, jumlahnya merupakan sudut lurus. Sedangkan ACB adalah sudut tumpul yang ukurannya 90o, pastilah ACD sudut lancip yang ukurannya 90o. Dengan demikian u ACD tidak lebih dari u ABC. Hal ini kontradiksi dengan teorema bahwa ukuran sudut pada eksterior segitiga adalah lebih dari sudut-sudut interiornya yang tidak bersisihan. Kesimpulannya, permisalan bahwa ACB dan ABC keduanya tumpul mengarah pada “tidak konsistennya sifat kelogisan”, yaitu u ACD tidak lebih dari u ABC dan u ACD u ABC. Menurut hukum kontradiksi keduanya tidak dapat dibenarkan pada saat yang sama. Jika uACD u ABC harus yang benar (menurut teorema), maka u ACD tidak lebih dari u ABC pastilah salah. Jadi untuk pernyataan bahwa ACB dan ABC keduanya sudut tumpul adalah salah. Tentu pernyataan ACB dan ABC tidak keduanya tumpul harus benar, yang merupakan satu-satunya pilihan yang mungkin.
c.
Bukti:
Diketahui : 1 2
Buktikan : garis l tidak berpotongan dengan m l m 2 1 P l m 2 1
Misal l dan m berpotongan di R, maka terbentuk PQR yang u 1 u 2. Padahal diketahui bahwa u 1 = u 2. Kesimpulannya, pemisalan bahwa l berpotongan dengan m mengarah pada adanya “tidak konsistennya sifat kelogisan”, yaitu u 1 = u 2 dan u 1 u 2. Menurut hukum kontradiksi keduanya tidak dapat dibenarkan pada saat yang sama. Jika u 1 = u 2 benar (menurut yang diketahui), maka u 1 u 2 harus salah. Sehingga pernyataan bahwa l berpotongan dengan m harus benar, yang merupakan satu-satunya pilihan yang mungkin.
DEFINISI 47: garis-garis yang sejajar adalah dua garis yang sebidang dan tidak berpotongan. Garis a sejajar dengan b dinotasikan dengan a//b.
DEFINISI 48 : suatu transversal adalah suatu garis yang memotong dua garis lain di dua titik yang berlainan.
Perhatikan gambar berikut.
n adalah transversal garis l dan m, dan perpotongannya di titik yang berbeda yaitu P dan Q. Sebarang titik A pada n (menurut pembagian letak), terletak pada daerah eksterior; demikian juga untuk A”. Sedangkan A’ terletak di daerah interior. Pembagian daerah ini ditentukan oleh pasangan l dan m dari transversal n.
n m l P Q A’ A’’
DEFINISI 49 : Sudut-sudut berseberangan dalam (alternate angles) adalah dua sudut yang dibentuk oleh transversal yang memotong dua garis; kedua sudut tersebut pada daerah eksterior di sisi yang berlawanan dari transversal, dan titik sudut titik sudutnya berlainan.
DEFINISI 50 : sudut-sudut berseberangan luar (alternate exterior) adalah dia sudut yang dibentuk oleh transversal yang memotong dua garis; kedua sudut tersebut pada daerah eksterior di sisi yang berlawanan dari transversal, dan titik sudut titik sudutnya berlainan.
DEFINISI 51 : sudut-sudut yang sehadap adalah dua sudut yang dibentuk oleh transversal yang memotong dua garis; sudut-sudut tersebut titik sudut titik sudutnya berlainan, satu terletak di daerah interior dan yang lain pada daerah eksteroir tetapi kedua sudut tersebut sepihak dengan transversal.
TEOREMA 23 : jika dua garis dipotong oleh suatu transversal sedemikian hingga sudut-sudut berseberangan dalamnya kongruen, maka kedua garis tersebut adalah sejajar. (buktikan sebagai latihan).
TEOREMA 24 : jika dua garis dipotong oleh suatu transversal sedemikian hingga sudut-sudut sehadapnya kongruen, maka kedua garis tersebut sejajar.
a. Pasangan sudut-sudut yang berseberangan dalam : 8 dan 2, 3 dan 5.
b. Pasangan sudut-sudut yang berseberangan luar : 1 dan 7, 4 dan 6.
c. Pasangan sudut-sudut sehadap : 4 dan 8, 1 dan 5, 3 dan 7, 2 dan 6. 2 3 4 8 5 6 7 1
Bukti: Pernyataan Alasan 1. 1 2 2. 3 2 3. 1 3 4. Jadi n // m 1. Diketahui
2. Dua sudut bertolak belakang 3. Dua sudut berseberangan dalam 4. Teorema 23
TEOREMA 25 : jika dua garis dipotong oleh suatu transversal sedemikian hingga sudut berseberangan luarnya kongruen, maka kedua garis tersebut sejajar (buktikan sebagai latihan).
TEOREMA 26 : jika dua garis keduanya tegak lurus pada garis yang sama, maka kedua garis tersebut sejajar (buktikan sebagai latihan).
POSTULAT 25 : melalui suatu titik yang tidak terletak pada garis yang diketahui ada satu dan hanya satu garis yang sejajar dengan garis yang diketahui tersebut (postulat kesejajaran atau postulat kelima Euclid).
TEOREMA 27 : jika dua garis sejajar dipotong oleh transversal, maka sudut-sudut berseberangan dalamnya kongruen (buktikan sebagai latihan).
Diketahui : 1 2 Buktikan : n//m 2 1 m l
TEOREMA 28 : jika dua garis sejajar dipotong transversal, maka sudut-sudut sehadapnya kongruen. Bukti : Pernyataan Alasan 1. a // b 2. 2 3 3. 1 3 4. Jadi 1 2 1. Diketahui 2. Teorema 27
3. Dua sudut bertolak belakang 4. Sifat transitif kongruensi
TEOREMA 29 : jika dua garis sejajar dipotong oleh transversal, maka sudut-sudut berseberangan luarnya kongruen (buktikan sebagai latihan).
TEOREMA 30 : jika suatu garis tegaklurus terhadap salah satu garis yang sejajar, maka garis tersebut juga tegaklurus terhadap yang lain (Buktikan sebagai latihan).
TEOREMA 31 : melalui titik yang terletak pada garis yang diketahui, tentu ada satu dan hanya satu garis yang tegaklurus terhadap garis tersebut.
TEOREMA 32 : dari suatu titik yang tidak terletak pada suatu garis, ada satu dan hanya satu garis yang tegaklurus terhadap garis yang diketahui tersebut.
Diketahui : a // b Buktikan : 1 2 2 1 b a
DEFINISI 52 : suatu segi empat adalah poligon yang bersisi empat.
DEFINISI 53 : jajar genjang adalah segi empat dengan sisi-sisi yang berhadapan sejajar.
DEFINISI 54 : persegi panjang adalah jajar genjang yang salah satu sudutnya siku-siku.
DEFINISI 55 : persegi adalah persegi panjang dengan dua sisi bersisihannya kongruen.
DEFINISI 56 : belah ketupat adalah jajar genjang dengan dua sisi bersisihannya kongruen.
DEFINISI 57 : trapesium adalah segi empat yang mempunyai satu dan hanya satu pasang sisi sejajar.
DEFINISI 58 : trapesium sama kaki adalah trapezium yang kedua sisi tidak sejajarnya kongruen.
CATATAN :
1. diagonal adalah segmen garis yang ditarik dari sebarang dua sudut yang tidak bersisihan pada poligon.
2. jajar genjang dinotasikan dengan
TEOREMA 34 : sudut-sudut yang berhadapan pada jajar genjang adalah kongruen.
TEOREMA 35 : diagonal-diagonal pada jajar genjang saling merupakan bisector terhadap yang lain.
TEOREMA 36 : semua sisi-sisi pada persegi adalah kongruen.
TEOREMA 37 : semua sisi-sisi pada belah ketupat adalah kongruen.
TEOREMA 38 : sudut-sudut alas pada trapezium sama kaki adalah kongruen.
TEOREMA 39 : jika sisi-sisi yang berhadapan pada segi empat adalah kongruen, maka segi empat tersebut merupakan jajar genjang.
TEOREMA 40 : jika diagonal-diagonal suatu segi empat saling merupakan bisektornya, maka segi empat tersebut merupakan jajar genjang.
TEOREMA 41 : jika segi empat mempunyai sepasang sisi-sisi yang kongruen dan sejajar, maka segi empat tersebut merupakan jajar genjang.
Soal-soal
1. Pada diagram di bawah , buktikan bahwa : u<ACD > u<B (teorema 22).
2. Dapatkah anda menjelaskan suatu pernyataan bahwa sebuah sudut alas suatu segitiga samakaki tidak dapat berupa sudut tumpul ?.
A
C D
3. Seperti no .2 ,untuk seggitiga siku-siku.
4. ABCD adalah poligon bersisi empat . Sedangkan ukuran sudut eksterior sebarang poligon lebih besar daripada ukuran sebarang sudut dalam yang berjauhan . Jelaskan jawaban anda yang terbatas pada poligon ABCD.
5. Segitiga samakaki ABCD , AB AC . Alasan BC diperluas ketitik D . Bisektor sudut ABC dan ACD berpotongan di E.
Dapatkah anda menjelaskan dalam sebarang keadaan apapun juga bahwa sudut ECD tidak dapat berupa sudut dari 300 .
6. Jika suatu sudut segitiga tidak terdapat dua sisi yang kongruen , maka sisi-sisinya dihadapannya tidak kongruen.
7. Jika suatu segitiga tidak terdapatdua sisi yang kongruen , maka bisektor yang tegak lurus satu sisi tidak melalui titik sudut dihadapannya .
8. Suatu sudut hanya mempunyai sebuah bisektor
9. Dari suatu titik yang tidak pada suatu garis yang dikketahui , dapat dibuat hanya sebuah garis yang tegak lurus terhadap garis yang diketahui tersebut.
10. Jika dua garis dipotong oleh transversal sedemikian hingga sudut-sudut yang berkorenspondensi kongruen , maka dua garis tersebut adalah pararel ( sejajar ). ( bukti tidak langsung ).
11. Jika bisektor sudut eksterior suatu segitiga adalah sejajar terhadap salah satu sisinya,
Mak segitiga tersebut samakaki .
12. Dengan bukti tidak langsung ; buktikan jika dua garis sejajar terhadap garis yang A
B
E D
13. Buktikan : Ada sebuah titik pada lingkaran yang berjarak sama dari dua titik lain pada lingkaran . Apakah titik tersebut tunggal ? dimana terdapat yang lain ? . 14. Jika garis-garis persekutuan titik –titik tengah sisi-sisi jajaran genjang
membentuk suatu belah ketupat , maka jajaran genjang tersebut merupakan persegi panjang.
Jika sepasang sudut yang berhadapan pada trapesium adalah bersuplemen , maka trapesium tersebut samakaki.
Tes Formatif
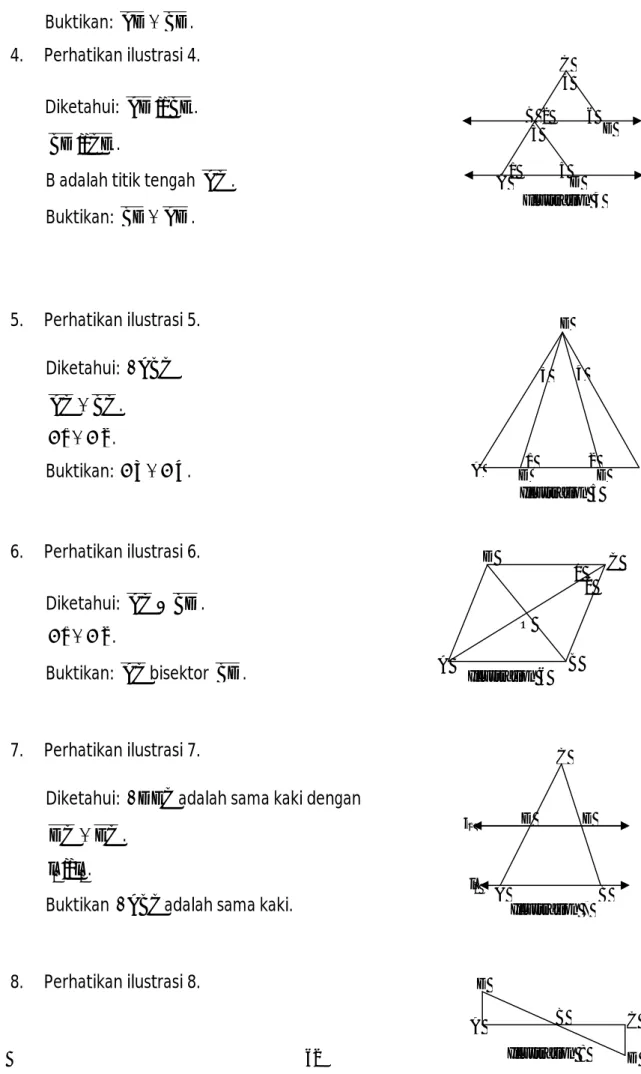
1. Perhatikan ilustrasi 1.
Diketahui: EDC adalah sama kaki dengan alas ED. 1 A . Buktikan: AB //ED. 2. Perhatikan ilustrasi 2.
Diketahui: Segmen AC dan EBbisektor satu sama lain di titik D.
Buktikan: AE //BC. 3. Perhatikan ilustrasi 3. Diketahui: ABE Illustration 1 E D C B A 1 E D Illustration 2 C B A E D C B A
CD AB // . CD AB // DE CE . Buktikan: AE BE. 4. Perhatikan ilustrasi 4. Diketahui: AD //BE. CE BD // .
B adalah titik tengah AC . Buktikan: BE AD. 5. Perhatikan ilustrasi 5. Diketahui: ABC BC AC . 2 1 . Buktikan: 34. 6. Perhatikan ilustrasi 6. Diketahui: AC BD.12. Buktikan: AC bisektor BD. 7. Perhatikan ilustrasi 7.
Diketahui: DEC adalah sama kaki dengan
Illustration 4 E D C B A 6 5 4 3 2 1 Illustration 5 D 3 B 4 A E E 1 2 A Illustration 6 D 1 O 2 C B E D C
Buktikan: ABC adalah sama kaki.
8. Perhatikan ilustrasi 8.
Diketahui: AC dan ED bisektor satu sama lain. Buktikan: AE //CD 9. Perhatikan ilustrasi 9. a. If 0 70 ) (A m dan 0 60 ) (B m , tentukan m ( C). b. If 0 70 ) (A m dan 0 60 ) (C m , tentukan m(1). c. If 0 50 ) (ABC m dan CB AB, tentukan m ( A). d. If 0 135 ) 1 ( m dan AC BC, tentukan ) ( C m . 10. Perhatikan ilustrasi 10. a. Tentukan m(2). b. Tentukan m ( ACB). c. Tentukan m(1). d. Tentukan m(3). Illustration 8 E D C B A Illustration 9 D C B A 1 Illustration 10 E D C B A 2 1 3 700 800
BAB VIII
SUDUT–SUDUT PADA POLIGON
TEOREMA 42 : Jumlah ukuran – ukuran sudut suatu segitiga sama dengan 180o. C 1
1 2 3 Diketahui : segitiga ABC Buktikan :
u < A + u < B + u < 2 = 180o
A B
Bukti :
Pernyataan Alasan
1. 1 adalah garis yang melalui B sedemikian hingga 1 // AB 2. u < 123 = 180o 3. u < 123 = u < 1 + u < 2 + u < 3 = 180o 4. < A < 1 dan < B < 3 5. Jadi u ( < A + < B + < 2 ) = 180o ( sebagai latihan )
TEOREMA 43 : jika dua sudut pada suatu segitiga adalah kongruen terhadap dua sudut segitiga yang kedua, maka sudut yang ketiganya kongruen (buktikan sebagai latihan).
TEOREMA 44 : dua segitiga adalah kongruen jika ada suatu korespodensi diantara 2 F E D C B A
berhadapan pada segitiga yang satu kongruen terhadap bagian–bagian yang berkorespodensi dengan segitiga yang lain (bukti sebagai latihan)
Ilustrasi :
Diketahui : < A < D, AC DF < B < E ,
Buktikan : ABC DEF
TEOREMA 45 : Ukuran sudut eksterior suatu segitiga adalah sama dengan jumlah ukuran – ukuran sudut dalam yang tidak bersisihan (bukti sebagai latihan).
TEOREMA 46 : sudut – sudut lancip pada segitiga siku – siku adalah bersuplemen (bukti sebagai latihan).
DEFINSI 54 : poligon konveks adalah poligon yang masing –masing sudutnya lebih kecil dari sudut lurus.
Poligon Konveks Poligon tidak konveks
TEOREMA 47 : jumlah ukuran-ukuran sudut suatu poligon dengan n sisi adalah 180 (n-2)
Diketahui :
Poligon ABCD …..bersisi n Buktikan :
u<A + u<B + u<C + ……= 180 (n-2) w P f s y F E D C B A E D C B A F D C E B A
Bukti :
Pernyataan Alasan
1. P titik interior poligggon ABCD ….dan PA garis yang melalui p dan A
2. Dibenarkan juga untuk PB , PC , PD , ……..
3. u<I + u<w + u<x =180 u<2 + u<y + u<z = 180 ………. * ………. 4. u<x + u<y = u<A
u<z + u<v = u<B ……… ** ……….
5. u<1 + u<2 + …=360 *** 6. u<P +u<A + u<B = n. 180 7. 360 + u<A + u<B = n. 180 8. u<A + u<B = n. 180 – 360 9. Jadi : u<A + u/B = 180 (n-2) = (n –2).180 (untuk latihan)
TEOREMA 48 : jumlah ukuran-ukuran sudut eksterior suatu poligon yang dibeeentuk oleh perpanjangan sisi-sisi pada urutan yang sama , sama dengan 360 (bukti sebagai latihan).
Diketahui : poligon ABCD …. dengan n sisi
Buktikan : jumlah ukuran-ukuran sudut eksterior =360o Ilustrasi :
u<D + u<E + …= n. 180o
(u<D2 + u<E4 + u<B8 + …) + (u<D1 + u<E3 + u<B7 +…) = n. 180o (n – 2 ). 180 + ( u<D1 + u<E3 + u<B7 + …) = n. 180o
n. 180 – 360 + (u<D1 + u<E3 + u<B7 + …) = n. 180o Jadi , u<D1 + u<E3 + u<B7 + …= 360o.
POSTULAT 26 : diketahui sebarang dua bilangan a dan b , satu dan hanya satu diantara tiga hubungan a<b , a=b , a.>b adalah benar (eksistensi dan ketunggalan urutan).
POSTULAT 27 : diketahui sebarang tiga bilangan a,b dan c dengan a.>b dan b>c, maka a>c (sifat transitif dari urutan).
Contoh : A 5 6 3 4 1 2 D 8 10 B 9 7 C E 1 D A
Diketahui : segitiga ABC u AC > u AB Buktikan : u < ABC > u<C
Bukti : (sebagai latihan)
Petunjuk : ukuran AB AD , dan tunjukkan u<D1 > u<C.
Soal-soal
1. Pada diagram sebelah , BD dan CD adalah bisektor sudut eksterior EBC dan FCB .
Tunjukkan dengan sebarang cara bahwa : u<D = 90 – ½ u<A
2. Dari titik tengah dari sebuah sisi segitiga , segmen-segmen ditarik tegak lurus terhadap dua sisi yang lain . Jika kedua segmen yang tegak lirus tersebut tidak kongruen , maka kedua sisi tersebut tidak kongruen . (tunjukkan dengan bukti tidak langsung ).
3. Ukuran masing-masing sudut pada sebuh poligon bersudut sama adalah lima kali sam dengan ukuran sebuh sudut eksterior poligon tersebut . Apa nama poligon itu ?.
4. Berapa bannyaknya sisi suatu poligon , jika jumlah ukuran sudut-sudutnya lima kali sama dengan jumlah ukuran sudut-sudut eksterior ? .
F E D C B A
u DA u CB Buktikan : u<C u <D
6. Jelaskan mengapa sebuah sudut pada poligon bersudut sama , tidak dapat 130o ? .
Tes Formatif
1. Perhatikan ilustrasi 1.
Diketahui: EDC adalah sama kaki dengan alas ED. 1 A . Buktikan: AB //ED. 2. Perhatikan ilustrasi 2.
Diketahui: Segmen AC dan EBbisektor satu sama lain di titik D.
Buktikan: AE //BC. 3. Perhatikan ilustrasi 3. Diketahui: ABE CD AB // . CD AB // DE CE . Illustration 1 E D C B A 1 E D Illustration 2 C B A E Illustration 3 D C B A
Buktikan: AE BE. 4. Perhatikan ilustrasi 4.
Diketahui: AD //BE. CE
BD // .
B adalah titik tengah AC . Buktikan: BE AD. 5. Perhatikan ilustrasi 5. Diketahui: ABC BC AC . 2 1 . Buktikan: 34. 6. Perhatikan ilustrasi 6. Diketahui: AC BD. 2 1 . Buktikan: AC bisektor BD. 7. Perhatikan ilustrasi 7.
Diketahui: DEC adalah sama kaki dengan EC
DC .
2 1// l
l .
Buktikan ABC adalah sama kaki.
Illustration 4 E D C B A 6 5 4 3 2 1 Illustration 5 D 3 B 4 A E E 1 2 A Illustration 6 D 1 O 2 C B Illustration 7 l2 l1 D E C B A
Diketahui: AC dan ED bisektor satu sama lain. Buktikan: AE //CD 9. Perhatikan ilustrasi 9. a. If 0 70 ) (A m dan 0 60 ) (B m , tentukan m ( C). b. If 0 70 ) (A m dan 0 60 ) (C m , tentukan m(1). c. If 0 50 ) (ABC m dan CB AB, tentukan m ( A). d. If 0 135 ) 1 ( m dan AC BC, tentukan ) ( C m . Illustration 9 D C B A 1
DAFTAR PUSTAKA
Greenberg, M.J. 1993. Eucledian and Non-Eucledian Geometries. New York: Freeman and Company.
Gustafson, R.D. 1991. Elementary Geometry. New York: John Wiley & Sons. Inc.
Kusno. 2002. Geometri Euclid Bidang Studi Luas Poligon, Lingkaran, dan Deformasi Objek Geometri Bidang. Jember: Fakultas Matematika dan Ilmu Pengetahuan Alam.
Lewis, H. 1968. Geometry a Contemporary Course. New York: Van Nostrand Company.
Moise, M.M. Elementary Geometry From an Advanced Standpoint. London: Addison Wesley.