PERBANDINGAN KEMAMPUAN KONEKSI MATEMATIS DAN
KEMANDIRIAN BELAJAR ANTARA SISWA YANG MEMPEROLEH
PEMBELAJARAN INKUIRI DAN PROBLEM BASED LEARNING
(Penelitian Quasi Eksperimen terhadap SMP Swasta di Kab. Bandung)
TESIS
Diajukan Untuk Memenuhi Sebagian Dari Syarat Memperoleh Gelar
Magister Pendidikan Program Studi Pendidikan Matematika
Di Susun Oleh:
NENG SORAYA LATIFAH
1308097
PROGRAM STUDI PENDIDIKAN MATEMATIKA
SEKOLAH PASCASARJANA
UNIVERSITAS PENDIDIKAN INDONESIA
PERNYATAAN
Dengan ini saya menyatakan bahwa tesis yang berjudul “Perbandingan
Kemampuan Koneksi Matematis Dan Kemandirian Belajar Antara Siswa Yang
Memperoleh Pembelajaran Inkuiri Dan Problem Based Learning (Penelitian Quasi Eksperimen Terhadap SMP Swasta di Kab. Bandung).” beserta seluruh isinya adalah benar-benar karya saya sendiri, dan saya tidak melakukan
penjiplakan atau pengutipan dengan cara-cara yang tidak sesuai dengan etika
keilmuan yang berlaku dalam masyarakat keilmuan. Atas pernyataan ini, saya siap
menanggung sanksi yang dijatuhkan kepada saya apabila kemudian ditemukan
adanya pelanggaran terhadap etika keilmuan dalam karya saya ini, atau ada klaim
dari pihak lain terhadap keaslian karya saya ini.
Bandung, Juli 2015
Yang membuat pernyataan
LEMBAR PENGESAHAN
Tesis
PERBANDINGAN KEMAMPUAN KONEKSI MATEMATIS DAN KEMANDIRIAN BELAJAR ANTARA SISWA YANG MEMPEROLEH
PEMBELAJARAN INKUIRI DAN PROBLEM BASED LEARNING (Penelitian Quasi Eksperimen terhadap SMP Swasta di Kab. Bandung)
Oleh
Neng Soraya Latifah 1308097
Disetujui dan disahkan Oleh, Pembimbing
Dr. Elah Nurlaelah, M.Si NIP. 196411231991032001
Mengetahui,
Ketua Program Studi Pendidikan Matematika
ABSTRAK
Neng Soraya Latifah. (1308097). Perbandingan Kemampuan Koneksi Matematis Dan Kemandirian Belajar Antara Siswa Yang Memperoleh Pembelajaran Inkuiri Dan Problem Based Learning (Penelitian Quasi Eksperimen Terhadap SMP Swasta di Kab. Bandung).
Penelitian ini bertujuan untuk mengetahui: (1) perbedaan pencapaian kemampuan koneksi matematis antara siswa yang mendapatkan pembelajaran Inkuiri dan pembelajaran problem based learning, (2) perbedaan peningkatan kemampuan koneksi matematis antara siswa yang mendapatkan pembelajaran Inkuiri dan pembelajaran problem based learning, (3) perbedaan peningkatan kemandirian belajar antara siswa yang mendapatkan pembelajaran Inkuiri dan pembelajaran problem based learning. Penelitian ini merupakan penelitian kuasi eksperimen yang terdiri dari kelas eksperimen yang memperoleh pembelajaran Inkuiri dan pembelajaran problem based learning. Populasi dalam penelitian ini adalah seluruh siswa kelas VII di salah satu SMP Swasta di Kab. Bandung dengan sampel diambil dua kelas dari lima kelas yang ada. Instrumen penelitian meliputi tes kemampuan koneksi matematis dan angket skala kemandirian siswa. Pengolahan data dilakukan dengan Uji-t dan uji Mann-Whitney. Hasil penelitian menunjukan bahwa (1) Tidak terdapat perbedaan pencapaian kemampuan koneksi matematis siswa yang menggunakan pembelajaran Inkuiri dan pembelajaran Problem Based Learning. (2) Tidak terdapat perbedaan peningkatan kemampuan koneksi matematis yang menggunakan pembelajaran Inkuiri dan pembelajaran Problem Based Learning. (3) Tidak terdapat perbedaan peningkatan kemandirian belajar yang menggunakan pembelajaran Inkuiri dan pembelajaran Problem Based Learning.
BAB I
PENDAHULUAN
A. Latar Belakang Masalah
Perubahan berbagai aspek kehidupan sangat dipengaruhi oleh perkembangan ilmu pengetahuan dan teknologi modern yaitu sebagai penunjang
segala aktivitas dan kebutuhan setiap orang. Matematika sebagai salah satu mata
pelajaran di sekolah merupakan salah satu ilmu dasar yang mempunyai peranan
penting dalam ilmu pengetahuan dan perkembangan teknologi dikarenakan
hampir di setiap disiplin ilmu matematika selalu digunakan baik dalam bahasan
yang sederhana sampai dengan bahasan yang sangat rumit. Sehingga matematika
perlu dikuasai dengan baik agar dapat dengan mudah mengantarkan kita
memahami ilmu-ilmu lainnya. Karena dalam matematika siswa pada akhirnya
mampu untuk berpikir logis, cermat dan kritis.
Namun pada kenyataanya prestasi siswa dalam mata pelajaran matematika
masih harus ditingkatkan. Salah satunya pemahaman siswa akan simbol yang
abstrak dan keterkaitannya fungsi matematika dalam kehidupan sehari-hari
menjadi hal yang perlu diasah dan ditingkatkan. Kebanyakan siswa hanya
menghafal rumus dan cara mengerjakannya, tanpa tahu makna apa yang
dipelajarinya dan kesulitan menyajikan masalah sehari-hari pada matematika.
Siswa tidak kesulitan menyelesaikan masalah-masalah matematika yang tidak rutin.
Siswa dalam mempelajari matematika seringkali menghadapi masalah,
karena kebanyakan dari mereka tidak berhasil dalam menyelesaikannya.
Matematika merupakan alat yang ampuh dalam pemecahan berbagai masalah ilmu
pengetahuan dan teknologi. Matematika juga dapat melatih kamampuan berpikir
logis, kritis, sistematis, kreatif dan kemampuan untuk dapat bekerjasama secara
efektif. Sikap dan cara berpikir ini salah satu nya dapat dikembangkan melalui
proses pembelajaran matematika, karena matematika memiliki struktur dan
siapapun yang mempelajarinya terampil berpikir rasional dalam memecahkan
masalah.
Pembelajaran matematika yang diberikan harus dapat mengasah siswa
agar mereka memiliki kompetensi dasar dalam matematika sesuai dengan tujuan
umum pembelajaran matematika yang dirumuskan National Council of Teachers of Mathematics (2000) yaitu:
1. Belajar untuk berkomunikasi (mathematical communication)
2. Belajar untuk bernalar (mathematical reasoning)
3. Belajar untuk memecahkan masalah (mathematiccal problem solving)
4. Belajar untuk mengaitkan ide (mathematical connection)
5. Pembentukan sikap positif terhadap matematika (positive attitudes towars
mathematics)
Hal tersebut sejalan dengan tujuan pembelajaran matematika yang
tercantum dalam permendikbud No. 58 tahun 2014 yang menyatakan bahwa
kecakapan matematika yang ditumbuhkan pada siswa merupakan sumbangan
mata pelajaran matematika kepada pencapaian kecakapan hidup yang ingin
dicapai melalui kurikulum matematika. Mata pelajaran matematika bertujuan agar
peserta didik dapat:
1. Memahami konsep matematika, merupakan kompetensi dalam menjelaskan keterkaitan antarkonsep dan menggunakan konsep maupun algoritma, secara luwes, akurat, efisien, dan tepat, dalam pemecahan masalah.
2. Menggunakan pola sebagai dugaan dalam penyelesaian masalah, dan mampu membuat generalisasi berdasarkan fenomena atau data yang ada.
3. Menggunakan penalaran pada sifat, melakukan manipulasi matematika baik dalam penyederhanaan, maupun menganalisa komponen yang ada dalam pemecahan masalah dalam konteks matematika maupun di luar matematika (kehidupan nyata, ilmu, dan teknologi) yang meliputi kemampuan memahami masalah, membangun model matematika, menyelesaikan model dan menafsirkan solusi yang diperolehtermasuk dalam rangka memecahkan masalah dalam kehidupan sehari-hari (dunia nyata).
4. Mengkomunikasikan gagasan,penalaran serta mampu menyusun bukti matematika dengan menggunakan kalimat lengkap, simbol, tabel, diagram, atau media lain untuk memperjelas keadaan atau masalah.
matematika dan pembelajarannya, seperti taat azas, konsisten, menjunjung tinggi kesepakatan, toleran, menghargai pendapat orang lain, santun, demokrasi, ulet, tangguh, kreatif, menghargai kesemestaan (konteks, lingkungan), kerjasama, adil, jujur, teliti, cermat, bersikap luwes dan terbuka, memiliki kemauan berbagi rasa dengan orang lain.
7. Melakukan kegiatan–kegiatan motorik yang menggunakan pengetahuan matematika.
8. Menggunakan alat peraga sederhana maupun hasil teknologi untuk melakukan kegiatan-kegiatan matematika.
Usaha awal yang harus dilakukan guru adalah bagaimana siswa menguasai
konsep matematika. Konsep menjadi landasan bagi jaringan ide yang menuntun
pemikiran siswa ke arah pemikiran yang lebih tinggi. Mempelajari konsep sangat
penting di sekolah sebagai bekal dalam kehidupan sehari-hari karena konsep
memungkinkan manusia untuk saling memahami dan menjadi dasar untuk
berinteraksi secara verbal.
Kemampuan koneksi merupakan salah satu tujuan dari belajar matematika.
Kemampuan koneksi matematika siswa diupayakan agar siswa dapat
menyelesaikan masalah yang saling berkaitan, menghubungkan ide – ide
matematika antar topik dalam matematika itu sendiri, mengubungkan topik
matematika dengan pelajararan lain ataupun topik matematika dengan kehidupan
sehari-hari. Selain kemampuan koneksi matematika, kemampuan pemecahan
masalah merupakan pendukung yang sangat penting agar siswa dapat
menyelesaikan masalah-masalah yang tidak rutin. Sebagaimana yang disarankan
oleh Ausubel (Ruseffendi, 2006) bahwa,
“Sebaiknya dalam pembelajaran digunakan pendekatan yang menggunakan
metode pemecahan masalah, inquiry, dan metode belajar yang dapat menumbuhkan berpikir kreatif dan kritis, sehingga siswa mampu menghubungkan/mengoneksikan antara masalah matematika, pelajaran lain
ataupun masalah yang berkaitan dengan kehidupan nyata”
Fenomena yang terjadi di lapangan menunjukkan bahwa kemampuan
koneksi matematis siswa masih rendah, sebagaimana dengan hasil penelitian
terdahulu Kurniawan (2011) dalam penelitiannya mengemukakan bahwa hasil tes
awal kemampuan koneksi matematis dari dua kelas masing-masing 30,54% dan
mempengaruhi kualitas belajar siswa, yang berdampak pula pada rendahnya
prestasi belajar siswa di sekolah.
Hal ini terlihat dari hasil pembelajaran siswa di berbagai jenjang
pendidikan yang tersirat dalam beberapa hasil penelitian para praktisi salah
satunya pengamatan yang telah dilakukan Kusmaydi (2010) menurutnya sebagian siswa mempunyai kemampuan rendah dalam pelajaran matematika. Hal ini
terlihat dari: 1) Kebanyakan siswa tidak mengetahui dan tidak mengerti materi
mana yang ada hubungannya dengan materi yang akan dipelajari berdasarkan
pertanyaan yang diajukan guru berkaitan dengan materi yang telah dipelajari
sebelumnya; 2) Masih banyak siswa yang tidak mampu menyatakan benda nyata,
gambar dan diagram ke dalam ide matematika dan juga tidak mampu menyatakan
peristiwa-peristiwa sehari-hari ke dalam bahasa atau bentuk simbol; 3) Sebagian
besar siswa tidak dapat menyelesaikan masalah-masalah yang berkaitan dengan
dunia nyata atau masalah yang ada di sekitar siswa; 4) Ada siswa yang mampu
menyelesaikan suatu masalah matematika tetapi tidak mengerti apa yang
dikerjakannya atau kurang memahami apa yang terkandung didalamnya. Seperti
halnya Coxford (1995) menyatakan bahwa mayoritas siswa tidak bisa
menghubungkan pengetahuan yang mereka miliki dengan konten matematika,
serta bisa tidak menghubungkan konten matematika dalam bidang studi lain dan
kehidupan nyata.
Hal ini erat kaitannya dengan kemandirian belajar matematika siswa itu sendiri, jika kemandirian belajarnya baik, maka pengetahuan prasyaratnya juga
akan baik. Kemandirian belajar matematika siswa merupakan faktor yang sangat
penting dalam menentukan keberhasilan mereka dalam belajar matematika.
Perkembangan teknologi yang sangat pesat berakibat pula pada semakin
banyaknya sumber-sumber belajar yang bisa diakses; hal ini akan sangat
mendukung bagi siswa yang punya kemandirian belajar yang tinggi.
Menurut Zimmerman (1995) kemandirian belajar atau Self Regulated
Learning adalah proses yang kita gunakan untuk aktif untuk mempertahankan
pemikiran, perilaku, dan emosi diri untuk mencapai tujuan. Kemandirian belajar
diri sendiri dalam belajar. Siswa yang memiliki kemandirian belajar yang tinggi
biasanya akan memiliki kemampuan matematika yang baik, hal ini dikarenakan
mereka lebih rajin dalam mempelajari matematika walaupun tidak atas perintah
guru di sekolah.
Kemandirian belajar dan kemampuan koneksi matematis siswa saling mempengaruhi, diantara keduanya terdapat hubungan satu sama lain.
Kemandirian belajar siswa akan berpengaruh terdapat tinggi rendahnya
kemampuan koneksi matematis siswa. Hal ini sejalan dengan hasil penelitian yang
telah dilakukan Qohar (2010), yang mengemukakan bahwa: (1) siswa yang
kemampuan koneksi matematisnya tinggi, sedang maupun rendah, maka
kemandirian belajar matematikanya cenderung sedang; (2) siswa yang
kemandirian belajar matematikanya tinggi, maka kemampuan koneksi
matematisnya cenderung sedang atau tinggi; (3) siswa yang kemandirian belajar
matematikanya sedang, maka kemampuan koneksi matematisnya cenderung
sedang; (4) siswa yang kemandirian belajar matematikanya rendah, maka
kemampuan koneksi matematisnya cenderung sedang.
Salah satu upaya untuk meningkatkan kemampuan koneksi matematis
siswa dan kemandirian belajar siswa adalah penggunaan pendekatan pembelajaran
yang tepat. Kegiatan pembelajaran perlu diupayakan yang dapat memaksimalkan
aktifitas siswa sehingga dapat mengembangkan kreatifitas siswa dan kemampuaan
siswa secara mandiri, mendorong siswa untuk menggali pengetahuan secara mandiri, dan melatih siswa dalam membuat kesimpulan. Sehingga pengetahuan
tersebut dapat tertanam dalam diri siswa secara mendalam, tidak mudah untuk
dilupakan.
Berdasarkan karakteristik tersebut, salah satu pendekatan yang dapat
digunakan yaitu pembelajaran Inkuiri yaitu suatu rangkaian kegiatan
pembelajaran yang menekankan pada proses berpikir secara kritis dan analitis
untuk mencari dan menemukan sendiri jawaban dari suatu masalah yang
dipertanyakan (Sanjaya, 2006). Pada pembelajaran inkuiri siswa mempunyai
prosesnya materi pembelajaran tidak diberikan secara langsung, dimana guru
sebagai fasilitator dan pembimbing siswa dalam belajar.
Langkah-langkah pembelajaran inkuiri yaitu, siswa dihadapkan dengan
suatu masalah, siswa mengajukan dugaan sementara, mengumpulkan data, siswa
menguji dugaan sementara, dan siswa merumuskan kesimpulan. Suchman (Joyce, et all, 2009) mengemukakan pembelajan inkuiri melibatkan siswa secara aktif
dalam suatu prosedur ilmiah dimana siswa harus mengolah informasi pengetahuan
dan menghasilkan suatu prinsip. Pendekatan pembelajaran Inkuiri mengajarkan
siswa untuk mengembangkan keterampilannya dan bahasa penelitian ilmiah.
Problem Based Learning juga merupakan sebuah pendekatan
pembelajaran yang menyajikan masalah kontekstual sehingga merangsang siswa
untuk belajar. Pembelajaran yang dilaksanakan secara berkelompok menantang
siswa untuk mencari solusi dari permasalahn dunia nyata, membuat siswa mahir
dalam memecahkan masalah, dan dapat mencari sendiri penyelesaian dari sebuah
masalah.
Problem Based Learning memberikan kesempatan kepada siswa untuk
memahami konsep atau materi pelajaran untuk menemukan masalah terlebih
dahulu dengan pengetahuan awal yang telah mereka miliki. Siswa diharuskan
menemukan masalah terlebih dahulu, menyatakan masalah, mengumpulkan fakta,
membangun pertanyaan-pertanyaan, mengajukan hipotesis, meneliti kembali
masalah dengan cara lain, membangun alternatif penyelesaian, dan mengusulkan solusi (Fogarty, 1997). Pendekatan pembelajaran ini memungkinan siswa untuk
memanfaatkan pengetahuan awalnya adalam mengembangkan dan menerapkan
pengetahuan akademik yang diperolehnya.
Hasil penelitian sebelumnya mengenai penerapan pembelajaran inkuiri
telah dilakukan oleh Risnanosanti (2010) dalam disertasinya menemukan secara
keseluruhan perkembangan kemampuan berpikir kreatif matematis siswa yang
memperoleh pembelajaran lebih baik daripada siswa yang memperoleh
pembelajaran biasa. Sedangkan untuk Problem Based Learning telah diterapkan
oleh beberapa peneliti salah satunya Ajai, et all. (2013) yang mendapatkan
strategi pembelajaran ataupun perangkat pembelajaran mandiri lebih efektif pada
aljabar daripada metode konvensional.
Berdasarkan latar belakang dan hasil temuan-temuan penelitan
sebelumnya, penulis tertarik untuk melakukan penelitian dibidang pendidikan
matematika dengan judul, “ Perbandingan Kemampuan Koneksi Matematis Dan Kemandirian Belajar Antara Siswa Yang Memperoleh Pembelajaran Inkuiri Dan
Problem Based Learning (Penelitian Quasi Eksperimen terhadap SMP Swasta di
Kab. Bandung)”
B. Rumusan Masalah
Berdasarkan latar belakang yang telah diuraikan, maka yang menjadi
masalah dalam penelitian ini adalah:
1. Apakah terdapat perbedaan pencapaian kemampuan koneksi matematis siswa
yang menggunakan pembelajaran Inkuiri dan pembelajaran Problem Based
Learning?
2. Apakah terdapat perbedaan peningkatan kemampuan koneksi matematis
siswa yang menggunakan pembelajaran Inkuiri dan pembelajaran Problem
Based Learning?
3. Apakah terdapat perbedaan peningkatan kemandirian siswa yang
menggunakan pembelajaran Inkuiri dan pembelajaran Problem Based
Learning?
C. Tujuan Penelitian
Berdasarkan rumusan masalah yang diuraikan diatas, maka penelitian ini
bertujuan:
1. Untuk mengetahui perbedaan pencapaian kemampuan koneksi matematis
siswa yang menggunakan pembelajaran Inkuiri dan pembelajaran Problem
Based Learning.
2. Untuk mengetahui perbedaan peningkatan kemampuan koneksi matematis
siswa yang menggunakan pembelajaran Inkuiri dan pembelajaran Problem
3. Untuk mengetahui perbedaan peningkatan kemandirian siswa yang
menggunakan pembelajaran Inkuiri dan pembelajaran Problem Based
Learning.
D. Manfaat Penelitian
Penelitian diharapkan dapat memberikan manfaat yang baik dalam kegiatan
pembelajaran dan memberi masukan dalam memilih model pembelajaran yang
tepat di kelas, khususnya dalam meningkatkan koneksi matematis dan
kemandirian belajar matematika siswa. Adapun manfaat lain dari penelitian ini
diantaranya sebagai berikut:
1. Secara teoritis, penelitian ini akan menguji sejauh mana keberlakuan dan
keterhandalan pembelajaran Inkuiri dan Problem Based Learning dalam
meningkatkan kemampuan koneksi matematis dan kemandirian belajar siswa.
2. Secara praktis, pembelajaran Inkuiri dan Problem Based Learning pada
matematika yang melibatkan guru dan siswa dalam penelitian dapat:
a. Dengan pembelajaran Inkuiri dan Problem Based Learning akan
memberikan dampak pada kebiasaan belajar yang baik dan berpandangan
positif terhadap matematika. Dengan meningkatmya kemampuan koneksi
matematis dan kemandirian belajar siswa, diharapkan dapat memberikan
dampak pada cara siswa menanggapi suatu permasalahan yang ditemui
dalam kehidupan sehari-hari.
b. Pembelajaran Inkuiri dan Problem Based Learning dapat dijadikan salah
satu pembelajaran alternatif dalam melaksanakan pembelajaran di kelas.
Guru dapat memilih pembelajaran ini untuk menggali kemampuan
koneksi matematis siswa dan membuat siswa mempunyai kemandirian
belajar yang kuat dalam proses pembelajarannya.
c. Memberikan pengalaman dan pengayaan pengetahuan sehingga dapat
mengembangkan penelitian-penelitian lanjut yang berguna untuk
d. Sebagai bahan pertimbangan untuk meningkatkan kemampuan koneksi
matematis dan kemandirian belajar siswa pada berbagai jenjang
pendidikan dan perluasan pada materi yang berbeda.
E. Definisi Operasional
1. Pembelajaran Inkuiri
Pembelajaran inkuiri adalah pembelajaran yang mengarahkan siswa untuk
mencari dan menemukan sendiri jawaban dari suatu masalah yang
dipertanyakan dalam memperoleh pengetahuannya. Adapun langkah dari
pembelajaran inkuiri yaitu: (1) orientasi masalah; (2) merumuskan masalah;
(3) merumuskan hipotesis; (4) mengumpulkan data; (5) menguji hipotesis; (6)
merumuskan kesimpulan.
2. Pembelajaran Problem Based Learning
Problem Based Learning atau pembelajaran berbasis masalah adalah
pendekatan pembelajaran yang dimulai dengan menyiapkan masalah-masalah
yang relevan dengan konsep yang akan dipelajari. Untuk menyelesaikan
masalah tersebut siswa harus bekerja secara berkelompok. Berikut adalah
langkah dasar dalam model pembelajaran tersebut, (1) Siswa diberikan
masalah; (2) Siswa mendiskusikan masalah tersebut dalam kelompok; (3)
Setiap siswa secara perorangan aktif terlibat mempelajari pengetahuan yang
diperlukan untuk menyelesaikan masalah mereka; (4) Bekerja kembali dengan berkelompok untuk menyelesaikan masalah; (5) Menyajikan
penyelesaian atas masalah tersebut; (6) Melihat dan menilai kembali apa yang
telah dipelajari siswa dari pengalaman memecahkan masalah tersebut.
3. Koneksi Matematis
Kemampuan koneksi matematis adalah kemampuan menyatakan dan
menerapkan hubungan antar obyek dan antar konsep matematika. Adapun
indikator kemampuan koneksi matematis adalah sebagai berikut: (1)
kemampuan mengaitkan suatu konsep matematika dengan konsep matematika
lain; (2) mengaitkan konsep matematika dengan bidang ilmu lain; (3)
4. Kemandirian Belajar
Kemandirian belajar adalah pandangan seseorang terhadap dirinya yang
meliputi: bernisiatif belajar; mendiagnosa kebutuhan belajar; menetapkan
target atau tujuan belajar; memilih dan menggunakan sumber belajar;
memanfaatkan dan mencari sumber yang relevan; memilih dan menerapkan strategi belajar; mengevaluasi proses dan hasil belajar; serta self efficacy
BAB III
METODE PENELITIAN
A. Desain Penelitian
Sejalan dengan tujuan penelitian, yaitu untuk mengetahui perbandingan pendekatan pembelajaran Inkuiri dan Problem Based Learning dalam
meningkatkan kemampuan koneksi matematis dan kemandirian belajar siswa,
metode penelitian yang digunakan dalam penelitian ini adalah metode kuasi
eksperimen yaitu metode yang tidak memungkinkan peneliti melakukan
pengontrolan penuh terhadap variabel dan kondisi eksperimen. Ruseffendi (2010)
mengemukakan bahwa pada kuasi eksperimen subjek tidak dikelompokkan secara
acak dan perlakuan dimanipulasikan, tetapi subjek yang telah ada yang berupa
kelas subjek yang telah berjalan.
Pada penelitian ini ada dua kelompok subjek eksperimen yang diberikan
perlakuan berbeda, yaitu kelompok eskperimen pertama melakukan pembelajaran
dengan menggunakan pembelajaran Inkuiri dan kelompok eksperimen kedua
menggunakan pembelajaran Problem Based Learning. Kedua kelas eksperimen
tersebut kemudian dibandingkan untuk melihat ada tidaknya perbedaan setelah
proses pembelajaran.
Untuk melihat perbedaan yang signifikan mengenai peningkatan
kemampuan koneksi matematis siswa pada kedua kelas tersebut, dilakukan pretes dan postes dengan instrumen yang sama. Pretes bertujuan untuk melihat
kesetaraan kemampuan awal koneksi matematis sebelum diberi perlakuan,
sedangkan postes dilakukan setelah proses kegiatan belajar mengajar berlangsung,
dengan tujuan untuk mengetahui bagaimana pengaruh pembelajaran yang
diberikan terhadap peningkatan kemampuan koneksi matematis dan kemandirian
belajar siswa serta melihat perbedaan yang signifikan antara siswa yang
mendapatkan pembelajaran dengan pendekatan Inkuiri dan siswa yang
mendapatkan pembelajaran Problem Based Learning.
Kelas eksperimen 1 : O X1 O
Kelas eksperimen 2 : O X2 O
Keterangan:
O : Prestes dan postes
X1 : Perlakuan dengan pembelajaran Inkuiri
X2 : Perlakuan dengan pembelajaran Problem Based Learning
B. Populasi Dan Sampel
Populasi dalam penelitian adalah seluruh siswa kelas VII di salah satu SMP Swasta di kabupaten Bandung Jawa Barat yang dilaksanakan pada semester
II (genap) yang terdiri dari lima kelas. Sampel diambil dua kelas dari lima kelas
yang ada dengan materi pembelajaran yaitu segi empat. Berdasarkan desain
penelitian, dari beberapa kelas akan dipilih dua kelas yang akan menjadi kelas
eksperimen. Sampel dipilih secara sengaja dengan pertimbangan tertentu
berdasarkan kesepakatan antara pihak sekolah dengan peneliti. Kelas A sebagai
kelompok eskperimen 1 yang akan melaksanakan pembelajaran dengan
pendekatan inkuiri sebanyak 35 orang siswa dan kelas B sebagai kelompok
eksperimen 2 yang melaksanakan pembelajaran dengan pendekatan Problem
Based learning sebanyak 34 orang siswa.
C. Variabel Penelitian
Menurut Sudjana (2005) penelitian eksperimen adalah suatu penelitian
yang berusaha mencari pengaruh variabel tertentu terhadap variabel lain dalam
kondisi yang terkontrol secara ketat. Pada penelitian ini terdapat dua variabel
yaitu variabel bebas dan variabel tidak bebas (variabel terikat).
1. Variabel Bebas
Variabel bebas adalah variabel yang mempengaruhi, disebut juga variabel
terhadap gejala yang diamati. Dalam penelitian ini pembelajaran Inkuiri ( X1) dan
pembelajaran Problem Based Learning (X2) merupakan variabel bebas.
2. Variabel terikat
Variabel terikat disebut juga variabel tak bebas, variabel akibat, variabel
tergantung, atau dependent variable (Arikunto, 1993). Dengan demikian yang menjadi variabel terikat pada penelitian ini adalah kemampuan koneksi matematis
dan kemandirian belajar siswa.
D. Instrumen Penelitian
Untuk memperoleh data yang diperlukan dalam penelitian ini, digunakan
instrument penelitian yaitu:
1. Tes Matematika
Tes matematika digunakan untuk mengukur kemampuan koneksi
matematis siswa. Soal dibuat dalam bentuk uraian karena dengan tipe uraian maka
proses berpikir, ketelitian, dan sistematika penyusunan dapat dilihat melalui
langkah-langkah penyelesaian soal dan dapat diketahui kesulitan yang dialami
siswa sehingga memungkinkan dilakukan perbaikan. Tes yang digunakan dalam
penelitian ini adalah untuk mengetahui kemampuan koneksi matematis siswa pada
saat pretes dan postes setelah menggunakan pendekatan pembelajaran Inkuiri dan
Problem Based Learning.
Materi tes diambil dari materi pelajaran matematika SMP kelas VII
kurikulum 2006 semester genap, yaitu materi segi empat. Penyusunan soal diawali dengan membuat kisi-kisi soal yang mencakup sub pokok bahasan, kemampuan
yang diukur, serta jumlah butir soal. Kemudian dilanjutkan dengan menyusun
soal-soal, membuat kunci jawaban dan pedoman penskoran tiap butir soal.
Untuk memberikan penilaian objektif, kriteria pemberian skor untuk soal
tes kemampuan koneksi matematis siswa berpedoman pada Holistic Scoring
Rubrics yang dikemukakan oleh Cai, lane, dan Jakabcsin (Izzati, 2010) yang
banyak tahapan yang dilalui pada soal tersebut. Kriteria skor untuk tes ini dapat
dilihat pada tabel berikut:
Tabel 3.1
Tabel Pedoman Pemberian Skor Kemampuan Koneksi Matematis Siswa
Kemampuan Menjawab Soal Skor
Tidak ada jawaban, kalaupun ada hanya memperlihatkan
ketidakpahaman tentang konsep sehingga informasi yang
diberikan tidak berarti apa-apa.
0
Hanya sedikit dari penjelasan yang benar 1
Penjelasan secara matematis masuk akal, namun hanya sebagian
lengkap dan benar 2
Penjelasan secara matematis masuk akal dan benar, meskipun
tidak tersusun secara logis atau terdapat sedikit kesalahan bahasa 3
Penjelasan secara matematis masuk akal dan jelas serta tersusun
secara logis dan sistematis 4
Untuk memperoleh soal tes yang baik dan dapat dipertanggungjawabkan
maka soal tes tersebut harus dinilai validitas, reliabilitas, tingkat kesukaran, dan daya beda. Soal tes diujicobakan pada siswa yang telah memperoleh materi
tersebut, yaitu kelas IX dan kemudian dilakukan analisis untuk menentukan
dipakai atau tidaknya soal tersebut.
a. Analisis validitas butir soal
Instrumen sebagai alat ukur yang akan digunakan dalam suatu penelitian
harus memenuhi validitas yang baik, agar hasil yang diperoleh sesuai yang
diharapkan. Ukuran validitas butir soal untuk menunjukkan seberapa jauh soal
tersebut mengukur yang hendak diukur. Analisis validitas butir soal digunakan
untuk mengetahui dukungan suatu butir soal terhadap skor total. Validitas yang
dinyatakan dalam penelitian ini adalah validitas instrument, yang tidak berlaku
secara umum. Artinya, apabila instrument tes yang digunakan dalam penelitian ini
untuk mencapai tujuan dalam penelitian ini), maka instrument tes ini tidak dapat
digunakan untuk mencapai tujuan yang lain diluar dari tujuan penelitian ini.
Perhitungan validitas butir soal dilakukan dengan menggunakan korelasi
Product Moment Pearson (Arikunto, 2006), yaitu sebagai berikut:
∑ ∑ ∑
√ ∑ ∑ ∑ ∑
Keterangan:
n = Banyaknya peserta tes
X = Skor item
Y = Skor total
rxy = Koefisien korelasi
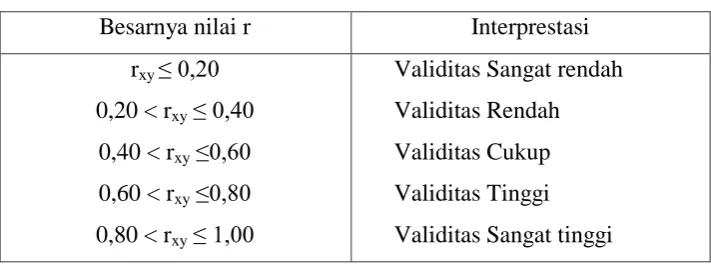
Adapun untuk menginterprestasikan nilai validitas digunakan kriteria koefisien korelasi seperti pada tabel di bawah ini.
Tabel 3.2
Tabel Interprestasi Nilai Validitas
Besarnya nilai r Interprestasi
rxy ≤ 0,20
0,20 < rxy≤ 0,40
0,40 < rxy≤0,60
0,60 < rxy≤0,80
0,80 < rxy≤ 1,00
Validitas Sangat rendah
Validitas Rendah
Validitas Cukup
Validitas Tinggi
Validitas Sangat tinggi
Setelah diperoleh nilai korelasi rxy diperoleh, maka untuk mengetahui valid atau
tidaknya butir soal diujikan, selanjutnya dilakukan uji-t dengan rumus berikut:
√
Nilai thitung yang dihasilkan kemudian dibandingkan dengan ttabel pada taraf
siginifikansi 0,05 dan derajat kebebasan dk = n – 2. Adapun instrumen tersebut
pobabilitas yang dihasilkan pada uji dua pihak (sig. 2 tailed ) < α = 0,05 maka butir soal tersebut valid. (Ruseffendi, 1998).
Hasil rekapitulasi uji validitas kemampuan koneksi matematis siswa
menggunakan Microsoft Excell disajikan pada tabel 3.3 berikut ini.
Tabel 3.3
Data Hasil Uji Validitas Butir Soal Kemampuan Koneksi Matematis Siswa
Nomor Soal Koefisien Korelasi (rxy) Interprestasi Kesimpulan
1 0,69 Validitas Tinggi Dipakai
2 0,81 Validitas Sangat Tinggi Dipakai
3 0,80 Validitas Tinggi Dipakai
4 0,85 Validitas Sangat Tinggi Dipakai
Tabel 3.3 menunjukkan bahwa koefisien korelasi soal 1 adalah 0,69 dan
soal 3 adalah 0,80 sehingga memiliki validitas yang tinggi, sedangkan untuk soal
2 memiliki nilai koefisien korelasi 0,81 dan soal 4 memiliki nilai 0,85 termasuk
kategori validitas yang sangat tinggi, sehingga semua soal dipakai.
b. Analisis reliabilitas tes
Suatu soal dikatakan memiliki reliabilitas yang baik bila soal itu dapat
memberikan hasil yang relatif tetap sama (konsisten) walaupun dikerjakan oleh
siapapun (pada level yang sama), dimanapun dan kapanpun. Untuk menghitung
reliabilitas soal tes kemampuan koneksi matematis siswa yang berbentuk uraian,
rumus yang digunakan menurut Arikunto (2006):
∑
Keterangan:
n = Banyaknya soal
r11 = Koefisien reliabilitas
= Varians total
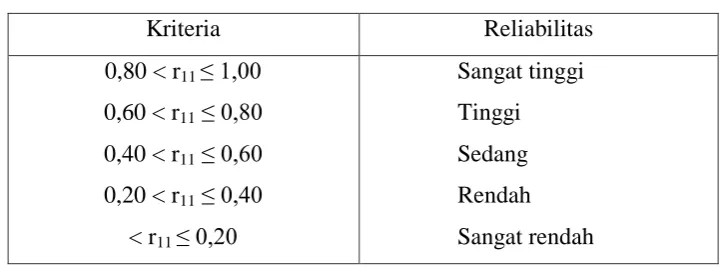
Adapun untuk menginterprestasikan nilai reliabilitas digunakan kriteria
koefisien reliabilitas seperti pada tabel dibawah ini.
Tabel 3.4
Tabel Klasifikasi Koefisien Reliabilitas
Kriteria Reliabilitas
0,80 < r11 ≤ 1,00
0,60 < r11≤ 0,80
0,40 < r11≤ 0,60
0,20 < r11≤ 0,40
< r11 ≤ 0,20
Sangat tinggi
Tinggi
Sedang
Rendah
Sangat rendah
Perhitungan uji reliabilitas menggunakan bantuan Microsoft Excell dengan
hasil rekapituasi dapat dilihat pada tabel 3.5 berikut.
Tabel 3.5
Data Hasil Uji Reabilitas Butir Soal Kemampuan Koneksi Matematis Siswa
r11 Interpretasi
0,79 Reliabilitas Tinggi
Hasil uji reabilitas pada tabel 3.5 menunjukkan bahwa soal koneksi
matematis siswa telah memenuhi karakteristik yang memadai untuk digunakan
dalam penelitian yaitu reliabilitas dengan kategori tinggi.
c. Analisis daya beda
Daya beda sebuah soal adalah kemampuan suatu soal tersebut untuk dapat
membedakan antara siswa yang berkemampuan tinggi dengan siswa yang
berkemampuan rendah. Sebuah soal dikatakan memiliki daya beda yang baik bila
siswa yang pandai dapat mengerjakan dengan baik, dan siswa yang kurang tidak
diberikan punya kemampuan dalam membedakan siswa yang termasuk kedalam
kategori yang memiliki kemampuan tinggi dan kemampuan rendah
Untuk mengetahui baik atau tidaknya soal yang di ujicobakan dengan
membagi dua subjek 50%-50% setelah diurutkan menurut peringkat, yaitu
kelompok atas dan kelompok bawah perolehan skor hasil tes, rumus yang digunakan menurut Arikunto (2006):
Keterangan:
DB = Daya beda
JA = Banyaknya siswa kelompok atas
JB = Banyaknya siswa kelompok bawah
BA = Banyaknya siswa kelompok atas yang menjawab soal yang benar
BB = Banyaknya siswa kelompok bawah yang menjawab benar
PA = Proporsi siswa kelompok atas yang menjawab benar
PB = Proporsi siswa kelompok bawah yang menjawab benar
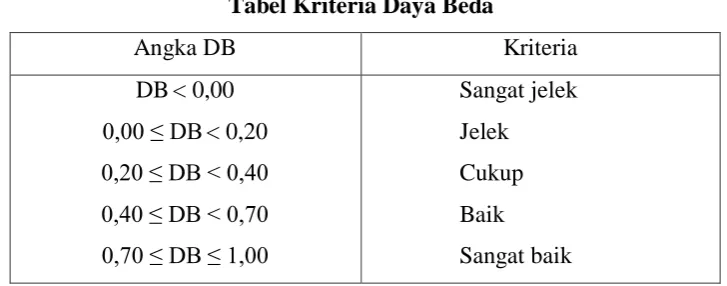
Adapun untuk mengetahui kriteria daya beda soal uji coba dapat dilihat
pada tabel berikut ini.
Tabel 3.6
Tabel Kriteria Daya Beda
Angka DB Kriteria
DB< 0,00
0,00 ≤ DB< 0,20
0,20 ≤ DB < 0,40 0,40 ≤ DB < 0,70 0,70 ≤ DB ≤ 1,00
Sangat jelek
Jelek
Cukup
Baik
Sangat baik
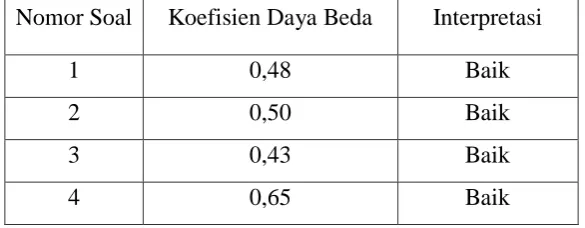
Hasil rekapitulasi uji daya beda tiap butir soal kemampuan koneksi
Tabel 3.7
Data Hasil Uji Daya Beda Butir Soal Kemampuan Koneksi Matematis Siswa
Nomor Soal Koefisien Daya Beda Interpretasi
1 0,48 Baik
2 0,50 Baik
3 0,43 Baik
4 0,65 Baik
Hasil uji daya beda pada Tabel 3.7 menunjukkan bahwa semua soal
memiliki koefisien daya beda diantara 0,40 sampai 0,65 yaitu termasuk kategori
yang baik, sehingga semua soal memadai untuk digunakan dalam proses
penelitian selanjutnya.
d. Analisis tingkat kesukaran
Tingkat mutu butir soal pada suatu tes dapat diketahui dari derajat
kesukaran atau taraf kesulitan yang dimiliki oleh masing-masing butir soal
tersebut. Soal yang baik adalah soal yang mempunyai tingat kesukaran yang
memadai dalam arti tidak terlalu mudah dan tidak terlalu sukar. Bilangan yang
menunjukan sukar dan mudahnya suatu soal disebut indeks kesukaran (difficulty
index). Untuk mengetahui tingkat kesukaran dari setiap item soal dihitung
berdasakan jawaban seluruh siswa yang mengikuti tes. Skor hasil tes yang
diperoleh siswa diklasifikasikan atas benar dan salah, sedangkan rumus yang
digunakan menurut Arikunto (2001) adalah:
Keterangan:
IK = Indeks kesukaran
JSA = Jumlah skor kelompok atas yang menjawab benar
N = Jumlah seluruh peserta tes
Si = Skor ideal
B = Banyaknya siswa yang menjawab benar
JS = Jumlah siswa yang mengikuti tes dikali skor ideal
Adapun klasifikasi tingkat kesukaran tiap butir soal uji coba dapat dilihat pada tabel berikut ini.
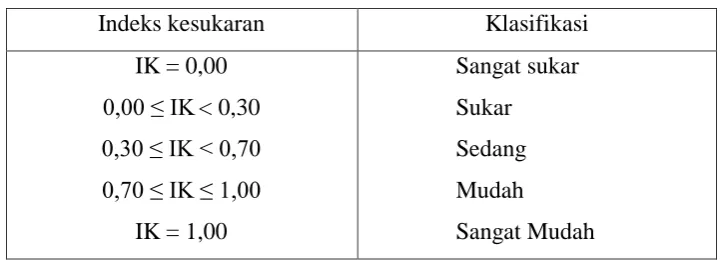
Tabel 3.8
Tabel Klasifikasi Tingkat Kesukaran
Indeks kesukaran Klasifikasi
IK = 0,00 0,00 ≤ IK< 0,30 0,30 ≤ IK < 0,70 0,70 ≤ IK ≤ 1,00
IK = 1,00
Sangat sukar
Sukar
Sedang
Mudah
Sangat Mudah
Hasil rekapitulasi uji kesukaran kemampuan koneksi matematis siswa
menggunakan Microsoft Excell 2007 disajikan pada Tabel 3.9.
Tabel 3.9
Data Hasil Uji Kesukaran Butir Soal Kemampuan Koneksi Matematis Siswa
Nomor Soal Koefisien Indeks Kesukaran Interprestasi
1 0,263 Sukar
2 0,298 Sukar
3 0,188 Sukar
4 0,382 Sedang
Hasil uji coba soal menunjukkan indeks kesukaran butir soal kemampuan
e. Kesimpulan Hasil Uji Coba Butir Soal Tes Kemampuan Koneksi
Matematis
Setelah dilakukan perhitungan validitas, reliabilitas, daya pembeda dan
tingkat kesukaran butir soal tes kemampuan koneksi matematis siswa, kesimpulan
hasil uji coba disajikan pada Tabel 3.10. Data hasil uji coba dan hasil validasi butir soal secara lengkap dapat dilihat pada lampiran.
Tabel 3.10
Kesimpulan Hasil Uji Coba Soal Kemampuan Koneksi Matematis Siswa
Nomor Soal Keterangan Kesimpulan
1 Memenuhi semua kriteria Digunakan
2 Memenuhi semua kriteria Digunakan
3 Memenuhi semua kriteria Digunakan
4 Memenuhi semua kriteria Digunakan
2. Skala Kemandirian Siswa
Kemandirian belajar matematika siswa diperoleh melalui angket yang
disusun dan dikembangkan berdasarkan Sembilan aspek kemandirian belajar
yaitu: inisiatif belajar; mendiagnosa kebutuhan belajar; menetapkan tujuan/ target
belajar; memonitor; mengatur dan mengontrol belajar; memandang kesulitan
sebagai tantangan; memanfaatkan dan mencari sumber yang relevan; memilih dan
menerapkan strategi belajar; mengevaluasi proses dan hasil belajar; serta
self-eficacy (konsep diri).
Skala kemandirian belajar matematika siswa terdiri dari 30 item
pernyataan yang diadopsi dari Sumarmo (Qohar, 2010). Masing-masing item
skala tersebut terdiri dari empat pilihan yaitu: STS (Sangat Tidak Setuju), S
(Setuju), TS (Tidak Setuju) dan SS (Sangat Setuju). Instrumen skala kemandirian
belajar matematika siswa ini sebelum digunakan terlebih dahulu di uji coba dan
dianalisis untuk menentukan validitas dan reliabilitasnya.
4, TS diberi skor 2, dan STS diberi skor 1. Sebaliknya untuk pernyataan negatif
SS diberi skor 1, S diberi skor 2, TS diberi skor 4, dan STS diberi skor 5.
3. Lembar Observasi
Lembar observasi digunakan untuk mengetahui aktivitas siswa dan guru
selama proses pembelajaran berlangsung. Observasi ini dilakukan dalam bentuk pengamatan terhadap keaktifan siswa dan semua aktifitas guru dalam kegiatan
pembelajaran pada kedua kelas eksperimen yang dilakukan oleh rekan sejawat
(guru) maupun oleh peneliti. Hal ini bertujuan untuk memberikan refleksi pada
proses pembelajaran kedua kelas eksperimen, agar pembelajaran berikutnya dapat
menjadi lebih baik daripada proses pembelajaran sebelumnya.
E. Prosedur Penelitian
Prosedur penelitian yang ditempuh dalam penelitian terbagi ke dalam tiga
tahap yaitu tahap persiapan, tahap pelaksanaan, dan tahap akhir.
1. Tahap persiapan
a. Melakukan persiapan dengan studi kepustakaan tentang teori-teori yang
berhubungan dengan kemampuan yang akan diukur.
b. Menyusun proposal penelitian dengan bimbingan dosen pembimbing
kemudian diseminarkan. Setelah mendapat masukan dari tim penguji
seminar proposal, proposal diperbaiki kemudian disetujui oleh tim
penguji.
c. Menyusun instrumen penelitian dan setelah disetujui dosen pembimbing kemudian melakukan uji instrumen.
d. Memvalidasi instrumen, menganalisis, dan merevisi sebelum melakukan
penelitian.
e. Merancang rencana pembelajaran kelas eksperimen dan lembar kerja
siswa.
a. Melakukan pemilihan sampel yaitu dengan memilih dua kelas dari kelas
yang ada untuk dijadikan dua kelas eksperimen.
b. Memberikan pretes terhadap kedua kelas eskperimen.
c. Melaksanakan pembelajaran pendahuluan.
d. Melaksanakan pembelajaran dengan pembelajaran Inkuiri dan Problem Base Learning pada kelas eksperimen.
e. Memberikan postes pada kedua kelompok kelas dan angket kemandirian
siswa.
3. Tahap akhir
a. Mengolah dan menganalisis hasil pretes dan postes serta hasil angket
untuk menguji hipotesis yang telah dirumuskan.
b. Mengolah hasil pengamatan pada lembar observasi siswa dan lembar
observasi guru.
c. Membuat kesimpulan hasil penelitian berdasarkan hasil analisis data dan
mengkaji hal-hal yang menjadi temuan, hambatan, dan dukungan dalam
menerapkan model pembelajaran.
d. Menyusun laporan.
F. Analisis Data
Data yang diperoleh dari hasil penelitian berupa data kuantitatif dan data
kualitatif. Data kuantitatif adalah data hasil tes kemampuan baik hasil pretes
maupun postes, sedangkan data kualitatif adalah data yang diperoleh dari hasil
angket siswa.
1. Analisis Data Kuantitatif
Langkah pertama yang dilakukan adalah menguji kenormalan distribusi,
apabila telah terpenuhi dilanjutkan dengan menguji homogenitas variansi, uji
kesamaan dua rata-rata, dan langkah terakhir adalah uji perbedaan dua rata-rata.
Pemilihan uji statistik yang dilakukan tergantung kenormalan distribusinya. Apabila hasil uji normalitas dan uji homogenitas diperoleh bahwa kedua data
data pretes menggunakan uji t-independent sample test sedangkan untuk data
yang berdistribusi normal tetapi tidak homogen akan dilanjutkan dengan uji t`,
dan untuk data yang tidak berdistribusi normal akan dilanjutkan dengan uji
non-parametrik Mann-Whitney. Perhitungan dalam penelitian ini diolah dengan
menggunakan bantuan software Microsoft excel 2007 dan IBM SPSS Versi 22.
a. Uji Normalitas
Uji normalitas dilakukan untuk mengetahui apakah data yang diperoleh
dari kedua kelas berdistribusi normal atau tidak. Uji normalitas dilakukan
terhadap dua data pretes dan data gain untuk kemampuan koneksi matematis dan
kemandirian siswa dengan menggunakan uji statistic Shapiro-Wilk. Adapun
rumsan hipotesisnya sebagai berikut:
Ho : Sampel berasal dari populasi yang berdistribusi normal
HA : Sampel tidak berasal dari populasi yang berdistribusi normal
Berdasarkan kriteria uji sebagai berikut:
Jika nilai Sig. (p-value) < α (α = 0,05), maka Ho ditolak
Jika nilai Sig. (p-value) ≥ α (α = 0,05), maka Ho tidak ditolak
Apabila data tidak berdistribusi normal, dapat dilanjutkan dengan pengujian
nonparametrik Mann-Whitney.
b. Uji Homogenitas
Uji homogenitas dilakukan apabia kedua data yang diperoleh berdistibusi
normal. Pengujian homogenitas variansi antara dua kelas dilakukan dengan tujuan untuk mengetahui apakah variansi kedua kelas sama atau berbeda. Uji
homogenitas dilakukan menggunakan uji Homogenitas of Varians (Levene
Statistic). Adapun hipotesis yang akan diuji yaitu:
Ho :
Varians sampel kedua kelas homogen
HA :
: Varians siswa kelas eksperimen 1
: Varians siswa kelas eksperimen 2
Dengan kriteria uji sebagai berikut:
Jika nilai Sig. (p-value) < α (α = 0,05), maka Ho ditolak
Jika nilai Sig. (p-value) ≥ α (α = 0,05), maka Ho tidak ditolak
c. Uji Kesamaan Dua Rata-rata
Apabila hasil uji normalitas dan uji homogenitas diperoleh bahwa kedua
data berdistribusi normal dan homogen, maka pengujian kesamaan dua rata-rata
untuk data pretes menggunakan uji t-independent sample test sedangkan untuk
data yang berdistribusi normal tetapi tidak homogen akan dilanjutkan dengan uji t`, dan untuk data yang tidak berdistribusi normal akan dilanjutkan dengan uji
non-parametrik Mann-Whitney.
Data pretes dianalisis menggunakan uji kesamaan dua rata-rata untuk
mengetahui kemampuan awal koneksi matematis siswa kelas eksperimen 1 dan
kelas eksperimen 2. Adapun rumusan hipotesis untuk kemampuan koneksi
matematis siswa untuk skor pretes adalah sebagai berikut:
Ho :
Tidak terdapat perbedaan yang signifikan rata-rata pretes kemampuan koneksi matematis siswa antara kelas eksperimen 1 dan kelas eksperimen 2.
Ho :
Terdapat perbedaan yang signifikan rata-rata pretes kemampuan koneksi
matematis siswa antara kelas eksperimen 1 dan kelas eksperimen 2.
Kriteria pengujian hipotesis berdasarkan P-value sebagai berikut:
Jika nilai Sig. (2-tailed) < α (α = 0,05), maka Ho ditolak
Jika nilai Sig. (2-tailed) ≥ α (α = 0,05), maka Ho tidak ditolak
Apabila hasil kesamaan dua rata-rata data pretes menunjukkan bahwa
kedua kelas memiliki kemampuan yang sama, untuk melihat peningkatannya
dilakukan uji perbedaan dua rata-rata . Akan tetapi, apabila kedua kelas memiliki
kemampuan yang berbeda maka untuk melihat peningkatannya dilakukan uji
d. Uji Gain Ternormalisasi
Untuk melihat peningkatan kemampuan koneksi matematis siswa dan
kemandirian belajar siswa antara sebelum dan sesudah pembelajaran Inkuiri dan
Problem Based Learning. Adapun rumus gain ternormalisasi menurut Meltzer
(2002) adalah sebagai berikut:
[image:30.595.150.438.305.417.2]
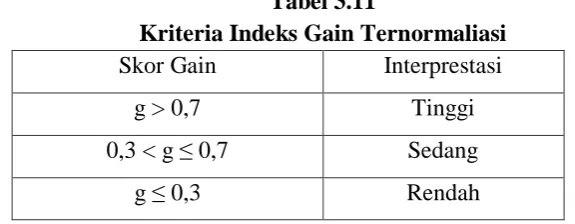
Dengan kriteria indeks gain berikut:
Tabel 3.11
Kriteria Indeks Gain Ternormaliasi Skor Gain Interprestasi
g > 0,7 Tinggi
0,3 < g ≤ 0,7 Sedang
g ≤ 0,3 Rendah
e. Uji Perbedaan Dua Rata-rata
Untuk menguji apakah terdapat perbedaan peningkatan kemampuan siswa
yang mendapat pembelajaran dengan pembelajaran Inkuiri dengan Problem
Based Learning, dilakukan uji perbedaaan dua rata-rata. Adapun rumusan
hipotesis untuk capaian kemampuan koneksi matematis siswa adalah:
Ho : =
Tidak terdapat perbedaan rata-rata capaian kemampuan koneksi matematis
siswa yang memperoleh model pembelajaran Inkuiri dengan Problem
Based Learning.
HA :
Terdapat perbedaan peningkatan rata-rata capaian kemampuan koneksi
matematis siswa yang memperoleh model pembelajaran Inkuiri dengan
Problem Based Learning.
Sedangkan rumusan masalah untuk peningkatan kemampuan koneksi matematis
Ho : =
Tidak terdapat perbedaan rata-rata peningkatan kemampuan koneksi
matematis siswa yang memperoleh model pembelajaran Inkuiri dengan
Problem Based Learning.
HA :
Terdapat perbedaan peningkatan rata-rata peningkatan kemampuan
koneksi matematis siswa yang memperoleh model pembelajaran Inkuiri
dengan Problem Based Learning.
Kriteria pengujian hipotesis berdasarkan P-value (sig) sebagai berikut:
Jika nilai Sig. (2-tailed) ≤ α (α = 0,05), maka Ho ditolak
Jika nilai Sig. (2-tailed) > α (α = 0,05), maka Ho tidak ditolak
2. Analisis Data Kualitatif
Data kualitatif dalam penelitian ini diperoleh dari angket kemandirian
belajar siswa. Angket bertujuan untuk mengetahui perbedaan peningkatan
kemandirian belajar siswa kelas eksperimen 1 dan kelas eksperimen 2. Adapun
langkah-langkah dalam menganalisis angket siswa adalah sebagai berikut:
1. Data yang diperoleh dari angket siswa dianalisis dengan cara menghitung
jumlah siswa yang menyatakan sangat setuju, setuju, tidak setuju, dan sangat
tidak setuju dari masing-masing pernyataan.
2. Skala kualitatif ditransfer kedalam skala kuantitatif. Untuk pernyataan positif
SS diberi skor 5, S diberi skor 4, TS diberi skor 2, dan STS diberi skor 1.
Sebaliknya untuk pernyataan negatif SS diberi skor 1, S diberi skor 2, TS
diberi skor 4, dan STS diberi skor 5 kemudian masing-masing indikator
dijumlahkan.
3. Menentukan gain ternormalisasi dari data pretes dan postes.
4. Menguji hipotesis dengan menggunakan uji nonparametrik Mann-Whitney.
Adapun untuk hipotesis kemandirian siswa sebagai berikut:
Ho : X =Y
Tidak terdapat perbedaan peningkatan sebaran kemandirian siswa yang
HA : X Y
Terdapat perbedaan peningkatan sebaran kemandirian siswa yang
memperoleh model pembelajaran Inkuiri dengan Problem Based Learning.
Kriteria pengujian hipotesis berdasarka P-value (sig) sebagai berikut:
Jika nilai Sig. (2-tailed) ≤ α (α = 0,05), maka Ho ditolak
Jika nilai Sig. (2-tailed) > α (α = 0,05), maka Ho tidak ditolak
3. Analisis Lembar Observasi
Lembar observasi siswa dan guru dihitung dengan menjumlahkan nilai
tiap indikator untuk seluruh pertemuan kemudian dicari rata-rata tiap indikator
tersebut. Pada penelitian ini dilakukan enam kali pengamatan dengan nilai
tertinggi setiap indikator adalah 5 dan nilai terendah terendah 1. Kemudian tiap indikator dipersentasekan dengan menggunakan rumus perhitungan persentase
sebagai berikut:
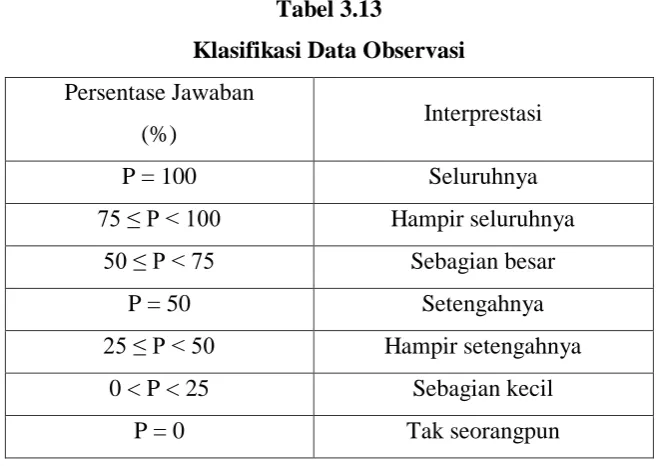
Penafsiran data observasi siswa dan guru dapat ditafsirkan pada kategori
[image:32.595.147.477.506.739.2]berdasarkan Hendro (Yulianti, 2009) terdapat pada Tabel 3.13 berikut ini.
Tabel 3.13
Klasifikasi Data Observasi
Persentase Jawaban
(%) Interprestasi
P = 100 Seluruhnya
75 ≤ P < 100 Hampir seluruhnya
50 ≤ P < 75 Sebagian besar
P = 50 Setengahnya
25 ≤ P < 50 Hampir setengahnya
0 < P < 25 Sebagian kecil
Keterangan:
Pk = Persentase ketercapaian aktivitas Q = Rata-rata skor kolektif yang diperoleh
R = Skor maksimum ideal dari suatu aspek aktivitas
Adapun untuk pengolahan data kuantitatif dapat disajikan seperti pada
Diagram berikut ini.
[image:33.595.117.490.275.716.2]Gambar 3.1
Diagram Alur Tahap Analisis Data Data Kemampuan Koneksi Matematis
siswa
Uji Statistik Parametrik
Uji Normalitas
Uji Statistik Non-Parametrik Kruskal Walis
Uji Homogenitas
Uji t` dua sampel Independen Uji t dua sampel
Independen
Kesimpulan
Kesimpulan Kesimpulan
Ya Tidak
KESIMPULAN DAN SARAN
A. Kesimpulan
Berdasarkan hasil analisis data dan temuan penelitian yang telah
dikemukakan sebelumnya, maka dapat diambil beberapa kesimpulan sebagai
berikut.
1. Tidak terdapat perbedaan pencapaian kemampuan koneksi matematis siswa
yang menggunakan pendekatan pembelajaran Inkuiri dan pendekatan
pembelajaran Problem Based Learning.
2. Tidak terdapat perbedaan peningkatan kemampuan koneksi matematis siswa
yang menggunakan pendekatan pembelajaran Inkuiri dan pendekatan pembelajaran Problem Based Learning. Peningkatan kemampuan koneksi
matematis siswa yang menggunakan pendekatan pembelajaran Inkuiri dan
pendekatan pembelajaran Problem Based Learning keduanya berada pada
kategori dengan klasifikasi sedang.
3. Tidak terdapat perbedaan peningkatan kemandirian siswa yang menggunakan
pendekatan pembelajaran Inkuiri dan pendekatan pembelajaran Problem
Based Learning. Peningkatan kemandirian belajar siswa yang menggunakan
pendekatan pembelajaran Inkuiri berada pada kategori dengan klasifikasi
rendah, sedangkan peningkatan kemandirian belajar siswa yang
menggunakan pendekatan pembelajaran Problem Based Learning berada
pada kategori sedang.
B. Saran
Berdasarkan kesimpulan dan hasil penelitian, maka penulis mengemukakan beberapa saran sebagai berikut:
1. Pembelajaran dengan menggunakan pendekatan Inkuiri dan pendekatan
itu, pembelajaran tersebut dapat digunakan untuk meningkatkan kemampuan
matematis siswa.
2. Dalam proses pembelajaran dengan pendekatan Inkuiri dan pendekatan
Problem Based Learning keberhasilan siswa tidak cukup diukur hanya
melalui tes tertulis tetapi diperlukan alat evaluasi lain untuk menganalisis
kegiatan siswa selama proses pembelajaran, seperti catatan perencanaan
belajar siswa, catatan refleksi siswa, dan jurnal kemajuan belajar siswa.
3. Perlu dikembangkan bahan ajar dan soal-soal beragam untuk meningkatkan
kemampuan koneksi matematis siswa dan dapat mendorong siswa mampu
belajar secara mandiri. Dengan demikian, siswa terbiasa mengerjakan