Perbandingan Kemampuan Koneksi Matematis dan Mathematics Self-Efficacy antara Siswa yang Memperoleh Pembelajaran Berbasis Masalah dengan Penemuan Terbimbing.

(1)

Ummi Hasanah, 2015

Perbandingan Kemampuan Koneksi Matematis Dan Mathematics Self-Efficacy Antara Siswa yang Memperoleh Pembelajaran Berbasis Masalah dengan Penemuan Terbimbing

Universitas Pendidikan Indonesia | repository.upi.edu | perpustakaan.upi.edu

ABSTRAK

Ummi Hasanah (2015): Perbandingan Kemampuan Koneksi Matematis dan Mathematics Self-Efficacy antara Siswa yang Memperoleh Pembelajaran Berbasis Masalah dengan Penemuan Terbimbing.

Penelitian ini dilatarbelakangi oleh pentingnya dan belum tercapainya kemampuan koneksi matematis dan mathematics self-efficacy siswa dengan optimal. Tujuan pada penelitian ini adalah untuk mengetahui dan menelaah: (1) perbedaan pencapaian dan peningkatan kemampuan koneksi matematis antara siswa yang memperoleh pembelajaran model PBM dan siswa yang memperoleh pembelajaran model penemuan terbimbing; (2) perbedaan pencapaian mathematics self-efficacy antara siswa yang memperoleh pembelajaran model PBM dan siswa yang memperoleh pembelajaran model penemuan terbimbing; dan (3) asosiasi antara kemampuan koneksi matematis dan mathematics self-efficacy siswa. Penelitian ini merupakan penelitian kuasi eksperimen dengan desain pretes-postes. Pelaksanaan penelitian ini dilakukan pada siswa kelas VIII di salah satu SMP Negeri di Bandung. Instrumen yang digunakan dalam penelitian ini adalah tes kemampuan koneksi matematis, skala mathematics self-efficacy, dan lembar observasi. Data kuantitatif yang diperoleh dianalisis menggunakan uji perbedaan rerata: Uji Mann Whitney dan Uji-t, serta uji asosiasi: Uji Chi-Kuadrat. Analisis data kualitatif dilakukan secara deskriptif. Hasil penelitian ini adalah (1a) terdapat perbedaan pencapaian kemampuan koneksi matematis antara siswa yang memperoleh pembelajaran model PBM dan siswa yang memperoleh pembelajaran model penemuan terbimbing. Perbedaan yang signifikan berada pada indikator menggunakan keterkaitan konsep matematika dengan kehidupan sehari-hari; (1b) terdapat perbedaan peningkatan kemampuan koneksi matematis antara siswa yang memperoleh pembelajaran model PBM dan siswa yang memperoleh pembelajaran model penemuan terbimbing. Secara umum, nilai rata-rata skor n-gain pada kedua kelas berada pada kategori sedang; (2) tidak terdapat perbedaan pencapaian mathematics self-efficacy antara siswa yang memperoleh pembelajaran model PBM dan siswa yang memperoleh pembelajaran model penemuan terbimbing; dan (3) tidak terdapat asosiasi antara kemampuan koneksi matematis dan mathematics self-efficacy siswa.

(2)

ABSTRACT

Ummi Hasanah (2015): Comparison of Mathematical Connection Ability and Mathematics Self-Efficacy between Students who Study in Problem-Based Learning Model and Guided Discovery Learning Model

This study was motivated by the importance of mathematical connection ability and mathematics self-efficacy. The aims of this study are to examine: (1) the difference of the achievement and the enhancement of mathematical connection ability between the students who studied under PBL model and those of under guided discovery leaning model; (2) the difference of mathematics self-efficacy between the students who studied under PBL model and those of under guided discovery learning model; (3) the association between the students’ mathematical connection ability and their mathematics self-efficacy. This quasi experimental study used pretest-posttest design and was conducted on 8th grader students in one of junior high schools in Bandung. The instruments of this study were mathematical connection ability test, mathematics self-efficacy scale, and observation sheets. The quantitative data were analyzed by mean difference test: Mann-Whitney test and t-test, and association test: Chi-Square test. The qualitative data was analyzed descriptively. The results of this study are: (1a) there is difference achievement in mathematical connection ability between the students who studied under PBL model and those of under guided discovery learning model. The significant difference was indicated in the second indicator: using the concepts of mathematics in daily life; (1b) there is difference enhancement in mathematical connection ability between the students who studied under PBL model and those of under guided discovery learning model. The n-gain of students who got PBL and guided discovery learning model for mathematical connection ability was medium; (2) there is no difference achievement in mathematics self-efficacy between the students who studied under PBL model and those of under guided discovery learning model (3) there is no association between students’ mathematical connection and their mathematics self-efficacy.

(3)

BAB I PENDAHULUAN

A. Latar Belakang Masalah

Beberapa tahun terakhir semakin berkembang penelitian tentang High-

Order Thinking Skill (HOTS) atau dalam bahasa Indonesia disebut kemampuan

berpikir tingkat tinggi. Terkait dengan HOTS, National Council of Teachers of

Mathematics (NCTM)(2000) menyatakan bahwa terdapat lima kemampuan

matematis yang perlu dimiliki oleh siswa, yaitu pemecahan masalah (problem

solving), penalaran dan pembuktian (reasoning and proofing), komunikasi

(communication), representasi (representation), dan koneksi (connection).

Disebutkan pula di NCTM bahwa mathematical connection merupakan

kemampuan matematis yang paling sulit untuk dicapai, namun yang paling

membantu dalam meningkatkan motivasi siswa khususnya pada siswa di kelas

menengah.

Sejalan dengan hal tersebut, Standar Isi Mata Pelajaran Matematika

Sekolah Menengah Pertama (SMP) (Depdiknas, 2006, hlm. 8) menyatakan bahwa

mata pelajaran matematika memiliki tujuan agar siswa memiliki kemampuan

sebagai berikut.

1. Memahami konsep matematika, menjelaskan keterkaitan antarkonsep dan mengaplikasikan konsep atau algoritma, secara luwes, akurat, efisien, dan tepat, dalam pemecahan masalah.

2. Menggunakan penalaran pada pola dan sifat, melakukan manipulasi matematika dalam membuat generalisasi, menyusun bukti, atau menjelaskan gagasan dan pernyataan matematika.

3. Memecahkan masalah yang meliputi kemampuan memahami masalah, merancang model matematika, menyelesaikan model dan menafsirkan solusi yang diperoleh.

4. Mengomunikasikan gagasan dengan simbol, tabel, diagram, atau media lain untuk memperjelas keadaan atau masalah.

5. Memiliki sikap menghargai kegunaan matematika dalam kehidupan, yaitu memiliki rasa ingin tahu, perhatian, dan minat dalam mempelajari matematika, serta sikap ulet dan percaya diri dalam pemecahan masalah.

Berdasarkan Standar Isi Mata Pelajaran Matematika SMP dapat

disimpulkan bahwa kemampuan koneksi matematis merupakan salah satu

(4)

2

Kemampuan koneksi matematis tampak pada poin pertama, yaitu kemampuan

siswa menjelaskan keterkaitan antar konsep dan mengaplikasikannya dalam

pemecahan masalah. Pemecahan masalah berarti menerapkan keterkaitan konsep

matematika pada masalah di mata pelajaran lain maupun pada masalah di

kehidupan sehari-hari.

Afgani (2011) menyatakan bahwa koneksi matematis muncul berdasarkan

kenyataan matematika sebagai body of knowledge, yakni ilmu yang terstruktur

dan utuh, yang terdiri dari bagian-bagian yang saling berhubungan. Hal ini

menunjukkan bahwa matematika merupakan ilmu yang memiliki konsep-konsep

yang saling berkaitan dan tidak berdiri sendiri. Matematika dapat digunakan pada

pemecahan masalah dalam berbagai konteks. Oleh karena itu, kemampuan

koneksi matematis perlu untuk dimiliki dan ditingkatkan oleh siswa.

Siswa yang memiliki kemampuan koneksi matematis yang baik akan

memperoleh prestasi yang baik dalam matematika (Fauzi, 2011; Sulistyaningsih,

Waluyo, & Kartono, 2012; Mandur, Sadra, & Suparta, 2013). Siswa dapat

mengaitkan antar topik matematika yang telah ia pelajari dengan yang sedang

dipelajari, mengaitkan matematika dengan bidang ilmu lain, dan juga mengaitkan

matematika dengan kehidupan sehari-hari. Lebih lanjut, dengan menghubungkan

berbagai macam gagasan atau ide matematis yang mereka terima mengakibatkan

kemampuan pemahaman matematis siswa juga dapat berkembang secara optimal

(Qohar, 2011; Cheeseman, McDonough, & Ferguson, 2012).

Dalam pembelajaran matematika, kemampuan koneksi antar konsep atau

ide-ide matematika akan memfasilitasi kemampuan siswa untuk merumuskan dan

memeriksa dugaan-dugaan sementara. Selanjutnya, konsep atau ide-ide matematis

yang baru dikembangkan dapat diterapkan untuk menyelesaikan masalah lain

dalam matematika (Permana&Sumarmo, 2007, hlm. 117-118). Dengan begitu,

koneksi matematis sangat berperan penting dalam penyelesaian soal-soal

pemecahan masalah. Glacey (2011) juga menyatakan bahwa siswa yang memiliki

kemampuan koneksi matematis akan menjadi seorang pemikir yang baik dan

berjiwa kritis.

Berdasarkan pemaparan di atas, kemampuan koneksi matematis

(5)

Namun, beberapa hasil penelitian terdahulu mengindikasikan bahwa kemampuan

koneksi matematis siswa masih belum mencapai hasil yang menggembirakan.

Sugiman (2008) melakukan penelitian pada siswa SMP kelas IX materi

Perbandingan. Hasil penelitiannya mengungkapkan bahwa pencapaian pada setiap

aspek koneksi siswa adalah 63% untuk koneksi antar topik, 41% untuk koneksi

matematika dengan bidang studi lain, dan 55% untuk koneksi matematika dengan

kehidupan sehari-hari. Penelitian Mustopa (2014) tentang materi Segitiga dan

Segiempat pada siswa kelas VII menemukan bahwa kemampuan koneksi siswa

masih perlu untuk ditingkatkan dilihat dari hasil postes siswa hanya sebesar

42,35%. Hasil tersebut masuk kedalam kategori rendah dengan pencapaian

terendah pada indikator koneksi antar konsep matematika.

Penelitian lain menyatakan bahwa siswa sekolah menengah pertama

merasa kesulitan dalam menyelesaikan masalah yang berhubungan dengan

kehidupan sehari-hari, dan topik dalam bidang studi lain. Siswa juga merasa

kesulitan dalam menjawab hubungan atau konsep matematis terkait yang

digunakan dalam soal (Gordah, 2009; Yusmanita, 2012). Kusmaydi (2010)

menyatakan bahwa kemampuan koneksi sebagian siswa masih rendah terlihat dari

beberapa hal, yaitu (1) siswa tidak dapat menentukan hubungan antar materi yang

sedang dipelajari dengan materi yang telah mereka pelajari; (2) siswa merasa

kebingungan dalam menyatakan benda nyata, diagram, maupun gambar ke dalam

peristiwa kehidupan sehari-hari; (3) siswa kurang mampu menyelesaikan masalah

yang berkaitan dengan kehidupan sehari-hari; (4) sebagian siswa dapat

menyelesaikan permasalah dalam kehidupan sehari-hari namun hanya bersifat

prosedural tanpa memahami apa yang mereka kerjakan.

Selain kemampuan kognitif siswa, kemampuan afektif siswa juga penting

untuk ditingkatkan. Salah satunya adalah keyakinan siswa atas kemampuannya

dalam melakukan tugas-tugas, menyelesaikan masalah, serta mengikuti kegiatan

pembelajaran dengan baik untuk mencapai tujuan yang diinginkan. Kemampuan

ini lebih dikenal dengan self-efficacy. Pengertian self-efficacy tersebut merujuk

pada pengertian yang dinyatakan oleh Bandura (Carmichael, Callingham, Hay, &

Watson, 2010), yaitu “beliefs in one’s capabilities to organize and execute the

(6)

4

Robins, et. al. (Carmichael, Callingham, Hay, & Watson, 2010)

menyatakan bahwa self-efficacy merupakan prediksi prestasi terbaik pada sebuah

konteks pendidikan. Siswa dengan self-efficacy yang baik akan memiliki prestasi

yang baik pula. Begitu juga sebaliknya pada siswa dengan self-efficacy yang

rendah. Hal ini disebabkan siswa yang memiliki self-efficacy tinggi akan memiliki

keyakinan tinggi dalam mengikuti kegiatan pembelajaran sehingga dapat

melakukan tugas yang diberikan guru dengan lebih baik. Hal ini menunjukkan

pentingnya menumbuhkembangkan aspek self-efficacy dalam diri siswa.

Secara lebih khusus self-efficacy dalam matematika disebut mathematics

self-efficacy. Pengertian mathematics self-efficacy merujuk pada pengertian yang

dinyatakan oleh Causapin (2012), yaitu “Mathematics self-efficacy is the belief in

a one’s ability to learn and succeed in school mathematics”. Berdasarkan pengertian tersebut mathematics self-efficacy diartikan sebagai keyakinan siswa

mengenai kemampuannya dalam menyelesaikan tugas-tugas matematika yang

diberikan, mengikuti pembelajaran matematika dengan baik, dan sukses dalam

matematika.

Pajares & Schunk (2001) menyatakan bahwa siswa dengan mathematics

self-efficacy yang tinggi biasanya menetapkan target yang lebih tinggi,

menerapkan usaha yang lebih keras, dan lebih tekun dalam menghadapi situasi

sulit serta lebih mandiri. Di sisi lain, siswa dengan mathematics self-efficacy yang

rendah, cenderung mudah menyerah dan tidak yakin terhadap kemampuan yang

mereka miliki sehingga mereka bahkan tidak mencoba untuk mengatasi hal-hal

sulit dalam matematika. Dengan demikian, siswa yang memiliki mathematics

self-efficacy tinggi akan mencapai prestasi matematika yang tinggi. Begitu pula

sebaliknya, siswa yang memiliki mathematics self-efficacy rendah akan mencapai

prestasi matematika yang rendah pula.

Hal tersebut menunjukkan bahwa terdapat hubungan yang positif antara

mathematics self-efficacy dengan prestasi matematika. Berdasarkan pemaparan

tersebut, maka ada indikasi bahwa kemampuan koneksi matematis juga memiliki

asosiasi dengan mathematics self-efficacy siswa. Dimana kemampuan koneksi

(7)

Menurut Usher & Pajares (2009), self-efficacy tidak selalu konsisten

dengan hasil yang diharapkan. Tidak sedikit terjadi di lapangan, siswa

berkemampuan tinggi memiliki mathematics self-efficacy yang rendah. Demikian

pula sebaliknya. Hal tersebut juga ditunjukkan pada hasil studi pendahuluan yang

dilakukan oleh peneliti. Dalam studi pendahuluan, peneliti memberikan

pernyataan-pernyataan yang dapat mengukur tingkat mathematics self-efficacy

siswa dan membandingkannya dengan perolehan nilai ujicoba tes kemampuan

koneksi matematis. Ternyata diperoleh hasil bahwa siswa yang mendapatkan nilai

tertinggi memiliki taraf keyakinan matematis yang lebih rendah daripada siswa

yang mendapatkan nilai tes rendah. Hal tersebut memerlukan perhatian baik dari

guru maupun dari dalam diri siswa.

Salah satu perhatian yang dapat diberikan oleh guru adalah pada saat

proses pembelajaran berlangsung. Guru merupakan salah seorang yang dapat

berperan aktif dalam meningkatkan mathematics self-efficacy pada diri siswa

(Pajares & Usher, 2009). Hal ini dikarenakan kemampuan mathematics

self-efficacy merupakan kemampuan yang harus dilatih dan diatur secara efektif.

Kemampuan ini tidak akan terbentuk dengan baik apabila tidak mendapatkan

perhatian.

Salah satu alternatif solusi untuk meningkatkan kemampuan koneksi

matematis dan mathematics self-efficacy siswa adalah melalui penerapan model

pembelajaran yang dapat melibatkan keaktifan siswa dan memberikan kesempatan

untuk meningkatkan kedua kemampuan siswa tersebut. Dijelaskan pula dalam

Permendikbud No.65 Tahun 2013 tentang standar proses bahwa “pengetahuan

diperoleh melalui aktivitas mengingat, memahami, menerapkan, melalui aktivitas,

mengevaluasi, dan mencipta.” Dengan demikian, pengetahuan akan diperoleh melalui suatu kegiatan yang aktif, tidak terkecuali dengan kemampuan koneksi

matematis. Kemampuan ini dapat dikembangkan dengan baik melalui

pembelajaran yang melibatkan siswa untuk mencari ilmu pengetahuan bukan

hanya menerima.

Pembelajaran yang melibatkan siswa secara aktif seringkali dilakukan

melalui kegiatan pembelajaran berkelompok. Siswa aktif mendiskusikan materi

(8)

6

yang kurang pandai akan dibantu oleh siswa yang lebih pandai. Kegiatan seperti

ini memungkinkan siswa lebih percaya diri dan yakin untuk lebih sukses dalam

belajar. Hal ini sejalan dengan Bandura (1997, hlm. 234) yang mengemukakan

bahwa belajar bersama dalam kelompok dapat menumbuhkembangkan potensi

self-efficacy siswa. Pembelajaran aktif seperti dikemukakan di atas dianjurkan

dalam pelaksanaan Kurikulum 2013.

Proses pembelajaran pada Kurikulum 2013 untuk semua jenjang

pendidikan dilaksanakan menggunakan pendekatan ilmiah (saintifik).

Langkah-langkah pendekatan ini meliputi: mengamati, bertanya, pengumpulan data atau

informasi, menganalisis, dan mengomunikasikan hasil yang diperoleh dalam

berbagai representasi. Hosnan (2014, hlm. 36) mengemukakan bahwa pendekatan

ilmiah merupakan salah satu pendekatan yang berpusat pada siswa, melibatkan

keterampilan proses sains dalam mengontruksi konsep, dan melibatkan

proses-proses kognitif yang potensial dalam merangsang perkembangan intelektual,

khususnya kemampuan berpikir tingkat tinggi siswa, serta dapat mengembangkan

karakter siswa.

Terdapat tiga model pembelajaran yang disarankan dalam Kurikulum

2013, yaitu pembelajaran berbasis masalah (PBM), penemuan (discovery), dan

proyek berbasis masalah. Pada ketiga model ini siswa diberikan kesempatan untuk

aktif dalam pembelajaran. Siswa tidak bergantung pada pengetahuan yang

ditransfer oleh guru, namun siswa aktif mencari, mengolah, mengkonstruksi, dan

menggunakan pengetahuan. Siswa juga dibiasakan untuk melakukan

pembelajaran secara berkelompok. Dengan demikian, kemampuan sosial siswa

dapat tercipta dengan baik. Siswa akan membiasakan diri untuk berkomunikasi,

menghargai, bekerjasama, dan bertanggungjawab dengan kelompok belajar. Hal

ini juga memungkinkan terjadinya pertukaran pengetahuan yang baik antara siswa

dengan siswa lainnya.

Walaupun ketiga model pembelajaran tersebut disarankan untuk

diterapkan dalam pembelajaran namun guru tetap diberikan kebebasan untuk

menentukan model manakah yang paling tepat untuk digunakan dalam setiap

(9)

karakteristik dari ketiga model tersebut sehingga baik guru dan siswa tidak

mengalami kesulitan dalam belajar.

Model PBM adalah model pembelajaran dimana siswa diberikan pada

masalah auntentik sehingga siswa dapat menyusun pengetahuannya sendiri,

menumbuhkembangkan keterampilan yang lebih tinggi, memandirikan siswa, dan

meningkatkan kepercayaan diri sendiri (Arends, 2009, hlm. 396). Model ini

bercirikan penyajian masalah kontekstual yang akan didiskusikan siswa dalam

kelompok. Model PBM tidak ditujukan bagi guru yang tetap menganggap dirinya

sebagai pusat dalam pembelajaran. Model PBM akan berjalan dengan baik jika

guru merancang lingkungan pembelajaran yang melibatkan siswa aktif dalam

kegiatan dan diskusi. Siswa bekerja dalam kelompok untuk membagi ide dengan

sesama anggota kelompok dalam memecahkan masalah.

Di lain pihak model pembelajaran penemuan terbimbing juga diduga dapat

membantu menumbuhkembangkan kemampuan koneksi matematis dan

mathematics self-efficacy siswa. Model pembelajaran penemuan terbimbing

memfasilitasi siswa untuk belajar secara mandiri melalui kegiatan yang dirancang

oleh guru. Siswa menyusun konjektur, hipotesis, melakukan verifikasi, dan

generalisasi untuk membangun pengetahuan baru.

Ibrahim (2012, hlm. 13) menyatakan bahwa kedua model pembelajaran

penemuan dan PBM memiliki karakteristik yang tidak jauh berbeda. Kedua model

pembelajaran ini memfasilitasi siswa untuk terlibat aktif dalam pembelajaran,

lebih menekankan pada proses induktif daripada deduktif, dan siswa menemukan

dan mengkonstruksi pengetahuan secara mandiri. Perbedaan antara model

pembelajaran penemuan dan PBM terletak pada masalahnya. Pada pembelajaran

penemuan, masalah atau pertanyaan yang akan dijawab oleh siswa sebagian besar

berdasarkan disiplin ilmu, penyelidikan siswa berlangsung di bawah bimbingan

guru terbatas di dalam lingkup kelas. Pada PBM pembelajaran dimulai dari

masalah yang berdasarkan pada masalah sehari-hari atau berdasarkan kehidupan

nyata sehingga lebih bermakna. Siswa memiliki kesempatan untuk melakukan

penyelidikan di dalam maupun di luar kelas selama diperlukan untuk

(10)

8

Pada model PBM, kemampuan koneksi matematis akan terbentuk pada

Fase 2 dan Fase 3. Pada Fase 2 siswa mencermati masalah yang diberikan. Siswa

mulai mencari kaitan materi yang sedang dipelajari dengan berbagai topik

matematika. Pada Fase 3, siswa bersama kelompoknya mencari informasi dan

melaksanakan kegiatan untuk menyelesaikan masalah. Pada tahap ini, siswa

membangun kemampuan koneksi matematis antar konsep, koneksi dengan bidang

studi lain, ataupun koneksi dengan kehidupan sehari-hari bergantung pada

masalah yang diberikan oleh guru.

Pada model pembelajaran penemuan terbimbing, kemampuan koneksi

matematis siswa akan terbentuk pada tahapan eksplorasi dimana siswa membuat

konjektur, melakukan proses penemuan, dan menganalisis data yang diberikan

guru. Pada tahap ini siswa menggunakan konsep yang telah ia miliki sebelumnya

untuk menemukan konsep baru. Hal ini sesuai dengan pendapat Roshendi (2011)

yang meneliti tentang penerapan model pembelajaran terbimbing pada siswa

SMA materi Turunan. Proses koneksi muncul pada pertanyaan-pertanyaan yang

disajikan di lembar aktivitas siswa.

Dengan memperhatikan uraian di atas, maka peneliti berupaya

mengungkapkan perbandingan kemampuan koneksi matematis dan mathematics

self-efficacy antara siswa yang memperoleh pembelajaran model PBM dengan

penemuan terbimbing.

B. Rumusan Masalah

Masalah yang dikaji dalam penelitian ini adalah bagaimana perbedaan

kemampuan koneksi matematis dan mathematics self-efficacy antara siswa yang

memperoleh pembelajaran model PBM dengan penemuan terbimbing. Secara

terperinci masalah-masalah dalam penelitian ini dijabarkan dalam rumusan

masalah sebagai berikut.

1. Apakah terdapat perbedaan pencapaian dan peningkatan kemampuan koneksi

matematis antara siswa yang memperoleh pembelajaran model PBM dan

(11)

2. Apakah terdapat perbedaan pencapaian mathematics self-efficacy antara siswa

yang memperoleh pembelajaran model PBM dan siswa yang memperoleh

pembelajaran penemuan terbimbing?

3. Apakah terdapat asosiasi antara kemampuan koneksi matematis dan

mathematics self-efficacy siswa.

C. Tujuan Penelitian

Berdasarkan rumusan masalah yang telah dijelaskan di atas, maka tujuan

penelitian ini antara lain untuk mengetahui dan menelaah:

1. Ada atau tidaknya perbedaan pencapaian dan peningkatan kemampuan

koneksi matematis antara siswa yang memperoleh pembelajaran model PBM

dan siswa yang memperoleh pembelajaran penemuan terbimbing.

2. Ada atau tidaknya perbedaan pencapaian mathematics self-efficacy antara

siswa yang memperoleh pembelajaran model PBM dan siswa yang

memperoleh pembelajaran penemuan terbimbing.

3. Ada atau tidaknya asosiasi antara kemampuan koneksi matematis dan

mathematics self-efficacy siswa.

D. Manfaat Penelitian

Penelitian ini diharapkan dapat memberikan manfaat yang dapat dilihat

dari beberapa aspek sebagai berikut:

1. Dari segi teori: diharapkan dapat dijadikan penguat teori yang menjelaskan

tentang penerapan model PBM, penemuan terbimbing, kemampuan koneksi

matematis, dan mathematics self-efficacy.

2. Dari segi praktik:

a) Bagi siswa, diharapkan mendapatkan pengalaman belajar yang dapat

menumbuhkembangkan kemampuan koneksi matematis dan mathematics

self-efficacy siswa.

b) Bagi guru, diharapkan dapat membantu kesulitan guru dalam mengajar

dengan memberikan gambaran pembelajaran melalui model PBM dan

(12)

10

dari keduanya terhadap kemampuan koneksi matematis dan mathematics

self-efficacy.

3. Dari segi kebijakan: diharapkan dapat menjadi salah satu pertimbangan dalam

menerapkan dan mengembangkan Kurikulum 2013 di sekolah dalam upaya

lebih memperhatikan keaktifan siswa.

E. Definisi Operasional

Untuk memperoleh kesamaan persepsi tentang istilah yang digunakan

dalam penelitian ini maka perlu dijelaskan definisi operasional dari istilah-istilah

tersebut, yaitu:

1. Kemampuan koneksi matematis adalah kemampuan mengaitkan

konsep-konsep matematika antar konsep-konsep dalam matematika itu sendiri maupun

mengaitkan konsep matematika dengan konsep dalam bidang studi lain serta

mengaitkan konsep matematika dengan kehidupan sehari-hari. Indikator

kemampuan koneksi matematis siswa dalam penelitian ini adalah: (1)

menggunakan keterkaitan antar konsep matematika; (2) menggunakan

keterkaitan matematika dengan bidang studi lain; dan (3) menggunakan

matematika dalam kehidupan sehari-hari.

2. Mathematics self-efficacy diartikan sebagai keyakinan siswa mengenai

kemampuannya dalam menyelesaikan tugas-tugas matematika yang diberikan,

mengikuti pembelajaran matematika dengan baik, dan sukses dalam

matematika berdasarkan pengalaman keberhasilan. Mathematics self-efficacy

dalam penelitian ini diperoleh dari pernyataan-pernyataan dalam skala

Mathematics self-efficacy yang menggunakan 11 respon skala dengan interval

0-10.

3. Model pembelajaran berbasis masalah (PBM) adalah model pembelajaran

yang diawali dengan pemberian masalah, menekankan pada keaktifan siswa

dalam melakukan pengamatan, dan menerapkan pengetahuan untuk

membangun konsep secara mandiri dan memecahkan masalah. Model ini

terdiri dari lima tahapan pembelajaran, yaitu orientasi pada masalah,

pengorganisasian belajar, membimbing penyelidikan kelompok atau individu,

(13)

4. Model pembelajaran penemuan terbimbing adalah model pembelajaran yang

menekankan pada pentingnya membantu siswa dalam memahami ide utama

materi melalui pembelajaran aktif dimana memungkinkan siswa untuk

mengaitkan topik yang telah ia pelajari sebelumnya untuk menemukan konsep

baru. Model ini terdiri dari empat tahapan pembelajaran, yaitu menyajikan

masalah, melakukan eksplorasi di bawah bimbingan guru, verifikasi dan

generalisasi.

(14)

BAB III

METODE PENELITIAN

A. Desain Penelitian

Fraenkel, Wallen, & Hyun (2012, hlm. 275) menyebutkan apabila peneliti

tidak dapat melakukan pengambilan sampel secara acak maka penelitian tersebut

merupakan penelitian kuasi eksperimen. Dalam penelitian ini peneliti tidak dapat

melakukan pengambilan sampel secara acak dikarenakan hal tersebut dapat

mengganggu jadwal yang sudah diterapkan oleh pihak sekolah. Oleh karena itu,

penelitian ini merupakan penelitian kuasi eksperimen.

Pada penelitian ini dipilih dua kelas, yaitu kelas eksperimen 1 dan kelas

eksperimen 2. Sebelum pembelajaran, pada kedua kelompok diberikan

pra-respon, yaitu pretes kemampuan koneksi matematis dan skala mathematics

efficacy awal untuk melihat kemampuan koneksi matematis dan mathematics

self-efficacy siswa sebelum diberikan perlakuan. Kelas eksperimen 1 diberikan

perlakuan model PBM, sedangkan kelas eksperimen 2 diberikan perlakuan model

pembelajaran penemuan terbimbing. Setelah penelitian kedua kelompok diberikan

pos-respon, yaitu postes kemampuan koneksi matematis dan skala mathematics

self-efficacy akhir yang berfungsi untuk melihat pencapaian kemampuan koneksi

matematis dan mathematics self-efficacy siswa setelah pembelajaran dilaksanakan.

Selain itu, data yang diperoleh dari pretes dan postes kemampuan koneksi

matematis juga digunakan untuk menentukan peningkatan (N-gain) kemampuan

koneksi matematis siswa. Penentuan N-gain perlu dilakukan karena meskipun

pencapaian siswa berbeda ada kemungkinan peningkatan tidak berbeda begitu

pula sebaliknya. Tabel 3.1 berikut menggambarkan kegiatan pra-respon,

perlakuan, dan pos-respon yang dilaksanakan.

Tabel 3.1 Pola Desain Eksperimen

(15)

Desain penelitian yang digunakan, yaitu desain pretes-postes yang

dimodifikasi berdasarkan desain pretes-postes dari Fraenkel, Wallen, & Hyun

(2012, hlm. 275) dapat digambarkan sebagai berikut.

Tabel 3.2 Desain Pretes-Postes

Kelompok Pretest Perlakuan Postest

Eksperimen 1 O X1 O

Eksperimen 2 O X2 O

Keterangan:

O : pra-respon/pos-respon (soal dan skala yang digunakan sama)

X1 : perlakuan pada kelas eksperimen 1 menggunakan model PBM

X2 : perlakuan pada kelas eksperimen 2 menggunakan model pembelajaran

penemuan terbimbing

--- : subjek tidak dikelompokkan secara acak

B. Variabel Penelitian

Penelitian ini mengkaji perbandingan kemampuan koneksi matematis dan

mathematics self-efficacy antara siswa yang belajar melalui model PBM dengan

siswa yang belajar melalui penemuan terbimbing di SMP. Variabel bebas dalam

penelitian ini adalah model PBM dan penemuan terbimbing. Variabel terikat,

yaitu kemampuan koneksi matematis dan tingkat mathematics self-efficacy.

Keterkaitan antara variabel bebas dan terikat disajikan pada Tabel 3.3 berikut ini.

Tabel 3.3 Keterkaitan antara Variabel Penelitian

Koneksi (K) Mathematics Self Efficacy (MSE)

Model Pemb.

K-PBM adalah kemampuan koneksi matematis siswa di kelas model PBM.

K-PT adalah kemampuan koneksi matematis siswa di kelas model

pembelajaran penemuan terbimbing.

MSE-PBM adalah mathematics self-efficacy siswa di kelas model PBM.

MSE-PT adalah mathematics self-efficacy siswa di kelas model pembelajaran

(16)

36

C. Populasi dan Sampel

Populasi dalam penelitian ini adalah seluruh siswa kelas VIII salah satu

SMP di Bandung, semester genap Tahun Pelajaran 2014/2015. Pengambilan

sampel menggunakan teknik purposive, yaitu berdasarkan pertimbangan guru di

sekolah tersebut. Hal ini bertujuan agar tidak mengganggu jadwal pelajaran yang

sudah ada di sekolah tersebut dan mempermudah dalam urusan administratif.

Dari segi kemampuan, sekolah yang dipilih adalah sekolah dengan

kategori menengah. Hal ini dengan pertimbangan pada sekolah kategori

menengah model pembelajaran yang dipilih dapat diterapkan. Siswa yang berada

di sekolah tersebut memiliki kemampuan yang heterogen sehingga diharapkan

pada tahap implementasi dapat dilihat respon dari siswa yang pintar hingga siswa

yang kurang pintar.

Alasan pemilihan kelas VIII adalah dikarenakan materi matematika yang

diperoleh kelas VIII memadai untuk melihat kemampuan koneksi matematis

siswa. Apabila dipilih siswa kelas VII materi matematika yang diperoleh belum

cukup memadai sedangkan jika dipilih kelas IX dikhawatirkan mengganggu

persiapan Ujian Nasional siswa dan tidak mendapatkan izin dari sekolah. Selain

itu, umumnya siswa SMP kelas VIII masih berada pada masa remaja. Pada masa

ini terjadi proses pencarian jati diri dan pertumbuhan self-efficacy.

D. Bahan Ajar

Dalam penelitian ini dirancang perangkat pembelajaran dan bahan ajar

yang didasarkan pada prinsip dan karakteristik model PBM untuk kelas

eksperimen 1 dan model pembelajaran penemuan terbimbing untuk kelas

eksperimen 2. Perangkat pembelajaran dalam penelitian ini adalah Rencana

Pelaksanaan Pembelajaran (RPP) yang terdiri dari 7 kali tatap muka. Bahan ajar

yang digunakan dalam penelitian ini berupa Lembar Masalah Kelompok (LMK)

untuk kelas PBM dan Lembar Aktivitas Siswa (LAS) untuk kelas penemuan

terbimbing.

Sebelum digunakan pada kelas kedua eksperimen, perangkat dan bahan

(17)

mengetahui kualitas perangkat pembelajaran dan bahan ajar apakah sudah sesuai

dengan model pembelajaran yang diterapkan.

E. Instrumen Penelitian

Instrumen yang digunakan dalam penelitian ini terdiri dari tes kemampuan

koneksi matematis, skala mathematics self-efficacy, dan lembar observasi. Berikut

ini merupakan penjelasan tentang instrumen yang digunakan dalam penelitian ini.

1. Tes Kemampuan Koneksi Matematis

Kemampuan koneksi matematis diukur menggunakan instrumen tes

berbentuk tes uraian. Hal ini dikarenakan tes uraian lebih memberikan gambaran

tentang proses penyelesaian jawaban sehingga didapatkan kemampuan koneksi

matematis yang akurat. Adapun indikator kemampuan koneksi matematis, yaitu:

(1) menggunakan keterkaitan antar topik matematika; (2) menggunakan

keterkaitan matematika dengan bidang studi lain; dan (3) menggunakan

matematika dalam kehidupan sehari-hari.

Data hasil tes berupa jawaban-jawaban siswa terhadap soal kemampuan

koneksi matematis dengan penilaian berdasarkan pedoman penskoran yang

dibuat. Data kemampuan koneksi matematis berasal dari pretes dan postes yang

digunakan untuk mencari peningkatan kemampuan koneksi matematis siswa (gain

ternormalisasi). Adapun pedoman penskoran yang digunakan dalam menilai hasil

pretes-postes kemampuan koneksi matematis siswa berdasarkan Cai, Lane, dan

Jakabcsin (Utami; 2014). Pedoman tersebut dapat dilihat pada Tabel 3.4 berikut.

Tabel 3.4 Pedoman Penskoran Kemampuan Koneksi Matematis

Skor

0 Tidak ada jawaban, kalaupun ada hanya melibatkan ketidakpahaman tentang konsep sehingga informasi yang diberikan tidak berarti apa-apa. 1 Hanya sedikit dari penjelasan yang benar.

2 Penjelasan secara matematis masuk akal dan mengarah pada solusi atau jawaban jika diterapkan dengan benar.

3 Penjelasan secara matematis masuk akal dan benar, meskipun tidak tersusun secara logis atau terdapat sedikit kesalahan perhitungan.

(18)

38

2. Skala Mathematics Self-efficacy

Skala mathematics self-efficacy digunakan untuk mengukur keyakinan

siswa dalam menyelesaikan tugas-tugas matematika yang diberikan, mengikuti

pembelajaran matematika dengan baik, dan memiliki motivasi untuk sukses dalam

matematika. Skala mathematics self-efficacy diberikan kepada masing-masing

kelompok siswa sebelum dan sesudah diberikan perlakuan. Skala mathematics

self-efficacy awal digunakan untuk melihat mathematics self-efficacy yang

dimiliki siswa sebelum diberikan perlakuan sedangkan skala mathematics

self-efficacy akhir digunakan untuk melihat mathematics self-self-efficacy yang dimiliki

siswa setelah diberikan perlakuan.

Format respon skala Likert pada umumnya menggunakan lima pernyataan

sikap. Namun, menurut Bandura (2006) skala self-efficacy lebih baik

menggunakan 11 respon skala dengan interval 0-10 atau 0-100. Hal ini didukung

oleh Panjares, Hartley, & Valiante (Bandura, 2006) yang menyatakan bahwa

format respon 0-100 merupakan prediktor yang lebih baik dari pada skala dengan

format 1-5. Peneliti lebih memilih menggunakan format respon skala dengan

interval 0-10 dengan pertimbangan format ini lebih mudah dimengerti oleh siswa

SMP. Bentuk skala ini termasuk dalam skala bentuk ordinal.

Terdapat beberapa langkah yang dilakukan untuk mendapatkan instrumen

skala mathematics self-efficacy yang baik, yaitu.

a. Penyusunan kisi-kisi skala mathematics self-efficacy.

b. Menyusun pernyataan skala mathematics self-efficacy berdasarkan dengan

kisi-kisi yang telah ditentukan.

c. Melakukan uji validitas teoritik, yaitu dengan meminta pertimbangan ahli

yang merupakan salah satu dosen dan pemerhati dunia psikologi.

d. Melakukan uji validitas empirik serta uji reliabilitas dengan cara melakukan

uji coba skala mathematics self-efficacy pada siswa non subyek penelitian.

e. Melakukan analisis hasil uji coba instrumen untuk melihat apakah diperlukan

revisi atau tidak.

f. Melakukan revisi dan meminta pertimbangan dosen ahli untuk menentukan

pernyataan-pernyataan yang digunakan.

(19)

3. Lembar Observasi

Lembar observasi digunakan untuk melihat aktivitas siswa selama proses

pembelajaran berlangsung di kedua kelas. Tujuan observasi ini adalah untuk

melihat apakah proses pembelajaran di kedua kelas telah diterapkan dengan

maksimal. Perangkat pendukung lainnya adalah tabel ringkasan hasil observasi

aktivitas siswa. Kategori atau aktivitas yang diamati dalam instrumen ini disusun

dengan memperhatikan prinsip-prinsip maupun karakteristik pembelajaran di

kedua kelas eksperimen. Observasi ini dapat dijadikan sebagai bahan refleksi agar

pembelajaran berikutnya dapat menjadi lebih baik. Data hasil penilaian lembar

observasi aktivitas siswa yang diperoleh selama penelitian adalah berupa data

dalam lima kriteria penilaian, yaitu kriteria “Sangat baik” diberi skor 5, kriteria “Baik” diberi skor 4, kriteria “Cukup” diberi skor 3, kriteria “Kurang” diberi skor 2, dan kriteria “sangat kurang” diberi nilai 1. Selanjutnya, dihitung nilai rata-rata dan dipersentasekan.

F. Teknik Analisis Instrumen

Sebelum soal dan skala mathematics self-efficacy digunakan, dilakukan

ujicoba terlebih dahulu. Hal ini bertujuan untuk menguji apakah instrumen

tersebut memenuhi kriteria instrumen yang layak digunakan. Kriteria tersebut

meliputi validitas dan reliabilitas (Fraenkel, 2012; Sugiyono, 2014; Creswell,

2014). Analisis taraf kesukaran juga dilakukan sebagai analisis tambahan. Uji

coba ini dilakukan pada kelas di luar sampel, yaitu kelas IX di sekolah yang sama.

Pengolahan data ini menggunakan analisis teori respon butir model Rasch.

Analisis dilakukan menggunakan Software MiniStep 3.78. Berikut ini adalah

teknik analisis instrumen penelitian yang dilakukan.

1. Tes Kemampuan Koneksi Matematis a. Uji Validitas

Untuk mengetahui tingkat keabsahan atau kevalidan butir soal maka

dilakukan uji validitas teoritik dan emprik butir soal. Uji validitas teroritik

dilakukan dengan cara meminta validasi dari empat orang ahli, yaitu tiga orang

(20)

40

guru matematika di jenjang SMP yang memiliki pengalaman mengajar dengan

kualifikasi sarjana pendidikan matematika. Tes yang dikategorikan valid adalah

yang telah dinyatakan sesuai dengan indikator yang diukur, kesesuaian isi tes

dengan isi kisi-kisi tes yang diukur, dan kesesuaian bahasa yang digunakan dalam

tes dengan kemampuan bahasa siswa yang dilakukan menggunakan daftar check

list.

Untuk mendapatkan kesimpulan apakah hasil timbangan para penimbang

tersebut sama atau tidak, dilakukan analisis menggunakan statistik Uji Q-Cochran

dengan bantuan Software IBM SPSS 20. Adapun kriteria uji yang digunakan

adalah terima H0 jika asym.sig yang diperoleh lebih besar dari taraf signifikansi α

= 0,05. Tabel 3.5 Berikut adalah ringkasan hasil uji Q-Cochran.

Tabel 3.5 Hasil Uji Q-Cochran Instrumen Kemampuan Koneksi Matematis

Aspek Asym. Sig Keputusan Uji Kesimpulan

Validitas Muka 0,063 H0 diterima Para penimbang memberikan pertimbangan yang seragam atau sama. Validitas Isi 0,013 H0 ditolak Para penimbang

memberikan pertimbangan yang tidak seragam atau berbeda

Berdasarkan Tabel 3.5 di atas, dapat diketahui bahwa pada aspek validitas

muka diperoleh nilai asym.sig sebesar 0,063. Hal ini berarti para penimbang

memberikan pertimbangan yang seragam atau sama. Berbeda dengan aspek

validitas isi, nilai asym.sig yang diperoleh sebesar 0,013. Hal ini berarti para

penimbang memiliki pertimbangan yang berbeda. Perbedaan ini terjadi

dikarenakan ada ahli menimbang bahwa soal-soal yang diajukan sudah sesuai

untuk mengukur indikator namun tergolong mudah sehingga ia memberikan nilai

0 pada poin ini. Di lain pihak penimbang yang lain tidak terlalu memperhatikan

tingkat kesulitan soal.

Berdasarkan pertimbangan para ahli maka dilakukan revisi pada soal-soal

yang diajukan. Revisi dilakukan berdasarkan saran-saran yang diberikan oleh para

penimbang, yaitu mengganti soal, meningkatkan kompleksitas soal, dan

(21)

A B

C

D E

F

memberikan pertimbangan. Tabel 3.6 berikut merupakan revisi soal yang

dilakukan.

Tabel 3.6 Revisi Soal

Soal Soal Revisi

Indikator 3: Menggunakan keterkaitan luas permukaan balok dalam kehidupan sehari-hari.

Ayah akan membuat sebuah akuarium berbentuk kubus dengan panjang rusuk 90 cm. Rangka akuarium terbuat dari kaca dengan bagian atas akuarium terbuka. Jika harga kaca per meter persegi adalah Rp 80.000,00. Hitunglah biaya yang diperlukan untuk membeli kaca tersebut.

Ayah membuat sebuah akuarium berbentuk kubus dengan panjang rusuk 90 cm. Akuarium terbuat dari kaca dengan bagian atas akuarium terbuka. Harga kaca per meter persegi adalah Rp 60.000,00. Biaya lain-lain yang dihabiskan ayah adalah Rp 50.000,00. Ayah ingin menjual akuarium tersebut dan mendapatkan keuntungan 20% dari total biaya yang dikeluarkan untuk membuat akuarium. Berapakah harga jual akuarium tersebut?

Indikator 1: Menggunakan keterkaitan antar konsep (unsur-unsur dan volum prisma dengan konsep phytagoras dan jumlah sudut dalam segitiga) Perhatikan gambar di samping.

ABC.DEF adalah sebuah prisma dengan alas berbentuk

segitiga siku-siku di C. a. Tentukanlah 4 pasang

(22)

42

Indikator 2: Menggunakan keterkaitan konsep volum balok dengan konsep massa jenis pada bidang studi fisika.

Pada saat kelas 7 kamu sudah mempelajari tentang massa jenis zat ( ). Dapatkah kamu menentukan massa jenis sebuah besi berbentuk kubus dengan panjang rusuk 5 cm dan massa besi tersebut adalah 500 gr?

(diberikan: )

Sebuah bak penampungan air berbentuk balok berukuran panjang 120 cm, lebar 70 cm, dan tinggi 50 cm terisi air penuh. Sebuah kayu dengan massa jenis 0,8 gr/cm3 dan massa 800 gr dimasukkan ke dalam bak air tersebut sehingga ada air yang tertumpah keluar. Berapakah volum air yang tersisa di dalam bak penampungan tersebut?

(keterangan: massa jenis suatu benda adalah hasil bagi massa benda dengan volum benda tersebut)

Indikator 1: Menggunakan keterkaitan antar konsep (konsep luas permukaan kubus dan limas dengan konsep perbandingan) Akan dibuat balok dengan perbandingan

panjang : lebar : tinggi = 4 : 3 : 2. Jika lebar balok tersebut 12 cm. Tentukanlah volume balok tersebut.

Diketahui sebuah limas segiempat dengan panjang alas = 12 cm dan lebar alas = 4 cm. Jika perbandingan volum limas dengan volum kubus yang memiliki panjang rusuk 8 cm adalah 1 : 4. Tentukan tinggi limas segiempat tersebut.

Indikator 3: Menggunakan keterkaitan luas permukaan kubus dan limas dalam kehidupan sehari-hari.

Andi membuat mainan rumah-rumahan seperti tampak pada gambar di bawah. Rumah-rumahan tersebut merupakan gabungan kubus sebagai bagian bawah dan limas sebagai atapnya. Panjang rusuk bagian bawah adalah 40 cm. Pada salah satu sisi, Andi membuat celah berbentuk lingkaran dengan jari-jari 7 cm. Andi ingin menutupi setiap bagian luar mainan tersebut dengan kertas kado. Berapakah luas minimal kertas kado yang dibutuhkan?

Andi membuat mainan rumah-rumahan seperti tampak pada gambar di bawah. Rumah-rumahan tersebut merupakan

(23)

Indikator 3: Menggunakan keterkaitan volum kubus dan balok dalam kehidupan sehari-hari.

Ibu memiliki kotak kue besar berbentuk balok dengan panjang 50 cm, lebar 20 cm, dan tinggi 35 cm. Ke dalam kotak tersebut akan diisi kotak kue kecil dengan panjang rusuk 10 cm. Berapa paling banyak kotak kue kecil yang dapat dimasukkan kedalam kotak kue besar?

Ditiadakan (karena soal untuk mengukur indikator ini sudah ada sebanyak 2 soal)

Indikator 2: Menggunakan keterkaitan konsep volum prisma dengan konsep debit pada bidang studi fisika.

Debit air adalah kecepatan aliran zat cair persatuan waktu. Misalnya debit air sungai adalah 3.000 liter/detik. Artinya setiap 1 detik air yang mengalir di sungai adalah 3.000 liter.

Jika terdapat tangki penampungan air berbentuk prisma yang alasnya berbentuk belah ketupat yang panjang diagonal-diagonalnya adalah 4 m dan 3 m. Tinggi tangki 2,5 m. Pada dasar tangki terdapat kran yang dapat mengalirkan air rata-rata 75 liter setiap menitnya. Jika tangki terisi air penuh, berapa lama waktu yang diperlukan untuk mengeluarkan air dari tangki itu sampai habis?

(keterangan: Debit = )

Ditiadakan.

40 cm

55 cm 15 cm

(24)

44

Setelah instrumen direvisi berdasarkan validitas teoritik dan mendapatkan

persetujuan dosen pembimbing, dilakukan uji validitas empirik dengan cara

mengujicobakan instrumen kepada non subjek penelitian.

Dalam penelitian ini, validitas ítem dihitung menggunakan model rasch

berbantuan Software MiniStep 3.78. Menurut Sumintono & Widhiarso (2013, hlm.

111) validitas ítem tes dapat dilihat berdasarkan nilai Output Mean Square

(MNSQ), Out-fit Z-Standard (ZSTD), dan Point Measure Correlation (Pt Mean

Corr). Kriteria validitas ítem tes dapat dilihat pada Tabel 3.7 berikut.

Tabel 3.7 Kriteria Validitas Item Tes

Nilai Interval Penerimaan

Output Mean Square (MNSQ) 0,5 < MNSQ < 1,5 Out-fit Z-Standard (ZSTD) - 2,0 < ZSTD < +2,0 Point Measure Correlation (Pt Mean Corr) 0,4 < Pt Mean Corr < 0,85

Jika ítem tes memenuhi minimal dua kriteria di atas, maka butir soal atau

pernyataan tersebut dapat dikatakan valid. Dengan kata lain ítem tersebut dapat

digunakan. Tabel 3.8 adalah hasil dari uji validitas tes kemampuan koneksi

matematis siswa.

Tabel 3.8 Hasil Uji Validitas Tes Kemampuan Koneksi Matematis

No Soal Outfit MNSQ

Outfit ZSTD

Pt Mean

Corr Kesimpulan Keterangan

1 1,65 1,7 0,55 Diterima Digunakan

2 0,78 -0,7 0,69 Diterima Digunakan

3 1,30 0,9 0,64 Diterima Digunakan

Berdasarkan Tabel 3.8 di atas kelima soal yang diujikan memiliki nilai

MNSQ, ZSTD, dan Pt. Mean Corr. yang masuk kedalam daerah kriteria validitas.

Oleh karena ini, dapat disimpulkan bahwa kelima soal kemampuan koneksi

matematis layak untuk digunakan.

b. Uji Reliabilitas

Reliabilitas tes adalah tingkat keajegan (konsistensi) suatu tes, yaitu sejauh

mana suatu tes dapat dipercaya untuk menghasilkan skor yang relatif tidak

(25)

Pada penelitian ini uji koefisien reliabilitas dihitung dengan bantuan Software

MiniStep 3.78. Pada software tersebut, tidak hanya dapat diketahui reliabilitas tes

namun juga reliabilitas item. Adapun klasifikasi nilai reliabilitas tes dan

reliabilitas item dimodifikasi berdasarkan pendapat Sumintono & Widhiarso

(2013, hlm. 109). Klasifikasi nilai reliabilitas tersebut dapat dilihat pada Tabel 3.9

dan Tabel 3.10 sebagai berikut.

Tabel 3.9 Klasifikasi Nilai Test Reliability Nilai Alpha Cronbach Klasifikasi

0,00 r < 0,50 Buruk 0,50 r < 0,60 Jelek 0,60 r < 0,70 Cukup 0,70 r < 0,80 Bagus

0,80 r ≤ 1,00 Bagus Sekali

Tabel 3.10 Klasifikasi Nilai Item Reliability Nilai Item Reliability Klasifikasi

0,00 r < 0,67 Lemah 0,67 r < 0,80 Cukup 0,80 r <0,90 Bagus 0,90 r < 0,94 Bagus Sekali 0,94 r ≤ 1,00 Istimewa

Tabel 3.11 berikut ini adalah hasil dari uji reliabilitas tes kemampuan

koneksi matematis siswa.

Tabel 3.11 Hasil Uji Reliabilitas Tes Kemampuan Koneksi Matematis Nilai Reliabilitas Klasifikasi Reliabilitas Tes

(Crobanch Alpha) 0,71 Bagus

Reliabilitas Item 0,90 Bagus Sekali

Berdasarkan Tabel 3.11, koefisien reliabilitas tes dan reliabilitas ítem

pada tes kemampuan koneksi matematis berturut-turut adalah 0,71 dan 0,90.

Berdasarkan klasifikasi nilai reliabilitas pada Tabel 3.9 dan Tabel 3.10, nilai

tersebut termasuk dalam klasifikasi bagus dan bagus sekali. Hal ini berarti

instrumen tes kemampuan koneksi matematis akan memberikan hasil yang hampir

(26)

46

c. Tingkat Kesukaran

Arikunto (2012) menyatakan bahwa “soal yang baik adalah soal yang tidak terlalu mudah dan tidak terlalu sukar”. Soal yang terlalu mudah tidak memberikan tantangan bagi siswa. Soal yang terlalu sukar dapat menyebabkan

siswa putus asa dan tidak bersemangat dalam mengerjakan soal. Pada hasil

perhitungan menggunakan bantuan Software MiniStep 3.78 tingkat kesukaran soal

dapat dilihat dari nilai logit item (measure). Soal diurutkan dari tingkat kesulitan

tersulit hingga termudah. Berikut ini urutan tingkat kesulitan tes kemampuan

koneksi matematis.

Tabel 3.12 Hasil Uji Tingkat Kesulitan Tes Kemampuan Koneksi Matematis

Item Measure

5 1,05

2 0,01

4 -0,21

3 -0,36

1 -0,49

Berdasarkan tabel di atas dapat disimpulkan bahwa soal nomor 5

merupakan soal tersulit atau soal yang paling sedikit siswa dapat mengerjakannya.

Diikuti dengan soal nomor 2, 4, dan 3. Soal termudah atau soal yang paling

banyak siswa dapat mengerjakannya adalah soal nomor 1.

2. Skala Mathematics Self-Efficacy a. Uji Validitas

Sama halnya dengan tes kemampuan koneksi matematis, skala

mathematics self-efficacy juga dilakukan uji validitas teoritik dan empirik. Uji

validitas teoritik dilakukan dengan cara meminta pertimbangan dari satu dosen

ahli bidang psikologi di Universitas Pendidikan Indonesia (UPI) menggunakan

daftar ceklis untuk menyatakan ítem-item yang dibuat sudah sesuai dengan

dimensi dan indikator yang diukur. Berdasarkan validitas teoritik tersebut, ada

beberapa hal yang perlu diperbaiki antara lain:

1) Memperbaiki pemilihan kalimat agar lebih mudah dipahami oleh siswa dan

(27)

2) Pernyataan yang digunakan hanya pernyataan positif dengan pertimbangan

bahwa keyakinan tidak memuat keyakinan negatif. Perbedaannya hanyalah

tingkat atau taraf keyakinan saja, mulai dari keyakinan tertinggi hingga

keyakinan terendah.

Setelah melakukan revisi berdasarkan saran-saran yang diberikan pada

saat uji validitas teoritik dan mendapatkan persetujuan dari ahli, dilakukan uji

validitas empirik dengan cara mengujicobakan skala mathematics self-efficacy

kepada siswa non subjek penelitian. Hasil uji validitas skala mathematics

self-efficacy dapat dilihat pada tabel berikut.

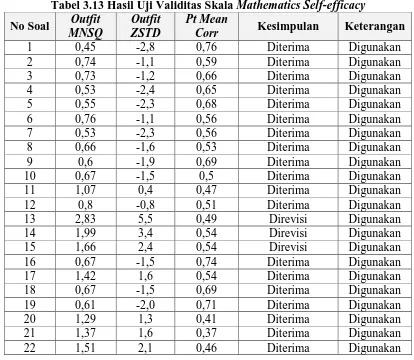
Tabel 3.13 Hasil Uji Validitas Skala Mathematics Self-efficacy

No Soal Outfit MNSQ

Outfit ZSTD

Pt Mean

Corr Kesimpulan Keterangan

pernyataan nomor 13, 14, dan 15 memiliki nilai MNSQ dan ZSTD yang berada di

luar jangkauan kriteria pernyataan yang dapat digunakan. Oleh karena itu, ketiga

ítem tersebut tidak memenuhi kriteria dan perlu direvisi. Namun, dikarenakan

(28)

48

dan berhubungan maka peneliti memutuskan untuk merevisi juga ítem nomor 16.

Revisi yang dilakukan adalah memperbaiki tata bahasa pada pernyataan tersebut.

Revisi yang dilakukan dapat dilihat pada Tabel 3.14 berikut.

Tabel 3.14 Revisi Skala Mathematics Self-Efficacy

No. Pernyataan Pernyataan Revisi

JIKA DIBERIKAN 5 SOAL TENTANG BANGUN RUANG SISI DATAR,

…

Hasil yang diperoleh berdasarkan uji reliabilitas skala mathematics

self-efficacy adalah sebagai berikut.

Tabel 3.15 Hasil Uji Reliabilitas Skala Mathematics Self-efficacy Nilai Reliabilitas Klasifikasi Reliabilitas Tes

(Crobanch Alpha) 0,90 Bagus Sekali

Reliabilitas Item 0,83 Bagus

Koefisien reliabilitas tes dan reliabilitas ítem pada skala mathematics

self-efficacy berturut-turut adalah 0,90 dan 0,83. Berdasarkan klasifikasi nilai

reliabilitas pada Tabel 3.9 dan Tabel 3.10, nilai tersebut termasuk dalam

klasifikasi bagus sekali dan bagus. Hal ini berarti instrumen skala mathematics

self-efficacy akan memberikan hasil yang hampir sama jika diujikan kembali

(29)

c. Tingkat Kesukaran

Untuk tingkat kesukaran, pada model Rasch juga diperlihatkan urutan

butir pernyataan yang paling sulit. Urutan kesulitan yang dimaksud, yaitu

pernyataan yang berada pada urutan pertama adalah pernyataan yang paling sulit

bagi siswa untuk menyatakan keyakinannya. Tabel 3.16 berikut menunjukkan

urutan kesulitan pernyataan mathematics self-efficacy.

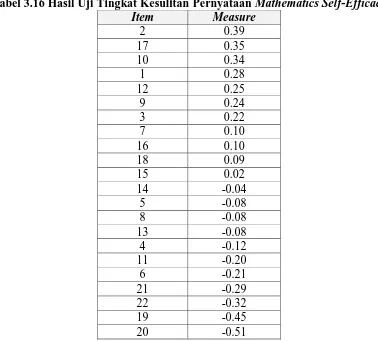
Tabel 3.16 Hasil Uji Tingkat Kesulitan Pernyataan Mathematics Self-Efficacy

Item Measure

2 0.39

17 0.35

10 0.34

1 0.28

12 0.25

9 0.24

3 0.22

7 0.10

16 0.10

18 0.09

15 0.02

14 -0.04

5 -0.08

8 -0.08

13 -0.08

4 -0.12

11 -0.20

6 -0.21

21 -0.29

22 -0.32

19 -0.45

20 -0.51

Berdasarkan tabel di atas dapat disimpulkan bahwa pernyataan nomor 2

merupakan pernyataan yang paling sulit dinyakatan keyakinannya. Diikuti dengan

pernyataan nomor 17, 10, 1, 12, 9, 3, 7, 16, 18, 15, 14, 5, 8, 13, 4, 11, 6, 21, 22,

dan 19. Pernyataan termudah atau pernyataan yang paling banyak siswa jawab

dengan yakin adalah soal nomor 20.

G. Analisis Data

Dari penelitian ini diperoleh dua jenis data, yaitu (1) data kuantitatif

(30)

50

mathematics self-efficacy, (2) data kualitatif berupa data hasil observasi. Data-data

yang telah dikumpulkan selanjutnya dianalisis dengan bantuan software IBM

SPSS 20 dan Microsoft Excel 2010. Berikut ini diuraikan tahap analisis untuk

kedua jenis data tersbut.

1. Data Kuantitatif

Terdiri dari data hasil tes kemampuan koneksi matematis dan data hasil

skala mathematics self-efficacy.

a. Pengolahan Data Hasil Tes Kemampuan Koneksi Matematis

Analisis data digunakan untuk menjawab pertanyaan penelitian tentang

ada atau tidaknya perbedaan pencapaian dan peningkatan kemampuan koneksi

matematis antara siswa yang belajar melalui model PBM dengan siswa yang

belajar melalui model pembelajaran penemuan terbimbing. Data diperoleh melalui

tahap-tahap sebagai berikut.

1) Memberikan skor jawaban siswa sesuai dengan kunci jawaban dan pedoman

penskoran yang digunakan.

2) Membuat tabel yang berisikan skor pretes-postes hasil kedua kelas

eksperimen.

3) Membuat tabel yang berisikan skor peningkatan kemampuan koneksi

matematis. Besarnya peningkatan akan dihitung dengan rumus N-gain

dikarenakan Meltzer (2002) mengemukakan bahwa kebanyakan penelitian

sebelumnya mendapatkan bahwa gain absolut yang diperoleh dari selisih

antara pretes dan postes berkorelasi negatif tinggi terhadap skor pretes. Hal ini

berarti siswa yang memperoleh skor pretes rendah cenderung akan

mendapatkan gain yang lebih tinggi dibandingkan dengan siswa yang

memperoleh skor pretes tinggi. Rumus N-gain dikembangkan oleh Hake

(Meltzer, 2002, hlm. 3), yaitu.

N-gain

=

4) Melakukan interpretasi hasil perhitungan n-gain dengan klasifikasi

(31)

Tabel 3.17 Klasifikasi N-Gain

Besarnya n-gain Klasifikasi

g ≥ 0.7 Tinggi

0.30 ≤ g < 0.7 Sedang

g < 0.30 Rendah

5) Melakukan uji normalitas untuk mengetahui kenormalan distribusi data skor

pretes, skor postes, dan skor n-gain menggunakan uji statistik One-sample

Kolmogorov-smirnov. Adapun hipotesis dinyatakan sebagai berikut.

H0: Data berasal dari populasi berdistribusi normal.

H1: Data berasal dari populasi berdistribusi normal.

Kriteria uji sebagai berikut:

Jika nilai Sig. (p-value) < α (α =0,05), maka H0 ditolak.

Jika nilai Sig. (p-value) ≥ α (α =0,05), maka H0 diterima.

6) Menguji homogenitas varians skor pretes, skor postes, dan skor n-gain

menggunakan uji statistik Homogenity of Variance (Levene-statistic). Adapun

hipotesis dinyatakan sebagai berikut.

H0: Varians skor kelas ekperimen 1 dan kelas eksperimen 2 homogen.

H1: Varians skor kelas ekperimen 1 dan kelas kelas eksperimen 2 tidak

homogen.

Jika nilai Sig. (p-value) < α (α =0,05), maka H0 ditolak.

Jika nilai Sig. (p-value) ≥ α (α =0,05), maka H0 diterima.

7) Melakukan uji hipotesis, dengan langkah sebagai berikut.

a) Apabila diperoleh kedua kelas berdistribusi normal dan memenuhi

homogenitas varians maka dilanjutkan dengan uji-t menggunakan uji

statistik Compare Mean Independent Sample Test. Adapun hipotesis

dinyatakan sebagai berikut.

: Rataan skor kelas eksperimen-1 sama dengan rataan skor

kelas eksperimen-2.

: Rataan skor kelas eksperimen tidak sama dengan rataan skor

kelas eksperimen-2.

Jika nilai Sig. (p-value) < α (α =0,05), maka H0 ditolak.

(32)

52

b) Apabila diperoleh kedua kelas berdistribusi normal namun tidak homogen

maka analisis yang digunakan adalah uji-t’ menggunakan uji statistik

Compare Mean Independent Sample Test.

c) Apabila diperoleh salah satu atau keduanya tidak normal maka tidak perlu

melakukan uji homogenitas varians, dan analisis yang digunakan adalah

uji nonparametrik sebagai pengganti uji-t, yaitu uji Mann-Witney.

8) Pengambilan kesimpulan.

b. Pengolahan Data Hasil Skala Mathematics Self-Efficacy

Sebagai analisis yang lebih mendalam, skor akhir mathematics

self-efficacy siswa dari masing-masing kelas dikelompokkan kedalam tiga kategori.

Kategori tersebut adalah kategori tinggi, sedang, dan rendah. Menurut Azwar

(2012, hlm. 154) acuan dalam mengelompokkan ke dalam tiga kategori adalah

sebagai berikut.

Tabel 3.18. Kriteria Kategori Mathematics Self-Efficacy

Skor Kategori

s Tinggi

s Sedang

s Rendah

Keterangan:

x : skor yang diperoleh

: rerata skor

s : deviasi standar skor

Setelah dilakukan pengelompokan, kemudian dihitung frekuensi

masing-masing kategori dan dihitung persentasenya. Analisis deskriptif juga dilakukan

pada kasus-kasus ekstrim yang ditemukan. Hal tersebut bertujuan diperoleh hasil

penelitian dan pembahasan yang lebih mendalam.

Untuk menjawab pertanyaan penelitian tentang ada atau tidaknya

perbedaan pencapaian mathematics self-efficacy antara siswa yang belajar melalui

model PBM dengan siswa yang belajar melalui model pembelajaran penemuan

terbimbing dilakukan analisis data melalui tahapan sebagai berikut.