SOLUSI ANALITIK DAN NUMERIK KONDUKSI PANAS PADA PEMBANGKIT ENERGI. Elfrida Saragi *

SOLUSI ANALITIK DAN NUMERIK

KONDUKSI PANAS PADA PEMBANGKIT ENERGI Elfrida Saragi*

ABSTRAK

SOLUSI ANALITIK DAN NUMERIK KONDUKSI PANAS PADA PEMBANGKIT ENERGI. Problem konduksi panas yang timbul karena pembangkit energi dalam benda padat terdapat

pada beberapa aplikasi enginering seperti perpindahan panas pada bahan bakar reaktor nuklir, disipasi panas dari sumber panas secara elektrik dan lain – lain. Dalam tulisan ini diterangkan teknik solusi analitik dan numerik untuk menentukan distribusi temperatur dan aliran panas pada konduksi panas dalam keadaan tunak berdimensi satu akibat pembangkit energi pada benda yang mempunyai bentuk seperti bidang datar, silinder. Formulasi masalah konduksi panas yang dikenalkan adalah beda hingga.

ABSTRACT

ANALYTIC AND NUMERICAL SOLUTIONS ON THE HEAT CONDUCTION WITH ENERGY GENERATION. Heat conduction problems involving energy generation in the solid come up

in numerous engineering applications, including heat removal from the fuel elements of nuclear reactor, heat dissipation from electrically heat source, and many others. This paper presents analytic and numerical solution techniques for determining temperature distribution and heat flow in one dimensional steady state heat conduction with energy generation in solids having shape such as plane walls, cylinders. The finite difference formulation of heat conduction problem is introduced.

PENDAHULUAN

Solusi analitik untuk masalah konduksi panas seperti pada geometrik yang komplek, problem nonlinear, sistem termal yang meliputi coupling antara elemen – elemen sangat rumit. Untuk menyelesaikan masalah konduksi panas satu dimensi pada keadaan tunak dengan pembangkit energi adalah menentukan distribusi temperatur dan aliran rata – rata panas pada medium dengan bentuk geometrinya diambil contoh yaitu; bidang datar, silinder.

*

SOLUSI ANALITIK

Bidang Datar dengan Pembangkit Energi dan Temperatur Permukaan Konstan Pada gambar 1 untuk ketebalan permukaan datar adalah L, syarat batas permukaan x = 0 dan x = L yang konstan tetapi temperaturnya berbeda yaitu T1 dan

T2. Konduktiviti termal papan datar adalah k dan pembangkit energi adalah g dalam

W/m3.

Gambar 1. Distribusi temperatur asimetrik Secara matematik formulasi konduksi panas adalah;

0 ) ( 2 2 = + k g dx x T d _{pada 0<x<L 1-1a} T(x) = T1 pada x = 0 1-1b T(x) = T2 pada x = L 1-1c

Distribusi temperatur T(x) untuk bidang datar ditentukan dengan integrasi langsung dari persamaan differensial. Integral persamaan 1-1a menjadi

2 1 2

2

)

(

x

C

x

C

k

g

x

T

=

−

+

+

1-2

Untuk syarat batas pertama (boundary condition) ;

C2 = T1 1-3

Syarat kondisi yang kedua;

L T T k gL C₁ 2 1 2 − + = 1-4

C1 dan C2 diketahui, distribusi panas dari persamaan 1-2 menjadi;

1 1 2 2 2

)

(

2

)

(

T

L

x

T

T

L

x

L

x

k

gL

x

T

+

−

+





























−

=

1-5

Bentuk pertama pada samping kanan adalah distribusi pembangkit energi dalam medium ke distribusi temperatur, dan bentuk kedua adalah kontribusi temperatur pada batas permukaan. Dari persamaan 1-5 diperoleh beberapa syarat yaitu;

a. Jika pembangkit energi (g) = 0 maka pers 1-5 menjadi

T(x ) Q2 Q1 T(L) =T2 T(0)=T1 L

1 1 2

)

(

)

(

T

L

x

T

T

x

T

=

−

+

1-6

T(x)= distribusi temperatur linear. b. Syarat temperatur permukaan adalah sama

Jika syarat temperatur permukaan adalah T1 dan T2 adalah sama,yaitu

T1 = T2

≡

Tw,

Maka distribusi temperatur;

w

T

L

x

L

x

k

gL

x

T

+





























−

=

2 2

2

)

(

1-7

di mana distribusi temperatur parabolik dan simetrik mempunyai temperatur maximum pada sumbu simetri x = L/2 seperti gambar 2. Formulasi matematik untuk problem yang tergantung pada ½ plat, 0<x<L/2 sebagai berikut;

Gambar 2. Distribusi temperatur simetrik

0

1

)

(

2 2

=

+

g

k

dx

x

T

d

pada 0 < x < L/2 1-8a

0

)

(

=

dx

x

dT

pada x = 0 1-8b w

T

x

T

(

)

=

pada x = L/2 1-8c

Problem ini diselesaikan dengan mengintegralkan pers 1-8a dua kali dan memasukkan syarat batas x = 0 dan x = L/2. Ekspresi temperatur menjadi;

w

T

L

x

k

gL

x

T

+





























−

=

2 2

4

1

2

)

(

1-9

di mana koordinat x merupakan garis pusat slab seperti pada gambar 2. Temperatur pada garis pusat, x = 0 diperoleh dari pers 1-9 dengan menentukan x = 0;

T(L/2)=Tw

x T(-L/2)=Tw

Tc

w c

T

k

gL

T

=

+

8

2 1-10

Sisa Energi Plat

Sisa energi plat pada batas permukaan merupakan kuantiti yang terkait untuk menentukan fluks panas. Sisa energi pada batas permukaan kanan x = L/2 adalah;

2

)

(

2

L x

dx

x

dT

k

L

q

=

−

=













1-11a

Pers 1-9 dimasukkan pada pers 1-11a dan menentukan x = L/2, maka fluks panas pada batas permukaan x = L/2 menjadi;

2

/

2

2

W

m

gL

L

q



=











1-11b Fluks panas di batas permukaan kiri x = -L/2 ;

2

/

2

2

W

m

gL

L

q



=

−









−

1-12

di mana kuantiti –gL/2 adalah negatip dan q(-L/2) adalah negatip.

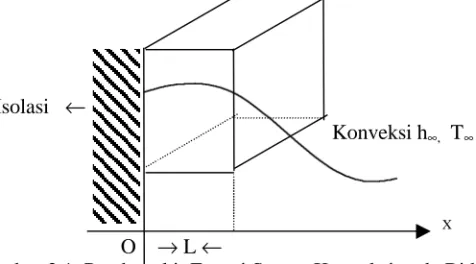
Bidang Datar dengan Pembangkit Energi dan Konveksi

Gambar 2.1 untuk batas permukaan x = 0 merupakan isolasi dan batas permukaan x = L, terjadi disipasi panas dengan koefisien perpindahan panas adalah h∞

pada temperatur T∞.

Isolasi ←

Konveksi h∞, T∞

X

O → L ←

Formulasi matematik dapat ditulis persamaan :

L

x

k

g

dx

x

T

d

<

<

=

+

0

pada

0

)

(

2 2 1-13a

0

pada

0

)

(

₌

₌

x

dx

x

dT

1-13b

[

T

x

T

]

x

L

h

dx

x

dT

k

=

−

=

−

(

)

_∞

(

)

_∞

pada

1-13c 1 ) ( C x k g dx x dT _{=− +} 1-14

Dari pers 1-14, jika syarat batas C1 = 0 maka x k g dx x dT( ) ₌₋ 1-15 Untuk syarat batas kedua dari pers 1-2 bila C1 = 0 maka;

2 2 2 ) ( x C k g x T =− + 1-16 ∞ ∞ ∞ ∞ + + =      _{− + −} =      − − T h gL k gL C T C L k g h L k g k 2 2 2 2 2 2 1-17

Distribusi temperatur menjadi;

∞ ∞ + +               − = T h gL L x k gL x T 2 2 1 2 ) ( _1-18

Koefisien perpindahan panas (h∞) mempunyai dua batasan yaitu ;

a. h∞ ∞ yang bernilai besar maka resistan termal pada batas permukaan hilang

dan persamaan 1-34 menjadi;

∞ +               − = T L x k gL x T 2 2 1 2 ) ( _1-19

b. h∞ 0 maka distribusi temperatur T(x) menjadi tak terhingga dan syarat batas

menjadi;

(

)

→

0

dx

x

dT

Benda yang Berbentuk Silinder dengan Pembangkit Energi dan Temperatur Permukaan Konstan

Pada gambar 3 benda silinder dengan radius r = b , di mana temperatur permukaan disebut temperatur yang sama yaitu Tw, konduktiviti termal dan pembangkit energi konstan.

T(b) = Tw Konveksi h∞, T∞

Gambar 3. Benda Silinder dengan Pembangkit Energi Persamaan konduksi panas, di mana,

0

)

(

1

₊

₌









k

g

dr

r

dT

r

dr

d

r

pada 0 < r < b 1-20a 0 ) ( ₌ dr r dT pada r = 0 1-20b Temperatur permukaan = Tw w T r T( )= pada r = b 1-20c

Persamaan 1-20a diselesaikan dengan integrasi pertama;

r C r k g dr r dT ₁ 2 ) ( _{=− +} 1-21 Untuk C1 = 0 maka distribusi temperatur menjadi

r k g dr r dT 2 ) ( ₌₋ 1-22 Integrasi dari persamaan 1-22 menjadi;

2 2 4 ) ( r C k g r T =− + 1-23

Untuk syarat batas C2 pada temperatur T(r) = Tw menjadi; w T k gb C = + 4 2 2 1-24 Pembangkit Energi, g b 0 r

Distribusi temperatur dari pers 1-24 dimasukkan ke pers 1-23 menjadi ; w T b r k gb r T +               − = 2 2 1 4 ) ( 1-25

Fluks panas dalam medium didefenisikan sebagai berikut;

dr r dT k r q( )=− ( ) 1-26

Untuk fluks panas pada batas permukaan adalah;

2 )

(r gr

q = 1-27

Jika r = b maka fluks panas menjadi;

2 )

(r gb

q = W/m2 1-28

Jika temperatur tinggi terjadi ditengah silinder maka temperatur digaris tengah diperoleh dari pers 1-25 dengan menentukan r = 0 menjadi;

w c T k gb T = + 4 2 1-29

Benda Berbentuk Silinder dengan Pembangkit Energi dan Konveksi

Pada gambar 4, aplikasi energi pada disipasi energi secara konveksi yang berasal dari luar permukaan menuju ke dalam dengan temperatur yang konstan T∞.

Gambar 4. Benda berbentuk silinder dengan pembangkit energi ke kondisi batas konveksi

Secara matematik dapat ditulis persamaan;

0 ) ( 1 = +     k g dr r dT r dr d r di 0 < r< b 1-30a Pembangkit energi,g b 0 r Konveksi h∞, T∞

0 ) ( ₌ dr r dT pada r = 0 1-30b

[

∞

]

∞ − = − h t r T dr r dT k ( ) ( ) pada r = b 1-30c

Persamaan 1-30a diintegrasikan dan diaplikasikan ke syarat batas pers 1-30b dengan menentukan C1 = 0 maka; r k g dr r dT 2 ) ( ₌₋ 1-31

Persamaan diatas diintegrasikan untuk mendapatkan distribusi temperatur pada C2

menjadi; 2 2 4 ) ( r C k g r T =− + 1-32

Pers 1-30c diintegrasikan dengan syarat batas r = b maka C2 menjadi; ∞ ∞ + + = b T h g b k g C 2 4 2 2 1-33

Distribusi temperatur pada silinder menjadi;

∞ ∞ + +               − + = T h gb b r k gb r T 2 1 4 ) ( 2 2 1-34

Secara fisika koefisien perpindahan panas (h ∞) mempunyai 2 batasan yaitu ;

• Distribusi temperatur pada bidang datar (slab) pada koefisien perpindahan panas h∞ ∞ maka; ∞

+





























−

+

=

T

b

r

k

gb

r

T

2 2

1

4

)

(

1-35

• h∞ 0 . Koefisien perpindahan panas yang bernilai kecil di mana temperatur

T(r) menjadi tak terhingga, maka syarat batas pada pers 1-30b menjadi;

0

)

(

₌

dr

r

dT

pada h∞ 0

Flux panas q(r) didefenisikan menjadi;

dr

r

dT

k

r

q

(

)

=

−

(

)

1-36

Pers 1-32 dimasukkan ke pers 1-36 maka flux panas menjadi;

r

g

r

q

2

)

(

=

1-37

SOLUSI NUMERIK

Rumus Beda Hingga yang Digunakan pada Bidang Datar.

Persamaan konduksi panas pada bidang datar dengan syarat batas permukaan x = 0 dan x = L , pembangkit energi adalah g(x) dalam W / m3 menjadi;

0

)

(

1

)

(

2 2

=

+

g

x

k

dx

x

T

d

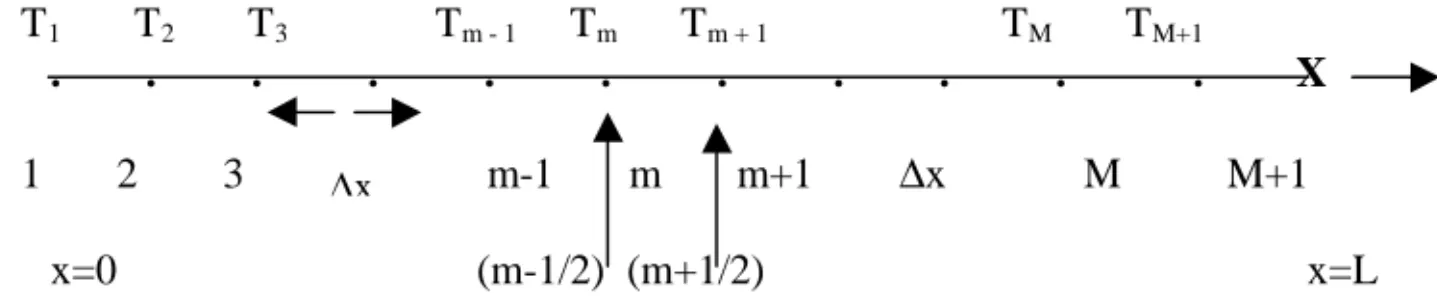
dalam 0 < x < L 2-1 Distribusi temperatur pada bidang datar dengan menentukan titik node l pada medium seperti gambar 5.

T1 T2 T3 Tm - 1 Tm Tm + 1 TM TM+1

. . . . . . . . . X 1 2 3 m-1 m m+1 ∆x M M+1

x=0 (m-1/2) (m+1/2) x=L

Gambar 5. Seleksi node pada bidang datar. Analisa pertama dengan membagi ke dalam bagian ke dalam M

M

L

x

=

∆

2-2

di mana node-node dimulai dari m=1 ke m = M+1 pada gambar 5, besar node m sama dengan lokasi pada koordinat x yang diberikan;

x = (m-1) ∆x untuk m = 1,2,3,…,M+1 2-3 di mana m =1 sama dengan ke syarat permukaan pada x = 0 dan m = M +1 sama dengan dengan syarat permukaan x = L. Temperatur T(x) pada node m menjadi;

(

)

[

m

x

]

T

m

T

x

T

(

)

=

−

1

∆

≡

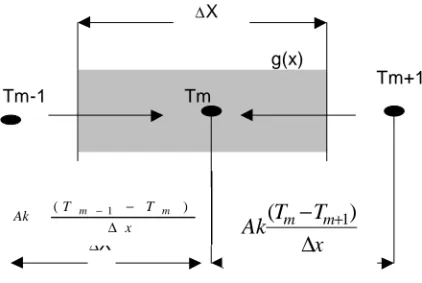
2-4 ∆x

Gambar 6. Kesetimbangan energi pada internal node m

Persamaan kesetimbangan energi pada keadaan tunak pada gambar 6 adalah; Rata – rata panas yang masuk melalui konduksi + Rata –rata pembangkit energi = 0

[

(

₁

−

2

+

₁

)

] [

+

∆

]

=

0

∆

T

m−

T

m

T

m+

A

xg

m

x

Ak

2-5

di mana A= luas permukaan slab, gm adalah pembangkit energi.

Bentuk beda hingga untuk persamaan konduksi panas pada keadaan tunak

(

2

)

( ) 0 2 1 1 = ∆ + + − ₊ − k g x T T T m m m m untuk m = 2,3,…,M 2-6

Menentukan Syarat Batas Fluks Panas

Kesetimbangan energi dengan ketebalan ∆x/2 pada node m=1;

0

2

1 1 2 0

=

∆

+

∆

−

+

x

Ag

x

T

T

kA

A

q

Pada gambar 7 ini ketebalan elemen = ∆x/2, pada batas permukaan (x) = 0 di node m = 1 qo ∆x/2 T1 T2 T3 X=0 ∆X Tm _Tm ∆X ∆X g(x) Tm+1 Tm-1 x T T Ak m m ∆ − − ) ( 1 x T T Ak m m ∆ − +) ( ₁ ∆x

Gambar 7. Syarat batas fluks panas pada node x = 0

Bentuk beda hingga untuk persamaan fluks panas dengan syarat batas permukaan = 0 dari node m = 1 menjadi;

0

2

)

(

2

2

1 0 2 1 2

=

∆

+

∆

+

−

k

xq

k

g

x

T

T

untuk m= 1 2-7

Untuk batas permukaan x = L dengan ketebalan elemen = ∆x/2 pada node m = M + 1 maka bentuk persamaan beda hingga fluks panas menjadi;

0

2

)

(

2

2

1 2 1

=

∆

+

∆

+

−

+ +

k

xq

k

g

x

T

T

M L M M untuk m = M + 1 2-8

Pada batas isolasi (geometrik dan kondisi simetrik termalnya) jika q0 = 0 dan qL = 0

maka persamaan 2-7 dan persamaan 2-8 menjadi ;

0 ) ( 2 2 1 2 1 2 = ∆ + − k g x T T 0 ) ( 2 2 1 2 1 = ∆ + − + + k g x T T M M M 2-9

Syarat Batas Konveksi.

Kesetimbangan energi pada elemen dengan ketebalan ∆x/2 pada node m = 1,seperti pada gambar di bawah ini di mana batas permukaan x = 0 dan koefisien perpindahan panas h∞1 kedalam temperatur T∞1 adalah;

(

)

0

2

1 1 2 1 1 1

=

∆

+

∆

−

+

−

∞ ∞

Ag

x

x

T

T

kA

T

T

A

h

2-10

( )

0

2

2

2

1 1 1 2 1 1 2

=

∆

+

∆

+













₊

∆

−

∞ ∞

_T

_∞

k

xh

k

g

x

T

k

xh

T

2-11

Jika batas permukaan x=L dan node m = M + 1 maka persamaan beda hingga untuk konveksi menjadi;

( )

0

2

2

2

1 2 ₂ 2 1 2



+

∆

+

∆

=











₊

∆

−

+ ∞ _∞ + ∞

_T

k

xh

k

g

x

T

k

xh

T

M M M 2-12

Sebagai contoh;

Sebuah papan dengan ketebalan potongannya = 0.1 m, konduktivitas termal k = 40 W/(m.0C) di mana energi yang timbul rata – rata konstan sebesar 106 W/m3. Batas permukaan x = 0 dan x =0.1 m, koefisien perpindahan panas sebesar 200 W /(m2.0C) dan temperatur sebesar 150 0C. Tentukanlah persamaan beda hingga jika papan tersebut di bagi kedalam M = 5 bagian.

a. Penyelesaian secara numerik.

∆x = L/M = 0.1/5 = 0.02m

Maka persamaan beda hingga untuk perpindahan panas pada node m =2 s/d m = 5

(

)

(

2

)

10

0

untuk

m

2

,

3

,

4

,

5

(

atau

0

40

10

)

02

.

0

(

2

1 1 6 2 1 1

=

=

+

+

−

=

×

+

+

−

+ − + − m m m m m m

T

T

T

T

T

T

Untuk batas isolasi pada x = 0 maka ;

0

)

(

2

2

1 2 1 2

=

∆

+

−

k

g

x

T

T

0 40 10 ) 02 . 0 ( 2 2 6 2 1 2 = × + − T T 2T2 - 2T1 + 10 = 0 untuk m = 1

Batas konveksi pada x = L, maka

( )

2 ₀ 2 2 1 2 ₂ 2 1 2_ + ∆ + ∆ =      ₊∆ − + ∞ _∞ + ∞ _T k xh k g x T k xh T M M M

( )

0 150 40 200 02 . 0 2 40 10 02 . 0 40 200 02 . 0 2 2 2 6 2 6 5 = × × + × +       ₊ × × − T T 2T5 – 2.2 T6 + 40 = 0 untuk m = 6

Kemudian diperoleh 6 persamaan secara matriks yaitu; -2T1 + 2T2 = -10 untuk m = 1 T1 - 2T2 + T3 = -10 untuk m = 2 T2 - 2T3 + T4 = -10 untuk m = 3 T3 - 2T4 + T5 = -10 untuk m = 4 T4 - 2T5 + T6 = -10 untuk m = 5 2T5 - 2.2T6 = -10 untuk m = 6

Maka bentuk matriksnya adalah;                     − − − − − − =                                         − − − − − − 10 10 10 10 10 10 2 . 2 2 0 0 0 0 1 2 1 0 0 0 0 1 2 1 0 0 0 0 1 2 1 0 0 0 0 1 2 1 0 0 0 0 2 2 6 5 4 3 2 1 T T T T T T

Hasilnya pada : Node Temperatur Node Temperatur

1 775 4 730

2 770 5 695

3 755 6 650

b. Penyelesaian secara analitk.

Temperatur permukaan isolasi pada x=0

∞ ∞ + +               − = T h gL L x k gL x T 2 2 1 2 ) (

[

x

]

C x x X x T 2 0 6 2 2 6 775 650 100 1 125 150 200 1 . 0 10 1 . 0 1 40 2 ) 1 . 0 ( 10 ) ( + + = − + =               − =

Temperatur pada batas konveksi x=L

[

x

]

C x x X x T 2 0 6 2 2 6 650 650 100 1 125 150 200 1 . 0 10 1 . 0 1 40 2 ) 1 . 0 ( 10 ) ( + + = − + =               − =

Formulasi Beda Hingga pada Silinder.

Untuk persamaan konduksi panas dengan syarat batas r = 0 dan r = b maka;

b

r

r

g

k

dr

r

dT

r

dr

d

r



+

=

<

<







(

)

1

₍

₎

₀

_pada

₀

1

Bentuk beda hingga untuk persamaan energi dibagi kedalam M bagian, dan ketebalannya (∆r) adalah;

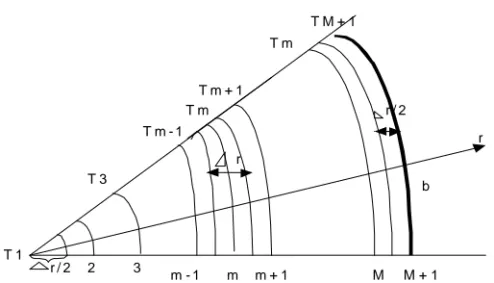
Pada gambar 8, setiap bagian 0 ≤ r ≤ b berisi M + 1 pada lokasi ; r = (m-1) ∆r pada m = 1,2,…, M+1 2-14 r r / 2 T M + 1 T m r b T m - 1 T m T 3 T 1 r / 2 2 3 m - 1 m m + 1 M M + 1 T m + 1 G a m b a r 5 .

Gambar 8. Seleksi Node pada Benda yang Berbentuk Silinder

dengan node – node m =1 dan m = M+1 sebanding dengan pusat dan luar batas permukaan benda silinder, dan node m=2,3,…,M adalah node dalam (seperti gambar diatas). Untuk temperatur node M+1 dinyatakan sebagai;

T(r) = T[(m-1) ∆r ] ≡ Tm pada m =1,2,…,M+1 2-15

Panas yang timbul pada element dengan ketebalan ∆r pada node m maka;

(

)

r

T

T

k

A

r

T

T

k

A

m m m m m m m m

∆

−

+

∆

−

=

+ + − − 1, 1 1 , 1

konduksi

Panas

di mana ;

H

r

r

m

A

H

r

r

m

A

m m m m









₋

_∆

₊

_∆

=









₋

_∆

₋

_∆

=

+ −

2

1

)

1

(

2

2

1

)

1

(

2

, 1 , 1

π

π

H = panjang silinder Energi generasi =

A

_m

∆

rg

_m = 2πH(m-1)(∆r)2 gm

Kesetimbangan energi pada silinder ;

0

)

(

)

1

(

2

1

1

2

)

1

(

2

1

1

2 1 1

=

∆

+













−

+

+

−













−

−

_{− +}

k

g

r

T

M

T

T

m

m m m m untuk m = 2,3,…,M (2-16) untuk m = 2, 3,…, M 2-16

Untuk node m = 1 dengan radius ∆r/2 maka;

Rata –rata panas yang masuk secara konduksi =

π

Hk

(

T

₂

−

T

₁

)

2-17 Rata panas yang timbul = ₁

2

2

Hg

r











 ∆

π

2-18

Persamaan beda hingga untuk kesetimbangan konduksi panas pada tengah node m =1 ;

0

)

(

)

(

4

1 2 1 2

=

∆

+

−

k

g

r

T

T

2-19

Pada syarat batas r = b maka perlu menentukan syarat batas temperatur , fluks panas dan konveksi.

Menentukan Syarat Batas Temperatur.

Jika temperatur pada batas permukaan di node M yang spesifik yang disebut fM+1 maka

TM+1 = fM+1 pada m = M + 1

Syarat Batas Fluks Panas

H

r

M

H

r

r

M

A

H

r

M

A

H

r

r

M

A

g

r

A

q

A

r

T

T

k

A

M M M M m M M M M M M M

)

(

2

)

4

1

(

2

)

(

2

)

2

1

(

2

mana

di

0

2

1 * 1 1 , 1 1 * 1 1 1 1 ,

∆

≅

∆

−

∆

=

∆

=

∆

−

∆

=

=

∆

+

+

∆

−

+ + + + + + + + +

π

π

π

π

2-20 H= panjang silinder

Dari ekspresi diatas maka diperoleh;

0 2 ) ( 2 1 1 2 1 1 1 2 1 = ∆ + ∆ +       − −       − + ∞ ∞ + k g r T k rh T M T M M M M untuk m = M + 1

Syarat batas konveksi

H

r

M

H

r

r

M

A

H

r

M

A

H

r

r

M

A

g

r

A

T

T

h

A

r

T

T

k

A

M M M M m M M M M M M M

)

(

2

)

4

1

(

2

)

(

2

)

2

1

(

2

mana

di

0

2

)

(

1 * 1 1 , 1 1 * 1 1 1 1 1 ,

∆

≅

∆

−

∆

=

∆

=

∆

−

∆

=

=

∆

+

−

+

∆

−

+ + + + + + ∞ ∞ + + +

π

π

π

π

2-21

Pers 2-21 dimasukkan ke persamaan kesetimbangan energi dan persamaan beda hingga dengan syarat batas r = b pada m = M + 1 maka dapat ditulis sebagai berikut;

0

2

)

(

2

1

1

2

1

1

1 2 1

=

∆

+

∆

+









₊

∆











 −

−











 −

+ ∞ ∞ + ∞

k

g

r

T

k

rh

T

k

rh

M

T

M

M M M

Contoh benda yang berbentuk silinder.

Benda sejenis chrome nikel yang berbentuk batang dengan diameter 10 Cm, konduktiviti termal 20 W/(m.0C), energi yang timbul dari panas elektrik dengan rata – rata 107 W/m3.Permukaan batang dipanasi secara konveksi dengan koefisien perpindahan panas h=200 W/(m.0C) pada temperatur 300C. Tentukanlah persamaan beda hingga jika radius batang dibagi kedalam 5 interval.

Jawab; b=0.05 m, k = 20 W/(m.0C), g = 107 W/m, T∞=30 0C, h∞ = 200 W/(m.0C), dan

M = 5 maka ∆r = b/M = 0.05/5 = 0.01 (∆r)2g/k = (0.01)2 (107) / 20 = 50

∆r h∞ / k = 0.01X 200 / 20 = 1/10

Persamaan beda hingga dipusat pada node m =1 maka diperoleh; 4(T2 – T1) + 50 = 0 untuk m = 0

Persamaan beda hingga dari persamaan 2-16 untuk node m =2 s/d 5 maka diperoleh ;

0

50

)

1

(

2

1

1

2

)

1

(

2

1

1

₁

_

₁

+

=











−

+

+

−













−

−

m₋ m

T

m₊

M

T

T

m

Hasil akhir persamaan beda hingga untuk syarat batas konveksi pada node m = M+1 = 6 maka diperoleh;

0

2

)

(

2

1

1

2

1

1

1 2 1

=

∆

+

∆

+









₊

∆











 −

−











 −

+ ∞ ∞ + ∞

k

g

r

T

k

rh

T

k

rh

M

T

M

M M M

0

25

30

10

1

10

1

10

1

1

10

1

1

_{5 6}

+

+

=









₊











 −

−











 −

T

T

0.9 T5 – T6 + 28 = 0 untuk m = 6

Diperoleh persamaan berbentuk matrik 6 X 6 untuk 6 node temperatur Tm, m = 1 s/d 6.

-4T1 + 4 T2 = -50 untuk m = 1 0.5T1 - 2T2 + 1.5 T3 = -50 untuk m = 2 0.75T2 - 2T3 + 1.25 T4 = -50 untuk m = 3 0.8333T3 - 2T4+ 1.1666 T5 = -50 untuk m = 4 0.875T4 - 2T5 + 1.125 T6 = -50 untuk m = 5 0.9T5 - T6 = -50 untuk m = 6

Dari persamaan diatas ditulis dalam bentuk matriks;                   − − − − − − =                                     − − − − − − 50 50 50 50 50 50 1 9 . 0 0 0 0 0 125 . 1 2 875 . 0 0 0 0 0 1666 . 1 2 8333 . 0 0 0 0 0 25 . 1 2 75 . 0 0 0 0 0 5 . 1 2 5 . 0 0 0 0 0 4 4 6 5 4 3 2 1 T T T T T T

Solusi Komputer / Numerik

Dari persamaan diatas diperoleh matrix tridiagonal maka dapat dibuat program aplikasi dengan memasukkan data seperti contoh pada bidang datar maupun pada silinder dengan persamaan ; [A] {X} = {D}

Secara umum dapat ditulis;

                      =                                             − − − − − N N N N N N N N N N d d d d X X X X c b a c b a c b a c b 1 2 1 1 2 1 1 1 1 2 2 2 1 1 . . . . . . 0 0 0 0 . 0 . . . . . . . . . . . . . . . . . . 0 0 0 0 0 0 0 Matriks A(I,J)                     = − − − − ' ' 1 1 1 1 ' 3 3 3 3 ' 2 2 2 2 ' 1 1 1 0 ) , ( N N N N N N N N d c b a d c b a d c b a d c b a d c b J I A

KESIMPULAN

• Untuk menentukan distribusi temperatur pada benda yang berbentuk bidang datar maupun berbentuk silinder atau lingkaran dengan cara membagi – bagi benda tersebut kedalam beberapa bagian.

• Perpindahan panas secara konduksi harus menentukan syarat batas permukaan, dalam dan luar benda agar diperoleh temperatur dimasing - masing node yang telah dibagi kedalam N bagian.

• Secara analitik temperatur permukaan isolasi pada x=0 diperoleh sebesar 750 0C , temperatur pada batas konveksi x = L diperoleh sebesar 750 0C sedangkan secara numerik hasilnya sama dengan secara analitik.

DAFTAR PUSTAKA

1. BAYAZITOGLU, Yilzid, OZISIK, M. Necati, Elements of Heat Transfer, McGraw-Hill Book, (1988)

2. HILL, J. M., DEWYNNE, J.N., Heat Conduction, Blackwell Scientific Publications, (1987)

3. HOLMAN, J.P., Heat Transfer, McGraw-Hill, (1981) 4. OZISIK, M. Necati, Heat Conduction, Jhon Willey & Sons.

DISKUSI

UTAJA

Untuk bentuk dan syarat batas sederhana, penyelesaian distribusi suhu lebih mudah dilakukan dengan analitik. Mohon dijelaskan mengapa Anda menggunakan metode numerik?

ELFRIDA SARAGI

Secara analitik dapat dilakukan. Dalam hal ini saya menggunakan metode secara numerik karena untuk membuat program komputer, untuk mengetahui distribusi temperatur pada benda.

SARIFUDDIN MADENDA

Dalam menghitung konduksi panas pada batang, silinder dan lingkaran, apakah ada perbandingan antara panjang bahan atau diameter bahan terhadap jumlah pembagian daerah perhitungan konduksi panas? Bila ada berapa kira-kira idealnya?

ELFRIDA SARAGI

Pembagian elemen ke dalam beberapa bagian harus ditentukan dan pembagian tersebut harus sama antara node pertama dengan node kedua dan node selanjutnya.

DAFTAR RIWAYAT HIDUP

1. Nama : ELFRIDA SARAGI

2. Tempat/Tanggal Lahir : Medan, 1 Juni 1963 3. Instansi : P2TIK - BATAN 4. Pekerjaan / Jabatan : Staf Bidang Komputasi

5. Riwayat Pendidikan : (setelah SMA sampai sekarang)

• FMIPA-USU, Jurusan Fisika (S1) 6. Pengalaman Kerja : - PT Benang Indah Jakarta

- P2TIK - BATAN 7. Organisasi Professional : GMK I Medan