Analisis Data
Kegiatan 1. Gerak dari C ke A Hasil pengukuran berulang pada waktu
1.
Jarak tempuh (x
CA ) = 40,60cm
Waktu tempuh (
t
CA )t
CA(1) = t1 = 1,518 st
CA(2) =t
2 = 1,511s
t
CA(3) = t3 = 1,536 s´
t
CA = tCA(1)+tCA(2)+tCA(3) 3
¿
1,518
+
1,511
+
1,536
3
´
t
CA = 1,522 sδ
1=
|
t
1−´
t
|
=|
1,518
−
1,522
|
s
=
0,004
s
δ
2=
|
t
2−´
t
|
=|
1,511−1,522|
s=0,011sδ
3=
|
t
3−´
t
|
=|
1,536
−
1,522
|
s
=
0,014
s
=δmaks
maka ∆ t=0,014sKR
=
∆ t
t
x 100 % =0,014
s
1,522
s
x 100%¿
0,92
= 3 AB Hasil pengukuran waktunya yaitu : t =|
1,5 2±0,01|
s2.
Jarak tempuh ( xCA ) = 37,50 cmWaktu tempuh ( tCA )
t
CA(1) =t
1 = 1,243s
t
CA(2) = t2 = 1,263 st
CA(3) =t
3 = 1,276s
t´CA =
t
CA(1)+
t
CA(2)+
t
CA(3)3
¿
1,243
+
1,263
+
1,276
3
t´CA = 1,261 s
δ
1=
|
t
1−´
t
|
=|
1,243−1,261|
s=0,018s = δmaksδ
2=
|
t
2−´
t
|
=|
1,263
−
1,261
|
s
=
0,002
s
KR
=
∆ t
t
x 100 % =0,018
s
1,261
s
x 100% ¿1,43 = 3 AB Hasil pengukuran waktunya yaitu :t
=|
1,2 6
±
0,01
|
s
3.
Jarak tempuh (x
CA ) = 31,80cm
Waktu tempuh (
t
CA )t
CA(1) = t1 = 1,114 st
CA(2) =t
2 = 1,123s
t
CA(3) = t3 = 1,172 s´
t
CA = tCA(1)+tCA(2)+tCA(3) 3¿
1,114
+
1,123
+
1,172
3
´
tCA = 1,136 s
δ
1=
|
t
1−´
t
|
=|
1,114−1,136|
s=0,022sδ
2=
|
t
2−´
t
|
=|
1,123
−
1,136
|
s
=
0,013
s
δ
3=
|
t
3−´
t
|
=|
1,172−1,136|
s=0,036s = δmaks maka∆ t
=
0,036
s
KR
=
∆ t
t
x 100 % =0,036
s
1,136
s
x 100% ¿3,17 = 3 AB Hasil pengukuran waktunya yaitu :t
=|
1,1 3
±
0,03
|
s
4.
Jarak tempuh (x
CA ) = 29cm
Waktu tempuh (
t
CA )t
CA(1) = t1 = 0,816 st
CA(2) =t
2 = 0,836s
t
CA(3) = t3 = 0,898 st
´
CA =
tCA(1)+tCA(2)+tCA(3)
3
¿
0,816
+
0,836
+
0,898
3
t
´
CA = 0,85 s
δ
1=
|
t
1−´
t
|
=|
0,816
−
0,85
|
s
=
0,034
s
δ
2=
|
t
2−´
t
|
=|
0,836−0,85|
s=0,014sKR
=
∆ t
t
x 100 % =0,048
s
0,85
s
x 100% ¿5,65 = 2 AB Hasil pengukuran waktunya yaitu :t
=|
0,85
±
0,04
|
s
5.
Jarak tempuh (x
CA ) = 24,50cm
Waktu tempuh (
t
CA )t
CA(1) = t1 = 0,781 st
CA(2) =t
2 = 0,798s
t
CA(3) = t3 = 0,785 st
´
CA =
tCA(1)+tCA(2)+tCA(3) 3
¿
0,781
+
0,798
+
0,785
3
t
´
CA = 0,788 s
δ
1=
|
t
1−´
t
|
=|
0,781
−
0,788
|
s
=
0,007
s
δ
2=
|
t
2−´
t
|
=|
0,798−0,788|
s=0,010s = δmaksδ
3=
|
t
3−´
t
|
=|
0,785
−
0,788
|
s
=
0,003
s
maka ∆ t=0,010s
KR
=
∆ t
t
x 100 % =0,010
s
0,788
s
x 100%¿
1,270
= 3 AB Hasil pengukuran waktunya yaitu : t =|
0,788±0,010|
s6.
Jarak tempuh ( xCA ) = 20,30 cmWaktu tempuh ( tCA )
t
CA(1) =t
1 = 0,587s
t
CA(2) = t2 = 0,587 st
CA(3) =t
3 = 0,593s
t´CA =
t
CA(1)+
t
CA(2)+
t
CA(3)3
¿
0,587
+
0,587
+
0,593
3
t´CA = 0,589 s
δ
1=
|
t
1−´
t
|
=|
0,587−0,589|
s=0,002sδ
2=
|
t
2−´
t
|
=|
0,587
−
0,589
|
s
=
0,002
s
KR
=
∆ t
t
x 100 % =0,004
s
0,589
s
x 100% ¿0,680 = 3 AB Hasil pengukuran waktunya yaitu :t
=|
0,589
±
0,004
|
s
7. Jarak tempuh (x
CA ) = 14,70cm
Waktu tempuh (
t
CA )t
CA(1) = t1 = 0,423 st
CA(2) =t
2 = 0,420s
t
CA(3) = t3 = 0,424 st
´
CA =
tCA(1)+tCA(2)+tCA(3)
3
¿
0,423
+
0,420
+
0,424
3
t
´
CA = 0,422 s
δ
1=
|
t
1−´
t
|
=|
0,423
−
0,422
|
s
=
0,001
s
δ
2=
|
t
2−´
t
|
=|
0,420−0,422|
s=0,002s = δmaksδ
3=
|
t
3−´
t
|
=|
0,424
−
0,422
|
s
=
0,002
s
maka ∆ t=0,002s
KR
=
∆ t
t
x 100 % =0,002
s
0,422
s
x 100%¿
0,473
= 4 AB Hasil pengukuran waktunya yaitu : t =|
0,4220±0,0020|
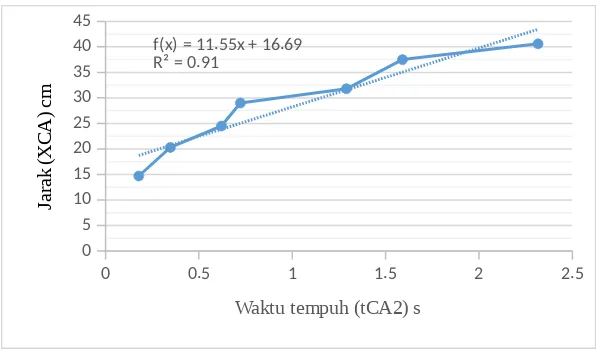
s1. Buatlah grafik antara XCA terhadap t2CA. dari grafik hitunglah percepatan benda M2 + m1. Bandingkan nilai percepatan yang diperoleh dengan percepatan dari perhitungan dengan persamaaan 3.5
0 0.5 1 1.5 2 2.5 0
5 10 15 20 25 30 35 40 45
f(x) = 11.55x + 16.69 R² = 0.91
Waktu tempuh (tCA2) s
Ja
ra
k
(X
C
A
) c
m
Grafik 1. Hubungan antara jarak (XCA) terhadap waktu tempuh(t2CA)
y
=
mx
+
c
y=11,55x+16,685
R
2=
0,9087
XCA=mt2+c
v
=
δx
δt
v
=
δ
(
mt
2
+
c
)
δ t
v=2mt
a
=
δv
δt
a
=
δ
(
2
mt
)
δ t
a
=
2
m
a
=
2
(
11,55
)
cm
s
2a=23,1
cm
s
2DK
=
0,9087
×
100
DK=90,87
KR
=
100
−
DK
=
100
−
90,87
=
9,13
( 2 AB )KR
=
9,13
=
0,0913
∆ a=KR× a=0,0913×23,1=2,11cm/s2
a
=
|
a ± ∆ a
|
cm
/
s
2a =
|
23,1±2,1|
cm
/
s
2Perhitungan percepatan dari perhitungan dengan persamaaan 3.5
a
=
(
m
+
M
1)−
M
2m
+
M
1+
M
2+
I
/
R
2. g
a
=
(
4,05
+
63,22
)−
63,22
4,05
+
63,22
+
63,22
+
1132,88
/
5,95
2.980
cm
/
s
2a
=
4,05
130,49
+
1132,88
/
35,4025
.980
cm
/
s
2a
=
3969
cm
/
s
2
130,49
+
1132,88
/
35,4025
a
=
3969
cm
/
s
2
162,49
2
m
+
2
M
1+
I
R
2¿
¿
∆ M
2+
|
(
m
+
M
1+
M
2)/
R
2(
m
+
M
1+
M
2+
I
R
2)
(
m
+
M
1−
M
2)
|
∆ I
+
|
2
I
R
3(
m
+
M
1−
M
2)
(
m
+
M
1+
M
2+
I
R
2)
(
m
+
M
1−
M
2)
|
∆ R
−
¿
|
2
M
2+
I
R
2(
m
+
M
1+
M
2+
I
R
2)
(
m
+
M
1−
M
2)
|
∆ m
+
|
2
M
2+
I
R
2(
m
+
M
1+
M
2+
I
R
2)
(
m
+
M
1−
M
2)
|
∆ M
1+
¿
∆ a
=
¿
a
2
(
4,05
)+
2
(
63,22
)+
1132,88
5,95
2¿
¿
0,01
+
|
(
4,05
+
63,22
+
63,22
)/
5,95
2(
4,05
+
63,22
+
63,22
+
1132,88
5,95
2)
(
4,05
+
63,22
−
63,22
)
|
19,20
+
|
2
(
1132,88
)
5,95
3(
4,05
+
63,22
−
63,22
)
(
4,05
+
63,22
+
63,22
+
1132,88
5,95
2)
(
4,05
+
63,22
−
63,22
)
|
0,05
−
¿
|
2
(
63,22
)+
1132,88
5,95
2(
4,05
+
63,22
+
63,22
+
1132,88
5,95
2)
(
4,05
+
63,22
−
63,22
)
|
0,01
+
|
2
(
63,22
)+
1132,88
5,95
2(
4,05
+
63,22
+
63,22
+
1132,88
5,95
2)
(
4,05
+
63,22
−
63,22
)
|
0,01
+
¿
∆ a
=
¿
24,43
¿
{
|
158,44
658,0845
|
0,01
+
|
158,44
658,0845
|
0,01
+
|
−
1 66,54
658,0845
|
0,01
+
|
0,1144
658,0845
|
19,20
+
|
43,563
658,0845
|
0,05
}
24,43
¿{
|
0,0024|
+|
0,0024|
+|
−0,0025|
+|
0,0033|
+|
0,0033|
}
24,43¿
|
0,0089
|
24,24
= 0,2174
KR
=
∆ a
a
=
0,2174
a
=
|
a ± ∆ a
|
=
|
24,4
±
0,2
|
cm
/
s
2a
=
|
a ± ∆ a
|
=
|
24,43
±
40,1
|
cm
/
s
2Perbandingan percepatan dari grafik dengan perhitungan = (23,1 : 24,4) cm/s2
2. Hitung momen inersia katrol dari hasil percobaan dengan memanipulasi persamaan 3.5, gunakan percepatan a yang kamu peroleh dari grafik. Bandingkan hasilnya dengan nilai momen inersia katrol dengan menggunakan persamaan 3.3
Percepatan dengan memanipulasi persamaan 3.5
m
+
M
1−
M
2. g
¿
¿
a
=
¿
a
(
m
+
M
1+
M
2)
+
aI
R
2=
(
m
+
M
1−
M
2)
g
I
=
[
(
m
+
m
1−
m
2)
g
a
−(
m
+
m
1+
m
2)
]
R
2∆ I
=
|
∂ I
∂ m
|
∆ m
+
|
∂ I
∂ m
1|
∆ m
1
+
|
∂ I
∂ m
2|
∆ m
2
+
|
∂ I
∂ a
|
∆ a
+
|
∂ I
∂ R
|
∆ R
2
∆ I
=
|
(
g
a
−
1
)
R
2|
∆ m
+
|
(
g
a
−
1
)
R
2|
∆ m
1
+
|
−
(
g
a
+
1
)
R
2
|
∆ m
2
+
|
2
R
(
g
(
m
+
M
1−
M
2)
a
−
m
−
M
1−
M
2)
|
∆ R
+
|
(
−
g
(
m
+
M
1−
M
2)
R
2a
2)
|
∆ a
∆ I
=
|
[
(
g
a
−
1
)
R
2]
∆ m
|
+
|
[
(
g
a
−
1
)
R
2]
∆ m
1|
+
|
−
[
(
g
a
+
1
)
R
2]
∆ m
2|
+
|
[
2
R
(
g
(
m
+
M
1−
M
2)
a
−
m
−
M
1−
M
2)
]
∆ R
|
+
|
(
−
g
(
m
+
M
1−
M
2)
R
2a
2)
∆ a
|
I
=
[
(
m
+
m
1−
m
2)
g
a
−(
m
+
m
1+
m
2)
]
R
2I
=
[
(
4,05
+
63,22
−
63,22
)
980
23,1
−(
4,05
+
63,22
+
63,22
)
]
5,95
2I
=
[
(
4,05
)
980
I
=
[
(
4,05
)
42,4242
−
130,49
]
35,4025
I
=
[
41,32801
]
35,4025
I=1463,1148gram/cm2∆ I
=
|
[
(
g
a
−
1
)
R
2]
∆ m
|
+
|
[
(
g
a
−
1
)
R
2]
∆ m
1|
+
|
−
[
(
g
a
+
1
)
R
2]
∆ m
2|
+
|
[
2
R
(
g
(
m
+
M
1−
M
2)
a
−
m
−
M
1−
M
2)
]
∆ R
|
+
|
(
−
g
(
m
+
M
1−
M
2)
R
2a
2)
∆ a
|
∆ I
=
|
[
(
980
23,1
−
1
)
5,95
2]
0,01
|
+
|
[
(
980
23,1
−
1
)
5,95
2]
0,01
|
+
|
−
[
(
980
23,1
+
1
)
5,95
2]
0,01
|
+
|
[
2
(
5,95
)
(
980
(
4,05
+
63,22
−
63,22
)
23,1
−
4,05
−
63,22
−
63,22
)
]
0,05
|
+
|
(
−
980
(
4,05
+
63,22
−
63,22
)
23,1
25,95
2)
2,11
|
∆ I=|
14,6652|
+|
14,6652|
+|
−15,3732|
+|
24,5902|
+|
−555,6144|
∆ I
=
¿
517,067KR
=
∆ I
I
KR
=
517,067
1463,1148
×
100
KR
=
35,34
(2 AB)I
=
|
I ± ∆ I
|
I
=
|
1,4
±
0,5
|
10
3Untuk I =
1
2
m
k R2∆ I
=
|
∂ I
∂ m
|
dm
+
|
∂ I
∂ R
|
dR
¿
|
∂
(
1
2
m R
2
)
∂m
|
dm
+
|
∂
(
1
2
m R
2)
∂ R
|
dR
∆ I
I
=
|
1
2
R
2dm
1
2
mR
2
|
+
|
mRdR
1
2
mR
2
|
∆ I
=
|
∆ m
m
+
2
∆ R
I =
1
2
m
k R2=
1
2
64,00x (5,95) 2 = 1132,88 gram/cm2∆ I
=
|
∆ m
m
+
2
∆ R
R
|
I
=|
0,01
64,00
+
2
(
0,05
)
5,95
|
1132,88
=|
0,00015
+
0,01680
|
1132,88
= 19,20 gram/cm2KR =
∆ I
I
x 100% =19,20
1132,88
x 100% = 1,7 % (3 AB)I =
|
I ± ∆ I|
gram /cm2 =|
11,3
±
0,19
|
102 gram /cm2Kegiatan 2
1. Buatlah grafik hubungan antara XAB terhadap tAB. Dari grafik tentukan besar kecepatan rata-rata benda M2 dan A ke B. Bandingkan nilai kecepatan rata-rata dari v grafik dengan nilai kecepatan benda (M2 + m) pada saat di A yang dperoleh dari persamaan GLBB dengan menggunakan percepatan a yang diperoleh dari kegiatan 1.
Hasil pengukuran berulang pada waktu 1. Jarak tempuh (
x
AB ) = 42,50cm
Waktu tempuh (
t
AB )t
AB(1) = t1 = 1,143 st
AB(2) =t
2 = 1,113s
t
AB(3) = t3 = 1,122 s´
t
AB = tAB(1)+tAB(2)+tAB(3) 3¿
1,143
+
1.113
+
1,122
3
´
tAB = 1,126 s
δ
3=
|
t
3−´
t
|
=|
1,122
−
1,126
|
s
=
0,004
s
maka ∆ t=0,017sKR
=
∆ t
t
x 100 % =0,017
s
1,126
s
x 100%¿
1,51
= 3 AB Hasil pengukurannya waktu yaitu : t =|
1,1 26±0,017|
s 2. Jarak tempuh ( xAB ) = 38,30 cmWaktu tempuh ( tAB )
t
AB(1) =t
1 = 1,002s
t
AB(2) = t2 = 1,008 st
AB(3) =t
3 = 1,010s
´
tAB =
t
AB(1)+
t
AB(2)+
t
AB(3)3
¿
1,002
+
1,008
+
1,010
3
´
t
AB = 1,007 sδ
1=
|
t
1−´
t
|
=|
1,002
−
1,007
|
s
=
0,005
s
=δmaks
δ
2=
|
t
2−´
t
|
=|
1,008−1,007|
s=0,001sδ
3=
|
t
3−´
t
|
=|
1,010
−
1,007
|
s
=
0,003
s
maka ∆ t=0,005sKR
=
∆ t
t
x 100 % =0,005
s
1,007
s
x 100%¿
0,5
= 4 AB Hasil pengukurannya waktu yaitu : t =|
1,007±0,005|
s 3. Jarak tempuh ( xAB ) = 36,50 cmWaktu tempuh ( tAB )
t
AB(1) =t
1 = 0,947s
t
AB(2) = t2 = 0,942 st
AB(3) =t
3 = 0,940s
´
tAB =
t
AB(1)+
t
AB(2)+
t
AB(3)3
¿
0,947
+
0,942
+
0,940
3
´
t
AB = 0,943 sδ
1=
|
t
1−´
t
|
=|
0,947
−
0,943
|
s
=
0,004
s
=δmaks
δ
2=
|
t
2−´
t
|
=|
0,942−0,943|
s=0,001smaka
∆ t
=
0,004
s
KR
=
∆ t
t
x 100 % =0,004
s
0,943
s
x 100% ¿0,424 = 4 AB Hasil pengukurannya waktu yaitu :t
=|
0,9430
±
0,0040
|
s
4. Jarak tempuh (x
AB ) = 31cm
Waktu tempuh (
t
AB )t
AB(1) = t1 = 0,781 st
AB(2) =t
2 = 0,781s
t
AB(3) = t3 = 0,790 s´
t
AB = tAB(1)+tAB(2)+tAB(3) 3¿
0,781
+
0,781
+
0,790
3
´
tAB = 0,784 s
δ
1=
|
t
1−´
t
|
=|
0,781−0,784|
s=0,003sδ
2=
|
t
2−´
t
|
=|
0,781
−
0,784
|
s
=
0,003
s
δ
3=
|
t
3−´
t
|
=|
0,790−0,784|
s=0,006s = δmaks maka∆ t
=
0,006
s
KR
=
∆ t
t
x 100 % =0,006
s
0784
s
x 100% ¿0,765 = 3 AB Hasil pengukurannya waktu yaitu :t
=|
0,784
±
0,006
|
s
5. Jarak tempuh (x
AB ) = 25,60cm
Waktu tempuh (
t
AB )t
AB(1) = t1 = 0,648 st
AB(2) =t
2 = 0,631s
t
AB(3) = t3 = 0,639 s´
t
AB =tAB(1)+tAB(2)+tAB(3)
3
¿
0,648
+
0,631
+
0,639
3
´
tAB = 0,640 s
δ
1=
|
t
1−´
t
|
=|
0,648−0,640|
s=0,008sδ
2=
|
t
2−´
t
|
=|
0,631
−
0,640
|
s
=
0,009
s
=δmaks
δ
3=
|
t
3−´
t
|
=|
0,639−0,640|
s=0,001sKR
=
∆ t
t
x 100 % =0,008
s
0,640
s
x 100% ¿1,25 = 3 AB Hasil pengukurannya waktu yaitu :t
=|
0,640
±
0,008
|
s
6. Jarak tempuh (x
AB ) = 20,60cm
Waktu tempuh (
t
AB )t
AB(1) = t1 = 0,508 st
AB(2) =t
2 = 0,507s
t
AB(3) = t3 = 0,506 s´
t
AB = tAB(1)+tAB(2)+tAB(3)3
¿
0,508
+
0,507
+
0,5063
3
´
tAB = 0,507 s
δ
1=
|
t
1−´
t
|
=|
0,508−0,507|
s=0,001s = δmaksδ
2=
|
t
2−´
t
|
=|
0,507
−
0,507
|
s
=
0
s
δ
3=
|
t
3−´
t
|
=|
0,506−0,507|
s=0,001s maka∆ t
=
0,001
s
KR
=
∆ t
t
x 100 % =0,001
s
0,507
s
x 100% ¿1,754 = 3 AB Hasil pengukurannya waktu yaitu :t
=|
0,507
±
0,001
|
s
7. Jarak tempuh (x
AB ) = 15,50cm
Waktu tempuh (
t
AB )t
AB(1) = t1 = 0,365 st
AB(2) =t
2 = 0,369s
t
AB(3) = t3 = 0,371 s´
t
AB = tAB(1)+tAB(2)+tAB(3) 3¿
0,365
+
0,369
+
0,371
3
´
tAB = 0,368 s
δ
1=
|
t
1−´
t
|
=|
0,365−0,368|
s=0,003s = δmaksδ
2=
|
t
2−´
t
|
=|
0,369
−
0,368
|
s
=
0,001
s
KR
=
∆ t
t
x 100 % =0,003
s
0,368
x 100% ¿0,815 = 3 AB Hasil pengukurannya waktu yaitu :t
=|
0,368
±
0,003
|
s
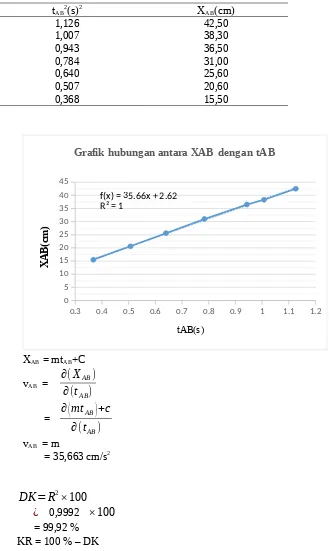
Tabel 4 .Hubungan antara jarak XAB dengan tABtAB2(s)2 XAB(cm)
1,126 42,50
1,007 38,30
0,943 36,50
0,784 31,00
0,640 25,60
0,507 20,60
0,368 15,50
0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1.1 1.2 0
5 10 15 20 25 30 35 40 45
f(x) = 35.66x + 2.62 R² = 1
Grafik hubungan antara XAB dengan tAB
tAB(s)
X
A
B
(c
m
)
XAB = mtAB+C vAB =
∂
(
X
AB)
∂
(
t
AB)
=
∂
(
mt
AB)
+
c
∂
(
t
AB)
vAB = m
= 35,663 cm/s2
DK=R2×100
¿
0,9992×
100
= 99,92 %= 100 % – 99,92 % = 0,8 % 3 AB
∆ v
=
KR× v
¿
0,8
×
35,663
¿
28,5304v
=
|
v ± Δv
|
cm
/
s
2¿
|
35, 6 63
±
28,530
|
cm
/
s
2Kecepatan pada benda yang telah ditetapkan jaraknya dikegiatan 1 (XCA) vt2-v02 = 2as
vt2- 0 = 2as vt =
√
2
as
∆v = |∂ v
∂ a
|da+|∂ v
∂ a
|ds= |
∂
√
2
as
∂ a
|da+|∂
√
2
as
∂ s
|ds∆ v
v
= |√
2
as da
a
√
2
as
|+|√
2
as ds
s
√
2
as
|∆ v
=
|
∆ a
2
a
|
+
¿
∆ s
2
s
∨
v
(XCA) =
|
14,70±0,05|
cm vt =√
2
as
=
√
2.47,02.14,70
=√
1382,38
= 37,18cm/s2∆ v
=
|
∆ a
2
a
|
+
¿
∆ s
2
s
∨
v
¿
|
6,86
47,02
|
+
¿
0,05
KR =
∆ v
v
×100% =5,50
37,18
×100% = 14,8 % 2 AB V = | v ± ∆v | = | 37,18 ± 5,50| cm/s2