Persamaan Non Linear. Nilai x yang memenuhi syarat disebut akar fungsi (square root); akar-akar ini adalah solusi dari persamaan f(x) = 0.

Persamaan Non Linear

Nilai x yang memenuhi syarat disebut akar fungsi (square root); akar-akar ini adalah solusi dari

persamaan f(x) = 0.

0 )

(x  f

(a) No Roots

(b) One Root

Contoh Akar dari Beberapa Fungsi

Two Roots

Three Roots

Direct-Search Method

• Ini adalah pendekatan trial-and-error

• Tidak didapatkan nilai pasti untuk root; hanya diperoleh perkiraan dari akar (hingga dalam tingkat presisi tertentu).

• Step 1:

Tentukan rentang atau interval untuk x sebagai akar yang diasumsikan terjadi. Interval awal yang lebih kecil akan membutuhkan lebih sedikit perhitungan untuk mendapatkan nilai akar sampai ke akurasi yang diinginkan

• Step 2:

Bagilah interval menjadi sub-interval yang lebih kecil dan berjarak sama. Ukuran sub-interval ini akan ditentukan oleh ketepatan yang diperlukan untuk estimasi nilai akar

Step 3: Cari melalui semua subinterval hingga subinterval yang berisi root ditemukan

Jika root tidak terletak di dalam subinterval [A, B], maka f (A) dan f (B) memiliki tanda yang sama.

(a) no roots in the interval [A, B]

(b) Tidak ada akar pada interval [A, B]

(c) Satu akar pada interval [A, B]

(d) Satu akar pada interval [A, B]

• Metode pencarian langsung akan menemukan akar dari fungsi apa pun selama semua akar adalah nyata dan dalam interval yang ditentukan.

• Beberapa akar mungkin terlewatkan seluruhnya jika subinterval terlalu besar sehingga lebih dari satu akar terjadi dalam satu subinterval.

• Metode pencarian langsung mengasumsikan bahwa hanya ada satu dan satu root dalam setiap subinterval.

• Jika ada jumlah akar genap dalam interval pencarian, maka f (A) dan f (B) akan memiliki tanda yang sama, dan proses pencarian akan kehilangan akar dalam interval tersebut.

• Contoh: Finding Eigenvalues

0 504188

. 0 3146

. 2 3 ²

3      



 f()  f()  f() 0.0 -0.504 0.1 -0.302 0.2 -0.153 0.3 -0.053 0.4 0.006 0.5 0.199 0.6 0.021 0.7 -0.011 0.8 -0.061 0.9 -0.122 1.0 -0.190 1.1 -0.257 1.2 -0.319 1.3 -0.368 1.4 -0.400 1.5 -0.407 1.6 -0.385 1.7 -0.326 1.8 -0.226 1.9 -0.077 2.0 0.125 Roots: 0.3    0.4, 0.6    0.7, 1.9    2.0

Kita bisa mendapatkan perkiraan yang lebih baik dengan interpolasi linier.

4- 9

Metode Bisection

Step 1:

Untuk interval x, tentukan titik awal x^s, dan titik akhir x^e, tentukan titik tengah x^m di tengah interval.

Step 2: Tentukan nilai dari

f(x_s), f(x_m), and f(x_e).

Step 3: Tentukan nilai f(x_s)f(x_m) dan f(x_m)f(x_e).

Jika f(x_s)f(x_m) <0, maka x_{s <} root < x_m.

Jikaf(x_m)f(x_e) <0, maka x_{m <} root <x_e.

Step 4:

• Jika belum menemukan air, lanjutkan kembali ke Langkah 1.

• Metode bisection akan selalu bertemu pada akar, asalkan hanya satu akar yang terletak di dalam interval awal untuk x.

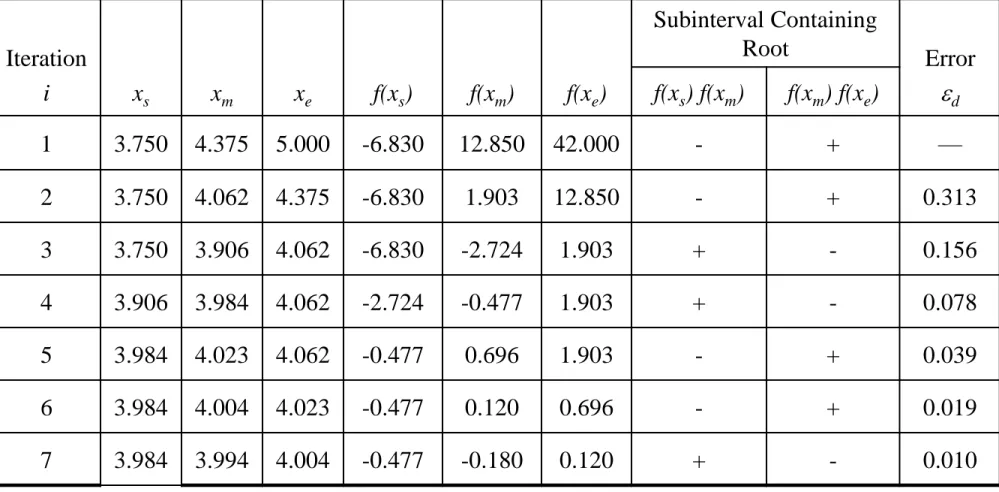
 Example: Bisection Method

0 8

10 )

(x  x³  x²  x   f

• Selesaikan persamaan di atas. Tent root (akar) persamaan di atas

• Perkiraan akhir dari root adalah 3.994.

• The true root=4

Iteration

i x_s x_m x_e f(x_s) f(x_m) f(x_e)

Subinterval Containing

Root Error

_d f(x_s) f(x_m) f(x_m) f(x_e)

1 3.750 4.375 5.000 -6.830 12.850 42.000 - + —

2 3.750 4.062 4.375 -6.830 1.903 12.850 - + 0.313

3 3.750 3.906 4.062 -6.830 -2.724 1.903 + - 0.156

4 3.906 3.984 4.062 -2.724 -0.477 1.903 + - 0.078

5 3.984 4.023 4.062 -0.477 0.696 1.903 - + 0.039

6 3.984 4.004 4.023 -0.477 0.120 0.696 - + 0.019

7 3.984 3.994 4.004 -0.477 -0.180 0.120 + - 0.010

Table 4-2 Example Polynomial Solved Using the Bisection Method

Newton-Raphson Iteration

• Metode iterasi Newton-Rahpson adalah metode yang lebih cepat untuk menemukan kondisi

konvergen pada satu akar fungsi.

• Ini menggunakan bagian linier dari deret Taylor:

dx x x df

f x

f ( ₁)  ( ₀)   ) (

) (

0 ₀ x₁ x₀

dx x df

f  



) (

) (

1

i i i

i f x

x x f

x _   

) (

) (

0 0 0

1 f x

x x f

x   

dx df

x x f

x ( ₀)

0

1 

General formula untuk metodeNewton- Raphson method:

Newton-Raphson Method

1 1

) ( 0

) ) (

(



  



 



i i

i i

i i

i x x

x f x

x x x f

f ( )

) (

1

i i i

i f x

x x f

x _   

Derivation

f(x)

f(x_i)

xi+1 xi

X B

C  A

) (

) (

1

i i i

i f x

x x f

x _   

1

) ) (

( '

 



i i

i i

x x

x x f

f

AC

 AB

 tan(

Derivation of the Newton-Raphson method.

8 10

)

(x  x³  x²  x  f

Turunan :

10 2

3 )

(  ²  

 x x x

f

Assume an initial estimate of the root x₀=6.0.

6977 .

4 3023

. 1 10 6

) 6 ( 2 )

6 ( 3

8 ) 6 ( 10 )

6 ( )

6

6 ( ₂

2 3

1   









 

 x

 Contoh: Newton-Raphson Method

1289 .

4 5688

. 0 6977

. 4

10 )

6977 .

4 ( 2 )

6977 .

4 ( 3

8 ) 6977 .

4 ( 10 )

6977 .

4 ( )

6977 .

4 6977 (

.

4 ₂

2 3

2















 

 　 　 x

Iteration i x_i x_i - x_i-1 x_i – x_t

0 6.0000 ─ 2.0000

1 4.6977 1.3023 0.6977

2 4.1289 0.5688 0.1289

3 4.0057 0.1232 0.0057

4 4.0000 0.0057 0.0000

Error Analysis (x_t: true root)

Iterasi Titik Tetap

 adalah suatu metode pencarian akar sebuah fungsi f(x) secara sederhana dengan menggunakan satu titik awal.

 Metode Iterasi Titik Tetap kadang-kadang dinamakan metode iterasi sederhana atau metode langsung atau metode substitusi beruntun.

 Perlu diketahui bahwa fungsi f(x) yang ingin dicari hampiran akarnya harus

konvergen. Misal x adalah Fixed Point (Titik Tetap); fungsi f(x) bila g(x) = x dan f(x) = 0.

Prosedur Metode Titik Tetap

1. Memisalkan f(x) adalah fungsi yang konvergen dengan f(x) = 0 2. Mengubah ke dalam bentuk x = g(x).

3. Mentukan nilai titik awal, misal x₁.

4. Mensubstitusikan titik awalnya ke persamaan g(x) sehingga g(x₁) = x₂, setelah itu titik x₂ yang diperoleh substitusikan lagi ke g(x) sehingga menghasilkan g(x₂) =

x₃.

Jika dituliskan, dapat dilihat sebagai berikut:

x₁ (penentuan titik awal) x₂= g(x₁) (iterasi pertama) x₃= g(x₂) (iterasi kedua)

hingga x_n= g(x_n-1) (iterasi ke-n)

Iterasi ini akan berhenti jika x = g(x) dan f(x) = 0 atau sudah mencapai nilai error yang cukup kecil (|x_n– x_n-1| < ε).

Nilai ε telah ditetapkan sebelumnya.

Contoh 1

Selesaikan persamaan x – e^-x = 0 dengan menggunakan Fixed Point dengan 10 iterasi atau sampai dua angka dibelakang koma tidak berubah.

Penyelesaian:

f(x) = x – e^-x

ubah terlebih dahulu ke dalam bentuk x = g(x), sehingga diperoleh x = e^-X misal kita ambil titik awalnya x₁ = 0.5, maka iterasinya adalah x_n+1 = e^-Xn akan diperoleh:

x₁ = 0.5 (penetuan titik awal) f(x₁) = 0.5 – e^-0.5 = -0.1065

x₂= g(x₁) = e^-0.5 = 0.6065 (iterasi pertama) f(x₁) = 0.6065 – e^-0.6065= 0.0612

Contoh 1 (Lanjutan)

x₃= g(x₂) = e^-0.6065= 0.5452 (iterasi ke-2) f(x₁) = 0.5452 – e^-0.5452= -0.0345

x₄= g(x₃) = e^-0.5452 = 0.5797 (iterasi ke-3) f(x₁) = 0.5797 – e^-0.5797= 0.0196

dan seterusnya hingga,

x₉= g(x₈) e^-0.5664= 0.5675 (iterasi ke-9) f(x₁) = 0.5 – e^-0.5 = -0.1065

x₁₀= g(x₉) e^-0.5675 = 0.5669 (iterasi ke-10) f(x₁) = 0.5 – e^-0.5 = -0.1065

sehingga apabila ditulis dalam bentuk tabel akan diperoleh:

Jadi, hampiran akar yang diperoleh menggunakan Metode Titik Tetap adalah 0.5675.

n x_n g(x_n-1) f(x_n)

1 2 3 4 5 6 7 8 9 10

0.5 0.6065 0.5452 0.5797 0.5600 0.5712 0.5648 0.5684 0.5664 0.5675

0.6065 0.5452 0.5797 0.5600 0.5712 0.5648 0.5684 0.5664 0.5675 0.5669

-0.1065 0.0612 -0.0345

0.0196 -0.0112

0.0006 -0.0003 0.00019 -0.00011

0.00005

Contoh 2

Hitunglah hampiran akar dari persamaan

x² – 2x – 3 = 0 pada interval [1, 4] menggunakan Fixed Point.

Penyelesaian:

Misal persamaan x² – 2x – 3 = 0 diubah menjadi x(x – 2) – 3 = 0, sehingga diperoleh: x = 3/X-2 dan iterasinya menjadi x_n+1 = 3/Xn-2.

ambil titik awal x₁ = 4.

Sehingga apabila ditulis dalam tabel diperoleh:

Jadi, akar dari f(x) = x² – 2x – 3 = 0 adalah -1 .

n x_n g(x_n-1) f(x_n)

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

4 1.5

-6 -0.375 -1.2631 -0.9193 -1.0276 -0.9908 -1.003 -0.999 -1.00033

-0.9989 -1.00036 -0.99988 -1.00004 -0.99998 -1.00001 -0.99999 -1.00000

1.5 -6 -0.375 -1.2631 -0.9193 -1.0276 -0.9908 -1.003 -0.999 -1.00033

-0.9989 -1.00036 -0.99988 -1.00004 -0.99998 -1.00001 -0.99999 -1.00000 -1.00000

5 -3.75

45 -2.1093

1.1216 -0.3162 0.1111 -0.0367 0.012 -0.00039

0.00013 -0.00043

0.00014 -0.00004 0.000016 -0.000008

0.00004 -0.000004

0

Secant Method

• Metode Secant sama dengan Metode Raphson, dengan perbedaan turunan pada Metode Secant f’(x) dihitung secara numerik, bukan secara

analitik

• Metode secant membutuhkan dua perkiraan awal dari sebuah root.

 Example: Metode Secant

Ada estimasi initial : x₀ = 4 and x₁ = 5.5.

Example 1

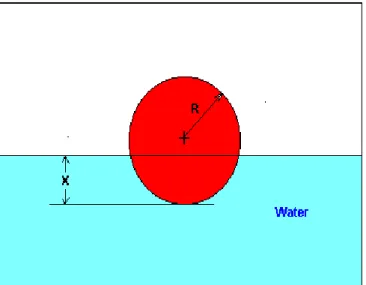
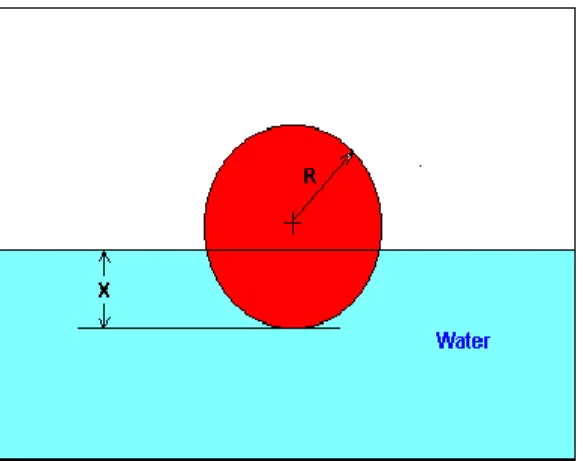
Sebuah Bola apung memiliki berat jenis 0,6 dan memiliki radius 5,5 cm. Anda diminta untuk menemukan kedalaman

tempat bola terendam saat mengapung di air. (Gunakan metode newton rapshon)

Figure 3 Floating ball problem.

27

Example 1 Cont.

Persamaan yang memberikan kedalaman x dalam meter di mana bola terendam air diberikan oleh

 

^{x x3-0.165x2+3.993 10-4}

f  

Gunakan metode Newton untuk mencari akar persamaan untuk mencari kedalaman 'x' dimana bola terendam di bawah air.

a) Lakukan tiga iterasi untuk memperkirakan akar persamaan di atas.

b) Perkiraan kesalahan relatif absolut di akhir setiap iterasi, dan

28

Figure 3 Floating ball problem.

Example 1 Cont.

 

^{x x3-0.165x2+3.993 10-4}

f  

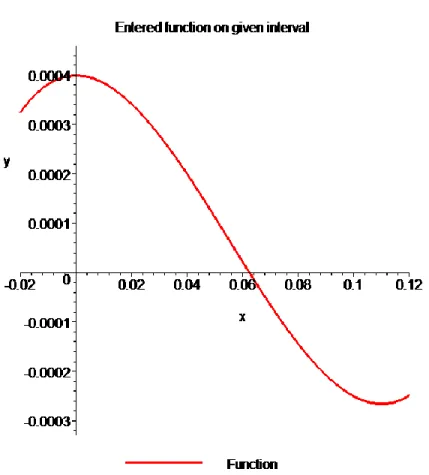
Untuk membantu

pemahaman tentang cara kerja metode ini untuk mencari akar persamaan, grafik f (x) ditampilkan di sebelah kanan,

dimana Solution

Figure 4 Graph of the function f(x)

Example 1 Cont.

 

 

^{x x - x}

f

. + x .

- x x

f ^-

33 . 0 3

'

10 993

3 165

0

2

4 2

3







Let us assume the initial guess of the root of is . This is a reasonable guess (discuss why

and are not good choices) as the extreme values of the depth x would be 0 and the diameter (0.11 m) of the ball.

 

^{x  0}

f m

05 .

0  0 x

 0

x x  0.11m

Solve for ^{f '}

 

^x

Example 1 Cont.

  

   

   

 

06242 .

0

01242 .

0 0.05

10 9

10 118

. 0.05 1

05 . 0 33 . 0 05

. 0 3

10 .993

3 05

. 0 165 .

0 05

. 05 0

. 0

'

3 4

2

2 4 3

0 0 0

1













 









 













x f

x x f

x

Iteration 1

The estimate of the root is

Example 1 Cont.

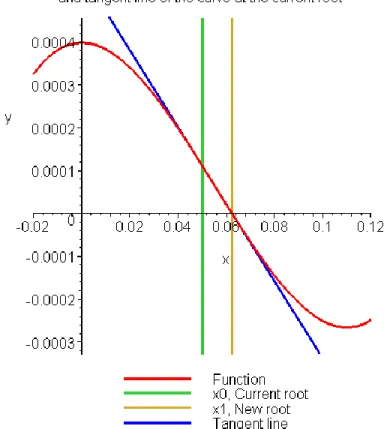
Figure 5 Estimate of the root for the first iteration.

Example 1 Cont.

% 90 . 19

06242 100 .

0

05 . 0 06242

. 0

100

1 0 1



 



 



 x

x x

a

33

The absolute relative approximate error at the end of Iteration 1

is ^a

The number of significant digits at least correct is 0, as you need an absolute relative approximate error of 5% or less for at least one significant digits to be correct in your result.

Example 1 Cont.

  

   

   

 

06238 .

0

10 4646

. 4 06242

. 0

10 90973

. 8

10 97781

. 06242 3

. 0

06242 .

0 33 . 0 06242

. 0 3

10 .993

3 06242

. 0 165 .

0 06242

. 06242 0

. 0

'

5 3 7

2

2 4 3

1 1 1

2















 









 















x f

x x f

x

Iteration 2

The estimate of the root is

Example 1 Cont.

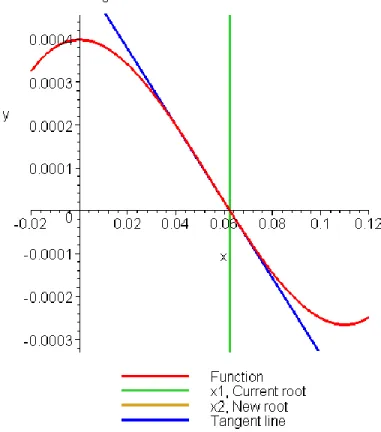
Figure 6 Estimate of the root for the Iteration 2.

Example 1 Cont.

% 0716 .

0

06238 100 .

0

06242 .

0 06238

. 0

100

2 1 2



 



 



 x

x x

a

The absolute relative approximate error at the end of Iteration 2

is ^a

The maximum value of m for which is 2.844.

Hence, the number of significant digits at least correct in the answer is 2.

m a

 



 0.5 10²

Example 1 Cont.

   

   

   

 

06238 .

0

10 9822

. 4 06238

. 0

10 91171

. 8

10 44

. 06238 4

. 0

06238 .

0 33 . 0 06238

. 0 3

10 .993

3 06238

. 0 165 .

0 06238

. 06238 0

. 0

'

9 3 11

2

2 4 3

2 2 2

3















 









 















x f

x x f

x

Iteration 3

The estimate of the root is

Example 1 Cont.

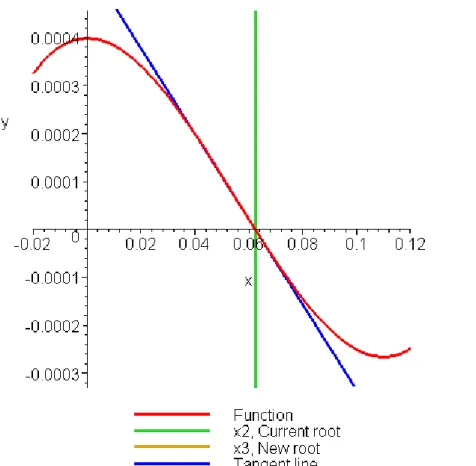
Figure 7 Estimate of the root for the Iteration 3.

Example 1 Cont.

% 0

06238 100 .

0

06238 .

0 06238

. 0

100

2 1 2



 



 



 x

x x

a

The absolute relative approximate error at the end of Iteration 3

is ^a

The number of significant digits at least correct is 4, as only 4 significant digits are carried through all the calculations.

END

4- 40