2.1 Teori Probabilitas (Peluang)
Probabilitas adalah suatu nilai untuk mengukur tingkat kemungkinan terjadinya suatu peristiwa (event) akan terjadi di masa mendatang yang hasilnya tidak pasti (uncertain event). Probabilitas dinyatakan antara 0 (nol) sampai 1 (satu) atau dalam persentase. Probabilitas 0 menunjukkan peristiwa yang tidak mungkin terjadi, sedangkan probabilitas 1 menunjukkan peristiwa yang pasti terjadi. P(A) = 0,99 artinya probabilitas bahwa kejadian A akan terjadi sebesar 99 % dan probabilitas A tidak terjadi adalah sebesar 1%.
Ada tiga hal penting dalam rangka membicarakan probabilitas, yaitu percobaan (experiment), ruang sampel (sample space) dan kejadian (event).
Percobaan (experiment) adalah pengamatan terhadap beberapa aktivitas atau proses yang memungkinkan timbulnya paling sedikit 2 (dua) peristiwa tanpa memperhatikan peristiwa mana yang akan terjadi.
Contoh :
Kegiatan melempar mata uang akan menghasilkan peristiwa muncul gambar atau angka, kegiatan jual beli saham akan menghasilkan peristiwa membeli atau menjual, perubahan harga-harga akan menghasilkan peristiwa inflasi atau deflasi, pertandingan sepak bola akan menghasilkan peristiwa menang, kalah atau seri. Kegiatan-kegiatan yang menimbulkan peristiwa tersebut dikenal sebagai percobaan.
ruang sampel adalah seluruh kemungkinan peristiwa yang akan terjadi akibat adanya suatu percobaan atau kegiatan.
Contoh :
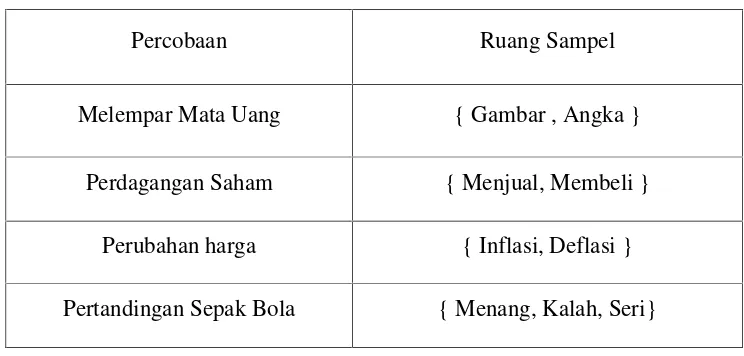
Dari kegiatan diatas dapat diperoleh hasil sebagai berikut : Tabel 2.1 Percobaan dan Hasil
Percobaan Ruang Sampel
Melempar Mata Uang { Gambar , Angka }
Perdagangan Saham { Menjual, Membeli }
Perubahan harga { Inflasi, Deflasi }
Pertandingan Sepak Bola { Menang, Kalah, Seri}
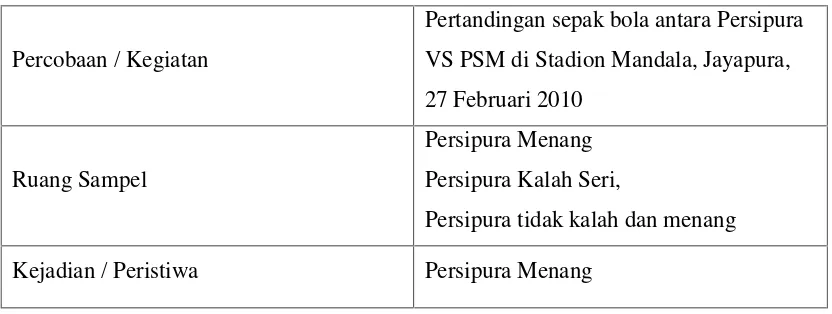
Tabel 2.2 Urutan Percobaan, Hasil, dan Peristiwa
Percobaan / Kegiatan
Pertandingan sepak bola antara Persipura
VS PSM di Stadion Mandala, Jayapura,
27 Februari 2010
Ruang Sampel
Persipura Menang
Persipura Kalah Seri,
Persipura tidak kalah dan menang
Kejadian / Peristiwa Persipura Menang
Nilai probabilitas dapat dihitung berdasarkan nilai hasil observasi (sifatnya subjektif) atau berdasarkan pertimbangan pembuat keputusan atau tenaga ahli dalam bidangnya secara subjektif.
Besarnya nilai kemungkinan bagi munculnya suatu kejadian adalah selalu diantaa 0 (nol) dan 1 (satu). Pernyataan ini dapat ditulis sebagai 0 P(A) 1, dimana P(A) menyatakan nilai kemungkinan bagi munculnya kejadian A. Jika suatu percobaan dapat menghasilkan N macam hasil yang berkemungkinan sama (equallylikely) dan jika tepat terdapat sebanyak n hasil yang berkaitan dengan kejadian A, maka probabilitas kejadian A adalah : P(A) =
Contoh:
Dari soal diketahui bahwa: N = 100 buah barang
n = 12 buah barang yang rusak A = barang yang diambil secara acak Jadi, probabilitas memperoleh barang yang rusak adalah :
P (A) =
P (A) = = 0,12
Jika n = 0, berarti tidak ada barang yang rusak, P (A) = = 0, kejadian ini disebut impossible event (tidak mungkin terjadi). Tetapi jika n = N = 100, berarti semua barang rusak, P (A) = = 1, kejadian ini disebut sure event (pasti terjadi).
2.2 Operasi-Operasi dalam Kejadian
Ada beberapa operasi-operasi dalam kejadian yaitu: gabungan (union), irisan (intersection), komplemen (complement), selisih dan kejadian majemuk
2.2.1 Gabungan (Union)
Gabungan dua kejadian A dan B, dinyatakan dengan A B, merupakan kejadian yang mengandung semua elemen yang termasuk A atau B atau keduanya.
A∪ B= {x : x A atau x B}
Gambar 2.1 Gabungan
2.2.2 Irisan (Intersection)
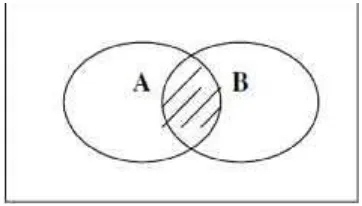
Irisan dua kejadian A dan B, dinyatakan dengan A∩ B,merupakan kejadian yang elemen-elemennya merupakan anggota dari A dan B.
A∩ B= {x : x A atau x B}
Jika digambarkan pada diagram Venn maka daerah yang diarsir merupakan himpunan A∩ B
Gambar 2.2 Irisan
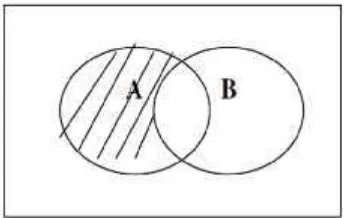
2.2.3 Komplemen (Complament)
Ac= {x : x S, x A}
Jika digambarkan pada diagram Venn maka daerah yang diarsir merupakan himpunan Ac.
Gambar 2.3 Komplemen
2.2.4 Selisih
Selisih kejadian B dari kejadian A dinyatakan dengan A – B adalah kejadian dari elemen-elemen yang merupakan anggota dari A tetapi bukan anggota dari B.
A - B = {x : x A, x B}
Jika digambarkan pada diagram Venn maka daerah yang diarsir merupakan himpunan A - B.
2.2.5 Kejadian Majemuk
1. Bila A and B mutually exclusive (kejadian yang terpisah), maka : P(A ∪B) =P(A) +P(B)
2. Bila A dan B dua kejadian sembarang, maka : P(A ∪B) =P(A) +P(B) -P(A ∩B)
4.Bila A dan B independent (bebas), maka : P(A ∩B) = P(A)P(B)
5. Bila A dan B dependent (tidak bebas), maka : P(A ∩B) = P(A)P(B | A)
P(A ∩B) = P(B)P(A | B), dimana P(A) 0, P(B) 0.
2.3 Probabilitas Bersyarat
Peluang terjadinya suatu kejadian A bila diketahui bahwa kejadian B telah terjadi disebut peluang bersyarat dan dinyatakan dengan P(A|B).
P (A|B) = ( )
Sama halnya dengan peluang terjadinya suatu kejadian B bila diketaui bahwa kejadian A telah terjadi dan dinyatakan dengan P(B|A).
P(B|A)= ( )
( )
Dengan mengkombinasikan kedua persamaan maka diperoleh :
P(A|B)P(B)= P(A∩ B)= P(B|A)P(A)
P(A|B) = (( ))= ( | ) ( )( )
Contoh:
Dari 900 nama, terdapat 500 orang pria dengan status 460 orang bekerja, sedangkan 40 orang lagi tidak bekerja, dan 400 orang wanita dengan status 140 orang bekerja sedangkan 260 orang lagi tidak bekerja. Berapa probabilitas terpilihnya pria dengan status telah bekerja?
A = pria terpilih
B = orang yang terpilih berstatus bekerja
P(B) = =
P(B∩ A) = =
P(A|B) = = = 0,77
2.4 Titik Sampel
Titik sampel (sample point) merupakan tiap anggota atau elemen dari ruang sampel. Jika suatu operasi dapat dilakukan dengan n1cara, dan bila untuk setiap cara ini operasi
kedua dapat dilakukan dengan n2 cara, dan bila untuk setiap cara ini operasi ketiga
dapat dilakukan dengan n3cara, dst, maka deretan k operasi dapat dilakukan dengan n1
n2...nkcara.
Contoh:
Tiga buah koin (uang logam) dilemparkan sekali. Banyaknya titik sampel dalam ruang sampel ?
Koin I dapat menghasilkan 2 hasil yang mungkin, muka (M) atau belakang (B) Koin II dapat menghasilkan 2 hasil yang mungkin, M atau B
Koin III dapat menghasilkan 2 hasil yang mungkin, M atau B Jumlah titik sampel yang dihasilkan = (2) (2) (2) = 8
2.4.1 Kombinasi (Combination)
Kombinasi merupakan susunan dari suatu himpunan obyek yang dapat dibentuk tanpa memperhatikan urutan. Kombinasi berkaitan dengan penentuan banyaknya cara memilih r obyek dari sejumlah n obyek tanpa memperhatikan urutannya. Kombinasi merupakan sekatan dengan dua sel, sel pertama berisi r obyek yang dipilih dan (n –r) obyek sisanya. Jumlah kombinasi dari n obyek yang berlainan jika diambil sebanyak r.
= !
! ( )!
Contoh:
Banyaknya cara memilih 2 dari 4 pria = = !
! != 6
Banyaknya cara memilih 1 dari 3 wanita = = !
! != 3
Banyaknya panitia yang dapat dibentuk = (6) (3) = 18
2.4.2 Permutasi (Permutation)
Permutasi merupakan susunan dari suatu himpunan obyek yang dapat dibentuk yang memperhatikan urutan. Banyaknya permutasi n obyek berlainan adalah n! Banyaknya permutasi n obyek berlainan bila diambil r sekaligus. = ( !)! Banyaknya permutasi n benda berlainan yang disusun melingkar adalah (n–1)!
Banyaknya permutasi yang berlainan dari n obyek bila n1adalah jumlah obyek
jenis pertama, n2 adalah jumlah obyek jenis kedua, ..., nk jumlah obyek ke-k adalah: !
! ! . !
Banyaknya cara menyekat n obyek dalam r sel bila masing-masing berisi n1obyek pada
sel pertama, n2obyek pada sel kedua, dan seterusnya adalah :
!
! ! . ! dengann1+
n2+ ... +nr=n
2.5 Distribusi Probabilitas Diskrit
Oleh karena itu perubah acak diskrit yang berkenaan dengan percobaan tersebut dapat dilukiskan dengan distribusi probabilitas yang sama, dan dapat dinyatakan dengan rumus yang sama.
Dalam banyak praktek yang sering di jumpai, hanya memerlukan beberapa distribusi probabilitas yang penting untuk menyatakan banyak perubah acak diskrit.
2.5.1 Distribusi Seragam
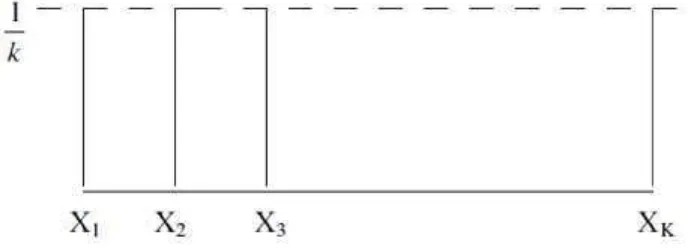
Distribusi probabilitas yang paling sederhana adalah yang semua perubah acaknya mempunyai probabilitas yang sama. Distribusi ini disebut distribusi probabilitas seragam diskrit.
Jika perubah acak X mendapat nilai x1, x2, , xk dengan probabilitas yang
sama, maka distribusi probabilitas diskrit diberikan oleh:
f ( x; k ) = ; untuk x = x1, x2, … , xk
Lambang f(x;k) sebagai pengganti f(x), yang menunjukan bahwa distribusi seragam tersebut bergantung pada parameter x
Rata-rata dan varians dari distribusi seragam diskrit adalah :
Sebuah dadu seimbang dilemparkan satu kali, maka tiap unsur dalam ruang sampel S={1, 2,3 4, 5, 6}. Muncul dengan probabilitas 1/6. Jadi jika X menyatakan mata dadu yang muncul, maka X terdistribusi peluang seragam (uniform) yakni f(x;6)=1/6, untuk x = 1, 2, 3, 4, 5, 6.
2.5.2 Distribusi Binomial
Suatu percobaan yang terdiri atas beberapa usaha, tiap-tiap usaha, memberikan hasil yang dapat dikelompokan menjadi 2-kategori yaitu sukses atau gagal, dan tiap-tiap ulangan percobaan bebas satu sama lainnya. Probabilitas kesuksesan tidak berubah dari percobaan satu ke percobaan lainnya. Proses ini disebut proses Bernoulli. Jadi proses Bernoulli harus memenuhi persyaratan berikut:
1. Percobaan terdiri atas n-eksperimen yang berulang.
2. Setiap eksperimen memiliki 2 (dua) kemungkinan hasil (outcomes), yakni Sukses dan Gagal yang saling meniadakan (mutually axclusive).
4. Eksperimen sebanyak n kali adalah bersifat bebas (independent), artinya hasil setiap eksperimen tidak mempengaruhi hasil dari eksperimen yang lain. Istilah sukses dan gagal merupakan istilah statistik dan tidak perlu disama-artikan dengan istilah sehari-hari yang sering didengar mengingat dalam pengertian ini kondisi cacat (defective items) hasil dari suatu proses produksi bisa dikatakan sebagai kondisi sukses.
Besarnya nilai probabilitas setiap x peristiwa sukses dari n kali eksperimen ditunjukkan oleh probabilitas sukses p dan probabilitas kegagalan 1-p.
f(x) = P(X=x) = b(x,n,p) = = !
!( )!
Dengan: p = probabilitas sukses q = 1-p
n = jumlah total percobaan
x = jumlah sukses dari n kali percobaan
Distribusi binomial mempunyai nilai rata-rata μ = np dan nilai simpangan
baku = .
2.5.3 Nilai Harapan Distribusi Binomial Untuk mencari rata-rata (μ ) digunakan Rumus :
Jadi ekspektasi dari distribusi binomial adalah np. 2.5.4 Variansi Distribusi Binomial
( ) =[ 2]–( [ ])2
[ ]2 = n(n−1)p2(qn-2+(n−2)pqn-3+ +pn-2)+np = n(n−1)p2(q+p)n-2+np
= n(n−1)pn+np
maka,
Var ( ) =[ 2]–( [ ])2 = n(n−1)p2+np− 2 2
= np(1-p) = npq
Jadi, varian dari distribusi binomial adalah npq
2.6 Distribusi Normal
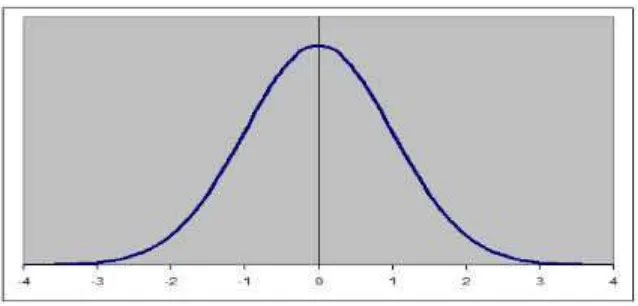
Distribusi probailitas kontinyu yang terpenting di bidang statistik adalah distribusi Normal. Grafiknya disebut kurva normal, berbentuk lonceng. Distribusi ini ditemukan Karl Friedrich Gauss (1777-1855) yang juga disebut distribusi Gauss. Perubah acak X yang bentuknya seperti lonceng disebut perubah acak normal dengan persamaan matematik distribusi probabilitas yang bergantung paramerter μ (mean) dan σ
Gambar 2.6 Kurva Normal
Fungsi padat perubah acak normal X, dengan rata-rata μ dan simpangan baku σ dinyatakan sebagai :
n( ; ; ) ,untuk−∞ < <∞
Dengan : μ = mean
σ = simpangan baku
π = 3,14159...
e = 2,71828...
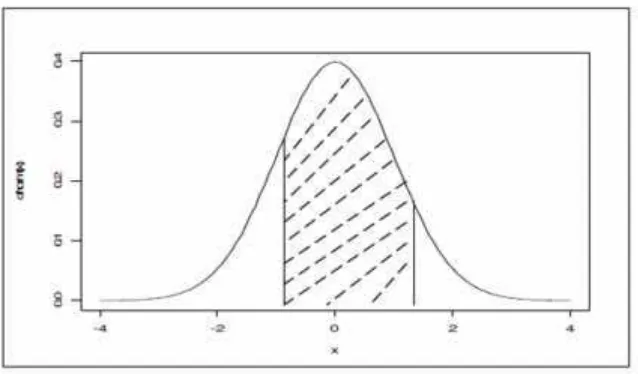
Luas daerah kurva normal antara x = a dan x = b dinyatakan sebagai berikut:
( ≤ ≤ ) = ( )
Gambar 2.7 Luas Derah P(a < x < b) = Luas Daerah Diarsir
2.6.1 Nilai Harapan Variabel acak Normal
E [X] = ( )
= /
= /
z= ; + = ; dz = ; dx =
= ( + )
= ( + )
Untuk = ( + )
y = ; = ; =
= ( + )
untuk = = = [ ]
dimana lim = 0 ; = 0
akibatnya = (0 + 0)= 0
untuk = ( + )
y = = 2
dy = =
= +
= ( + )
= + =
Sehingga:
E [X] = +
2.6.2 Variansi Variabel Acak Normal Var (X) = E [X2] - (E [X])2
E [x2] =
=
z = +
= =
= ( + )
= ( + 2 + )
= + 2 +
= + +
= + 0 + ( 2 )
= +
Untuk = ( + )
= ( 2 + 2 )
= ( + )
= ( 2 1 + 2 1 )
= +
= Sehingga : E[X2] = + Maka :
Var (X) = E[X2]–(E[X])2
= +
=
2.6.3 Distribusi Normal Standard
Keluarga distribusi normal memiliki jumlah yang banyak sekali, akibat pengaruh rata-rata dan simpangan baku. Akan tetapi, untuk mencari probabilitas suatu interval dari variabel random kontinu dapat di permudah dengan menggunakan bantuan distribusi normal standard.
Distribusi normal standard adalah distribusi normal yang memiliki rata-rata (μ ) = 0dan simpangan baku ( ) = 1. Bentuk fungsinya adalah:
Untuk mengubah distribusi normal umum menjadi distribusi normal standard di gunakan nilai Z (standard units). Bentuk rumusnya adalah:
Z =
Dengan:
Z = Skor Z atau nilai normal baku
X = Nilai dari suatu pengamatan atau pengukuran m = Nilai rata-rata hitung suatu distribusi
s = Standart deviasi suatu distribusi
Nilai Z (standard units) adalah angka atau indeks yang menyatakan penyimpangan suatu nilai variabel random (X) dari rata-rata ( ) dihitung dalam satuan simpangan baku ( ).
2.6.4 Sifat-Sifat Normal Standard
Sifat-sifat penting dalam distribusi normal standard yaitu: 1) Grafiknya selalu ada di atas sumbu datar x
2) Bentuknya simetrik terhadap x =
3) Mempunyai satu modus, jadi kurva unimodal, tercapai pada x =
4) Grafiknya mendekati (berasimtutkan) sumbu datar x di mulai dari x = + 3 ke kanan dan x = - 3 ke kiri
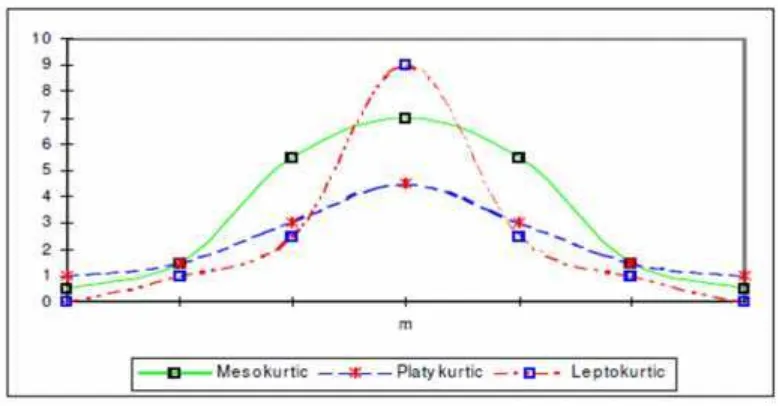
Untuk tiap pasang dan , sifat-sifat di atas selalu di penuhi, hanya bentuk kurvanya saja yang berlainan. Jika makin besar, kurvanya makin rendah (platikurtik) dan untuk makin kecil, kurvanya makin tinggi (leptokurtik).
Gambar 2.8 Distribusi Kurva Normal dengan μ Sama dan Berbeda Pada Gambar 2.8 menunjukkan bentuk distribusi dan kurva normal dengan nilai tengah sama dan standart deviasi yang berbeda. Kurva normal demikian mempunyai μ = Md = Mo yang sama, namun mempunyai s yang berbeda. Semakin besar s, maka kurva semakin pendek dan semakin tinggi nilai s, maka semakin runcing. Oleh sebab itu, s yang tinggi menunjukkan bahwa nilai data semakin menyebar dari nilai tengahnya (μ ). Sebaliknya apabila s semakin rendah, maka nilai
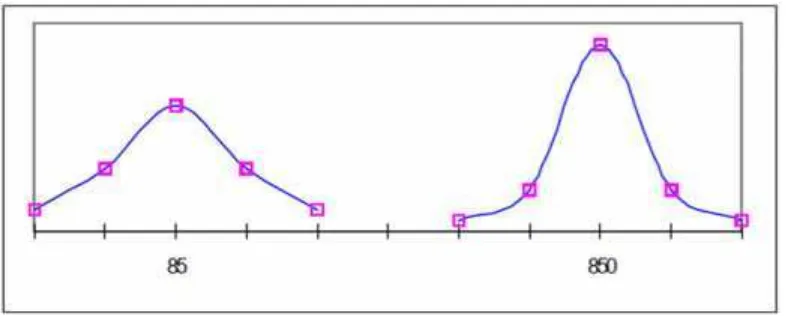
Gambar 2.9Distribusi Kurva Normal dengan μ Berbeda dan Sama Pada Gambar 2.9 menunjukkan bentuk distribusi probabilitas dan kurva normal dengan μ berbeda dan s sama, mempunyai jarak antara kurva yang berbeda, namun bentuk kurva tetap samGaa. Hal demikian bisa terjadi karena kemampuan antar populasi berbeda, namun setiap populasi mempunyai keragaman yang hampir sama.
Gambar 3.0 Distribusi Kurva Normal dengan dan Berbeda