2007 Pendugaan Statistik Area Kecil dengan Metode Empirical Constrained Bayes

PENDUGAAN STATISTIK AREA KECIL DENGAN METODE EMPIRICAL CONSTRAINED BAYES 1

Kismiantini

Jurusan Pendidikan Matematika FMIPA Universitas Negeri Yogyakarta

Abstrak

Metode empirical Bayes (EB) merupakan metode yang lebih aplikatif pada pendugaan area kecil. Metode ini mampu menangani data kontinu, biner maupun cacahan serta mampu menurunkan galat baku dibandingkan penduga langsung. Penduga empirical Bayes diperoleh dengan menduga parameter model melalui fungsi kepekatan peluang marjinal lalu disubstitusikan dalam penduga Bayes. Namun penduga Bayes ini akan mengalami underdispersi pada kuadrat galat dengan model dua tahap. Untuk mengatasi permasalahan ini, dapat dengan memasukkan kendala (constraint) pada posterior expected squared error loss, sehingga penduga yang diperoleh disebut penduga constrained Bayes. Selanjutnya dengan mensubstitusikan nilai dugaan parameternya diperoleh penduga empirical constrained Bayes (ECB). Kebaikan ketiga penduga statistik area kecil yaitu penduga langsung, empirical Bayes dan empirical constrained Bayes dengan melihat besarnya kuadrat tengah galat.

Kata-kata kunci : pendugaan area kecil, empirical Bayes, empirical constrained Bayes

PENDAHULUAN

Pendugaan area kecil (small area estimation) adalah suatu teknik statistika untuk

menduga parameter-parameter subpopulasi yang ukuran contohnya kecil (Rao 2003).

Pendugaan sederhana area kecil yang didasarkan pada penerapan model desain penarikan

contoh (design-based) dengan ukuran contoh dari subpopulasi disebut sebagai pendugaan

langsung (direct estimation). Bila ukuran contohnya kecil maka statistik yang dihasilkan

akan memiliki ragam yang besar bahkan pendugaan tidak dapat dilakukan.

Berbagai metode pendugaan area kecil (small area estimation) telah dikembangkan

khususnya menyangkut metode yang berbasis model (model-based area estimation)

sebagai alternatif dari pendugaan langsung. Metode tersebut adalah empirical best linear

unbiased prediction (EBLUP), empirical Bayes (EB), dan hierarchical Bayes (HB).

Metode EB dan HB merupakan metode yang lebih umum yang mampu menangani data

kontinu, biner maupun cacahan.

1

Pada model area kecil, pendugaan dengan metode empirical Bayes dimulai dengan

mengasumsikan model dua tahap. Selanjutnya dengan memaksimumkan fungsi marjinal

akan diperoleh nilai dugaan parameternya, yang kemudian disubstitusikan dalam penduga

Bayes. Menurut Rao (2003) penduga Bayes ini akan menunjukkan underdispersi dengan

model dua tahap tersebut, yang dapat dilihat pada kuadrat galatnya. Untuk mengatasi

permasalahan ini dapat dilakukan dengan memasukkan suatu kendala (constraint) pada

kuadrat galatnya (Ghosh, 1992). Dalam makalah ini akan dibahas pendugaan statistik area

kecil dengan menggunakan penduga empirical constrained Bayes (ECB) berdasarkan

asumsi normal.

METODE EMPIRICAL BAYES

Metode empirical Bayes (EB) merupakan metode yang lebih umum untuk

menangani model dengan data kontinu, biner maupun cacahan. Berdasarkan asumsi

normal, model area kecil (basic area level) dapat diekspresikan sebagai model dua tahap

(Rao, 1999) sebagai berikut :

(i)

θ

ˆ_i =

θ

_i+e_i dengan

(

_i

)

iid

i N

e

~

0,

ψ

, i=1,2, ,m (1) (ii)

θ

~

(

µ

i,

σ

_ν2

)

iid

i N sebagai prior,

µ

β

T i

i =x (2)

Berdasarkan teorema Bayes maka diperoleh sebaran posterior yaitu :

( )

(

i i i

)

B i ind

i

i

θ

β

σ

N

θ

g

σ

γ

ψ

θ

_{ν ν}2 =

1 2

, ˆ ,

,

ˆ

~

_dengan

(

)

i

i

σ

σ

ψ

γ

= _ν2 _ν2+

/ (3)

Penduga Bayes bagi

θ

_i adalah nilai harapan dari sebaran posterior sebagai berikut : E

(

θ

_i

θ

ˆ_i,

β

,

σ

_ν2

)

=

θ

ˆ_iB =

γ

_i

θ

ˆ_i +

(

1−

γ

_i

)

µ

_i ,

γ

_i =

σ

_ν2

(

σ

_ν2+

ψ

_i

)

/ ,

µ

_i = xT_i

β

(4) Penduga Bayes

θ

ˆ_iB tergantung pada parameter

β

dan

σ

_ν2, yang dapat diperoleh dari

sebaran marjinal :

(

_{i i}

)

ind

i N

µ

σ

ψ

θ

ν +

2 , ˆ

~

. Penduga empirical Bayes (EB) bagi

θ

_i

diperoleh dengan mensubstitusikan

β

dengan

β

ˆ dan

σ

_ν2dengan

σ

ˆ_ν2, yaitu :

θ

ˆ_iEB

θ

ˆ_iB

(

β

ˆ,

σ

ν

)

γ

ˆ_i

θ

ˆ_i

(

1

γ

ˆ_i

)

µ

ˆ_i

2

− + =

= ,

γ

ˆ_i

σ

ˆ_ν2/

(

σ

ˆ_ν2

ψ

ˆ_i

)

+

= dan

µ

ˆ T

β

ˆ

i

i =x (5)

Pada makalah ini akan diasumsikan bahwa ragam sampling sama. Menurut Morris

(1983) bila ragam sampling sama yaitu

ψ

_i =

ψ

maka penduga tak bias bagi

γ

γ

= −

− 1

(

m p 2

)

/S

1−

γ

* =

ψ

− − dengan =

(

ˆ − ˆ

)

2

i LS

T i

i x

S

θ

β

,

β

ˆ_LS merupakan

penduga kuadrat terkecil bagi

β

. Sehingga penduga EB bagi

θ

_i adalah

(

)

LS

T i i

EB

i

γ

θ

γ

x

β

θ

ˆ ₌ *ˆ ₊ 1₋ * ˆ

(6)

Pendugaan kuadrat tengah galat (MSE) bagi penduga EB (

θ

ˆEB) dengan menggunakan metode jackknife yang dikemukakan oleh Jiang, Lahiri dan Wan (2002)

yaitu

( ) (

)

(

)

(

)

( )

i i i B i EB i i B i B i EB i EB i M M g E E E MSE 1 2 2 1 2 2 2 : ˆ ˆ ˆ ˆ ˆ ˆ + = + − = − + − = ν

σ

θ

θ

θ

θ

θ

θ

θ

(7)

METODE EMPIRICAL CONSTRAINED BAYES

Metode constrained Bayes merupakan metode yang digunakan untuk mengatasi

permasalahan underdispersi pada penduga Bayes. Misalkan model dua tahap berikut

(

ˆ , 1

)

ˆ

~

θ

θ

λ

θ

θ

_{i i}ind f _{i i} dan

θ

~

(

θ

_i

λ

₂

)

iid

i f , maka dapat diperoleh penduga Bayes bagi

θ

i

yaitu

θ

ˆ_iB =E

(

θ

_i

θ

ˆ_i,

λ

)

. Persamaan (8) menunjukkan bahwa penduga Bayes mengalami underdispersi pada kuadrat tengah galatnya.

(

)

(

)

(

)

(

−

)

− > − − + − − = − − i B B i i B B i i i i i m m V m m E 2 . 2 . 2 . 2 . ˆ ˆ 1 1 ˆ ˆ 1 1 ˆ 1 1 1 1

θ

θ

θ

θ

θ

θ

θ

θ

θ

(8)

dengan

θ

ˆ=

(

θ

ˆ₁, ,

θ

ˆ_m

)

T, =

i B i

B _{ˆ /m}

ˆ

.

θ

θ

.

Selanjutnya untuk mengatasi permasalahan underdispersi tersebut adalah dengan

meminimumkan posterior expected squared error loss E

[

_i

(

θ

_i−t_i

)

2

θ

ˆ

]

terhadap

kendala (constraint) berikut :

B

t_. =

θ

ˆ_. (9)

(

)

(

−

)

− = −

− i ti t E _m i i

m

θ

θ

θ

ˆ 1 1 1 1 2 . 2

dengan t_. = _{i i}t /m. Dengan perkalian Lagrange, dapat diperoleh penduga constrained Bayes (CB) sebagai solusi masalah minimisasi berikut (Rao, 2003) :

( )(

B B

)

i B i CB i opt i a

t_, =

θ

ˆ =

θ

ˆ +

θ

ˆ,

λ

θ

ˆ −

θ

ˆ_. (11)

dengan

( )

(

)

(

)

{

}

(

)

2 / 1 2 . ˆ ˆ ) 1 /( 1 , ˆ / 1 1 , ˆ − − + = i B B i

i i i

m V m a

θ

θ

λ

θ

θ

λ

θ

(12)

Dari persamaan (11) dapat diketahui bahwa

(

−

)

>

(

−

)

i B B i i CB CB i 2 . 2 . ˆ ˆ ˆ ˆ

θ

θ

θ

θ

karena

( )

θ

ˆ,

λ

a >1 dan

θ

ˆ_.CB =

θ

ˆ_.B (Rao, 2003).

Pada makalah ini akan dibahas untuk model berdasarkan asumsi normal dengan

ragam sampling sama. Misalkan model dua tahap yaitu

θ

ˆ_i =

θ

_i+e_i dengan

(

0,

ψ

)

~

N e

iid

i dan saling bebas dengan

(

)

2 ,

~

µ

σ

ν

θ

_i

iid

i N sebagai prior. Sehingga sebaran

posteriornya adalah

θ

θ

β

σ

_ν

(

θ

( )

σ

_ν2 =

γψ

)

1 2 , ˆ , , ˆ

~

i B i ind i

i N g . Penduga Bayes diberikan oleh

(

)

i

i B

i

γ

θ

γ

µ

θ

ˆ = ˆ + 1− dengan

γ

=

σ

_ν2

(

σ

_ν2 +

ψ

)

/ ,

µ

_i = x_iT

β

. Menurut Rao (2003), penduga constrained Bayes pada model dua tahap ini adalah :

(

)

[

]

(

)

{

}

(

)

(

.

)

2 / 1 2 . . ˆ ˆ ˆ ˆ 1 / 1 / 1 1 ˆ ˆ

γ

θ

θ

θ

θ

γ

ψ

µ

γ

θ

γ

θ

− − − + + − + = _i i i i CB i m (13)

Diketahui bahwa

θ

(

µ

σ

_ν2+

ψ

)

,

ˆ

~

i

iid

i N , bila m → ∞ maka

θ

ˆ. konvergen peluang terhadap

i

µ

dan

(

ˆ ˆ_.

)

2

1 1

− − i i

m

θ

θ

konvergen peluang terhadap

ψ

+

σ

ν =

ψ

/

(

1−

γ

i

)

2

, sehingga

penduga constrained Bayes bagi

θ

_i dapat dinyatakan sebagai berikut :

(

)

i

i CB

i

γ

θ

γ

µ

θ

ˆ _≈ 1/2ˆ _{+ 1−} 1/2

(14)

Selanjutnya penduga empirical constrained Bayes bagi

θ

_i diperoleh dengan mensubstitusikan

µ

_i dengan

µ

ˆ_idan

γ

dengan

γ

ˆ pada persamaan (14), yaitu :

(

)

i

i ECB

i

γ

θ

γ

µ

θ

ˆ ₌ ˆ1/2ˆ ₊ 1₋ ˆ1/2 ˆ

dengan

γ

ˆ

σ

ˆ_ν2/

(

σ

ˆ_ν2

ψ

ˆ

)

+

= dan

µ

ˆ T

β

ˆ

i

i =x . Kuadrat tengah galat bagi ECB

θ

ˆ diperoleh dengan menggunakan metode jackknife pula.

PENERAPAN PADA DATA BPS

Peubah yang diamati dan menjadi perhatian dalam ilustrasi ini adalah rata-rata

pengeluaran perkapita rumah tangga. Sumber data yang digunakan adalah SUSENAS

2003 dengan materi informasi berbasis rumah tangga, serta PODES 2003 sebagai sumber

data peubah penyerta. Peubah penyertanya adalah peubah-peubah yang diasumsikan

mempengaruhi dan atau menggambarkan pengeluaran rumah tangga pada suatu wilayah,

meliputi: persentase rumah tangga prasejahtera dan sejahtera 1, persentase pengangguran,

persentase rumah tangga pelanggan listrik PLN, dan persentase rumah tangga pelanggan

telepon.

Analisis menggunakan SAS 9.1 meliputi: PROC TABULATE untuk memperoleh

penduga langsung, PROC MIXED untuk mendapatkan penduga

β

,

σ

_ν2,

ψ

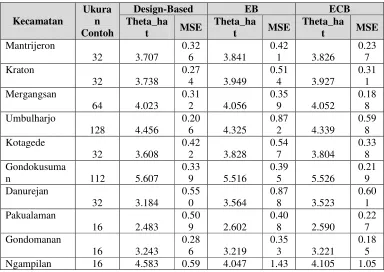
, dan PROC IML untuk mendapatkan penduga EB dan ECB.

Tabel 1. Pendugaan rata-rata pengeluaran per kapita (× Rp.100.000,-) berdasarkan design-based, empirical Bayes (EB) dan empirical constrained Bayes (ECB)

Kecamatan

Ukura n Contoh

Design-Based EB ECB

Theta_ha

t MSE

Theta_ha

t MSE

Theta_ha

t MSE

Mantrijeron

32 3.707

0.32

6 3.841

0.42

1 3.826

0.23 7 Kraton

32 3.738

0.27

4 3.949

0.51

4 3.927

0.31 1 Mergangsan

64 4.023

0.31

2 4.056

0.35

9 4.052

0.18 8 Umbulharjo

128 4.456

0.20

6 4.325

0.87

2 4.339

0.59 8 Kotagede

32 3.608

0.42

2 3.828

0.54

7 3.804

0.33 8 Gondokusuma

n 112 5.607

0.33

9 5.516

0.39

5 5.526

0.21 9 Danurejan

32 3.184

0.55

0 3.564

0.87

8 3.523

0.60 1 Pakualaman

16 2.483

0.50

9 2.602

0.40

8 2.590

0.22 7 Gondomanan

16 3.243

0.28

6 3.219

0.35

3 3.221

0.18 5

[image:5.612.127.511.439.711.2]

2 5 7 Wirobrajan

48 4.212

0.33

2 3.723

1.27

0 3.776

0.92 4 Gedong tengen

32 2.596

0.19

8 2.645

0.38

9 2.640

0.21 2 Jetis

48 3.609

0.27

7 3.560

0.35

9 3.566

0.19 0 Tegalrejo

64 3.740

0.26

7 3.909

0.54

4 3.891

0.33 5

Kajian empirik pada Tabel 1 memperlihatkan bahwa pendugaan dengan metode empirical

constrained Bayes memberikan hasil yang lebih baik dibanding metode empirical Bayes

yang ditunjukkan oleh nilai kuadrat tengah galat (MSE) yang relatif lebih kecil.

Pendugaan langsung berdasarkan design-based untuk kasus data Susenas di kota

Yogyakarta relatif memberikan hasil yang baik, hal ini mengindikasikan bahwa ukuran

contoh untuk area kecamatan di kota Yogyakarta cukup memadai untuk digunakan dalam

pendugaan langsung. Namun pendugaan langsung ini belum memasukkan unsur

pembobot padahal pembobot merupakan salah satu hal penting pada pendugaan

berdasarkan design-based.

SIMPULAN

Pendugaan statistik area kecil dengan metode empirical constrained Bayes (ECB)

memberikan hasil yang lebih baik dibanding metode empirical Bayes (EB). Pada

pendugaan langsung berdasarkan metode design-based perlu dilakukan pengkajian

tentang besarnya pembobot.

DAFTAR PUSTAKA

Ghosh, M. 1992. Constrained Bayes estimation with applications. Journal of the American Statistical Association 87: 533-540.

Jiang, J., Lahiri, P., & Wan, S.M. 2002. A unified jackknife theory for empirical best prediction with M-estimation. The Annals of Statistics 30:1782-1810.

Morris, C.A. 1983. Parametric empirical Bayes inference: Theory and applications. Journal of the American Statistical Association 78: 47-54.

Rao, J.N.K. 1999. Some recent advances in model-based small area estimation. Survey Methodology 25: 175-186.