STUDI TERHADAP SEBARAN STASIONER PADA
SISTEM BONUS MALUS SWISS
Oleh :
RENSY ERMAWATY
G05400005
PROGRAM STUDI MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
ABSTRAK
RENSY ERMAWATY. Studi Terhadap Sebaran Stasioner pada Sistem Bonus-Malus Swiss. Dibimbing oleh I GUSTI PUTU PURNABA dan I WAYAN MANGKU.
Sistem Bonus-Malus Swiss (BMS) merupakan salah satu sistem pada asuransi mobil. Sistem BMS memiliki jumlah state (x) yang terbatas yaitu 22 state dan premi yang dibayarkan oleh setiap pemegang polis tergantung pada state tersebut. Tiap tahun state dari seorang pemegang polis ditentukan oleh state tahun sebelumnya dan banyaknya kecelakaan yang dilaporkan pada tahun tersebut. Jika tidak ada kecelakaan yang dilaporkan pada jangka waktu satu tahun maka state akan berkurang sebanyak satu dan untuk setiap kecelakaan yang dilaporkan maka state akan mengalami kenaikan sebanyak s. Sebelum tahun 1990 nilai s yang digunakan pada sistem BMS adalah 3, tetapi sejak tahun 1990 berubah menjadi 4.
Penetapan state dalam sistem BMS didasarkan pada pencarian sebaran stasioner F
( )
x yang menyatakan banyaknya pemegang polis dalam tiap state. Untuk menentukan sebaran stasioner F( )
x digunakan metode rekursif.Dalam karya tulis ini penghitungan sebaran stasioner didasarkan pada 2 asumsi, yaitu : (a) banyaknya kecelakaan menyebar Poisson dengan parameter
λ
dan (b) banyaknya kecelakaan menyebar Binomial Negatif dengan parameter α dan1 1
+
β .
Selain penghitungan sebaran stasioner, diukur juga suatu ukuran efisiensi dari sistem BMS yaitu efisiensi asimtotik. Ukuran efisiensi ini dihitung berdasarkan rataan frekuensi kecelakaan
λ
dan rataan premi jangka panjang b( )
λ .Berdasarkan penghitungan sebaran stasioner dan nilai dari maksimal efisiensi asimtotik, dapat disimpulkan bahwa sistem BMS yang lama (s = 3) lebih efisien dibanding sistem BMS yang baru (s = 4).
STUDI TERHADAP SEBARAN STASIONER PADA
SISTEM BONUS MALUS SWISS
Skripsi
Sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains
Pada Fakultas Matematika dan Ilmu Penetahuan Alam
Institut Pertanian Bogor
Oleh :
RENSY ERMAWATY
G05400005
PROGRAM STUDI MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
Judul
: Studi Terhadap Sebaran Stasioner Pada Sistem Bonus-Malus Swiss
Nama
: Rensy Ermawaty
NIM :
G05400005
Menyetujui :
Pembimbing I,
Pembimbing II,
Dr. Ir. I Gusti Putu Purnaba, DEA.
Dr. Ir. I Wayan Mangku, M.Sc.
NIP. 131 878 945
NIP. 131 633 020
Mengetahui :
Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam
Institut Pertanian Bogor
Prof. Dr. Ir. Yonny Koesmaryono, MS.
NIP. 131 473 999
Tanggal Lulus :
RIWAYAT HIDUP
Penulis dilahirkan di Sukabumi 15 Oktober 1981 sebagai anak ke tiga dari empat bersaudara, anak dari pasangan Babas Permana dan Yetty Nurhayaty.
Penulis menyelesaikan pendidikan Sekolah Dasar pada tahun 1994 di SD Negeri Cikole 1 Sukabumi. Kemudian penulis melanjutkan pendidikan ke jenjang Sekolah Lanjutan Tingkat Pertama Negeri 1 Sukabumi tahun 1994 dan lulus tahun 1997. Selanjutnya ke jenjang Sekolah Menengah Umum Negeri 1 Sukabumi tahun 1997 dan lulus tahun 2000. Selepas SMU tahun 2000, penulis diterima sebagai mahasiswa Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor melalui jalur USMI.
Selama mengikuti perkuliahan, penulis pernah menjadi Staf Pengajar Bimbel Prestasipb (2002/2003), Staf Pengajar Bimbel Sinar Ilmu (2003/2004) dan Staf Pengajar Bimbel Bina Madani (2005/2006).
PRAKATA
Alhamdulillahirobbil’alamin. Segala puji syukur penulis panjatkan kepada Allah SWT atas ijin-Nya
penulis dapat menyelesaikan karya ilmiah ini. Dalam kesempatan ini penulis ingin menyampaikan penghargaan setinggi-tingginya kepada :
1. Bapak I Gusti Putu Purnaba yang telah menuangkan ide dan pikirannya selama penyusunan karya ilmiah ini.
2. Bapak I Wayan Mangku yang telah memberikan arahan dan tuntunan selama penyusunan karya ilmiah ini.
3. Bapak Siswandi atas kesediaannya menjadi penguji.
4. Keluargaku tercinta : Papah, Mamah, Asti, A iki, dan A aji . “Do’a dan kasih sayang kalianlah yang telah mengembalikan penulis menjadi bagian dari kalian”.
5. Dwi Ade (akhirnya kita jadi sarjana juga ya …).
6. Teman-teman seperjuanganku : Endah, Marita, Cahyadi, Rudi, Ribut, dan Wahyu (terus berjuang ya)
7. Adik-adikku yang manis (angkatan 38,39 dan 40) terutama Indah dan Mika, makasih ya udah bantuin kak echi.
8. Sahabatku yang manis Iin, “denganmu aku menjadi sekarang….”. 9. Ian, makasih ya komputernya udah disimpen di wangun.
10. Abang Fadli, Mas Sambodo, Rama, Adji dan Ahmad, “kalian telah memberi warna kehidupanku selama ini”.
11. Bu Susi dan Bu Ade atas dukungan dan kekeluargaan yang telah diberikan kepada penulis sehingga menjadi betah di kampus.
12. Mas Bono, Mas Yono, Mas Deni, Ibu Marizi atas bantuannya dalam mensukseskan jalannya seminar dan sidang penulis.
13. Semua pihak yang tidak bisa penulis sebutkan satu persatu. Terima kasih atas segala bantuannya yang telah diberikan selama ini, semoga menjadikannya ibadah. Amin.
Bogor, Januari 2007 Rensy Ermawaty
DAFTAR ISI
Halaman
DAFTAR TABEL ... vii
DAFTAR GAMBAR... vii
DAFTAR LAMPIRAN ... vii
PENDAHULUAN... 1
Latar Belakang... 1
Tujuan ... 1
LANDASAN TEORI ... 1
PEMBAHASAN ... 3
Sistem Bonus-Malus Swiss... 3
Sebaran Stasioner... 3 Model Portfolio... 6 Efisiensi Asimtotik ... 8 SIMPULAN... 9 DAFTAR PUSAKA ... 10 LAMPIRAN ... 11
DAFTAR TABEL
Halaman
Tabel 1 : Neraca premi (%) ... 3
DAFTAR GAMBAR
Halaman Gambar 1: Grafik Sebaran Stasioner Sistem BMS dengan s = 3... 5Gambar 2: Grafik Sebaran Stasioner Sistem BMS dengan s = 4... 6
Gambar 3: Grafik Sebaran Stasioner Model Porfolio... 8
Gambar 4: Grafik Efisiensi Asimtotik dari Sistem BMS... 9
DAFTAR LAMPIRAN
Halaman Lampiran 1: Penjabaran rumus rekursif untuk menghitung A(
x+1)
jika s = 3 ... 12Lampiran 2: Penjabaran rumus rekursif untuk menghitung A
(
x+1)
jika s = 4 ... 27Lampiran 3: Tabel 2. Sebaran stasioner sistem BMS dengan s = 3... 37
Tabel 3. Fungsi kepekatan peluang Sistem BMS dengan s = 3 ... 38
Lampiran 4: Tabel 4. Sebaran stasioner sistem BMS dengan s = 4... 39
Tabel 5. Fungsi kepekatan peluang sistem BMS dengan s = 4... 40
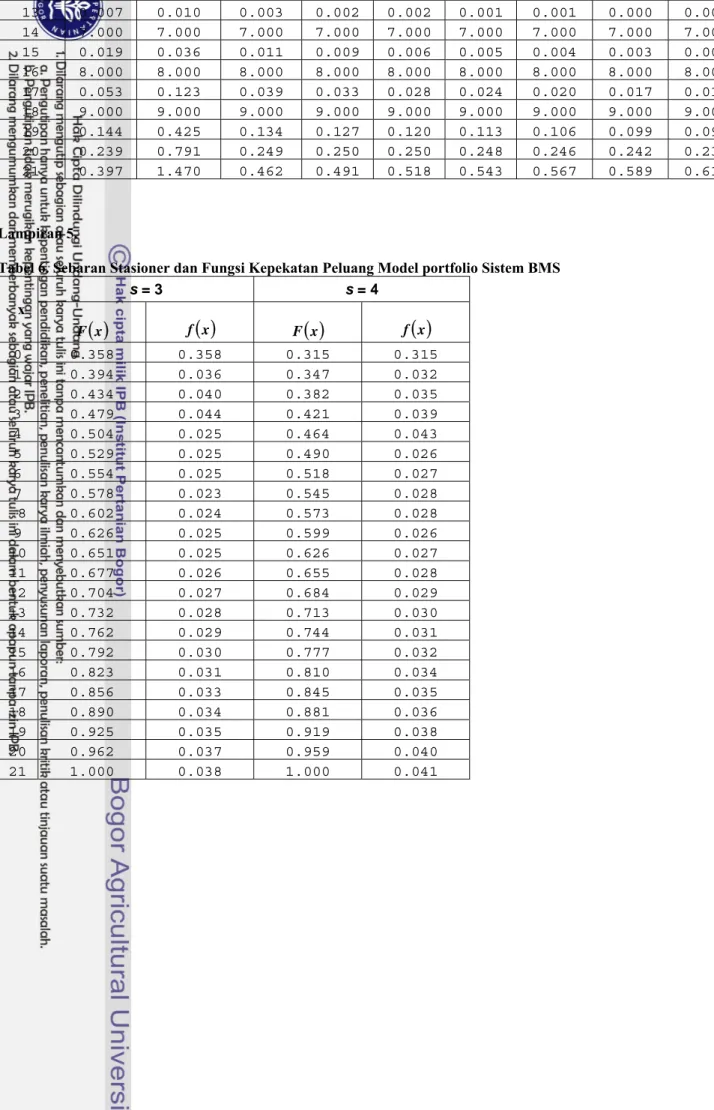
Lampiran 5 :Tabel 6. Sebaran stasioner dan fungsi kepekatan peluang model portfolio sistem BMS ... 41
PENDAHULUAN
Latar Belakang
Untuk mengantisipasi kemungkinan adanya kerugian secara finansial yang mungkin timbul akibat kejadian-kejadian yang tidak diharapkan maka seseorang biasanya mengikuti asuransi. Salah satu kejadian yang sering terjadi pada pemilik mobil adalah kecelakaan akibat tabrakan dan lain-lain.
Berbagai jenis sistem asuransi ditawarkan oleh perusahaan asuransi mobil untuk menarik banyak orang agar menjadi pemegang polis perusahaan tersebut. Salah satu jenis sistem dalam asuransi mobil adalah sistem bonus-malus. Sistem ini mempunyai jumlah state yang terbatas dan Pemi yang harus dibayar oleh setiap pemegang polis tergantung pada state masing-masing.
Sistem bonus-malus yang akan dibahas pada tulisan ini adalah sistem Bonus-Malus Swiss (BMS).
Penetapan state dalam sistem BMS didasarkan pada pencarian sebaran stasioner yang menyatakan banyaknya pemegang polis dalam tiap state. Tiap tahun state seorang pemegang polis ditentukan oleh
state pada tahun sebelumnya dan banyaknya
kecelakaan yang dilaporkan pada tahun tersebut. Jika tidak ada kecelakaan yang dilaporkan pada tahun ini maka tahun depan pemegang polis akan
memperoleh bonus yang dinyatakan dengan state yang lebih rendah dengan Pemi yang lebih kecil. Tetapi jika tahun ini terjadi kecelakaan maka pemegang polis akan memperoleh malus yang dinyatakan dengan state yang lebih tinggi dengan Pemi yang lebih besar.
Pada tahun 1990, sistem BMS mengalami perubahan aturan perpindahan state. Pada sistem BMS yang baru untuk setiap laporan kecelakaan, kenaikan state akan berubah menjadi 4 state yang semula hanya 3 state.
Tujuan
Tujuan penulisan karya ilmiah ini adalah sebagai berikut :
• Mempelajari metode yang digunakan untuk mencari sebaran stasioner pada sistem BMS. • Mengukur tingkat efisiensi dari sistem BMS
berdasarkan ukuran efisiensi asimtotik.
• Membandingkan sistem BMS yang baru dengan yang lama berdasarkan penghitungan sebaran stasioner dan ukuran efisiensi asimtotik.
LANDASAN TEORI
Definisi 1 (Percobaan acak)
Percobaan acak adalah suatu percobaan yang dapat diulang dalam kondisi yang sama namun hasil pada percobaan berikutnya tidak dapat ditebak dengan tepat. Tetapi kita bisa mengetahui semua kemungkinan hasil yang muncul.
[Hogg dan Craig, 1995] Definisi 2 (Ruang Contoh dan Kejadian)
Himpunan dari semua kemungkinan dari suatu percobaan disebut ruang contoh, dinotasikan dengan
Ω
. Suatu kejadian A adalah himpunan bagian dari ruang contohΩ
.[Grimmett dan Stirzaker, 1992] Definisi 3 (Medan –σ)
Medan – σ adalah suatu himpunan Y yang anggotanya terdiri atas semua himpunan bagian ruang contoh Ω yang memenuhi kondisi berikut :
1. φ Y ∈ 2. Jika A1 ,A2 ,... ∈ Y maka ∈ ∞ =
U
i 1Ai Y. 3. Jika A ∈Y maka Ac ∈Y.[Grimmett dan Stirzaker, 1992] Definisi 4 (Ukuran Peluang)
Ukuran peluang adalah suatu fungsi P : Y →
[ ]
0,1pada (Ω, Y ) yang memenuhi : 1. P
( )
φ =0,P( )
Ω =1.2. Jika A1 ,A2 ,... ∈Y adalah himpunan-himpunan yang saling lepas, yaitu
φ
=
∩ j
i A
A untuk setiap pasangan i ≠ j, maka
( )
∑
∞ = ∞ = = ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ 1 1 P P i i i i A AU
.Pasangan (Ω, Y , P) disebut ruang peluang.
[Grimmett dan Stirzaker, 1992] Definisi 5 (Kejadian Saling Bebas)
Kejadian A dan B dikatakan bebas jika
(
A B) ( ) ( )
PA PBP ∩ = .
Secara umum, jika I adalah himpunan indeks, himpunan kejadian
{
Ai ,i∈I}
dikatakan salingbebas jika
( )
∏
∈ ∈ = ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ J i i J i i A A P PI
untuk setiap himpunan bagian berhingga J dari I. [Grimmett dan Stirzaker, 1992] Definisi 6 (Peubah Acak)
Suatu peubah acak X adalah suatu fungsi
R
X :Ω→ dengan sifat bahwa
( )
{
ω∈Ω :X ω ≤x}
∈Y, untuk setiap x ∈ . R[Grimmett dan Stirzaker, 1992] Peubah acak dinotasikan dengan huruf kapital seperti X, Y, Z. Sedangkan nilai peubah acak dinotasikan dengan huruf kecil seperti x, y, z. Setiap peubah acak mempunyai fungsi sebaran.
Definisi 7 (Fungsi Sebaran)
Fungsi sebaran dari suatu peubah acak X adalah suatu fungsi F :R→
[ ]
0,1yang didefinisikan oleh( ) (
x X x)
FX =P ≤ .[Grimmett dan Stirzaker, 1992] Definisi 8 (Peubah Acak Diskret)
Peubah acak X dikatakan diskret jika nilainya hanya pada himpunan bagian tercacah
{
x1,x2,x3,...}
dariR.
[Grimmett dan Stirzaker, 1992] Suatu himpunan bilangan C disebut tercacah
jika terdiri dari bilangan terhingga atau anggota C dapat dikorespondesikan 1-1 dengan bilangan bulat positif.
Definisi 9 (Fungsi Kerapatan Peluang)
Fungsi kerapatan peluang dari peubah acak diskret
X adalah fungsi f :R→
[ ]
0,1yang diberikan oleh :( ) (
x X x)
X
p =P = .
[Grimmett dan Stirzaker, 1992] Definisi 10 (Peubah Acak Kontinu)
Suatu peubah acak X disebut kontinu jika fungsi sebarannya dapat dinyatakan sebagai
( )
∫
( )
∞ ∈ = x X X x f u du x R F ,dengan f R : → 0,
[
∞)
adalah fungsi yang terintegralkan. Fungsi f disebut fungsi kerapatan peluang dari peubah acak X.[Grimmett dan Stirzaker, 1992] Definisi 11 (Peubah Acak Bebas-Mutual dan
Identik)
Misalkan X1 ,X2 ,...,Xn adalah n peubah acak dengan fungsi kerapatan peluang bersama
(
x x xn)
f 1, 2 ,..., dan fungsi kerapatan peluang
marjinal f1
( )
x1 , f2( )
x2 , ..., fn( )
xn . Peubah acak nX X
X1 , 2 ,..., dikatakan bebas-mutual dan identik
jika dan hanya jika untuk setiap k peubah acak dengan 2≤k≤n dipenuhi
(
xi xi xik) ( ) ( ) ( )
f xi f xi fk xik f 1 , 2 ,..., = 1 1 2 2 ... dan( )
x f( )
x f( )
x f1 = 2 =...= kdimana i1 ,i2 ,...,ik adalah sebarang nilai dari 1,...,n. [Hogg dan Craig, 1995] Definisi 12 (Sebaran Poisson)
Suatu peubah acak X dikatakan menyebar Poisson dengan parameter λ , jika memiliki fungsi kerapatan peluang
( )
, 0,1,2,... ! e -= = x x x p λ λx dengan λ >0.[Hogg dan Craig, 1995] Definisi 13 (Sebaran Gamma)
Suatu peubah acak X dikatakan menyebar Gamma dengan parameter α dan β , dinotasikan Gamma
(
α,β)
, jika memiliki fungsi kerapatan peluang( )
( )
+ − − ∈ Γ = x e x R x f 1 α α 1 xβ , β αdengan α>0,β >0 ,dan Γ
( )
α >0,
dimana( )
=∫
∞ − − Γ 0 1e dy yα y α.
[Hogg dan Craig, 1995] Definisi 14 (Sebaran Binomial Negatif)
Suatu peubah acak N dikatakan menyebar Binomial Negatif dengan parameter r dan p, dinotasikan BN
( )
r,p , jika memliki fungsi kerapatan peluang( )
P[
]
-1 , 0,1,2,... P ⎟⎟ = ⎠ ⎞ ⎜⎜ ⎝ ⎛ + = = = p q n n n r n N n r n N[Hogg dan Craig, 1995]
Poses Stokastik dan Rantai Markov Definisi 15 (Poses Stokastik)
Poses stokastik
{
X( )
t ,t∈T}
adalah suatu himpunan dari peubah acak yang memetakan suatu ruang contohΩ
ke ruang state S.[Ross, 1996] Definisi 16 (Rantai Markov dengan Waktu
Diskret)
Poses stokastik
{
Xn ,n=0,1,2,...}
dengan ruang state{
0 ,1,2,...}
disebut rantai Markov denganwaktu diskret jika untuk setiap n =
{
0 ,1,2,...}
berlaku :(
)
(
)
P ,..., i i, P 1 0 0 1 -n 1 -1 i X j X i X X X j X n n n n n = = = = = = = + +untuk semua kemungkinan nilai dari
{
0,1,2,...}
, , ,..., , 1 1 0 i i − i j∈ i n . [Ross, 1996] Definisi 17 (Rantai Markov Homogen)Rantai Markov disebut homogen jika
(
) (
)
j i n n p i X j X i X j X , 0 1 1 P P = = = = = = + untuk semua n dan i,j∈{
0 ,1,2,...}
.[Ross, 1996]
PEMBAHASAN
1. Sistem Bonus-Malus Swiss
Sistem Bonus-Malus Swiss memiliki 22 state (kelas Pemi), dan Pemi yang harus dibayarkan oleh setiap pemegang polis tergantung pada state mereka berada. Tiap tahun perubahan state setiap pemegang polis hanya ditentukan oleh state
sebelumnya dan banyaknya kecelakaan yang terjadi dalam jangka waktu tersebut. Pada Tabel 1 ditunjukkan suatu neraca Pemi dari persentase Pemi yang dibayarkan dengan Pemi dasar pada state 9 (Dufresne 1988). Misal bx adalah persentase dari
Pemi pada state x Tabel 1. Neraca Pemi (%)
State (x) Pemi (bx) State (x)
Pemi (bx) State (x) Pemi (bx) State (x) Pemi (bx) 0 45 6 75 12 130 18 215 1 50 7 80 13 140 19 230 2 55 8 90 14 155 20 250 3 60 9 100 15 170 21 270 4 65 10 110 16 185 5 70 11 120 17 200
Dari data tersebut diketahui bahwa :
• Terdapat 22 state dari 0, 1, 2,..., 21. Kita katakan kelas 0 sebagai kelas superbonus dan kelas 21 sebagai kelas supermalus.
• Skala Pemi b=
(
b0,b1,...,b21)
, dengan asumsi 211
0 b ... b
b ≤ ≤ ≤ .
Setiap pemegang polis yang baru masuk pada sistem akan ditempatkan pada state 9, dengan pembayaran Pemi dasar (100%) untuk tahun pertamanya.
Menurut aturan untuk tahun-tahun berikutnya, jika state sebelumnya x maka state baru adalah :
x – 1 jika tidak ada kecelakaan x + n.s jika ada n kecelakaan
dengan kondisi bahwa state yang baru tidak boleh kurang dari 0 atau lebih dari 21. Apabila tidak ada kecelakaan yang dilaporkan pada jangka waktu satu tahun maka state akan berkurang sebanyak satu dan untuk setiap kecelakaan yang dilaporkan maka state akan mengalami kenaikan sebanyak s. Nilai s yang
digunakan pada sistem BMS adalah 3, tetapi sejak tahun 1990 berubah menjadi 4 (Dufresne 1995). 2. Sebaran Stasioner
Pada umumnya pencarian sebaran stasioner dilakukan dengan menggunakan matriks peluang transisi. Namun pada sistem BMS, penggunaan matriks peluang transisi tidak efisien karena jumlah
state pada sistem tersebut cukup besar sehingga
untuk memudahkan penentuan sebaran stasioner digunakan suatu formula rekursif.
Jika total langkah pada neraca Pemi untuk tahun t +1 dinotasikan dengan Yt+1 maka didefinisikan : kecelakaan ada jika . kecelakaan ada tidak jika 1 -1 ⎩ ⎨ ⎧ = + sn n Yt (1)
Diasumsikan Y1,Y2,... menyebar bebas-mutual dan identik dengan fungsi kerapatan peluang
( )
y P[
Y y]
, y -1, s ,2s ,3s ,...q = t = = (2) Jika Xt +1 merupakan state pemegang polis pada saat t +1 dan diasumsikan bahwa state untuk tahun berikutnya adalah unik yang ditentukan oleh state pada tahun sebelumnya dan banyaknya kecelakaan pada tahun tersebut, maka Xt +1 didefinisikan 21 jika 21 1 - jika 0 21 0 jika 1 1 1 1 1 ⎪ ⎩ ⎪ ⎨ ⎧ > + = + ≤ + ≤ + = + + + + + t t t t t t t t t Y X Y X Y X Y X X (3)
Karena Xt +1 hanya dipegaruhi oleh Xt maka { Xt }
merupakan suatu rantai Markov.
Fungsi sebaran dari Xt +1 dapat didefinisikan sebagai berikut :
(
) (
)
(
)
(
)
(
)
( )
(
) ( )
(
X x y) ( )
q y y q x y X y q y Y x Y X y Y y Y x X t x x X t x F x y t x y t x y t t t x y t t t t P P P P P 0,1,... 21 0,1,2,..., , P 1 , 1 1 1 1 1 1 1 1 1 1∑
∑
∑
∑
− = − = − = + + − = + + + + − ≤ = ≤ + = = ≤ + = = = ≤ = = = ≤ = + sehingga diperoleh :(
, 1)
(
- ,) ( )
, 0,1,...,21 1 -= = +∑
= x y q t y x F t x F x y (4) dengan F(
21,t+1)
=1.Fungsi sebaran stasioner dari F(x) ditunjukkan dengan :
( )
= lim(
+1)
∞ → F xt x F t ,(
x y t) ( )
q y F x y tlim - , 1 -∑
= ∞ → =( )
y F(
x yt)
q t x y , lim 1 − = ∞ → − =∑
(
-) ( )
, 0,1,...,21 1 - = =∑
= x y q y x F x y (5) dengan F( )
21=1. Persamaan (5) dapat diuraikan sebagai berikut:( ) (
) ( )
(
) ( )
(
) ( ) ( )
(
) ( )
(
) ( ) ( )
(
-) ( )
. 1 1 1 -1 1 -1 1 0 0 0 ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − − = + ⇔ − = − + ⇔ + − + =∑
∑
∑
= = = x y x y x y y q y x F x F q x F y q y x F x F q x F y q y x F q x F x FRumus di atas merupakan rumus rekursif, tetapi karena nilai F
( )
0 tidak diketahui maka nilai F( )
xUntuk mencari nilai F
( )
x dapat dibangkitkan fungsi-fungsi pembantu A( )
x , x = 0, 1, 2, … yang sebanding dengan nilai-nilai F( )
xdengan memilih sembarang A
( )
0 >0, sehingga :(
) ( ) ( )
(
) ( )
⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ∑ = − − = + x y A x y q y x A q x A 0 -1 1 1.
Rumus rekursif di atas dapat ditulis dengan menggunakan persamaan algoritma sebagai berikut (Dufresne 1988): 1. Tentukan A(0) = 1 2. Hitung untuk x = 0, 1, 2, ... , 21
(
) ( ) ( )
(
) ( )
⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ − − = +∑
= x y y q y x A x A q x 0 -1 1 1 A (6) 3. Hitung( )
( )
( )
untuk 0,1,2,...,21 21 = = x A x A x F (7)4. Selisih dari F
( ) (
x −F x−1)
merupakan fungsi kerapatan peluang f( )
x .Jika diasumsikan untuk setiap pemegang polis dengan frekuensi harapan banyaknya kecelakaan λ maka peluang dia mengalami n kecelakaan mengikuti sebaran Poisson dengan parameter λ > 0, yaitu :
[
]
, 0,1,2... ! P = = − n= n e n Nt λλn (8) dimana Nt adalah peubah acak dari banyaknyakecelakaan.
Jika fungsi peluang q
( )
y menyebar Poisson dengan parameter λ dan s = 3 maka :( )
− =[
=]
=e−λ t N q 1 P 0( ) ( ) ( )
0 =q1 =q2 =0 q( )
=[
=]
=λ −e λ t N q3 P 1( ) ( )
4 = q5 =0 q( )
6 =P[
Nt =2]
=λ2e−λ 2! q (9) ...dan seterusnya.Sedangkan jika fungsi peluang q
( )
y menyebar Poisson dengan parameter λ dan s = 4 maka :( )
− =[
=]
=e−λ t N q 1 P 0( ) ( ) ( ) ( )
0 =q1 =q2 =q3 =0 q( )
=[
=]
=λ −e λ t N q4 P 1( ) ( ) ( )
5 =q6 =q7 =0 q( )
8 =P[
Nt =3]
=λ2e−λ 2! q(10) ...dan seterusnya.
Misalkan diambil 6 tingkatan resiko (Dufresne 1988), yaitu λ=0,05i,i=1 ,2,... ,6 maka untuk masing-masing nilai λ , penentuan sebaran kumulatifnya dapat dilakukan dengan rumus rekursif pada persamaan (6) dan (7).
Penghitungan tersebut dapat dilakukan menggunakan Microsoft Excel. Penjabaran rumus rekursif A
( )
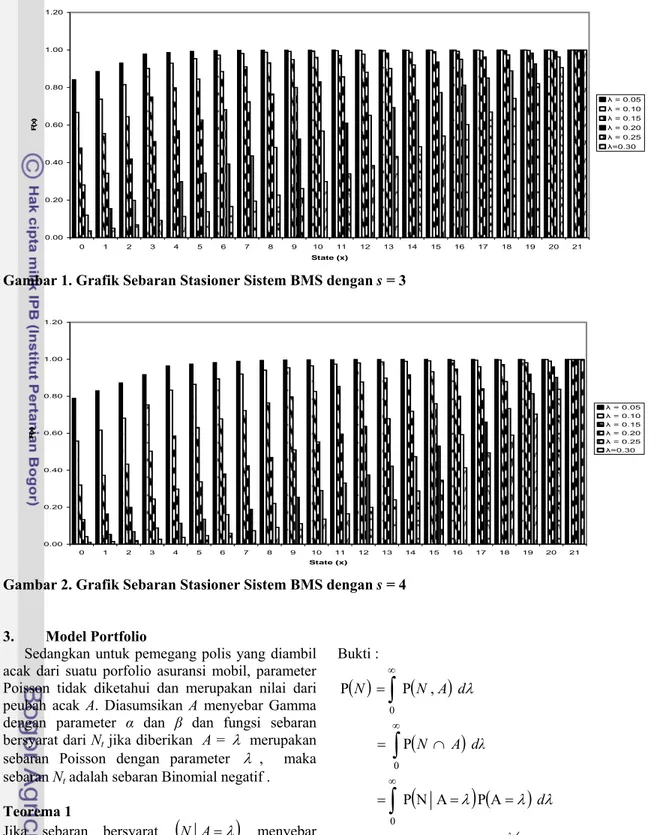
x untuk s = 3 dan s = 4 ditunjukkan pada Lampiran 1 dan Lampiran 2. Hasil penghitungan sebaran stasioner dan fungsi kerapatan peluang untuk s = 3 dan s = 4 ditunjukkan pada Lampiran 3 dan Lampiran 4. Sedangkan grafik sebarannya untuk s = 3 dan s = 4 digambarkan pada Gambar 1 dan Gambar 2.Dari hasil yang diperoleh dapat diketahui bahwa nilai sebaran stasioner untuk s = 3 lebih besar dari nilai sebaran stasioner untuk s = 4. Berdasarkan Gambar 1 dan Gambar 2 dapat dilihat bahwa kecenderungan pemegang polis berada di
state 0 semakin besar untuk nilai λ yang semakin kecil. Hal ini sesuai dengan asumsi yang digunakan bahwa λ adalah frekuensi harapan dari banyaknya kecelakaan, sehingga semakin sedikit banyaknya kecelakaan yang dilaporkan maka pemegang polis akan semakin mendekati state 0.
0.00 0.20 0.40 0.60 0.80 1.00 1.20 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 State (x) F( x ) λ = 0.05 λ = 0.10 λ = 0.15 λ = 0.20 λ = 0.25 λ=0.30
Gambar 1. Grafik Sebaran Stasioner Sistem BMS dengan s = 3
0.00 0.20 0.40 0.60 0.80 1.00 1.20 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 State (x) F( x ) λ = 0.05 λ = 0.10 λ = 0.15 λ = 0.20 λ = 0.25 λ=0.30
Gambar 2. Grafik Sebaran Stasioner Sistem BMS dengan s = 4 3. Model Portfolio
Sedangkan untuk pemegang polis yang diambil acak dari suatu porfolio asuransi mobil, parameter Poisson tidak diketahui dan merupakan nilai dari peubah acak A. Diasumsikan A menyebar Gamma dengan parameter α dan β dan fungsi sebaran bersyarat dari Nt jika diberikan A = λ merupakan
sebaran Poisson dengan parameter λ , maka sebaran Nt adalah sebaran Binomial negatif .
Teorema 1
Jika sebaran bersyarat
(
N A=λ)
menyebar Poisson dengan parameter λ serta A menyebar Gamma(
α ,β)
, maka N menyebar Binomial negatif dengan parameter ⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ +1 1 , β α . Bukti :
( )
N P(
N ,A)
dλ P 0∫
∞ =(
)
∫
∞ ∩ = 0 P N A dλ(
N A λ)
P(
A λ)
dλ P 0∫
∞ = = =( )
∫
∞ − − − Γ = 0 1 ! λ β α λ λ α β λ α λ d e n e n( )
∫
∞ − ⎜⎜⎝⎛ + ⎟⎟⎠⎞ + − Γ = 0 1 1 1 ! λ β λ α α β λ d α n e n( )
∫
∞ − + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − Γ = 0 1 1 1 ! 1 λ λ β α β λ α e d α n n.
Misalkan : . 1 1 1 1 1 1 λ β β λ β λ d dt t t ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + = ⇔ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + = Sehingga :( )
( )
⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + Γ = − + ∞ −∫
β β β α α α 1 1 1 1 ! 1 P 1 0 dt t e n N n t( )
e t dt n n n t ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + Γ = + −+ − ∞ −∫
β β β α α α α 1 1 1 1 1 ! 1 1 1 0( )
e t dt n n n t∫
∞ + − + − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + Γ = 0 1 1 1 ! 1 α α α β β α ( )( )
∫
∞ − + − + − Γ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + = 0 1 ! 1 1 e t dt n n t n α α α β α β ( )( )
α β(
α)
β α α + Γ Γ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + = + − n n n ! 1 1 ( )(
)
( )
α α β α α β β Γ + Γ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + = + − ! 1 n n n(
)
( )(
)
( )( )
(
)
( )
(
)
( ) n n n n n n n n − + − + − + − + Γ + Γ = Γ + Γ + = β β α α α β β α β α α α α 1 ! ! 1(
)
(
)
(
) (
)
α α β β β α α β β β α α ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − + = + + − − + = − − − − 1 1 1 1 1 1 1 ! 1 ! ! 1 n n n n n n α β β β α α ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − + = 1 1 1 1 1 n n(
p)
n p n − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − + = 1 1 1 α α α dimana : ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + = = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + = 1 -1 dan 1 1 β β β q p p . terbukti Sebaran Binomial negatif dengan parameter⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ +1 1 , β
α memiliki nilai harapan dan ragam sebagai berikut :
[ ]
αβ ENt = (11) dan[ ]
2 VarNt =αβ +αβ.
(12) Fungsi sebaran stasioner dan transien jika diberikan A = λ dinotasikan F( )λ( )
x dan( )
x t Fλ , sehingga :( )
x F( )λ( ) ( )
x dU λ F 0∫
∞ = (13) dan( )
=∫
∞ ( )( ) ( )
0 , ,t F λ xt dU λ x F(14)
dimana U
(
x ;α,β)
merupakan sebaran Gamma. Jika fungsi peluang q( )
y menyebar Binomial Negatif dengan parameter ⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ +1 1 , β α dan s = 3 maka :
( )
[
]
β ⎟⎟α ⎠ ⎞ ⎜⎜ ⎝ ⎛ + = = = − 1 1 0 P 1 Nt q( ) ( ) ( )
0 =q1 =q 2 =0 q( )
[
]
(
)
⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − = = = 1 1 1 ! 1 ! 1 P 3 β β α β α α t N q( ) ( )
4 =q5 =0q
...dan seterusnya.
Sedangkan jika fungsi peluang q
( )
y menyebar binomial Negatif dengan parameter ⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ +1 1 , β α dan s = 4 maka :
( )
[
]
β ⎟⎟α ⎠ ⎞ ⎜⎜ ⎝ ⎛ + = = = − 1 1 0 P 1 Nt q( ) ( ) ( ) ( )
0 =q1 =q 2 =q3 =0 q( )
[
]
(
)
⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − = = = 1 1 1 ! 1 ! 1 P 4 β β α β α α t N q( ) ( ) ( )
5 =q6 =q7 =0 q ...dan seterusnya.Penghitungan sebaran stasioner F
( )
x untuk model portfolio dapat dilakukan juga dengan menggunakan rumus rekursif pada persamaan (6) dan (7) dengan asumsi bahwa q( )
y menyebar Binomial Negatif dengan parameter ⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ +1 1 , β α .
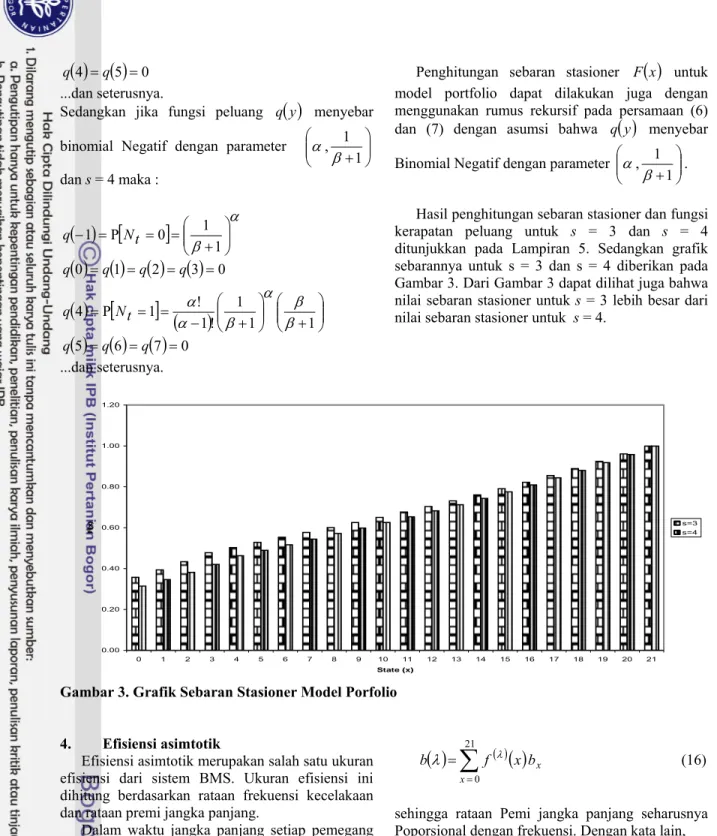
Hasil penghitungan sebaran stasioner dan fungsi kerapatan peluang untuk s = 3 dan s = 4 ditunjukkan pada Lampiran 5. Sedangkan grafik sebarannya untuk s = 3 dan s = 4 diberikan pada Gambar 3. Dari Gambar 3 dapat dilihat juga bahwa nilai sebaran stasioner untuk s = 3 lebih besar dari nilai sebaran stasioner untuk s = 4.
0.00 0.20 0.40 0.60 0.80 1.00 1.20 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 State (x) F( x ) s=3 s=4
Gambar 3. Grafik Sebaran Stasioner Model Porfolio 4. Efisiensi asimtotik
Efisiensi asimtotik merupakan salah satu ukuran efisiensi dari sistem BMS. Ukuran efisiensi ini dihitung berdasarkan rataan frekuensi kecelakaan dan rataan premi jangka panjang.
Dalam waktu jangka panjang setiap pemegang polis dapat membayar rata-rata dari Poporsi Pemi untuk setiap rataan frekuensi. Hal ini sesuai dengan kenyataan bahwa kecelakaan tidak dapat diambil dari suatu laporan dan diasumsikan bahwa setiap rataan Pemi tidak sama untuk setiap asuransi.
Rataan Pemi jangka panjang merupakan fungsi Poisson yang dinotasikan b
( )
λ , yang ditunjukkan dengan( )
∑
( )( )
= = 21 0 x x b x f bλ λ (16) sehingga rataan Pemi jangka panjang seharusnya Poporsional dengan frekuensi. Dengan kata lain,( )
( )
λ λb
db seharusnya sama dengan
λ λ
d sehingga
nilai efisiensi asimtotik dapat didefinisikan (Dufresne 1995) :
( ) ( )
( )
λ λ λ λ λ η d db b = (17)( ) ( )
λ λ λ ' b b = .Dengan menggunakan pendekatan turunan maka dapat dituliskan :
( ) ( )
(
) ( )
⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + − ≈ → h b h b b h λ λ λ λ λ η 0 lim .Misalkan diambil suatu nilai h yang sangat kecil (h = 0,01) maka:
( ) ( )
(
) ( )
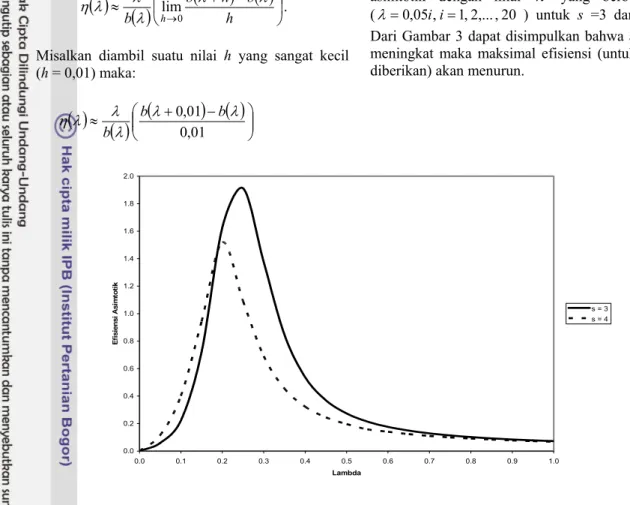
⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − ≈ 01 , 0 01 , 0 λ λ λ λ λ η b b b dengan λ > 0.Gambar 3 menunjukkan bahwa efisiensi asimtotik dengan nilai λ yang berbeda-beda (λ=0,05i,i=1 ,2,... ,20 ) untuk s =3 dan s = 4. Dari Gambar 3 dapat disimpulkan bahwa apabila s meningkat maka maksimal efisiensi (untuk s yang diberikan) akan menurun.
0.0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8 2.0 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 Lambda E fi s ie n s i A s im to ti k s = 3 s = 4
Gambar 4. Grafik Efisiensi Asimtotik dari Sistem BMS
SIMPULAN
Sistem Bonus-Malus Swiss (BMS) memiliki 22
state yang memiliki sifat Markov. Karena sebaran
stasioner pada sistem ini sangat sulit diperoleh secara analitik, maka digunakan suatu metode rekursif. Sebaran stasioner tersebut diberikan oleh :
( )
( )
( )
, 0 ,1,2,...,21, 21 = = x A x A x F dengan(
) ( ) ( )
(
) ( )
⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ − − = +∑
= x y y q y x A x A q x 0 -1 1 1 A .Fungsi A
( )
x adalah fungsi pembantu dengan sebarang nilai A( )
0 >0.Sebaran stasioner diperoleh berdasarkan 2 asumsi, yaitu :
a) Banyaknya kecelakaan (n) ~ Poisson (λ ) dengan λ = 0,05i , i = 0, 1 , 2 , ..., 6.
b) Banyaknya kecelakaan ~ Binomial Negatif. Untuk kejadian dengan banyaknya kecelakaan yang menyebar Poisson (λ ) dengan λ = 0,05i , i = 0, 1 , 2 , ..., 6, diperoleh hasil bahwa untuk state tertentu (x), makin besar λ maka Fλ
( )
x makin kecil. Nilai sebaran stasioner ini juga akan semakin kecil jika penalti yang diberikan semakin ketat yang dicerminkan oleh step (s) yang semakin besar.Sedangkan untuk kejadian dengan banyaknya kecelakaan yang menyebar Binomial Negatif, diperoleh hasil bahwa untuk state tertentu (x) nilai sebaran stasioner juga akan semakin kecil jika step (s) semakin besar.
Diperoleh juga hasil bahwa nilai dari maksimal efisiensi asimtotik akan semakin besar jika step (s) semakin kecil.
Berdasarkan penghitungan sebaran stasioner dan nilai dari maksimal efisiensi asimtotik, dapat
disimpulkan bahwa sistem BMS yang lama (s = 3) lebih baik dibanding dengan sistem BMS yang baru (s = 4).
DAFTAR PUSTAKA
Dufresne, F. 1988. Distributions Stationnaires d’un Systeme Bonus-Malus et Pobabilite de Ruine.
ASTIN Bulletin, 18:31-46.
Dufresne, F. 1995. The Efficiency of The Swiss Bonus-Malus System. Bulletin of The Swiss
Association of Actuaries. 1:29-42.
Grimmett, G. R. dan D. R. Stirzaker. 1992.
Pobability and Random Pocesses. Ed. Ke-2.
Clarendon Pess. Oxpord.
Hogg, R. V. dan A. T. Craig. 1995. Introduction to
Mathematic Statistics. Ed. Ke-5. Pentice Hall.
Englewood Cliffs. New Jersey.
Ross, S. M. 1996. Stochastic Pocesses. Ed. Ke-2. John Willey & Sons. New York.
Lampiran 1. Penjabaran Rumus Rekursif untuk menghitung A
(
x+1)
jika s = 3 1. Diket : A( )
0 =1. 2. Jika x = 0 maka :( ) ( ) ( )
(
) ( )
( ) ( )
1[
0(
( ) ( )
0 . 0)
]
[ ]
1 . 1 0 0 . 0 1 1 1 λ λ e e q A A q y Ax y q y A q A = = − − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ∑ = − − − = 3. Jika x = 1 maka :( ) ( ) ( )
(
) ( )
( ) ( )
1[
1(
( ) ( ) ( ) ( )
1. 0 0. 1)
]
[ ]
2 . 1 1 0 . 1 1 1 2 λ λ λ e e e q A q A A q y Ax y q y A q A = = + − − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ∑ = − − − = 4. Jika x = 2 maka :( ) ( ) ( )
(
) ( )
( ) ( )
1[
2(
( ) ( ) ( ) ( ) ( ) ( )
2. 0 1. 1 0. 2)
]
[ ]
. 1 . 2 1 1 3 3 2 2 0 λ λ λ e e e q A q A q A A q y q y x A A q A y = = + + − − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − − − =∑
= 5. Jika x = 3 maka :( ) ( ) ( )
(
) ( )
( ) ( )
[
(
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
)
]
(
)
[
1.] [
]
. 3 . 0 2 . 1 1 . 2 0 . 3 3 1 1 . 3 1 1 4 4 3 3 3 0 λ λ λ λ λ λ λ λ λ λ − = − = − = + + + − − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − − − = − − =∑
e e e e e e e q A q A q A q A A q y q y x A A q A y 6. Jika x = 4 maka :( ) ( ) ( )
(
) ( )
( ) ( )
[
(
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
)
]
(
) (
(
)
)
[
.] [
2]
2 . 4 . 0 3 . 1 2 . 2 1 . 3 0 . 4 4 1 1 . 4 1 1 5 5 4 4 4 0 λ λ λ λ λ λ λ λ e λ e λe e e λ e λe e q A q A q A q A q A A q y q y x A A q A y − = − = − − = + + + + − − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − − − = − =∑
7. Jika x = 5 maka :( ) ( ) ( )
(
) ( )
( ) ( )
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
(
) (
)
[
]
[
(
)
]
. 2 3 6 3 5 . 2 2 5 5 . 0 4 . 1 3 . 2 2 . 3 1 . 4 0 . 5 5 1 1 5 0 . 5 1 1 6 λ λ λ λ λ λ λ λ λ λ λ λ λ λ e e e e e e e e e e q A q A q A q A q A q A A q y Ax y q y A q A − = − = − − − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + + + + − − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ∑ = − − − =8. Jika x = 6 maka ;
( ) ( ) ( )
(
) ( )
( ) ( )
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
(
) (
)
. ! 2 4 ! 2 4 ! 2 . 1 . 3 6 . 0 5 . 1 4 . 2 3 . 3 2 . 4 1 . 5 0 . 6 6 1 1 . 6 1 1 7 2 3 7 2 2 6 2 3 2 6 6 0 λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ − − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + − − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + + + + + − − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − − − = − − − =∑
e e e e e e e e e e e e q A q A q A q A q A q A q A A q y q y x A A q A y 9. Jika x = 7 maka :( ) ( ) ( )
(
) ( )
( ) ( )
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( ) ( )
(
)
(
)
(
)
. ! 2 2 5 ! 2 2 5 ! 2 ! 2 4 ! 2 . ! 2 4 7 . 0 6 . 1 5 . 2 4 . 3 3 . 4 2 . 5 1 . 6 0 . 7 7 1 1 7 0 . 7 1 1 8 2 2 4 8 2 2 3 7 2 2 3 2 3 7 2 4 2 3 7 λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + − − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + − − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + + + + + + − − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ∑ = − − − = − − − − e e e e e e e e e e e e e e e e e e e q A q A q A q A q A q A q A q A A q y Ax y q y A q A 10. Jika x = 8 maka :( ) ( ) ( )
(
) ( )
( ) ( )
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
(
)
(
)
(
)
. 3 ! 2 3 6 3 ! 2 3 6 ! 2 2 ! 2 2 5 ! 2 . 2 ! 2 2 5 8 . 0 7 . 1 6 . 2 5 . 3 4 . 4 3 . 5 2 . 6 1 . 7 0 . 8 8 1 1 . 8 1 1 9 2 2 2 5 9 2 2 4 8 2 2 4 2 2 4 8 2 2 5 2 2 4 8 8 0 λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ e e e e e e e e e e e e e e e e e e e e e e e q A q A q A q A q A q A q A q A q A A q y q y x A A q A y + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + − − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + − − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + + + + + + + − − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − − − = − − − =∑
11. Jika x = 9 maka :
( ) ( ) ( )
(
) ( )
( ) ( )
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
(
)
(
)
(
)
. ! 3 6 ! 2 4 7 ! 3 6 ! 2 4 7 ! 3 ! 2 3 3 ! 2 3 6 ! 3 . 1 ! 2 . 3 3 ! 2 3 6 9 . 0 8 . 1 7 . 2 6 . 3 5 . 4 4 . 5 3 . 6 2 . 7 1 . 8 0 . 9 9 1 1 . 9 1 1 10 3 2 2 3 2 6 10 3 2 2 2 5 9 3 2 2 2 5 2 2 2 5 9 3 2 3 2 6 2 2 2 5 9 9 0 λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + + − − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + − − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + + + + + + + + − − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − − − = − − − − − =∑
e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e q A q A q A q A q A q A q A q A q A q A A q y q y x A A q A y 12. Jika x = 10 maka :( ) ( ) ( )
(
) ( )
( ) ( )
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
( ) ( )
(
)
. ! 2 3 2 ! 3 3 2 3 2 10 4 ! 2 2 5 7 8 11 ! 2 3 2 ! 3 3 2 2 2 10 3 ! 2 2 5 6 8 10 ! 3 3 ! 2 3 3 ! 2 2 ! 2 3 2 2 4 6 ! 3 3 2 2 6 3 ! 2 2 4 6 7 10 ! 3 3 . ! 2 2 4 ! 2 2 3 4 7 ! 3 3 2 2 6 3 ! 2 2 4 6 7 10 10 . 0 9 . 1 8 . 2 7 . 3 6 . 4 5 . 5 4 . 6 3 . 7 2 . 8 1 . 9 0 . 10 10 1 1 10 0 . 10 1 1 11 ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + − − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − − − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − = ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ + + + + + + + + + + − − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ∑ = − − − = λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e q A q A q A q A q A q A q A q A q A q A q A A q y Ax y q y A q A13. Jika x = 11 maka :
( ) ( ) ( )
(
) ( )
( ) ( )
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
(
)
. 3 ! 2 3 6 2 ! 3 3 3 4 2 15 5 ! 2 2 6 8 9 12 3 ! 2 3 6 ! 3 3 3 3 2 15 4 ! 2 2 6 7 9 11 ! 3 3 ! 2 3 2 4 ! 2 2 3 ! 2 3 2 3 2 5 7 ! 2 3 2 ! 3 3 2 3 2 10 4 ! 2 2 5 7 8 11 ! 3 3 . 2 ! 2 2 2 5 2 ! 2 2 2 4 5 8 ! 2 3 2 ! 3 3 2 3 2 10 4 ! 2 2 5 7 8 11 11 . 0 10 . 1 9 . 2 8 . 3 7 . 4 6 . 5 5 . 6 4 . 7 3 . 8 2 . 9 1 . 10 0 . 11 11 1 1 11 0 . 11 1 1 12 λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − + ⎟⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎝ ⎛ − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − = ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ + + + + + + + + + + + − − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ∑ = − − − = e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e q A q A q A q A q A q A q A q A q A q A q A q A A q y Ax y q y A q A14. Jika x = 12 maka :
( )
( ) ( )
(
) ( )
( ) ( )
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( ) ( )
(
)
. ! 4 4 3 4 2 ! 2 3 12 3 ! 3 3 4 5 2 21 6 ! 2 2 7 9 10 13 ! 4 4 3 4 ! 2 3 12 2 ! 3 3 4 3 2 21 5 ! 2 2 7 8 10 12 ! 4 4 2 ! 3 3 ! 2 3 3 5 ! 2 2 3 3 ! 2 3 3 4 2 6 8 3 ! 2 3 6 2 ! 3 3 3 4 2 15 5 ! 2 2 6 8 9 12 ! 4 4 . 1 ! 3 3 . 3 ! 2 2 2 3 6 2 3 2 ! 2 2 3 5 6 9 3 ! 2 3 6 2 ! 3 3 3 4 2 15 5 ! 2 2 6 8 9 12 12 . 0 11 . 1 10 . 2 9 . 3 8 . 4 7 . 5 6 . 6 5 . 7 4 . 8 3 . 9 2 . 10 1 . 11 0 . 12 12 1 1 12 0 . 12 1 1 13 ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ − + + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − + ⎟⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎝ ⎛ − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − = ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ + + + + + + + + + + + + − − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ∑ = − − − = λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e q A q A q A q A q A q A q A q A q A q A q A q A q A A q y Ax y q y A q A15. Jika x = 13 maka :
( ) ( ) ( )
(
) ( )
( ) ( )
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
(
)
. ! 2 ! 2 ! 3 2 ! 4 2 10 ! 2 20 ! 3 5 28 ! 2 8 11 ! 2 ! 2 ! 3 2 ! 4 2 10 ! 2 20 ! 3 5 28 ! 2 8 11 ! 4 ! 3 ! 3 ! 2 ! 2 ! 2 4 ! 2 ! 3 6 ! 2 4 7 ! 4 4 ! 2 12 ! 3 4 21 ! 2 7 10 ! 4 . ! 3 ! 2 ! 2 4 ! 3 6 ! 2 4 7 ! 4 4 ! 2 12 ! 3 4 21 ! 2 7 10 13 . 0 12 . 1 11 . 2 10 . 3 9 . 4 8 . 5 7 . 6 6 . 7 5 . 8 4 . 9 3 . 10 2 . 11 1 . 12 0 . 13 13 1 1 . 13 1 1 14 4 4 4 2 3 3 3 4 3 6 2 7 2 10 14 4 4 4 3 2 3 3 3 5 2 6 2 9 13 4 4 3 3 4 2 3 6 2 4 3 2 3 5 2 9 4 3 2 3 3 3 5 2 6 2 9 13 4 3 4 2 2 3 7 3 2 2 3 2 6 10 4 3 2 3 3 3 5 2 6 2 9 13 13 0 λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − = ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ + − + − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − = ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ + + + + + + + + + + + + + − − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − − − = − − − − − − − − − =∑
e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e q A q A q A q A q A q A q A q A q A q A q A q A q A q A A q y q y x A A q A y16. Jika x = 14 maka
( ) ( ) ( )
(
) ( )
( ) ( )
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
(
)
. ! 2 3 ! 2 ! 2 3 ! 3 6 ! 4 3 20 ! 2 30 ! 3 6 36 ! 2 9 12 ! 2 3 ! 2 ! 2 3 ! 3 6 ! 4 3 20 ! 2 30 ! 3 6 36 ! 2 9 12 ! 4 ! 3 2 ! 3 ! 2 ! 2 ! 2 2 ! 2 5 ! 2 ! 2 2 ! 3 2 10 ! 2 5 8 ! 2 ! 2 3 2 ! 4 2 10 ! 2 20 ! 3 5 28 ! 2 8 11 ! 4 . ! 3 2 ! 2 ! 2 2 5 ! 2 2 ! 3 2 10 ! 2 5 8 ! 2 ! 2 ! 3 2 ! 4 2 10 ! 2 20 ! 3 5 28 ! 2 8 11 14 . 0 13 . 1 12 . 2 11 . 3 10 . 4 9 . 5 8 . 6 7 . 7 6 . 8 5 . 9 4 . 10 3 . 11 2 . 12 1 . 13 0 . 14 14 1 1 . 14 1 1 15 4 4 4 2 4 3 3 4 3 5 3 7 2 8 2 11 15 4 4 4 4 2 3 3 3 4 3 6 2 7 2 10 14 4 4 4 3 4 4 3 3 7 2 4 4 2 3 3 3 6 2 10 4 4 4 2 3 3 3 4 3 6 2 7 2 10 14 4 2 3 5 2 2 2 4 8 3 3 3 2 4 2 7 11 4 4 4 2 3 3 3 4 3 6 2 7 2 10 14 14 0 ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − = ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − − ⎟⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − − ⎟⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − = ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ + + + + + + + + + + + + + + − − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − − − = − − − − − − − =∑
λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ λ e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e q A q A q A q A q A q A q A q A q A q A q A q A q A q A q A A q y q y x A A q A y17. Jika x = 15 maka :