ABSTRAK
Fransiska Dwi Handriyani. 2013. Metode Banyak Langkah Linear
untuk Menyelesaikan Masalah Nilai Awal dalam Persamaan Diferensial Biasa.
Skripsi. Program Studi Matematika, Jurusan Matematika, Fakultas Sains dan Teknologi, Universitas Sanata Dharma, Yogyakarta.
Topik yang dibahas dalam skripsi ini adalah menyelesaikan masalah nilai
awal dalam persamaan diferensial biasa dengan menggunakan metode banyak
langkah linear. Pembahasan mengenai metode tersebut dalam skripsi ini dibatasi
untuk persamaan diferensial linear tingkat pertama. Metode banyak langkah linear
menggunakan beberapa nilai sebelumnya, yaitu ��, ��−1, ��−2, … untuk
menentukan nilai ��+1. Masalah nilai awal mempunyai satu nilai awal, sedangkan
metode banyak langkah linear memerlukan beberapa nilai sebelumnya untuk
menentukan nilai ��+1. Oleh karena itu, digunakan metode lain untuk menentukan
nilai-nilai tersebut, di antaranya yaitu dengan menggunakan metode Euler dan
metode Deret Taylor.
Metode banyak langkah linear dapat dibuat dalam bermacam-macam
bentuk, tergantung nilai yang diberikan pada koefisien-koefisiennya. Suatu
metode banyak langkah linear akan menghasilkan penyelesaian yang akurat jika
metode tersebut konvergen. Oleh karena itu, metode tersebut harus diuji dulu
konvergensinya. Suatu metode banyak langkah linear adalah konvergen jika dan
ABSTRACT
Fransiska Dwi Handriyani. 2013. Linear Multistep Methods to Solve
Initial Value Problems in Ordinary Differential Equations. A Thesis.
Mathematics Study Program, Department of Mathematics, Faculty of Science and Technology, Sanata Dharma University, Yogyakarta.
The topic covered in this thesis is linear multistep methods for solving
initial value problems in ordinary differential equations. The discussion about
these methods, is limited to first order linear differential equations. Linear
multistep methods use some previous values, that are ��, ��−1, ��−2, … to
determine the value of ��+1. Initial value problems have one initial value, while
linear multistep methods require some previous values to determine the value of
��+1. Therefore, other methods are used to determine these values, among which
are the Euler method and Taylor Series method.
Linear multistep methods can be made in a variety of forms, depending on
the value assigned to the coefficients. They will produce accurate solution if they
are convergence. Therefore, the convergence of the method should be tested first.
A linear multistep method is convergent if and only if the method is consistent
i
METODE BANYAK LANGKAH LINEAR UNTUK
MENYELESAIKAN MASALAH NILAI AWAL DALAM
PERSAMAAN DIFERENSIAL BIASA
Skripsi
Diajukan Untuk Memenuhi Salah Satu Syarat
Memperoleh Gelar Sarjana Sains
Program Studi Matematika
Oleh:
Fransiska Dwi Handriyani 093114010
PROGRAM STUDI MATEMATIKA
JURUSAN MATEMATIKA
FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA
YOGYAKARTA
iv
HALAMAN PERSEMBAHAN
“Dan siapa pun yang memaksa engkau berjalan sejauh satu mil, berjalanlah bersama dia sejauh dua mil.”
(Matius 5:41)
“Barangsiapa tidak memikul salibnya dan mengikut Aku, ia tidak layak
bagi-Ku.” (Matius 10:38)
Karya ini aku persembahkan untuk orang-orang terkasih:
Keluargaku tercinta
Teman-teman Matematika’09
Teman-teman OMK
vi
ABSTRAK
Fransiska Dwi Handriyani. 2013. Metode Banyak Langkah Linear
untuk Menyelesaikan Masalah Nilai Awal dalam Persamaan Diferensial Biasa.
Skripsi. Program Studi Matematika, Jurusan Matematika, Fakultas Sains dan Teknologi, Universitas Sanata Dharma, Yogyakarta.
Topik yang dibahas dalam skripsi ini adalah menyelesaikan masalah nilai
awal dalam persamaan diferensial biasa dengan menggunakan metode banyak
langkah linear. Pembahasan mengenai metode tersebut dalam skripsi ini dibatasi
untuk persamaan diferensial linear tingkat pertama. Metode banyak langkah linear
menggunakan beberapa nilai sebelumnya, yaitu ��, ��−1, ��−2, … untuk
menentukan nilai ��+1. Masalah nilai awal mempunyai satu nilai awal, sedangkan
metode banyak langkah linear memerlukan beberapa nilai sebelumnya untuk
menentukan nilai ��+1. Oleh karena itu, digunakan metode lain untuk menentukan
nilai-nilai tersebut, di antaranya yaitu dengan menggunakan metode Euler dan
metode Deret Taylor.
Metode banyak langkah linear dapat dibuat dalam bermacam-macam
bentuk, tergantung nilai yang diberikan pada koefisien-koefisiennya. Suatu
metode banyak langkah linear akan menghasilkan penyelesaian yang akurat jika
metode tersebut konvergen. Oleh karena itu, metode tersebut harus diuji dulu
konvergensinya. Suatu metode banyak langkah linear adalah konvergen jika dan
vii
ABSTRACT
Fransiska Dwi Handriyani. 2013. Linear Multistep Methods to Solve
Initial Value Problems in Ordinary Differential Equations. A Thesis.
Mathematics Study Program, Department of Mathematics, Faculty of Science and Technology, Sanata Dharma University, Yogyakarta.
The topic covered in this thesis is linear multistep methods for solving
initial value problems in ordinary differential equations. The discussion about
these methods, is limited to first order linear differential equations. Linear
multistep methods use some previous values, that are ��, ��−1, ��−2, … to
determine the value of ��+1. Initial value problems have one initial value, while
linear multistep methods require some previous values to determine the value of
��+1. Therefore, other methods are used to determine these values, among which
are the Euler method and Taylor Series method.
Linear multistep methods can be made in a variety of forms, depending on
the value assigned to the coefficients. They will produce accurate solution if they
are convergent. Therefore, the convergence of the method should be tested first. A
linear multistep method is convergent if and only if the method is consistent and
viii
KATA PENGANTAR
Puji syukur penulis panjatkan kepada Tuhan Yesus yang selalu memberikan
hikmat dan menyertai penulis sehingga mampu menyelesaikan skripsi ini dengan
baik dan lancar. Skripsi ini dimaksudkan untuk memenuhi salah satu syarat dalam
menyelesaikan pendidikan Strata 1 (S1) dan memperoleh gelar Sarjana Sains pada
Program Studi Matematika di Universitas Sanata Dharma Yogyakarta.
Penulis menyadari bahwa proses penulisan skripsi ini tidak lepas dari
bantuan serta dukungan dari banyak pihak. Oleh karena itu, pada kesempatan ini
penulis sudah selayaknya mengucapkan terima kasih kepada:
1. Lusia Krismiyati Budiasih, S.Si., M.Si., selaku Ketua Program Studi
Matematika atas dukungannya.
2. Hartono, S.Si., M.Sc., Ph.D., selaku dosen pembimbing yang telah dengan
sabar memberikan bimbingan, pengetahuan baru, dan saran-saran kepada
penulis selama proses penulisan skripsi.
3. Bapak, Ibu, dan Romo, dosen-dosen yang telah memberi pengetahuan kepada
penulis selama proses perkuliahan.
4. Markus Ngatemin (Kakek) dan Martina Martinah (Nenek) terima kasih atas
cinta dan jerih payahnya. Martinus Tumar (Bapak), Yordana Riyani (Ibu),
Mas Eka, Dek Tri, dan Dek Rina, serta saudara-saudara yang telah
ix
5. Teman-teman Matematika’09: Yohana, Faida, Etik, Rossi, Jojo, Sekar,
Erlika, dan Dimas, terima kasih untuk semangat dan keceriaan yang selalu
diberikan kepada penulis. Kalian sahabat-sahabat yang hebat.
6. Teman-teman OMK dan adik-adik PASAYES, terima kasih atas kebersamaan
dan semangat yang selalu diberikan kepada penulis.
7. Santi, Mbak Cicil, dan Nica, terima kasih sudah menjadi teman untuk berbagi
cerita dan menumbuhkan semangat.
8. Semua pihak yang tidak dapat disebutkan satu per satu yang telah terlibat
dalam proses penulisan skripsi ini.
Penulis menyadari bahwa masih ada kekurangan dalam penulisan skripsi
ini. Oleh karena itu, penulis mengharapkan kritik dan saran demi penyempurnaan
skripsi ini. Akhirnya, penulis berharap semoga skripsi ini dapat bermanfaat bagi
para pembaca.
Yogyakarta, 17 Desember 2013
DAFTAR ISI
Halaman
HALAMAN JUDUL... i
HALAMAN PERSETUJUAN PEMBIMBING... ii
HALAMAN PENGESAHAN... iii
HALAMAN PERSEMBAHAN... iv
PERNYATAAN KEASLIAN KARYA... v
ABSTRAK... vi
ABSTRACT... vii
KATA PENGANTAR... viii
PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH... x
DAFTAR ISI... xi
DAFTAR TABEL... xiv
DAFTAR GAMBAR... xv
DAFTAR LAMPIRAN... xvi
BAB I PENDAHULUAN... 1
A. Latar Belakang Masalah... 1
B. Rumusan Masalah... 4
C. Batasan Masalah... 4
D. Tujuan Penulisan... 4
E. Manfaat Penulisan... 5
F. Metode Penulisan... 5
BAB II MASALAH NILAI AWAL DALAM PERSAMAAN DIFERENSIAL
BIASA... 8
A. Persamaan Diferensial... 8
1. Klasifikasi Persamaan Diferensial... 8
2. Penyelesaian Persamaan Diferensial... 12
3. Masalah Nilai Awal... 14
4. Teorema Eksistensi dan Ketunggalan... 17
B. Persamaan Beda dengan Koefisien Konstan... 27
1. Persamaan Orde Pertama... 28
2. Persamaan Orde Kedua... 31
3. Persamaan Orde Tinggi... 34
C. Deret Taylor dan Orde Penghampiran... 34
1. Deret Taylor... 35
2. Orde Penghampiran... 35
D. Metode Satu Langkah... 37
1. Metode Euler... 37
2. Metode Deret Taylor... 47
BAB III METODE BANYAK LANGKAH LINEAR... 56
A. Pendahuluan... 56
B. Metode Adams-Bashforth... 56
C. Metode Dua Langkah Linear dan Konsistensi... 61
BAB IV STABILITAS DAN KONVERGENSI... 74
A. Stabil Nol... 74
B. Syarat Perlu untuk Konvergensi... 82
C. Syarat Cukup untuk Konvergensi ... 92
BAB V KESIMPULAN DAN SARAN... 103
A. Kesimpulan... 103
B. Saran ... 104
xiv
DAFTAR TABEL
Halaman
Tabel 2.4.1 Tabel Galat Total ... 47
Tabel 2.4.2 Tabel Galat Total Maksimum dan Jumlahan Galat Total... 50
Tabel 2.4.3 Tabel Galat Total... 55
Tabel 3.2.1 Tabel Galat Total Maksimum dan Jumlahan Galat Total... 60
xv
DAFTAR GAMBAR
Gambar 2.1.1 � < (kiri), � > (kanan)... 20
Gambar 2.4.1 Grafik penyelesaian sejati, hampiran, dan galat total... 41
Gambar 2.4.2 Grafik penyelesaian sejati dan hampiran dengan metode
Euler (kiri) dan grafik galat total (kanan)... 42
Gambar 2.4.3 Grafik penyelesaian sejati dan penyelesaian hampiran
dengan menggunakan metode Euler... 46
Gambar 2.4.4 Grafik penyelesaian sejati dan hampiran dengan metode
Deret Taylor orde dua (kiri) dan grafik galat total (kanan)... 49
Gambar 2.4.5 Grafik penyelesaian sejati dan penyelesaian hampiran
dengan metode Deret Taylor orde dua... 55
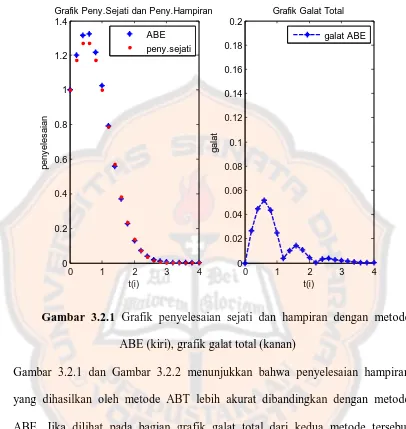
Gambar 3.2.1 Grafik penyelesaian sejati, hampiran dengan metode ABE
(kiri) dan grafik galat total (kanan)... 59
Gambar 3.2.2 Grafik penyelesaian sejati dan hampiran dengan metode
ABT (kiri), grafik galat total (kanan)... 60
Gambar 3.3.1 Grafik penyelesaian sejati dan hampiran... 67
Gambar 3.4.1 Grafik penyelesaian sejati dan hampiran dengan metode
ABT (kiri), grafik galat total... 71
Gambar 3.4.2 Grafik penyelesaian sejati dan hampiran dengan metode tiga
xvi
DAFTAR LAMPIRAN
Lampiran A Pembuktian Teorema
BAB I PENDAHULUAN
A. LATAR BELAKANG
Persamaan diferensial adalah persamaan yang memuat turunan (derivatif)
dari suatu fungsi. Jika fungsi yang belum diketahui dalam persamaan diferensial
bergantung pada satu variabel bebas, maka persamaan tersebut disebut persamaan
diferensial biasa. Persamaan diferensial dapat diklasifikasikan berdasarkan dengan
tingkatnya, yaitu tingkat turunan tertinggi yang muncul dalam persamaan tersebut.
Selain itu persamaan diferensial juga dibedakan dalam dua jenis, yaitu persamaan
diferensial linear dan nonlinear. Persamaan diferensial dikatakan linear jika
me-menuhi persyaratan berikut: fungsi yang belum diketahui dan turunan-turunannya
secara aljabar hanya berderajat satu, tidak ada hasil kali yang berkaitan dengan
fungsi yang belum diketahui dan turunannya atau dua atau lebih
turunan-nya, dan tidak ada fungsi transendental dari fungsi yang belum diketahui dan
tu-runan-turunannya. Persamaan diferensial yang tidak memenuhi ketiga syarat
ter-sebut diter-sebut persamaan diferensial nonlinear. Semua persamaan diferensial yang
akan dibahas dalam tugas akhir ini adalah persamaan diferensial linear tingkat
pertama.
Penyelesaian persamaan diferensial adalah fungsi yang turunannya termuat
dalam persamaan tersebut. Jika fungsi tersebut disubstitusikan ke dalam
persa-maan diferensial akan menghasilkan suatu identitas. Persapersa-maan diferensial
khu-sus. Penyelesaian umum adalah penyelesaian yang masih memuat konstanta,
se-dangkan penyelesaian khusus adalah penyelesaian yang sudah tidak memuat
kons-tanta. Penyelesaian khusus ditentukan dengan bantuan syarat bantu, yaitu syarat
awal (nilai awal) atau syarat batas.
Persamaan diferensial yang disajikan beserta syarat awalnya seperti berikut
�′= �(�,�), � �
0 = �0
disebut masalah nilai awal. Penyelesaian masalah nilai awal adalah penyelesaian
dari persamaan diferensial yang memenuhi syarat awal yang diberikan. Jika
per-masalahan tersebut dapat diselesaikan secara analitik, maka penyelesaian yang
dihasilkan disebut penyelesaian sejati (penyelesaian yang sesungguhnya). Namun,
terkadang masalah nilai awal muncul dalam bentuk yang rumit, sehingga tidak
dapat diselesaikan dengan metode analitik. Jika metode analitik tidak dapat lagi
diterapkan, maka penyelesaian tersebut dapat dicari dengan metode numerik.
Penyelesaian yang dihasilkan metode numerik disebut penyelesaian hampiran
(pendekatan terhadap penyelesaian sejati). Penyelesaian hampiran tidak tepat
sa-ma dengan penyelesaian sejati, sehingga ada selisih antara keduanya. Selisih
ter-sebut diter-sebut galat. Semakin kecil galatnya berarti penyelesaian terter-sebut semakin
baik.
Terdapat beberapa metode numerik yang digunakan untuk menyelesaikan
masalah nilai awal, diantaranya yaitu Metode Euler dan Metode Deret Taylor.
Metode-metode tersebut dikelompokkan ke dalam metode satu langkah karena
untuk menentukan nilai ��+1 hanya dibutuhkan satu nilai sebelumnya, yaitu ��.
kurang akurat karena mereka hanya menggunakan informasi dari satu titik
sebelumnya.
Tugas akhir ini akan membahas mengenai Metode Banyak Langkah Linear
untuk menyelesaikan masalah nilai awal. Metode Banyak Langkah Linear
memer-lukan beberapa nilai sebelumnya, yaitu ��, ��−1, ��−2, … untuk menentukan nilai
��+1. Tujuan utama dari Metode Banyak Langkah Linear adalah menggunakan
informasi dari beberapa nilai di titik sebelumnya untuk menentukan nilai ��+1
yang lebih akurat.
Persamaan diferensial biasa hanya mempunyai satu nilai awal, yaitu
� �0 =�0, sedangkan Metode Banyak Langkah Linear memerlukan beberapa
nilai sebelumnya untuk menentukan nilai ��+1. Oleh karena itu, untuk
menentu-kan nilai-nilai tersebut diperlumenentu-kan prosedur pendahuluan. Prosedur pendahuluan
ini dilakukan dengan menggunakan salah satu dari metode-metode satu langkah
yang disebutkan di atas. Setelah diperoleh nilai-nilai yang dibutuhkan, selanjutnya
Metode Banyak Langkah Linear dapat diterapkan untuk menentukan nilai ��+1.
Jadi metode tersebut lebih efisien karena menggunakan informasi dari titik-titik
yang sudah ada.
Keakuratan penyelesaian yang dihasilkan oleh suatu metode ketika
diterapkan dalam masalah nilai awal juga tergantung dari kebaikan metode
tersebut. Metode yang baik akan menghasilkan penyelesaian yang lebih akurat
dan ditandai dengan dihasilkannya penyelesaian yang konvergen. Suatu metode
akan konvergen jika metode tersebut memenuhi syarat konsisten dan stabil nol.
stabilitas, dan konvergensi, yang berpengaruh terhadap kebaikan suatu Metode
Banyak Langkah Linear.
B. RUMUSAN MASALAH
Pokok permasalahan yang akan dibahas dalam tulisan ini yaitu:
1. Apa yang dimaksud dengan Metode Banyak Langkah Linear?
2. Bagaimana menyelesaikan masalah nilai awal dalam persamaan diferensial
biasa dengan Metode Banyak Langkah Linear dan bagaimana penerapannya
dengan program Matlab?
3. Bagaimana hubungan antara konsistensi, stabilitas, dan konvergensi?
C. BATASAN MASALAH
1. Penerapan Metode Banyak Langkah Linear dalam tugas akhir ini hanya untuk
masalah nilai awal dalam persamaan diferensial linear tingkat pertama.
2. Penyelesaian masalah nilai awal secara analitik hanya menggunakan metode
integral langsung.
D. TUJUAN PENULISAN
Tujuan penulisan ini yaitu untuk menyelesaikan masalah nilai awal dalam
persamaan diferensial biasa dengan Metode Banyak Langkah Linear dan
menerapkannya dengan program Matlab, serta membahas mengenai hubungan
antara konsistensi, stabilitas, dan konvergensi dari suatu Metode Banyak Langkah
E. MANFAAT PENULISAN
Memperoleh pengetahuan tentang penyelesaian masalah nilai awal secara
numerik menggunakan Metode Banyak Langkah Linear dan penerapannya dengan
program Matlab, serta mengetahui hubungan antara konsistensi, stabilitas, dan
konvergensi dari suatu metode Metode Banyak Langkah Linear.
F. METODE PENULISAN
Metode yang digunakan penulis adalah metode studi pustaka, yaitu dengan
mempelajari buku-buku yang berkaitan dengan Metode Banyak Langkah Linear
untuk menyelesaikan masalah nilai awal dalam persamaan diferensial biasa.
G. SISTEMATIKA PENULISAN
BAB I PENDAHULUAN
A. Latar Belakang
B. Rumusan Masalah
C. Batasan Masalah
D. Tujuan Penulisan
E. Manfaat Penulisan
F. Metode Penulisan
BAB II MASALAH NILAI AWAL DALAM PERSAMAAN
DIFEREN-SIAL BIASA
A. Persamaan Diferensial
1. Klasifikasi Persamaan Diferensial
2. Penyelesaian Persamaan Diferensial
3. Masalah Nilai Awal
4. Teorema Eksistensi dan Ketunggalan
B. Persamaan Beda dengan Koefisien Konstan
1. Persamaan Orde Pertama
2. Persamaan Orde Kedua
3. Persamaan Orde Tinggi
C. Deret Taylor dan Orde Penghampiran
1. Deret Taylor
2. Orde Penghampiran
D. Metode Satu Langkah
1. Metode Euler
2. Metode Deret Taylor
BAB III METODE BANYAK LANGKAH LINEAR
A. Pendahuluan
B. Metode Adams-Bashforth
C. Metode Dua Langkah Linear dan Konsistensi
BAB IV STABILITAS DAN KONVERGENSI
A. Stabil Nol
B. Syarat Perlu untuk Konvergensi
C. Syarat Cukup untuk Konvergensi
BAB V PENUTUP
A. Kesimpulan
BAB II
MASALAH NILAI AWAL DALAM PERSAMAAN DIFERENSIAL BIASA
A. PERSAMAAN DIFERENSIAL
Definisi 2.1.1
Persamaan diferensial adalah persamaan yang memuat turunan (derivatif) dari
suatu fungsi.
Contoh 2.1.1
Ketiga persamaan di bawah ini merupakan contoh persamaan diferensial:
a. = 2
b. = ( 2+ )
c. ′′ + 4 = ( 2+ 1)3
1. Klasifikasi Persamaan Diferensial
Persamaan diferensial dapat diklasifikasikan dengan berbagai macam cara.
Jika fungsi yang belum diketahui dalam persamaan diferensial bergantung pada
satu variabel bebas, maka persamaan itu disebut persamaan diferensial biasa. Di
sisi lain, jika fungsi yang belum diketahui bergantung pada lebih dari satu variabel
Contoh 2.1.2
a. = 2+
b. ′′ + 4 = ( 2+ 1)3
Kedua persamaan pada contoh (a) dan (b) merupakan persamaan diferensial
biasa, dimana menyatakan fungsi yang belum diketahui (variabel tak
bebas) dan menyatakan variabel bebas.
c. �
� + � � = 0
d. �2
� 2 +
�2
� 2 = 1 +
Kedua persamaan pada contoh (c) dan (d) merupakan persamaan diferensial
parsial, dimana menyatakan fungsi yang belum diketahui (variabel tak
bebas), sedangkan dan menyatakan variabel bebas.
Definisi 2.1.2
Tingkat persamaan diferensial adalah tingkat turunan tertinggi yang muncul
dalam persamaan diferensial.
Klasifikasi persamaan diferensial berdasarkan tingkatnya adalah sebagai berikut:
1) Persamaan diferensial tingkat pertama
Bentuk umum:
, , ′ = 0
Contoh 2.1.3
b. ′ = + 2
2) Persamaan diferensial tingkat kedua
Bentuk umum:
, , ′, ′′ = 0
Contoh 2.1.4
a. ′′ + 2 = −1
b. ′′ = ′ + −
3) Persamaan diferensial tingkat ke-
Bentuk umum:
, , ′, ′′,…, ( ) = 0
Contoh 2.1.5
a. (4)−5 ′′ = 4 + 2
b. (3)= ′′ − ′ +
Definisi 2.1.3
Persamaan diferensial biasa tingkat ke- disebut linear dalam jika persamaan
diferensial itu dapat ditulis dalam bentuk
+
−1 −1 +⋯+ 1 ′ + 0 = ( )
dimana 0, 1,…, dan adalah fungsi-fungsi kontinu pada suatu interval yang memuat dan ( ) ≠0 pada interval itu. Fungsi ( ) disebut fungsi-fungsi
Jadi persamaan diferensial biasa adalah linear jika memenuhi syarat-syarat
berikut:
a. Fungsi yang belum diketahui dan turunan-turunannya secara aljabar hanya
berderajat satu.
b. Tidak ada hasil kali yang berkaitan dengan fungsi yang belum diketahui dan
turunan-turunannya atau dua atau lebih turunan.
c. Tidak ada fungsi transendental dari fungsi yang belum diketahui dan
turunan-turunannya.
Persamaan diferensial yang tidak linear disebut nonlinear.
Contoh 2.1.6
a. ′′ −3 ′ + 3 = 3, merupakan persamaan diferensial linear.
b. ′′′ + + 5 = 0, merupakan persamaan diferensial linear.
c. ( ′)3+ 2 = , merupakan persamaan diferensial nonlinear karena turunan pertama dari fungsi yang belum diketahui berderajat tiga.
d. ′ + 3 = 0, merupakan persamaan diferensial nonlinear karena ′ adalah
hasil kali dari fungsi yang belum diketahui dengan turunannya.
e. ′′ + 5 = cos , merupakan persamaan diferensial nonlinear karena cos
2. Penyelesaian Persamaan Diferensial
Definisi 2.1.4
Penyelesaian persamaan diferensial tingkat ke- pada interval adalah
suatu fungsi yang mempunyai semua turunan yang diperlukan, yang jika
menggantikan , ′, ′′,…, ( ) menjadikan persamaan diferensial itu suatu identitas.
Contoh 2.1.7
Tunjukkan bahwa fungsi = 2 + − adalah penyelesaian dari persamaan
diferensial ′ + −2 = 0.
Penyelesaian:
Diketahui = 2 + − , maka diperoleh ′ = − − .
Kemudian substitusikan kedua fungsi tersebut ke dalam persamaan diferensial
sehingga diperoleh
− − + 2 + − −2 = 0
Ruas kiri dari persamaan tersebut bernilai 0 (sama dengan ruas kanan), maka
fungsi = 2 + − merupakan penyelesaian dari persamaan diferensial ′ + −
2 = 0.
Contoh 2.1.8
Tentukan penyelesaian dari persamaan diferensial berikut ini
′ = 3
2+5
Penyelesaian persamaan tersebut disajikan oleh
= 32+5
= 32+5
= 3 2+ 5 −12
Misalkan = ( 2+ 5), maka = 2 atau
2 = , sehingga = 3
1 2+ .
Karena = ( 2+ 5), maka penyelesaian dari persamaan diferensial tersebut adalah
= 3 ( 2+ 5)
1
2+ = 3 2+ 5 +
Persamaan diferensial mempunyai tak hingga banyak penyelesaian.
Misalnya pada Contoh 2.1.8 penyelesaiannya berbentuk = 3 2+ 5 + , dimana adalah kontanta real. Penyelesaian itu disebut keluarga penyelesaian.
Pemberian nama untuk keluarga penyelesaian adalah berdasarkan banyaknya
parameter yang termuat dalam penyelesaian, dalam kasus di atas maka =
3 2+ 5 + disebut keluarga berparameter-satu.
Definisi 2.1.5
Suatu keluarga berparameter- dari penyelesaian persamaan diferensial tingkat
ke- disebut penyelesaian umum dari persamaan diferensial, jika semua
Definisi 2.1.6
Suatu penyelesaian persamaan diferensial tingkat ke- yang diperoleh dari
penyelesaian umum dengan menentukan nilai parameter disebut penyelesaian
khusus.
Contoh 2.1.9
Penyelesaian umum dari ′′ + 9 = 0 adalah keluarga berparameter-dua =
1cos 3 + 2sin 3 . Jika diambil 1 = 2 dan 2 = 1, maka penyelesaian khusus dari persamaan diferensial tersebut adalah = 2 cos 3 + sin 3 .
3. Masalah Nilai Awal
Penyelesaian umum dari persamaan diferensial tingkat ke- memuat
konstanta sembarang. Sedangkan, penyelesaian khusus dari suatu persamaan
diferensial diperoleh dari penyelesaian umum dengan memasukkan syarat bantu
pada fungsi penyelesaian umum tersebut. Ada dua macam cara penentuan syarat
bantu untuk memperoleh penyelesaian khusus dari suatu persamaan diferensial
seperti dijelaskan dalam definisi berikut ini.
Definisi 2.1.7
1) Jika syarat bantu pada persamaan diferensial yang diketahui berhubungan
dengan sebuah nilai , syarat itu disebut syarat awal. Persamaan diferensial
2) Jika syarat bantu pada persamaan diferensial yang diketahui berhubungan
dengan dua atau lebih nilai , syarat itu disebut syarat batas atau nilai batas.
Persamaan diferensial dengan syarat batasnya disebut masalah nilai batas.
Contoh 2.1.10
a. ′ + = 3, 0 = 1 merupakan masalah nilai awal.
b. ′′ − ′ + = 3, 0 = 2, ′ 1 =−1, merupakan masalah nilai batas.
Contoh 2.1.11
Penyelesaian umum dari persamaan diferensial ′ + = 1 adalah keluarga
berparameter-satu = 1 + − . Diberikan syarat bantu 0 = 0, tentukan
penyelesaian khusus dari persamaan diferensial tersebut.
Penyelesaian:
Diketahui 0 = 0, maka diperoleh
0 = 1 + 0
= −1
Jadi penyelesaian khusus dari persamaan diferensial tersebut adalah = 1− − .
Contoh 2.1.12
Selesaikan masalah nilai awal berikut ini
Penyelesaian:
Penyelesaian persamaan diferensial tersebut disajikan oleh
= 2
−2 =
Ruas kiri dari persamaan di atas mudah untuk diintegralkan langsung. Sedangkan
untuk ruas kanan digunakan pengintegralan parsial dengan dimisalkan = dan
= sehingga = dan = , maka
−2 =
− −1 = − − −1 = − +
= −−1 +
Diketahui bahwa 0 = 2, sehingga = 1 2.
Jadi penyelesaian dari masalah nilai awal tersebut adalah
= −2
2 −2 +1
Berikut ini diberikan definisi mengenai syarat Lipschitz yang akan
digunakan dalam pembuktian teorema eksistensi dan ketunggalan.
Definisi 2.1.8
Fungsi ( , ) dikatakan memenuhi syarat Lipschitz terhadap variabel pada
himpunan ⊂ �2 jika ada konstanta > 0 dengan
, 1 − ( , 2) 1− 2
Contoh 2.1.13
Tunjukkan bahwa , = 1−2 memenuhi syarat Lipschitz pada interval
= , |1 2,−2 5 .
Penyelesaian:
Untuk sembarang titik ( , 1) dan ( , 2) di , maka
, 1 − ( , 2) = 1−2 1− 1−2 2
= 1−2 ( 1− 2)
= 1−2 ( 1− 2)
5 1− 2
Maka memenuhi syarat Lipschitz pada terhadap variabel . Sedangkan,
konstanta Lipschitznya adalah 5.
4. Teorema Eksistensi dan Ketunggalan
Bentuk umum dari masalah nilai awal adalah sebagai berikut
′ = ( , ),
0 = 0 (2.1) Andaikan masalah nilai awal tersebut mempunyai titik awal ( 0, 0) pada titik (0, 0), maka
′ = ( , ), 0 = 0 (2.2)
Secara umum, jika titik awalnya tidak berada pada titik (0, 0) , maka dapat
yang memenuhi syarat yang disebutkan dalam teorema nanti akan mempunyai
penyelesaian dan penyelesaian tersebut adalah tunggal.
Teorema 2.1.1
Jika dan �
� kontinu pada bidang �: , , maka ada suatu interval
dimana ada penyelesaian tunggal = �( ) dari masalah nilai awal
(2.2).
Bukti:
Andaikan ada = �( ), yaitu fungsi yang terdiferensial dan memenuhi masalah
nilai awal. Oleh karena itu, =�( ) merupakan fungsi kontinu dan karena
kontinu, maka [ ,� ] merupakan fungsi yang kontinu pada . Jadi dengan
mengintegralkan ′ = ( , ) dari = 0 sampai ke sembarang nilai , diperoleh
� = 0 [ ,� ] (2.3) yang disebut persamaan integral.
Ketika = 0, maka � 0 = 0, yang memenuhi syarat awal. Andaikan ada
fungsi kontinu =�( ) yang memenuhi persamaan integral (2.3), maka fungsi
ini juga memenuhi masalah nilai awal (2.2). Karena fungsi yang diintegralkan
pada persamaan (2.3) kontinu, maka berdasarkan teorema dasar kalkulus
diperoleh bahwa � terdiferensial dan �′ = [ ,�( )]. Oleh karena itu,
masalah nilai awal (2.2) ekuivalen dengan persamaan integral (2.3), sehingga
penyelesaian yang memenuhi persamaan integral juga memenuhi masalah nilai
eksplisit, maka digunakan metode iterasi Picard untuk mencari hampirannya.
Metode tersebut dimulai dengan menentukan syarat awal �0 0 = 0. Kemudian
�1 diperoleh dengan mensubstitusikan �0 untuk �( ) pada ruas kanan persamaan (2.3), sehingga diperoleh
�1 = 0 [ ,�0 ] �1 0 = 0
�2 diperoleh dari �1
�2 = 0 [ ,�1 ] �2 0 = 0
dan secara umum,
� +1 = 0 [ ,� ] � +1 0 = 0
Jadi setiap anggota barisan � =�0,�1,�2,…,� ,… memenuhi syarat awal. Jika pada suatu tahap, misalnya = , � +1 =� , maka
� +1 = 0 [ ,� ] � +1 = �
� = 0 [ ,� ]
sehingga � merupakan penyelesaian dari persamaan integral (2.3). Jadi � juga
merupakan penyelesaian dari masalah nilai awal (2.2) karena masalah nilai awal
dan persamaan integral tersebut adalah ekuivalen.
Pembuktian bahwa persamaan integral tersebut mempunyai penyelesaian dan
tunggal akan dilakukan dalam beberapa langkah:
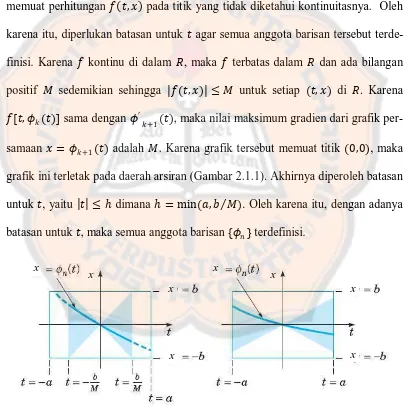
a. Pertama, akan dibuktikan bahwa semua anggota barisan � ada. Dari
teo-rema tersebut diketahui bahwa dan �
� kontinu hanya pada bidang �: ,
. Anggota dari barisan � tidak dapat dihitung secara eksplisit dan jika
pada suatu tahap, misal = grafik dari =� memuat titik yang berada di
luar bidang �, maka perhitungan untuk � +1 tidak dapat dilakukan karena memuat perhitungan , pada titik yang tidak diketahui kontinuitasnya. Oleh
karena itu, diperlukan batasan untuk agar semua anggota barisan tersebut
terde-finisi. Karena kontinu di dalam �, maka terbatas dalam � dan ada bilangan
positif sedemikian sehingga , untuk setiap , di �. Karena
,� sama dengan �′ +1 , maka nilai maksimum gradien dari grafik per-samaan = � +1 adalah . Karena grafik tersebut memuat titik 0,0 , maka grafik ini terletak pada daerah arsiran (Gambar 2.1.1). Akhirnya diperoleh batasan
untuk , yaitu dimana = min( , ). Oleh karena itu, dengan adanya
batasan untuk , maka semua anggota barisan � terdefinisi.
Gambar 2.1.1 < (kiri), > (kanan)
b. Kedua, akan dibuktikan bahwa barisan � konvergen. Misalkan
,� −1( ) dan ,� ( ) adalah dua titik sembarang di dalam �. Dengan
meng-x
x
x
x
x
x
gunakan teorema nilai rata-rata pada dan menganggap ( , ) sebagai fungsi
dari , maka diperoleh
,� −1( ) − ,� ( ) = �� ,� ( ) � −1 − � ( ) (2.5)
dimana � ( ) berada di antara � −1( ) dan � ( ). Karena �
� kontinu di dalam �,
maka terbatas di dalam �, sehingga ada bilangan positif sedemikian sehingga
�
� ( , ) untuk setiap ( , ) di dalam � (2.6)
Dari (2.5) dan (2.6) berlaku bahwa untuk setiap pasang titik ,� −1( ) dan ,� ( ) di dalam �, fungsi memenuhi syarat
,� −1( ) − ,� ( ) � −1 − � ( ) (2.7) Suatu fungsi yang terdefinisi di dalam suatu himpunan � dan memenuhi syarat
(2.7) untuk suatu konstanta positif dan setiap pasang titik ,� −1( ) dan ,� ( ) di dalam � disebut kontinu Lipschitz dalam di � dengan konstanta
Lipschitz .
Selanjutnya akan dibuktikan bahwa � ( ), untuk = 0, 1, 2,… ada di dalam
dan kontinu pada interval ini serta memenuhi ketaksamaan
� ( ) untuk , = 0, 1, 2,… (2.8)
Pembuktian ini adalah untuk menunjukkan bahwa barisan (2.4) benar terdefinisi.
Dibuktikan dengan induksi:
Untuk = 0, �0 = 0 kontinu dalam (karena fungsi konstan kontinu dimana-mana). Jadi �0 = 0 , sehingga (2.8) benar untuk = 0.
Misalkan � kontinu dalam dan bahwa (2.8) berlaku untuk = ,
� +1 terdefinisi oleh (2.4), maka kontinu pada interval (karena integral dari fungsi kontinu akan kontinu juga) dan diperoleh
� +1( ) = 0 ,� ( )
0 ,� ( )
0
.
Dipilih = , maka diperoleh
� +1( ) =
Terbukti bahwa (2.8) berlaku untuk semua .
Berikutnya akan dibuktikan pula dengan induksi bahwa untuk
ketaksa-maan berikut ini berlaku untuk = 0, 1, 2,…
� − � −1( )
−1
!
−1
! (2.9) Untuk = 1
�1 − �0 = 0 ,�0
0 =
Jadi (2.9) benar untuk = 1.
Misalkan (2.9) benar untuk = , yaitu dimisalkan untuk
� − � −1( )
−1
!
−1
Berdasarkan (2.4) dan (2.7), maka
Langkah selanjutnya dalam pembuktian ini yaitu menunjukkan bahwa barisan
� ( ) konvergen seragam ke suatu limit fungsi pada interval . Barisan
� dapat dinyatakan sebagai jumlahan dari deret berikut
� − � −1( )
∞
=1 (2.11) Jadi deret (2.11) dan barisan � mempunyai sifat-sifat kekonvergenan yang
sama. Berdasarkan (2.9), maka deret (2.11) dipengaruhi oleh deret dengan
suku-suku konstanta
−1
!
∞
=1
Deret terakhir ini adalah konvergen dan dapat dinyatakan dalam bentuk yang lebih
Menurut uji− Weierstrass, deret (2.11) konvergen mutlak dan seragam pada
interval . Oleh karena itu, barisan � konvergen seragam pada interval
. Jadi dengan menyatakan limit fungsi dengan �( ), maka diperoleh
� = lim →∞� (2.12)
c. Ketiga, akan dibuktikan bahwa � memenuhi persamaan integral, sehingga
merupakan penyelesaian dari masalah nilai awal (2.2). Berdasarkan (2.4), maka
� memenuhi syarat awal
� 0 = 0, = 0, 1, 2,…
Diambil limit dari kedua ruasnya, maka untuk → ∞ diperoleh � 0 = 0. �
kontinu pada interval karena � merupakan limit seragam dari fungsi
kontinu � di dalam interval untuk = 0, 1, 2,…. Berdasarkan (2.8),
dengan mengambil limit dari kedua ruasnya juga bila → ∞, maka untuk
�( )
Jadi fungsi ( ,� ) benar terdefinisi dan kontinu pada interval ,
sehing-ga
,�( )
0
ada. Berdasarkan (2.7), untuk diperoleh
,� ( ) − ,�( ) � − �( )
Karena barisan � konvergen seragam ke � pada interval , maka
barisan ,� ( ) juga konvergen seragam ke ,�( ) dan akibatnya
Diambil limit pada kedua ruas dari (2.4) bila → ∞ dan berdasarkan (2.12) dan
(2.13), diperoleh
� = 0 ,�( ) (2.14)
Jadi terbukti bahwa �( ) memenuhi persamaan integral dan berarti merupakan
penyelesaian dari masalah nilai awal (2.2).
d. Terakhir, akan dibuktikan bahwa � merupakan penyelesaian tunggal dari
masalah nilai awal (2.2). Misalkan ada penyelesaian lain dari masalah nilai awal
(2.2), yaitu �( ), maka
�′( )− �′ = ,� − ,�( ) (2.15)
Karena kedua penyelesaian tersebut memenuhi syarat awal, maka � 0 = 0 =
� 0 , sehingga dengan mengintegralkan kedua ruas (2.15) dari 0 sampai ,
dipe-roleh
�( )− � = 0 ,� − ,�( ) (2.16)
Kemudian berdasarkan (2.7) maka diperoleh
�( )− � �0 ( )− � (2.17)
Misalkan
= �0 ( )− � (2.18)
dimana
0 = 0 (2.19)
Berdasarkan (2.17) dan (2.18) maka diperoleh
′ ( )
atau
′( )− ( ) 0 (2.21)
Kalikan kedua ruas pertidaksamaan (2.21) dengan faktor pengintegralan − ,
maka diperoleh
− ′( )− ( ) 0
− ′ − − ( ) 0
− ( ) ′ 0
Integralkan kedua ruas (2.22) dari 0 sampai dan berdasarkan (2.19), maka
dipe-roleh
− 0 untuk 0
Karena − tidak pernah bernilai kurang dari atau sama dengan nol, maka
( ) 0 untuk 0, sehingga berdasarkan (2.20), diperoleh bahwa
0 ( ) 0
atau
( ) ≡0 (2.23)
Jadi berdasarkan (2.18) dan (2.23) dapat diambil kesimpulan bahwa � = � ,
sehingga terbukti bahwa � merupakan penyelesaian tunggal dari masalah nilai
awal (2.2).
Persamaan diferensial pada masalah nilai awal yang diberikan dalam
contoh-contoh sebelumnya dapat diselesaikan secara analitik dengan
menggunakan metode pengintegralan langsung. Namun, masih ada beberapa
metode analitik lain yang juga dapat digunakan untuk menyelesaikan persamaan
diferensial tersebut, antara lain yaitu Metode Faktor Integral, Metode Substitusi,
Metode Bernoulli. Akan tetapi masih tetap ada persamaan diferensial yang rumit
jika diselesaikan secara analitik. Oleh karena itu, dibutuhkan metode numerik
untuk menentukan penyelesaian hampiran (pendekatan) untuk persamaan
diferensial tersebut.
B. PERSAMAAN BEDA DENGAN KOEFISIEN KONSTAN
Pembahasan mengenai metode numerik untuk menyelesaikan masalah nilai
awal tidak lepas dari penggunaan persamaan beda. Oleh karena itu, dalam subbab
ini akan dibahas mengenai persamaan beda linear dengan koefisien konstan
(li-near constant-coefficient difference equations). Persamaan beda adalah relasi
an-tara + 1 suku berturut-turut dari barisan 0, 1,…, ,…, yang mana bentuk umumnya adalah
+ + −1 + −1+⋯+ 0 = (2.24) dimana , −1,…, 0 merupakan koefisien dan adalah barisan bilangan.
Diberikan > 0, atur koefisien-koefisien dan barisan sehingga diperoleh
rumus untuk suku ke- dari barisan yang memenuhi (2.24). Penyelesaian umum
untuk (2.24) disusun dari penjumlahan antara fungsi pelengkap (complementary
penyele-saian khusus (particular solution), yaitu suatu penyelepenyele-saian dari persamaan beda
yang diberikan. Konstanta-konstanta sembarang pada penyelesaian umum dapat
ditentukan dengan memasukkan nilai yang sesuai dari nilai-nilai awal yang
di-ketahui, yaitu = � untuk = 0, 1,…, −1.
1. Persamaan Orde Pertama
Diberikan masalah koefisien konstan orde pertama
+1 = + , = 0, 1,… (2.25) Kemudian untuk = 0, 1, 2 diperoleh
1 = 0+
2 = 1+ = 0+ + = 2 0+ + 1
3 = 2+ = 2 0+ + 1 +
= 3
0+ 2+ + 1
dan jika dilanjutkan akan diperoleh suatu suku dalam barisan , meskipun suku
ke- yang sesungguhnya mungkin tidak dapat ditemukan.
Pertama, akan dicari fungsi pelengkap untuk (2.25). Diberikan persamaan
homogen +1 = , dimana 1 = 0, 2 = 1 = 2
0 dan dengan induksi diperoleh suku ke- barisan tersebut, yaitu = 0, untuk suatu nilai 0. Di-ambil 0 = , yaitu sembarang konstanta, maka diperoleh fungsi pelengkap
= .
Selanjutnya akan dicari penyelesaian khusus dari (2.25), yaitu dalam bentuk
+1 = +
− =
1− =
= 1− Maka,
=
1− , ≠1
Jumlahan dari fungsi pelengkap dan penyelesaian khusus menghasilkan
= +
1− , ≠1 (2.26) yang merupakan penyelesaian umum dari (2.25) ketika ≠ 1. Sedangkan, ketika
= 1, maka
+1 − =
dan dengan syarat deret teleskop diperoleh
= − −1 + −1− −2 +⋯+ 1− 0 + 0
= + +⋯+ + 0
= + 0
Sehingga penyelesaian umum dari persamaan tersebut adalah
= +
dimana adalah sembarang konstanta.
Jadi penyelesaian umum dari (2.25) adalah
= + 1− ( ≠ 1)
Setelah diperoleh penyelesaian umum dari (2.25), maka dapat dicari juga
penyelesaian umum dari persamaan beda berikut
+1 = + , = 0, 1,… (2.28) Substitusikan = ke dalam (2.28), maka diperoleh
+1
+1 = + +1 = +1 + +1
= +
Jadi memenuhi
+1 = + (2.29) dimana bentuknya sama seperti (2.25). kemudian dengan membandingkan
penye-lesaian umum dari (2.25), maka dapat ditunjukkan bahwa (2.29) mempunyai
pe-nyelesaian umum
= + 1− ≠1 + = 1
Karena = , maka
=
= +
1−
= +
= + 1−
= + −1
1−
= +
−
= +
= +
= +
= + −1
Jadi penyelesaian umum dari (2.28) adalah
= + − ( ≠ )
+ −1 ( = ) (2.30)
2. Persamaan Orde Kedua
Diberikan persamaan homogen
+2+ +1 + = 0 (2.31) Persamaan tersebut akan mempunyai penyelesaian dalam bentuk = ,
di-mana adalah sembarang kontanta.
Maka,
+2 + +1+ = 0
( 2+ + ) = 0
Karena ≠0, maka
yang disebut persamaan tambahan (auxiliary equation). Andaikan bahwa
persa-maan tersebut mempunyai akar-akar dan , maka
− − = 2− + +
Sehingga
=− + dan =
Jadi persamaan tak homogen berikut
+2 + +1+ = (2.33) dapat ditulis menjadi
+2 − + +1 + = atau
+2− +1 − ( +1 − ) = Didefinisikan = +1− , maka
+1 − =
Jadi (2.33) dapat dinyatakan dengan sistem persamaan orde satu dari persamaan
beda dengan koefisien konstan berikut
(i) +1− =
(ii) +1− =
Ketika ≡0, yaitu untuk kasus homogen, (ii) pada (2.34) menjadi
+1 − = 0
yang mempunyai penyelesaian umum = , dimana adalah sembarang
konstanta. Jadi (i) pada (2.34) menjadi
dimana bentuknya sama seperti (2.28), sehingga berdasarkan (2.30) diperoleh
penyelesaian umum dari (2.34), yaitu
= + − ( ≠ )
+ −1 ( = ) (2.36) dimana dan adalah sembarang konstanta.
Persamaan tak homogen (2.33) yang akan dijelaskan yaitu untuk kasus
Substitusikan kedua penyelesaian tersebut ke (i) pada (2.34) sehingga diperoleh
+1 − = +1− untuk ≠1 dan
+1 − = + untuk = 1
Penyelesaian umum dari kedua persamaan tersebut adalah
3. Persamaan Orde Tinggi
Bentuk umum dari pesamaan beda dengan koefisien konstan homogen
ada-lah
+ + −1 + −1+⋯+ 0 = 0 (2.37) Penyelesaian umum dari (2.37) adalah dalam bentuk
=
Sehingga untuk menentukan penyelesaian tersebut dibutuhkan , yaitu akar dari
persamaan tambahan
+ −1 −1+⋯+ 0 = 0 (2.38) Andaikan bahwa setiap akar dari (2.38) mempunyai multiplisitas , maka
kontribusi untuk fungsi pelengkap adalah
( )
dimana ( ) adalah polinomial dalam berderajat ( −1) (memuat
semba-rang koefisien). Sebagai contoh, ketika = 1, polinomial ( ) berderajat 0,
yai-tu = . Ketika = 2, polinomial ( ) berderajat 1 dan bentuk umumnya
adalah = + .
C. DERET TAYLOR DAN ORDE PENGHAMPIRAN
Kegunaan dari Deret Taylor adalah untuk menghampiri suatu fungsi dengan
bentuk polinom yang disebut fungsi hampiran. Perhitungan dengan menggunakan
fungsi yang sesungguhnya akan menghasilkan penyelesaian sejati, sedangkan
dengan fungsi hampiran akan menghasilkan penyelesaian hampiran, sehingga
yang dihasilkan akan bergantung pada seberapa teliti polinom menghampiri
dapat diperluas ke dalam Deret Taylor
= 0 + −0
Persamaan (2.39) merupakan penjumlahan dari suku-suku yang disebut
deret. Jika dimisalkan − 0 = , maka juga dapat ditulis menjadi Deret Taylor panjangnya tak berhingga sehingga untuk alasan praktis deret
tersebut dipotong sampai suku orde tertentu. Deret Taylor yang dipotong sampai
suku orde ke- dinyatakan dengan
= 0 + −0
Salah satu cara untuk menyatakan tingkat ketelitian suatu hampiran adalah
(big-Oh). Misalkan fungsi ( ) dihampiri dengan fungsi ( ). Jika − ( )
, dimana > 0 adalah konstanta real, maka dapat dikatakan bahwa ( )
menghampiri dengan orde penghampiran ( ) dan ditulis
= + ( )
( ) juga dapat diartikan sebagai orde galat dari fungsi hampiran. Nilai
adalah kurang dari 1, maka semakin tinggi nilai akan semakin kecil galat yang
dihasilkan sehingga hampiran fungsinya semakin teliti. Misalnya, metode yang
berorde ( 2) akan lebih teliti dibandingkan metode dengan orde ( ).
Definisi 2.3.2
Andaikan dan semua turunannya ′, ′′, ′′′,… kontinu di dalam interval [ , ].
Misalkan +1 = + , = 0, 1, 2,… adalah titik-titik selebar , hampiran untuk
( +1) dengan menggunakan deret Taylor di sekitar adalah
+1 = +1! ′ +
2
2!
′′
+⋯+
!
+� (
+1) (2.41) dimana � +1 = +1
+1 !
+1 , < <
+1, maka orde penghampiran untuk fungsi tersebut adalah +1 =� +1 .
Persamaan (2.41) juga dapat ditulis menjadi
Persamaan (2.42) menyatakan bahwa jika fungsi ( ) dihampiri dengan deret
Taylor derajat , maka suku sisanya cukup dinyatakan dengan lambang ( +1). Suku sisa ( +1), yaitu suku yang dimulai dengan perpangkatan +1.
D. METODE SATU LANGKAH
Masalah nilai awal yang telah dijelaskan pada contoh-contoh dalam subbab
sebelumnya dapat diselesaikan secara analitik sehingga penyelesaiannya disebut
penyelesaian sejati. Jika metode analitik tidak bisa lagi diterapkan, maka
penyelesaian masalah nilai awal dapat dicari dengan menggunakan metode
numerik. Penyelesaian yang dihasilkan oleh metode numerik adalah berupa
hampiran (pendekatan) terhadap penyelesaian sejati sehingga terdapat selisih
antara keduanya. Selisih tersebut disebut galat total. Ada beberapa metode
numerik yang dapat digunakan untuk menyelesaikan masalah nilai awal,
diantaranya yaitu metode Euler dan metode Deret Taylor. Kedua metode tersebut
merupakan metode satu langkah dimana untuk menghitung pendekatan pada titik
tertentu digunakan data pada satu titik sebelumnya.
1. Metode Euler
Metode Euler merupakan metode yang paling sederhana untuk
menyelesaikan masalah nilai awal dalam bentuk
′ = , , >
0 0 =�
yang mempunyai penyelesaian tunggal pada interval ∈ [ 0, ].
Langkah awal dari penyusunan metode Euler yaitu dengan membagi
interval ( 0, ) ke dalam subinterval yang sama besar. Sehingga dapat dihitung pendekatan terhadap penyelesaian sejati dari masalah nilai awal pada titik
= 0+ untuk = 0, 1, 2,…,
dimana merupakan ukuran langkah. Metode Euler diturunkan dari deret Taylor
pada ( + ) yang dipotong sampai suku orde dua
+ = + ′ +�1( ) (2.44) Kemudian substitusikan ′ = ( , ( )) ke dalam deret Taylor (2.44) sehingga
diperoleh
+ = + , +�1 (2.45) Ketika = , maka persamaan (2.45) menjadi
+1 = + , +�1 , = 0, 1, 2,…, −1
Suku �1 dapat dibuat sangat kecil dengan mengambil ukuran langkah yang cukup kecil, sehingga diperoleh bentuk umum dari metode Euler
+1 = + , untuk = 0, 1, 2,…, −1 (2.46) dimana = ( , ), +1 merupakan pendekatan terhadap +1 , merupakan pendekatan terhadap , dan merupakan pendekatan terhadap
, .
Selanjutnya, karena metode Euler disusun dari deret Taylor yang dipotong
sampai suku orde dua, maka metode tersebut mempunyai galat pemotongan, yaitu
Galat pemotongan tersebut juga dapat dinyatakan dengan
= �1 = +1 − − ,
yang diperoleh dengan memasukkan penyelesaian sejati dari masalah nilai awal
ke dalam metode numerik dan membaginya dengan ukuran langkah . Pemberian
pembagi tidak berpengaruh terhadap keakuratan metode tersebut karena ini
hanya untuk pembobotan saja.
Seperti disebutkan di awal bahwa terdapat selisih antara penyelesaian sejati
dengan penyelesaian hampiran dari suatu masalah nilai awal yang disebut galat
total. Besar galat total dari suatu metode numerik didefinisikan dengan
= − ,
dimana merupakan penyelesaian sejati dan merupakan penyelesaian
hampiran pada titik .
Contoh 2.4.1
Gunakan metode Euler dengan ukuran langkah = 0.3 untuk menghitung
penyelesaian hampiran masalah nilai awal
′ = 1−2 , > 0
0 = 1
pada interval 0 0.9, dimana penyelesaian sejati dari masalah nilai awal
Penyelesaian:
Dari masalah nilai awal yang diketahui maka diperoleh bahwa 0 = 0, 0 = 1,
′ 0 = 1.
Kemudian dengan menggunakan informasi tersebut ditarik garis singgung melalui
titik P0 0, 0 = (0,1) dengan gradien ′0 = ′ 0 = 1 dan berhenti di titik P1 1, 1 (lihat Gambar 2.4.1 (a)).
Perhitungan pada langkah selanjutnya diperoleh
1 = 0+ = 0.3
1 = 0+ ′0 = 1 + 0.3 = 1.3
′1 = 1−2 1 1 = 1−0.6 1.3 = 0.52
Kemudian ditarik garis melalui titik P1 1, 1 = (0.3, 1.3) dengan gradien
′
1 = 0.52 dan berhenti di titik P2 2, 2 (lihat Gambar 2.4.1 (b)). Pada langkah berikutnya diperoleh
2 = 1+ = 0.6
2 = 1+ ′1 = 1.3 + 0.3 × 0.52 = 1.456
′2 = 1−2 2 2 = 1−1.2 1.456 =−0.2912
Kemudian ditarik garis melalui titik P2 2, 2 = (0.6, 1.456) dengan gradien
′
2 = −0.2912 dan berhenti di titik P3 3, 3 (lihat Gambar 2.4.1 (c)). Perhitungan untuk langkah terakhir diperoleh
3 = 2+ = 0.9
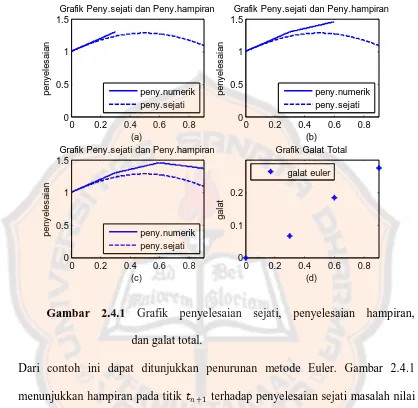
Gambar 2.4.1 Grafik penyelesaian sejati, penyelesaian hampiran,
dan galat total.
Dari contoh ini dapat ditunjukkan penurunan metode Euler. Gambar 2.4.1
menunjukkan hampiran pada titik +1 terhadap penyelesaian sejati masalah nilai awal dihitung dengan menggunakan persamaan garis yang melalui titik ( , )
dengan gradien ′ sehingga +1 = + ′ yang tidak lain merupakan metode Euler.
Contoh 2.4.2
Gunakan metode Euler untuk menyelesaikan masalah nilai awal berikut
Penyelesaian:
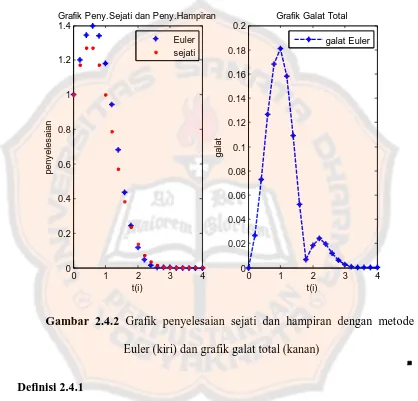
Hasil perhitungan dengan menggunakan program Matlab ditunjukkan pada
Gam-bar 2.4.2 berikut:
Gambar 2.4.2 Grafik penyelesaian sejati dan hampiran dengan metode
Euler (kiri) dan grafik galat total (kanan)
Definisi 2.4.1
Metode numerik dikatakan konvergen terhadap penyelesaian ( ) dari masalah
Berikut ini diberikan lemma yang nanti akan digunakan dalam pembuktian
teorema konvergensi dari Metode Euler.
Lemma 2.4.1
1 + untuk semua 0.
Bukti:
Dibuktikan dengan menggunakan fakta bahwa 1 untuk semua 0.
Kemudian dengan mengambil integral dari kedua ruasnya pada interval 0
(dimana 0), maka diperoleh
0 0 1 − 0 −0
1 +
Jadi terbukti bahwa 1 + .
Teorema 2.4.1
Metode Euler akan diterapkan terhadap masalah nilai awal
′ =� + ( ), 0 <
0 = 1
dimana � ∈ ℂ dan adalah fungsi yang turunannya kontinu. Metode tersebut
Bukti:
Metode Euler untuk masalah nilai awal tersebut adalah
+1 = +� +
= 1 +� + ( ) (2.47)
Sementara dari ekspansi deret Taylor (2.44) diperoleh
+1 = + ′ +�1( )
= + � + +�1
= 1 +� + +�1 (2.48) Kemudian kurangkan (2.48) dengan (2.47) diperoleh
+1 = 1 + � + +�1 +1 = 1 + � + ( )
+1 = 1 + � +�1
Selanjutnya untuk menyederhanakan penyimbolan, maka �1 diganti dengan
+1, sehingga
+1 = 1 + � + +1 (2.49) Karena 0 = 0 = �, maka 0 = 0. Persamaan (2.49) menunjukkan bahwa galat total pada langkah berikutnya ( +1) merupakan penjumlahan dari galat pemotongan lokal pada langkah tersebut ( +1) dan galat total pada langkah sebelumnya ( ). Persamaan tersebut tetap berlaku untuk persamaan diferensial
Kemudian substitusikan = 0, 1, 2 ke dalam persamaan (2.49) (gunakan 0 = 0), maka diperoleh
1 = 1
2 = 1 + � 1+ 2 = 1 + � 1+ 2
3 = 1 + � 2+ 3 = 1 + � 2 1+ 1 + � 2+ 3 Sehingga rumus umumnya adalah
= 1 + � −1
1+ 1 + � −2 2+⋯+
= =1 1 + � − (2.50) Ruas kanan dari persamaan (2.50) harus dibatasi agar nilainya mendekati nol
ketika →0.
Berdasarkan Lemma 2.4.1 (dengan = � ), maka
1 + � 1 + � �
dan karena − = − untuk dan 0 < , maka
1 + � − e(n−j) � = e � − e � .
Kemudian karena 2 untuk suatu kontanta (tidak bergantung pada atau ), setiap suku pada ruas kanan persamaan (2.50) dibatasi oleh 2 e �
sehingga
2 � = �
(dengan = ). Selama berhingga, maka = ( ) dan terbukti bahwa
Contoh 2.4.3
Jika interval pada Contoh 2.4.1 diperluas menjadi 0 3 dan dengan
mengambil ukuran langkah = 0.3, = 0.15, dan = 0.075, maka dengan
menggunakan program Matlab diperoleh hasil sebagai berikut:
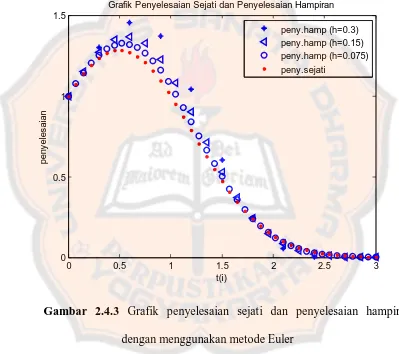
Gambar 2.4.3 Grafik penyelesaian sejati dan penyelesaian hampiran
dengan menggunakan metode Euler
Gambar 2.4.3 menunjukkan bahwa ketika ukuran langkah diperkecil, maka nilai
penyelesaian hampiran akan semakin mendekati penyelesaian sejati dari masalah
nilai awal yang diberikan. Dengan program Matlab, penghitungan galat total pada
titik 0.09 diperoleh hasil sebagai berikut,
h 0.3 0.15 0.075
Euler 0.2745 0.1325 0.0649
Tabel 2.4.1 Tabel Galat Total
Dari Tabel 2.4.1 nampak bahwa ketika ukuran langkah diperkecil setengah
kalinya, maka galat totalnya akan mengecil sekitar setengah kalinya juga. Jadi
sesuai dengan Teorema 2.4.1, metode Euler konvergen dengan orde satu, sehingga
∝ (galat total sebanding dengan ukuran langkah).
2. Metode Deret Taylor
Metode Euler yang dijelaskan sebelumnya disusun dari deret Taylor pada
( + ) di sekitar titik = yang dipotong sampai suku orde dua. Keakuratan
penyelesaian hampiran yang dihasilkan oleh metode tersebut dipengaruhi oleh
besarnya ukuran langkah yang diambil. Metode tersebut menjadi kurang efektif
karena untuk mencapai keakuratan yang baik, maka diperlukan ukuran langkah
yang kecil dan berarti diperlukan komputasi yang lebih mahal. Oleh karena itu,
dibutuhkan metode yang lebih efektif, yaitu metode deret Taylor dimana bisa
menghasilkan penyelesaian hampiran yang lebih akurat ketika diambil ukuran
langkah yang sama besar atau penyelesaian hampiran dengan keakuratan sama
ketika diambil ukuran langkah yang lebih besar.
Diberikan masalah nilai awal
′ = ( , ), >
0 0 = �
Sebelum masuk ke dalam pembahasan metode deret Taylor orde-� (bentuk
umum), terlebih dahulu akan dijelaskan mengenai metode deret Taylor orde dua.
Ekspansi deret Taylor orde dua adalah sebagai berikut
+ = + ′ + 1
2!
2 ′′ +� 2( ) dimana �2 = ( 3). Substitusikan = , dan karena
+1 = + , maka diperoleh
+1 = + ′ + 1 2!
2 ′′ + ( 3)
Suku sisa ( 3) dapat dibuat sangat kecil sehingga bisa diabaikan. Jadi diperoleh bentuk umum dari metode deret Taylor orde dua
+1 = + ′ + 1 2
2 ′′ (2.51)
dimana , ′, dan ′′ menyatakan pendekatan terhadap ( ), ′( ), dan
′′( ). Suku ′′( ) diperoleh dengan menurunkan persamaan diferensial yang
diketahui.
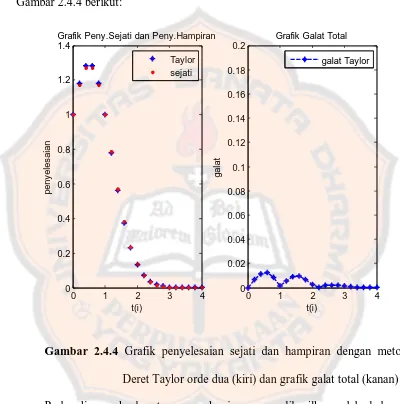
Contoh 2.4.4
Gunakan metode Deret Taylor orde dua untuk menyelesaikan masalah nilai awal
berikut
′ = 1−2
0 = 1
Penyelesaian:
Hasil perhitungan dengan menggunakan program Matlab ditunjukkan pada
Gambar 2.4.4 berikut:
Gambar 2.4.4 Grafik penyelesaian sejati dan hampiran dengan metode
Deret Taylor orde dua (kiri) dan grafik galat total (kanan)
Perbandingan keakuratan penyelesaian yang dihasilkan oleh beberapa
Berdasarkan Gambar 2.4.2 (pada Contoh 2.4.2) dan Gambar 2.4.4 (pada
Contoh 2.4.4), maka galat total maksimum dan jumlahan galat total dari metode
Euler dan Deret Taylor orde dua adalah seperti ditunjukkan dalam tabel di bawah
ini.
Metode Galat Total Maksimum Jumlahan Galat Total
Euler 0.1808 0.9853
Taylor 0.0127 0.0842
Tabel 2.4.2 Tabel Galat Total Maksimum dan Jumlahan Galat Total
Tabel 2.4.2 menunjukkan bahwa galat total maksimum dan jumlahan galat total
dari metode Deret Taylor orde dua lebih kecil daripada metode Euler. Jadi
penyelesaian yang lebih akurat adalah penyelesaian yang dihasilkan oleh metode
Deret Taylor orde dua.
Selanjutnya akan dijelaskan mengenai metode deret Taylor secara umum.
Deret Taylor orde-� pada ( + ) beserta dengan suku sisanya adalah sebagai
berikut
+ = + ′ + 1
2!
2 ′′ +⋯+ 1
�!
� � +�
�( ) (2.52)
dimana �� = �1 +1 !
�+1 �+1 (�), � ∈( , + ). Jika ada bilangan positif
sedemikian sehingga �+1 ( ) untuk semua ∈( 0, ), maka �� �+1 ! �+1,
sehingga �� = ( �+1).
Substitusikan = dan dengan mengabaikan suku sisa, maka diperoleh bentuk
+1 = + ′ +
Berikut ini diberikan lemma yang nanti akan digunakan untuk membuktikan
teorema konvergensi dari Metode Deret Taylor.
1 + + 1
Metode deret Taylor akan diterapkan terhadap masalah nilai awal
′ =� + ( ), 0 <
0 = 1
dimana � ∈ ℂ dan adalah fungsi terdiferensial kontinu � kali. Metode tersebut
konvergen dan galat totalnya pada sembarang ∈ [0, ] adalah ( �).
Bukti:
Metode deret Taylor untuk masalah nilai awal tersebut adalah
+1 = + ′ +
Sementara dengan menggunakan ekspansi deret Taylor adalah
′( ) =� ( ) + ( )
′′( ) =� ′( ) + ′ =�2 ( ) +� + ′( )
…
� = �� +��−1 +��−2 ′ +⋯+� �−2 + �−1 ( ) Kemudian kurangkan (2.57) dengan (2.56), maka diperoleh
+1 − +1 = − + � − � + Ruas kanan dari (2.58) harus dibatasi agar nilainya mendekati nol ketika →0.
Berdasarkan Lemma 2.4.2, maka untuk = � diperoleh bahwa
� �
Dan karena − = − untuk dan 0 < , maka
� − ( − ) � = � − �
Kemudian karena �+1 untuk semua konstanta , maka
�+1 � = � �
Jadi terbukti bahwa = ( �) dan metode deret Taylor konvergen pada orde �.
Contoh 2.4.5
Diketahui masalah nilai awal berikut
′ = 1−2 ( ), > 0
0 = 1
dimana mempunyai penyelesaian sejati = − 2. Gunakan metode deret
Taylor orde dua untuk menyelesaikan masalah nilai awal tersebut dengan
mengambil = 0.3, = 0.15, dan = 0.075 pada interval 0 4.
Penyelesaian:
Hasil perhitungan dengan menggunakan program Matlab ditunjukkan pada
Gambar 2.4.5 di bawah. Jika grafik pada Gambar 2.4.5 dibandingkan dengan
grafik pada Gambar 2.4.3, maka untuk nilai yang sama nampak bahwa
penyelesaian hampiran yang dihasilkan oleh metode deret Taylor orde dua lebih
akurat dibandingkan yang dihasilkan oleh metode Euler. Dengan program Matlab,