Pengintegralan numeris dengan metode gauss legendre.

vii

ABSTRAK

Integrasi numeris adalah metode yang digunakan oleh ilmuwan untuk memperoleh pendekatan penyelesaian intergral tentu yang tidak dapat diselesaikan secara analitik. Ada beberapa metode pengintegralan numeris, yaitu metode Newton-Cotes dan metode Gauss. Metode Newton-Cotes merupakan metode integrasi numeris, dimana fungsi yang akan diintegralkan didekati dengan polinom interpolasi berderajat n. Salah satu metode Newton-Cotes bentuk tertutup adalah metode trapesium. Secara Geometris, metode trapesium adalah metode yang menghampiri luas daerah berbentuk trapesium di bawah garis lurus yang menghubungkan nilai fungsi pada batas awal dan batas akhir.

viii

ABSTRACT

Numerical integration is a kind of method which is used by some scientists in gaining approaches to solve a certain integral, which cannot be solved analytically. There are some of numerical integral methods; they are Newton-Cotes method and Gauss method. Newton-Newton-Cotes method is a kind of numerical integration method, in which integral function is approached by n degrees interpolated polynomial. One of the Newton-Cotes closed methods is trapezoid method. Geometrically, trapezoid method is a kind of method which approaching the wide area of trapezoid below the straight line connecting the function numbers on the first limit and the last limit.

i

PENGINTEGRALAN NUMERIS

DENGAN METODE GAUSS-LEGENDRE

MAKALAH

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Disusun oleh: Gigih Adiguna NIM: 063114005

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA

FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA

YOGYAKARTA

ii

NUMERICAL INTEGRATION

USING GAUSS-LEGENDRE METHODS

A PAPER

Presented As Partial Fulfillment Of The Requirements to Obtain The Sarjana Sains Degree Of

Mathematics Study Program

Written by: Gigih Adiguna Student ID: 063114005

MATHEMATICS STUDY PROGRAM MATHEMATICS DEPARTMENT

FACULTY OF SCIENCE AND TECHNOLOGY

SANATA DHARMA UNIVERSITY

YOGYAKARTA

v

HALAMAN PERSEMBAHAN

"if you think you are too small to

make a difference, try sleeping

with MOSQUITO"

vi

PERNYATAAN KEASLIAN KARYA

Saya menyatakan dengan sesungguhnya bahwa makalah yang saya tulis ini tidak memuat karya atau bagian karya orang lain, kecuali yang telah disebut dalam kutipan dan daftar pustaka, sebagaimana layaknya karya ilmiah.

Yogyakarta, 31 Januari 2013 Penulis

vii

ABSTRAK

Integrasi numeris adalah metode yang digunakan oleh ilmuwan untuk memperoleh pendekatan penyelesaian intergral tentu yang tidak dapat diselesaikan secara analitik. Ada beberapa metode pengintegralan numeris, yaitu metode Newton-Cotes dan metode Gauss. Metode Newton-Cotes merupakan metode integrasi numeris, dimana fungsi yang akan diintegralkan didekati dengan polinom interpolasi berderajat n. Salah satu metode Newton-Cotes bentuk tertutup adalah metode trapesium. Secara Geometris, metode trapesium adalah metode yang menghampiri luas daerah berbentuk trapesium di bawah garis lurus yang menghubungkan nilai fungsi pada batas awal dan batas akhir.

viii

ABSTRACT

Numerical integration is a kind of method which is used by some scientists in gaining approaches to solve a certain integral, which cannot be solved analytically. There are some of numerical integral methods; they are Newton-Cotes method and Gauss method. Newton-Newton-Cotes method is a kind of numerical integration method, in which integral function is approached by n degrees interpolated polynomial. One of the Newton-Cotes closed methods is trapezoid method. Geometrically, trapezoid method is a kind of method which approaching the wide area of trapezoid below the straight line connecting the function numbers on the first limit and the last limit.

In the Newton-Cotes method, the condition before conducting integration we must decide the points with the same space limit. Those points have to start and stop on the points of interval between first and last limit. It becomes different when in Newton-Cotes method, in the Gauss method, to evaluate the wide area below the lines, it’s chosen a random point. One of the special formulas from Gauss is Gauss-Legendre. In the Gauss-Legendre method, before conducting

ix

LEMBAR PERNYATAAN PERSETUJUAN

PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS

Yang bertanda tangan di bawah ini, saya mahasiswa Universitas Sanata Dharma: Nama

Nomor Mahasiswa

: Gigih Adiguna : 063114005

Demi pengembangan ilmu pengetahuan, saya memberikan kepada Perpustakaan Universitas Sanata Dharma karya ilmiah saya yang berjudul:

PENGINTEGRALAN NUMERIS

DENGAN METODE GAUSS-LEGENDRE

beserta perangkat yang diperlukan (bila ada). Dengan demikian saya memberikan kepada Perpustakaan Universitas Sanata Dharma hak untuk menyimpan, mengalihkan dalam bentuk media lain, mengelolanya dalam bentuk pangkalan data, mendistribusikannya secara terbatas, dan mempublikasikan di internet atau media lain untuk kepentingan akademis tanpa meminta ijin dari saya maupun memberikan royalti kepada saya selama tetap mencantumkan nama saya sebagai penulis.

Demikian pernyataan ini saya buat dengan sebenarnya. Dibuat di Yogyakarta

Pada tanggal : 31 Januari 2013 Yang menyatakan

x

KATA PENGANTAR

Puji dan syukur kepada Tuhan Yang Maha Esa, atas berkat dan rahmat yang telah diberikan sehingga penulis dapat menyelesaikan makalah ini.

Dalam menulis makalah ini banyak hambatan dan kesulitan yang penulis temukan. Namun, berkat bantuan dan dukungan dari banyak pihak, akhirnya makalah ini dapat selesai. Oleh sebab itu penulis ingin mengucapkan terimakasih kepada:

1. Ibu Paulina Heruningsih Prima Rosa, S.Si., M.Sc., selaku Dekan Fakultas Sains dan Teknologi Universitas Sanata Dharma Yogyakarta.

2. Ibu Lusia Krismiyati Budiasih, S.Si., M.Si selaku Ketua Program Studi Matematika sekaligus dosen pembimbing makalah yang telah meluangkan waktu, pikiran, serta kesabarannya dalam membimbing penulis dalam menyusun makalah ini.

3. Ibu Maria Vianney Any Herawati, S.Si., M.Si selaku dosen pembimbing akademik sekaligus dosen penguji tugas akhir yang telah memberikan masukan dan saran.

4. Bapak Ir. Ig. Aris Dwiatmoko, M.Sc., selaku dosen penguji tugas akhir yang telah memberikan masukan dan saran.

5. Bapak dan Ibu Dosen Program Studi Matematika yang telah memberikan ilmu yang sangat berguna bagi penulis.

xi

7. Teman-teman angkatan 2006 tanpa terkecuali yang telah memberikan semangat kepada penulis.

Yogyakarta, 31 Januari 2013

xii

DAFTAR ISI

Halaman

HALAMAN JUDUL ………..

HALAMAN PERSETUJUAN PEMBIMBING ………

HALAMAN PENGESAHAN ………

HALAMAN PERSEMBAHAN ……….

HALAMAN PERNYATAAN KEASLIAN KARYA ………

i iii iv v vi

ABSTRAK ………..

ABSTRACT ………

HALAMAN PUBLIKASI ………..

KATA PENGANTAR ………

DAFTAR ISI ………...

DAFTAR GAMBAR ………..

vii viii

ix x xii xiv

BAB I. PENDAHULUAN ………..

A. Latar Belakang ………...

B. Perumusan Masalah ………...

C. Pembatasan Masalah ………..

D. Tujuan Penulisan ………...

E. Manfaat Penulisan ………..

F. Metode Penulisan ………...

G. Sistematika Penulisan ………

xiii

BAB II. PENGINTEGRALAN NUMERIS DENGAN METODE

NEWTON-COTES……….

A. Fungsi dan Integral Fungsi ..……….. B. Metode Newton-Cotes ………...

C. Metode Trapesium………..

6 6 33 38 BAB III. PENGINTEGRALAN NUMERIS DENGAN METODE

GAUSS-LEGENDRE ……….………

A. Metode Gauss-Legendre………... B. Metode Koefisien Tak Tentu...………... C. Metode Gauss-Legendre Dua Titik……… D. Metode Gauss-Legendre Tiga Titik ………..

BAB IV. PENUTUP ………

A. Kesimpulan ………

B. Saran ………..

DAFTAR PUSTAKA .……….

LAMPIRAN .………...

xiv

DAFTAR GAMBAR

Halaman

Gambar 2.1 ………... 7

Gambar 2.2 ………...

Gambar 2.3 ………...

Gambar 2.4 ………...

Gambar 3.1 ………...

Gambar 3.2 ………...

Gambar 3.3 ………...

Gambar 3.4 ………...

1

BAB I

PENDAHULUAN

A. LATAR BELAKANG MASALAH

Integrasi numeris adalah metode yang digunakan oleh ilmuwan untuk memperoleh pendekatan penyelesaian intergral tentu yang tidak dapat diselesaikan secara analitik. Metode analitik adalah metode penyelesaian model matematika dengan rumus-rumus aljabar yang sudah baku, yakni rumus-rumus yang sudah dibuktikan kebenarannya dan memberikan hasil sebenarnya yang memiliki galat sama dengan nol. Integrasi numeris dilakukan dengan mengevaluasi integral tentu pada batas integrasi. Ada beberapa metode pengintegralan numeris, yaitu metode Newton-Cotes dan metode Gauss. Metode Newton-Cotes terdiri dari metode trapesium dan metode Simpson. Cara kerja metode tersebut biasanya diawali dengan membagi interval integrasi menjadi beberapa subinterval dengan ukuran yang sama, kemudian mencari pendekatan luas dari setiap daerah yang terbentuk pada subinterval dan kemudian menjumlahkannya. Jika perhitungan dilakukan secara manual pada umumnya dipilih sehingga ujung setiap interval jatuh pada nilai yang mudah dihitung.

merupakan rumus paling sederhana untuk integrasi numeris. Galat rumus ini lebih besar dibandingkan dengan semua metode integrasi yang lainnya, tetapi karena kemudahan pada tekniknya, yakni fungsi yang akan diintegralkan didekati dengan fungsi linear, membuat aturan ini menjadi menarik. Metode ini penting pada setiap kasus karena menunjukkan ide dasar rumus pengintegrasi dengan ukuran interval tertentu, yakni menghampiri fungsi

) (x

f dengan garis lurus yang menghubungkan f(a) dan f(b). Dalam penerapannya, metode ini membagi seluruh interval menjadi sub-subinterval dan mendekati kurva dalam beberapa subinterval dengan kurva yang lebih sederhana, yakni kurva linear, sehingga nilai integralnya dapat dihitung secara analitis.

relatif lebih teliti dan rumusnya tidak lebih kompleks daripada metode trapesium , yakni mendekati fungsi yang akan diintegralkan dengan parabola (polinom interpolasi berderajat dua atau tiga). Karakteristik inilah yang menyebabkan metode Simpson lebih luas penggunaannya.

Berbeda dengan metode Newton-Cotes, metode Gauss dalam menghitung luas daerah di bawah garis dipilih titik sembarang secara bebas. Titik-titik tersebut dipilih untuk meminimalkan galat. Jika galat minimum, maka nilai hampirannya akan mendekati nilai sebenarnya.

B. PERUMUSAN MASALAH

Pokok – pokok permasalahan yang akan dibahas dalam tulisan ini dirumuskan sebagai berikut:

1. Apa yang dimaksud metode Gauss-Legendre?

2. Bagaimana mengintegralkan secara numeris dengan metode Gauss-Legendre?

C. PEMBATASAN MASALAH

D. TUJUAN PENULISAN

Tujuan penulisan ini adalah untuk memahami pengintegralan numeris dengan metode Gauss-Legendre dan untuk memperoleh pendekatan penyelesaian integral tentu yang memberikan ketelitian yang lebih tinggi.

E. MANFAAT PENULISAN

Manfaat yang akan diperoleh setelah mempelajari topik ini adalah dapat memahami pengintegralan numeris dengan metode Gauss-Legendre yang memberikan ketelitian yang lebih tinggi dalam mendapatkan pendekatan penyelesaian integral tentu.

F. METODE PENULISAN

Metode yang digunakan penulis adalah metode studi pustaka yaitu dengan mempelajari buku-buku yang berkaitan dengan topik makalah ini, sehingga tidak ada hal-hal baru.

G. SISTEMATIKA PENULISAN

BAB I PENDAHULUAN

A. LATAR BELAKANG MASALAH B. RUMUSAN MASALAH

D. TUJUAN PENULISAN E. MANFAAT PENULISAN F. METODE PENULISAN G. SISTEMATIKA PENULISAN

BAB II PENGINTEGRALAN NUMERIS DENGAN METODE NEWTON-COTES

A. FUNGSI DAN INTEGRAL FUNGSI B. METODE NEWTON-COTES

C. METODE TRAPESIUM

BAB III PENGINTEGRALAN NUMERIS DENGAN METODE GAUSS- LEGENDRE

A. METODE GAUSS-LEGENDRE B. METODE KOEFISIEN TAK TENTU

C. METODE GAUSS-LEGENDRE DUA TITIK D. METODE GAUSS-LEGENDRE TIGA TITIK BAB IV PENUTUP

6

BAB II

PENGINTEGRALAN NUMERIS

DENGAN METODE NEWTON-COTES

A. FUNGSI DAN INTEGRAL FUNGSI

Definisi 2.1

Relasi adalah hasil pemasangan elemen-elemen dari satu himpunan dengan elemen-elemen dari suatu himpunan kedua. Fungsi adalah relasi di mana setiap elemen dalam daerah asal dipasangkan dengan tunggal satu elemen dalam daerah hasil. Untuk memberi nama fungsi dipakai sebuah huruf tunggal seperti f _dan f(x) _{menunjukkan nilai yang diberikan oleh} f kepada x.

Daerah asal adalah himpunan semua komponen pertama dari pasangan terurut dari relasi, sedangkan daerah hasil adalah himpunan komponen keduanya. Fungsi belum dapat ditentukan bila daerah asalnya belum diberikan.

Contoh 2.1

Jika f(x)x34, tentukan daerah hasilnya untuk x2,x3,x4 dan 5

Penyelesaian

Gambar 2.1

Dari gambar 2.1 di atas himpunan



2,3,4,5



menunjukkan daerah asal fungsi, sedangkan himpunan



4,23,60,121



menunjukkan daerah hasil fungsi.

Definisi 2.2

Contoh 2.2

Buktikan fungsi f dengan f(x)4x, pada interval 1x1 adalah terbatas

Penyelesaian

Jelas f(x) 5,x

 

1,1 . Jika dipilih M 5 _maka f(x) 5 )

(x f

 terbatas untuk x

 

1,1

Definisi 2.3

Missal AR, fungsi f adalah fungsi dari A ke R. Dikatakan bahwa

L x f

c

x ( )

lim berarti bahwa untuk tiap  0 yang diberikan (betapapun kecilnya), terdapat  0 yang berpadanan sedemikian sehingga

 

L

x

f( ) asalkan bahwa 0 xc  ; yakni, 

   

 

 x c f(x) L

0

Teorema 2.1

Andaikan n bilangan bulat positif, k adalah konstanta, dan f dan g adalah fungsi-fungsi yang memiliki limit di c. Maka

1. k k

c x 

2. x c

c x 

lim ,

3. kf

 

x k f

 

x

c x c

x  lim

lim ,

4.



f

   

x g x



f

 

x g

 

x

c x c

x c

x  lim lim

lim ,

5.



f

   

x g x



f

 

x g

 

x

c x c

x c

x  lim lim

lim ,

6.



f

   

x g x



f

 

x g

 

x

c x c x c

x . lim .lim

lim ,

7. Jika g

 

x L

c

x 

lim dan lim f

 

x f(L)

c

x  , maka limxc f



g

 

x



 f(L) 8.

 

 

 

 

x g

x f

x g

x f

c x

c x c

x

    _lim

lim

lim asalkan lim

 

0

cg x

x ,

9. lim

x®céëf x

( )

ùû n

= lim

x®c f(x)

é

ë ùû

n

,

10. lim

x®c f x

( )

n = _lim

x®c f(x)

n asalkan lim

 

0

c f x

x jika n genap.

Bukti

1. Akan dibuktikan  0  0 sehingga



0 xc   kk 



Ambil sebarang  0, akan dicari  0 sehingga



     





x R 0 x c k k

Diketahui 0 xc  bila 

  1 jadi 

 

  

k 0x c 0.1 k

Menurut definisi 2.3, maka

k k

c

x 





lim

2. Akan dibuktikan  0  0 sehingga



0 xc   xc 



Ambil sebarang  0, akan dicari  0 sehingga



     





x R 0 x c x c

Ambil  0, perhatikan bahwa xc 1xc

Diketahui 0 xc  bila   jadi xc 1xc 1  Menurut definisi 2.3, maka

c x

c

x 





lim

3. Akan dibuktikan  0  0 sedemikian hingga 

   

 

 x c kf(x) kL

0

ambil sebarang  0 pilih k 

  sehingga untuk 0 xc 

Maka        

k k L x f k kL x

kf( ) ( )

 

x k f

 

x kf

c x c

x  

lim lim

4. Missal f x L

c

x ( )

lim dan g x K

c

x ( )

lim

Akan dibuktikan  0 ₁ 0 sehingga

2 )

(

0 xc ₁ f x L 

Akan dibuktikan  0 ₂ 0 sehingga

      _{     }  2 ) (

0 x c ₂ g x K  x Perhatikan bahwa K x g L x f K L x g x f K L x g x f            ) ( ) ( ) ( ) ( ) ( ) ( ) ( K x g L x

f   

 ( ) ( )

Ambil sebarang  0, jika dipilih  min



₁,₂



maka              2 2 ) ( ) ( ) ( ) ( )

(x g x L K f x L g x K

f

Menurut definisi 2.3, maka

   



f x g x



f

 

x g

 

x

c x c

x c

x     

lim lim lim

5. Akan dibuktikan



f

   

x g x



f

 

x g

 

x

c x c

x c

x  lim lim

Menurut Teorema 2.1 ) ( lim ) ( lim ) 3 ( ) ( lim ) 1 ( ) ( lim ) 4 ( ) ( ) 1 ( lim ) ( lim )) ( ) 1 ( ) ( ( lim )) ( ) ( ( lim x g x f x g x f x g x f x g x f x g x f c x c x c x c x c x c x c x c x                    

6. Akan dibuktikan  0 1 0 sehingga lim

x®c f(x)=L dan limx®cg(x)=M

) 1 ( 2 ) ( 0 ₁        M L x f c

x  

Akan dibuktikan  0 2 0 sehingga

L M x g c x 2 ) (

0  ₂   

Perhatikan bahwa

f(x)g(x)- LM

LM x Lg x Lg x g x

f   

 ( ) ( ) ( ) ( ) LM x Lg x Lg x g x

f   

 ( ) ( ) ( ) ( ) M x g L L x f x

g   

 ( ) ( ) ( )

Akan dibuktikan g(x)  M 1

- e < g(x)- M <e

M x

g

M   ( ) 

- M - 1<M- e <g(x)<M+e < M +1

1 )

(x  M  g

Sehingga

f(x)g(x)- LM £ M +1 f(x)- L +L g(x)- M

Ambil sebarang  0, Jika dipilih  min



₁,₂



maka



  

  



 

 



 

 

  

  

L L M

M

M x g L L x f M LM x g x f c

x

2 1 2

1

) ( )

( 1 )

( ) ( 0

Menurut definisi 2.3, maka





f

   

x g x



f

 

x g

 

x

c x c x c

x . lim .lim

lim

7. Akan dibuktikan  0  0 sedemikian hingga



  



   

 

 x c f g(x) f L

0

Dari f

 

y L

c

x 

lim ambil sebarang  0 pilih ₁ 0 sehingga

Dari g

 

x L

c

x 

lim ambil sebarang  0 pilih  0 sehingga untuk 

   x c

0 Maka g

 

x L ₁ atau yL ₁ dimana

 

x

g y

Dari (1) dapat dilihat bahwa

Jika 0 xc  maka f



g

 

x

  

 f L  f

   

y  f L 

8. Misalkan g x L

c x ( )

lim dan lim

x®c f(x)=M

Akan dibuktikan  0 $

d

>0 sedemikian hingga

0< x- c <d Þ f(x) g(x)

-M L <e

Ambil sebarang  0

Akan dibuktikan lim

x®c

1

g(x)= 1

L

Diketahui  0

$

d

₁

>

0

sedemikian hingga 0< x- c <d ₁Þ g(x)- L <a

Perhatikan bahwa

- a < - g(x)- L < g(x)- L

Dipilih 0

2 1



 L



- a + L < g(x)

g(x) >1 2 L 1

g(x) < 2

L

Jadi 1

g(x) -1

L =

L- g(x)

Lg(x)

= 1

Lg(x) L- g(x)

= 1

g(x) 1

L L- g(x)

< 2

L2 L- g(x)

Diketahui "

e

>0 $ d 2 >0 sedemikian hingga

0< x- c <d ₂ Þ 0< g(x)- L <1

2 L 2

e

Ambil sebarang  0, Jika dipilih d =max

{

d ₁,d ₂

}

maka 1

g(x) -1

L <

2

L2 L- g(x) <

2

L2.

1 2 L

2 .e =e

jadi terbukti bahwa \ lim

x®c

1

g(x)= 1

L

Sehingga menurut Teorema 2.1 no. 6, misal 1

lim

x®c f(x).h(x)=limx®c f x

( )

. limx®ch x

( )

=M.1

L

= M

L

=lim

x®c

f(x)

g(x)

 

 

 

 

c x

c x c

x _{g x}

x f x

g x f

   



lim lim

lim asalkan lim

 

0

cg x x

9. Misal

lim

x®c

f

(

x

)

=

L

Untuk n1 lim

x®c

[

f(x)

]

1 =lim

x®c f(x)

= lim

x®c f(x)

(

)

1

=

( )

L 1

=L

Pn yaitu lim

x®c

[

f(x)

]

n

= lim

x®c f(x)

é

ë ùû

n

benar untuk n1

Diasumsikan Pn benar untuk n=kÎ N, yaitu lim

x®c

[

f(x)

]

k

= lim

x®c f(x)

é

ë ùû

k

=Lk, kÎN









 













1 1 . ) ( lim . ) ( lim ) ( lim . ) ( lim ) ( . ) ( lim ) ( lim              k k c x k c x c x k c x k c x k c x L L L x f x f x f x f x f x f x f

jadi Pn benar untuk n=k+1, maka menurut induksi matematika



f x





f x



n n N

c x n c

x   



  ( ) lim ( )

lim

10. Misalkan n=2k, k=1 lim

x®cg(x)=L

k k

c

x g x L

2 2 _{( )}

lim 



f(x)=2kx

Menurut Teorema 2.1 no 7 maka lim

x®c g(x)

2k =_lim

x®c f(g(x))

= f lim

x®cg(x)

(

)

= lim

x®cg(x)

Contoh 2.3

Buktikan lim(3 7) 5

4  

 x

x

Penyelesaian

Menurut Teorema 2.1 lim

x®4(3x- 7)=limx®43x- limx®47 (5) =3lim

x®4x- 7 (3)dan(1)

=3.4- 7 (2)

=12- 7 =5

Definisi 2.4

Andaikan f terdefinisi pada suatu selang terbuka yang memuat c. Dikatakan bahwa f kontinu di c jika

lim f(x) f(c)

c

x  .

Contoh 2.4

Apakah

2 4 )

(

2 

 

x x x

f kontinu di titik x2

Penyelesaian

maka f(2) tidak terdefinisi Jadi f tidak kontinu di x2

Definisi 2.5

Fungsi f adalah kontinu di kanan di a _{jika lim}

x®a+ f(x)= f(a) dan

kontinu di

kiri pada b jika lim

x®b- f(x)= f(b)

Dikatakan bahwa f kontinu pada suatu selang terbuka jika f kontinu di setiap titik selang tersebut. Ia kontinu pada selang tertutup

[ ]

a,b jika kontinu pada (a,b), kontinu kanan di a dan kontinu kiri di b

Contoh 2.5

x x

f( )1 kontinu pada I (0,1)

Definisi 2.6

Turunan fungsi f adalah fungsi lain f' yang nilainya pada sebarang bilangan x adalah

h x f h x f x

f

h

) ( ) ( lim ) ( '

0

  



Jika limitnya ada, dikatakan bahwa f terdiferensialkan di x. Pencarian turunan disebut pendiferensialan. Secara umum turunan fungsi f , ditulis (n)

f , adalah suatu fungsi yang diperoleh dengan cara menghitung turunan dari fungsi f(n1),n1,2,3,... dengan f(0)(x) f(x).Turunan ke-

n dari fungsi pada titik x dapat dihitung dengan definisi

) ( ) ( ,..., 3 , 2 , 1 , ) ( ) ( lim ) ( ) ( lim ) ( ) 0 ( ) 1 ( ) 1 ( 0 ) 1 ( ) 1 ( ) ( x f x f n h x f h x f x t x f t f x f n n h n n x t n               Contoh 2.6

Hitunglah turunan pertama dari fungsi f(x)13x6, untuk x4

Penyelesaian

Turunan pertama dari fungsi f(x)13x6 untuk x4 adalah

Teorema 2.2

Jika f'(c) ada, maka f kontinu di c.

Bukti

Akan ditunjukan lim f(x) f(c)

c

x  .

c x c x c x c f x f c f x

f  

    ( ) ( ) ( ).( ), ) (

oleh karena itu, jika diambil limitnya di x®c

) ( 0 ). ( ' ) ( ) ( lim . ) ( ) ( lim ) ( lim ) .( ) ( ) ( ) ( lim ) ( lim c f c f c f c x c x c f x f c f c x c x c f x f c f x f c x c x c x c x c x             _         

Teorema 2.3

Jika f(x)k dengan k suatu konstanta, maka untuk sebarang x, f'(x)0, yakni

0 ) (k  Dx

Bukti

0 0 lim lim

) ( ) ( lim ) ( '

0 0

0

 

 

  

 



h h

h

h k k

h x f h x f x

f

Teorema 2.4

Jika f(x)x, maka f'(x)1, yakni

1 ) (x  D_x

Bukti

1 lim lim

) ( ) ( lim ) ( '

0 0

0

 

  

  

 



h h h

x h x

h x f h x f x

f

h h

Teorema 2.5

Jika n

x x

f( ) , dengan n bilangan bulat positif, maka f'(x)nxn1, yakni 1

) ( n  n

x x nx

D Bukti h h nxh h x n n nx h h x h nxh h x n n h nx x h x h x h x f h x f x f n n n n h n n n n n n h n n h h      _{  }                            1 2 2 1 0 1 2 2 1 0 0 0 ... 2 ) 1 ( lim ... 2 ) 1 ( lim ) ( lim ) ( ) ( lim ) ( '

Di dalam kurung, semua suku kecuali yang pertama mempunyai h sebagai faktor, sehingga masing-masing suku ini mempunyai limit nol bila h mendekati nol. Jadi

1

) (

' x nxn f

Teorema 2.6

Jika k suatu konstanta dan f suatu fungsi yang terdeferensialkan, maka ) ( ' . ) ( )'



k.f(x)



k.D f(x)

Dx  x

Bukti

Andaikan F(x)k.f(x). Maka

) ( ' .

) ( ) ( lim .

) ( ) ( . lim

) ( . ) ( . lim

) ( ) ( lim ) ( '

0 0 0 0

x f k

h x f h x f k

h x f h x f k

h

x f k h x f k

h x F h x F x

F

h h h h



  

  

  

  

   

Teorema 2.7

Jika f dan g adalah fungsi-fungsi yang terdiferensialkan, maka )

( ' ) ( ' ) ( )'

(f g x  f x g x yakni, D_x



f(x)g(x)



D_xf(x)D_xg(x)

Bukti



 



) ( ' ) ( ' ) ( ) ( lim ) ( ) ( lim ) ( ) ( ) ( ) ( lim ) ( ) ( ) ( ) ( lim ) ( ' 0 0 0 0 x g x f h x g h x g h x f h x f h x g h x g h x f h x f h x g x f h x g h x f x F h h h h                             Teorema 2.8

Jika f dan g adalah fungsi-fungsi yang terdiferensialkan, maka ) ( ' ) ( ' ) ( )'

(f g x  f x g x yakni, Dx



f(x)g(x)



Dxf(x)Dxg(x)

Bukti













) ( ) ( ) ( ) 1 ( ) ( ) ( ) 1 ( ) ( ) ( ) 1 ( ) ( ) ( ) ( x g D x f D x g D x f D x g D x f D x g x f D x g x f D x x x x x x x x             Teorema 2.9

Misalkan f C

 

a,b dan f terdeferensial pada

 

a,b . Jika f(a) f(b) , maka ada paling sedikit satu bilangan c

 

a,b sedemikian sehingga

Bukti

Karena f(x) kontinu pada selang axb, berarti f(x) mempunyai nilai maksimum M dan nilai minimum m dalam

 

a,b , jadi m f(x)M dalam

 

a,b . Bila mM, maka f(x)= konstan, berarti f(x)0.

Karena mM dan f(a) f(b), maka paling sedikit salah satu m atau M tidak sama dengan f(a) f(b), misalnya M  f(a). Maka nilai maksimum

M tidak pada titik akhir dari

 

a,b , melainkan terletak di xc , (acb)

dan berarti f'(c)0.

Teorema 2.10

Jika f kontinu pada selang tertutup

 

a,b dan terdefinisikan pada titik-titik dalam dari

 

a,b , maka terdapat paling sedikit satu bilangan c dalam

 

a,b dengan

) ( ' ) ( ) (

c f a

b a f b f

 



Bukti

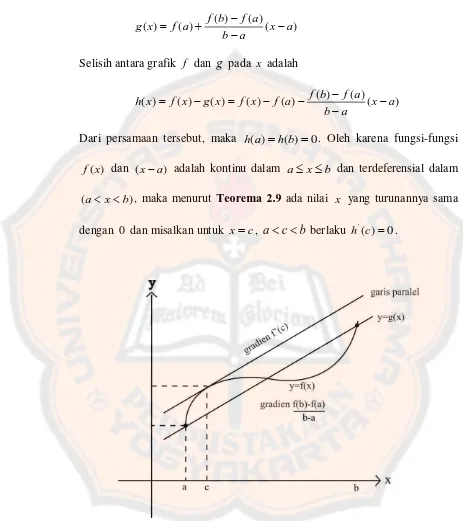
[image:42.612.69.532.196.622.2]

) ( ) ( ) ( ) ( )

( x a

a b

a f b f a f x

g 

  



Selisih antara grafik f dan g pada x adalah

) ( ) ( ) ( ) ( ) ( ) ( ) ( )

( x a

a b

a f b f a f x f x g x f x

h 

  

 

 

Dari persamaan tersebut, maka h(a)h(b)0. Oleh karena fungsi-fungsi

) (x

f dan (xa) adalah kontinu dalam a xb dan terdeferensial dalam

)

[image:43.612.69.532.103.624.2]

(a xb , maka menurut Teorema 2.9 ada nilai x yang turunannya sama dengan 0 dan misalkan untuk xc, acb berlaku h'(c)0.

diperoleh

a b

a f b f x f x h

  

 ( ) ( ) ( )

)

( '

'

Untuk persamaan xc, menjadi

a b

a f b f c f c h

  

 ( ) ( ) ( )

)

( '

'

a b

a f b f c f

  

 ( ) ( ) ( )

0 '

a b

a f b f c f

 

 ( ) ( )

) ( '

Definisi 2.7

Fungsi F dikatakan anti turunan dari fungsi f pada selang I jika )

( ) (

' x f x

F  untuk semua xdi I .

Leibniz menggunakan lambang



...dxuntuk menunjukkan anti turunan terhadap x, sama seperti D_x menunjukkan turunan terhadap x. Perhatikan bahwa Dx



f(x)dx f(x).

Teorema 2.11



  

 

1 ,

1

1 1

n c x n dx

xn n

Bukti

Untuk menunjukkan hasil berbentuk



f(x)dxF(x)c

maka ditunjukan



F(x) c



f(x)

Dx  

n

n n

x

x n n c n

x Dx



      

 

 



) 1 ( 1 1 1

1

 c

n x dx x

n

n 



 



1₁

Teorema 2.12

Jika f adalah fungsi yang terintegralkan dan k suatu konstanta maka



kf(x)dxk



f(x)dx.

Bukti

Berdasarkan Teorema 2.6





) (

) ( )

(

x kf

x f kDx dx

x f k Dx









Teorema 2.13

Jika f dan g adalah fungsi-fungsi yang terintegralkan maka







f(x)g(x) dx



f(x)dx



g(x)dx.

Bukti

Diferensialkan ruas kanan Berdasarkan Teorema 2.7





) ( ) (

) ( )

( )

( )

(

x g x f

dx x g Dx dx x f Dx dx x g dx x f Dx

 

 











Teorema 2.14

Jika f dan g adalah fungsi-fungsi yang terintegralkan maka



f x g x



dx f x dx g x dx

Bukti

Berdasarkan Teorema 2.8





) ( ) (

) ( )

( )

( )

(

x g x f

dx x g Dx dx x f Dx dx x g dx x f Dx

 

 











Definisi 2.8

Andaikan f suatu fungsi yang didefinisikan pada selang tertutup

 

a,b . Jika





 

n

i

i i

P f x x

1 0 ( )

lim ada maka f _dikatakan terintegralkan pada

 

a,b .

selanjutnya



b

a

dx x

f( ) disebut integral tentu f dari a ke b dan diberikan

oleh







 

 n

i

i i P

b

a

x x f dx

x f

1 0 ( ) lim

)

(

Teorema 2.15

Andaikan f kontinu pada

 

a,b dan andaikan F sebarang anti turunan dari f di selang

 

a,b . Maka

) ( ) ( )

(x dx F b F a f

b

a

 

Bukti

Andaikan P:ax₀x₁x₂...x_n1x_nb adalah partisi sebarang dari

 

a,b . Maka







               n i i i n n n n x F x F x F x F x F x F x F x F a F b F 1 1 0 1 2 1 1 ) ( ) ( ) ( ) ( .... ) ( ) ( ) ( ) ( ) ( ) (

Menurut Teorema 2.10 yang diterapkan pada F pada selang



x_i1,x_i



, i i i i i i

i F x F x x x f x x

x

F( ) ( _1) '( )(  _1) ( )

untuk suatu pilihan xi dalam selang terbuka



xi1,xi



. Jadi



    n i i i x x f a F b F 1 ) ( ) ( ) (

Bilamana kedua ruas diambil limitnya untuk P 0, diperoleh





      b a n i i i

P f x x f x dx

a F b

F( ) ( ) lim ( ) ( )

1 0

Contoh 2.7

Tentukan



x2dx dan



3

0 2

Penyelesaian

c x dx

x  



2 3

3 1

dan



  

3

0

3

3 _{3 0 9}

3 1 dx x

B. METODE NEWTON-COTES

Metode Newton-Cotes merupakan metode integrasi numeris, dimana fungsi yang akan diintegralkan didekati dengan polinom interpolasi pn(x).

Definisi 2.9

Misal n0. Diberikan fungsi bernilai real f , terdefinisi dan kontinu pada selang tertutup

 

a,b , dan titik-titik interpolasinya xi

 

a,b,i0,...,n,

polinomial p_n didefinisikan dengan

 



   



 n

k

h k

n x L x f x

p

0

dengan

 





 

  n

i k i

i k

k i

x x

x x x

L

0

Contoh 2.8

Akan disusun polinom interpolasi Lagrange berderajat 2 untuk fungsi x

x

f : 3 pada interval

 

1,1 , dengan titik-titik interpolasi

1 , 0 ,

1 _{1 2}

0  x  x 

x

Penyelesaian

Karena n2, maka

  













1



2

1

2 0 1 0

2 1

0 _{ }  

 

 x x

x x x x

x x x x x L

 

2

1 x 1 x

L  

 



1



2 1 2 x  x x L

Oleh karena itu

 



  





 



1

  

31 2

1 0 3 1 1 3 1 2

1 2

2 x  x x   x  x x

p

 







1



2 3 1 2

3

2 x  x x  x x

p

Teorema 2.16

ada dan kontinu pada

 

a,b . Maka untuk setiap x

 

a,b , terdapat

 

a b

x c

c ( ) , _{sedemikian hingga}

) ( )! 1 (

) ( )

( )

( ₁

1

x n

c f x p x

f _n

n

n 



 

  (2.1)

dengan

) )...( (

)

( ₀

1 n

n x  xx xx

 (2.2)

Bukti

Jika xx_i, untuk suatu i, i0,1,...,n, kedua ruas pada persamaan (2.1) sama dengan 0, dan persamaan tersebut akan dipenuhi secara trivial. Misalkan x

 

a,b dan x xi,i0,1,...,n. Untuk nilai x yang demikian,

pertimbangkan sembarang fungsi tg

 

t , yang terdefinisi pada interval

 

a,b dengan

 

) ( )

( ) ( ) ( ) ( )

( ₁

1

t x

x p x f t p t f t

g _n

n n

n 



 



 

 _(2.3)

Khususnya, jika n0, maka berdasarkan Teorema Rolle, ada cc

 

x pada interval

 

a,b sehingga g'

 

c 0. Karena p₀

   

x  f x₀ dan

 

0

1 t tx

 , menurut persamaan (2.3) maka

 

 

 

   

 

 

     

   

 

 

) ( ) ( ' ) ( ' 0 ) ( ) ( ' ) ( ' 0 ) ( ) ( ) ( ) ( 1 0 1 0 1 1 0 0 1 1 0 0 x x p x f c f c g x x f x f c f c g c x x f x f x f c f c g t x x p x f t p t f t g                      

Sekarang misalkan n1. Karena g'(t) bernilau nol pada n1 titik di

 

a,b , berdasarkan Teorema Rolle, g" bernilai nol di n titik yang berbeda.

Jika langkah ini dilakukan sebanyak n1 maka g(n1) akan bernilai nol di suatu titik c

 

a,b , nilai dari ctergantung pada nilai x. Dengan menurunkan fungsi g(t) sebanyak n1kali maka

 

 

  

! 1 ) ( ) ( ) ( 0 1 0 ) 1 (

1    

Polinom interpolasi menjadi dasar metode Newton-Cotes. Gagasannya adalah menghampiri fungsi f(x) dengan polinom interpolasi p_n

 

x . Secara umum integral suatu fungsi didekati dengan persamaan berikut







 b a

b

a

n x dx p dx x f

I ( ) ( ) (2.4)

dimana

n n n n

n x a a x a x a x a x

p ( ) ₀ ₁  ₂ 2... _1 1 (2.5) adalah polinomial berderajat n.

[image:54.612.68.539.101.595.2]

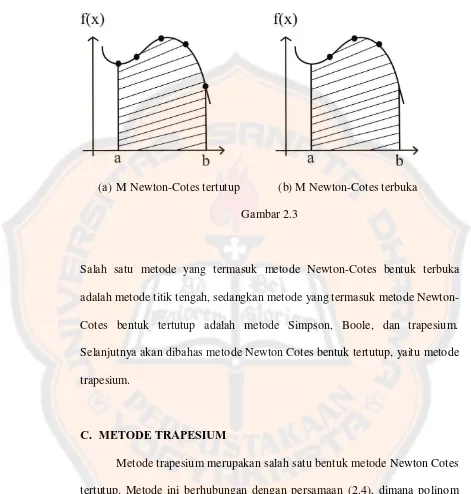
(a) M Newton-Cotes tertutup (b) M Newton-Cotes terbuka

Gambar 2.3

Salah satu metode yang termasuk metode Newton-Cotes bentuk terbuka adalah metode titik tengah, sedangkan metode yang termasuk metode Newton-Cotes bentuk tertutup adalah metode Simpson, Boole, dan trapesium. Selanjutnya akan dibahas metode Newton Cotes bentuk tertutup, yaitu metode trapesium.

C. METODE TRAPESIUM

[image:55.612.73.537.95.636.2]

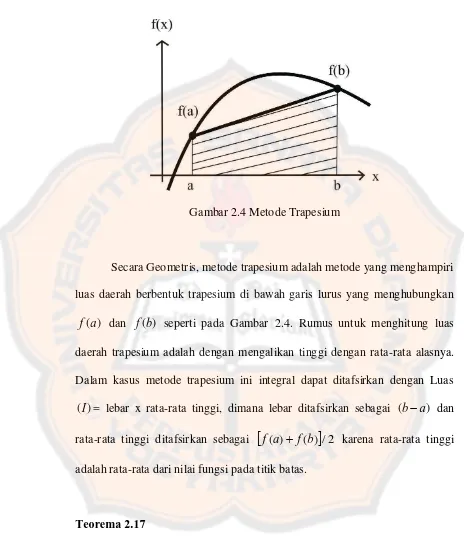
Gambar 2.4 Metode Trapesium

Secara Geometris, metode trapesium adalah metode yang menghampiri luas daerah berbentuk trapesium di bawah garis lurus yang menghubungkan

) (a

f dan f(b) seperti pada Gambar 2.4. Rumus untuk menghitung luas daerah trapesium adalah dengan mengalikan tinggi dengan rata-rata alasnya. Dalam kasus metode trapesium ini integral dapat ditafsirkan dengan Luas

)

(I = lebar x rata-rata tinggi, dimana lebar ditafsirkan sebagai (ba) dan rata-rata tinggi ditafsirkan sebagai



f(a) f(b)



/2 karena rata-rata tinggi adalah rata-rata dari nilai fungsi pada titik batas.

Teorema 2.17

3 ) )( ( '' 12 1 2 ) ( ) ( ) ( )

(x b a f a f b f c b a

f b a     



, dengan c(a,b) (2.6)

Bukti

Pada Gambar 2.4 fungsi f(x) dihampiri dengan garis lurus yang melalui titik



a,f(a)



dan



b, f(b)



. Persamaan garis lurus yang melalui kedua titik

tersebut adalah a b a x a f b f a f x f      ) ( ) ( ) ( ) ( atau



f(x) f(a)



ba

 

 xa



f(b) f(a)





 









a b a f b f a x a f x f      ( ) ( ) ( ) ) ( ) ( ) ( ) ( ) ( )

( x a

a b a f b f a f x f    

 (2.7)

dengan demikian persamaan 2.4 dapat ditulis sebagai

dx a x a b a f b f a f dx x f I b a b a





_  _      ( ) ( ) ( ) ( )( ) b a a x a b a f b f x a f _      _     2 ) ( ) ( 2 ) ( ) ( ) ( 2 ) ( ) ( 2 ) ( ) ( ) )(

( b a

   



 

 



2 ) ( ) ( ) ( )

(b a f a f b f a

2 ) ( ) ( )

(ba f b  f a 

sehingga menghasilkan persamaan

2 ) ( ) ( )

(b a f a f b

I    (2.8)

Persamaan (2.8) disebut metode Trapesium.

Ketika bekerja pada daerah integral di bawah garis lurus untuk menghampiri integral di bawah kurva, akan memunculkan sebuah galat. Penafsiran untuk galat pemotongan dari penggunaan metode trapesium adalah



( ) ( )



2

)

(x dx h f a f b f

E b

a

t 



  , dengan hba

Menguraikan f(x) ke dalam deret Taylor di sekitar x_a a diperoleh

... '' )' ( 6 1 ' )' ( 2 1 )' ( ) ( )

(x  f a xf a  x2f a  x3f a  f

Menguraikan f(b) f(xb) f(h) ke dalam deret Taylor di sekitar xa a diperoleh

 

( )''

2 1 ) ( ) ( )

( )

(b f x f h f a hf a ' h2f a

f  _b     +...

    _{  }       _{   } 



... ' )' ( 2 1 )' ( ) ( 2 ) ( 2 ... '' )' ( 6 1 | ' )' ( 2 1 )' ( ) ( 2 3 2 a f h a hf a f h a f h dx a f x a f x a xf a f E b a                 _{  }        _{  }  ... )" ( 4 1 )' ( 2 ) ( ... )" ( 6 1 )' ( 2 1 ) ( ... )" ( 6 1 )' ( 2 1 ) ( 3 2 3 2 3 2 a f h a f h a hf a f a a f a a af a f b a f b a bf                 _{  }

 ( )" ...

4 1 )' ( 2 ) ( ... )" ( 6 1 )' ( 2 1 ) ( 3 2 3 2 a f h a f h a hf a f h a f h a hf ... )" ( 12 1 ₃  

 h f a

b c a c

f

h  



 "( ), 12 1 ₃ Jadi 3 '' ) )( ( 12 1 a b c f

E_t   (2.9)

Contoh 2.9

Gunakan metode trapesium untuk menghampiri nilai integral 5 4 3 2 400 900 675 200 25 2 . 0 )

(x x x x x x

f      

dari a0ke b0.8

Penyelesaian

Nilai fungsi f(x) di titik a0dan b0,8 masing-masing adalah 5 4 3 2 ) 0 ( 400 ) 0 ( 900 ) 0 ( 675 ) 0 ( 200 ) 0 ( 25 2 . 0 ) 0 (       f 2 . 0  dan 5 4 3 2 ) 8 . 0 ( 400 ) 8 . 0 ( 900 ) 8 . 0 ( 675 ) 8 . 0 ( 200 ) 8 . 0 ( 25 2 . 0 ) 8 . 0 (       f 232 . 0 072 . 131 64 . 368 6 . 345 128 20 2 . 0       

Bila kedua hasil diatas disubstitusikan ke dalam persamaan (2.8) maka diperoleh 1728 . 0 2 232 . 0 2 . 0 ) 0 8 . 0 (     I

Bila



8 , 0 0 ) (x

f ditentukan secara analitik maka diperoleh



    







x x x x x dx

   

 _{    } 0,8

0 6 5 4 3 2 6 400 5 900 4 675 3 200 2 25 2 .

0 x x x x x x

6438 , 1 48 , 17 9824 , 58 12 , 69 13 , 34 8 16 ,

0      

Dengan demikian nilai analitiknya adalah 1,6438

Menghampiri nilai galat sangat diperlukan agar dapat diketahui besar kesalahan perhitungan. Untuk mendapatkan nilai hampiran galat tersebut, turunan kedua fungsi pada interval dapat ditentukan dengan menurunkan fungsi asli dua kali sehingga menghasilkan

4 512 1728 1620 400 ) 8 . 0 , 0 ( ), 4 . 0 ( 8000 ) 4 . 0 ( 10800 ) 4 . 0 ( 4050 400 8000 10800 4050 400 ) ( 3 2 3 2 ''                  x dengan x x x x f 1706 . 0 ) 8 . 0 )( 4 ( 12

1 3 

  t E Sehingga 00213 . 0 1706 . 0 1728 .

0  



Et

45

BAB III

PENGINTEGRALAN NUMERIS

DENGAN METODE GAUSS-LEGENDRE

Metode yang umum untuk memperoleh nilai hampiran dengan metode integrasi numeris adalah metode Newton-Cotes. Metode ini dijabarkan dengan mengintegralkan polinom interpolasi. Polinom interpolasi digunakan karena suku-suku polinom mudah diintegralkan dengan rumus integral yang sudah baku. Metode Newton-Cotes memiliki 3 metode integrasi numeris yaitu metode trapesium, metode Simpson 1/3, dan metode Simpson 3/8 yang masing-masing menghampiri fungsi f(x)dengan polinom interpolasi derajat 1, derajat 2, dan derajat 3. Hampiran nilai integrasi yang lebih baik dapat ditingkatkan dengan menggunakan polinom interpolasi berderajat yang lebih tinggi. Dalam metode Newton-Cotes sebelum melakukan integrasi harus menentukan titik-titik yang berjarak sama. Titik-titik tersebut harus berawal dan berakhir di ujung-ujung selang a yang disebut batas awal dan b yang disebut batas akhir. Selanjutnya akan dibahas metode integrasi numeris yang juga digunakan untuk memperoleh nilai hampiran, metode tersebut adalah metode Gauss.

Titik- titik x1,x2,...,xn pada interval

 

a,b dan koefisien c1,c2,...,cn dipilih untuk meminimalkan galat sehingga diperoleh rumus hampiran



b 



_ a

n

i

i if x c dx x f

1

) ( )

( (3.1)

Salah satu rumus khusus Gauss adalah Rumus Gauss-Legendre.

A. METODE GAUSS-LEGENDRE

[image:63.612.68.536.93.645.2]

Gambar 3.1

[image:64.612.71.541.90.715.2]

Gambar 3.2

Dalam metode Gauss-Legendre tidak lagi ditentukan titik-titik diskret yang berjarak sama seperti pada metode Newton-Cotes. Pada sub bab selanjutnya akan dijelaskan mengenai pemilihan titik-titik tersebut untuk memperkecil kesalahan memperoleh nilai hampiran.

B. METODE KOEFISIEN TAK TENTU

Persamaan garis yang melalui dua titik (a,f(a))dan



b,f

 

b



adalah

a b

a x a f b f

a f y

   

 ) ( ) (

) (

(3.2)

atau

 

a b

a f b f a x a f y

  



dan luas daerah trapesium di bawah garis adalah



    

2 b f a f a b

I    (3.4)

Persamaan (3.4) dapat dinyatakan sebagai ) ( )

( _{1 2 2}

1f x c f x c

I   (3.5) dimana c₁ dan c₂ adalah konstanta.

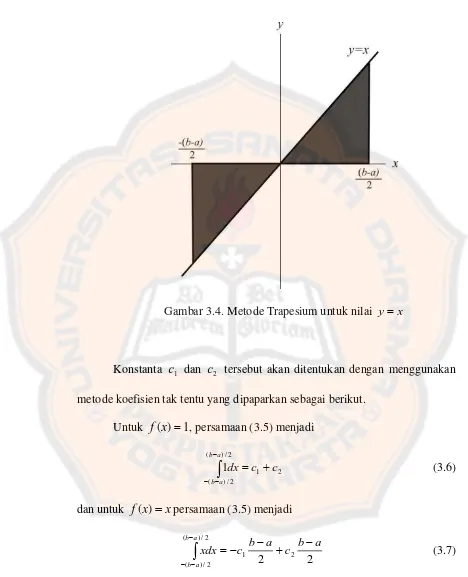
[image:65.612.67.537.136.615.2]

Metode trapesium dapat menghasilkan hasil yang tepat ketika fungsi yang diintegrasikan tersebut adalah suatu konstanta atau garis lurus. Dua persamaan yang sederhana ditunjukan pada kasus y 1 dan y x. Keduanya diilustrasikan pada Gambar 3.3.

[image:66.612.71.539.92.669.2]

Gambar 3.4. Metode Trapesium untuk nilai y x

Konstanta c_{1 dan} c_{2 tersebut akan ditentukan dengan menggunakan} metode koefisien tak tentu yang dipaparkan sebagai berikut.

Untuk f(x)1, persamaan (3.5) menjadi

2 1 2 / ) (

2 / ) (

1dx c c

a b

a b

 



  

(3.6)

dan untuk f(x) xpersamaan (3.5) menjadi

2

2 2

1 2

/ ) (

2 / ) (

a b c a b c xdx

a b

a b

    



  

(3.7)

2 2

2 1

a b a b c

c     

a b c

c₁  ₂   (3.8)

dan untuk persamaan (3.7) menjadi

2 2

2 1

2 2 1 2

2 1 2

2 

 



 

         

  

c b a c b a b a b a

0 2

2 2

1 

  

c b a c b a (3.9)

Persamaan (3.8) dan (3.9 ) merupakan dua persamaan dengan dua koefisien yang tidak diketahui. Penyelesaian dari sistem persamaan tersebut untuk c₁danc₂adalah

2

2 2

1

a b c a b

c   

2 1 c c 

2 2 c c a b  

2 2c a b 

2

2 c

a b _

2 2 1

a b c

c    (3.10)

) ( 2 ) (

2 1 f x2

a b x f a b

I     (3.11)

Persamaan tersebut ekuivalen terhadap metode trapesium.

C. METODE GAUSS-LEGENDRE DUA TITIK

Seperti halnya metode trapesium, tujuan metode Gauss-Legendre 2-titik adalah menentukan koefisien sebuah persamaan dalam bentuk

) ( )

( _{1 2 2}

1f x c f x c

I   (3.12)

Teorema 3.1 Gauss-Legendre Dua Titik

Jika f fungsi kontinu pada

 

1,1 maka dengan metode Gauss-Legendre

2-titik ) (