www.elsevier.com/locate/dsw
Elementary closures for integer programs
(
Gerard Cornuejols
∗, Yanjun Li
Graduate School of Industrial Administration, Carnegie Mellon University, Schenley Park, Pittsburgh, PA 15213-1342, USA
Received 19 June 2000; received in revised form 1 October 2000
Abstract
In integer programming, theelementary closureassociated with a family of cuts is the convex set dened by the intersection of all the cuts in the family. In this paper, we compare the elementary closures arising from several classical families of cuts: three versions of Gomory’s fractional cuts, three versions of Gomory’s mixed integer cuts, two versions of intersection cuts and their strengthened forms, Chvatal cuts, MIR cuts, lift-and-project cuts without and with strengthening, two versions of disjunctive cuts, Sherali–Adams cuts and Lovasz–Schrijver cuts with positive semi-deniteness constraints. c2001 Published by Elsevier Science B.V.
Keywords:Integer programming; Cutting plane; Elementary closure
1. Introduction
Recently, the integer programming community has emphasized that many of the cuts found in the lit-erature are essentially the same. Chvatal cuts [12] are equivalent to Gomory fractional cuts [20,21,23]. Lift-and-project cuts [4] are disjunctive cuts [3]. Go-mory mixed integer cuts [22], disjunctive cuts [2,9,24] and mixed integer rounding cuts [28] are equivalent [26]. It is natural to ask which of these cuts are in-trinsically dierent. This is the purpose of this pa-per. Our approach is to compare the corresponding elementary closures. Given an integer program PI ≡
{(x; y)∈Z+n ×R
p
+|Ax+Gy6b}and a familyF of
inequalitiesx+y6generated fromP≡ {(x; y)∈
(
Supported by NSF grant DMI-9802773 and ONR grant N00014-97-1-0196.
∗Corresponding author.
E-mail address:[email protected] (G. Cornuejols).
Rn++p|Ax+Gy6b}and valid forPI, theelementary
closurePFis a convex set obtained as the intersection of all the inequalities in F. This concept was intro-duced by Chvatal [12] for a specic family of cuts. In this paper, we consider elementary closures associ-ated with other families of cuts. Some of the cuts that we consider are designed for mixed integer programs, others just for mixed 0,1 programs or pure integer pro-grams. They can all be applied to pure 0,1 propro-grams. We compare 18 families of cuts that have appeared in the literature by comparing the corresponding 18 elementary closures. We show that ten of these sets are distinct and we establish all inclusion relationships between them.
2. Several classical families of cuts
Let A and G be given rational matrices (dimen-sionsm×n andm×p, respectively) andb a given
rational column vector (dimension m). Consider the polyhedron P ≡ {(x; y) ∈ Rn+p|Ax+Gy6b}. A
cut is a valid inequality for the set PI ≡ {(x; y) ∈
Zn×Rp|Ax+Gy6b}. We will sometimes restrict our attention to the pure case (p= 0) or to the mixed 0,1 case (the constraintsAx+Gy6b contain the in-equalities 06x61). In all cases, we assume, without loss of generality, thatx¿0 andy¿0 are part of the constraints forP.
2.1. Chvatal cuts andPC
In the pure case, the inequality⌊uA⌋x6⌊ub⌋is valid forPIfor anyu∈Rm+. Here,⌊uA⌋denotes the vector
obtained from the vectoruAby rounding down every component to an integer. These cuts are known as
Chvatal cuts [12]. Let PC denote the corresponding
elementary closure.
2.2. Gomory fractional cuts andPF,PFB,PFBF
In the pure case, Gomory [20,21,23] introduced fractional cuts when the constraints are in equality form. Assume, without loss of generality, that Aand
bare integral. Note thatP={x∈Rn|Ax6b}can be
Pluggings=b−Axinto it, we get thefractional cut
⌊uA⌋x− ⌊u⌋Ax6⌊ub⌋ − ⌊u⌋bin the space ofx. LetPF
denote the elementary closure of the fractional cuts. Originally, Gomory proposed to generate fractional cuts from basic feasible solutions ofP′. Letz= (x
s)∈
R+n+m. ThenP′={z∈R+n+m|(A; I)z=b}. Consider a
basic feasible solution zofP′. LetBandNbe the index
sets of its basic and nonbasic variables, respectively. Then, fori∈B,
is obtained as a linear combination of the equations in the original systemAx+s=bwith some multipli-ers u∈Rm. Clearly,u depends on zandi, and there is only a nite number of such choices. Any Gomory fractional cut obtained this way is called afractional cut from a basic feasible solution. Let PFBF be the
corresponding elementary closure. Similarly, let PFB
be the elementary closure of the fractional cuts gen-erated from all the basic solutions.
2.3. Gomory mixed integer cuts andPMI,PMIB,
PMIBF
In [22], Gomory introduced cuts that are at least as strong as his fractional cuts in the pure case and, in addition, can be applied to the mixed case. LetP′=
{(x; y; s)∈Rn+p+m|Ax+Gy+s=b; s¿0}andP′
The following inequality, known as Gomory mixed integer cuts[22], is valid forP′
I: for PI. LetPMI denote the corresponding elementary
closure.
Just as we dened fractional cuts from basic feasible solutions, we can also denemixed integer cuts from basic feasible solutions.
LetPMIBF be the elementary closure of the mixed
integer cuts generated from basic feasible solutions and letPMIB be the elementary closure of the mixed
integer cuts generated from all the basic solutions.
2.4. Mixed integer rounding cuts andPMIR
Letc1x+hy6c1
is valid for PI [28]. These cuts were introduced by
Nemhauser and Wolsey [28] and are calledmixed in-teger rounding cuts. Let PMIR be the corresponding
elementary closure.
2.5. Disjunctive cuts andPD
For any (; 0) ∈ Zn+1, dene P(; 0) to be the
{x60} and P ∩ {x¿0 + 1}. Inequalities that
are valid for someP(; 0) are calleddisjunctive cuts
orD-cuts. Disjunctive cuts were introduced by Balas [3]. They are also called split cuts [15]. D-cuts can be obtained as follows [2,9,24]: ifcx+hy−(x−
0)6c0 andcx+hy+(x−0−1)6c0 are two
valid inequalities forP, where¿0,¿0, (; 0)∈
Zn+1, thencx+hy6c0is aD-cut and, conversely, all
D-cuts can be obtained this way.
PD ≡ T(; 0)∈Zn+1P(; 0) is the elementary
clo-sure of theD-cuts.
2.6. Simple disjunctive cuts andPSD
In the mixed 0;1 case, the D-cuts can be special-ized to those arising from the disjunction (xj60) or (xj¿1), i.e., valid inequalities for the union of the polyhedraP∩ {xj60}andP∩ {xj¿1}. LetPSD
de-note the elementary closure of thesesimple D-cuts.
2.7. Lift-and-project cuts andPL&P,PL&P+S
These cuts can be obtained in the mixed 0,1 case. For a givenj∈ {1; : : : ; n}, form the nonlinear system (1−xj)(b−Ax−Gy)¿0;
xj(b−Ax−Gy)¿0;
and linearize it by substituting xj for x2j; zi for
xixj; i6=j; andwi forxjyi. Then project this higher dimensional polyhedron back into the (x; y) space. The resulting polyhedron is denoted byPj. It is easy to see thatPI⊆Pj. Therefore any valid inequality for
PL&P ≡ TjPj is valid forPI. Valid inequalities for
PL&P are calledlift-and-project cuts[4]. See Sherali
and Adams [30] and Lovasz and Schrijver [25] for earlier related work.
It can be shown [3,4] that any valid inequality
(yx)¿ for Pj corresponds to a feasible solution (; )∈Rn+p+1of the polyhedral coneQ
(∗)
+u(A; G)−u0ej¿0;
+v(A; G)−v0ej¿0;
−ub=;
−vb+v0=;
u; v¿0;
whereejdenotes thejth unit vector. Furthermore the extreme rays of the coneQ correspond to the facets ofPjwhenPj6=∅. Notice that if (; ) is an extreme ray ofQ, then= max{1; 2}, where
1=u0ej−u(A; G);
2=v0ej−v(A; G):
The lift-and-project cut (xy)¿is derived from the 0 –1 condition on a single variablexj, even though we allow the choice ofxj to be arbitrary. These cuts can be strengthened by using integrality conditions on the other variables xi for i 6= j as shown by Balas and Jeroslow [5,7]. Thestrengthened lift-and-project cut
(yx)¿is dened as follows:
k= min{1k+u0⌈mk⌉; 2k−v0⌊mk⌋} for k= 1; : : : ; n;
k= max{1k; k2} for k=n+ 1; : : : ; n+p;
where1 and2 are dened above and m
k= (2k−
1
k)=(u0+v0).
The strengthened lift-and-project cuts can be viewed as valid inequalities for the union of the poly-hedra P∩ {x60} and P∩ {x¿1} for a special choice of(see proof of Theorem 2:2 in [5]).
The elementary closure of the strengthened lift-and-project cuts is denoted byPL&P+S.
2.8. Intersection cuts andPIBF,PIB,PIBF+S,PIB+S
LetP′={(x; y; s)∈Rn+p+m|Ax+Gy+s=b; s¿0} and let ( x;y; s) be a basic feasible solution. Let ( x;y) be the corresponding point in (n+p)-space. Note that ( x;y) is an extreme point of P and the n+p
nonbasic variables in ( x;y; s) uniquely dene n+p
extreme rays originating at ( x;y). Let C denote the cone dened by thesen+prays. Valid inequalities for
C∩{xk60}andC∩{xk¿0+ 1}where0∈Z, are
calledintersection cuts from basic feasible solutions. This notion was introduced by Balas in a more general context [1]. LetPIBFbe the corresponding elementary
closure.
is called an intersection cuts from a basic solution. Denote the corresponding elementary closure byPIB.
Just as lift-and-project cuts, intersection cuts can be strengthened by using integrality conditions on the other variablesxifori6=k. The elementary closures of thestrengthened intersection cuts from basic feasible solutionsand thestrengthened intersection cuts from basic solutionsare respectively denoted byPIBF+Sand
PIB+S.
2.9. Sherali–Adams cuts andPSA
The Sherali–Adams cuts can be obtained in the mixed 0,1 case as follows. Form the nonlinear system
(1−x1)(b−Ax−Gy)¿0;
x1(b−Ax−Gy)¿0
: : :
(1−xn)(b−Ax−Gy)¿0;
xn(b−Ax−Gy)¿0;
and linearize it by substituting xj for xj2; zij for
xixj; i6=j; andwikforxiyk. Then project this higher dimensional polyhedronM back into the (x; y) space. The resulting polyhedron is denoted by PSA. Any
valid inequality for PSA is valid forPI and is called
a Sherali–Adams cut [30]. Sherali and Adams also introduced other families, obtained with more mul-tiplication of terms, but we do not consider them here.
2.10. Lovasz–Schrijver cuts andPLS
The Lovasz–Schrijver cuts are obtained in the mixed 0,1 case by imposing an additional constraint on the polyhedron M dened in Section 2.9. Let Z
be the square matrix with n+ 1 rows and columns dened as follows. Row 0 is the vector (1; x), col-umn 0 is its transpose, and for i; j¿1, Z has entry
zij if i6=jandzii=xi otherwise. Lovasz and Schri-jver [25] proposed to tighten the set M by impos-ing that the matrix Z be positive semi-denite. Let
M∗=M∩ {Z| Z is a positive semi-denite matrix}.
The projection ofM∗ into the (x; y) space is denoted
byPLS. One can verify thatPI⊆PLS⊆P. Any valid
inequality forPLSis aLovasz–Schrijver cut.
3. Comparison of the elementary closures
All the cuts dened in Section 2 are meaningful in the case of pure 0;1 programs. The purpose of this section is to compare the corresponding 18 elemen-tary closures in this case. When appropriate, we state the results in more general cases (for example, pure integer programs, mixed 0;1 programs).
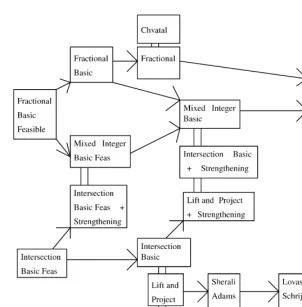
The comparison between the 18 elementary closures is illustrated in Fig. 1. If A andB denote two kinds of cuts, we use the following convention in Fig. 1:
A=Bmeans that the elementary closuresPAandPBare identical,A→Bmeans thatPA⊇PBand the inclusion is strict for some instances, andAnot related toBin the gure means that for some instancesPA*PBand for other instancesPB*PA.
(1) PC=PF. Now we are in the pure caseAx6b
with x ∈ Zn
+. Without loss of generality, A and b
are assumed to be integral. The proof of Theorem 6:34 in [13] implies that any Chvatal cut has the form
⌊uA⌋x6⌊ub⌋ for some multiplier vector 06u ¡1. Since⌊u⌋=0, this is the Gomory fractional cut⌊uA⌋x− ⌊u⌋Ax6⌊ub⌋ − ⌊u⌋b. Conversely, any fractional cut
⌊uA⌋ − ⌊u⌋Ax6⌊ub⌋ − ⌊u⌋bcan be written as⌊uA− ⌊u⌋A⌋x6⌊ub− ⌊u⌋b⌋, sinceAandbare integral. But this is a Chvatal cut⌊A⌋6⌊b⌋, where=u− ⌊u⌋. (2) PSD = PL&P. In the mixed 0,1 case, (P ∩
{xj60})∪(P∩ {xj¿1}) =P∩ {(x; y)∈Rn+p:xj∈
{0;1}}). Therefore PSD= Tn
j=1 conv(P∩ {(x; y) ∈
Rn+p: x
j ∈ {0;1}}), which is PL&P by Theorem 2:1
in [4].
(3)PMIR=PD=PMI. Nemhauser and Wolsey [28]
showed these two equalities.
To show thatPMIR⊆PD, we show that anyD-cut
can be obtained by the MIR procedure. Let cx +
hy6c0 be a D-cut. Then there exist (; 0) ∈ Zn+1
and; ¿0 such thatcx+hy−(x−0)6c0and
cx+hy+(x−0−1)6c0are both valid
inequal-ities forP. Multiplying both inequalities by 1=(+) and applying the MIR procedure with==(+) gives, after simplications,cx+hy6c0.
PD⊆PMI, since it is well known that Gomory mixed
integer cuts can be derived from a disjunction express-ing integrality conditions on thexvariables.
Now we show thatPMI⊆PMIR. We show that any
MIR cut can be obtained using Gomory’s mixed inte-ger procedure. Consider two valid inequalities forP, sayc1x+hy6c1
Fig. 1. Comparison of elementary closures.
Zn. After introducing two nonnegative slack variables
s1 ands2, we getc1x+hy+s1=c10 andc2x+hy+
s2=c20. Subtracting the rst equation from the
sec-ond, we get (c2−c1)x−s
1+s2=c20−c10. The
Go-mory mixed integer cut generated from this equation is=(1−)s1+s2¿, where=c20−c10− ⌊c20−c10⌋, or
equivalently (c2−c1)x−1=(1−)s
16⌊c20−c10⌋.
Plug-gings1=−c1x−hy+c10into it, we obtain the mixed
integer rounding cutx+ (c1x+hy−c1
0)=(1−)60,
where0=⌊c20−c10⌋.
(4)PIB=PL&P; PIB+S=PL&P+S=PMIB; PIBF+S=
PMIBF. These are new results of Balas and Perregaard
[8]. They are obtained by establishing the correspon-dence between the basic feasible solutions of (∗) in Section 2.7 and Gomory mixed integer cuts from ba-sic solutions ofP′.
(5) PL&P+S⊆PL&P and the inclusion is strict for
some P. Obviously PL&P+S⊆PL&P from their
def-initions. To see that the inclusion can be strict,
consider the polytope P={x ∈ R+2 | −1=26x1−
x260; x161; x261}. Then PL&P ={x ∈ R2|x1−
x260; −2x1+x260; −x1+2x261}, whilePL&P+S=
conv(PI) ={x∈R2+|x1−x2= 0; x161; x261}.
(6) PF⊆PFB⊆PFBF; PMI⊆PMIB⊆PMIBF⊆PFBF,
PMIB⊆PFB; PIB+S⊆PIB⊆PIBF; PIBF+S⊆PIBF and
each of these inclusions is strict for some P. These inclusions follow from the denitions. The fact that they can be strict follows from the following results, established later: The results in (15), (4) and (12) imply the strict inclusions in PF⊆PFB⊆PFBF, and
the results in (7), (15), (4), (12) and (11) imply the strict inclusions in PMI⊆PMIB⊆PMIBF⊆PFBF.
The strict inclusion inPMIB⊆PFBfollows from (11),
and the strict inclusions in PIB+S⊆PIB⊆PIBF
fol-low from (5), (4) and (13). The strict inclusion in
PIBF+S⊆PIBFholds because of (10).
(7) PMI⊆PC and the inclusion is strict for some
obtained from the multiplier vectoruis a strengthening of the Gomory fractional cut obtained from the same
u. The fact that the inclusion can be strict will be established in (11).
(8)PSA⊆PL&P and the inclusion is strict for some
P. The inclusionPSA⊆PL&Pfollows from the
deni-tions. The fact that the inclusion can be strict follows from (14).
(9) PLS⊆PSA and the inclusion is strict for some
P. The inclusion follows from the denitions. Next we show that it can be strict. For a graphG= (V; E) and P={x ∈ Rn
+|xi+xj61; ∀(i; j) ∈ E}, the set
PI is the stable set polytope conv({x ∈ {0;1}n|xi+
xj61; ∀(i; j)∈E}). Lovasz and Schrijver [25] char-acterized PSA as the polytope dened exactly by the
constraints of P and the odd hole constraints. They showed that there are other constraints, like clique, odd wheel and odd antihole constraints, which are valid forPLSbut not forPSA.
(10)PLS*PFBFfor someP. LetP={x∈R2| −
x1+x261=2; 06x161;6x261}. ThenPFBF={x∈
R2|x1 − x2¿0; 06x161; 06x261} = conv(PI),
since the Gomory fractional cut generated from the basic feasible solution (0;1=2) isx1−x2¿0. However,
the vector (x1; x2)T=(1=2−;1=2+)T6∈ conv(PI) is
inPLS, whereis a suciently small positive number,
because (x1; x2; y12) = (1=2−;1=2 +;1=2−)
sat-ises both the inequalities in the higher dimensional polyhedron M and the positive semi-deniteness constraint. See also [14].
(11)PC*PIBF for someP. ForP={(x1; x2)| −
2x1+x260; 2x1+x262; 06x1; 06x261}, we have
PIBF= conv(PI) ={(x1; x2)|06x161; x2= 0}.
In order to show conv(PI)⊂PC for this P, let us
consider an arbitrary valid inequality forPand justify that (1=2;1=2) satises the corresponding Chvatal cut. Any valid inequality forPmust either be valid for both (0;0) and (1;1) or be valid for both (1;0) and (0;1). Hence the Chvatal rounding procedure will keep either both (0;0) and (1;1) or both (1;0) and (0;1) valid for the corresponding Chvatal cut. Therefore, the center point (1=2;1=2) is valid for the cut. cuts generated from basic feasible solutions do not
yield x1 +x261, whereas PFB= conv(PI) ={x ∈
R2
+|x1 +x261}, since the Gomory fractional cut
generated from the basic infeasible solution (9=10;1) isx1+x261.
of the Steiner triple systemA9[11,18]. Theorem 4:4 of
[11] tells us that the inequality1x¿27=7 is a Sherali– Adams cut.
The pointx∗= (x∗
1; x2∗; : : : ; x∗9) = (3=7;3=7; : : : ;3=7)
satises1x¿27=7 as equality and satises all the con-straints of P as strict inequalities. If we could show thatx∗satises anyD-cut as a strict inequality, thenx∗
is in the interior ofPD, which means that the Sherali–
Adams cut 1x¿27=7 is not valid for PD. Hence we
sides of all the above inequalities and resetting the variables, we see thatx60 is aD-cut if and only if
x∗= (3=7;3=7; : : : ;3=7). We conclude thatx∗is in the
interior of PD, which leads to PD * PSA for this
polytopeP.
(15)PL&P+S*PCfor someP. Consider the
poly-tope P={x ∈ R10 +|
P
j6=ixij61; for i= 1;2; : : : ;5} for the matching problem on the complete graph with ve nodes. The facet-dening inequalityP
ij∈Exij62 of conv(PI) is a Chvatal cut of rank one. We will
show that this facet-dening inequality cannot be generated from any disjunction of P∩ {x60} and
P∩ {x¿1}, whereis integral. By the property of strengthened lift-and-project cuts shown in Section 2.7,P
ij∈Exij62 is not valid forPL&P+S.
By the argument and (∗ ∗ ∗) in (14), an inequal-ity x60 can be generated from a disjunction of
P ∩ {x60} and P ∩ {x¿1}, where P ={x ∈
Rn|Ax6b}, if and only if the following linear integer system is feasible:
6+1A;
′6−+′2A;
0¿1b;
0′¿′2b−1;
′¿0; 1; ′2∈Rm+;
(; 0)∈Zn+1:
ForP
ij∈Exij62 andP={x∈R10+ | P
j6=ixij61; for i= 1;2; : : : ;5}, we used LINDO to check numerically that the corresponding linear integer system is infeasible.
4. Properties of elementary closures
In this section we address two questions about the elementary closures introduced above: Are they poly-hedra? Can linear functions be optimized in polyno-mial time over these elementary closures?
PIBF; PFBF; PFB; PMIBF (or PIBF+S) and PMIB (or
PIB+S; PL&P+S) are polyhedra, since there are only
nitely many constraints for them. But it is unknown whether one can optimize linear functions over them in polynomial time.
PC(orPF) is a polyhedron [12,29], but it is NP-hard
to optimize linear functions over it [16]. Recently, Bockmayr and Eisenbrand [10] showed that, in xed dimension, PC has a description with polynomially
many inequalities.
PL&P(orPSD; PIB) is obtained by projecting a
poly-hedron and therefore is a polypoly-hedron. Furthermore, optimizing a linear function over it can be done by solving a polynomial size linear program in the higher dimensional space. Hence this optimization problem is solvable in polynomial time. So isPSAfor the same
reason.
PLS is a convex set. It is not a polyhedron in
gen-eral, but one can optimize linear functions overPLSin
polynomial time [25]. Recently, Goemans and Tun-cel [9] gave some conditions under whichPLS=PSA.
Cook and Dash [14] considered combining Lovasz– Schrijver cuts with Chvatal cuts.
PMI (orPMIR,PD) is a polyhedron [15]. However,
it is still an open problem whether the optimization of linear functions over it can be done in polynomial time.
5. For further reading
The following references are also of interest to the reader: [6,17,19,27]
References
[1] E. Balas, Intersection cuts – a new type of cutting planes for integer programming, Oper. Res. 19 (1971) 19–39. [2] E. Balas, Disjunctive programming: cutting planes from
logical conditions, in: O.L. Mangasarian et al., (Eds.) Nonlinear Programming, Vol. 2, Academic Press, New York, 1975, pp. 279–312.
[3] E. Balas, Disjunctive programming, Ann. Discrete Math. 5 (1979) 3–51.
[4] E. Balas, S. Ceria, G. Cornuejols, A lift-and-project cutting plane algorithm for mixed 0 –1 programs, Math. Programming 58 (1993) 295–324.
[5] E. Balas, S. Ceria, G. Cornuejols, Mixed 0 –1 programming by lift-and-project in a branch-and-cut framework, Manage. Sci. 42 (1996) 1229–1246.
[6] E. Balas, S. Ceria, G. Cornuejols, G. Pataki, Polyhedral methods for the maximum clique problem cuts, DIMACS Ser. Discrete Math. Theoret. Comput. Sci. 26 (1996) 11–27. [7] E. Balas, R. Jeroslow, Strengthening cuts for mixed integer
programs, European J. Oper. Res. 4 (1980) 224–234. [8] E. Balas, M. Perregaard, A precise correspondence between
lift-and-project cuts, simple disjunctive cuts, and mixed integer Gomory cuts for 0 –1 programming, Proceedings of the 17th International Symposium on Mathematical Programming, Atlanta, GA, 2000.
[10] A. Bockmayr, F. Eisenbrand, Cutting planes and the elementary closure in xed dimension, preprint, Max-Planck-Institut fur Informatik, Saabrucken, Germany, 1999, to appear in Math. Oper. Res., to appear.
[11] S. Ceria, Lift-and-project methods for mixed 0 –1 programs, Ph.D. Dissertation, GSIA, Carnegie Mellon University, 1993. [12] V. Chvatal, Edmonds polytopes and a hierarchy of combinatorial optimization, Discrete Math. 4 (1973) 305– 337.
[13] W. Cook, W. Cunningham, W. Pullyblank, A. Schrijver, Combinatorial Optimization, Wiley, New York, 1998. [14] W. Cook, S. Dash, On the matrix-cut rank of polyhedra,
preprint, Department of Computational and Applied Mathematics, Rice University, Houston, TX, 1999, Math. Oper. Res., to appear.
[15] W. Cook, R. Kannan, A. Schrijver, Chvatal closures for mixed integer programming problems, Math. Programming 47 (1990) 155–174.
[16] F. Eisenbrand, On the membership problem for the elementary closure of a polyhedron, Combinatorica 19 (1999) 297–300. [17] F. Eisenbrand, A. Schulz, Bounds on the Chvatal rank of polytopes in the 0=1-cube, in: G. Cornuejols et al. (Eds.), Integer Programming and Combinatorial Optimization, Proceedings of the Seventh International IPCO Conference, Graz Austria, Lecture Notes in Computer Science, Vol. 1610, 1999, pp. 137–150.
[18] D. Fulkerson, G. Nemhauser, L. Trotter Jr., Two computationally dicult set covering problems that arise in computing the 1-width of incidence matrices of Steiner triple systems, Math. Programming Study 2 (1974) 72–81. [19] M. Goemans, L. Tuncel, When does the positive
semideniteness constraint help in lifting procedures, preprint, Department of Combinatorics and Optimization, University
of Waterloo, Ontario, Canada, 2000, Math. Oper. Res., to appear.
[20] R. Gomory, Outline of an algorithm for integer solutions to linear programs, Bull. Amer. Math. Soc. 64 (1958) 275–278. [21] R. Gomory, Solving linear programming problems in integers, in: R.E. Bellman, M. Hall Jr. (Eds.), Combinatorial Analysis, American Mathematical Society, Providence, RI, 1960, pp. 211–216.
[22] R. Gomory, An algorithm for the mixed integer problem, Technical Report RM-2597, The RAND Corporation, 1960. [23] R. Gomory, An algorithm for integer solutions to linear programs, in: R. Graves, P. Wolfe (Eds.), Recent Advances in Mathematical Programming, McGraw-Hill, New York, 1963, pp. 269–302.
[24] R. Jeroslow, Cutting plane theory: disjunctive methods, Ann. Discrete Math. 1 (1972) 293–330.
[25] L. Lovasz, A. Schrijver, Cones of matrices and set-functions and 0-1 optimization, SIAM J. Optim. 1 (1991) 166–190. [26] H. Marchand, A. Martin, R. Weismantel, L. Wolsey, Cutting
planes in integer and mixed integer programming, preprint, CORE, Louvain-la-Neuve, Belgium, 1999.
[27] G. Nemhauser, L. Wolsey, Integer and Combinatorial Optimization, Wiley, New York, 1988.
[28] G. Nemhauser, L. Wolsey, A recursive procedure to generate all cuts for 0-1 mixed integer programs, Math. Programming 46 (1990) 379–390.
[29] A. Schrijver, On cutting planes, Ann. Discrete Math. 9 (1980) 291–296.