kalkulus bab iv differensiasi

(1)

BAB IV DIFFERENSIASI

4.1 Garis singgung

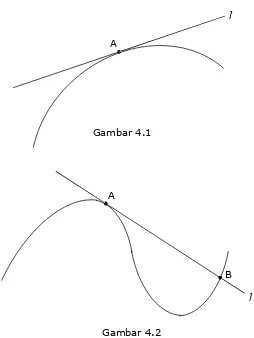
Garis singgung adalah garis yang menyinggung suatu titik tertentu pada suatu kurva. Pengertian garis singgung tersebut dapat dilihat pada Gambar 4.1. Akan tetapi jika terdapat dua buah titik pada suatu kurva maka berkemungkinan garis singgung yang menyinggung salah satu titik akan memotong kurva pada titik lainnya. Untuk lebih jelasnya dapat dilihat pada Gambar 4.2.

Untuk mendapatkan pengertian yang lebih jelas mengenai garis singgung kita perlu mendefinisikan kemiringan garis singgung

l

pada titik A(x1,f(x1)) yang terletak pada grafik fungsi. Selanjutnya pada grafik fungsi tersebut kita pilih

A

[image:1.595.205.459.313.651.2]

l

Gambar 4.1

Gambar 4.2 A

B

(2)

suatu titik B(x,f(x)). Jika kita hubungkan titik A dan B maka akan terbentuk garis

l

1 yang mempunyai kemiringan :

m1 =

x -x

f(x) -) x ( f

1

1 _{( 4.1 )}

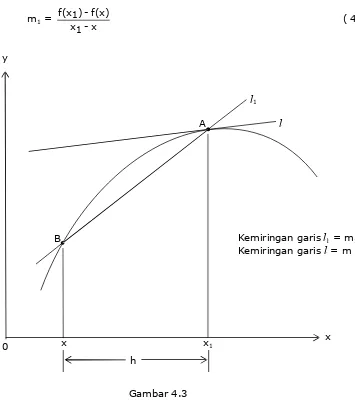
Jika f(x) kontinu pada selang [A,B] maka kita dapat mendekatkan titik B ke titik A dengan jalan memperkecil jarak antara x dan x1. Dalam bentuk limit hal tersebut dapat ditulis dalam bentuk :

x x

f(x) -) x ( f lim m

lim

1 1 x x 1 x

x 1 1

-=

®

® ( 4.2 )

Persaman (4.2) adalah kemiringan garis

l

1 jika x mendekati x1. Jika kita perhatikan Gambar 4.3 maka kita dapat melihat bahwa kemiringan garis

l

1

jika

x mendekati x1 adalah mendekati kemiringan garis

l

.

Dalam bentuk limit dapat ditulis :

m x x

f(x) -) x ( f lim m

lim

1 1 x x 1 x

x® ₁ = ® ₁ - =

l

1

A

l

B

x x1 h

x 0

y

Gambar 4.3

[image:2.595.141.496.131.536.2]

(3)

Jadi :

x x

f(x) -) x ( f lim m

1 1 x

x 1

-=

® ( 4.3 )

Karena x1– x = h, maka

h f(x) -) h x ( f lim m

0 h

+ =

® ( 4.4 )

Jika dimisalkan h = Dx, maka

x f(x) -) x x ( f lim m

0

x D

D + =

®

D

( 4.5 ) Persamaan 4.3 s/d 4.5 adalah kemiringan garis

l

pada titik (x, f(x))

Contoh 4.1

Diketahui f(x) = 3x2 + 5

Tentukan kemiringan dan persamaan garis singgung yang melalui titik (a,a2) Penyelesaian :

x f(x) -) x x ( f lim m

0

x D

D + =

®

D

x

5 x 3 5 x) 3( x x 6 x 3 lim x

5 3x -5 ) x x ( 3 lim

2 2

2

0 x 2

2

0

x D

-+ D + D + =

D

-+

D + =

®

D

®

D

x 6 x 3 x 6 lim

0

x + D =

=

®

D

Jadi m = 6x (*)

Persamaan garis singgung : y = mx + n (**) Karena garis singgung melalui titik (a,a2) maka : persamaan (*) menjadi :m = 6a

persamaan (**) menjadi : a2 = 6a2 + n. Sehingga n = -5a2 Persamaan garis singgung menjadi : y = 6ax – 5a2

4.2 Turunan

Turunan adalah hasil dari proses differensiasi suatu fungsi. Untuk mendapatkan pengertian yang jelas dari turunan dan differensiasi perhatikan Gambar 4.4 berikut. Differensiasi dapat dimisalkan sebagai suatu mesin yang memproses masukan f(x) menjadi turunan f(x) atau f’(x).

Selanjutnya turunan didefinisikan sebagai kemiringan garis yang menyinggung kurva f(x) di titik (x,f(x)). Berdasarkan persamaan 4.3 dan Gambar 4.3 maka definisi turunan dapat ditulis dalam bentuk :

x x

) x ( f ) x ( f lim ) x ( ' f

1 1 x

x 1

-=

® , jika nilai limitnya ada ( 4.6 )

Jika persamaan 4.6 dapat dipenuhi berarti f(x) dapat didifferensiasikan (differensiable) pada x. Maka dikatakan f(x) mempunyai turunan pada x.

Differensiasi

f(x) f’(x)

(4)

Contoh 4.2

Jika f(x) = 2x2_{+ 5x}_–_{7, tentukan f}_’_{(x), f}_’_{(c) dan f}_’₍₃₎ Penyelesaian :

f(x) = 2x2 + 5x – 7

f(x+Dx) = 2(x+Dx)2_{+ 5(x+}_D_x)_–_{7 = 2x}2_{+ 4x}_D_{x +2(}_D_x)2_{+ 5x + 5}_D_x_–₇ f(x+Dx) – f(x) = 4xDx + 2(Dx)2 _{+ 5}

Dx

5 x 4 5 x 2 x 4 lim x

x 5 ) x ( 2 x x 4 lim x

) x ( f ) x x ( f lim ) x ( ' f

0 x 2

0 x 0

x

+ = + D + =

D

D + D + D =

D -D + =

®

D

®

D

®

D

Jadi : f'(x) = 4x+5 5 c 4 ) c ( '

f = +

17 5 ) 3 ( 4 ) 3 ( '

f = + =

4.3 Notasi turunan

Pada pasal terdahulu kita telah menggunakan notasi turunan dengan lambang f’

yaitu lambang turunan dari suatu fungsi f yang diperkenalkan pertama kali oleh matematikawan Perancis Louis Lagrange (1646 – 1716). Selain notasi tersebut masih terdapat notasi lain yang sering digunakan yaitu notasi double “d”. Jadi kita juga dapat menulis lambang turunan sebagai dy/dx, dy/dz, … dimana x dan z adalah peubah-peubah bebas dan y sebagai peubah tak bebas. Hubungan antara notasi-notasi turunan yang disebut diatas adalah sebagai berikut : Jika terdapat suatu persamaan y = f(x), maka : dy/dx = f’(x).

4.4 Differensiabilitas dan kontinuitas

Jika f adalah fungsi yang differensiabel pada x maka f dikatakan kontinu pada x. Bukti :

Pada uraian terdahulu telah dijelaskan bahwa suatu fungsi f dikatakan differensiable jika memenuhi persamaan 4.6, yaitu :

Jika :

x ) x ( f ) x x ( f lim

0

x D

-D +

®

D

ada, maka

x ) x ( f ) x x ( f lim ) x ( ' f

0

x D

-D + =

®

D

f(x+Dx)-f(x)= x

x ) x ( f ) x x ( f

D

·

D -D +

x lim . x

) x ( f ) x x ( f lim )) x ( f ) x x ( f ( lim

0 x 0

x 0

x D D

-D + =

-D +

®

D

®

D

®

D

=f’(x) . 0 = 0 Sehingga : lim f( x x) lim f(x)

0 x 0

x® D ®

D

= +

D ® lim f(x) f(x)

0

x® =

D

(terbukti)

Sebaliknya jika f adalah fungsi yang kontinu pada x, maka tidak secara otomatis f differensiable pada x.

4.5 Teorema-teorema

4.5.1 Turunan bilangan konstan

(5)

y = f(x) = c maka f'(x) 0 dx

dy

=

= ( 4.7 )

Bukti :

f(x) = c ; f(x+Dx) = c

x ) x ( f ) x x ( f lim ) x ( ' f

0 x dx

dy

D -D + =

=

®

D

= 0

x c c lim

0

x D =

-®

D

(terbukti)

4.5.2 Jika n adalah sembarang bilangan bulat, k adalah sembarang bilangan ril dan jika y didefinisikan sebagai :

y = f(x) = kxn maka f'(x) knxn 1 dx

dy

-=

= ( 4.8 )

Bukti : f(x) = kxn

f(x+Dx) = k(x+Dx)n

Dengan mengunakan teorema binomial didapat : k(x+Dx)n

=

! n

x ! kn !

) 1 n (

x ! 1) -k(n !

2

) x ( x ) 1 n ( kn !

1 x knx !

0

kxn n 1 n 2 2 n-1 D n

+

-D +

+ D

-+ D +

-L

1 n 0

x

knx x

) x ( f ) x x ( f lim ) x ( ' f dx

dy

-®

D

= D

-D + =

= (terbukti)

Contoh 4.3

Tentukan turunan pertama dari f(x) = 5x7 Penyelesaian :

6 1

7 ₃₅_x

x ) 7 )( 5 ( ) x ( ' f dx dy

= =

=

-4.5.3 Aturan penjumlahan

Jika f dan g adalah dua buah fungsi dan h adalah fungsi yang didefinisikan sebagai :

y = h(x) = f(x) + g(x) maka f'(x) g'(x) dx

dy

+

= ( 4. 9 )

Bukti :

h(x) = f(x) + g(x)

h(x+Dx) = f(x+Dx) + g(x+Dx) h’(x) =

x

) x ( g ) x ( f ) x x ( g ) x x ( f lim x

) x ( h ) x x ( h lim

0 x 0

x D

-D + + D + =

D -D +

®

D

®

D

= f'(x) g'(x)

x ) x x ( g lim x

) x ( f ) x x ( f lim

0 x 0

x

+ = D

D + +

D -D +

®

D

®

D

(terbukti)

Contoh 4.4

(6)

Tentukan dx dy

Penyelesaian :

f(x) = 5x6 g(x) = 2x-3 f’(x) = 30x5 g’(x) = -6x-4

=

dx dy

f’(x) + g’(x) = 30x5– 6x-4

4.5.4 Aturan perkalian

y = h(x) = f(x).g(x) maka f'(x)g(x) f(x)g'(x) dx

dy

+

= (4.10)

Bukti : h’(x) =

x

) x ( g ). x ( f ) x x ( g ). x x ( f lim

0

x D

-D + D

+

®

D

=

x

) x ( g ). x ( f ) x ( g ). x x ( f ) x ( g ). x x ( f ) x x ( g ). x x ( f lim

0

x D

-D

+ + D

+ -D + D

+

®

D

=

x ) x ( g ) x x ( g ) x x ( f lim

0

x D

-D + D

+

®

D

+

x ) x ( f ) x x ( f ) x ( g lim

0

x D

-D +

®

D

= f(x).g’(x) + g(x).f’(x) (terbukti)

Contoh 4.5

Diketahui y = (3x5 + 2x-2)(7x+3) Tentukan

dx dy

Penyelesaian :

f(x) = 3x5 + 2x-2 g(x) = 7x+3 f’(x) = 15x4– 4x-3 g’(x) = 7

dx dy

= f’(x).g(x) + g’(x).f(x) = (15x4-4x-3

)

(7x+3) + (3x5 + 2x-2)(7) = 105x5-28x-2 +45x4– 12x-3 +21x5 + 14x-2

= 126x5 + 45x4 - 14x-2– 12x-3

4.5.5 Aturan pembagian

y = h(x) = ) x ( g

) x ( f

maka

[

_g₍_x₎

]

2

) x ( ' g ) x ( f ) x ( g ) x ( ' f dx

dy

-= (4.11)

(7)

h(x) = ) x ( g ) x ( f

; h(x+Dx) =

) x x ( g ) x x ( f D + D +

h’(x) =

x ) x ( g ) x ( f ) x x ( g ) x x ( f lim x ) x ( h ) x x ( h lim 0 x 0 x D -D + D + = D -D + ® D ® D = ) x ( g ). x x ( g . x ) x ( f ). x x ( g ) x x ( f ). x ( g lim 0

x D +D

D + -D + ® D = ) x ( g ). x x ( g . x ) x ( g ). x ( f ) x ( f ). x x ( g ) x ( g ). x ( f ) x x ( f ). x ( g lim 0

x D +D

+ D + -D + ® D = ) x ( g ). x x ( g . x ) x ( f ) x x ( f ) x ( g lim 0

x D +D

-D + ® D - ) x ( g ). x x ( g . x ) x ( g ) x x ( g ) x ( f lim 0

x D +D

-D + ® D = ú ú ú ú û ù ê ê ê ê ë é D + D -D + ®

D g(x x).g(x)

x ) x ( f ) x x ( f ) x ( g lim 0 x - ú ú ú ú û ù ê ê ê ê ë é D + D -D + ®

D g(x x).g(x)

x ) x ( g ) x x ( g ) x ( f lim 0 x =

[

_g₍_x₎

]

2

) x ( f ). x ( ' g ) x ( ' f ). x ( g (terbukti) Contoh 4.6

Tentukan h’(x) jika h(x) =

3 2 4 x 4 x 3 x 2 -Penyelesaian :

f(x) = 2x4– 3x2 f’(x) = 8x3– 6x g(x) = 4x3 g’(x) = 12x2 h’(x) =

2 3 2 2 4 3 3

2 ₍₄_x ₎

) x 12 )( x 3 x 2 ( ) x 4 )( x 6 x 8 ( )] x ( g [ ) x ( ' g ). x ( f ) x ( g ). x ( '

f - -

-= = 6 4 6 6 4 6 4 6

16

12

8

16

36

24

32

x

+

=

+

-= 2 2

4

3

2

x

+

4.5.6 Turunan fungsi komposisi

Jika y = f(u) dan u = g(x) maka

dx du du dy dx dy = (4.12) Bukti :

Jika y = f(u) dan u = g(x) maka y = f(g(x)). Fungsi tersebut mempunyai bentuk komposisi dan dapat ditulis sebagai (fog)(x).

u = g(x)

Du= g(x+Dx) – g(x) ® g(x+Dx) = g(x) + Du = u + Du Jadi Du ® 0 maka Dx ® 0

y = f(g(x))

(8)

x )) x ( g ( f )) x x ( g ( f x y D -D + = D D u u x )) x ( g ( f )) x x ( g ( f D D D -D + = = D D x y x u u ) u ( f ) u u ( f D D D -D + ® = D D ® D x y lim 0 x dx dy x u u ) u ( f ) u u ( f lim 0

x D =

D D -D + ® D dx du du dy x u lim . u ) u ( f ) u u ( f lim dx dy 0 x 0 x = D D D -D + = ® D ® D (terbukti)

Persamaan 4.12 disebut aturan rantai Contoh 4.7

Tentukan dx dy

jika y = (4x3 + 5x2– x + 4)3 Penyelesaian :

Misal u = 4x3 + 5x2– x + 4 y = u3 1 x 10 x 12 dx du 2 -+

= 3u2

du dy = ) 1 x 10 x 12 ( u 3 dx du du dy dx

dy ₌ ₌ 2 2 ₊

-2 2

3

2 ₁₀_x ₁₎₍₄_x ₅_x _x ₄₎ x

12 (

3 + - + - +

=

Soal-soal

Tentukan turunan pertama dari fungsi-fungsi berikut ! 1. f(t) = at2_–_{bt + 7} _{6. f(x) =}

ú û ù ê ë é + ú û ù ê ë é x 1 5 x 4 3x -x 4 5

2. f(x) = 3x-5 + 35x2 7. g(t) = (at2+bt+c)2(3at–7)5 3. g(x) = _ú

û ù ê ë é + 2 x x 2

8. h(w) = c w 2 aw b +

-4. h(x) =

2 x 1 5 x 4 ú û ù ê ë é

+ 9. v(t) =

3 ) d ct ( 2 ) bt 2 at (

-5. w(x) =

3 3 2x -x 4 7 ú û ù ê ë é

+ 10. g(t) =

3 -t ) 3 (2t t 2 +

4.6 Turunan fungsi-fungsi trigonometri

Jika y = f(x) = sin x maka f'(x) cosx dx

dy

=

= (4.13)

(9)

x

x sin x sin x cos x cos x sin lim

0

x D

-D +

D =

®

D

x

x sin x cos ) 1 x (cos x sin lim

0

x D

D +

-D =

®

D

ú û ù ê

ë é

D D +

D -D

®

D =

x x sin x cos x

) 1 x (cos x sin 0 xlim

x x sin lim x cos x

1 x cos lim x sin

0 x 0

x D

D +

D -D =

®

D

®

D

= (sinx)(0) + (cosx)(1) = cosx (terbukti) Jika y = sin u dan u = f(x) maka

dx du u cos dx dy

= (4.14)

Bukti :

y = sin u cosu

du dy

=

u = f(x) f'(x) dx du

=

dx du u cos dx du du dy dx dy

=

= (terbukti)

Jika y = f(x) = cos x maka f'(x) sinx dx

dy

-=

= (4.15)

Bukti :

x

x cos ) x x cos(

0 xlim x

) x ( f ) x x ( f

0 xlim ) x ( ' f dx dy

D -D +

®

D = D

-D +

®

D = =

x

x cos x sin x sin x cos x cos 0

xlim D

-D

®

D =

x

x sin x sin ) 1 x (cos x cos

0

xlim D

D

-D

®

D =

ú û ù ê

ë é

D D

-D -D

®

D =

x x sin x sin x

) 1 x (cos x cos 0 xlim

x x sin 0 xlim x sin x

1 x cos 0 xlim x cos

D D

®

D -D

-D

®

D =

= (cosx)(0) - (sinx)(1) = -sinx (terbukti)

Jika y = cos u dan u = f(x) maka

dx du u sin dx dy

-= (4.16)

Bukti :

y = cos u sinu

du dy

-=

(10)

dx du u sin dx du du dy dx dy

-=

= (terbukti)

Contoh 4.8

Jika y = sin(p-2x), tentukan dx dy

Penyelesaian :

Misal u = p - 2x y = sin u

2

dx du

-= cosu

du dy

=

) x 2 cos( 2 ) 2 )( u (cos dx du du dy dx dy

-p -= -=

=

Contoh 4.9 Jika y =

2 x

cos tentukan dx dy

Penyelesaian : Misal u =

2

x _{y = cos u}

1/2

dx du

= sinu

du dy

-=

2 x sin 2 1 -) 2 1 )( u sin ( dx du du dy dx dy

=

-= =

Contoh 4.10

Jika y = sin2x cos3x, tentukan dx dy

Penyelesaian :

Misal u = sin 2x v = cos 3x 2cos2x

dx du

= 3sin3x

dx dv

-=

) x 3 sin 3 )( x 2 (sin ) x 3 )(cos x 2 cos 2 ( dx dv u v . dx du dx dy

-+

= + =

x 3 sin . x 2 sin 3 x 3 cos . x 2 cos

2

-=

Contoh 4.11 Jika y =

x 4 cos

x 3

sin _{, tentukan}

dx dy

Penyelesaian :

Misal u = sin 3x v = cos 4x 3cos3x

dx du

= 4sin4x

dx dv

-=

2 ) x 4 (cos

) x 4 sin 4 )( x 3 (sin ) x 4 )(cos x 3 cos 3 ( 2

v dx dv . u v . dx du

dx

dy -

-= -=

x 4 cos

x 4 sin . x 3 sin 4 x 4 cos . x 3 cos 3

2

(11)

Jika y = f(x) = tan x maka f'(x) sec x dx

dy ₂

=

= (4.16)

Bukti : y = tan x =

x cos

x sin

u = sin x v = cos x

cosx

dx du

= sinx

dx dv

-=

2 v

dx dv . u v . dx du

dx

dy

-= =

2 ) x (cos

) x sin )( x (sin ) x )(cos x

(cos -

-=

x cos

x sin x cos

2 2 2 ₊

= sec x

x cos

1 ₂

2 = (terbukti)

Jika y = tan u maka

dx du u) (sec dx

dy ₂

= (4.17)

Bukti :

y = tan u sec u

du

dy ₂

=

dx du ) u (sec dx du du dy dx

dy ₂

=

= (terbukti)

Contoh 4.12

Jika y = 5 tan 3x, tentukan dx dy

Penyelesaian :

Misal u = 3x y = 5 tan u

3

dx du

= 5sec u

du

dy ₂

=

x 3 sec 15 u sec 15 ) 3 )( u sec 5 ( dx du du dy dx

dy ₂ ₂ ₂

= =

Jika y = f(x) = cot x maka f'(x) csc x dx

dy ₌ ₌_- 2 _(4.18)

Bukti : y = cot x =

x sin

x cos

u = cos x v = sin x

sinx

dx du

-= cosx

dx dv

(12)

2 v

dx dv . u v . dx du

dx

dy

-= =

2 ) x (sin

) x )(cos x (cos ) x )(sin x sin

(-

-=

x sin

) x cos x (sin

2 2 2 ₊

-= csc x

x sin

1 ₂

2 =

-- (terbukti)

Jika y = cot u maka

dx du u) csc ( dx

dy ₂

-= (4.19)

Bukti :

y = cot u csc u

du

dy ₂

-=

=

dx du ) u csc ( dx du du dy dx

dy ₌ ₌ _- 2 _(terbukti)

Contoh 4.13

Jika y = x

3 1 cot 2 1

, tentukan dx dy

Penyelesaian : Misal u = x

3 1

y = cotu 2 1

3 1 dx du

= csc u

2 1 du

dy ₂

-=

x 3 1 csc 6 1 u csc 6 1 ) 3 1 )( u csc 2 1 ( dx du du dy dx

dy ₌ ₌ _- 2 ₌_- 2 ₌ _- 2

Jika y = f(x) = sec x maka f'(x) secxtanx dx

dy

=

= (4.20)

Bukti : y = sec x =

x cos

1

u = 1 v = cos x

0

dx du

= sinx

dx dv

-=

2 v

dx dv . u v . dx du

dx

dy

-= =

2 ) x (cos

) x sin )( 1 ( ) x )(cos 0

( -

-= secxtanx

x 2 cos

x sin

(13)

Jika y = sec u maka

dx du tanu) u (sec dx dy

= (4.21)

Bukti :

y = sec u secutanu du

dy

=

dx du u) tan u (sec dx du du dy dx dy

=

= (terbukti)

Jika y = f(x) = csc x maka f'(x) cscxcotx dx

dy

-=

= (4.22)

Bukti : y = csc x =

x sin

1

u = 1 v = sin x

0 dx du

= cosx

dx dv

=

2 v

dx dv . u v . dx du

dx

dy

-= =

2 ) x (sin

) x )(cos 1 ( ) x )(sin 0

(

= cscxcotx x

2 sin

x cos

-=

(terbukti)

Jika y = csc u maka

dx du cotu) u csc ( dx dy

-= (4.23)

Bukti :

y = csc u cscucotu du

dy

-=

=

dx du u) cot u csc ( dx du du dy dx dy

-=

= (terbukti)

Contoh 4.15 Jika y = csc( x)

3 1

-p , tentukan dx dy

Penyelesaian :

Misal u = p-x y = cscu 3 1

1

dx du

-= cscucotu

3 1 du dy

-=

x) -cot( ) x csc( 3 1 cotu u csc 3 1 ) 1 )( cotu u csc 3 1 ( dx du du dy dx dy

p

-p =

=

-= =

Soal-soal

Tentukan turunan pertama dari fungsi-fungsi berikut ! PR : 2, 5, 6 & 9

1. f(x) = )

3 2 x

sin( - p 6. f(x) = x)

(14)

-2. f(x) = cos ) 3 x 2

(p - 7. g(t) = sin2tcos t 2

1

p

3. g(x) = tan3x 8. h(w) =

) bw cos(

) aw sin(

-p

p

-4. h(x) = cot3x 9. v(t) =

) t b cos(

t 2 sin at2

-5. w(x) = )

3 2 x (

sec5 - p 10. g(t) =

t 3 sin cos2t t sin

4.7 Turunan fungsi-fungsi trigonometri invers

Jika y = f(x) = arcsin x maka

2 x 1

1 ) x ( ' f dx dy

-=

= (4.24)

Bukti :

y = arcsinx ® sin y = x ® 1

dx dx dx dy y

cos = = ®

y cos

1 dx dy

=

Selanjutnya perhatikan segitiga berikut ini !

sin y = x cos y = ₁_-_x2

2

x 1

1 dx dy

-= (terbukti)

2

x 1

-Jika y = arcsin u dan u = f(x) maka

dx du u 1

1 dx dy

2

-= (4.25)

Bukti :

y = arcsin u ®

2

u 1

1 du dy

-=

dx du

u 1

1 dx du . du dy dx dy

2 -=

= (terbukti)

Contoh 4.16

Jika y = x)

3 1 arcsin( 8 3

- , tentukan

dx dy

3 1

- y = arcsinu 8

3

1 x

(15)

3 1 dx du

-=

2

u 1

1 8 3 du dy

-=

2 2

x 9 1 1 8

1 3

1

u 1

1 8 3 dx du du dy dx dy

-=

ú û ù ê ë é

-= =

Jika y = f(x) = arccos x maka

2

x 1

1 )

x ( ' f dx dy

-=

= (4.26)

Bukti :

y = arccosx ® cos y = x ® 1

dx dx dx dy y

sin = =

- ®

y sin

1 dx dy

-=

cos y = x sin y = ₁ _x2

-2

x 1

1 dx

dy

-= (terbukti) ₁ _x2

-x

Jika y = arccos u dan u = f(x) maka

dx du u 1

1 dx

dy

2

-= (4.27)

Bukti :

y = arccos u ®

2

u 1

1 du

dy

-=

dx du

u 1

1 dx

du . du dy dx dy

2 -=

= (terbukti)

Contoh 4.17

Jika y =-3arccos2x, tentukan

dx dy

Penyelesaian :

Misal u = 2x y = -3arccosu

2

dx du

=

2 u 1

1 3 du dy

-=

2

2 ₁ ₄_x

6 ) 2 ( u 1

1 3 dx du du dy dx dy

-=

-= =

1

(16)

Jika y = f(x) = arctan x maka

2 x 1

1 ) x ( ' f dx dy

+ =

= (4.28)

Bukti :

y = arctanx ® tan y = x ® sec2y 1 dx dx dx dy

=

= ®

y sec

1 dx dy

2 =

tan y = x sec2_{y =} ₁ _x2

-2

x

1+ x

2

x 1

1 dx dy

-= (terbukti)

1

Jika y = arctan u dan u = f(x) maka

dx du u 1

1 dx dy

2

+

= (4.29)

Bukti : y = arctan u ®

2

u 1

1 du dy

+ =

dx du u 1

2 + =

= (terbukti)

Contoh 4.18

Jika y = x

3 1 arctan 5 3

, tentukan dx dy

3

1 _{y =}

arctan

u

5

3

3 1 dx du

= ₂

u 1

1 5 3 du dy

+ =

) x 9 1 1 ( 5

1 3

1 u 1

1 5 3 dx du du dy dx dy

2 2

+ =

ú û ù ê ë é

+ = =

Jika y = f(x) = arccot x maka

2

x 1

1 ) x ( ' f dx dy

+ -=

= (4.30)

Bukti : y = arccotx ® cot y = x ® -csc2_y

1 dx dx dx dy

=

= ®

y csc

1 dx

dy

2 -=

cot y = x csc2_{y =}₁ _x2

+

2

x

1+ 1

(17)

2

x 1

1 dx

dy

+

-= (terbukti)

x

Jika y = arccot u dan u = f(x) maka

dx du u 1

1 dx

dy

2

+

-= (4.31)

Bukti : y = arccot u ® ₂

u 1

1 du dy

+ -=

dx du u 1

1 dx

du . du dy dx dy

2 + -=

= (terbukti)

Contoh 4.19

Jika y = 2 arccot 3x, tentukan dx dy

Penyelesaian :

Misal u = 3x y = 2 arccot u

3

dx du

=

2

u 1

1 2 du dy

+ -=

2

2 ₁ ₉_x

6 )

3 ( u 1

1 2 dx du du dy dx dy

+ -= +

-= =

Jika y = f(x) = arcsec x maka

1 x x

1 ) x ( ' f dx dy

2 -=

= (4.32)

Bukti : y = arcsecx ® sec y = x ® secy tany 1 dx dx dx dy

=

= ®

y tan y sec

1 dx

dy

-=

sec y = x

sec y tan y = x x2-1

x x2-1

1 x x

1 dx

dy

2

-= (terbukti)

1

Jika y = arcsec u dan u = f(x) maka

dx du

1 u u

1 dx dy

2

-= (4.33)

Bukti : y = arcsec u ®

1 u u

1 du dy

2 -=

dx du

1 u u

2 -=

= (terbukti)

y

(18)

Contoh 4.20

Jika y = arcsec x) 2

(p- , tentukan dx dy

2

-p _{y = arcsec u}

1

dx du

-=

1 u u

1 du dy

2 -=

1 ) x 2 ( ) x 2 (

1 )

1 ( 1 u u

1 dx du du dy dx dy

2 2

-p -p -= -= =

Jika y = f(x) = arccsc x maka

1 x x

1 )

x ( ' f dx dy

2 -=

= (4.34)

Bukti :

y = arccscx ® csc y = x ® -csc y cot y 1 dx dx dx dy

=

= ®

y cot y csc

1 dx

dy

-=

csc y = x

csc y cot y = x x2-1

x 1

1 x x

1 dx

dy

2

-= (terbukti)

1 x2

Jika y = arcsec u dan u = f(x) maka

dx du

1 u u

1 dx

dy

2

-= (4.35)

Bukti : y = arccsc u ®

1 u u

1 du

dy

2 -=

dx du

1 u u

1 dx

du . du dy dx dy

2 -=

= (terbukti)

Contoh 4.21

Jika y = arccsc ) 2 x

( -p , tentukan dx dy

Penyelesaian : Misal u =

2

x- p y = arccsc u

1

dx du

=

1 u u

1 du

dy

2 -=

(19)

1 ) 2 x ( ) 2 x ( 1 ) 1 ( 1 u u 1 dx du du dy dx dy 2 2 -p -p -= -= = Soal-soal

Carilah turunan pertama dari soal-soal berikut ! 1. y = arcsin(p-x) 3.

x arccos x 2 cos y=

2. y = -3 arccos 4x 4. y = arctan x – sin 3x

4.8 Turunan fungsi Eksponen

Jika y = f(x) = ex maka =f'(x)=

dx

dy _ex

(4.36) Bukti :

ex didefinisikan sebagai n n x 1 nlim úû

ù ê ë é + ¥ ®

Dengan menggunakan teorema binomial didapat : n n x 1 _ú û ù ê ë é

+ = L

n x 3! 1 ). 2 n )( 1 n ( n n x ! 2 1 ). 1 n ( n n x ! 1 1 n 1 . n n x ! 0 n

1 0 1 n 2 2 n 3 3

+ ú û ù ê ë é -+ ú û ù ê ë é -+ ú û ù ê ë é -+ ú û ù ê ë é - -n n x 1 _ú û ù ê ë é

+ = x L

3! ) n / 2 1 )( n / 1 1 ( x ! 2 ) n / 1 1 ( x

1+ + - 2+ - - 3+

n

n x 1 nlim úû

ù ê ë é + ¥ ® = úû ù ê ë é + -+ -+ + ¥

® 3! x L

) n / 2 1 )( n / 1 1 ( x ! 2 ) n / 1 1 ( x 1 nlim 3 2

ex = _L

3 x ! 2 x x 1 3 2 + + + + (4.37)

Sehingga : e = + + + +L= + + + +L ! 3 1 ! 2 1 1 1 3 1 ! 2 1 1 1 3 2 (4.38)

Jika y = f(x) = ex Maka x ) 1 e ( e lim x e e lim x ) x ( f ) x x ( f lim ) x ( ' f dx

dy x x

0 x x x x 0 x 0 x D -= D -= D -D + = = D ® D D + ® D ® D

Karena ex = L

3 x ! 2 x x 1 3 2 + + +

+ , maka eDx

–

1 = L

3 x ! 2 x x 3 2 + D + D + D Sehingga x ) 1 e ( e lim x x 0 x D -D ® D

= x

2 x

0

x 3 e

x ! 2 x 1 e lim = ú ú û ù ê ê ë é + D + D + ® D L (terbukti)

Jika y = eu dan u = f(x) maka

dx du e dx dy u = (4.39)

Bukti : y = eu eu du dy

= u = f(x) f'(x)

dx du

(20)

dx du e dx du du dy dx

dy ₌ ₌ u _(terbukti)

Contoh 4.22

Jika y = -2ea-bx, tentukan

dx dy

Penyelesaian :

Misal : u = a – bx

dx du

= -b

(ea bx)( b) bea bx dx

dy -

-= -=

4.9 Turunan fungsi logaritma

Jika y = f(x) = ln x maka =f'(x)=

dx dy

x

1 _(4.40)

Bukti :

y = f(x) = ln x

x x x 1 ln lim x x ln ) x x ln( lim x ) x ( f ) x x ( f lim ) x ( ' f dx dy 0 x 0 x 0 x D ú û ù ê ë é D + = D -D + = D -D + = = ® D ® D ® D = ú û ù ê ë é D + D = ® D x x 1 ln x 1 lim 0

x úû=

ù ê ë é D + D = ® D x x 1 ln x x lim x 1 0 x x x 0 x x x 1 ln lim x 1 D ®

D úû

ù ê ë é D + =

Berdasarkan teorema binomial maka :

L + ú û ù ê ë éD ú û ù ê ë é -D ú û ù ê ë é D + ú û ù ê ë éD ú û ù ê ë é D + = ú û ù ê ë é D + -D -D D D ! 2 x x 1 1 x x x x ! 1 x x 1 x x ! 0 1 x x 1 2 2 x x 1 x x x x x x Jadi : ú ú ú ú ú ú û ù ê ê ê ê ê ê ë é + ú û ù ê ë éD ú û ù ê ë é -D ú û ù ê ë é D + ú û ù ê ë éD ú û ù ê ë é D + = ú û ù ê ë é D + -D -D D ® D D ®

D 2! L

x x 1 1 x x x x ! 1 x x 1 x x ! 0 1 ln lim x 1 x x 1 ln lim x 1 2 2 x x 1 x x x x 0 x x x 0 x ú ú ú ú û ù ê ê ê ê ë é + ú û ù ê ë é D -ú û ù ê ë é D -+ ú û ù ê ë é D -+ + = ú û ù ê ë é D + ® D D ®

D 3! L

x x 2 1 x x 1 ! 2 x x 1 1 1 ln lim x 1 x x 1 ln lim x 1 0 x x x 0 x

( )

x 1 1 x 1 e ln x 1 ! 3 1 ! 2 1 1 1 ln x 1 = = = ú û ù ê ë é + + + +

(21)

Jika y = ln u dan u = f(x) maka

dx du u 1 dx dy

= (4.41)

Bukti : y = ln u

u 1 du dy

= u = f(x) f'(x)

dx du

=

dx du u 1 dx du du dy dx dy

=

= (terbukti)

Contoh 4.23 Jika y = e2x ln x

3

1 _tentukan dx dy

Penyelesaian :Misal : u = e2x v = ln x 3 1

2e2x

dx du

=

x 1 dx dv

=

ú û ù ê

ë é

+ =

x 1 x 3 1 ln 2 e x 1 e x 3 1 ln e 2 dx dv . u v . dx du dx

dy 2x 2x 2x

Jika y = f(x) = alog x maka =f'(x)=

dx dy

x ) a (ln

1 _(4.42)

Bukti :

y = alog x ® ay = x

y ln a = ln x ® y = lnx a ln

1

x ) a (ln

1 dx dy

= (terbukti)

Jika y = alog u dan u = f(x) maka

dx du u ) a (ln

1 dx dy

= (4.43)

Bukti :

y = alog u ®

u ) a (ln

1 du dy

=

dx du . u ) a (ln

=

= (terbukti)

Contoh 4.24

Jika y = 7log(3-5x) tentukan

dx dy

Penyelesaian :Misal : u = 3 – 5x ® 5 dx du

-=

) x 5 3 )( 7 (ln

5 dx

du u ) a (ln

1 dx dy

(22)

Soal-soal

Tentukan turunan pertama dari fungsi-fungsi berikut !

1. y = xe3x 4. y = x 4 2

e x 3 ln x

7. y = x 4 ln

e x 3 1

10. y =

x ln e

e x 5 ln x

x x

-2. y = x 3 e 2

2 x 3

- 5. y = 2x x

e ) e x 4 (ln

x +

8. y =

x 2 3 5

e

) x 1 log( 3

-3. y = x3 _{ln2x 6. y =}

x 6 5

x 3 ln 2

- 9. y = _log₄_x e x

3 bx a 3

-4.10 Turunan fungsi hiperbolik

Jika y = f(x) = sinhx maka =f'(x)=

dx

dy _coshx _(4.44)

Bukti :

y = f(x) = sinhx = (e e ) 2

1 x -x

-) x ( ' f dx dy

= = (e e )

2

1 x -x

+ = coshx (terbukti)

Jika y = sinh u dan u = f(x) maka =

dx dy

cosh u

dx du

(4.45) Bukti :

y = sinh u ® coshu du

dy

=

dx du u cosh dx du . du dy dx dy

=

= (terbukti)

Contoh 4.25 Jika y = 3 sinh x

5 1

, tentukan

dx dy

Penyelesaian :

Misal : u = x 5 1

y = 3 sinh u

5 1 dx du

= 3coshu

du dy

(23)

x 3 1 cosh 5 3 ) 5 1 u)( cosh 3 ( dx du du dy dx dy

= =

=

Jika y = f(x) = coshx maka =f'(x)=

dx

dy _sinhx _(4.46)

Bukti :

y = f(x) = coshx = (e e ) 2

1 x₊ -x

) x ( ' f dx dy

= = (e e )

2

1 x_- -x _{= sinhx (terbukti)}

Jika y = cosh u dan u = f(x) maka =

dx

dy _{sinh u} dx

du _(4.47)

Bukti :

y = cosh u ® sinhu du

dy

=

dx du u sinh dx du . du dy dx dy

=

= (terbukti)

Contoh 4.26

Jika y = cosh (1-2x), tentukan

dx dy

Penyelesaian :

Misal : u = 1-2x y = cosh u

2

dx du

-=

=

sinh

u

du

dy

(sinh

u)(-2

)

2

sinh(

1

2

x

)

dx

du

dy

dx

dy

-=

=

Jika y = f(x) = tanhx maka =f'(x)=

dx

dy _sech2_x _(4.48)

Bukti :

y = f(x) = tanhx = x cosh

x sinh

) x ( ' f dx dy

= =

x cosh

x sinh x cosh )

x (cosh

) x )(sinh x (sinh ) x )(cosh x (cosh

2 2 2

2

-=

-= sech x

x cosh

1 2

2 = (terbukti)

Jika y = tanh u dan u = f(x) maka =

dx

dy _sech2_u

dx

du _(4.49)

(24)

y = tanh u ® sech u du

dy 2

=

dx du u h sec dx du . du dy dx

dy ₌ ₌ 2 _(terbukti)

Contoh 4.27

Jika y = tanh (a+bx), tentukan

dx dy

Penyelesaian :

Misal : u = a+bx y = tanh u

b

dx du

= sech u

du

dy 2

=

(sech u)(b) bsech (a bx)

dx du du dy dx

dy ₌ ₌ 2 ₌ 2 ₊

Jika y = f(x) = cothx maka =f'(x)=

dx dy

-csch2 x (4.50)

Bukti :

y = f(x) = cothx =

x sinh

x cosh

) x ( ' f dx dy

= =

x sinh

x cosh x sinh

) x (sinh

) x )(cosh x (cosh ) x )(sinh x (sinh

2 2 2

2

-=

-= csch x

x sinh

1 2

2 =

(terbukti)

Jika y = coth u dan u = f(x) maka =

dx

dy _{- csch}2_u

dx

du _(4.51)

Bukti : y = tanh u ® csch u du

dy 2

-=

dx du u h csc dx du . du dy dx

dy ₌ ₌_- 2 _(terbukti)

Contoh 4.28

Jika y = coth (a+bt), tentukan

dt dy

Penyelesaian :

Misal : u = a+bt y = coth u

b

dt du

= csch u

du

dy ₌_- 2

( csch u)(b) bcsch (a bt)

dt du du dy dt

dy ₌ ₌ _- 2 ₌_- 2 ₊

Jika y = f(x) = sechx maka =f'(x)=

dx dy

-csch2 x (4.52)

Bukti : y = f(x) = sechx = x cosh

(25)

Misal u = 1 ® 0 dx du

=

V = coshx ® sinhx

dx dv

=

2 v

dx dv . u v . dx du

dx

dy

-= =

2 ) x (cosh

) x )(sinh 1 ( ) x )(cosh 0

(

-=

x cosh

x sinh

2

= - tanhx sechx (terbukti)

Jika y = sech u dan u = f(x) maka =

dx dy

- tanhu sechu

dx du

(4.53)

Bukti : y = sech u ® tanhusechu du

dy

-=

dx du u sech u tanh dx

du . du dy dx dy

-=

= (terbukti)

Contoh 4.29

Jika y = 2sech x) 5 1 3 1

( - , tentukan

dt dy

Penyelesaian :

Misal : u = x 5 1 3 1

- y = 2 sech u

5 1 dx du

-= tanhu sechu

du dy

-=

x)

5 1 3 1 sech( ) x 5 1 3 1 tanh( 5 2 ) 5 1

u tanh 2 ( dt du du dy dt dy

-=

-= =

y = f(x) = cschx maka =f'(x)=

dx dy

-csch x cothx (4.54)

Bukti :

y = f(x) = sechx =

x sinh

1

Misal u = 1 ® 0

dx du

=

V = sinhx ® coshx

dx dv

=

2 v

dx dv . u v . dx du

dx

dy

-= =

2 ) x (sinh

) x )(cosh 1 ( ) x )(sinh 0

(

-=

x sinh

x cosh

2

= - cothx cschx (terbukti)

Jika y = csch u dan u = f(x) maka =

dx dy

- cothu cschu dx du

(4.55) Bukti :

y = csch u ® cothucschu du

dy

(26)

dx du u csch u coth dx

du . du dy dx dy

-=

= (terbukti)

Contoh 4.30

Jika y = -3csch x) 2 1 5 1

( + , tentukan

dt dy

Penyelesaian :

Misal : u = x 2 1 5 1

+ y = -3 csch u

2 1 dx du

= 3cothu cschu du

dy

=

x)

2 1 5 1 sech( ) x 2 1 5 1 coth( 2 3 ) 2 1 cschu)( u coth 3 ( dt du du dy dt dy

+ +

= =

=

Soal-soal

Tentukan turunan pertama dari fungsi-fungsi berikut !

1. y = sinh(2-3x) 6. y =

) x 2 1 coth(

c bx ax2

+ + +

2. y = cosh(a2x – b) 7. y =

x 2 h sec

e-ax

3. y = x2 sinh5x 8. y =

) x 5 4 ln(

x 3 h sec

-4. y = emx cosh2x 9. y = x csch(x-1) 5

1 3

5. y = ln(2-x) tanh3x 10. y = e csch(a-bx) x

3 1

4.11 Turunan fungsi hiperbolik invers

Jika y = f(x) = sinh-1_{x maka}

= =f'(x) dx dy

1 x

1 2₊

(4.56)

Bukti : y = f(x) = sinh-1x = ln(x+ x2+1)

1 x

1

1 x x

1 . 1 x

x 1 x

1 x x

1 x

x 1

dx dy

2 2

2 2 2

2

+ = + + +

+ + = + +

+ +

= (terbukti)

Jika y = sinh-1 u dan u = f(x) maka =

dx dy

dx du

1 u

1

2₊ (4.57)

Bukti : y = sinh-1 u ®

1 u

1 du dy

2₊

=

dx du

1 u

2

+ =

(27)

Contoh 4.31 Jika y = -3sinh-1

x 2

1 _{, tentukan} dt dy

Penyelesaian :

Misal : u = x 2

1 _{y = -3 sinh}-1_u

2 1 dx du

=

1

3

2

+

-=

u

du

dy

1

4

1

2

3

)

2

1

)(

1

3

(

2 2

+

-=

+

-=

=

x

u

dt

du

dy

dt

dy

Jika y = f(x) = cosh-1x maka =f'(x)=

dx dy

1 x

1 2

, x > 1 (4.58)

Bukti : y = f(x) = cosh-1_{x =}

) 1 x x

ln( + 2-

1 x

1

1 x x

1 . 1 x

x 1 x

1 x x

1 x

x 1

dx dy

2 2

2 2 2

2

-= -+

-+ -= -+

-+

= , x > 1 (terbukti)

Jika y = cosh-1_{u dan u = f(x) maka}

=

dx dy

dx du

1 u

1 2

, u > 1 (4.59)

Bukti : y = cosh-1_u _®

1 u

1 du dy

2

-=

dx du

1 u

2

-=

= , u > 1 (terbukti)

Contoh 4.32 Jika y = cosh-1

x 4

3 _{, tentukan} dx dy

Penyelesaian :

Misal : u = x 4

3 _{y = cosh}-1_u

4 3 dx du

=

1 u

1 du dy

2

-=

1 x 16

9 4

3 )

4 3 )( 1 u

1 ( dt du du dy dt dy

2 2

+ =

-= =

Jika y = f(x) = tanh-1x maka =f'(x)=

dx dy

2 x 1

1

-, x <1 (4.60)

Bukti : y = f(x) = tanh-1_{x =}

1 x , x 1

x 1 ln 2 1

<

(28)

₂ ₂ x 1

1 x 1

x 1 . ) x 1 (

2 2 1 dx dy

-= +

-= , x <1 (terbukti)

Jika y = tanh-1_{u dan u = f(x) maka}

=

dx dy

dx du

u 1

1 2

-, u <1 (4.61)

Bukti : y = tanh-1 u ® ₂

u 1

1 du dy

-=

dx du

u 1

2

-=

= , u <1 (terbukti)

Contoh 4.33

Jika y = tanh-1_{(2x-1), tentukan}

dx dy

Penyelesaian :

Misal : u = 2x - 1 y = tanh-1u

2

dx du

= ₂

u 1

1 du dy

-=

2 2 ₁ ₍₂_x ₁₎

2 )

2 )( u 1

1 ( dx du du dy dx dy

-=

-= =

Jika y = f(x) = coth-1_{x maka}

= =f'(x) dx dy

2 x 1

1

-, x >1 (4.62)

Bukti : y = f(x) = tanh-1x = , x 1 1

x 1 x ln 2 1

>

-+

2 2

2 ₁ _x

1

1 x

1 1

x 1 x . ) 1 x (

2 2 1 dx dy

-= -= +

-= , x >1 (terbukti)

Jika y = coth-1 u dan u = f(x) maka =

dx dy

dx du

u 1

1 2

-, u >1 (4.63)

Bukti : y = tanh-1 u ® ₂

u 1

1 du dy

-=

dx du

u 1

2

-=

= , u >1 (terbukti)

Contoh 4.34

Jika y = 3 coth-1(2-3x), tentukan dx dy

Penyelesaian :

Misal : u = 2-3x y = 3 tanh-1u

3

dx du

-=

2 u 1

3 du dy

-=

2 2 ₁ ₍₂ ₃_x₎

9 )

3 )( u 1

(29)

Jika y = f(x) = sech-1x maka =f'(x)=

dx dy

2 x 1 x

1

-- , 0<x<1 (4.64)

Bukti : y = f(x) = sech-1x = , 0 x 1 x

x 1 1 ln

2

< <

-+

2 x 1 x

1 dx

dy

-= , 0<x<1 (terbukti)

Jika y = sech-1 u dan u = f(x) maka =

dx dy

dx du

u 1 u

1 2

-- , 0<u<1 (4.65)

Bukti : y = sech-1 u ®

2 u 1 u

1 du

dy

-=

dx du

u 1

1 dx

du . du dy dx dy

2

-=

= , 0<u<1 (terbukti)

Contoh 4.35

Jika y = -2 sech-1_{(1-x), tentukan}

dx dy

Penyelesaian :

Misal : u = 1-x y = 2 sech-1u

1

dx du

-=

2 u 1 u

2 du

dy

-=

2 2 ₍₁ _x₎ ₁ ₍₁ _x₎

2 )

1 )( u 1 u

-= -= =

Jika y = f(x) = csch-1x maka =f'(x)=

dx dy

2 x 1 x

1

+

- (4.66)

Bukti : y = f(x) = csch-1_{x =}

x x 1 1 ln

2

+ +

2 x 1 x

1 dx

dy

+

-= (terbukti)

Jika y = csch-1 u dan u = f(x) maka =

dx dy

dx du

u 1 u

1 2

+

- (4.67)

Bukti : y = csch-1_u _®

2 u 1 u

1 du

dy

+ -=

dx du

u 1 u

1 dx

du . du dy dx dy

2

+ -=

= (terbukti)

(30)

Jika y = csch-1(sinx), tentukan dx dy

Penyelesaian :

Misal : u = sinx y = csch-1_u

cosx

dx du

=

2

u 1 u

1 du

dy

+ -=

x sin 1 x sin

x cos

) x )(cos u 1 u

2 2

+

-= +

-= =

Soal-soal

Tentukan turunan pertama dari fungsi-fungsi : 1. y = sinh-1(cosx) 4. y = x2 coth-1x 2. y = cosh-1(sin2x) 5. y = sech-1(x sinx) 3. y = tanh-1_(3x+_p₎ _{6. y = e}-2x

csch-1_(1-2x)

4.12 Turunan tingkat tinggi

Jika terdapat suatu fungsi f(x) yang differensiable, maka kita dapat mencari turunan pertamanya yaitu f’(x). Jika turunan pertama tersebut juga differensiable maka kita dapat menentukan turunan kedua dari fungsi tersebut. Secara umum jika turunan ke (n-1) differensiable maka kita dapat menentukan turunan ke n dari fungsi tersebut. Biasanya turunan kedua dan seterusnya dari suatu fungsi disebut turunan tingkat tinggi. Turunan pertama, kedua dan ketiga ditulis dengan lambang :

2 2 dx y d , dx

dy _dan 3 3 dx y

d _{atau f}_’_{(x), f}_’’_{(x) dan f}_’’’_{(x). Sedangkan untuk turunan ke n,}

dimana n ³4, maka kita gunakan lambang : n n dx y

d _{atau f}(n)

(x). Contoh 4.37

Tentukan turunan pertama sampai dengan turunan keempat dari f(x) = (x2_-4)3 Penyelesaian :

f'(x) 3(x2 4)2(2x) 6x(x2 4)2 dx

dy

-=

-= =

f''(x) 6(x 4) 6x(4x)(x 4) 6(x 4) 24x (x 4) dx

y

d 2 2 2 2 2 2 2

2 2

-+

-= -+

-= =

f'''(x) 24x(x 4) 48x(x 4) 48x 120x 288x dx

y

d 2 2 3 3

3 3

-=

+ -+

-=

=

288 x 360 ) x ( f dx

y

d (4) 2

4 4

-=

=

Soal-soal

Tentukan turunan kedua dari fungsi-fungsi :

1. f(x) = 2x e-x 2. f(x) = ln(a-bx) 3. f(x) = 1 x

x 2

(31)

4. f(x) = 2 2

x 1

4 x

-+

5. f(x) = sin2(a-bx)

6.f(x) = cos2 (mx+n)

4.13 Differensial

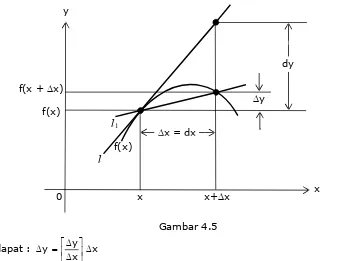
Pada pembahasan mengenai masalah turunan kita telah menggunakan lambang dy/dx sebagai suatu kesatuan dan merupakan lambang dari turunan pertama suatu fungsi x. Pada pasal ini kita akan membahas pengertian dy dan dx secara terpisah. Misal terdapat suatu persamaan y = f(x). Dari Gambar 4.5

didapat : x

x y

y _ú D

û ù ê ë é

D D =

D (4.68)

Jika harga Dx sangat kecil, maka Dy menjadi sangat kecil juga. Sehingga persamaan 4.68 dapat ditulis menjadi :

dx ) x ( f

dy = ¢ (4.69)

Pada persamaan 4.69 diatas dx dan dy disebut differensial dari x dan y. Differensial y atau dy adalah perubahan kecil pada peubah y akibat adanya perubahan kecil pada peubah x atau dx.

Contoh 4.38

Jika y = x2 - 2x – 3, tentukan differensial y Penyelesaian :

f(x) = x2 - 2x – 3 f’(x) = 2x – 2

Sehingga : dy = (2x-2) dx = 2(x-1) dx

Contoh 4.39

Dx = dx

l

1

f(x)

l

f(x + Dx)

f(x)

Dy dy y

[image:31.595.138.475.253.514.2]

x x+Dx x 0

(32)

Volume sebuah silinder adalah V = pr2_{h. Jika jari-jari silinder tersebut} membesar 1% dari jari-jari asal, tentukan perubahan volumenya.

Penyelesaian : f(r) = pr2_h f’(r) = 2prh

dV = f’(r) dr = 2prh (0,01r) = 0,02 pr2_h

Jadi perubahan volume silinder adalah sebesar 0,02 pr2h

Soal-soal

1. Sebuah bola mempunyai jari-jari 15 cm. Akibat meningkatnya temperatur maka jari-jari bola tersebut meningkat menjadi 15,02 cm. Berapakah perubahan volume bola tersebut ?

2. Sebuah kolam renang berisi penuh dengan air.Ukuran kolam renang tsb adalah sebagai berikut : panjang = 50 m, lebar = 20 meter dan kedalaman = 3 meter. Akibat adanya penguapan kedalaman air berkurang menjadi 2,98 m. Berapakah volume air yang menguap ?

Penjelasan :

Kerjakan kedua soal tersebut diatas dengan metode differensial !

4.14 Turunan fungsi implisit

Pada pasal-pasal sebelumnya kita telah mempelajari turunan fungsi-fungsi eksplisit, yaitu fungsi yang mempunyai bentuk y =f(x). Akan tetapi tidak semua fungsi mempunyai bentuk eksplisit. Sebagian mempunyai bentuk implisit, yaitu fungsi yang mempunyai bentuk F(x,y) = 0. Untuk mencari turunan fungsi implisit kita gunakan aturan sebagai berikut :

1. Jika pada F(x,y) = 0 mengandung suku g(x), maka : )

x ( ' g ) x ( g dx

d

= (4.70)

2. Jika pada F(x,y) = 0 mengandung suku h(y), maka :

dx dy ) y ( ' h ) y ( h dx

d

= (4.71)

3. Jika pada F(x,y) = 0 mengandung suku u(x) dan v(y), maka :

[

]

dx dy ) y ( ' v ). x ( u ) y ( v ). x ( ' u ) y ( v ). x ( u dx

d

+

= (4.72)

=

Contoh 4.40 Tentukan

dx dy

dari : x2– 3xy +y2 = 4 Penyelesaian :

(33)

2x – 3y – 3x dx dy

+ 2y dx dy

- 0 = 0

( 2y – 3x ) dx dy

= 3y - 2x ®

x

y

x

y

dx

dy

3

2

3

-=

Contoh 4.41 Tentukan

dx dy

dari : x2_{y + xy}2_{= 6 pada titik (1,2)} Penyelesaian :

x2y + xy2 = r2® x2y + xy2 - r2 = 0 2xy + x2

dx dy

+ y2_{+ 2xy} dx dy

= 0

(x2_{+ 2xy)} dx dy

= -(2xy + y2₎_®

) xy 2 x (

) y xy 2 ( dx dy

2 2

+ +

-= ®

5 8 dx

dy

2 y

1 x =

-= =

Soal-soal 1.Tentukan

dx dy

dari : i) x + y = sinxy ii)xy = cos (x+y) iii) y = exy

iv) y = ln(xy)

2.Tentukan nilai dx dy

pada titik (1,0) dari : i) 3xy2_{+ e}x+y_{= e}

ii) x2 + y2 + xy = 1

4.15 Turunan fungsi parameter

Fungsi parameter adalah fungsi yang mempunyai bentuk :

x = f(t) dan y = g(t) , dengan t adalah parameter (4.73)

Untuk menentukan turunan pertama atau dy/dx dari fungsi parameter, terlebih dahulu kita tentukan dx/dt dan dy/dt. Serlanjutnya dy/dx dicari dengan rumus:

dt / dx

dt / dy dx dy

= (4.74)

Soal-soal Tentukan

dx dy

(34)

1.

ïî ï í ì

-=

+ =

2 2

3

) 4 t ( y

) 3 t ( x

3.

î í ì

=

p -=

t 2 cos y

) t sin( x

2.

ïî ï í ì

-=

=

) 7 t 5 ln( y

e

x 2t _4.

ï ï î ï ï í ì

-=

+ + =

t t 1 y

1 t

1 t x

2 2