BAB 3 PENGEMBANGAN TEOREMA DAN PERANCANGAN PROGRAM

PENGEMBANGAN TEOREMA DAN PERANCANGAN PROGRAM

3.1. Pengembangan Teorema

Dalam penelitian dan perancangan algoritma ini, akan dibahas mengenai beberapa teorema uji primalitas yang terbaru. Teorema-teorema ini akan dipergunakan dalam pengembangan algoritma yang akan dirancang. Berikut ini adalah teorema-teorema uji primalitas.

Teorema 3.1.1.Teorema Lucas-Lehmer

Terdapat sebuah bilangan prima ganjil p. Mp adalah bilangan prima jika dan hanya jika S₍p₋₁₎ = 0

(

mod Mp

)

di mana S1 = 4 dan S_n = S_n²₋₁ − 2.

Bukti :

Misalkan w = 2 + 3 dan v = 2 − 3. Maka, dengan mudah dapat kita tunjukkan bahwa S_n = w²ⁿ⁻¹ + v²ⁿ⁻¹. Jadi, Mp membagi Sp-1 berarti terdapat sebuah bilangan bulat positif R sedemikian sehingga w^2p−2 + v^2p−2 = RM_p.

Atau, setelah kita kalikan dengan w^2p−2 dan dikurangi satu, akan kita dapatkan

2 1

1 2

2^p− = R ⋅M ⋅w ^p− −

w _p ………...(1) dan setelah

dikuadratkan ^{w2p =}

(

^{R ⋅ M}p ^{⋅ w2p−2 −1}

)

²………...(2)

Dengan menggunakan pembuktian secara kontradiksi, kita asumsikan Mp

adalah bilangan komposit dan pilih salah satu faktor pembagi primanya q yang tidak lebih besar dari akar kuadratnya.

Anggap grup G = Ζq

[ ]

³ terdiri dari semua bilangan dengan bentuk q

b

a + 3 mod yang memiliki invers, dengan catatan G memiliki paling banyak

2 −1

q elemen. Melihat w mod q, persamaan (1) dan (2) di atas menjadi

1 1

2^p− = −

w dan w^2p = 1, menunjukkan bahwa w adalah sebuah elemen dari G dengan order 2^p. Karena order dari sebuah elemen dalam suatu grup tidak akan lebih besar dari order grup itu sendiri, sehingga kita dapatkan

1 2 1

2^p ≤ q² − < M_p = ^p − suatu kontradiksi, memenuhi syarat cukup.

Untuk memenuhi syarat perlu, sekarang kita asumsikan Mp adalah bilangan prima. Hukum dua arah (resiprok) mengimplikasikan :

1 3

3  = −



 



−

 =











 _p

p

M

M

1 1

−

 =











 − Mp

Karena 12M_p ≡ 7 mod dengan p adalah bilangan prima ganjil. Sehingga

kita tahu bahwa G memiliki order 2p dan S_i ⁼ Tr_GΖ_q

(

^{2 + 3}

)

^2i−1,i ^{= 1,2,....}

Sekarang kita selesaikan dalam G saja, karena

( ) ( ) (

^{4 2 3}

)

^{2 3}

2 3 1 2 4 2 3

1

2 ¹

2 2

1

+

= +

= +

 =



 



 ^p− + ^p− sehingga

(

^{2 3}

)

^{2p1 2p21}

(

^{1 3}

)

^{2p = 2(p 1)2p1}

(

^{1+ 3}

)

^2p



 



 +

=

+ ^{− − − −}

Karena 2p = 1 dan

(

p −1

)

2^p−1 ≡ −1mod p, kita tahu bahwa 2^{(p−1)2p−1} = 12. Juga dengan teorema binomial,

(

^{1 + 3}

)

^{2p = 1+ 2p 3 + 2p}

( )

^{3 2p−1 +}

( )

^{3 2p}

(tiap unit di bagian tengah merupakan sebuah pembagi dari q dalam koefisien binomialnya.)

^{= 1+ 32p−1 +}

(

^{1+ 32p−1−1}

)

³

Berdasarkan hukum dua arah di atas, kita dapat bahwa 3 bukanlah kuadrat sempurna dalam Ζ , sehingga kita dapat membuat _q

(

q −1

)

2 = 2^p−1 −1 berpasangan dari 1 sampai q −1. Dengan demikian, hasil dari tiap pasangan adalah 3, dan hal ini mengimplikasikan

3^2p−1−1 =

(

q −1

)

!= −1 Dengan Lemma Wilson, kita dapatkan

(

^{1 + 3}

)

^{2P =}

⁽

^{1− 3}

⁾

^{+ 3}

⁽

^{1 −1}

⁾

^{= −2}

Sehingga

(

^{2 + 3}

)

^{2p−1 = −1} dengan persamaan di atas kita dapatkan

(

^{2+ 3}

)

^{2p−2 =α 3}

Untuk beberapa

α ∈ Ζ

q dimana hasil kuadratnya adalah -1/3. Sehingga

(

^{2 3}

)

/ ^{3 0}

2 /

1

2 = =

+

= _{Ζ Ζ}

−

− _{G q}α

q G

p Tr Tr

a

p

Yang membuktikan pernyataan tersebut.

Contoh :

Akan dibuktikan bahwa 2⁷ – 1 adalah bilangan prima :

( )

( )

( )

( )

(

111 *111 2

)

mod127 0 111 127

mod 2 42

* 42

42 127 mod 2 67

* 67

67 127 mod 2 14

* 14

14 127 mod 2 4

* 4 4

5 4 3 2 1 0

=

−

=

=

−

=

=

−

=

=

−

=

=

−

=

=

S S S S S S

Terbukti bahwa S_p−2 = 0, maka 2⁷ – 1 = 127 merupakan bilangan prima.

Teori uji primalitas ini merupakan inisiatif dari Lucas pada akhir tahun 1870 dan disederhanakan oleh Lehmer pada tahun 1930. Setiap barisan Sp dimodulokan 2^p - 1 untuk mempercepat perhitungan. Uji ini ideal untuk komputer biner karena pembagian oleh 2^p - 1 dapat dilakukan hanya dengan menggunakan perputaran dan penjumlahan saja.

Teorema 3.1.2. Teorema Pocklington

Andaikan n adalah bilangan bulat dengan n – 1 = FR, dimana ( F, R) = 1 dan R

F > . Bilangan bulat n tersebut adalah prima jika ada sebuah bilangan bulat a sedemikian sehingga (a ^{(n -1) / q} – 1, n) = 1 dengan q adalah bilangan prima dengan q

F danaⁿ⁻¹ ≡ 1

(

mod n

)

. Bukti :

Misalkan p adalah pembagi prima untuk n. Karena a^{n – 1} ≡ 1(mod n) (dimana a adalah sebuah bilangan bulat yang dimisalkan memiliki sifat khusus),

jika p | n, kita lihat bahwa a^{n – 1} ≡ 1(mod p). Hal ini sesuai dengan ordp(a) | (n – 1).

Akibatnya, ada sebuah bilangan bulat t sedemikian sehingga n – 1 = t . ordp(a).

Sekarang, misalkan q adalah bilangan prima dengan q | F. Akan ditunjukkan t

q | . Untuk mendapatkan ini, ingat bahwa q | t, maka a(n – 1) / q = a ordp(a) t / q = 1 (mod p).

Hal ini mengimplikasikan bahwa p | (a(n – 1) / q -1, n) karena p | a^{(n – 1)/q} – 1). Ini menjadi kontradiksi dengan hipotesis bahwa (a^(n-1)/q – 1, n) = 1. Akibatnya, q tidak habis membagi t. Hal ini sesuai dengan pernyataan bahwa semua pembagi prima dari F membagi ordp(a). Akibatnya, F | ordp(a). Karena ordp(a) | p -1, sesuai dengan F p −1, mengimplikasikanF < p.

Karena F > Rdan n −1= FR, sehingga n − 1 > F. karena keduanya, n −1 dan F , adalah bilangan bulat, didapatkan ² n −1 ≤ F , sehingga ² p > F ≥ n. dapat disimpulkan bahwa n adalah bilangan prima.

3.2. Perancangan Program 3.2.1 Struktur Program

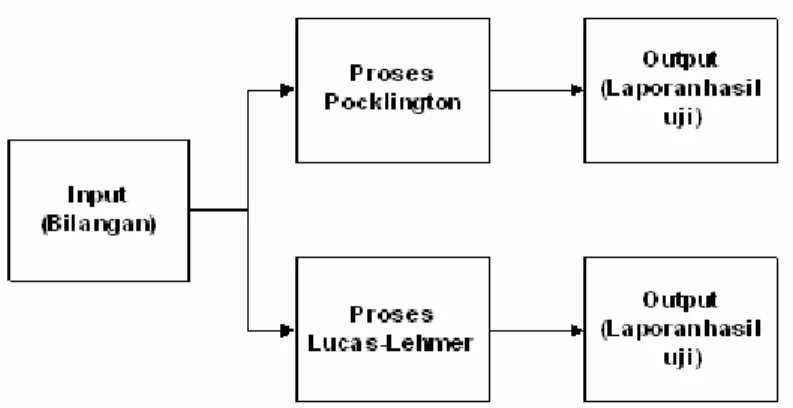
Gambar 3.1 Struktur Chart

Input yang digunakan dalam program ini berupa bilangan yang merupakan bilangan ganjil dan harus lebih besar daripada 2. Output dari program ini merupakan laporan hasil uji berdasarkan kedua teorema yang digunakan.

Laporan uji tersebut menyatakan bilangan yang diinput bilangan prima atau bukan serta waktu yang diperlukan untuk menguji bilangan tersebut.

Pengujian berdasarkan teorema uji primalitas Pocklington menggunakan 2 tahap, yaitu tahap modulo dan pencarian gcd. Sedangkan pengujian berdasarkan teorema uji primalitas Lucas-Lehmer menggunakan tahap pengkuadratan cepat.

3.2.2 Tipe Data yang digunakan

Untuk dapat menguji bilangan yang cukup besar diperlukan penampung data (tipe data) yang besar pula. Pada metode yang penulis gunakan, terdapat suatu pengujian berdasarkan rumus gcd(a_n^(n−1)/pi −1,n)=1, di mana n sangat menentukan besar a_n^(n−1)/pi yang akan ditampung. Nilai a_n^(n−1)/pi jauh lebih besar dari daya tampung tipe data yang telah tersedia, sehingga hasil perhitungan menjadi tidak akurat. Oleh karena itu diperlukanlah suatu tipe data baru yang dapat menampung hasil perhitungan di atas dan dukungan algoritma – algoritma perhitungan untuk tipe data yang baru tersebut.

Tipe data baru yang akan penulis gunakan adalah tipe data String, di mana tipe data ini dapat menampung bilangan yang sangat besar. Supaya tipe data ini dapat kita gunakan dalam perhitungan, maka diperlukanlah modul – modul untuk mengoperasikan tipe data tersebut. Modul dasar operasinya adalah

Modul Penjumlahan, Modul Pengurangan, Modul Perkalian dan Modul Pembagian. Kemudian modul – modul ini digunakan sebagai dasar perhitungan dari fungsi – fungsi / modul – modul yang lain. Modul Penjumlahan dan Modul Pengurangan sama seperti dasar algoritma penjumlahan dan pengurangan bilangan. Modul Perkalian dari bilangan a dan b menggunakan Modul Penjumlahan bilangan a diulang sebanyak b kali. Sedangkan Modul Pembagian (a membagi b) menggunakan Modul Pengurangan b dengan a terus menerus hingga b lebih kecil dari a. Jumlah perulangan dari pengurangan terserbut adalah hasil bagi, dan nilai b terakhir yang lebih kecil dari a merupakan sisa.

3.2.3 Tahap – Tahap yang digunakan 3.2.3.1 Tahap Validasi

Pada tahap ini, input yang dimasukkan oleh user akan diperiksa. Input harus berupa bilangan ganjil dan lebih besar dari 1. Jika input tidak memenuhi syarat tersebut, maka akan ditampilkan pesan kesalahan.

3.2.3.2 Tahap Utama Uji Primalitas

Ada 2 tahap uji primalitas, yaitu tahap uji Lucas-Lehmer dan Uji Pocklington. Pada tahap Lucas-Lehmer, terdapat 2 tahap pengujian yaitu tahap pengujian dengan kuadrat cepat dan tahap pencarian faktor.

Tahap pertama dari Modul Uji Lucas-Lehmer adalah menguji bilangan Mersenne berdasarkan rumus S_n =

(

S_n−1² − ²

) (

^{mod2 p} −¹

)

. Bilangan Mersenne dihasilkan dari p, dimana p adalah bilangan yang diinput. Pengujian bilangan tersebut dilakukan berdasarkan dengan teorema Lucas-Lehmer. Proses

pengkuadratan dilakukan dengan cara membagi proses pengkuadratan menjadi dua bagian sama besar kemudian dijalankan proses kuadrat biasa terhadap kedua bagian tersebut, baru kemudian digabungkan kembali dan didapatkan hasil kuadrat dengan waktu dua kali lebih cepat dari pengkuadratan biasa. Sebagai langkah awal pengujian ditetapkan S = 4, kemudian dilakukan perulangan sebanyak p − 3 kali untuk mendapatkan S_p−2 = 0. Jika didapatkan

2 = 0

p−

S , maka bilangan Mersenne tersebut merupakan bilangan prima.

Namun, jika S_p−2 ≠ 0 maka bilangan Mersenne tersebut bukanlah bilangan prima.

Tahap kedua adalah pencarian faktor. Tahap ini hanya dilakukan bila bilangan Mersenne, Mn yang diuji dinyatakan sebagai bilangan komposit.

Pencarian faktor ini dilakukan untuk membuktikan bahwa bilangan tersebut memang bukan bilangan prima. Faktor yang didapat akan ditampilkan sebagai output. Pemfaktoran Mn – 1 berdasarkan Teorema Fundamental Aritmetika dan Metode Eratosthenes, di mana nilai Mn – 1 diuraikan satu – persatu dimulai dari bilangan prima terkecil, yaitu 2, dengan menggunakan Modul Pembagian sampai dengan M , hingga didapatlah faktor – faktor primanya. Kemudian dari faktor-_n faktor prima tersebut didapatkanlah suatu variabel m dan j, di mana

Mn

m j m

p = ⋅ , > dan m = p₁^k1p₂^k2...p^ks_s . Untuk suatu n = a / b, di mana a

≥ b, nilai n akan semakin kecil jika nilai b semakin besar. Sehingga untuk memperkecil proses perhitungan, nilai m sebagai pembagi dari (Mn – 1),

sebaiknya diperoleh dari perkalian faktor – faktor prima Mn – 1 yang terbesar, hingga memenuhi syarat m > M_n .

Sedangkan pada tahap Pocklington terdapat 3 tahap pengujian, yaitu tahap pencarian faktor n – 1, dan 2 tahap pengujian.

Tahap pertama dari Modul Uji Pocklington adalah mencari faktor dari n – 1, di mana n adalah bilangan yang diinput / akan diuji. Pemfaktoran dilakukan dengan cara yang sama dengan pencarian faktor pada tahap Uji Lucas-Lehmer di atas.

Tahap kedua dari Modul Uji Primalitas adalah pengujian dari faktor – faktor n – 1 terhadap n dengan rumus a_iⁿ⁻¹ ≡1(modn) untuk sembarang basis ai. Basis ai merupakan bagian dari faktor – faktor pi. Untuk mempermudah pengujian maka sebaiknya kita gunakan basis ai yang relatif kecil, misal ai = 2.

Sehingga hasil pemangkatan ai tidak terlalu besar, sehingga proses perhitungan dapat memakan waktu yang lebih cepat. Perhitungan a_iⁿ⁻¹ ≡1(modn) dapat dipermudah dengan menggunakan Teorema Fermat. Jika a_iⁿ⁻¹ ≡1(modn) telah terpenuhi maka pengujian tahap ketiga dapat dilakukan.

Tahap ketiga dari Modul Uji Primalitas adalah pengujian terakhir berdasarkan rumus gcd(a_n^(n−1)/pi −1,n)=1. Pengujian ini adalah perhitungan yang paling sulit untuk dilakukan oleh karena besarnya bilangan yang akan diuji akan sangat besar, yaitua_n^(n−1)/pi, sehingga perlu waktu perhitungan yang relatif lama.

Jika bilangan masukan telah lulus dari kedua tahap pengujian, maka akan dinyatakan bahwa bilangan tersebut adalah bilangan prima. Sebaliknya jika bilangan terserbut tidak lulus dari salah satu atau kedua tahap pengujian tersebut maka akan dinyatakan bahwa bilangan tersebut bukanlah bilangan prima.

3.2.4 Diagram Alir Modul

Berikut ini adalah diagram alir dari program aplikasi yang dibuat oleh penulis.

3.2.4.1 Diagram Alir Modul Input

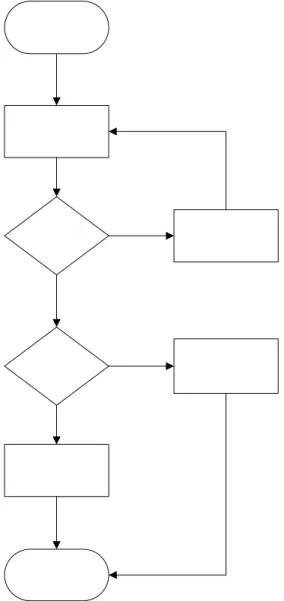
Berikut ini adalah diagram alir modul input yang menjelaskan proses validasi input

Gambar 3.2 Gambar Diagram Alir Modul Input

3.2.4.2 Diagram Alir Modul GCD

Berikut ini adalah diagram alir modul GCD yang menjelaskan tentang proses pencarian Greatest Common Divisor dari 2 bilangan.

Gambar 3.3 Gambar Diagram Alir Modul GCD

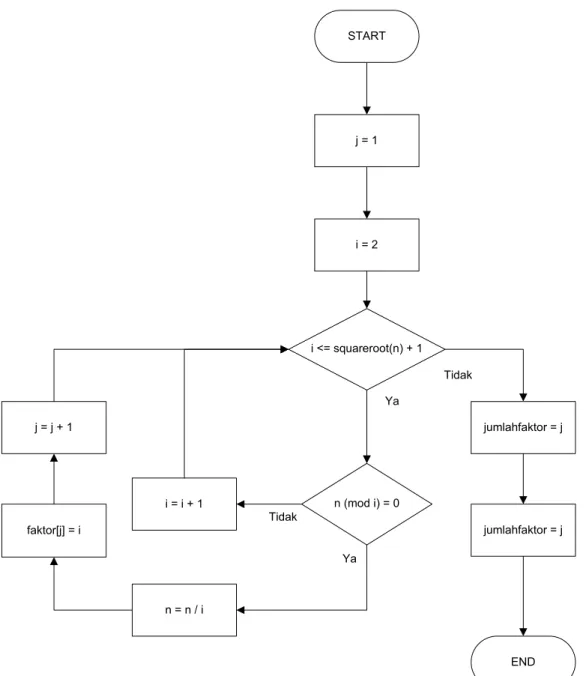
3.2.4.3 Diagram Alir Modul Faktorisasi

Berikut ini adalah diagram alir modul Faktorisasi yang menjelaskan proses faktorisasi suatu bilangan hingga didapat faktor – faktor dari suatu bilangan.

i <= squareroot(n) + 1 i = 2

n (mod i) = 0

n = n / i

Ya i = i + 1

Tidak

Ya

jumlahfaktor = j Tidak

j = 1

faktor[j] = i j = j + 1

jumlahfaktor = j START

END

Gambar 3.4 Gambar Diagram Alir Modul Faktorisasi

3.2.4.4 Diagram Alir Modul Utama

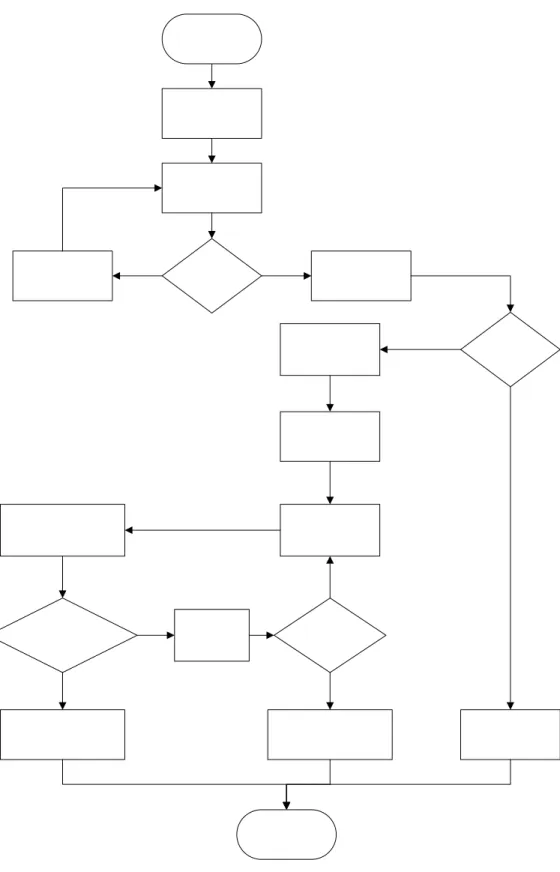
Berikut ini adalah diagram alir Modul Lucas-Lehmer yang menjelaskan pengujian primalitas suatu bilangan Mersenne.

START

3 <= i <= p

s := (s² - 2) mod (2^p - 1)

i++ s = 0

End

Mp prima Mp bukan prima

Tidak Ya

Ya Tidak

Input p Mp = 2^p -1

s:= 4

Gambar 3.5 Gambar Diagram Alir Modul Utama Lucas-Lehmer

Gambar 3.6 Gambar Diagram Alir Modul Utama Pocklington