BAB I LIMIT-LIMIT Limit-limit Fungsi

BAB I LIMIT-LIMIT

1.1. Limit-limit Fungsi

1.1.1. Definisi. Misalkan A⊆R. Suatu titik c∈R adalah titik cluster dari A jika setiap lingkungan-δ dari c, Vδ(c) = (c-δ,c+δ), memuat paling sedikit satu titik dari A yang berbeda dengan c.

Catatan : Titik c merupakan anggota dari A atau bukan, tetapi meskipun demikian itu tidak menentukan apakah c suatu titik cluster dari A atau bukan, karena secara khusus yang diperlukan adalah bahwa adanya titik- titik dalam V_δ(c)∩A yang berbeda dengan c agar c menjadi titik Cluster dari A, dengan demikian c akan menjadi titik cluster dari A jika dan hanya jika Vδ(c)∩A\{c} ≠ ∅.

1.1.2. Teorema. Suatu bilangan c∈R merupakan titik cluster dari A⊆R jika dan hanya jika terdapat barisan bilangan real (an) dalam A dengan an ≠ c untuk semua n∈N sedemikian sehingga lim (an) = c.

Bukti. Jika c merupakan titik cluster dari A, maka untuk setiap n∈N, lingkungan-(1/n) dari c, V1/n(c), memuat paling sedikit satu titik yang berbeda dengan c. Jika titik yang dimaksud adalah an, maka an∈A, a_n ≠ c, dan lim (a_n) = c.

Sebaliknya, jika terdapat suatu barisan (an) dalam A\{c} dengan lim(an) = c, maka untuk sebarang δ>0 terdapat bilangan asli K(δ) sedemikian sehingga jika n≥K(δ), maka a_n∈V_δ(c). Oleh karena itu lingkungan-δ dari c, V_δ(c), memuat titik-titik an, n≥K(δ), yang mana termuat dalam A dan berbeda dengan c.

Contoh-contoh berikut ini menekankan bahwa suatu titik cluster dari suatu himpunan dapat masuk dalam himpunan tersebut atau tidak. Bahkan lebih dari itu, suatu himpunan bisa mungkin tidak mempunyai titik cluster.

1.1.3. Contoh-contoh. (a) Jika A₁ = (0,1), maka setiap titik dalam interval tutup [0,1]

merupakan titik cluster dari A1. Perhatikan bahwa 0 dan 1 adalah titik cluster dari A1, meskipun titik- titik itu tidak termuat dalam A1. Semua titik dalam A1 adalah titik cluster dari A1 (mengapa?)

(b) Suatu himpunan berhingga tidak mempunyai titik cluster (mengapa?) (c) Himpunan tak berhingga N tidak mempunyai titik cluster.

(d) Himpunan A4 = {1/n : n∈N} hanya mempunyai 0 sebagai titik clusternya. Tidak satu pun titik dalam A4 yang merupakan titik cluster dari A4.

(e) Himpunan A5 = I∩Q yaitu himpunan semua bilangan rasional dalam interval tutup I=[0,1]. Ini menunjukkan bahwa setiap titik dalam I merupakan titik cluster dari A5.

Sekarang kita kembali kepada pengertian limit dari suatu fungsi pada titik cluster domainnya.

Definisi Limit

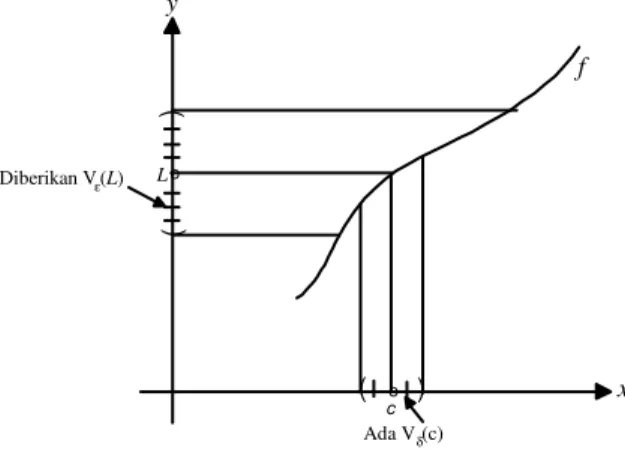
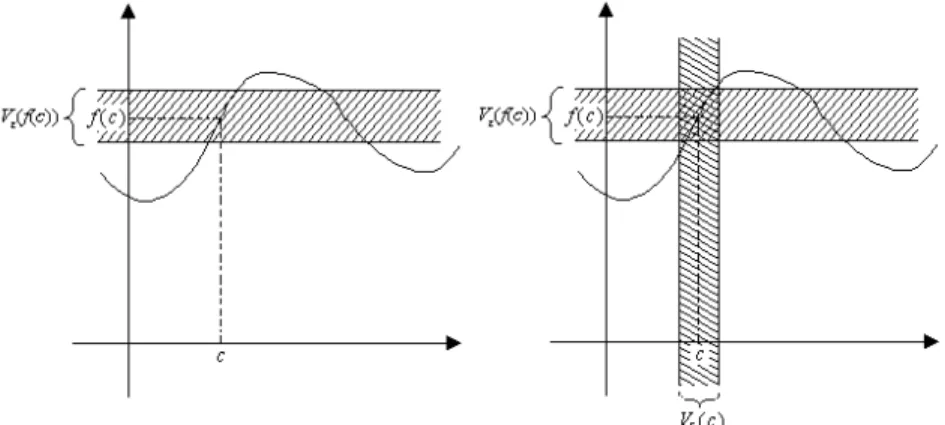
1.1.4 Definisi. Misalkan A⊆R, f : A → R, dan c suatu titik cluster dari A. Kita katakan bahwa suatu bilangan real L merupakan limit dari f pada c jika diberikan sebarang lingkungan-ε dari L, V_ε(L),

terdapat lingkungan-δ dari c, Vδ(c) sedemikian sehingga jika x ≠ c sebarang titik dari Vδ(c)∩A, maka f(x) termasuk dalam Vε(L). (Lihat Gambar 1.1.1)

Gambar 1.1 1. Limit dari f pada c adalah L

Jika L merupakan suatu limit dari f pada c, maka kita juga mengatakan bahwa f konvergen ke L pada c. Sering dituliskan L = f

x→c

lim atau L = ^f

( )

^x

x→c

lim

Kita juga mengatakan bahwa “f(x) menuju L sebagaimana x mendekat ke c”, atau “f(x) menuju L sebagaimana x menuju ke c”. Simbol F(x) → L sebagaimana x → c

juga dipergunakan untuk menyatakan fakta bahwa f mempunyai limit L pada c. Jika f tidak mempunyai suatu limit pada c, kita akan sering mengatakan bahwa f divergen pada c.

1.1.5. Teorema. Jika f : A → R dan c suatu titik cluster dari A, maka f hanya dapat mempunyai satu limit pada c.

Bukti. Andaikan kontradiksi, yaitu terdapat bilangan real L’ ≠ L” yang memenuhi definisi 1.1.4. Kita pilih ε>0 sedemikain sehingga lingkungan-ε dari L’ daan L”, yaitu V_ε(L’) dan Vε(L”) saling lepas. Sebagai contoh, kita dapat mengambil sebarang ε yang lebih kecil dari ½L’ – L”.

Maka menurut definisi 1.1.4, terdapat δ’ > 0 sedemikian sehingga jika x sebarang titik dalam A∩V_δ’(c) dan x ≠ c, maka f(x) termuat dalam V_ε(L’). Secara serupa, terdapat δ” > 0 sedemikian sehingga jika x sebarang titik dalam A∩Vδ”(c) dan x ≠ c, maka f(x) termuat dalam Vε(L”). Sekarang ambil δ = inf{δ’,δ”}, dan misalkan V_δ(c) lingkungan-δ dari c. Karena c titik cluster dari A, maka terdapat paling sedikit satu titik x0 ≠ c sedemikian sehingga x₀∈A∩Vδ(c). Akibatnya, f(x0) mesti termasuk dalam V_ε(L’) dan Vε(L”), yang mana kontradiksi dengan fakta bahwa kedua himpunan ini saling lepas. Jadi asumsi bahwa L’ ≠ L” merupakan limit-limit f pada c menimbulkan kontradiksi.

Kriteria εεεε-δδδδ untuk Limit

1.1.6 Teorema. Misalkan f : A → R dan c suatu titik cluster dari A, maka x y

Ada V_δ(c)

( (

((

o

o Diberikan V_ε(L) L

c

f

(ii) untuk sebarang ε > 0 terdapat suatu δ(ε) > 0 sedemikian sehingga jika x∈A dan 0 < x - c <

δ(ε), maka f(x) - L < ε.

Bukti. (i) ⇒ (ii) Anggaplah bahwa f mempunyai limit L pada c. Maka diberikan ε > 0 sebarang, terdapat δ = δ(ε) > 0 sedemikian sehingga untuk setiap x dalam A yang merupakan unsur dalam lingkungan-δ dari c, V_δc), x ≠ c, nilai f(x) termasuk dalam lingkungan-ε dari L, V_ε(L). Akan tetapi, x∈Vδ(c) dan x≠c jika dan hanya jika 0 < x - c < δ. (Perhatikan bahwa 0 < x - c adalah cara lain untuk menyatakan bahwa x ≠ c). Juga, f(x) termasuk dalam V_ε(L) jika dan hanya jika f(x) – L <

ε. Jadi jika x∈A memenuhi 0 < x - c< δ, maka f(x) memenuhi f(x) - L <ε.

(ii) ⇒ (i) Jika syarat yang dinyatakan dalam (ii) berlaku, maka kita ambil lingkungan-δ dari c, V_δ(c) = (c - δ,c + δ) dan lingkungan-ε dari L, Vε(L) = (L - ε,L + ε). Maka syarat (ii) berakibat jika x masuk dalam Vδ(c), dimana x∈A dan x≠c, maka f(x) termasuk dalam V_ε(L). Oleh karena itu, menurut definisi 1.1.4, f mempunyai limit L pada c.

Sekarang akan memberikan beberapa contoh untuk menunjukkan bagaimana Teorema 1.1.6.

sering dipergunakan.

1.1.7. Contoh-contoh. (a) b

x→c

lim = b.

Untuk menjadi lebih eksplisit, misalkan f(x) = b untuk semua x∈R; kita claim bahwa f

x→c

lim

= b. Memang, jika diberikan ε > 0, misalkan δ = ε. Maka jika 0 <x - c< ε, kita mempunyai f(x) - b

= b - b = 0 < δ =ε. Karena ε > 0 sebarang, kita simpulkan dari 1.1.6(ii) bahwa f

x→c

lim = b.

(b). x

c x

lim→ = c.

Misalkan g(x) = x untuk semua x∈R. Jika ε > 0 misalkan δ(ε) = ε. Maka jika 0 <x - c <

δ(ε), maka secara trivial kita mempunyai g(x) - c = x - c < ε. Karena ε > 0 sebarang, maka kita berkesimpulan bahwa g

x→c

lim = c.

(c). lim x ²

x→c = c².

Misalkan h(x) = x² untuk semua x∈R. Kita ingin membuat selisih h(x) – c² = x² – c² lebih kecil dari suatu ε > 0 yang diberikan dengan pengambilan x yang cukup dekat dengan c. Untuk itu, kita perhatikan bahwa x² – c² = (x – c)(x + c). Selain itu, jka x - c < 1, maka

x ≤ c + 1 dengan demikian x + c ≤ x + c ≤ 2c + 1.

Oleh karena itu, jika x - c < 1, kita mempunyai

(*) x² – c² = x – cx + c ≤ (2c + 1)x - c

Selain itu suku terakhir ini akan lebih kecil dari ε asalkan kita mengambil x - c < ε/(2c + 1).

Akibatnya, jika kita memilih δ(ε) = inf













+1 ,2 1 c

ε , maka jika 0 <x - c < δ(ε), pertama akan berlaku

bahwa x - c < 1 dengan demikian (*) valid. Selanjutnya, karena x - c < ε/(2c + 1) maka x² – c² < ε/(2c + 1)x - c < ε. Karena kita mempunyai pilihan δ(ε) > 0 untuk sebarang pilihan dari ε >

0, maka dengan demikian kita telah menunjukkan bahwa lim h(x)

x→c = lim x ²

x→c = c². (d) lim x c

c x

1 1 =

→ , jika c > 0.

Misalkan ϕ(x) = 1/x untuk x > 0 dan misalkan c > 0. Untuk menunjukkan bahwa lim ϕ

x→c = 1/c kita ingin membuat selisih

( )

x −1c

ϕ =

c x

1 −1 lebih kecil dari ε > 0 yang diberikan dengan pengambilan x cukup dekat dengan c > 0. Pertama kita perhatikan bahwa

c x

1 −1 =

(

c x

)

cx1 −

= x c

cx1 −

untuk x > 0. Itu berguna untuk mendapatkan batas atas dari 1/(cx) yang berlaku dalam suatu lingkungan c. Khususnya, jika x - c < ₂¹ c, maka ₂¹ c < x < ₂³ c (mengapa?), dengan demikian 0 <

cx 1 < 2₂

c untuk x - c < ₂¹ c. Oleh karena itu, untuk nilai-nilai x ini kita mempunyai

(#)

( )

x −1c

ϕ < x c

c2₂ − .

Agar suku terakhir lebih kecil dar ε, maka cukup mengambil x – c < ₂¹ c²ε. Akibatnya, jika kita memilih δ(ε) = inf{₂¹ c, ₂¹ c²ε}, maka apabila 0 < x - c < δ(ε), pertama yang berlaku bahwa x - c

< ¹₂c dengan demikian (#) valid, dan olehnya itu, karena x – c < ₂¹c²ε maka berlaku

( )

x −c1

ϕ =

c x

1 −1 < ε. Karena kita mempunyai pilihan δ(ε) > 0 untuk sebarang pilihan dari ε > 0, maka dengan

demikian kita telah menunjukkan bahwa lim (x)

c

x ϕ

→ =

x

c x

1 lim→ =

c 1.

(e).

5 4 1 4 lim 2

3 =

+

−

→ x x

c x

Misalkan ψ(x) = (x³ – 4)/(x² + 1) untuk x∈R. Maka sedikit manipulasi secara aljabar memberikan

( )

5 4

−

ψ x = ^{5 5}

(

^{42 1}

)

²⁴

2 3

+

−

− x

x x

= ^{5 5}

(

^{26 1}

)

¹²

2

+

− + x

x

x x - 2

Untuk mendapatkan suatu batas dari koefisien x - 2, kita membatasi x dengan syarat 1 < x < 3.

Untuk x dalam interval ini, kita mempunyai 5x² + 6x + 12 ≤ 5(3²) + 6(3) + 12 =75 dan 5(x² + 1) ≥ 5(1 + 1) = 10, dengan demikian

( )

5 4

−

ψ x ≤

1075 x - 2 =

15 x - 2. 2 Sekarang diberikan ε > 0, kita pilih δ(ε) = inf







 ε

15 , 2

1 . Maka jika 0 <x - 2 < δ(ε), kita mempunyai

ψ(x) – (4/5) ≤ (15/2)x - 2 < ε. Karena ε > 0 sebarang, maka contoh (e) terbukti.

Kriteria Barisan Untuk Limit

1.1.8. Teorema. (Kriteria Barisan) Misalkan f : A → R dan c suatu titik cluster dari A;

maka :

(i) f

x→c

lim = L jika dan hanya jika

(ii) untuk sebarang barisan (xn) dalam A yang konvergen ke c sedemikian sehingga x ≠ c untuk semua n∈N, barisan (f(xn)) konvergen ke L.

Bukti. (i) ⇒ (ii). Anggaplah f mempunyai limit L pada c, dan asumsikan (xn) barisan dalam A dengan

( )

_n

c x

→ x

lim = c dan xn ≠ c untuk semua n∈N. Kita mesti membuktikan bahwa barisan (f(x_n)) konvergen ke L. Misalkan ε > 0 sebarang, maka dengan Kriteria ε-δ 1.1.6, terdapat δ > 0 sedemikian sehingga jika x memenuhi 0 <x - c < δ, dimana x∈A maka f(x) memenuhi f(x) - L < ε. Sekarang kita akan menggunakan definisi kekonvergenan barisan untuk δ yang diberikan untuk memperoleh bilangan asli K(δ) sedemikian sehingga jika n > K(δ) maka xn – c < δ. Akan tetapi untuk setiap xn

yang demikian kita mempunyai f(xn) - L < ε. Jadi, jika n > K(δ), maka f(x_n) - L < ε. Oleh karena itu, barisan (f(xn)) konvergen ke L.

(ii) ⇒ (i). [Pembuktian ini merupakan argumen kontrapositif.] Jika (i) tidak benar, maka terdapat suatu lingkungan-ε0 dari L, ^V_ε0

( )

^L , sedemikian sehingga lingkunga-δ dari c apapun yang kita pilih, akan selalu terdapat paling kurang satu xδ dalam A∩V_δ(c) dengan xδ ≠ c sedemikian sehingga f(xδ)∉V

( )

L

ε0 . Dari sini untuk setiap n∈N, lingkungan-(1/n) dari c memuat suatu bilangan xn sedemi- kian sehingga 0 <xn - c < 1/n dan xn∈A, tetapi sedemikian sehingga f(x_n) - L ≥ ε₀ untuk semua n∈N. Kita menyimpulkan bahwa barisan (x_n) dalam A\{c} konvergen ke c, tetapi barisan (f(xn)) tidak konvergen ke L. Oleh karena itu kita telah menunjukkan bahwa jika (i) tidak benar, maka (ii) juga tidak benar. Kita simpulkan bahwa (ii) menyebabkan (i).

Kriteria Kedivergenan

1.1.9. Kriteria Divergensi. Misalkan A⊆R, f : A → R dan c∈R suatu titik cluster dari A.

(a). Jika L∈R, maka f tidak mempunyai limit L pada c jika dan hanya jika terdapat suatu barisan (xn) dalam A dengan xn ≠ c untuk semua n∈N sedemikian sehingga barisan (xn) konvergen ke c tetapi barisan (f(xn)) tidak konvergen ke L.

(b). Fungsi f tidak mempunyai limit pada c jika dan hanya jika terdapat suatu barisan (xn) dalam A dengan xn ≠ c untuk semua n∈N sedemikian sehingga barisan (xn) konvergen ke c tetapi barisan (f(xn)) tidak konvergen dalam R.

1.1.10. Contoh-contoh. (a).

( )

x

x 1/

lim→0 tidak ada dalam R.

Seperti Contoh dalam 1.1.7(d), misalkan ϕ(x) = 1/x untuk x > 0. Akan tetapi, disini kita menyelidiki pada c = 0. Argumen yang diberikan pada contoh 1.1.7(d) gagal berlaku jika c = 0 karena kita tidak akan memperoleh suatu batas sebagaimana dalam (#) pada contoh tersebut. Jika kita mengambil barisan (xn) dengan xn = 1/n untuk n∈N, maka lim(xn) = 0, tetapi ϕ(x_n) = 1/1/n = n. Seperti kita ketahui bahwa barisan (ϕ(x_n)) = (n) tidak konvergen dalam R, karena barisan ini tidak terbatas.

Dari sini, dengan Teorema 1.1.9(b),

( )

^x

x 1/ lim

→0 tidak ada dalam R. [Akan tetapi, lihat contoh 1.3.9(a).]

(b) limsgn

( )

x

x→0 tidak ada.

Misalkan fungsi signum didefinisikan dengan

sgn(x) =







<

−

=

>

+

0 untuk , 1

0 untuk 0,

0 untuk , 1

x x x

Perhatikan bahwa sgn(x) = x/x untuk x ≠ 0. (Lihat Gambar 1.1.2) Kita akan menunjukkan bahwa sgn tidak mempunyai limit pada x = 0. Kita akan mengerjakan ini dengan menunjukkan bahwa terdapat barisan (xn) sedemikian sehingga lim(xn) = 0, tetapi sedemikian sehingga (sgn(xn)) tidak konvergen.

Misalkan xn = (-1)ⁿ/n untuk n∈N dengan demikian lim(x_n) = 0. Akan tetapi , karena sgn(xn) =

Gambar 4.1.2 Fungsi Signum

.

⁽

) -1 1

0

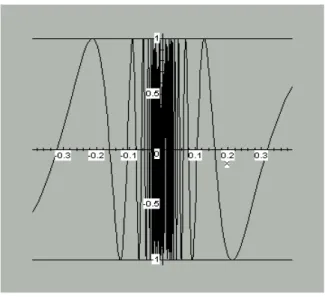
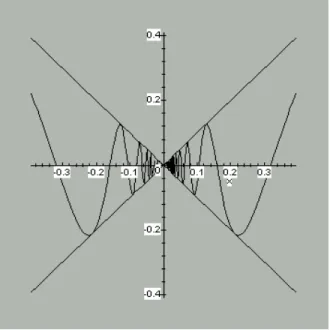
(c) xlim→0 sin(1/x) tidak ada dalam R.

Misalkan g(x) = sin(1/x) untuk x ≠ 0. (Lihat Gambar 1.1.3.) Kita akan menunjukkan bahwa g tidak mempunyai limit pada c = 0, dengan memperlihatkan dua barisan (xn) dan (yn) dengan xn ≠ 0 dan y_n ≠ 0 untuk semua n∈N dan sedemikian sehingga lim(xn) = 0 = lim(yn), tetapi sedemikian sehingga lim(g(xn)) ≠ lim(g(yn)). Mengingat Teorema 1.1.9, ini mengakibatkan g

x

lim

→0 tidak ada. (Jelaskan mengapa.)

Gambar 1.1 3. Grafik f(x) = sin(1/x), x ≠ 0

Kita mengingat kembali dari kalkulus bahwa sin t = 0 jika t = nπ untuk n∈Z, dan sin t = +1 jika t = ½π + 2πn untuk n∈Z. Sekarang misalkan xn = _n¹_π untuk n∈N; maka lim (xn) = 0 dan g(xn) = 0 untuk semua n∈N, dengan demikian lim(g(xn)) = 0. Di pihak lain, misalkan yn = (½π + 2πn)^-1 untuk n∈N; maka lim (y_n) = 0 dan g(yn) = sin(½π + 2πn) = 1 untuk semua n∈N, dengan demikian lim (g(yn)) = 1. Kita simpulkan bahwa

→0

xlim sin(1/x) tidak ada.

Soal-soal Latihan

1. Tentukan suatu syarat pada x - 1 yang akan menjamin bahhwa : (a) x² - 1 < ½,

(b) x² - 1 < 1/10³

(c) x² - 1 < 1/n untuk suatu n∈N yang diberikan, (d) x³ - 1 < 1/n untuk suatu n∈N yang diberikan.

2. Misalkan c suatu titik cluster dari A⊆R dan f : A → R. Buktikan bahwa ^lim

( )

^x

0 f

x→ = L jika dan hanya jika

( )

L f

x −

→ x

lim

0 = 0.

3. Misalkan f : R → R, dan c∈ R. Tunjukkan bahwa lim f

( )

x

x→c = L jika dan hanya jika f

(

c

)

x +

→ x

lim

0 = L.

4. Misalkan f : R → R, I⊆R suatu interval buka, dan c∈I. Jika f1 merupakan pembatasan dari f pada I, tunjukkan bahwa f1 mempunyai suatu limit pada c jika dan hanya jika f mempunyai suatu limit pada c dan tunjukkan pula bahwa f

c x

lim→ = lim f₁

x→c .

5. Misalkan f : R → R, J⊆R suatu interval tutup, dan c∈J. Jika f2 merupakan pembatasan dari f pada I, tunjukkan bahwa jika f mempunyai suatu limit pada c dan hanya jika f2 mempunyai suatu limit pada c.

Tunjukkan bahwa tidak berlaku bahwa jika f2 mempunyai suatu limit pada c dan hanya jika f mempunyai suatu limit pada c.

6. Misalkan I = (0,a), a > 0, dan misalkan g(x) = x² untuk x∈I. Untuk sebarang x,c dalam I, tunjukkan bahwa

g(x) – c² ≤ 2ax - c. Gunakan ketaksamaan ini untuk membuktikan bahwa limx²

x→c = c² untuk sebarang c∈I.

7. Misalkan I⊆R suatu interval, f : I → R, dan c∈I. Misalkan pula terdapat K dan L sedemikian sehingga

f(x) - L≤Kx - c untuk x∈I. Tunjukkan bahwa f

c x

lim→ = L.

8. Tunjukkan bahwa lim x³

x→c = c³ untuk sebarang c∈ R.

9. Tunjukkan bahwa x c

c

x =

lim→ untuk sebatang c ≥ 0.

10. Gunakan formulasi ε-δ dan formulasi formulasi barisan dari pengertian limit untuk memperlihatkan berikut : (a) ^x→ 1−x

lim 1

2 = -1 (x > 1), (b)

2 1 lim1

1 =

+

→ x

x

x (x > 0),

(c) x

x

x 2

0

lim→ = 0 (x ≠ 0), (d)

2 1 1 lim 1

2

1 =

+ +

−

→ x

x x

x (x > 0).

11. Tunjukkan bahwa limit-limit berikut ini tidak ada dalam R:

(a) 0 2

1 lim

x→ x (x > 0), (b)

x x 1 lim

→0 (x > 0), (c) .

(

x

( )

x

)

x sgn

lim

0 +

→ , (d) 



 





→1 2

sin 1

lim^x x (x ≠ 0).

12. Misalkan fungsi f : R → R mempunyai limit L pada 0, dan misalkan pula a > 0. Jika g : R → R didefinisikan oleh g(x) = f(ax) untuk x∈R, tunjukkan bahwa g

x

lim

→0 = L.

13. Misalkan c titik cluster dari A⊆ R dan f : A → R sedemikian sehingga lim

(

f

( )

x

)

²

x→c = L. Tunjukkan bahwa jika L =,0, maka f

( )

x

c x

lim→ = 0. Tnjukkan dengan contoh bahwa jika L ≠ 0, maka f bisa mungkin tidak mempunyai suatu limit pada c.

14. Misalkna f : R → R didefinisikan oleh f(x) = x jika x rasional, dan f(x) = 0 jika x irasional. Tunjukkan bahwa f mempunyai suatu limit pada x = 0. Gunakan argumen barisan untuk menunjukkan bahwa jika c ≠ 0, maka f tidak mempunyai limit pada c.

1.2.1 Definisi. Misalkan A⊆R, f : R → R, dan c∈R suatu titik cluster dari A. Kita mengatakan bahwa f terbatas pada suatu lingkungan dari c jika terdapat lingkungan-δ dari c, V_δ(c) dan suatu konstanta M > 0 sedemikian sehingga f(x) ≤ M untuk semua x ∈ A∩Vδ(c).

1.2.2 Teorema Jika A⊆ R dan f : A → R mempunyai suatu limit pada c∈ R, maka f terbatas pada suatu lingkungan dari c.

Bukti. Jika L = lim f(x)

x→c , maka oleh Teorema 1.1.6, dengan ε = 1, terdapat δ > 0 sedemikian sehingga jika 0 <x - c < δ, maka f(x) - L < 1; dari sini

f(x) - L ≤ f(x) - L < 1.

Oleh karena itu, jika x∈A∩V_δ(c), x≠c, maka f(x) ≤ L + 1. Jika c∉A, kita pilih M = L+ 1, sedangkan jika c∈A kita pilih M = sup{f(c),L+1}. Ini berarti bahwa jika c∈A∩Vδ(c), maka f(x)

≤ M. Ini menunjukkan bahwa f terbatas pada V_δ(c) suatu lingkungan-δ dari c.

1.2.3 Definisi Misalkan A⊆R dan misalkan pula f dan g fungsi-fungsi yang terdefinisi pada A ke R. Kita mendefinisikan jumlah f + g, selisih f – g, dan hasil kali fg pada A ke R sebagai fungsi- fungsi yang diberikan oleh

(f + g)(x) = f(x) + g(x), (f - g)(x) = f(x) - g(x), dan (fg)(x) = f(x)g(x), untuk semua x∈A. Selanjutnya, jika b∈R, kita definisikan kelipatan bf sebagai fungsi yang diberikan oleh

(bf)(x) = bf(x) untuk semua x∈A.

Akhirnya, jika h(x) ≠ 0 untuk x∈A, kita definisikan hasil bagi f/h adalah fungsi yang didefinisikan sebagai

( ) ( ) ( )

x h

x x f h f  =



 



 untuk semua x∈A.

1.2.4 Teorema. Misalkan A⊆R, f dan g fungsi-fungsi pada A ke R, dan c∈R titik cluster dari A. Selanjutnya, misalkan b∈R.

(a) Jika f

x→c

lim = L dan g

x→c

lim = M, maka

(

f g

)

c

x +

lim→ = L + M,

(

f g

)

c

x −

lim→ = L - M,

( )

fg

x→c

lim = LM,

( )

bf

x→c

lim = bL.

(b) Jika h : A → R, h(x) ≠ 0 untuk semua x∈A, dan jika

h

x→c

lim

= H ≠ 0, maka

H L h

f

c

x =



 





lim→ .

Bukti. Salah satu cara pembuktian dari teorema-teorema ini sangat serupa dengan pembuktian Teorema 3.2.3. Secara alternatif, teorema ini dapat dibuktikan dengan menggunakan Teorema 3.2.3 dan Teorema 1.1.8. Sebagai contoh, misalkan (xn) sebarang barisan dalam A sedemikain sehingga xn ≠ c untuk semua n∈N,dan c = lim (xn). Menurut Teorema 1.1.8, bahwa

Lim (f(xn)) = L, lim (g(xn)) = M.

Di pihak lain, Definisi 1.2.3 mengakibatkan (fg)(xn) = f(xn)g(xn) untuk semua n∈N. Oleh karena itu suatu aplikasi dari Teorema 3.2.3 menghasilkan

Lim ((fg)(xn)) = lim (f(xn)g(xn)) = (lim f(xn)) (lim (g(xn))) = LM.

Bagian lain dari teorema ini dibuktikan dengan cara yang serupa. Kita tinggalkan untuk dilakukan oleh pembaca.

Catatan (1) Kita perhatikan bahwa, dalam bagian (b), asumsi tambahan dibuat bahwa H = h

x→c

lim ≠ 0.

Jika asumsi ini tidak dipenuhi, maka

( ) ( )

x h

x f

c x

lim→ tidak ada. Akan tetapi jika limit ini ada, kita tidak dapat menggunakan Teorema 1.2.4(b) untuk menghitungnya.

(2) Misalkan A∈R, dan f1, f2, …, f_n fungsi-fungsi pada A ke R, dan c suatu titk cluster dari A. Jika Lk = lim f _k

x→c untuk k = 1,2, …, n,

maka ,menurut Teorema 1.2.4 dengan argumen induksi kita peroleh bahwa L₁ + L₂ + … + Ln =

(

n

)

c x

f f

f + + +

→ L

2

1

lim dan L₁ · L₂ · … · L_n =

(

n

)

c x

f f f ⋅ ⋅ ⋅

→ L

2

1

lim (3) Khususnya, kita deduksi dari (2) bahwa jika L = f

x→c

lim dan n∈N, maka Lⁿ =

( ( ) )

ⁿ

c

x f x

lim→

1.2.5 Contoh-contoh (a) Beberapa limit yang diperlihatkan dalam Pasal 1.1 dapat dibuktikan dengan menggunakan Teorema 1.2.4. Sebagai contoh, mengikuti hasil ini bahwa karena x

c x

lim→ = c,

maka limx²

x→c = c², dan jika c > 0, maka

c x

c x

1 1 lim =

→ .

(b) lim2

→

x (x² + 1)(x³ – 4) = 20

Berdasarkan Teorema 1.2.4, kita peroleh bahwa

2

lim→

x (x² + 1)(x³ – 4) = (

2

lim→

x (x² + 1))(

2

lim→ x (x³ – 4)) = 5(4) = 20.

(c) .

5 4 1 lim 4

2 3

2 =









 +

−

→ x

x

x

Jika kita menggunakan Teorema 1.2.4(b), maka kita mempunyai











 +

−

→ 1

lim 4

2 3

2 x x

x =

( )

(

¹

)

^54.

lim 4 lim

2 2

3

2 =

+

−

→

→

x x

x x

Perhatikan bahwa karena limit pada penyebut [yaitu ^lim

(

^{2 1}

)

2 +

→ x

x = 5] tidak sama dengan 0, maka Teorema 1.2.4(b) dapat dipergunakan.

(d) . 3 4 6 3 lim 4

2

2 =











−

−

→ x

x

x

Jika kita misalkan f(x) = x² – 4 dan h(x) = 3x – 6 untuk x∈R, maka kita tidak dapat menggunakan Teorema 1.22.4(b) untuk meneghitung

2

lim→

x (f(x)/h(x)) sebab H = ^h

( )

^x

x

lim

→2 =

(

3 6

)

lim

2 −

→ x

x = 3 x

x

lim

→2 - 6 = 3(2) – 6 = 0. Akan tetapi, jika x ≠ 2, maka berarti bahwa 6 3

2 4

−

− x x =

( )( )

(

2

)

3 2 2

− +

− x

x

x = ¹₃(x + 2). Oleh karena itu kita mempunyai 











−

−

→ 3 6

lim 4

2

2 x x

x = lim₃¹

(

2

)

2 +

→ x

x =



 



 +

→ 2

lim2 3

1 x

x = ₃¹(2 + 2) = ₃⁴

Perhatikan bahwa fungsi g(x) = (x² – 4)/(3x – 6) mempunyai limit pada x = 2 meskipun tidak terdefinisi pada titik tersebut.

(e) ^x x 1

lim→0 tidak ada dalam R.

Tentu saja

0

lim→

x 1 = 1 dan H = x

x lim

→0 = 0. Akan tetapi, karena H = 0, kita tidak dapat menggunakan Teorema 1.2.4(b) untuk menghitung

x

x

1

lim→0 . Kenyataannya, seperti kita telah lihat pada Contoh 1.1.10(a), fungsi ϕ(x) = 1/x tidak mempunyai limit pada x = 0. Kesimpulan ini mengikuti juga Teorema 1.2.2 karena fungsi ϕ(x) = 1/x tidak terbatas pada lingkungan dari x = 0. (Mengapa?)

(f) Jika p fungsi polinimial, maka lim p(x)

x→c = p(c).

Misalkan p fungsi polinimial pada R dengan demikian p(x) = anxⁿ + an-1x^n-1 + … + a1x + a0 untuk semua x∈R. Menurut Teorema 1.2.4 dan fakta bahwa lim x ^k

x→c = c^k, maka )

( lim p x

x→c =

[

1 0

]

1

1

lim a_nxⁿ a_n xⁿ a x a

c x

+ + +

+ ₋ ⁻

→ L = lim ( _n ⁿ)

c x

x

→ a + lim ( ₋₁ ⁻¹)

→

n c n

x

x

a +

… + lim (a₁x)

x→c + lim a ₀

x→c = ancⁿ + an-1c^n-1 + … + a1c + a0 = p(c).

Dari sini lim p(x)

x→c = p(c) untuk ssebarang fungsi polinomial p.

(g) Jika p dan q fungsi-fungsi polinomial pada R dan jika q(c) ≠ 0, maka

( ) ( ) ( )

^c

q c p x q

x p

c

x =

→

) (

lim .

Karena q(x) suatu fungsi polinomial, berarti menurut sutu teorema dalam aljabar bahwa terdapat paling banyak sejumlah hingga bilangan real α₁, α₂, … ,α_m [pembuat nol dari q(x)] sedemikain sehingga q(α_j) = 0 dan sedemikian sehingga jika x∉{α₁, α₂, …, α_m} maka q(x) ≠ 0. Dari sini, jika

x∉{α₁, α₂, …, α_m} kita dapat mendefinisikan r(x) =

( ) ( )

^x

q x

p . Jika c bukan pembuat nol dari q(x), maka

q(c) ≠ 0, dari berdasarkan bagian (f) bahwa q

( )

x

c x

lim→ = q(c). ≠ 0. Oleh karena itu kita dapat

menggunakan Teorema 1.2.4(b) untuk menyimpulkan bahwa

( ) ( ) ( ) ( )

^c

q c p x q

x p x

q x p

c x

c x c

x = =

→

→

→ lim

) ( ) lim (

lim .

1.2.6 Teorema Misalkan A⊆R. f : A → R dan c∈R suatu titik cluster dari A. Jika a ≤ f(x) ≤ b untuk semua x∈A, x ≠ c,

dan jika f

c x

lim→ ada, maka a ≤ f

c x

lim→ ≤ b.

Bukti. Jika L = f

c x

lim→ , maka menurut Teorema 1.1.8 bahwa jika (xn) sebarang barisan bilangan real sedemikain sehingga c≠ x_n∈A untuk semua n∈N dan jika barisan (x_n) konvergen ke c, maka barisan (f(xn)) konvergen ke L. Karena a ≤ f(xn) ≤ b untuk semua n∈N, berarti menurut Teorema 3.2.6 bahwa a ≤ L ≤ b.

1.2.7 Teorema Apit. Misalkan A⊆R, f,g,h : A → R, dan c∈R suatu titik cluster dari A. Jika f(x) ≤ g(x) ≤ h(x) untuk semua x∈A, x ≠ c, dan jika f

c

limx

→ = L = h

c xlim

→ , maka g

c xlim

→ = L.

1.2.8 Contoh-contoh (a) ^3/2 lim x0

x→ = 0 (x > 0).

Misalkan f(x) = x^3/2 untuk x > 0. Karena ketaksamaan x < x^1/2 ≤ 1 berlaku untuk 0 < x ≤ 1, maka berarti bahwa x² < f(x) = x^3/2 ≤ x untuk 0 < x ≤ 1. Karena ²

0

lim x

x→ = 0 dan x

x

lim

→0 = 0, maka dengan menggunakan Teorema Apit 1.2.7 diperoleh ^3/2

0

lim x

x→ = 0.

(b) x

x sin lim→0 = 0.

Dapat dibuktikan dengan menggunakan pendekatan deret Taylor (akan dibahas pada lanjutan dari tulisan ini) bahwa -x ≤ sin x ≤ x untuk semua x ≥ 0. Karena

( )

x

x ±

lim→

0 = 0, maka menurut Teorema Apit bahwa x

x sin lim

→0 = 0.

(c) x

x cos

lim

→0 = 1.

Dapat dibuktikan dengan menggunakan pendekatan deret Taylor (akan dibahas pada lanjutan dari tulisan ini) bahwa

(*) 1 - ½x² ≤ cos x ≤ 1 untuk semua x ∈ R.

Karena ^lim

(

^1−1x2

)

= 1, maka menurut Teorema Apit bahwa limcosx = 1.

(d) 



 



 −

→ x

x

x

1 lim cos

0 = 0.

Kita tidak dapat menggunakan Teorema 1.2.4 (b) secara langsung untuk menghitung limit ini. (Mengapa?) Akan tetapi, dari ketaksamaan (*) dalam bagian (c) bahwa -½x ≤ (cos x – 1)/x ≤ 0 untuk x > 0 dan juga bahwa 0 ≤ (cos x – 1)/x ≤ ½x untuk x < 0. Sekarang misalkan f(x) = - x/2 untuk x ≥ 0 dan f(x) = 0 untuk x < 0, dan misalkan pula h(x) = 0 untuk x ≥ 0 dan h(x) = -x/2 untuk x < 0.

Maka kita mempunyai f(x) ≤ (cos x – 1)/x ≤ h(x) untuk x ≠ 0. Karena , mudah dilihat (Bagaimana?)

bahwa f

xlim

→0 = h

xlim

→0 , maka menurut Teorema Apit bahwa

x x

x

1 limcos

0

−

→ = 0.

(e) 



 





→ x

x

x

lim sin

0 = 1.

Sekali lagi, kita tidak dapat menggunakan Teorema 1.2.4(b) untuk menghitung limit ini.

Akan te-tapi, dapat dibuktikan (pada lanjutan diktat ini) bahwa x - ₆¹x³ ≤ sin x ≤ x untuk x≥0 dan bahwa x ≤ sin x ≤ x - ₆¹x³ untuk x ≤ 0. Oleh karena itu berarti (Mengapa?) bahwa 1 - ₆¹x² ≤ (sin x)/x ≤ 1 untuk semua x ≠ 0. Tetapi karena

(

₆^{1 2}

)

01

lim x

x −

→ = 1 - ²

6 0 1lim x

x→ = 1, kita simpulkan dari Teorema

Apit bahwa 



 





→ x

x

x

lim sin

0 = 1.

(f)

(

^x

( )

^x

)

x sin1/ lim

→0 = 0.

Misalkan f(x) = x sin (1/x) untuk x ≠ 0. Karena –1 ≤ sin z ≤ 1 untuk semua z ∈ R, kita mempunyai ketaksamaan -x ≤ f(x) = x sin(1/x) ≤ x untuk semua x R, x ≠ 0. Karena x

x 0

lim→ = 0, maka dari Teorema Apit diperoleh bahwa f

x 0

lim→ = 0.

1.2.9 Teorema Misalkan A⊆R, f : A → R dan c∈R suatu titik cluster dari A. Jika f

x→c

lim > 0 [ atau, f

x→c

lim < 0],

maka terdapat suatu lingkungan dari c Vδ(c) sedemikian sehingga f(x) > 0 [atau f(x) < 0] untuk semua x∈A∩Vδ(c), x ≠ c.

Bukti. Misalkan L = f

x→c

lim and anggaplah L > 0. Kita ambil ε = ½L > 0 dalam Teorema 1.1.6(b), dan diperoleh suatu bilangan δ > 0 sedemikain sehingga jika 0 <x - c< δ dan x∈A, maka

f(x) - L < ½L. Oleh karena itu (Mengapa?) berarti bbahwa jika x∈A∩V_δ(c), x≠c, maka f(x)>½L>0.

Jika L < 0, dapat digunakan argumen yang serupa.

Latihan 1.2

1. Gunakan Teorema 1.2.4 untuk menentukan limit-limit berikut :

(a)

1

limx→ (x + 1)(2x + 3) (x∈R), (b)

2 lim 2

2 2

1 −

+

→ x x

x (x > 0),

(c) 



 



 −

+

→ x x

x 2

1 1 lim 1

2

(x > 0), (d)

2 lim 1

0 2+ +

→ x x

x (x∈R)

2. Tentukan limit-limit berikut dan nyatakan teorema-teorema mana yang digunakan dalam setiap kasus. (Anda bisa menggunakan latihan 14 di bawah.)

(a)

3 1 lim 2

2 +

+

→ x

x

x (x > 0), (b)

2 lim 4

2

2 −

−

→ x x

x (x > 0),

(c)

( )

x x

x

1 lim 1

2

0

− +

→ (x > 0), (d)

1 lim 1

1 −

−

→ x x

x (x > 0)

3. Carilah ₂

0 2

3 1 2 lim 1

x x

x x

x +

+

− +

→ dimana x > 0.

4. Buktikan bahwa

( )

x

x cos1/ lim

→0 tidak ada, akan tetapi x

( )

x

x cos1/

lim

→0 = 0.

5. Misalkan f,g fungsi-fungsi yang didefinisikan pada A⊆R ke R, dan misalkan c suatu titik cluster dari A.

Anggaplah bahwa f terbatas pada suatu lingkungan dari c dan g

x→c

lim = 0. Buktikan bahwa fg

x→c

lim = 0.

6. Gunakanlah formuasi ε-δ dari limit fungsi untuk membuktikan pernyataan pertama dalam Teorema 1.2.4(a).

7. Gunakanlah formulasi sekuensial untuk limit fungsi untuk membuktikan Teorema 1.2.4(b).

8. Misalkan n∈N sedemikian sehingga n ≥ 3. Buktikan ketaksamaan –x² ≤ xⁿ ≤ x² untuk –1 < x < 1.

Selanjutnya, gunakan fakta bahwa ²

0

lim x

x→ = 0 untuk menunjukkan bahwa ⁿ

x x

0

lim→ = 0.

9. Misalkan f,g fungsi-fungsi yang didefinisikan pada A⊆R ke R, dan misalkan c suatu titik cluster dari A.

(a) Tunjukkan bahwa jika f

x→c

lim dan

(

f g

)

c

x +

lim→ ada, tunjukkanlah bahwa f

x→c

lim ada.

(b) Jika f

x→c

lim dan fg

x→c

lim ada, apakah juga g

x→c

lim ada ?

10. Berikan contoh fungsi-fungsi f dan g sedemikian sehingga f dan g tidak mempunyai limit pada suatu titik c, tetapi sedemikian sehingga fungsi-fungsi f + g dan fg mempunyai limit pada c.

11. Tentukan apakah limit-limit berikut ada dalam R.

(a)

( )

²

0sin1/

lim x

x→ (x ≠ 0), (b)

( )

²

0 sin1/

limx x

x→ (x ≠ 0),

(c)

( )

x

x sgn sin1/ lim

→0 (x ≠ 0), (d)

( )

²

0 sin1/

lim x x

x→ (x > 0)

12. Misalkan f : R → R sedemikian sehingga f(x + y) = f(x) + f(y) untuk semua x,y dalam R. Anggaplah f

x 0

lim→

= L ada. Buktikan bahwa L = 0, dan selanjutnya buktikan bahwa f mempunyai suatu limit pada setiap titik c∈R. [Petunjuk : Pertama-tama catat bahwa f(2x) = f(x) + f(x) = 2f(x) untuk semua x∈R. Juga perhatikan bahwa f(x) = f(x – c) + f(c) untuk semua x,c dalam R.]

13. Misalkan A⊆R, f : A → R dan c suatu titik cluster dari A. Jika f

x 0

lim→ ada, dan jika f menyatakan fungsi yang terdefinisi untuk x∈A dengan f(x) = f(x), buktikan bahwa f

x 0

lim→ =  f

x 0

lim→ .

14. Misalkan A⊆R, f : A → R dan c suatu titik cluster dari A. Tambahan, anggaplah bahwa f(x) ≥ 0 untuk semua x ∈ A, dan misalkan f suatu fungsi yang terdefinisi pada A dengan f (x) = ^f

( )

^{x untuk}

semua x∈A. Jika f

x 0

lim→ ada, buktikan bahwa f

x 0

lim→ = f

x 0

lim→ .

1.3 Beberapa Perluasan dari Konsep Limit Limit-limit Sepihak

1.3.1 Definisi. Misalkan A⊆R dan f : A → R

(i)

Jika c∈R suatu titik cluster dari A∩(c,∞) = {x∈A:x > c}, maka kita mengatakan bahwa L∈R adalah suatu limit-kanan dari f pada c dan dituliskan f

c

xlim→ ⁺ = L jika diberikan sebarang ε > 0 terdapat suatu δ = δ(ε)> 0 sedemikian sehingga untuk semua x∈A dengan 0 < x – c < δ, maka f(x) – L < ε.

(ii)

Jika c∈R suatu titik cluster dari A∩(-∞,c) = {x∈A : x < c}, maka kita mengatakan bahwa L∈R adalah suatu limit-kiri dari f pada c dan dituliskan f

c

xlim→ ⁻ = L jika diberikan sebarang ε

> 0 terdapat suatu δ = δ(ε)> 0 sedemikian sehingga untuk semua x∈A dengan 0 < c – x < δ, maka

f(x) - L < ε.

Catatan: (1) Jika L suatu limit kanan dari f pada c, kita kadang-kadang mengatakan bahwa L adalah limit dari kanan pada c. Kita menggunakan notasi f

( )

x

c

xlim→+ = L. Terminologi dan notasi yang serupa digunakan juga untuk limit-kiri.

(2) Limit-limit f

c

xlim→+ dan f

c xlim-

→ disebut limit-limit sepihak dari f pada c. Ini dimungkinkan kedua limit sepihak dimaksud ada. Juga bisa mungkin salah satu saja yang ada. Serupa, seperti kasus pada fungsi f(x) = sgn (x) pada c = 0, limit-limit ini ada, meskipun berbeda.

(3) Jika A suatu interval dengan titik ujung kiri c, maka jelas nampak bahwa f : A → R mempunyai suatu limit pada c jika dan hanya jika f mempunyai suatu limit kanan pada c. Selain itu, dalam kasus ini limit

f

x→c

lim dan limit pihak kanan f

c

xlim→+ sama. (Situasi serupa juga akan berlaku untuk limit-kiri suatu interval dengan titik ujung kanan adalah c.

1.3.2 Teorema Misalkan A⊆R, f : A → R dan c suatu titik cluster dari A∩(c,∞). Maka pernyataan-pernyataan berikut ini eqivalen.

(i) f

c

xlim→ ⁺ = L∈R;

(ii) Untuk sebarang barisan (xn) yang konvergen ke c sedemikian sehingga xn∈A dan x_n > c untuk semua n∈N, barisan (f(x_n)) konvergen ke L∈R.

Kita tinggalkan pembuktian Teorema ini (dan formulasi dan pembuktian dari teorema yang analog dengannya untuk limit-kiri) untuk dilakukan oleh pembaca.

1.3.3 Teorema. Misalkan A⊆R, f : A → R dan c ∈ R suatu titik Cluster dari A∩(c,∞) dan A ∩ (-∞,c). Maka f

x→c

lim = L∈R jika dan hanya jika f

c

xlim→ ⁺ = L = f

c xlim→⁻ .

1.3.4 Contoh-contoh (a) Misalkan f(x) = sgn(x).

Kita telah lihat dari contoh 1.1.10(b) bahwa sgn tidak mempunyai limit pada c = 0. Ini jelas bahwa lim sgn

( )

x

x→0⁺ = +1 dan bahwa lim sgn

( )

x

x→0⁻ = -1. Karena limit-limit satu pihak ini berbeda, maka mengikuti Teorema 1.3.3 bahwa sgn tidak mempunyai limit pada 0.

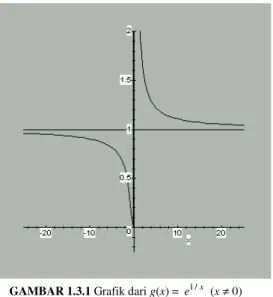
(b) Misalkan g(x) = e^1/x untuk x ≠ 0. (Lihat gambar 1.3.1)

Pertama kita tunjukkan bahwa g tidak mempunyai limit kanan hingga pada c = 0 karena g tidak terbatas pada sebarang lingkungan kanan (0,∞) dari 0. Kita akan menggunakan ketaksamaan (*) 0 < t < e^t untuk t > 0

yang pada bagian ini tidak akan diberikan pembuktiannya. Berdasarkan (*), jika x > 0 maka 0 < 1/x <

e^1/x.

GAMBAR 1.3.1 Grafik dari g(x) = e^1/x (x ≠ 0)

Dari sini, jika kita mengambil xn = 1/n, maka g(xn) > n untuk semua n∈N. Oleh karena itu ^x

x

e^1/

0

lim₊

→

tidak ada dalam R.

Akan tetapi, ^x

x

e^1/

0

lim₋

→ = 0. Kita perhatikan bahwa, jika x < 0 dan kita mengambil t = 1/x dalam (*) kita peroleh 0 < -1/x < e^-1/x. Karena x < 0, ini mengakibatkan 0 < e^1/x < -x untuk semua x < 0.

Mengikuti ketaksamaan ini diperoleh ^x

x

e^1/

0

lim₋

→ = 0.

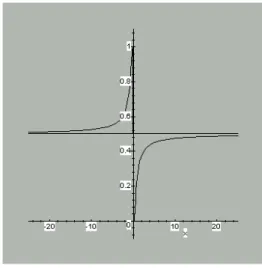
(c) Misalkan h(x) = 1/(e^1/x + 1) untuk x ≠ 0. (lihat gambar 1.3.2).

Kita telah melihat bagian (b) bahwa 0 < 1/x < e^1/x untuk x > 0, dengan demikian 0 <

1 1

/ 1 ^x + e

< _x e^1/

1 < x yang mengakibatkan bahwa ₊ lim→0 x

h = 0. Karena kita telah melihat dalam bagian (b)

bahwa ₊

lim→0 x

e^1/x = 0, maka dari analog Teorema 1.2.4(b) untuk untuk limit-kiri, kita peroleh



 



 +

→ − 1

lim 1

/ 0 1 x

x e ^{= lim}

(

^{11/ 1}

)

0

− +

→ x x

e ⁼ 0 1

1

+ = 1 Perhatikan bahwa untuk fungsi ini, limit sepihak kedua- duanya ada, akan tetapi tidak sama.

GAMBAR 1.3.2. Grafik dari h(x) = 1/(e^1/x+1) (x ≠ 0) Limit-limit Tak Hingga

1.3.5 Definisi. Misalkan A⊆R, f : A → R dan c∈R suatu titik cluster dari A.

(i) Kita katakan bahwa f menuju ke ∞ apabila x→c, dan ditulis =∞

→ f

c x

lim jika untuk setiap α∈R terdapat δ = δ(α) > 0 sedemikain sehinggauntuk semua x∈A dengan 0 <x-c < δ, maka f(x)>α.

(ii) Kita katakan bahwa f menuju ke ∞ apabila x→c, dan ditulis =−∞

→ f

c x

lim jika untuk setiap β∈R terdapat δ = δ(β) > 0 sedemikian sehingga untuk semua x∈A dengan 0 < x - c < δ, maka f(x) < β.

1.3.6 Contoh-contoh (a) _→

( )

^{2 =−∞}

01/ lim x

x .

Karena, jika α > 0 diberikan, misalkan δ = 1/ α . Ini erarti bahwa jika 0 <x<δ, maka x² <

1/α dengan demikian 1/x² > α.

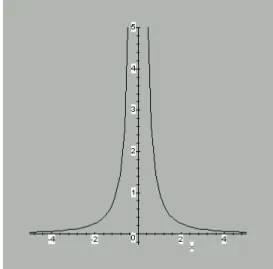
(b) Misalkan g(x) = 1/x untuk x ≠ 0. (Lihat Gambar 1.3.4)

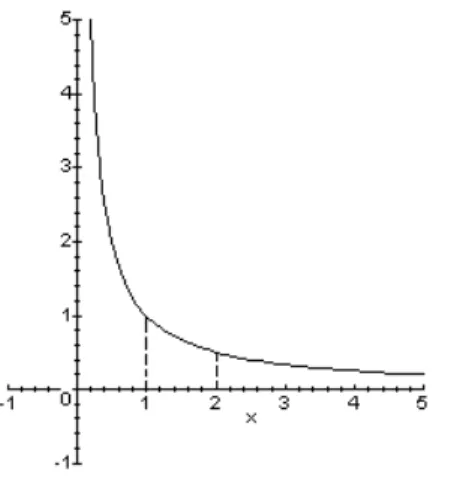
Fungsi g tidak menuju ke ∞ atau ke -∞ sebagaimana x→0. Karena, jika α > 0 maka g(x) < α untuk semua x < 0, dengan demikian g tidak menuju ke ∞ apabila x→0. Serupa juga, jika β < 0 maka g(x) > β untuk semua x > 0, dengan demikian g tidak menuju ke -∞ apabila x→0.

Hasil berikut analog dengan Teorema Apit 1.2.7. (Lihat juga Teorema 3.6.4).

1.3.7 Teorema Misalkan A⊆R, f,g : A → R dan c∈R suatu titik cluster dari A.

Anggaplah bahwa f(x) ≤ g(x) untuk semua x∈A, x ≠ c.

(a) Jika =∞

→ f

c

xlim , maka =∞

→ g

c

xlim .

(b) Jika =−∞

→ g

c x

lim , maka =−∞

→ f

c x

lim .

Bukti. (a) Jika

= ∞

→

f

c

lim

x dan α∈R diberikan, maka terdapat δ(α) > 0 sedemikian sehingga jika 0 <x - c < δ(α) dan x∈A, maka f(x) > α. Akan tetapi, jika f(x) ≤ g(x) untuk semua x∈A x ≠ c, maka berarti jika 0 <x - c < δ(α) dan x∈A, maka g(x) > 0. Oleh karena itu =∞

→ g

c

limx . Pembuktian bagian (b) dilakukan dengan cara serupa.

Fungsi g(x) = 1/x dalam Contoh 1.3.6(b) menyarankan bahwa itu dapat berguna untuk memandang limit-limit sepihaknya.

GAMBAR 1.3.3 Grafik dari f(x) = 1/x² (x ≠ 0)

GAMBAR 1.3.4 Grafik dari g(x) = 1/x (x ≠ 0) 1.3.8 Definisi Misalkan A⊆R dan f : A → R.