Penulis : RUGIANTO Editor Materi : ASMUNIV Editor Bahasa :
Ilustrasi Sampul :
Desain & Ilustrasi Buku : PPPPTK BOE MALANG
Hak Cipta © 2013, Kementerian Pendidikan & Kebudayaan MILIK NEGARA
TIDAK DIPERDAGANGKAN
Semua hak cipta dilindungi undang-undang.
Dilarang memperbanyak(mereproduksi), mendistribusikan, atau memindahkan sebagian atau seluruh isi buku teks dalam bentuk apapun atau dengan cara apapun, termasuk fotokopi, rekaman, atau melalui metode (media) elektronik atau mekanis lainnya, tanpa izin tertulis dari penerbit, kecuali dalam kasus lain, seperti diwujudkan dalam kutipan singkat atau tinjauan penulisan ilmiah dan penggunaan non-komersial tertentu lainnya diizinkan oleh perundangan hak cipta. Penggunaan untuk komersial harus mendapat izin tertulis dari Penerbit. Hak publikasi dan penerbitan dari seluruh isi buku teks dipegang oleh Kementerian Pendidikan & Kebudayaan.
Untuk permohonan izindapat ditujukan kepada Direktorat Pembinaan Sekolah Menengah Kejuruan, melalui alamat berikut ini:
Pusat Pengembangan & Pemberdayaan Pendidik & Tenaga Kependidikan Bidang Otomotif & Elektronika:
DISKLAIMER (DISCLAIMER)
Penerbit tidak menjamin kebenaran dan keakuratan isi/informasi yang tertulis di dalam buku tek ini. Kebenaran dan keakuratan isi/informasi merupakan tanggung jawab dan wewenang dari penulis.
Penerbit tidak bertanggung jawab dan tidak melayani terhadap semua komentar apapun yang ada didalam buku teks ini. Setiap komentar yang tercantum untuk tujuan perbaikan isi adalah tanggung jawab dari masing-masing penulis.
Setiap kutipan yang ada di dalam buku teks akan dicantumkan sumbernya dan penerbit tidak bertanggung jawab terhadap isi dari kutipan tersebut. Kebenaran keakuratanisi kutipan tetap menjadi tanggung jawab dan hak diberikan pada penulis dan pemilik asli. Penulis bertanggung jawab penuh terhadap setiap perawatan (perbaikan) dalam menyusun informasi dan bahan dalam buku teks ini.
Penerbit tidak bertanggung jawab atas kerugian, kerusakan atau
ketidaknyamanan yang disebabkan sebagai akibat dari ketidakjelasan, ketidaktepatan atau kesalahan didalam menyusun makna kalimat didalam buku teks ini.
Kewenangan Penerbit hanya sebatas memindahkan atau menerbitkan mempublikasi, mencetak, memegang dan memproses data sesuai dengan undang-undang yang berkaitan dengan perlindungan data.
Katalog Dalam Terbitan (KDT)
TEKNIK JARINGAN AKSES, Edisi Pertama 2013 Kementerian Pendidikan & Kebudayaan
KATA PENGANTAR
Puji syukur kami panjatkan kepada Tuhan yang Maha Esa atas tersusunnya buku teks ini, dengan harapan dapat digunakan sebagai buku teks untuk siswa Sekolah Menengah Kejuruan (SMK) Bidang Studi Keahlian Teknik Informasi dan Komunikasi.
Penerapan kurikulum 2013 mengacu pada paradigma belajar kurikulum abad 21 menyebabkan terjadinya perubahan, yakni dari pengajaran (teaching) menjadi BELAJAR (learning), dari pembelajaran yang berpusat kepada guru ( teachers-centered) menjadi pembelajaran yang berpusat kepada peserta didik ( student-centered), dari pembelajaran pasif (pasive learning) ke cara belajar peserta didik aktif (active learning-CBSA) atau Student Active Learning-SAL.
Buku teks ″TEKNIK DASAR ELEKTRONIKA KOMUNIKASI” ini disusun berdasarkan tuntutan paradigma pengajaran dan pembelajaran kurikulum 2013 diselaraskan berdasarkan pendekatan model pembelajaran yang sesuai dengan kebutuhan belajar kurikulum abad 21, yaitu pendekatan model pembelajaran berbasis peningkatan keterampilan proses sains.
Penyajian buku teks untuk Mata Pelajaran ″TEKNIK DASAR ELEKTRONIKA KOMUNIKASI″ ini disusun dengan tujuan agar supaya peserta didik dapat melakukan proses pencarian pengetahuan berkenaan dengan materi pelajaran melalui berbagai aktivitas proses sains sebagaimana dilakukan oleh para ilmuwan dalam melakukan eksperimen ilmiah (penerapan scientifik), dengan demikian peserta didik dia`rahkan untuk menemukan sendiri berbagai fakta, membangun konsep, dan nilai-nilai baru secara mandiri.
Kementerian Pendidikan dan Kebudayaan, Direktorat Pembinaan Sekolah Menengah Kejuruan, dan Direktorat Jenderal Peningkatan Mutu Pendidik dan Tenaga Kependidikan menyampaikan terima kasih, sekaligus saran kritik demi kesempurnaan buku teks ini dan penghargaan kepada semua pihak yang telah berperan serta dalam membantu terselesaikannya buku teks siswa untuk Mata Pelajaran TEKNIK DASAR ELEKTRONIKA KOMUNIKASI kelas X/Semester 2 Sekolah Menengah Kejuruan (SMK).
DAFTAR ISI
DISKLAIMER (DISCLAIMER) ... III
KATA PENGANTAR ... IV
DAFTAR ISI ... V
PETA KEDUDUKAN MODUL ... VIII
5.2URAIAN MATERI
... 157
5.3 RANGKUMAN
... 166
5.4 LEMBAR KERJA PESERTA DIDIK
... 168
5.4.1TUGASKEGIATAN BELAJAR 4-1 ... 168
5.4.2TUGASKEGIATAN BELAJAR 4-2 ... 177
5.4.3TUGASKEGIATAN BELAJAR 4-3 ... 185
5.4.4TUGASKEGIATAN BELAJAR 4-4 ... 200
VI. PENERAPAN ... 209
6.1ATTITUDE SKILLS ... 209
6.2KOGNITIF SKILLS ... 210
6.3PSIKOMOTORIK SKILLS ... 211
6.4PRODUK/BENDA KERJA SESUAI KRITERIA STANDARD ... 213
PETA KEDUDUKAN MODUL
BIDANG STUDI KEAHLIAN : TEKNIK INFORMASI dan KOMUNIKASI
PROGRAM STUDI KEAHLIAN : TEKNIK TELEKOMUNIKASI
PAKET KEAHLIAN : 1. TEKNIK TRANSMISI TELEKOMUNIKASI (057)
2. TEKNIK SUITSING (058)
3. TEKNIK JARINGAN AKSES (060) Kelas X
Semester : Ganjil / Genap
Materi Ajar : Teknik Listrik Telekomunikasi
Jarin
Kelas XI dan Kelas XII
C3:Teknik Elektronika Komunikasi
Teknik Kerja Bengkel
Teknik Listrik Dasar
Elektronika
Fisika Pemrograman Dasar Sistem computer
Kelas X, XI
C1. Dasar Bidang Kejuruan KELOMPOK C (Kejuruan)
Seni Budaya
(termasuk muatan
Prakarya dan Kewirausahaan Pendidikan Jasmani,
Kelas X, XI, XI
KELOMPOK B (WAJIB)
Pendidikan Agama
dan Budi
Pekerti
Pendidikan
Pancasila dan
Kewarganegaraan
Bahasa Indonesia
Matematika Sejarah Indonesia
Bahasa Inggris
Kelas X, XI, XI
GLOSARIUM
Desimal : Sistem bilangan 0, 1, 2, 3, 4, 5, 6, 7, 8, dan 9
Biner : Sistem bilangan dengan dua simbol, yaitu 0 dan 1
Karnaugh map : Metode untuk mendapatkan persamaan rangkaian digital dari tabel kebenarannya
I. PENDAHULUAN
1.1 Deskripsi
Teknik Elektronika Digital adalah merupakan dasar dalam melakukan melakukan pekerjaan-pekerjaan yang berkaitan dengan rangkaian maupun peralatan telekomunikasi. Untuk itu pada pekerjaan ini siswa diharapkan dapat melakukan dan menguasai dengan benar karena akan menunjang pada proses pembelajaran berikutnya.
Teknik Elektronika Digital merupakan salah satu bentuk dan alat bantu ajar yang dapat digunakan baik di laboratorium elektronika pada saat siswa melakukan praktek di laboratorium elektronika telekomunikasi. Dengan modul ini maka diharapkan dapat meningkatkan efisiensi dan efektifitas proses belajar mengajar yang berorientasi pada proses pembelajaran tuntas. Dengan modul ini diharapkan proses belajar mengajar akan menjadi program dan terencana untuk meningkatkan pengetahuan dan ketrampilan pada siswa didik.
1.2 Prasyarat
Sebelum siswa mempelajari materi teknik elektronika digital ini, siswa sudah harus mengetahui metode dan cara pengukuran menggunakan berbagai macam alat ukur di bidang elektronika dan materi teknik elektronika analog untuk menunjang kegiatan agar proses belajar mengajar menjadi lebih lancar.
1.3 Petunjuk Penggunaan
Langkah - langkah yang harus dilakukan untuk mempelajari modul ini: a. Bagi siswa atau peserta didik:
1. Bacalah tujuan antara dan tujuan akhir dengan seksama,
2. Bacalah Uraian Materi pada setiap kegiatan belajar dengan seksama sebagai teori penunjang,
3. Baca dan ikuti langkah kerja yang ada pada modul ini pada tiap proses pembelajaran sebelum melakukan atau mempraktekkan,
b. Bagi guru pembina / pembimbing:
1. Dengan mengikuti penjelasan didalam modul ini, susunlah tahapan penyelesaian yang diberikan kepada siswa / peserta didik.
2. Berikanlah penjelasan mengenai peranan dan pentingnya materi dari modul ini.
3. Berikanlah penjelasan serinci mungkin pada setiap tahapan tugas yang diberikan kepada siswa.
4. Berilah contoh gambar-gambar atau barang yang sudah jadi, untuk memberikan wawasan kepada siswa.
5. Lakukan evaluasi pada setiap akhir penyelesaian tahapan tugas. 6. Berilah penghargaan kepada siswa didik yang setimpal dengan hasil
karyanya. 1.4 Tujuan Akhir
1. Peserta / siswa dapat menerapkan sistem konversi bilangan pada
1.5 Kompetensi Inti dan Kompetensi Dasar
Dengan menguasai modul ini diharapkan peserta / siswa didik dapat menjelaskan dasar elektronika digital dalam teknik telekomunikasi.
1.6 Cek Kemampuan Awal
Pada awal pembelajaran siswa didik diberi tugas untuk menyebutkan aplikasi elektronika digital dalam teknik telekomunikasi
Apabila siswa telah dapat melaksanakan tugas tersebut dengan benar, maka siswa yang bersangkutan sudah dapat ujian untuk mendapatkan sertifikat, dan tidak perlu mengikuti modul ini serta diperbolehkan langsung mengikuti
II. Kegiatan Belajar 1.
SISTEM BILANGAN (ELEKTRONIKA DIGITAL)
2.1 Tujuan Pembelajaran
Peserta diklat / siswa dapat :
Memahami sistem bilangan desimal, biner, oktal, dan heksadesimal
Memahami konversi sistem bilangan desimal ke sistem bilangan
Memahami sistem bilangan pengkode biner (binary encoding)
2.2 Uraian Materi
1. Sistem bilangan desimal, biner, oktal, dan heksadesimal a) Bilangan Desimal
Bilangan 9 menunjukkan satuan (100), angka 6 memiliki bobot nilai (101) dan angka 3 menunjukkan bobot nilai ratusan (102). Cara penulisan bilangan desimal yang memiliki radik atau basis 10 dapat dinyatakan seperti berikut:
300 60 9
(369)10
2 1 0
10 3 x 10 6 x 10 9 x 10
(369)
sehingga untuk mengetahui nilai bilangan desimal (bobot bilangan) dari suatu bilangan desimal dengan radik yang lainnya secara umum dapat dinyatakan seperti persamaan (1) berikut:
Penulisan dengan menggunakan persamaan (3.1) 0
atau dapat dinyatakan juga dengan menggunakan persamaan (2)
Berbeda dengan bilangan desimal, bilangan biner hanya menggunakan dua simbol, yaitu 0 dan 1. Bilangan biner dinyatakan dalam radik 2 atau disebut juga dengan sistem bilangan basis 2, dimana setiap biner atau biner digit disebut bit. Tabel 1 kolom sebelah kanan memperlihatkan pencacahan bilangan biner dan kolom sebelah kiri memnunjukkan nilai sepadan bilangan desimal.
Sistem bilangan oktal sering dipergunakan dalam prinsip kerja digital computer. Bilangan oktal memiliki basis delapan, maksudnya memiliki kemungkinan bilangan 1,2,3,4,5,6 dan 7. Posisi digit pada bilangan oktal adalah :
Tabel 2. Posisi digit bilangan oktal
84 83 82 81 80 8-1 8-3 8-3 8-4 8-5
Penghitungan dalam bilangan oktal adalah:
0,1,2,3,4,5,6,7,10,11,12,13,14,15,16,17,20………65,66,67, 70,71………….275,276,277,300…….dst.
d) Bilangan Heksadesimal
Sistem bilangan heksadesimal memiliki radik 16 dan disebut juga dengan sistem bilangan basis 16. Penulisan simbol bilangan heksadesimal berturut-turut adalah 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E dan F. Notasi huruf A menyatakan nilai bilangan 10, B untuk nilai bilangan 11, C menyatakan nilai bilangan 12, D menunjukkan nilai bilangan 13, E untuk nilai bilangan 14, dan F adalah nilai bilangan 15. Manfaat dari
bilangan heksadesimal adalah kegunaannya dalam
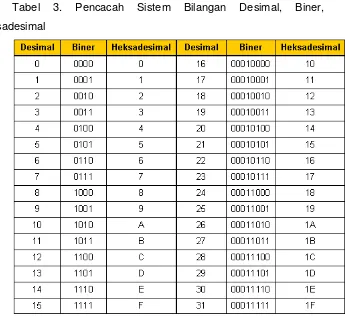
Tabel 3. Pencacah Sistem Bilangan Desimal, Biner, Heksadesimal
Hitungan heksadesimal pada nilai yang lebih tinggi adalah ……38,39. 3A, 3B, 3C, 3D, 3E, 3F, 40,41………... ...6F8,6F9,6FA, 6FB,6FC,6FD,6FE,6FF, 700……….
Tabel 7 memperlihatkan pencacahan sistem bilangan desimal, biner dan heksadesimal. Terlihat jelas bahwa ekivalen-ekivalen heksadesimal memperlihatkan tempat menentukan nilai. Misal 1 dalam 1016 mempunyai makna/bobot nilai 16 satuan, sedangkan angka 0 mempunyai rnilai nol.
yang paling signifikan (MSB). Urutan penulisan bilangan biner dimulai dari VII ke I.
Tabel 4 Konversi Desimal ke Biner
Sehingga didapatkan hasil konversi bilangan desimal 83 ke bilangan biner basis 2 adalah 83(10) = 0 1 0 1 0 0 1 1(2).
Berikut adalah contoh konversi bilangan desimal pecahan ke bilangan biner. Berbeda dengan penyelesaian bilangan desimal bukan pecahan (tanpa koma), Pertama (I) bilangan desimal 0,84375 dikalikan dengan basis 2 menghasilkan 1,6875. Langkah berikutnya bilangan pecahan dibelakang koma 0,6875 dikalikan bilangan basis 2 sampai akhirnya didapatkan nilai bilangan genap 1,0. Semua bilangan yang terletak didepan koma mulai dari urutan (I) sampai (V) merepresentasikan bilangan biner pecahan.
Sehingga konversi bilangan desimal 0,87375(10) terhadap bilangan biner adalah = 0,1 1 0 1 1(2).
Berikut adalah contoh konversi bilangan desimal pecahan 5,625 ke bilangan biner basis 2. Berbeda dengan penyelesaian bilangan desimal bukan pecahan (tanpa koma), Pertama (I) bilangan desimal 5 dibagi dengan basis 2 menghasilkan 2 sisa 1, berulang sampai dihasilkan hasil bagi 0. Langkah berikutnya adalah menyelesaikan bilangan desimal pecahan dibelakang koma 0,625 dikalikan dengan basis 2 menghasilkan 1,25, berulang sampai didapatkan nilai bilangan genap 1,0. Penulisan diawali dengan bilangan biner yang terletak didepan koma mulai dari urutan (III) berturut-turut sampai (I), sedangkan untuk bilangan biner pecahan dibelakang koma ditulis mulai dari (I) berturut-turut sampai ke (III).
Tabel 6. Konversi Desimal ke Biner Pecahan
Sehingga didapatkan hasil konversi bilangan 5,625(10) = 1 0 1 , 1 0 1(2).
Tabel 7 Konversi Desimal ke Oktal
Maka hasilnya 26610 = 4128
Sisa pembagian yang pertama disebut dengan Least Significant Digit (LSD) dan sisa pembagian terakhhir disebut Most Significant Digit (MSD).
4. Konversi sistem bilangan desimal ke sistem bilangan heksadesimal.
Konversi desimal ke heksadesimal bisa dilakukan dengan dua tahapan. Yang pertama adalah melakukan konversi bilangan desimal ke bilangan biner, kemudian dari bilengan biner ke bilangan heksadesimal.
Contoh :
Konversi bilangan desimal 250 ke bilangan heksadesimal. Tabel 8 Konversi Desimal ke Heksadesimal.
Byte pertama adalah 1111(2) = F(16) Byte ke dua adalah
1010(1) = A(16)
Maka bilangan heksadesimal, 1111.1010 (2) = FA (16) Sehingga 250 (10) = FA (16)
5. Konversi sistem bilangan biner ke sistem bilangan desimal Konversi bilangan biner basis 2 ke bilangan desimal basis 10 dapat dilakukan seperti pada tabel 3.2 berikut.
Tabel 9 Konversi Desimal ke Biner
Pangkat 24 23 22 21 20
Nilai 16 8 4 2 1
Biner 1 0 0 0 1
Desimal 16 + 1
Hasil 17
Oleh karena bilangan biner yang memiliki bobot hanya kolom paling kiri dan kolom paling kanan, sehingga hasil konversi ke desimal adalah sebesar 16 + 1 = 17.
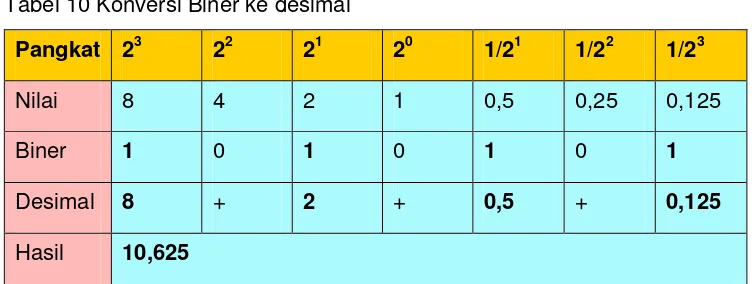
Tabel 10 Konversi Biner ke desimal
Pangkat 23 22 21 20 1/21 1/22 1/23
Nilai 8 4 2 1 0,5 0,25 0,125
Biner 1 0 1 0 1 0 1
Desimal 8 + 2 + 0,5 + 0,125
Tabel 10 memperlihatkan contoh konversi dari bilangan biner pecahan ke besaran desimal. Biner yang memiliki bobot adalah pada bilangan desimal 8 + 2 + 0,5 + 0,125 = 10,6125.
6. Konversi sistem bilangan oktal ke sistem bilangan desimal
Bilangan oktal bisa dikonversikan dengan mengalikan bilangan oktal dengan angka delapan dipangkatkan dengan posisi pangkat.
Contoh :
2268 = 2 x 82+ 2 x 81+ 6 x 80 = 2x64 + 2 x 8 + 6x1 = 128 + 16 + 6 =15010
7. Konversi sistem bilangan heksadesimal ke sistem bilangan desimal. Bila kita hendak mengkonversi bilangan heksadesimal ke bilangan desimal, hal penting yang perlu diperhatikan adalah banyaknya bilangan berpangkat menunjukkan banyaknya digit bilangan heksadesimal tersebut. Misal 3 digit bilangan heksadesimal mempunyai 3 buah bilangan berpangkat yaitu 162, 161, 160.
Tabel 11. Konversi bilangan heksadesimal ke desimal
Tabel 12 berikut memperlihatkan contoh konversi bilangan pecahan heksadesimal ke desimal. Metode penyelesaiannya adalah sama seperti metode yang digunakan tabel 11.
Tabel 12 Konversi bilangan pecahan heksadesimal ke desimal
No Pangkat 162 161 160 . 1/161
Langkah pertama adalah bilangan heksadesimal A pada kolom 256-an dikalik256-an deng256-an 10 sehinggga didapatk256-an nilai desimal sebesar 2560. Bilangan heksadesimal 3 pada kolom 16-an menghasilkan nilai desimal sebesar 3 x 16 = 48. Selanjutnya bilangan F menyatakan nilai desimal 1 x 15 = 15. Terakhir bilangan pecahan heksadesimal adalah 0,625 x 12 = 0,75. sehingga hasil akhir bilangan desimal adalah 2560 + 48 + 15 + 0,75 = 2623,75(10).
8. Sistem bilangan pengkode biner (binary encoding)
mesin hitung (kalkulator), komputer dan alat komunikasi handphone yang menggunakan bilangan logika biner 1 dan 0. Peralatan-peralatan tersebut termasuk kelompok perangkat digital yang hanya mengolah data berupa bilangan biner.
Untuk menghubungkan perhitungan logika perangkat digital dan perhitungan langsung yang dimengerti manusia, diperlukan sistem pengkodean dari bilangan biner ke desimal. Sistem pengkodean dari bilangan logika biner menjadi bilangan desimal lebih dikenal dengan sebutan BCD (Binary Coded Desimal).
Kode BCD
Sifat dari logika biner adalah sukar untuk dipahami secara langsung. Suatu kesulitan, berapakah nilai konversi jika kita hendak merubah bilangan biner 10010110(2) menjadi bilangan desimal?. Tabel 13 Kode BCD 8421
8421. Tabel 13 memperlihatkan kode BCD 4bit untuk digit desimal 0 sampai 9. Maksud sistem desimal terkode biner atau kode BCD (Binary Coded Desimal) bertujuan untuk membantu agar supaya konversi biner ke desimal menjadi lebih mudah. Kode BCD ini setiap biner memiliki bobot nilai yang berbeda tergantung posisi bitnya. Untuk bit paling kiri disebut MSB-Most Significant Bit mempunyai nilai desimal 8 dan bit paling rendah berada pada posisi bit paling kiri dengan nilai desimal 1 disebut LSB-Least Significant Bit. Oleh karena itu sistem pengkode ini dinamakan juga dengan sebutan kode BCD 8421. Bilangan 8421 menunjukkan besarnya pembobotan dari masing-masing bilangan biner 4bit.
Contoh 1 memperlihatkan pengubahan bilangan desimal 352 basis 10 ke bentuk kode BCD 8421.
Desimal 3 5 2
BCD 0011 0101 0010
Contoh 2 menyatakan pengubahan BCD 0110 1001 ke bentuk bilangan desimal basis 10.
BCD 0110 1001 .
Desimal 6 9 .
Contoh 3 memperlihatkan pengubahan bilangan desimal pecahan 53.52 basis 10 ke bentuk BCD 8421.
Desimal 5 3 . 5 2
BCD 0101 0011 . 0101 0010
Contoh 4 menyatakan pengubahan pecahan BCD 8421 ke bentuk bilangan desimal basis 10.
BCD 0111 0001 . 0000 1000
Contoh 5 menyatakan pengubahan pecahan BCD 8421 ke bentuk bilangan desimal basis 10 dan ke konversi biner basis 2.
BCD 0101 0100 . 0101
Desimal 5 4 . 5
Desimal ke biner
2.3 Rangkuman
1. Sistem bilangan desimal, biner, oktal, dan heksadesimal
Sistem bilangan desimal, urutan penulisan sistem bilangan ini adalah 0, 1, 2, 3, 4, 5, 6, 7, 8, dan 9. Sehingga bilangan desimal disebut dengan bilangan yang mempunyai bobot radik 10. Nilai suatu sistem bilangan desimal memiliki karakteristik dimana besarnya nilai bilangan tersebut ditentukan oleh posisi atau tempat bilangan tersebut berada.
Sistem bilangan oktal sering dipergunakan dalam prinsip kerja digital computer. Bilangan oktal memiliki basis delapan, maksudnya memiliki kemungkinan bilangan 1,2,3,4,5,6 dan 7. Sistem bilangan heksadesimal memiliki radik 16 dan disebut
bilangan heksadesimal adalah kegunaannya dalam
pengubahan secara langsung dari bilangan biner 4-bit.
2. Konversi sistem bilangan desimal ke sistem bilangan biner
Langkah konversi bilangan desimal basis 10 ke bilangan biner basis 2. Pertama (I) bilangan desimal 80 dibagi dengan basis 2 menghasilkan 40 sisa 1. Untuk bilangan biner sisa ini menjadi bit yang kurang signifikan (LSB), sedangkan sisa pembagian pada langkah ketujuh (VII) menjadi bit yang paling signifikan (MSB). Urutan penulisan bilangan biner dimulai dari VII ke I.
3. Konversi sistem bilangan desimal ke sistem bilangan oktal
Bilangan desimal bisa dikonversikan ke dalam bilangan oktal dengan cara yang sama dengan sistem pembagian yang dterapkan pada konversi desimal ke biner, tetapi dengan faktor pembagi 8.
4. Konversi sistem bilangan desimal ke sistem bilangan heksadesimal. Konversi desimal ke heksadesimal bisa dilakukan dengan dua tahapan. Yang pertama adalah melakukan konversi bilangan desimal ke bilangan biner, kemudian dari bilengan biner ke bilangan heksadesimal.
Pada konversi bilangan biner basis 2 ke bilangan desimal basis 10, bilangan biner yang memiliki bobot hanya kolom paling kiri dan kolom paling kanan, sehingga hasil konversi ke desimal
6. Konversi sistem bilangan oktal ke sistem bilangan desimal
Bilangan oktal bisa dikonversikan dengan mengalikan bilangan oktal dengan angka delapan dipangkatkan dengan posisi pangkat.
7. Konversi sistem bilangan heksadesimal ke sistem bilangan desimal. Bila kita hendak mengkonversi bilangan heksadesimal ke bilangan desimal, hal penting yang perlu diperhatikan adalah banyaknya bilangan berpangkat menunjukkan banyaknya digit bilangan heksadesimal tersebut. Misal 3 digit bilangan heksadesimal mempunyai 3 buah bilangan berpangkat yaitu 162, 161, 160
8. Sistem bilangan pengkode biner (binary encoding)
Untuk menghubungkan perhitungan logika perangkat digital dan perhitungan langsung yang dimengerti manusia, diperlukan sistem pengkodean dari bilangan biner ke desimal. Sistem pengkodean dari bilangan logika biner menjadi bilangan desimal lebih dikenal dengan sebutan BCD (Binary Coded Desimal).
2.4 Tugas
Lakukan pengukuran materi berikut ini menggunakan langkah-langkah pada lembar kerja:
1. Pengalih desimal ke biner . 2. Pengalih biner ke desimal.
2.5 Tes Formatif
1. Jelaskan pengertian sistem bilangan desimal ! 2. Jelaskan pengertian sistem bilangan biner ! 3. Jelaskan pengertian sistem bilangan oktal !
5. Jelaskan cara mengkonversi sistem bilangan desimal ke sistem bilangan biner !
6. Jelaskan cara mengkonversi sistem bilangan desimal ke sistem bilangan oktal !
7. Jelaskan cara mengkonversi sistem bilangan desimal ke sistem bilangan heksadesimal !
8. Jelaskan cara mengkonversi sistem bilangan biner ke sistem bilangan desimal !
9. Jelaskan cara mengkonversi sistem bilangan oktal ke sistem bilangan desimal !
10. Jelaskan cara mengkonversi sistem bilangan heksadesimal ke sistem bilangan desimal !
11. Jelaskan pengertian sistem bilangan pengkode biner (binary encoding)
2.6 Lembar Jawab Tes Formatif
1. Sistem bilangan desimal, urutan penulisan sistem bilangan ini adalah 0, 1, 2, 3, 4, 5, 6, 7, 8, dan 9. Sehingga bilangan desimal disebut dengan bilangan yang mempunyai bobot radik 10. Nilai suatu sistem bilangan desimal memiliki karakteristik dimana besarnya nilai bilangan tersebut ditentukan oleh posisi atau tempat bilangan tersebut berada.
2. Bilangan biner hanya menggunakan dua simbol, yaitu 0 dan 1. Bilangan biner dinyatakan dalam radik 2 atau disebut juga dengan sistem bilangan basis 2, dimana setiap biner atau biner digit disebut bit.
3. Sistem bilangan oktal sering dipergunakan dalam prinsip kerja digital computer. Bilangan oktal memiliki basis delapan, maksudnya memiliki kemungkinan bilangan 1,2,3,4,5,6 dan 7.
nilai bilangan 11, C menyatakan nilai bilangan 12, D menunjukkan nilai bilangan 13, E untuk nilai bilangan 14, dan F adalah nilai bilangan 15. Manfaat dari bilangan heksadesimal adalah kegunaannya dalam pengubahan secara langsung dari bilangan biner 4-bit.
5. Konversi sistem bilangan desimal ke sistem bilangan biner:
Langkah konversi bilangan desimal basis 10 ke bilangan biner basis 2. Pertama (I) bilangan desimal 80 dibagi dengan basis 2 menghasilkan 40 sisa 1. Untuk bilangan biner sisa ini menjadi bit yang kurang signifikan (LSB), sedangkan sisa pembagian pada langkah ketujuh (VII) menjadi bit yang paling signifikan (MSB). Urutan penulisan bilangan biner dimulai dari VII ke I.
6. Konversi sistem bilangan desimal ke sistem bilangan oktal
Bilangan desimal bisa dikonversikan ke dalam bilangan oktal dengan cara yang sama dengan sistem pembagian yang dterapkan pada konversi desimal ke biner, tetapi dengan faktor pembagi 8. 7. Konversi sistem bilangan desimal ke sistem bilangan heksadesimal.
Konversi desimal ke heksadesimal bisa dilakukan dengan dua tahapan. Yang pertama adalah melakukan konversi bilangan desimal ke bilangan biner, kemudian dari bilengan biner ke bilangan heksadesimal.
8. Konversi sistem bilangan biner ke sistem bilangan desimal
Pada konversi bilangan biner basis 2 ke bilangan desimal basis 10, bilangan biner yang memiliki bobot hanya kolom paling kiri dan kolom paling kanan, sehingga hasil konversi ke desimal
9. Konversi sistem bilangan oktal ke sistem bilangan desimal
Bilangan oktal bisa dikonversikan dengan mengalikan bilangan oktal dengan angka delapan dipangkatkan dengan posisi pangkat.
11. Sistem bilangan pengkode biner (binary encoding)
2.7 Lembar Kerja Peserta Didik
2.7.1 Tugas Kegiatan Belajar 1 - 1
Pengalih Desimal ke Biner
Tujuan Instruksional Umum
Setelah pelajaran selesai, peserta harus dapat:
Memahami rangkaian dan aturan pengalih bilangan desimal ke Biner.
Tujuan Instruksional Khusus
Peserta harus dapat:
Membangun rangkaian pengalih bilangan Desimal ke bilangan Biner Menyusun tabel kebenaran rangkaian pengalih
Memeriksa tabel kebenaran dengan valensi Biner
Menerapkan aturan pengalih bilangan Desimal ke Bilangan Biner.
Waktu 5 x 45 menit
Alat dan Bahan
Alat Alat:
Catu daya 5V 1 buah
Trainer digital 1 buah
Kabel penghubung Secukupnya
Bahan:
IC 74LS32 2 buah
1. Persiapan alat dan bahan
2. Buatlah rangkaian seperti gambar 2
3. Lakukan percobaan sesuai tabel kebenaran 4. Buatlah rangkaian seperti gambar 3
5. Lakukan percobaan sesuai tabel kebenaran 6. Buatlah rangkaian seperti gambar 4
7. Lakukan percobaan sesuai tabel kebenaran 8. Buatlah rangkaian seperti gambar 5
9. Lakukan percobaan sesuai tabel kebenaran
10. Periksa apakah data percobaan pada tabel kebenaran sesuai dengan valensi Biner
11. Definisikan aturan pengalihan dari bilangan Desimal ke bilangan Biner 12. Gambarkan data-data dan tabel; kebenaran ke gambar bentuk pulsa
Cara Kerja / Petunjuk
1. Konstruksi IC
2. Periksakan rangkaian yang anda buat pada instruktur sebelum rangkaian dihubungkan ke sumber tegangan
2.7.2 Tugas Untuk langkah 2
Untuk langkah 4
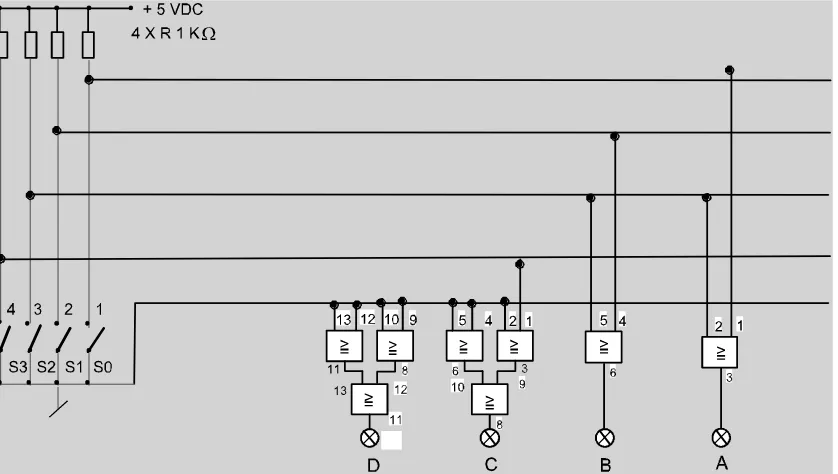
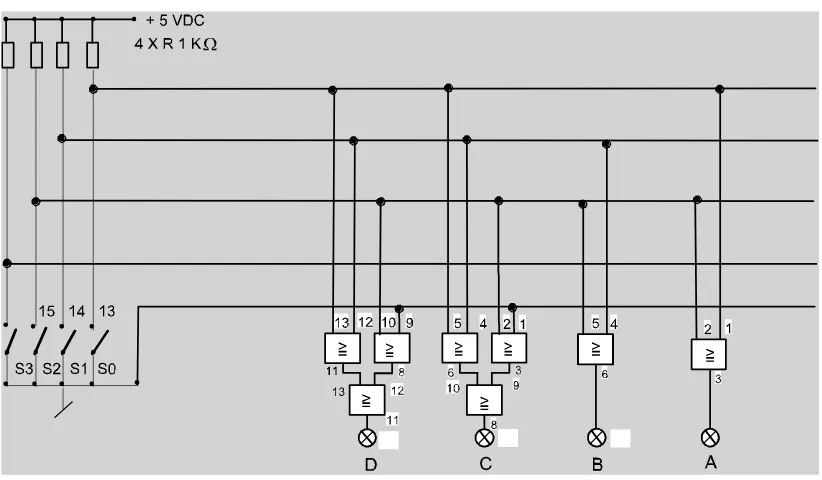
Rangkaian pengalih bilangan Desimal (5-8) ke bilangan Biner Gambar 3.
Untuk langkah 6
Untuk langkah 8
Rangkaian pengalih bilangan Desimal (13-15) ke bilangan Biner Gambar 5.
INPUT OUTPUT
Desimal S3 S2 S1 S0 D C B A Biner
1 0 0 0 1
2 0 0 1 0
3 0 1 0 0
4 1 0 0 0
Untuk langkah 5
5 0 0 0 1
6 0 0 1 0
7 0 1 0 0
8 1 0 0 0
Untuk langkah 7
9 0 0 0 1
10 0 0 1 0
11 0 1 0 0
12 1 0 0 0
Untuk langkah 9
15 0 1 0 0
Untuk langkah 10
1. Nilai valensi dari digit Code Biner
Digit Code Biner pada D C B A
Nilai Valensi
2. Bagaimana cara memeriksa kembali data pengalihan bilangan desimal ke bilangan Biner ?
Bilangan Desimal = ...+...+...+...
3. Periksalah kembali data-data dibawah ini, dengan menentukan nilai valensinya
Desimal Nilai valensi Biner
3 5 10 15
Untuk langkah 11
1. Sebuah rangkaian pengalih bilangan desimal ke bilangan Biner dapat bdibuat dengan mempergunakan :...
2. Aturan yang berlaku untuk pengalihan bilangan desimal ke bilangan Biner adalah
Untuk A : Amempunyai nilai ...
bila A = 1 berlaku untuk semua bilangan desimal ...oleh sebab itu A adalah terjadi secara ...
Bila B = 1 berlaku untuk bilangan desimal, yang mengandung sebuah ...oleh sebab itu B berubah dalam irama ...
Untuk C : C mempunyai nilai ...
Bila C = 1 berlaku untuk bilangan desimal yang mengandung sebuah ...oleh karena itu Cberubah dalam irama ...
Untuk D : D mempunyai nilai...
Bila D = 1 berlaku untuk bilangan desimal yang mengandung sebuah ...oleh sebab itu D berubah dalam irama ...
Untuk langkah 12
Jawaban
Tabel kebenaran Untuk langkah 3
INPUT OUTPUT
Untuk langkah 5
5 0 0 0 1 0 0 0 0 0111
6 0 0 1 0 0 0 0 0 0110
7 0 1 0 0 0 0 0 0 0111
8 1 0 0 0 0 0 0 0 1000
Untuk langkah 7
9 0 0 0 1 0 0 0 0 1001
10 0 0 1 0 0 0 0 0 1010
11 0 1 0 0 0 0 0 0 1011
12 1 0 0 0 0 0 0 0 1100
Untuk langkah 9
14 0 0 1 0 0 0 0 0 1110
15 0 1 0 0 0 0 0 0 1111
Untuk langkah 10
1. Nilai valensi dari digit Code Biner
Digit Code Biner pada D C B A
Nilai Valensi 23 22 21 20
2. Bagaimana cara memeriksa kembali data pengalihan bilangan desimal ke bilangan Biner ?
Bilangan Desimal = D3.+ D2 + D1 + D0
3. Periksalah kembali data-data dibawah ini, dengan menentukan nilai valensinya
Desimal Nilai valensi Biner 3 0 + 0 + 21 + 20 0 0 1 1 5 0 + 22 + 0 + 20 0 1 0 1 10 23 + 0 + 21 + 0 1 0 1 0 15 23 + 22 + 21 + 20 1 1 1 1
Untuk langkah 11
1. Sebuah rangkaian pengalih bilangan desimal ke bilangan Biner dapat
bdibuat dengan mempergunakan : gerbang dasar OR
2. Aturan yang berlaku untuk pengalihan bilangan desimal ke bilangan Biner adalah
Untuk A : A mempunyai nilai 20 = 1
Untuk B : B mempunyai nilai 21 = 2
Bila B = 1 berlaku untuk bilangan desimal, yang mengandung sebuah
nilai 2 oleh sebab itu D1 berubah dalam irama dua-dua ( dua kali B= 0
dan dua kali B = 1 ) : 0011001100110011 dst
Untuk C : C mempunyai nilai 22 = 4
Bila C = 1 berlaku untuk bilangan desimal yang mengandung sebuah
nilai 4 oleh karena itu C berubah dalam irama empat-empat :
0000111100001111 dst
Untuk D : D mempunyai nilai 23 = 8
Bila D = 1 berlaku untuk bilangan desimal yang mengandung sebuah
nilai 8 oleh sebab itu D berubah dalam irama delapan-delapan :
0000000011111111 dst
Untuk langkah 12
2.7.3 Tugas Kegiatan Belajar 1 - 2
Pengalih Biner Ke Desimal
Tujuan Instruksional Umum
Setelah pelajaran selesai, peserta harus dapat:
Memahami rangkaian dan aturan pengalih bilangan biner ke desimal
Tujuan Instruksional Khusus
Peserta harus dapat:
Membangun rangkaian pengalih bilangan biner ke bilangan desimal. Menyusun tabel kebenaran rangkaian pengalih.
Memeriksa tabel kebenaran dengan valensi biner.
Menerapkan hukum pengalih bilangan biner ke bilangan desimal.
Waktu 4 x 45 Menit
Alat dan Bahan
Gunakan pakaian kerja dengan benar Hati - hati memasang dan melepas IC Hindari hubung singkat
Langkah Kerja
1. Buat rangkaian seperti gambar 1 sampai dengan 4. 2. Gunakan saklar, letakkan pada input bilangan biner. 3. Catat hasil tingkat keluaran dalam tabel kebenaran. 4. Periksa apakah sesuai dengan valensi biner.
5. Definisikan dari pengalih bilangan biner ke bilangan desimal.
Cara Kerja / Petunjuk
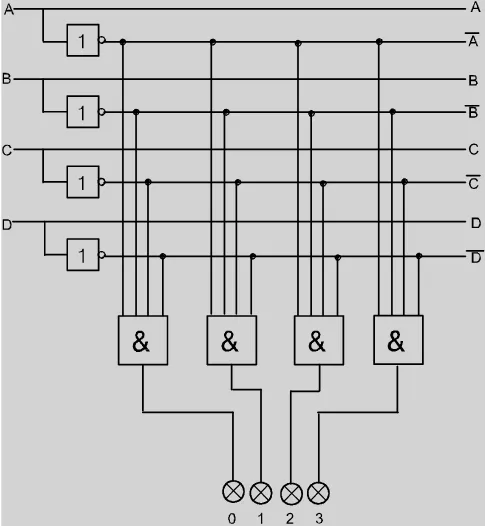
Rangkaian Pengalih bilangan biner ke bilangan desimal ( 0-3 )
Rangkaian Pengalih bilangan biner ke bilangan desimal ( 4-7 )
Gambar 2.
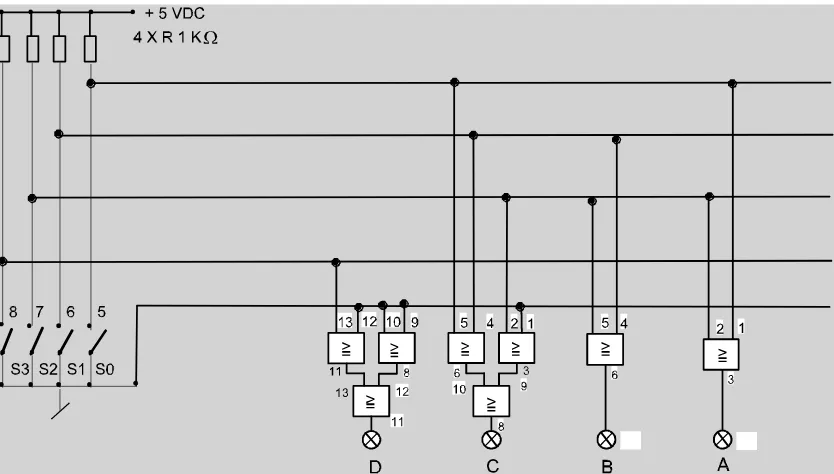
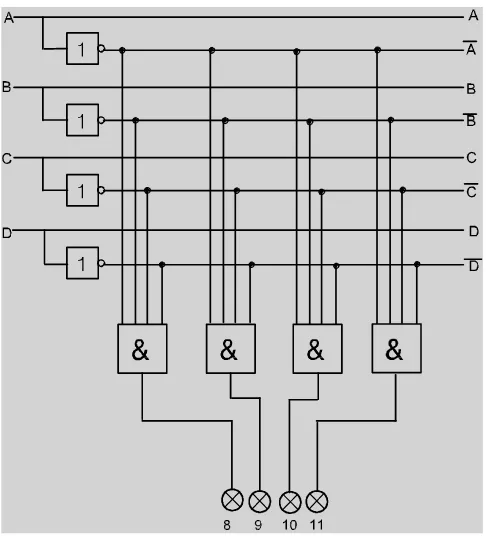
Rangkaian Pengalaih bilangan biner ke bilangan desimal ( 8-11 )
Rangkaian Pengalih bilangan biner ke bilangan desimal ( 12-15 )
Gambar 4.
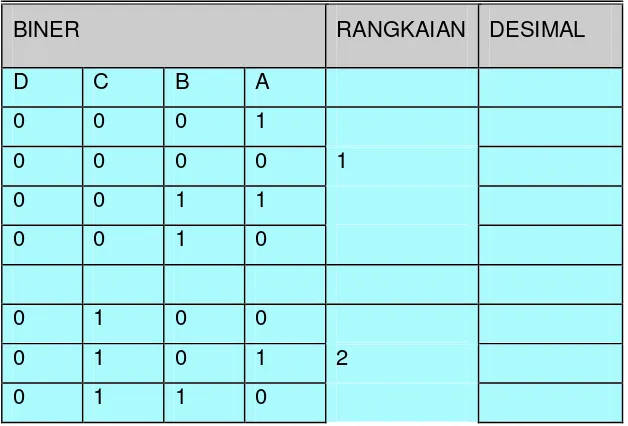
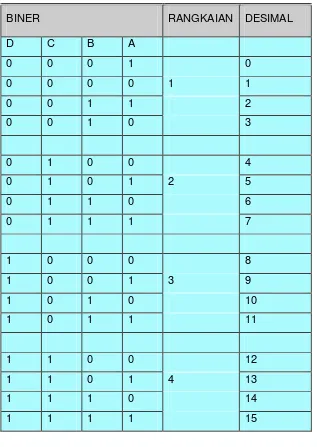
Untuk Langkah 3 Tabel Kebenaran
BINER RANGKAIAN DESIMAL
D C B A
0 0 0 1
0 0 0 0 1
0 0 1 1
0 0 1 0
0 1 0 0
0 1 1 1
Untuk Langkah 4
1. Berapa hasil, yang harus diperhitungkan
2. Alihkan bilangan biner ini ke bilangan desimal. a. 0001 = ... b. 0101 = ... c. 1001 = ... d. 1010 = ... e. 1111 = ...
Untuk Langkah 5
Pengalih bilangan biner ke bilangan desimal dapat dibangun dengan gerbang
Hukum dari pengalihan.
a. Untuk A... ... b. Untuk B
... c. Untuk C
... d. Untuk D
Jawaban
Untuk Langkah 3
Tabel Kebenaran untuk pengalih bilangan biner ke bilangan desimal.
BINER RANGKAIAN DESIMAL
D C B A
Untuk Langkah 4
2. Alihakan bilangan biner ini ke bilangan desimal.
Untuk Langkah 5
Pengalih bilangan biner ke bilangan desimal dapat dibangun dengan gerbang
AND atau NAND
nilainya :
4, 5, 6, 7, 12, 14, 15.
d. Untuk D.
D mempunyai nilai 23 = 8.
Yang mana D = 1, bagi / untuk bilangan desimal yang nilainya :
III. Kegiatan Belajar 2. ALJABAR BOOLEAN 3.1 Tujuan Pembelajaran
Peserta diklat / siswa dapat:
Menjelaskan konsep dasar aljabar Boolean pada gerbang logika digital.
Mentabulasikan macam macam Karnaugh map untuk mendapatkan
persamaan rangkaian digital
3.2 Uraian Materi
3. Aljabar Boole
Untuk menyelesaikan disain rangkaian digital tentunya dibutuhkan rangkaian yang benar, efektif, sederhana, hemat komponen serta ekivalen gerbang dasar bila terjadi keterbatasan komponen yang tersedia. Untuk itu diperlukan penyelesaian secara matematis guna mencapai tujuan-tujuan tersebut di atas. Aljabar boole adalah cara meyelesaikan permasalahan dengan penyederhanaan melalui beberapa persamaan sebagai berikut :
Postulate 2 x + 0 = x
Theorems 4 Associative x+(y+z)=(x+y)+z x(yz) = (xy)z Postulate 4 Distributive x(y+z) = xy + xz x+yz = (x+y)(x+z) Theorems 5 De Morgan (x+y)‟ = x‟y‟
(x.y)‟ = x‟+y‟
Theorems 6 Absorption x+xy = x x (x+y) = x
4. Karnaugh Map
Karnaugh map adalah metode untuk mendapatkan persamaan rangkaian digital dari tabel kebenarannya. Aplikasi dari Karnaugh map adalah dengan cara memasukkan data keluaran dari tabel kebenaran ke dalam tabel karnaugh map. Dengan menggunakan metode Sume of Product, maka keluaran yang berlogik “1” dan berdekatan atau berderet ditandai dengantanda hubung. Kemudian tuliskan persamaannya dengan metode SOP.
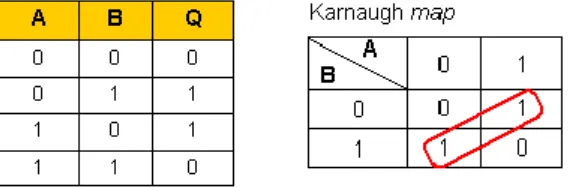
Karnaugh map dua masukan satu keluaran
Tabel sebuah rangkaian yang memiliki dua masukan A,B dan satu keluaran Q :
Contoh soal 1:
Dengan menggunakan Karnaugh map, tentukan persamaan dari data keluaran yang ada pada tabel kebenaran berikut :
Tabel 2 Tabel kebenaran contoh 1
Maka persamaan rangkaian tersebut adalah : Q = A.B
Contoh soal 2 :Dengan menggunakan Karnaugh map, tentukan persamaan dari data keluaran yang ada pada tabel kebenaran berikut :
Tabel 3 Tabel kebenaran contoh 2
Maka persamaan rangkaian tersebut adalah : QABABAB Bentuk-bentuk lain penyelesaian Karnaugh map adalah sebagai berikut:
Persamaan Q = B
Contoh lain : bila diketahui data-data seperti pada tabel 3.28, tuliskan persamaan rangkaian tersebut.
Tabel 5 Tabel kebenaran contoh 4
Persamaan adalah Q = A
Karnaugh map tiga masukan satu keluaran
Karnaugh map ada yang memiliki tiga buah masukan A,B,C dan sebuah keluaran Q seperti pada tabel 6.
Tabel 6 Tabel Karnaugh Map 3 masukan 1 keluaran
Tabel 7 Tabel kebenaran contoh 5
Persamaan rangkaian adalah Q=
A
.
C
A
B
C
Bentuk-bentuk karnaugh map yang lain untuk 3 masukan 1 keluaran:
Tabel 8 Tabel kebenaran contoh 5
Contoh 6.
Diketahui tabel kebenaran di bawah, cari persamaan rangkaian. Tabel 9 Tabel kebenaran contoh 6
Persamaan rangkaian adalah Q = B Contoh 7.
Diketahui tabel kebenaran di bawah, cari persamaan rangkaian. Tabel 10 Tabel kebenaran contoh 7
Contoh 8.
Diketahui tabel kebenaran di bawah, cari persamaan rangkaian. Tabel 11 Tabel kebenaran contoh 8
Persamaan rangkaian adalah Q =
B
.
C
Karnaugh map yang memiliki empat buah masukan dan satu buah keluaran adalah seperti pada tabel 12 di atas.
Karnaugh Map
Aplikasi dari model Karnaugh map 4 masukan 1 keluaran adalah sebagai berikut :
Contoh 9.
Persamaan adalah : Q =
B
.
D
BD
Karnaugh Map Lima Masukan A,B,C,D,E dan Satu Keluaran Q Karnaugh map yang memiliki lima buah masukan dan satu buah keluaran adalah seperti pada Tabel 14, table ini merupakan Tabel Kebenaran 5 masukan 1.
Karnaugh map harus dipecah menjadi dua bagian, yaitu untuk kondisi masukan A=0 dan A=1. Sehingga Karnaugh map-nya sebagai berikut:
Aplikasi dari model Karnaugh map 5 masukan 1 keluaran adalah sebagai berikut :
Contoh10.
Tabel 16 Tabel kebenaran contoh 10
3.3 Rangkuman
1. Konsep dasar aljabar Boolean pada gerbang logika digital.
Untuk menyelesaikan disain rangkaian digital tentunya dibutuhkan rangkaian yang benar, efektif, sederhana, hemat komponen serta ekivalen gerbang dasar bila terjadi keterbatasan komponen yang tersedia. Untuk itu diperlukan penyelesaian secara matematis guna mencapai tujuan-tujuan tersebut di atas. Aljabar boole adalah cara meyelesaikan permasalahan dengan penyederhanaan melalui beberapa persamaan
2. Mentabulasikan macam macam Karnaugh map untuk mendapatkan
persamaan rangkaian digital abulasikan macam macam Karnaugh map untuk mendapatkan persamaan rangkaian digital
3.4 Tugas
3.5 Tes Formatif
1. Jelaskan konsep dasar aljabar Boolean pada gerbang logika digital ! 2. Jelaskan pengertian Some Of Product dalam aplikasi dari Karnaugh
map !
3.6 Lembar Jawab Tes Formatif
1. Aljabar boole adalah cara meyelesaikan permasalahan dengan penyederhanaan melalui beberapa persamaan.
3.7 Lembar Kerja Peserta Didik
Kunci Jawaban
Tabel kebenaran Aplikasi dari model Karnaugh map 5 masukan 1 keluaran berikut berdasarkan contoh 10 diatas.
IV. Kegiatan Belajar 3. GERBANG DASAR 4.1 Tujuan Pembelajaran
Peserta diklat / siswa dapat :
Memahami konsep dasar rangkaian logika digital.
Memahami prinsip dasar gerbang logika AND, OR, NOT, NAND, NOR.
Memahami prinsip dasar gerbang logika eksklusif OR dan NOR. 4.2 Uraian Materi
1. Konsep dasar rangkaian logika digital.
Besaran digital adalah besaran yang terdiri dari besaran level tegangan High dan Low, atau dinyatakan dengan logika “1” dan “0”. Level high adalah identik dengan tegangan “5 Volt” atau logika “1”, sedang level low identik dengan tegangan “0 Volt” atau logika “0”. Untuk sistem digital yang menggunakan C-MOS level yang digunakan adalah level tegangan “15 Volt” dan “0 Volt”
Sebagai gambaran perbedaan besaran digital dan analog adalah seperti penunjukan alat ukur. Alat ukur analog akan menunjukkan besaran analog, sedangkan alat ukur digital akan menunjukkan display angka yang disusun secara digital (7-segment).
Pada Gambar 1 diperlihatkan alat ukur analog (gambar c) dan alat ukur digital pada gambar d.
Gambar 1a dan b memperlihatkan besaran digital yang hanya ada harga 0 dan 5V untuk di peralatan yang menggunakan TTL serta 0 dan 15V untuk di peralatan yang menggunakan C-MOS
c Besaran Analog d Besaran Digital
e Tegangan Analog f Tegangan digital
Gambar 1 Besaran Analog dan Digital
2. Prinsip dasar gerbang logika AND, OR, NOT, NAND, NOR. Gerbang AND
Gerbang dasar AND adalah ekivalen dengan dua buah saklar terbuka yang terpasang seri seperti terlihat pada gambar 2 di bawah.
Gambar 2 Rangkaian listrik ekivalen AND
saklar atau semua saklar diputus (off). Sehingga bisa dirumuskan hanya akan terjadi keluaran “1” bila A=”1” dan B=”1”.
Rangkaian listrik :
Simbol standar IEC standar USA
Gambar 3 Simbol gerbang AND
Fungsi persamaan dari gerbang AND
f(A,B) = A
B (1)Tabel 1 Tabel kebenaran AND
B A Q=f(A,B)
0 0 0
0 1 0
1 0 0
1 1 1
Gerbang OR
Gerbang dasar OR adalah ekivalen dengan dua buah saklar terbuka yang terpasang parallel / jajar seperti terlihat pada gambar 3.5 di bawah. Rangkaian terdiri dari dua buah saklar yang terpasang secara parallel, sebuah relay dan lampu. Lampu akan menyala bila salah satu atau ke dua saklar A dan B dihubungkan (on). Sebaliknya lampu hanya akan padam bila semua saklar A dan B diputus (off). Maka bisa dirumuskan bahwa akan terjadi keluaran “1” bila salah satu saklar A=”1” atau B=”1”, dan akan terjadi keluaran “0” hanya bila saklar Rangkaian listrik : A=”1” dan B=”1”.
Gambar 5 Rangkaian listrik ekivalen gerbang OR
Gambar 6 simbol gerbang OR
Fungsi dari gerbang OR adalah :
f(A,B) = A + B (2)
B A Q=f(A,B)
0 0 0
0 1 1
1 0 1
1 1 1
Gambar 7 Diagram masukan-keluaran gerbang OR
Diagram masukan-keluaran diperlihatkan seperti gambar di bawah. Pada keluaran A+B hanya akan memiliki logik low “0” bila semua masukan - masukannya A dan B memiliki logik “0”
Gerbang NOT
Gambar 8 Rangkaian listrik ekivalen gerbang NOT
Gambar 9 Gambar symbol gerbang NOT
Fungsi persamaan dari gerbang NOT adalah:
f(A)=A (3)
Tabel 3 Tabel kebenaran NOT
A Q=A
0 1
1 0
Gambar 9 Diagram masukan-keluaran gerbang NOT Gerbang NAND
Gerbang dasar NAND adalah ekivalen dengan dua buah saklar terbuka yang terpasang seri. Akan terjadi keluaran Q=“1” hanya bila A=”0” dan B=”0”. Gerbang NAND sama dengan gerbang AND dipasang seri dengan gerbang NOT. Rangkaian listrik :
Gambar 10 Rangkaian listrik ekivalen gerbang NAND
Gambar 11 Gambar symbol gerbang NAND Fungsi persamaan gerbang NAND
Diagram masukan-keluaran dari gerbang NAND, keluaran memiliki logik “0” hanya bila ke dua masukannya berlogik “1”
Gerbang NOR
Gerbang dasar NOR adalah ekivalen dengan dua buah saklar terbuka yang terpasang parallel / jajar.
Gambar 13 Rangkaian listrik ekivalen gerbang NOR
Akan terjadi keluaran “1” bila semua saklar A=”0” atau B=”0”. Gerbang NOR sama dengan gerbang OR dipasang seri dengan gerbang NOT.
Gambar 14 Gerbang NOR
Fungsi persamaan gerbang NOR
f(A,B)=AB (5)
Diagram masukan keluaran seperti terlihat pada gambar di bawah. Keluaran hanya akan memiliki logik „1‟, bila semua masukannya berlogik “0”
Gambar 15 Diagram masukan-keluaran gerbang NOR
3. Prinsip dasar gerbang logika eksklusif OR dan NOR. Exclusive OR (EX-OR)
Gambar 16 Rangkaian listrik ekivalen gerbang EX-OR
Gambar 17 Simbol gerbang EX-OR Fungsi persamaan gerbang EX-OR
B A B A B A B)
f(A, (6)
Tabel 6 Tabel kebenaran EX-OR
Keluaran hanya akan memiliki logik “1” bila masukan-masukannya memiliki kondisi logik berlawanan.
Gambar 18 Diagram masukan-keluaran gerbang EX-OR
Gerbang EX-NOR (Exlusive-NOR)
Gambar 20 Rangkaian listrik ekivalen gerbang EX-NOR
Gambar 21 Simbol gerbang EX-NOR Fungsi persamaan gerbang EX-NOR
f(A,B)=ABAB =A B (7)
Tabel 3.23 Tabel kebenaran gerbang EX=NOR
masukan-masukannya memiliki kondisi logik sama, logik “0” maupun logik “1”.
4.3 Rangkuman
1. Konsep dasar rangkaian logika digital.
Besaran digital adalah besaran yang terdiri dari besaran level tegangan High dan Low, atau dinyatakan dengan logika “1” dan “0”. Level high adalah identik dengan tegangan “5 Volt” atau logika “1”, sedang level low identik dengan tegangan “0 Volt” atau logika “0”. Untuk sistem digital yang menggunakan C-MOS level yang digunakan adalah level tegangan “15 Volt” dan “0 Volt”
2. Prinsip dasar gerbang logika AND, OR, NOT, NAND, NOR.
Gerbang dasar AND adalah ekivalen dengan dua buah saklar terbuka yang terpasang seri. Diagram masukan-keluaran dari gerbang AND terlihat bahwa pada keluaran akan memiliki logik high “1” bila semua masukan A dan B berlogik “1”.
Gerbang dasar OR adalah ekivalen dengan dua buah saklar terbuka yang terpasang parallel / jajar , bahwa akan terjadi keluaran “1” bila salah satu saklar A=”1” atau B=”1”, dan akan terjadi keluaran “0” hanya bila saklar Rangkaian listrik : A=”1” dan B=”1”.
Gerbang dasar NOT adalah rangkaian pembalik / inverter , bahwa akan terjadi keluaran Q=“1” hanya bila masukan A=”0”. Gerbang dasar NAND adalah ekivalen dengan dua buah saklar
terbuka yang terpasang seri. Akan terjadi keluaran Q=“1” hanya bila A=”0” dan B=”0”. Gerbang NAND sama dengan gerbang AND dipasang seri dengan gerbang NOT.
Gerbang dasar NOR adalah ekivalen dengan dua buah saklar terbuka yang terpasang parallel / jajar. Akan terjadi keluaran “1” bila semua saklar A=”0” atau B=”0”. Gerbang NOR sama dengan gerbang OR dipasang seri dengan gerbang NOT.
3. Prinsip dasar gerbang logika eksklusif OR dan NOR.
Gerbang EX-OR hanya akan memiliki keluaran Q=”1” bila masukan-masukan A dan B memiliki kondisi berbeda.
Pada gerbang EX-NOR bila saklar A dan B masing-masing dihubungkan (on) atau diputus (off) maka lampu akan menyala. Namun bila saklar A dan B dalam kondisi yang berlawanan, maka lampu akan mati. Sehingga bisa disimpulkan bahwa gerbang EX-NOR hanya akan memiliki keluaran Q=”1” bila masukan-masukan A dan B memiliki kondisi yang sama.
4.4 Tugas
Lakukan praktek pengukuran untuk mengetahui prinsip kerja gerbang rangkaian logika berikut sesuai lembar kerja:
1. Gerbang DAN (AND Gate) 2. Gerbang ATAU (OR-Gate) 3. Gerbang NOT , NAND dan NOR
4. Gerbang Exsclusive OR ( EX - OR ) dan Exsclusive NOR ( EX - NOR )
5. Logika AND dan NAND Mengggunakan Teknik NOR.
4.5 Tes Formatif
1. Jelaskan pengertian besaran digital pada rangkaian logika digital ! 2 Jelaskan pengertian rangkaian Gerbang dasar AND !
3 Jelaskan pengertian rangkaian Gerbang dasar OR ! 4 Jelaskan pengertian rangkaian Gerbang dasar NOT ! 5 Jelaskan pengertian rangkaian Gerbang dasar NAND ! 6 Jelaskan pengertian rangkaian Gerbang dasar NOR ! 7 Jelaskan pengertian rangkaian Gerbang dasar EX-OR ! 8 Jelaskan pengertian rangkaian Gerbang dasar EX-NOR !
4.6 Lembar Jawab Tes Formatif
Untuk sistem digital yang menggunakan C-MOS level yang digunakan adalah level tegangan “15 Volt” dan “0 Volt”.
2. Gerbang dasar AND adalah ekivalen dengan dua buah saklar terbuka yang terpasang seri. Diagram masukan-keluaran dari gerbang AND terlihat bahwa pada keluaran akan memiliki logik high “1” bila semua masukan A dan B berlogik “1”.
3. Gerbang dasar OR adalah ekivalen dengan dua buah saklar terbuka yang terpasang parallel / jajar , bahwa akan terjadi keluaran “1” bila salah satu saklar A=”1” atau B=”1”, dan akan terjadi keluaran “0” hanya bila saklar Rangkaian listrik : A=”1” dan B=”1”. 4. Gerbang dasar NOT adalah rangkaian pembalik / inverter , bahwa
akan terjadi keluaran Q=“1” hanya bila masukan A=”0”.
5. Gerbang dasar NAND adalah ekivalen dengan dua buah saklar terbuka yang terpasang seri. Akan terjadi keluaran Q=“1” hanya bila A=”0” dan B=”0”. Gerbang NAND sama dengan gerbang AND dipasang seri dengan gerbang NOT.
6. Gerbang dasar NOR adalah ekivalen dengan dua buah saklar terbuka yang terpasang parallel / jajar. Akan terjadi keluaran “1” bila semua saklar A=”0” atau B=”0”. Gerbang NOR sama dengan gerbang OR dipasang seri dengan gerbang NOT.
7. Gerbang EX-OR sering ditulis dengan X-OR adalah gerbang yang paling sering dipergunakan dalam teknik komputer. Gerbang EX-OR hanya akan memiliki keluaran Q=”1” bila masukan-masukan A dan B memiliki kondisi berbeda.
4.7 Lembar Kerja Peserta Didik
4.7.1 TUGAS Kegiatan Belajar 3 - 1
Gerbang DAN (AND Gate)
Tujuan Instruksional Umum
Setelah pelajaran selesai, peserta harus dapat: Memahami prinsip kerja gerbang DAN
Tujuan Instruksional Khusus Peserta harus dapat:
Menerangkan prinsip kerja gerbang DAN sesuai dengan tabel kebenaran
Menggambarkan rangkaian persamaan gerbang DAN sesuai dengan standar IEC
Alat dan Bahan Alat Alat:
Multimeter 1 buah
Catu daya 1 buah
Papan Percobaan 1 buah
Kabel penghubung secukupnya
IC 7408 1 buah
IC 7421 1 buah
Keselamatan Kerja
Hati-hatilah dengan arus dan tegangan 220 Volt
Hati-hati memasukkan sumber tegangan jangan sampai lebih dari 5 Volt DC.
Langkah Kerja
1. Persiapan alat dan bahan
2. Buat rangkaian seperti gambar 1.2
3. Lapor pada Instruktur sebelum rangkaian dihubungkan ke sumber tegangan.
4. Hubungkan ke sumber tegangan 5 V DC
5. Lakukan percobaan sesuai tabel kebenaran dan perhatikan perubahan pada keluaran, kemudian catat pada tabel kebenaran
6. Gambarkan rangkaian persamaan logikanya dari gerbang AND 7. Serta tuliskan persamaan Aljabar Boolenya dari gerbang AND 8. Gambarkan Diagram Pulsa pada kurva diagram
Percobaan I (B) (Gerbang AND 3 masukan)
9. Ulangi langkah percobaan 2 - 8 untuk percobaan A dan percobaan B dengan menggunakan gambar 1.3
Percobaan I (C) (Gerbang AND 4 masukan)
10. Ulangi langkah percobaan 2 - 8 untuk percobaan A dan percobaan C dengan menggunakan gambar 1.4
Percobaan II
(Gerbang AND dengan menggunakan IC 7421 (IC AND 4 masukan)
Cara Kerja / Petunjuk
1. Cara memegang IC yang benar diperlihatkan oleh gambar di bawah :
3. Jangan memasang/melepas IC secara paksa 4. Pasang IC dengan tepat, jangan terbalik 5. Simbol untuk gerbang AND ().
4.7.2 Tugas
Gerbang DAN (IC-7408)
Gerbang DAN dengan 2 masukan (Percobaan IA) Untuk langkah 1
Gambar 1
Untuk langkah 5 Untuk langkah 7
Tabel kebenaran Persamaan aljabar Boole
Untuk langkah 8 Diagram Pulsa :
Gerbang DAN dengan 3 masukan. (Percobaan 1B)
A
B
C
Q
-Gambar 3
Untuk langkah 5 Untuk langkah 6
Tabel kebenaran : Rangkaian
Persamaan :
C B A Q
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
Untuk langkah 7
Untuk langkah 8 Diagram Pulsa
Gerbang DAN dengan 4 masukan (IC 7408) (Percobaan 1C)
Tabel Kebenaran Rangkaian Persamaan :
MASUKAN KELUARAN
Untuk langkah 8 Diagram Pulsa
Gerbang DAN dengan 4 masukan (IC - 7421) (Percobaan II)
Untuk langkah 1
GND
Untuk langkah 5 Untuk langkah 6
Tabel Kebenaran : Rangkaian persamaan
MASUKAN KELUARAN
D C B A Q
0 0 0 0
0 0 0 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
1 0 1 1 Untuk langkah 7
1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1
Untuk langkah 8 Diagram Pulsa :
Jawaban
Gerbang DAN (IC-7408)
Gerbang DAN dengan 2 masukan (Percobaan 1A)
gambar 1
Untuk langkah 5 Untuk langkah 7
Tabel kebenaran Persamaan aljabar Boole
MASUKA
Untuk langkah 6 Rangkaian persamaan
Untuk langkah 8 Diagram Pulsa :
Gerbang DAN dengan 3 masukan.
A
Untuk langkah 5 Untuk langkah 6
Tabel kebenaran : Rangkaian
Persamaan :
MASUKAN KELUARAN
Untuk langkah 7
Persamaan aljabar Boole
Untuk langkah 8 Diagram Pulsa
Gerbang DAN dengan 4 masukan (percobaan 1C)
Q
-+ A
B
C D
Q1
Q2
3
Gambar 4
Untuk langkah 5 Untuk langkah 6
Tabel Kebenaran Rangkaian Persamaan :
MASUKAN KELUARAN
0 0 0 0 0 0 0
0 0 0 1 0 0 0
0 0 1 0 0 0 0
0 0 1 1 1 0 0
0 1 0 0 0 0 0
0 1 0 1 0 0 0
0 1 1 0 0 0 0
0 1 1 1 1 0 0
1 0 0 0 0 0 0
1 0 0 1 0 0 0
1 0 1 0 0 0 0
1 0 1 1 1 0 0 Untuk langkah 7
1 1 0 0 0 1 0
1 1 0 1 0 1 0
1 1 1 0 0 1 0
1 1 1 1 1 1 1
Untuk langkah 8 Diagram Pulsa
Gerbang DAN dengan 4 masukan (IC - 7421) (Percobaan II)
Untuk langkah 6 Untuk langkah 5
Tabel Kebenaran : Rangkaian persamaan
MASUKAN KELUARAN
4.7.3 TUGAS Kegiatan Belajar 3 - 2
Gerbang ATAU (OR-Gate)
Tujuan Instruksional Umum
Setelah pelajaran selesai, peserta harus dapat: Menjelaskan prinsip kerja gerbang dasar ATAU
Tujuan Instruksional Khusus Peserta harus dapat:
Menentukan kaki-kaki masukan, dan keluaran gerbang ATAU sesuai gambar petunjuk kaki IC dengan benar.
Menerangkan prinsip kerja gerbang ATAU sesuai dengan tabel kebenaran.
Menggambar rangkaian persamaan gerbang ATAU sesuai dengan standar IEC.
Alat dan Bahan Alat Alat:
Catu daya 5V 1 buah
Papan Percobaan / trainer digital 1 buah
Kabel penghubung secukupnya
Keselamatan Kerja
Output catu daya harus 5 Volt DC Peganglah IC sesuai petunjuk
Pelajari petunjuk-petunjuk sebelum anda melakukan praktik
Langkah Kerja
1. Persiapan alat dan bahan
2. Lengkapi gambar 1.1 dengan tanda masukan dan keluaran 3. Buat rangkaian seperti gambar 1.1
4. Lapor pada Instruktur sebelum rangkaian dihubungkan ke sumber tegangan.
5. Lakukan percobaan sesuai tabel kebernaran
6. Perhatikan perubahan pada keluaran, catat di tabel kebenaran. 7. Buat gambar rangkaian persamaan.
8. Tuliskan Aljabar Boole nya. 9. Buat diagram pulsa
10. Ulangi langkah 2-8 untuk gambar 1.2 dan 1.3 Cara Kerja / Petunjuk
1. Cara memegang IC yang benar diperhatikan oleh gambar di bawah :
3. Jangan memasang/melepas IC secara paksa 4. Pasang IC dengan tepat, jangan terbalik 5. Simbol untuk gerbang AND ()
Tugas
Gerbang ATAU (IC-7432)
Untuk langkah 1
gambar 1
Untuk langkah 5 Untuk langkah 7
Tabel kebenaran Persamaan aljabar Boole
1 1
Untuk langkah 6 Rangkaian persamaan
Untuk langkah 8
Gerbang ATAU dengan 3 masukan.
Untuk langkah 5 Untuk langkah 6
Tabel kebenaran : Rangkaian
Persamaan :
MASUKAN KELUARAN
C B A Q
Untuk langkah 7
V. Gerbang ATAU dengan 4 masukan
Tabel Kebenaran Rangkaian Persamaan :
MASUKAN KELUARAN
Untuk langkah 8 Diagram Pulsa
Jawaban
Untuk langkah 1
gambar 1.1
Untuk langkah 5 Untuk langkah 7
Tabel kebenaran Persamaan aljabar Boole
MASUKAN KELUARAN
B A Q
0 0 0
1 0 1
1 1 1
Untuk langkah 6 Rangkaian persamaan
Untuk langkah 8 Diagram Pulsa :
Gerbang ATAU dengan 3 masukan.
A
B
C
Q
-+
Untuk langkah 5 Untuk langkah 6
Tabel kebenaran : Rangkaian
Persamaan :
MASUKAN KELUARAN
C B A Q
0 0 0 0
0 0 1 1
0 1 0 1
0 1 1 1
1 0 0 1
1 0 1 1
1 1 0 1
1 1 1 1
Untuk langkah 7
Untuk langkah 8 Diagram Pulsa
Gerbang ATAU9 dengan 4 masukan
Tabel Kebenaran Rangkaian Persamaan :
MASUKAN KELUARAN
4.7.4. TUGAS Kegiatan Belajar 3 - 3
Gerbang NOT , NAND dan NOR
Tujuan Instruksional Umum
Setelah pelajaran selesai, /peserta harus dapat:
Menganalisa prinsip kerja gerbang Not, Nand dan Nor-gate.
Tujuan Instruksional Khusus
Peserta harus dapat:
Menentukan kaki-kaki masukan, dan keluaran pada IC berdasarkan gambar bukaannya dengan benar
Menerangkan prinsip kerja gerbang NOT,NAND dan NOR.
berdasarkaan hasil percobaan dalam tabel kebenaran dengan benar. Menggambarkan rangkaian persamaan listrik dari gerbang NOT,
NAND dan NOR berdasarkan tabel kebenaran dengan benar.
Menuliskan persamaan fungsi "Aljabar Boole" dari gerbang NOT, NAND dan NOR berdasarkan tabel kebenaran dengan benar.
Menggambar kan pulsa .keluaran gerbang-gerbang NOT, NAND dan NOR berdasarkan tabel kebenaran dengan benar.
Waktu 8 x 45 menit
Alat dan Bahan
Alat Alat:
Catu daya 5 VDC 1 buah
Papan percobaan 1 buah
Bahan:
IC 7400 1 buah
IC 7402 1 buah
IC 4002 1 buah
IC 7404 1 buah
IC 7408 1 buah
IC 7420 1 buah
Keselamatan Kerja
Hati-hati dalam memasang IC pada papan percobaan Hati-hati dengan tegangan 220 Volt
A semua masukan tidak berlogika 1
Q semua masukan berlogika 0
Langkah Kerja
1. Lengkapi gambar bukaan IC dari gerbang NOT, NAND, NOR, dengan tanda masukan dan keluaran (lihat keterangan)
2. Buat rangkaian seperti gambar 1.2 pada papan percobaan
3. Lapor instruktur sebelum rangkaian dihubungkan ke sumber tegangan. 4. Hubungkan rangkaian ke sumber tegangan 5 VDC
6. Buatlah rangkaian persamaan kelistrikannya. 7. Tuliskan fungsi "Aljabar Boole" nya ke dalam kolom 8. Ulangi langkah 1 s/d 7 untuk percobaan berikutnya 9. Buat kesimpulan untuk tiap-tiap percobaan.
Cara Kerja / Petunjuk
1. Cara memegang IC yang benar diperlihatkan oleh gambar di bawah.
2. Perhatikan penunjuk (indeks) di bawah untuk menetapkan nomor kaki IC secara tepat.
4.7.5 Tugas
Gerbang NOT (IC - 7404)
Untuk Langkah 1
GND
Untuk langkah 5 Untuk langkah 6
Tabel kebenaran : Rangkaian persamaan
Masukan Keluaran
A Q
0 1
Untuk langkah 7
Persamaan aljabar boole
NAND dibangun dari gerbang AND + NOT
Untuk langkah 1
GND
Untuk langkah 5 Untuk langkah 6
Tabel kebenaran Rangkaian persamaan
Masukan Keluaran
B A Q1 Q2
0 0
0 1
1 0
1 1
Untuk langkah 7
GERBANG NAND (IC -7400)
Untuk langkah 1
GND
Untuk langkah 5 Untuk langkah 6
Tabel kebenaran Rangkaian persamaan
Masukan Keluaran
B A Q
0 0
0 1
1 0
Untuk langkah 7
Persamaan aljabar boole
Untuk langkah 8 Diagram pulsa
NAND dengan 4 masukan (7420)