Materi Matematika Wajib Kelas XII KK13

(1)

M A T R I K S 3

B. Invers Perkalian Matriks ordo (2 x 2)

Matriks identitas perkalian (dilambangkan dengan I) adalah sebuah matriks persegi yang memenuhi sifat: Jika A adalah matriks persegi yang berordo sama dengan I, maka berlaku

A x I = I x A = A

Untuk matriks identitas ordo (2 x 2) dapat dinyatakan sebagai I = 

Jika A sebuah matriks persegi maka terdapat invers perkalian dari matriks A yang dilambangkan dengan A1 dan memenuhi sifat:

A x A1 = A1 x A = I

Untuk matriks ordo (2 x 2), invers dari matriks A = 

(2)

Dari (1)(2) ap + br = 1 (c) acp + bcr = c dimana ad – bc dinamakan determinan.

Jika matriks A mempunyai determinan 0 maka A dikatakan matriks singular, yaitu matriks yang tidak mempunyai invers.

Terdapat beberapa sifat yang berkenaan dengan invers matriks, yaitu : Sifat 1

Jika A adalah matriks berordo (2 x 2) dan k adalah bilangan real, maka

(3)

Sifat 2

Jika A adalah transpose matriks A maka berlaku (At)1(A1)t

Bukti Jika A =

   

d c

b a

, maka At =

   

d b

c a

sehingga (At)1₌

bc ad

1

   

a b

c d

…...(1)

1 A =

bc ad

1

 

 

 

 a c

b d

sehingga (A1)t₌

bc ad

1

 

 

 

 a b

c d

...(2)

Dari (1) dan (2) terbukti bahwa (At)1(A1)t

Sifat 2

Jika A adalah matriks berordo (2 x 2) maka berlaku 1 1

)

(A  = A Bukti

Misalkan : 1 1

)

(A  = B ... (1) Maka 1

A (A1)1 = 1

A . B (kedua ruas dikalikan dengan 1

A dari kiri) I = 1

A . B A x I = A x 1

A . B (Kedua ruas dikalikan dengan A) A = I x B

A = B ... (2) Dari (1) dan (2) terbukti bahwa 1 1

)

(A  = A Sifat 3

Jika A dan B adalah matriks berordo (2 x 2) maka berlaku :(A x B)1  B1 x A1 Bukti

Misalkan (A x B)1 = C ………(1) maka

1 1

) ) B A x (

(   = C1 (kedua ruas di inverskan) A x B = C1

A1 x A x B = A1 x C1 (Kedua ruas dikalikan dengan 1

A dari kiri) I x B = A1 x C1

B = A1 x C1

B x C = A1 x C1 x C (Kedua ruas dikalikan dengan C dari kanan) B x C = A1 x I

B x C = A1

B1 x B x C = B1 x A1 (Kedua ruas dikalikan dengan 1

(4)

Sifat 4

Jika A, B dan C adalah matriks-matriks berordo (2 x 2) maka :

(1) Tidak berlaku sifat komutatif perkalian, sehingga A x B ≠ B x A

(2) Berlaku sifat asosiatif perkalian, sehingga : (A x B) x C = A x (B x C) (3) Berlaku sifat distributif, sehingga A(B + C) = AB + AC

Untuk lebih jelasnya akan diuraikan dalam contoh soal berikut ini 01. Jika A =

maka buktikanlah bahwa matriks A dan B saling invers

(5)

1

merupakan matriks singular maka tentukanlah nilai x

(6)

05. Jika matriks A =

adalah invers dari matriks B =

 tentukanlah nilai x dan y

(7)

M A T R I K S 3

B. Invers Perkalian Matriks ordo

(3 x 3

)

Seperti yang telah diuraikan di atas, bahwa setiap matriks persegi mempunyai identitas perkalian (dilambangkan dengan I ) dan invers perkalian, sehingga berlaku :

Jika 1

A adalah invers dari matriks A, maka 1

A x A = A x 1 A = I

Selanjutnya akan dibahas tentang matriks identitas dan invers perkalian matriks persegi ordo (3 x 3).

Matriks identitas perkalian ordo (3 x 3) adalah I =

    

    

1 0 0

0 1 0

0 0 1

Sedangkan untuk

menentukan invers perkalian matriks (3 x 3) dapat dilakukan dengan dua cara, yaitu :

(1) Dengan metoda mereduksi elemen baris.

Untuk menentukan invers matriks dengan metoda ini, dilakukan dengan cara :

Jika A =

    

    

i h g

f e d

c b a

maka invers matriks A didapat dengan cara mereduksi elemen

baris matriks A, sehingga :

a b c 1 0 0 1 0 0 p q r d e f 0 1 0 diubah menjadi 0 1 0 s t u g h i 0 0 1 0 0 1 v w x

dalam hal ini A1 =

    

    

x w v

u t s

r q p

Terdapat beberapa aturan dalam reduksi elemen baris, yaitu :

(1) Setiap elemen baris dapat dikali (atau dibagi) dengan bilangan real

(2) Setiap elemen baris dapat ditambah (atau dikurang) dengan elemen baris yang lain

(3) Setiap elemen baris dapat ditukar posisi dengan baris lain

(8)

01. Tentukanlah invers matriks A =

    

    

  

1 5 0

2 3 2

1 2 1

Jawab

1 –2 1 1 0 0 b₁ x 2 2 –3 2 0 1 0

0 –5 1 0 0 1

2 –4 2 2 0 0

2 –3 2 0 1 0 b₂ – b₁ 0 –5 1 0 0 1

2 –4 2 2 0 0 0 1 0 –2 1 0 b₂ x 5 0 –5 1 0 0 1

2 –4 2 2 0 0 0 5 0 –10 5 0 b₂ x 5 0 –5 1 0 0 1

2 –4 2 2 0 0 0 5 0 –10 5 0

0 0 1 –10 5 1 b₃ + b₂

1 –2 1 1 0 0 b₁: 2 0 1 0 –2 1 0 b₂: 5 0 0 1 –10 5 1

1 –2 0 11 –5 –1 b₁ – b₃ 0 1 0 –2 1 0

(9)

1 –2 0 11 –5 –1 0 2 0 –4 2 0 b₂x 2 0 0 1 –10 5 1

1 0 0 7 –3 –1 b₁+ b₂ 0 2 0 –4 2 0

0 0 1 –10 5 1

1 0 0 7 –3 –1 0 1 0 –2 1 0 b₂: 2 0 0 1 –10 5 1

maka A1 =

    

    

 

f e 10

0 d c

b 3 a

=

    

    

 

1 5 10

0 1 2

1 3 7

02. Tentukanlah invers matriks A =

    

    

  

5 2 4

0 1 2

3 2 1

Jawab

–1 2 –3 1 0 0 b₁ x 5 2 1 0 0 1 0

4 –2 5 0 0 1 b₃ x 3

–5 10 –15 5 0 0 b₁ + b₃ 2 1 0 0 1 0

12 –6 15 0 0 3

7 4 0 5 0 3

(10)

–1 0 0 5 –4 3 b₁ – b₂ 8 4 0 0 4 0

12 –6 15 0 0 3

–4 0 0 20 –16 12 b₁ x 4 8 4 0 0 4 0

4 –2 5 0 0 1 b₃: 3

–4 0 0 20 –16 12 8 4 0 0 4 0

0 –2 5 20 –16 13 b₃ + b₁

–2 0 0 10 –8 6 b₁: 2 2 1 0 0 1 0 b₂: 4 0 –2 5 20 –16 13

–2 0 0 10 –8 6

0 1 0 10 –7 6 b₂+ b₁ 0 –2 5 20 –16 13

–2 0 0 10 –8 6

0 2 0 20 –14 12 b₂x 2 0 –2 5 20 –16 13

–2 0 0 10 –8 6 0 2 0 20 –14 12

0 0 5 40 –30 25 b₃+ b₂

(11)

maka A1 =

(2) Dengan menggunakan Minor-Kofaktor

Menentukan invers matriks dengan Minor-kofaktor ini, dilakukan dengan

menggunakan konsep determinan (dilambangkan dengan det) dan konsep adjoint (dilambangkan dengan adj).

Misalkan A =

maka langkah-langkah menentukan invers matriks

dengan metoda ini adalah sebagai berikut :

1. Menentukan minor matriks A untuk baris p dan kolom q (Mpq)

2. Menentukan kofaktor matriks A

Kofaktor matriks A baris ke-p kolam ke-q dilambangkan Cpq ditentukan dengan

rumus :

Sehingga diperoleh matriks kofaktor C sebagai berikut :

(12)

3. Menentukan determinan matriks A

Determinan matriks A ditulis det(A) atau │A│ ditentukan dengan rumus:

det(A) =

3 3 3

2 2 2

1 1 1

c b a

= a1.b2.c3 + b1.c2.a3 + c1.a2.b3– c1.b2.a3– a1.c2.b3– b1.a2.c3

atau dengan menggunakan kofaktor C_pq dengan rumus : det(A) = a1C₁₁ – b1C₁₂ + c1C₁₃

det(A) = a2C₂₁ – b2C₂₂ + c2C₂₃

det(A) = a3C₃₁ – b3C₃₂ + c3C₃₃

4. Menentukan matriks adjoint A, yakni transpose dari kofaktor matriks A, atau dirumuskan :

Adj A = Ct

5. Menentukan invers matriks A dengan rumus :

1

A =

det(A) 1

adj A

Untuk lebih jelasnya ikutilah contoh soal berikut ini :

03. Tentukanlah Determinan matriks A =

    

     



1 3 0

3 2 1

2 1 2

Jawab

2 1 –2 2 1

–1 2 3 –1 2 0 3 1 0 3

det = (2)(2)(1) + (1)(3)(0) + (–2)(–1)(3) – (–2)(2)(0) – (2)(3)(3) – (1)(–1)(1) det = 4 + 0 + 6 – 0 – 18 + 1

det = –7

04. Dengan menggunakan kofaktor, tentukanlah invers matriks A =

    

    

  

2 2 1

1 3 2

0 5 3

Jawab

(13)

11

M =

2 2

1 3 

= (–3)(2) – (1)(2) = –6 – 2 = –8

12

M = 2 1

1 2

 = (2)(2) – (1)( –1) = 4 + 1 = 5

13

M =

2 1

3 2 



= (2)( 2) – (–3)( –1) = 4 – 3 = 1

21

M =

2 2

0 5 

= (–5)(2) – (0)(2) = –10 – 0 = –10

22

M =

2 1

0 3

 = (3)(2) – (0)( –1) = 6 – 0 = 6

23

M =

2 1

5 3 



= (3)(2) – (–5)( –1) = 6 – 5 = 1

31

M =

1 3

0 5  

= (–5)(1) – (0)( –3) = –5 – 0 = –5

32

M = 1 2

0 3

= (3)(1) – (0)(2) = 3 – 0 = 3

33

M =

3 2

5 3

 

= (3)( –3) – (–5)(2) = –9 + 10 = 1

Langkah 2 (menentukan kofaktor matriks)

11

C = (1)11 M₁₁ = (1)(–8) = –8

12

C = (1)12 M₁₂ = (–1)(5) = –5

13

C = (1)13 M₁₃ = (1)(1) = 1

21

C = (1)21 M₂₁ = (–1)(–10) = 10

22

C = (1)22 M₂₂ = (1)(6) = 6

23

C = (1)23 M₂₃ = (–1)(1) = –1

31

C = (1)31 M₃₁ = (1)(1) = 1

32

(14)

Matriks kofaktornya : C =

Langkah 3 (menentukan Determinan matriks) Menggunakan ekspansi baris pertama

det(A) = a₁₁C₁₁ + a₁₂C₁₂ + a₁₃C₁₃ = (3)(–8) + (–5)(–5) + (0)(1) = 1

Langkah 4 (menentukan Adjoint matriks)

Matiks kofaktor C =

Langkah 4 (menentukan Invers matriks)

1

05. Dengan menggunakan kofaktor, tentukanlah invers matriks A =



Langkah 1 (menentukan minor matriks)

(15)

13

M = 3 1

2 1

= (1)( 3) – (2)(1) = 3 – 2 = 1

21

M = 1 3

3 3

= (3)(1) – (3)(3) = 3 – 9 = –6

22

M = 1 1

3 1

= (1)(1) – (3)(1) = 1 – 3 = –2

23

M = 3 1

3 1

= (1)(3) – (1)(3) = 3 – 3 = 0

31

M = 1 2

3 3

= (3)(1) – (3)(2) = 3 – 6 = –3

32

M = 1 1

3 1

= (1)(1) – (3)(1) = 1 – 3 = –2

33

M = 2 1

3 1

= (1)(2) – (3)(1) = 2 – 3 = –1

Langkah 2 (menentukan kofaktor matriks)

11

C = (1)11 M₁₁ = (1)(–1) = –1

12

C = (1)12 M₁₂ = (–1)(0) = 0

13

C = (1)13 M₁₃ = (1)(1) = 1

21

C = (1)21 M₂₁ = (–1)(–6) = 6

22

C = (1)22 M₂₂ = (1)(2) = 2

23

C = (1)23 M₂₃ = (–1)(0) = 0

31

C = (1)31 M₃₁ = (1)(–3) = –3

32

C = (1)32 M₃₂ = (–1)(–2) = 2

33

C = (1)33 M₃₃ = (1)(–1) = –1

    

    

 



1 2 3

0 2 6

(16)

Langkah 3 (menentukan Determinan matriks) Menggunakan ekspansi baris pertama

det(A) = a₁₁C₁₁ + a₁₂C₁₂ + a₁₃C₁₃ = (1)(–1) + (3)(0) + (3)(1) = –1 + 0 + 3 = 2

Langkah 4 (menentukan Adjoint matriks)

Matiks kofaktor C =

    

    

 



1 2 3

0 2 6

1 0 1

adjoin nya adj(A) =

    

    

  

1 0 1

2 2 0

3 6 1

Langkah 4 (menentukan Invers matriks)

1

A =

det(A) 1

adj(A)

1

A = 2 1

    

    

  

1 0 1

2 2 0

3 6 1

1

A =

    

    

  

2 / 1 0 2 / 1

1 1 0

(17)



A. Menyelesaikan Sistem Persamaan Linier Dua Variabel

Salah satu diantara penggunaan invers matriks adalah untuk menyelesaikan sistim persamaan linier. Tentu saja teknik penyelesaiannya dengan aturan persamaan matriks, yaitu :

Jika maka _

Selain dengan persamaan matriks, teknik menyelesaikan sistem persamaan linier juga dapat dilakukan dengan determinan matriks. Aturan dengan cara ini adalah : Jika matriks A =

Untuk lebih jelanya, ikutolah contoh soal berikut ini:

01. Tentukan himpunan penyelesaian sistem persamaan 2x – 3y = 8 dan x + 2y = –3 dengan metoda:

(a) Invers matriks (b) Determinan

Jawab 2x – 3y = 8 x + 2y = –3

(18)



(b) Dengan metoda determinan matriks diperoleh D =

02. Tentukan himpunan penyelesaian sistem persamaan y =

2 dengan metoda:

(19)

 dengan metoda:

(a) Invers matriks (b) Determinan Jawab

2y – 3x = –4 3x – 2y = 4 x + 2y = –3 2x + y = 5

(b) Dengan metoda invers matriks diperoleh

(20)

Maka x = D D_x

= 7 14

= 2

y = D D_y

= 7 7

(21)

M A T R I K S 4

B. Menyelesaikan Sistem Persamaan Linier Tiga Variabel

Salah satu diantara penggunaan matriks adalah untuk menyelesaikan

sistim persamaan linier. Sepeti halnya pada sistem persamaan linier dua variabel, menyelesaikan sistem persamaan linier tiga variabel dengan matriks juga terdiri dari dua cara, yakni dengan menggunakan determinan matriks dan dengan menggunakan aturan invers perkalian matriks. Berikut ini akan diuraikan masing masing cara

tersebut.

(1) Menyelesaikan sistem persamaan linier tiga variabel dengan determinan matriks Aturan menyelesaikan sistem persamaan linier dengan cara ini adalah dengan menentukan terlebih dahulu matriks koefisien dari sistem persamaan itu. Selanjutnya ditentukan empat nilai determinan sebagai berikut:

(1) D yakni determinan matriks koefisien

(2) Dx yakni determinan matriks koefisien dengan koefisien x diganti konstanta

(3) Dy yakni determinan matriks koefisien dengan koefisien y diganti konstanta

(4) Dz yakni determinan matriks koefisien dengan koefisien z diganti konstanta

Rumus masing-masingnya adalah sebagai berikut : a1x + b1y + c1z = d1

Jika a2x + b2y + c2z = d2 diperoleh nilai determinan :

a3x + b3y + c3z = d3

D =

3 3 3

2 2 2

1 1 1

c b a

= a1.b2.c3 + b1.c2.a3 + c1.a2.b3– c1.b2.a3– a1.c2.b3– b1.a2.c3

Dx =

3 3 3

2 2 2

1 1 1

c b d

= d1.b2.c3 + b1.c2.d3 + c1.d2.b3– c1.b2.d3– d1.c2.b3– b1.d2.c3

Dy =

3 3 3

2 2 2

1 1 1

c d a

= a1.d2.c3 + d1.c2.a3 + c1.a2.d3– c1.d2.a3– a1.c2.d3– d1.a2.c3

Dz =

3 3 3

2 2 2

1 1 1

d b a

(22)

Untuk lebih jelasnya, ikutilah contoh soal berikut ini:

(23)

(24)

(25)

(2) Menyelesaikan sistem persamaan linier tiga variabel dengan invers matriks Aturan menyelesaikan sistem persamaan linier dengan cara ini adalah dengan menentukan invers matriks koefisien melalui tahapan berikut ini :

a1x + b1y + c1z = d1

Karena A adalah matriks koefisien berordo (3 x 3) maka A1 adalah invers perkalian matriks berordo (3 x 3). Berikut ini tatacara menentukan invers matriks ordo (3 x 3)

maka langkah-langkah menentukan invers matriks

adalah sebagai berikut :

1. Menentukan minor matriks A untuk baris p dan kolom q (Mpq)

2. Menentukan kofaktor matriks A

Kofaktor matriks A baris ke-p kolam ke-q dilambangkan Cpq ditentukan

(26)

Sehingga diperoleh matriks kofaktor C sebagai berikut :

C =

    

    

33 32 31

23 22 22

13 12 11

C C C

3. Menentukan determinan matriks A

Determinan matriks A ditulis ditentukan dengan menggunakan kofaktor C_pq dengan rumus : det(A) = a1C₁₁– b1C₁₂ + c1C₁₃

det(A) = a2C₂₁ – b2C₂₂ + c2C₂₃

det(A) = a3C₃₁ – b3C₃₂ + c3C₃₃

4. Menentukan matriks adjoint A, yakni transpose dari kofaktor matriks A, atau dirumuskan :

Adj A = Ct

5. Menentukan invers matriks A dengan rumus :

1

A =

det(A) 1

adj A Untuk lebih jelasnya, ikutilah contoh soal berikut ini:

04. Tentukanlah himpunan penyelesaian sistem persamaan linier x + y – 2z = 2

x – 3y + z = –3 dengan menggunakan metoda inver matriks x – y + z = 1

Jawab

Matriks koefisien untuk sistem persamaan linier diataas adalah :

A =

    

    

 



1 1 1

1 3 1

2 1 1

sehingga

Pertama akan ditentukan minor matriks, yaitu

11

M =

1 1

1 3  

= (–3)(1) – (1)( –1) = –3 + 1 = –2

12

M = 1 1

1 1

= (1)(1) – (1)(1) = 1 – 1 = 0

13

M =

1 1

3 1

 

= (1)(–1) – (–3)(1) = –1 + 3 = 2

21

M =

1 1

2 1 



(27)

22

M = 1 1

2 1 

= (1)(1) – (–2)(1) = 1 + 2 = 3

23

M = 1 1

1 1

 = (1)(–1) – (1)(1) = –1 – 1 = –2

31

M =

1 3

2 1 



= (1)(1) – (–2)(–3) = 1 – 6 = –5

32

M = 1 1

2 1 

= (1)(1) – (–2)(1) = 1 + 2 = 3

33

M = 3 1

1 1

 = (1)(–3) – (1)(1) = –3 – 1 = –4

Kemudian menentukan kofaktor matriks

11

C = (1)11 M₁₁ = (1)(–2) = –2

12

C = (1)12 M₁₂ = (–1)(0) = 0

13

C = (1)13 M₁₃ = (1)(2) = 2

21

C = (1)21 M₂₁ = (–1)(–1) = 1

22

C = (1)22 M₂₂ = (1)(3) = 3

23

C = (1)23 M₂₃ = (–1)(–2) = 2

31

C = (1)31 M₃₁ = (1)(–5) = –5

32

C = (1)32 M₃₂ = (–1)(3) = –3

33

C = (1)33 M₃₃ = (1)(4) = 4

    

    

   

4 3 5

2 3 1

2 0 2

Setelah itu menentukan Determinan matriks menggunakan ekspansi baris pertama

(28)

Berikutnya menentukan Adjoint matriks dari matriks kofaktor

Akhirnya dimasukkan kedalam rumus invers matriks:

1

Setelah mendapatkan invers matriks, maka system persamaan linier diatas dielesaikan dengan persamaan matriks sebagai berikut :



05. Tentukanlah himpunan penyelesaian sistem persamaan linier 2x + 2y + 3z = 4

–x + y + 3z = 1 dengan menggunakan metoda inver matriks –2x + y + 2z = –3

Jawab

A =

(29)

12

M =

2 2

3 1 



= (–1)(2) – (3)(–2) = –2 + 6 = 4

13

M =

1 2

1 1

 = (–1)(1) – (1)(–2) = –1 + 2 = 1

21

M = 2 1

3 2

= (2)(2) – (3)(1) = 4 – 3 = 1

22

M =

2 2

3 2

 = (2)(2) – (3)(–2) = 4 + 6 = 10

23

M =

1 2

2 2

 = (2)(1) – (2)(–2) = 2 + 4 = 6

31

M = 3 1

3 2

= (2)(3) – (3)(1) = 6 – 3 = 3

32

M =

3 1

3 2

 = (2)(3) – (3)(–1) = 6 + 3 = 9

33

M =

1 1

2 2

 = (2)(1) – (2)(–1) = 2 + 2 = 4

11

C = (1)11 M₁₁ = (1)(–1) = –1

12

C = (1)12 M₁₂ = (–1)(4) = –4

13

C = (1)13 M₁₃ = (1)(1) = 1

21

C = (1)21 M₂₁ = (–1)(1) = –1

22

C = (1)22 M₂₂ = (1)(10) = 10

23

C = (1)23 M₂₃ = (–1)(6) = –6

31

C = (1)31 M₃₁ = (1)(3) = 3

32

C = (1)32 M₃₂ = (–1)(9) = –9

33

(30)

det(A) = a₁₁C₁₁ + a₁₂C₁₂ + a₁₃C₁₃ = (2)(–1) + (2)(–4) + (3)(1) = –7

Jika kofaktor C =

1

(31)

06. Tentukanlah himpunan penyelesaian sistem persamaan linier 2x – 2y – z = 3

3x + y + 2z = 7 dengan menggunakan metoda inver matriks 2x + 3y + 4z = 8

Jawab

A =

    

   

  

4 3 2

2 1 3

1 2 2

sehingga

11

M = 4 3

2 1

= (1)(4) – (2)(3) = 4 – 6 = –2

12

M = 4 2

2 3

= (3)(4) – (2)(2) = 12 – 4 = 8

13

M = 3 2

1 3

= (3)(3) – (1)(2) = 9 – 2 = 7

21

M =

4 3

1 2  

= (–2)(4) – (–1)(3) = –8 + 3 = –5

22

M = 4 2

1 2 

= (2)(4) – (–1)(2) = 8 + 2 = 10

23

M = 3 2

2 2 

= (2)(3) – (–2)(2) = 6 + 4 = 10

31

M =

2 1

1 2  

= (–2)(2) – (–1)(1) = –4 + 1 = –3

32

M = 2 3

1 2 

= (2)(2) – (–1)(3) = 4 + 3 = 7

33

M = 1 3

2 2 

= (2)(1) – (–2)(3) = 2 + 6 = 8

11

(32)

21

det(A) = a₁₁C₁₁ + a₁₂C₁₂ + a₁₃C₁₃ = (–2)(2) + (–8)(–2) + (7)(–1) = 5

Jika kofaktor C =

1

(33)

    

    

z y x

=     

     

3 2 1

(34)

M A T R I K S 4

C. Penerapan Matriks pada Transformasi

1. Transformasi Pergeseran (Translasi) Segitiga ABC pada gambar di

samping digeser menjadi segitiga

A’B’C’. Artinya setiap titik pada

segitiga ABC tersebut digeser dengan jarak dan arah yang tetap sehingga diperoleh segitiga

A’B’C’.

Transformasi yang berciri demikian dinamakan pergeseran atau translasi.

Sebuah titik P(x,y) digeser sejauh T = 

maka akan diperoleh bayangan P’(x’,y’), dan dirumuskan x’ = x + a

Untuk pemantapan lebih lanjut, ikutilah contoh soal berikut ini

01. Diketahui dua titik A(–2, 3) dan B(5, 1). Tentukanlah bayangan ruas garis AB jika ditranslasikan sejauh T =



Atau dengan matriks Titik A :

(35)

02. Diketahui titik A(3, -5) digeser sehingga diperoleh bayangan A’(7, 2). Dengan translasi yang sama titik B(-4, -8) akan bergeser menjadi B’. Tentukan

koordinat B’

2. Transformasi Perputaran (Rotasi) Segitiga ABC pada gambar berikut ini diputar dengan pusat putaran di O(0, 0) dan sudut putar sejauh α ,

sehingga menjadi segitiga A’B’C’.

Artinya setiap titik pada segitiga ABC tersebut diputar denganpusat dan sudut putar yang tetap sehingga

diperoleh segitiga A’B’C’.

(36)

Untuk α positif, maka perputarannya berlawanan arah jarum jam. Sedangkan untuk

α negatif, maka perputarannya searah jarum jam

Sebuah titik P(x,y) diputar dengan pusat O(0, 0) sejauh α akan diperoleh bayangan

P’(x’,y’) dimana : x’ = x.cosα– y.sinα

y’ = x.sinα + y.cosα

Atau :    

' y

' x

=

  

 

  cos  sin

sin cos

    y x

Bukti:

Didalam segitiga OAP diperoleh hubungan : OA = OP cos atau x = r.cos AP = OP sin atau y = r.sin Di dalam segitiga OBP diperoleh hubungan

(i) OB = OP cos (+α) x' = r. cos ( +α)

x' = r cos . cosα – r sin . sinα x' = xcosα – y sinα

(ii) BP = OP sin (+α) y' = r. sin ( +α)

y' = r sin . cosα + r cos . sinα y' = ycosα + x sinα

Walaupun rumus di atas diturunkan dengan mengambil α_{sudut positip, tetapi dapat} ditunjukkan bahwa berlaku untuk semua α (α positip atau α negatif)

Jika pusat putaran di A(h, k) dan sudut putaran sejauh α , maka rumus menentukan bayangannya dapat diturunkan dengan menggeser titik pusat O(0, 0) sejauh

    k h

Sehingga jika titik P(x,y) diputar dengan pusat A(h, k) sejauh α akan diperoleh

bayangan P’(x’,y’) dimana : x’– h = (x – h)cosα – (y – k)sinα y’– k = (x – h) sinα_{+ (y}– k)cosα Atau :

   

' y

' x

=

  

 

  cos sin

sin cos

      

k -y

h x

+ _

    

k h

O B A

C

D P(x,y)

) y' , (x' P'

x y

α



r

(37)

03. Diketahui segitiga ABC dimana titik A(6, 2), B(1, 3) dan C(4, 6) diputar sejauh 900 dengan pusat O(0, 0). Tentukanlah koordinat titik bayangan segitiga tersebut Jawab Gambarnya

04. Sebuah titik A(x, y) dirotasikan dengan pusat O(0, 0) sejauh 450, sehingga diperoleh

(38)



05. Tentukan bayangan titik P(4, –6 3) jika diputara sejauh 1/3 putaran berlawanan arah

jarum jam dengan pusat O(0, 0) ….

Jawab

α Bernilai positip karena perputaran berlawanan arah jarum jam α = (360 )

06. Jika titik P(5,-7) dirotasikan sejauh 1800 dengan pusat A(3, 1) sehingga diperoleh

bayangan P’. Tentukanlah koordinat P’

(39)

cermin garis

y’– k = (x – h) sin 1800_{+ (y}– k) cos 1800

y’– 1 = (5 – 3) sin 1800_{+ (}–7 – 1) cos 1800

y’–_{1 = (2)(0) + (}–8)( –1)

y’–_{1 = 0 + 8} y’– 1 = 8

y’ = 9 Jadi titiknya P’(1, 9)

3. Transformasi Pencerminan (Refleksi)

Segitiga ABC pada gambar di

samping dicerminkan terhadap garis tertentu menjadi segitiga A’B’C’. Pada pencerminan ini segitiga asal ABC akan berhadapan dengan

segitiga bayangan A’B’C’.

Transformasi yang berciri demikian dinamakan pencerminan atau

tranformasi.

Terdapat beberapa macam jenis pencerminan, tergantung pada posisi garis cerminnya, yaitu:

a. Pencerminan terhadap sumbu x

Misalkan P’(x’, y’) merupakan bayangan hasil pencerminan titik P(x, y) terhadap sumbu X, maka dirumuskan : x’ = x

y’ = –y Atau :

   

' y

' x

=

   

1 0

0 1

   

y x

Misalkan titik P(5, 2) dicerminkan terhadap sumbu X, maka bayangannya

adalah P’(5, -2)

b. Pencerminan terhadap sumbu Y

Misalkan P’(x’, y’) merupakan bayangan hasil pencerminan titik P(x, y) terhadap

sumbu Y, maka dirumuskan : x’ = –x

y’ = y

Atau :    

' y

' x

=

   

1 0

0 1

   

y x

Misalkan titik P(-4, 3) dicerminkan

.

P(5, 2)

.

P’(5, -2)

.

P(-4, 3)

.

P’(4, 3) A

B C

A' B'

(40)

c. Pencerminan terhadap garis y = x

Misalkan P’(x’, y’) merupakan bayangan hasil pencerminan titik P(x, y) terhadap garis y = x, maka dirumuskan : x’ = y

Misalkan titik P(4, 2) dicerminkan

terhadap garis y = x, maka bayangannya

adalah P’(2, 5)

d. Pencerminan terhadap garis y = –x

Misalkan titik P(-6, 3) dicerminkan

terhadap garis y = x, maka bayangannya

adalah P’(-3, 6)

i. Pencerminan terhadap titik asal

Misalkan P’(x’, y’) merupakan bayangan hasil pencerminan titik P(x, y) terhadap titik O(0, 0) maka dirumuskan : x’ = –x

Misalkan titik P(–5, 3) dicerminkan terhadap y = x + 4, maka

bayangannya adalah P’(5, –3)

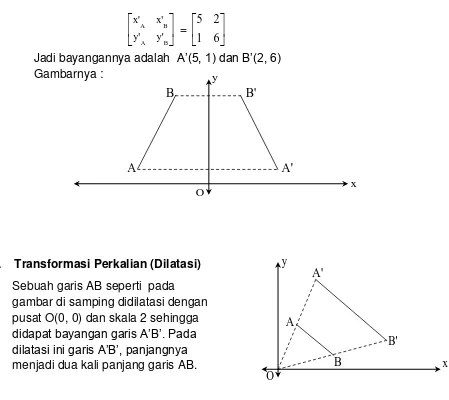
01. Diketahui titik A(–5, 1) dan B(–2, 6). Tentukanlah bayangan ruas garis AB oleh refleksi terhadap sumbu-Y dan gambarkan

(41)



Jadi bayangannya adalah A’(5, 1) dan B’(2, 6) Gambarnya :

4. Transformasi Perkalian (Dilatasi) Sebuah garis AB seperti pada gambar di samping didilatasi dengan pusat O(0, 0) dan skala 2 sehingga

didapat bayangan garis A’B’. Pada dilatasi ini garis A’B’, panjangnya

menjadi dua kali panjang garis AB.

Transformasi yang berciri demikian dinamakan perkalian atau dilatasi.

Sebuah titik P(x, y) didilatasi dengan pusat O(0, 0) dan skala k akan menghasilkan

bayangan P’(x’, y’) dimana : x’ = k.x

Sedangkan jika titik P(x, y) didilatasi dengan pusat A(m, n) dan skala k akan

menghasilkan bayangan P’(x’, y’) dimana : x’ = k(x – m) + m

(42)

y

04. Tentukanlah bayangan garis AB jika titik A(2, 5) dan B(6, 1) diperbesar dengan pusat O(0, 0) dan faktor skala 2 serta gambarkan

Jawab

Jadi bayangannya adalah

A’(4, 10) dan B’(12, 1)

05. Tentukanlah bayangan segitiga ABC jika titik A(–1, 4), B(4, 2) dan C(2, 5) didilatasi dengan pusat O(0, 0) dan faktor skala –2 serta gambarkan

(43)

A

B C

A' B'

C'

x

O

06. Jika titik P(9, –6) didilatasi dengan skala k dan pusat O(0, 0) sehingga diperoleh

bayangan P’(a, 4) maka tentukanlah nilai a

Jawab

Misalkan P’(a, 4) adalah bayangan titik P(9, –6) oleh dilatasi dengan pusat O(0, 0) dan skala k

Maka : x’ = kx y’ = ky

a = 9k……… (1) 4 = k(–6)

k = –2/3 ……… (2)

Dari (1) dan (2) diperoleh : a = 9(–2/3) a = –6

07. Titik P(2, -5) diperbesar dengan skala -3 dan pusat A(1, 3) sehingga didapat

bayangan P’. Tentukanlah koordinat P’

Jawab

Misalkan P’(x’, y’) adalah bayangan titik P(2, –5) oleh dilatasi dengan pusat A(1, 3) dan skala –3

dimana : x’ = k(x – m) + m y’ = k(y – n) + n

x’ = –3(2 – 1) + 1 y’ = –3(–5 – 3) + 3

x’ = –2 y’ = 27

(44)

BARISAN DAN DERET 3

B. Bunga Tunggal dan Bunga Majemuk

Salah satu apliksai barisan dan deret pada bidang ekonomi adalah pada perhitungan bunga pada simpanan uang di bank atau koperasi atau lembaga lain sejenisnya. Terdapat dua macam jenis bunga pada simpanan, yaitu :

(1) Bunga Tunggal (Barisan Aritmatika)

Yaitu metoda pemberian imbalan jasa bunga simpanan yang dihitung berdasarkan modal pokok pinjaman atau modal awal simpanan saja. Rumus bunga tunggal : Mn = Mo (1 + in)

Dimana : Mn = Nilai modal simpanan periode ke-n Mo = Nilai modal awal simpanan

i = Persentase bunga simpanan n = Periode pembungaan

(2) Bunga Majemuk (Barisan geometri)

Yaitu metoda pemberian imbalan jasa bunga simpanan yang dihitung berdasarkan besar modal atau simpanan pada periode bunga berjalan Rumus bunga majemukl : Mn = Mo (1i)n

Dimana : Mn = Nilai modal simpanan setelah periode ke-n Mo = Nilai modal awal simpanan

i = Persentase bunga simpanan n = Periode pembungaan

Untuk lebih jelasnya, ikutilah contoh soal berikut ini :

01. Pak Ahmad memerlukan tambahan modal untuk usahanya berdagang makanan,

sehingga ia meminjam uang dikoperasi “Maju Jaya” sebesar Rp. 4.000.000

dengan imbalan jasa berupa bunga sebesar 2% dari pokok pinjaman per bulan. Jika pak Ahmad akan melunasi pinjaman itu beserta bunganya setelah 6 bulan, maka tentukanlah total pengembalian pak Ahmad

Jawab

Diketahui : Mo = 40.000.000 i = 2% = 0,02 n = 6

maka Mn = Mo (1 + in)

6

M = 40.000.000(1 + 0,02(6))

6

M = 40.000.000(1,12)

6

M = 4.480.000

(45)

02. Tina menginvestasikan uangnya di koperasi “Bangun bersama” sebesar Rp. 2.000.000. Dengan sistem bunga tunggal sebesar 2% per-bulan, berapakah besar modal Tina setelah 1,5 tahun ?

Jawab

Diketahui : Mo = 2.000.000 i = 2% = 0,02

n = 1,5 tahun = 18 bulan maka Mn = Mo (1 + in)

18

M = 2.000.000(1 + 0,02(18))

18

M = 2.000.000(1 + 0,36)

18

M = 2.000.000(1,36)

18

M = 2.720.000

Jadi besar modal Tina setelah 1,5 tahun adalah Rp. 2.720.000

03. Arman menabung sejumlah uang disebuah bank. Jenis tabungan yang dipilih Arman adalah tabungan dengan sistem bunga tunggal sebesar 3% per

caturwulan. Jika setelah 3 tahun tabungan Arman menjadi Rp. 25.400.000 maka tentukanlah besar tabungan awal Arman di bank itu

Jawab

Diketahui : Mn = 25.400.000 i = 3% = 0,03 n =

bulan 4

tahun 3

=

bulan 4

bulan 36

= 9

25.400.000 = Mo (1 + 0,03(9)) 25.400.000 = Mo (1 + 0,27) 25.400.000 = Mo (1,27)

0 M =

1,27 25.400.000

0

M = 20.000.000

Jadi besar tabungan awal Arman di bank itu adalah Rp. 20.000.000

04. Pak Budi menabung sebesar Rp. 8.000.000 di suatu bank. Jika bank

memberlakukan sistem bunga tunggal sebesar 3% setiap triwulan, maka setelah berapa lamakah uang tabungan pak Budi menjadi Rp. 10.400.000

Jawab

(46)

10.400.000 = 8.000.000 (1 + 0,03n) 10.400.000 = 8.000.000 + 240.000n 2.400.000 = 240.000n

n =

240.000 2.400.000

n = 10

sehingga n = 10 triwulan = (10x3) bulan = 30 bulan = 2,5 tahun

05. Pak Mulyo adalah seorang pengusaha batik. Ia menyimpan uangnya sebesar Rp. 100.000.000 di sebuah bank. Bank tersebut memberikan bunga tabungan dengan sistem bunga majemuk sebesar 1,2% per bulan. Berapakah besarnya tabungan pak Mulyo setelah 5 bulan ?

Jawab

Diketahui : Mo = 100.000.000 i = 1,2% = 0,12 n = 5

Ditanya : Mn = …. ? Jawab

Mn = Mo (1i)n

10

M = 100.000.000(10,12)5

10

M = 100.000.000(1,12)5

10

M = 100.000.000.(1,762)

10

M = 176.200.000

02. La Ode Ahdan, seorang mahasiswa dari Sulawesi Tenggara, menginvestasikan uangnya sebesar Rp. 200.000.000 di salah satu bank. Andaikan pihak bank memberikan bunga majemuk sebesar 4% per-semester, berapa besar modal investasi itu setelah 2 tahun ?

Jawab

Diketahui : Mo = 200.000.000 i = 4% = 0,04

n = 2 tahun = 4 semester Ditanya : Mn = …. ?

Jawab

Mn = Mo (1i)n

4

M = 200.000.000(10,04)4

4

M = 200.000.000(1,04)4

4

M = 200.000.000.(1,169)

4

(47)

03. Santi menyimpan uangnya di sebuah bank sebesar Rp. 2.000.000. Setelah tiga tahun uang tabungan Santi menjadi Rp. 2.662.000. Jika bank tersebut

menerapkan sistem bunga majemuk , berapa persenkah per-tahun bunga bank tersebut ?

Jawab

Diketahui : Mo = 2.000.000 Mn = 2.662.000 n = 3

Ditanya : i = …. ?

Jawab

Mn = Mo (1i)n

2.662.000 = 2.000.000(1 i )3

2000000 2662000

= (1 i )3 1,331 = (1 i )3

3

1,1 = (1 i )3 Maka : 1 + i = 1,1

i = 1,1 – 1

(48)

BARISAN DAN DERET 3

C. Pertumbuhan dan Peluruhan.

(1) Pertumbuhan yaitu bertambahnya jumlah / nilai suatu objek yang mengikuti pola aritmatika atau geometri.

Contoh : (1) Perkembangbiakan bakteri (2) Pertumbuhan penduduk

(2) Peluruhan yaitu berkurangnya jumlah / nilai suatu objek yang mengikuti pola aritmatika atau geometri

Contoh : (1) Penurunan nilai jual mobil

(2) Penurunan jumlah populasi hewan

Rumus Pertumbuhan aritmatika :

Mn = Mo (1 + pn) atau Mn = Mo + bn

Dimana : Mn = Jumlah/Nilai suatu objek setelah n waktu Mo = Jumlah/Nilai suatu objek mula-mula p = Persentase pertumbuhan

b = Nilai beda pertumbuhan n = jangka waktu pertumbuhan Rumus Pertumbuhan geometri :

Mn = Mo (1p)n atau Mn = Mo .rn

Dimana : Mn = Jumlah/Nilai suatu objek setelah n waktu Mo = Jumlah/Nilai suatu objek mula-mula i = Persentase pertumbuhan

r = Ratio pertumbuhan (r > 1) n = jangka waktu pertumbuhan

01. Elsa mulai bekerja pada suatu perusahaan pada awal tahun 2005 dengan gaji permulaan sebesar Rp. 3.000.000. Jika dia mendapatkan kenaikan gaji secara berkala setiap tahunnya sebesar Rp. 200.000 maka berapakah gaji yang

diterima Elsa pada awal tahun 2011? Jawab

Diketahui : Mo = 3.000.000 b = 200.000 n = 6

(49)

Jawab

Mn = Mo + bn

Mn = 3.000.000 + 200.000(6) Mn = 3.000.000 + 1.200.000 Mn = Rp. 4.200.000

02. Suatu koloni bakteri akan membelah menjadi dua setiap lima menit. Jika pada permulaan trdapat 90 bakteri, maka tentukanlah jumlah bakteri setelah setengah jam ?

Jawab

Diketahui : Mo = 90 r = 2 n = 4 Ditanya : Mn = …. ? Jawab

Mn = Mo rn Mn = 90 x24 Mn = 90 (16) Mn = 1440 bakteri

03. Jumlah penduduk suatu kota bertambah menurut pola geometri sebesar 0,1% per bulan. Berarti jika jumlah penduduk kota itu semula 3 juta orang maka pada akhir bulan ke-3 jumlahnya telah menjadi sekitar … orang

Jawab

Diketahui : Mo = 3.000.000 i = 0,1% = 0,001 n = 3

Mn = Mo (1i)n

Mn = 3.000.000(10,001)3 Mn = 3.000.000(1,001)3 Mn = 3.000.000(1,003003) Mn = 3.009.009 orang

Rumus Peluruhan aritmatika :

Mn = Mo (1 – in) atau Mn = Mo – bn

(50)

Rumus Peluruhan geometri :

Mn = Mo (1p)n atau Mn = Mo .rn

Dimana : Mn = Jumlah/Nilai suatu objek setelah n waktu Mo = Jumlah/Nilai suatu objek mula-mula i = Persentase peluruhan

r = Ratio peluruhan (r < 1) n = jangka waktu peluruhan

04. Sebuah mobil dibeli dengan harga Rp.200.000.000. Jika setiap tahun harganya mengalami penyusutan 20% dari nilai tahun sebelumnya, maka tentukanlah harga mobil itu setelah dipakai selama 5 tahun

Jawab

Diketahui : Mo = 200.000.000 i = 20% = 0,2 n = 5

Mn = Mo (1i)n

Mn = 200.000.000(10,2)5 Mn = 200.000.000(0,8)5 Mn = 200.000.000(0,32768) Mn = 65.536.000

05. Suatu pabrik kendaraan bermotor roda dua mulai memproduksi pertama pada tahun 2010 sebanyak 20.000 unit kendaraan. Tiap tahun produksi pabrik tersebut turun 100 unit. Berapakah jumlah produksi pada tahun 2016? Jawab

Diketahui : Mo = 20.000 b = 100 n = 6 Ditanya : Mn = …. ? Jawab

Mn = Mo – bn

(51)

06. Suatu jenis hewan langka setiap tahun mengalami penurunan jumlah populasi sebanyak 1/3 dari jumlah populasi tahun sebelumnya. Jika pada tahun 2015 diperkirakan jumlah populasi hewan tersebut disuatu pulau sebanyak 720 ekor, maka berapakah perkiraan jumlah hewan itu pada tahun 2019 ?

Jawab

Diketahui : Mo = 360 r = 1/4 n = 4 Ditanya : Mn = …. ? Jawab

Mn = Mo rn

Mn = 360 x (1/3)4 Mn = 360 x (1/81) Mn = 14,44 = 14 ekor

07. Dengan pesatnya pembangunan pemukiman, maka daerah pesawahan semakin lama semakin sempit. Menurut data statistik, pada tahun 2003 total areal sawah di daerah itu sekitar 400 ha dan setiap tahun berkurang 5% dari total areal sawah semula . Berapakah diperkirakan areal sawah pada tahun 2015?

Jawab

Diketahui : Mo = 400 i = 5% = 0,05 n = 12

Mn = Mo (1 – in)

(52)

BARISAN DAN DERET 3

A. Barisan dan Deret Geometri Tak Hingga

Barisan geometri tak hingga adalah suatu barisan geometri yang mempunyai tak hingga banyaknya suku-suku. Barisan geometri tak hingga dikatakan konvergen jika suku ke tak hingga dari barisan itu menuju ke suatu nilai tertentu. Syaratnya jika nilai rasio terletak antara -1 dan 1.

Deret geometri tak hingga yang konvergen ini dapat ditentukan jumlahnya, dengan aturan sebagai berikut :

Jika -1< r < 1 maka jumlah sampai takhingga suku-sukunya (n = ) diperoleh :

Sn =

1 r

1) a(rn

 

1 r

1) a(r

 



 S

1 r

1) a(0

   S

1 r

a

    S

r 1

a S





 ………. (6)

Untuk lebih memantapkan pemahaman konsep di atas ikutilah contoh soal berikut ini: 01. Suatu deret geometri diketahui suku pertamanya 4. Jika jumlah tak hingga

suku-suku deret geometri itu adalah 12, tentukanlah rasionya ! Jawab

a = 4 

S = 12 Maka

r 1

a S



 

12 = r 1

4  12(1 – r) = 4 12 – 12r = 4

(53)

02. Suatu deret geometri tak hingga diketahui suku pertamanya 24 dan rasionya 1/3. Tentukanlah jumlah suku-suku genapnya !

Jawab

a + ar + ar2 + ar3 + ar4 + ar5 + ar6 + ar7 + ar8 + ar9 + ar10 + ... = S_ suku-suku genapnya adalah :

ar + ar3 + ar5 + ar7 + ar9 + ... = S_

sehingga : suku pertama = ar dan rasio = ar ar3

= r2

Jumlah sampai tak hingga suku-suku genap :

2 r 1

ar S

  

2

) 3 / 1 ( 1

24(1/3) S

  

) 9 / 1 ( 1

8 S

  

9 / 8

8 S_ 



S = 9

03. Sebuah bola dijatuhkan ke lantai dari ketinggian 12 m. Jika setiap kali jatuh, bola memantul kembali ke atas dengan ketinggian 2/3 dari ketinggian sebelumnya, maka hitunglah panjang lintasan bola dari mulai dijatuhkan hingga berhenti !

Jawab

Lintasan ke bawah : 12, 8, 16/3, 32/9 , 64/27 , ....

r 1

a S





 =

(2/3) 1

12

 = 1/3 12

= 36

Lintasan ke atas : 8, 16/3, 32/9, 64/27 , ....

r 1

a S





 =

(2/3) 1

8

 = 1/3 8

(54)

Jika dianalisa secara umum, rumus menentukan panjang lintasan benda yang

dijatuhkan dari ketinggian h dan setelah menyentuh lantai bola memantul sejauh r kali tinggi sebelumnya dapat ditentukan sebagai berikut :

Lintasan ke bawah :

r 1

h S

 



Lintasan ke bawah :

r 1

hr S

 



Sehingga total lintasan seluruhnya = r 1

h

 + 1 r hr

 =

r 1

hr h

 

= h

r 1

     

(55)

INDUKSI MATEMATIKA

A. Induksi Matematika Pada Pembuktian Rumus

Dalam kehidupan sehari hari, kita sering mengambil suatu kesimpulan berdasarkan data-data yang sudah ada.

Kesimpulan tersebut belum valid, karena masih bersifat dugaan (hipotesa)

Kesimpulan akan lebih valid jika hipotesa tersebut diuji berdasarkan fakta yang sudah ada. Cara seperti ini merupakan inti dari prinsip induksi

Langkah langkah pembuktian rumus dengan induksi matematika : (1) Langkah mengambil data (base case)

- Ambil beberapa data (n = 1, 2, 3, … )

- Tetapkan kesimpulan sementara /hipotesa (rumus dianggap benar untuk n= k) (2) Langkah menguji hipotesa (inductive step)

- Rumus diuji dengan pengambilan n = k + 1

Atau Rumus diuji dengan rumus lain yang sudah valid Untuk lebih jelasnya ikutilah contoh soal berikut ini

01. Dengan induksi matematika buktikanlah bahwa 72n11 habis dibagi 8 untuk n bilangan asli

Jawab

Untuk n = 1, diperoleh 72(1)1 1 = 344 habis dibagi 8 (terbukti)

Untuk n = 2, diperoleh 72(2)1 1 = 16.808 habis dibagi 8 (terbukti)

Untuk n = 3, diperoleh 72(3)1 1 = 823.544 habis dibagi 8 (terbukti)

Dari data diatas anggap bahwa rumus benar untuk n = k, artinya 1

72k1 habis dibagi 8 (hipotesa)

Akan dibuktikan bahwa rumus juga benar untuk n = k + 1, artinya 1

72(k1)1 juga habis dibagi 8 Tinjau : 72(k1)11 = 72k31

= 72k1.72 1

= 49

 

72k1 + 49 – 8 = 49



72k11



– 8

Karena 49



72k11



habis dibagi 8 (menurut hipotesa) maka 49



72k11



– 8 juga habis dibagi 8

(56)

02. Dengan induksi matematika buktikanlah bahwa 34n– 1 habis dibagi 80 untuk n bilangan asli

Jawab

Untuk n = 1, diperoleh 34(1)1 = 81 – 1 = 80 habis dibagi 80 (terbukti)

Dari data diatas anggap bahwa rumus benar untuk n = k, artinya 1

34k  habis dibagi 80 (hipotesa)

Akan dibuktikan bahwa rumus juga benar untuk n = k + 1, artinya 1

34(k1)  juga habis dibagi 80 Tinjau : 34(k1) 1 = 34k4 1

= 34k.34 1 = 81.34k.1

= 81.34k – 81 + 80 = 81(34k.1) + 80

Karena 34k 1 habis dibagi 80 (menurut hipotesa) maka 81(34k 1) juga habis dibagi 80

Sehingga 81(34k.1) + 80 habis diabgi 80

Jadi terbukti bahwa 34n – 1 habis dibagi 80 untuk n bilangan asli

03. Dengan induksi matematika buktikanlah bahwa 11n – 6 habis dibagi 5 untuk setiap n bilangan asli

Jawab

Untuk n = 1, diperoleh 111 – 6 = 11 – 6 = 5 habis dibagi 5 (terbukti)

Dari data diatas anggap bahwa rumus benar untuk n = k, artinya k

11 – 6 habis dibagi 5 untuk setiap k bilangan asli (hipotesa) Akan dibuktikan bahwa rumus juga benar untuk n = k + 1, artinya

1 k

11  – 6 juga habis dibagi 5 Tinjau : 11k1 – 6 = 11k11 – 6

= 1111k – 66 + 60 = 11(11k – 6) + 60

Karena 11k – 6 habis dibagi 5 (menurut hipotesa) maka 11(11k – 6) juga habis dibagi 5, sehingga 11( 11k – 6) + 60 habis diabgi 5

(57)

04. Buktikanlah bahwa 32n22n2 habis dibagi 5 untuk n bilangan asli Jawab

Ambil n = 1 maka 32(1)22(1)2 = 3224 = 9 + 16 = 25 (habis dibagi 5) Ambil n = 2 maka 32(2)22(2)2 = 3426 = 81 + 64 = 155 (habis dibagi 5) Ambil n = 3 maka 32(3)22(3)2 = 36 28 = 81 + 64 = 985 (habis dibagi 5) Disimpulkan sementara (hipotesis), bahwa

Untuk n = k maka 32k22k2 habis dibagi 5

Akan dibuktikan bahwa Untuk n = k + 1 maka 32(k1)22(k1)2 juga habis dibagi 5 Bukti : 32(k1)22(k1)2 = 32(k1)22(k1)2

= 32k2 + 22k4 = 32k.32 + 22k2.22 = 9

 

32k + 4

 

22k2

= 5

 

32k + 4

 

32k + 4

 

22k2 = 5

 

32k + 4



32k 22k2



Karena 4



32k 22k2



habis dibagi 5 (berdasarkan hipotesa) dan 5

 

32k juga habis dibagi 5, maka dapat disimpulkan 5

 

32k + 4



32k 22k2



habis dibagi 5

Jadi terbukti bahwa 32n22n2 habis dibagi 5 untuk n bilangan asli

05. Buktikanlah bahwa n3 + 2n habis dibagi 3 untuk n bilangan asli Jawab

Ambil n = 1 maka (1)3 + 2(1) = 1 + 2 = 3 (habis dibagi 3) Ambil n = 2 maka (2)3 + 2(2) = 8 + 4 = 12 (habis dibagi 3) Ambil n = 3 maka (3)3 + 2(3) = 27 + 6 = 33 (habis dibagi 3) Disimpulkan sementara (hipotesis), bahwa

Untuk n = k maka k3 + 2k habis dibagi 3 untuk k bilangan asli

Akan dibuktikan bahwa Untuk n = k + 1 maka (k1)3 + 2(k+1) juga habis dibagi 3 Bukti : (k1)3 + 2(k+1) = k3 + 3k2+ 3k + 1 + 2k + 2

= k3 + 2k + 3k2+ 3k + 3 = (k3 + 2k) + 3(k2+ k + 1)

Karena (k3 + 2k) habis dibagi 3 (berdasarkan hipotesa) dan 3(k2+ k + 1) juga habis dibagi 3, maka dapat disimpulkan (k3 + 2k) + 3(k2+ k + 1) habis dibagi 3

(58)

06. Buktikanlah bahwa untuk setiap bilangan bulat n, berlaku (2n + 1)2 selalu bernilai ganjil

Jawab

Ambil n = 1 maka (2(1) + 1)2 = (3)2 = 9 (bilangan ganjil) Ambil n = 2 maka (2(2) + 1)2 = (5)2 = 25 (bilangan ganjil) Ambil n = 3 maka (2(3) + 1)2 = (7)2 = 49 (bilangan ganjil) Disimpulkan sementara (hipotesis), bahwa

Untuk n = k maka (2k + 1)2 selalu bernilai ganjil untuk k bilangan asli Akan dibuktikan bahwa Untuk n = k + 1 maka (2[k+1] + 1)2 juga ganjil Bukti : (2[k+1] + 1)2 = (2k+2 + 1)2

= ([2k+1] + 2)2

= (2k + 1)2 + 4(2k + 1) + 4 = (2k + 1)2 + 8k + 4 + 4 = (2k + 1)2 + 8k + 8 = (2k + 1)2 + 8(k + 1)

Karena (2k + 1)2 adalah bilangan ganjil (berdasarkan hipotesa) dan 8(k + 1) adalah bilangan genap, maka (2k + 1)2 + 8(k + 1) selalu bernilai ganjil

Jadi terbukti bahwa untuk setiap bilangan bulat n, berlaku (2n + 1)2 selalu bernilai ganjil

07. Buktikanlah bahwa untuk setiap n bilangan asli, berlaku 2n ≤ 2n Jawab

Ambil n = 1 maka 2(1) ≤ 21 artinya 2 ≤ 2 (bernilai benar) Ambil n = 2 maka 2(2) ≤ 22 artinya 4 ≤ 4 (bernilai benar) Ambil n = 3 maka 2(3) ≤ 23 artinya 6 ≤ 8 (bernilai benar) Disimpulkan sementara (hipotesis), bahwa

Untuk n = k maka 2k ≤ 2k untuk setiap k bilangan asli

Akan dibuktikan bahwa Untuk n = k + 1 maka 2(k + 1) ≤ 2(k1) Bukti : 2(k + 1) ≤ 2(k1)

2k + 2 ≤ 2k.21 2k + 2 ≤ 2

 

2k 2k + 2 ≤ 2k + 2k

Karena 2k ≤ 2k (berdasarkan hipotesa) dan 2 ≤ 2k untuk setiap k bilangan asli, maka 2k + 2 ≤ 2k + 2k

(59)

08. Buktikanlah bahwa untuk n ≥ 4 dan n bilangan asli berlaku 3n > n3 Jawab

Ambil n = 4 maka 34 > 43 artinya 81 > 64 (bernilai benar) Ambil n = 5 maka 35 > 53 artinya 243 > 125 (bernilai benar) Ambil n = 6 maka 36 > 63 artinya 729 > 216 (bernilai benar) Disimpulkan sementara (hipotesis), bahwa

Untuk n = k maka 3k > k3 untuk setiap k bilangan asli dan k ≥ 4 Akan dibuktikan bahwa Untuk n = k + 1 maka 3k1 > (k+1)3 Bukti : 3k1 > (k+1)3

k

3 . 31_{> k}3 + 3k2 + 3k + 1 3

 

3k > k3 + 3k2 + 3k + 1

 

₃k ₊

 

₃k ₊

 

₃k

> k3 + 3k2 + 3k + 1

Karena untuk k ≥ 4 maka 3k > k3 (berdasarkan hipotesa)

k ≥ 4 maka k

3 > 3.k2

k ≥ 4 maka ₃k_{> 3k + 1}

Sehingga terbukti bahwa

 

3k +

 

3k +

 

3k _{> k}3 + 3k2 + 3k + 1 untuk setiap k bilangan asli, dan k ≥ 4.

Artinya untuk n ≥ 4 dan n bilangan asli berlaku 3n > n3

09. Buktikanlah bahwa xn – 1 habis dibagi (x – 1) untuk setiap n bilangan asli Jawab

Untuk n = 1, maka x1 – 1 = x – 1 habis dibagi (x – 1)

Untuk n = 2, maka x2 – 1 = (x – 1)(x + 1) habis dibagi (x – 1) Untuk n = 3, maka x3 – 1 = (x – 1)(x2 + x + 1) habis dibagi (x – 1) Dari data diatas anggap bahwa rumus benar untuk n = k, artinya

k

x – 1 habis dibagi (x – 1) untuk setiap n bilangan asli (hipotesa) Akan dibuktikan bahwa rumus juga benar untuk n = k + 1, artinya

1 k

x  – 1 habis dibagi (x – 1) Bukti : xk1 – 1 = xk_.x1– 1

= xxk – x + x – 1 = x(xk – 1) + (x – 1)

(60)

10. Dengan induksi matematika buktikanlah bahwa n(n + 1)(n + 2) habis dibagi 3 untuk n bilangan asli

Jawab

Untuk n = 1, diperoleh 1(1 + 1)(1 + 2) = 6 habis dibagi 3 (terbukti)

Dari data diatas anggap bahwa rumus benar untuk n = k, artinya k(k + 1)(k + 2) habis dibagi 3 (hipotesa)

Akan dibuktikan bahwa rumus juga benar untuk n = k + 1, artinya [k+1]( [k+1] + 1)( [k+1] + 2) juga habis dibagi 3

Tinjau : [k+1]( [k+1] + 1)( [k+1] + 2) = (k+1)(k+2)(k+3)

= (k+1)(k+2)k + (k+1)(k+2)3

Karena (k+1)(k+2)k habis dibagi 3 (menurut hipotesa) dan (k+1)(k+2)3 juga habis dibagi 3 maka 81((k+1)(k+2)k + (k+1)(k+2)3 habis dibagi 3

Sehingga [k+1]( [k+1] + 1)( [k+1] + 2) habis diabgi 3

(61)

INDUKSI MATEMATIKA

B. Penerapan Induksi Matematika pada Barisan dan deret

Langkah-langkah pembuktian :

(1) Tunjukkan bahwa rumus S(n) benar untuk n = 1, 2, 3 (2) Anggap bahwa rumus S(n) benar untuk n = k

(3) Akan dibuktikan bahwa rumus Sn benar untuk n = k + 1

Untuk lebih jelasnya ikutilah contoh soal berikut ini

01. Dengan induksi matematika buktikanlah rumus 3 + 7 + 11 + 15 + … + (4n – 1) = n(2n + 1)

Jawab

Untuk n = 1, diperoleh 3 = 1(2[1] + 1) = 3 (terbukti)

Untuk n = 2, diperoleh 3 + 7 = 2(2[2] + 1) = 10 (terbukti)

Untuk n = 3, diperoleh 3 + 7 + 11 = 3(2[3] + 1) = 21 (terbukti)

Dari data diatas anggap bahwa rumus benar untuk n = k, artinya

3 + 7 + 11 + 15 + … + (4k – 1) = k(2k + 1) adalah benar (hipotesa) Akan dibuktikan bahwa rumus juga benar untuk n = k + 1, artinya

3 + 7 + 11 + 15 + … + (4k – 1) + (4[k+1] – 1) = [k+1](2[k+1] + 1) k(2k + 1) + (4[k+1] – 1) = [k+1](2[k+1] + 1)

2k2 + k + 4k + 4 – 1 = [k+1](2[k+1] + 1) 2k2 + 5k + 3 = [k+1](2[k+1] + 1) (k + 1)(2k + 3) = [k+1](2[k+1] + 1)

(k + 1)(2k + 2 + 1) = [k+1](2[k+1] + 1)

(k + 1)(2[k+1] + 1) = [k+1](2[k+1] + 1) (terbukti) Jadi terbukti rumus 3 + 7 + 11 + 15 + … + (4n – 1) = n(2n + 1)

02. Dengan induksi matematika buktikanlah rumus 2 + 5 + 8 + 11 + … + (3n – 1) =

2 1

n(3n + 1)

Jawab

Untuk n = 1, diperoleh 2 = 2 1

(1)(3[1] + 1) = 2 (terbukti)

Untuk n = 2, diperoleh 2 + 5 = 2 1

(62)

2 + 5 + 8 + 11 + … + (3k – 1) = 2 1

k(3k + 1) adalah benar (hipotesa) Akan dibuktikan bahwa rumus juga benar untuk n = k + 1, artinya

2 + 5 + 8 + 11 + … + (3k – 1) + (3[k+1] – 1) = 2 1

[k+1](3[k+1] + 1)

2 1

k(3k + 1) + (3[k+1] – 1) = 2 1

[k+1](3[k+1] + 1)

2 1

(3k2 + k) + (3k + 3 – 1) = 2 1

[k+1](3[k+1] + 1)

2 1

(3k2 + k) + 2 2

(3k + 2) = 2 1

[k+1](3[k+1] + 1)

2 1

[ (3k2 + k) + (6k + 4) ] = 2 1

[k+1](3[k+1] + 1)

2 1

(3k2 + 7k + 4) = 2 1

[k+1](3[k+1] + 1)

2 1

(3k + 4)(k + 1) = 2 1

[k+1](3[k+1] + 1)

2 1

(k + 1)(3k + 3 + 1) = 2 1

[k+1](3[k+1] + 1)

2 1

(k + 1)(3[k + 1] + 1) = 2 1

[k+1](3[k+1] + 1) (terbukti)

Jadi terbukti rumus 2 + 5 + 8 + 11 + … + (3n – 1) = 2 1

n(3n + 1)

03. Dengan induksi matematika buktikanlah bahwa 3 + 5 + 7 + 9 +… + (2n + 1) = n2 + 2n untuk n bilangan asli

Jawab

Untuk n = 1, diperoleh 3 = 1(2[1] + 1) = 3 (terbukti)

Untuk n = 2, diperoleh 3 + 7 = 2(2[2] + 1) = 10 (terbukti)

Untuk n = 3, diperoleh 3 + 7 + 11 = 3(2[3] + 1) = 21 (terbukti)

3 + 7 + 11 + 15 + … + (4k – 1) = k(2k + 1) adalah benar (hipotesa) Akan dibuktikan bahwa rumus juga benar untuk n = k + 1, artinya

3 + 7 + 11 + 15 + … + (4k – 1) + (4[k+1] – 1) = [k+1](2[k+1] + 1) k(2k + 1) + (4[k+1] – 1) = [k+1](2[k+1] + 1)

(63)

(k + 1)(2k + 2 + 1) = [k+1](2[k+1] + 1)

(k + 1)(2[k+1] + 1) = [k+1](2[k+1] + 1) (terbukti) Jadi terbukti rumus 3 + 7 + 11 + 15 + … + (4n – 1) = n(2n + 1)

04. Dengan induksi matematika buktikanlah bahwa :

8 + 16 + 32 + 64 +… + 2n2 = 2n3 – 8 untuk n bilangan asli Jawab

Untuk n = 1, diperoleh 8 = 213 – 8 = 16 – 8 = 8 (terbukti) Untuk n = 2, diperoleh 8 + 16 = 223 – 8 = 32 – 8 = 24 (terbukti) Untuk n = 3, diperoleh 8 + 16 + 32 = 233 – 8 = 64 – 8 = 64 (terbukti) Dari data diatas anggap bahwa rumus benar untuk n = k, artinya 8 + 16 + 32 + 64 +… + 2k2 = 2k3 – 8 adalah benar (hipotesa) Akan dibuktikan bahwa rumus juga benar untuk n = k + 1, artinya 8 + 16 + 32 + 64 +… + 2k2 + 2(k1)2 = 2(k1)3 – 8

Bukti :

8 + 16 + 32 + 64 +… + 2k2 + 2(k1)2 = 2(k1)3 – 8 2k3 – 8 + 2(k1)2 = 2(k1)3 – 8 2k3 – 8 + 2k3 = 2(k1)3 – 8

2.2k3 –_{8 =}2(k1)3 _– 8

21.2k3 – 8 = 2(k1)3 – 8

2(k1)3 – 8 = 2(k1)3 – 8 terbukti Jadi : 8 + 16 + 32 + 64 +… + ₂n2

= 2n3 – 8 untuk n bilangan asli

6 + 18 + 54 + 162 +… + _2.₃n

= 3n1 _– 3 untuk n bilangan asli Jawab

Untuk n = 1, diperoleh 6 = 311 _–_{3 = 9}– 3 = 6 (terbukti)

(64)

6 + 18 + 54 + 162 +… + _2.₃k

= 3k1 – 3 adalah benar (hipotesa) Akan dibuktikan bahwa rumus juga benar untuk n = k + 1, artinya

6 + 18 + 54 + 162 +… + _2.₃k

+ 2.3k1 = 3(k1)1 – 3 Bukti :

6 + 18 + 54 + 162 +… + _2.₃k

+ 2.3k1 = 3(k1)1 – 3 3k1 _– 3 + 2.3k1 = 3(k1)1 _– 3 3.3k1 – 3 = 3(k1)1 – 3 31.3k1 – 3 = 3(k1)1 – 3

3(k1)1 _– 3 = 3(k1)1 _– 3 terbukti

Jadi : _{6 + 18 + 54 + 162 +… +}2.3n₌3n1 _–_{3 untuk n bilangan asli}

1

2 + 22 + 23 + 24 + ... + 2n = 2(2n– 1) untuk n bilangan asli Jawab

n = 1 maka 21 = 2(21– 1) 2 = 2 (benar)

n = 2 maka 21 + 22 = 2(22– 1)

2 + 4 = 2(4 – 1)(benar) n = 3 maka 21 + 22 + 23 = 2(23– 1)

2 + 4 + 8 = 2(8 – 1) (benar)

Hipotesa : n = k maka 21 + 22 + 23 + 24 + ... + 2k = 2(2k– 1) (benar) Uji hipotesa

n = k + 1 maka 21 + 22 + 23 + 24 + ... + 2k + 2k1 = 2(2k1– 1) 2(2k– 1) + 2k1 = 2(2k1– 1) 2.2k– 2 + 2k1 = 2(2k1– 1) 2k1– 2 + 2k1 = 2(2k1– 1) 2.2k1 + 2k1 = 2(2k1– 1)

(65)

2

5 ₊53₊54₊55 _{+… +}5n1₌ ( 25) 4

1 ₅n2 _

untuk n bilangan asli Jawab

Untuk n = 1, diperoleh 52 = ( 25) 4

1 ₅12 _ _{= 25 (terbukti)}

Untuk n = 2, diperoleh 52₊53 = ( 25) 4

1 ₅22 _ _{= 150 (terbukti)}

Untuk n = 3, diperoleh 52₊53₊54 = ( 25) 4

1 ₅32 _ _{= 775 (terbukti)}

2

5 ₊53₊54₊55 _{+… +}5k1₌ ( 25) 4

1 ₅k2 _

adalah benar (hipotesa) Akan dibuktikan bahwa rumus juga benar untuk n = k + 1, artinya

2

5 + 53 + 54 + 55 +… + 5k1 + 5(k1)1 = ( 25) 4

1 ₅(k1)2 _

Bukti :

2

5 + 53 + 54 + 55 _{+… +}5k1 + 5(k1)1 = ( 25) 4

1 ₅(k1)2 _

( 25) 4

1 ₅k2 _

+ 5k2 = ( 25) 4

1 (k 1) 2

5   

( 25) 4

1 ₅k2 _

+ (4. ) 4

1 ₅k2

= ( 25)

4

1 ₅(k1)2 _

( 25 4. ) 4

1 ₅k2 _ _ ₅k2

= ( 25)

4

1 ₅(k1)2 _

(5. 25) 4

1 ₅k2 _

= ( 25)

4

1 ₅(k1)2 _

( 25) 4

1 ₅(k1)2 _

= ( 25)

4

1 ₅(k1)2 _ _terbukti

Jadi : 52₊53₊54₊55 _{+… +}5n1₌ ( 25) 4

1 ₅n2 _

untuk n bilangan asli

1x2 1

+ 2x3

1 +

3x4 1

+ 4x5

1

+ ... +

1) n(n

1

 = 1 – n 1 1

 untuk n bilangan asli Jawab

n = 1 maka 1x2

1

= 1 – 1 1

1 

2 1

= 1 – 2 1

(66)