MODEL DINAMIS : AUTOREGRESSIVE DAN DISTRIBUSI LAG

MODEL DINAMIS : AUTOREGRESSIVE DAN

DISTRIBUSI LAG

SKRIPSI

Diajukan kepada Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Yogyakarta

untuk memenuhi sebagian persyaratan guna memperoleh gelar Sarjana Sains

Oleh:

Natalia Jatiningrum 04305144021

PROGRAM STUDI MATEMATIKA JURUSAN PENDIDIKAN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS NEGERI YOGYAKARTA

ii

PERSETUJUAN

SKRIPSI

MODEL DINAMIS : AUTOREGRESSIVE DAN DISTRIBUSI LAG

Telah disetujui dan disahkan pada tanggal 15 Agustus 2008

Untuk dipertahankan di depan Tim Penguji Skripsi Fakultas Matematika dan Ilmu Pengetahuan Alam

Universitas Negeri Yogyakarta

Pembimbing I

Endang Listyani, M.S NIP. 131569343

Pembimbing II

Elly Arliani, M.Si NIP. 131993532

iii

PERNYATAAN

Yang bertanda tangan di bawah ini, saya :

Nama : Natalia Jatiningrum

NIM : 04305144021

Jurusan : Pendidikan Matematika Prodi : Matematika

Fakultas : Matematika dan Ilmu Pengetahuan Alam

Judul Skripsi : Model Dinamis : Autoregressive dan Distribusi Lag

Menyatakan bahwa skripsi ini adalah benar-benar hasil pekerjaan saya sendiri, dan sepanjang pengetahuan saya tidak berisi materi yang dipublikasikan atau ditulis orang lain, kecuali pada bagian-bagian tertentu yang saya ambil sebagai bahan acuan. Demikianlah pernyataan ini dibuat dengan sebenar-benarnya, apabila pernyataan ini terdapat kekeliruan sepenuhnya menjadi tanggung jawab saya.

Yogyakarta, 13 Juni 2008 Yang menyatakan,

Natalia Jatiningrum NIM.04305144021

iv

PENGESAHAN SKRIPSI

MODEL DINAMIS : AUTOREGRESSIVE DAN DISTRIBUSI LAG

Disusun oleh: Natalia Jatiningrum

NIM. 04305144021

Telah dipertahankan di depan Tim Penguji Skripsi Jurusan Pendidikan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam

Universitas Negeri Yogyakarta pada tanggal 27 Agustus 2008

dan dinyatakan telah memenuhi syarat guna memperoleh gelar Sarjana Sains

Susunan Tim Penguji

Nama Lengkap Tanda Tangan Tanggal

Ketua Penguji : Endang Listyani, M.S

NIP. 131569343 ... ... Sekretaris : Elly Arliani, M.Si

NIP. 131993532 ... ... Penguji

Utama

: Mathilda Susanti, M.Si

NIP. 131808672 ... ... Penguji Pendamping : Kismiantini, M.Si NIP. 132296139 ... ... Yogyakarta, September 2008

Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Yogyakarta

Dekan

Dr. Ariswan NIP. 131791367

v MOTTO

There is no rose without a thorn, there is no royal road to success (Tiada mawar yang tak berduri, tiada jalan enak menuju keberhasilan)

Strike the iron while it is hot

(Tempalah besi selagi panas. Berbuatlah ketika ada kesempatan. Pergunakanlah masa muda sebelum tua)

Education is an ornament in prosperity and a refuge in adversity (Pendidikan adalah perhiasan di waktu senang

dan tempat berlindung di waktu susah) Don’t put off till tomorrow what you can do to day

(Janganlah menunda pekerjaan yang dapat dilakukan disaat sekarang) Mawar takkan sempurna tanpa duri

Mentari takkan sempurna tanpa cahaya Kebahagiaan takkan sempurna tanpa kesengsaraan

Manusiapun takkan sempurna tanpa cinta demikian juga dengan

vi

PERSEMBAHAN

Skripsi ini kupersembahkan untuk : Ayah & Ibu

Kedua adikku Yayan & Bondan

Terima kasih telah memberikan kasih sayang, pengorbanan, perhatian, motivasi dan doa.

Teman-Teman Math’04 :

Anggi, Nely, Ria, Nopek, Mami, , Ana, Henik, Soe_See, Do_Why, Nia, Nufus,Irma, Hendro, Sofyan, Sigit, Fajar Yusfi, Johan

Terima kasih buat kebersamaan kita baik dalam suka maupun duka. Sahabat-sahabatkoe:

Pikachu, Desty, Martina, Sinta, Mbak Lina, Mbak Nia, Juve, Ris, ,Mas Andie, Mas Andri, Mas Kris dll Terima kasih telah memberikan makna indahnya persahabatan.

Temen-temen KKN Magelang 3 : Bona, Rong-Rong, Miss. Pusing, Oet-Oet, Huda, Wahyu, Andri, and Sinta. Terima kasih buat kebersamaan kita selama ini.

Kalian adalah kelurga baruku.

Teman-teman seperjuangan, senasib dan sepenanggungan : Mbak Eko, Mbak Yuni, Mbak Atun,

Mbak Audi, Mbak Isti, Mas Farid dll. Temen-temen Kos Samirono CT VI No. 151

Semua guru dan dosen

Engkau adalah pelita dalam kegelapan dan laksana embun penyejuk dalam kehausan.. Seseorang yang selalu ada dalam suka dan duka

Tiada kata yang pantas terucap selain terima kasih atas motivasi dan semua bantuannya.

vii

MODEL DINAMIS : AUTOREGRESSIVE DAN DISTRIBUSI LAG Oleh :

Natalia Jatiningrum NIM. 04305144021

ABSTRAK

Model Dinamis : Autoregresive dan Distribusi Lag merupakan model regresi linear yang memperhitungkan pengaruh waktu. Tujuan penulisan skripsi ini adalah menentukan persamaan dinamis autoregressive dugaan dan persamaan dinamis distribusi lag dugaan.

Metode yang digunakan dalam menentukan persamaan dinamis distribusi

lag dugaan adalah metode Koyck dan metode Almon. Metode Koyck digunakan jika panjang beda kala (lag) tidak diketahui sedangkan metode Almon digunakan jika panjang beda kala (lag) diketahui. Bedakala adalah waktu yang diperlukan bagi variabel bebas X dalam mempengaruhi variabel tak bebas Y. Langkah pertama dalam metode Almon adalah transformasi Almon hingga didapat persamaan Yˆ_t =αˆ +αˆ₀ Z_0t +αˆ₁Z_1t +αˆ₂ Z_2t dengan

∑

= − = k i t t X Z 0 1 0 ,

∑

= − = k i t t iX Z 0 1 1 ,

∑

= − = k i t t i X Z 0 1 2

2 . Nilai-nilai αˆ,αˆ0,αˆ1,αˆ2 untuk mencari nilai

k β β β β α_ˆ, ˆ _, ˆ _, ˆ _{, ,} ˆ 2 1

0 K dalam persamaan dinamis distribusi lag dugaan yaitu dengan

rumus βˆ_k =αˆ₀ +kαˆ₁+k2αˆ₂. Y. Langkah pertama dalam metode Koyck adalah transformasi Koyck hingga didapat persamaan Yˆ_t =αˆ

( )

1−Cˆ +βˆ₀ X_t +C) Y_t−1. Nilai αˆ,βˆ₀,C) untuk mencari nilai αˆ,βˆ₀,βˆ₁,βˆ₂,_K,βˆ_k dalam persamaan dinamis distribusi lag dugaan yaitu dengan rumus βˆ_k =βˆ₀Cˆk. Metode Koyck juga dapat digunakan untuk menentukan persamaan dinamis autoregressive dugaan, tetapi dilakukan uji lanjutan dengan uji statistik h Durbin-Watson. Uji ini perlu dilakukan sebab dalam persamaan dinamis autoregressive terdapat Y_t−1 sebagai salah satu variabel bebas sehingga kemungkinan menyebabkan autokorelasi. Penggunaan program Eviews 5 juga diperlukan untuk mempermudah perhitungan.

Hasil akhir persamaan dinamis distribusi lag dugaan yang diperoleh dengan metode Koyck adalah Y∧_t =αˆ +βˆ₀X_t+βˆ₁X_t−1+βˆ₂X_t−2 +... sedangkan persamaan dinamis distribusi lag dugaan yang diperoleh dengan menggunakan metode Almon adalah Yt Xt Xt− Xt− kXt−k

∧ + + + + =α_ˆ βˆ βˆ βˆ _...βˆ 2 2 1 1 0 dengan t

menyatakan waktu sekarang, dan t−1,t−2,_K menyatakan periode waktu sebelumnya, k menyatakan panjang beda kala (lag). Hasil akhir persamaan dinamis autoregressive dugaan adalah ˆ ˆ0 ˆ1 −1

∧ + + = t t t X Y Y α β β .

viii

KATA PENGANTAR

Puji syukur penulis panjatkan ke hadirat Tuhan Yang Maha Esa yang telah memberikan berkat dan karunia-Nya sehingga penyusunan skripsi yang berjudul “Model Dinamis : Autoregressive dan Distribusi Lag ” dapat terselesaikan.

Skripsi ini disusun untuk memenuhi salah satu persyaratan guna memperoleh gelar Sarjana Sains Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Yogyakarta.

Penulis menyadari sepenuhnya bahwa selama penyusunan skripsi ini telah banyak menerima bantuan dari berbagai pihak. Oleh karena itu, pada kesempatan ini penulis bermaksud menyampaikan ucapan terima kasih kepada:

1. Bapak Dr. Ariswan selaku Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Yogyakarta yang telah memberikan izin dan kesempatan kepada penulis dalam menyelesaikan studi.

2. Bapak Dr. Hartono selaku Ketua Jurusan Pendidikan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Yogyakarta sekaligus Penasehat Akademik yang telah memberikan kemudahan dan kelancaran pelayanan dalam urusan akademik. selama penulisan skripsi.

3. Ibu Atmini Dhoruri, M.S. selaku Ketua Program Studi Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Yogyakarta yang telah memberikan kemudahan dan kelancaran pelayanan dalam urusan akademik.

4. Ibu Endang Listyani, M.S selaku Dosen Pembimbing Utama yang berkenan memberikan waktu bimbingan serta dengan penuh kesabaran memberi pengarahan dalam menyusun skripsi.

5. Ibu Elly Arliani, M.Si selaku Dosen Pembimbing Pendamping yang berkenan memberikan waktu bimbingan serta dengan penuh kesabaran memberi pengarahan dalam menyusun skripsi.

6. Ibu Mathilda Susanti, M.Si selaku Dosen Penguji Utama yang telah memberikan saran dan kritik untuk perbaikan skripsi ini.

ix

7. Ibu Kismiantini, M.Si selaku Dosen Penguji Pendamping yang telah memberikan saran dan kritik untuk perbaikan skripsi ini.

8. Seluruh dosen Jurusan Pendidikan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Yogyakarta yang telah mengajarkan ilmu selama kuliah.

9. Pihak-pihak yang telah membantu penyusunan skripsi yang tidak dapat disebutkan satu persatu.

Penulis menyadari sepenuhnya bahwa skripsi ini masih jauh dari kesempurnaan. Seperti peribahasa mengatakan “Akal Tak Sekali Datang Runding Tak Sekali Tiba” yang berarti bahwa segala sesuatu tidak akan datang dengan kesempurnaan, harus berangsur-angsur. Namun, penulis berharap semoga skripsi ini dapat bermanfaat.

Yogyakarta, 13 Juni 2008 Penulis

x

DAFTAR ISI

Halaman

HALAMAN JUDUL ... i

HALAMAN PERSETUJUAN ... ii

HALAMAN PERNYATAAN ... iii

HALAMAN PENGESAHAN... iv

MOTTO ... v

PERSEMBAHAN ... vi

ABSTRAK ... vii

KATA PENGANTAR ... viii

DAFTAR ISI ... x

DAFTAR SIMBOL ... xiii

DAFTAR GAMBAR ... xiv

DAFTAR TABEL ... xv

DAFTAR LAMPIRAN... xvi

BAB I PENDAHULUAN A. Latar Belakang ... 1

B. Rumusan Masalah ... 5

C. Tujuan Penulisan... 6

xi BAB II LANDASAN TEORI

A. Data ... 7

1. Data Berkala (Time Series) ... 7

2. Data Seleksi Silang (Cross Section) ... 7

B. Variansi ... 7 C. Matriks ... 8 1. Definisi Matriks ... 8 2. Transpose Matriks... 8 3. Invers Matriks ... 9 4. Operasi Matriks... 9 D. Regresi Linier... 11

1. Regresi Linear Sederhana ... 11

2. Regresi Linear Berganda... 12

E. Korelasi ... 13

1. Koefisien Determinasi... 13

2. Koefisien Korelasi... 14

F. Metode Kuadrat Terkecil (Least Square Method) ... 15

G. Kesalahan Standar Estimasi ... 21

H. Asumsi Klasik ... 22

xii BAB III PEMBAHASAN

A. Metode-Metode dalam Menentukan Persamaan Dinamis Distribusi

Lag Dugaan ... 26

1. Metode Koyck... 26

2. Metode Almon ... 29

B. Metode-Metode dalam Menentukan Persamaan Dinamis Autoregressive Dugaan ... 33 C. Aplikasi ... 39 BAB IV PENUTUP A. Kesimpulan ... 56 B. Saran ... 60 DAFTAR PUSTAKA ... 60 LAMPIRAN ... 63

xiii

DAFTAR SIMBOL

2

σ : variansi populasi

µ : rata-rata hitung untuk populasi

N : banyaknya data pengamatan

Y : variabel tak bebas

X : variabel bebas

α : intersep

β : koefisien regresi / slope

ε : kesalahan pengganggu n : ukuran populasi 2 r : koefisien determinasi r : koefisen korelasi i

e : taksiran dari faktor gangguan ε_i X' : transpose dari matriks X

βˆ : penaksir koefisien regresi

e

S : kesalahan standar estimasi (standar error of estimate)

C : rata-rata tingkat penurunan dari distribusi lag

C −

xiv

DAFTAR GAMBAR

Gambar 2.1 Metode Kuadrat Terkecil ... 15

Gambar 3.1 Penurunan Koefisien β dalam model Koyck ... 27

Gambar 3.2 Perubahan Koefisien β ... 29

Gambar 3.3 Perubahan Koefisien β ... 29

Gambar 3.4 Perubahan Koefisien β ... 29

Gambar 3.5 Perubahan Koefisien β ... 29

xv

DAFTAR TABEL

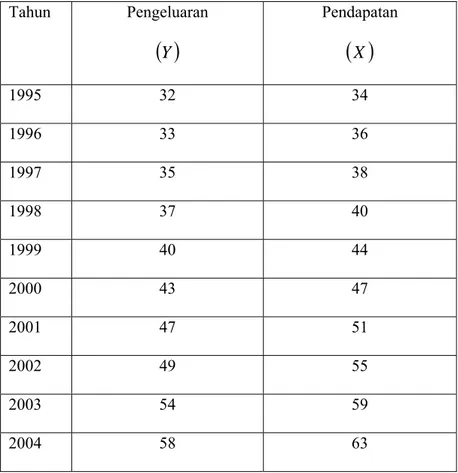
Tabel 3.1 Pengeluaran dan Pendapatan... 41

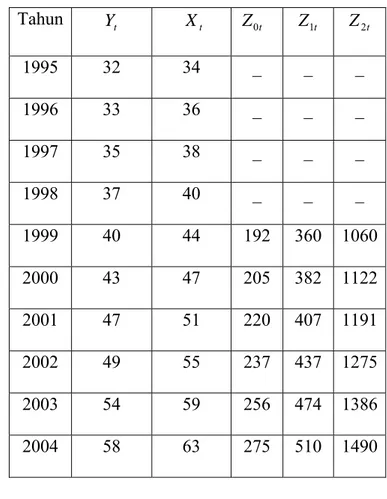
Tabel 3.2 Nilai Z Data Pengeluaran dan Pendapatan... 43

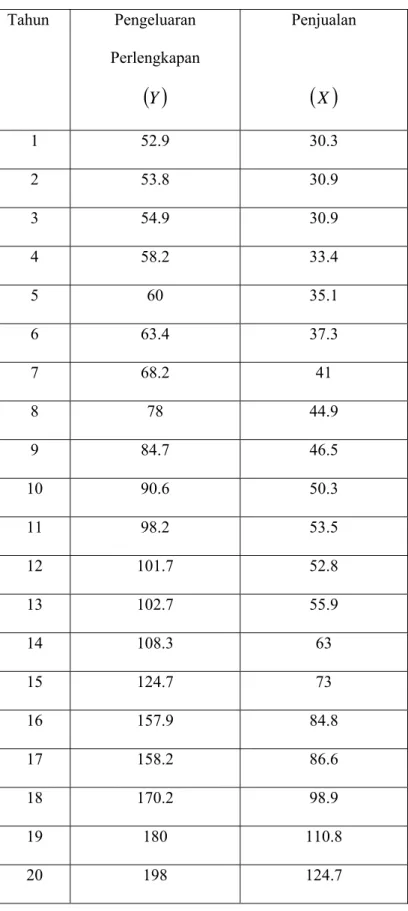
Tabel 3.3 Pembelian Perlengkapan dan Penjualan... 48

Tabel 3.4 Pembelian Perlengkapan dan Penjualan Setelah

Dimasukkan Variabel Lag... 49

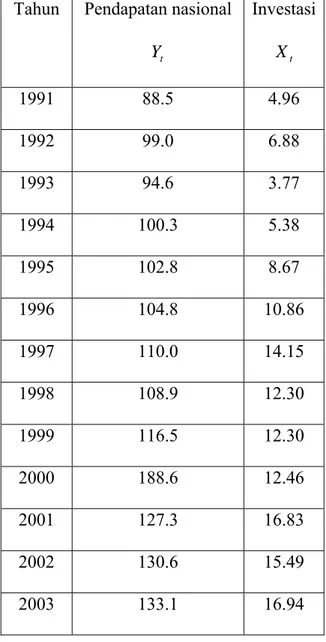
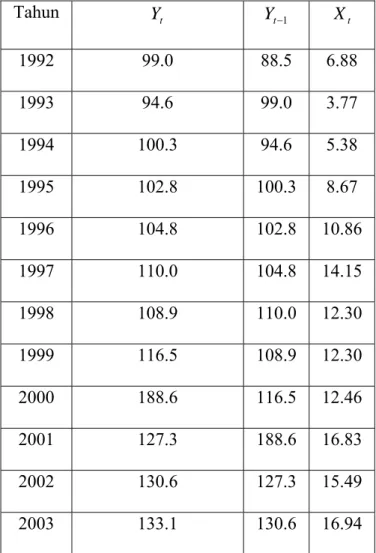
Tabel 3.5 Pendapatan Nasional dan Investasi ... 52

Tabel 3.6 Pendapatan Nasional dan Investasi ... 53

xvi

DAFTAR LAMPIRAN

Lampiran 1 Output Eviews metode Koyck ... 63

Lampiran 2 Output Eviews metode Almon ... 64

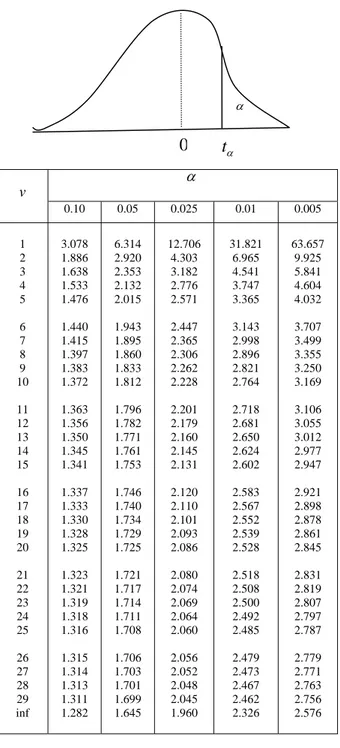
Lampiran 3 Tabel Nilai Kritik Sebaran t ... 65

1 BAB I PENDAHULUAN

A. Latar Belakang

Kehidupan manusia sehari-hari tidak pernah lepas dari pengamatan. Ketika

seseorang melihat atau mengamati suatu kejadian dalam suatu waktu sering

timbul pertanyaan apa yang akan terjadi pada waktu yang akan datang dan

bagaimana kejadian pada waktu sebelumnya. Begitu pula saat melihat suatu

kejadian di suatu tempat, muncul pertanyaan apa yang terjadi di daerah sekitarnya.

Pertanyaan menyangkut waktu tersebut mendasari munculnya suatu kajian runtun

waktu (time series analysis).

Runtun waktu merupakan serangkaian pengamatan terhadap suatu

peristiwa, kejadian, yang diambil dari waktu ke waktu, serta dicatat secara teliti

berdasarkan urutan waktu, kemudian disusun sebagai data statistik (Sutrisno,

1998: 353). Analisis runtun waktu merupakan analisis sekumpulan data dalam

suatu periode waktu yang lampau yang berguna untuk mengetahui atau

meramalkan kondisi masa mendatang. Hal ini didasarkan bahwa perilaku manusia

banyak dipengaruhi kondisi atau waktu sebelumnya sehingga dalam hal ini faktor

waktu sangat penting peranannya (Gujarati, 1995: 5).

Penganalisaan runtun waktu dahulu menjadi pertentangan antara dua

kelompok ahli yaitu para ahli ekonometrika dan para ahli runtun waktu. Para ahli

ekonometrika menganalisis data runtun waktu dengan metode yang berbeda

2

menformulasikan model regresi klasik untuk menganalisis perilaku data runtun

waktu, menganalisis tentang masalah simultanitas, dan kesalahan autokorelasi.

Sebaliknya, ahli runtun waktu membuat model perilaku runtun waktu dengan

mekanisme sendiri serta tidak begitu memperhatikan peranan variabel bebas X

dan variabel tak bebas Y. Perbedaan pendapat ini membuat para ahli

ekonometrika mengkaji ulang pendekatannya terutama dalam menganalisis runtun

waktu.

Ekonometrika merupakan suatu ilmu yang menganalisis fenomena

ekonomi dengan menggunakan teori ekonomi, matematika, dan statistika, yang

berarti teori ekonomi tersebut dirumuskan melalui hubungan matematika

kemudian diterapkan pada suatu data untuk dianalisis menggunakan metode

statistika (Awat, 1995: 3). Hal yang banyak mendapat perhatian dalam

ekonometrika adalah kesalahan pengganggu terutama dalam membuat perkiraan

atau estimasi. Model ekonometrika yang digunakan untuk mengukur hubungan

antara variabel-variabel dapat dinyatakan dalam bentuk model regresi linear.

Model regresi linear merupakan salah satu model ekonometrika yang hubungan

antar variabelnya satu arah, yang berarti variabel tak bebas ditentukan oleh

variabel bebas (Sumodiningrat, 1995: 135). Hubungan antara satu variabel bebas

X dengan variabel tak bebas Y dapat dimodelkan dengan Y =α+β X +ε atau beberapa variabel bebas X terhadap variabel tak bebas Y dapat dimodelkan

dengan : i in n i i i X X X X Y=β0+β1 1+β2 2+β3 3+_K+β +ε .

3

Pada skripsi ini akan dibahas tentang model regresi linear yang

memperhitungkan pengaruh waktu, karena kebanyakan dari model regresi linear

kurang memperhatikan waktu. Data yang digunakan adalah data runtun waktu

(time series). Model regresi dengan menggunakan data runtun waktu tidak hanya

menggunakan pengaruh perubahan variabel bebas terhadap variabel tak bebas

dalam kurun waktu yang sama dan selama periode pengamatan yang sama, tetapi

juga menggunakan periode waktu sebelumnya. Waktu yang diperlukan bagi

variabel bebas X dalam mempengaruhi variabel tak bebas Y disebut bedakala

atau lag (Supranto, 1995: 188).

Model regresi yang memuat variabel tak bebas yang dipengaruhi oleh

variabel bebas pada waktu t, serta dipengaruhi juga oleh variabel bebas pada

waktu t−1, t−2 dan seterusnya disebut model dinamis distribusi lag, sebab pengaruh dari suatu atau beberapa variabel bebas X terhadap variabel tak bebas

Y menyebar (spread or distributed) ke beberapa periode waktu dengan

t t

t t

t X X X

Y =α +β₀ +β_{1 −1}+β_{2 −2} +_K+ε . Model regresi yang memuat variabel tak bebas yang dipengaruhi oleh variabel bebas pada waktu t, serta dipengaruhi

juga oleh variabel tak bebas itu sendiri pada waktu t−1 disebut model

autoregressive dengan Y_t =α +β₀ X_t +β₁Y_t−1 +ε_t (Awat, 1995: 410).

Metode-metode yang digunakan dalam menentukan persamaan distribusi

lag dugaan antara lain metode Koyck, metode Almon, metode Jorgenson dan

metode Pascal. Pada skripsi ini hanya akan dibahas metode Koyck dan metode

Almon sebab kedua metode ini lebih mudah diterapkan dalam membuat

4

menentukan persamaan dinamis distribusi lag dugaan yang panjang beda kala

(lag) diketahui. Langkah pertama yang dilakukan adalah membuat persamaan

Almon yaitu : t t t t Z Z Z Yˆ =αˆ +αˆ_{0 0} +αˆ_{1 1} +αˆ_{2 2} dengan

∑

= − = k i t t X Z 0 1 0 ,

∑

= − = k i t t iX Z 0 1 1 ,

∑

= − = k i t t i X Z 0 1 2 2

Selanjutnya, nilai-nilai αˆ,αˆ₀ ,αˆ₁,αˆ₂ pada Yˆ_t =αˆ +αˆ₀ Z_0t +αˆ₁Z_1t +αˆ₂ Z_2t digunakan untuk mencari αˆ,βˆ₀,βˆ₁,βˆ₂,_K,βˆ_k dalam persamaan dinamis distribusi

lag dugaan dengan panjang beda kala (lag) sebesar k. Metode Koyck digunakan

untuk menentukan persamaan dinamis distribusi lag dugaan yang panjang beda

kala (lag) tidak diketahui. Langkah pertama yang dilakukan adalah membuat

persamaan Koyck yaitu :

( )

1 ˆ ˆ0 1 ˆ ˆ − + + − = _{t t} t C X C Y Y α β )

Selanjutnya, nilai-nilai αˆ,βˆ₀,C) digunakan untuk mencari nilai k β β β β α_ˆ, ˆ _, ˆ _, ˆ _{, ,} ˆ 2 1

0 K dalam persamaan dinamis distribusi lag dugaan yang panjang

beda kala (lag) tidak diketahui.

Pada persamaan Koyck terdapat Y_t−1 sebagai variabel bebas maka bersifat

autoregressive sehingga metode Koyck juga dapat digunakan untuk menentukan

persamaan dinamis autoregressive dugaan sedangkan persamaan hasil

transformasi Almon tidak bersifat autoregressive. Namun, setelah menggunakan

metode Koyck perlu dilakukan uji lanjutan dengan menggunakan uji statistik h

5

autoregressive. Uji statistik h Durbin-Watson perlu dilakukan karena adanya Yt−1

sebagai variabel bebas dalam model dinamis autoregressive kemungkinan

menyebabkan autokorelasi.

Keistimewaan dari model dinamis autoregressive dan model dinamis

distribusi lag adalah model tersebut telah membuat teori statis menjadi dinamis

karena model regresi yang biasanya mengabaikan pengaruh waktu, melalui model

autoregressive dan model dinamis distribusi lag waktu ikut diperhitungkan

(Supranto, 1995: 200). Oleh karena itu, model autoregressive dan model dinamis

distribusi lag sering disebut satu rangkaian dengan nama “Model Dinamis :

Autoregressive dan Distribusi Lag”.

B. Rumusan Masalah

Berdasarkan latar belakang, penulis dapat mengemukakan rumusan masalah

sebagai berikut :

1. Bagaimana menentukan persamaan dinamis distribusi lag dugaan dengan

metode Koyck dan metode Almon?

2. Bagaimana menentukan persamaan dinamis autoregressive dugaan dan

mendeteksi autokorelasi dengan statistik h Durbin-Watson?

6

C. Tujuan Penulisan

Tujuan penulisan skripsi ini adalah :

1. Menjelaskan tentang metode Koyck, metode Almon, dan uji statistik h

Durbin-Watson dalam menentukan persamaan dinamis : autoregressive dan

distribusi lag dugaan.

2. Menjelaskan tentang aplikasi model dinamis autoregressive dan distribusi lag.

D. Manfaat Penulisan

Berdasarkan rumusan masalah dan tujuan penulisan yang telah dikemukakan,

maka manfaat penulisan skripsi ini adalah :

1. Bagi Penulis

Dengan mengetahui cara menentukan persamaan dinamis : autoregressive dan

distribusi lag, diharapkan dapat menambah pengetahuan tentang analisis

regresi beserta aplikasinya.

2. Bagi Ilmu Pengetahuan

Penulisan ini dapat dijadikan salah satu referensi bagi pihak yang

7 BAB II

LANDASAN TEORI

A. DATA

Data merupakan bentuk jamak dari datum. Data merupakan kumpulan informasi yang diperoleh melalui pengamatan (Hasan, 2005: 12). Berdasarkan waktu pengambilannya data dibedakan menjadi 2 yaitu :

1. Data berkala (time series data)

Data berkala (time series data) adalah data yang terkumpul dari waktu ke

waktu untuk memberikan gambaran perkembangan suatu hal.

Contoh : Data perkembangan harga 9 bahan pokok selama 10 bulan terakhir yang dikumpulkan tiap bulan.

2. Data seleksi silang (cross section data)

Data seleksi silang (cross section data) merupakan data yang terkumpul dari

suatu waktu tertentu untuk memberikan gambaran keadaan atau kegiatan pada waktu itu.

Contoh : Sensus penduduk 1990.

B. Variansi Populasi

Variansi populasi adalah jumlah kuadrat selisih nilai data pengamatan dengan rata-rata hitung dibagi dengan banyaknya data pengamatan.

(

)

2 1 2 1

∑

= − = N i i X N µ σ (2.1)

8

Akar dari variansi populasi adalah simpangan baku populasi (σ) (Walpole, 1995: 33).

C. Matriks

Pada pembahasan berikut ini akan dikaji tentang matriks, transpose matriks, invers matriks dan operasi matriks.

1. Definisi 2.1 Matriks (Anton, 1987: 22)

Sebuah matriks adalah susunan segi empat siku-siku dari bilangan-bilangan. Suatu matriks A berukuran m×n adalah susunan mn bilangan real di dalam tanda kurung siku dan disusun dalam m baris dan n kolom sebagai berikut :

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = mn m m n n a a a a a a a a a K M M M L L 2 1 2 22 21 1 12 11 A

2. Definisi 2.2Transpose Matriks (Anton, 1987: 27).

Jika ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = = mn m m n n ij a a a a a a a a a a K M M M L L 2 1 2 22 21 1 12 11 ] [

A adalah matriks berukuran m×n maka

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = = mn n n m m T ij T a a a a a a a a a a K M M M L L 2 1 2 22 12 1 21 11 ] [ A dimana ji T ij a a = , 1≤i≤m, 1≤ j≤n.

9

3. Definisi 2.3Invers Matriks (Anton, 1987: 34).

Jika terdapat matriks A yang berukuran n×n dan matriks B yang berukuran n

n× sedemikian sehingga AB=BA=I maka matriks B disebut inversA. 4. Operasi Matriks

a. Penjumlahan Dua Matriks

Jika A=[a_ij] dan B=[b_ij] adalah matriks-matriks berukuran m×n maka B

A+ adalah matriks C=[c_ij] berukuran m×n, dengan c_ij =a_ij +b_ij,

m i≤ ≤ 1 , 1≤ j≤n. Diketahui matriks ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = mn m m n n a a a a a a a a a K M M M L L 2 1 2 22 21 1 12 11 A dan matriks ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = mn m m n n b b b b b b b b b K M M M L L 2 1 2 22 21 1 12 11 B sehingga ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + + + + + + + + + = + = mn mn m m m m n n n n b a b a b a b a b a b a b a b a b a K M M M K K 2 2 1 1 2 2 22 22 21 21 1 1 12 12 11 11 B A C

10

b. Selisih Dua Matriks

Jika A=[a_ij] dan B=[b_ij] adalah matriks-matriks berukuran m×n maka Selisih antara A dan B adalah matriks D=[dij] dengan dij =aij −bij,

m i≤ ≤ 1 , 1≤ j≤n. Diketahui matriks ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = mn m m n n a a a a a a a a a K M M M L L 2 1 2 22 21 1 12 11 Α dan ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = mn m m n n b b b b b b b b b K M M M L L 2 1 2 22 21 1 12 11 B sehingga ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − − − − − − = − = mn mn m m m m n n n n b a b a b a b a b a b a b a b a b a K M M M K K 2 2 1 1 2 2 22 22 21 21 1 1 12 12 11 11 B A D c. Perkalian Matriks

Jika ]A=[aij adalah matriks berukuran m×p dan B=[bij] adalah matriks berukuran p×n dengan1≤i≤m 1≤ j≤n maka perkalian A

dan B adalah matriks C=[cij] yang berukuran m×n dengan

∑

= = + + + = p k kj ik pj ip i i j i ij a b a b a b a b c 1 2 2 1 1 K , 1≤i≤m, 1≤ j≤n

11 Diketahui matriks ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = mp m m p p a a a a a a a a a K M M M L L 2 1 2 22 21 1 12 11 A dan matriks ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = pn p p n n b b b b b b b b b K M M M L L 2 1 2 22 21 1 12 11 B sehingga ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + + + + + + + + + + + + = × = pn mp n m n m p mp m m pn p n n p p pn p n n p p b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a K K K M M K L K K L K 2 2 1 1 1 21 2 11 1 1 2 12 1 21 1 2 21 22 21 21 1 2 12 1 11 1 1 21 12 11 11 B A C D. Regresi Linear

Regresi linear adalah regresi yang variabel bebasnya (variabelX )

berpangkat paling tinggi 1. Regresi linear dibedakan menjadi 2 yaitu : 1. Regresi Linear Sederhana

Regresi linear sederhana adalah regresi linear yang hanya melibatkan dua variabel yaitu variabel bebas X dan variabel tak bebas Y (Hasan, 2005:

250). Model regresi linear sederhana dari Y terhadapX ditulis dalam bentuk :

ε β α+ + = X Y dengan

Y : variabel tak bebas X : variabel bebas

α : intersep

β : koefisien regresi / slope

ε : kesalahan penggangu yang berarti nilai-nilai variabel lain tidak dimasukkan dalam persamaan, dengan _{ε ~}

(

_0;σ2

)

N ) 2 . 2 (

12

2. Regresi Linear Berganda

Regresi linear berganda adalah regresi yang variabel tak bebasnya

( )

Y dihubungkan lebih dari satu variabel bebas

(

X1, X2,X3,K,Xn

)

(Hasan, 2005: 269).

Bentuk umum model regresi linear berganda : i in n i i i i X X X X Y =β₀ +β_{1 1} +β_{2 2} +β_{3 3} +_K+β +ε

( )

2.3 dengan i

Y : variabel tak bebas

0 β : intersep n β β β β₁, ₂, _3K, : koefisien regresi ik i i i X X X X ₁, ₂, _3K, : variabel bebas i

ε : kesalahan penggangu yang berarti nilai-nilai variabel lain tidak dimasukkan dalam persamaan, dengan _{ε ~}

(

_0;σ2

)

N

i .

i : pengamatan ke-i

(

i=1,2,_K,n

)

n : ukuran sampel

( )

2.3 dapat diuraikan menjadi :

n nn n n n n n n n n n X X X X Y X X X X Y X X X X Y ε β β β β β ε β β β β β ε β β β β β + + + + + + = + + + + + + = + + + + + + = K M K K 3 3 2 2 1 1 0 2 2 23 3 22 2 21 1 0 2 1 1 13 3 12 2 11 1 0 1

Apabila dituliskan dalam bentuk matriks menjadi :

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ n n nn n n n n n n X X X X X X X X X X X X Y Y Y ε ε ε β β β β β β M M M M M M M M 2 1 2 1 3 2 1 2 23 22 21 1 13 12 11 0 0 0 2 1

13

Secara ringkas dapat dituliskan : ε

B X

Y= + .

( )

2.4

E. Analisis Korelasi

Analisis Korelasi adalah analisis yang dilakukan untuk mengetahui derajat hubungan linear antara suatu variabel dengan variabel yang lain (Algifari, 2000: 45). Ukuran statistik yang dapat menggambarkan hubungan antara suatu variabel dengan variabel yang lain adalah :

1. Koefisien Determinasi

Koefisien determinasi digunakan untuk mengetahui ada tidaknya hubungan antara dua variabel (Algifari, 2000: 45). Besarnya koefisien determinasi dapat dihitung dengan rumus :

( )

2 __ 2 2 ₁ ˆ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − − = Y Y Y Y r

( )

2.5 dengan 2 r : koefisien determinasi Y : variabel tak bebas

__

Y : rata-rata hitung dari nilai Y Yˆ : Y dugaan dengan Yˆ =αˆ+βˆX

Rumus

( )

2.5 digunakan untuk menghitung besarnya koefisien determinasi pada regresi linear sederhana.

14

2. Koefisien Korelasi

Menurut Algifari (2000: 51) koefisien korelasi

( )

r dapat digunakan untuk :

a. Mengetahui keeratan hubungan antara dua variabel.

Besarnya koefisien korelasi antara dua variabel adalah −1≤r ≤1. Jika dua variabel mempunyai nilai r =0 berarti antara dua variabel tidak ada hubungan tetapi jika dua variabel mempunyai r =+1atau 1r =− maka

dua variabel tersebut mempunyai hubungan sempurna. b. Menentukan arah hubungan antara dua variabel.

Tanda (+) dan (-) yang terdapat pada koefisien korelasi menunjukkan arah hubungan antara dua variabel.

Tanda (+) pada r menunjukkan hubungan yang searah atau positif.

Tanda (-) pada r menunjukkan adanya hubungan berlawanan arah atau

negatif.

Besarnya koefisien korelasi dapat ditentukan dengan rumus :

(

)

2 2

( )

2 2 Y Y n X X n Y X XY n r ∑ − ∑ − ∑ − ∑ ∑ ∑ − ∑ =

( )

2.6 dengan

r : besarnya koefisien korelasi X : variabel bebas

Y : variabel tak bebas

15

F. Metode Kuadrat Terkecil (Least Square Method)

Berikut ini adalah gambar persamaan regresi yang sebenarnya dan persamaan regresi taksiran.

Keterangan :

Persamaan regresi sebenarnya dinyatakan dengan Yi =α+β Xi Persamaan regresi dugaan dinyatakan dengan Yˆi =αˆ +βˆXi AA’ adalah garis regresi sebenarnya

BB’ adalah garis regresi dugaan

Titik P merupakan salah satu titik dari pengamatan data sampel i

e taksiran dari faktor gangguan εi

Metode kuadrat terkecil adalah metode yang digunakan untuk menaksir

β. Prinsip dasar metode kuadrat terkecil adalah meminimumkan jumlah kuadrat galat yaitu meminimumkan ∑ei2 (Suryanto, 1998: 140).

Untuk mendapatkan penaksir-penaksir bagi β, ditentukan dua vektor βˆ dan e

sebagai berikut : ei i ε i Yˆ B A A’ i i X Y =α +β Y_i B’ Y P i

X

X i i X Yˆ =αˆ +βˆ

16 k 1 0 β β β β ˆ ˆ ˆ ˆ M = dan n 2 1 e e e e M =

Persamaan hasil estimasi dapat ditulis : e β X Y= ˆ + β X Y e = − ˆ

( )

2.7 sehingga

(

)(

)

(

)(

)

(

)(

)

β X X' ' β Y X' ' β ' β X' Y' Y Y' β X Y X' ' β Y' β X Y ' β X' Y' β X Y β X Y e e' ' ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ + − − = − − = − − = − − = β X X' ' β Y X' ' β 2 Y Y' e' e = − ˆ +ˆ ˆ

( )

2.8

Untuk meminimumkan e'e, dapat diperoleh dengan menurunkan secara parsial terhadap βˆ serta menyamakan turunan dengan 0.

( )

Y' X' β X' X' β X' X' Y' X' e' e β β = = + − = ∂ ∂ = ∂ ∂

∑

∑

= = ˆ 0 ˆ 2 2 0 ˆ 0 ˆ 1 1 2 n i n i i e

17

Selanjutnya kalikan kedua ruas dengan

(

X'X

)

−1 diperoleh

(

)

(

)

(

X'X

)

X' β I Y X' X X' β X X' X X' Y X' β X X' 1 1 1 − − − = = = ˆ ˆ ˆ

(

X'X

)

X'Y β_{ˆ =} −1

( )

9 . 2 dengan

X' : transpose dari matrik X

βˆ : penaksir koefisien regresi

Menurut (Sumodiningrat, 1995: 188) untuk menguji sifat-sifat taksiran parameter digunakan asumsi sebagai berikut :

1. E

( )

ε =0 2. E

[

ε ε'

]

=

σ

2 I Bukti : n ε ε ε ε M 2 1 = dan ε'= ε1 ε2 K ε_n 2 2 1 2 2 2 1 2 1 2 1 2 1 n n n n n ε ε ε ε ε ε ε ε ε ε ε ε ε ε ε ε' ε K M M M K K =

18

[ ]

[ ]

[

]

[

]

[

]

[ ]

[

]

[

] [

]

[ ]

2 2 2 0 0 0 0 0 0 σ σ σ K M M M K K K M M M K K = = 2 n 2 n 1 n n 2 2 2 1 2 n 1 2 1 2 1 ε ε ε ε ε ε ε ε ε ε ε ε ε ε ε ε' ε E E E E E E E E E E

[ ]

2 _=σ2 i ε E dan E

[ ]

ε_iε_j =0

(

i≠ j

)

[ ]

I E 2 2 1 0 0 0 1 0 0 0 1 ' =σ = =σ K M M M K K ε ε

Apabila asumsi-asumsi sudah dipenuhi maka estimasi yang diperoleh dengan metode kuadrat terkecil akan bersifat linear, tak bias, dan variansinya minimum yang dikenal dengan sifat Best, Linear, Unbiased estimator (BLUE). Sifat-sifat penaksir (estimator) dalam metode kuadrat terkecil adalah :

1. Linear (Linearity)

(

)

(

)

(

)

(

)

(

)

(

)

(

X'X

)

Xε β Xε X X' Iβ Xε X X' Xβ X' X X' ε Xβ X' X X' Y X' X X' β 1 1 1 1 1 1 − − − − − − + = + = + = + = = ˆ

19

2. Tak bias (Unbiasedness)

Sifat tak bias berarti nilai harapan dari estimator yaitu E[βˆ]=β.

(

)

[ ]

[

(

)

]

(

X'X

)

X'

[ ]

ε β ε X' X X' β ε] X' X X' [β β 1 1 1 E E E E E − − − + = + = + = ] ˆ [ Karena E

[ ]

ε =0 maka E[βˆ]=βˆ

Jadi, βˆ merupakan penaksir tak bias. 3. Variansi minimum

Estimator variansi minimum adalah estimator dengan variansi terkecil di antara semua estimator untuk koefisien yang sama. Menurut Sudjana (1996 : 199) jika βˆ₁ dan βˆ merupakan dua estimator untuk ₂ β dengan

( )

βˆ1 Var

( )

βˆ2

Var < maka βˆ₁ merupakan estimator bervariansi minimum.

( )

βˆ1

Var dapat dicari sebagai berikut :

( ) (

)

(

)(

)

(

)

{

}

{

(

)

}

[

]

(

)

[ ]

(

)

(

)

(

)

(

)

(

)

(

)

1 1 1 1 1 1 1 1 1 X X' X X' X X' X X' X X' X I X' X X' X X' X ε ε X' X X' ε X' X X' ε X' X X' β β β β β β β − − − − − − − − − = = = = = ⎥⎦ ⎤ ⎢⎣ ⎡ _{− −} = ⎥⎦ ⎤ ⎢⎣ ⎡ ₋ = 2 2 2 ' 1 1 2 1 1 ' ' ˆ ˆ ˆ ˆ ε ε ε σ σ σ E E E E Var

20

Misalkan β_ˆ2 =

[

(

X'X

)

−1 +B

]

Y dengan

2

βˆ : penaksir alternatif yang linear dan tak bias bagiβ B : matriks konstanta yang diketahui

(

)

[

]

(

)

[

]

(

)

(

)

(

)

(

)

[ ]

[

(

)

(

)

(

)

]

(

)

(

)

[

]

( )

0 ˆ ˆ = + = + + + = + + + = + + + = + + = + = − − − − − − ε B X B β ε B Xβ B ε X' X X' Xβ X' X X' ε Xβ B ε Xβ X' X X' β ε Xβ B ε Xβ X' X X' ε Xβ B X' X X' Y B X' X X' β 1 1 1 2 1 1 1 2 E karena E E E

Oleh karena diasumsikan βˆ merupakan estimator tak bias untuk ₂ β maka

[ ]

βˆ₂ =β

E atau dengan kata lain BXB merupakan matriks 0.

Variansi dari penaksir alternatif tersebut dapat dicari sebagai berikut :

( )

(

)

(

)(

)

(

)

[

]

{

}

{

[

(

)

]

}

[

]

(

)

[

]

(

)

{

}

{

[

(

)

]

(

)

}

[

]

(

)

(

)

{

}

[

(

)

(

)

{

}

]

(

)

{

}

{

(

)

}

[

]

(

)

{

}

{

(

)

}

[

]

(

)

{

}

{

(

)

}

[

]

(

)

{

}

[ ]

{

(

)

}

(

)

{

}

{

(

)

}

(

)

(

)

(

)

(

)

{

}

(

)

{

}

karena 0 0 karena ' ˆ ˆ ˆ ˆ 2 2 2 ' ' ' = + = + + + = + + = + + = + + = + + = = + + = − + + + − + + + = − + + − + + = − + − + = − − = ⎥⎦ ⎤ ⎢⎣ ⎡ ₋ = − − − − − − − − − − − − − − − − − − − − − − − X B B' B X X' B' B B' X' X X' X X' X B X X' X X' X X' B' X X X' B X' X X' I B' X X X' ε' ε E B X' X X' B' X X X' ε' ε B X' X X' B' ε' X X X' ε' ε B ε X' X X' X B ε B ε X' X X' ε B ε X' X X' β Bε β X B ε X' X X' β X X' X X' β Bε β X B ε X' X X' β X X' X X' β ε β X B X' X X' β ε β X B X' X X' β Y B X' X X' β Y B X' X X' β β β β β β β 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ' 1 1 1 1 2 2 2 2 2 ε ε ε σ σ σ E E E E E E E E Var

21

( )

β_ˆ2 = 2

(

X'X

)

−1 +σ_ε2BB'

ε

σ

Var

Jadi, Var

( )

βˆ₁ ≤Var

( )

βˆ₂ sehingga terbukti memiliki variansi minimum.

G. Kesalahan Standar Estimasi (Standar Error Of Estimate)

Proses selanjutnya dalam analisis regresi adalah menentukan ketepatan persamaan yang dihasilkan untuk mengestimasi nilai variabel tak bebas dengan metode kuadrat terkecil. Kesalahan standar estimasi (standar error of estimate)

yang dinotasikan dengan S_e. Besarnya kesalahan standar estimasi menunjukkan

ketepatan persamaan estimasi untuk menjelaskan nilai variabel tak bebas yang sesungguhnya. Semakin kecil nilai kesalahan standar estimasi makin tinggi ketepatan persamaan estimasi, sebaliknya jika semakin besar nilai kesalahan standar estimasi makin rendah ketepatan persamaan estimasi (Sugiarto, 1993: 20). Cara mengetahui ketepatan persamaan estimasi dapat digunakan kesalahan standar estimasi (standar error of estimate) ditentukan dengan rumus :

2 2 − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = ∧ n Y Y S_e

(

2.10

)

Rumus alternatif yang dapat digunakan untuk menentukan kesalahan standar estimasi (standar error of estimate) adalah sebagai berikut :

2 ˆ ˆ 2 − ∑ − ∑ − ∑ = n XY Y Y S_e α β

(

2.11

)

Rumus

(

2.10

)

dan

(

2.11

)

digunakan untuk menghitung besarnya kesalahan standar estimasi (standar error of estimate) pada model regresi linear sederhana

22

yaitu : Y =α +β X +ε. Nilai 2 dalam n−2 menunjukkan banyaknya parameter dalam model regresi linear sederhana yaitu α dan β sehingga dalam rumus

(

2.10

)

dan

(

2.11

)

dibagi dengan n−2. H. Asumsi Klasik

Model regresi yang diperoleh dari metode kuadrat terkecil merupakan model regresi yang menghasilkan estimator linear tak bias yang terbaik (BLUE). Menurut Supranto (1987: 281), kondisi BLUE ini akan terjadi jika dipenuhi beberapa asumsi klasik sebagai berikut :

1. Non-Multikolinearitas

Non-Multikolineritas berarti antara variabel bebas yang satu dengan variabel bebas yang lain dalam model regresi tidak saling berhubungan secara sempurna atau mendekati sempurna.

2. Homoskedasitisitas Homoskedasitisitas berarti

( )

_{ε =}

( )

_{ε =σ}2 j i E Var . 3. Non-Autokorelasi

Non-Autokorelasi berarti model tidak dipengaruhi waktu yang berarti

(

)

i j

Cov εi,εj =0, ≠ . Menurut model asumsi klasik, nilai suatu variabel saat ini tidak akan berpengaruh terhadap nilai variabel lain pada masa yang akan datang.

4. Nilai rata-rata kesalahan pengganggu (error) populasi adalah 0 atau E

( )

εi =0 untuk i = 1, 2, ..., n.

23

5. Variabel bebas adalah non-stokastik yang berarti tetap dari sampel ke sampel atau tidak berkorelasi dengan kesalahan pengganggu εt.

6. Distribusi kesalahan (error) adalah normal _{ε ~}

(

_0;σ2

)

N

i atau kesalahan pengganggu mengikuti distribusi normal dengan rata-rata 0 dan variansi _σ2_.

I. Penyimpangan Asumsi Klasik

Penyimpangan terhadap asumsi-asumsi dasar tersebut dalam regresi akan menimbulkan beberapa masalah seperti kesalahan standar estimasi untuk masing-masing koefisien kemungkinan akan sangat besar, pengaruh masing-masing-masing-masing variabel bebas tidak dapat dideteksi atau variansinya tidak minimum lagi. Akibatnya, estimasi koefisiennya kurang akurat lagi yang akhirnya dapat menimbulkan kesimpulan yang salah. Penyimpangan dari asumsi dasar tersebut meliputi :

1. Multikolinearitas

Definisi 2.4 ( Supranto, 1989: 293 )

Multikolinearitas berarti bahwa antar variabel bebas yang terdapat dalam model regresi memiliki hubungan sempurna atau mendekati sempurna atau dengan kata lain koefisien korelasinya tinggi bahkan mendekati 1.

2. Heteroskedastisitas

Definisi 2.5 ( Supranto, 1989: 281 )

Heteroskedastisitas berarti variansi variabel Y dalam model tidak sama untuk

24

3. Autokorelasi

Definisi 2.6 ( Supranto, 1989: 285 )

Autokorelasi berarti terdapatnya korelasi antaranggota sampel Y atau data

pengamatan diurutkan berdasarkan waktu. Autokorelasi biasanya muncul pada regresi yang menggunakan data berkala (time series) karena dalam data

berkala (time series), data masa sekarang dipengaruhi oleh data pada

25 BAB III PEMBAHASAN

Model regresi linear yang sering ditemui biasanya tidak memperhatikan pengaruh waktu karena pada umumnya model regresi linear cenderung mengasumsikan bahwa pengaruh variabel bebas terhadap variabel tak bebas terjadi dalam kurun waktu yang sama. Namun, dalam model regresi linear juga terdapat model regresi yang memperhatikan pengaruh waktu. Waktu yang diperlukan bagi variabel bebas X dalam mempengaruhi variabel tak bebas Y

disebut bedakala atau “a lag” atau “a time lag” (Supranto, 1995: 188). Ada 2

macam model regresi linear yang memperhatikan pengaruh waktu yaitu : 1. Model Dinamis Distribusi Lag

Suatu variabel tak bebas apabila dipengaruhi oleh variabel bebas pada waktu t, serta dipengaruhi juga oleh variabel bebas pada waktu t−1, t−2 dan seterusnya disebut model dinamis distribusi lag. Model dinamis distribusi lag ada 2 jenis yaitu :

a. Model InfiniteLag

Model : Y_t =α +β₀ X_t +β₁ X_t−1+β₂ X_t−2 +_K+ε_t

( )

3.1

Model

( )

3.1 disebut model infinite lag sebab panjang beda kalanya tidak

26

b. Model FiniteLag

Model : Y_t =α+β₀ X_t+β₁X_t−1+β₂ X_t−2 +_K+β_k X_t−k +ε_t

( )

3.2

Model

( )

3.2 disebut model finite lag sebab panjang beda kalanya

diketahui yaitu sebesar k. 2. Model Dinamis Autoregressive

Apabila variabel tak bebas dipengaruhi oleh variabel bebas pada waktu

t, serta dipengaruhi juga oleh variabel tak bebas itu sendiri pada waktu t−1 maka model tersebut disebut autoregressive dengan

t t t

t X Y

Y =α+β₀ +β_{1 −1}+ε .

A. Metode-Metode dalam Menentukan Persamaan Dinamis Distribusi Lag Dugaan

Dua metode yang dapat digunakan untuk menentukan persamaan dinamis distribusi lag dugaan adalah :

1. Metode Koyck

Metode Koyck didasarkan asumsi bahwa semakin jauh jarak lag variabel

bebas dari periode sekarang maka semakin kecil pengaruh variabel lag terhadap

variabel tak bebas. Koyck mengusulkan suatu metode untuk memperkirakan model dinamis distribusi lag dengan mengasumsikan bahwa semua koefisien β

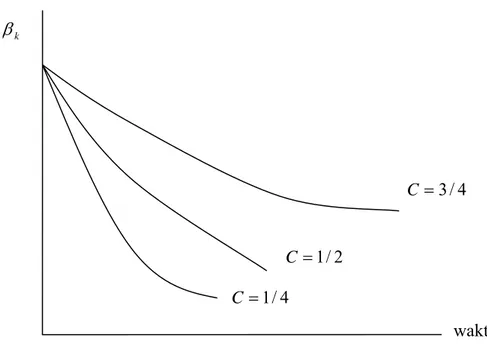
mempunyai tanda sama. Koyck menganggap bahwa koefisien menurun secara geometris sebagai berikut :

k k β0C

27

dengan :

C : rata-rata tingkat penurunan dari distribusi lag dengan nilai 0<C <1 C

−

1 : kecepatan penyesuaian.

( )

3.3 mempunyai arti bahwa nilai setiap koefisien β lebih kecil dengan nilai sebelumnya atau yang mendahuluinya

(

0<C <1

)

. Secara grafis, dapat dilihat pada gambar sebagai berikut :

Gambar 3.1 Penurunan Koefisien β dalam model Koyck

( )

3.3 apabila diuraikan akan menjadi :

M 3 0 3 2 0 2 0 1 0 0 C C C β β β β β β β β = = = =

( )

3.4

Dalam prakteknya Koyck menggunakan model

( )

3.1 .

Sebagai akibat dari

( )

3.4 model

( )

3.1 dapat dituliskan menjadi : t t t t t X CX C X Y =α +β₀ +β_{0 −1} +β₀ 2 ₋₂+K+ε .

( )

3.5 4 / 1 = C 2 / 1 = C 4 / 3 = C k β waktu

28

Model

( )

3.5 sukar digunakan untuk memperkirakan koefisien-koefisien yang banyak sekali dan juga parameter C yang masuk ke dalam model dalam bentuk yang tidak linear. Akhirnya Koyck mencari jalan keluar dengan mengambil beda kala 1 periode berdasarkan

( )

3.5 yaitu :

1 3 2 0 2 0 1 0 1 − − − − − = + t + t + t + + t t X CX C X Y α β β β _K ε .

( )

3.6

( )

3.6 dikalikan dengan C diperoleh :

1 3 3 0 2 2 0 1 0 1 − − − − − = + t + t + t + + t t C C X C X C X C Y C α β β β _K ε .

( )

3.7

( )

3.5 dikurangi

( )

3.7 menjadi :

(

)

0

(

1

)

1 1 − − = − + + − − _{t t t t} t CY C X C Y α β ε ε .

( )

3.8

Secara umum

( )

3.8 dapat dituliskan menjadi :

(

)

t t t

t C X C Y V

Y =α 1− +β₀ + ₋₁+

( )

3.9

dengan V_t =ε_t−Cε_t−1.

Prosedur sampai ditemukannya model

( )

3.9 dikenal dengan nama Transformasi Koyck. Model

( )

3.9 inilah yang disebut dengan model Koyck.

Pada model

( )

3.1 parameter α dan β yang diperkirakan banyaknya tak terhingga, sedangkan pada model

( )

3.9 lebih sederhana karena hanya memperkirakan tiga parameter yaitu α , β, dan C. Nilai α , β, dan C selanjutnya digunakan untuk menetukan koefisien distribusi lag dugaan yaitu

dengan rumus : k k β0C

β = . Namun, ada hal yang harus diperhatikan dalam transformasi Koyck yaitu adanya Y_t−1 yang diikutsertakan sebagai salah satu

29

2. Metode Almon

Metode Koyck memang banyak digunakan dalam distribusi lag.

Penerapan dengan metode Koyck berdasarkan asumsi bahwa koefisien β menurun secara geometris sepanjang beda kala (lag). Namun, apabila diagram

pencar antara β dengan lag itu naik kemudian menurun maka metode Koyck

tidak dapat diterapkan. Gambar berikut ini akan menunjukkan perubahan koefisien β.

Gambar 3.2 Perubahan Koefisien β Gambar 3.3 Perubahan Koefisien β

30

Model yang digunakan dalam metode Almon adalah model finite lag sebagai

berikut : t k t k t t t t X X X X Y =α +β₀ +β_{1 −1}+β_{2 −2} +_K+β ₋ +ε

(

3.10

)

atau t k i i t i t X Y =α +

∑

β +ε =0 − .

(

3.11

)

Berdasarkan teori matematik yang dikenal dengan nama Weir-Strass’s Theorem, Almon berasumsi bahwa βi dapat didekati oleh suatu polinomial dalam

i yang memiliki derajat, dengan i merupakan panjangnya beda kala (lag).

Polinomial tersebut bisa berderajat 0, 1, 2, … dst. Apabila scatter diagram digambarkan seperti gambar 3.2 maka model bisa dituliskan sebagai berikut :

2 2 1 0 i i i α α α β = + + .

(

3.12

)

(

3.12

)

merupakan polinomial dalam i yang kuadratik atau berpangkat dua

(second-degree polynomial in i).

Namun, apabila koefisien β mengikuti gambar 3.4 maka model bisa dituliskan sebagai berikut : 3 3 2 2 1 0 i i i i α α α α β = + + + .

(

3.13

)

(

3.13

)

merupakan polinomial dalam i yang berpangkat tiga (third-degree polynomial in i).

Secara umum, model dituliskan sebagai berikut : m m i α α i α i α i β = + + 2 +_K+ 2 1 0 .

(

3.14

)

31

(

3.14

)

merupakan polinomial dalam i yang berpangkat m (m-degree polynomial in i) dengan m<k (panjang beda kala maksimum).

Almon mengasumsikan bahwa polinomial berpangkat dua adalah yang paling tepat digunakan.

Apabila

(

3.12

)

disubstitusikan ke

(

3.11

)

maka diperoleh :

(

)

∑

= − + + + + = k i t t t i i X Y 0 1 2 2 1 0 α α ε α α

∑

∑

∑

= − = − = − + + + + = k i t k i t k i t t iX i X X 0 0 1 2 0 1 1 1 0 α ε α α

(

3.15

)

Apabila didefinisikan :

∑

= − = k i t t X Z 0 1 0

∑

= − = k i t t iX Z 0 1 1

(

3.16

)

∑

= − = k i t t i X Z 0 1 2 2 maka

(

3.15

)

menjadi : t t t t t Z Z Z Y =α +α_{0 0} +α_{1 1} +α_{2 2} +ε

(

3.17

)

Apabila dituliskan dengan persamaan regresi dugaan menjadi : t

t t

t Z Z Z Yˆ =αˆ+αˆ_{0 0} +αˆ_{1 1} +αˆ_{2 2} .

Model

(

3.17

)

dapat diperkirakan koefisiennya dengan metode kuadrat terkecil. Perkiraan α) dan α_i yang diperoleh akan mempunyai sifat-sifat yang diinginkan asalkan kesalahan pengganggu εt memenuhi asumsi dari model linear yang

32

klasik. Setelah semua αi diperkirakan dari

(

3.17

)

, koefisien βˆ dapat dihitung berdasarkan rumus

(

3.14

)

sebagai berikut :

0 0 ˆ ˆ _α β = 2 1 0 1 ˆ ˆ ˆ ˆ _{α α α} β = + + 2 1 0 2 ˆ 2ˆ 4ˆ ˆ _{α α α} β = + + 2 1 0 3 ˆ 3ˆ 9ˆ ˆ _{α α α} β = + + M 2 2 1 0 ˆ ˆ ˆ ˆ _{α α α} βk = +k +k

(

3.18

)

dengan 0 ˆ β merupakan perkiraan β₀ i βˆ _{merupakan perkiraan} i β k i=1,2,K,

Sebelum menerapkan metode Almon, harus melakukan langkah-langkah sebagai berikut :

1. Menentukan panjang maksimum dari beda kala (k).

Hal ini merupakan kelemahan terbesar dalam teknik Almon. harus memutuskan panjangnya beda kala maksimum (k) dengan tepat berdasarkan

anggapan, pengalaman, maupun dasar teori yang sudah memperhitungkan kondisi dan situasi.

2. Menentukan nilai m.

Setelah menentukan nilai k, m juga harus ditentukan, m merupakan derajat atau pangkat polinomial (degree of the polynomial). Derajat atau

33

pangkat polinomial harus paling sedikit lebih besar satu dibandingkan dengan banyaknya titik belok dalam kurva yang menghubungkan β_i dengan i.

Misalkan gambar

( )

3.2 dan

( )

3.3 hanya ada satu titik belok, sehingga polinomial yang cocok digunakan adalah polinomial berpangkat dua. Namun, prakteknya banyaknya titik belok seringkali tidak diketahui sehingga m biasanya ditentukan secara subjektif yaitu dengan menggunakan asumsi umum

2 2 1

0 i i

i α α α

β = + + seperti yang dilakukan Almon. Kelebihan metode Almon :

1. Almon memberikan metode yang fleksibel yaitu mempersatukan berbagai struktur beda kala, yang berarti bahwa koefisien β bisa naik dan bisa turun sedangkan dalam metode Koyck sangat kaku karena koefisien β harus menurun secara geometris.

2. Metode Almon tidak perlu mengkhawatirkan tentang adanya variabel tak bebas beda kala sebagai suatu variabel bebas baik dalam model maupun persoalan yang timbul dalam estimasi.

B. Metode dalam Menentukan Persamaan Dinamis Autoregressive Dugaan Pada pembahasan model dinamis distribusi lag dikenal model Koyck yaitu :

(

1−

)

+ 0 + −1+

(

− −1

)

= _{t t t t}

t C X CY C

Y α β ε ε

(

3.19

)

Model

(

3.19

)

mempunyai bentuk sama dengan model dinamis autoregressive :

t t t

t X Y V

Y =α₀ +α₁ +α_{2 −1} +

(

3.20

)

34

Namun, metode kuadrat terkecil tidak dapat digunakan dalam persamaan dinamis

autoregressive dugaan karena :

1. Adanya variabel-variabel bebas yang stokastik. 2. Adanya autokorelasi.

Oleh karena itu, untuk mengetahui adanya autokorelasi dalam model dinamis

autoregressive perlu mengenali sifat-sifat Vt terlebih dahulu.

Asumsikan bahwa εt atau kesalahan pengganggu asli memenuhi asumsi klasik antara lain :

1. Homoskedastisitas

( )

_{ε =}

( )

_=σ2 j i E e

Varian , sama untuk semua kesalahan penggangu. 2. Non-Autokorelasi

(

)

i j Cov ε_i,ε_j =0, ≠

Berdasarkan asumsi tentang ε_t, jika V_t adalah autokorelasi maka harus

dibuktikan bahwa :

(

)

2 1 Cσ V V E _{t t−} =−

(

3.21

)

Bukti :

Misalnya dalam model Koyck ada kesalahan penggangu Vt =

(

εt −Cεt₋₁

)

. Adanya E

(

V_tV_t−1

)

maka ada Y_t−1 muncul dalam model Koyck sebagai variabel bebas, sehingga Y_t−1 tersebut akan berkorelasi dengan kesalahan pengganggu

t