Rata-rata Nilai. 2 saudara 25%

(1)

7

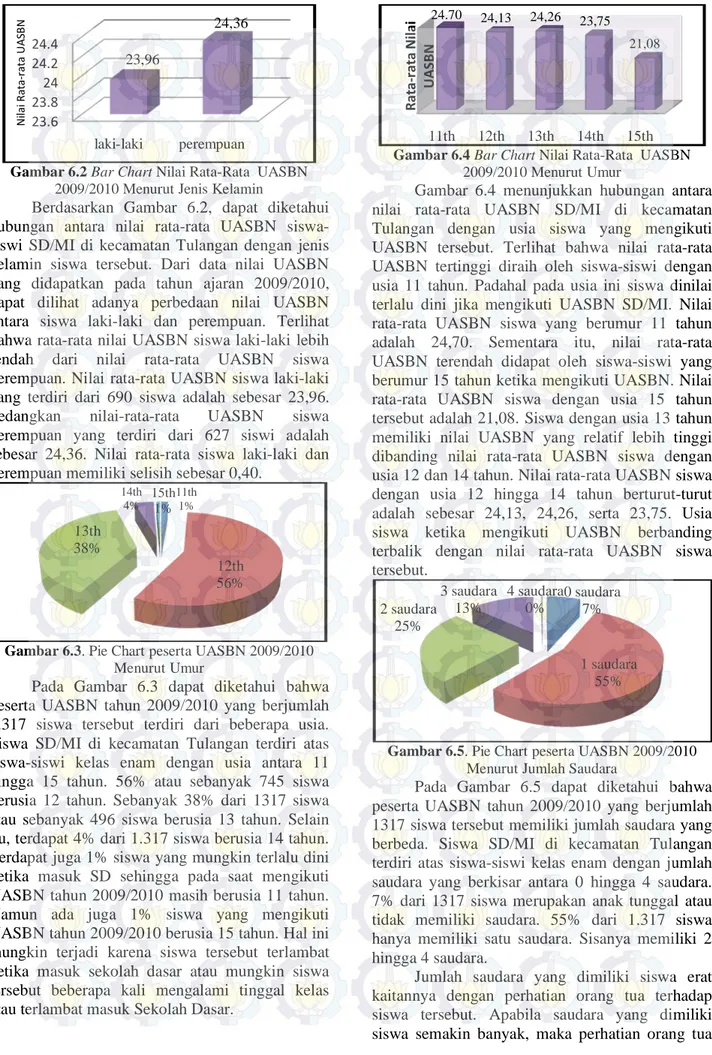
Gambar 6.2 Bar Chart Nilai Rata-Rata UASBN

2009/2010 Menurut Jenis Kelamin

Berdasarkan Gambar 6.2, dapat diketahui hubungan antara nilai rata-rata UASBN siswa-siswi SD/MI di kecamatan Tulangan dengan jenis kelamin siswa tersebut. Dari data nilai UASBN yang didapatkan pada tahun ajaran 2009/2010, dapat dilihat adanya perbedaan nilai UASBN antara siswa laki-laki dan perempuan. Terlihat bahwa rata-rata nilai UASBN siswa laki-laki lebih rendah dari nilai rata-rata UASBN siswa perempuan. Nilai rata-rata UASBN siswa laki-laki yang terdiri dari 690 siswa adalah sebesar 23,96. Sedangkan nilai-rata-rata UASBN siswa perempuan yang terdiri dari 627 siswi adalah sebesar 24,36. Nilai rata-rata siswa laki-laki dan perempuan memiliki selisih sebesar 0,40.

Gambar 6.3. Pie Chart peserta UASBN 2009/2010

Menurut Umur

Pada Gambar 6.3 dapat diketahui bahwa peserta UASBN tahun 2009/2010 yang berjumlah 1.317 siswa tersebut terdiri dari beberapa usia. Siswa SD/MI di kecamatan Tulangan terdiri atas siswa-siswi kelas enam dengan usia antara 11 hingga 15 tahun. 56% atau sebanyak 745 siswa berusia 12 tahun. Sebanyak 38% dari 1317 siswa atau sebanyak 496 siswa berusia 13 tahun. Selain itu, terdapat 4% dari 1.317 siswa berusia 14 tahun. Terdapat juga 1% siswa yang mungkin terlalu dini ketika masuk SD sehingga pada saat mengikuti UASBN tahun 2009/2010 masih berusia 11 tahun. Namun ada juga 1% siswa yang mengikuti UASBN tahun 2009/2010 berusia 15 tahun. Hal ini mungkin terjadi karena siswa tersebut terlambat ketika masuk sekolah dasar atau mungkin siswa tersebut beberapa kali mengalami tinggal kelas atau terlambat masuk Sekolah Dasar.

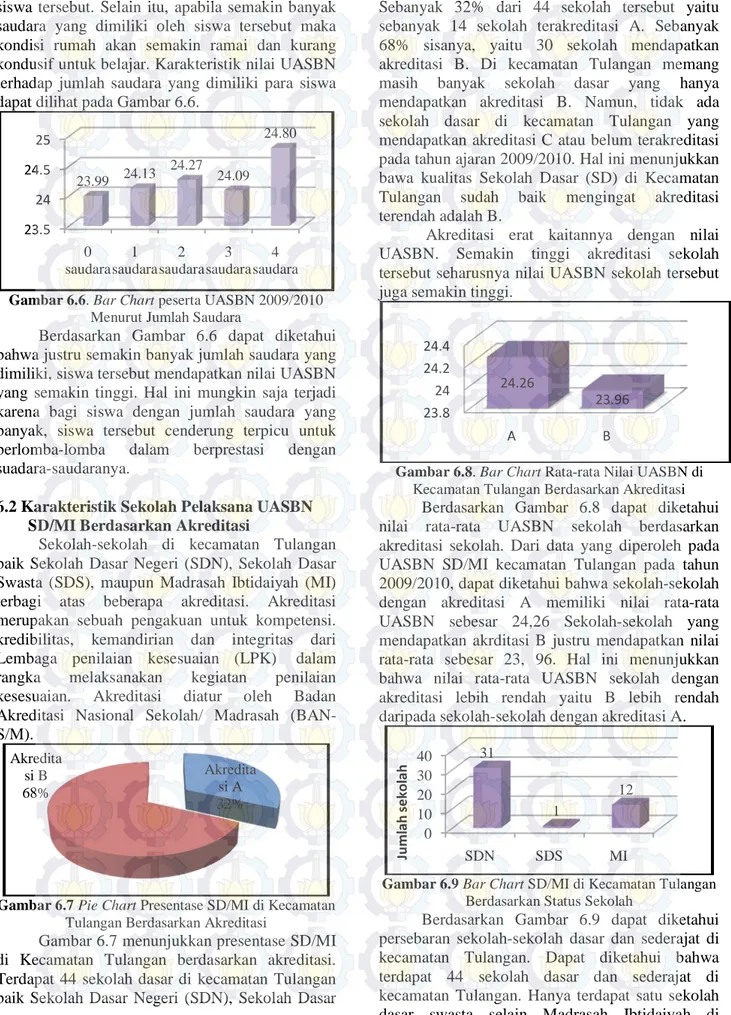
Gambar 6.4 Bar Chart Nilai Rata-Rata UASBN

2009/2010 Menurut Umur

Gambar 6.4 menunjukkan hubungan antara nilai rata-rata UASBN SD/MI di kecamatan Tulangan dengan usia siswa yang mengikuti UASBN tersebut. Terlihat bahwa nilai rata-rata UASBN tertinggi diraih oleh siswa-siswi dengan usia 11 tahun. Padahal pada usia ini siswa dinilai terlalu dini jika mengikuti UASBN SD/MI. Nilai rata-rata UASBN siswa yang berumur 11 tahun adalah 24,70. Sementara itu, nilai rata-rata UASBN terendah didapat oleh siswa-siswi yang berumur 15 tahun ketika mengikuti UASBN. Nilai rata-rata UASBN siswa dengan usia 15 tahun tersebut adalah 21,08. Siswa dengan usia 13 tahun memiliki nilai UASBN yang relatif lebih tinggi dibanding nilai rata-rata UASBN siswa dengan usia 12 dan 14 tahun. Nilai rata-rata UASBN siswa dengan usia 12 hingga 14 tahun berturut-turut adalah sebesar 24,13, 24,26, serta 23,75. Usia siswa ketika mengikuti UASBN berbanding terbalik dengan nilai rata-rata UASBN siswa tersebut.

Gambar 6.5. Pie Chart peserta UASBN 2009/2010

Menurut Jumlah Saudara

Pada Gambar 6.5 dapat diketahui bahwa peserta UASBN tahun 2009/2010 yang berjumlah 1317 siswa tersebut memiliki jumlah saudara yang berbeda. Siswa SD/MI di kecamatan Tulangan terdiri atas siswa-siswi kelas enam dengan jumlah saudara yang berkisar antara 0 hingga 4 saudara. 7% dari 1317 siswa merupakan anak tunggal atau tidak memiliki saudara. 55% dari 1.317 siswa hanya memiliki satu saudara. Sisanya memiliki 2 hingga 4 saudara.

Jumlah saudara yang dimiliki siswa erat kaitannya dengan perhatian orang tua terhadap siswa tersebut. Apabila saudara yang dimiliki siswa semakin banyak, maka perhatian orang tua

23.6 23.824 24.2 24.4 laki-laki perempuan 23,96 24,36 N ilai R at a-rat a U AS BN 11th 1% 12th 56% 13th 38% 14th 4% 15th 1% 11th 12th 13th 14th 15th 24.70 _24,13 24,26 _23,75 21,08 Ra ta -r at a N ila i UA SB N 0 saudara 7% 1 saudara 55% 2 saudara 25% 3 saudara 13% 4 saudara 0%

(2)

8

akan terpecah dan kurang terkonsentrasi pada siswa tersebut. Selain itu, apabila semakin banyak saudara yang dimiliki oleh siswa tersebut maka kondisi rumah akan semakin ramai dan kurang kondusif untuk belajar. Karakteristik nilai UASBN terhadap jumlah saudara yang dimiliki para siswa dapat dilihat pada Gambar 6.6.

Gambar 6.6. Bar Chart peserta UASBN 2009/2010

Menurut Jumlah Saudara

Berdasarkan Gambar 6.6 dapat diketahui bahwa justru semakin banyak jumlah saudara yang dimiliki, siswa tersebut mendapatkan nilai UASBN yang semakin tinggi. Hal ini mungkin saja terjadi karena bagi siswa dengan jumlah saudara yang banyak, siswa tersebut cenderung terpicu untuk berlomba-lomba dalam berprestasi dengan suadara-saudaranya.

6.2 Karakteristik Sekolah Pelaksana UASBN SD/MI Berdasarkan Akreditasi

Sekolah-sekolah di kecamatan Tulangan baik Sekolah Dasar Negeri (SDN), Sekolah Dasar Swasta (SDS), maupun Madrasah Ibtidaiyah (MI) terbagi atas beberapa akreditasi. Akreditasi merupakan sebuah pengakuan untuk kompetensi. kredibilitas, kemandirian dan integritas dari Lembaga penilaian kesesuaian (LPK) dalam rangka melaksanakan kegiatan penilaian kesesuaian. Akreditasi diatur oleh Badan Akreditasi Nasional Sekolah/ Madrasah (BAN-S/M).

Gambar 6.7 Pie Chart Presentase SD/MI di Kecamatan

Tulangan Berdasarkan Akreditasi

Gambar 6.7 menunjukkan presentase SD/MI di Kecamatan Tulangan berdasarkan akreditasi. Terdapat 44 sekolah dasar di kecamatan Tulangan baik Sekolah Dasar Negeri (SDN), Sekolah Dasar

Swasta (SDS), maupun Madrasah Ibtidaiyah. Sebanyak 32% dari 44 sekolah tersebut yaitu sebanyak 14 sekolah terakreditasi A. Sebanyak 68% sisanya, yaitu 30 sekolah mendapatkan akreditasi B. Di kecamatan Tulangan memang masih banyak sekolah dasar yang hanya mendapatkan akreditasi B. Namun, tidak ada sekolah dasar di kecamatan Tulangan yang mendapatkan akreditasi C atau belum terakreditasi pada tahun ajaran 2009/2010. Hal ini menunjukkan bawa kualitas Sekolah Dasar (SD) di Kecamatan Tulangan sudah baik mengingat akreditasi terendah adalah B.

Akreditasi erat kaitannya dengan nilai UASBN. Semakin tinggi akreditasi sekolah tersebut seharusnya nilai UASBN sekolah tersebut juga semakin tinggi.

Gambar 6.8. Bar Chart Rata-rata Nilai UASBN di

Kecamatan Tulangan Berdasarkan Akreditasi

Berdasarkan Gambar 6.8 dapat diketahui nilai rata-rata UASBN sekolah berdasarkan akreditasi sekolah. Dari data yang diperoleh pada UASBN SD/MI kecamatan Tulangan pada tahun 2009/2010, dapat diketahui bahwa sekolah-sekolah dengan akreditasi A memiliki nilai rata-rata UASBN sebesar 24,26 Sekolah-sekolah yang mendapatkan akrditasi B justru mendapatkan nilai rata-rata sebesar 23, 96. Hal ini menunjukkan bahwa nilai rata-rata UASBN sekolah dengan akreditasi lebih rendah yaitu B lebih rendah daripada sekolah-sekolah dengan akreditasi A.

Gambar 6.9 Bar Chart SD/MI di Kecamatan Tulangan

Berdasarkan Status Sekolah

Berdasarkan Gambar 6.9 dapat diketahui persebaran sekolah-sekolah dasar dan sederajat di kecamatan Tulangan. Dapat diketahui bahwa terdapat 44 sekolah dasar dan sederajat di kecamatan Tulangan. Hanya terdapat satu sekolah dasar swasta selain Madrasah Ibtidaiyah di

23.5 24 24.5 25 0 saudara 1 saudara 2 saudara 3 saudara 4 saudara 23.99 24.13 24.27 24.09 24.80 Akredita si A 32% Akredita si B 68% 23.8 24 24.2 24.4 A B 24.26 23.96 0 10 20 30 40 SDN SDS MI 31 1 12 Ju m la h s ek ola h

(3)

9

kecamatan Tulangan. Sekolah dasar tersebut adalah Sekolah Dasar (SD) Muhammadiyah 2. Selain itu, terdapat 12 sekolah dasar swasta berbasis Madrasah Ibtidaiyah di kecamatan Tulangan. Sisanya yaitu 31 sekolah dasar merupakan Sekolah Dasar (SD) yang dikelola oleh pemerintah atau disebut juga Sekolah Dasar Negeri (SDN).

Gambar 6.10 Pie Chart Peserta UASBN di Kecamatan

Tulangan Berdasarkan Status Sekolah

Dari 44 sekolah dasar penyelenggara UASBN SD/MI di kecamatan Tulangan pada tahun 2009/2010 dapat diketahui pula jumlah siswa yang menjadi peserta UASBN SD/MI di kecamatan Tulangan pada tahun 2009/2010 berdasarkan status sekolahnya. Dapat dilihat dari Gambar 4.8 bahwa 19% dari peserta UASBN SD/MI di kecamatan Tulangan pada tahun 2009/2010 tersebut berasal dari Madrasah Ibtdaiyah (MI) swasta di kecamatan Tulangan. 25 dari peserta UASBN SD/MI di kecamatan Tulangan pada tahun 2009/2010 berasal dari Sekolah Dasar (SD) swasta non MI. Selain itu, 79% dari 1317 siswa yang menjadi peserta UASBN SD/MI di kecamatan Tulangan pada tahun 2009/2010 merupakan siswa Sekolah Dasar Negeri (SDN) yang tersebar di seluruh wilayah kecamatan Tulangan.

Gambar 6.11 Bar Chart Rata-rata Nilai UASBN di

Kecamatan Tulangan Berdasarkan Status Sekolah

Berdasarkan Gambar 6.11, diketahui bahwa rata-rata nilai UASBN SDN di kecamatan Tulangan pada tahun ajaran 2009/2010 adalah sebesar 24,07. Nilai rata-rata UASBN untuk sekolah dasar swasta non MI adalah sebesar 25,68. Selain itu, diketahui pula nilai rata-rata UASBN Madrasah Ibtidaiyah (MI) swasta di kecamatan Tulangan adalah sebesar 24,07. Dapat dilihat bahwa sekolah dasar swasta non madrasah memiliki nilai rata-rata UASBN tertinggi di

kecamatan Tulangan. Sekolah Dasar Negeri (SDN) dengan Madrasah Ibtidaiyah memiliki nilai rata-rata UASBN yang relatif sepadan yaitu sekitar 24,075.

Gambar 6.12 Pie Chart Guru Kelas 6 Berdasarkan

Pendidikan Terakhir

Berdasarkan Gambar 6.12, dapat diketahui pendidikan guru kelas 6 dari masing-masing 44 sekolah baik Sekolah Dasar Negeri (SDN), Sekolah Dasar Swasta (SDS) non madrasah, serta Madrasah Ibtidaiyah (MI). Sebanyak 43% dari 44 sekolah dasar di kecamatan Tulangan menempatkan guru dengan pendidikan bukan Pendidikan Guru Sekolah Dasar (PGSD) sebagai guru kelas 6. Sedangkan sebanyak 57% dari 44 sekolah dasar menempatkan guru yang memang merupakan lulusan Pendidikan Guru Sekolah Dasar (PGSD) sebagai guru kelas 6. Siswa siswi yang dididik oleh masing-masing guru kelas baik dengan pendidikan terakhir Pendidikan Guru Sekolah Dasar (PGSD) maupun dari jurusan lain tentunya memiliki hasil yang berbeda. Pengaruh pendidikan terakhir guru terhadap nilai UASBN sekolah dapat dilihat berdasarkan gambar dibawah ini.

Gambar 6.13. Bar Chart Rata-rata UASBN Sekolah

Berdasarkan Pendidikan Terakhir Guru Kelas 6

Gambar 6.13 menunjukkan hubungan antara pendidikan terakhir guru kelas 6 dengan rata-rata nilai UASBN sekolah tempat guru tersebut mengajar. Nilai rata-rata UASBN sekolah dengan guru kelas 6 yang berpendidikan terakhir PGSD adalah sebesar 24,43. Namun, rata-rata nilai UASBN sekolah dengan guru kelas 6 yang memiliki pendidikan terakhir selain PGSD adalah sebesar 23,57. 1036 siswa 79% 33 siswa 2% 248 siswa 19% SDN SDS MI 23 24 25 26 SDN SDS MI 24,07 25.68 24.07 Ra ta -r at a U AS BN PGSD 57% jur.lain 43% 23 24 25 PGSD jur.lain 24.43 23.57

(4)

10

1.1 Uji Signifikansi Serentak Variabel Prediktor Terhadap Variabel Respon

Untuk mengetahui signifikan atau tidaknya suatu variabel pada model dapat diketahui melalui pengujian signifikansi parameter. Berikut adalah pengujian signifikansi secara serentak dengan menggunakan pengujian chi-square.

H0 : γ00 = γ01 = ⋯ = γrp = 0

H1 : Minimal ada satu

γ

_rp≠ 0, r = 0,1,…,s dan p =

0,1,…,s Statistik hitung: χ2 statistik = 2.0462,929073 df = 9 p-value = <0.001

Berdasarkan hasil pengujian di atas, dapat diketahui bahwa nilai p-value dari pengujian signifikansi secara serentak yang didapatkan adalah kurang dari α yang ditentukan yaitu 0,05. Hal ini menunjukkan bahwa terjadi penolakan terhadap hipotesis nol sehingga menunjukkan bahwa minimal terdapat satu variabel yang koefisiennya tidak sama dengan nol.

1.2 Uji SignifikansiIndividu Variabel Prediktor Terhadap Variabel Respon

Berpengaruh atau tidaknya masing-masing variabel prediktor tersebut dapat diketahui melalui pengujian signifikansi individu. Berikut adalah pengujian signifikansi individu setelah dilakukan pemodelan multilevel awal dengan sotware HLM7. Pengujian dilakukan dengan menggunakan uji

T-rasio.

H0 : Tidak ada hubungan antara variabel prediktor

dengan variabel respon

H1 : Ada hubungan antara variabel prediktor

dengan variabel respon

Tabel 6.1 Uji Signifikansi Individu Variabel Prediktor

terhadap Variabel Respon

Efek Tetap t-rasio P-value Keterangan

Intersep 16.30 0,00 Tolak H0

W1

(ukuran kelas) 0,80 0,43 Gagal Tolak H0

W2

(pendidikan guru) -2,30 0,03 Tolak H0

W3

(pengalaman guru kelas)

1,09 0,28 Gagal tolak H0

W4

(akreditasi sekolah) -0,91 0,37 Gagal Tolak H0

X1

(jenis kelamin) 4,87 0,00 Tolak H0

X2

(umur) -3,85 0,00 Tolak H0

X3

(jumlah saudara) 1,34 0,18 Gagal Tolak H0

X4

(nilai raport kls 4 smt 1) 5,95 0,00 Tolak H0

*) signifikan pada ∝= 0,05

Tabel 6.1 menunjukkan ada hubungan antara pendidikan guru kelas 6 (W2), jenis kelamin siswa

(X1), umur siswa (X2), serta nilai raport kelas 4

semester 1 siswa tersebut (X4) dengan nilai

UASBN siswa tersebut. Namun terdapat 4 variabel yang tidak signifikan terhadap nilai UASBN siswa. Variabel-variabel tersebut adalah ukuran kelas (W1), pengalaman guru kelas (W3), akreditasi

sekolah (W4) serta jumlah saudara dari siswa

tersebut (X3). Keempat variabel yang signifikan

tersebut kemudian akan dianalisis lebih lanjut menggunakan analisis regresi multilevel.

6.4 Analisis Regresi Multilevel Random Intersep

Setelah dilakukan pemodelan regresi multilevel random intersep dan didapatkan variabel-variabel yang signifikan, dilakukan kembali analisis lebih lanjut terhadap variabel-variabel yang signifikan tersebut. Pemodelan regresi multilevel random intersep dilakukan kembali pada variabel-variabel yang signifikan tersebut. Berikut adalah model regresi multilevel random intersep yang akan dibentuk.

Model Level-1

Yij = β0j+ β1j∗ Jkij + β2j∗ umurij + β3j

∗ raportij + εij

Model Level-2

β0j = γ00+ γ01∗ pendidikan guru kelasj+ δ0j

β1j= γ10

β2j = γ20

β3j = γ30

Setelah persamaan digabungkan, maka akan didapatkan persamaan berikut.

Yij = γ00+ γ01∗ pendidikan guru kelasj+ γ10∗

Jkij + γ20∗ umurij + γ30∗ raportij + εij +

δ0j

Untuk mendapatkan model tersebut, digunakan suatu software yang khusus menangani tentang kasus multilevel model. Software tersebut adalah Hierarchial Linier Model (HLM7). Berikut adalah hasil output dari model yang dibentuk dan analisisnya.

Tabel 6.2 Pemodelan Variabel Prediktor terhadap

Variabel Respon

Efek Tetap Koefisian Error t-rasio d.f. P-value

𝛽𝛽0 Intersep 22.33 1,19 18,80 42 <0,001 W1(pendidikan guru kelas) -0,90 0,35 -2,62 42 0,012 X1(jk) 0,40 0,08 4,81 1.270 <0,001 X2(umur) -0,26 0,07 -3,81 1.270 <0,001 X3(raport) 0,22 0,04 6,08 1.270 <0,001

(5)

11

Berdasarkan Tabel 6.2 diatas dapat diketahui model regresi multilevel yang didapatkan dari analisis adalah sebagai berikut.

yij� = 22,33 − 0,90(W1j) + 0,40(X1ij) − 0,26(X2ij) + 0,22(X3ij)

Interpretasi dari model di atas adalah sebagai berikut.

1. Untuk siswa yang bersekolah dengan guru kelas berpendidikan PGSD berjenis kelamin laki-laki, didapatkan model regresi multilevel sebagai berikut.

y� = 22,33 − 0,26(Xij 2ij) + 0,22(X3ij)

Setiap peningkatan umur siswa, nilai UASBN cenderung berkurang sebesar 0,26 dan pada setiap peningkatan nilai raport kelas 4 semester 1 pada tiga pelajaran UASBN, nilai UASBN cenderung bertambah sebesar 0,22 satuan dengan perpotongan pada sumbu x pada y senilai 22,33.

2. Untuk siswa yang bersekolah dengan guru kelas berpendidikan non PGSD berjenis kelamin laki-laki, didapatkan model regresi multilevel sebagai berikut.

y� = 21,43 − 0,26(Xij 2ij) + 0,22(X3ij)

3. Untuk siswa yang bersekolah dengan guru kelas berpendidikan PGSD berjenis kelamin perempuan didapatkan model regresi multilevel sebagai berikut.

y� = 22,73 − 0,26(Xij 2ij) + 0,22(X3ij)

4. Untuk siswa yang bersekolah dengan guru kelas berpendidikan non PGSD berjenis kelamin perempuan didapatkan model regresi multilevel sebagai berikut.

yij

� = 21,83 − 0,26(X2ij) + 0,22(X3ij)

Setiap peningkatan umur siswa, nilai UASBN cenderung berkurang sebesar 0,26 dan pada setiap peningkatan nilai raport kelas 4 semester 1 pada tiga pelajaran UASBN, nilai UASBN cenderung bertambah sebesar 0,22

satuan dengan perpotongan pada sumbu x pada y senilai 21,83.

Setelah didapat model regresi multilevel, maka diketahui pula nilai σ2 dan τ dari model regresi tersebut. Dengan menggunakan nilai σ2 dan τ, dapat dihitung nilai Intra Class Correlation (ICC) dari masing-masing variabel dalam model tersebut. Perhitungan ICC model tersebut adalah sebagai berikut.

ICC = τ τ + σ� 2

= 1.16141 1.16141 + 2.16569� = 0,349076

Nilai dari Intra Class Correlation (ICC) tersebut menunjukkan nilai korelasi atau hubungan dari masing-masing unit pada level 2(sekolah). Semakin tinggi nilai ICC menunjukkan bahwa masing-masing sekolah tersebut memiliki hubungan yang semakin berkaitan. Berdasarkan perhitungan didapatkan bahwa nilai ICC adalah sebesar 0,349. Hal tersebut menunjukkan bahwa terdapat 34% variansi pada nilai UASBN yang merupakan variansi antar sekolah, sedangkan 66% sisanya merupakan variansi yang terdapat pada level siswa (individu).

Dengan menggunakan HLM, dapat pula diketahu R2 dari model yang terbentuk. R2 merupakan proporsi pereduksian varians setelah dimasukkan variabel-variabel yang dianggap signifikan. Nilai R2 menunjukkan berapa besar varians yang dijelaskan dalam model. Persentase variansi yang dijelaskan (proporsi pereduksian variansi) berdasarkan prediktor pada level 1 adalah sebagai berikut.

R2_{level 1}

₌

𝜎𝜎2𝑚𝑚𝑚𝑚𝑚𝑚𝑚𝑚𝑚𝑚 ℎ𝑎𝑎𝑎𝑎𝑎𝑎𝑎𝑎 𝑖𝑖𝑎𝑎𝑖𝑖𝑚𝑚𝑖𝑖𝑖𝑖𝑚𝑚𝑖𝑖−𝜎𝜎2𝑚𝑚𝑚𝑚𝑚𝑚𝑚𝑚𝑚𝑚 𝑖𝑖𝑖𝑖𝑠𝑠𝑎𝑎𝑖𝑖𝑠𝑠𝑖𝑖𝑠𝑠𝑎𝑎𝑎𝑎

𝜎𝜎2𝑚𝑚𝑚𝑚𝑚𝑚𝑚𝑚𝑚𝑚 ℎ𝑎𝑎𝑎𝑎𝑎𝑎𝑎𝑎 𝑖𝑖𝑎𝑎𝑖𝑖𝑚𝑚𝑖𝑖𝑖𝑖𝑚𝑚𝑖𝑖

=2.29108 − 2.16569_2.29108 = 0,0547 ~ 5,5%

Berdasarkan perhitungan tersebut dapat diketahui bahwa variansi yang dijelaskan oleh variabel–variabel prediktor pada level 1 terhadap model adalah sebesar 5,5 %. Hal ini terjadi karena kemungkinan besar masih banyak faktor-faktor lain yang mempengaruhi nilai UASBN siswa SD/MI di Kecamatan Tulangan pada tahun ajaran 2009/2010 dan belum masuk dalam model level satu tersebut. Persentase variansi yang dijelaskan (proporsi pereduksian variansi) berdasarkan prediktor pada level 2 adalah sebagai berikut.

(6)

12

R_{level 2}2

₌

τmodel hanya intersep−τmodel signifikan

τmodel hanya intersep

= 1.35452 − 1.16141_1.35452 = 0,142567 ~ 14,26% Berdasarkan hasil berhitungan R2 berdasarkan variabel prediktor level 2 tersebut dapat diketahui bahwa nilai R_{level 2}2 adalah 14,26 persen. Hal tersebut menunjukkan bahwa variabel prediktor pada level dua yaitu pendidikan guru kelas enam mampu mereduksi variansi awal atau mampu menjelaskan nilai UASBN siswa sebesar 14,26 %. Nilai R_{level 2}2 tersebut relatif kecil mengingat masih banyak variabel lain pada sekolah penyelenggara UASBN yang mempengaruhi nilai UASBN siswa di sekolah tersebut.

2. Kesimpulan dan Saran 7.1 Kesimpulan

Berdasarkan hasil analisis data terhadap faktor-faktor yang mempengaruhi UASBN SD/MI di Kecamatan Tulangan pada tahun ajaran 2009/2010 dengan menggunakan analisis regresi multilevel, diperoleh hasil sebagai berikut.

1. Karakteristik peserta UASBN dan sekolah penyelenggara UASBN SD/MI di Kecamatan Tulangan pada tahun 2009/2010 adalah sebagai berikut.

a. Siswa peserta UASBN terdiri dari 48% laki-laki dan 52% perempuan. 38% siswa berusia 13 tahun, 56% berusia 12 tahun dan sisanya berusia 11, 14, dan 15 tahun. 55% peserta UASBN memiliki 1 saudara, 25% memiliki 2 saudara, 13% memiiki 3 saudara, 7% anak tunggal dan sisanya memiliki 4 saudara.

b. Sekolah penyelenggara UASBN terdiri dari 68% sekolah dengan akreditasi B dan 32% berakreditasi A. 31 sekolah adalah SD Negeri, 1 SD swasta non madrasah, dan 12 MI. 57% sekolah memiliki guru kelas 6 berpendidikan PGSD dan 43% guru kelas 6 non-PGSD.

2. Faktor-faktor yang mempengaruhi nilai UASBN SD/MI di Kecamatan Tulangan tahun ajaran 2009/2010 adalah jenis kelamin, umur, nilai raport kelas IV, dan pendidikan guru. Setiap peningkatan umur siswa, nilai UASBN cenderung berkurang sebesar 0,26 dan pada setiap peningkatan nilai raport kelas 4 semester 1 pada tiga pelajaran UASBN, nilai UASBN cenderung bertambah sebesar 0,22 satuan. Perpotongan pada sumbu x (intersep) untuk siswa laki-laki dengan pendidikan guru kelas PGSD dan non PGSD maupun siswa

perempuan dengan pendidikan guru kelas PGSD maupun non PGSD berturut-turut adalah sebesar 22,33, 21,43, 22,73 dan 21,83.

7.2 Saran

Adapun saran yang dapat diberikan setelah melakukan penelitian adalah perlu digali lebih lanjut akan faktor-faktor yang mempengaruhi nilai UASBN siswa disamping faktor-faktor yang telah diteliti di atas. Hal tersebut mengingat masih banyak lagi faktor-faktor yang mungkin mempengaruhi ketidak-berhasilan seorang siswa dalam UASBN.

3. PUSTAKA

BSNP. (2008). Standar Nasional Pendidikan. Jakarta : BSNP dan BALITBANG. Dewi L., Anastasia. (2008). Estimasi Parameter

Regresi Logistik Multilevel. Jakarta:

Skripsi FMIPA UI.

Ermawati. (2008). Perbandingan Prestasi Belajar

Siswa dengan Mengunakan Multigroup Structural Equation model. Surabaya:

Tesis Jurusan Statistika ITS.

Mendiknas. (2009). Permendiknas No.74 Th.2009

Tentang Ujian Akhir Sekolah Berstandar Nasional (UASBN) Sekolah Dasar/Madrasah Ibtidaiyah/Sekolah Dasar Luar Biasa (SD/MI/SDLB) Tahun

Pelajaran 2009/2010. Jakarta:

Mendiknas press.

Dalyono, M. dan TIM MKDK IKIP Semarang. (1997). Psikologi Pendidikan. Semarang: IKIP Semarang Press.

Drapper, N.R. dan Smith, H. (1981). Applied

Regression Analysis. New York: John

Wiley & Sons.

Goldstein, H. (2003). Multilevel Statistical Models. London: Arnold Publishers.

Hox, J.J. (2002). Multilevel Analysis: Techniques

and Applications. Mahwah: Lawrence

Erlbaum Associates.

Kreft, I. dan De Leeuw. (1998). Introducing

Multilevel Modeling. London: Sage.

Raudenbush, S., dkk. (2001). HLM 7: Hierarchical

Linear and Nonlinear Model. USA: SSI,

Inc.

Singer, J.D. dan Willet, J.B. (2003). Applied

Longitudinal Data Analysis: Modelling Change and Event Occurrence. London:

Oxford University Press.

Sutarsih. (2008). Pemodelan Nilai UNAS Dengan

Pendekatan Regresi Spline. Surabaya : Tesis