2-EKSPONEN DARI DIGRAPH DWIWARNA ASIMETRIK YANG MEMUAT CYCLE PRIMITIF TESIS

2-EKSPONEN DARI DIGRAPH DWIWARNA ASIMETRIK

YANG MEMUAT CYCLE PRIMITIF

TESIS

Oleh

TITIK NGATMINTARSIH 067021030/MT

SEKOLAH PASCASARJANA

UNIVERSITAS SUMATERA UTARA

MEDAN

2008

2-EKSPONEN DARI DIGRAPH DWIWARNA ASIMETRIK

YANG MEMUAT CYCLE PRIMITIF

TESIS

Untuk Memperoleh Gelar Magister Sains dalam

Program Studi Magister Matematika pada Sekolah Pascasarjana Universitas Sumatera Utara

Oleh

TITIK NGATMINTARSIH 067021030/MT

SEKOLAH PASCASARJANA

UNIVERSITAS SUMATERA UTARA

MEDAN

2008

Judul Tesis : 2-EKSPONEN DARI DIGRAPH DWIWARNA ASIMETRIK YANG MEMUAT CYCLE PRIMITIF

Nama Mahasiswa : Titik Ngatmintarsih

Nomor Pokok : 067021030

Program Studi : Matematika

Menyetujui, Komisi Pembimbing

(Dr. Saib Suwilo, M.Sc) (Drs. Opim Salim S, M.IKom, PhD)

Ketua Anggota

Ketua Program Studi Direktur

(Prof. Dr. Herman Mawengkang) (Prof. Dr. Ir. T.Chairun Nisa. B,M.Sc)

Telah diuji pada : Tanggal 6 Juni 2008

PANITIA PENGUJI TESIS

Ketua : Dr. Saib Suwilo, M.Sc

Anggota : Drs. Opim Salim Sitompul, MI.Kom, PhD

Dr. Tulus, M.Si

2-EKSPONEN DARI DIGRAPH DWIWARNA ASIMETRIK YANG MEMUAT CYCLE PRIMITIF

TESIS

Saya mengakui bahwa tesis ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, 20 Juni 2008

TITIK NGATMINTARSIH 067021030

ABSTRAK

Suatu digraph dwiwarna adalah sebuah digraph dengan setiap arcnya terwarnai, merah atau biru. Sebuah digraph dwiwarna D dikatakan terhubung kuat bila ada bilangan tak negatif h dan k sehingga untuk setiap pasangan verteks u dan v ditemukan walk yang panjangnya h + k dengan h arc merah dan k arc biru. Bila-ngan bulat terkecil h + k dikatakan 2-eksponen dari D. Sebuah asimetrik digraph dwiwarna adalah sebuah simetrik digraph dwiwarna sedemikian bila (u, v) adalah arc merah maka (v, u) adalah arc biru, demikian sebaliknya. Sebuah digraph dwi-warna asimetrik yang mempunyai cycle primitif adalah sebuah digraph dwidwi-warna asimetrik dengan n verteks yang mempunyai cycle dengan panjang s dan path dengan panjang n − s yang terhubung dengan cycle dan tidak terhubung dengan cycle. Dalam tulisan ini ditunjukkan bahwa, sebuah digraph dwiwarna asimetrik yang memuat cycle primitif dengan panjang s ≥ 3 dan merupakan bilangan ganjil, memiliki 2 − exp(D) ≤ (s2− 1)/2 + (s + 1)(n − s).

Kata Kunci : Digraph Dwiwarna, Primitif, 2-Eksponen.

ABSTRACT

A two-colored digraph is a digraph in which each of arc colored by either red or blue. A strongly connected two-colored digraph D is primitive provided there are nonnegative integers h and k such that for each pair of vertices u and v one can find a walk from u to v of length h + k consisting of h red arc and k blue arc. The smallest positive integer h + k among all such nonnegative h and k is the 2-exponent of D. An asymmetric two-colored digraph is a symmetric digraph such that (u, v) is a red arc if and only if (v, u) is a blue arc and vice versa. An asymmetric two-colored digraph consisting of a cycles of length s and a path of length n − s connects a vertex on the cycle and a vertex not on the cycle. For an asymmetric two-colored digraph consisting of primitive cycle, odd length s ≥ 3, we show that 2 − exp(D) ≤ (s2_{− 1)/2 + (s + 1)(n − s)}

KATA PENGANTAR

Allhamdulillahirabbilalamin, segala Puji dan Syukur hanyalah untuk Allah SWT yang telah memberikan Rahamat dan Hidayah-Nya kepada seluruh makhluk-Nya. Oleh karena Rahmat-Nya pula penulis dapat menyelesaikan tulisan ini yang berjudul ”2-Eksponen dari Digraph Dwiwarna Asimetrik yang Memuat Cycle Primitif”. Tulisan ini sebagai salah satu mata kuliah wajib yang harus diselesaikan oleh seluruh mahasiswa Sekolah Pascasarjana Universitas Sumatera Utara.

Pada kesempatan ini, penulis juga menyampaikan ucapan terima kasih dan penghargaan yang sebesar-besarnya kepada : Kepala Bappeda Propinsi Sumatera Utara beserta stafnya yang telah memberikan beasiswa kepada penulis, Kepala Dinas Pendidikan Kota Medan yang telah memberi izin mengikuti perkuliahan Program Pascasarjana di Universitas Sumatera Utara. Prof. dr. Chairuddin P. Lubis, DTM&H, Sp.Ak selaku Rektor Universitas Sumatera Utara dan Prof. Dr. Ir. T. Chairun Nisa B, M.Sc selaku Direktur Sekolah Pascasarjana Universitas Sumatera Utara beserta Stafnya yang telah memberi kesempatan kepada penulis untuk mengikuti perkuliahan pada Angkatan ke II Program Educator Tahun 2006. Penulis juga mengucapkan terima kasih kepada Pemerintah Propinsi Su-matera Utara yang telah memberi beasiswa kepada penulis, Bapak Prof. Herman Mawengkang dan Bapak Dr. Saib Siwilo, M. Sc selaku Ketua dan Sekretaris Pro-gram Studi matematika di Sekolah Pascasarjana Universitas Sumatera Utara. Ba-pak Dr. Saib Suwilo, M Sc selaku dosen pembimbing I, dan Drs. Opim S. Sitom-pul, M Ikom, Ph.D, selaku dosen pembimbing II yang telah memberi dukungan, waktu, tenaga, motivasi dan ilmu pengetahuan dalam menyelesaikan penelitian ini. Seluruh Staf Pengajar di Program Studi matematika Sekolah Pascasarjana

Universitas Sumatera Utara.

Dr. Tulus, MSi dan Drs. Marihat Situmorang, MKom selaku pembanding atas saran dan bantuannya untuk kesempurnaan penulisan tesis ini serta bimbi-ngan selama perkuliahan berlangsung.

Seluruh Staf Administrasi SPs USU, Ibu Misiani, S.Si, Saudari Sri Rayani Tanjung, S.Si, Indra Syahputra, S.Si, M. Idris, S.Si, Didi Febrian, S.Si dan Richad Albert Nasution, S.Si yang telah memberikan bantuan dan pelayanan yang baik kepada penulis.

Juandi Sidabutar dan Fauziah Hasibuan selaku ketua kelas dan bendahara atas kebersamaan dan bantuan dalam mengatasi masalah selama perkuliahan berlangsung.

Secara pribadi penulis mengucapkan ribuan terima kasih kepada Suami Dr. Sumarno, M.Pd dan Ananda Ilman, Fadhil dan Farid tercinta yang telah mem-berikan dukungan, semangat dan doa kepada penulis.

Drs. Ramly selaku Kepala Sekolah SMAN 11 Medan yang telah memberikan kesempatan dan dorongan kepada penulis hingga penulisan tesis ini selesai tepat waktu.

Selain itu, penulis mengucapkan ribuan terima kasih kepada Bapak, Ibu dan adik-adik yang telah memberikan doa dan motivasi, serta teman-teman setambuk dan seluruh rekan-rekan mahasiswa yang turut membantu penyelesaian tulisan ini. Semoga Allah SWT membalas semua jasanya.

Akhir kata penulis berharap bahwa tulisan ini bermanfaat terutama kepada penulis maupun para pembaca serta semua pihak yang berhubungan dengannya. Saya menyadari sepenuhnya bahwa tulisan ini sangat jauh dari sempurna. Oleh karena itu kritik dan saran yang membangun sangat diharapkan demi perbaikan.

Medan, 20 Juni 2008 Penulis,

Titik Ngatmintarsih

RIWAYAT HIDUP

Titik Ngatmintarsih dilahirkan di Simpang Periuk (Lubuk Linggau) tanggal 11 Maret 1966 dan merupakan anak pertama dari Bapak Supangat dan Ibu Sri Suwati. Menamatkan Sekolah Dasar (SD) Negeri di Simpang Periuk pada tahun 1979, Sekolah Menengah Pertama (SMP) Negeri Tugu Mulyo pada tahun 1982 dan Sekolah Menengah Atas (SMA) Negeri I Lubuk Linggau jurusan IPA pada tahun 1985. Pada tahun 1985 memasuki perguruan tinggi Negeri FKIP UNSRI Jurusan Matematika dan memperoleh Gelar Sarjana (S1) pada tahun 1990. Pada tahun 1993 penulis diangkat menjadi guru di SMA Negeri 1 Muara Keling. Pada tahun 1996 pindah tugas di SMA Negeri 11 Medan. Tahun 2001 sampai 2005 mengajar di SMA Negeri 7 Yogyakarta. Tahun 2005 sampai sekarang mengajar di SMA Negeri 11 Medan. Dan pada tahun 2006 diperkenankan mengikuti pendidikan Program Studi Magister Matematika di Sekolah Pascasarjana Universitas Sumatera Utara dengan program beasiswa dari Bappeda Propinsi Sumatera Utara.

DAFTAR ISI

Halaman

ABSTRAK . . . i

ABSTRACT . . . ii

KATA PENGANTAR . . . iii

RIWAYAT HIDUP . . . vi

DAFTAR ISI . . . vii

DAFTAR GAMBAR . . . ix BAB 1 PENDAHULUAN . . . 1 1.1 Latar Belakang . . . 1 1.2 Rumusan Masalah . . . 3 1.3 Tinjauan Pustaka . . . 3 1.4 Tujuan . . . 4 1.5 Kontribusi . . . 4 1.6 Metode Penelitian . . . 4

BAB 2 DIGRAPH DWIWARNA PRIMITIF . . . 5

2.1 Digraph . . . 5

2.2 Digraph Dwi Warna Atau 2- Digraph . . . 9

2.3 Digraph Dwiwarna Asimetrik . . . 15

2.4 Eksponen dari Digraph Dwiwarna atau 2-Digraph . . . 18

BAB 3 2-EKSPONEN DARI DIGRAPH DWIWARNA ASIMETRIK YANG MEMUAT CYCLE PRIMITIF . . . 25

3.1 Batas atas dari 2-exp(D) . . . 25

3.2 Digraph dwiwarna D yang memenuhi batas atas . . . 31

BAB 4 KESIMPULAN DAN SARAN . . . 33

4.1 Kesimpulan . . . 33

4.2 Saran . . . 33

DAFTAR GAMBAR

Nomor Judul Halaman

2.1 Representasi dari digraph . . . 6

2.2 (7,5)-lollipop . . . 9

2.3 Representasi Digraph Dwiwarna . . . 10

2.4 Representasi Digraph Dwiwarna 2 arc merah dan 3 arc biru . 12

2.5 Digraph Dwiwarna Terhubung kuat dan tidak Terhubung Kuat 13

2.6 Digraph Dwiwarna Terhubung Kuat Yang Primitif . . . 14

2.7 (1,5,3)-Lollipop Dua Tangkai . . . 18

2.8 Digraph Dwiwarna dengan 3 verteks, 3 arc biru dan 3 arc merah 21

BAB 1 PENDAHULUAN

1.1 Latar Belakang

Banyak situasi di dunia yang dapat digambarkan dengan memakai dia-gram yang terdiri atas sekumpulan titik-titik dan garis-garis, dimana garis-garis tersebut yang menghubungkan pasangan titik-titik. Misalnya, titik-titik tersebut mewakili seseorang, dengan garis-garis yang menghubungkan pasangan teman; atau titik-titik merupakan pusat-pusat komunikasi dengan garis mewakili hubu-ngan komunikasi. Pada diagram di atas seorang terutama tertarik pada apakah dua titik yang ada dihubungkan dengan garis atau tidak; cara bagaimana mereka (orang, atau pusat komunikasi) berhubungan tidak jadi persoalan. Abstraksi matematika dari situasi seperti ini memunculkan konsep graph.

Teori graph lahir pada tahun 1736 melalui tulisan Euler yang berisi tentang upaya pemecahan masalah jembatan Konigsberg di Eropa. Walaupun banyak formulasi graph secara teoritis, tetapi konsep-konsep graph kadang kala tidak cukup memadai untuk mengatasi masalah. Misalnya, berkenaan dengan problem arus lalu lintas.

Pada tahun 1859 Sir W.R. Hamilton menemukan suatu permainan yang kemudian dijualnya ke sebuah pabrik mainan di Dublin. Permainan tersebut dari kayu berbentuk dodecahedron beraturan yakni berupa sebuah polihedron dengan 11 muka dan 20 pojok. Tiap muka berbentuk sebuah pentagon beraturan dan tiap pojoknya dibentuk oleh tiga sisi berbeda. Tiap pojok dari dodekahedron tersebut

2

dipasangkan dengan sebuah kota terkenal seperti London, New York, Paris, dll. Masalah dalam permainan ini adalah diminta untuk mencari suatu rute melalui sisi-sisi dari dodecahedron sehingga tiap kota dari 20 kota yang ada dapat dilalui tepat satu kali.

Untuk mengatasi situasi seperti di atas graph tidak banyak berguna. Yang dibutuhkan adalah suatu graph yang masing-masing link mempunyai orientasi tetap/tertentu yang disebut dengan graph berarah (digraph). Digraph adalah salah satu disiplin ilmu dalam bidang matematika yang dapat digunakan untuk menganalisis dan memberikan hasil yang diharapkan guna mengatasi masalah-masalah seperti di atas.

Beberapa penelitian yang pernah dilakukan berkenaan dengan digraph, an-tara lain: Wielandt (1950) tentang digraph primitif (D) dengan n vertex. Dulmage dan Mendelsohn (1964) untuk digraph primitif (D) dengan n vertex dan panjang cycle terkecil s. Shao (1987) untuk digraph primitif simetrik dengan n vertex. Liu et al (1990) untuk digraph primitif simetrik tanpa loop (D) dengan n vertex. Suwilo dan Mardiningsih (2005) untuk digraph primitif simetrik D dan untuk (n, s)lollipop simetrik. Suwilo (2007) untuk (n, s)-lollipop asimetrik.

Mengacu pada penelitian-penelitian yang telah dilakukan di atas, baik yang berkenaan dengan digraph primitif, digraph primitif simetrik maupun 2-digraph, khususnya tentang 2-eksponen dwiwarna asimetrik (n, s)-lollipop, masih diper-lukan adanya penelitian lanjutan yang merupakan perluasan dari hasil pada lol-lipop dwiwarna, dalam menentukan batas atas dan batas bawah dari 2-eksponen. Pada tesis ini, penulis berkeinginan untuk meneliti 2-EKSPONEN DARI DI-GRAPH DWIWARNA ASIMETRIK YANG MEMUAT CYCLE PRIMITIF.

3

1.2 Rumusan Masalah

Misalkan D adalah digraph dwiwarna asimetrik untuk n verteks yang memuat cycle primitif dengan panjang s ≥ 3 merupakan bilangan ganjil, ditemukan batas atas dari 2-exp(D).

1.3 Tinjauan Pustaka

Shader dan Suwilo (2003) memperlihatkan bahwa 2-eksponen terbesar dari 2-digraph primitif terletak di interval [{n3− 5n2}/2, {3n3+ 2n2 − 2n}/2]. Batas bawah pada interval tersebut ditemukan dengan menggunakan 2-digraph yang terdiri dari dua cycle dan batas atas ditemukan secara teoritis. Sehingga masih terdapat gap antara empiris dan batas teoritis.

Suwilo (2001) memberikan definisi dari content matriks cycle M . Andaikan D suatu 2-digraph dan y = {γ1, γ2, . . . , γt} merupakan himpunan semua cycle di

D, suatu matriks cycle M dari D adalah matriks berukuran 2 × t yang masing-masing kolomnya terdiri dari cycle-cycle di D. Yang dinyatakan oleh

M = "

r(γ1) r(γ2) · · · r(yt)

b(γ1) b(γ2) · · · b(γt)

#

content dari M dinotasikan dengan cont(M ). Content(M ) = 0 jika rank (M ) = 1 dan Cont(M ) sama dengan pembagi persekutuan terbesar dari determinasi sub-matriks berukuran 2 × 2 dari M bila, rank(M ) = 2. Suwilo (2001) memberikan formula bagi 2-eksponen dari 2-digraph, yang terdiri atas cycle. Dan memperli-hatkan bahwa untuk 2-digraph yang asimetrik komplit maka 2 ≤ exp₂(D) ≤ 4.

4

1.4 Tujuan

Penelitian ini bertujuan mencari batas atas dari 2-eksponen digraph dwi-warna asymetrik yang memuat cycle primitive.

1.5 Kontribusi

Menemukan teorema baru dalam bidang digraph pada umumnya dan 2-eksponen dari digraph pada khususnya.

1.6 Metode Penelitian

Metodologi penilitian ini bersifat literatur atau kepustakaan dengan langkah-langkah sebagai berikut:

1. Menggambar digraph dwiwarna asimetrik yang memuat cycle primitif de-ngan panjang s ≥ 3 merupakan bilade-ngan ganjil, dimana warna arc dari masing-masing gambar berbeda.

2. Mengambil beberapa contoh gambar untuk ditentukan 2-Eksponennya. 3. Menguji rumusan yang telah diperoleh dengan software sederhana Twoexp. 4. Menentukan 2-Eksponen semua gambar dengan software sederhana Twoexp. 5. Mempelajari hubungan setiap gambar dengan 2-Eksponennya sehingga

di-peroleh kesimpulan.

6. Membuat sebuah teorema baru yang berkenaan dengan permasalahan yang diangkat

BAB 2

DIGRAPH DWIWARNA PRIMITIF

Pada bab ini akan dijelaskan mengenai teori-teori yang berhubungan dengan penelitian ini sehingga dapat dijadikan sebagai landasan berfikir dalam melakukan penelitian ini dan akan mempermudah dalam hal pembahasan hasil utama pada bab berikutnya. Adapun teori tersebut mencakup penjelasan digraph, digraph dwiwarna, serta eksponen dari digraph dan digraph dwiwarna.

2.1 Digraph

Digraph adalah sekumpulan titik-titik yang dihubungkan oleh garis-garis berarah. Titik (O) disebut dengan verteks. Garis berarah (→) disebut denga arc. Suatu digraph D (graph berarah) adalah suatu objek yang terdiri atas dua himpunan, yaitu himpunan hingga dan tak kosong V , bersama dengan himpunan bagian A dari himpunan pasangan berurut V ×V . Unsur dari himpunan V disebut verteks dari digraph D dan unsur dari himpunan A disebut arc dari digraph D. Pada sebuah arc (u, v) verteks u disebut verteks inisial dan verteks v disebut verteks terminal.

Definisi 2.1 Sebuah graph berarah (directed graph) atau digraph D adalah suatu

objek yang dibentuk oleh himpunan tak kosong V yang unsurnya disebut verteks dari digraph D, dan himpunan A ⊆ V × V yang unsurnya disebut arc dari D.

6

Jika diberikan a, b ∈ V dengan (a, b) ∈ A, maka terdapat arc dari verteks a ke verteks b di digraph D. Verteks a disebut sebagai verteks awal dan verteks b disebut sebagai verteks akhir.

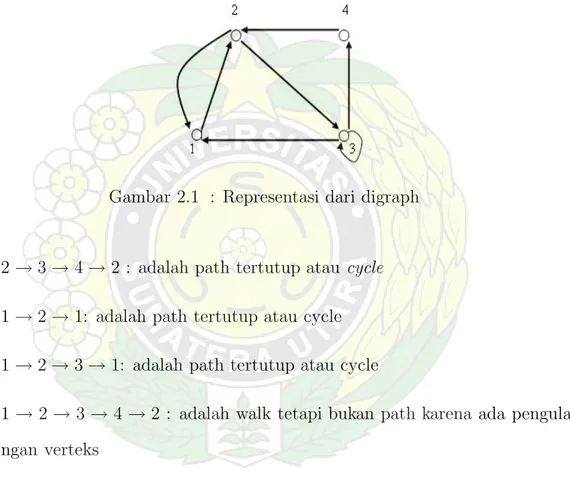
Contoh 2.1 Merupakan representasi dari digraph, gambarnya sebagai berikut:

Gambar 2.1 : Representasi dari digraph

2 → 3 → 4 → 2 : adalah path tertutup atau cycle

1 → 2 → 1: adalah path tertutup atau cycle

1 → 2 → 3 → 1: adalah path tertutup atau cycle

1 → 2 → 3 → 4 → 2 : adalah walk tetapi bukan path karena ada pengula-ngan verteks

3 → 3: adalah sebuah loop

Untuk memaparkan tentang digraph, penulis mengikuti notasi dan termi-nologi yang disampaikan oleh Brualdi dan Ryser (1991), dan digraph dwiwarna oleh Shader dan Suwilo (2003). Sebuah directed walk dengan panjang m dari u ke v adalah suatu barisan m arc dalam bentuk:

7

yang dinotasikan oleh (u, v)-walk atau wuv dan panjangnya dinotasikan oleh

l(wuv). Suatu (u, v)-walk adalah tertutup bila u = v dan terbuka untuk yang

lainnya. Suatu directed path dari u ke v adalah (u, v)-walk dengan tidak ada pengulangan verteks, kecuali mungkin u = v. Suatu directed cycle adalah path tertutup. Suatu loop adalah cycle tertutup dengan panjang 1.

Suatu digraph D adalah dikatakan terhubung kuat (strongly connected) bila untuk setiap pasangan verteks u dan v di D ada suatu (u, v)-walk dan (v, u)-walk. Suatu digraph terhubung kuat D dikatakan primitif bila terdapat bilangan bulat positif k sehingga untuk setiap pasangan verteks u dan v di D dapat ditemukan suatu (u, v)-walk dan (v, u)-walk dengan panjang k. Bilangan k terkecil demikian dikatakan eksponen dari D yang dinotasikan oleh exp(D). Suatu digraph ter-hubung kuat D adalah primitif jika dan hanya jika pembagi persekutuan terbesar dari panjang semua cycle di D adalah 1 (Dulmage dan Mendelsohn, 1964).

Lemma 2.2 Andaikan D adalah suatu digraph dwiwarna terhubung kuat maka

setiap verteks terletak pada cycle.

Bukti. Ambil sebarang verteks v di D dan sebarang arc dari verteks u ke verteks v di D. Karena terhubung kuat, maka terdapat path dari verteks v dan u dan dari verteks u ke v, akibatnya diperoleh suatu path tertutup di D, yang dibentuk oleh arc dari verteks u ke v dan verteks v ke u di D. Oleh defenisi verteks v terletak pada suatu cycle.

Suatu digraph dwiwarna terhubung kuat D dikatakan primitif jika terdapat bilangan bulat tak negatif h dan k sehingga untuk setiap pasangan verteks u dan v di D terdapat (h, k)-walk dari u ke v.

8

Andaikan himpunan C = {c1, c2, . . . , ct} adalah himpunan semua cycle di D.

Misalkan M adalah suatu matriks baris dengan kolom ke-i untuk i = 1, 2, . . . , t dari M adalah panjang cycle ci(l(ci)). Misalkan hM i sebagai subgroup dari grup

bilangan bulat Z yang dibangun oleh kolom-kolom dari M yakni

hM i = {zil(c1) + z2l(c2) + · · · + ztl(ct) : zi∈Z, i = 1, 2, 3, . . . , t}

Andaikan D adalah digraph imprimitif dengan indeks imprimitifitas k, dan k = gcd {l(c1), l(c2), . . . , l(ct)} Suatu digraph dikatakan primitive jika k = 1 dan

im-primitif jika k 6= 1

Teorema 2.3 Andaikan D adalah sebuah digraph terhubung kuat. Digraph D

adalah primitif jika dan hanya jika pembagi persekutuan terbesar (gcd) dari pan-jang cycle-cycle di D adalah 1.

Bukti. Andaikan D adalah primitif. Maka untuk setiap pasangan verteks u dan v di D, u ∼ v. Karena l(wuv) ∈ H untuk setiap pasang verteks u dan v di

D dan setiap walk wuv dari u ke v maka u ∼ v. Di ambil walk dengan

pan-jang 1, maka 1 ∈ H, karena H = { gcd (l(γ1), l(γ1), . . . , l(γi))} maka pembagi

persekutuan dari cycle-cycle di D haruslah sama dengan 1. Sebaliknya andaikan gcd(l(γ1), l(γ1), . . . , l(γi)) = 1, maka H = Z sehingga untuk setiap pasangan

verteks u dan v di D dan setiap walk wuv dari u dan v di D diperoleh l(wuv) ∈ H.

Sehingga masing-masing pasangan verteks di D adalah ekivalen. Akibatnya D adalah primitif.

Sebuah simetrik digraph D adalah suatu digraph sedemikan hingga arc (u, v) dan arc (v, u) ada di D. Karena sebuah simetrik digraph mempunyai suatu cycle

9

dengan panjang 2, maka sebuah simetrik digraph adalah primitif jika dan hanya jika mengandung cycle dengan panjang ganjil.

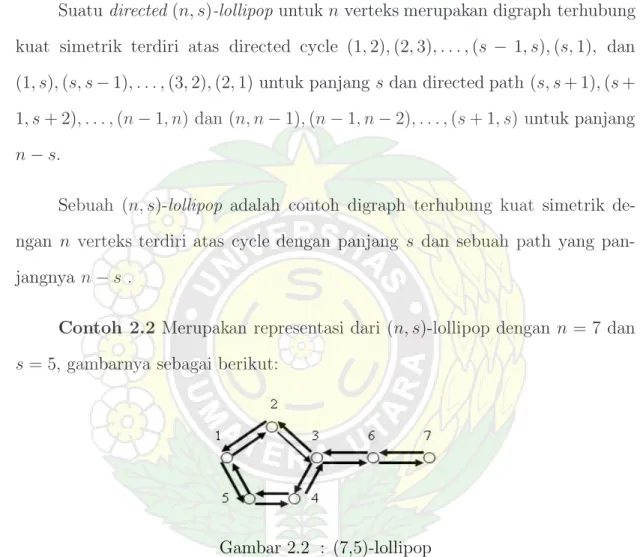
Suatu directed (n, s)-lollipop untuk n verteks merupakan digraph terhubung kuat simetrik terdiri atas directed cycle (1, 2), (2, 3), . . . , (s − 1, s), (s, 1), dan (1, s), (s, s − 1), . . . , (3, 2), (2, 1) untuk panjang s dan directed path (s, s + 1), (s + 1, s + 2), . . . , (n − 1, n) dan (n, n − 1), (n − 1, n − 2), . . . , (s + 1, s) untuk panjang n − s.

Sebuah (n, s)-lollipop adalah contoh digraph terhubung kuat simetrik de-ngan n verteks terdiri atas cycle dede-ngan panjang s dan sebuah path yang pan-jangnya n − s .

Contoh 2.2 Merupakan representasi dari (n, s)-lollipop dengan n = 7 dan

s = 5, gambarnya sebagai berikut:

Gambar 2.2 : (7,5)-lollipop

2.2 Digraph Dwi Warna Atau 2- Digraph

Suatu digraph dwiwarna atau 2-digraph adalah suatu digraph yang masing-masing arcnya diberi warna misalnya merah atau biru. Dalam 2-digraph, walknya dibedakan oleh banyaknya arc yang merah atau biru. Dengan sebuah (h, k)T_-walk

dari u ke v,diartikan sebuah (u, v)-walk dengan panjang h + k yang terdiri dari h arc merah dan k arc biru. Sehingga walk (1, 3)T _{dapat berupa walk dengan}

10

panjang 4 yang seluruh arcnya berwarna biru kecuali arc pertama, atau seluruh arcnya berwarna biru kecuali arc kedua, atau seluruh arcnya berwarna biru ke-cuali arc ketiga, atau seluruh arcnya berwarna biru keke-cuali arc keempat. Secara umum (r(w), b(w))T_{-walk w diartikan suatu walk w yang terdiri dari r(w) arc}

merah dan b(w) arc biru. Vektor (r(w), b(w))T _{disebut komposisi walk w.}

Contoh 2.3 Digraph dwiwarna, gambarnya sebagai berikut:

Gambar 2.3 : Representasi Digraph Dwiwarna

Berdasarkan gambar 2.3 dapat ditunjukkan bahwa:

1−m→ 2−m→ 3−→ 3 adalah sebuah path tertutup atau cycle dari 1 ke 1 denganb komposisi " 2 1 # .

1−m→ 2−→ 1 adalah sebuah cycle dari 1 ke 1 dengan komposisib "

1 1 #

.

1−m→ 2−m→ 3−→ 1b −→ 3 adalah walk dari 1 ke 3 dengan komposisim "

3 1 #

tetapi bukan suatu path karena path adalah walk tanpa melalui lebih dari satu verteks kecuali mungkin verteks awal dan akhir

1−m→ 3−→ 1 adalah sebuah cycle dari 1 ke 1 dengan komposisib "

1 1 #

11

Suatu 2-digraph D terhubung kuat adalah primitif bila terdapat bilangan bulat tak negatif h dan k sehingga untuk setiap pasangan verteks u dan v terdapat walk dari u dan v dengan panjang h + k yang terdiri dari h arc berwarna merah dan k arc berwarna biru.

Suwilo (2001) memberikan definisi dari content matriks cycle M . Andaikan D suatu 2-digraph dan y = {γ1, γ2, . . . , γt} merupakan himpunan semua cycle di

D, suatu matriks cycle M dari D adalah matriks berukuran 2 × t yang masing-masing kolomnya terdiri dari cycle-cycle di D. Yang dinyatakan oleh

M = " r(γ1) r(γ2) · · · r(yt) b(γ1) b(γ2) · · · b(γt) # .

Content dari M dinotasikan dengan cont(M ). Content(M ) = 0 jika rank (M ) = 1 dan Cont(M) sama dengan pembagi persekutuan terbesar dari deter-minasi submatiks berukuran 2 × 2 dari M bila, rank(M ) = 2.Hasil berikut ini, menurut Fornasini dan Valcher (1997) memberikan syarat penting dan memadai untuk digraph dwiwarna primitif.

Teorema 2.4 Misalkan D adalah digraph dwiwarna yang terhubung kuat dengan

sedikitnya satu arc dari setiap warna. Digraph dwiwarna D adalah primitif jika dan hanya jika content matriks cycle adalah 1

Sebuah digraph dwiwarna D dengan n verteks dapat dinyatakan oleh matriks, yang entri dari matriks tersebut adalah bilangan 1 atau 0, matriks yang demikian disebut sebagai matriks adjacency, dinyatakan sebagai berikut.

12

Matriks adjacency merah, R = [rij] pada D adalah matriks n × n dengan

rij =       

1 jika arc (i, j) adalah arc merah 0 jika sebaliknya

matriks adjacency biru B = [bij] pada D adalah matriks n × n, dengan

bij =       

1 jika arc (i, j) adalah arc biru 0 jika sebaliknya

berikut ini akan diberikan sebuah digraph dwiwarna dan dipresentasikan ke dalam matriks adjacencynya.

Contoh 2.4 Representasi lain dari sebuah digraph dwiwarna:

Gambar 2.4 : Representasi Digraph Dwiwarna 2 arc merah dan 3 arc biru

Dari representasi digraph dwiwarna diatas, dapat dibuat sebuah matriks adjacency merah (R) dan matriks adjacency biru (B) sebagai berikut:

R =         0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0         B =         0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0        

13

Digraph dwiwarna D dikatakan terhubung kuat (strongly connected) jika untuk setiap pasangan verteks u dan v di D terdapat walk berarah dari verteks u ke v dan walk berarah dari verteks v ke u, dengan mengabaikan komposisi arc yang ada.

Berikut ini diberikan contoh digraph dwiwarna yang terhubung kuat dan digraph dwiwarna yang tidak terhubung kuat.

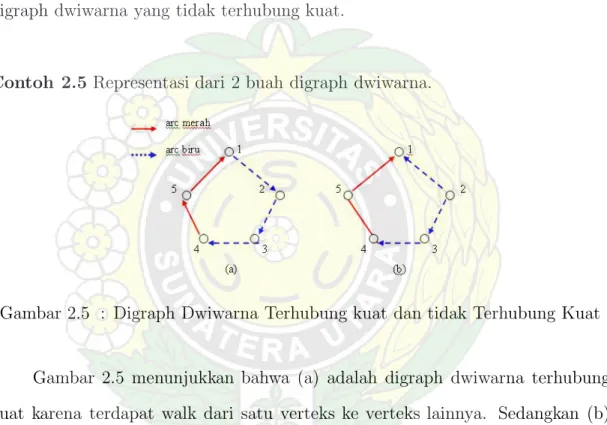
Contoh 2.5 Representasi dari 2 buah digraph dwiwarna.

Gambar 2.5 : Digraph Dwiwarna Terhubung kuat dan tidak Terhubung Kuat

Gambar 2.5 menunjukkan bahwa (a) adalah digraph dwiwarna terhubung kuat karena terdapat walk dari satu verteks ke verteks lainnya. Sedangkan (b) adalah diagrap dwiwarna tidak terhubung kuat, karena tidak terdapat walk dari 1 ke 2.

Proposisi 2.5 Andaikan D adalah digraph dwiwarna terhubung kuat, dan

misal-kan u dan v adalah verteks di D dan misalmisal-kan w1 dan w2 adalah walk dari u ke

v di D. Maka: _" r (w1) b (w1) # − " r (w2) b (w2) # ∈ hM i

14

Bukti. Karena D adalah digraph dwiwarna terhubung kuat, maka terdapat walk wvu dari v ke u. Misalkan w01 adalah walk tertutup yang dibentuk oleh u

w1

−→ v wvu

−−→ u dan misalkan w0

2adalah walk tertutup yang dibentuk oleh u w2

−→ v wvu

−−→ u. Karena untuk setiap walk tertutup dapat dikomposisi menjadi cycle,

" r (w0 1) b (w0 1) # , " r (w0₂) b (w0 2) # ∈ hM i sehingga " r (w1) b (w1) # − " r (w2) b (w2) # = " r (w0₁) b (w0 1) # − " r (w0₂) b (w0 2) # ∈ hM.i

Diberikan D adalah sebuah digraph dwiwarna dan z adalah verteks di D. Dua vertks u dan v di D dikatakan ekivalen, di notasikan u ∼2 v, bila terdapat

sebuah walk wzu dari z ke u dan sebuah walk wzv dari z ke v dengan komposisi

yang sama. Dalam kasus verteks ekivalen, definisi dari ekivalen verteks adalah verteks di D yang dipilih secara bebas. Lebih lanjut, hal itu ditunjukkan oleh hubungan ∼2 adalah hubungan ekivalen dengan himpunan dari verteks di D dan

partisi dari himpunan verteks di D ke dalam kelas ekivalen. Bilangan dari kelas ekivalen k2 dari D disebut dengan index imprimitifitas dari D. Sebuah digraph

dwiwarna terhubung kuat dikatakan primitif bila k2 = 1 dan imprimitif bila

sebaliknya.

Contoh 2.6 Representasi dari digraph dwiwarna terhubung kuat yang primitif.

15

Perhatikan gambar diatas, dimulai dari verteks 2. Walk 2 −→ 3 dan 2r −→ 1r adalah walk dari 2 ke 3 dan dari 2 ke 1 dengan komposisi yang sama. Sehingga 3 ∼2 1. Walk 2

r

−

→ 1 −→ 2b −→ 2 dan 2r −→ 2r −→ 1r −→ 2 adalah walk dari 2 ke 3 danb dari 2 ke 2. Sehingga 3 ∼2 2, dengan sifat transitif kita peroleh 1 ∼2 2 akibatnya,

D adalah primitif.

2.3 Digraph Dwiwarna Asimetrik

Sebuah digraph dwiwarna asimetrik D adalah digraph simetrik D sedemikian sehingga arc (u, v) merah bilamana arc (v, u) biru, dan sebaliknya. Sebuah di-graph D adalah sebuah didi-graph komplit bila untuk masing-masing pasangan verteks yang berbeda u dan v keduanya (u, v) dan (v, u) adalah arc pada D. Sebuah digraph dwiwarna asimetrik komplit D adalah sebuah digraph asimetrik sedemikian sehingga digraph adalah komplit.

Teorema 2.6 Andaikan D sebuah digraph dwiwarna asimetrik primitif komplit

dengan verteks n ≥ 3, maka 2-exp(D) ≤ 4.

Bukti: Misal u dan v adalah verteks di D. Akan ditunjukkan bahwa ada (2,2)-walk dari u ke v sehingga D mempunyai verteks n ≥ 3, ada sebuah verteks x di D dimana x 6= u, v. Jika u = v, maka walk u → x → u → x → u adalah (2,2)-walk dari u ke u. Asumsi bahwa u 6= u.

Andaikan

VR(u) = {x ∈ V : x 6= v dan arc(u, x) adalah arc merah} dan

16

Jika ada x ∈ VR(u) sehingga arc (x, v) adalah arc biru, maka walknya

u−→ xr −→ vb −→ xr −→ vb

walk diatas adalah (2,2)-walk dari u ke v di D. dengan cara yang sama jika ada y ∈ VB(u) sehingga arc (y, v) adalah arc merah, maka walknya

u−→ yb −→ vr −→ yb −→ vr

walk diatas adalah (2,2)-walk dari u ke v. Karena diasumsikan bahwa (x, y) merah untuk setiap x ∈ VR(u), dan (y, v) adalah biru untuk setiap y ∈ VB(u).

Jika n ≥ 3, VR(u) 6= ∅ atau VB(u) 6= ∅ Berikut ini disajikan tiga kasus:

Kasus 1: VR(u) = ∅ dan VB(u) = ∅

Andaikan x ∈ VR(u). Jika arc (u, v) merah, maka walknya u r

−

→ v −→ xb −→b u −→ v adalah (2, 2)-walk dari u ke v. Andaikan arc (u, v) biru. Cycle u →r x → u, u → v → u, x → v → x, u → x → v → u dan x → u → v → x mempunyai komposisi berturut-turut

" 1 1 # , " 1 1 # , " 1 1 # , " 3 0 # dan " 0 3 # . Sehingga D

adalah 2-primitif dan content dari "

1 1 1 3 0 1 1 1 0 3 #

adalah bukan 1, |VR(u) > 1|.

Andaikan x1 dan x2 verteks yang berbeda di VR(u). Jika arc (x1, x2) merah, maka

u−→ vb −→ xb 1 r − → x2 r −

→ v adalah (2,2)-walk dari u ke v. Jika arc (x1, x2) biru, maka

u−→ vb −→ xb 2 r − → x1 r −

→ v adalah (2,2)-walk dari u ke v.

Kasus 2: VR(u) = ∅ dan VB(u) 6= ∅.

Sebuah argumen yang serupa dengan VR(u) = ∅ dan VB(u) = ∅ dari kasus 1

menunjukkan bahwa untuk masing-masing pasangan verteks u dan v di D ada (2,2)-walk dari u ke v.

17

Kasus 3 : VR(u) = ∅ dan VB(u) = ∅

Pilih x ∈ VR(u) dan y ∈ VB(u). Jika arc (u, v) merah maka walknya u r

− → v −→b x −→ ub −→ v adalah (2,2)-walk dari u ke v. Jika arc (u, v) biru maka walknya,r maka walknya u−→ vb −→ yr −→ ur −→ v adalah (2,2)-walk dari u ke v.b

Oleh karena itu, untuk masing-masing pasangan verteks u dan v, ada (2,2) walk dari u ke v.

Catatan bahwa sebuah digraph dwiwarna terhubung kuat untuk n verteks yang terdiri atas sebuah loop merah dan sebuah loop biru pada verteks yang sama, maka 2-exp(D) ≤ 2n − 2, menyatakan secara tidak langsung hasil tersebut tentang tipe khusus digraph dwiwarna primitif asimetrik.

Proposisi 2.7 Andaikan sebuah digraph dwiwarna asimetrik terhubung kuat yang

terdiri atas path 1 → 2 · · · → n − 1 → n, n → n − 1 · · · → 2 → 1 dan loop (n, n). Maka 2-exp(D) ≤ 2n − 2.

Andaikan digraph D pada proposisi diatas diwarnai sehingga 1 → 2 · · · → n−1 → n adalah path merah dan dan path n → n − 1 · · · → 2 → 1 adalah path biru, maka 2-exp(D) ≤ 2n − 2 dan dicapai dengan (n − 1, n − 1)-walk.

Misalkan D adalah 2-primitif asimetrik dengan n cycle. Karena digraph D adalah primitif, n ganjil. Karena D simetriks, cycle di D mempunyai panjang 2 atau n. Selanjutnya D mempunyai tepat 2 cycle yang panjangnya n.

Andaikan:

γ1 adalah cycle 1 → 2 · · · → n − 1 → n dan

masing-18

masing cycle di D berturut-turut " 1 1 # , " n − a a # atau " a n − a # untuk a bilangan bulat tak negatif.

Sebuah (n1, s, n2)-lollipop dua tangkai adalah digraph dwiwarna yang

ter-diri atas cycle dengan panjang s dan sebuah path yang panjangnya n−s = n1+n2.

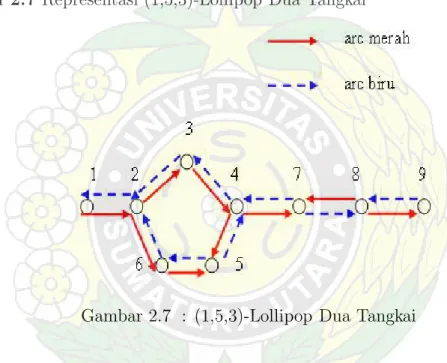
Contoh 2.7 Representasi (1,5,3)-Lollipop Dua Tangkai

Gambar 2.7 : (1,5,3)-Lollipop Dua Tangkai

Gambar di atas merupakan representsi digraph dwiwarna asimetriks dengan 9 verteks yang terdiri atas cycle dengan panjang 5 dan sebuah path yang pan-jangnya 4.

2.4 Eksponen dari Digraph Dwiwarna atau 2-Digraph

Studi batas eksponen dari suatu digraph dimulai oleh Wielandt. Wielandt (1950) menyatakan, andaikan D adalah digraph terhubung kuat dan primitif de-ngan n verteks maka exp(D) ≤ (n − 1)2 + 1. Sejak saat itu studi eksponen

19

pada suatu digraph dengan sifat-sifat khusus mulai dikembangkan. Secara khusus, Dulmage dan Mendelsohn (1964) memberikan batasan yang lebih umum untuk eksponen digraph primitif berdasarkan panjang cycle terkecilnya. Mereka mem-perlihatkan bahwa jika D adalah digraph primitif dengan n verteks dan cycle terkecil s, maka exp(D) ≤ n + s(n − 2).

Beasley dan Kirkland (1997) mendiskusikan suatu batas eksponen dari di-graph primitif yang berkenaan eksponen dari subdidi-graph primitif. Untuk didi-graph simetrik primitif untuk n verteks, Shao (1987) membuktikan bahwa exp(D) ≤ 2n − 2, dan menunjukkan bahwa eksponen 2n − 2 dicapai jika dan hanya jika digraph D isomofik dengan simetrik digraph yang mengandung directed path (1, 2), (2, 3), . . . , (n − 1, n) dan (n, n − 1), (n − 1, n − 2), . . . , (2, 1), dan loop (1, 1). Andaikan D adalah digraph primitif dan simetrik tanpa loop untuk n verteks,

Liu et. al. (1990) menunjukkan bahwa exp(D) ≤ 2n − 4,dan membuktikan

bahwa batas atas dicapai jika dan hanya jika D isomorfik dengan directed (n, 3)-lollipop. Dengan mengikuti Dulmage dan Mendelson (1964), Suwilo dan Mar-diningsih (2005) memperlihatkan bahwa batas atas eksponen digraph primitif dan simetrik adalah (s − 1) + 2l dengan s adalah panjang cycle terkecil dan l adalah panjang path terpanjang yang menghubungkan pada cycle terkecil dan verteks di D tetapi bukan pada cycle terkecil. Secara khusus mereka memperlihatkan bahwa eksponen dari (n, s)-lollipop simetrik adalah 2n − s − 1 yang kemudian mengimplikasikan bahwa eksponen cycle yang simetrik dengan panjang ganjil n adalah (n − 1).

Pada digraph dwiwarna D, eksponen didefenisikan sebagai bilangan bulat terkecil h + k sehingga untuk setiap pasangan verteks u dan v di D terdapat walk

20

dari u ke v dengan panjang h + k yang terdiri dari h arc merah dan k arc biru. Eksponen dari digraph dwiwarna D dinotasikan oleh exp2(D).

Misalkan D adalah digraph dwiwarna terhubung kuat pada n verteks. Mi-salkan R = (aij) adalah n × n (0,1)-matriks dengan rij = 1 jika dan hanya jika

arc (i, j) di D adalah arc merah, dan B = (bij) adalah matriks n × n

(0,1)-matriks dengan bij = 1 jika dan hanya jika arc (i, j) arc biru di D. Matrik R

dan B berturut-turut adalah matriks adjacency merah dan biru. Sebaliknya un-tuk pasangan (A, B) dari matriks tak negatif n × n dapat ditemukan digraph dwiwarna D pada n verteks yang berhubungan dengan (A, B) sebagai berikut:

Arc (i, j) pada D adalah arc merah jika dan hanya jika entri aij > 0 dan arc

(i, j) pada D adalah arc biru jika dan hanya jika bij > 0. Untuk setiap pasangan

matriks tak negatif (A, B) dan bilangan bulat tak negatif h dan k didefinisikan oleh (h, k)-hurwitz product, (A, B)(h,k) _{dari A dan B merupakan jumlah semua}

matriks dari perkalian A sebanyak h kali dan B sebanyak k kali.

Lemma 2.8 Jika (R, B) adalah matriks adjacency dari 2-digraph D. Maka entri

(i, j) dari (R, B)(h,k) _{adalah jumlah (h, k)-walk dari 2-digraph D.}

Bukti. Akan dibuktikan dengan induksi pada h + k, jika h + k = 1, h = 0 dan k = 1 atau jika h = 1 dan k = 0. Jika h = 0 maka entri (i, j) dari (R, B)(0,1)_{= B}

adalah walk dengan komposisi "

0 1 #

di 2-digraph D. Dengan cara yang sama, jika k = 0 maka (R, B)(1,0) _{= R adalah walk dengan entri (i, j) menyatakan walk}

dengan komposisi " 1 0 # di 2-digraph D.

21

Andaikan lemma 2.3.1 benar untuk semua bilangan bulat tak negative h dan k dengan h + k ≤ h + k akan diperlihatkan untuk h + k + 1 adalah benar, dengan catatan sebagai berikut:

(R, B)(h+1,k) = R(R, B)(h,k)+ B(R, B)(h+1,k−1)

dengan induksi entri (i, j) pada R(R, B)(h,k) _{adalah walk dari i ke j diikuti}

de-ngan sebuah arc merah dan diikuti oleh sebuah (h, k)-walk dari entri (i, j) pada B(R, B)(h+1,k−1) _{adalah jumlah walk dari i ke j yang dimulai dengan sebuah arc}

biru dan diikuti oleh sebuah (h + 1, k − 1)-walk sedemikian hingga entri (i, j) dari (R, B)(h+1,k) _{adalah jumlah (h + 1, k)-walk dari i ke j.}

Dari Lemma 3.2.1 dapat diambil kesimpulan bahwa 2-eksponen digraph dwi-warna primitif dapat dihitung dengan mencari bilangan bulat positif terkecil h + k sehingga seluruh entri matriks (A, B)(h,k) adalah positif untuk bilangan bulat tak negatif h dan k.

Contoh 2.8 Representasi grafis digraph dwiwarna asimetrik.

22

Berdasarkan Gambar 2.8 diatas didapat matriks adjacency sebagai berikut: Matriks adjacency merah R =

   0 0 0 1 0 0 1 1 0  

 dan Matriks adjacency biru B =    0 0 1 0 0 1 0 0 0    a. Untuk h + k = 1 (a) (R, B)(1,0)= R =    0 0 0 1 0 0 1 1 0    (b) (R, B)(0,1)_{= B =}    0 1 1 0 0 1 0 0 0    b. Untuk h + k = 2 (a) (R, B)(2,0)_{= RR =}    0 0 0 0 0 0 1 0 0    (b) (R, B)(1,1)= RB + BR =    2 1 0 1 2 1 0 1 2    (c) (R, B)(0,2)_{= BB =}    0 0 1 0 0 0 0 0 0    c. Untuk h + k = 3 (a) (R, B)(3,0)_{= RR}2 ₌    0 0 0 0 0 0 0 0 0   

23 (b) (R, B)(2,1)_{= R(R, B)}(1,1)_{+ B(R, B)}(2,0)₌    1 0 0 3 1 0 3 3 1    (c) (R, B)(1,2)= R(R, B)(0,2)+ B(R, B)(1,1)=    1 3 3 0 1 3 0 0 1    (d) (R, B)(0,3)= B3 =    0 0 0 0 0 0 0 0 0    d. Untuk h + k = 4 (a) (R, B)(4,0)= R4 = R.R3 =    0 0 0 0 0 0 0 0 0    (b) (R, B)(3,1)_{= R(R, B)}(2,1)_{+ B(R, B)}(3,0)₌    0 0 0 1 0 0 4 1 0    (c) (R, B)(2,2)= R(R, B)(1,2)+ B(R, B)(2,1)=    6 4 1 4 6 4 1 4 6   

Untuk h + k = 4 merupakan matriks positif dengan komposisi arc "

2 2 #

, 2 arc merah dan 2 arc biru, artinya terdapat walk dari tiap pasangan verteks u dan v di digraph dwiwarna D, sehingga digraph dwiwarna pada contoh 7 diatas memiliki eksponen 4 dengan komposisi arc

" 2 2 #

, 2 arc merah dan 2 arc biru.

Penelitian tentang 2-eksponen digraph dwiwarna diawali oleh Shader dan Suwilo (2003). Mereka membuktikan bahwa 2-eksponen terbesar dari digraph dwiwarna primitif pada n verteks terletak pada interval [(n3_−5n2_{)/2, (3n}3_+2n2₋

24

2n)/2]. Sejak itu banyak paper telah dipublikasikan tentang subyek yang sama.Lee dan Yang (2005) tentang 2-eksponen digraph extremal ministrong berada dalam interval [2n2 _{− 8n + 7, 2n}2 _{− 5n + 3]. Suwilo (2001) tentang 2-eksponen digraph}

primitif asimetrik komplit berada dalam interval [2,4] dan ada tepat k dengan 2 ≤ k ≤ 4. Suwilo dan Shader (2006) tentang 2-eksponen digraph dwiwarna n verteks primitif berada dalam interval 2n2_{− 8n + 7, 2n}2_{− 7n + 6]. Suwilo (2007)}

tentang 2-eksponen suatu (n, s)- lollipop dwiwarna primitif asimetrik 2−exp(D) ≤ (s2_{− 1)/2 + (s + 1)(n − s).}

BAB 3

2-EKSPONEN DARI DIGRAPH DWIWARNA ASIMETRIK YANG MEMUAT CYCLE PRIMITIF

Pada bab ini akan dipaparkan hasil penelitian ini yang diperoleh berdasarkan penjelasan-penjelasan yang telah dipaparkan pada bab-bab sebelumnya. Pertama-tama disini akan di tunjukkan bahwa 2-eksponen dari digraph dwiwarna yang memuat cycle primitif mempunyai batas atas (s2 _{− 1)/2 + (s + 1)(n − s) dan}

batasan tersebut dapat di representasikan sebagai (q, q)T_{-walk dengan t = (s}2 ₋

1)/4 + (s + 1)(n − s)/2. Selanjutnya akan dibahas mengenai karakteristik atas batasan dari 2-eksponen dari digraph dwiwarna asimetrik yang memuat cycle primitif.

3.1 Batas atas dari 2-exp(D)

Andaikan D adalah suatu digraph dwiwarna asimetrik (n1, s, n2)-lollipop dua

tangkai yang memuat cycle primitif dengan s ≥ 3 maka s harus ganjil. Karena D asimetrik, maka D mempunyai cycle yang panjangnya 2 dengan komposisi (1, 1)T _{dan juga mempunyai dua cycle γ}

1 dan γ2 yang panjangnya masing-masing

n dengan

γ1 : 1 → 2 → 3 → · · · → s → 1 dan

γ2 : s → (s − 1) → · · · → 2 → 1.

Sehingga D mempunyai komposisi cycle yang berbentuk (1, 1)T_{, (a, s − a)}T _dan

26 D berbentuk M = " a s − a 1 1 · · · 1 s − a a 1 1 · · · 1 #

Dari matriks M diatas menghasilkan matriks minor M , yaitu:

M1 =

"

a s − a

s − a a

#

Determinan matriks M1 = s(2a − s)

M2 = " s − a 1 a 1 # Determinan matriks M2 = s − 2a M3 = " a 1 s − a 1 # Determinan matriks M3 = 2a − s

Karena D primitif, maka oleh Teorema 2,1,1 content matriks M adalah 1. Akibatnya

1 = gcd(s(2a − s), s − 2a, 2a − s) = ±(s − 2a)

Dari 1 = ±(s − 2a) diperoleh:

s − 2a = 1 maka a = (s + 1)/2 −(s − 2a) = 1 maka a = (s − 1)/2

Sehingga a = (s + 1)/2 atau a = (s − 1)/2. Tanpa kehilangan keumumannya, dapat diasumsikan M = " (s − 1)/2 (s + 1)/2 1 1 · · · 1 (s + 1)/2 (s − 1)/2 1 1 · · · 1 #

27

Teorema 3.1 Andaikan D adalah suatu digraph dwiwarna asimetrik (n, s) yang

memuat cycle primitif dengan bilangan ganjil s ≥ 3 maka 2-exp(D) ≤ (s2_{− 1)/2 + (s + 1)(n − s)}

Bukti. Untuk setiap pasangan verteks u dan v ditunjukkan ada sebuah (q, q)T

-walk dari u ke v dengan q = (s2_{− 1)/4 + (s + 1)(n − s)/2. Karena D asimetrik,}

maka untuk setiap (h, k)T_{-walk dapat dibentuk menjadi (h + t, k + t)}T_{-walk untuk}

suatu t ≥ 1. Akibatnya cukup ditunjukkan bahwa ada (e, e)T_{-walk dengan e ≤ q.}

Andaikan u dan v adalah dua verteks berbeda di D dan puv adalah path terpendek

dari u ke v. Tanpa kehilangan keumumannya, dapat diasumsikan bahwa r(puv) ≥

b(puv).

Pertama diasumsikan bahwa path puv tidak mempunyai verteks persekutuan

dengan cycle γ1 atau γ2. Hal ini berakibat, walknya dimulai dengan verteks u,

bergerak menuju x sepanjang path pus dilanjutkan mengelilingi cycle γ1 sebanyak

(r(puv − b(puv)) dan kembali ke x, serta berakhir di verteks v sepanjang path

psv. Perjalanan walk ini menghasilkan (e, e)T-walk terpendek dari u ke v, dengan

komposisi walknya " r(wuv) b(wuv) # = " r(puv) b(puv) # + [r(puv) − b(puv)] " (s − 1)/2 (s + 1)/2 # + luv " 1 1 #

dengan luv = d(u, x) bila d(u, x) < d(v, x)) dan luv = d(v, x) bila d(v, x) < d(u, x).

28 " r(wuv) b(wuv) # ≤ " r(puv) b(puv) # + [r(puv) − b(puv)] " (s − 1)/2 (s + 1)/2 # + luv " (s + 1)/2 (s + 1)/2 # = [r(puv) + b(puv) + luv] " (s + 1)/2 (s + 1)/2 # − b(puv) " s s # ≤ (n − s) " (s + 1)/2 (s + 1)/2 # ≤ [(s − 1)/2 + (n − s)] " (s + 1)/2 (s + 1)/2 # = " (s2_{− 1)/4 + (n − s)(s + 1)/2} (s2_{− 1)/4 + (n − s)(s + 1)/2} #

Kedua diasumsikan bahwa path puv mempunyai verteks persekutuan dengan

cycle γ1 atau γ2. Hal ini berakibat, walknya dimulai dengan verteks u, bergerak

path puv menuju verteks v dan dilanjutkan dengan mengelilingi cycle γ1 sebanyak

(r(puv) − b(puv)). Perjalanan walk ini menghasilkan (e, e)Twalk terpendek, dengan

komposisi walknya " r(wuv) b(wuv) # = [r(puv) + b(puv)] " (s + 1)/2 (s + 1)/2 # − b(puv) " s s # .

Dalam kasus ini, dapat dipilih path puv sehingga (r(puv) + b(puv)) ≤ (n − s) + (s −

1)/2 akibatnya (r(puv) − b(puv)) ≤ r(puv) ≤ (r(puv) + b(puv)) ≤ (n − s) + (s − 1)/2 Sehingga diperoleh " r(wuv) b(wuv) # ≤ [(n − s) + (s − 1)/2] " (s + 1)/2 (s + 1)/2 # ≤ [(s − 1)/2 + (n − s)] " (s + 1)/2 (s + 1)/2 # = " (s2− 1)/4 + (n − s)(s + 1)/2 (s2_{− 1)/4 + (n − s)(s + 1)/2} # .

Ketiga diasumsikan bahwa path puv mempunyai verteks persekutuan

de-ngan cycle γ1 atau γ2. Hal ini walknya dimulai dengan verteks u bergerak

menuju x sepanjang path pux dilanjutkan dengan mengelilingi cycle γ1 sebanyak

29

terpendek, dengan komposisi walknya " r(wuv) b(wuv) # = " r(pux) b(pux) # + [r(puv) − b(puv)] " (s − 1)/2 (s + 1)/2 # + " r(pxv) b(pxv) # = " r(puv) b(puv) # + [r(puv) − b(puv)] " (s − 1)/2 (s + 1)/2 # = [r(puv) + b(puv)] " (s + 1)/2 (s + 1)/2 # − b(puv) " s s # ≤ (n − s) " (s + 1)/2 (s + 1)/2 # ≤ [(s − 1)/2 + (n − s)] " (s + 1)/2 (s + 1)/2 # = " (s2− 1)/4 + (n − s)(s + 1)/2 (s2_{− 1)/4 + (n − s)(s + 1)/2} # " r(wuv) b(wuv) # ≤ " (s2_{− 1)/4 + (n − s)(s + 1)/2} (s2_{− 1)/4 + (n − s)(s + 1)/2} # .

Keempat diasumsikan bahwa path puv mempunyai verteks persekutuan dengan

cycle γ1 atau γ2. Hal ini walknya dimulai dengan verteks u bergerak menuju x

sepanjang path pux menuju verteks vkemudian dilanjutkan mengelilingi cycle γ1

sebanyak (r(puv) − b(puv)). Perjalanan walk ini menghasilkan (e, e)T-walk

terpen-dek, dengan komposisi walknya " r(wuv) b(wuv) # = " r(pux) b(pux) # + " r(pxv) b(pxv) # + [r(puv) − b(puv)] " (s − 1)/2 (s + 1)/2 # = " r(puv) b(puv) # + [r(puv) − b(puv)] " (s − 1)/2 (s + 1)/2 # = [r(puv) + b(puv)] " (s + 1)/2 (s + 1)/2 # − b(puv) " s s # ≤ [r(puv) + b(puv)] " (s + 1)/2 (s + 1)/2 # .

30

Karena dapat dipilih path puv sehingga (r(puv) + b(puv)) ≤ (n − s) + (s − 1)/2

maka " r(wuv) b(wuv) # ≤ [r(puv) + b(puv)] " (s + 1)/2 (s + 1)/2 # ≤ [(s − 1)/2 + (n − s)] " (s + 1)/2 (s + 1)/2 # = " (s2− 1)/4 + (n − s)(s + 1)/2 (s2_{− 1)/4 + (n − s)(s + 1)/2} # " r(wuv) b(wuv) # ≤ " (s2_{− 1)/4 + (n − s)(s + 1)/2} (s2_{− 1)/4 + (n − s)(s + 1)/2} # .

Kelima diasumsikan bahwa path puv mempunyai verteks persekutuan dengan

cycle γ1 atau γ2. Hal ini walknya dimulai dengan verteks u bergerak menuju y

sepanjang path puy kemudian ke x dilanjutkan mengelilingi cycle γ1 sebanyak

(r(puv) − b(puv)) dan berakhir di verteks v. Perjalanan walk ini menghasilkan

(e, e)T_{-walk terpendek, dengan komposisi walknya}

" r(wuv) b(wuv) # = " r(puy) b(puy) # + " r(pyx) b(pyx) # + " r(pxv) b(pxv) # + [r(puv) − b(puv)] " (s − 1)/2 (s + 1)/2 # = " r(puv) b(puv) # + [r(puv) − b(puv)] " (s − 1)/2 (s + 1)/2 # = [r(puv) + b(puv)] " (s + 1)/2 (s + 1)/2 # − b(puv) " s s # ≤ [r(puv) + b(puv)] " (s + 1)/2 (s + 1)/2 # .

31

Karena dapat dipilih path puv sehingga (r(puv) + b(puv)) ≤ (n − s) + (s − 1)/2,

maka: " r(wuv) b(wuv) # ≤ [r(puv) + b(puv)] " (s + 1)/2 (s + 1)/2 # ≤ [(s − 1)/2 + (n − s)] " (s + 1)/2 (s + 1)/2 # = " (s2− 1)/4 + (n − s)(s + 1)/2 (s2− 1)/4 + (n − s)(s + 1)/2 # " r(wuv) b(wuv) # ≤ " (s2− 1)/4 + (n − s)(s + 1)/2 (s2− 1)/4 + (n − s)(s + 1)/2 # .

dengan menggunakan (1, 1)T_{-walk, walk w}

uv dapat diubah menjadi (q, q)T-walk

dengan q = (s2 _{− 1)/4 + (n − s)(s + 1)/2. Karena untuk setiap pasangan}

verteks u dan v dapat ditemukan sebuah (q, q)T_{-walk dari u ke v dengan q =}

(s2_{− 1)/4 + (n − s)(s + 1)/2 maka 2-exp(D) ≤ (s}2_{− 1) + (n − s)(s + 1).}

3.2 Digraph dwiwarna D yang memenuhi batas atas

Pada bagian ini dibahas mengenai digraph dwiwarna asimetrik yang memuat cycle primitif dengan sifat 2-exp(D) = (s2_{− 1) + (n − s)(s + 1).}

Teorema 3.2 Andaikan D adalah suatu digraph dwiwarna asimetrik yang memuat

cycle primitif dengan bilangan ganjil s ≥ 3. Jika D mempunyai path merah de-ngan panjang (s + 1)/2 + (n − s) maka 2-exp(D) = (s2_{− 1) + (n − s)(s + 1)}

Bukti. Misalkan puv adalah sebuah path merah dengan panjang (s + 1)/2 + (n − s)

di D, maka satu dari verteks u atau v berada pada cycle γ1 atau γ1. Karena D

asimetrik maka D memiliki sebuah path biru dengan panjang (s + 1)/2 + (n − s). Karena s merupakan bilangan ganjil, maka ada sebuah path terpendek merah puv

32

dari u ke v di D dengan panjang q = (s+1)/2+(n−s). Karena D asimetrik, maka ada sebuah path terpendek biru dari v ke u dengan panjang q = (s+1)/2+(n−s). Misalkan wuv dan wvu masing-masing merupakan walk dari u ke v dan walk dari

v ke u dengan komposisi yang sama dan mempunyai bentuk " r(wuv) b(wuv) # = " q 0 # + α " 1 0 # + x1 " 1 1 # + x2 " (s − 1)/2 (s + 1)/2 # + x3 " (s + 1)/2 (s − 1)/2 # dan " r(wvu) b(wvu) # = " 0 q # + β " 0 1 # + y1 " 1 1 # + y2 " (s − 1)/2 (s + 1)/2 # + y3 " (s + 1)/2 (s − 1)/2 # ,

untuk suatu bilangan bulat tak negatif x1, x2, x3, y1,y2, y3 dan α, β ∈ {0, 1} Bila

α = 0 maka digunakan path merah dengan panjang q = (s + 1)/2 + (n − s) untuk mengkonstruksikan walk wuv. Bila α = 1, maka digunakan path merah

dengan panjang (s + 1)/2 + (n − s) untuk mengkonstruksikan walk wuv. Dengan

argumentasi yang sama untuk β. Jika α = β = 0, maka " −q q # = (x1− y1) " 1 1 # + (x2− y2) " (s − 1)/2 (s + 1)/2 # + (x3− y3) " (s + 1)/2 (s − 1)/2 # .

Dari persamaan di atas, diperoleh (x2 − y2) + (y3 − x3) = 2q Sehingga

x2+ y3 ≥ 2q yang berakibat x2 ≥ q atau y3 ≥ q. Dengan cara yang sama, untuk

α = 1 dan β = 0 atau untuk α = 0 dan β = 1 diperoleh x2 ≥ q atau y3 ≥ q.

Terakhir untuk α = 1 dan β = 1 diperoleh x2 ≥ q + 1 dan y3 ≥ q + 1. Karena

dari semua kasus, mengakibatkan " r(wuv) b(wuv) # ≥ " (s2_{− 1)/4 + (s + 1)(n − s)/2} (s2_{− 1)/4 + (s + 1)(n − s)/2} #

maka 2-exp(D) ≥ (s2− 1)/2 + (s + 1)(n − s). Berdasarkan Teorema 3.1, diperoleh 2-exp(D) = (s2− 1)/2 + (s + 1)(n − s).

BAB 4

KESIMPULAN DAN SARAN

4.1 Kesimpulan

Pada digraph dwiwarna asimetrik yang memuat cycle primitif D, untuk memperoleh batas atas dari 2-eksponennya dilakukan dengan peninjauan dua ka-sus. Pertama, path puv tidak mempunyai verteks persekutuan dengan cycle γ1

atau cycle γ2. Pada kasus pertama dilakukan dengan peninjauan terhadap satu

asumsi. Kedua, path puv mempunyai verteks persekutuan dengan cycle γ1 atau

cycle γ2. Pada kasus kedua dilakukan dengan peninjauan terhadap empat asumsi.

Pada digraph dwiwarna asimetrik yang memuat cycle primitif D, batas atas dari 2-eksponennya dicapai bila D mempunyai path merah dengan panjang (s + 1)/2 + (n − s).

4.2 Saran

Pada tulisan ini penulis hanya membahas mengenai batas atas pada digraph dwiwarna asismetrik yang memuat cycle primitif. Penelitian lanjutan diharapkan dapat menentukan 2-eksponen digraph dwiwarna primitif secara umum, yakni andaikan D adalah sebuah digraph dwiwarna n verteks primitif. Apa batas atas dan batas bawah dari 2-eksponennya ?.

DAFTAR PUSTAKA

Beasley, L.A and Kirkland,S. 1997. On the exponent of primitive matrices contai-ning primitive submatrices. Linier Algebra Appl. 261, 195-205.

Brualdi, R, A dan Ryser, H. J. 1991. Combinational Matrix Theory. Cambridge: Cambridge University Press.

Dulmage, A.L and Mendelsohn, N.S. 1964. The Exponent of Incidence Matrices. Duke Math 31, 575-584

Fornasini, E.and M. E. Valcher. 1997. Directed graphs, 2D State Models, and charateristic polynomials of irreducible matrix pairs. Linear Algebra Appl.,

263, 275-310

Liu, B., McKay, B.D, Wormald, N. C dan Min, Z. K. 1990. The exponent set of symmeteric primitive (0,1) matrices with zero trace. Linear Algebra Appl.,133, 121 131

S.G Lee and J.M Yang. 2005. Bound for 2-exponent of primitive extremal min-istrong digraph, Commun. Korean. Math. 51-62

Schneider, H. 2002. Wielandts proof of the exponent inequality for primitive non-negative matrices. Linear Algebra Appl. 353, 5-10.

Shader, B.l and Suwilo,S. 2003. Exponents of nonnegative matrices pairs. Linier Algebra Appl.363, 275-293.

Shao, J.Y. 1987.The exponent set of symmetric primitive matrices. Scientia sinica Ser. A 30(4): 348-358.

Suwilo, S. 2001. On 2-Exponents of 2-digraph. Disertasi, University of Wyoming. Suwilo, S. 2007. 2-Exponents of two-colored lollipops. Proceeding Icoms 2007. Suwilo dan Mardiningsih. 2005. On exponent of primitive graphs. Mawengkang,

Suwilo, Sutarman (ed.), Proceedings of the 1st IMT-GT Regional Conference on Mathematics, Statistics and Their Applications, 37 - 42

Wielandt. 1950. Unzerlegbare nicht negative Matrizen, Math. Z, 52, 642-645.