PROGRAM LINEAR BILANGAN BULAT DUAL SKRIPSI

PROGRAM LINEAR BILANGAN BULAT DUAL

SKRIPSI

Diajukan Untuk Memenuhi Salah Satu Syarat

Memperoleh Gelar Sarjana Sains (S.Si)

Program Studi Matematika

Oleh:

Bernadeta Widiasih

NIM : 013114017

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SANATA DHARMA

YOGYAKARTA

iv

HALAMAN PERSEMBAHAN

 

Terima kasih 

Telah mengajariku membedakan yang benar dan yang salah 

Mendorongku untuk mempertahankan mimpi­mimpiku 

Menunjukkan padaku untuk tidak terpengaruh oleh rintangan 

Dan untuk mengubah kebingunganku menjadi senyuman 

 

Telah mengatakan bahwa kalian menyayangiku 

Menunjukkan betapa istimewanya cinta itu 

Menghapuskan air mataku kala aku sedih 

Dan untuk menenangkanku saat aku ingin marah 

 

Telah membantu sesama dengan perbuatan baik kalian 

Mengajariku bahwa aku pun mesti menolong sesama 

Memelukku ketikaaku merasa sunyi 

Dan membisikkan padaku 

AKU SAYANG PADAMU

Terima kasih keluargaku atas segala yang kalian lakukan 

Entah bagaimana jadinya diriku tanpa kalian  

 

Kupersembahkan karya ini untuk:

Tuhan Yesus Kristus dan Bunda Maria

Almarhum Bapak, Ibu, Mba eta, Lia dan

Semua Keluarga Besarku.

vi

ABSTRAK

Program linear bilangan bulat merupakan bagian dari program linear di mana

menginginkan penyelesaian dalam bentuk bilangan bulat. Dalam program linear

bilangan bulat terdapat dua model, yakni program linear bilangan bulat fraksional

dual dan program linear bilangan bulat dual. Program linear bilangan bulat fraksional

dual memungkinkan adanya nilai variabel berupa bilangan pecahan dalam

perhitungannya, sedangkan dalam program linear bilangan bulat dual semua nilai

variabel dalam perhitungan haruslah berupa bilangan bulat. Masalah program linear

bilangan bulat dapat diselesaikan dengan menggunakan beberapa metode, seperti

metode bidang pemotong, metode cabang dan batas, dan metode enumerasi. Pada

penulisan ini masalah program linear bilangan bulat akan diselesaikan dengan

metode bidang pemotong.

Penyelesaian masalah program linear bilangan bulat dengan metode bidang

pemotong dimulai dengan mengubah bentuk baku menjadi bentuk kanonik, dan

menyusun tabel awal. Setelah itu dilanjutkan dengan mencari baris sumber dan

kolom pivot serta menentukan bentuk kendala bidang pemotong. Bentuk kendala

bidang pemotong tersebut kemudian ditambahkan ke dalam tabel, yang selanjutnya

diselesaikan dengan metode simpleks. Proses iterasi ini diulang hingga penyelesaian

optimum dicapai.

vii

ABSTRACT

Integer programming is a part of linear programming where its solutions are

integer. There are two models of integer programming, dual fractional integer

programming and dual all-integer integer programming. The value of variables in

calculations of dual fractional integer programming can be in the form of fractional,

while in dual all-integer integer programming all of variable values in calculations

must be in the form of integer. Some methods, such as cutting plane method, branch

and bound method and enumeration method can solve the integer programming

problem. In this paper, we use cutting plane method to solve integer programming

problem.

The first step in solving integer programming problem by cutting plane

method is changing standard form to canonic form, and arranging the beginning

table. After that, we choose the source row and pivot column, and then determine the

form of the Gomory Cut. We will add the Gomory Cut into the table and solve it by

dual simplex method. We repeat this iteration process until optimum integer solution.

viii

KATA PENGANTAR

Puji syukur penulis panjatkan kepada Tuhan Yesus atas segala kasih dan

perlindungan-Nya sehingga penulisan skripsi ini dapat terselesaikan. Skripsi ini

disusun dalam rangka melengkapi salah satu syarat untuk memperoleh gelar Sarjana

Sains pada Program Studi Matematika, Jurusan Matematika, Fakultas Matematika

dan Ilmu Alam, Universitas Sanata Dharma Yogyakarta.

Penulisan skripsi ini tidak lepas dari bantuan dan dukungan dari berbagai

pihak. Oleh karena itu, pada kesempatan ini penulis ingin menyampaikan ucapan

terima kasih kepada:

1.

Ibu Lusia Krismiyati, S.Si, M.Si sebagai dosen pembimbing yang penuh

perhatian dan kesabaran telah membimbing serta memberi saran dan kritik

kepada penulis selama proses penulisan skripsi ini.

2.

Bapak Ir. Ig. Aris Dwiatmoko, M.Sc selaku Dekan fakultas MIPA yang telah

memberi dukungan dalm penulisan skripsi ini.

3.

Bapak Y.G. Hartono, S.Si, M.Sc selaku Ketua Program Studi Matematika, dan

dosen penguji yang memberikan dukungan, saran dan kritik dalam skripsi ini.

4.

Ibu Any Herawati, S.Si, M.Si selaku dosen penguji yang telah memberikan saran

dan kritik dalam skripsi ini.

5.

Bapak dan Ibu dosen di Fakultas MIPA yang telah membimbing dan mendidik

penulis selama menuntut ilmu di Universitas Sanata Dharma.

6.

Bapak dan Ibu karyawan Universitas Sanata Dharma, khususnya sekretariat

fakultas MIPA dan perpustakaan Universitas Sanata Dharma atas segala bantuan

dan fasilitas yang telah diberikan.

7.

Almarhum Bapak (pak aku belum bisa buat bapak bahagia dengan kelulusan ini

tapi aku tau bapak selalu menyertai hidupku, makasih pak aku sayang bapak),

ix

Ibu, Mba eta, Lia dan semua keluargaku tercinta atas kasih sayang, doa,

semangat, dukungan dan kesabarannya menanti kelulusan ini.

8.

Sahabat-sahabatku seperjuangan angkatan 2001: Maria(jangan lupain masa2 qta

nunggu 21 ya!!!), Indah, Erika, Ajeng(tunggu aku dijakarta ya), Very, Upik,

Yuli, Dani, Tabita, Fanya(makasih laptopnya), Andre, Ariel, Agnes, Wiwit,

Rita+Alam (makasih semangat n bantuannya), Vrysca, Daniel, Tedy, Ray, April,

Ardi, serta kakak-kakak angkatan 1998, 1999, 2000 dan adik-adik angkatan

2002, 2003, 2004 yang telah membantu dan mendukung penulis.

9.

Untuk seseorang yang selama ini mengisi hatiku yang telah memberi dukungan,

semangat, nasehat, doa, cinta dan rasa sayangnya.

10.

Untuk saudara-saudaraku yang menemaniku dijogja: Wahyu(makasih dah mau

anter aku n pinjemin komputernya), Nita, Wiwit, mas Lus dan keluargaku yang

telah memberi dukungan, semangat, saran dan doanya.

11.

Anak-anak kost gang endro no 8 : Mba lina(makasih atas perhatiannya hingga ku

bisa mengerti arti hidup), Mba rini, Mba armi, Ayu, Tia, Mery, F3, Cu2, Weni,

Rini, Ika, Lia, Ratna, Riska, Winda,Beni dan teman-teman kost dari awal sampai

akhir aku kuliah yang telah memberi dukungan, semangat, doa dan candanya.

12.

Semua pihak yang telah membantu penulis baik secara langsung maupun tidak

langsung hingga selesainya penulisan skripsi ini.

Penulis menyadari bahwa skripsi ini masih banyak kekurangannya. Oleh

karena itu, penulis mengucapkan terima kasih bila ada kritik dan saran yang dapat

membangun penulis. Penulis berharap semoga skripsi ini dapat bermanfaat dan

menjadi referensi bagi pembaca.

x

DAFTAR ISI

Halaman

HALAMAN JUDUL ………..…… i

HALAMAN PERSETUJUAN PEMBIMBING ………. ii

HALAMAN PENGESAHAN ……… iii

HALAMAN PERSEMBAHAN ………..…….. iv

PERNYATAAN KEASLIAN KARYA ……….…... v

ABSTRAK ……….…… vi

ABSTRACT ……….………... vii

KATA PENGANTAR ……….…….. viii

DAFTAR ISI ……….……. x

DAFTAR GAMBAR ……….……. xii

DAFTAR TABEL ……….……. xiii

BAB I

PENDAHULUAN ………..……. 1

A.

Latar Belakang Masalah ……….…… 1

B.

Rumusan Masalah ………...…….. 2

C.

Pembatasan Masalah ………...….. 2

D.

Tujuan Penulisan ………. 3

E.

Manfaat Penulisan ……….. 3

F.

Metode Penulisan ………..…………..……... 3

G.

Sistematika Penulisan ……….……… 4

xi

BAB II PROGRAM LINEAR DENGAN DUAL………..……... 5

A.

Program Linear ……….…… 5

B.

Metode Grafik ……….…… 9

C.

Metode simpleks………...………... 10

D.

Metode Simpleks Dual ………..…….. 16

E.

Program Linear Bilangan Bulat ..………...…… 21

BAB III

PROGRAM LINEAR BILANGAN BULAT FRAKSIONAL DUAL 25

A.

Masalah Program Linear Bilangan Bulat...………... 25

B.

Penyelesaian Masalah Program Linear Bilangan Bulat Fraksional

Dual ……….….…… 29

BAB IV PROGRAM LINEAR BILANGAN BULAT DUAL ... 60

A.

Masalah Program Linear Bilangan Bulat Dual Dengan Metode

Bidang Pemotong...…… 60

B.

Penyelesaian Masalah Program Linear Bilangan Bulat Dual... 68

BAB IV PENUTUP ...….. 81

A.

Kesimpulan ………...…….. 81

B.

Saran ………...…… 82

xii

DAFTAR GAMBAR

Halaman

Gambar 2.1.Ilustrasi Penyelesaian Masalah Program Linear dengan metode

grafik……… 10

Gambar 3.1.Ilustrasi Penyelesaian Masalah Program Linear Bilangan Bulat dengan

metode bidang pemotong …………..……....………... 26

Gambar 3.2.Penyelesaian Masalah Program Linear Bilangan Bulat Fraksional

Dual……….. 51

Gambar 4.1. Penyelesaian Masalah Program Linear Bilangan Bulat Dual……... 80

xiii

DAFTAR TABEL

Halaman

Tabel 2.1 Tabel Awal Simpleks……… 14

Tabel 2.2 Tabel Awal Simpleks Dual………...…… 19

Tabel 3.1 Tabel Awal Program Linear Bilangan Bulat Fraktional Dual...…………... 30

Tabel 3.2. Tabel Dengan Bentuk Kendala Bidang Pemotong... ………. 32

Tabel 3.3. Tabel Awal Pada Contoh Masalah Program Linear Bilangan Bulat………… 40

Tabel 3.4. Tabel Setelah Operasi Baris Elementer Pada Iterasi 1.………...…. 41

Tabel 3.5. Tabel Setelah Operasi Baris Elementer Pada Iterasi 2……….. 42

Tabel 3.6. Tabel Dengan Bentuk Pembatas Sekunder Pada Iterasi 1………...…. 45

Tabel 3.7. Tabel Setelah Dilakukan Operasi Baris Elementer Pada Iterasi 1...…….. 46

Tabel 3.8. Tabel Dengan Bentuk Pembatas Sekunder Pada Iterasi 2... 48

Tabel 3.9. Tabel Setelah Dilakukan Operasi Baris Elementer Pada Iterasi 2... 49

Tabel 3.10. Tabel Dengan Bentuk Pembatas Sekunder Pada Iterasi 3... 54

Tabel 3.11. Tabel Setelah Dilakukan Operasi Baris Elementer Pada Iterasi 3... 55

Tabel 3.12. Tabel Dengan Bentuk Pembatas Sekunder Pada Iterasi 4... 57

Tabel 3.13. Hasil setelah dilakukan operasi baris elementer pada iterasi 4... 58

Tabel 4.1. Tabel Awal Program Linear Bilangan Bulat... 65

Tabel 4.2. Tabel Awal Pada Contoh Masalah Program Linear Bilangan Bulat... 73

Tabel 4.3. Tabel Bentuk Kendala Bidang Pemotong Pada Iterasi 1... 75

Tabel 4.4. Tabel Setelah Dilakukan Operasi Baris Elementer Pada Iterasi 1... 75

Tabel 4.5. Tabel Dengan Bentuk Kendala Bidang Pemotong Pada Iterasi 2... 78

BAB I P ENDAHULUAN

A. Latar Belakang Masalah

Program linear adalah teknik optimasi yang bertujuan untuk menentukan pemecahan masalah dari suatu program matematika yang linear sehingga dapat ditemukan nilai sasaran yang optimal. Hasil akhir penyelesaian masalah program linear bisa dapat berupa bilangan pecahan atau bilangan bulat. Dalam penyelesaian masalah yang berupa bilangan bulat diperlukan suatu penyelesaian khusus untuk menjawabnya, yaitu program linear bilangan bulat.

Program linear bilangan bulat merupakan salah satu bentuk dari program linear dengan satu variabel atau lebih. Dalam masalah program linear bilangan bulat ini variabel masukannya bernilai bilangan bulat. Banyak sekali ditemukan permasalahan program linear bilangan bulat dalam kehidupan sehari-hari dan industri. Permasalahan tersebut tidak dapat diselesaikan hanya dengan program linear biasa, misalnya masalah produksi, masalah transportasi, masalah penjadwalan para pekerja dan mesin-mesin kantor, desain jaringan telekomunikasi dan masalah salesmen yang berpergian (traveling salesman).

Dalam program linear bilangan bulat terdapat dua model, yakni program linear bilangan bulat fraksional dual dan program linear bilangan bulat dual. Program linear bilangan bulat fraksional dual memungkinkan adanya nilai variabel berupa bilangan pecahan dalam perhitungannya, sedangkan dalam

program linear bilangan bulat dual semua nilai variabel dalam perhitungan haruslah berupa bilangan bulat.

Masalah program linear bilangan bulat dapat diselesaikan dengan menggunakan beberapa metode, seperti metode bidang pemotong, metode cabang dan batas, dan metode enumerasi. Pada penulisan ini masalah program linear bilangan bulat akan diselesaikan dengan metode bidang pemotong. Metode bidang pemotong untuk pertama kalinya diaplikasikan pada masalah program linear bilangan bulat fraktional dual kemudian diperbaiki menjadi masalah program linear bilangan bulat dual. Penyelesaian kedua masalah program linear bilangan bulat tersebut menggunakan metode simpleks dual.

B. Rumusan Masalah

Pokok permasalahan yang akan dibahas dalam skripsi ini dapat dituliskan dengan beberapa pertanyaan sebagai berikut :

1. Bagaimana menyelesaikan masalah program linear bilangan bulat fraksional dual dengan metode bidang pemotong ?

2. Bagaimana menyelesaikan masalah program linear bilangan bulat dual dengan metode bidang pemotong ?

C. Pembatasan Masalah

Dalam skripsi ini hanya akan dibahas tentang program linear bilangan bulat, yakni program linear bilangan bulat fraksional dual dan program linear bilangan bulat dual yang diselesaikan dengan metode bidang pemotong yang

menggunakan metode simpleks dual dan landasan teori yang berkaitan dengan aljabar linear seperti sistem persamaan linear, matriks dan ruang vektor yang telah dipelajari pada saat kuliah tidak akan dibahas dalam skripsi ini.

D. Tujuan Penulisan

Sesuai dengan latar belakang di atas, penulisan skripsi ini bertujuan untuk dapat menyelesaikan masalah program linear bilangan bulat khususnya tentang masalah program linear bilangan bulat fraksional dual dan masalah program linear bilangan bulat dual dengan metode bidang pemotong dan dapat dipertanggungjawabkan langkah demi langkah.

E. Manfaat Penulisan

1. Dapat menyelesaikan masalah program linear bilangan bulat fraksional dual

2. Dapat menyelesaikan masalah program linear bilangan bulat dual

F. Metode Penulisan

Metode penulisan yang digunakan dalam penulisan skripsi ini adalah metode studi pustaka, yaitu dengan membaca dan mempelajari materi dari buku - buku acuan yang berkaitan dengan topik skripsi ini, sehingga tulisan ini tidak ada penemuan hal-hal yang baru.

G. Sistematika Penulisan

Sistem penulisan skripsi ini terdiri dari 5 bab dengan urutan sebagai berikut:

Bab I PENDAHULUAN

Bab ini menjelaskan uraian mengenai hal-hal yang menjadi dasar dalam pembahasan skripsi ini. Uraian tersebut berisi latar belakang masalah, perumusan masalah, pembatasan masalah, tujuan penulisan, manfaat penulisan, metode penulisan dan sistematika penulisan.

BAB II PROGRAM LINEAR DENGAN DUAL

Bab ini memberikan penjelasan secara singkat beberapa dasar pengetahuan, yaitu tentang program linear, metode grafik, metode simpleks, metode simpleks dual dan program linear bilangan bulat. BAB III PROGRAM LINEAR BILANGAN BULAT FRAKSIONAL DUAL

Bab ini membahas tentang langkah-langkah penyelesaian masalah program linear bilangan bulat fraksional dual menggunakan metode bidang pemotong.

BAB IV PROGRAM LINEAR BILANGAN BULAT DUAL

Bab ini membahas tentang langkah-langkah penyelesaian masalah program linear bilangan bulat dual menggunakan metode bidang pemotong.

BAB V Penutup

Bab ini berisi beberapa kesimpulan dan saran berdasarkan hasil pembahasan dan keseluruhan proses penyusunan skripsi.

BAB II

PROGRAM LINEAR DENGAN DUAL

A. Program Linear

Penerapan program linear untuk pertama kalinya adalah di bidang perencanaan militer, yakni pada perang dunia II oleh angkatan bersenjata Amerika Serikat dan Inggris. Kemudian pada tahun1930-an ahli matematika seperti Von Neuman dan Leontief melahirkan teknik-teknik penyelesaian masalah program linear dengan menggunakan pendekatan aljabar linear (aljabar matriks). Karya Leontif yang terkenal adalah model input-output. Setelah itu ahli matematika Dr George B. Dantzig, seorang anggota dari pasukan Angkatan Udara tersebut, memformulasikan masalah program linear secara umum dan menemukan penyelesaian dengan metode simpleks pada tahun 1947.

Program linear adalah suatu metode optimasi yang digunakan untuk menyelesaikan masalah dengan fungsi sasaran dan kendala-kendala berbentuk linear.

Secara umum masalah program linear dapat dinyatakan sebagai berikut : 1. Bentuk Baku Masalah Program Linear :

Minimumkan ( atau maksimumkan) :

n nx c x c x c z= 1 1+ 2 2+K+ (2.1)

dengan kendala-kendala : ⎪ ⎪ ⎭ ⎪ ⎪ ⎬ ⎫ ≥ = ≤ + + + ≥ = ≤ + + + ≥ = ≤ + + + m n mn m m n n n n b x a x a x a b x a x a x a b x a x a x a } , , { } , , { } , , { 2 2 1 1 2 2 2 22 1 21 1 1 2 12 1 11 K M O O M K K (2.2) xj ≥0, j=1,2,K,n (2.3)

Rumus di atas dapat diringkas sebagai berikut : Minimumkan ( atau maksimumkan) :

∑

= = n j j jx c z 1 (2.4) dengan kendala

∑

= = ≥ = ≤ n j ij j i m i b x a 1 , , 2 , 1 , ) , , ( _K (2.5) n j x_j ≥0 , =1,2,_K, (2.6) 2. Bentuk Matriks Masalah Program linear :

Minimumkan (atau maksimumkan) : z=cx (2.7) dengan kendala-kendala :

{

0 } , , ≥ ≥ = ≤ x b Ax _(2.8) dengan : ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = mn m m n n a a a a a a a a a K M O M K K 2 1 2 22 21 1 12 11 A , ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = n x x x M 2 1 x , ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = n b b b M 2 1 b ,c=

(

c₁,c₂,_K,c_n

)

Definisi 2.1Fungsi sasaran atau fungsi tujuan Fungsi sasaran masalah program linear berbentuk

∑

= = p j j jx c z 1

dengan p merupakan banyaknya variabel, x_j merupakan variabel ke- j, dan c_j

merupakan koefisien ongkos dari variabel ke- j.

Definisi 2.2Kendala utama dan kendala tak negatif

Persamaan atau pertidaksamaan dalam masalah program linear

(

, ,

)

, 1 ,

∑

= ≥ = ≤ n j i j j i x b a i=1,2,...,m disebut kendala utama, dengan m merupakan banyaknya kendala, dan a_i,j

(koefisien teknis) merupakan koefisien kendala ke-i dari variabel ke-j dan bi

menyatakan konstanta di ruas kanan untuk kendala ke-i.

Sedangkan x_j ≥0; j=1,2,...,p disebut kendala tak negatif

Untuk mengembangkan suatu metode penyelesaian, secara umum harus sesuai dengan karakter dari masalah program linear. Karakter tersebut dinyatakan dalam bentuk baku sebagai berikut :

1. Fungsi sasarannya berpola minimum atau maksimum.

2. Semua kendalanya berbentuk persamaan. Bentuk ini disebut bentuk kanonik dari masalah program linear.

Definisi 2.3Penyelesaian layak

Penyelesaian layak adalah penyelesaian yang memenuhi semua kendala yakni kendala utama dan kendala tak negatif.

Definisi 2.4Penyelesaian optimum

Penyelesaian optimum adalah penyelesaian layak yang takhingga banyak yang mengoptimumkan fungsi sasaran.

Definisi 2.5Penyelesaian basis

Suatu vektor x merupakan penyelesaian basis, jika:

(i) x memenuhi persamaan kendala utama dalam program linear.

(ii) kolom-kolom matriks kendala yang bersesuaian dengan vektor tak nol x

adalah bebas linear.

Definisi 2.6Penyelesaian layak basis

Suatu vektor x disebut penyelesaian layak basis jika x adalah penyelesaian basis dan memenuhi kendala tak negatif x≥0.

Definisi 2.7Penyelesaian layak basis optimum

Suatu vektor x disebut penyelesaian layak basis optimum jika x adalah penyelesaian layak basis yang juga mengoptimumkan fungsi sasaran.

Masalah program linear biasanya diselesaikan dengan dua metode penyelesaian, yaitu metode grafik dan metode simpleks. Masalah program linear dapat diselesaikan dengan menggunakan metode grafik bila masalah tersebut hanya memiliki dua variabel keputusan. Tetapi untuk masalah yang memiliki variabel keputusan lebih dari dua tidak mungkin menggunakan metode grafik. Lalu pada tahun 1947 George Dantzig dan pakar-pakar lainnya mengembangkan metode simpleks yang dapat menyelesaikan masalah program linear yang memuat tiga variabel keputusan atau lebih.

B. Metode Grafik

Masalah program linear dengan dua variabel dapat diselesaikan menggunakan metode grafik. Meskipun masalah program linear jarang yang hanya memuat dua variabel tetapi metode grafik memudahkan dalam penyelesaian masalah tersebut. Masalah program linear dapat diilustrasikan dengan melihat Gambar 2.1, yakni Pasangan

(

x₁,x₂

)

yang memenuhi semua kendala disebut penyelesaian layak (feasible solution). Titik-titik dalam daerah layak disebut titik layak. Himpunan titik layak yang terlihat dalam Gambar 2.1, yakni daerah OABCD adalah daerah layak yang diperoleh dari perpotongan kendala-kendala utama. Grafik fungsi sasaran ini berupa garis lurus z dan disebut garis selidik karena menggambarkan pasangan-pasangan

(

x1,x2

)

yang memberikan nilai z yang sama. Pada masalah program linear yang memaksimumkan fungsi sasaran z maka akan ditemukan penyelesaian optimum titik B, yakni titik yang memaksimumkan fungsi sasaran.

0 x1 2 x A B D C z

Gambar2.1. Ilustrasi Penyelesaian Masalah Program Linear dengan metode grafik

C. Metode simpleks

Untuk menyelesaikan masalah program linear dengan metode simpleks, kendala yang masih berbentuk pertidaksamaan ini harus diubah dahulu ke bentuk persamaan dengan penambahan variabel slack atau variabel pengetat yang mempunyai koefisien ongkos nol. Jika kendala berpola kurang dari (≤) , yakni kendala berbentuk pertidaksamaan :

k n kn k k x a x a x b a 1 1+ 2 2 +K+ ≤

maka kendala tersebut dapat diubah ke bentuk persamaan dengan menambah variabel pengetat xn+₁dengan 0xn+1 > . Dengan demikian , persamaan untuk kendala tersebut adalah

0 , ₁ 1 2 2 1 1 + k + + kn n + n+ = k n+ > k x a x a x x b x a _K .

Dengan cara yang sama, kendala berpola lebih besar dari (≥), yakni kendala berbentuk pertidaksamaan :

ak1x1+ak2x2 +K+aknxn ≥bk

dapat diubah ke bentuk persamaan dengan mengurangi pertidaksamaan tersebut dengan variabel pengetat xn+1 dengan xn+1 >0

a_k1x₁+a_k2x₂+_K+a_knx_n −x_n+1=b_k ,x_n+1>0

Untuk menyesuaikan dengan bentuk kendala baru, fungsi sasaran yang semula berbentuk z=c1x1+c2x2+K+c_nx_n diubah menjadi

p n n j x x c x c x c x c z= 1 1+ 2 2 +K+ n n + j( n+1+K+ p) , = +1, +2,K,

dengan 0cn+1 =cn+2 =K=cp = danxi,i=n+1,n+2,K,p adalah variabel

pengetat.

Dengan demikian masalah yang telah diubah kedalam bentuk kanonik akan menjadi seperti ini :

Minimumkan ( atau maksimumkan ) :

∑

= = n j j jx c z 1 (2.9) dengan kendala

∑

= = = n j i j ijx b i m a 1 , , 2 , 1 , K (2.10) n j x_j ≥0 , =1,2,_K, (2.11)

Definisi 2.8Bentuk kanonik

Bentuk pertidaksamaan yang sudah diubah dalam bentuk persamaan disebut bentuk kanonik dari masalah program linear.

Berikut ini akan diberikan contoh masalah program linear yang diubah ke bentuk kanonik

Contoh 2.1

Ubah soal dibawah ini ke bentuk kanonik. Maksimumkan :z=10x1−20x2+5x3 dengan kendala 10 2 8 3 2 1 3 2 1 ≤ + − ≤ + − x x x x x x Penyelesaian :

Pada masing-masing kendala yang masih berbentuk pertidaksamaan ditambahkan satu variabel pengetat, misalkan x4 dan x5 sehingga masala program linear di atas menjadi : Maksimumkan : z=10x₁−20x₂+5x₃+0x₄ +0x₅ Dengan kendala : 10 2 8 5 3 2 1 4 3 2 1 = + + − = + + − x x x x x x x x Soal ini sudah berbentuk kanonik dan berpola maksimum, dengan x₁,x₂,x₃

Jika masalah program linear yang telah diubah ke dalam bentuk persamaan berpola maksimum maka masalah sudah dapat diselesaikan dengan metode simpleks. Bila masalah program linear berpola maksimum atau berpola minimum dan mempunyai penyelesaian basis yang tidak layak, karena memuat nilai negatif untuk variabel pengetat, maka masalah program linear tersebut belum bisa diselesaikan dengan metode simpleks.

Masalah program linear yang masih memuat nilai negatif pada variabel pengetatnya memerlukan variabel semu, yaitu variabel yang ditambahkan kedalam persamaan kendala-kendala. Jika a adalah variabel semu yang disisipkan pada persamaan yang memuat variabel pengetat bernilai negatif maka masalah program linear tersebut sudah memuat suatu penyelesaian layak basis. Variabel semu ini bersifat sebagai katalisator (penghubung) dan mempunyai nilai nol supaya masalah semula mempunyai penyelesaian optimum. Bila ada variabel semu yang dipakai maka fungsi sasaran yang baru untuk pola maksimum berbentuk z=z−Ma, sedangkan fungsi sasaran yang baru untuk pola minimum berbentuk z=z+Ma dengan M bilangan positif yang cukup besar.

Salah satu cara untuk menyelesaikan masalah program linear dengan menggunakan metode simpleks adalah melalui tabel simpleks.

Langkah-langkah penyelesaian masalah program linear dengan menggunakan metode simpleks melalui tabel simpleks adalah sebagai berikut :

Langkah 1:

Membentuk masalah program linear menjadi bentuk kanonik yaitu kendalanya harus berbentuk persamaan, dengan menambahkan variabel pengetat, variabel semu dan b_i ≥0 sehingga memenuhi bentuk baku program linear.

Langkah 2 :

Menyusun tabel awal seperti dalam tabel berikut ( Tabel 2.1 )

Tabel 2.1 Tabel Awal Simpleks

j c c₁ c_{2 K} c_n i c x_i \x_j x1 x2 K xn bi Ri m c c c M 2 1 m x x x M 2 1 mn m m n n a a a a a a a a a K M O M K K 2 1 2 22 21 1 12 11 m b b b M 2 1 m R R R M 2 1 j z z₁ z_{2 K} z_n z j j c z − z Keterangan : j x : variabel-variabel keputusan ij a : koefisien teknis i

b : suku tetap (tak negatif)

j

c : koefisien ongkos

i

x : variabel yang menjadi basis dalam tabel yang ditinjau

n n c z c z c z₁− _{1 2}− _{2 K} −

i

c : koefisien ongkos milik variabel basis xi

j z :

∑

= m i ij ia c 1 z :

∑

= m i i ib c 1 j j c z − : selisih z_j denganc_j i R : ik i a b hanya untuk

a

_i

≥

0

Langkah 3 :

Menguji keoptimuman, dengan memperhatikan nilai z_j −c_j. Untuk masalah dengan pola maksimum, tabel dikatakan optimum bila nilai zj −cj ≥0 untuk semua j. Sedangkan untuk masalah dengan pola minimum tabel dikatakan optimum bila nilai z_j −c_j ≤0 untuk semua j. Bila sudah optimum berarti sudah didapatkan penyelesaiannya. Jika belum optimum maka dilanjutkan ke Langkah 4.

Langkah 4 :

Memperbaiki tabel. Dalam hal ini artinya memilih variabel baru yang masuk menjadi variabel basis. Untuk masalah yang berpola maksimum adalah dengan memilih kolom pivot, yaitu kolom dengan nilai zj −cj terkecil atau

paling minimum. Untuk masalah yang berpola maksimum adalah dengan memilih nilai zj −cj terbesar atau paling maksimum. Setelah ditemukan

kolom pivot maka selanjutnya dicari nilai rasio (Ri ) untuk setiap baris,

yaitu bi dibagi unsur-unsur pada kolom pivot yang bernilai positif. Tidak

berbeda untuk pola maksimum dan pola minimum, dipilih nilai Ri terkecil

atau _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ik i i a b

R min . Baris dengan Ri terkecil kemudian menjadi baris

pivot. Setelah baris pivot dan kolom pivot terpilih, maka perpotongan antara baris pivot dan kolom pivot

( )

a_rs disebut sebagai elemen pivot dimana variabelnya akan menjadi variabel basis baru yang akan menggantikan variabel basis lama dan selanjutnya menuju ke Langkah 5.

Langkah 5 :

Pada tabel selanjutnya elemen ars diubah supaya bernilai satu dan semua

elemen pada kolom yang bersesuaian diubah menjadi nol dengan melakukan operasi baris elementer. Variabel basis baru dan koefisien ongkos menyesuaikan dengan variabel basis baru tersebut. Selanjutnya kembali ke langkah 3.

D. Metode Simpleks Dual

Masalah program linear memiliki dua macam metode simpleks, yaitu metode simpleks primal dan metode simpleks dual. Untuk setiap masalah program linear dapat diubah ke bentuk dual dimana kendala dan variabelnya adalah kebalikan dari primal, yakni koefisien variabel dalam masalah primal menjadi koefisien kendala dalam masalah dual. Jika dalam masalah primal mempunyai n

variabel dan m kendala maka masalah dualnya akan menjadi m variabel dan n

kendala. Dapat dikatakan bahwa jumlah kendala dalam masalah primal sama dengan jumlah variabel dalam masalah dual. Bila masalah primal memaksimumkan fungsi sasaran maka masalah dualnya pasti meminimumkan fungsi sasaran, dan begitu sebaliknya.

Berikut akan diberikan contoh bentuk dual dari bentuk primal pada masalah program linear

Contoh 2.2 Masalah primal Minimumkan z=6x₁+2x₂ −x₃+2x₄ dengan kendala 4x₁+3x₂−2x₃+2x₄ ≥10 188x₁+x₂+2x₃+4x₄ ≥ dan x1,x2,x3,x4≥0 Penyelesaian : Masalah dual Maksimumkan g =10y1+18y2 dengan kendala 4y₁+8y₂ ≤6 2 3y1+y2 ≤ 1 2 2 1+ 2 ≤− − y y 2 4 2y₁+ y₂≤ dan y₁,y₂ ≥0

Dalam metode simpleks dual penyelesaiannya dimulai dari penyelesaian basis yang tidak layak dan memenuhi ciri optimum sedangkan metode simpleks primal penyelesaiannya dimulai dari penyelesaian layak basis tetapi tidak harus optimum.

Masalah program linear yang akan dicari dualnya harus berpola maksimum baku atau minimum baku yang memiliki bentuk baku sebagai berikut :

Pola maksimum baku : Maksimumkan z=cx

memenuhi Ax≤b ( semua berbentuk ≤ )

Pola minimum baku : Minimumkan z=cx

memenuhi Ax≥b ( semua berbentuk ≥ )

Untuk dapat menyusun suatu masalah primal kedalam bentuk dual maka harus dibuat kedalam bentuk kanonik sebagai berikut :

Pola maksimum (atau pola minimum):

Maksimumkan (atau minimumkan) z=cx (2.12) yang memenuhi Ax=b (2.13)

Langkah-langkah metode simpleks dual adalah sebagai berikut : Langkah 1 :

Membentuk masalah program linear menjadi bentuk kanonik, yaitu kendalanya harus berbentuk persamaan, dengan menambahkan variabel pengetat, variabel semu dan b_i ≥0 sehingga memenuhi bentuk baku program linear.

Langkah 2 :

Menyusun tabel awal dual simpleks yang disajikan sebagai berikut

Tabel 2.2 Tabel Awal Simpleks Dual

i c c1 c2 K cn j c _{xi \xj} x₁ x_{2 K} x_n b_i m c c c M 2 1 m x x x M 2 1 mn m m n n a a a a a a a a a K M O M K K 2 1 2 22 21 1 12 11 m b b b M 2 1 j z z₁ z_{2 K} z_n z j j c z − z i R R1 R2 K R_n Keterangan : ij j j i a c z R = − , hanya untuk aij <0 n n c z c z c z1− 1 2− 2 K −

Langkah 3 :

Memilih baris pivot, yakni dengan memilih baris i yang mempunyai nilai bi

paling minimum dengan (bi<0)

Jika ada nilai b_i yang sama maka dipilih sembarang b_i.

Langkah 4 :

Memilih kolom pivot, yakni mencari nilai rasio. Nilai rasio R_i diperoleh dengan membagi z_j−c_j dan nilai mutlak dari koefisien teknis yang

berkoefisien negatif atau R_{i ⎟}⎟

⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ₋ = ij j j a c z

dengan aij < 0. Untuk masalah

yang berpola minimum dipilih nilai rasio yang terkecil atau R_i

⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ₋ = ij j j a c z

min , sedangkan masalah yang berpola maksimum dipilih nilai

rasio aij yang terkecil atau R_i

⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ₋ = ij j j a c z

min . Jika koefisien teknis aij

bernilai positif atau nol maka masalah program linear tersebut tidak ada penyelesaian yang layak.

Langkah 5 :

Melakukan operasi baris elementer agar perpotongan antara baris pivot dan kolom pivot (a_rs) yang disebut elemen pivot ini bernilai 1 dan yang lainnya bernilai 0.

Langkah 6 :

Menguji keoptimuman. Jika semua bi ≥0 maka penyelesaian sudah optimum, jadi iterasi harus dihentikan. Jika belum optimum maka harus dilanjutkan ke Langkah 2.

Perbedaan masalah program linear dengan menggunakan metode simpleks primal dan metode simpleks dual adalah sebagai berikut :

1. Jika masalah program linear dalam primal memiliki pola maksimum maka dalam dualnya masalah program linear tersebut akan memiliki pola minimum.

2. Jumlah variabel primal sama dengan jumlah kendala pada bentuk dualnya. 3. Dalam masalah primal, matriks koefisien teknis adalah

( )

a_ij tetapi dalam

masalah dualnya berbentuk tranpose dari matriks tersebut, yakni

( )

t.

ij

a

4. b_i dalam masalah program linear yang berbentuk primal disebut suku tetap tetapi dalam bentuk dualnya b_i menjadi koefisien ongkos.

5. c_j dalam masalah program linear yang berbentuk primal disebut koefisien ongkos tetapi dalam bentuk dualnya cj menjadi suku tetap.

6. Dalam masalah dual, koefisien kendala ke-i berasal dari koefisien variabel ke-i masalah primal.

7. Dalam masalah dual, koefisien variabel ke-j berasal dari koefisien kendala ke-j masalah primal.

D. Program Linear Bilangan Bulat

Program linear bilangan bulat merupakan bagian dari program linear dengan tambahan kendala, dimana beberapa atau semua variabel keputusannya memiliki nilai-nilai bilangan bulat. Masalah-masalah program linear bilangan bulat menyangkut masalah-masalah yang harus diselesaikan dengan bentuk bilangan bulat.

Program linear bilangan bulat ada dua model, yaitu program linear bilangan bulat murni atau biasa disebut program linear bilangan bulat (integer

programming) dan program linear bilangan bulat campuran (mixed integer

programming). Program linear bilangan bulat murni adalah suatu model program linear yang semua variabelnya adalah bilangan bulat, sedangkan program bilangan bulat campuran adalah suatu model program linear dengan beberapa variabelnya berupa bilangan bulat .

Secara umum bentuk masalah program linear bilangan bulat murni dan campuran adalah sebagai berikut :

1. Bentuk baku masalah program linear bilangan bulat murni. Maksimumkan (atau minimumkan ) :

n nx c x c x c Z = _{1 1}+ _{2 2}+_K+ (2.14) dengan kendala-kendala : ⎪ ⎪ ⎭ ⎪ ⎪ ⎬ ⎫ ≥ = ≤ + + + ≥ = ≤ + + + ≥ = ≤ + + + m n mn m m n n n n b x a x a x a b x a x a x a b x a x a x a } , , { } , , { } , , { 2 2 1 1 2 2 2 22 1 21 1 1 2 12 1 11 K M O O M K K (2.15) n j xj ≥0, =1,2,K, (2.16)

Rumus di atas dapat diringkas sebagai berikut : Maksimumkan (atau minimumkan)

∑

= = n j j jx c Z 1 (2.17) dengan kendala :

(

)

∑

= ≥ = ≤ n j i j ijx b a 1 , , (2.18) . , , 2 , 1 , , , 2 , 1 , 0 n j m i bulat bilangan x x_{j j} K K = = ≥ (2.19) 2. Bentuk baku masalah program linear bilangan bulat campuran.

Maksimumkan (atau minimumkan) :

∑

∑

= = + = n j p k k k j jx d y c Z 1 1 (2.20) dengan kendala : . , , 2 , 1 , , , 2 , 1 , , , 2 , 1 , 0 , 0 1 1 p k n j m i bulat bilangan x y x b atau y g x a j k j i p k k ik n j j ij K K K = = = ≥ ≥ ≥ ≤

∑

∑

= = (2.21)

Dalam tulisan ini hanya akan dibahas program linear bilangan bulat murni (integer programming).

Masalah program linear bilangan bulat dapat diselesaikan dengan menggunakan beberapa metode, seperti metode bidang pemotong (cutting plane

method), metode cabang dan batas (branch and bound method), dan metode

enumerasi (enumerative methods). Secara umum, langkah pertama dalam menyelesaikan masalah program linear bilangan bulat adalah dengan

merupakan bilangan bulat maka penyelesaian program linear bilangan bulat sudah dicapai. Jika ternyata masih terdapat penyelesaian yang merupakan bilangan pecahan maka dilakukan suatu proses untuk menentukan penyelesaian bilangan bulat dari masalah tersebut. Dalam tulisan ini hanya akan dibahas menggunakan metode bidang pemotong untuk menyelesaikan masalah program linear bilangan bulat.

Pada tahun 1958 Ralph Gomory mengembangkan metode bidang pemotong (cutting plane method) yang untuk pertama kalinya diaplikasikan pada masalah program linear bilangan bulat fraktional dual (dual fractional integer

programming) adalah penyelesaian metode bidang pemotong yang menggunakan

metode simpleks dual dan memungkinkan adanya bilangan pecahan dalam perhitungannya. Lalu pada tahun 1960 Ralph Gomory memperbaiki metode bidang pemotong tersebut, yakni menjadi masalah program linear bilangan bulat dual (dual all-integer integer programming) yang dalam perhitungannya harus berupa bilangan bulat. Metode bidang pemotong dalam kedua masalah program linear bilangan bulat ini menggunakan metode simpleks dual. Uraian untuk kedua masalah program linear bilangan bulat tersebut akan dijelaskan pada bab-bab berikutnya.

BAB III

PROGRAM LINEAR BILANGAN BULAT FRAKSIONAL DUAL

A. Masalah Program Linear Bilangan Bulat

Salah satu langkah yang dilakukan dalam penyelesaian masalah program linear bilangan bulat yang menggunakan metode bidang pemotong adalah dengan menambahkan kendala baru. Penambahan kendala baru dalam metode ini diperoleh dengan menyusun suatu persamaan yang memenuhi setiap penyelesaian layak dari masalah program linear bilangan bulat yang semula. Penambahan kendala tersebut memungkinkan diperolehnya penyelesaian yang optimum dari masalah program linear yang berupa bilangan bulat.

Masalah program linear bilangan bulat yang diselesaikan dengan metode bidang pemotong dapat diilustrasikan dengan melihat Gambar 3.1. ABCDE adalah daerah layak yang diperoleh dari perpotongan kendala-kendala utama. Penyelesaian dari masalah program linear bilangan bulat dapat digambarkan sebagai titik-titik layak pada daerah layak tersebut dan titik D adalah penyelesaian optimum program linear yang pertama kali diperoleh. Sebuah kendala baru x′≥0 ditambahkan sehingga titik D terbuang dari daerah layak dan jika dilakukan optimisasi kembali akan didapat penyelesaian optimum program linear yang baru, yakni titik F sehingga daerah layak yang baru adalah ABCGFE. Sebuah kendala baru kedua x′′≥0 ditambahkan agar menghapus titik F dari daerah layak sehingga diperoleh daerah layak yang baru adalah ABCGHIE. Dalam

m p G d b l b s menyelesaik penyelesaian Gambar 3.1. b Perb dengan masa bernilai -1. Perh linear bilang berpola mak sebagai berik kan kembali n optimum b Ilustrasi Peny bidang pemoto edaan metod alah program atikan kemb gan bulat. S ksimum dap kut : masalah pr bilangan bula yelesaian Masa ong de simpleks m linear bila bali pada b ecara umum pat dinyataka rogram linea at, yakni titi

alah Program dual yang su angan bulat a bab sebelum m masalah pr an dalam be ar bilangan ik H. Linear Bilang udah dibahas adalah pada mnya menge rogram linea entuk kanon bulat akan

gan Bulat den

s pada bab s elemen pivo

enai masalah ar bilangan nik dan bent

ditemukan ngan metode ebelumnya otnya yaitu h program bulat yang tuk matriks

1. Bentuk kanonik masalah program linear bilangan bulat : Maksimumkan : n nx c x c x c z= 1 1+ 2 2+K+ (3.1) dengan kendala-kendala :

⎪

⎪

⎭

⎪

⎪

⎬

⎫

+

+

+

+

=

+

+

+

+

=

+

+

+

+

+ + + m m n n mn m m n n n n n n

b

x

x

a

x

a

x

a

b

x

x

a

x

a

x

a

b

x

x

a

x

a

x

a

K

M

O

O

M

K

K

2 2 1 1 2 2 2 2 22 1 21 1 1 1 2 12 1 11 (3.2) n j x_j ≥0, =1,2,_K, (3.3) dan x_j bilangan bulat.

2. Bentuk matriks masalah program linear bilangan bulat : Maksimumkan :

cx = z (3.4)

dengan kendala-kendala :

Ax ≤ b (3.5) x ≥0 dan komponen-komponen x adalah bilangan bulat. (3.6) dengan A=

( )

a_ij matriks kendala berukuran m x n.

Bentuk kanonik pada masalah program linear bilangan bulat disusun ke dalam bentuk seperti dibawah ini :

Maksimumkan :

(

c x

)

(

c

(

x

)

)

(

cn

(

xn

)

)

dengan kendala-kendala :

(

)

(

)

(

(

)

)

(

(

)

)

(

)

(

)

(

(

)

)

(

(

)

)

(

)

(

m

)

(

m

(

)

)

(

mn

(

n

)

)

n m m n n n n n n b x x a x a x a b x x a x a x a b x x a x a x a = + − − + + − − + − − = + − − + + − − + − − = + − − + + − − + − − + + + K M M M O O M K K 2 2 1 1 2 2 2 2 22 1 21 1 1 1 2 12 1 11 (3.8) n j xj ≥0, =1,2,K,

dan x_j bilangan bulat.

Bentuk kanonik di atas dapat diubah ke dalam bentuk seperti dibawah ini : Maksimumkan :

(

x

)

a

(

x

)

a n

(

xn

)

a a x₀ = ₀₀ + ₀₁ − ₁ + ₀₂ − ₂ +_K+ ₀ − (3.9) dengan kendala-kendala :

( )

( )

( )

⎪

⎪

_⎭

⎪

⎪

⎬

⎫

−

−

=

−

−

=

−

−

=

n n

x

x

x

x

x

x

1

1

1

2 2 1 1

O

M

(3.10)

( )

( )

( )

( )

( )

( )

⎪

⎭

⎪

⎬

⎫

−

+

+

−

+

−

+

=

−

+

+

−

+

−

+

=

+ + + + + + + + + + n n m n m n m n m n m n n n n n n n n

x

a

x

a

x

a

a

x

x

a

x

a

x

a

a

x

, 2 2 , 1 1 , 0 , , 1 2 2 , 1 1 1 , 1 0 , 1 1

K

M

O

O

O

O

M

K

(3.11) dengan x_j ≥0,j=1,2,_K,n+m

dan xj bilangan bulat untuk j=0,1,K,n+m.

Persamaan (3.10) merupakan persamaan kendala untuk variabel keputusan (original variables), yakni variabel awal pada masalah program linear bilangan bulat. Persamaan (3.11) merupakan persamaan kendala untuk kendala utama (original constraints) yang ada pada masalah program linear bilangan

bulat. Pada bentuk di atas, n dan m masing-masing menunjukkan banyaknya variabel keputusan dan variabel slack yang muncul dari kendala utama.

Dengan membandingkan persamaan (3.7), (3.8), (3.10) dan (3.11) dapat didefinisikan x0 = z, a00 =0, cj =−a0j, ( j=1,K,n), bi =an+i,0

(

i=1,_K,m

)

, dan a_ij =a_n+_i,j

(

i=1,_K,m; j=1=1,_K,n

)

.

B. Penyelesaian Masalah Program Linear Bilangan Bulat Fraksional Dual Metode yang digunakan untuk mencari penyelesaian program linear bilangan bulat fraksional dual merupakan perluasan dari metode simpleks dual, yakni dengan menambah kendala baru pada masalah tersebut. Langkah-langkah masalah program linear bilangan bulat fraksional dual adalah sebagai berikut : 1. Mengubah bentuk baku menjadi bentuk kanonik seperti persamaan (3.2)

2. Menyusun tabel awal dari masalah program linear bilangan bulat. Pada persamaan (3.2) tabel awal tersebut disajikan sebagai berikut :

Tabel 3.1 Tabel Awal Program Linear Bilangan Bulat Fraktional Dual. 1

(

−x₁

)

_K

( )

−x_{j K}

(

−x_n

)

= 0 x a00 a01 K a0j K a0n 0 0 0 M M 0 0 1 M M − K O L O K 0 1 0 M M − K O L O K 1 0 0 − M M = = + + m n n x x M 1 0 , 0 , 1 m n n a a + + M 1 , 1 , 1 m n n a a + + M K O K j m n j n a a , , 1 + + M K O K Keterangan : j j a c a z x0 = , 00 =0, =− 0 , ( j=1,K,n), bi =an+i,0 (i=1,K,m), dan

(

i m j n

)

a a_ij = _n+i,j =1,_K, ; =1=1,_K, , x_i ≥0(i=1,_K,n+m).

3. Masalah program linear bilangan bulat ini diselesaikan dahulu sebagai masalah program linear, yakni dengan menggunakan metode simpleks dual. Dengan langkah-langkah sebagai berikut :

Langkah 1: Memilih baris pivot, yakni dengan memilih baris v yang mempunyai nilai a_v0 paling minimum dengan a_v0 <0 ,v≠0

= = = n j x x x M M 1 n m n n n a a , , 1 + + M

Langkah 2 : Memilih kolom pivot, yakni kolom dengan nilai rasio yang paling minimum dan nilai rasio =

⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ vj j a a₀ min

Langkah 3 : Mengganti variabel nonbasis pada kolom pivot dengan variabel

v

x , yakni variabel pada baris pivot.

Langkah 4 : Melakukan operasi kolom agar elemen-elemen baris x_v pada kolom pivot bernilai -1 dan yang lain bernilai 0.

Langkah 5 : Bila nilai a_v0 masih ada yang bernilai negatif maka kembali ke langkah 1. Jika sudah tidak ada lagi yang bernilai negatif maka langkah dihentikan dan penyelesaian masalah program linear bilangan bulat sudah optimum.

4. Menguji keoptimuman.

Bila penyelesaian optimum yang diperoleh pada langkah sebelumnya adalah bilangan bulat maka masalah program linear bilangan bulat sudah selesai. Jika penyelesaian optimumnya belum berupa bilangan bulat maka langkah-langkah penyelesaian dilanjutkan lagi menggunakan metode bidang pemotong dengan menambahkan kendala bidang pemotong yang baru yang memuat variabel pengetat x_n+m+k. Lalu kendala bidang pemotong yang baru ditambahkan pada tabel yang ditulis pada baris terakhir maka bentuk tabel akan menjadi :

Tabel 3.2. Tabel Dengan Bentuk Kendala Bidang Pemotong 1

(

−x₁

)

_K

( )

−x_{j K}

(

−x_n

)

= 0 x a00 a01 K a0j K a0n = = + + m n n x x M 1 0 0 0 M M 0 , 0 , 1 m n n a a + + M 0 0 1 M M − K O L O K 0 1 0 M M − K O L O K 1 0 0 − M M 1 , 1 , 1 m n n a a + + M K O K j m n j n a a , , 1 + + M K O K = + +m k n x an+m+k,0 an+m+k,1Kan+m+k,j K an+m+k,n

Dalam menentukan kendala bidang pemotong harus ditentukan dahulu baris sumber. Berikut ini akan dijelaskan bagaimana cara menentukan bentuk kendala bidang pemotong dan cara memilih baris sumber :

a. Memilih baris sumber

Cara memilih baris sumber adalah dengan memilih baris yang memuat variabel-variabel basis yang nilainya belum berupa bilangan bulat. Dalam hal ini variabel yang akan terpilih harus memberikan ketaksamaan yang kuat yaitu nilai dengan bilangan pecahan terbesar supaya dapat mempercepat pencapaian penyelesaian program linear bilangan bulat yang optimum.

= = = n j x x x M M 1 n m n n n a a , , 1 + + M

Jika variabel basis xi pada persamaan ke-i bukan merupakan bilangan bulat

maka variabel tersebut dapat dinyatakan sebagai :

(

_{( )}

)

₀ 1 J j i n j ij i a x a x −

∑

− = = (3.12)

Keterangan : ai0bukan bernilai bilangan bulat aij dapat berbentuk bilangan bulat

J adalah himpunan indeks variabel nonbasis

J(j) adalah elemen j di dalam J

xJ_{( )}j adalah variabel nonbasis j di dalam J

Persamaan (3.12) dapat ditulis sebagai berikut

n

(

_{J( )j}

)

j ij i i a a x x = +

∑

− =1 0 (3.13)

Setiap persamaan seperti di atas dinyatakan sebagai baris sumber (source row). Misalkan : a_i0 =

[ ]

a_i0 + f_i dan a_ij =

[ ]

a_ij + f_ij (3.14) dengan :

[ ]

ai0 adalah bilangan bulat terbesar yang kurang dari atau sama dengan ai0, dan

[ ]

aij adalah bilangan bulat terbesar yang kurang dari atau sama dengan aij

maka 10< fi < dan 0≤ fij <1

Ada dua cara untuk memilih baris sumber yaitu : 1. Baris dengan nilai fi0 yang paling maksimum.

2. Baris dengan nilai

⎪ ⎪ ⎭ ⎪⎪ ⎬ ⎫ ⎪ ⎪ ⎩ ⎪⎪ ⎨ ⎧

∑

= n j ij i f f 1

0 _{yang paling maksimum.}

Jika nilai fi0 atau

⎪ ⎪ ⎭ ⎪⎪ ⎬ ⎫ ⎪ ⎪ ⎩ ⎪⎪ ⎨ ⎧

∑

= n j ij i f f 1

0 _{untuk setiap baris selalu sama maka dapat dipilih}

sebarang baris untuk menjadi baris sumber. b. Menentukan bentuk kendala bidang pemotong

Dari uraian pemilihan baris sumber, dengan persamaan (3.13) akan menjadi :

[ ]

(

[ ]

)

(

J_{( )}j

)

n j ij ij i i i a f a f x x = + +

∑

+ − =1 0

[ ]

[ ]

(

_{( )}

)

n

(

_{J( )j}

)

j ij j J n j ij i i f a x f x a + + − + − =

∑

∑

= =1 1 0 atau ( )

(

)

[ ]

[ ]

(

J( )j

)

n j ij i i j J n j ij i f x x a a x f +

∑

− = − −

∑

− = = 1 0 1 (3.15)

Supaya nilai x_i dan

(

−x_{J( )j}

)

adalah bilangan bulat, maka ruas kanan dari persamaan (3.15) harus bernilai bilangan bulat yang mengakibatkan ruas kiri persamaan (3.15) haruslah bernilai bilangan bulat. Karena fij ≥0 dan

( )

(

−xJ j

)

≤0 untuk setiap nilai i dan j, maka

( )

(

)

0 1 ≤ −

∑

= J j n j ij x f dengan demikian n

(

_{J( )j}

)

_i j ij i f x f f +

∑

− ≤ =1 . Karena fi <1 maka

(

( )

)

1 1 < − +

∑

= J j n j ij i f x f (3.16) atau ( )

(

J j

)

n j ij i f x f < −

∑

− =1 1

Karena ruas kiri persamaan (3.15) harus bernilai bilangan bulat, maka berdasarkan persamaan (3.15), haruslah

( )

(

)

0 1 ≤ − +

∑

= J j n j ij i f x f

Jika bentuk di atas ditambahkan dengan variabel pengetat x_n+m+k dengan 0

≥

+ +m k n

x bilangan bulat, maka didapat :

( )

(

)

0 1 = + − + + + =

∑

J j n m k n j ij i f x x f atau ( )

(

J j

)

i n j ij k m n f x f x =−

∑

− − = + + 1 (3.17)

Persamaan (3.17) merupakan bagian pecahan (fractional cut) atau disebut juga pembatas sekunder. Jika pembatas sekunder ini sudah dimasukkan ke dalam tabel yang berada pada baris terakhir dalam tabel dan dilakukan operasi kolom maka tabel terakhir didapat

(

−xJ_{( )}j

)

=0 sehingga xn+m+k = fi, yang berarti

tidak layak. Hal ini berarti pembatas sekunder yang baru tersebut tidak dipenuhi oleh penyelesaian yang diperoleh karena mengakibatkan nilai yang didapat belum berupa bilangan bulat sehingga untuk mengatasi ketidaklayakan ini dapat digunakan metode simpleks dual, yang pada dasarnya sama dengan memotong daerah layak ke arah penyelesaian optimum yang berupa bilangan bulat.

Dari penjelasan yang sudah dijabarkan di atas dan cara-cara memilih baris sumber serta menentukan pembatas sekunder, secara umum langkah pertama yang dilakukan dalam menyelesaikan masalah program linear bilangan bulat fraksional dual adalah mengubah masalah ke dalam bentuk kanonik dan menyusun tabel awal, menyelesaikan masalah program linear bilangan bulat dengan cara simpleks biasa dan dilanjutkan dengan langkah-langkah sebagai berikut :

Langkah 1 :

Memilih baris sumber x_v dengan dua cara di bawah ini :

1. Baris dengan nilai f_v0 yang paling maksimum.

2. Baris dengan nilai

⎪ ⎪ ⎭ ⎪⎪ ⎬ ⎫ ⎪ ⎪ ⎩ ⎪⎪ ⎨ ⎧

∑

= n j vj v f f 1

yang paling maksimum.

Langkah 2 :

Menentukan bentuk kendala bidang pemotong yang baru, yakni pembatas sekunder seperti persamaan (3.17)

( )

(

J j

)

v n j vj k m n f x f x =−

∑

− − = + + 1 Langkah 3 :

Langkah 4 :

Mencari baris pivot dengan melihat nilai koefisien av0 yang bernilai negatif dan dipilih yang paling minimum

Langkah 5 :

Mencari kolom pivot dengan melihat niali R=

vj j a a0 yang terkecil. Langkah 6 :

Menggantikan variabel non basis pada kolom pivot dengan Variabel xv.

Langkah 7 :

Melakukan operasi kolom agar elemen-elemen baris x_v pada kolom pivot bernilai -1 dan yang lainnya bernilai 0.

Langkah 8 :

Jika masih ada nilai x_v yang nilainya belum berupa bilangan bulat maka dilanjutkan ke Langkah 1. Jika sudah tidak ada maka proses dihentikan dan diperoleh tabel optimum.

Masalah program linear bilangan bulat fraksional dual tidak membedakan antara variabel keputusan dan variabel pengetat yakni bahwa semua variabel harus berupa bilangan bulat. Adanya koefisien yang tidak bulat dalam kendala tidak

memungkinkan untuk variabel pengetat berupa bilangan bulat. Dalam hal ini, masalah program linear bilangan bulat fraksional dual dapat menyatakan bahwa tidak terdapat penyelesaian layak, sekalipun masalah tersebut mempunyai penyelesaian layak yang bernilai bilangan bulat dalam bentuk bukan variabel pengetat.

Berikut akan diberikan contoh penyelesaian masalah program linear bilangan bulat menggunakan metode bidang pemotong

Contoh 3.1

Selesaikan masalah program linear bilangan bulat berikut: Maksimumkan: z=−4x1−5x2

Dengan kendala: −x₁−4x₂ ≤−5 −3x₁−2x₂ ≤−7 dan x₁,x₂ ≥0

Penyelesaian :

Masalah program linear di muka dapat dibuat ke bentuk kanonik sebagai berikut : Maksimumkan: z=−4x₁−5x₂

Dengan kendala: −x1−4x2 +x3 =−5 −3x1 −2x2 +x4 =−7 dan x₁,x₂,x₃,x₄ ≥0

1. Menyusun tabel awal simpleks.

Tabel 3.3. Tabel Awal Pada Contoh Masalah Program Linear Bilangan Bulat

1

(

−x₁

)

(

−x₂

)

0 x 0 4 5 4 3 2 1 x x x x 7 5 0 0 − − 3 1 0 1 − − − 2 4 1 0 − − −

2. Menyelesaikan dengan metode simpleks dual. ITERASI 1

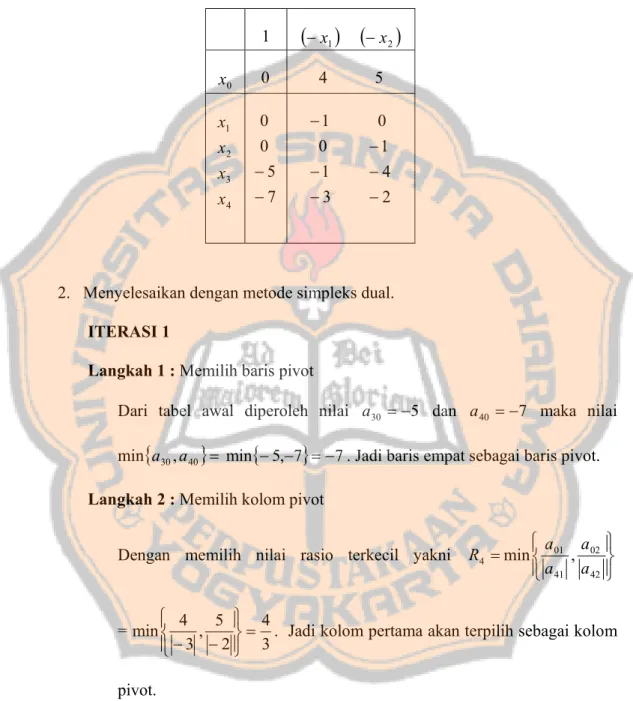
Langkah 1 : Memilih baris pivot

Dari tabel awal diperoleh nilai a30 =−5 dan a40 =−7 maka nilai min

{

a30,a40

}

= min

{

−5,−7

}

=−7. Jadi baris empat sebagai baris pivot.

Langkah 2 : Memilih kolom pivot

Dengan memilih nilai rasio terkecil yakni R4 =min

⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ 42 02 41 01 _, a a a a = min 3 4 2 5 , 3 4 ₌ ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ −

− . Jadi kolom pertama akan terpilih sebagai kolom

pivot.

Langkah 3 : Menggantikan variabel x₁ dengan variabel x₄

Tabel 3.4. Tabel Setelah Operasi kolom Pada Iterasi 1 1

(

−x₄

)

(

−x₂

)

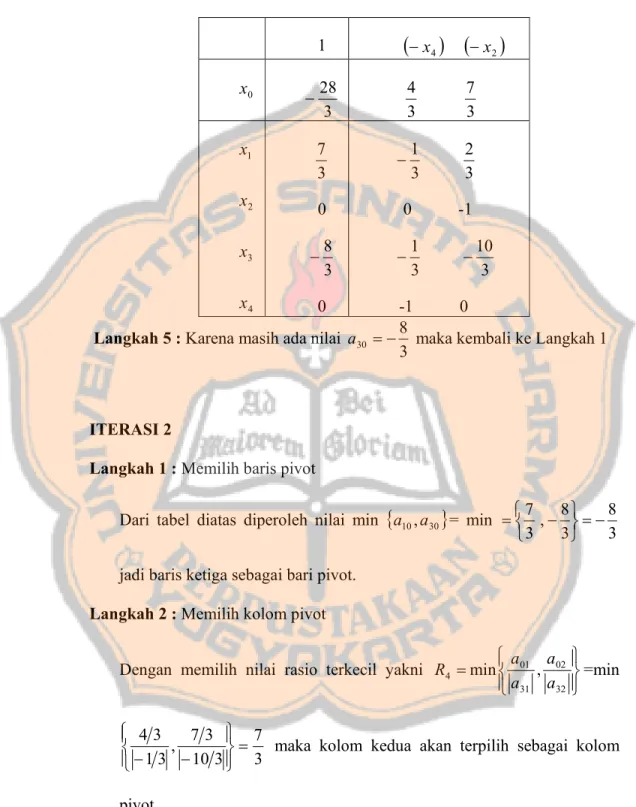
0 x 3 28 − 3 4 3 7 4 3 2 1 x x x x 3 7 0 3 8 − 0 3 1 − 3 2 0 -1 3 1 − 3 10 − -1 0 Langkah 5 : Karena masih ada nilai

3 8 30 =−

a maka kembali ke Langkah 1

ITERASI 2

Langkah 1 : Memilih baris pivot

Dari tabel diatas diperoleh nilai min

{

a₁₀,a₃₀

}

= min

3 8 3 8 , 3 7 ₌₋ ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ₋ =

jadi baris ketiga sebagai bari pivot. Langkah 2 : Memilih kolom pivot

Dengan memilih nilai rasio terkecil yakni R4 =min

⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ 32 02 31 01 _, a a a a =min 3 7 3 10 3 7 , 3 1 3 4 ₌ ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ −

− maka kolom kedua akan terpilih sebagai kolom

pivot.

Langkah 4 : Melakukan operasi kolom, sehingga diperoleh tabel baru sebagai berikut

Tabel 3.5. Tabel Setelah Operasi kolom Pada Iterasi 2

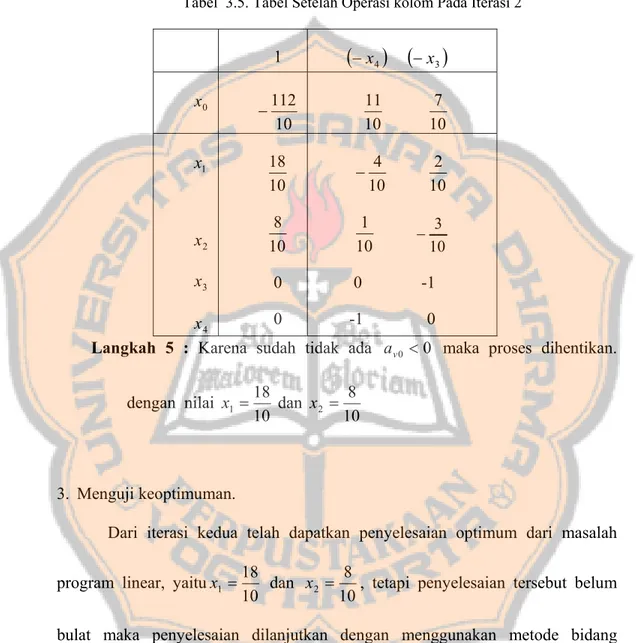
1

(

−x₄

)

(

−x₃

)

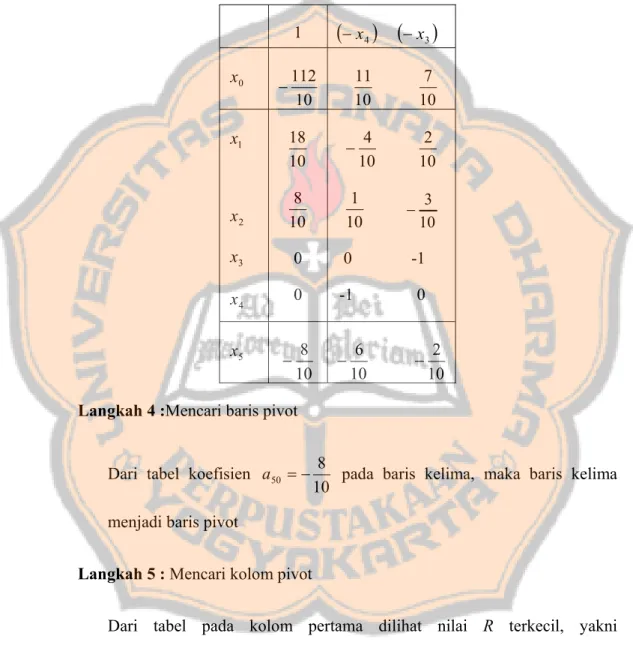
0 x 10 112 − 10 11 10 7 2 x 3 x 4 x 10 18 10 8 0 0 10 4 − 10 2 10 1 0 -1 -1 0

Langkah 5 : Karena sudah tidak ada a_v0 <0 maka proses dihentikan. dengan nilai 10 18 1 = x dan 10 8 2 = x 3. Menguji keoptimuman.

Dari iterasi kedua telah dapatkan penyelesaian optimum dari masalah program linear, yaitu

10 18 1 = x dan 10 8 2 =

x , tetapi penyelesaian tersebut belum bulat maka penyelesaian dilanjutkan dengan menggunakan metode bidang pemotong. 1 x 10 3 −