49-364 / H/IT

ITS I

i 1 T 5

m

^{InstitutTeknologi}

SepuluhNopember

538 /

•

Hid P - '

TUGASAKHIR-SF091321

2012

PENDEKATAN KARTESIAN UNTUK SISTEM POTENSIAL LISTRIK GEOMETRI CAMPURAN KARTESIAN - POLAR

FITRIANARICHA HIDAYATI NRP

.

1107100046

DosenPembimbing M

.

Ariel Bustomi,M

.

Si JURUSAN FISIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUTTEKNOLOGI SEPULUH NOPEMBER

SURABAYA2012

» Term

* own

-^m-

Mo

Agenda

Teknologi

SepuluhNopember

FINALPROJECT

-

^SF091321

CARTESIAN APPROACH FOR ELECTRIC POTENTIAL OF MIXTURE GEOMETRY SYSTEM CARTESIAN

^-

POLAR

FITRIANARICHA HIDAYATI NRP

.

1107100046

Advisor

M

.

ArielBustomi,M

.

^Si

DEPARTEMEN OF PHYSICS

Facultyof MathematicandNaturalScience SepuluhNovember InstituteofTechnology Surabaya 2012

CAMPURAN KARTESIAN-POLAR TUGAS AKHIR

Diajukan Untuk Memenuhi SalahSatuSyarat

Memperoleh GelarSarjanaPada Bidang Studi Optoelektronika Program Studi S

-

l Jurusan Fisika

Fakultas Matematikadan IlmuPengetahuanAlam InstitutTeknologi Sepuluh Nopember

Oleh:

Fitriana RichaHidavati NRP. 1107100 046

Disetujui olehPembimbingTugas Akhir :

M

.

AriefBustomi M^.Si

12012

'

'^ORUS

^

lam/O iO XIMT3IJ JAI_AAjei

-

_/

^

^{/ fTO i}

*

^{MATSIA / JT/! I}

Ai

« ; rr «

^{yvi/ /}

a

^JSM/

>

HfHtfA >/

.

^{» fT}

)SIB^/AUJK

< '

^{Inis?iflunon,•£/ jli}

.

^lri-1fiE

^

^ujtiO

r

.

^/itisoifcteteoKjO_RAibmZ

- -

¹_nsjjOfibif_•.

-

^.V

*

^!eta

-

^{<* '-i' x}

-

^nnui?.mB»B<

^

^{'i O i}

-

^uibi

'

^f;rl

^

^orxjrmf/

fTUilAladmoqoinaurtaJogns

^

^{insl> B}

^

^iJf

.

^rnstsfV'

^

^tlu/irI

^

^{riuluq*j<!igoionAA uni nl}

k

dl

-

^{fl 00f Tull}

.

^Htttf

:i i <1 i’ t h k^, i u n i i w t l

i^? 1^/ irrif ^j:-^;cf iM/> f/

S I0£ l/ L

.

^{/ f t ’l M i n}

KARTESIAN

-

^POLAR

NamaMahasiswa :Fitriana RichaHidayati

NRP :1107 100 046

Jurusan : Fisika FMIPA ITS DosenPembimbing : M.AriefBustomi,M

.

Si Abstrak

Sistem potensial listrik dengan geometri campuran kartesian ^- polar dianalisa dengan menggunakan pendekatan /cartesian

.

Untuk penelitian ini hanya dibatasi pada pengaruh jumlah titik data syarat batas pada pendekatan kartesian. Ada beberapa tahapan yang dilakukan dalam penelitian ini yaitu melakukan perhitungan analitik dalam koordinat campuran kartesian - polar, menentukan syarat batas untuk pendekatan kartesian^, menghitung potensial listrik dengan pendekatan kartesian pada masing

-

^masing jumlah titik datasyarat batas dan membandingkannya dengan basil perhitungannya secara langsung.Berdasarkanpenelitian inisemakinbanyak jumlah titik datayang digunakan^, maka selisih nilai potensial listrik antara pendekatan kartesian dan perhitungan langsung akan mendekati suatu nilai tertentu. Dari penelitian ini juga diperoleh bahwa perhitungan pada pendekatan kartesian untuk sistem geometri campuran kartesian

-

^polar temyata diperoleh nilai yang berbeda darinilaiperhitungan langsungnya.

Kata kunci

:

pendekatan kartesian, jumlah titik data, syarat batas, sistem geometricampurankartesian-polar

IV

POLAR Student Name :FitrianaR.H

:1107100 046 NRP

:FisikaFMIPA ITS Department

: M.Arief Bustomi,M.Si Advisor

Abstract

Electrical potential system with a mixture geometry of cartesian^-polar analyzed using cartesian approach. This study wasonly limited by the influence of thenumberofpoints onthe boundary condition cartesian approach. There are several steps in this study, first analytical calculation in cartesian ^- polar coordinate, second determine the boundary conditions for cartesian approach, third calculate the electric potential with cartesianapproachfor each number of data points in boundary conditions and compared with the result of direct calculation

.

Basedon the study the more number ofdata points used,then the differencein the electricalpotentialbetween cartesian and direct calculationapproachwillapproach a particular value.Fromthis study also found that the calculation of the cartesian approach for mixed system of cartesian-polargeometrywas obtained by thedifferent values ofthedirect calculation.

Keywords: cartesianapproach,the numberof datapoints,the boundary conditions,amixture geometry system of cartesian

-

^polar.

v

Bismillaahirrohmaanirrohiim DenganNamaAllah Yang MahaPengasihLagiMahaPenyayang

AlhamdulillaahiRobbiPAalamiin, segala puji bagi Allah SWT, Tuhan seluruh alam, karena atas limpahan rahmat serta karunia

-

Nya penulis dapat menyelesaikan LaporanTugasAkhir yang beijudul “ PENDEKATAN KARTESIAN UNTUK SISTEM POTENSIAL LISTRIK GEOMETRICAMPURAN KARTESIAN

-

POLAR

”

^.Adapun tujuan dari penulisan Tugas Akhir ini adalah sebagai syarat untuk menyelesaikan program studi Strata

-

1 di JurusanFisika,FakultasMatematika dan Ilmu PengetahuanAlam, Institut Teknologi Sepuluh Nopember Surabaya.

Ucapan terima kasih pertama kalipenulissampaikan kepada:

MamadanAyah

atas segala do’a yang telah dipanjatkan, mendengarkan segala keluh kesah

,

dan motivasi yang diberikan sehingga penulis dapat menyelesaikanTugas akhir ini

.

Penulis juga ingin menyampaikan ucapan terima kasih atas segalabantuan maupun dukungan sehingga terselesaikannya tugasakhir ini kepada:

1

.

^M

.

^{Arief Bustomi, M.Si}

.

selaku dosen pembimbing yang telah berkenan dengan segala kesabaran dan keikhlasan membimbing penulis dalam penulisan Tugas Akhir ini sehinggabeijalandengan lancar.

2

.

Dosen penguji yangtelah memberikan banyak sarandalam Tugas Akhir ini.

3

.

^{Bapak Dr.Yono Hadi Pramono,} M.Eng. sebagai Ketua Jurusan Fisika MIPA ITS,IbuDr

.

Melania Suwentini,M

.

T

.

sebagai Sekretaris Jurusan Fisika MIPA ITS, serta Bapak Drs

.

Gatut Yudoyono,M

.

T sebagai Koordinator Tugas Akhir Program SI JurusanFisikaFMIPAITS

.

vi

5

.

Seluruh dosen dan

staf

karyawanJurusan Fisika yang telah membantupenulisselama perkuliahan.

6 . Teman -

^teman

kosan

^,

orang - orang yang telah

menyayangi ku ,

^{keluarga besar angkatan}

2007

Jurusan Fisika,

serta semua pihak

yang

tidak dapat disebutkan satu - persatu yang telah membantu dalam penelitian dan penyusunan Tugas Akhir ini .

Semoga Tugas Akhir ⁱⁿⁱ memberikan kontribusi dan menginspirasi terutama bagi pihak

-

^pihak yang menekuni tema terkait, saran dan kritik sangat penulis harapkan untuk pengembanganpenelitian Tugas Akhirberikutnya.

Surabaya, Juni2012

Penulis

VII

ABSTRAK ABSTRACT

KATAPENGANTAR DAFTAR ISI

DAFTARGAMBAR DAFTAR TABEL

IV

v

V I V I I I X X U

BABIPENDAHULUAN 1.1Latar Belakang 1.2PerumusanMasalah 1.3 Batasan Masalah 1.4Tujuan Penelitian 1.5Manfaat Penelitian

1 1 1 2 2 BABII DASAR TEORI

2.1Persamaan Laplace 2.2DeretFourier 2.3 Integrasi Numerik 2.4Penelitian Sebelumnya

3 8 9 1 1 BABIII METODOLOGI

3.1Langkah-LangkahPenelitian 3.2 DiagramAlirPenelitian

13 14 BABIVANALISADATA PEMBAHASAN

4.1 Potensial Listrik Sistemyangditeliti 4.2 Perhitungan Langsung Potensial^Listrik

4.2

.

1Perhitungan Potensial Atas(V^] ) 4.2.2Perhitungan Potensial SisiKanan 4.2

.

3 Perhitungan Potensial Sisi Bawah 4.2.4 Perhitungan PotensialSisiKiri

15 20 21

23

24

26

Vlll

Kartesian

Potensial Listrik

Untuk

15titik data Potensial Listrik Untuk30titik data Potensial Listrik Untuk60titik data PotensialListrik

Untuk

120 titik

data

Potensial Listrik

Untuk

240titik data Potensial Listrik

Untuk

480titik data

Selisih Potensial ListrikPerhitungan Langsung danPendekatan Kartesian

SelisihV

untuk

15titik data SelisihV

untuk

30 titik data SelisihVuntuk60titik data SelisihVuntuk 120 titik data Selisih V untuk240titik data SelisihVuntuk480 titikdata

Pembahasan

GrafikPerbandinganVi

untuk

15 titik data Grafik Perbandingan V2untuk 15 titik data Grafik PerbandinganV₃untuk15titik data GrafikPerbandinganV₄untuk15titik data GrafikNilai PotensialV pada titik ( 0,2;0,4 ) Grafik Nilai PotensialVpada titik( 0,4;0,2) GrafikNilai Potensial V pada titik( 0,

2

;0 ) Grafik Nilai Potensial V pada titik^{( 0 ;0,}2) 4.3^.1 29

4.3.2 34 4.3.3 39 4.3^.4 44 4.3^.5 49 4.3.6 53 4.4 58

4.4.1 59 4.4.2 63 4.4.3 68 4.4.4 73 4.4.5 77 4.4.6 82 4.5 87

4.5^.1 87 4.5^.2 88 4.5.3 89 4.5.4 90 4.5.5 91 4.5^.6 93 4.5^.7 94 4.5.8 96

BAB V KESIMPULAN DAN SARAN 99 DAFTARPUSTAKA

LAMPIRANA LAMPIRAN B LAMPIRANC

101 103 132 155

tx

Gambar 2.1 Syarat Batas untuk sistem kartesian 4 Gambar 2.2 KaidahTrapesium

Gambar2.3Kaidah Trapesium Gabungan Gambar 3.1 Diagram Alir Penelitian

Gambar4.1 GeometrisystemdanSyarat Batas Potensial Listrik

Gambar4.2PotensialListrik dalam Koordinat Kartesian secara^umur 16 Gambar4.3 Potensial Listrik ditinjau dari sisi kanan⁽

Vkn

⁾

Gambar4.4Potensial Listrik ditinjau darisisikiri(

Vkr

⁾

Gambar 4.5 Potensial Listrikditinjau darisisi atas(Vpoiar) Gambar 4.6 Perhitunganpotensiallangsung

Gambar 4.7PotensialListrikditinjaudarisisiatas (

Vi

⁾

Gambar 4.8 PotensialLisrik ditinjaudarisisikanan (V₂) Gambar 4.9 Potensial Listrik ditinjau dari sisi bawah⁽V3) Gambar 4.10 Potensial Listrikditinjaudarisisi kiri⁽V₄)

Gambar4.11 Hubungan potensialatas Vlangsungdengan Vkartesian 88 Gambar4.12 Hubunganpotensial kanan Vlangsung dengan

Vkartesian15

Gambar4.13 Hubungan potensialbawah Vlangsung dengan Vkartesian 15

Gambar4.14 Hubungan potensial kiri Vlangsung^dengan Vkartesian 15

Gambar 4.15 Hubungan antara jumlah titik data syarat batas dan Seli^: 92 bedapotensial listrik padatitik(0,2;0,4)

Gambar 4.16 Hubungan antarajumlahtitikdatasyarat batas dan Selisih beda potensial pada titik(0,4 ; 0,2) Gambar4.17 Hubunganantarajumlahtitikdata syarat batas dan

Selisih bedapotensial padatitik(0,2;0)

Gambar4.18 Hubungan antarajumlahtitik data syarat batas dan Selisih bedapotensial padatitik (0;0,2)

GambarC

.

l Potensial atas 30 GambarC

.

2Potensial atas60 GambarC

.

3Potensial atas120

9 10 14 15 17 17 18 20 21 23 25 26

89 90 91

94 95 97 155 155 156

x

GambarC

.

5Potensialatas480 GambarC

.

6Potensialkanan30 Gambar C

.

7Potensial kanan 60 GambarC.8 Potensialkanan120 GambarC.9Potensial kanan 240 GambarC

.

10 Potensialkanan 480 GambarC

.

l1 Potensial bawah 30 GambarC.l2Potensial bawah60 GambarC

.

^l3Potensial bawah 120 Gambar C.14 Potensial bawah240 Gambar C.l5Potensial bawah 480 Gambar C.l 6 Potensial kiri 30 GambarC

.

l7Potensialkiri60 GambarC

.

^{l 8}Potensial kiri 120 GambarC.19Potensial kiri 240 GambarC.20 Potensial kiri 480

157 157 158 158 159 159 160 160 161 161 162 162 163 163 164 164

xi

Tabel 4.1 Selisihnilai V untuk 15^{titik data} 59 Tabel 4.2Selisih nilai Vuntuk 30 titik data Tabel4.3Selisih nilai V untuk 60 titik data Tabel4.4 SelisihnilaiV untuk120titik data Tabel4.5 Selisih nilai V untuk 240 titik data Tabel 4.6 Selisih niali Vuntuk 480 titik data Tabel4.7 Selisihtitik data syarat batasdengan

Bedapotensialpada titik(0,2 ; 0,4 ) Tabel4.8Selisih titikdatasyarat batas dengan Beda potensialpada titik(0,4;0,2) Tabel4.9 Selisih titik data syarat batas dengan

Bedapotensial padatitik(0,2;0) Tabel4.10 Selisihtitik data syarat batas dengan

Beda potensial pada titik(0 ; 0,2) Tabel B.l Perhitungan V|secara langsun Tabel B.2PerhitunganV₂secara langsung TabelB.3 Perhitungan V₃secara langsung Tabel B.4 PerhitunganV4secara langsung

Tabel B.5

Vi

pendekatan kartesian untuk 15 titik data Tabel B.6 V2pendekatan kartesian untuk 15 titik data Tabel B^.7V3pendekatankartesian untuk15titikdata Tabel B.8V₄pendekatankartesian untuk15titik data Tabel B.9

Vi

pendekatan kartesian untuk 30 titik data Tabel B.10 V2pendekatankartesian untuk30titik data TabelB.l1 V3pendekatan kartesian untuk 30 titik data Tabel B.12 V4pendekatan kartesian untuk 30 titik data Tabel B.l3V^] pendekatan kartesian untuk 60 titik data Tabel B.14 V2pendekatankartesianuntuk60titik data Tabel B.l5V3pendekatan kartesian untuk 60 titik data Tabel B. l 6V4pendekatan kartesian untuk60titikdata Tabel B.l7 V^|pendekatankartesian untuk120titik data Tabel B.18 V2pendekatan kartesian untuk 120 titik data Tabel B.19V3pendekatankartesian untuk 120 titik data

63 68 73 77 82 92 93 94 96 132 132 133 134 135 135 136 137 138 139 139 140 141 142 143 143 144 145 146

X l l

Tabel B.21 V^|pendekatan kartesian untuk240titikdata Tabel B.22 V₂pendekatan kartesian untuk 240 titikdata TabelB.23V3pendekatan kartesian untuk 240 titik data Tabel B.24V4pendekatankartesianuntuk240titikdata Tabel B.25V|pendekatankartesian untuk480titikdata Tabel B.26V2pendekatankartesianuntuk480titikdata Tabel B.27 V3pendekatan kartesianuntuk480 titik data Tabel B.28V₄pendekatan kartesian untuk 480 titik data

147 148 149 150 151 151 152 153

Xlll

PENDAHULUAN 1.1 LatarBelakang

Sebagaian besar persoalan matematika dalam Fisika adalah persoalan penyelesaian suatu persamaan differensial^dalam fisika harus memenuhi suatu syarat batas tertentu yang merupakan kondisi fisis dari sistem

.

Untuk kondisi yang demikian analisa yang digunakan harus disesuaikan dengan bentuk geometri sistemnya.

Permasalahannya adalah bagaimana jika suatu sistem tersebutmempunyaibentukgeometri campuran

.

Dalampenelitian Tugas Akhir sebelumnya

telah

^{dipelajari suatu metode} pendekatan perhitungan menggunakan koordinat yang tidak sesuai dengan bentuk geometri sistemnya. Penelitian tersebut sebagai langkahawal untuk mempelajarisistem dengan geometri campuran.

Dalam Tugas Akhir ini akan diteliti sistem dengan geometri campuranyaitu kartesian dan pola

.

Sistem tersebut akan dicoba untuk dianalisa dengan pendekatan perhitungan menggunakan koordinat kartesian.

1.2PerumusanMasalah

Dalam penelitian Tugas Akhir ini akan dipelajari suatu sistem dengan geometri campuran kartesian - polar . Dalam penilitian ini diteliti variasi jumlah titik data syarat batas pada pendekatan kartesian untuk sistem potensial listrik geometri campuran kartesian - polar .

1J BatasanMasalah

Batasan masalah untuk penyederhaaan analisa dalam Penelitian Tugas Akhir ini adalah sebagai berikut :

1 . Sistem yang dianalisa adalah 2 dimensi

1

2 .

Analisamenggunakan pendekatan

kartesian .

3 . Pendekatan suku fourier kartesiannya hanya sampai 10 suku .

4 . Hanya diteliti pengaruh jumlah titik data pada pendekatan kartesiannya .

1.4 Tujuan

Tujuan pada penelitian Tugas Akhir ini adalah :

1 . Untuk menguji apakah transformasi

^syarat

batas untuk sistem geometri campuran kartesian - polar dapat

didekati menggunakan kartesian .

2 . Untuk menentukan jumlah titik data pada pendekatan kartesian yang optimum untuk sistem geometri campuran kartesian - polar .

1.5 Manfaat

Manfaaat

Tugas

Akhir

ini

adalah

agar dapat

diketahui

seberapa baik pendekatan kartesian dapatdigunakanuntuksistem geometricampurankartesian^-polar.

TINJAUAN PUSTAKA 2.1 Persamaan Laplace

Dalam persoalan listrik statik tertentu yang melibatkan penghantar seluruh muatan terdapat padapermukaan penghantar atau dalam bentuk muatan titik yang tetap. Daiam hal ini p di sebagian besartitik dalam ruangsama dengan nol.Dan di tempat yangrapat muatannyanol,persamaanPoisson mempunyai bentuk yanglebih sederhana.

vV = 0

^(2.1)

Didalam persamaan Laplace ini akan digunakan dibahas dua metodeseparasiyaitu:

1. Metode separasi variabel koordinat kartesian 2. Metodeseparasi variabel koordinat polar

2.1.1 MetodeSeparasi Variabel Koordinat Kartesian

Diketahui persamaan Laplace

V

^“2⁽

p = 0

^{yang dalam}

koordinat kartesian berbentuk:

|

d V

-

p

dx²

dy

²

Dengan metode pemisahan variabel maka ⁽p disajikan dalam bentuk :

(2.2)

<P

= X

⁽

x

⁾

Y

^(y)

Dan fungsi ini disubstitusikankepersamaan(2.2)menjadi

J

-

^ - 0

Y ( y )

d y²

(2.3)

1 d

²

X

(2.4)

X

{ x ) d x²

3

Karena persamaan inihams samadengan nol untuk semuanilaix dan y maka kedua sukunya bisa disamakan dengan konstanta^:

1

d²

X

= -

^{k2 (2 . 5 )}

^

⁽

x

⁾

dx

²

1

d

²

Y

k²

Y

⁽

y )

dy^{2 (2.6)}

Yang solusinyaadalah :

X

(

x

)

=

^Asin(

fcc

^{) +}

B cos

⁽

fcc

⁾

..

^.

Y^{y)

-

^C

sinh

⁽

Ay

^{) +D}

cosh

⁽

Ay

⁾

(2 . 7) (2.8)

y

<p₂

%

^<

P *

+ _X

<p

*

Gambar2.1Syarat batas untuksistemkartesian

Jika system dikondisikan

q

⁾_x

=

⁽

p

2

—

⁽

p

³

= 0

^{dan hanya (p4}

=

^V4

yang memilikinilai,maka :

v = v

₄

Untuksistem di x

=

⁰

V₄(

0 ,

y)

= B

^{

c sinh

⁽

^

^{y) +D}

sinh

^(fcy))

=

^O

, O '

⁾

= 0

(2 . 9)

(2.10) diperoleh konstanta B bemilai nol

.

Sistem di x

=

a menghasilkan potensial:

V₄(

a , y

)

=

^Asin(

l

^<2)(

Csinh

⁽

^ y

^{) +}

Dcosh

⁽

^ v

⁾⁾

= 03

^... .

(

(^j2.11⁾

= 0

) Untuk menghindari solusi trivial ( karena B

=

0 ) maka didefinisikan k

= nn /

^{u ,}kemudian untuksistemdiy

=

^a

)(Csinh(nsr) +Dcosh(nn))

-

^<

t

^>2(x)

=

⁰

(2.12) Sehingga diperoleh konstanta C bemilai

C = - D

^coi\i{nn)

.

sistem di y

=

0 menghasilkanpotensial :

VA

^(x

,

⁰⁾

=

^{ADsin(~a )}

= 0

^>4(x)

= £

^TT

yn sin

⁽

^ a

ri7DC

V₄(

x ,

a)

=

^Asin(

a

) (2.13) Denganmenggunakan ekspansi Deret Fourier, diperoleh koefisien Fourier dari persamaantersebutbemilai:

-^a o

]

^(p4(

x

⁾

sin ^ a -

^dx

Sehingga persamaan potensial disetiap titik adalah :

V

₄(

x, y

)

= V

i

yn sin

⁽

«

^;

r

⁾⁽

cosh

⁽

^ a ^ ) - coth

^(w

^ ) sinh ( ^

^a

^ ))

(2.15) (Vanderlinde,2004)

(2.14) Y n

=

2.1.2 MetodeSeparasiVariabel KoordinatPolar

Selanjutnya,untuk masalah nilai batasdidalam sifat dasar benttuk geometri polar, dimana potensial adalah suatu fungsi lebih dari satu koordinat. Dianggap potensial

-

potensial itu adalah suatu fungsi dari p dan

^

saja. Seperti timbul potensial

-

potensial didalam keadaan dimana ada suatu simetri sepanjang

sumbu

—

^Z

.

Dalam daerah meniadakan batas beban, potensial memenuhipersamaan:

1 d

,

50 , 1 520 „

-

7 (

^7*

)

⁺

—

T7^'

0

p op op p dtp

^(2.16)

Metode separasi variabel digunakan diatas untuk menyelesaikan potensial dalam koordinat polar. «

J

^{> merupakan}

hasil dari 2 fiingsi, O

= R(

^{p )}

Y

^{<

/

^{)),dan jika} disubstitusikan ke persamaan(2.16)menjadi:

R d dR

1

d²

Y

,

(

^

^T)

=

p dp dp

Y

d_<

/

^{>2 (2.17)}

Kedua sisi dari persamaan(2.14 )akan disamakan ke K²,yang mana K merupakankonstantaseparasi variabel

d²

Y

T⁺ K²

Y = 0

^(2.18)

d<}>

Mempunyaisolusi

cos

(

K

_{<f> )}dan

sin

(

A

^

⁾

.

^{Besaran dari K harus}

dibatasi dalam orde tertentu untuk membuat solusi ini mempunyai nilai fungsi tunggal dari <f_>

.

Atau dalam kata lain, solusi untuk membuat pengertianfisikanyaseharusnyasamasetelah diputar2JI

atau

CosK SinK

( <f(_\>

i

^>+⁺

2n) In

⁾

= = sin cos

⁽⁽

X A ^

⁾

^

⁾

.

^(2.19)

Dimanamenghendaki bahwa K

=

n

,

dan

n

adalah nol atau suatu bilangan positif. Memasukkan bilangan negative tidak akan menghasilkan dalam mengabaikan beberapa solusi yang mungkin^, sebab

cos

(^-

n

^

⁾

= cos

⁽

w ^

^{) dan}

sin

^(-

n ^

⁾

= - sin

⁽

n ^

⁾

.

^Suatu

sifat pentingdari solusi ini adalah kenyataan bahwa sindan soc orthogonal:

1*2/r r2n

Jo

tin

cos

⁽

m ^

⁾

cos

⁽

« ^

^)<

/ ^ = Jo sin

⁽

w ^

⁾

sin( n

^<f>)d<

p =

^mo

Jo c o s c o s

( n_<f_{> )}d<

/

^>

= 0

mn

(2.20)

Dimana

8

m„adalah delta kronecker.

Ketergantungan radial dari potensial selanjutnya dapat diperoleh. Pengaturan sisi sebelah kiri persamaan ⁽ 2.14 ) menyamakan

K =

ⁿ didapatkan :

d

,

dR

^.

rrR

-

_dp

r

⁽

p

^-_dp

r

⁾

p

Untuk n

=

0, potensial memenuhi persamaan yang sama ditemukan dalam kasus dimana potensial tidak mempunyai ketergantungan anguler yaitu:

-_dp

<

^/

>

^-_dp

> =

⁰

Dimana memiliki solusi

R

( p )

=

^{Konstanta dan}

R

^{( p)}

=

^\np

untuk n

=

^£0 persamaan memiliki dua solusi

pn

dan p^~n oleh karena itu,solusiyang palingumum adalah :

= 0

^(2.21)

( 2.22)

oo

<

b

( p

,

6 ) =

^A()

In

^

^»=i

An

⁽

pn

^{+ p}

”

⁾

cosn&

⁺

Bn ( pn

^{+ p}

” ) sinnB

O0

O( p,0)

=

^{A0 + AoInp+}

^

^n=l

[ An cosn

⁰⁺

Bn +

jr \

^A

cos

ⁿ⁶⁺

B

ⁿ

sin

ⁿ⁶

\ p

^~n

n=¹

(2.23) Dimana A

„

,

An

^,

Bn

^,B

„

untuk n 0 adalah konstanta untuk nilai dari syarat batas

.

(Andrews,2006)

ITS _

2.2DenetFourier

Pada tahun

1822

, Joseph Fourier, ahli matematika dari perancis menemukanbahwasetiap fiingsi periodic⁽sinyal)dapat dibentuk dari penjumlahan gelombang

-

gelombang sinus atau cosines.

Teorema fourier menyatakan bahwa fiingsi bemilai tunggal f(

x

) pada selang [

-

^71,71] dapat diungkapkan sebagai kombinasi linier dari fiingsi sinus dan cosinus.

f

( x

) = a

0

cosx

+

a

₂

cos 2x ± a

3

cos3x +

...

bj sin x

+

b

₂

sin 2

x

+ b

₃

sin 3x +

...

°° (

= a

⁰

+ E

_n

ancos

=^1\

Y17DC

nm

^.

.

—

+^{h sin}

L ⁽2.24)

L

)

Dengan koefisien:

2 ^ {

^f(

x

^{)d x}

1 ⁷¹

= — J / ( x

⁾

cos

^{(nx )dx}

b

_„

= Y

^~

] f

⁽

x

⁾

sm

^{(nx )dx}

an

(2.25) -^It

Deret persamaan (2.25) dikenal sebagai deret fourier dan koefisiena

„

, b

„

disbutkoefisienfourier.(Boas^,1985)

2.3 Integrasi Numerik

Integrasi numerik dapat diturunkan dengan metode pias

.

Daerah integrasi dibagi atas sejumlah pias yang berbentuk segiempat. Luas daerah integrasi dihampiri dengan luas seluruh pias

.

Y

4

*

h

+

X

Xo X ,

Gambar2.2Kaidah Trapesium

Salah satu kaidah integrasi numerik yang dapat diturunkan dengan metodepias adalahkaidah Trapesium

.

Sebuah pias berbentuk trapesium dipandang dari x

=

^{Xo sampai x}

=

^xj

sepertigambar 2.2

.

Luassatu trapesiumadalah:

|

*^{0 f ( x )d x}

= 11 f

^{( x0)+}

/ ( *, ) ]

^(2.26)

Persamaan(2.26⁾dikenaldengannamakaidahtrapesium.

f

(

x

xn = b x

a = x

o

h

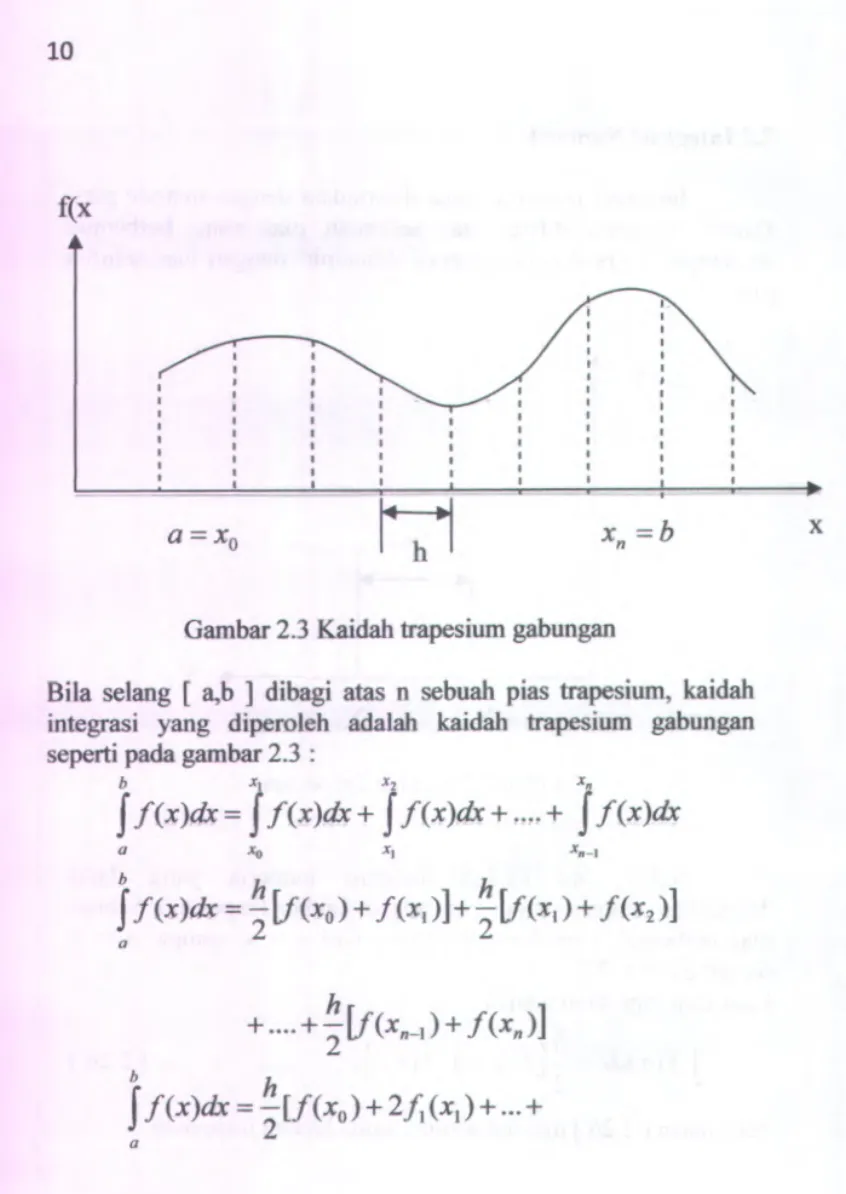
Gambar 2.3Kaidahtrapesium gabungan

Bila selang

[

a,b

]

dibagi atas n sebuah pias trapesium, kaidah integrasi yang diperoleh adalah kaidah trapesium gabungan seperti padagambar2.3:

j f

^{(x)d x}

| =

^{f ( x)d x+}

|

^{f(x)d x+....}

+ ] f

^{( x )d x}

a x0 i

J

^{f (x )d x}

= | [ / O

⁰

) + / (x ,

⁾

]

⁺

11 /

⁽

*,

^{) +}

/ (

^x2

) ]

^ lf

^{( x„-i)+ f (}

xn

⁾

]

} / ( x )d x =

^ [ / (x

⁰

)

⁺²

f (x , )

^+...

+....+

+

2 /0

^„-i

)

⁺

/

⁽

*

^„

) ]

\

^{f ( x)d x}

=

^ /

^e

+ 2 ^ /

ⁱ

+ /

^{» •}

0

^

^{V 1=1 )}

Dengan

fr = /

⁽

xr

^{) ,}

r =

^0,1,2,.

..

^{.,n(Mathewdan Frank,1999)}

(2.27⁾

2.4Penelitian Sebelumnya

Pada2 penelitiansebelumnyayang berjudul yaitu : a. Pengaruh jumlah titik data Syarat Batas Pada Kartesian

UntukSistem potensialListrik GeometriPolar.

b

.

Analisis menggunakan Koordinat Polar Untuk Sistem PotensialListrikGeometri CampuranKartesian

-

Polar. Pada penelitian a sistem potensial bentuk lingkaran dianalisis dengan menggunakan koordinat kartesian. Sedangkan pada penelitian b sistem potensial berbentuk persegi panjang dianalisis dengan menggunakan koordinat polar. Berikut ini penjelsannya lebih lanjut.

2.4.1 Pengaruh Jumlah Titik Data Syarat Batas Pada Kartesian Untuk Sistem Potensial Listrik Geometri Polar

Sistem potensial listrik dalam koordinat polar dapat dianalisa dengan menggunakan pendekatan kartesian

.

Dalam penelitian ini hanya dibatasi pada pengaruh jumlah titik data syarat batas pada pendekatan kartesian^.Ada beberapa tahapyang harus dilakukan, yaitu: melakukan perhitungan analitik dalam koordinat polar, menentukan syarat batas untuk pendekatan kartesian, menghitung potensial listrik dengan pendekatan kartesian pada masing

-

^{masing titik} data syarat batas dan membandingkannya dengan hasil perhitungan koordinat polar.

Dalam penelitian ini jumlah titik ^data syarat batas

yang

digunakan adalah 16, 32, 64, 128, 256 dan 512. Hasil penelitian

memperlihatkan bahwa semakin banyak jumlah titik data syarat batas yang digunakan dalam pendekatan kartesian akan memberikan hasil yang semakin mendekati perhitungan langsung dalam koordinat polar(Agustina tri Wahyudi,2012)

.

2.4.2 Analisis Menggunakan Koordinat Polar Untuk Sistem Potensial Listrik Geometri Campuran Kartesian - Polar

Sistem potensial listrik dengan geometri campuran kartesian

-

polar dianalisa dengan menggunakan pendekatan polar. Untuk penelitian ini hanyadibatasi pada pengaruh jumlah titik data syarat batas pada pendekatan polar. Ada beberapa tahapan yang dilakukan dalam penelitian ini yaitu melakukan perhitungan analitikdalam koordinatcampuran kartesian

-

^polar,

menentukan syarat batas untuk pendekatan polar, menghitung potensial listrik dengan pendekatan polar pada masing

-

^masing

jumlah titik data syarat batas dan membandingkannya dengan hasil perhitungannya secara langsung. Berdasarkan penelitian ini pendekatan polar untuk sistem geometri campuran kartesian

-

polar yang sangat berbeda dengan nilainya bila dihitung

secara

langsung

.

Dari penelitian ini juga diperoleh bahwa empat macam variasijumlahtitik data syarat batas yaitu360,720,1080,dan 1440 temyata tidak terlalu berpengaruh pada nilai selisih potensial listrik pendekatan polar dan perhitungan langsung (M. Najik, 2012).

Dalam bab ini akan dibahas mengenai langkah

-

Iangkah penelitian dan metode yang akan digunakan dalam penelitian Tugas Akhir ini. Didalam proses perhitungannya meggunakan aplikasiprogram matlab

.

3.1 Langkah

-

Iangkah Penelitian

Langkah

-

^Iangkahpenelitian dari Tugas Akhir ini adalah: 1

.

Pengumpulan teori

-

^{teori tentang} persamaan laplace,

separasi variabel koordinat kartesian danpolarsertaderet fourier sebagai acuan dalam perhitungan terhadap rumusandasar

.

2

.

Perhitungan analitik menggunakan koordinatpolar. 3

.

Mencari syarat batas untukkoordinatkartesian.

4

.

Perhitungan potensial listrik dengan menggunakan pendekatankartesian yangakan dicari berdasarkan variasi jumlahtitik datasyaratbatasyang digunakan.

5

.

Membuat perbandingan perhitungan koordinat polar dan pendekatan kartesian untuk masing-masing titik data.

6

.

Membuat analisa seberapa baik pendekatan kartesian terhadapkoordinatpolar

.

7

.

Kesimpulan

3.2 DiagramAlirPenelitian

Langkah

-

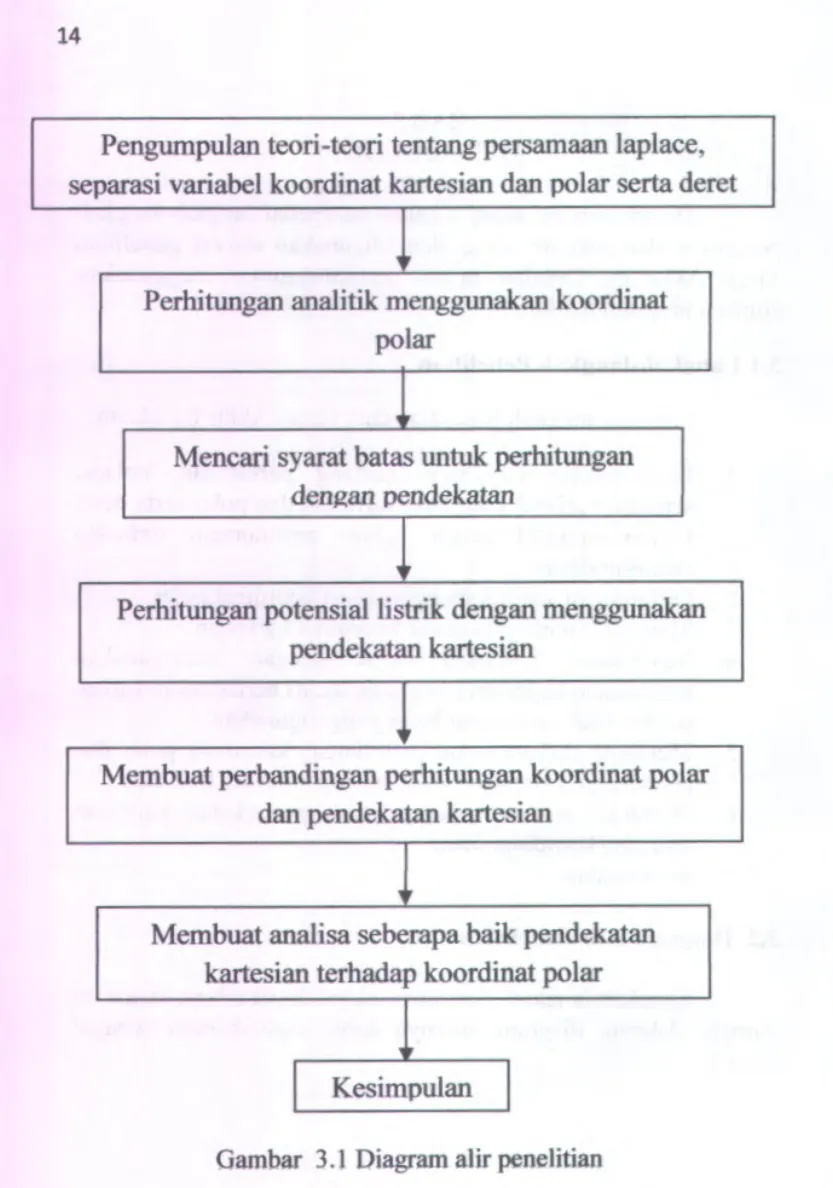
Iangkah penelitian diatas dapatdibuatdiagaram alimya

.

Adapun diagram alaimya dapat digambarkan sebagai berikut :

13

Pengumpulan teori - teori

^tentang

persamaan laplace ,

separasi

variabel koordinat kartesian dan

polar serta

deret

Perhitungan

analitik

menggunakan koordinat polar

Mencari

syarat

batas I untuk perhitungan

denganpendekatan

Perhitungan potensial listrik dengan menggunakan I

pendekatan kartesian

Membuat

perbandingan perhitungan koordinat polar dan pendekatan kartesian

Membuat analisa seberapa baik pendekatan

kartesian

terhadap koordinat polar

Kesimpulan

I

Gambar 3.1Diagramalirpenelitian

4.1PotensialListrik Sistem yangditeliti

Didalam kasus ini, akan dihitungnilai potensialpada sebuahsistem dengan geometri polar seperti gambar di bawah ini

r

=

^0,5

Vj

=

^cos6

V₂

=

^l

V4

=

^l

V₃

=

⁰

Gambar4.1 Geometri Sistem dan Syarat Batas Potensial Listriknya

Dalam menghitung potensial pada sistem diatasdapat digunakan solusi umumnyayaitu:

@_total ~ ®polarT $katesian kananT $kartesian kiri

(4 . 1 )

Padakoordinatkartesiandimisalkan mempunyaipanjangx

=

^a

dan y

=

bdenganV( potensial listrik)pada setiap sisinya

15

yaitu

Vki =

¹ pada sisi sampingkanan,

= -

^{1 padasisi bawah}

V3

=

⁰

.

Seperti pada Gambar4.2dibawah ini: y

a

Vi

V4 V₂

V₃ a x

Gambar4.2Potensial Listrik dalam Koordinat Kartesian

Pada perumusan persamaan potensial listrik diatas dapat ditinjau satu persatudari setiap sisinya dan setiapsisi lainnyadianggap V

=

^0.Berikut iniuraian dari setiap sisi

:

Tinjaundari sisi kanan(0kn)

Persamaan potensial listrikdengan sisi atas

x -

a sebagai 1.

berikut :

4

00 Yin nn

< Hx

^.y)

=

n=

X

^ganjilnnsxvfann

1 sin

a

xsinh —

a^-y (4 . 2) Sehinggadalam koordinatpolar menjadi:

®( ^ ) = X 4

ao Yin

nn

(rcos

#)sinh —

^rsin6

Yinsinhnn lsin

a a

n=^ganjil

(4.3)

v = o

a

V

=

⁰

Vk

^„

x V

=

^{0 a}

Gambar4.3Potensial Listrik ditinjau dari sisi ^{kanan (}

Vkn

⁾

2

.

Tinjauandarisisi kiri (

0

kr)

Persamaan potensial listrikdengan sisi kanan

x =

^{a sebagai} berikut:

co

4

^{Yin Yin}

<

Hx -

^y)

= Z

_n7rsinhrM

(

^-

1

⁾

sin

_a

xsinh

_a ^y

n=^ganjil (4.4)

Sehingga dalam koordinatpolar menjadi :

CO

4

Yin ^Yin

< t ( x

^ ) =

ⁿ⁼

Y

^ganjil

.

rt

^

^-

sinhw ^ (

^-

1 ) sin

^{a (r}

cost ?

⁾

sinh

^{—a r}

sint

^?

y

v = o

a

Vkr v = o

/ m >

X

V

=

^{0 a}

Gambar 4.4 Potensial Listrikditinjaudarisisi kiri(

Vkr

⁾

3

.

Tinjauandarisisiatas(

0

po2ar)

Untuk meninjau potensial listrik sisi atas dapatdihitung dengan menggunakan koordinatpolar. Maka persamaan potensial listrik dengansisikananV

=

^cos6adalah:

Gambar4.5PotensialListrikditinjaudarisisiatas (Vpoia

,

) Persamaanpotensial listrik dengan sisi kiri,x

=

0 sebagai berikut :

00

4>(

r

,

e

⁾

=

^{A0 +}

£

_n ⁽

An cos n

^{9 +B}

„

^sin

n

⁰⁾

r

^"

=¹

UntukTugas Akhir inihanya dibatasi sampaisukufourier ke tiga maka hanya dihitung nilai A0, A(, A₂, A3,

Bi

^{, B2,dan B3 yang}

akan digunakan dalam rumus koordinat polardengan persamaan sebagaiberikut:

A₀

=

(4.6)

i 2K

^

^-

\ v

^(0)d0

(4.7)

|^{2K I 2}*

-

—

_{i t}

j

^{V (0)cos n O d O A m -}

—— j

^{V(0)cos n O d6}

0 i t r ₀

r a A m

(4.8)

i 2f

j ^2K

— f

^{V(0)sin n O d O}

=

^>

Bn

⁼

f

^{V (0)sin n O d O}

n ^J₀ 7

trn

^J0

rnBn =

(4.9) Maka didapatkan nilai

—

nilai konstantasepertidibawahini:

A0

=

0 A

, =

¹ A₂

=

0 A₃

=

^O

B

, =

0 B2

=

^1,699 B3

=

⁰

Setelah nilai konstanta didapatkan maka persamaan potensial polamya adalah:

<

J

^>poiar(r,0)

=

^A

-

^jcos9

+

^B2r²sin26

=

^{r cos9}

+

^{1,699r2sin26 (4.10)} Sehinggapersamaan potensialtotalnya adalah:

= tppolar

^~b

^

^{kn ~b}

^

^{fcr (4.11)}

Dimana :

<

Ppoiar —

^rcos9

+

^1,699

r

^{2sin29 (4.11a)}

oo

4 nn rm

<

J

>(x

-

^y)

= X n

^{lsin (rcos}

#

^{)sinh rsin(?}

^ rsinhn ^ a

^a

n=^ganjil

(4.11 b)

4

CO nn nn

<

t * * y

⁾

= E

_nnsivkwn⁽

- 1

⁾

sin — a

⁽

rcos #

⁾

sinh —

_a ^r

sin6

n=^ganjil (4.11c)

Dari persamaan 4.11,4.11a, 4.11 b,4.11c dapat dibuat program MATLABnyadengan jari

-

jari0,5(lampiran A no1, 2, 3, dan 4)

.

Sehingga didapatkan nilai potensial totalnya

4

^{> nya (}

lampiran B no 1,2,3,dan4)

.

4.2PerhitunganLangsungPotensialListrik

Dalam memudahkan untuk menganalisa dapat dilakukan translasi kotak potensial ke tengah

-

tengah sumbu koordinat sehingga menjadi

cos

6

1

\

0 1

Gambar 4.6perhitungan potensiallangsung

Dalam gambar 4.6 adalah gambar sistem potensial listrik yang telahditranslasi

.

Untuk kasus ini, potensial listrik ^dalam koordinat kartesian mempunyai panjang

x =

^{1 dan y}

=

^0,5

.

Sedangkan V( potensial )dalam setiap sisinya adalah sisi atas

= Vt

, sisi samping kanan

=

^V2,sisi bawah

=

^V3, dan sisi samping kiri

=

^V4. Untuk mendapatkan persamaan potensial listrik dengan pendekatan kartesian dapat dicari satu persatu dari setiapsisinya

.

Jika yang ditinjausisiatas

Vi

^{maka sisiyanglainnyaV}

=

^0.

4.2.1 PerhitunganPotensialatas(Vj)

Untuk menghitungpotensialatas (

Vi

⁾dapat dicari dengan sisi-sisi yang lain dibuat 0(nol). Adapundi tinjau dari sisi atas(

V i

⁾

y

Vl (x) 0,5

0 0

0 1 x

Gambar 4.7Potensial Listrik ditinjau dari sisi atas (

Vt

⁾

Padasisi atas,y

=

^{0,5 makapersamaan} potensial listriknya

:

00

" —

_{a \}

(

^coshnn( b

—

^y)

= £

_n

=

_l^Ynsin

a

nnb m nn(b

—

^y)

)

—

^coth _a ^sin _a

(4.12) Untuk nilai konstanta yn dihitung dengan menggunakan deret fourier dan di batasi sampai 10suku. Adapun persamaan untuk mencarinilaiyn sebagai berikut:

Yn

= \ V i

^(x

. a

^{)sin~ d x}

Y i

= lloVi

^~

fg

V^{( x,}

a

^{)s i n}

^

^{d x}

^

^x,

a )

^{sin d x}

Y3

=

^~

IQ VI

^(X

.

^O

.

^{)sin dor}

X4

=

^ /

⁰

aVri

⁽

x

^,

a

^)sin

^

^dx

Xs

=

^ /

^0a

^

ⁱ⁽

^ a

^)sin

^ dx

Xe

= f /

⁰

“

⁽

* . «

^{)sin~ dx}

X

?

= \ /

^0a

Vi

⁽

x

^,

a

^{) sin7-}

f

^{- d x}

~

fg Vi

^{( x,}

a

^)sin

pp

^dx

X9

=

^~

/

0

“ Vi

⁽

* . «

^)sin

^

^dx

X i o

=

^-

J

0

Vi

⁽

x . a

^{) sln}

—

^dx

(4.13) (4.13a) (4.13b) X2

=

(4.13c) (4.13d) (4.13e) (4.131) (4.13g) (4.13b) Xs

=

(413i) (4.13j)

4.2.2 Perhitungan Potensial SisiKanan(V₂)

Untukmenghitungpotensial atas(V₂)dapatdicari dengansisi

-

sisiyanglain dibuat 0(nol).Adapun ditinjaudari sisi atas(V2)

y

o

0,5

0

Vk

²

0 1 x

Gambar 4.8Potensial Listrik ditinjaudari sisi kanan Pada sisisampingkanan,x

=

^a

=

^1,persamaanpotensialnya adalah :

d>₂(

x

,y )

=

Voo ,, nny

L .

^I,nn(a-x)

iLn

=^iyriSin

^ ^

^COSh

^

coth

^ ^

^{b sinh}

Untuk nilai konstanta yn dihitung dengan menggunakan deret fourier dan di batasi sampai 10 suku

.

Adapun persamaan untuk mencarinilai ynsebagai berikut :

nn(a^-x)\

b ) ^(4.14)

sin

^

^{d y}

\ JQa ^

^{2(a»y)sin d y}

(4.15) Yn

=

(4.15a) Yi

=

/2

=

^ /

^0a

^

⁽

a .

^y)sin

^

^dy

ys

= \ /

⁰

“ v

²⁽

a .

^y

)

^sin

22

^dy

X

* = ; J

0

av

2(

a .

^y)sin

^

^dy

Xs

=

^ /

^0a

^

⁽

a .

^y)sin

^

^dy

^ /

^0a

^

⁽

a .

^y)sin

^

^dy

| /

0

a

^

⁽

a . y

⁾

sinz ^

^dy

Xs

= \ /

^0a

^

²⁽

a .

^y)sin

22

^dy

Y9

= I C ^

²⁽

a .

^y)sin

22

^dy

Xio

=

^ /

^0a

^

²⁽

a

^>

y

^{)sin~~ dy}

(4.15b) (4.15c) (4.15d) (4.15e) (4.15f) Ye

=

(4.15g)

x

^?

=

(4.15h) (4.15i) (4.15j) 4.2.3PerhitunganPotensialSisiBawah

Untukmenghitung potensial^atas(V₃)dapatdicari dengan sisi

-

sisiyanglain dibuat0⁽nol)

.

Adapun di tinjau dari sisiatas (V₃)

y

o

0,5

0 0

V3(x) 1

Gambar4.9 Potensial Listrik ditinjau dari sisi bawah(V3) Padasisi sampingkanan,y

=

0, persamaanpotensialnya adalah:

x

OO nnb

4

hix .

^{y )}

=

^

^{Ynsinnnxa \(coshnnya coth a sinh}

n=¹

(4.16⁾ Untuk nilai konstanta yn dihitung dengan menggunakan deret fourier dan di batasi sampai 10 suku. Adapun persamaan untuk mencari nilai ynsebagai berikut:

0)sin

^

^{d x}

~

fo ^

³⁽

*

^{»0)sin d x}

^ lfoVi f o V

³⁽⁽

*

x^,>⁰⁾

°

^{)sinsin~~d xd x}

i /

0

V

3(

x

^,0) sin

* =

^d

*

(4.17) Yn

=

(4.17a) Yl

=

(4.17b) Y2

=

(4.17c) /3

=

(4.17d) Y4

=

X5

= g f o

^~

/ ^

³⁽

*

^»0)Sin“

^

^{~ dX}

0

°

^

³⁽

*

^{»0)sin dx}

X?

=

^ /

^0a

^

³⁽

^

⁰⁾

sinZ ^

^dx

Ya

= \ ICV ^

³

⁰

^»0)sin

^

^{d x}

^

^X’

°

^)sin~"dx

yio

= iUV

³

( * .

^{0) sin}

^ d *

(4.17e) (4.17f) Y6

=

(4.17g) (4.17h) (4

-

¹⁷ⁱ⁾

Y9

=

(4

-

^17j)

4.2.4 Perhitungan PotensialSisiKiri

Untuk menghitungpotensialatas ( V4)dapatdicari dengan sisi

-

^{sisiyanglaindibuat0(nol)}

.

^Adapundi tinjau dari sisiatas (V4)

y

o

0,5

V₄( y) 0

0 x

Gambar4.10Potensial Listrikditinjaudari kiri(V4)

Pada sisi sampingkanan,

x =

0, persamaan potensialnya adalah:

00 nnx^\

b

^~

)

nny

r nnx nna

—

^{( cosh}

—

^{7 coth}

—

b

v

_b b

^ O . y

⁾

=

ⁿ

^

^{=lYnsm sinh(4.18)}

Untuk nilai konstanta yn dihitung dengan menggunakan deret fourier dan di batasi sampai 10 suku. Adapun persamaan untuk mencari nilaiynsebagai berikut:

2

f

a ⁿⁿ

Yn

⁼

bJ

^o

V

^*(

°

^{'y) sin}

_

^b

dy

(4.19)

Yi

= lj Kt

^(0,

y

⁾

0

Tdy

ny

sin

(4.19a)

2

f

²

ny

r

²

= b J

0

^

^(O

.

^yjsin

—

2 f 37ry

Y³

= b j

^y4(0,y)sin

—

o

d y

(4.19b)

dy

(4.19c) Y

* = IJ

_o

v *

⁽

°

^>y)

sm Any Tdy

(4.19d)

Sny

Ys

=

^

⁰

j v

^4(0,y)sin

Vdy

^(4.19e)

Ye

= lj Wy

⁾

0

6n y

v d y

2 f 7n y

£

_o

J K

^{( 0}

.

^y)sin

- y -

^dy

8rry