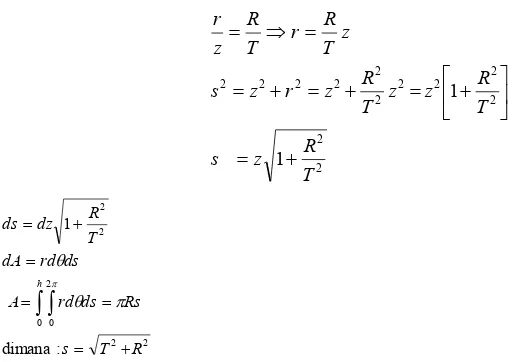Integral Lipat Dalam Menghitung Volume dan Luas Permukaan Benda Geometri Sederhana dan Terpancung

(1)

260

_{Isu-Isu Kontemporer Sains, Lingkungan, dan Inovasi Pembelajarannya}

INTEGRAL LIPAT DALAM MENGHITUNG VOLUME DAN LUAS PERMUKAN

BENDA GEOMETRI SEDERHANA DAN TERPANCUNG

Ulil Azmi1, Lilik Hendrajaya2

Pengajaran Fisika ITB, Bandung E-mailkorespondensi: ulil.hasbi88@gmail.com

Abstrak: Pemahaman konsep fisika matematika sangat dibutuhkan dalam memecahkan berbagai persoalan fisika. Dalam studi ini, telah disusun sebuah acuan modul praktikum sebagai penguatan konsep fisika matematika mengenai integral lipat yang dapat digunakan untuk menghitung volume benda. Benda yang digunakan adalah benda bangun ruang sederhana (silinder, silinder pancung, bola, bola pancung, kerucut, dan kerucut pancung), di dalam modul praktikum ini berisi langkah-langkah menghitung volume benda ruang tersebut.

Kata Kunci: Integral lipat, volume, luas permukaan.

1. PENDAHULUAN

Fisika matematika adalah mata matakuliah yang dapat meningkatkan dan mengembangkan kemampuan peserta didik dalam berfikir analitik dan kuantitatif dalam menyelesaikan persoalan fisika. Melihat peranannya, maka perlu perlu dirancang pembelajaran yang lebih strategis. contoh-contoh soal dan penyelesaiannya, dan soal-soal latihan melainkan diikuti dengan praktikum yang sesuai dengan materi- materi yang di ajarkan.

Dalam tulisan ini dibahas sebuah acuan modul untuk materi integral lipat dan penggunaannya dalam menentukan volume- volume bangun ruang sederhana, bola terpancung, dan kerucut terpancung. pembahasan bola terpancung dan kerucut terpancung dapat menjadi hal yang mebagi peserta didik sebagai bahan belajar yang dapat mengembangkan nalar dalam memahami materi integral lipat untuk menentukan volume bangun ruang tersebut.

Integral

Integral suatu fungsi f(x terhadap x yang didefinisikan dengan



f(x)dx. Jika g(x)



f(x)dx maka berarti g(x) adalah fungsi yang turunannya terhadap x sama dengan f(x).Integral dengan batas a dan b yang dinyatakan dengan



b

a

dx x

f( ) dinamakan integral tertentu. Integral ini diartikan sebagai sebagai luas daerah yang dibentuk

antara kurva f(x), sumbu x, garis x = a dan garis x = b. Integral Lipat Dua dan Integral Lipat Tiga

Integral lipat dua dari suatu fungsif(x,y) pada suatu daerah A dalam bidang xydinyatakan sebagai volume di bawahfungsi f(x,y) dan dibatasi luasan A. Integral ini biasanya ditulis sebagai

f

x

y

dxdy

A

(

,

)



. Selain itu,

integral lipat dua ini dapat ditafsirkan sebagai luas suatu daerah dengan batas dari suatu kurva tertentu.

3. METODE PENELITIAN

Metode yang digunakan dalam penelitian ini adalah studi pustaka.Dalam tahap ini dicari sumber pustaka dan dipilih bagian dari sumber pustaka untuk menentukan voume geometri (bola terpancung, silinder

terpancuk, dan kerucut terpancung).

x

(2)

4. HASIL DAN PEMBAHASAN

a. Luas Permukaan Bangun Simetris Tabung (Silinder)

Gambar 1. Elemen luas dan elemen volume dalam sistem koordinat silinder (Boas, 2006). Luas Permukaan Tabung

Luas selimut tabung:

Rh dz R dz d R L

dz Rd dA

h

z h

z o

SS   







2 2

0 0

2

 



 

_

  Luas lingkaran:

2 0 2 0

0 0

2

2 1 2

2 rdr r R

drd r L

rdrd dA

R

r R

r o

lingkaran    





  

    

 



 

_

  Luas permukaan tabung (silinder):

Rh R

L L

LPS lingkaran ss  2

2

  

Volume tabung (silinder):

h R dr d d r V

R

r o

h

z tabung

2

0 0

2

sin    



 

  

  

Kerucut

Luas Permukaan Kerucut:

Gambar 2. Kerucut (perbandingan segitiga) Luas permukaan kerucut dapat ditentukan melalui persamaan sederhana sebagai berikut:

sR A s R s A s R s

A _

    

     



2 2 2

2

lingkaran keliling

kerucut alas keliling lingkaran

luas

kerucut selimut luas

2 2

(3)

262

2 2

2 2 2 2 2 2 2 2 2 2

1

T R z s

T R z z T R z r z s

z T R r T R z r

 

           

  

Dengan menggunakan integral lipat tiga, volume kerucut dapat ditentukan sebagai berikut:

3

2 1

) 2 ( 2 1 2

2 1 2

) (

0 3 3 3 2

2 0

2 2

0

) (

0 2 0

) (

0 2

0

RT

T T T T

R

dz z Tz T T R

dz r

d rdr dz

drdz d r dv

T z T R r z T

r T R

T T

z

T

z

T z T R

r T

z T

z T R

r

  

  







   



 _ _



  

 



    







 



 

Bola

Gambar 3. Elemen luas dan elemen volume dalam sistem koordinat bola

2 2

0 2 2

0 2

2

4 ) 2 ( 2 2 ) cos ( sin

sin ) sin )( (

R R

R d d R A

d d R d R Rd dA

o

   

 

   

 

 

 

    



 

 

_ _

Volume bola:

2 2 0

2 0

2 2

: dimana

1

R T s

Rs ds rd A

ds rd dA

T R dz ds

h

 

 

  

 

 



(4)

3 3

0 3

0 0

2

0 2

2

3 4 ) 2 ( 3 2 2 ) cos ( 3 1

sin

sin )

)( )( sin

(

R R

R

dr d d r

V

dr d d r

rd dr d d r dv

R

r bola

















 

 



 

  

 

  

  

b. Volume Kerucut Terpancung Miring

Dalam pembahasan ini, kerucut dipancung miring. Kerucut yang dipancung ini dibagi menjadi 2 bagian, yaitu kerucut bagian atas (kerucut miring) dan pancungan bagian bawah.Kerucut miring berbeda dengan kerucut biasa. Kerucut miring adalah kerucut yang sumbunya tidak tegak lurus dengan alas. Kerucut miring memiliki ketinggian yang tegak lurus dengan alasnya.

Berikut adalah langkah untuk mendapatkan volume kedua bagian kerucut yg terpancung tersebut:

Gambar 3. Tampak depan atau samping dari kerucut yang terpancung

Volume pancungan bagian bawah (Vt) dapat diperoleh dengan mengurangkan volume kerucut penuh (Vp) dengan volume kerucut miring atas (Vm):

Vm Vp Vt 

Dimana :

3 3 1

r Vp 

kerucut puncak ke elips dari tinggi (LE) miring elips luas 3 1

 



Vm Dengan

  

   

  

2 2

pendek sumbu panjang sumbu

b a LE

 

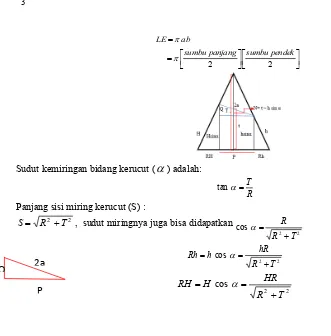
Sudut kemiringan bidang kerucut (



) adalah:

R T  

tan

Panjang sisi miring kerucut (S) :

2 2 _T

R

S  , sudut miringnya juga bisa didapatkan

2 2 cos

T R

R   

2 2 cos

T R

hR h

Rh

 

 

2 2

cos

T R

HR H

RH

 

 

Q

(5)

264

_{Isu-Isu Kontemporer Sains, Lingkungan, dan Inovasi Pembelajarannya} Untuk menetukan besar P,



cos ) ( 2 ) ( 2 R

-2R 2

2 2

2 2 2 2

h H R T R

h H

T R

hR

T R

HR Rh

RH R P

      

 

   

   

  

Besar Q,

 

 sin ( ) ( )sin

sin

2

2 _T H h

R T h H h

H

Q  

    

Besar a,

2 2

2 2 2

2 1 2 ) 2 (

P Q a

 

Menetukan sumbu pendek (2b)

Dengan perbandingan segitiga (P,Q), dapat ditentukan t, maka:

 

  



sin ) sin ) (( cos ) ( 2

cos

) sin ) (( cos ) ( 2

cos sin

cos ) ( 2

cos sin

) (

) sin (

h h

H h

H R

h R t

h H h

H R

h R h

t

h H R

h R h

H h t

 

   

 

   

    



 

   

sin ) sin ) (( ) cos ) ( 2 (

) cos (

tan tan

h h

H h

H R T

h R R

T R t R T

t t t l l t

 

   

    

Maka besar b :

 



 ₍₍ ₎_sin ₎ _sin

) cos ) ( 2 (

) cos (

h h

H h

H R T

h R R R

l R b

 

   

  

Luas elips (LE) adalah:

t

*

T

H

Hsin

α

h

α

P

RH

R

2

a

β

γ

t

(T-t)

(6)

 

  

 



sin ) (

cos ) ( 2

,

sin ) sin ) (( ) cos ) ( 2 (

) cos ( 2

1 2 2

h H Q

h H R P dengan

h h H h

H R T

h R R R

x P Q

b a LE

   

   



 _ _

   

  

 _

 

Tinggi kerucut ke puncak elips (t*₎

    

  

    

 

  

 _ _

  

  

 

  

  

2 2

) sin ) (( ) cos ) ( 2 (

cos ) ( 2

sin ) sin ) (( cos ) ( 2

cos

-T *

) sin ) (( ) cos ) ( 2 (

cos ) ( 2 2

cos

cos t) -(T sin t) -(T *

 



  



 

 

 

h H h

H R P

h H R

x h h H h H R

h R t

h H h

H R P

h H R a

P t

Volume kerucut miring atas(Vm):

* 3 1

kerucut puncak ke elips dari tinggi (LE) miring elips luas 3 1

t ab Vm

 

 



Volume pancungan bagian bawah (Vt):

* 3 1 3 1

(Vm) atas miring kerucut volume (Vp) penuh kerucut volume

2

t ab t ab Vt



 



 

c. Volume Bola Terpancung (Tembereng Bola)

Tembereng bola adalah bangun ruang bagian dari potongan atau pancungan bola yang dibatasi oleh sebagian bidang bola dan sebuah daerah lingkaran dari sisi potonganya. Daerah lingkaran itu dari sisi tersebut disebut alas, bagian bolanya disebut bidang lengkung. Tembereng bola dapat ditentukan dengan bantuan volume bola.

Dalam pembahasan ini, tembereng dibagi menjadi 2 segmen, yaitu tembereng besar dan tembereng kecil. Tembereng besar adalah bangun ruang (tembereng) yang memiliki ukuran lebih besar dan berada dibagian bawah, sedangkan tembereng kecil adalah tembereng yang bervolume kecil dan berada pada bagian atas (dengan tebal h).Untuk menentukan volume tembereng kecil, hal yang perlu diperhatikan dari Gambar III.3. adalah batas-batas yang akan digunakan yaitu dari R-h sampai dengan R,dengan h adalah ketebalan dari tembereng kecil dan R adalah jari-jari bola.

Gambar 4. Bola terbancung menjadi dua bagian (tembereng besar dan tembereng kecil)

Volume tembereng kecil dapat ditentukan dengan menggunakan intergral, melalui phytagoras didapatkan R2

(7)

266











3 3 2 2 3



2 3 3 2 3 2 . 2 2 3 3 3 ) ( 3 3 ) ( 2 h Rh h R R R h R h R R h R R R z z R dz z R dz y dv R h R R h R R h R                   







































3 )



3 ) 3 3 ) 2 2 2 3 ) 2 2 ( 2 3 ) )( 2 ( 3 3 2 ) )( 2 ( 3 3 ) )( 2 ( 3 ) ( ) ( 2 3 ) ( ) ( 2 3 2 2 3 3 3 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 h R h V h Rh h h hR hR R R h h hR hR R R h h R h R h h R h R h R h h R h R h R h R R h h R h R h h R R R h h R h R h h R R R h h R h Rh Rh R R h h R h Rh R h h R

T  

                                                                  

Setelah didapatkan volume tembereng kecil, juga bisa didapatkan volume tembereng besar. Volume tembereng besar dapat ditetukan dengan mengurangi volume bola dengan volume tembereng kecil

3 )

3 3 4 ) (V tembereng Volume ) (V utuh bola Volume (VB) bawah Volume 2 3 T bola h R h

R  



 

 

4. Kesimpulan

Adapun kesimpulan yang dapat di ambil dari tulisan ini adalah:

1. Integral lipat dapat digunakan dalam menentukan volume benda ruang seperti tabung, bola silinder dan lain lain.

2. Dari perhitungan penentuan volume bangun ruang terpancung ini dapat dijadikan sebagai bahan dasar bagi peserta untuk memahami materi integral lipat.

5. DAFTAR PUSTAKA

Boas, L. m. (2006). Mathematical Methods In The Physical Science. Canada: John Willey and sons. Clemens, S. R. (1984). Geometry. USA: Addision-Westley Publishing Company, inc.