ABSTRAK
DWI SETIANTO. Penjadwalan Kereta Api Menggunakan Pemrograman Linear Integer. Dibimbing oleh PRAPTO TRI SUPRIYO dan TEDUH WULANDARI MAS’OED
Karya ilmiah ini memberikan formulasi masalah penjadwalan kereta api menggunakan model pemrograman linear integer. Penjadwalan kereta api tersebut didasarkan pada jalur tunggal yang menghubungkan antar stasiun. Formulasi yang dibangun bertujuan meminimumkan keterlambatan serta menjamin bahwa tidak ada kereta api yang mengalami tabrakan baik searah maupun berlawanan arah. Input model berupa jadwal keberangkatan kereta api yang direncanakan (aktual), sedangkan outputnya berupa jadwal keberangkatan dan kedatangan kereta api yang faktual.
ABSTRACT
DWI SETIANTO. Train Scheduling Using Integer Linear Programming. Supervised by PRAPTO TRI SUPRIYO and TEDUH WULANDARI MAS’OED
I PENDAHULUAN
1.1 Latar Belakang
Semakin tingginya mobilitas penduduk di suatu negara terutama di kota besar tentulah memiliki banyak permasalahan, mulai dari kemacetan yang tak terselesaikan hingga moda transportasi yang efisien. Salah satu moda transportasi yang tepat dalam mengurangi kemacetan adalah kereta api, karena kereta api memiliki daya angkut yang besar dibandingkan angkutan kota pada umumnya.
Jumlah penumpang kereta api yang meningkat akan membuat frekuensi keberangkatan kereta semakin padat. Hal ini tentunya harus ditopang dengan perencanaan yang baik. Perencanaan yang dimaksud adalah perencanaan jadwal perjalanan kereta api yang tepat dan efisien dengan memperhatikan segala kendala semisal ketersediaan rangkaian kereta maupun jalur di setiap stasiun. Tentu
tidak mudah ketika telah mendapatkan jadwal perjalanan kereta api tetapi masih memiliki delay (keterlambatan) kereta yang besar.
Dalam karya ilmiah ini, akan dibahas penentuan jadwal kereta api menggunakan PLI (Pemrograman Linear Integer) yang meminimumkan delay. Solusi yang didapat menggunakan bantuan software LINGO 8.0. Karya ilmiah ini merupakan rekonstruksi dari sebagian artikel yang berjudul A Heuristic for the Train Pathing and Timetabling Problem yang ditulis oleh Yusin Lee dan Chuen-Yih Chen tahun 2009.
1.2 Tujuan
Tujuan penulisan karya ilmiah ini adalah mencari penyelesaian masalah penjadwalan kereta api yang meminimumkan delay (keterlambatan) menggunakan PLI (Pemrograman Linear Integer).
II LANDASAN TEORI
Untuk membuat model penjadwalan kereta api diperlukan pemahaman teori Pemrograman Linear (PL) atau Linear Programming (LP), Pemrograman Linear Integer (PLI) atau Integer Linear Programming (ILP), dan metode branch-and-bound.
Definisi 1 (Fungsi linear)
Suatu fungsi f dalam variabel-variabel
1, 2,..., n
x x x adalah suatu fungsi linear jika
dan hanya jika untuk suatu himpunan konstanta c c1, 2,...,c , n fungsi dapat
dituliskan sebagai
. ... )
,..., ,
(x1 x2 xn c1x1 c2x2 cnxn f
(Winston 2004)
Sebagai contoh, f x x( ,1 2) 2x1 3x 2
merupakan fungsi linear, sementara
2 2 1 2 1 2
( , )
f x x
x x
bukan fungsi linear.Definisi 2 (Pertidaksamaan dan persamaan linear)
Untuk sembarang fungsi linear )
,..., , (x1 x2 xn
f dan sembarang bilangan b,
pertidaksamaan f(x1,x2,...,xn) b dan
b x x x
f( 1, 2,..., n) adalah pertidaksamaan linear, sedangkan suatu persamaan
b x x x
f( 1, 2,..., n) merupakan persamaan linear.
(Winston 2004)
2.1 Pemrograman Linear
Pemrograman Linear (PL) adalah suatu masalah optimisasi yang memenuhi ketentuan-ketentuan berikut:
a) Tujuan masalah tersebut adalah memaksimumkan atau meminimumkan suatu fungsi linear dari sejumlah variabel keputusan. Fungsi yang akan dimaksimumkan atau diminimumkan ini disebut fungsi objektif.
b) Nilai variabel-variabel keputusannya harus memenuhi suatu himpunan kendala. Setiap kendala harus berupa persamaan linear atau pertidaksamaan linear.
c) Ada pembatasan tanda untuk setiap variabel dalam masalah ini. Untuk sembarang variabel , pembatasan tanda menentukan harus tak-negatif ( ) atau tidak dibatasi tandanya (unrestricted in sign).
I PENDAHULUAN
1.1 Latar Belakang
Semakin tingginya mobilitas penduduk di suatu negara terutama di kota besar tentulah memiliki banyak permasalahan, mulai dari kemacetan yang tak terselesaikan hingga moda transportasi yang efisien. Salah satu moda transportasi yang tepat dalam mengurangi kemacetan adalah kereta api, karena kereta api memiliki daya angkut yang besar dibandingkan angkutan kota pada umumnya.
Jumlah penumpang kereta api yang meningkat akan membuat frekuensi keberangkatan kereta semakin padat. Hal ini tentunya harus ditopang dengan perencanaan yang baik. Perencanaan yang dimaksud adalah perencanaan jadwal perjalanan kereta api yang tepat dan efisien dengan memperhatikan segala kendala semisal ketersediaan rangkaian kereta maupun jalur di setiap stasiun. Tentu
tidak mudah ketika telah mendapatkan jadwal perjalanan kereta api tetapi masih memiliki delay (keterlambatan) kereta yang besar.
Dalam karya ilmiah ini, akan dibahas penentuan jadwal kereta api menggunakan PLI (Pemrograman Linear Integer) yang meminimumkan delay. Solusi yang didapat menggunakan bantuan software LINGO 8.0. Karya ilmiah ini merupakan rekonstruksi dari sebagian artikel yang berjudul A Heuristic for the Train Pathing and Timetabling Problem yang ditulis oleh Yusin Lee dan Chuen-Yih Chen tahun 2009.
1.2 Tujuan
Tujuan penulisan karya ilmiah ini adalah mencari penyelesaian masalah penjadwalan kereta api yang meminimumkan delay (keterlambatan) menggunakan PLI (Pemrograman Linear Integer).
II LANDASAN TEORI
Untuk membuat model penjadwalan kereta api diperlukan pemahaman teori Pemrograman Linear (PL) atau Linear Programming (LP), Pemrograman Linear Integer (PLI) atau Integer Linear Programming (ILP), dan metode branch-and-bound.
Definisi 1 (Fungsi linear)
Suatu fungsi f dalam variabel-variabel
1, 2,..., n
x x x adalah suatu fungsi linear jika
dan hanya jika untuk suatu himpunan konstanta c c1, 2,...,c , n fungsi dapat
dituliskan sebagai
. ... )
,..., ,
(x1 x2 xn c1x1 c2x2 cnxn f
(Winston 2004)
Sebagai contoh, f x x( ,1 2) 2x1 3x 2
merupakan fungsi linear, sementara
2 2 1 2 1 2
( , )
f x x
x x
bukan fungsi linear.Definisi 2 (Pertidaksamaan dan persamaan linear)
Untuk sembarang fungsi linear )
,..., , (x1 x2 xn
f dan sembarang bilangan b,
pertidaksamaan f(x,x,...,x ) b dan
b x x x
f( 1, 2,..., n) adalah pertidaksamaan linear, sedangkan suatu persamaan
b x x x
f( 1, 2,..., n) merupakan persamaan linear.
(Winston 2004)
2.1 Pemrograman Linear
Pemrograman Linear (PL) adalah suatu masalah optimisasi yang memenuhi ketentuan-ketentuan berikut:
a) Tujuan masalah tersebut adalah memaksimumkan atau meminimumkan suatu fungsi linear dari sejumlah variabel keputusan. Fungsi yang akan dimaksimumkan atau diminimumkan ini disebut fungsi objektif.
b) Nilai variabel-variabel keputusannya harus memenuhi suatu himpunan kendala. Setiap kendala harus berupa persamaan linear atau pertidaksamaan linear.
c) Ada pembatasan tanda untuk setiap variabel dalam masalah ini. Untuk sembarang variabel , pembatasan tanda menentukan harus tak-negatif ( ) atau tidak dibatasi tandanya (unrestricted in sign).
2
Suatu PL mempunyai bentuk standar seperti yang didefinisikan sebagai berikut.
Definisi 3 (Bentuk Standar suatu PL) Suatu pemrograman linear dalam bentuk standar didefinisikan sebagai:
max z = (atau min) s.t.
(2.1) Dengan mendefinisikan:
A =
,
Maka kendala pada (2.1) dapat ditulis dengan sistem persamaan Ax = b (2.2)
(Winston 2004)
2.1.1 Solusi suatu Pemrograman Linear Suatu masalah PL dapat diselesaikan dalam berbagai teknik, salah satunya adalah metode simpleks. Metode ini dapat menghasilkan suatu solusi optimum bagi masalah PL dan telah dikembangkan oleh Dantzig sejak tahun 1947 (Winston 2004), dan dalam perkembangannya merupakan metode yang paling umum digunakan untuk menyelesaikan PL. Metode ini berupa metode iteratif untuk menyelesaikan PL berbentuk standar.
Pada masalah PL (2.2), vektor x yang memenuhi kendala Ax = b disebut sebagai solusi dari PL (2.2). Misalkan matriks A dapat dinyatakan sebagai A = (B N), dengan B adalah matriks taksingular berukuran m × m yang elemennya berupa koefisien variabel basis dan N merupakan matriks berukuran m × (n – m) yang elemennya berupa koefisien variabel nonbasis pada matriks kendala. Dalam hal ini matriks B disebut matriks basis untuk PL (2.2).
Misalkan x dinyatakan sebagai vektor x =
, dengan xB adalah vektor variabel basis
dan xN adalah vektor variabel nonbasis, maka
Ax = b dapat dinyatakan sebagai:
Ax =
= BxB + NxN= b (2.3)
Karena matriks B adalah matriks tak singular, maka B memiliki invers, sehingga dari (2.3) xB dapat dinyatakan sebagai:
xB = B-1b - B-1NxN (2.4) Kemudian, fungsi objektifnya berubah menjadi:
min z =
(Winston 2004)
Definisi 4 (Daerah Fisibel)
Daerah fisibel suatu PL adalah himpunan semua titik yang memenuhi semua kendala dan pembatasan tanda pada PL tersebut.
(Winston 2004)
Definisi 5 (Solusi Basis)
Solusi basis adalah solusi pada PL yang didapatkan dengan mengatur variabel n–m sama dengan nol dan nilai untuk penyelesaiannya adalah dari sisa variabel m. Hal ini mengasumsikan bahwa mengatur variabel n–m sama dengan nol sehingga membuat nilai yang unik untuk sisa variabel m atau sejenisnya, dan kolom-kolom untuk sisa dari variabel m adalah bebas linear.
(Winston 2004)
Definisi 6 ( Solusi Fisibel Basis)
Solusi fisibel basis adalah solusi basis pada PL yang semua variabel-variabelnya tak-negatif.
(Winston 2004)
Definisi 7 (Solusi Optimum)
Untuk masalah maksimisasi, solusi optimum suatu PL adalah suatu titik dalam daerah fisibel dengan nilai fungsi objektif terbesar. Untuk masalah minimisasi, solusi optimum suatu PL adalah suatu titik dalam daerah fisibel dengan nilai fungsi objektif terkecil.
(Winston 2004)
Ilustrasi untuk solusi basis dan solusi fisibel basis diberikan dalam Contoh 1 di bawah ini.
Contoh 1
Misalkan diberikan PL berikut: minimumkan z = -2 - 3 terhadap -x1 + 2x2 + x3 = 10 -2x1 + x2 + x4 = 2 2x1 + x5 = 3
3
Dari PL (2.5) didapatkan:
A = , b =
Misalkan dipilih
= T dan = T maka matriks basisnya adalah
B = ,
N = .
.
Dengan menggunakan matriks basis tersebut diperoleh
.
(2.6) .
Solusi (2.6) merupakan solusi basis, karena solusi tersebut memenuhi kendala PL (2.5) dan kolom-kolom pada matriks kendala yang berpadanan dengan komponen taknol dari (2.6) yaitu B adalah bebas linear (kolom yang satu bukan merupakan kelipatan dari kolom yang lain). Solusi (2.6) juga merupakan solusi fisibel basis, karena nilai-nilai variabelnya lebih dari atau sama dengan nol.
2.2 Pemrograman Linear Integer
Pemrograman linear integer (PLI) adalah suatu model pemrograman linear dengan variabel yang digunakan berupa bilangan bulat (integer). Jika semua variabel harus berupa integer, maka masalah tersebut dinamakan pure integer programming. Jika hanya sebagian yang harus berupa integer, maka disebut mixed integer programming (MIP). PLI dengan semua variabelnya harus bernilai 0 atau 1 disebut 0-1 PLI
(Garfinkel & Nemhauser 1972)
Definisi 8 (Relaksasi Pemrograman Linear) Relaksasi pemrograman linear atau sering disebut relaksasi-PL merupakan suatu pemrograman linear yang diperoleh dari suatu PLI dengan menghilangkan kendala integer atau kendala 0-1 pada setiap variabelnya.
Untuk masalah maksimisasi, nilai optimum fungsi objektif relaksasi-PL lebih besar atau sama dengan nilai optimum fungsi objektif PLI, sedangkan untuk masalah
minimisasi, nilai optimum fungsi objektif relaksasi-PL lebih kecil atau sama dengan nilai optimum fungsi objektif PLI.
(Winston 2004)
2.3 Metode Branch and Bound
Dalam penulisan karya ilmiah ini, untuk memperoleh solusi optimum dari masalah PLI digunakan software LINGO 8.0, yaitu sebuah program yang dirancang untuk menentukan solusi model linear, nonlinear, dan optimisasi integer. Software LINGO 8.0 ini menggunakan metode branch-and-bound untuk menyelesaikan masalah PLI.
Prinsip dasar metode branch-and-bound adalah memecah daerah fisibel dari masalah relaksasi-PL dengan membuat subproblem-subproblem. Terdapat dua konsep dasar dalam algoritma branch-and-bound.
1. Branch (Cabang)
Branching (pencabangan) adalah proses membagi permasalahan menjadi subproblem-subproblem yang mungkin mengarah ke solusi.
2. Bound (Batas)
Bounding (pembatasan) adalah suatu proses untuk mencari atau menghitung batas atas (dalam masalah minimisasi) dan batas bawah (dalam masalah maksimisasi) untuk solusi optimum pada subproblem yang mengarah ke solusi.
Metode branch-and-bound diawali dari menyelesaikan relaksasi-PL dari suatu pemrograman linear integer. Jika semua nilai variabel keputusan solusi optimum sudah berupa integer, maka solusi tersebut merupakan solusi optimum PLI. Jika tidak, dilakukan pencabangan dan penambahan batasan pada relaksasi-PLnya kemudian diselesaikan.
4
artinya fungsi objektif dan semua variabelnya sudah bernilai integer.
Sebelumnya akan dibahas terlebih dahulu pengertian subproblem yang terukur. Menurut Winston (2004), suatu subproblem dikatakan terukur (fathomed) jika salah satu kondisi berikut terpenuhi:
a. Subproblem tersebut takfisibel, sehingga tidak dapat menghasilkan solusi optimum bagi PLI.
b. Subproblem tersebut menghasilkan suatu solusi optimum dengan semua variabelnya bernilai integer. Jika solusi optimum ini mempunyai nilai fungsi objektif yang lebih baik daripada solusi fisibel yang diperoleh sebelumnya, maka solusi ini menjadi kandidat solusi optimum dan nilai fungsi objektifnya menjadi batas bawah (dalam masalah maksimisasi) dan batas atas (dalam masalah minimisasi) nilai fungsi objektif optimum bagi masalah PLI pada saat itu. Bisa jadi subproblem ini menghasilkan solusi optimum untuk masalah PLI.
c. Nilai fungsi objektif optimum untuk subproblem tersebut tidak melebihi batas bawah saat itu (untuk masalah maksimisasi). Suatu subproblem dapat dieliminasi apabila subproblem tersebut takfisibel dan batas bawah kandidat solusi lebih kecil (untuk masalah maksimisasi) dari nilai fungsi objektif optimum untuk subproblem tersebut.
Berikut ini adalah langkah-langkah penyelesaian suatu masalah maksimisasi dengan metode branch-and-bound :
Langkah 0
Didefinisikan z sebagai batas bawah dari solusi PLI yang optimum. Pada awalnya tetapkan z = − dan i = 0.
Langkah 1
Subproblem PL(i) dipilih sebagai bagian masalah berikutnya untuk diteliti. Subproblem PL(i) diselesaikan dan diukur dengan kondisi yang sesuai.
a) Jika PL(i) terukur, maka batas bawah z dapat diperbarui. Batas bawah z dapat diperbaharui jika solusi PLI yang lebih baik telah ditemukan. Jika tidak, maka bagian masalah (subproblem) baru i dipilih dan langkah 1 diulangi. Jika semua subproblem telah diteliti, maka proses dihentikan.
b) Jika PL(i) tidak terukur, lanjutkan ke langkah 2 untuk melakukan pencabangan PL(i).
Langkah 2
Pilih satu variabel xj yang nilai optimumnya, yaitu xj*, tidak memenuhi batasan integer dalam solusi PL(i). Singkirkan bidang [xj*] xj [xj*]+1 dengan membuat dua bagian masalah PL yang berkaitan menjadi dua batasan yang tidak dapat dipenuhi secara bersamaan yaitu:
xj ≤ [xj*] dan xj ≥ [xj*]+1,
dengan [xj*] didefinisikan sebagai integer terbesar yang kurang dari atau sama dengan xj*. Jika PL(i) masih tidak terukur, maka kembali ke Langkah 1.
(Taha 1996)
Untuk memudahkan pemahaman mengenai metode branch-and-bound diberikan contoh sebagai berikut:
Contoh 2
Misalkan diberikan PLI sebagai berikut: Maksimumkan z = 5 x1 + 4 x2
terhadap x1 + x2 5 10 x1 + 6 x2
x1, x2 0 dan integer (2.7)
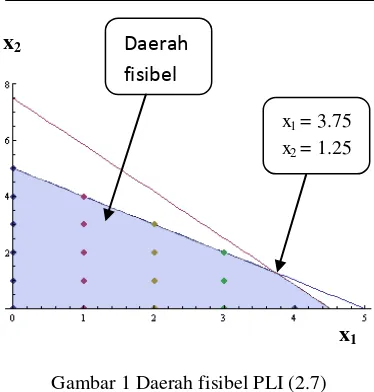
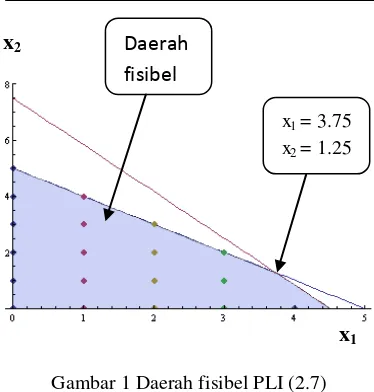
Solusi optimal relaksasi-PL dari masalah PLI (2.7) adalah x1=3.75, x2=1.25, dan z =23.75 (lihat Lampiran 1). Jadi batas atas nilai optimal fungsi objektif masalah PLI (2.7) adalah z= 23.75. Daerah fisibel relaksasi-PL masalah (2.7) ditunjukkan pada Gambar 1 (daerah yang diarsir) sedangkan titik-titik merupakan solusi fisibel masalah PLI (2.7).
Gambar 1 Daerah fisibel PLI (2.7)
Langkah berikutnya adalah memartisi daerah fisibel relaksasi-PL menjadi dua bagian berdasarkan variabel yang bernilai pecahan (non-integer). Karena x1= 3.75 dan x2=1.25 variabel bernilai pecahan maka dipilih
x
2x
1Daerah
fisibel
5
salah satu variabel, misalkan x1, sebagai dasar pencabangan. Jika masalah relaksasi-PL dari PLI (2.7) diberi nama Subproblem 1 dan Subproblem 1 dicabangkan atas x1, maka pencabangan tersebut menghasilkan 2 subproblem, yaitu:
Subproblem 2: Subproblem 1 ditambah kendala x1 ≥ 4
Subproblem 3: Subproblem 1 ditambah kendala x1 ≤ 3.
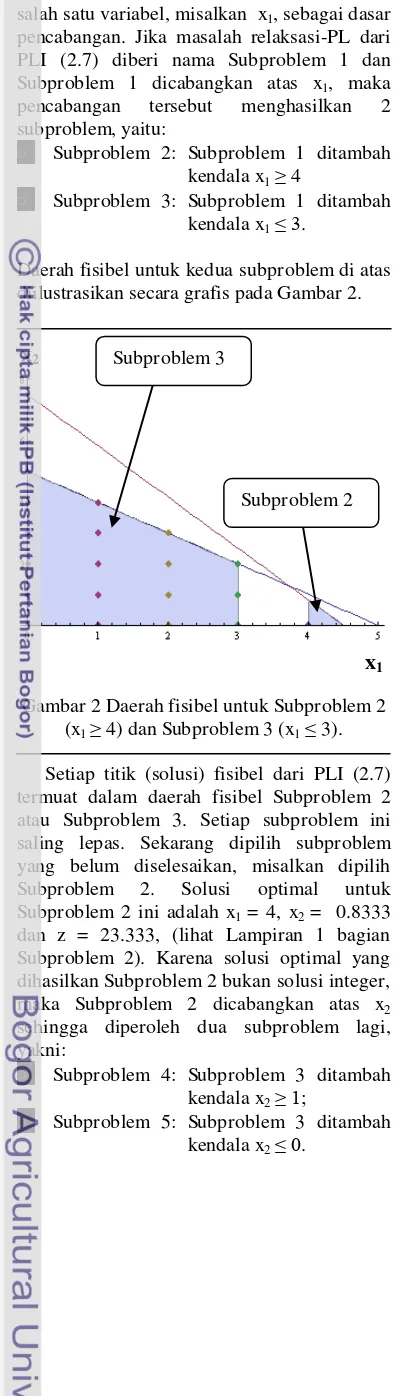
Daerah fisibel untuk kedua subproblem di atas diilustrasikan secara grafis pada Gambar 2.
Gambar 2 Daerah fisibel untuk Subproblem 2 (x1 ≥ 4) dan Subproblem 3 (x1 ≤ 3). Setiap titik (solusi) fisibel dari PLI (2.7) termuat dalam daerah fisibel Subproblem 2 atau Subproblem 3. Setiap subproblem ini saling lepas. Sekarang dipilih subproblem yang belum diselesaikan, misalkan dipilih Subproblem 2. Solusi optimal untuk Subproblem 2 ini adalah x1 = 4, x2 = 0.8333 dan z = 23.333, (lihat Lampiran 1 bagian Subproblem 2). Karena solusi optimal yang dihasilkan Subproblem 2 bukan solusi integer, maka Subproblem 2 dicabangkan atas x2 sehingga diperoleh dua subproblem lagi, yakni:
Subproblem 4: Subproblem 3 ditambah kendala x2 ≥ 1;
Subproblem 5: Subproblem 3 ditambah kendala x2 ≤ 0.
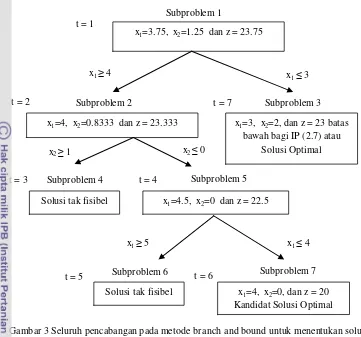
Saat ini subproblem yang belum diselesaikan adalah Subproblem 3, 4 dan 5. Salah satu subproblem dipilih, misalnya dengan aturan LIFO (last in first out). Dengan aturan ini berarti dipilih Subproblem 4 atau Subproblem 5. Subproblem 4 takfisibel (lihat Lampiran 1 bagian Subproblem 4) maka subproblem ini tidak dapat menghasilkan solusi optimal, yang tersisa adalah Subproblem 3 dan Subproblem 5.
Karena aturan LIFO, dipilih Subproblem 5, yang kemudian menghasilkan solusi optimal x1=4.5, x2=0 dan z=22.5 (lihat Lampiran 1 bagian Subproblem 5). Karena x1=4.5 bukan integer, maka dilakukan kembali pencabangan atas x1, sehingga diperoleh:
Subproblem 6: Subproblem 5 ditambah kendala x1≥5;
Subproblem 7: Subproblem 5 ditambah kendala x1≤4.
Misalkan dipilih Subproblem 6. Ternyata Subproblem 6 ini juga takfisibel (lihat Lampiran 1 bagian Subproblem 6), sehingga tidak dapat menghasilkan solusi optimal. Dengan demikian subproblem-subproblem yang belum diselesaikan adalah Subproblem 3 dan Subproblem 7. Karena aturan LIFO, dipilih Subproblem 7. Subproblem ini kemudian menghasilkan solusi opimal x1=4, x2= 0, dan z= 20 (lihat Lampiran 1 bagian Subproblem 7). Dapat dilihat bahwa solusi optimal subproblem ini semuanya berupa integer, sehingga merupakan kandidat solusi untuk PLI (2.7). Nilai z pada kandidat solusi ini merupakan batas bawah bagi nilai optimal PLI. Penyelesaian Subproblem 3 menghasilkan solusi optimal x1= 3, x2= 2 dan z= 23 (lihat Lampiran 1 bagian Subproblem 3). Batas bawah yang ditetapkan dari solusi optimal Subproblem 7 tidak lebih baik dari nilai solusi optimal yang dihasilkan Subproblem 3. Dengan demikian, nilai solusi optimal Subproblem 3, yakni z = 23 menjadi batas bawah yang baru. Semua solusi optimal telah berupa integer dan tidak perlu dilakukan pencabangan kembali, sehingga solusi optimal dari Subproblem 3 merupakan solusi optimal PLI (2.7), yakni x1= 3, x2= 2 dan z= 23. Pohon pencabangan yang menunjukkan proses penyelesaian masalah PLI (2.7) secara keseluruhan ditunjukkan pada Gambar 3.
x
1x
2 Subproblem 36
Gambar 3 Seluruh pencabangan pada metode branch and bound untuk menentukan solusi PLI (2.7)
III DESKRIPSI DAN PEMODELAN MASALAH
3.1 Deskripsi masalah
Untuk mendeskripsikan masalah penjadwalan kereta api di setiap stasiun, hal utama yang harus diketahui adalah banyaknya rangkaian kereta yang ditugaskan di stasiun tersebut. Kemudian dari kereta api yang ditugaskan tadi, seberapa banyak ketersedian jalur yang dapat dilalui. Banyaknya kereta api yang beroperasi juga bergantung pada kebutuhan atau permintaan penumpang.
Dalam memenuhi keinginan penumpang, tersedia dua jenis kereta api yaitu kereta api reguler dan kereta api ekspress. Untuk kereta api regular, waktu tunggu di dalam stasiun lebih lama dibandingkan jenis yang kedua yaitu kereta api ekspress. Selain itu kecepatan kereta api jenis reguler lebih rendah dibandingkan kereta api jenis ekspress.
Berikut ini adalah gambaran dari suatu penjadwalan kereta api. Misalkan terdapat n buah stasiun yang masing-masing stasiun memiliki dua buah jalur pemberhentian dan
dari keseluruhan stasiun tersebut saling dihubungkan oleh jalur tunggal. Stasiun ke-1 dan stasiun ke-n adalah stasiun pemberangkatan, sedangkan stasiun ke-2 hingga stasiun ke−(n-1) adalah stasiun pemberhentian. Andaikan dioperasikan p kereta api ekspress dan q kereta api reguler. Kereta api tersebut ada yang diberangkatkan dari stasiun ke-1 dan juga dari stasiun ke-n. Pengelola stasiun dihadapkan pada masalah penjadwalan kereta sedemikian rupa sehingga dapat meminimumkan delay (keterlambatan), dengan memperhatikan kebutuhan pengguna kereta api.
3.2 Formulai masalah
Model penjadwalan kereta api bergantung pada ketersedian rangkaian kereta api dan jumlah jalur yang dapat dilalui. Selanjutnya, penjadwalan kereta api dapat diformulasikan dalam bentuk PLI.
x1=3.75, x2=1.25 dan z = 23.75
x1=4, x2=0.8333 dan z = 23.333 x1=3, x2=2, dan z = 23 batas bawah bagi IP (2.7) atau
Solusi Optimal
Solusi tak fisibel x1=4.5, x2=0 dan z = 22.5 t = 1
t = 2
x2 ≥ 1 x2 ≤ 0
Solusi tak fisibel x1=4, x2=0, dan z = 20 Kandidat Solusi Optimal
x1 ≤ 4 x1 ≥ 5
t = 5 t = 6
t = 7
t = 3 t = 4
Subproblem 1
Subproblem 3 Subproblem 2
Subproblem 4 Subproblem 5
Subproblem 7 Subproblem 6
6
Gambar 3 Seluruh pencabangan pada metode branch and bound untuk menentukan solusi PLI (2.7)
III DESKRIPSI DAN PEMODELAN MASALAH
3.1 Deskripsi masalah
Untuk mendeskripsikan masalah penjadwalan kereta api di setiap stasiun, hal utama yang harus diketahui adalah banyaknya rangkaian kereta yang ditugaskan di stasiun tersebut. Kemudian dari kereta api yang ditugaskan tadi, seberapa banyak ketersedian jalur yang dapat dilalui. Banyaknya kereta api yang beroperasi juga bergantung pada kebutuhan atau permintaan penumpang.
Dalam memenuhi keinginan penumpang, tersedia dua jenis kereta api yaitu kereta api reguler dan kereta api ekspress. Untuk kereta api regular, waktu tunggu di dalam stasiun lebih lama dibandingkan jenis yang kedua yaitu kereta api ekspress. Selain itu kecepatan kereta api jenis reguler lebih rendah dibandingkan kereta api jenis ekspress.
Berikut ini adalah gambaran dari suatu penjadwalan kereta api. Misalkan terdapat n buah stasiun yang masing-masing stasiun memiliki dua buah jalur pemberhentian dan
dari keseluruhan stasiun tersebut saling dihubungkan oleh jalur tunggal. Stasiun ke-1 dan stasiun ke-n adalah stasiun pemberangkatan, sedangkan stasiun ke-2 hingga stasiun ke−(n-1) adalah stasiun pemberhentian. Andaikan dioperasikan p kereta api ekspress dan q kereta api reguler. Kereta api tersebut ada yang diberangkatkan dari stasiun ke-1 dan juga dari stasiun ke-n. Pengelola stasiun dihadapkan pada masalah penjadwalan kereta sedemikian rupa sehingga dapat meminimumkan delay (keterlambatan), dengan memperhatikan kebutuhan pengguna kereta api.
3.2 Formulai masalah
Model penjadwalan kereta api bergantung pada ketersedian rangkaian kereta api dan jumlah jalur yang dapat dilalui. Selanjutnya, penjadwalan kereta api dapat diformulasikan dalam bentuk PLI.
x1=3.75, x2=1.25 dan z = 23.75
x1=4, x2=0.8333 dan z = 23.333 x1=3, x2=2, dan z = 23 batas bawah bagi IP (2.7) atau
Solusi Optimal
Solusi tak fisibel x1=4.5, x2=0 dan z = 22.5 t = 1
t = 2
x2 ≥ 1 x2 ≤ 0
Solusi tak fisibel x1=4, x2=0, dan z = 20 Kandidat Solusi Optimal
x1 ≤ 4 x1 ≥ 5
t = 5 t = 6
t = 7
t = 3 t = 4
Subproblem 1
Subproblem 3 Subproblem 2
Subproblem 4 Subproblem 5
Subproblem 7 Subproblem 6
7
Model penjadwalan pada karya ilmiah ini menggunakan dua parameter utama sebagai penyusun jadwal, yaitu:
1. Kereta, yaitu seluruh rangkaian kereta api yang terlibat dalam penjadwalan.
2. Jalur, yaitu jalur yang dapat dilalui oleh kereta api dan yang terlibat dalam penjadwalan. Sebagai contoh, pandang penamaan jalur kereta api antara dua buah stasiun di bawah ini.
Gambar 4 Contoh peta jaringan jalur kereta api antara dua stasiun
Variabel-variabel yang digunakan dalam model penjadwalan kereta api ini sebagai berikut:
s : indeks stasiun. k,m : indeks kereta.
V : himpunan seluruh kereta. h : indeks jalur.
B : himpunan semua jalur.
Bk : himpunan semua jalur yang dilewati oleh kereta k.
Bs : himpunan jalur yang terletak di dalam stasiun.
Bk \ Bs : himpunan jalur yang terletak di luar stasiun.
: lama waktu minimum kereta k menyelesaikan seluruh perjalanannya (menit).
: lama waktu minimum kereta k di jalur h (menit).
: lama waktu perpanjangan atau maksimum yang diizinkan untuk kereta k di jalur h apabila mengalami delay (menit). : jalur pertama yang digunakan
oleh kereta k.
: jalur terakhir yang digunakan oleh kereta k.
: jalur yang telah digunakan kereta k sebelum memasuki jalur h.
: Selisih minimum waktu antara dua kereta menggunakan jalur h secara berurutan (menit). : waktu ketika kereta k memasuki
jalur pertama yang digunakannya.
Selain itu, diperlukan pula pendefinisian suatu variabel keputusan:
delayk : total waktu keterlambatan kereta k (menit)
yhk : keterlambatan kereta k di jalur h (menit)
ahk : waktu ketika kereta k memasuki jalur h.
dhk : waktu ketika kereta k meninggalkan jalur h.
dhm : waktu ketika kereta m meninggalkan jalur h.
: waktu ketika kereta k meninggalkan jalur terakhir yang digunakannya.
: waktu ketika kereta k meninggalkan jalur yang telah digunakannya tepat sebelum memasuki jalur h.
Fungsi objektif dari permasalahan ini adalah meminimumkan keterlambatan seluruh kereta api, sehingga dimodelkan sebagai berikut:
minimumkan
dengan kendala-kendala sebagai berikut: 1) Mengatur waktu kedatangan dan
keberangkatan kereta berdasarkan lama waktu operasi minimum kereta. Apabila kereta mengalami delay maka akan diatur di kendala 2.
≥ +
h , k V
2) Menyatakan bahwa jika panjang waktu kereta yang dijadwalkan melebihi waktu operasi minimumnya, maka kelebihan waktu ini dianggap sebagai keterlambatan yang dijadwalkan.
≤ + +
h , k V
Dari kendala 1 dan 2 didapat persamaan berikut:
+ ≤ ≤ + +
Misalkan 7:03 ≤ ≤ 7:06, yang artinya adalah waktu kereta k meninggalkan jalur h adalah pukul 7:03 (tanpa delay) sedangkan apabila mengalami delay maka batas waktu maksimumnya adalah sampai pukul 7:06.
3) Kendala berikut menjelaskan aturan penggunaan satu jalur oleh dua kereta pada saat yang bersamaan baik untuk satu arah maupun berlawanan arah.
- ≥
h \ , k,m V 2
stasiun A stasiun B
3
1 4
8
Perhatikan ilustrasi berikut ini: (contoh berlawanan arah)
Kereta m (dari A ke B) dan kereta k (dari B ke A) menggunakan jalur yang sama (h), maka harus ada selisih minimum waktu ( ) agar kedua kereta tersebut tidak bertabrakan.
(contoh satu arah)
Diperlukan selisih minimum waktu (Chmk) antara kereta k dan m untuk menghindari kemungkinan terjadinya tabrakan. Kereta k mengalami delay terutama di jalur h = 2.
4) Waktu kereta k meninggalkan jalur yang telah digunakannya tepat sebelum memasuki jalur h sama dengan waktu kereta k memasuki jalur h.
= h , k V
Misal kereta k = 1 melalui jalur h = 1, 2, dan 3 (Bk = 1,2,3)
h = 2 makaB21 = 1 sehingga d11 = a21 h = 3 makaB = 2 sehingga d21 = a31 31 5) Lama waktu kereta api yang dibutuhkan
mulai dari stasiun awal hingga stasiun tujuan.
- = + , k V
Kendala ketaknegatifan ≥ 0 dan bilangan integer
delayk ≥ 0 dan delayk bilangan integer
IV CONTOH KASUS DAN PENYELESAIANNYA
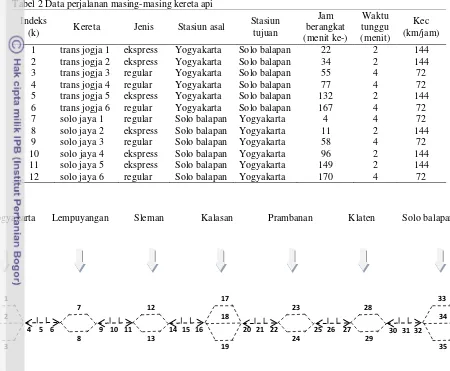
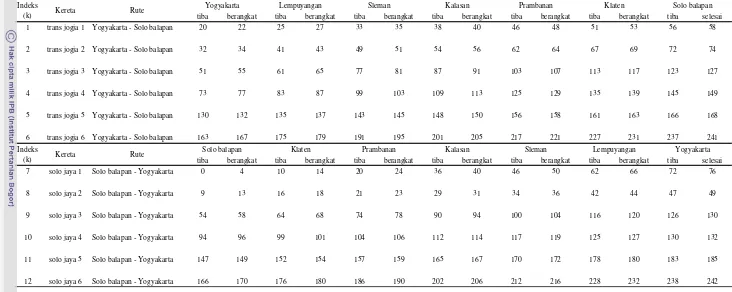
Pada bagian ini akan diberikan contoh kasus dengan data hipotetik seperti penamaan stasiun, rangkaian kereta yang digunakan dan jumlah jalur yang tersedia. Misalkan PT KAI (Kereta Api Indonesia) memiliki tujuh stasiun (s) yang jarak dari stasiun satu ke stasiun berikutnya beragam (Tabel 1).
Tabel 1Jarak antar stasiun
Stasiun 1 Stasiun 2 Jarak (m) Yogyakarta Lempuyangan 7200 Lempuyangan Sleman 14400 Sleman Kalasan 7200 Kalasan Prambanan 14400 Prambanan Klaten 7200 Klaten Solo balapan 7200
Kemudian dari ketujuh stasiun tersebut ada yang memiliki dua maupun tiga jalur kereta api. Sehingga setiap kereta api yang akan melalui jalur (h) tersebut harus sesuai kapasitas masing-masing stasiun. Untuk kereta api sendiri terbagi kedalam dua jenis, yaitu kereta api ekspress dan kereta api reguler. Untuk kereta api ekspress, kecepatan rata-ratanya adalah 144 km/jam dengan waktu
tunggu di dalam stasiun dua menit sedangkan untuk kereta api reguler, kecepatan rata-ratanya adalah 72 km/jam dengan waktu tunggu di dalam stasiun empat menit. Selanjutnya ada 12 perjalanan kereta api (k) yang siap untuk diberangkatkan yang terbagi ke dalam 6 kereta untuk rute Yogyakarta ke Solo balapan dan 6 kereta lagi untuk rute sebaliknya.
Tabel 2 memberikan jam keberangkatan yang direncanakan dengan periode waktu menit (0 – 1440). Jam keberangkatan sesungguhnya akan ditentukan pada hasil perhitungan yang dilakukan oleh model. Dari seluruh kereta api tersebut telah ditentukan urutan jalur atau rute yang akan dilalui oleh masing-masing kereta (Bk) seperti yang tertera pada Tabel 4 (Lampiran 2).
Lama waktu yang dibutuhkan oleh masing-masing kereta untuk melalui jalur antar stasiun (Bk \ Bs) tergantung pada kecepatan kereta api tersebut, selengkapnya dapat dilihat pada Tabel 5 (lama waktu minimum kereta) dan Tabel 6 (lama waktu perpanjangan kereta) di setiap jalur yang dilaluinya pada Lampiran 2. Dalam
Kereta 1
h = 1 h = 2 h = 3 stasiun A jalur h stasiun B
kereta k kereta m
kereta k kereta m
h = 1 h = 2 h = 3
stasiun A stasiun B (7:00) (7:02)
(7:04) (7:04)
(7:03) (7:02)
(7:06)
8
Perhatikan ilustrasi berikut ini: (contoh berlawanan arah)
Kereta m (dari A ke B) dan kereta k (dari B ke A) menggunakan jalur yang sama (h), maka harus ada selisih minimum waktu ( ) agar kedua kereta tersebut tidak bertabrakan.
(contoh satu arah)
Diperlukan selisih minimum waktu (Chmk) antara kereta k dan m untuk menghindari kemungkinan terjadinya tabrakan. Kereta k mengalami delay terutama di jalur h = 2.
4) Waktu kereta k meninggalkan jalur yang telah digunakannya tepat sebelum memasuki jalur h sama dengan waktu kereta k memasuki jalur h.
= h , k V
Misal kereta k = 1 melalui jalur h = 1, 2, dan 3 (Bk = 1,2,3)
h = 2 makaB21 = 1 sehingga d11 = a21 h = 3 makaB = 2 sehingga d21 = a31 31 5) Lama waktu kereta api yang dibutuhkan
mulai dari stasiun awal hingga stasiun tujuan.
- = + , k V
Kendala ketaknegatifan ≥ 0 dan bilangan integer
delayk ≥ 0 dan delayk bilangan integer
IV CONTOH KASUS DAN PENYELESAIANNYA
Pada bagian ini akan diberikan contoh kasus dengan data hipotetik seperti penamaan stasiun, rangkaian kereta yang digunakan dan jumlah jalur yang tersedia. Misalkan PT KAI (Kereta Api Indonesia) memiliki tujuh stasiun (s) yang jarak dari stasiun satu ke stasiun berikutnya beragam (Tabel 1).
Tabel 1Jarak antar stasiun
Stasiun 1 Stasiun 2 Jarak (m) Yogyakarta Lempuyangan 7200 Lempuyangan Sleman 14400 Sleman Kalasan 7200 Kalasan Prambanan 14400 Prambanan Klaten 7200 Klaten Solo balapan 7200
Kemudian dari ketujuh stasiun tersebut ada yang memiliki dua maupun tiga jalur kereta api. Sehingga setiap kereta api yang akan melalui jalur (h) tersebut harus sesuai kapasitas masing-masing stasiun. Untuk kereta api sendiri terbagi kedalam dua jenis, yaitu kereta api ekspress dan kereta api reguler. Untuk kereta api ekspress, kecepatan rata-ratanya adalah 144 km/jam dengan waktu
tunggu di dalam stasiun dua menit sedangkan untuk kereta api reguler, kecepatan rata-ratanya adalah 72 km/jam dengan waktu tunggu di dalam stasiun empat menit. Selanjutnya ada 12 perjalanan kereta api (k) yang siap untuk diberangkatkan yang terbagi ke dalam 6 kereta untuk rute Yogyakarta ke Solo balapan dan 6 kereta lagi untuk rute sebaliknya.
Tabel 2 memberikan jam keberangkatan yang direncanakan dengan periode waktu menit (0 – 1440). Jam keberangkatan sesungguhnya akan ditentukan pada hasil perhitungan yang dilakukan oleh model. Dari seluruh kereta api tersebut telah ditentukan urutan jalur atau rute yang akan dilalui oleh masing-masing kereta (Bk) seperti yang tertera pada Tabel 4 (Lampiran 2).
Lama waktu yang dibutuhkan oleh masing-masing kereta untuk melalui jalur antar stasiun (Bk \ Bs) tergantung pada kecepatan kereta api tersebut, selengkapnya dapat dilihat pada Tabel 5 (lama waktu minimum kereta) dan Tabel 6 (lama waktu perpanjangan kereta) di setiap jalur yang dilaluinya pada Lampiran 2. Dalam
Kereta 1
h = 1 h = 2 h = 3 stasiun A jalur h stasiun B
kereta k kereta m
kereta k kereta m
h = 1 h = 2 h = 3
stasiun A stasiun B (7:00) (7:02)
(7:04) (7:04)
(7:03) (7:02)
(7:06)
9
melakukan penjadwalan kereta api juga diperlukan sketsa peta jaringan rel kereta seperti yang tersaji di Gambar 5.
Model penjadwalan kereta api ini menggunakan beberapa asumsi. Asumsi yang digunakan diantaranya adalah:
1. Jalur yang menghubungkan antar stasiun adalah jalur tunggal.
2. Tidak ada prioritas kereta.
Tabel 2 Data perjalanan masing-masing kereta api
Indeks
(k) Kereta Jenis Stasiun asal
Stasiun tujuan
Jam berangkat (menit ke-)
Waktu tunggu (menit)
Kec (km/jam)
1 trans jogja 1 ekspress Yogyakarta Solo balapan 22 2 144 2 trans jogja 2 ekspress Yogyakarta Solo balapan 34 2 144 3 trans jogja 3 regular Yogyakarta Solo balapan 55 4 72 4 trans jogja 4 regular Yogyakarta Solo balapan 77 4 72 5 trans jogja 5 ekspress Yogyakarta Solo balapan 132 2 144 6 trans jogja 6 regular Yogyakarta Solo balapan 167 4 72 7 solo jaya 1 regular Solo balapan Yogyakarta 4 4 72 8 solo jaya 2 ekspress Solo balapan Yogyakarta 11 2 144 9 solo jaya 3 regular Solo balapan Yogyakarta 58 4 72 10 solo jaya 4 ekspress Solo balapan Yogyakarta 96 2 144 11 solo jaya 5 ekspress Solo balapan Yogyakarta 149 2 144 12 solo jaya 6 regular Solo balapan Yogyakarta 170 4 72
Gambar 5 Peta jaringan jalur (rel) kereta api Yogyakarta-Solo balapan
Model penjadwalan tersebut selanjutnya dapat diformulasikan ke dalam bentuk PLI dengan fungsi objektif:
Minimumkan 12
1 k
k
delay
Dengan kendala :
1) Waktu kereta k meninggalkan jalur h harus lebih besar atau sama dengan waktu kereta k memasuki jalur h ditambah lama waktu minimum kereta k di jalur h.
hk
d
a
hk +T
hkmin , h BkSebagai contoh, dengan memperhatikan Tabel 4 (Lampiran 2) untuk kereta k = 3 dan jalur h = 6, diperoleh pertidaksamaan d63 ≥ a63 + . Sehingga diperoleh seluruhnya 300 pertidaksamaan.
2) Waktu kereta k meninggalkan jalur h harus lebih kecil atau sama dengan waktu kereta k memasuki jalur h ditambah masa keterlambatan kereta k di jalur h dan lama waktu perpanjangan kereta k di jalur h.
hk
d
a
hk+y
hk+ext hk
T
, h Bk Sebagai contoh, dengan memperhatikan Tabel 4 (Lampiran 2) untuk kereta k = 1Yogyakarta Lempuyangan Sleman Kalasan Prambanan Klaten Solo balapan
3 19 35
1
2
4 5 6 8 7
9 10 11 12
15 16 17
18
13
23
14 20 21 22 24
26 27 29 28
30 31 32 33
34
25
min 63
10
dan jalur h = 8, diperoleh pertidaksamaan d81 ≤ a81 + y81 + . Sehingga diperoleh seluruhnya 300 pertidaksamaan.
3) Waktu kereta k memasuki jalur h dikurangi waktu kereta m meninggalkan jalur h lebih besar atau sama dengan selisih minimum waktu antara kereta m dan k di jalur h.
hk
a
–d
hmc
hmkh Bk \ Bs atau jalur antar stasiun, yaitu jalur 4, 5, 6, 9, 10, 11, 14, 15, 16, 20, 21, 22, 25, 26, 27, 30, 31, dan 32.
Untuk contoh kasus ini diasumsikan nilai
hmk
c
= 14) Waktu kereta k meninggalkan jalur yang telah digunakannya tepat sebelum memasuki jalur h sama dengan waktu kereta k memasuki jalur h.
k Bhk
d
=a
hk , h BkSebagai contoh, dengan memperhatikan Tabel 4 (Lampiran 2) untuk kereta k = 1 dan jalur h = 4 , diperoleh persamaan d11 = a41. Sehingga diperoleh seluruhnya 300 pertidaksamaan.
5) Waktu kereta k meninggalkan jalur terakhir dikurangi waktu kereta k memasuki jalur pertama yang digunakannya sama dengan total waktu keterlambatan kereta k ditambah lama waktu minimum kereta k menyelesaikan perjalanannya.
k BkF
d
- k Bka
0 = delayk + TripkSebagai contoh, dengan memperhatikan Tabel 4 (Lampiran 2) untuk kereta k = 1, jalur pertama yang digunakannya ( ) = 1 dan jalur terakhir yang digunakan ( ) = 33, diperoleh persamaan d331 – a11 = delay1 + Trip1. Sehingga diperoleh seluruhnya 12 persamaan.
Pada uraian contoh kasus di PT KAI banyak sekali persamaan maupun pertidaksamaan yang harus diselesaikan, hal ini menjadi sulit apabila menggunakan metode branch-and-bound secara manual. Oleh karena itu diperlukan suatu alat bantu yaitu dengan menggunakan software LINGO 8.0. Syntax program dan hasil komputasi dicantumkan pada Lampiran 3. Solusi yang didapat merupakan solusi optimum dengan nilai fungsi objektifnya adalah 8 menit dengan rincian sebagai berikut:
Kereta 1 tidak mengalami delay Kereta 2 mengalami delay 4 menit Kereta 3 tidak mengalami delay Kereta 4 tidak mengalami delay Kereta 5 tidak mengalami delay Kereta 6 mengalami delay 2 menit Kereta 7 tidak mengalami delay Kereta 8 mengalami delay 2 menit Kereta 9 tidak mengalami delay Kereta 10 tidak mengalami delay Kereta 11 tidak mengalami delay Kereta 12 tidak mengalami delay
Berikut hasil penjadwalan kereta api yang tertera di Tabel 3 yang didapatkan dari software Lingo 8.0.
ext
Tabel 3 Jadwal keberangkatan kereta di masing-masing stasiun
tiba berangkat tiba berangkat tiba berangkat tiba berangkat tiba berangkat tiba berangkat tiba selesai
1 trans jogja 1 Yogyakarta - Solo balapan 20 22 25 27 33 35 38 40 46 48 51 53 56 58
2 trans jogja 2 Yogyakarta - Solo balapan 32 34 41 43 49 51 54 56 62 64 67 69 72 74
3 trans jogja 3 Yogyakarta - Solo balapan 51 55 61 65 77 81 87 91 103 107 113 117 123 127
4 trans jogja 4 Yogyakarta - Solo balapan 73 77 83 87 99 103 109 113 125 129 135 139 145 149
5 trans jogja 5 Yogyakarta - Solo balapan 130 132 135 137 143 145 148 150 156 158 161 163 166 168
6 trans jogja 6 Yogyakarta - Solo balapan 163 167 175 179 191 195 201 205 217 221 227 231 237 241
tiba berangkat tiba berangkat tiba berangkat tiba berangkat tiba berangkat tiba berangkat tiba selesai
7 solo jaya 1 Solo balapan - Yogyakarta 0 4 10 14 20 24 36 40 46 50 62 66 72 76
8 solo jaya 2 Solo balapan - Yogyakarta 9 13 16 18 21 23 29 31 34 36 42 44 47 49
9 solo jaya 3 Solo balapan - Yogyakarta 54 58 64 68 74 78 90 94 100 104 116 120 126 130
10 solo jaya 4 Solo balapan - Yogyakarta 94 96 99 101 104 106 112 114 117 119 125 127 130 132
11 solo jaya 5 Solo balapan - Yogyakarta 147 149 152 154 157 159 165 167 170 172 178 180 183 185
12 solo jaya 6 Solo balapan - Yogyakarta 166 170 176 180 186 190 202 206 212 216 228 232 238 242
Kalasan Sleman Lempuyangan Yogyakarta
Kalasan Prambanan Klaten Solo balapan
Prambanan Indeks
(k) Kereta Rute
Yogyakarta Lempuyangan Sleman
Indeks
(k) Kereta Rute
Solo balapan Klaten
12
V SIMPULAN DAN SARAN
5.1 Simpulan
Dalam penulisan karya ilmiah ini telah diperlihatkan penyelesaian dari masalah penjadwalan kereta api yang bertujuan untuk menentukan nilai keterlambatan (delay) yang minimum. Masalah ini dipandang sebagai masalah 0-1 PLI.
5.2 Saran
Pada karya ilmiah ini data yang digunakan merupakan data hipotetik, saran untuk penulisan selanjutnya adalah dengan menggunakan data yang asli. Model penjadwalan kereta api ini juga dapat dikembangkan semisal meminimumkan biaya operasional kereta tentunya dengan menambahkan beberapa kendala.
DAFTAR PUSTAKA
Garfinkel, R.S & G.L. Nemhauser. 1972. Integer Programming. John Willey & Sons, New York.
Lee, Yusin. & Chen, Chuen-Yih. 2009. A heuristic for the train pathing and timetabling problem. Transportation research part B,43:837-851.
Taha, H.A. 1996. Pengantar Riset Operasi. Alih Bahasa:k Drs. Daniel Wirajaya. Binarupa Aksara, Jakarta. Terjemahan dari: Operations Research.
PENJADWALAN KERETA API MENGGUNAKAN
PEMROGRAMAN LINEAR INTEGER
DWI SETIANTO
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
PENJADWALAN KERETA API MENGGUNAKAN
PEMROGRAMAN LINEAR INTEGER
DWI SETIANTO
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
ABSTRAK
DWI SETIANTO. Penjadwalan Kereta Api Menggunakan Pemrograman Linear Integer. Dibimbing oleh PRAPTO TRI SUPRIYO dan TEDUH WULANDARI MAS’OED
Karya ilmiah ini memberikan formulasi masalah penjadwalan kereta api menggunakan model pemrograman linear integer. Penjadwalan kereta api tersebut didasarkan pada jalur tunggal yang menghubungkan antar stasiun. Formulasi yang dibangun bertujuan meminimumkan keterlambatan serta menjamin bahwa tidak ada kereta api yang mengalami tabrakan baik searah maupun berlawanan arah. Input model berupa jadwal keberangkatan kereta api yang direncanakan (aktual), sedangkan outputnya berupa jadwal keberangkatan dan kedatangan kereta api yang faktual.
ABSTRACT
DWI SETIANTO. Train Scheduling Using Integer Linear Programming. Supervised by PRAPTO TRI SUPRIYO and TEDUH WULANDARI MAS’OED
PENJADWALAN KERETA API MENGGUNAKAN
PEMROGRAMAN LINEAR INTEGER
DWI SETIANTO
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains pada Fakultas Matematika dan Ilmu Pengetahuan Alam
Institut Pertanian Bogor
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
Judul
: Penjadwalan Kereta Api Menggunakan Pemrograman Linear
Integer
Nama
: Dwi Setianto
NIM
: G54062111
Menyetujui,
Mengetahui,
Ketua Departemen Matematika
Dr. Berlian Setiawaty, M.S.
NIP. 19650505 198903 2 004
Tanggal Lulus :
Pembimbing I
Drs. Prapto Tri Supriyo, M.Kom.
NIP. 19630715 199002 1 002
Pembimbing II
KATA PENGANTAR
Puji dan syukur penulis panjatkan kehadirat Allah SWT atas segala nikmat, rahmat dan karunia -NYA sehingga penulis dapat menyelesaikan karya ilmiah ini. Tema yang dipilih adalah Riset Operasi dengan judul Penjadwalan Kereta Api Menggunakan Pemrograman Linear Integer. Skripsi ini merupakan syarat untuk menyelesaikan studi pada Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor.
Pada kesempatan ini penulis menyampaikan ucapan terima kasih kepada :
1. Allah SWT atas limpahan Rahmat dan Karunia-NYA
2. Keluarga tercinta: bapak dan ibu atas kasih sayangnya yang tulus dan ikhlas, untuk kakak Purwo Saputro dan Ema yang telah memberikan saran dan nasihat buat penulis.
3. Drs. Prapto Tri Supriyo, M.Kom. selaku dosen pembimbing I yang telah meluangkan waktu, tenaga dan pikiran dalam membimbing penulis.
4. Teduh Wulandari Mas’oed, M.Si. selaku dosen pembimbing II yang memberikan arahan dan masukan pada penulisan karya ilmiah ini.
5. Dr. Ir. Amril Aman, M.Sc. selaku dosen penguji yang telah memberikan saran dan masukan demi kesempurnaan karya ilmiah ini.
6. Seluruh dosen Departemen Matematika, terima kasih atas segala ilmu yang telah diberikan.
7. Staf Departemen Matematika: Bapak Yono, Bapak Deni, Bapak Hery, Bapak Epul, Bapak Bono, Ibu Susi dan Ibu Ade atas saran dan dedikasinya.
8. Fajar Yuliawan dan Salman Farid, terima kasih atas ilmu, saran, waktu dan segala dukungannya.
9. Sahabat yang selalu memberi inspirasi: Elly, Apri, Slamet Riyadi, Ratna, Adin, Kukuh, Ali, Popo, Angga, Widi, Yanti dan Avi.
10. Semua teman Matematika 42 yang selalu menjadi panutan yang baik. 11. Semua teman Matematika 43 yang telah menjadi bagian keluarga. 12. Semua teman Matematika 44 atas segala dukungannya.
13. Semua pihak yang telah membantu sehingga bisa terselesaikannya karya ilmiah ini.
Semoga karya ilmiah ini dapat bermanfaat bagi dunia ilmu pengetahuan khususnya Matematika dan dapat menjadi inspirasi bagi penelitian selanjutnya.
Bogor, Oktober 2011
RIWAYAT HIDUP
Penulis dilahirkan di Jakarta pada tanggal 27 Desember 1987 sebagai putra kedua dari dua bersaudara dengan ayah Drs. H. Ngatidjan, M.Pd. dan ibu Suratinah.
Tahun 2006 penulis lulus dari SMA Negeri 105 Jakarta dan pada tahun yang sama lulus seleksi masuk IPB melalui jalur Undangan Seleksi Masuk IPB (USMI). Penulis memilih Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.
DAFTAR ISI
Halaman
DAFTAR TABEL ... viii
DAFTAR GAMBAR ... viii
LAMPIRAN ... viii
I PENDAHULUAN
1.1Latar Belakang ... 1 1.2Tujuan ... 1
II LANDASAN TEORI
2.1 Pemrograman Linear ... 1 2.2 Pemrograman Linear Integer ... 3 2.3 Metode Branch and Bound ... 3
III DESKRIPSI DAN PEMODELAN MASALAH
3.1 Deskripsi Masalah ... 6 3.2 Formulasi Masalah ... 6
IV CONTOH KASUS DAN PENYELESAIANNYA ... 8
V SIMPULAN DAN SARAN
5.1 Simpulan ... 12 5.2 Saran ... 12
DAFTAR PUSTAKA ... 12
DAFTAR TABEL
Halaman
1 Jarak antar stasiun ... 8 2 Data perjalanan masing-masing kereta api ... 9 3 Jadwal keberangkatan kereta di masing-masing stasiun ... 11 4 Rute jalur yang digunakan oleh masing-masing kereta (Bk) ... 17 5 Waktu operasi minimum kereta ( min
hk
T ) ... 17 6 Waktu perpanjangan kereta ( ext
hk
T ) ... 18
DAFTAR GAMBAR
Halaman
1 Daerah fisibel PLI (2.7) ... 4 2 Daerah fisibel untuk Subproblem 2 (x1 ≥ 4) dan Subproblem 3 (x1 ≤ 3) ... 5 3 Seluruh pencabangan pada metode branch and bound untuk menentukan solusi PLI (2.7) ... 6 4 Contoh peta jaringan jalur kereta api antara dua stasiun ... 7 5 Peta jaringan jalur (rel) kereta api Yogyakarta – Solo balapan ... 9
LAMPIRAN
Halaman
1 Syntax Program LINGO 8.0 untuk menyelesaikan linear programming dengan Metode Branch and Bound ... 14 2 Data hipotetik awal untuk implementasi penyelesaian masalah penjadwalan kereta api ... 17 3 Syntax Program LINGO 8.0 untuk mencari penjadwalan dan keterlambatan masing - masing
I PENDAHULUAN
1.1 Latar Belakang
Semakin tingginya mobilitas penduduk di suatu negara terutama di kota besar tentulah memiliki banyak permasalahan, mulai dari kemacetan yang tak terselesaikan hingga moda transportasi yang efisien. Salah satu moda transportasi yang tepat dalam mengurangi kemacetan adalah kereta api, karena kereta api memiliki daya angkut yang besar dibandingkan angkutan kota pada umumnya.
Jumlah penumpang kereta api yang meningkat akan membuat frekuensi keberangkatan kereta semakin padat. Hal ini tentunya harus ditopang dengan perencanaan yang baik. Perencanaan yang dimaksud adalah perencanaan jadwal perjalanan kereta api yang tepat dan efisien dengan memperhatikan segala kendala semisal ketersediaan rangkaian kereta maupun jalur di setiap stasiun. Tentu
tidak mudah ketika telah mendapatkan jadwal perjalanan kereta api tetapi masih memiliki delay (keterlambatan) kereta yang besar.
Dalam karya ilmiah ini, akan dibahas penentuan jadwal kereta api menggunakan PLI (Pemrograman Linear Integer) yang meminimumkan delay. Solusi yang didapat menggunakan bantuan software LINGO 8.0. Karya ilmiah ini merupakan rekonstruksi dari sebagian artikel yang berjudul A Heuristic for the Train Pathing and Timetabling Problem yang ditulis oleh Yusin Lee dan Chuen-Yih Chen tahun 2009.
1.2 Tujuan
Tujuan penulisan karya ilmiah ini adalah mencari penyelesaian masalah penjadwalan kereta api yang meminimumkan delay (keterlambatan) menggunakan PLI (Pemrograman Linear Integer).
II LANDASAN TEORI
Untuk membuat model penjadwalan kereta api diperlukan pemahaman teori Pemrograman Linear (PL) atau Linear Programming (LP), Pemrograman Linear Integer (PLI) atau Integer Linear Programming (ILP), dan metode branch-and-bound.
Definisi 1 (Fungsi linear)
Suatu fungsi f dalam variabel-variabel
1, 2,..., n
x x x adalah suatu fungsi linear jika
dan hanya jika untuk suatu himpunan konstanta c c1, 2,...,c , n fungsi dapat
dituliskan sebagai
. ... )
,..., ,
(x1 x2 xn c1x1 c2x2 cnxn f
(Winston 2004)
Sebagai contoh, f x x( ,1 2) 2x1 3x 2
merupakan fungsi linear, sementara
2 2 1 2 1 2
( , )
f x x
x x
bukan fungsi linear.Definisi 2 (Pertidaksamaan dan persamaan linear)
Untuk sembarang fungsi linear )
,..., , (x1 x2 xn
f dan sembarang bilangan b,
pertidaksamaan f(x,x,...,x ) b dan
b x x x
f( 1, 2,..., n) adalah pertidaksamaan linear, sedangkan suatu persamaan
b x x x
f( 1, 2,..., n) merupakan persamaan linear.
(Winston 2004)
2.1 Pemrograman Linear
Pemrograman Linear (PL) adalah suatu masalah optimisasi yang memenuhi ketentuan-ketentuan berikut:
a) Tujuan masalah tersebut adalah memaksimumkan atau meminimumkan suatu fungsi linear dari sejumlah variabel keputusan. Fungsi yang akan dimaksimumkan atau diminimumkan ini disebut fungsi objektif.
b) Nilai variabel-variabel keputusannya harus memenuhi suatu himpunan kendala. Setiap kendala harus berupa persamaan linear atau pertidaksamaan linear.
c) Ada pembatasan tanda untuk setiap variabel dalam masalah ini. Untuk sembarang variabel , pembatasan tanda menentukan harus tak-negatif ( ) atau tidak dibatasi tandanya (unrestricted in sign).
2
Suatu PL mempunyai bentuk standar seperti yang didefinisikan sebagai berikut.
Definisi 3 (Bentuk Standar suatu PL) Suatu pemrograman linear dalam bentuk standar didefinisikan sebagai:
max z = (atau min) s.t.
(2.1) Dengan mendefinisikan:
A =
,
Maka kendala pada (2.1) dapat ditulis dengan sistem persamaan Ax = b (2.2)
(Winston 2004)
2.1.1 Solusi suatu Pemrograman Linear Suatu masalah PL dapat diselesaikan dalam berbagai teknik, salah satunya adalah metode simpleks. Metode ini dapat menghasilkan suatu solusi optimum bagi masalah PL dan telah dikembangkan oleh Dantzig sejak tahun 1947 (Winston 2004), dan dalam perkembangannya merupakan metode yang paling umum digunakan untuk menyelesaikan PL. Metode ini berupa metode iteratif untuk menyelesaikan PL berbentuk standar.
Pada masalah PL (2.2), vektor x yang memenuhi kendala Ax = b disebut sebagai solusi dari PL (2.2). Misalkan matriks A dapat dinyatakan sebagai A = (B N), dengan B adalah matriks taksingular berukuran m × m yang elemennya berupa koefisien variabel basis dan N merupakan matriks berukuran m × (n – m) yang elemennya berupa koefisien variabel nonbasis pada matriks kendala. Dalam hal ini matriks B disebut matriks basis untuk PL (2.2).
Misalkan x dinyatakan sebagai vektor x =
, dengan xB adalah vektor variabel basis
dan xN adalah vektor variabel nonbasis, maka
Ax = b dapat dinyatakan sebagai:
Ax =
= BxB + NxN= b (2.3)
Karena matriks B adalah matriks tak singular, maka B memiliki invers, sehingga dari (2.3) xB dapat dinyatakan sebagai:
xB = B-1b - B-1NxN (2.4) Kemudian, fungsi objektifnya berubah menjadi:
min z =
(Winston 2004)
Definisi 4 (Daerah Fisibel)
Daerah fisibel suatu PL adalah himpunan semua titik yang memenuhi semua kendala dan pembatasan tanda pada PL tersebut.
(Winston 2004)
Definisi 5 (Solusi Basis)
Solusi basis adalah solusi pada PL yang didapatkan dengan mengatur variabel n–m sama dengan nol dan nilai untuk penyelesaiannya adalah dari sisa variabel m. Hal ini mengasumsikan bahwa mengatur variabel n–m sama dengan nol sehingga membuat nilai yang unik untuk sisa variabel m atau sejenisnya, dan kolom-kolom untuk sisa dari variabel m adalah bebas linear.
(Winston 2004)
Definisi 6 ( Solusi Fisibel Basis)
Solusi fisibel basis adalah solusi basis pada PL yang semua variabel-variabelnya tak-negatif.
(Winston 2004)
Definisi 7 (Solusi Optimum)
Untuk masalah maksimisasi, solusi optimum suatu PL adalah suatu titik dalam daerah fisibel dengan nilai fungsi objektif terbesar. Untuk masalah minimisasi, solusi optimum suatu PL adalah suatu titik dalam daerah fisibel dengan nilai fungsi objektif terkecil.
(Winston 2004)
Ilustrasi untuk solusi basis dan solusi fisibel basis diberikan dalam Contoh 1 di bawah ini.
Contoh 1
Misalkan diberikan PL berikut: minimumkan z = -2 - 3 terhadap -x1 + 2x2 + x3 = 10 -2x1 + x2 + x4 = 2 2x1 + x5 = 3
3
Dari PL (2.5) didapatkan:
A = , b =
Misalkan dipilih
= T dan = T maka matriks basisnya adalah
B = ,
N = .
.
Dengan menggunakan matriks basis tersebut diperoleh
.
(2.6) .
Solusi (2.6) merupakan solusi basis, karena solusi tersebut memenuhi kendala PL (2.5) dan kolom-kolom pada matriks kendala yang berpadanan dengan komponen taknol dari (2.6) yaitu B adalah bebas linear (kolom yang satu bukan merupakan kelipatan dari kolom yang lain). Solusi (2.6) juga merupakan solusi fisibel basis, karena nilai-nilai variabelnya lebih dari atau sama dengan nol.
2.2 Pemrograman Linear Integer
Pemrograman linear integer (PLI) adalah suatu model pemrograman linear dengan variabel yang digunakan berupa bilangan bulat (integer). Jika semua variabel harus berupa integer, maka masalah tersebut dinamakan pure integer programming. Jika hanya sebagian yang harus berupa integer, maka disebut mixed integer programming (MIP). PLI dengan semua variabelnya harus bernilai 0 atau 1 disebut 0-1 PLI
(Garfinkel & Nemhauser 1972)
Definisi 8 (Relaksasi Pemrograman Linear) Relaksasi pemrograman linear atau sering disebut relaksasi-PL merupakan suatu pemrograman linear yang diperoleh dari suatu PLI dengan menghilangkan kendala integer atau kendala 0-1 pada setiap variabelnya.
Untuk masalah maksimisasi, nilai optimum fungsi objektif relaksasi-PL lebih besar atau sama dengan nilai optimum fungsi objektif PLI, sedangkan untuk masalah
minimisasi, nilai optimum fungsi objektif relaksasi-PL lebih kecil atau sama dengan nilai optimum fungsi objektif PLI.
(Winston 2004)
2.3 Metode Branch and Bound
Dalam penulisan karya ilmiah ini, untuk memperoleh solusi optimum dari masalah PLI digunakan software LINGO 8.0, yaitu sebuah program yang dirancang untuk menentukan solusi model linear, nonlinear, dan optimisasi integer. Software LINGO 8.0 ini menggunakan metode branch-and-bound untuk menyelesaikan masalah PLI.
Prinsip dasar metode branch-and-bound adalah memecah daerah fisibel dari masalah relaksasi-PL dengan membuat subproblem-subproblem. Terdapat dua konsep dasar dalam algoritma branch-and-bound.
1. Branch (Cabang)
Branching (pencabangan) adalah proses membagi permasalahan menjadi subproblem-subproblem yang mungkin mengarah ke solusi.
2. Bound (Batas)
Bounding (pembatasan) adalah suatu proses untuk mencari atau menghitung batas atas (dalam masalah minimisasi) dan batas bawah (dalam masalah maksimisasi) untuk solusi optimum pada subproblem yang mengarah ke solusi.
Metode branch-and-bound diawali dari menyelesaikan relaksasi-PL dari suatu pemrograman linear integer. Jika semua nilai variabel keputusan solusi optimum sudah berupa integer, maka solusi tersebut merupakan solusi optimum PLI. Jika tidak, dilakukan pencabangan dan penambahan batasan pada relaksasi-PLnya kemudian diselesaikan.
4
artinya fungsi objektif dan semua variabelnya sudah bernilai integer.
Sebelumnya akan dibahas terlebih dahulu pengertian subproblem yang terukur. Menurut Winston (2004), suatu subproblem dikatakan terukur (fathomed) jika salah satu kondisi berikut terpenuhi:
a. Subproblem tersebut takfisibel, sehingga tidak dapat menghasilkan solusi optimum bagi PLI.
b. Subproblem tersebut menghasilkan suatu solusi optimum dengan semua variabelnya bernilai integer. Jika solusi optimum ini mempunyai nilai fungsi objektif yang lebih baik daripada solusi fisibel yang diperoleh sebelumnya, maka solusi ini menjadi kandidat solusi optimum dan nilai fungsi objektifnya menjadi batas bawah (dalam masalah maksimisasi) dan batas atas (dalam masalah minimisasi) nilai fungsi objektif optimum bagi masalah PLI pada saat itu. Bisa jadi subproblem ini menghasilkan solusi optimum untuk masalah PLI.
c. Nilai fungsi objektif optimum untuk subproblem tersebut tidak melebihi batas bawah saat itu (untuk masalah maksimisasi). Suatu subproblem dapat dieliminasi apabila subproblem tersebut takfisibel dan batas bawah kandidat solusi lebih kecil (untuk masalah maksimisasi) dari nilai fungsi objektif optimum untuk subproblem tersebut.
Berikut ini adalah langkah-langkah penyelesaian suatu masalah maksimisasi dengan metode branch-and-bound :
Langkah 0
Didefinisikan z sebagai batas bawah dari solusi PLI yang optimum. Pada awalnya tetapkan z = − dan i = 0.
Langkah 1
Subproblem PL(i) dipilih sebagai bagian masalah berikutnya untuk diteliti. Subproblem PL(i) diselesaikan dan diukur dengan kondisi yang sesuai.
a) Jika PL(i) terukur, maka batas bawah z dapat diperbarui. Batas bawah z dapat diperbaharui jika solusi PLI yang lebih baik telah ditemukan. Jika tidak, maka bagian masalah (subproblem) baru i dipilih dan langkah 1 diulangi. Jika semua subproblem telah diteliti, maka proses dihentikan.
b) Jika PL(i) tidak terukur, lanjutkan ke langkah 2 untuk melakukan pencabangan PL(i).
Langkah 2
Pilih satu variabel xj yang nilai optimumnya, yaitu xj*, tidak memenuhi batasan integer dalam solusi PL(i). Singkirkan bidang [xj*] xj [xj*]+1 dengan membuat dua bagian masalah PL yang berkaitan menjadi dua batasan yang tidak dapat dipenuhi secara bersamaan yaitu:
xj ≤ [xj*] dan xj ≥ [xj*]+1,
dengan [xj*] didefinisikan sebagai integer terbesar yang kurang dari atau sama dengan xj*. Jika PL(i) masih tidak terukur, maka kembali ke Langkah 1.
(Taha 1996)
Untuk memudahkan pemahaman mengenai metode branch-and-bound diberikan contoh sebagai berikut:
Contoh 2
Misalkan diberikan PLI sebagai berikut: Maksimumkan z = 5 x1 + 4 x2
terhadap x1 + x2 5 10 x1 + 6 x2
x1, x2 0 dan integer (2.7)
[image:31.595.322.509.487.683.2]Solusi optimal relaksasi-PL dari masalah PLI (2.7) adalah x1=3.75, x2=1.25, dan z =23.75 (lihat Lampiran 1). Jadi batas atas nilai optimal fungsi objektif masalah PLI (2.7) adalah z= 23.75. Daerah fisibel relaksasi-PL masalah (2.7) ditunjukkan pada Gambar 1 (daerah yang diarsir) sedangkan titik-titik merupakan solusi fisibel masalah PLI (2.7).
Gambar 1 Daerah fisibel PLI (2.7)
Langkah berikutnya adalah memartisi daerah fisibel relaksasi-PL menjadi dua bagian berdasarkan variabel yang bernilai pecahan (non-integer). Karena x1= 3.75 dan x2=1.25 variabel bernilai pecahan maka dipilih
x
2x
1Daerah
fisibel
5
salah satu variabel, misalkan x1, sebagai dasar pencabangan. Jika masalah relaksasi-PL dari PLI (2.7) diberi nama Subproblem 1 dan Subproblem 1 dicabangkan atas x1, maka pencabangan tersebut menghasilkan 2 subproblem, yaitu:
Subproblem 2: Subproblem 1 ditambah kendala x1 ≥ 4
Subproblem 3: Subproblem 1 ditambah kendala x1 ≤ 3.
[image:32.595.105.303.84.782.2]Daerah fisibel untuk kedua subproblem di atas diilustrasikan secara grafis pada Gambar 2.
Gambar 2 Daerah fisibel untuk Subproblem 2 (x1 ≥ 4) dan Subproblem 3 (x1 ≤ 3). Setiap titik (solusi) fisibel dari PLI (2.7) termuat dalam daerah fisibel Subproblem 2 atau Subproblem 3. Setiap subproblem ini saling lepas. Sekarang dipilih subproblem yang belum diselesaikan, misalkan dipilih Subproblem 2. Solusi optimal untuk Subproblem 2 ini adalah x1 = 4, x2 = 0.8333 dan z = 23.333, (lihat Lampiran 1 bagian Subproblem 2). Karena solusi optimal yang dihasilkan Subproblem 2 bukan solusi integer, maka Subproblem 2 dicabangkan atas x2 sehingga diperoleh dua subproblem lagi, yakni:
Subproblem 4: Subproblem 3 ditambah kendala x2 ≥ 1;
Subproblem 5: Subproblem 3 ditambah kendala x2 ≤ 0.
Saat ini subproblem yang belum diselesaikan adalah Subproblem 3, 4 dan 5. Salah satu subproblem dipilih, misalnya dengan aturan LIFO (last in first out). Dengan aturan ini berarti dipilih Subproblem 4 atau Subproblem 5. Subproblem 4 takfisibel (lihat Lampiran 1 bagian Subproblem 4) maka subproblem ini tidak dapat menghasilkan solusi optimal, yang tersisa adalah Subproblem 3 dan Subproblem 5.
Karena aturan LIFO, dipilih Subproblem 5, yang kemudian menghasilkan solusi optimal x1=4.5, x2=0 dan z=22.5 (lihat Lampiran 1 bagian Subproblem 5). Karena x1=4.5 bukan integer, maka dilakukan kembali pencabangan atas x1, sehingga diperoleh:
Subproblem 6: Subproblem 5 ditambah kendala x1≥5;
Subproblem 7: Subproblem 5 ditambah kendala x1≤4.
Misalkan dipilih Subproblem 6. Ternyata Subproblem 6 ini juga takfisibel (lihat Lampiran 1 bagian Subproblem 6), sehingga tidak dapat menghasilkan solusi optimal. Dengan demikian subproblem-subproblem yang belum diselesaikan adalah Subproblem 3 dan Subproblem 7. Karena aturan LIFO, dipilih Subproblem 7. Subproblem ini kemudian menghasilkan solusi opimal x1=4, x2= 0, dan z= 20 (lihat Lampiran 1 bagian Subproblem 7). Dapat dilihat bahwa solusi optimal subproblem ini semuanya berupa integer, sehingga merupakan kandidat solusi untuk PLI (2.7). Nilai z pada kandidat solusi ini merupakan batas bawah bagi nilai optimal PLI. Penyelesaian Subproblem 3 menghasilkan solusi optimal x1= 3, x2= 2 dan z= 23 (lihat Lampiran 1 bagian Subproblem 3). Batas bawah yang ditetapkan dari solusi optimal Subproblem 7 tidak lebih baik dari nilai solusi optimal yang dihasilkan Subproblem 3. Dengan demikian, nilai solusi optimal Subproblem 3, yakni z = 23 menjadi batas bawah yang baru. Semua solusi optimal telah berupa integer dan tidak perlu dilakukan pencabangan kembali, sehingga solusi optimal dari Subproblem 3 merupakan solusi optimal PLI (2.7), yakni x1= 3, x2= 2 dan z= 23. Pohon pencabangan yang menunjukkan proses penyelesaian masalah PLI (2.7) secara keseluruhan ditunjukkan pada Gambar 3.
x
1x
2 Subproblem 36
Gambar 3 Seluruh pencabangan pada metode branch and bound untuk menentukan solusi PLI (2.7)
III DESKRIPSI DAN PEMODELAN MASALAH
3.1 Deskripsi masalah
Untuk mendeskripsikan masalah penjadwalan kereta api di setiap stasiun, hal utama yang harus diketahui adalah banyaknya rangkaian kereta yang ditugaskan di stasiun tersebut. Kemudian dari kereta api yang ditugaskan tadi, seberapa banyak ketersedian jalur yang dapat dilalui. Banyaknya kereta api yang beroperasi juga bergantung pada kebutuhan atau permintaan penumpang.
Dalam memenuhi keinginan penumpang, tersedia dua jenis kereta api yaitu kereta api reguler dan kereta api ekspress. Untuk kereta api regular, waktu tunggu di dalam stasiun lebih lama dibandingkan jenis yang kedua yaitu kereta api ekspress. Selain itu kecepatan kereta api jenis reguler lebih rendah dibandingkan kereta api jenis ekspress.
Berikut ini adalah gambaran dari suatu penjadwalan kereta api. Misalkan terdapat n buah stasiun yang masing-masing stasiun memiliki dua buah jalur pemberhentian dan
dari keseluruhan stasiun tersebut saling dihubungkan oleh jalur tunggal. Stasiun ke-1 dan stasiun ke-n adalah stasiun pemberangkatan, sedangkan stasiun ke-2 hingga stasiun ke−(n-1) adalah stasiun pemberhentian. Andaikan dioperasikan p kereta api ekspress dan q kereta api reguler. Kereta api tersebut ada yang diberangkatkan dari stasiun ke-1 dan juga dari stasiun ke-n. Pengelola stasiun dihadapkan pada masalah penjadwalan kereta sedemikian rupa sehingga dapat meminimumkan delay (keterlambatan), dengan memperhatikan kebutuhan pengguna kereta api.
3.2 Formulai masalah
Model penjadwalan kereta api bergantung pada ketersedian rangkaian kereta api dan jumlah jalur yang dapat dilalui. Selanjutnya, penjadwalan kereta api dapat diformulasikan dalam bentuk PLI.
x1=3.75, x2=1.25 dan z = 23.75
x1=4, x2=0.8333 dan z = 23.333 x1=3, x2=2, dan z = 23 ba