Metode Lexicographic dalam Masalah Transportasi

METODE LEXICOGRAPHIC DALAM MASALAH TRANSPORTASI

SKRIPSI

MANUEL S. MARBUN 100803019

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

METODE LEXICOGRAPHIC DALAM MASALAH TRANSPORTASI

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains

MANUEL S. MARBUN 100803019

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

PERSETUJUAN

Judul : MetodeLexicographic dalam Masalah Trans-portasi

Kategori : Skripsi

Nama : Manuel S. Marbun

Nomor Induk Mahasiswa : 100803019

Program Studi : Sarjana (S1) Matematika

Departemen : Matematika

Fakultas : Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara

Disetujui di Medan, Juli 2014

Komisi Pembimbing

Pembimbing 2, Pembimbing 1,

Dr. Faigiziduhu Bu’ulolo, M.Si. Dr. Mardiningsih, M.Si.

NIP. 195312181980031003 NIP. 196304051988112001

Disetujui Oleh

Departemen Matematika FMIPA USU Ketua,

PERNYATAAN

METODE LEXICOGRAPHIC DALAM MASALAH

TRANSPORTASI

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil karya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, Juli 2014

PENGHARGAAN

Puji dan syukur penulis panjatkan kepada Tuhan Yang Maha Pemurah dan Maha Penyayang, dengan limpah karunia-Nya Penulis dapat menyelesaikan penyusunan skripsi ini dengan judul MetodeLexicographic dalam Masalah Transportasi.

METODE LEXICOGRAPHIC DALAM MASALAH

TRANSPORTASI

ABSTRAK

Masalah transportasi adalah salah satu jenis pemodelan matematika untuk menen-tukan strategi terbaik dalam distribusi barang dari beberapa gudang ke sejumlah pelanggan agar biaya dapat diminimumkan. Pada tulisan ini, masalah trans-portasi dikembangkan dengan menggunakan lebih dari satu fungsi tujuan, yaitu meminimumkan biaya transportasi, meminimumkan kekosongan kapasitas mobil, dan meminimumkan kerusakan barang selama perjalanan. MetodeLexicographic juga akan dikaji untuk menyelesaikan masalah transportasi. Di akhir tulisan ini, diberikan suatu pendekatan numerik untuk memperlihatkan keragaman nilai op-timal setiap fungsi tujuan seiring perbedaan urutan prioritas fungsi tujuan.

LEXICOGRAPHIC METHOD FOR TRANSPORTATION

PROBLEM

ABSTRACT

Transportation problem is a kind of mathematical programming to find the best strategy in distributing goods from several warehouses to several customers in order that the total cost can be minimized. In this paper, transportation prob-lem is developed by using more than one objectives, such as minimizing the total cost, minimizing the underused capacity, and minimizing the number of broken goods in travel. Lexicographic Method will be discussed to solve transportation problem. In the end of this paper, given a numerical approach to show varieties of objectives based on different order of priority.

DAFTAR ISI

Halaman

Persetujuan i

Pernyataan ii

Penghargaan iii

Abstrak iv

Abstract v

Daftar Isi vi

Daftar Tabel vii

Daftar Lampiran viii

Bab 1. Pendahuluan 1

1.1 Latar Belakang Penelitian 1

1.2 Perumusan Masalah 2

1.3 Batasan Masalah 2

1.4 Tujuan Penelitian 2

1.5 Kontribusi Penelitian 2

1.6 Metodologi Penelitian 3

1.6.1 Alat 3

1.6.2 Langkah-langkah 3

Bab 2. Tinjauan Pustaka 5

2.1 Masalah Transportasi 5

2.3 Program Tujuan Ganda dan Solusi Pareto-Optimal 7

2.4 MetodeLexicographic 9

Bab 3. Pembahasan 11

3.1 Masalah Transportasi 11

3.1.1 Asumsi 11

3.1.2 Formulasi Model 12

3.2 MetodeLexicographic 15

3.2.1 Algoritma Metode Lexicographic 17

3.3 Pendekatan Numerik 17

Bab 4. Kesimpulan dan Saran 26

4.1 Kesimpulan 26

4.2 Saran 26

DAFTAR TABEL

No.

Judul

Hal.

3.1 Jumlah persediaan barang pada gudang i 18

3.2 Jumlah permintaan pelangganj 18

3.3 Biaya penggunaan sebuah mobil dari gudang ike pelanggan j 18 3.4 Biaya kekosongan sebuah barang dari gudangi ke pelanggan j 19 3.5 Peluang sebuah barang rusak dari gudang i ke pelangganj 19 3.6 Nilai optimal setiap fungsi tujuan dari berbagai urutan prioritas 21 3.7 Nilaif∗

i dan f +

i 21

DAFTAR LAMPIRAN

No.

Judul

Hal.

METODE LEXICOGRAPHIC DALAM MASALAH

TRANSPORTASI

ABSTRAK

Masalah transportasi adalah salah satu jenis pemodelan matematika untuk menen-tukan strategi terbaik dalam distribusi barang dari beberapa gudang ke sejumlah pelanggan agar biaya dapat diminimumkan. Pada tulisan ini, masalah trans-portasi dikembangkan dengan menggunakan lebih dari satu fungsi tujuan, yaitu meminimumkan biaya transportasi, meminimumkan kekosongan kapasitas mobil, dan meminimumkan kerusakan barang selama perjalanan. MetodeLexicographic juga akan dikaji untuk menyelesaikan masalah transportasi. Di akhir tulisan ini, diberikan suatu pendekatan numerik untuk memperlihatkan keragaman nilai op-timal setiap fungsi tujuan seiring perbedaan urutan prioritas fungsi tujuan.

LEXICOGRAPHIC METHOD FOR TRANSPORTATION

PROBLEM

ABSTRACT

Transportation problem is a kind of mathematical programming to find the best strategy in distributing goods from several warehouses to several customers in order that the total cost can be minimized. In this paper, transportation prob-lem is developed by using more than one objectives, such as minimizing the total cost, minimizing the underused capacity, and minimizing the number of broken goods in travel. Lexicographic Method will be discussed to solve transportation problem. In the end of this paper, given a numerical approach to show varieties of objectives based on different order of priority.

Bab 1

PENDAHULUAN

1.1

Latar Belakang Penelitian

Operasi Riset merupakan disiplin ilmu matematika aplikasi yang telah membawa pengaruh besar pada dunia sejak perang dunia kedua. Beberapa contoh masalah Operasi Riset adalah sebagai berikut:

1. Selain mengharapkan keuntungan yang besar, seorang Manajer perlu menger-jakan proyeknya dengan waktu yang singkat.

2. Selain mengharapkan keuntungan maksimal, seorangDeveloper properti ingin membangun rumah sewa dengan jumlah yang besar.

3. Selain mengharapkanreturn saham yang menggiurkan, seorang Investor perlu meminimumkan risiko atau kerugian dari Investasi yang akan dilakukannya.

4. Perusahaan yang memproduksi galon air mineral, harus memperhatikan vo-lume air yang harus 19 liter, desain yang elegan, biaya produksi yang mini-mum, penyusunan yang baik saat distribusi, dan keuntungan yang maksimal

5. Seorang manajer meminimumkan biaya transportasi saat mengantar barang dari beberapa gudang ke sejumlah pelanggan.

2

Ada beberapa metode untuk menyelesaikan program linier tujuan ganda, salah satunya adalah MetodeLexicographic. Dalam Wikipedia.org, metode lexi-cographic berasumsi bahwa setiap fungsi tujuan dapat diurutkan (ranking) dalam urutan kepentingan menurut pembuat keputusan (Decision Maker). Dengan kata lain, metode lexicographic memerlukan preferensi dari pembuat keputu-san sendiri agar dapat dikerjakan. Secara intuisi, akan terlihat suatu relativitas dalam metode lexicographic karena hasil optimal akan berbeda-beda bila ma-salah transportasi tersebut dikerjakan oleh orang yang berbeda-beda pula. Se-mentara, pengguna operasi riset tetap menginginkan solusi terbaik dari prosedur lexicographic. Oleh karena itu, penulis mengangkat judul, ”Metode lexicographic dalam Masalah Transportasi”.

1.2

Perumusan Masalah

Metodelexicographic membutuhkan preferensi urutan kepentingan fungsi tujuan dari pembuat keputusan. Masalah penelitian ini adalah menentukan urutan yang bagaimanakah yang memberikan hasil paling optimal kepada pembuat keputu-san.

1.3

Batasan Masalah

1. Penulis membahas metodelexicographic hanya dalam masalah transportasi.

2. Penulis membatasi penelitian dengan 3 fungsi tujuan dalam model.

1.4

Tujuan Penelitian

Tujuan penelitian ini adalah untuk mengkaji metode lexicographic dan menye-lesaikan masalah transportasi berbentuk program linier tujuan ganda.

1.5

Kontribusi Penelitian

Dari penelitian ini, penulis optimis dapat memberikan kontribusi kepada pem-baca berupa:

1. literatur tentang masalah transportasi

3

1.6

Metodologi Penelitian

1.6.1

Alat

Untuk membantu menganalisis data, penulis menggunakansoftwareLINGO 13.0 dan AIMMS 3.13.

1.6.2

Langkah-langkah

1.6.2.1 Mengkaji Masalah Transportasi

Tahap ini dilakukan dengan studi literatur dan pengamatan di lapangan. Akan diamati kondisi truk saat akan berangkat, saat dalam perjalanan, dan saat truk tiba di tempat pelanggan karena dicurigai bahwa hal-hal tersebut mempengaruhi strategi transportasi yang optimal. Sebagai contoh, dalam perjalanan, truk yang memuat barang dengan jumlah yang besar justru akan memperlambat trans-portasi dan juga akan membuat kondisi lalu lintas tidak kondusif.

Setelah studi literatur dan pengamatan dilakukan, masalah transportasi tersebut dimodelkan dalam bentuk program linier tujuan ganda sehingga diper-oleh model matematika yang lebih kompleks daripada model transportasi dalam program linier.

1.6.2.2 Mengkaji Metode

Lexicographic

Tahap ini dilakukan dengan studi literatur, yaitu dengan mengkaji karakteristik metode lexicographic sehingga dapat diamati pengaruh urutan prioritas fungsi tujuan terhadap hasil optimal. Pada tahap ini, juga dilakukan suatu pendekatan numerik dengan langkah-langkah sebagai berikut:

1. Mengambil sebuah contoh masalah transportasi

2. Mendaftarkan seluruh urutan prioritas fungsi tujuan

3. Mengambil hipotesis urutan yang memberikan hasil minimal

4

5. Menentukan nilai minimal dari hasil-hasil optimal tersebut.

6. Mengamati apakah urutan yang memberikan hasil minimal sesuai dengan uru-tan dugaan (hipotesis). Bila sesuai, kembali melakukan langkah 4 hingga langkah 6 dengan masalah transportasi yang lain. Bila tidak sesuai, maka lanjut ke langkah 7.

7. Mengambil kesimpulan bahwa “tidak terdapat urutan fungsi tujuan tertentu yang selalu memberikan hasil optimal dalam masalah transportasi berbentuk program linier tujuan ganda”.

8. MengkajiAnalytic Hierarchy Processuntuk menentukan urutan prioritas fungsi tujuan.

9. Menentukan algoritma untuk menyelesaikan masalah transportasi berbentuk program linier tujuan ganda dengan metode lexicographic.

1.6.2.3. Membuat Kesimpulan

Bab 2

TINJAUAN PUSTAKA

2.1

Masalah Transportasi

Masalah transportasi pertama kali digunakan pada awal perang dunia kedua un-tuk menenun-tukan bagaimana mengirimkan pasukan yang terletak disuatu tempat latihan Amerika Serikat ke medan perang di Eropa dan Asia, kemudian dikem-bangkan oleh F. L. Hitchcock sejak 1941 sebagai persoalan distribusi atau trans-portasi produk dari gudang ke pelanggan. Ilustrasinya adalah sebagai berikut:

Gambar 1. Jaringan Masalah Transportasi

6

Model 2.1

minf(g) = M X i=1 N X j=1

cijgij 2.1

kendala:

N X

j=1

gij ≤Si,∀i 2.2

M X

i=1

gij =Dj,∀j 2.3

M X

i=1

Si = N X

j=1

Dj 2.4

gij ≥0,∀i, j 2.5

Persamaan (2.1) adalah fungsi tujuan model transportasi untuk memini-mumkan total biaya transportasi. Total jumlah barang yang diangkut dari suatu gudang untuk didistribusikan tidak lebih dari kapasitas gudang tersebut, seperti yang dinyatakan oleh persamaan (2.2). Persamaan (2.3) adalah persamaan yang menunjukkan bahwa total jumlah barang yang diangkut dari setiap gudang ke suatu pelanggan tepat memenuhi jumlah barang kebutuhan setiap pelanggan. Persamaan (2.4) menunjukkan bahwa total jumlah produk yang tersedia di selu-ruh gudang harus sama dengan total jumlah permintaan seluselu-ruh pelanggan, dan persamaan (2.5) menunjukkan bahwa persamaan (2.2), persamaan (2.3), dan persamaan (2.4) adalah kendala yang tak negatif.

7

2.2

Program Tujuan Ganda dan Solusi Pareto-Optimal

Dalam Caramiaet al, sebuah persoalan optimisasi dengan fungsi tujuan tunggal dapat diformulasikan sebagai berikut:

minf(x)

x∈S

di manaf adalah sebuah fungsi skalar dan S adalah daerah fisibel yang didefin-isikan sebagai

S ={x∈Rm :

Ax

= 0}.

di mana

A

adalah matriks koefisien

x

pada kendala. Program Tujuan Ganda dapat dimodelkan secara matematis sebagai berikut:

min [f1(x), f2(x), . . . , fn(x)]

x∈S,

di mana n > 1. Definisikan Ruang Objektif adalah ruang yang mengandung seluruh fungsi tujuan, dan definisikan

C ={y∈R:y=f(x), x∈S}.

Konsep skalar dari ”optimalitas” tidak dapat langsung diaplikasikan pada Program Tujuan Ganda. Di sini, notasi optimalitas Pareto akan diperkenalkan sebagai berikut:

• Sebuah titikx∗

dikatakan Pareto optimum lemah atau sebuah solusi efisien lemah untuk masalah Program Tujuan Ganda jika dan hanya jika tidak terdapat x∈S sehingga fi(x)< fi(x∗

) untuk setiap i∈ {1, . . . , n}.

• Sebuah titik x∗

dikatakan Pareto optimum kuat atau sebuah solusi efisien yang tepat untuk masalah Program Tujuan Ganda jika dan hanya jika tidak terdapat x∈S sehingga fi(x)≤fi(x∗

8

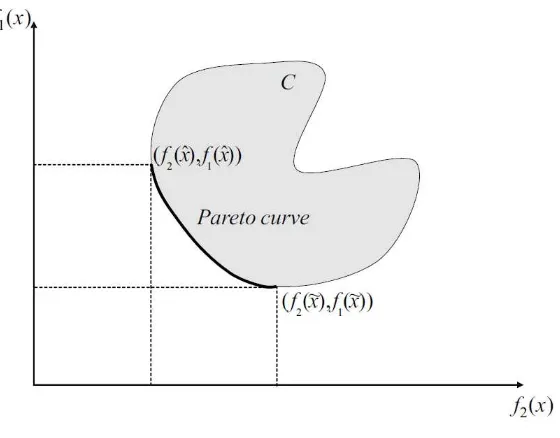
disebut Pareto front atau Kurva Pareto. Bentuk dari permukaan Pareto meng-indikasikan hubungan antara setiap fungsi tujuan. Sebuah contoh kurva Pareto ditampilkan pada Gambar 2, di mana setiap titik di antara (f2(ˆx), f1(ˆx)) dan (f2(˜x), f1(˜x)) disebut Pareto front. Titik-titik tersebut disebut titik non-inferior atau titik tak-terdominasi.

Gambar 2. Contoh Kurva Pareto

Contoh Pareto optimum lemah dan kuat ditunjukkan pada Gambar 3: titikp1 dan p5 adalah Pareto optimum lemah; titik p2, p3, danp4 adalah Pareto optimum kuat.

9

2.3

Metode

Lexicographic

Mathias Ehrgott mengemukakan bahwa dalam optimisasi lexicographic, setiap fungsi tujuan akan dipertimbangkan berdasarkan tingkat kepentingan atau pri-oritas. Sebuah solusi optimal ˆxdari suatu masalah disebut optimallexicographic dan ˆy = f(ˆx) adalah sebuah vector minimal lexicographicdalam Y = f(X), di manaX adalah himpunan vektorxyang memenuhi kendala (fisibel). Optimisasi lexicographicjuga dapat ditulis dengan notasi “lexmin” sebagai berikut:

lexmin

x∈X (f1(x), f2(x), . . . , fp(x)) 2.6

Notasi “lexmin” pada persamaan (3.4) di atas menunjukkan proses meminimum-kan setiap fungsi tujuan secaralexicographi atau berurutan, yaitu dari fungsi tu-juan 1 hingga fungsi tutu-juanp. Algoritma optimisasilexicographicakan dijelaskan lebih rinci pada Bab 3. Berikut diberikan definisi solusi dari sebuah optimisasi lexicographic.

Definisi 2.1.

Sebuah solusi fisibel xˆ∈ X adalah solusi lexicographic, jika tidak terdapat x∈ X sehinggaf(x)<lex f(ˆx).

Misalkan y1

= f(x1) dan y2

= f(x2) adalah dua buah nilai fungsi tujuan dengan x1, x2 ∈ X. Perhatikan kembali bahwa y1 <lex y2 jika yq1 < y

2

q, di mana

q = min{k : y1 k 6=y

2 k}, y

1

q =fq(x1), dan y 2

q =fq(x2) serta asumsi bahwa seluruh fungsi tujuan telah diurutkan secara lexicographic. Pada definisi di atas, dapat dinyatakan bahwa ˆx∈ X adalah optimal lexicographic, jika

f(ˆx)≤lexf(x),∀x∈ X.

10

diaplikasikan: untuka, b∈Rm, ketidaksamaan lexicographic kuat (the strict lex-icographic inequality)a≻bdipenuhi, jika dan hanya jika,ai ≻bi dipenuhi untuk

i = min{1, . . . , m | ak 6= bk}; dan ketidaksamaan lexicographic lemah (the weak lexicographic inequality) a %b dipenuhi, jika dan hanya jika, a ≻ b atau a =b. Untuk setiap dua matriks berorde (m×n),A = (a1, . . . , an), B = (b1, . . . , bn).

Bab 3

PEMBAHASAN

3.1

Masalah Transportasi

3.1.1

Asumsi

Seperti yang telah dijelaskan di Bab 2 pada bagian Masalah Transportasi, masa-lah transportasi perlu dikaji lebih jauh dalam fungsi tujuan untuk mendapatkan hasil optimal dan praktikal atau lebih dekat dengan dunia nyata. Perusahaan dapat menambahkan fungsi tujuan lain ke dalam Model 2.1, yaitu fungsi tu-juan yang dapat berkaitan dengan kuantitas barang yang didistribusikan, ruang kosong dalam mobil pengangkut, konsumsi energi, total waktu distribusi, dan lain-lain. Pada Model 2.1, masalah transportasi menggunakan asumsi sebagai berikut:

1. Transportasi atau distribusi barang dilakukan oleh perusahaan secara serem-pak dari seluruh gudang.

2. Mobil pengangkut yang telah mendistribusikan barang ke pelanggan, langsung kembali ke gudang masing-masing. Dengan kata lain, mobil pengangkut tidak melanjutkan perjalanan ke pelanggan lain.

3. Total jumlah barang yang tersedia di seluruh gudang sama dengan total jum-lah barang yang dipesan seluruh pelanggan.

4. Biaya transportasi dihitung berdasarkan kuantitas barang yang didistribusikan dari suatu gudang ke suatu pelanggan.

5. Waktu transportasi diabaikan.

Pada tulisan ini, masalah transportasi dimodifikasi dengan asumsi 1 dan 2 di atas dan beberapa asumsi tambahan sebagai berikut:

12

2. Setiap mobil pengangkut bersifat identik dan memiliki kapasitas angkut yang sama.

3. Biaya distribusi dihitung berdasarkan banyak mobil yang digunakan.

4. Kondisi setiap jalan dari gudang ke pelanggan sama.

5. barang yang didistribusikan hanya satu jenis.

6. Total jumlah barang yang tersedia di seluruh gudang dapat memenuhi per-mintaan seluruh pelanggan.

Asumsi-asumsi di atas berlaku untuk masalah transportasi dengan skala besar karena biaya transportasi dihitung berdasarkan kuantitas mobil yang digunakan.

3.1.2

Formulasi Model

Berdasarkan asumsi-asumsi di atas, misalkan:

xij = kuantitas barang yang didistribusikan dari gudang i ke pelang-gan j

mij = kuantitas mobil yang bergerak dari gudang i ke pelanggan j

cij = biaya distribusi sebuah mobil dari gudang i ke pelanggan j

eij = biaya ruang kosong sebuah barang dalam mobil pengangkut, dari gudang i ke pelangganj

pij = peluang sebuah barang rusak dalam perjalanan dari gudangike pelanggan j

Si = kuantitas barang yang tersedia di gudangi

Dj = kuantitas barang yang dipesan pelangganj

k = kapasitas atau daya angkut sebuah mobil

M = kuantitas gudang

N = kuantitas pelanggan

13

1. Total Waktu Transportasi

Biaya transportasi yang diperlukan dari gudangike pelangganjadalahmijcij. Sehingga, fungsi total biaya transportasi adalah:

f1(x) = M X i=1 N X j=1

mijcij 3.1

2. Kekosongan Mobil Pengangkut

Kekosongan dalam mobil pengangkut terjadi karena jumlah barang yang didis-tribusikan lebih sedikit dari kapasitas mobil, atau dengan kata lain, xij tidak sama dengan kelipatank. Misalkan banyak ruang kosong dalam sebuah mobil yang bergerak dari gudangike pelangganj adalahrij. Dengan mendefinisikan

mij = xij

k

, maka

xij +rij = (k)(mij); 0 ≤rij < k

sehingga 0 ≤ (k)(mij)−xij < k dan fungsi total biaya ruang kosong dalam mobil adalah:

f2(x) = M X i=1 N X j=1

((k)(mij)−xij)eij

3. Kerusakan Barang

Dalam perjalanan dari gudangike pelanggan j, banyak barang yang diperki-rakan akan rusak adalah pijxij. Sehingga, fungsi total barang rusak adalah:

f3(x) = M X i=1 N X j=1

pijxij

Selanjutnya, ditentukan kendala pada model transportasi sebagai berikut:

1. Total jumlah barang yang dapat diangkut dari suatu gudang untuk didis-tribusikan tidak lebih dari kapasistas gudang tersebut, yaitu:

N X

14

2. Total jumlah barang yang diangkut dari setiap gudang ke suatu pelanggan tepat memenuhi jumlah barang kebutuhan pelanggan, yaitu:

M X

i=1

xij =Dj ;∀j 3.3

3. Banyak ruang kosong dalam mobil adalah paling sedikit 0 dan tidak melebihi kapasitas atau daya angkut mobil, yaitu:

0≤(k)(mij)−xij < k; ∀i, j

4. Nilai variabel keputusanxij dan mij adalah bilangan bulat tak negatif, yaitu:

xij, mij ∈Z +

∪ {0}

Dengan demikian, model transportasi dalam bentuk program tujuan ganda ada-lah:

Model 3.1

minf1(x) = M X i=1 N X j=1

mijcij

minf2(x) = M X i=1 N X j=1

((k)(mij)−xij)eij

minf3(x) = M X i=1 N X j=1

pijxij

kendala:

N X

j=1

xij ≤Si ;∀i

M X

i=1

xij =Dj ;∀j

0≤(k)(mij)−xij < k ;∀i, j

mij, xij ∈Z +

15

3.2

Metode

Lexicographic

Program tujuan ganda menggunakan lebih dari satu fungsi tujuan. Berbeda dengan program linier biasa yang secara mudah dapat ditentukan solusi opti-mal tunggal, program tujuan ganda tidak memiliki solusi yang mengoptiopti-malkan seluruh fungsi tujuan sekaligus. Dalam masalah tersebut, pembuat keputusan mencari solusi yang paling dapat diterima. Konsep optimalitas pada program tujuan ganda menggunakan konsep efisiensi atau optimum Pareto. Dalam ma-tematika, solusi efisien didefinisikan sebagai berikut:

Definisi 3.1.

Sebuah solusi fisibelx˜∈ X dalam program tujuan ganda dikatakan efisien jika tidak terdapat solusi fisibel lainnya,x∈ X, yang menyebabkanfk(x)≤

fk(˜x) untuk setiap k ∈ {1,2, . . . , p} dengan paling sedikit satu ketidaksamaan.

Solusi yang diinginkan pembuat keputusan adalah solusi yang paling da-pat diterima atau yang paling memenuhi permasalahan dunia nyata. Karena keterbatasan informasi, tidak terdapat solusi yang dapat dikatakan lebih baik daripada solusi lainnya. Biasanya penilaian pembuat keputusan dibutuhkan se-bagai informasi atau preferensi untuk menentukan solusi yang paling diterima. Penilaian tersebut berupa pandangan terhadap prioritas atau tingkat kepentin-gan fungsi tujuan. Salah satu metode yang menggunakan preferensi pembuat keputusan adalah metodelexicographic.

Metode lexicographic adalah salah satu metode yang tidak mengombi-nasikan seluruh fungsi tujuan menjadi satu fungsi tujuan sebagaimana halnya MetodeWeighted Sum, tetapi mengoptimalkan setiap fungsi tujuan secara berta-hap dan berurutan. Perlu diketahui bahwa dalam optimisasi multi fungsi tujuan, tidak terdapat suatu metode yang selalu menjamin memberikan sebuah solusi op-timal.

16

bel). Optimisasilexicographic juga dapat ditulis dengan notasi “lexmin” sebagai berikut:

lexmin

x∈X (f1(x), f2(x), . . . , fp(x)) 3.4

Definisi 3.2.

Sebuah solusi fisibel xˆ∈ X adalah solusi lexicographic, jika tidak terdapat x∈ X sehinggaf(x)<lex f(ˆx).

Misalkan y1

= f(x1) dan y2

= f(x2) adalah dua buah nilai fungsi tujuan dengan x1, x2 ∈ X. Perhatikan kembali bahwa y1 <lex y2 jika yq1 < y

2

q, di mana

q = min{k : y1 k 6=y

2 k}, y

1

q =fq(x1), dan y 2

q =fq(x2) serta asumsi bahwa seluruh fungsi tujuan telah diurutkan secara lexicographic. Pada definisi di atas, dapat dinyatakan bahwa ˆx∈ X adalah optimal lexicographic, jika

f(ˆx)≤lexf(x),∀x∈ X.

Hubungan antara optimal lexicographic dengan solusi efisien diberikan pada lema berikut.

Lema 3.3.

Misalkanxˆ∈ X sehinggaf(ˆx)≤lex f(x)untuk setiapx∈ X. Maka, ˆ

x∈ XE.

Bukti. Dengan kontraposisi, akan dibuktikan bahwa jika x /∈ XE, maka ter-dapat x ∈ X sehingga f(ˆx) >lex f(x). Oleh karena itu, misalkan ˆx bukan solusi efisien sehingga terdapat x ∈ X sehingga fk(x) ≤ fk(ˆx) untuk setiap

k ∈ {1,2, . . . , p}. Misalkan q = min{k : fk(x) < fk(ˆx)}. Maka, fk(x) = fk(ˆx) untuk k = 1,2, . . . , q−1 dan fk(x)< fk(ˆx) untuk k =p. Hal itu menyebabkan

f(x)<lex f(ˆx).

17

j < k sebagai kendala.

3.2.1

Algoritma Metode

Lexicographic

Misalkan terdapat p fungsi tujuan, maka algoritma metode lexicographic untuk menyelesaikan masalah program tujuan ganda diberikan sebagai berikut.

Input: Himpunan fisibel

X dan fungsi-fungsi tujuan f

Inisialisasi: Definisikan

X1 := X dan k := 1 Selesaikan optimisasi fungsi tujuan tunggal

min

x∈X_kfk(x) 3.5

While k ≤p

,

do

• Jika fungsi (3.5) memberikan solusi optimal tunggal ˜

xk, BERHENTI. ˜xkadalah solusi optimal dari masalah optimisasi lexicographic.

• Jika solusi fungsi (3.5) tidak terbatas atau “ un-bounded”, BERHENTI. Masalah optimisasi lexico-graphic tidak terbatas.

• Jika k = p, BERHENTI. Himpunan so-lusi optimal masalah optimisasi lexicographic adalah:

x∈ Xp :fp(x) = min x∈Xp

fp(x)

.

Definisikan Xk+1 :=

x∈ Xk:fk(x) = min x∈X_kfk(x)

dan k :=

k+ 1.

End While

Output: Himpunan solusi optimal

lexicographic.

3.3

Pendekatan Numerik

18

meminimumkan biaya ruang kosong pada mobil pengangkut, dan meminimum-kan kerusameminimum-kan barang selama perjalanan. Berikut contoh kasus dan data yang dibangkitkan penulis sebagai parameter model transportasi.

Sebuah perusahaan akan mendistribusikan barang barangsinya dari tiga gudang ke empat pelanggan. Jumlah barang yang tersedia digudang diberikan pada Tabel 3.1 dan jumlah permintaan setiap pelanggan diberikan pada Tabel 1.2.. Pembuat keputusan perusahaan akan menyelesaikan masalah transportasi tersebut, yaitu mengatur strategi pengiriman barang agar ketiga tujuan dapat dioptimalkan. Diberikan data masalah transportasi sebagai berikut:

Tabel 3.1 Jumlah persediaan barang pada gudang i i Si

1 179

2 107

3 221

[image:30.595.269.354.439.532.2]

Jumlah 507

Tabel 3.2 Jumlah permintaan pelangganj j Dj

1 94

2 132

3 157

4 115

[image:30.595.224.400.582.642.2]

Jumlah 498

Tabel 3.3 Biaya penggunaan sebuah mobil dari gudang i ke pelangganj cij 1 2 3 4

1 48,13 88,57 68,64 72,24 2 96,26 98,19 66,76 94,27 3 60,78 19,61 87,02 47,75

[image:31.595.225.401.104.163.2]

19

Tabel 3.4 Biaya kekosongan sebuah mobil dari gudang i ke pelanggan j eij 1 2 3 4

1 0.235 0.233 0.249 0.242 2 0.271 0.245 0.258 0.260 3 0.256 0.256 0.264 0.257

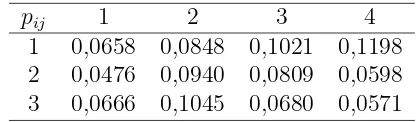
Tabel 3.5 Peluang sebuah barang rusak dari gudang i ke pelanggan j pij 1 2 3 4

1 0,0658 0,0848 0,1021 0,1198 2 0,0476 0,0940 0,0809 0,0598 3 0,0666 0,1045 0,0680 0,0571

minf1(x) = 48,13m11+ 88,57m12+ 68,64m13+ 72,24m14+ 96,26m21 + 98,19m22+ 66,76m23+ 94,27m24+ 60,78m31+ 19,61m32 + 87,02m33+ 47,75m34

minf2(x) = (13m11−x11)(0,235) + (13m12−x12)(0,233) + (13m13−x13)(0,249) + (13m14−x14)(0,242) + (13m21−x21)(0,271) + (13m22−x22)(0,245) + (13m23−x23)(0,258) + (13m24−x24)(0,260) + (13m31−x31)(0,256) + (13m32−x32)(0,256) + (13m33−x33)(0,264) + (13m34−x34)(0,257)

[image:31.595.206.415.197.258.2]

20

kendala:

x11+x12+x13+x14 ≤179

x21+x22+x23+x24 ≤107

x31+x32+x33+x34 ≤221

x11+x21+x31 = 94

x12+x22+x32 = 132

x13+x23+x33 = 157

x14+x24+x34 = 115 0≤(k)(mij)−xij < k ;∀i, j

mij, xij ∈Z +

∪ {0}

Dalam penelitian, penulis berhipotesis bahwa model di atas akan mem-berikan nilai yang optimal dan praktikal bila urutan prioritas fungsi tujuan adalahf1(x),f3(x),f2(x). Preferensi ini diambil berdasarkan konsep utama Ma-salah Transportasi klasik, yaitu meminimumkan biaya transportasi. Sehingga, penulis menjadikan f1(x) sebagai prioritas 1. Kemudian, penulis memandang bahwa kerusakan barang dalam perjalanan harus lebih dipertimbangkan daripada kekosongan mobil karena kerusakan barang sangat berpengaruh pada kepuasan dan kepercayaan pelanggan pada pelayanan perusahaan. Pandangan ini men-jadikanf3(x) sebagai prioritas 2 dan f2(x) sebagai prioritas 3.

Dengan menggunakan metode lexicographic, model transportasi tersebut diselesaikan dengan bantuan software LINGO 13.0. Model transportasi dalam program LINGO 13.0 diberikan pada Lampiran 1. Karena terdapat tiga fungsi tujuan, maka penggunaan metode lexicographic dalam masalah transportasi memberikan solusi sebanyak 3! = 6 urutan seperti pada Tabel 3.6.

[image:33.595.208.413.104.207.2]

21

Tabel 3.6 Nilai optimal setiap fungsi tujuan dari berbagai urutan prioritas Urutan f1(x) f2(x) f3(x)

(1,2,3) 1954,8800 8,7580 41,9372 (1,3,2) 1954,8800 8,7580 41,9372 (2,1,3) 2025,7200 8,3850 41,8360 (2,3,1) 3306,6400 8,3850 34,2674 (3,1,2) 3347,0500 8,9220 33,7398 (3,2,1) 3347,0500 8,9220 33,7398

dalam Babaeiet al.(2009) menggunakan fungsi keanggotaan linier untuk mengek-spresikan derajat optimalitas individu sebagai berikut:

µ(fi(x)) = fi(x)−f ∗ i

f+ i −f

∗ i

; i= 1,2,3 3.6

dengan

f∗

i = min x∈Xfi(x)

f+

i = max_x∈Xfi(x)

Dapat dilihat bahwaf∗

i adalah nilai terbaik (minimal) fungsi tujuani, sebaliknya,

f+

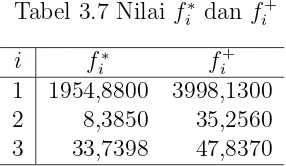
i adalah nilai terburuk fungsi tujuan i. Oleh karena itu, derajat optimalitas individu µ(fi(x)) dapat dipandang sebagai besar penyimpangan nilai fungsi tu-juan i dari nilai fungsi tujuan terbaik. Tabel 3.7 berikut memberikan nilai f∗ i dan f+

i yang digunakan untuk menentukanµ seperti pada Tabel 3.8. Tabel 3.7 Nilaif∗

i dan f + i

i f∗

i f + i 1 1954,8800 3998,1300 2 8,3850 35,2560 3 33,7398 47,8370

[image:33.595.239.382.550.633.2]

[image:34.595.179.443.103.207.2]

ma-22

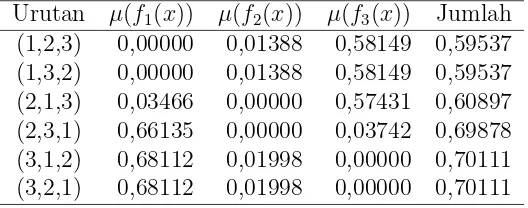
Tabel 3.8 Proporsi penyimpangan nilai fungsi tujuan Urutan µ(f1(x)) µ(f2(x)) µ(f3(x)) Jumlah

(1,2,3) 0,00000 0,01388 0,58149 0,59537 (1,3,2) 0,00000 0,01388 0,58149 0,59537 (2,1,3) 0,03466 0,00000 0,57431 0,60897 (2,3,1) 0,66135 0,00000 0,03742 0,69878 (3,1,2) 0,68112 0,01998 0,00000 0,70111 (3,2,1) 0,68112 0,01998 0,00000 0,70111

salah program tujuan ganda”.

Pada masalah transportasi atau masalah program tujuan ganda lainnya, bila terdapat tiga fungsi tujuan, maka tidak sulit untuk menentukan solusi op-timal lexicographic dengan menguraikan seluruh solusi dari 3!=6 urutan, yaitu dengan cara yang telah dijelaskan sebelumnya. Akan tetapi, bila terdapat lebih dari tiga fungsi tujuan, atau p > 3, maka akan lebih sulit untuk menguraikan seluruh solusi dari p! urutan. Namun demikian, pendekatan tetap dapat di-lakukan, yaitu dengan menggunakan preferensi pembuat keputusan. Pembuat keputusan dapat menentukan urutan prioritas fungsi tujuan dengan memband-ingkan tingkat kepentingan antar fungsi tujuan.

Urutan prioritas fungsi tujuan dapat ditentukan dengan menggunakan An-alytic Hierarchy Process sebagaimana telah dipaparkan oleh Saaty (1990), yaitu dengan menentukan bobot setiap fungsi tujuan. Pada dasarnya, Saaty menggu-nakan matriks perbandinganA untuk membandingkan setiap atribut (dalam hal ini fungsi tujuan) dengan persamaan berikut:

AW =pW

        w1 w1 w1

w2 · · ·

w1

wp

w2

w1

w2

w2 · · ·

w2 wp ... ... ... wp w1 wp

w2 · · ·

23

wi = bobot fungsi tujuan i

p = banyak fungsi tujuan

Langkah awal untuk menentukan bobot adalah menentukan nilai setiap unsur matriks A′

berdasarkan preferensi pembuat keputusan. Unsur matriks A′ ditentukan dengan membandingkan setiap fungsi tujuan dengan skala standar sebagai berikut:

Tabel 3.9 Interpretasi skala standar Analytic Hierarchy Process

aij Interpretasi

1 Bila fungsi tujuan i sama pentingnya dengan fungsi tujuan j

3 Bila fungsi tujuan i sedikit lebih penting daripada fungsi tujuan j

5 Bila fungsi tujuan i lebih penting daripada fungsi tujuan j

7 Bila fungsi tujuan i sangat lebih penting daripada fungsi tujuan j

9 Bila fungsi tujuan i mutlak lebih penting daripada fungsi tujuanj

Saaty menerangkan bahwa A′

harus konsisten dengan hirarki matriks A

seperti yang diuraikan pada persamaan (3.7), yaitu memenuhi persamaan berikut:

ajk =

aik

aij

; i, j, k= 1,2, ..., p 3.8

Untuk menguji konsistensi matriks A′

, digunakan indeks konsistensi (CI) dan rasio konsistensi (CR) yang akan dijelaskan secara prosedural. Oleh karena itu, penulis mengasumsikan nilai setiap unsur matriksA′

sebagai berikut:

A′ = 

   

1 9 3 1 9 1

1 5 1 3 5 1

     3.9

Diperoleh nilai eigen matriks A′

sebagai berikut:

λ1 = 3,02906

λ2 =−0,0145319 + 0,296353i

24

tensi (=CI)

CI = λmax−p

p−1 = 3,02906−3

3−1 = 0,02906

2 = 0,01453

Dengan menggunakan nilai CI di atas, diperoleh rasio konsistensi (CR) sebagai berikut:

CR= CI

RI

= 0,01453 0,58 = 0,02505

KarenaCR <0,1, maka dapat dikatakan bahwa matriks perbandingan A

konsisten. Dengan menggunakanLeast Square Method, akan ditentukan nilaiw1,

w2, dan w3.

minz = 3 X

i=1 3 X

j=1

(aijwj−wi) 2

3.10

kendala:

w1+w2+w3 = 1

Model di atas meminimumkan penyimpangan unsur matriks A′

yang terdefin-isi pada persamaan (3.7) dengan unsur matriks A yang diasumsikan pembuat keputusan (preferensi) seperti yang diberikan pada persamaan (3.9). Kendala

25

atas dapat diuraikan menjadi:

minz =(w1−w1) 2

+ (9w2−w1) 2

+ (3w3−w1) 2

+ (1

9w1−w2) 2

+ (w2−w2) 2

+ (1

5w3−w2) 2

+ (1

3w1−w3) 2

+ (5w2−w3) 2

+ (w3−w3) 2

kendala:

w1+w2+w3 = 1

Dengan menggunakan bantuansoftware LINGO 13.0, diperoleh bobot-bobot se-bagai berikut:

w1 = 0,68798

w2 = 0,06985

w3 = 0,24217

Bab 4

KESIMPULAN DAN SARAN

4.1

Kesimpulan

Berdasarkan hasil penelitian yang telah dibahas pada bab sebelumnya, dapat diambil beberapa kesimpulan sebagai berikut:

1. Dari pendekatan numerik, diketahui bahwa tidak terdapat urutan tertentu yang secara umum memberikan solusi optimal pada masalah program tujuan ganda.

2. Pada kondisi tertentu, Metode Lexicographic tidak dapat digunakan untuk menyelesaikan masalah transportasi atau masalah program tujuan ganda lain-nya, karena bila pada suatu iterasi tidak terdapat solusi optimal, maka fungsi tujuan berikutnya tidak dapat dioptimalkan. Dengan kata lain, fungsi tujuan tersebut sama sekali tidak diperhitungkan dalam masalah.

3. PenggunaanAnalytic Hierarchy ProcessdanLeast Square Methoduntuk menen-tukan prioritas fungsi tujuan, tidak menjamin solusi paling optimal dari p! urutan prioritas yang dapat dibentuk dari p fungsi tujuan.

4.2

Saran

Berdasarkan proses dan hasil penelitian, penulis menyampaikan beberapa saran sebagai berikut:

1. Peneliti selanjutnya diharapkan meneliti masalah program tujuan ganda yang menggunakan lebih dari tiga fungsi tujuan.

27

3. Sebelum menyelesaikan masalah transportasi, peneliti selanjutnya perlu men-ganalisa kembali setiap fungsi tujuan yang digunakan agar seluruh fungsi tu-juan dapat dioptimalkan.

28

DAFTAR PUSTAKA

Caramia,M. dan Dell’Olmo, P..2008.Multi-objective Management in Freight Lo-gistics Increasing Capacity, Service Level and Safety with Optimization Al-gorithms. Springer

Djelatova, Mariana.2001.A Lexicographic Algorithm Solving a Problem of a Mul-tiobjective Flow in a Network.Sofia:Institute of Information Technologies Ehrgott, Mathiass.2005.Multicriteria Optimization.Auckland:Springer

Ehrgott, Mathiass.2007.Multiobjective Linear Programming.Han sur Lesse: In-ternational Doctoral School Algorithmic Decision

Gupta, Prem Kumar., Hira, D.S..2007.Operations Research.India: S.Chand Gamal, M.D.H..2007.Program Linier dan Integer.Pekanbaru: Pusat

Pengemban-gan Pendidikan Universitas Riau

Isermann, H.. 1982. OR Spektrum—Linear Lexicographic Optimization. Springer-Verlag

Lewis, Catherine.2008.Linear Programming: Theory and Its Applications

Mandler, Michael.2012.The Lexicographic Method in Preference Theory.University of London

Marler, R. Timothy dan Arora, Jasbir S..2010.The Weighted Sum Method for Multiobjective Optimization:new insights.Springer-Verlag

Nunkeaw, Wuttinan and Phruksaphanrat, Busaba.2009.A Multiobjective Pro-gramming for Transportation Problem with Consideration of both Depot to Customer and Customer to Customer Relationships

Ojha, Dr.A.K.,Biswal, K.K..2009.Lexicographic Multi-objective Geometric Pro-gramming Problems.India:International Journal of Computer Science Is-sues, Vol. 6, No. 2

Rueda, A.J..1987.A Lexicographic Method for Multiple Objective Binary Linear Programming.Springer Berlin Heidelberg

Siang, Jong Jek.2011.Riset Operasi dalam Pendekatan Algoritmis.Yogyakarta: C.V ANDI OFFSET

Siagian, P..1987.Penelitian Operasional.Jakarta:UI-Press

29

Lampiran 1. Program Lingo 13.0 pada Masalah Transportasi

MODEL:

SETS:

GUDANG: STOK;

PELANGGAN: PERMINTAAN;

LINKS(GUDANG,PELANGGAN): B_MOBIL, PELUANG, MOBIL, JUMLAH, HARGA_KOSONG; ENDSETS

! Datanya diberikan sebagai berikut:; DATA:

!Anggota Himpunan; GUDANG = G1..G3; PELANGGAN = P1..P4;

!Nilai-nilai;

STOK = 179 107 221;

PERMINTAAN = 94 132 157 115;

B_MOBIL = 48.13 88.57 68.64 72.24 96.26 98.19 66.76 94.27

60.78 19.61 87.02 47.75;

PELUANG = 0.0658 0.0848 0.1021 0.1198 0.0476 0.0940 0.0809 0.0598

0.0666 0.1045 0.0680 0.0571;

HARGA_KOSONG = 0.235 0.233 0.249 0.242 0.271 0.245 0.258 0.260

0.256 0.256 0.264 0.257; ENDDATA

!======================================================;

!FUNGSI TUJUAN1 : Meminimumkan Biaya Penggunaan Mobil;

MIN = @SUM(LINKS(I,J): @IF(JUMLAH(I,J) #GE# 0,1,0)*MOBIL(I,J)* B_MOBIL(I,J));

!FUNGSI TUJUAN2 : Meminimumkan Biaya Ruang Kosong pada Mobil

MIN = @SUM(LINKS(I,J): (13*MOBIL(I,J) - JUMLAH(I,J))*HARGA_KOSONG(I,J));

!FUNGSI TUJUAN3 : Meminimumkan Jumlah Barang Rusak Selama Perjalanan MIN = @SUM(LINKS(I,J): PELUANG(I,J)*JUMLAH(I,J));

30

!Kendala Stok/Kapasitas; @FOR(GUDANG(I):

@SUM(PELANGGAN(J):JUMLAH(I,J)) <= STOK(I));

@FOR(LINKS(I,J):

13*MOBIL(I,J) - JUMLAH(I,J) >= 0);

@FOR(LINKS(I,J):

13*MOBIL(I,J) - JUMLAH(I,J) < 13);

@FOR(LINKS: @GIN(MOBIL)); @FOR(LINKS: @GIN(JUMLAH));

!KENDALA FUNGSI TUJUAN3 : Jumlah Barang Rusak Selama Perjalanan @SUM(LINKS(I,J): PELUANG(I,J)*JUMLAH(I,J))=...;

!KENDALA FUNGSI TUJUAN2 : Biaya Ruang Kosong pada Mobil

@SUM(LINKS(I,J): (13*MOBIL(I,J) - JUMLAH(I,J))*HARGA_KOSONG(I,J))=...;

!KENDALA FUNGSI TUJUAN1 : Biaya Penggunaan Mobil

@SUM(LINKS(I,J): @IF(JUMLAH(I,J) #GE# 0,1,0)*MOBIL(I,J)* B_MOBIL(I,J)) = ...;

31

Lampiran 2. Hasil perhitungan urutan prioritas fungsi tujuan: f1,f2, f3.

Tahap 1.

Meminimumkan f1(x)

f1(x) = 1954,880

mij 1 2 3 4

1 8 0 4 2

2 0 0 9 0

3 0 11 0 7

xij 1 2 3 4

1 94 0 50 26

2 0 0 107 0

3 0 132 0 89

Tahap 2.

Meminimumkan f2(x)

f1(x) = 1954,8800

f2(x) = 8,7580

mij 1 2 3 4

1 8 0 4 2

2 0 0 9 0

3 0 11 0 7

xij 1 2 3 4

1 94 0 50 26

2 0 0 107 0

3 0 132 0 89

Tahap 3.

Meminimumkan f3(x)

f1(x) = 1954,8800

f2(x) = 8,7580

f3(x) = 41,9372

mij 1 2 3 4

1 8 0 4 2

2 0 0 9 0

3 0 11 0 7

xij 1 2 3 4

1 94 0 50 26

2 0 0 107 0

32

Lampiran 3. Hasil perhitungan urutan prioritas fungsi tujuan: f1,f3, f2.

Tahap 1.

Meminimumkan f1(x)

f1(x) = 1954,880

mij 1 2 3 4

1 8 0 4 2

2 0 0 9 0

3 0 11 0 7

xij 1 2 3 4

1 94 0 50 26

2 0 0 107 0

3 0 132 0 89

Tahap 2.

Meminimumkan f3(x)

f1(x) = 1954,8800

f3(x) = 41,9372

mij 1 2 3 4

1 8 0 4 2

2 0 0 9 0

3 0 11 0 7

xij 1 2 3 4

1 94 0 50 26

2 0 0 107 0

3 0 132 0 89

Tahap 3.

Meminimumkan f2(x)

f1(x) = 1954,8800

f3(x) = 41,9372

f2(x) = 8,7580

mij 1 2 3 4

1 8 0 4 2

2 0 0 9 0

3 0 11 0 7

xij 1 2 3 4

1 94 0 50 26

2 0 0 107 0

33

Lampiran 4. Hasil perhitungan urutan prioritas fungsi tujuan: f2,f1, f3.

Tahap 1.

Meminimumkan f2(x)

f2(x) = 8,3850

mij 1 2 3 4

1 3 1 6 6

2 4 0 3 1

3 1 10 4 2

xij 1 2 3 4

1 29 2 66 76

2 52 0 39 13

3 13 130 52 26

Tahap 2.

Meminimumkan f1(x)

f2x) = 8,3850

f1(x) = 2025,720

mij 1 2 3 4

1 8 1 5 2

2 0 0 8 0

3 0 10 0 7

xij 1 2 3 4

1 94 2 53 24

2 0 0 104 0

3 0 130 0 91

Tahap 3.

Meminimumkan f3(x)

f2x) = 8,3850

f1(x) = 2025,720

f3(x) = 41,8360

mij 1 2 3 4

1 8 1 5 2

2 0 0 8 0

3 0 10 0 7

xij 1 2 3 4

1 94 2 53 24

2 0 0 104 0

34

Lampiran 5. Hasil perhitungan urutan prioritas fungsi tujuan: f2,f3, f1.

Tahap 1.

Meminimumkan f2(x)

f2(x) = 8,3850

mij 1 2 3 4

1 3 1 6 6

2 4 0 3 1

3 1 10 4 2

xij 1 2 3 4

1 29 2 66 76

2 52 0 39 13

3 13 130 52 26

Tahap 2.

Meminimumkan f3(x)

f2x) = 8,3850

f3(x) = 34,26740

mij 1 2 3 4

1 3 11 1 1

2 5 0 0 3

3 0 0 12 5

xij 1 2 3 4

1 29 132 1 11

2 65 0 0 39

3 0 0 156 65

Tahap 3.

Meminimumkan f1(x)

f2x) = 8,3850

f3(x) = 34,26740

f1(x) = 3306,640

mij 1 2 3 4

1 3 11 1 1

2 5 0 0 3

3 0 0 12 5

xij 1 2 3 4

1 29 132 1 11

2 65 0 0 39

35

Lampiran 6. Hasil perhitungan urutan prioritas fungsi tujuan: f3,f1, f2.

Tahap 1.

Meminimumkan f3(x)

f3(x) = 33,7398

mij 1 2 3 4

1 3 11 1 1

2 5 1 1 4

3 1 1 13 5

xij 1 2 3 4

1 38 132 0 0

2 56 0 0 51

3 0 0 157 64

Tahap 2.

Meminimumkan f1(x)

f3(x) = 33,7398

f1(x) = 3347,0500

mij 1 2 3 4

1 3 11 0 0

2 5 0 0 4

3 0 0 13 5

xij 1 2 3 4

1 38 132 0 0

2 56 0 0 51

3 0 0 157 64

Tahap 3.

Meminimumkan f2(x)

f3(x) = 33,7398

f1(x) = 3347,0500

f2(x) = 8,9220

mij 1 2 3 4

1 3 11 0 0

2 5 0 0 4

3 0 0 13 5

xij 1 2 3 4

1 38 132 0 0

2 56 0 0 51

36

Lampiran 7. Hasil perhitungan urutan prioritas fungsi tujuan: f3,f2, f1.

Tahap 1.

Meminimumkan f3(x)

f3(x) = 33,7398

mij 1 2 3 4

1 3 11 1 1

2 5 1 1 4

3 1 1 13 5

xij 1 2 3 4

1 38 132 0 0

2 56 0 0 51

3 0 0 157 64

Tahap 2.

Meminimumkan f2(x)

f3(x) = 33,7398

f2(x) = 8,9220

mij 1 2 3 4

1 3 11 0 0

2 5 0 0 4

3 0 0 13 5

xij 1 2 3 4

1 38 132 0 0

2 56 0 0 51

3 0 0 157 64

Tahap 3.

Meminimumkan f1(x)

f3(x) = 33,7398

f2(x) = 8,9220

f1(x) = 3347,0500

mij 1 2 3 4

1 3 11 0 0

2 5 0 0 4

3 0 0 13 5

xij 1 2 3 4

1 38 132 0 0

2 56 0 0 51