OPTIMASI BERSYARAT DENGAN KENDALA PERSAMAAN
MENGGUNAKAN MULTIPLIER LAGRANGE SERTA
PENERAPANNYA
SKRIPSI
SANDRA RIZAL
060803016
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
OPTIMASI BERSYARAT DENGAN KENDALA PERSAMAAN
MENGGUNAKAN MULTIPLIER LAGRANGE SERTA
PENERAPANNYA
SKRIPSI
Diajukan untuk memenuhi syarat mendapat gelar Sarjana Sains
SANDRA RIZAL
060803016
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
PERSETUJUAN
Judul : OPTIMASI BERSYARAT DENGAN KENDALA PERSAMAAN MENGGUNAKAN MULTIPLIER
LAGRANGE SERTA PENERAPANNYA
Kategori : SKRIPSI
Nama : SANDRA RIZAL
Nomor Induk Mahasiswa : 060803016
Program Studi : SARJANA (SI) MATEMATIKA Departemen : MATEMATIKA
Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA
Diluluskan di Medan, Juni 2010
Komisi Pembimbing :
Pembimbing 2 Pembimbing 1
Drs. Henry Rani Sitepu, M.Si. Prof. Dr. Herman Mawengkang NIP. 195303031983031002 NIP. 194611281974031001
Diketahui/Disetujui oleh
Departemen Matematika FMIPA USU Ketua,
Dr. Saib Suwilo, M.Sc. NIP: 196401091988031004
PERNYATAAN
OPTIMASI BERSYARAT DENGAN KENDALA PERSAMAAN MENGGUNAKAN MULTIPLIER LAGRANGE SERTA
PENERAPANNYA
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, Juni 2010
PENGHARGAAN
Puji dan syukur penulis panjatkan ke hadirat Allah SWT Yang Maha Esa dan Kuasa atas limpahan rahmat dan karunia-Nya sehingga skripsi ini dapat diselesaikan dalam waktu yang telah ditetapkan.
Dalam kesempatan ini, penulis ingin mengucapkan terima kasih yang sebesar-besarnya kepada semua pihak yang telah membantu dan membimbing penulis dalam penyusunan skripsi ini, ucapan terima kasih penulis sampaikan kepada :
1. Bapak Prof. Dr. Herman Mawengkang selaku pembimbing I dan Bapak Drs. Henry Rani Sitepu, M.Si selaku pembimbing II yang telah memberikan banyak bimbingan dan penuh kepercayaan kepada saya untuk menyempurnakan tugas akhir ini.
2. Bapak Drs. H. Haluddin Panjaitan dan Bapak Drs, Ramli Barus, M.Si selaku komisi penguji atas masukan dan saran yang telah diberikan demi perbaikan skripsi ini.
3. Bapak Dr. Saib Suwilo M.Sc dan Bapak Drs. Henry Rani Sitepu, M.Si selaku ketua dan Sekretaris Departemen Matematika FMIPA USU.
4. Dekan dan Pembantu Dekan FMIPA USU.
5. Semua Dosen dan Pegawai pada Departemen Matematika FMIPA USU. 6. Ayahanda tercinta Abdurrahman dan Ibunda Hamdiah yang sangat saya kasihi
dan sayangi atas doa dan dukungan moril maupun materil yang diberikan selama ini.
7. Saudara kandung Faisal, Andi, Rina, Putri, Faiza yang selalu memberikan motivasi, saran dan bantuannya.
8. Rekan-rekan kuliah matematika serta semua stambuk 2006 yang tidak terlupakan dukungan dan bantuannya.
9. Semua pihak yang tidak dapat penulis sebutkan satu persatu.
Penulis juga menyadari masih banyak kekurangan dalam skripsi ini, baik dalam teori maupun penulisannya. Oleh karena itu, penulis mengharapkan saran dari pembaca demi perbaikan bagi penulis, semoga segala kebaikan dalam bentuk bantuan yang telah diberikan mendapat balasan dari Yang Maha Kuasa.
Akhir kata, kiranya skripsi ini dapat bermanfaat bagi pihak pembaca.
Hormat saya, Penulis
ABSTRAK
CONDITIONAL OPTIMIZATION WITH THE EQUATION CONSTRAINT USING MULTIPLIER LAGRANGE
AND ALSO Its APPLYING
ABST`RACT
The aim of this paper is to alter the problem form the optimization burdened to become the problem optimization without constraint, and also its applying determination is economic area modeled in the form of optimization. To facilitate the optimization have constraint to or used by conditional of function Lagrange. Stage Steps determine the optimum value use the multiplier Lagrange that is with forming a new function representing quantifying from function which will be optimum added by result of times rill of coefficient Lagrange λ with the its constraint function.
DAFTAR ISI
Halaman
Persetujuan ii
Pernyataan iii
Penghargaan iv
Abstrak v
Abstract vi
Daftar Isi vii
Daftar Tabel viii
Daftar Gambar ix
Bab 1 Pendahuluan 1
1.1Latar Belakang 1
1.2Perumusan Masalah 3
1.3Batasan Masalah 3
1.4Tinjauan Pustaka 4
1.5Tujuan Penelitian 6
1.6Manfaat Penelitian 7
1.7Metode Penelitian 7
Bab 2 Landasan Teori 9
2.1 Optimasi 9
2.1.1 Optimasi Tak Bersyarat 9
2.1.2 Optimasi Bersyarat 10
2.2 Metode Pengali Lagrange 13
2.3 Matrik Hessian 14
2.4 Matrik Definit Positif 17
2.5 Maksimum dan Minimum 19
2.6 Fungsi Utilitas Marginal 22
2.7 Produk Marginal 24
Bab 3 Pembahasan 26
3.1 Optimasi Dengan Kendala Persamaan Menggunakan Multiplier
Lagrange 26
3.2 Utilitas Marjinal Parsial Serta Keseimbangan Konsumsi 29 3.3 Produk Marjinal Parsial Dan Keseimbangan Produksi. 33
Bab 4 Kesimpulan dan Saran
4.1 Kesimpulan 36
4.2 Saran 36
DAFTAR TABEL
Tabel Halaman
DAFTAR GAMBAR
Gambar Halaman
1. Gambar. 2.1 grafik dari + + + 16
2. Gambar 2.2. Grafik 1 20
3. Gambar 2.3. Grafik nilai maksimum dan minimum 21 4. Gambar 2.4. Bentuk kurva utilitas 22 5. Gambar 2.5 Bentuk kurva fungsi U = f(Q) = 90Q – 5Q2dan 23
ABSTRAK
Tujuan dari tulisan ini adalah untuk mengubah persoalan bentuk optimasi terkendala menjadi persoalan optimasi tanpa kendala, serta penentuan penerapannya dibidang ekonomi dimodelkan dalam bentuk optimasi. Untuk memudahkan optimasi berkendala atau bersyarat digunakan fungsi lagrange. Langkah-langkah menentukan nilai optimum menggunakan multiplier lagrange yaitu dengan membentuk sebuah fungsi baru yang merupakan penjumlahan dari fungsi yang hendak dioptimumkan ditambah hasil kali pengganda lagrange λ dengan fungsi kendalanya.
CONDITIONAL OPTIMIZATION WITH THE EQUATION CONSTRAINT USING MULTIPLIER LAGRANGE
AND ALSO Its APPLYING
ABST`RACT
BAB 1
PENDAHULUAN
1.1Latar Belakang
Dalam kehidupan sehari-hari baik disadari maupun tidak, sebenarnya orang selalu melakukan optimasi untuk memenuhi kebutuhannya. Tetapi optimasi yang dilakukan masyarakat awam lebih banyak dilandasi oleh intuisi daripada teori optimasi. Dalam masalah optimasi terdapat dua bentuk optimasi yaitu fungsi optimasi tak bersyarat dan fungsi optimasi bersyarat. Banyak aplikasi dari pemodelan matematika dalam optimasi fungsi yang mensyaratkan beberapa kondisi atau syarat untuk diperoleh suatu solusi optimal. Syarat ini yang mengoptimumkan fungsi tujuan. Persoalan dengan model tersebut dinamakan optimasi bersyarat. Optimasi merupakan masalah yang berhubungan dengan keputusan yang terbaik, maksimum, minimum dan memberikan cara penentuan solusi yang memuaskan.
Multiplier Lagrange adalah sebuah konsep populer dalam menangani permasalahan ini untuk program-program non-linear. Sesuai namanya, konsep ini dikemukakan oleh Joseph Louis Langrange (1736-1813). Teori ini dapat digunakan untuk menangani optimalitas dari permasalahan program non-linear.
dioptimumkan menghadapi suatu kendala (constraint). Kasus optimasi bersyarat semacam ini banyak dijumpai dalam bidang ekonomi, misalnya seseorang hendak memaksimumkan utilitas. Fungsi utilitas ialah fungsi yang menjelaskan besarnya utilitas (kepuasan, kegunaan) yang diperoleh seseorang dari mengkonsumsi suatu barang atau jasa.
Pada umumnya semakin banyak jumlah suatu barang dikonsumsi semakin besar utilitas yang diperoleh, kemudian mencapai titik puncaknya (titik jenuh) pada jumlah konsumsi tertentu, sesudah itu justru menjadi berkurang atau bahkan negatif jika jumlah barang yang dikonsumsi terus-menerus ditambah. Utilitas total merupakan fungsi dari jumlah barang yang dikonsumsi. Persamaan utilitas total (total utility, U)
dari mengkonsumsi suatu jenis barang berupa fungsi kuadrat parabolik, dengan kurva berbentuk parabola terbuka ke bawah.
Utilitas marginal (marginal utility, MU) ialah utilitas tambahan yang diperoleh dari setiap satu unit barang yang dikonsumsi. Secara matematik, fungsi utilitas marginal merupakan derivatif pertama dari fungsi utilitas total. Jika fungsi utilitas total dinyatakan dengan U = f (Q) dimana U melambangkan utilitas total dan Q
jumlah barang yang dikonsumsi atau tingkat kepuasannya tetapi terikat pada fungsi pendapatan, atau sebuah perusahaan yang ingin memaksimumkan labanya namun terikat pada fungsi produksi. Maka suatu cara yang dapat digunakan untuk menentukan titik ekstrim dari suatu fungsi yang bersyarat adalah dengan menggunakan Pengali Lagrange, yakni dengan cara membentuk sebuah fungsi baru yang merupakan penjumlahan dari fungsi yang hendak dioptimumkan di tambah hasil kali pengali Lagrangeλ dengan fungsi kendalanya.
Berdasarkan uraian optimasi diatas penulis mencoba menuangkannya yang hasilnya akan disajikan dalam bentuk karya ilmiah yang berjudul “Optimasi Bersyarat dengan Kendala Persamaan Menggunakan Multiplier Langrange
1.2 Perumusan Masalah
Metode Multiplier Lagrange digunakan untuk menentukan persoalan optimasi dengan kendala menjadi optimasi tanpa kendala. Selanjutnya menerapkan metode tersebut untuk menyelesaikan masalah optimasi bersyarat yang dimodelkan dalam bentuk optimasi didalam bidang ekonomi.
Bentuk umum dari optimasi fungsi dengan kendala adalah sebagai berikut: Tentukan nilai dari variabel keputusan (nilai ekstrim) x = {x1, x2, …, xn} yang
memaksimumkan (meminimumkan) fungsi dari permasalahan:
Maksimumkan (Minimumkan) z = f(x)
Dengan kendala g1(x)(≤, =, ≥) b1 g2(x)(≤, =, ≥) b2 ………. gm(x)(≤, =, ≥) bm
dimana:
f(x) merupakan fungsi tujuan (objective function), dan
gm(x)(≤, =, ≥) bm merupakan fungsi kendala.
Untuk menentukan nilai ekstrim dari persoalan tersebut digunakan pangali λi
dengan fungsi kendala ke i dan persamaan fungsi Lagrangenya:
L(x, λ) = f(x) +
m
i1
λigi (x)
1.3 Batasan Masalah
Dalam tulisan ini penulis hanya membatasi permasalahannya pada pembahasan tentang masalah optimasi bersyarat dengan metode Lagrange. Metode tersebut digunakan untuk menentukan masalah optimasi dengan kendala menjadi tanpa kendala dan menerapkan metode tersebut untuk menyelesaikan masalah optimasi bersyarat yang dimodelkan dalam bentuk optimasi didalam bidang ekonomi.
1.4 Tinjauan Pustaka
Luknanto (2000), dalam bukunya yang berjudul “Pengantar Optimasi Non-Linier”.
Menyatakan bahwa optimasi multi-variabel dengan kendala persamaan mempunyai bentuk umum sebagai berikut:
Minimumkan f = f(x) (1) Kendala gj(x) = 0 untuk j=1,2,…,m (2)
Metode pengali Lagrange dapat dipakai untuk menyelesaikan optimasi yang dirumuskan persamaan (1) dan (2). Metode ini dimulai dengan pembentukan fungsi Lagrange yang didefinisikan sebagai:
L(x, λ) = f(x) +
m
i1
λigi (x) (3)
Teorema:
Syarat perlu bagi sebuah fungsi f(x) dengan kendala gj(x) = 0, untuk j = 1,2,…,m agar
mempunyai minimum relatif pada titik X* adalah derivasi parsial pertama dari fungsi
Lagrangenya yang didefinisikan sebagai L(x, λ) = ( x1,x2,…,xn, 1, 2,..., m ) terhadap setiap argumennya mempunyai nilai nol.
Teorema:
Syarat perlu bagi sebuah fungsi f(x) agar mempunyai minimum atau maksimum relatif pada titik X* adalah jika fungsi kuadrat, Q yang didefinisikan sebagai:
n i n j j i j i dx dx x x L Q 1 1 2 (4)
Dievaluasikan pada X = X* harus definit positif (atau negatif) untuk setiap nilai dx
yang memenuhi semua kendala.
Bronson and wospakrik, (1988) dalam bukunya yang berjudul “Teori dan soal-soal operations research”. Menyatakan bahwa bentuk umum fungsi lagrange:
L(x, λ) = f(x) +
m
i1
λigi (x) (1)
) ,..., 2 , 1 ( , 0 ) ,.., 2 , 1 ( , 0 m i L n j x l i i (2)
Dengan x = {x1, x2, …, xn} maka bentuk standar untuk program non linear
dengan kendala kesamaan adalah Maksimumkan z = f(x)
Dengan kendala g1(x) = 0
g2(x) = 0
gm(x) = 0
Barnet, Ziegler, and Byleen (1987), Dalam bukunya yang berjudul “Calculus
For Business Economics, Life, and Social Sciences”. Menyatakan bahwa adapun langkah – langkah Metode multiplier Lagrange sebagai berikut :
Langkah 1. Tentukan masalah
Maksimum (minimum) z = f(x, y)
Dengan kendala g(x, y) = 0
Langkah 2. Tentukan fungsi F:
F(x, y, λ) = f(x, y) + λg(x, y)
Langkah 3. Tentukan point dari F , masalah sistem Fx (x, y, λ) = 0
Fy (x, y, λ) = 0
F λ (x, y, λ) = 0
Langkah 4. Jika (x0, y0, λ0 ) merupakan point dari F, di asumsikan bahwa (x0, y0)
selalu diberikan solusi permasalahannya. Jika F lebih dari satu kriktikal point, dengan evaluasi z = f(x,y) di (x0, y0) untuk setiap
kritikal point (x0, y0, λ0 ) dari F. Untuk setiap masalah, dengan
asumsi untuk maksimum dari f(x,y), dengan kendala g(x,y) = 0, dan minimumnya dari f(x,y) dengan kendala g(x,y) = 0.
Dumairy (1996), dalam bukunya yang berjudul “Matematika Terapan Untuk Bisnis dan Ekonomi” menyatakan bahwa: Fungsi utilitas ialah fungsi yang menjelaskan besarnya utilitas (kepuasan, kegunaan) yang diperoleh seseorang dari mengkonsumsi suatu barang atau jasa. Pada umumnya semakin banyak jumlah suatu barang dikonsumsi semakin besar utilitas yang diperoleh, kemudian mencapai titik puncaknya (titik jenuh) pada jumlah konsumsi tertentu, sesudah itu justru menjadi berkurang atau bahkan negatif jika jumlah barang yang dikonsumsi terus menerus ditambah. Utilitas total merupakan fungsi dari jumlah barang yang dikonsumsi. Persamaan utilitas total (total utility, U) dari mengkonsumsi suatu jenis barang berupa fungsi kuadrat parabolik, dengan kurva berbentuk parabola terbuka ke bawah. Utilitas marginal (marginal utility, MU) ialah utilitas tambahan yang diperoleh dari setiap satu unit barang yang dikonsumsi. Secara matematik, fungsi utilitas marginal merupakan derivatif pertama dari fungsi utilitas total. Jika fungsi utilitas total dinyatakan dengan
U = f (Q) dimana U melambangkan utilitas total dan Q jumlah barang yang dikonsumsi, maka utilitas marjinalnya : MU =U’ = dQ / dU
1.5 Tujuan Penelitian
Tujuan dari penelitian ini adalah sebagai berikut :
1. Mengubah persoalan bentuk optimasi dengan kendala menjadi persoalan optimasi tanpa kendala, serta penentuan penerapannya dibidang ekonomi dimodelkan dalam bentuk optimasi.
2. Untuk memudahkan optimasi berkendala atau bersyarat digunakan fungsi Lagrange.
1.6 Manfaat Penelitian
Manfaat dari penelitian ini adalah sebagai berikut.
mengikuti perkuliahan serta mampu menerapkan ilmunya dalam kehidupan nyata.
2. Menambah wawasan penulis tentang metode Multiplier Lagrange, serta dapat mencari solusi Optimal dari kasus yang berhubungan dengan Multiplier Lagrange.
b. Bagi Departemen
1. Dapat dijadikan sebagai bahan studi kasus bagi pembaca dan acuan bagi mahasiswa.
2. Dapat digunakan sebagai tambahan informasi dan referensi bacaan untuk mahasiswa matematika, terlebih bagi mahasiswa yang hendak melakukan penelitian serupa.
1.7 Metode Penelitian
Metode penelitian dalam tulisan ini dilakukan dengan melakukan penelitian melalui tinjauan pustaka. Adapun langkah – langkahnya adalah:
1. Membuat langkah – langkah menentukan nilai ekstrim suatu fungsi dengan kendala fungsi lain menggunakan Multiplier Lagrange.
Maksimumkan (Minimumkan) z = f(x), x = {x1, x2, …, xn}
Dengan kendala g1(x) (≤, =, ≥) = b1 g2(x) (≤, =, ≥) = b2 …
gm(x)(≤, =, ≥) bm
2. Fungsi baru Lagrange yang telah dimodifikasi menjadi
L(x, λ) = f(x) +
m
i1
λigi (x)
3. Menentukan syarat perlu untuk mendapatkan titik ekstrim
=
4. Mencari semua solusi syarat cukup untuk ekstrim relatif
Syarat cukup pada kasus ini juga diekspresikan dalam bentuk determinan. Posisi determinan matriks Hessian pada optimasi dengan kendala persamaan digantikan dengan apa yang disebut Bordered Hessian. Syarat cukup ini diterapkan setelah syarat perlu dipenuhi dan digunakan untuk mengetahui prilaku dari L(x , λ ) pada nilai kritisnya.
5. Menentukan solusi optimal dari persoalan optimasi bersyarat menggunakan Multiplier Lagrange serta penerapannya didalam bidang ekonomi.
6. Menarik beberapa kesimpulan
Yaitu menyimpulkan hasil dan informasi dari penyelesaian permasalahan optimasi yang telah diselesaikan.
BAB 2
LANDASAN TEORI
Pada bab ini akan dibahas beberapa pengertian dari optimasi bersyarat dengan kendala persamaan menggunakan multiplier lagrange serta penerapannya yang akan digunakan sebagai landasan berfikir dalam melakukan penelitian ini, yang akan dipergunakan pada bab pembahasan.
2.1 Optimasi
Suatu permasalahan optimasi disebut nonlinear jika fungsi tujuan dan kendalanya mempunyai bentuk nonlinear pada salah satu atau keduanya. Optimasi merupakan masalah yang berhubungan dengan keputusan yang terbaik, maksimum, minimum dan memberikan cara penentuan solusi yang memuaskan. Salah satu bentuk umum masalah optimasi adalah untuk menentukan bersyarat x = (x1, x2, … , xn) sehingga
mencapai tujuannya untuk memaksimumkan/ meminimumkan f(x) dengan kendala
gn(x) ≥ 0 dan untuk x ≥ 0 . dengan f(x) dan gn(x) adalah fungsi yang diketahui dengan n variabel keputusan.
Dalam masalah optimasi terdapat dua bentuk masalah optimasi yaitu optimasi bersyarat dan optimasi tak bersyarat.
2.1.1 Optimasi Tak Bersyarat
Optimasi tak bersyarat merupakan masalah optimasi yang tidak memiliki syarat atau tidak memiliki batasan- batasan , sehingga untuk x = (x1, x2, … , xn) mempunyai fungsi
Syarat perlu dan syarat cukup untuk suatu penyelesaian x = x* merupakan
penyelesian optimal saat f(x) merupakan fungsi yang dapat diturunkan adalah
pada x = x*, untuk j = 1,2, … , n. Dimana f(x) dengan kondisi ini juga mencukupi, sehingga mencari solusi untuk x* tereduksi menjadi penyelesaian dari sistem n
persamaan yang diperoleh dengan n turunan parsial sama dengan nol.
2.1.2 Optimasi Bersyarat
Optimasi bersyarat adalah masalah optimasi yang memiliki syarat atau memiliki batasan - batasan yang merupakan masalah pemodelan matematika dalam optimasi fungsi yang mensyaratkan beberapa kondisi atau syarat untuk diperoleh solusi optimal yaitu syarat yang mengoptimumkan fungsi tujuan.
Maksimumkan / Minimumkan z = f(x), x = {x1, x2, …, xn}
Dengan kendala g1(x) (≤, =, ≥) = b1 g2(x) (≤, =, ≥) = b2 …
gm(x) (≤, =, ≥) = bm
Disini jika terjadi bahwa m > n maka tidak dapat diselesaikan. Akan tetapi untuk dapat menyelesaikannya maka m ≤ n (jumlah kendala lebih kecil daripada variabel).
Metode yang dapat digunakan untuk menyelesaikan masalah optimasi adalah metode pengali Lagrange, karena metode Lagrange tersebut prinsip kerjanya sederhana dan mudah dimengerti. Metode ini dimulai dengan pembentukan fungsi Lagrange yang didefinisikan sebagai :
L(x, λ) = f(x) +
m
i1
Teorema :
Syarat perlu bagi sebuah fungsi f(x) dengan kendala gj (x) = 0, untuk j = 1, 2, … , m
agar mempunyai minimum relatif pada titik x* adalah derivasi parsial pertama dari fungsi Lagrangenya yang didefinisikan sebagai L(x, λ) = ( x1,x2,…,xn, 1, 2,..., m ) terhadap setiap argumennya mempunyai nilai nol.
(Luknanto, 2000: 12)
Teorema:
Syarat harus bagi sebuah fungsi f(x) agar mempunyai minimum(atau maximum) relatif pada titik x* adalah jika fungsi kuadrat Q, yang didefinisikan sebagai
n i n j j i j i dx dx x x L Q 1 1 2
Dievaluasi pada x = x* harus definit positif (atau negatif) untuk semua nilai dx yang memenuhi semua kendala.
(Luknanto, 2000: 13)
Syarat perlu agar
n i n j j i j i dx dx x x L Q 1 1 2
menjadi definit positif( atau
negatif) untuk setiap variasi nilai dx adalah setiap akar dari polynomial zi, yang
didapat dari determinan persamaan dibawah ini harus positif (atau negatif).
(L11- z) L12 L13 … L1n g11 g12 … gm1
L21 (L22-z) L23 … L2n g12 g22 … g2n
… …
Ln1 Ln2 Ln3 … (Lnn-z) gm1 gm2 … gmn
g11 g12 g13 … g1n 0 0 … 0
g21 g22 g23 … g2n 0 0 … 0
… …
gm1 gm2 gm3 … gmn 0 0 … 0 = 0
Dengan L11 = dan gij =
Arti dari pengali Lagrange secara fisik yang menarik dimisalkan terdapat permasalahan optimasi dengan satu kendala sebagai berikut: maksimumkan/ minimumkan f(x) dengan kendala g(x) = b
Fungsi Lagrangenya adalah
L (x, λ) = f (x) + λ(b-g (x))
Syarat perlu untuk penyelesaian diatas adalah
= 0
Maka persamaan diatas menghasilkan :
b – g(x) = 0 atau b = g(x)
didapat;
Atau
Atau
Atau
menghasilkan yang final yaitu
df =λdb karena b = g(x) atau df = λ*db
Dapat diambil suatu kesimpulan bahwa dari persamaan diatas pada penyelesaian optimum, perubahan fungsi tujuan f, berbanding lurus dengan perubahan Kendala b dengan faktor sebesar pengali Lagrange λ.
2.2 Metode Pengali Lagrange
Sejauh ini proses optimasi dilakukan tanpa menggunakan kendala, padahal seringkali persoalan optimasi dihadapkan pada kendala - kendala tertentu. Sebagai contoh persoalan dasar dalam teori konsumen adalah bagaimana menentukan tingkat konsumsi yang memberikan kepuasan optimal dengan tingkat pendapatan tertentu.
Multiplier Langrange adalah sebuah konsep populer dalam menangani permasalahan ini untuk program-program non-linear. Sesuai namanya, konsep ini dikemukakan oleh Joseph Louis Langrange (1736-1813). Teori ini dapat digunakan untuk menangani optimalitas dari permasalahan program non-linear.
Metode pengali Lagrange merupakan sebuah tehnik dalam menyelesaikan masalah optimasi dengan kendala persamaan. Inti dari metode pengali Lagrange adalah mengubah persoalan titik ekstrem terkendala menjadi persoalan ekstrem bebas kendala. Fungsi yang terbentuk dari tranformasi tersebut dinamakan fungsi Lagrange.
misalkan permasalahan yang dihadapi adalah
Maksimumkan (Minimumkan) z = f(x), x = {x1, x2, …, xn}
Dengan kendala g1(x) (≤, =, ≥) = b1 g2(x(≤, =, ≥)) = b2 …
gm(x) (≤, =, ≥) = bm
Fungsi baru Lagrange yang telah dimodifikasi menjadi
L(x, λ) = f(x) +
m
i1
λigi (x)
2.3 Matrik Hessian
Matrik adalah susunan bilangan yang diatur berdasarkan baris dan kolom. Bilangan – bilangan tersebut dinamakan entri dalam matrik atau disebut juga elemen (unsur).
Matrik Hessian adalah matrik yang setiap elemennya dibentuk dari turunan parsial kedua dari suatu fungsi. Misalkan f(x) fungsi dengan n variabel yang memiliki turunan parsial kedua dan turunannya kontinu, matrik Hessian f(x) ditulis H adalah :
…
…
…
…
…
…
H =
Matrik Hessian dapat digunakan untuk melakukan uji turunan kedua fungsi lebih dari satu variabel, yaitu untuk mengidentifikasi optimum relatif dari nilai fungsi tersebut. Penggolongan titik stasioner fungsi dua variabel dengan menggunakan matriks Hessian misalkan f(x) = F(x1, …, xn) adalah fungsi bernilai real dimana semua
Titik stasioner dapat digolongkan sebagai berikut :
1. x0. Adalah suatu minimum relatif dari F jika jika H(x0.) definit positif
2. x0. Adalah suatu maksimum relatif dari F jika H(x0.) definit negatif
3. x0. Adalah suatu titik pelana dari F jika H(x0.) indefinite
(Leon,1998 : 313)
Contoh : 1
Untuk mendapatkan titik ekstrim dari suatu fungsi dipakai sebuah contoh sebagai berikut :
+ + +
Solusi :
Titik ekstrim harus memenuhi syarat :
+4
+8
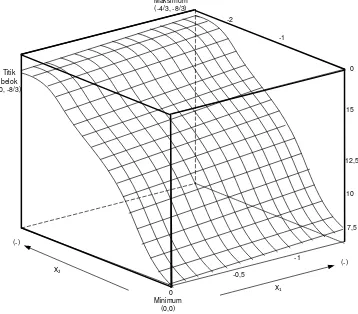
Persamaan diatas dipenuhi oleh titik – titik (0, 0), (0, -8/3), (-4/3, 0), dan (-4/3, -8/3) Untuk mengetahui titik maksimum dan minimum maka digunakannya matrik Hessian untuk menyelidikinya. Derivasi kedua dari f adalah :
, , dan
Jadi matrik Hessian menjadi
6x1 + 4 0
0 6x2 + 8
sehingga H1 = [6x1 + 4] dan
6x1 + 4 0
0 6x2 + 8 H2 =
Tabel 2.1. Nilai matrik Hessian untuk masing – masing titik ekstrim.
( x1 ,x2) Matrik H H1 H2 Sifat H Sifat ( x1 ,x2) f(x1, x2)
(0, 0)
4 0 0 8
+4 +32 Definit
positif Minimum 6
(0, -8/3) 4 0
0 - 8
+4 -32 Tak tentu Titik belok 418 / 27
(-4/3, 0) -4 0
0 8
- 4 - 32 Tak tentu Titik belok 194/ 27
(-4/3, -8/3) -4 0
0 -8
- 4 + 32 nefgatifDefinit Maksimum 50/ 3
Grafik f(x) disajikan dalam ruang tiga dimensi diperlihatkan dalam gambar dibawah ini :
[image:28.595.151.509.396.710.2]Maksimum (-4/3, -8/3) 0 -1 -2 7,5 10 12,5 15 Titik belok (0, -8/3) 0 Minimum (0,0) -0,5 -1 (-) X2 X1 (-)
2.4 Matrik Definit Positif
Bentuk kuadrat pada ( x1, x2, … xn ) adalah ekspresi yang dapat kita tulis sebagai
X1
X2
Xn
[ x1, x2, … xn ] A
Dengan A merupakan matrik simetrik n x n . Jadi misalkan
X1
X2
Xn
X =
maka bentuk ini dapat ditulis sebagai X t AX
contoh : 2
Misalkan sebuah matrik simetrik berikut :
2 -1 0
-1 2 -1
0 -1 2 A =
Untuk mengkaji apakah matriks A bersifat definite positif, maka;
2 -1 0
-1 2 -1
0 -1 2
X1
X2
X3
X t AX = [x1 x2 x3 ]
X t AX = [x1 x2 x3 ]
2x1–x2
-x1 + 2x2–x3
-x2 + 2x3
Sehingga hasilnya adalah
X t AX = x1(2x1-x2) + x2(-x1 + 2x2– x3) + x3(-x2 + 2x3) X t AX = 2 - x1x2 - x1x2 + - x2x3 - x2x3 +
X t AX = 2 - 2x1x2 + - 2x2x3 +
X t AX = + ( 2x1x2 + ) + ( -2x2x3 + ) +
X t AX = + ( )2 + ( - )2 +
Dari sini dapat disimpulkan bahwa matrik A bersifat definit positif karena memenuhi:
+ ( )2 + ( - )2 + > 0 kecuali jika x1 = x2 = x3 = 0
Sebaliknya matrik A dan bentuk kuadrat X t AX disebut : 1. Definit negatif jika X t AX < 0, untuk semua x 0
2. Semidefinit positif jika X t AX ≥ 0, untuk semua x
3. Semidefinit negatif jika X t AX ≤ 0, untuk semua x
4. Indefinit bila tidak termasuk golongan diatas
Himpunan syarat perlu dan syarat cukup untuk bentuk – bentuk definit positif dan negatif yaitu :
1. Syarat perlu dan syarat cukup untuk bentuk definit positif
Suatu himpunan syarat perlu dan syarat cukup bentuk X t AX sebagai definit positif adalah
> 0, h11 > 0, h11 h12
h21 h22
h11 h12 h13
h21 h22 h23
h31 h32 h33
Jika n minor dari A adalah positif, maka X t AX adalah definit positif dan X t AX
hanya definit positif, jika minor – minor ini positif.
2. Syarat perlu dan syarat cukup untuk bentuk definit negatif
Suatu himpunan syarat perlu dan syarat cukup bentuk X t AX sebagai definit negatif atau setaranya untuk X t (-A)X sebagai definite positif adalah
> 0, h11 h12
h21 h22
h11 h12 h13
h21 h22 h23
h31 h32 h33
A > 0
h11 < 0, < 0, … , (-1)n
Dimana aij adalah elemen – elemen dari A (bukan –A).
2.5 Maksimum dan Minimum
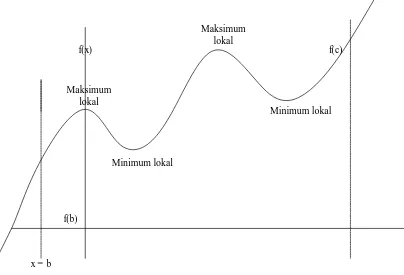
Suatu fungsi y = f(x) dikatakan mempunyai maksimum lokal (maksimum relatif) dimana x = a bila f(a) lebih besar dari sembarang nilai f(x) lainnya dari x sekitar a, dan dikatakan mempunyai minimum lokal (minimum relatif) pada x = a bila f(a) lebih kecil dari sembarang nilai f(x) lain untuk x sekitar a. Maksimum dan minimum local suatu fungsi adalah maksimum dan minimum absolut dari suatu fungsi mempunyai jarak yang lebih besar lagi dan terletak pada titik yang paling tinggi atau paling rendah dari jarak tersebut, melebihi maksimum atau minimum lokal. Jadi f(x) mempunyai nilai maksimum absolute pada nilai x = a1 dengan batas b apabila nilai f(x)
pada x = a1 mempunyai nilai paling tinggi , f(a1) > f(x), sedangkan f(x) mempunyai
nilai maksimum lokal pada batas b , apabila f(x) pada x =a2. Dengan
demikian suatu fungsi yang mempunyai titik maksimum kurvanya berbentuk cembung keatas dan fungsi yang mempunyai titik minimum kurvanya berbentuk cembung kebawah.
f(x)
x = b f(b)
f(c)
Minimum lokal
Minimum lokal Maksimum
lokal
Maksimum lokal
Gambar. 2.2. Grafik 1
Sebaliknya, titik kritis x dan f dapat dianalisa dengan menggunakan turunan kedua dari f di x :
1. Jika turunan kedua bernilai positif, x adalah minimum 2. Jika turunan kedua bernilai negatif, x adalah maksimum
3. Jika turunan kedua bernilai nol, x mungkin maksimum, minimum, ataupun tidak kedua- duanya.
[image:32.595.112.516.96.371.2]Contoh : 3
Tentukan nilai ekstrim dari fungsi f(x) = pada (-∞,∞)
Penyelesaian :
Turunan pertama dari f(x) adalah f’(x) = 0 maka
0 f’(x) = ( x + 1)(x –3) = 0 sehingga nilai x = -1 dan x = 3 maka titik kritis f
(x) adalah -1 dan 3. Maka turunan kedua dari f(x) adalah f”(x) = 2x– 2 sehingga nilai untuk mengujinya maka bahwa (x + 1)(x - 3) > 0 pada (-∞, -1) dan (3, ∞) maka menurut uji dari turunan pertama dapat disimpulkan bahwa merupakan
nilai minimum dan untuk merupakan nilai minimum grafiknya diperlihatkan oleh gambar dibawah ini.
1 -1
1
-1
0 2
2
3
-2 4
-2
-3
-4
-5 3
Minimum maksimum
x y
Gambar 2.3. Grafik nilai maksimum dan minimum
2.6 Fungsi Utilitas Marginal
Fungsi utilitas merupakan fungsi yang menjelaskan besarnya utilitas (kepuasan, kegunaan) yang diperoleh seseorang dari mengkonsumsi suatu barang atau jasa. Pada umumnya semakin banyak jumlah suatu barang dikonsumsi semakin besar utilitas yang diperoleh, kemudian mencapai titik puncaknya (titik jenuh) pada jumlah konsumsi tertentu, sesudah itu justru menjadi berkurang atau bahkan negatif jika jumlah barang yang dikonsumsi terus menerus ditambah.
Utilitas total merupakan fungsi dari jumlah barang yang dikonsumsi. Adapun persamaan utilitas total (total utility, U) dari mengkonsumsi suatu jenis barang berupa fungsi kuadrat parabolic, dengan kurva berbentuk parabola terbuka kebawah. Utilitas marginal (marginal utility, MU) merupakan utilitas tambahan yang diperoleh dari setiap unit barang yang dikonsumsi. Secara matematik, fungsi utilitas marginal merupakan derivative pertama dari fungsi utilitas total. Jika fungsi utilitas total dinyatakan dengan U= f(Q) dimana U melambangkan utilitas total dan Q jumlah barang yang dikonsumsi, maka utilitas marginal : MU = U’ = dU / dQ
(Dumairy, 1996 : 226 )
U = f(Q) U
MU
0 Q
Karena fungsi utilitas total yang non liner pada umumnya berbentuk fungsi kuadrat, fungsi utilitas marginalnya akan berbentuk fungsi liner. Kurva utilitas marginal (MU) selalu mencapai nol tepat pada saat kurva utilitas total (U) berada pada posisi puncaknya.
Contoh : 4
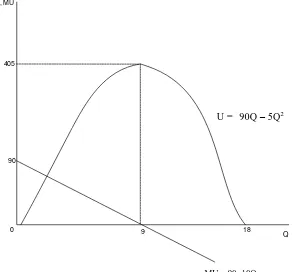
U = f(Q) = 90Q – 5Q2
MU = U’ = 90 – 10Q U maksimum pada MU = 0
MU = 0
Sehingga nilai Q = 9
Maka, Umaksimum = 90(9) – 5(9)2
= 810 – 405 = 405
Diperlihatkan oleh gambar dibawah ini :
MU = 90 -10Q
9 18
0 90 405
U = 90Q – 5Q2
[image:35.595.121.413.423.695.2]Q U, MU
Gambar 2.5. Grafik kurva fungsi U = f(Q) = 90Q – 5Q2 dan MU = U’ = 90 – 10Q
2.7 Produk Marginal
Produk marginal ( marjinal product, MP) ialah produk tambahan yang dihasilkan dari suatu unit tambahan faktor produksi yang digunakan. Secara matematik fungsi produk marjinal merupakan derivative pertama dari fungsi produk total. Jika fungsi produk total dinyatakan P = f(x) dimana P melambangkan jumlah produk total dan x adalah jumlah masukan, maka produk marginal :
MP = P’ = dp/ dx
Karena fungsi produk total yang non liner pada umumnya berbentuk fungsi kubik, fungsi produk marjinalnya akan berbentuk fungsi kuadrat. Kurva produk marginal (MP) selalu mencapai nilai ektrimnya, dalam hal ini nilai maksimum, tepat pada saat kurva produk total ( P) berada pada posisi titik beloknya. Produk total mencapai puncaknya ketika produk marjinalnya nol. Produk total menurun bersamaan dengan produk marginal menjadi negatif. Produk marjinal negatif menunjukkan bahwa penambahan penggunaan masukan yang bersangkutan justru akan mengurangi jumlah produk total.
(Dumairy, 1996: 227)
Contoh 5.
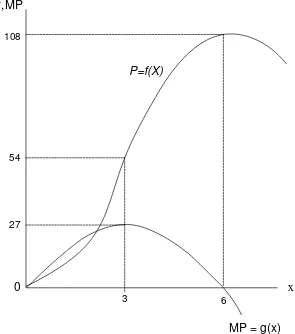
Produksi total P = f(x) = 9x2 – x3 produk marjinalnya adalah
MP = P’ = 18x – 3x2
Sehingga Pmaksimum pada P’ = 0 yaitu pada x = 6 dengan Pmaksimum = 108
Diperlihatkan oleh gambar dibawah ini :
x
6
P,MP
108
54
27
3
0
P=f(X)
MP = g(x)
[image:37.595.124.419.166.500.2]Gambar. 2.6. Kurva fungsi P = f(x) = 9x2 – x3dan MP = P’ = 18x – 3x2
BAB 3
PEMBAHASAN
Dalam masalah optimasi terdapat dua bentuk optimasi yaitu optimasi tak bersyarat dan optimasi bersyarat. Ada beberapa cara untuk menyelesaikan bentuk yang pertama seperti uji turunan pertama, uji turunan kedua, untuk fungsi satu variabel. Sedangkan optimasi bersyarat merupakan jenis yang paling banyak dijumpai dalam kehidupan nyata. Banyak aplikasi dalam pemodelan matematika dari optimasi fungsi yang menggunakan syarat untuk memperoleh solusi optimal. Syarat yang mengoptimumkan fungsi tujuan yang dinamakan dengan optimasi bersyarat. Bentuk umum dari optimasi fungsi dengan kendala adalah menentukan nilai dari variabel keputusan ( nilai ekstrim) x = (x1, x2, … xn) yang memaksimumkan ataupun meminimumkan fungsi dari
permasalahan :
Maksimumkan/ minimumkan : z = f(x)
Dengan kendala : g1(x) (≤, =, ≥) b1 ………..
gm(x)(≤, =, ≥) bm
Dimana f(x) merupakan fungsi tujuan dan g1(x) (≤, =, ≥) b1merupakan fungsi
kendala. Akan tetapi dalam penulisan skripsi ini akan di uraikan optimasi fungsi dengan kendala persamaan.
3.1 Optimasi Dengan Kendala Persamaan Menggunakan Multipilier Lagrange.
optimasi dengan kendala persamaan dalam suatu bentuk sedemikian hingga syarat perlu bagi masalah optimasi tanpa kendala masih bisa diterapkan. Metode ini banyak digunakan karena cara kerjanya sederhana dan mudah dimengerti.
Bentuk persoalan dari optimasi bersyarat dengan kendala persamaan dirumuskan sebagai berikut :
Maksimumkan/ minimumkan : z = f(x)
Dengan kendala g1(x) (≤, =, ≥) b1
…
gm(x)(≤, =, ≥) bm
Dimana f(x) merupakan fungsi tujuan dan g1(x) (≤, =, ≥) b1 merupakan fungsi
kendala. Akan tetapi dalam penulisan skripsi ini akan di uraikan optimasi fungsi dengan kendala persamaan, dari persoalan tersebut digunakan pengali lagrange λi
dengan fungsi kendala ke i dan persamaan fungsi Lagrangenya adalah
L(x, λ) = f(x) +
m
i1
λigi (x)
Seperti pada kasus optimasi tanpa kendala, syarat cukup pada kasus ini juga diekspresikan dalam bentuk determinan. Posisi determinan matriks Hessian pada optimasi dengan kendala persamaan digantikan dengan apa yang disebut Bordered Hessian. Syarat cukup ini diterapkan setelah syarat perlu dipenuhi dan digunakan untuk mengetahui prilaku dari L(x ,λ ) pada nilai kritisnya.
Contoh : 1
Carilah fungsi f(x, y) = x3 + y3 + xy dengan syarat x + y – 4 = 0
Penyelesaian :
Optimumkan : f(x, y) = x3 + y3 + xy
Dengan kendala : g(x,y) = x + y – 4 = 0
Maka fungsi baru lagrangennya
F(x, y, λ) = f(x, y) + λg(x + y - 4)
F(x, y, λ) = x3
+ y3+ xy + λ(x + y – 4)
Syarat perlu untuk mendapatkan titik ekstrim :
Sehingga turunan pertama terhadap setiap variabel adalah sebagai berikut :
Dari persamaan (1) dan (2) didapat :
λ = - ( 3x2 + y)
λ = - ( 3y2 + x)
sehingga persamaannya menjadi λ = λ maka
3y2 + x = 3x2 + y (4)
dari persamaan (3) didapat y = 4 – x maka disubtitusikan ke persamaan yang ke (4)
3(4 – x )2 + x = 3x2 + (4 – x )
48 – 24x + 3x2 + x = 3x2– x + 4
22 x = 44
x = 2
maka
x = 2 → x + y – 4= 0 → y = 2
pada x = 2 dan y = 2 fungsi tujuannya memberikan nilai ekstrim f(x ,y) = 20
syarat cukup untuk menguji sifat titik stasioner untuk mengetahui perilaku fungsi
F(x, y, λ) = x3
x g y g 0 x g 2 2 x L y x L 2 y g x y L 2 2 2 y L 2 H
0
1 1
2
H
1
6
x
1
1
1
6yPada titik (2,2) diproleh nilai H2
0
1 1
2
H
1
12 1
1
1
12
Maka untuk mendapatkan nilai determinan dari H2 adalah
H2 = 0 + 1
H2 = 0 – 11 + (-11) = -22
Jadi pada nilai L pada (2, 2) dengan H2 = -22 adalah minimum relatif
3.2. Utilitas Marjinal Persial Serta Keseimbangan Konsumsi
Dalam kenyataan sehari - hari, seorang konsumen tidak hanya mengkonsumsi satu macam barang tetapi berbagai macam. Jika kepuasan konsumen dilambangkan dengan
U dan barang-barang yang dikonsumsinya dilambangkan dengan qi (i = 1,2, …n),
maka fungsi utilitasnya dapat dituliskan dengan notasi U = f (q1, q2…..qn). seandainya
untuk menyederhanakan dianggap bahwa seorang konsumen hanya mengkonsumsi dua macam barang, misalnya x dan y, maka fungsinya utilitasnya adalah : U = f (x, y)
Derivatif pertama dari U merupakan utilitas marjinal parsialnya.
adalah utilitas marjinal berkenaan dengan barang x.
adalah utilitas marjinal berkenaan dengan barang y
Untuk U = konstanta tertentu, fungsi utilitas U= f(x, y) merupakan suatu persamaan kurva indiferensi, yaitu kurva yang menunjukan berbagai kombinasi konsumsi barang x dan y yang memberikan tingkat kepuasan yang sama.
Keseimbangan konsumsi maksudnya adalah suatu keadaan atau tingkat kombinasi konsumsi beberapa macam barang yang memberikan kepuasan optimum. Keseimbangan terjadi pada persinggungan kurva idenferensi dengan garis anggaran komsumen (budget line).
Garis anggaran adalah garis yang mencerminkan kemampuan komsumen membeli berbagai macam barang berkenaan dengan harganya masing-masing dan pendapatan konsumen. Jika pendapatan konsumen berjumlah M serta harga barang x
dan barang y masing-masing Px dan Py persamaan budget line-nya dapat ditulis dengan notasi
M = x.Px + y.Py.
Tingkat kombinasi konsumsi yang memberikan kepuasan optimum atau keseimbangan konsumsi dapat dicari dengan Multiplier Lagrange. Dalam hal ini fungsi utilitas U = f (x,y) dimaksimumkan terhadap fungsi anggaran M = x.Px + y.Py.
diproleh fungsi Lagrange:
F (X,y) = f (x,y) + λ (x.Px + y.Py-M)
Agar F maksimum :
Fx (x,y) = 0 fx (x, y) + λ.Px = 0 (1)
Fy (x, y) = 0 fy (x, y) + λ.Py = 0 (2) Selanjutnya perhatikan :
Utilitas total : U = f(x,y)
Utilitas marjinal barang x : MUx = fx (x, y) =
Utilitas marjinal barang y : MUy = fx (x, y) =
Dari persamaan (1)
fx(x, y) + λ.Px = 0 -λ=
Dari persamaan (2)
fy(x, y) + λ.Py = 0 -λ =
Diperoleh
= berakibat
Dapat diartikan pula bahwa keseimbangan konsumsi akan tercapai apabila hasil bagi utilitas marjinal masing-masing barang terhadap harganya bernilai sama.
Contoh 2.
Kepuasan konsumen dari kombinasi dua pakaian dan makanan ditunjukkan oleh fungsi U = 4x2 + 2y2 + 5, dengan x menyatakan pakaian dan y menyatakan makanan. Jumlah pendapatan konsumen 90000 rupiah, harga pakaian dan harga makanan per unit masing – masing 5000 rupiah dan 1000 rupiah. Hitunglah kombinasi konsumsi pakaian dan makanan yang memberikan kepuasan optimum.
Penyelesaian :
Diketahui : U = 4x2 + 2y2 + 5
Jumlah pendapatan (M) = 90000 Harga pakaian (Px) = 5000
Harga makanan (Py) = 1000
Maka persamaannya menjadi
M = xPx + yPy
90000 = 5000x + 1000y
5000x + 1000y –90000 = 0
Dari persamaan yang diatas maka diperoleh persamaan Lagrangeyang baru :
F(x, y) = 4x2 + 2y2+ 5 + λ(5000x + 1000y – 90000)
F(x, y) = 4x2 + 2y2 + 5 + 5000 λx + 1000 λ y –90000 λ
Supaya F menjadi maksimum maka :
Fx= 8x + 5000 λ = 0 , maka - λ = 8x / 5000 (1) Fy= 4y + 1000 λ = 0, maka - λ = 4y / 1000 (2)
Dari persamaan (1) dan (2) didapat
8x / 5000 = 4y / 1000 maka 8000x = 20000y
Sehingga
Maka 5000x + 1000y – 90000 = 0
5000x + 1000 ( ) – 90000 = 0
5000x – 400x = 90000 4600x = 90000
x = 90000/ 4600 maka nilai x = 19, 57
Didapat nilai x = 19, 57 dan y =
y = = 7, 83
Sehingga,
U = 4x2 + 2y2 + 5 = 4 ( 19,57)2 + 2 (7, 83)2 + 5 = 1531, 94 + 122,61 + 5 = 1659,55. Jadi kombinasi konsumsi yang memberikan kepuasan optimum adalah 19, 57 unit pakaian dan 7, 83 unit makanan, dengan nilai kepuasan U = 1659,55
Contoh 3
Fungsi utilitas untuk dua komoditas yang diberikan oleh fungsi U = x2y dan anggaran pengeluaran 3x + 6y = 18, berapa nilai x dan y yang memberikan kepuasan optimum.
Penyelesaian :
Maksimumkan U = x2y
Dengan kendala 3x + 6 y = 18
Dari persamaan diatas diperoleh fungsi baru Lagrange ;
L = x2y + λ( 3x + 6 y – 18) L = x2y + 3 λ x + 6 λy –18 λ
Agar L maksimum
Ly = x2+ 6λ = 0 maka–λ = x2 / 6 (2)
Berdasarkan persamaan (1) dan (2) didapat
2xy/ 3 = x2 / 6 maka 12xy = 3x2 y = x / 4
sehingga 3x + 6 y– 18 = 0
3x + 6 y = 18 maka 3x + 6( ) = 18
x = 4
karena nilai x = 4 maka y = x / 4 = 4/ 4 =1 U = x2y = 42 . 1 = 16
Jadi kombinasi konsumsi yang memberikan kepuasan optimum adalah 4 unit x dan 1 unit y, dengan nilai kepuasan U = 16
3.3 Produk Marjinal Parsial Dan Keseimbangan Produksi.
Untuk memproduksi suatu barang pada dasarnya diperlukan beberapa macam faktor produksi seperti tanah, modal, tenaga kerja, bahan baku, mesin-mesin dan sebagainya. Jika jumlah keluaran yang dihasilkan dilambangkan dengan P dan masukan yang digunakan dilambangkan untuk xj dimana( j= 1, 2, …..,n), maka fungsi
produksinya dapat dituliskan dengan notasi P = f(x1, x2, x3, ….xn).
Sebagian dari masukan yang digunakan sudah barang tentu merupakan masukan tetap, sementara sebagain lainya adalah masukan variabel. Selanjutnya jika untuk memproduksi suatu barang dianggap hanya ada dua macam masukan variabel (misalkan K dan L), maka fungsi produksinya secara pasti dapat dinyatakan dengan,
P= f(k,l)
Derivatif pertama merupakan produk marjinal parsialnya ∂P/∂k adalah produk marginal berkenaan dengan masukan K. ∂P / ∂l adalah produk marginal berkenaan dengan masukan L. Dimana P = konstanta tertentu, fungsi produksi P = f (k, l)
merupakan suatu persamaan, yaitu kurva yang menunjukkan berbagai kombinasi penggunaan masukan K dan L yang menghasilkan keluaran dalam jumlah sama.
Keseimbangan produksi adalah suatu keadaan atau tingkat penggunaan kombinasi faktor – faktor produksi secara optimum, yakni suatu tingkat pencapaian produksi dengan kombinasi biaya terendah. Jika jumlah dana yang dianggarkan untuk membeli masukan K dan L adalah sebesar M, serta harga masukan K dan masukan L
masing – masing Pk dan Pl , persamaan tersebut ditulis dengan notasi M = k. Pk + l Pl
Tingkat kombinasi penggunaan masukan yang optimum dapat dicari dengan
multiplier Lagrange, untuk fungsi produksi P = f(k, l) dimaksimumkan terhadap fungsi M = k. Pk + l Pl
Sedangkan fungsi tujuannya yang hendak dioptimumkan P = f(k, l), untuk fungsi kendalanya adalah M = k. Pk + l Pl
k. Pk + l Pl– M = 0
Fungsi baru LagrangeF(k, l) = f(k, l) + λ(k Pk + l Pl - M)
syarat perlu agar F(k,l) maksimum :
Fk(k, l) = 0 maka fk(k,l)+ λ Pk = 0 (1) Fl(k, l) = 0 maka fl(k,l)+ λ Pl = 0 (2)
Dari persamaan (1) dan (2) nilai k dan nilai l dapat dicari selanjutnya nilai P
maksimum dapat dihitung. Produksi total : P = f(k, l)
Produksi marjinal barang K: MPK = fk(k, l) = ∂P / ∂k
Produksi marjinal barang L : MPL = fl(k, l) = ∂P / ∂l
Pengembangannya dari persamaan menjadi
1. fk (k, l) + λ Pk = 0 maka fk (k, l) = - λ Pk , - λ = fk (k, l) / Pk
2. fl (k, l) + λ Pl = 0 maka fl (k, l) = - λ Pl , - λ = fl (k, l) / Pl
Sehingga dengan demikian, syarat keseimbangan produksi dapat juga dirumuskan dengan fk (k, l) / Pk = fl (k, l) / Pl berakibat MPK / Pk = MPL / Pl , dapat
Contoh 4.
Suatu pabrik memproduksi dua jenis mesin, x dan y fungsi biaya gabungan dari dua mesin tersebut adalah F(x, y) = x2 + 3xy – 6y , untuk meminimalkan biaya, berapa banyak mesin dari keduanya harus diproduksi jika total mesin yang diproduksi 42. Penyelesaian
Minimalkan F(x, y) = x2 + 3xy – 6y
Dengan kendala x + y = 42
Maka diperoleh persamaan fungsi baru Lagrange F(x, y) = x2 + 3xy –6y + λ(x + y – 42)
Agar F minimum maka,
Fx(x, y) = 2x + 3y + λ = 0 , -λ = 2x + 3y (1) Fy (x, y) = 3x - 6 + λ = 0 , -λ = 3x – 6 (2) Fλ (x, y) = x + y – 42= 0 , x = - y + 42 (3) Berdasarkan persamaan (1) dan (2) maka
2x + 3y = 3x – 6
x = 3y + 6 (4) Berdasarkan persamaan (3) dan (4)
x = 42 – y = 3y + 6 y = 9
maka x = 33
Jadi, biaya minimum yang diperoleh jika x = 33 dan y = 9
KESIMPULAN DAN SARAN
4.1. Kesimpulan
1. Mencari semua solusi syarat cukup untuk ekstrim relatif
Syarat cukup pada kasus ini juga diekspresikan dalam bentuk determinan. Posisi determinan matriks Hessian pada optimasi dengan kendala persamaan digantikan dengan apa yang disebut Bordered Hessian. Syarat cukup ini diterapkan setelah syarat perlu dipenuhi dan digunakan untuk mengetahui prilaku dari L(x ,λ ) pada nilai kritisnya.
2. Metode Lagrange dapat digunakan untuk menyelesaikan permasalahan optimasi yang dihadapi yaitu contoh kasus dalam bidang ekonomi.
4.2. Saran
1. Bagi pembaca yang berminat untuk mendalami optimasi bersyarat, dapat mengembangkan skripsi ini lebih lanjut, khususnya optimasi bersyarat dengan kendala pertidaksamaan.
DAFTAR PUSTAKA
Barnet, R. Ziegler, Michael, R. & Byleen, karl, E. 1987. “Calculus For Busines Economics,Life, and Social Sciences”. New Jersey: PEI.
Bronson, Richard. Wospakrik, Hans, J.1988. “Teori Dan Soal-Soal Operations
Research”. Jakarta: Erlangga.
Com S. 2008.”lagrange-multiplier”.
http://www.cs.iastate.edu/~cs577/handouts/lagrange-multiplier.pdf.Diakses tanggal 17 Maret 2010.
Dumairy, 1996. “Matematika Terapan Untuk Bisnis dan Ekonomi”.Yogyakarta: BPFE Yogyakarta
Hillier, F.S & Gerald J. L. 1990. “Pengantar Riset Operasi Terjemahan Ellen
Gunawan dan Ardi Wirda Mulia”. Jakarta: Erlangga.
Johannes, “Peranan Geometri dalam Mengoptimalkan Fungsi 2 Peubah atau
Lebih” http://library.usu.ac.id/download/fmipa/matematika-johannes.pdf Diakses pada tanggal 11 Maret 2010
Klein D. “Lagrange-Multipliers Without Permanent Scarring”.
http://diglib.stanford.edu:8091/~klein/lagrange-multipliers.pdf. Diakses tanggal 17 Maret 2010.
Leithold, L. 1991. Kalkulus dan Ilmu Ukur Analitik Edisi Kelima Terjemahan S. M. Nababan, dkk. Jakarta: Erlangga
Luknanto, J. 2000. “Pengantar Optimasi Non-linier”.
http:/luk.staff.ugm.ac.id/optimasi/pdf/nonliner2003.pdf. Diakses tanggal 15 Maret 2010.
Nadhifah, Siti . “Penerapan Differensial Fungsi Majemuk”
http://pksm.mercubuana.ac.id/new/elearning/files.../9301496999525784.doc .
Diakses pada tanggal 26 maret 2010
Purcell, E. J. & D. Varberg. 1987. Kalkulus dan Geometri Analitis Terjemahan I. Nyoman, S., Bana, K., dan Rawuh. Jakarta: Erlangga.
Rao, SS. 1978. “Optimization Theory And Application Second Edition”. Deptt. Of Mechanical Engg. USA: San Diego State University.
Sawyer , S. 2002. “The Method of Lagrange Multipliers”.
http://xbeams.chem.yale.edu/~batista/vaa/LagrangeMult.pdf. Diakses tanggal 25 Maret 2010.
http://djonhart.economicpolicy.info/lecture/meb1/catatan%20kuliah%2012.pdf Diakses pada tanggal 10 juni 2010
http://djonhart.economic-policy.info/lecture/mex/Bahan_Kul_5-6.pdf Diakses pada tanggal 11 juni 2010
http://mdwiner.files.wordpress.com/2009/01/mencari-nilai-maksimum-atau-minimum.pdf. Diakses pada tanggal 11 juni 2010
http://p4tkmatematika.org/downloads/smk/Matriks.pdf Diakses pada tanggal 11 juni 2010
http://staff.ui.ac.id/internal/131803524/material/Bab_IV.Penggunaan_Turunan.pdf Diakses pada tanggal 11 juni 2010
http://anwarazis.files.wordpress.com/2009/01/linier-c.pdf. Diakses pada tanggal 11 juni 2010