42
DAFTAR PUSTAKA
BSW, Pudjiastuti. 2006. Matriks, Teori dan Aplikasi. Graha Ilmu. Yogyakarta. C. Chiang, Alpha. 2005. Fundamental Methods of Mathematical Economics. Dumairy. 2000. Matematika untuk Ekonomi dan Bisnis. BPFE Yogyakarta.
Yogyakarta.
Effendi, Usman. 2012. Rekayasa dan Optimasi Proses Lagrange Multipliers. Gupta, P.K and D.S. Hira. 2007. Operations Research. Rajendra Ravindra.
Ramnagar – New Delhi.
Hillier, F. S. 1994. Pengantar Riset Operasi. Jilid 1. Ed ke- 5. Wahyarasmana, D. Erlangga. Jakarta.
Luknanto, J. 2000. Pengantar Optimasi Non Linier.
Maynard, H. B. 1971. Industrial Engineering Handbook. The McGraw-Hill Companies, Inc. New York.
Mulyono, Sri. 2004. Riset Operasi. Fakultas Ekonomi Universitas Indonesia. Jakarta.
Prayudi. 2009. Kalkulus Lanjut. Graha Ilmu. Yogyakarta.
Rao, S.S. 1985. Optimization Theory and Applications. Wiley Eastern Limited. New Delhi.
Supranto, J. 2005. Matematika untuk Ekonomi & Bisnis. FE-UI. Jakarta. Stewart, J. 1999. Kalkulus. Jilid 1. Ed ke- 4. Mahanani, N. Erlangga. Jakarta. Syaripuddin. 2011. Penerapan Metode Pengganda Lagrange dalam Bidang
Ekonomi.
Taha, H. A. 2007. Operation Research An Introduction. Ed ke – 8. University of Arkansas. Fayetteville.
Widayat, Wahyudi. 2011. Matematika Ekonomi. BPFE Yogyakarta. Yogyakarta. Wrede, Robert dan R. Spiegel, Murray. 2007. Schaum’s Outlines Teori dan
3.1 Optimasi dengan Metode Pengali Lagrange
Dalam masalah optimasi terdapat dua bentuk masalah optimasi yaitu optimasi bersyarat dan optimasi tak bersyarat. Banyak aplikasi dari pemodelan matematika dalam optimasi fungsi yang mensyaratkan beberapa kondisi atau syarat untuk memperoleh suatu solusi optimal di mana syarat tersebut yang mengoptimumkan fungsi tujuan. Persoalan dengan model tersebut dinamakan optimasi bersyarat.
Bentuk umum dari fungsi optimasi bersyarat adalah untuk menentukan , , … , , sehingga mencapai tujuan yaitu :
Maksimumkan/Minimumkan , , , … , 3.1
dengan kendala , ,
, ,
…
, , , 1, 2, … , 3.2
Metode pengali Lagrange merupakan salah satu cara yang dapat digunakan untuk menentukan titik ekstrim suatu fungsi berkendala, di mana kendalanya berbentuk persamaan. Metode pengali Lagrange dikembangkan untuk mengatasi masalah optimasi dengan kendala persamaan dalam suatu bentuk sedemikian hingga syarat perlu bagi masalah optimasi tanpa kendala masih bisa diterapkan. Metode pengali Lagrange paling banyak dipakai dengan pertimbangan prinsip kerjanya sederhana dan mudah dimengerti.
Bentuk persoalan dari optimasi fungsi dengan kendala persamaan dirumuskan sebagai berikut:
Maksimumkan/Minimumkan , , , … , 3.3
28
dengan kendala
…
, 1, 2, … , 3.4
Di mana adalah fungsi yang hendak dioptimumkan (fungsi tujuan) dan adalah fungsi kendala (equality constraint). Untuk menentukan nilai ekstrim dari persoalan tersebut digunakan pengali Lagrange λ dengan fungsi
kendala ke dan persamaan fungsi Lagrangenya:
,λ ∑ λ 3.5
Fungsi baru Lagrange dapat pula dibentuk dengan cara mengurangkan fungsi yang hendak dioptimumkan terhadap hasil kali pengali Lagrange λ dengan
fungsi kendala, hasilnya tetap sama kecuali pada tanda hasil perhitungan λ.
Pengali Lagrange atau λ adalah suatu variabel tak tentu yang hanya bersifat
pembantu. Contoh 3.1:
Tentukan nilai , , dan yang meminimumkan fungsi , ,
4 4 6 16 dengan kendala 15
Penyelesaian:
Minimumkan: , , 4 4 6 16
dengan kendala: 15
Maka fungsi baru Lagrangenya:
, , ,λ 4 4 6 16 λ 15
Syarat perlu untuk mendapatkan titik ekstrim:
sehingga turunan pertama terhadap setiap variabel adalah sebagai berikut:
"#
"$% 2 4
λ 0 →λ 2 4 3.6
"#
"$' 8 4 λ 0 →λ 8 4 3.7
"#
"$) 2 6 λ 0 →λ 2 6 3.8
"#
"λ 15 0 3.9
dari persamaan 3.6 dan 3.7 diperoleh:
2 4 8 4
6 12
2 3.10
dari persamaan 3.6 dan 3.8 diperoleh:
2 4 2 6
substitusi persamaan 3.10 ke persamaan 3.6 sehingga:
2 2 4 2 6
2 6 0
3
substitusi 3 dan persamaan 3.10 ke pesamaan 3.9 15 0
2 3 15 0
3 12 0
4
karena 2 maka 2 4 8.
30
Jadi, nilai optimal dari persoalan di atas adalah 8, 4, dan 3 dengan nilai ekstrim , , 7.
Untuk melihat apakah hasil di atas memberikan nilai minimum dari , maka uji syarat cukup fungsi. Sehingga persamaannya:
,, -= turunan untuk pada persamaan kendala larange ke . atau
3.2 Utilitas Marjinal Parsial dan Keseimbangan Konsumsi
Dalam kehidupan sehari-hari, seorang konsumen tidak hanya mengkonsumsi satu macam barang tetapi berbagai macam. Jika kepuasan konsumen dilambangkan dengan U dan barang-barang yang dikonsumsinya dilambangkan dengan
Derivatif pertama dari U merupakan utilitas marjinal parsialnya.
">
"$ adalah marjinal berkenaan dengan barang ">
"? adalah marjinal berkenaan dengan barang =
Untuk U konstanta tertentu, fungsi utilitas < , = merupakan suatu persamaan kurva indiferensi, yaitu kurva yang menunjukan berbagai kombinasi konsumsi barang dan = yang memberikan tingkat kepuasan yang sama.
Keseimbangan konsumsi adalah suatu keadaan atau tingkat kombinasi konsumsi beberapa macam barang yang memberikan kepuasan optimum. Secara geometri, keseimbangan konsumsi terjadi pada persinggungan kurva indiferensi dengan garis anggaran konsumen (budget line). Garis anggaran adalah garis yang mencerminkan kemampuan konsumen membeli berbagai macam barang berkenaan dengan harganya masing-masing dan pendapatan konsumen. Jika pendapatan konsumen berjumlah M serta harga barang dan barang = masing-masing A$ dan A? per unit, persamaan budget line-nya dapat ditulis dengan notasi:
B . A$ =. A? 3.12
Tingkat kombinasi konsumsi yang memberikan kepuasan optimum atau keseimbangan konsumsi dapat dicari dengan metode pengali Lagrange. Dalam hal
32
ini fungsi utilitas < , = dimaksimumkan terhadap fungsi anggaran B . A$ =. A?, diperoleh fungsi baru Lagrange:
D , = , = E4 . A$ =. A? B5 3.13
agar D maksimum:
D$ , = 0 → $ , = E. A$ 0 3.14
D? , = 0 → ? , = E. A? 0 3.15
Selanjutnya:
Utilitas total : < , =
Utilitas marjinal : B< <′ ′ , = 3.16
Utilitas marjinal barang : B<$ $ , = ">"$ 3.17
Utilitas marjinal barang = : B<? ? , = ">"? 3.18
dari persamaan 3.14: $ , = E. A$ 0 → E GHI$,? H
dari persamaan 3.15: ? , = E. A? 0 → E GJ$,?
IJ diperoleh
GH $,?
IH
GJ$,?
IJ berakibat
K>H
IH
K>J
IJ 3.19
Contoh 3.2:
Fungsi utilitas untuk dua komoditas yang diberikan oleh fungsi <
2= = dan anggaran pengeluaran = 35, berapa nilai , = dan yang memberikan kepuasan optimum.
Penyelesaian:
Maksimumkan < 2= =
dengan kendala = 35
dari persamaan di atas diperoleh fungsi baru Lagrange:
2= = E = 35
agar maksimum
$ 2 = E 0 → E 2 = 3.20
? 4= E 0 → E 4= 3.21
L 2 1 E 0 → E 2 1 3.22
M = 35 0 3.23 dari persamaan 3.20 dan 3.21 diperoleh:
2 = 4=
3 5=
5 3 =
dari persamaan 3.20 dan 3.22 diperoleh:
2 = 2 1
7
3 = 2 1
1 73= 2
34
Jadi, kombinasi konsumsi yang memberikan kepuasan optimum adalah 15 unit , 9 unit =, dan 11 unit dengan nilai kepuasan < 362.
Contoh 3.3:
Kepuasan seorang konsumen dari kombinasi dua barang pakaian dan makanan ditunjukan oleh fungsi < 4 2= 5, dengan menyatakan pakaian dan = menyatakan makanan. Jumlah pendapatan konsumen Rp 90.000,00, harga pakaian dan harga makanan per unit masing-masing Rp 5.000,00 dan Rp 2.500,00. Hitunglah kombinasi konsumsi pakaian dan makanan yang memberikan kepuasan optimum.
dari persamaan di atas diperoleh fungsi Lagrange yang baru: D , = 4 2= 5 E 5.000 2.500= 90.000
agar D maksimum:
D$ 8 5.000E 0 → E N.SSSR$ 3.24
dari persamaan 3.24 dan 3.25 diperoleh: 8
5.000 2.500 → 20.0004= 20.000= =
Maka 5.000 2.500= 90.000 0 5.000 2.500 90.000 0 7.500 90.000
12
karena = maka = 12.
Sehingga, < 4 2= 5 869.
Jadi, kombinasi konsumsi yang memberikan kepuasan optimum adalah 12 unit pakaian dan 12 unit makanan dengan nilai kepuasan < 869.
3.3 Produk Marjinal Parsial dan Keseimbangan Produksi
Untuk memproduksi suatu barang pada dasarnya diperlukan beberapa macam faktor produksi seperti tanah, modal, tenaga kerja, bahan baku, mesin-mesin dan sebagainya. Jika jumlah keluaran yang dihasilkan dilambangkan dengan P dan masukan yang digunakan dilambangkan dengan - . 1, 2, … , ; , maka fungsi produkasinya dapat dituliskan dengan notasi A , , , … , .
Sebagian dari masukan yang digunakan sudah barang tentu merupakan masukan tetap, sementara sebagian lainnnya adalah masukan variabel. Selanjutnya jika untuk memproduksi suatu barang dianggap hanya ada dua macam masukan variabel (misalkan U dan V), maka fungsi produksinya secara pasti dapat dituliskan dengan,
A U, V 3.26
Derivatif pertama merupakan produk marjinal parsialnya.
"I
"W adalah produk marjinal berkenaan dengan barang U
36
"I
"X adalah produk marjinal berkenaan dengan barang V
Untuk P konstanta tertentu, fungsi utilitas A U, V merupakan suatu persamaan isoquant, yaitu kurva yang menunjukan berbagai kombinasi penggunaan masukan U dan V yang menghasilkan keluaran dalam jumlah yang sama.
Keseimbangan produksi adalah suatu keadaan atau tingkat penggunaan kombinasi faktor-faktor produksi secara optimum, yakni suatu tingkat pencapaian produksi dengan kombinasi biaya terendah (least cost combination). Secara geometri, keseimbangan produksi terjadi pada persinggungan isocost dengan isoquant. Isocost adalah kurva yang mencerminkan kemampuan produsen membeli berbagai macam masukan berkenaan dengan harga masing-masing masukan dan jumlah dana yang dimilikinya. Jika jumlah dana yang dianggarkan untuk membeli masukan U dan masukan l adalah sebesar M, serta harga masukan k dan masukan l masing-masing AW dan AX, persamaan isocost-nya dapat dituliskan dengan notasi:
B U. AW V. AX 3.27
Tingkat kombinasi penggunaan masukan yang optimum atau least cost combination dapat dicara dengan metode pengali Lagrange. Dalam hal ini fungsi produksi A U, V dimaksimumkan terhadap fungsi isocost B U. AW V. AX.
Fungsi tujuan yang hendak dioptimumkan: A U, V Fungsi kendala yang dihadapi : B U. AW V. AX
U. AW V. AX B 0
Fungsi baru Lagrange : D U, V U, V E U. AW V. AX B 3.28 Syarat perlu agar D U, V maksimum:
DX U, V 0 → X U, V E. AX 0 3.30
Pengembangan lebih lanjut dari persamaan 3.29 dan 3.30 menghasilkan:
W U, V E. AW 0 → E GZIW,XZ
X U, V E. AX 0 → E G[IW,X[
Dengan demikian, syarat keseimbangan produksi dapat juga dirumuskan:
GZ W,X
Dapat diartikan pula bahwa produksi optimum dengan biaya terendah akan tercapai apabila hasil bagi produk marjinal masing-masing masukan terhadap harganya bernilai sama.
Contoh 3.4:
Sebuah perusahaan mempunyai tiga pabrik yang memproduksi barang dagangan yang sama. Jika pabrik A memproduksi satuan, pabrik B memproduksi = satuan, pabrik C memproduksi satuan, berturut-turut dengan biaya pembuatan
3 200 dolar, = 400 dolar, 2 300 dolar. Jika harus mengisi permintaan sebanyak 1.100 satuan, tentukan bagaimana produksi tersebut harus dibagikan kepada ketiga pabrik itu agar dicapai biaya pembuatan yang minimum.
38
Penyelesaian:
Minimumkan \ , =, 3 200 = 400 2 300
3 = 2 900
dengan kendala = 1.100 diperoleh fungsi baru Lagrange:
3 = 2 900 E = 1.100
agar minimum:
$ 6 E → E 6 3.34
? 2= E → E 2= 3.35
L 4 E → E 4 3.36
M = 1.100 → 1.100 = 3.37 dari persamaan 3.34 dan 3.35 diperoleh:
6 2= → = 3
dari persamaan 3.34 dan 3.36 diperoleh:
6 4 → 32
dari persamaan 3.37 diperoleh: 1.100 3 32
200
Maka = 600 dan 300.
Contoh 3.5:
Seorang petani mempunyai dua tanaman, ] dan ^. Biaya untuk memproduksi unit tanaman ] adalah 1.200 dan biaya untuk memproduksi = unit tanaman ^ adalah 3= 800. Jika petani mempunyai pesanan 1.200 unit. Berapa banyak masing-masing tanaman harus dipoduksi untuk memenuhi pesanan yang meminimumkan biaya produksi.
Penyelesaian:
Minimumkan \ , = 1.200 3= 800
3= 2.000
dengan kendala = 1.200
diperoleh fungsi baru Lagrange:
D , = 3= 2.000 E = 1.200
agar D maksimum:
D$ , = 2 E → E 2 3.38
D? , = 6= E → E 6= 3.39 DM , = = 1.200 → 1.200 = 3.40
dari persamaan 3.38 dan 3.39 diperoleh:
2 6=
3=
dari persamaan 3.40 diperoleh: 3= 1.200 =
= 300
Maka 900.
Jadi masing-masing tanaman yang harus diproduksi yang meminimumkan biaya produksi adalah 900 dan = 300.
BAB 4
KESIMPULAN DAN SARAN
4.1 Kesimpulan
Dari pembahasan pada bab sebelumnya dapat disimpulkan bahwa:
1. Langkah-langkah menentukan nilai ekstrim suatu fungsi dengan kendala fungsi lain menggunakan metode pengali Lagrange adalah sebagai berikut: a. Maksimumkan (Minimumkan) , , , … ,
dengan kendala
…
, 1,2, … , .
b. Diperoleh fungsi baru Lagrange:
,λ λ
c. Syarat perlu untuk mendapatkan titik ekstrim:
⋯ λ λ ⋯ λ 0
dengan menyelesaikan persamaan di atas diperoleh titik ekstrim ∗ d. Syarat cukup untuk ekstrim relatif
Mencari semua solusi syarat cukup untuk ektrim relatif pada kasus ini diekspresikan dalam bentuk determinan. Syarat cukup diterapkan setelah syarat perlu dipenuhi dan digunakan untuk mengetahui perilaku dari ,λ
pada nilai kritisnya.
4.2 Saran
1. Dalam skripsi ini, penulis hanya menguraikan tentang optimasi bersyarat dengan kendala persamaan dan penerapannya. Bagi pembaca yang berminat untuk mendalami teknik optimasi bersyarat dapat mengembangkan skripsi ini lebih lanjut, khususnya optimasi bersyarat dengan kendala pertidaksamaan. 2. Permasalahan yang dikaji dalam penelitian ini hanya metode pengali Lagrange
dengan 3 variabel keputusan. Oleh karena itu, diperlukan pengembangan yang lebih lanjut untuk permasalahan yang lebih rumit.
BAB 2
LANDASAN TEORI
2.1 Pemrograman Non linier
Pemrograman non linier adalah suatu bentuk pemrograman yang berhubungan dengan suatu perencanaan aktivitas tertentu yang dapat diformulasikan dalam model matematika yang memuat fungsi tujuan non linier dan fungsi kendala linier atau non linier. Hal ini didasarkan pada penemuan beberapa contoh penerapan dalam dunia usaha bisnis yang menggunakan asumsi ketaklinieran dalam membuat perencanaan. Bentuk umum dari pemrograman non linier adalah untuk menentukan , , … , , sehingga mencapai tujuan yaitu:
Memaksimumkan/meminimumkan : , , , … , 2.1
dengan kendala : , ,
0
1,2, … ,
di mana dan merupakan fungsi-fungsi dengan n variabel keputusan.
2.2 Maksimum dan Minimum
Dalam program non linier tidak selamanya terdapat satu titik maksimum ataupun minimum. Sebuah fungsi dapat memiliki lebih dari satu maksimum ataupun minimum.
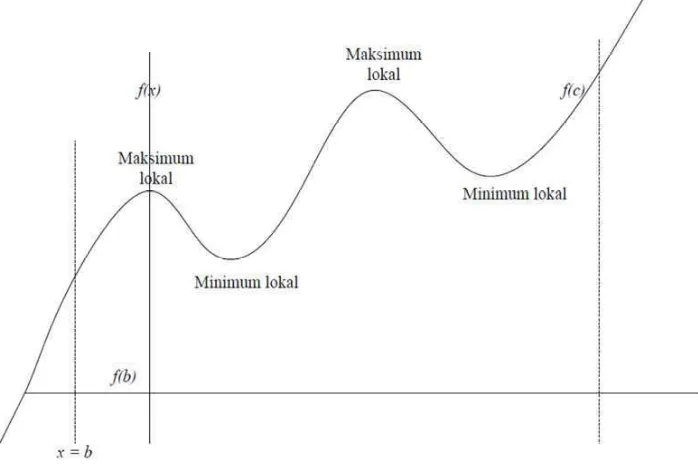
dan disebut nilai maksimum pada . Sebaliknya, minimum mutlak (minimum global) dari adalah nilai yang paling rendah dari seluruh nilai-nilai fungsi tersebut. Dengan kata lain, dikatakan memiliki minimum mutlak (global) di jika untuk semua di , di mana adalah daerah asal (domain) dari dan disebut nilai minimum pada . Jika memiliki maksimum atau minimum lokal di , maka adalah titik kritis . Jika tidak memiliki maksimum atau minimum dan memiliki kemiringan 0 di , maka adalah titik belok (saddle point) (Stewart, 1999). Dengan demikian suatu fungsi yang mempunyai titik maksimum kurvanya berbentuk cembung ke atas dan fungsi yang mempunyai titik minimum kurvanya berbentuk cembung ke bawah, diperlihatkan oleh Gambar 2.1.
Gambar 2.1 Grafik Maksimum dan Minimum Uji Turunan Pertama
Andaikan adalah titik kritis dari fungsi kontinu .
1. Jika berubah dari positif ke negatif pada , maka memiliki maksimum lokal pada .
2. Jika berubah dari negatif ke positif pada , maka memiliki minimum lokal pada .
8
3. Jika tidak berubah tanda dari positif ke negatif atau sebaliknya pada , maka tidak memiliki maksimum ataupun minimum lokal pada .
Uji Turunan Kedua
Andaikan kontinu dekat .
1. Jika 0 dan 0, maka memiliki minimum lokal pada . 2. Jika 0 dan 0, maka memiliki maksimum lokal pada .
Pada kasus suatu fungsi dengan satu variabel bebas nilai ekstrim dapat dilukiskan dalam suatu grafik dengan dua dimensi. Titik maksimum dilukiskan sebagai puncak suatu bukit dan titik minimum sebagai dasar suatu lembah. Dengan dua variabel bebas, fungsi , merupakan bidang yang berada dalam ruang berdimensi tiga. Meskipun titik maksimum dilukiskan sebagai puncak bukit dan titik minimum dilukiskan sebagai dasar lembah, akan tetapi baik bukit maupun lembah mempunyai sifat tiga dimensi.
Definisi 2.1:
Titik , dikatakan sebagai titik stasioner pada daerah asal fungsi jika
, 0 dan ! , 0.
Definisi 2.1, menyatakan bahwa syarat perlu adanya nilai ekstrim fungsi dua variabel adalah fungsi mempunyai turunan parsial pertama dan adanya titik yang memenuhi turunan pertama sedemikian sehingga nilainya nol.
Andaikan adalah fungsi dua variabel dari dan sedemikian sehingga dan turunan-turunan parsial orde kedua kontinu. Andaikan pula bahwa
, 0 dan ! , 0.
1. , dikatakan sebagai nilai maksimum , jika:
, !! , " # ! , $ 0, dan , 0 atau
!! , 0.
2. , dikatakan sebagai nilai minimum , jika:
, !! , " # ! , $ 0, dan , 0 atau
3. , !! , " # ! , $ 0, uji gagal dan , dikatakan bukan nilai ekstrim dan , disebut dengan titik pelana.
Pada fungsi multivariabel (lebih dari satu variabel bebas), yaitu
, , … , untuk uji syarat kedua dapat menggunakan suatu determinan yang dikenal dengan nama determinan Hessian.
Contoh 2.1:
Tentukan nilai ekstrim dari fungsi 12 %" 45 () 40 *) 5 pada
"∞, ∞
Penyelesaian :
Syarat perlu untuk mencari nilai ekstrim yang pertama adalah turunan pertama dari adalah 0. Maka 60 (" 3 *) 2 0, sehingga diperoleh titik-titik kritis dari yaitu 0, 1 dan 2. Turunan kedua dari adalah 60 4 *" 9 ) 4 , sehingga
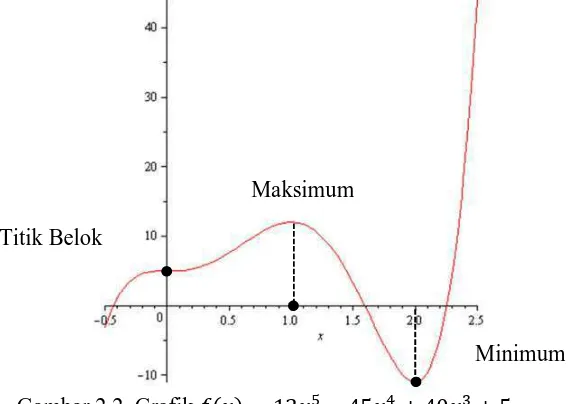
0 untuk 1 dan 0 untuk 2. Maka memiliki maksimum di 1 dan minimum di 2. Sehingga 1 12 merupakan nilai maksimum dari dan 2 "11 merupakan minimum dari . Grafiknya diperlihatkan oleh Gambar 2.2.
Gambar 2.2 Grafik 12 %" 45 () 40 *) 5 Maksimum
Minimum Titik Belok
10
2.3 Matriks Hessian
Matriks Hessian adalah matriks yang setiap elemennya dibentuk dari turunan pasial kedua dari suatu fungsi. Misalkan fungsi dengan / variabel yang memiliki turunan parsial kedua dan turunannya kontinu. Matriks Hessian dari
ditulis H adalah: menghapus / " @ baris dan kolom yang bersesuaian dari matriks tersebut.
Contoh 2.2:
Andaikan A adalah suatu matriks berukuran 3 ? 3 sebagai berikut:
A B2 6 31 5 2
Leading principal minor ke @ dari suatu matriks / ? / diperoleh dengan menghapus / " @ baris terakhir dan kolom yang bersesuaian. Dari matriks A di atas, maka leading principal minor ke-1 adalah 2 (hapus dua baris dan dua kolom terakhir). Leading principal minor ke-2 adalah:
D2 61 5E
Dengan demikian, leading principal minor ke-3 adalah matriks A itu sendiri. Determinan dari suatu leading principal minor adalah determinan leading principal. Banyaknya determinan leading principal dari suatu matriks / ? / adalah /.
Untuk menentukan apakah suatu matriks adalah definit positif, semidefinit positif, definit negatif, semidefinit negatif, atau indefinit dapat dilakukan suatu pengujian sederhana di mana hanya berlaku jika matriksnya simetris.
Uji Matriks Definit Positif
1. Semua elemen diagonal positif.
2. Semua determinan leading principal positif. Uji Matriks Semidefinit Positif
1. Semua elemen diagonal non negatif.
2. Semua determinan leading principal non negatif.
Suatu matriks dapat dikatakan definit negatif (semidefinit negatif), yaitu dengan melakukan uji negatif dari matriks untuk definit positif (semidefinit positif). Jika matriks tersebut memiliki sekurang-kurangnya dua elemen diagonal yang berlawanan tanda, maka matriks tersebut menjadi indefinit.
Contoh 2.3:
Untuk mendapatkan titik ekstrim dari suatu fungsi dipakai sebuah contoh sebagai berikut:
, *) " 4 ) 1
12
Maka solusi untuk menyelesaikannya tentukan titik ekstrim yang memenuhi syarat sehingga turunan pertama untuk setiap variabel adalah
46
4 7 3 ) " 4 0 2.3
46
4 5 2 " 4 2 " 2 0 2.4
0 atau 2
Kemudian substitusi masing-masing nilai dan ke persamaan 2.3. untuk 0, dan 4 46
Persamaan 2.3 dan 2.4 dipenuhi oleh titik-titik:
0,0 , 0,4 , L23 √3, 2M , L"23 √3, 2M
Untuk mengetahui titik maksimum dan minimum maka digunakan matriks Hessian untuk menyelidikinya sehingga turunan kedua dari adalah:
N
N
N 2 , dan
N
N NN 2 " 4
Jadi matriks Hessiannya menjadi
Q R 62 " 4 2 " 42 S
sehingga diperoleh Q T6 U, karena matriks Q merupakan matriks Q maka
Q Q R 62 " 4 2 " 42 S
Tabel 2.1 Nilai Matriks Hessian Untuk Masing-Masing Titik Ekstrim
, Matriks H Q Q Sifat H Sifat , ,
0,0 D 0 "4"4 0 E 0 -16 Tak tentu Titik belok 1
0,4 D0 44 0E 0 -16 Tak tentu Titik belok 1
L23 √3, 2M V4√30 40
3 √3W 4√3
16 Definit
positif Minimum "
16
9 √3 ) 1
L"23 √3, 2M V"4√30 "40
3 √3W "4√3
16 Definit
negatif Maksimum
16
9 √3 ) 1
14
L"23 √3, 2M
L23 √3, 2M
0,0
0,4
Grafik dalam ruang tiga dimensi diperlihatkan oleh Gambar 2.3.
Gambar 2.3 Grafik , *) " 4 ) 1
2.4 Optimasi
2.4.1 Optimasi Tak Bersyarat
Masalah optimasi tak bersyarat merupakan masalah optimasi yang tidak memiliki batasan-batasan, hanya memiliki fungsi tujuan yang sederhana, yaitu:
Memaksimumkan/meminimumkan: 2.5
untuk semua , , … , dan adalah sebuah fungsi yang dapat didiferensialkan. Syarat perlu dan cukup agar suatu penyelesaian ∗ merupakan penyelesaian optimal adalah
Y ∗ 46
4 Z 0 di
∗ untuk 1,2, … , / 2.6
Teorema Fermat:
Jika mempunyai minimum atau maksimum lokal di ∗ dan jika derivasi pertama dari memiliki nilai pada titik ∗ ,maka Y ∗ 0.
Teorema 2.1:
Titik ∗ adalah titik maksimum lokal dari jika dan hanya jika:
(i) Y ∗ 0
(ii) H ∗ 0 definit negatif atau "1 |Q| 0 untuk 1,2, … , / dengan H adalah matriks Hessian
Teorema 2.2:
Titik ∗ adalah titik minimum lokal dari jika dan hanya jika:
(i) Y ∗ 0
(ii) H ∗ 0 definit positif atau |Q| 0 untuk 1,2, … , / dengan H adalah matriks Hessian
Matriks juga dapat digunakan untuk uji syarat kedua pada proses optimasi tak bersyarat terutama pada fungsi multivariabel (lebih dari satu variabel bebas), yaitu menggunakan suatu determinan yang dikenal dengan nama determinan Hessian (Hessian Determinant). Determinan Hessian diturunkan dari matriks
16
bujur sangkar di mana elemen-elemennya merupakan turunan kedua parsial. Jika
, , … , maka matriks Hessiannya mempunyai dimensi n ? n. Diagonal utama (principal diagonal) dari matriks Hessian terdiri dari turunan kedua parsial langsung, sedangkan elemen-elemen di luar diagonal utama merupakan turunan kedua silang.
Jadi penggunaan determinan Hessian untuk uji syarat kedua akan menghasilkan:
1. Maksimum relatif jika H ∗ definit negatif. 2. Minimum relatif jika H ∗ definit positif.
3. Jika kedua kondisi tidak dipenuhi maka tidak diperoleh suatu kesimpulan, apakah fungsi mempunyai maksimum atau minimum.
2.4.2 Optimasi Bersyarat
Optimasi bersyarat adalah masalah optimasi yang memiliki syarat atau memiliki batasan-batasan yang merupakan masalah pemodelan matematika dalam optimasi fungsi yang mensyaratkan beberapa kondisi atau syarat untuk diperoleh solusi optimal yaitu syarat yang mengoptimumkan fungsi tujuan. Masalah optimasi bersyarat dengan kendala persamaan merupakan masalah optimasi yang dibatasi dengan batasan-batasan berupa persamaan dengan bentuk umum sebagai berikut:
Memaksimumkan/meminimumkan : 2.7
kendala. Matriks Hessian Terbatas adalah matriks yang entri-entrinya adalah turunan parsial kedua dari fungsi Lagrange berikut:
a , , b , ) b ,
Qc disebut bordered Hessian yaitu determinan Hessian asli yang dibatasi oleh turunan pertama dari fungsi kendala dengan nol sebagai principal diagonal. Ordo dari bordered principal minor ditentukan oleh principal minor yang dibatasi.
Determinan Hessian asli adalah eaa aa e.
Qc Qc disebut second bordered principal minor karena principal minor yang dibatasi mempunyai dimensi 2 ? 2.
Untuk fungsi dengan n variabel determinan Hessiannya sebagai berikut:
18
2. Minimum relatif jika Qc definit positif, di mana Qc 0 atau |Qc| 0 untuk
2,3, … , / dengan Qc adalah matriks Hessian terbatas (bordered Hessian). Uji syarat kedua dengan bordered Hessian dimulai dari Qc bukan Qc .
2.5 Metode Pengali Lagrange
Salah satu metode yang digunakan untuk menyelesaikan masalah ekstrim terbatas adalah dengan cara substitusi. Dengan metode substitusi, salah satu variabel bebas dari persamaan terkendala disubstitusikan pada fungsi tujuan yang akan dicari nilai ekstrimnya. Sebagai hasilnya, masalah ekstrim terkendala diselesaikan melalui ekstrim bebas fungsi. Namun demikian, metode substitusi tidak selalu membawa hasil, jika batasan-batasannya tidak hanya melibatkan satu persamaan kendala.
Disamping itu, masalah-masalah ekstrim terbatas sering timbul dalam masalah-masalah nyata, di mana batasan-batasannya tidak hanya satu fungsi. Masalah yang sering timbul dengan metode substitusi adalah tidak mudah untuk menentukan titik kritisnya. Salah satu metode untuk mengatasi masalah ekstrim terkendala adalah metode pengali Lagrange. Metode pengali Lagrange dikembangkan didasarkan pada kenyataan bahwa ekstrim terbatas, nilai ekstrimnya selalu terletak pada titik kritisnya. Metode pengali Lagrange menyediakan suatu metode aljabar yang cukup baik untuk menentukan titik kritis, sehingga masalah ekstrim terkendala dengan metode pengali Larange dapat di atasi.
optimalitas dari permasalahan program nonlinier. Metode pengali Lagrange dimulai dengan pembentukan fungsi Lagrange yang didefinisikan sebagai:
a ,λ ) ∑ij λ 2.9
Asumsikan masalah maksimisasi suatu fungsi kontinu dan dapat diturunkan , , … , dengan kendala , , … , , di mana juga kontinu dan dapat diturunkan. Kondisi tersebut menyarankan bahwa dapat dipilih variabel pada kendala dan menyatakan variabel yang lain, sehingga Q , , … , k . Kemudian disubstitusikan ke fungsi tujuan untuk mendapatkan:
T , , … , k , Q , , … , k U 2.10
Dalam bentuk persamaan 2.10, metode klasik dapat diterapkan karena fungsinya tanpa kendala. Suatu syarat perlu untuk titik ekstrim adalah dengan menghilangkan semua turunan pertama yaitu 4l
4 Z 0, di mana 1,2, … , / " 1.
Dengan menggunakan dalil rantai diperoleh: 4l
substitusi persamaan 2.12 ke persamaan 2.11, sehingga:
20 turunan parsial pertama dari fungsi Lagrangenya yang didefinisikan sebagai
Syarat cukup sebuah fungsi agar mempunyai minimum/maksimum dapat ditentukan dengan matriks Hessian terbatas. Matriks Hessian Terbatas (Bordered Hessian) didefinisikan sebagai berikut:
P• adalah transpose dari matriks P,
dan
j ~ ~ menjadi definit positif atau negatif untuk setiap variasi nilai ~ adalah setiap akar dari polinomial , yang diperoleh dari determinan persamaan di bawah ini harus positif atau negatif.
f
= turunan untuk pada persamaan kendala larange ke
22
~ ~
2.24 Pengali Lagrange mempunyai arti secara fisik yang menarik, dimisalkan terdapat permasalahan optimasi dengan satu kendala sebagai berikut:
Maksimumkan / minimumkan 2.18
dengan kendala
Fungsi Lagrangenya adalah
a ,λ )λy " z 2.19
Syarat perlu untuk penyelesaiannya adalah 4|
4 } 0 untuk ‡ 1,2, … , / dan 2.20
4|
4λ 0 2.21
Persamaan 2.23 dan 2.24 menghasilkan hasil yang final yaitu:
~ λ ~
atau ~ λ∗~ 2.25
Dari persamaan 2.22 pada penyelesaian optimum, perubahan fungsi tujuan berbanding lurus dengan perubahan kendala dengan faktor sebesar pengali Lagrange yaitu λ.
2.6 Utilitas Marjinal
Fungsi utilitas adalah fungsi yang menjelaskan besarnya utilitas (kepuasan, kegunaan) yang diperoleh seseorang dari mengkonsumsi suatu barang atau jasa. Pada umumnya semakin banyak jumlah suatu barang dikonsumsi semakin besar utilitas yang diperoleh, kemudian mencapai titik puncaknya (titik jenuh) pada jumlah konsumsi tertentu, sesudah itu justru menjadi berkurang atau bahkan negatif jika jumlah barang yang dikonsumsi terus menerus ditambah.
Utilitas total merupakan fungsi dari jumlah barang yang dikonsumsi. Persamaan utilitas total (U) dari mengkonsumsi suatu jenis barang berupa fungsi kuadrat parabolik, dengan kurva berbentuk parabola terbuka ke bawah. Utilitas marjinal (MU) adalah utilitas tambahan yang diperoleh dari setiap satu unit barang yang dikonsumsi. Secara matematik, fungsi utilitas marjinal merupakan derivatif pertama dari fungsi utilitas total. Jika fungsi utilitas total dinyatakan dengan
‰ { di mana U melambangkan utilitas total dan Q jumlah barang yang dikonsumsi, maka utilitas marjinal
Š‰ ‰ ‹Œ‹•. 2.26
24
Grafiknya kurva fungsi utilitas diperlihatkan oleh Gambar 2.4.
Gambar 2.4 Grafik Fungsi Utilitas
Karena fungsi utilitas total yang nonlinier pada umumnya berbentuk fungsi kuadrat, fungsi utilitas marjinalnya akan berbentuk fungsi linier. Kurva utilitas marjinal (MU) selalu mencapai nol tepat pada saat kurva utilitas total (U) berada pada posisi puncaknya.
Contoh 2.3:
Utilitas total ‰ { 90{ " 5{ , utilitas marjinalnya adalah
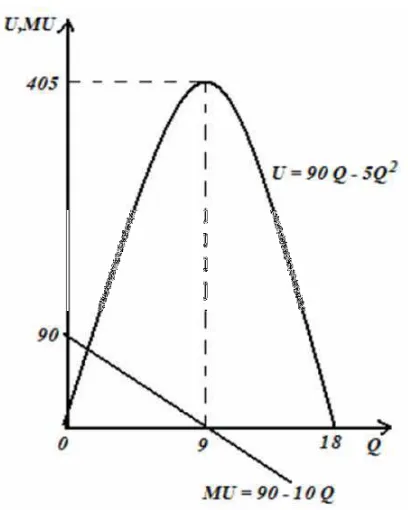
Š‰ ‰ 90 " 10{ ‰ maksimum pada Š‰ 0 sehingga 90 " 10{ 0 → { 9 maka ‰i••‘ i’i 90 9 " 5 9
Grafiknya diperlihatkan oleh Gambar 2.5.
Gambar 2.5 Grafik ‰ 90{ " 5{ dan Š‰ 90 " 10{
2.7 Produk Marjinal
Produk marjinal (MP) ialah produk tambahan yang dihasilkan dari suatu unit tambahan faktor produksi yang digunakan. Secara matematik, fungsi produk marjinal merupakan derivatif pertama dari fungsi produk total. Jika fungsi produk total dinyatakan ” di mana ” melambangkan jumlah produk total dan adalah jumlah masukan, maka produk marjinal:
Š” ” ‹•‹ 2.27
Karena fungsi produk total yang nonlinier pada umumnya berbentuk fungsi kubik, fungsi produk marjinalnya akan berbentuk fungsi kuadrat (parabolik). Kurva produk marjinal (MP) selalu mancapai nilai ekstrimnya. Dalam hal ini, nilai maksimum tepat pada saat kurva produk total (P) berada pada posisi titik beloknya. Produk total mancapai puncaknya ketika produk marjinalnya nol. Sesudah kedudukan ini, produk total menurun bersamaan dengan produk marjinal
26
menjadi negatif. Area di mana produk marjinal negatif menunjukan bahwa penambahan penggunaan masukan yang bersangkutan justru akan mengurangi jumlah produk total (Dumairy, 1996).
Contoh 2.4:
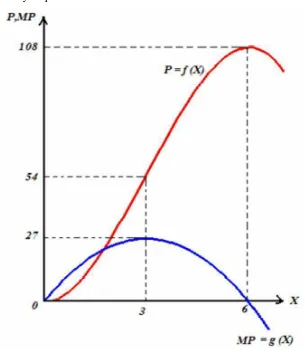
Produksi total ” 9 " *, produk marjinalnya adalah
Š” ” 18 " 3
sehingga ”i••‘ i’i pada ” 0 pada 6 dengan ”i••‘ i’i 108
” berada dititik belok dan Š” maksimum pada ”" Š” ′ 0 yaitu pada 3
Grafiknya diperlihatkan oleh Gambar 2.6.
PENDAHULUAN
1.1 Latar Belakang
Dalam kehidupan sehari-hari baik disadari maupun tidak, optimasi selalu dilakukan untuk memenuhi kebutuhan. Tetapi optimasi yang dilakukan masyarakat awam lebih banyak dilandasi oleh intuisi daripada teori optimasi. Dalam masalah optimasi terdapat dua bentuk optimasi yaitu fungsi optimasi tak bersyarat dan fungsi optimasi bersyarat. Banyak aplikasi dari pemodelan matematika dalam optimasi fungsi yang mensyaratkan beberapa kondisi atau syarat untuk memperoleh suatu solusi optimal di mana syarat tersebut yang mengoptimumkan fungsi tujuan. Persoalan dengan model tersebut dinamakan optimasi bersyarat. Optimasi merupakan masalah yang berhubungan dengan keputusan yang terbaik, maksimum, minimum dan memberikan cara penentuan solusi yang memuaskan.
Teori optimasi sangat aplikatif pada permasalahan-permasalahan yang menyangkut pengoptimalan, baik kasus maksimasi atau minimasi. Ada banyak metode optimasi yang berkembang mengikuti perkembangan terutama di bidang industri, perdagangan dan bidang-bidang lain yang juga menggunakan teori optimasi.
Metode pengali Lagrange (Multiplier Lagrange) adalah sebuah teknik yang dapat digunakan untuk menyelesaikan masalah optimasi dengan kendala persamaan. Sesuai namanya, konsep pengali Lagrange dikemukakan oleh Joseph Louis Lagrange (1736-1813). Inti dari metode pengali Lagrange adalah mengubah titik ekstrim terkendala menjadi persoalan titik ekstrim bebas kendala. Teori pengali Lagrange digunakan untuk menangani optimalitas dari permasalahan program nonlinier.
Pada diferensial fungsi majemuk dikenal konsep diferensial parsial. Dalam fungsi majemuk dapat dilakukan penyelidikan mengenai kedudukan-kedudukan
2
khusus dari sebuah fungsi seperti halnya diferensial pada sebuah fungsi dengan satu variabel bebas. Nilai-nilai ekstrim (maksimum atau minimum) dari sebuah fungsi majemuk dapat dicari dengan menggunakan konsep diferensial parsial. Dalam penerapannya sering kali diharuskan untuk mengoptimumkan (menentukan nilai ekstrim) dari sebuah fungsi, yakni menentukan nilai maksimum atau minimum suatu fungsi, tetapi ada syarat yang harus dipenuhi. Dengan kata lain fungsi yang hendak dioptimumkan menghadapi suatu kendala (constraint). Kasus optimasi bersyarat banyak dijumpai dalam berbagai bidang, di antaranya seorang insinyur teknik mungkin akan meminimumkan frekuensi kerusakan walaupun harus memperhatikan jumlah biaya untuk dua jenis alat pencegah kerusakan yang terbatas jumlahnya dan konsumen mungkin akan memaksimumkan utilitas yang diperoleh dari konsumsi barang-barang dengan memperhatikan penghasilannya yang terbatas.
Metode pengali Lagrange merupakan salah satu cara yang dapat digunakan untuk menentukan titik ekstrim suatu fungsi berkendala, di mana kendalanya berbentuk persamaan. Metode pengali Lagrange paling banyak dipakai dengan pertimbangan prinsip kerjanya sederhana dan mudah dimengerti. Untuk menentukan nilai ekstrim fungsi berkendala tersebut digunakan metode pengali Lagrange, yaitu dengan cara membentuk sebuah fungsi baru yang merupakan penjumlahan dari fungsi yang hendak dioptimumkan ditambah hasil kali pengali Lagrange atau λ dengan fungsi kendalanya. Metode pengali Lagrange digunakan untuk memperoleh maksimum atau minimum dari fungsi dengan pembatasan berbentuk persamaan.
1.2 Perumusan Masalah
1.3 Batasan Masalah
Dalam penulisan skripsi ini, penulis hanya membatasi permasalahannya pada pembahasan tentang masalah optimasi dengan metode pengali Lagrange. Metode pengali Lagrange digunakan untuk menentukan nilai ekstrim suatu fungsi dengan kendala fungsi lain dan menerapkan metode pengali Lagrange untuk menyelesaikan optimasi bersyarat khususnya dalam bidang ekonomi.
1.4 Tinjauan Pustaka
Alpha C. Chiang (2005), dalam bukunya yang berjudul Fundamental Methods of Mathematical Economics, menyatakan bahwa metode pengali Lagrange adalah sebuah teknik dalam menyelesaikan optimasi dengan kendala persamaan. Jika permasalahan yang dihadapi adalah memaksimalkan , dengan kendala
, , di mana c adalah konstanta. Maka fungsi Lagrangenya adalah:
, λ , 1.1
di mana λ adalah pengali Lagrange dengan kondisi optimalnya diperoleh melalui 0.
Prayudi (2009), dalam bukunya yang berjudul Kalkulus Lanjut, menyatakan bahwa Salah satu metode untuk mengatasi masalah ekstrim terkendala adalah metode pengali Lagrange. Metode pengali Lagrange dikembangkan didasarkan pada kenyataan bahwa ekstrim terbatas, nilai ekstrimnya selalu terletak pada titik kritisnya. Metode pengali Lagrange menyediakan suatu metode aljabar yang cukup baik untuk menentukan titik kritis, sehingga masalah ekstrim terkendala dengan metode pengali Larange dapat di atasi.
4
Sri Mulyono (2004), dalam bukunya yang berjudul Riset Operasi, menyatakan bahwa jika suatu fungsi tujuan , , … , dengan kendala
, , … , , maka fungsi Lagrangenya adalah:
, , … , , , … , 1.2
dan kemudian syarat perlu untuk suatu nilai stasioner adalah: ! 0
1.3
, , … , 0 1.4
Luknanto (2000), dalam bukunya yang berjudul Pengantar Optimasi Non linier, menyatakan bahwa optimasi multivariabel dengan kendala persamaan mempunyai bentuk umum sebagai berikut:
Minimumkan : " 1.5
kendala : # 0 untuk $ 1,2, … , ' 1.6
Metode pengali Lagrange dipakai untuk menyelesaikan optimasi yang dirumuskan persamaan 1.9 dan 1.10. Metode pengali Lagrange dimulai dengan pembentukan fungsi Lagrange yang didefinisikan sebagai:
,λ ∑)#* λ# # 1.7
1.5 Tujuan Penelitian
1.6 Manfaat Penelitian
Manfaat dari penelitian ini adalah sebagai berikut:
1. Membantu penulis dalam menerapkan ilmu-ilmunya sehingga dapat semakin memantapkan pemahaman mengenai teori-teori yang diperoleh selama mengikuti perkuliahan serta mampu menerapkan ilmunya dalam kehidupan nyata.
2. Menambah wawasan penulis tentang metode pengali Lagrange, serta dapat mencari solusi optimal dari kasus yang berhubungan dengan pengali Lagrange.
3. Dapat digunakan sebagai tambahan informasi dan referensi bacaan untuk mahasiswa matematika, terlebih bagi mahasiswa yang hendak melakukan penelitian serupa.
1.7 Metode Penelitian
Penelitian ini adalah penelitian literatur yang disusun dengan langkah-langkah sebagai berikut:
1. Mencari literatur dari beberapa buku, jurnal, situs dan karya tulis lainnya yang berhubungan dengan metode pengali Lagrange.
2. Penjabaran mengenai definisi dari program nonlinier, metode pengali Lagrange, matriks hessian, serta maksimum dan minimum.
3. Pengerjaan contoh yang dikerjakan dengan metode pengali Lagrange.
4. Penyelesaian masalah optimasi bersyarat dalam bidang ekonomi dengan metode pengali Lagrange.
5. Membuat kesimpulan.
METODE PENGALI LAGRANGE DAN APLIKASINYA DALAM BIDANG EKONOMI
ABSTRAK
Metode pengali Lagrange adalah sebuah teknik yang dapat digunakan untuk menyelesaikan masalah optimasi dengan kendala persamaan. Inti dari metode pengali Lagrange adalah mengubah titik ekstrim terkendala menjadi persoalan titik ekstrim bebas kendala. Teori Lagrange digunakan untuk menangani optimalitas dari permasalahan program nonlinier. Dalam tulisan ini akan ditunjukkan suatu persoalan mencari nilai optimum suatu fungsi optimasi bersyarat dengan menggunakan metode pengali Lagrange dan menyelesaikan masalah optimasi bersyarat di dalam bidang ekonomi. Langkah-langkah menentukan nilai optimum menggunakan metode pengali Lagrange yaitu dengan membentuk sebuah fungsi baru yang merupakan penjumlahan dari fungsi yang hendak dioptimumkan di tambah hasil kali pengali Lagrange λ dengan fungsi kendalanya.
v ABSTRACT
Lagrange multiplier method is a technique that can be used to solve optimization problems with equality constraint. The mean of this method is to change constrained extreme point into unconstrained extreme point. That theory is used to handle the optimalization for nonlinear programming problem. In this research will show problems to find optimum value for a condition optimate function with Lagrange multiplier method and solve problem from condition optimization in economy. Steps to get optimum value with Lagrange multiplier method is making a new function result to sum from the function that we want to optimate with multiply of multiplier Lagrange λ with its constraint function.
Keyword: Nonlinear Programming, Optimization, Optimum Value, Lagrange Multiplier
METODE PENGALI LAGRANGE DAN APLIKASINYA
DALAM BIDANG EKONOMI
SKRIPSI
RAHMAD HIDAYAT
110803018
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat
mencapai gelar Sarjana Sains
RAHMAD HIDAYAT
110803018
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
MEDAN
2015
PERSETUJUAN
Judul : Metode Pengali Lagrange dan Aplikasinya dalam Bidang Ekonomi
Kategori : Skripsi
Nama : Rahmad Hidayat
Nomor Induk Mahasiswa : 110803018
Program Studi : Sarjana (S1) Matematika
Departemen : Matematika
Fakultas : Matematika Dan Ilmu Pengetahuan Alam (FMIPA) Universitas Sumatera Utara
Diluluskan di Medan, Agustus 2015
Komisi Pembimbing:
Pembimbing 2, Pembimbing 1,
Dr. Elly Rosmaini, M.Si Dr. Sawaluddin, M.IT
NIP. 19600520 198503 2 002 NIP. 19591231 199802 1 001
Disetujui oleh:
Departemen Matematika FMIPA USU Ketua,
Prof. Dr. Tulus, M.Si
ii
METODE PENGALI LAGRANGE DAN APLIKASINYA DALAM BIDANG EKONOMI
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, Agustus 2015
Rahmad Hidayat 110803018
PENGHARGAAN
Puji dan syukur penulis panjatkan kepada Tuhan Yang Maha Esa dan Maha Penyayang, dengan limpahan karunia-Nya penulis dapat menyelesaikan penyusunan skripsi ini dengan judul Metode Pengali Lagrange dan Aplikasinya dalam Bidang Ekonomi.
Terima kasih penulis sampaikan kepada Bapak Dr. Sawaluddin, M.IT dan Ibu Dr. Elly Rosmaini, M.Si selaku pembimbing yang telah memberikan bimbingan dan telah meluangkan waktunya selama penulisan skripsi ini. Bapak Dr. Suwarno Ariswoyo, M.Si dan Bapak Dr. Faigiziduhu Bu’ulolo, M.Si selaku penguji yang telah memberikan saran dan kritik yang membangun dalam penyempurnaan skripsi ini. Terima Kasih kepada Bapak Prof. Dr. Tulus, M.Si. Ph.D dan Ibu Dr. Mardiningsih, M.Si selaku Ketua dan Sekretaris Departemen Matematika FMIPA USU. Terima kasih kepada Bapak Sutarman, M.Sc selaku Dekan FMIPA USU, Pembantu Dekan FMIPA USU, seluruh staff dan Dosen Matematika FMIPA USU, pegawai FMIPA USU seta rekan-rekan kuliah. Ucapan terima kasih juga ditujukan kepada kedua orang tua penulis Ayahanda Terimo dan Ibunda Erna Suryani serta keluarga yang selama ini memberikan dorongan yang diperlukan. Semoga Allah SWT akan membalasnya.
iv ABSTRAK
Metode pengali Lagrange adalah sebuah teknik yang dapat digunakan untuk menyelesaikan masalah optimasi dengan kendala persamaan. Inti dari metode pengali Lagrange adalah mengubah titik ekstrim terkendala menjadi persoalan titik ekstrim bebas kendala. Teori Lagrange digunakan untuk menangani optimalitas dari permasalahan program nonlinier. Dalam tulisan ini akan ditunjukkan suatu persoalan mencari nilai optimum suatu fungsi optimasi bersyarat dengan menggunakan metode pengali Lagrange dan menyelesaikan masalah optimasi bersyarat di dalam bidang ekonomi. Langkah-langkah menentukan nilai optimum menggunakan metode pengali Lagrange yaitu dengan membentuk sebuah fungsi baru yang merupakan penjumlahan dari fungsi yang hendak dioptimumkan di tambah hasil kali pengali Lagrange λ dengan fungsi kendalanya.
Kata kunci: Pemrograman Nonlinier, Optimasi, Nilai Optimum, Pengali Lagrange
LAGRANGE MULTIPLIER METHOD AND APLICATION IN ECONOMIC CASES
ABSTRACT
Lagrange multiplier method is a technique that can be used to solve optimization problems with equality constraint. The mean of this method is to change constrained extreme point into unconstrained extreme point. That theory is used to handle the optimalization for nonlinear programming problem. In this research will show problems to find optimum value for a condition optimate function with Lagrange multiplier method and solve problem from condition optimization in economy. Steps to get optimum value with Lagrange multiplier method is making a new function result to sum from the function that we want to optimate with multiply of multiplier Lagrange λ with its constraint function.
vi
1.4 Tinjauan Pustaka 3
1.5 Tujuan Penelitian 4
1.6 Manfaat Penelitian 5
1.7 Metodologi Penelitian 5
BAB 2 LANDASAN TEORI 6
2.1 Pemrograman Nonlinier 6
2.2 Maksimum Dan Minimum 6
2.3 Matriks Hessian 10
2.4 Optimasi 14
2.4.1 Optimasi Tak Besyarat 15
2.4.2Optimasi Bersyarat 16
2.5 Metode Pengali Lagrange 18
2.6 Utilitas Marjinal 23
2.7 Produk Marjinal 25
BAB 3 HASIL DAN PEMBAHASAN 27
3.1Optimasi dengan Metode Pengali Lagrange 27 3.2Utilitas Marjinal Parsial dan Keseimbangan Konsumsi 31 3.3Produk Marjinal Parsial dan Keseimbangan Produksi 35
BAB 4 KESIMPULAN DAN SARAN 40
4.1 Kesimpulan 40
4.2 Saran 41
DAFTAR PUSTAKA 42
DAFTAR TABEL
Nomor Judul Halaman
Tabel
viii
Nomor Judul Halaman
Gambar
2.1 Grafik Maksimum dan Minimum 6
2.2 Grafik 12 45 40 5 9
2.3 Grafik , 4 1 14
2.4 Grafik Fungsi Utilitas 24
2.5 Grafik 90 5 dan 90 10 25
2.6 Grafik 9 dan 18 3 26