2-Eksponen Digraph Dwiwarna Asimetrik Dengan Dua Cycle Yang Bersinggungan

(1)

SKRIPSI

INDRA SYAHPUTRA 040803003

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

(2)

2-EKSPONEN DIGRAPH DWIWARNA ASIMETRIK DENGAN DUA CYCLE YANG BERSINGGUNGAN

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains

INDRA SYAHPUTRA 040803003

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

(3)

PERSETUJUAN

Judul : 2-EKSPONEN DIGRAPH DWIWARNA

ASIMETRIK DENGAN DUA CYCLE YANG BERSINGGUNGAN

Kategori : SKRIPSI

Nama : INDRA SYAHPUTRA

Nomor Induk Mahasiswa : 040803003

Program Studi : SARJANA (S1) MATEMATIKA

Departemen : MATEMATIKA

Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN

ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA

Medan, Februari 2009

Komisi Pembimbing :

Pembimbing 2 Pembimbing 1

Dra. Mardiningsih, M.Si Dr. Saib Suwilo, MSc.

NIP.131803344 NIP. 131796149

Diketahui oleh

Departemen Matematika FMIPA USU Ketua,

(4)

ii

PERNYATAAN

2-EKSPONEN DIGRAPH DWIWARNA ASIMETRIK DENGAN DUA CYCLE YANG BERSINGGUNGAN

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, Februari 2009

(5)

PENGHARGAAN

Puji dan syukur penulis serahkan kehadirat Allah SWT yang telah mem-berikan berkat dan rahmatNya sehingga penulis dapat menyelesaikan skripsi yang berjudul ” 2-Eksponen Digraph Dwiwarna Asimetrik Dengan Dua Cy-cle Yang Bersinggungan”ini dengan baik. Skripsi ini sebagai salah satu mata kuliah wajib yang harus diselesaikan oleh seluruh mahasiswa Fakultas MIPA De-partemen Matematika.

Pada kesempatan ini penulis mengucapkan terima kasih kepada :

1. Bapak Dr. Eddy Marlianto, M.Sc, selaku Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Sumatera Utara.

2. Bapak Dr. Saib Suwilo, M.Sc, dan Bapak Henry Rani S, M.Si selaku Ketua dan Sekretaris Departemen Matematika di FMIPA USU Medan.

3. Bapak Dr. Saib Suwilo, M.Sc, selaku dosen pembimbing I dan Dra. Mar-diningsih, M.Si selaku dosen pembimbing II yang telah memberi dukungan moral, motivasi dan ilmu pengetahuan bagi penulis dalam menyelesaikan penelitian ini.

4. Seluruh Staf Pengajar Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Sumatera Utara.

5. Ayahanda Surajiman dan Ibunda Masitah yang selalu memberikan dukun-gan moril dan materiel serta doa yang tiada hentinya kepada penulis serta keluarga besar ayah dan ibu khususnya kepada bu idah dan tulang ucok yang telah banyak membantu penulis dari awal kuliah hingga selesai. Dan terima kasih juga untuk adik-adikku heri, yanti, nisa, dan irna yang telah memberikan dukungan moril yang sangat berarti bagi penulis.

Tak lupa, penulis juga mengucapkan terima kasih kepada para senior dan juniorku di departemen matematika yang telah membantu dalam penyelesaian skripsi ini, serta seluruh rekan-rekan math’04 seperjuangan yakni deni, darto, igun, hemi, ija, serta rekan-rekan lainnya yang tidak dapat disebutkan satu-persatu. Se-moga Allah SWT memberikan balasan atas jasa-jasa mereka yang telah diberikan kepada penulis.

Penulis menyadari masih banyak kekurangan dalam penulisan ini, untuk itu penulis meminta saran dan kritik yang membangun dari pembaca sekalian.

(6)

iv

ABSTRAK

Andaikan D adalah digraph-dwiwarna asimetrik atas n = 2m, m ≥ 4 verteks dengan dua cycle yang memiliki satu verteks persekutuan dengan panjang masing-masing cycle m dan m+ 1. Karena D adalah asimetrik maka ada dua cycle yang panjangnya m dinotasikan dengan γ1 dan γ2 dan dua cycle yang panjang m+ 1 dinotasikan denganγ3 danγ4 serta memiliki cycle-cycle dengan panjang2. Bilaγ1 danγ3 masing-masing memiliki tepat satu arc biru, penelitian ini memperlihatkan bahwa dengan menggunakan submatriks ordo2×2dengan determinan1dari cycle matriks di D maka diperoleh exp2(D)≤ 1

2(2n

(7)

2-EXPONENTS OF TWO-COLORED DIGRAPHS WITH TWO CYCLES WHICH HAVE A COMMON VERTEX

ABSTRACT

Let D be a asymmetric two-colored digraph on n = 2m, m ≥ 4 vertices which have a common vertex and the length of each cycles is m and m+ 1. Since D is asymmetric, there exists two cycles of length m are denoted by γ1 and γ2 and two cycles of length m+ 1 are denoted by γ3 and γ4 and also has cycles of length 2. If γ1 dan γ3 have each exactly one blue arc, This research will show that usedly a 2 by 2 submatrix with determinant1of cycle matrix inD then obtainedexp2(D)≤

1 2(2n

(8)

vi

DAFTAR ISI

Halaman

PERSETUJUAN i

PERNYATAAN ii

PENGHARGAAN iii

ABSTRAK iv

ABSTRACT v

DAFTAR ISI vi

DAFTAR GAMBAR vii

BAB

1. PENDAHULUAN 1

1.1. Latar Belakang Penelitian 1

1.2. Masalah Penelitian 2

1.3. Tinjauan Pustaka 3

1.4. Tujuan Penelitian 5

1.5. Manfaat Penelitian 5

1.6. Metodologi Penelitian 5

2. LANDASAN TEORI 7

2.1. Primitifitas dari Digraph Terhubung Kuat 7

2.2. Primitifitas dari Digraph-dwiwarna Terhubung Kuat 11

2.3. Matriks Adjancency 14

2.4. Eksponen Digraph 16

2.5. 2-Eksponen dari Digraph-dwiwarna 19

2.6. Beberapa Fakta Tentang Digraph-Dwiwarna Asimetrik Yang

Memuat Cycle Primitif 24

3. HASIL UTAMA 27

4. KESIMPULAN DAN SARAN 34

4.1. Kesimpulan 34

4.2. Saran 35

(9)

DAFTAR GAMBAR

Gambar Halaman

2.1 Digraph dengan 5 verteks dan 6 arc 8

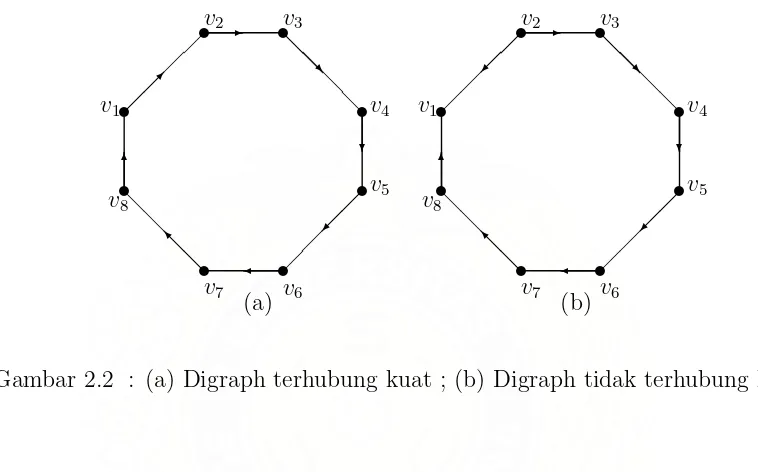
2.2 (a) Digraph terhubung kuat ; (b) Digraph tidak terhubung kuat 9

2.3 Digraph simetrik yang terdiri dari 6 verteks dan 12 arc 10

2.4 Digraph primitif dengan 3 verteks dan 4 arc 10

2.5 Digraph-dwiwarna dengan 3 verteks dan 4 arc 12

2.6 2-Digraph asimetrik yang terdiri dari 6 verteks dan 12 arc 13

(10)

BAB 1

PENDAHULUAN

1.1 Latar Belakang Penelitian

Digraph merupakan salah satu disiplin ilmu matematika. Suatu digraph

terdiri dari titik-titik yang dihubungkan oleh garis berarah. Titik-titik tersebut

disebut verteks dari digraph dan garis berarah yang menghubungkan titik-titik

tersebut disebut arc dari digraph. Suatu digraph dikatakan terhubung kuat bila

untuk setiap pasangan verteks u dan v terdapat walk dari u ke v dan walk dari

v ke u. Suatu digraph D adalah primitif jika dan hanya jika terdapat bilangan

bulat positifk sehingga untuk setiap pasangan verteksudan v terdapat walk dari

u ke v dengan panjang k. Bilangan bulat terkecil dari k yang demikian disebut

eksponen dari digraph yang dinotasikanexp(D).

Penelitian digraph sampai saat ini masih difokuskan pada digraph-dwiwarna.

Digraph-dwiwarna, disingkat 2-digraph adalah digraph yang arc-arcnya terdiri dari

dua warna, warna arc yang dipakai di sini adalah warna merah dan biru(Fornasini

dan Valcher, 1997). Suatu digraph-dwiwarna D adalah 2-primitif bila terdapat

bilangan bulat tak negatif h dan k sehingga untuk setiap pasangan verteks u

dan v di D terdapat walk dari u ke v dengan panjang h+ k dan terdiri dari

h arc berwarna merah dan k arc berwarna biru. Bilangan bulat positif terkecil

h+k diantara semua bilangan bulat tak negatif h dan k yang demikian disebut

2-eksponen digraph dwiwarnaD yang dinotasikan exp2(D).

Riset tentang 2-eksponen dari digraph-dwiwarna dimulai oleh Shader dan

Suwilo (2003). Mereka memperlihatkan bahwa bila D adalah digraph-dwiwarna

2-primitif atasn verteks, maka 2-eksponen terbesar dariD terletak pada interval

[1 2(n

3₋_5n2_), 3 2n

(11)

mulai berkembang (lihat Lee dan Yang 2005, Gao dan Shao 2005, Suwilo 2005,

Shader dan Suwilo 2006).

Selanjutnya, riset pada 2-eksponen digraph-dwiwarna berkembang pada

ke-las digraph-dwiwarna asimetrik. Riset pada keke-las digraph-dwiwarna asimetrik

telah dilakukan oleh Suwilo (2005) yang menentukan 2-eksponen dari digraph

dwiwarna komplit asimetrik. Pada tahun 2008, suwilo memperlihatkan bahwa

bila D adalah digraph-dwiwarna yang berbentuk lollipops dan asimetrik maka

exp2(D)≤(s2−1)/2 + (s+ 1)(n−s). Sehingga seperti riset yang dilakukan Goa

dan Shao (2005), Shader dan Suwilo (2006), dan Suwilo (2008) maka penelitian

un-tuk 2-eksponen dari digraph-dwiwarna asimetrik yang terdiri dari dua cycle perlu

dilakukan. AndaikanDadalah digraph-dwiwarna asimetrik dengan dua cycle yang

bersinggungan (memiliki satu verteks persekutuan). Karena D adalah asimetrik

maka komposisi cycle-cycle dari digraph-dwiwarna tersebut adalah

r(γ1) b(γ1)

,

r(γ2) b(γ2)

,

r(γ3) b(γ3)

,

r(γ4) b(γ4)

, dan

1 1

, yang mana γ1 dimulai dari vm → v1 → v2 → v3 →

... → vm−1 → vm, γ2 dimulai dari vm → vm−1 → ... → v2 → v1 → vm, γ3

dim-ulai dari vm → vm+1 → vm+2 → ... → vn−1 → vn → vm, dan γ4 dimulai dari

vm → vn → vn−1 → vn−2 → ... → vm+1 → vm. Penelitian ini difokuskan untuk

mencari batas atas 2-eksponen dari digraph-dwiwarnaD tersebut.

1.2 Masalah Penelitian

Masalah dalam penelitian ini adalah :

Bila digraph-dwiwarnaDadalah digraph-dwiwarna asimetrik atasn = 2m,m≥4

verteks dengan dua cycle yang memiliki satu verteks persekutuan dengan panjang

masing-masing cycle m dan m+ 1, γ1 dan γ3 masing-masing memiliki tepat satu

arc biru. FungsiF(n) manakah yang memenuhi sifatexp2(D)≤F(n). F(n) yang

(12)

3

adalah banyak verteks yang dikandung oleh digraph-dwiwarnaD.

1.3 Tinjauan Pustaka

Istilah-istilah baku digraph diambil dari (Brualdi dan Ryser, 1991) dan untuk

digraph-dwiwarna diambil dari (Shader dan Suwilo, 2003). Suatu digraph adalah

suatu himpunan tak kosong V = {v0, v1, ..., vn} yang elemen-elemennya disebut

verteksdan himpunan garis-garis berarahE yang elemen-elemennya disebut arc.

Suatuwalkdengan panjangtdari sebuahdigraph Dyang menghubungkan verteks

udan verteks v adalah suatu barisan arc diD dalam bentuk

u=v0 →v1 →v2 → · · · →vt−1 →vt =v.

Suatu walk dikatakan terbuka jika u 6= v dan tertutup jika u = v. Suatu path

adalah suatu walk tanpa perulangan verteks. Suatu uv-path tertutup disebut

cycle. Suatu digraph dikatakan terhubung kuat jika untuk setiap pasangan dari

verteks u dan v diD terdapat walk dariu ke v dan terdapat walk dariv keu.

Pada tahun 1997, Fornasini dan Valcher melakukan riset tentang digraph

dwiwarna. Suatu digraph-dwiwarna D, disingkat 2-digraph D adalah suatu

di-graph D yang arc-arcnya terdiri dari dua warna, warna arc yang dipakai di sini

adalah warna merah dan biru. Suatu digraph D dikatakan simetrik bila arc dari

ukev ada di Ddan arc dari v keu ada di D. Suatu digraph-dwiwarna dikatakan

asimetrik bila digraph-dwiwarna tersebut simetrik dan arc dari verteks u ke v

diwarnai merah jika dan hanya jika arc dari verteks v ke u di warnai biru atau

sebaliknya.

Suatu (h, k)-walk dari u kev pada suatu 2-digraphD adalah suatu uv-walk

yang terdiri dari h arc berwarna merah dan k arc berwarna biru. Banyaknya arc

berwarna merah pada walkwuv dinotasikan r(wuv) dan banyak arc berwarna biru

pada walkwuvdinotasikanb(wuv). Vektor

r(wuv)

b(wuv)

disebut sebagai komposisi dari

walkwuv. Andaikan 2-digraph terhubung kuat dan misalkan {γ1, γ2, ..., γt}adalah

(13)

Dyang kolom-kolomnya disusun dari cycle-cycle di Ddan banyak baris diperoleh

dari banyak warna diD sehingga

M =

r(γ1) r(γ2) · · · r(γt)

b(γ1) b(γ2) . . . b(γt)

Sebuah 2-digraph Ddikatakan 2-primitif jika dan hanya jika terdapat

bilan-gan bulat tak negatifhdan k sehingga untuk setiap pasangan dua verteksudanv

diDterdapat (h, k)-walk dariukevdan darivkeu. Suatu 2-digraphDdikatakan

2-primitif jika dan hanya jika content dari M yaitu pembagi persekutuan

terbe-sar dari determinan submatriks-submatriks 2×2 dari M adalah 1 (Fornasini dan

Valcher, 1997).

Riset tentang 2-eksponen dari 2-digraph 2-primitif pertama kali dilakukan

oleh Shader dan Suwilo (2003). Mereka membuktikan bahwa 2-eksponen terbesar

dari digraph dwiwarna 2-primitif atas n verteks berada dalam interval [1 2(n

3 ₋

5n2_),3 2n

3_+n2₋_{n)]. Kemudian beberapa peneliti memfokuskan untuk menentukan}

2-eksponen dari 2-digraph yang terdiri dari dua cycle dengan beberapa verteks

persekutuan. Pada tahun 2005, Lee dan Yang memperlihatkan bahwa 2-eksponen

dari ministrong 2-digraph dengann−3 verteks persekutuan berada dalam interval

[2n2₋_8n_{+ 7,}_2n2₋_5n_{+ 3]. Di tahun 2006, Suwilo memperbaiki batas 2-eksponen}

dari ministrong 2-digraph yang dibuat Lee dan Yang (2005) sehingga berada dalam

interval [2n2 ₋_8n_{+ 7,}_2n2₋_7n_{+ 6]. Gao dan Shao (2005) juga memperlihatkan}

bahwa 2-eksponen dari 2-digraph atasn+s,s ≥0,m≥s+ 1 verteks yang terdiri

dari dua cycle yang memiliki n−m verteks persekutuan berada dalam interval

[2n2₋_3n_{+ 1,}_2n2₋_2n_{+ 2sn}₋_{s] dan} _{exp2(D) = 2n}2₋_4n_{+ 1 .}

Sekarang beberapa periset memfokuskan pada digraph dwiwarna asimetrik.

Suwilo (2005) memperlihatkan bahwa digraph dwiwarna komplit asimetrik atas

n verteks, 2-eksponennya berada dalam interval [2, 4] dan membuktikan untuk

setiap bilangan bulatk, 26k 64, ada suatu digraph dwiwarna komplit asimetrik

(14)

5

verteks u dan v yang berbeda arc (u, v) dan arc (v, u) berada di D. Dan suatu

digraph-dwiwarna komplit asimetrik adalah digraph-dwiwarna komplit sedemikian

hingga arc dari verteksukev diwarnai merah jika dan hanya jika arc dari verteks

v ke u di warnai biru atau sebaliknya. Pada tahun 2008, Suwilo memperlihatkan

bahwa bila D adalah digraph-dwiwarna yang berbentuk lollipops dan asimetrik

maka batas atas 2-eksponen D adalahexp2(D)≤(s2₋_{1)/2 + (s}_{+ 1)(n}₋_s).

1.4 Tujuan Penelitian

Penelitian ini bertujuan untuk mencari batas atas F(n) dari 2-eksponen

digraph-dwiwarna asimetrik D atas n = 2m, m ≥ 4 verteks dengan dua cycle

yang memiliki satu verteks persekutuan dengan panjang masing-masing cycle m

dan m+ 1, γ1 dan γ3 masing-masing memiliki tepat satu arc biru sehingga

diper-olehexp2(D)≤F(n). F(n) yang dimaksudkan pada penelitian merupakan fungsi

dengan peubah bebas n dengan n adalah banyak verteks yang dikandung oleh

digraph-dwiwarna asimetrikD.

1.5 Manfaat Penelitian

Penelitian ini memberikan teori baru tentang 2-eksponen digraph-dwiwarna

asimetrik dengan dua cycle yang bersinggungan.

1.6 Metodologi Penelitian

Penelitian ini bersifat literatur atau kepustakaan. Untuk mencari batas atas

2-eksponen dari digraph-dwiwarna asimetrik atasn = 2m, m ≥4 verteks dengan

dua cycle yang memiliki satu verteks persekutuan yang panjang masing-masing

cyclemdanm+1,γ1danγ3 masing-masing memiliki tepat satu arc biru dilakukan

dengan pendekatan sebagai berikut :

1. Permasalahan pada masalah penelitian diselesaikan dengan menggunakan

(15)

persamaan

h k

=

r(puv)

b(puv)

+Mx

denganM adalah cycle matriks berordo 2×t yang kolom-kolomnya

berben-tuk

s q

,

q s

,

1 1

, danxadalah vektor yang komponen-komponennya bilan-gan bulat tak negatif dan memperhatikan beberapa hal berikut ini :

a. Faktanya bahwa dalam digraph-dwiwarna asimetrik D atas n = 2m,

m≥4 verteks dengan dua cycle yang memiliki satu verteks

persekutu-an ypersekutu-ang ppersekutu-anjpersekutu-ang masing-masing cycle m dan m+ 1,γ1 dan γ3

masing-masing memiliki tepat satu arc biru terdapat submatrik dari cycle

ma-trikM di digraph-dwiwarna asimetrik tersebut yang memiliki

determi-nan 1. Sehingga, (h, k)-walk untuk setiap pasangan verteks u dan v di

D dapat diperoleh dari path dari u ke v dan komposisi cycle-cycle di

submatriks tersebut.

b. Shader dan Suwilo (2006) memberikan suatu pendefenisian untuk

di-gunakan dalam menentukan 2-eksponen digraph dwiwarna yang terdiri

dari dua cycle, yaitu:

ℓ′

r = max_u,v

∈V{b(γ2)r(puv)−r(γ2)b(puv)},

ℓ′

b = max_u,v

∈V{r(γ1)b(puv)−b(γ1)r(puv)}.

dengan V adalah himpunan verteks di D.

2. Berdasarkan data empiris hasil simulasi memperlihatkan bahwa 2-eksponen

dari digraph-dwiwarna asimetrik atas n = 2m, m ≥ 4 verteks dengan dua

cycle bersinggungan yang panjang masing-masing cycle m dan m+ 1, γ1

dan γ3 masing-masing memiliki tepat satu arc biru, dapat diperoleh

meng-gunakan (h, k)-walk dengan h arc merah sama dengan k arc biru. Dengan

menggunakan teknik yang digunakan pada pembuktian menentukan batas

atas 2-eksponen dari (n, s)-lollipop dwiwarna primitif asimetrik didapatkan

(16)

BAB 2

LANDASAN TEORI

Pada bab ini akan dipaparkan mengenai materi-materi yang berhubungan

dan mendukung dalam penelitian 2-eksponen digraph-dwiwarna asimetrik dengan

dua cycle yang bersinggungan. Materi tersebut mencakup pengertian dari digraph,

digraph-dwiwarna dan digraph-dwiwarna asimetrik, contoh digraph-dwiwarna dan

digraph-dwiwarna asimetrik, pengertian 2-eksponen dari digraph dwiwarna,

fakta-fakta tentang 2-eksponen digraph-dwiwarna asimetrik 2-primitif. Dengan demikian,

akan mempermudah dalam hal pembahasan hasil utama pada bab berikutnya.

2.1 Primitifitas dari Digraph Terhubung Kuat

Pada bagian ini akan dijelaskan tentang pengertian digraph, digraph

ter-hubung kuat dan digraph terter-hubung kuat yang 2-primitif.

2.1.1 Digraph.

Suatu graph berarah D atau yang disingkat digraph D adalah sebuah

ob-jek matematika yang terdiri dari suatu himpunan tak kosong V = {v0, v1, v2,· ·

·, vn} dengan elemen-elemennya disebut verteks dan himpunan garis berarah yang

menghubungkan verteks-verteks tersebut dengan elemen-elemennya disebut arc.

Suatu arc yang menghubungkan verteks u ke verteks v di digraph D dinotasikan

dengan (u, v). u disebut verteks awal dan v disebut verteks akhir.

Suatu digraph dapat direpresentasikan secara grafis dengan cara setiap verteks

direpresentasikan sebagai sebuah titik dan setiap arc (u, v) direpresentasikan

se-bagai garis lurus berarah atau kurva berarah dari titik uke v.

(17)

dan himpunan arc

E ={(v0, v1),(v1, v2),(v2, v3),(v3, v4),(v1, v4),(v4, v0)}.

Representasi grafis dari digraphD diperlihatkan oleh Gambar 2.1

t

v4

t

v1

t

v3

t

v0

tv2

✠ ❘

✠ ■

✲

✻

Gambar 2.1 : Digraph dengan 5 verteks dan 6 arc

Suatu walk dari u kev dengan panjangt adalah barisan arc dalam bentuk

u=v0 →v1 →v2 → · · · →vt−1 →vt =v.

atau

(u=v0, v1),(v1, v2),· · ·,(vt−1, vt=v).

Suatu walk dariukevdinotasikan denganuv-walk atauwuv. Suatu walk dikatakan

terbuka jika u6=v dan tertutup bila sebaliknya. Suatu uv-path adalah suatu

uv-walk tanpa perulangan verteks kecuali mungkin u = v. Suatu uv-path tertutup

disebut cycle.

Berdasarkan Gambar 2.1 di atas, berikut ini akan diperlihatkan contoh dari

walk, path, dan cycle :

a. Barisan v0 → v1 → v2 → v3 → v4 → v0 → v1 adalah suatu walk terbuka

tetapi bukan path karena ada verteks yang berulang.

b. Barisan v0 → v1 → v2 → v3 adalah suatu path karena tidak ada verteks

(18)

9

c. Barisan v0 →v1 →v4 →v0 adalah sebuah cycle.

Suatu digraph D dikatakan terhubung kuat (strongly connected) jika untuk

setiap pasangan verteksudan v diDterdapat walk dariukev dan walk dariv ke

u. Berikut ini diberikan contoh dari digraph terhubung kuat dan tidak terhubung

kuat. t v1 t v2 t v7 t v3 tv4 tv5 t v6 t v8 ✒ ✲ ❅ ❅ ❅ ❅ ❅ ❅ ❘ ❄ ✠ ✛ ❅ ❅ ❅ ❅ ❅ ❅ ■ ✻ (a) t v1 t v2 t v7 t v3 tv4 tv5 t v6 t v8 ✠ ✲ ❅ ❅ ❅ ❅ ❅ ❅ ❘ ❄ ✠ ✛ ❅ ❅ ❅ ❅ ❅ ❅ ■ ✻ (b)

Gambar 2.2 : (a) Digraph terhubung kuat ; (b) Digraph tidak terhubung kuat

Lemma berikut ini akan menjamin bahwa setiap verteks di digraphDterletak

pada suatu cycle bila digraphD terhubung kuat.

Lemma 2.1 AndaikanDadalah suatu digraph terhubung kuat, maka setiap verteks di D terletak pada suatu cycle.

Bukti. Ambil sebarang verteksu dan sebarang arc dari verteks u ke verteksv di D. Karena D terhubung kuat, maka terdapat path dari verteks u ke v dan dari

verteks v ke u, yang berakibat diperoleh suatu path tertutup diD yang dibentuk

oleh arc dari verteksuke v dan path dari verteksv keu diD. Oleh definisi, path

tertutup adalah suatu cycle dan u sebarang verteks di D, maka setiap verteks u

(19)

Suatu digraph D dikatakan simetrik bila arc dari u ke v ada di D dan arc

dari v keu ada di D. Berikut ini akan diberikan satu contoh digraph simetrik :

t

v1

t

v2

t

v6

t

v3

tv4

tv5

✒ ✠

❘

■

✠ ✒

■❘

✒

❅ ❅ ❘ ❅

❅ ❅

❅ ✠

■

Gambar 2.3 : Digraph simetrik yang terdiri dari 6 verteks dan 12 arc

2.1.2 Digraph Primitif.

Suatu digraph terhubung kuat(strongly connected)D dikatakan primitif bila

terdapat suatu bilangan bulat positif k sehingga untuk setiap pasangan verteks

u dan v di D terdapat uv-walk dan vu-walk yang panjangnya k. Bilangan bulat

positifk terkecil yang demikian disebut sebagai eksponen dariD dan dinotasikan

denganexp(D). Suatu digraph terhubung kuat D adalah primitif jika dan hanya

jika pembagi persekutuan terbesar (greatest common divisor atau disingkat gcd)

dari panjang-panjang cycle diD adalah 1 (Brualdi dan Ryser, 1991).

Andaikan himpunan C = {γ1,γ2,...,γt} adalah himpunan semua cycle di D.

Maka panjang dari cycle-cycle yang ada digraph D dinotasikan dengan ℓ(γi)

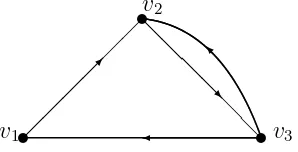
di-manai= 1,2,· · ·, t. Berikut ini diberikan contoh dari digraph primitif

t

v1

t

v2

tv3

✒ ❅

❅ ❅

❅ ❘ ■

✛

(20)

11

Dari Gambar 2.4 diperoleh dua cycle. Cycle pertamaγ1 diperoleh dariv1 →

v2 → v3 →v1 dengan panjang ℓ(γ1) = 3 dan cycle kedua γ2 diperoleh dari v2 →

v3 →v2dengan panjangℓ(γ2) = 2 sehinggagcd(3,2) = 1. Jadi digraphDtersebut

adalah primitif.

2.2 Primitifitas dari Digraph-dwiwarna Terhubung Kuat

Pada bagian ini akan dijelaskan tentang pengertian dwiwarna,

digraph-dwiwarna terhubung kuat dan digraph-digraph-dwiwarna terhubung kuat yang primitif.

2.2.1 Digraph-dwiwarna.

Suatu digraph-dwiwarna D, disingkat 2-digraph D adalah digraph D yang

arc-arcnya terdiri dari dua warna, warna arc yang dipakai di sini adalah warna

merah atau biru.

Suatu 2-digraph dapat direpresentasikan secara grafis dengan cara sebagai

berikut :

1. setiap verteks direpresentasikan sebagai suatu titik.

2. setiap arc merah dalam digraph dwiwarna direpresentasikan sebagai garis

berarah tak putus

3. setiap arc biru dalam digraph dwiwarna direpresentasikan sebagai garis

putus-putus berarah.

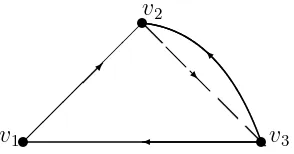
Contoh 2.2 Himpunan verteks V = {v1, v2, v3, v4} bersama dengan himpunan arc merahR={(v1, v2),(v3, v1),(v3, v2)}dan arc biruB ={(v2, v3)}adalah suatu

(21)

Representasi grafis dari digraph-dwiwarna dari Contoh 2.2 adalah sebagai berikut:

t

v1

t

v2

tv3 ✒

❅❅ ❅ ❅

❅ ❅

❅ ❅ ❘ ■

✛

Gambar 2.5 : Digraph-dwiwarna dengan 3 verteks dan 4 arc

Suatu (h, k)-walk dari u kev pada suatu 2-digraphD adalah suatu uv-walk

yang terdiri dari h arc berwarna merah dan k arc berwarna biru. Banyaknya

arc berwarna merah pada walk wuv dinotasikan dengan r(wuv) dan banyak arc

berwarna biru dinotasikan dengan b(wuv). Vektor

r(wuv)

b(wuv)

disebut komposisi dari

walk wuv. Suatu uv-path adalah suatu uv-walk tanpa perulangan verteks

ke-cuali mungkinu =v. Banyaknya arc berwarna merah pada path puv dinotasikan

dengan r(puv) dan banyak arc berwarna biru dinotasikan dengan b(puv). Vektor

r(puv)

b(puv)

disebut komposisi dari path puv. Suatuuv-path tertutup disebut cycle.

Dari Gambar 2.5 dapat ditemukan beberapa walk, path, dan cycle, antara

lain :

1. Barisan v1 −→r v2 −→b v3 −→r v1 −→r v2 adalah suatu walk dengan komposisi

3 1

2. Barisan v1 −→r v2 −→b v3 adalah sebuah path dengan komposisi

1 1

3. Barisan v1 −→r v2 −→b v3 −→r v1 adalah sebuah cycle dengan komposisi

2 1

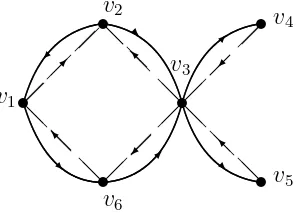
Suatu digraph-dwiwarna dikatakan asimetrik jika digraph tersebut simetrik

dan arc dari verteks u ke v diwarnai merah jika dan hanya jika arc dari verteks

v ke u di warnai biru atau sebaliknya. Berikut ini diberikan sebuah contoh dari

(22)

13 t v1 t v2 t v6 t v3 tv4 tv5 ✒ ✠ ❘ ■ ❅ ❅ ❅_❅ ❅ ❅ ✠ ✒ ■ ❅ ❅ ❅ ❅ ❅❅ ❘ ✠ ■ ❅❅ ❅_❅ ❅ ❅ ✒ ❘

Gambar 2.6 : 2-Digraph asimetrik yang terdiri dari 6 verteks dan 12 arc

2.2.2 Digraph-dwiwarna 2-Primitif.

Suatu digraph-dwiwarna dikatakan terhubung kuat (strongly connected) jika

digraphnya terhubung kuat. Berikut ini diberikan contoh dari digraph-dwiwarna

terhubung kuat dan tidak terhubung kuat.

t v1 t v2 t v7 t v3 tv4 tv5 t v6 t v8 ✒ ✲ ❅ ❅ ❅ ❅ ❅ ❅ ✠ ❘ ❄ ✠ ✛ ❅ ❅ ❅ ❅ ❅ ❅ ■ ✻ (a) t v1 t v2 t v7 t v3 tv4 tv5 t v6 t v8 ✠ ✲ ❅ ❅ ❅ ❅ ❅ ❅ ❘ ❄ ✠ ✛ ❅ ❅ ❅ ❅ ❅ ❅ ■ ✻ (b)

Gambar 2.7 : (a) 2-Digraph terhubung kuat ; (b)2-Digraph tidak terhubung kuat

Sebuah digraph-dwiwarnaDdikatakan 2-primitif jika dan hanya jika

terdap-at bilangan bulterdap-at tak negterdap-atifh dan k sehingga untuk setiap pasangan dua verteks

udanv diD terdapat (h, k)-walk dariu kev dan dariv keu. AndaikanDadalah

digraph-dwiwarna terhubung kuat dan andaikan C = {γ1, γ2,· · ·, γt} merupakan

himpunan semua cycle diD. MisalkanM adalah cycle matriks dariDyang

kolom-kolomnya disusun dari cycle-cycle di D dan banyak baris diperoleh dari banyak

warna arc di Dsehingga

M =

r(γ1) r(γ2) ... r(γt)

b(γ1) b(γ2) ... b(γt)

(23)

Suatu digraph-dwiwarnaDdikatakan primitif jika dan hanya jika pembagi

perseku-tuan terbesar dari determinan submatriks-submatriks 2×2 dari cycle matriks M

diD adalah 1 (Fornasini dan Valcher, 1997).

Contoh 2.3Dari Gambar 2.5 dapat diperoleh cycle matriks dari digraph-dwiwarna tersebut, yaitu :

M =

2 1 1 1

karena det(M)=1 maka digraph-dwiwarna tersebut 2-primitif.

2.3 Matriks Adjancency

Pada subbab ini akan dibahas hubungan antara digraph, digraph-dwiwarna

dengan matriks tak negatif.

2.3.1 Matriks tak negatif.

Suatu matriks bujursangkar A ordo n, A = (aij) dikatakan sebagai matriks

tak negatif jika aij ≥ 0 untuk setiap i, j = 1, 2, ..., n dan dinotasikan dengan A

≥ 0. Apabila aij > 0 untuk setiap i, j = 1, 2, ..., n maka matriks A tersebut

dikatakan matriks positif.

Contoh 2.4Matriks tak negatif dan matriks positif.

MatriksA=

0 2 0 5

adalah matriks tak negatif.

MatriksB =

1 2 3 1

adalah matriks positif.

2.3.2 Matriks Adjancency dari Digraph.

Andaikan V ={v1, v2, ..., vn−1, vn} merupakan himpunan verteks di digraph

D atas n verteks. Sebuah digraph D atas n verteks dapat dituliskan ke dalam

matriks adjacency. Matriks adjacency adalah sebuah matriks bujursangkarAordo

n, A=(aij) dengan entriaij sebagai

aij =

1, jika (vi, vj) merupakan arc di D

(24)

15

dimanai, j = 1,2,3, ..., n.

Berikut ini akan diberikan contoh matriks adjacency dari sebuah representasi

di-graph.

Contoh 2.5Dari Gambar 2.1 dapat diperoleh matriks adjacencynya yaitu :

A=      

0 1 0 0 0 0 0 1 0 1 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0      

2.3.3 Matriks Adjacency Digraph-dwiwarna.

Andaikan Dadalah sebuah digraph-dwiwarna atasn verteks. Misalkan V =

{v1, v2, ..., vn−1, vn}merupakan himpunan verteks di digraph dwiwarnaD. Matriks

adjacency merahdari Dadalah sebuah matriks bujursangkarR ordon,R = (rij)

dengan entri rij sebagai

rij =

1 , jika (vi, vj) adalah arc merah di D

0 , jika sebaliknya.

dimanai, j = 1,2,3, ..., n.

Matriks adjacency biru dari D adalah sebuah matriks bujursangkar B ordo n, B = (bij) dengan entribij sebagai

bij =

1 , jika (vi, vj) adalah arc biru di D

0 , jika sebaliknya.

dimanai, j = 1,2,3, ..., n.

Berikut ini akan diberikan sebuah digraph-dwiwarna yang direpresentasikan ke

dalam matriksadjacency.

Contoh 2.6 Dari Gambar 2.5 dapat diperoleh matriks adjacencynya yaitu :

MatriksR =  

0 1 0 0 0 0 1 1 0 

 adalah matriks adjacency merah ;

MatriksB =  

0 0 0 0 0 1 0 0 0 

(25)

Untuk sebarang matriks tak negatifRdanB dan bilangan bulat tak negatifh

dank, suatu (h, k)-Hurwitz product dariRdanBdapat didefinisikan secara

rekur-sif sebagai berikut. Definisikan (R, B)(h,0) ₌_Rh_,_{(R, B)}(0,k)₌_Bk_{dan (R, B)}(h,k) ₌ R(R, B)(h−1,k)₊_{B(R, B)}(h,k−1) _untuk _{h, k} _≥ _1. _{Sebagai contoh, (R, B)}(4,0) ₌ _R4_, (R, B)(0,5) ₌_B5_{dan (R, B)}(2,2) ₌_R2_B2_+RBRB+RB2_R+BR2_B+BRBR+B2_R2_.

2.4 Eksponen Digraph

Pada bagian digraph primitif, sudah dijelaskan bahwa suatu digraph D

ter-hubung kuat dikatakan primitif bila terdapat suatu bilangan bulat positif k

se-hingga untuk setiap pasangan verteksudan v diDterdapat uv-walk danvu-walk

yang panjangnyak. Bilangan bulat terkecil dari semuak tersebut dikatakan

seba-gai eksponen digraphD. Eksponen dari digraphD dinotasikan dengan exp(D).

Contoh 2.7Dari Gambar 2.4 akan diperlihatkan eksponen dari digraph tersebut adalah 5 :

1. Walk dengan panjang 1, yaitu :

v1 →v2 v2 →v3 v3 →v2 v3 →v1

Karena tidak ada walk dengan panjang 1 dari v1 ke v1 maka walk dengan

panjang 1 bukan eksponen dari digraph tersebut.

v1 →v2 →v3 v2 →v3 →v1 v3 →v2 →v3 v3 →v1 →v2 v2 →v3 →v2

v1 →v2 →v3 →v1 v1 →v2 →v3 →v2 v3 →v2 →v3 →v1 v2 →v3 →v1 →v2 v2 →v3 →v2 →v3

v3 →v2 →v3 →v2 v3 →v1 →v2 →v3

(26)

17

v1 →v2 →v3 →v1 →v2 v1 →v2 →v3 →v2 →v3 v2 →v3 →v2 →v3 →v1 v2 →v3 →v2 →v3 →v2 v2 →v3 →v1 →v2 →v3 v3 →v1 →v2 →v3 →v1 v3 →v1 →v2 →v3 →v2 v3 →v2 →v3 →v2 →v3

v1 →v2 →v3 →v2 →v3 →v1 v2 →v3 →v2 →v3 →v2 →v3 v1 →v2 →v3 →v2 →v3 →v2 v2 →v3 →v1 →v2 →v3 →v2 v1 →v2 →v3 →v1 →v2 →v3 v2 →v3 →v1 →v2 →v3 →v1 v3 →v1 →v2 →v3 →v1 →v2 v3 →v1 →v2 →v3 →v2 →v3 v3 →v2 →v3 →v2 →v3 →v1

Karena walk dengan panjang 5 merupakan panjang terkecil yang dapat

diper-oleh untuk setiap pasangan verteks udan v di digraph tersebut maka

ekspo-nen dari digraph tersebut adalah 5.

Pada tahun 1991, Brualdi dan Ryser menyatakan bahwa entri (i, j) dari Ak

merupakan banyaknya walk dari verteksvi kevj yang panjangnyak di digraph D.

Proposisi 2.2 AndaikanAadalah suatu matriks adjacency dari digraphD. Entri (i, j) dari Ak _{menyatakan banyaknya walk dari verteks} _v

i ke vj yang panjangnya

k di D.

Bukti Andaikan A adalah suatu matriks adjacency dari digraph D, maka setiap entri (i, j) dari A menyatakan arc dari verteks vi ke vj di digraph D. Hal ini

berakibat untukk= 1, maka setiap entria1

ij dari A1 menyatakan banyaknya walk

dari verteks vi ke vj yang panjangnya satu.

Asumsikan setiap entriak

ij dari Ak menyatakan banyaknya walk dari verteks

vi ke verteks vj yang panjangnya k di D, untuk k ≥ 1 adalah benar. Berikut ini

diperlihatkan ak+1

ij adalah banyaknya walk darivi kevj yang panjangnyak+ 1 di

(27)

Asumsikan entri (i, j) dari Ak+1 _{adalah banyaknya walk dari} _v

i ke vj yang

panjangnya k+ 1 di D, untuk k ≥ 1. Misalkan entri (i, j) dari Ak+1 _dinotasikan akij+1. Perhatikan setiap walk dari verteks vi ke verteks vj di D dengan panjang

k+ 1 yang terdiri dari walk vi ke vℓ dengan panjang k untuk ℓ = 1,2, ..., n dan

dilanjutkan dengan arc dari verteks vℓ ke vj, sehingga akiℓaℓj adalah walk yang

panjangnyak+1 dari verteksvikevj diDuntukk = 1,2, ..., n. Sehingga diperoleh

banyaknya walk yang panjangnyak+ 1 dari verteks vi ke verteksvj diD adalah :

ak

i1a1j +aki2a2j+....+akinanj = n

X

ℓ=1 ak

iℓaℓj

karena

Ak+1 =AkA

maka

akij+1 = n

X

ℓ=1 akiℓaℓj

Hal ini berakibat ak+1

ij adalah benar menyatakan banyaknya walk dari verteks vi

kevj yang panjangnyak+ 1 diD. Jadi, entri (i, j) dariAkadalah banyaknya walk

yang panjangnyak dari vi ke vj.

Berikut ini diberikan suatu contoh representasi grafis digraph yang akan

dicari eksponennya dengan menggunakan Proposisi. 2.2 diatas.

Contoh 2.8 Dari Gambar 2.4 dapat diperoleh matriks adjacencynya sebagai berikut:

A=  

0 1 0 0 0 1 1 1 0

 

Dari Proposisi 2.4 untuk mencari banyak walk dari verteks vi ke vj

den-gan panjang k adalah entri (i, j) dari Ak_{. Dengan demikian nilai} _k _{terkecil yang}

menghasilkan matriks positif adalah eksponen dari digraph. Perhatikan matriks

Ak _:

1. Untuk k = 1; diperoleh A =  

0 1 0 0 0 1 1 1 0



(28)

19

dari digraph karena tidak terdapat walk dengan panjang satu dari v1 kev1,

dari v1 kev3, dari v2 ke v1, dari v2 kev2, dan dari v3 kev3.

2. Untuk k = 2; diperoleh A2 ₌  

0 0 1 1 1 0 0 1 1 

, maka bukan merupakan eksponen

dari digraph karena tidak terdapat walk dengan panjang dua dari v1 ke v1,

dari v1 kev2, dari v2 ke v3, dan dari v3 kev1.

1 1 0 0 1 1 1 1 1 

dari digraph karena tidak terdapat walk dengan panjang tiga dari v1 ke v3,

dan dari v2 ke v1.

0 1 1 1 1 1 1 2 1 

dari digraph karena tidak terdapat walk dengan panjang empat dari v1 ke

v1.

1 1 1 1 2 1 1 2 2 

, karena untuk setiap pasangan

verteks di digraph tersebut terdapat walk dengan panjang lima maka

ekspo-nen dari digraph digraph tersebut adalah 5.

2.5 2-Eksponen dari Digraph-dwiwarna

Pada bagian digraph-dwiwarna 2-primitif, sudah dijelaskan bahwa suatu

di-graph dwiwarnaDterhubung kuat dikatakan 2-primitif jika dan hanya jika

terda-pat bilangan bulat tak negatifhdanksehingga untuk setiap pasangan dua verteks

u dan v di D terdapat (h, k)-walk dari u ke v dan dari v ke u. Bilangan bulat

positif terkecil dari semuah+k dikatakan sebagai 2-eksponen digraph-dwiwarna

D. 2-Eksponen dari digraph D dinotasikan denganexp2(D).

Contoh 2.9Dari Gambar 2.5 dapat diperoleh bahwa untuk setiap pasang verteks u dan v dalam digraph-dwiwarna tersebut terdapat walk terpendek yang

(29)

v1 −→r v2 −→b v3 −→r v2 →−b v3 −→r v2 −→b v3 −→r v1 v2 −→b v3 −→r v1 −→r v2 →−b v3 −→r v2 −→b v3 −→r v1 v1 −→r v2 −→b v3 −→r v2 →−b v3 −→r v2 −→b v3 −→r v2 v2 −→b v3 −→r v1 −→r v2 →−b v3 −→r v2 −→b v3 −→r v2 v1 −→r v2 −→b v3 −→r v1 →−r v2 −→b v3 −→r v2 −→b v3 v2 −→b v3 −→r v1 −→r v2 →−b v3 −→r v1 −→r v2 −→b v3 v3 −→r v2 −→b v3 −→r v2 →−b v3 −→r v2 −→b v3 −→r v1 v3 −→r v2 −→b v3 −→r v2 →−b v3 −→r v2 −→b v3 −→r v2 v3 −→r v1 −→r v2 −→b v3 →−r v2 −→b v3 −→r v2 −→b v3

Contoh 2.10 menjamin bahwa untuk setiap pasangan verteksu dan v di

digraph-dwiwarna tersebut, walk terpendek yang dapat diperoleh digraph digraph-dwiwarna

terse-but adalah 7 dengan komposisi

4 3

sehingga 2-eksponen dari digraph-dwiwarna

tersebut adalah 7 dengan komposisi

4 3

. Berikut ini akan ditunjukkan hubungan

2-eksponen digraph-dwiwarna dengan matrik tak negatif.

Lemma 2.3 AndaikanDadalah sebuah digraph-dwiwarna atasnverteks dan mis-alkan R dan B masing-masing adalah matriks adjacency merah dan biru dari di-graph dwiwarnaD. Maka entri (i, j) dari(R, B)(h,k) _{adalah banyaknya} _{(h, k)-walk} dari verteks vi ke verteks vj .

Bukti. Akan dibuktikan dengan induksi pada (h+k) dan (h+k+ 1), jika h= 0 maka k = 1 atau jika h = 1 maka k = 0. jika h = 0 maka entri (i, j) dari

(R, B)(0,1) ₌_B _{adalah walk dengan komposisi}

0 1

di digraph-dwiwarna D.

Den-gan cara yang sama, jika k = 0 maka (R, B)(1,0) ₌ _R _{adalah walk dengan entri} (i, j) menyatakan walk dengan komposisi

1 0

di digraph-dwiwarna D.

Andaikan Lemma 2.3 benar untuk semua bilangan bulat tak negatif h′

dan

k′

denganh′

+k′

≤h+k akan diperlihatkan untukh+k+ 1 adalah benar dengan

catatan sebagai berikut.

(R, B)(h+1,k) ₌_{R(R, B)}(h,k)₊_{B(R, B)}(h+1,k−1)

Oleh hipotesis induksi, entri(i, j) pada R(R, B)(h,k) _{adalah walk dari} _v

(30)

21

yang dimulai dengan arc merah dan diikuti oleh (h, k)-walk, dan entri (i, j) pada

B(R, B)(h+1,k−1)_{adalah walk dari}_v

ikevj yang dimulai dengan arc biru dan diikuti

oleh (h+ 1, k−1)−walk sedemikian hingga entri (i, j) dari (R, B)(h+1,k) _adalah jumlah (h+ 1, k)-walk darivi kevj. Jadi, entri (i, j) dari (R, B)(h,k) adalah jumlah

(h, k)-walk dari verteks vi ke verteks vj .

Berikut ini diberikan representasi grafis digraph-dwiwarna yang akan diberikan

2-eksponennya.

Contoh 2.10 Dari Gambar 2.5 dapat diperoleh matriks adjacencynya sebagai berikut:

MatriksR =  

0 1 0 0 0 0 1 1 0 

 adalah matriks adjacency merah.

MatriksB =  

0 0 0 0 0 1 0 0 0 

 adalah matriks adjacency biru.

Dari Contoh 2.10 kita cari 2-eksponennya, yaitu dengan melihat penjumlahan

h arc biru dank arc merahnya, dengan cara sebagai berikut:

a. Untuk h+k = 1

1. (R, B)(1,0) ₌_R₌  

0 1 0 0 0 0 1 1 0 

, bukan merupakan 2-eksponen dari

digraph-dwiwarna tersebut karena tidak terdapat walk dengan panjang 1 dengan

komposisi

1 0

dari v1 kev1,v1 kev3, v2 kev1, v2 kev2,v2 kev3, danv3

ke v3.

2. (R, B)(0,1) ₌_B ₌  

0 0 0 0 0 1 0 0 0 

digraph-dwiwarna tersebut karena tidak terdapat walk dengan panjang 1 dengan

komposisi

0 1

dari v1 kev1, v1 ke v2, v1 ke v3, v2 kev1, v2 ke v2,v3 ke

(31)

b. Untuk h+k = 2

1. (R, B)(2,0) ₌ _R2 ₌  

0 0 0 0 0 0 0 1 0 

di-graph dwiwarna tersebut karena tidak terdapat walk dengan panjang 2

dengan komposisi

2 0

dari v1 ke v1, v1 ke v2, v1 ke v3, v2 ke v1, v2 ke

v2,v2 kev3, v3 kev1 dan v3 kev3.

2. (R, B)(1,1) ₌_RB+BR₌  

0 0 1 1 1 0 0 0 1 

digraph-dwiwarna tersebut karena tidak terdapat walk dengan panjang

2 dengan komposisi

1 1

dari v1 ke v1, v1 ke v2, v2 ke v3, v3 kev1, dan

v3 kev2.

3. (R, B)(0,2) ₌ _B2 ₌  

0 0 0 0 0 0 0 0 0



dengan komposisi

0 2

v2,v2 kev3, v3 kev1, v3 ke v2, dan v3 kev3.

c. Untuk h+k = 3

1. (R, B)(3,0) ₌ _R3 ₌  

0 0 0 0 0 0 0 0 0 

dengan komposisi

3 0

2. (R, B)(2,1) ₌_{R(R, B)}(1,1)_{+B(R, B)}(2,0) ₌  

1 1 0 0 1 0 1 1 1 

, bukan merupakan

2-eksponen dari digraph-dwiwarna tersebut karena tidak terdapat walk

dengan panjang 3 dengan komposisi

2 1

dari v1 kev3, v2 ke v1, dan v2

ke v3.

3. (R, B)(1,2) ₌_{R(R, B)}(0,2)_{+B(R, B)}(1,1) ₌  

0 0 0 0 0 1 0 0 0 

(32)

23

1 2

dari v1 ke v1, v1 ke v2, v1 ke

v3,v2 kev1, v2 kev2, v3 ke v1, v3 ke v2, dan v3 kev3.

4. (R, B)(0,3) ₌ _B3 ₌  

0 0 0 0 0 0 0 0 0



dengan komposisi

0 3

d. Lakukan dengan cara yang sama sampai denganh+k = 7

1. (R, B)(7,0) ₌ _R7 ₌  

0 0 0 0 0 0 0 0 0 

dengan komposisi

7 0

2. (R, B)(6,1) ₌_{R(R, B)}(5,1)_{+B(R, B)}(6,0) ₌  

0 0 0 0 0 0 0 0 0 

2-eksponen dari digraph dwiwarna tersebut karena tidak terdapat walk

6 1

v3,v2 kev1, v2 kev2, v2 ke v3, v3 ke v1, v3 kev2, dan v3 kev3.

3. (R, B)(5,2) ₌_{R(R, B)}(4,2)_{+B(R, B)}(5,1) ₌  

0 1 0 0 0 0 1 3 0 

2-eksponen dari digraph dwiwarna tersebut karena tidak terdapat walk

5 2

v1,v2 kev2, v2 kev3, v3 ke v1, v3 ke v2, dan v3 kev3.

4. (R, B)(4,3) ₌ _{R(R, B)}(3,2) ₊_{B(R, B)}(4,2) ₌  

1 1 2 2 3 1 1 1 3 

, karena untuk

setiap pasangan verteksudanv di digraph tersebut terdapat walk

den-gan panjang 7 denden-gan komposisi

4 3

maka 2-eksponen dari

digraph-dwiwarna tersebut adalah 7 dengan komposisi

4 3

(33)

2.6 Beberapa Fakta Tentang Digraph-Dwiwarna Asimetrik Yang Memu-at Cycle Primitif

Asumsikan bahwa h dan k adalah bilangan bulat tak negatif sedemikian

hingga diantara pasangan verteksu kev ada sebuah (h, k)-walk dariu ke v.

Lemma 2.4 Andaikan D adalah digraph-dwiwarna yang terdiri dari dua cycle yang memiliki paling sedikit satu arc pada masing-masing warna. Misalkan s dan t merupakan bilangan bulat tak negatif sedemikian hingga

h k = M s t . Maka s t

≥M−1

r(puv)

b(puv)

, untuk beberapa path puv dari u ke v.

Bukti. Karena ada suatu (h, k)-walk dari ukev, sehingga (h, k)-walk merupakan komposisi pathpuv dari u kev dan cycle - cycle di D,

h k =M x1 x2 +

r(puv)

b(puv)

untuk beberapax1, x2 ≥0 dan beberapa path puv dari uke v.

Karena h k =M s t maka s t

−M−1

r(puv)

b(puv)

= x1 x2 ≥ 0 0 jadi, s t

≥M−1

r(puv)

b(puv)

Shader dan Suwilo (2006) memberikan suatu pendefenisian untuk digunakan

dalam menentukan 2-eksponen digraph dwiwarna yang terdiri dari dua cycle, yaitu:

Andaikan D adalah suatu digraph-dwiwarna primitif yang terdiri dari dua cycle

γ1 dan γ2 dan misalkan M =

r(γ1) r(γ2) b(γ1) b(γ2)

. Karena D adalah 2-primitif, tanpa

menghilangkan keumumannya asumsikan det(M) = 1. Untuk setiap pasangan

verteks u dan v, andaikanpuv adalah path terpendek dariu kev, didefenisikan

ℓ′

r = max_u,v

∈V{b(γ2)r(puv)−r(γ2)b(puv)} (2.11)

ℓ′

b = max_u,v

(34)

25

dengan V adalah himpunan verteks di D.

Pada tahun 2008, Suwilo memperlihatkan bahwa bilaDadalah digraph

dwi-warna yang berbentuk lollipops dan asimetrik maka batas atas 2-eksponen D

adalahexp2(D)≤(s2₋_{1)/2 + (s}_{+ 1)(n}₋_s).

Teorema 2.5 AndaikanDadalah (n, s)-lollipop dwiwarna primitif asimetrik den-gan s≥3. Maka exp(D)≤(s2₋_{1)/2 + (s}_{+ 1)(n}₋_s).

Bukti. Andaikan cycle matrik di D adalah C dengan C = {γ1, γ2}. Karena D adalah asimetrik cukup ditunjukkan bahwa untuk setiap verteksudan v diDada

sebuah (e, e)-walk dengan e= (s2₋_{1)/4 + (s}_{+ 1)(n}₋_{s)/2. Karena}_D _asimetrik,

untuk setiap verteks u di D ada (1,1)-walk dari u ke dirinya sendiri. Andaikan

u dan v merupakan dua verteks yang berbeda di D dan andaikan puv merupakan

path terpendek dari u ke v. Jika r(puv) = b(puv), maka bukti selesai. Jadi kita

asumsikan bahwar(puv)6=b(puv) dan tanpa menghilangkan keumumannya anggap

bahwar(puv)> b(puv). Pembuktian ini akan kita tunjukkan atas 2 kasus, yaitu :

Kasus 1. Pathpuv mempunyai verteks sekutu denganC.

Sebuah (e, e)-walk dari verteksukev dibentuk dengan cara sebagai berikut. Walk

dimulai di verteksu, kemudian ikuti pathpuvmenuju ke verteksv, lalu mengelilingi

γ1 sebanyak r(puv)−b(puv) kali dan kembali ke v sehingga terbentuk (e, e)-walk.

Komposisi dari walkwuv tersebut adalah

r(wuv)

b(wuv)

=

r(puv)

b(puv)

+ (r(puv)−b(puv))

(s−1)/2 (s+ 1)/2

.

r(wuv)

b(wuv)

=

b(puv) + (r(puv)−b(puv))(s+ 1)/2

b(puv) +r(puv)−b(puv))(s+ 1)/2

≤ (r(puv) +b(puv))

(s+ 1)/2 (s+ 1)/2

.

Karena (r(puv) +b(puv))≤(s+ 1)/2 + (n−s), maka

r(wuv)

b(wuv)

≤((s−1)/2 + (n−s))

(s+ 1)/2 (s+ 1)/2

=

(s2₋_{1)/2 + (s}_{+ 1)(n}₋_s)/2 (s2₋_{1)/2 + (s}_{+ 1)(n}₋_s)/2

(35)

Kasus 2. Semua path puv tidak mempunyai verteks sekutu dengan cycle C.

Sebuah (e, e)-walk dari verteksukev dibentuk dengan cara sebagai berikut. Walk

dimulai di verteksu, kemudian ikuti pathpusmenuju ke vertekss, lalu mengelilingi

γ1 sebanyak r(puv)−b(puv) kali dan kembali ke s, dan akhirnya ikuti path psv ke

verteksv sehingga terbentuk (e, e)-walk. Komposisi dari walkwuvtersebut adalah

r(wuv)

b(wuv)

=

r(puv)

b(puv)

+ℓuv

1 1

+ (r(puv)−b(puv))

(s−1)/2 (s+ 1)/2

dimanaℓuv=d(u, s) jikad(u, s)≤d(v, s) danℓuv =d(v, s) bila sebaliknya. Karena

(r(puv) +b(puv) +ℓuv)≤(n−s) maka

r(wuv)

b(wuv)

≤ ℓuv

(s+ 1)/2 (s+ 1)/2

+ (r(puv)−b(puv))

(s+ 1)/2 (s+ 1)/2

.

= (r(puv) +b(puv) +ℓuv)

(s+ 1)/2 (s+ 1)/2

≤

(s2₋_{1)/4 + (s}_{+ 1)(n}₋_s)/2 (s2₋_{1)/4 + (s}_{+ 1)(n}₋_s)/2

.

Dengan menggunakan (1,1)-walk, (e, e)-walk dari setiap kasus dapat diperpanjang

menjadi (e, e)-walk dengan e = (s2₋_{1)/4 + (s}_{+ 1)(n}₋_{s)/2. Hal ini berakibat}

(36)

BAB 3

HASIL UTAMA

Pada bab ini diberikan hasil utama tulisan ini yakni 2-eksponen

digraph-dwiwarna dengan dua cycle yang bersinggungan. Hasil utama dalam penelitian ini

berupa batas atas 2-eksponen digraph dwiwarna asimetrik dengan dua cycle yang

bersinggungan. Andaikan D adalah digraph-dwiwarna asimetrik atas n = 2m,

m ≥ 2 verteks dengan dua cycle yang bersinggungan dengan panjang

masing-masing cycle adalah m dan m+ 1. Karena D adalah asimetrik maka komposisi

cycle-cycle dari digraph-dwiwarna tersebut adalah

r(γ1) b(γ1)

,

r(γ2) b(γ2)

,

r(γ3) b(γ3)

,

r(γ4) b(γ4)

,

dan

1 1

, yang mana γ1 dimulai dari vm →v1 → v2 →v3 → ...→vm−1 → vm, γ2

dimulai dari vm → vm−1 → ... → v2 → v1 → vm, γ3 dimulai dari vm → vm+1 → vm+2 → ...→ vn−1 → vn →vm, dan γ4 dimulai dari vm →vn → vn−1 → vn−2 → ...→vm+1 →vm.

Dari bab sebelumnya, dikatakan bahwa untuk menentukan 2-eksponen dari

digraph-dwiwarna, tentunya digraph-dwiwarna tersebut harus dijamin 2-primitif.

Lemma berikut ini, akan memberikan jaminan untuk digraph-dwiwarna asimetrik

dengan dua cycle yang bersinggungan sehingga 2-primitif.

Lemma 3.1 Andaikan D adalah digraph-dwiwarna asimetrik dengan dua cycle yang memiliki satu verteks persekutuan. Misalkan cycle matriks M di D adalah

M =

a m−a b m−b+ 1 1 · · · 1

m−a a m−b+ 1 b 1 · · · 1

denganm ≥2, 0≤a≤m−a, dan 0≤b≤m−b+ 1. Maka D adalah 2-primitif jika dan hanya jika gcd(m−2a, m−2b+ 1) = 1.

Bukti. Andaikan ci menyatakan kolom ke-i dari cycle matriks M. Misalkan

(37)

matriks M. Kurangkan ci dengan x1i kali dari kolom ke-5 untuk i=1, 2, 3, 4.

Sehingga diperoleh matriks seperti berikut

0 0 0 0 1 · · · 1

m−2a 2a−m m−2b+ 1 2b−m−1 1 · · · 1

.

Contentdari matriks tersebut sama sepertiM, dan akan menjadi 1 jika dan hanya

jika gcd(m−2a, m−2b + 1)=1. Jadi, D adalah 2-primitif jika dan hanya jika

gcd(m−2a, m−2b+ 1)=1.

Andaikan D adalah digraph-dwiwarna asimetrik atas n = 2m, m ≥ 4

verteks dengan dua cycle bersinggungan yang panjang masing-masing cycle m

dan m + 1, γ1 dan γ3 masing-masing memiliki tepat satu arc biru. Lemma 3.1

menjamin bahwa terdapat submatriks dari cycle matriks M di D yang memiliki

determinan 1. Proposisi berikut ini akan memperlihatkan batas atas 2-eksponen

digraph-dwiwarna asimetrik D yang dapat dicapai dengan menggunakan

subma-triks tersebut.

Proposisi 3.2 AndaikanDmerupakan digraph-dwiwarna asimetrik atasn= 2m, m ≥ 4 verteks dengan dua cycle yang memiliki satu verteks persekutuan dengan panjang masing-masing cycle m dan m + 1, γ1 dan γ3 masing-masing memiliki tepat satu arc biru. Misalkan cycle matriks M di D mempunyai submatriks ordo 2×2 dengan determinan 1. Maka exp2(D)≤ 1₂(2n2₋_n₋_6).

Bukti. Andaikan cycle matrik dari D adalah M, M =

m−1 1 m 1 1 · · · 1

1 m−1 1 m 1 · · · 1

.

Dari cycle matrik M, diperoleh suatu submatrik N berordo 2×2 yang

determi-nannya 1, yaitu

N =

m m−1

1 1

dengan

m−1 1

dimulai dari vm → v1 → v2 → v3 → ... → vm−1 → vm,

m

1

(38)

29

cycle matriksM memiliki content 1. AkibatnyaDadalah 2-primitif. Untuk setiap

pasangan verteksudanv diD, andaikanpuv adalah sebuah path terpendek dariu

kev. Dari Persamaan 2.11 dan 2.12 maka diperoleh suatu persamaan baru, yakni

ℓ′r = max

u,v∈V{r(puv)−(m−1)b(puv)} (3.1)

ℓ′b = max

u,v∈V{mb(puv)−r(puv)} (3.2)

denganV adalah himpunan verteks di D.

Bila path puv mengandung paling banyak dua arc biru maka kemungkinan r(puv)

terbesar diperoleh dari verteks v2 ke v2m−1 atau dari verteks vm−2 ke vm+2 yang melalui γ1 dan γ3. Sehingga ℓ

′

r diperoleh apabila D memuat path merah r(puv)

dari u ke v dengan panjang 2m−3 dan tidak memuat path biru b(puv) dari u ke

v, ℓ′

b diperoleh apabilaD memuat path birub(puv) dari u ke v dengan panjang 2

dan tidak memuat path merah r(puv) dari u ke v. Dari Persamaan 3.1 dan 3.2

diperolehℓ′

r= 2m−3 dan ℓ

′

b = 2m.

Berdasarkan Lemma 2.4, (h, k)-walk dariukev diDdapat diperoleh dengan

komposisi sebagai berikut,

h k =N s t (3.3)

dengans dan t adalah bilangan bulat tak negatif.

Pilih s=ℓ′

r = 2m−3 dant =ℓ

′

b = 2m maka Persamaan 3.3 menjadi

h k =N

2m−3 2m

. (3.4)

Karena setiap (h, k)-walk dari verteksu kev dapat dibentuk melalui perjalanan u

kev yang mengelilingi cycle γ1 dan γ3 dan kemudian path puv dari u ke v, maka

h k =

r(puv)

b(puv)

+N x1 x2 (3.5) dengan x1 x2

adalah solusi bilangan bulat tak negatif.

Sekarang akan ditunjukkan bahwa

x1 x2

(39)

Dari Persamaan 3.4 dan 3.5 diperoleh

r(puv)

b(puv)

+N x1 x2 =N

2m−3 2m sehingga x1 x2 =

2m−3 2m

−N−1

r(puv)

b(puv)

=

2m−3 2m

−

1 −(m−1)

−1 m

r(puv)

b(puv)

=

2m−3 2m

−

r(puv)−(m−1)b(puv)

mb(puv)−r(puv)

=

2m−3−(r(puv)−(m−1)b(puv))

2m−(mb(puv)−r(puv))

.

Oleh Persamaan 3.1 dan 3.2 maka diperolehℓ′

r ≥r(puv)−(m−1)b(puv) danℓ

′

b ≥

mb(puv)−r(puv) untuk semua path terpendekpuv, makax1 ≥0 danx2 ≥0. Jadi,

Persamaan 3.5 mempunyai solusi bilangan bulat tak negatif. Ini mengakibatkan

bahwa untuk setiap pasangan verteksu dan v, adauv-walk di Dyang terdiri dari

( (2m−3) r(γ3)+ 2m r(γ1) ) arc merah dan ( (2m−3) b(γ3) + 2m b(γ1) ) arc

biru. Sehingga, sebuah (h, k)-walk dari verteksukev dapat dibentuk dengan cara

sebagai berikut. Walk dimulai dari verteks u, mengelilingi cycle γ3 sebanyak x1

kali dan cycle γ1 sebanyak x2 kali, kemudian kembali ke u dan selanjutnya ke v

melalui pathpuv.

Jadi, h+k ≤(m+ 1)(2m−3) +m.2m= 4m2₋_m₋_{3 =} 1

2(2n2−n−6).

Berdasarkan data empiris, bila D adalah digraph-dwiwarna asimetrik atas

n = 2m, m ≥ 4 verteks dengan dua cycle bersinggungan yang panjang

masing-masing cycle m dan m+ 1, dengan γ1 dan γ3 masing-masing memiliki tepat satu

arc biru, maka untuk setiap pasangan dua verteks u dan v di D dapat dibentuk

(h, k)-walk terpendek dariukev dan dariv keudenganharc merah sama dengan

k arc biru. Fakta baru ini, akan digunakan dalam pembuktian proposisi berikut

ini, sehingga akan diperlihatkan bahwa batas atas 2-eksponen digraph-dwiwarna

asimetrik D yang diperoleh lebih baik daripada batas atas 2-eksponen

(40)

31

Proposisi 3.3 AndaikanDmerupakan digraph-dwiwarna asimetrik atasn= 2m, m ≥ 4 verteks dengan dua cycle yang memiliki satu verteks persekutuan dengan panjang masing-masing cycle m dan m + 1, γ1 dan γ3 masing-masing memiliki tepat satu arc biru . Maka exp2(D)≤ 1₂(n2_{+ 2n).}

Bukti. KarenaDadalah asimetrik cukup ditunjukkan bahwa untuk setiap verteks udan v diD ada sebuah (e, e)-walk dengan e= 1₄(n2+ 2n). Karena D asimetrik,

untuk setiap verteksu diD ada (1,1)-walk dari u ke dirinya sendiri. Misalkan u

danv adalah dua verteks berbeda diDdan misalkanpuv adalah path berarah dari

u kev. Perhatikan bahwar(puv)≤ n < ₄1(n2+ 2n). Jika r(puv) =b(puv), dengan

menggunakan (1,1)-walk maka dapat dicapai (e, e)-walk sehingga bukti selesai.

Jadi, asumsikan bahwa r(puv) 6= b(puv) dan tanpa menghilangkan keumumannya

anggap bahwa r(puv) > b(puv). Pembuktian ini akan ditunjukkan atas 3 kasus,

yaitu :

Kasus 1 : Bila verteks u dan v terletak diγ1 atau γ2 .

Andaikanpum(γ1) adalah path dari verteksuke verteks m melaluiγ1 dan pmu(γ1)

adalah path dari verteksmke verteks umelaluiγ1. Sebuah (e, e)-walk dari verteks

u kev dibentuk dengan cara sebagai berikut. Walk dariu ke v tersebut di mulai

dari u, kemudian mengikuti pathpum(γ1) ke verteks m, lalu mengelilingi

1 m

se-banyak (r(puv)−b(puv)) kali dan kembali kem, setelah itu mengikuti pathpmu(γ1)

ke verteks u, kemudian mengelilingi

m−1 1

sebanyak (r(puv)−b(puv)−1) kali

dan kembali keu, akhirnya kev melaluipuv. Komposisi dari walk tersebut adalah

r(wuv)

b(wuv)

=

r(puv)

b(puv)

+ (r(puv)−b(puv)−1)

m−1

1

+ (r(puv)−b(puv))

1 m +

r(pum)

b(pum)

γ1 +

r(pmu)

b(pmu)

γ1 .

Karena

r(pum)

b(pum)

γ1 +

r(pmu)

b(pmu)

γ1 =

m−1

1

(41)

r(wuv)

b(wuv)

=

r(puv)

b(puv)

+ (r(puv)−b(puv))

m m+ 1

, sehingga

a. Untuk m bernilai genap,r(puv) +b(puv)≤

m 2 maka

r(wuv)

b(wuv)

=

b(puv) +r(puv)−b(puv)(m+ 1)

m+ 1 m+ 1

≤ m

2

m+ 1 m+ 1

= ₁

8(n 2 _{+ 4)} 1

8(n2 + 4)

.

b. Untuk m bernilai ganjil, r(puv) +b(puv)≤

m−1 2 maka

r(wuv)

b(wuv)

≤ m−1

2

m+ 1 m+ 1

= ₁

8(n 2₋₄₎ 1

8(n2−4)

.

Kasus 2 : Bila verteks u dan verteks v terletak di γ3 atau γ4 .

Andaikanpum(γ4) adalah path dari verteksuke verteks m melaluiγ4 dan pmu(γ4)

adalah path dari verteksmke verteks umelaluiγ4. Sebuah (e, e)-walk dari verteks

u kev dibentuk dengan cara sebagai berikut. Walk dariu ke v tersebut di mulai

dariu, kemudian mengikuti path pum(γ4) ke verteksm, lalu mengelilingi

m−1

1

sebanyak (r(puv) − b(puv)) kali dan kembali ke m, setelah itu mengikuti path

pmu(γ4) ke verteks u, kemudian mengelilingi

1 m

sebanyak (r(puv)−b(puv)−1)

kali dan kembali ke u, akhirnya ke v melalui puv. Komposisi dari walk tersebut

adalah

r(wuv)

b(wuv)

=

r(puv)

b(puv)

+ (r(puv)−b(puv))

m−1

1

+ (r(puv)−b(puv−1))

1 m +

r(pum)

b(pum)

γ4 +

r(pmu)

b(pmu)

γ4 .

Karena

r(pum)

b(pum)

γ4 +

r(pmu)

b(pmu)

γ4 = 1 m maka r(wuv)

b(wuv)

=

r(puv)

b(puv)

+ (r(puv)−b(puv))

m m+ 1

, sehingga

a. Untuk m+ 1 bernilai genap, r(puv) +b(puv)≤

(42)

33

r(wuv)

b(wuv)

=

m+ 1 m+ 1

≤ m+ 1

2

m+ 1 m+ 1

= ₁

8(n2+ 4n+ 4) 1

8(n

2_{+ 4n}_{+ 4)}

.

b. Untuk m+ 1 bernilai ganjil,r(puv) +b(puv)≤

m 2 maka

r(wuv)

b(wuv)

≤ m

2

m+ 1 m+ 1

= ₁

8(n

2 _{+ 2n)} 1

8(n

2 _{+ 2n)}

.

Kasus 3 : Bila verteksuberada di γ1 atau γ2 dan verteksv berada di γ3 atau γ4. Sebuah (e, e)-walk dari verteksukev dibentuk dengan cara sebagai berikut. Walk

dari u ke v tersebut di mulai dari u, kemudian mengelilingi

m−1 1

sebanyak

(r(puv)−b(puv)) kali dan kembali ke u, setelah itu mengikuti path puv ke verteks

v, kemudian mengelilingi

1 m

sebanyak (r(puv)−b(puv)) kali dan kembali ke v.

Komposisi dari walk tersebut adalah

r(wuv)

b(wuv)

=

r(puv)

b(puv)

+ (r(puv)−b(puv))

m−1

1

+ (r(puv)−b(puv))

1 m =

r(puv)

b(puv)

+ (r(puv)−b(puv))

m m+ 1

.

Karenar(puv) +b(puv)≤m maka

r(wuv)

b(wuv)

=

m+ 1 m+ 1

≤ m

m+ 1 m+ 1

= ₁

4(n

2_{+ 2n)} 1

4(n2+ 2n)

.

Dengan menggunakan (1,1)-walk, (e, e)-walk dari verteks u ke v di setiap kasus

maka dapat diperpanjang menjadi (e, e)-walk dari verteks u ke v dengan e =

1

4(n2+ 2n). Hal ini berakibat bahwa exp2(D)≤ 1

(43)

KESIMPULAN DAN SARAN

Pada bab ini akan diberikan kesimpulan yang didapat dari hasil penelitian

pada bab-bab sebelumnya, selanjutnya akan diberikan saran untuk dipergunakan

dalam penelitian lebih lanjut

4.1 Kesimpulan

Andaikan D merupakan digraph-dwiwarna asimetrik atas n = 2m, m ≥ 4

verteks dengan dua cycle yang memiliki satu verteks persekutuan dengan panjang

masing-masing cycle m dan m+ 1, γ1 dan γ3 masing-masing memiliki tepat satu

arc biru makaD memiliki matriks cycle M dengan

M =

m−1 1 m 1 1 · · · 1

1 m−1 1 m 1 · · · 1

.

Untuk (h, k)-walk dari verteks u ke verteks v di D dapat diperoleh dari

komposisi path puv dan cycle matriks M di D, sehingga batas atas 2-eksponen

dari D dapat disimpulkan sebagai berikut:

1. Bila (h, k)-walk dari verteks u ke verteks v diD dengan meggunakan teknik

yang dikembangkan oleh Shader dan Suwilo (2003) dan submatriks dari cycle

matrik M yang determinannya 1 maka batas atas 2-eksponen di D adalah

exp2(D)≤ 1₂(2n2₋_n₋_6).

2. Bila (h, k)-walk untuk setiap pasangan verteks u dan verteks v di D

meng-gunakan teknik yang dimeng-gunakan dalam pembuktian menentukan batas atas

2-eksponen dari (n, s)-lollipop dwiwarna primitif asimetrik dan fakta bahwa

(h, k)-walk terpendek untuk setiap pasangan verteks u dan verteks v di D

(44)

35

2-eksponen diDyang diperoleh akan lebih baik yaituexp2(D)≤ 1₂(n2_{+ 2n).}

4.2 Saran

Penelitian ini telah memperlihatkan batas atas 2-eksponen dari

digraph-dwiwarna asimetrik atasn = 2m, m ≥4 verteks dengan dua cycle yang memiliki

satu verteks persekutuan dengan panjang masing-masing cycle m dan m+ 1, γ1

danγ3 masing-masing memiliki tepat satu arc biru . Penelitian lebih lanjut

diper-lukan untuk menentukan batas atas 2-eksponen dari digraph-dwiwarna asimetrik

atas n = 2m verteks dengan dua cycle yang memiliki satu verteks persekutuan

dengan panjang masing-masing cyclem dan m+ 1 bila γ1 dan γ3 masing-masing

(45)

DAFTAR PUSTAKA

Beasley, L. B, dan Kirkland, S. 2003. A note onk-primitive digraphs.Linier Algebra Appl..373: hal. 67-74.

Brualdi, R. A dan Ryser, H. J. 1991. Combinatorial Matrix Theory. Cambridge : Cambridge University Press.

Fornasini, E. dan Valcher, M. E. 1997. Directed graphs, 2D State Models, and char-acteristic polinomials of irreducible matrix pairs. Linear Algebra Appl.. 263: hal. 275-310.

Gao, Y. dan Shao, Y. 2005. Exponents of two-colored digraph with two cycle.Linear Algebra Appl..407: hal. 263-276.

Lee S. G dan Yang J. M. 2005. Bound for 2-exponents of primitive extremal digraph. Commun.Korean.Math.Soc.20(1): hal. 51-62.

Shader, B. L. dan Suwilo, S. 2003. Exponents of nonnegative matrix pairs. Linear Algebra Appl..363: hal. 275-293.

Suwilo, S. 2005. ” The exponent set of complete asymmetric 2-digraphs ”. Dalam Mawengkang, H., Suwilo, S., dan Sutarman(eds.).Proceeding of the 1 st IMT-GT Regional Conference on mathematics,Statistics and Their Applications: hal. 51-56.

Suwilo, S. 2008. 2-Exponents of two-coloured lollipops.Mathematics Journal of Uni-versiti Teknologi Malaysia. 24(1): hal. 11-22.