Analisa Struktur Pelat Dua Arah Tanpa Balok (Flat Slab)

ANALISA STRUKTUR PELAT DUA ARAH TANPA BALOK

(FLAT SLAB)

Tugas Akhir

Diajukan untuk melengkapi tugas-tugas dan memenuhi Syarat untuk menempuh ujian sarjana Teknik Sipil

Disusun oleh:

JAKA PRAMANA KABAN 040404034

SUB JURUSAN STRUKTUR DEPARTEMEN TEKNIK SIPIL

FAKULTAS TEKNIK

UNIVERSITAS SUMATERA UTARA MEDAN

Disetujui oleh : Dosen Pembimbing

LEMBAR PENGESAHAN

ANALISA STRUKTUR PELAT DUA ARAH TANPA BALOK (FLAT SLAB)

Tugas Akhir

Diajukan untuk melengkapi tugas-tugas dan memenuhi Syarat untuk menempuh ujian sarjana Teknik Sipil

Disusun oleh:

JAKA PRAMANA KABAN 04 0404 034

SUB JURUSAN STRUKTUR Prof.Dr.Ing.Johannes Tarigan NIP.19561224 198103 1 002

DEPARTEMEN TEKNIK SIPIL FAKULTAS TEKNIK

UNIVERSITAS SUMATERA UTARA MEDAN

Abstrak

Penyusunan tugas akhir ini merupakan perhitungan sederhana mengenai gaya dalam yang terjadi pada flat slab. Perhitungan ini ditujukan untuk menemukan besaran gaya dalam yang terjadi pada setiap panel di dalam flat slab. Sehingga dari sini kita dapat mengetahui besarnya gaya dalam dan juga bentuk dari gaya dalam itu sendiri yang diaplikasikan ke dalam gambar.

Bentuk pelat yang diambil ada dua macam yaitu bujur sangkar dan persegi panjang. Alasan digunakannya dua bentuk pelat ini adalah agar di dalam tulisan kedua bentuk dapat diperbandingkan secara lebih nyata dan lebih kompleks. Dan akibat dari keterbatasan literatur mengenai pembahasan pelat ini maka penulis hanya mampu melakukan perhitungan sederhana dengan menggunakan data data yang ada.

Pembahasan yang dilakukan dalam tugas akhir ini antara lain perhitungan lendutan dan momen lentur. Perhitungan dilakukan secara manual dengan menggunakan rumus rumus yang terdapat di dalam literatur, untuk perhitungan data-data agar lebih akurat maka perhitungan dilakukan dengan menggunakan bantuan program microsoft excel dan penggambaran dilakukan dengan bantuan program AutoCAD .

1. Bapak Dr.Ing.Johannes Tarigan. Selaku dosen pembimbing dan juga selaku Ketua Departemen Teknik Sipil Universitas Sumatera Utara yang telah banyak meluangkan waktu, tenaga dan pikiran untuk memberikan bimbingan dalam menyelesaikan tugas akhir ini

KATA PENGANTAR

Puji syukur penulis ucapkan atas kehadirat Tuhan Yang Maha Esa yang telah memberikan anugrah, berkat dan karunia-Nya hingga terselesaikannya tugas akhir ini dengan judul “Analisa Struktur Pelat Dua Arah Tanpa Balok (Flat Slab)”.

Tugas akhir ini disusun untuk diajukan sebagai syarat dalam ujian sarjana teknik sipil bidang studi struktur pada fakultas teknik Universitas Sumatera Utara Medan. Penulis menyadari bahwa isi dari tugas akhir ini masih banyak kekurangannya. Hal ini disebabkan keterbatasan pengetahuan dan kurangnya pemahaman penulis. Untuk penyempurnaannya, saran dan kritik dari bapak dan ibu dosen serta rekan mahasiswa sangatlah penulis harapkan.

Penulis juga menyadari bahwa tanpa bimbingan, bantuan dan dorongan dari berbagai pihak, tugas akhir ini tidak mungkin dapat diselesaikan dengan baik. Oleh karena itu pada kesempatan ini penulis menyampaikan rasa terima kasih yang sebesar-besarnya kepada kedua orang tua yang senantiasa penulis cintai yang dalam keadaan sulit telah memperjuangkan hingga penulis dapat menyelesaikan perkuliahan ini.

2. Bapak Ir.Teruna Jaya, M.Sc. Selaku Sekretaris Departemen Teknik Sipil Universitas Sumatera Utara

3. Bapak/Ibu staf pengajar jurusan teknik sipil Universitas Sumatera Utara.

4. Seluruh pegawai administrasi yang telah memberikan bantuan dan kemudahan dalam penyelesaian administrasi

5. Untuk sahabat-sahabatku Leo, Topan, Suryo, Kingson, Joseph, Syawal, Benny, Meijen, Roy, Meijer, Mario, Pepeng, Fauzy, Suryadi, Budiman, Samuella, Egi, Ahmad, Emir, Joko, Asrul, Daniel, Widarto, Ilham, dan teman-teman stambuk 04 lainnya, buat doa, semangat dan dukungan kalian. 6. Seluruh rekan-rekan mahasiswa-mahasiswi jurusan teknik sipil.

Akhir kata penulis mengharapkan tugas akhir ini dapat bermanfaat bagi kita semua.

Medan, Agustus 2010

I.1. Latar Belakang ... 1

DAFTAR ISI

Abstrak ... i

Kata Pengantar ... ii

Daftar Isi ... iv

Daftar Notasi ... vi

Daftar Tabel ... viii

Daftar Gambar ... xi

BAB I Pendahuluan ... 1

I.2. Permasalahan ... 3

I.3. Tujuan Penulisan ... 5

I.4. Pembatasan Masalah ... 6

I.5. Metodologi Pembahasan ... 6

BAB II Tinjauan Pustaka ... 7

II.1. Teori Dasar Elastisitas ... 7

II.1.1. Komponen Tegangan ... 8

II.1.2. Komponen Regangan ... 14

II.1.3. Hubungan Tegangan dan Regangan (Hukum Hooke) ... 16

II.2. Analisa Pelat Lentur ... 20

II.2.1. Hubungan Regangan - Kelengkungan ... 21

II.2.2. Tegangan dan Resultan Tegangan ... 23

II.2.4. Persamaan Lendutan Pelat ... 30

II.2.5. Beberapa Syarat Batas ... 31

BAB III Metodologi Penelitian ... 34

III.1. Analisa Flat Slab ... 34

III.1.1.Lendutan ... 34

III.1.2.Momen Lentur ... 40

III.1.3.Tegangan ... 43

III.2. Analisa Flat Beam ... 44

III.2.1.Lendutan ... 44

III.2.2.Momen Lentur ... 47

BAB IV Aplikasi Flat Slab ... 49

IV.1. Gaya Dalam di Pusat Pelat ... 50

IV.2. Gaya Dalam Panel Pelat ... 54

BAB V Kesimpulan ... 81 Daftar Pustaka

v

DAFTAR NOTASI

A = luas tampang

a = sisi terpendek pelat b = sisi terpanjang pelat D = kekakuan lentur pelat E = modulus elastisitas

f’c = kekuatan tekan hancur beton G = modulus geser

h = tebal pelat

Mx = momen Lentur tegak lurus sumbu x My = momen lentur tegak lurus sumbu y Mxy = momen torsi/puntir tegak lurus sumbu x q = beban terbagi rata per satuan panjang Qx = gaya geser tegak lurus sumbu x Qy = gaya geser tegak lurus sumbu y

= rasio poisson x,y,z = koordinat pelat

σx = tegangan normal arah x

σy = tegangan normal arah y

τxy = tegangan geser arah xy

τyz = tegangan geser arah yz

Vx = gaya geser arah x

εx = regangan normal arah x

εy = regangan normal arah y

εz = regangan normal arah z

γyz = regangan geser arah yz

γxz = regangan geser arah xz

dx, dy, dz = panjang sisi elemen sumbu x,y,z

DAFTAR TABEL

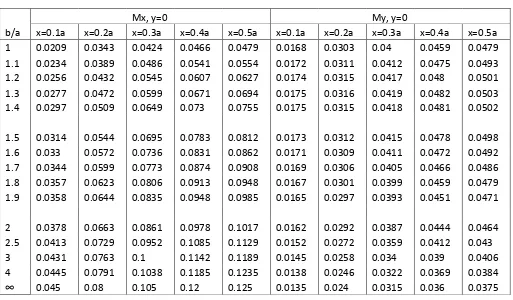
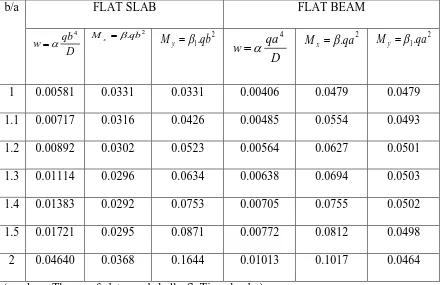
Tabel.III.1 : Faktor-Faktor Bilangan Untuk Momen Lentur Pelat Persegi

Panjang yang Mengalami Tekanan Merata q ... 48

Tabel.IV.1 : Faktor Bilangan Gaya Dalam Pelat ... 50

Tabel.IV.2 : Faktor Bilangan Gaya Dalam Pelat (Revisi) ... 51

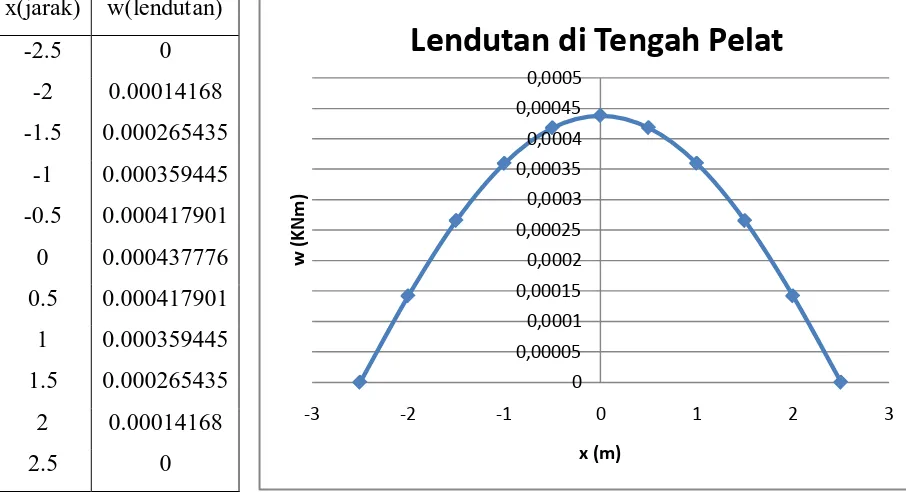
Tabel.IV.3 : Tabel dan Grafik Lendutan Pelat ... 52

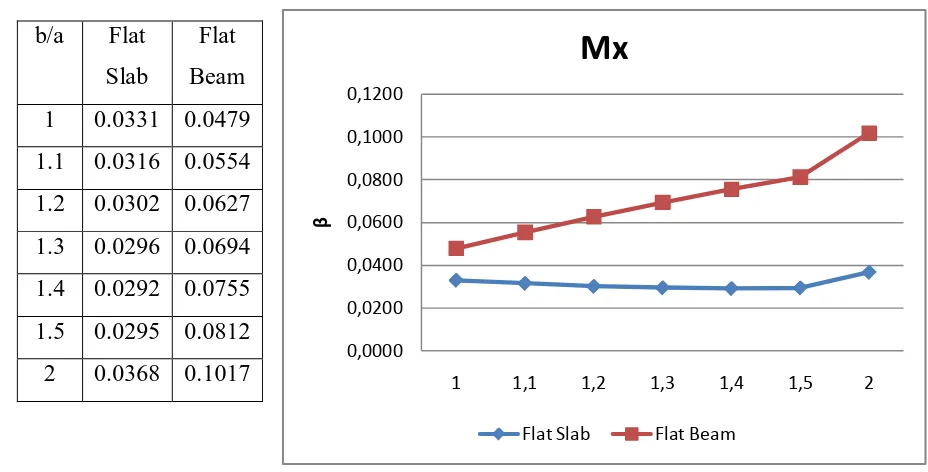
Tabel.IV.4 : Tabel dan Grafik Momen Lentur (Mx) Pelat ... 52

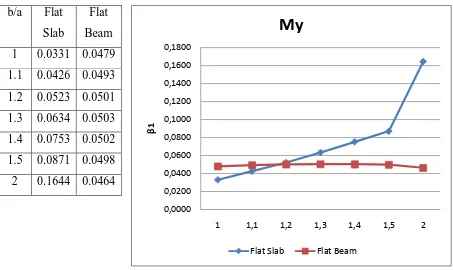
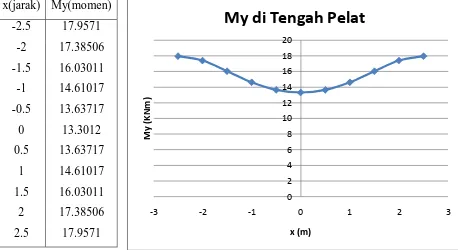
Tabel.IV.5 : Tabel dan Grafik Momen Lentur (My) Pelat ... 53

Tabel.IV.6 : Tabel dan Grafik Lendutan Flat Slab Bujur Sangkar di Tengah Pelat ... 56

Tabel.IV.7 : Tabel dan Grafik Lendutan Flat Slab Bujur Sangkar di Tepi Pelat ... 56

Tabel.IV.8 : Tabel dan Grafik Momen Lentur (Mx) Flat Slab Bujur Sangkar di Tengah Pelat ... 58

Tabel.IV.9 : Tabel dan Grafik Momen Lentur (Mx) Flat Slab Bujur Sangkar di Tepi Pelat ... 58

Tabel.IV.10 : Tabel dan Grafik Momen Lentur (My) Flat Slab Bujur Sangkar di Tengah Pelat ... 60

Tabel.IV.11 : Tabel dan Grafik Momen Lentur (My) Flat Slab Bujur Sangkar di Tepi Pelat ... 60

Tabel.IV.13 : Tabel dan Grafik Lendutan Flat Beam Bujur Sangkar di Tepi Pelat ... 62 Tabel.IV.14 : Tabel dan Grafik Momen Lentur (Mx) Flat Beam Bujur

Sangkar di Tengah Pelat ... 64 Tabel.IV.15 : Tabel dan Grafik Momen Lentur (Mx) Flat Beam Bujur

Sangkar di Tepi Pelat ... 64 Tabel.IV.16 : Tabel dan Grafik Momen Lentur (My) Flat Beam Bujur

Sangkar di Tengah Pelat ... 66 Tabel.IV.17 : Tabel dan Grafik Momen Lentur (My) Flat Beam Bujur

Sangkar di Tepi Pelat ... 66 Tabel.IV.18 : Tabel dan Grafik Lendutan Flat Slab Persegi Panjang di

Tengah Pelat ... 69 Tabel.IV.19 : Tabel dan Grafik Lendutan Flat Slab Persegi Panjang di

Tepi Pelat ... 69 Tabel.IV.20 : Tabel dan Grafik Momen Lentur (Mx) Flat Slab Persegi

Panjang di Tengah Pelat... 71 Tabel.IV.21 : Tabel dan Grafik Momen Lentur (Mx) Flat Slab Persegi

Panjang di Tepi Pelat ... 71 Tabel.IV.22 : Tabel dan Grafik Momen Lentur (My) Flat Slab Persegi

Panjang di Tengah Pelat... 73 Tabel.IV.23 : Tabel dan Grafik Momen Lentur (My) Flat Slab Persegi

Tabel.IV.24 : Tabel dan Grafik Lendutan Flat Beam Persegi Panjang di Tengah Pelat ... 75 Tabel.IV.25 : Tabel dan Grafik Lendutan Flat Beam Persegi Panjang di

Tepi Pelat ... 75 Tabel.IV.26 : Tabel dan Grafik Momen Lentur (Mx) Flat Beam Persegi

Panjang di Tengah Pelat... 77 Tabel.IV.27 : Tabel dan Grafik Momen Lentur (Mx) Flat Beam Persegi

Panjang di Tepi Pelat ... 77 Tabel.IV.28 : Tabel dan Grafik Momen Lentur (My) Flat Beam Persegi

Panjang di Tengah Pelat... 79 Tabel.IV.29 : Tabel dan Grafik Momen Lentur (My) Flat Beam Persegi

Gambar.4.5 : Momen Lentur (Mx) Flat Beam Bujur Sangkar ... 65

DAFTAR GAMBAR

Gambar.1.1 : Flat Slab ... 2

Gambar.1.2 : Flat Beam ... 3

Gambar.1.3 : Lendutan pada Flat Slab... 4

Gambar.1.4 : Lendutan Pada Flat Beam ... 5

Gambar.2.1 : Benda Tampang Sembarang yang Dibebani Gaya Gaya Luar ... 8

Gambar.2.2 : Komponen-Komponen Tegangan yang Bekerja Pada Potongan Kubus Kecil ... 10

Gambar.2.3 : Potongan Melintang Kubus yang Melalui Titik P ... 11

Gambar.2.4 : Komponen-Komponen Tegangan yang Bekerja Pada Potongan Kubus Kecil dimana Gaya per Satuan Volume X,Y,Z Bekerja ... 13

Gambar.2.5 : Elemen Kecil Berdimensi dx, dy, dz ... 14

Gambar.2.6 : Perpindahan Titik P, A, dan B... 15

Gambar.2.7 : Perubahan Bentuk Segi Empat Parallelogram ... 18

Gambar.3.1 : Lendutan Pelat Rata ... 34

Gambar.3.2 : Pelat di Atas Kolom Ruang ... 42

Gambar.4.1 : Lendutan Flat Slab Bujur Sangkar ... 57

Gambar.4.2 : Momen Lentur (Mx) Flat Slab Bujur Sangkar ... 59

Gambar.4.3 : Momen Lentur (My) Flat Slab Bujur Sangkar ... 61

Gambar.4.6 : Momen Lentur (My) Flat Beam Bujur Sangkar ... 67

Gambar.4.7 : Lendutan Flat Slab Persegi Panjang ... 70

Gambar.4.8 : Momen Lentur (Mx) Flat Slab Persegi Panjang ... 72

Gambar.4.9 : Momen Lentur (My) Flat Slab Persegi Panjang ... 74

Gambar.4.10 : Lendutan Flat Beam Persegi Panjang ... 76

Gambar.4.11 : Momen Lentur (Mx) Flat Beam Persegi Panjang ... 78

Abstrak

Penyusunan tugas akhir ini merupakan perhitungan sederhana mengenai gaya dalam yang terjadi pada flat slab. Perhitungan ini ditujukan untuk menemukan besaran gaya dalam yang terjadi pada setiap panel di dalam flat slab. Sehingga dari sini kita dapat mengetahui besarnya gaya dalam dan juga bentuk dari gaya dalam itu sendiri yang diaplikasikan ke dalam gambar.

Bentuk pelat yang diambil ada dua macam yaitu bujur sangkar dan persegi panjang. Alasan digunakannya dua bentuk pelat ini adalah agar di dalam tulisan kedua bentuk dapat diperbandingkan secara lebih nyata dan lebih kompleks. Dan akibat dari keterbatasan literatur mengenai pembahasan pelat ini maka penulis hanya mampu melakukan perhitungan sederhana dengan menggunakan data data yang ada.

Pembahasan yang dilakukan dalam tugas akhir ini antara lain perhitungan lendutan dan momen lentur. Perhitungan dilakukan secara manual dengan menggunakan rumus rumus yang terdapat di dalam literatur, untuk perhitungan data-data agar lebih akurat maka perhitungan dilakukan dengan menggunakan bantuan program microsoft excel dan penggambaran dilakukan dengan bantuan program AutoCAD .

BAB I

PENDAHULUAN

I.1. LATAR BELAKANG

Pada saat ini, pesatnya perkembangan teknologi telah memunculkan berbagai jenis struktur pelat yang cukup rumit misalnya pada struktur jembatan, pesawat terbang, bangunan, dan produk industri lainnya. Pada analisa struktur yang demikian kompleks, metode eksak akan sulit digunakan. Kompleksitas struktur tersebut menyangkut beberapa hal, antara lain: kerumitan bentuk struktur yang kerap kali tidak simetris, karakteristik material yang non-linier dan kondisi pembebanan yang rumit. Perhitungan menggunakan metode eksak tidak mungkin digunakan pada struktur dengan kompleksitas yang sedemikian rumit, karena penyelesaian eksak hanya dapat diperoleh untuk kasus yang paling sederhana.

Dalam model teori yang telah dikembangkan, analisa dan dan modelisasi struktur pelat dapat disederhanakan menjadi sebuah bidang datar yang disebut permukaan referensi, yaitu bidang tengah pelat atau bidang xy (z = 0). Dengan pemodelan ini semua relasi (persamaan keseimbangan, tegangan, deformasi, hukum hooke dan ekspresi energi) struktur solid 3 dimensi akan digeneralisasikan menjadi model solid 2 dimensi dengan mengikuti hipotesa-hipotesa yang diambil sesuai dengan model teori yang dipergunakan.

kecil dibandingkan dengan dimensi yang lain. Ditinjau dari segi statika, kondisi tepi pelat bisa bebas, jepit-jepit elastis, bertumpuan sederhana, bertumpuan elastis atau dalam beberapa hal dapat berupa tumpuan titik terpusat. Beban statis dan dinamis yang dipikul oleh pelat umumnya tegak lurus terhadap permukaan pelat sehingga peralihan yang terjadi pada pelat merupakan akibat dari aksi lentur pelat. Sementara perkembangan mekanika struktur secara keseluruhan dimulai dengan penelitian masalah keseimbangan, analisa dan percobaan yang pertama kali terhadap pelat terutama dilakukan terhadap getaran bebas.

Dalam hal yang lebih khusus, Pelat Flat-Slab memiliki keistimewaan dibandingkan dengan pelat lain yaitu pada pelat ini tidak menggunakan balok sebagai penahan bebannya melainkan pelat itu sendiri yang menahan beban diatasnya. Hal ini pasti menimbulkan pemikiran, tanpa adanya balok sebagai penahan pada pelat flat-slab ini pasti akan mengalami momen dan lendutan yang besar terutama pada bagian tengah pelat. Hal inilah yang mendasari penulisan tugas akhir ini, yaitu untuk menganalisa seberapa besar momen dan lendutan yang terjadi pada pelat flat-slab ini dan membandingkannya dengan pelat lain sehingga kita dapat mengetahui perbedaan yang konkrit antara pelat flat-slab ini dengan pelat biasa sehingga hal ini dapat dijadikan pedoman untuk mendesain pelat.

Gambar.1.2. Flat Beam

Setelah membaca dan mempelajari literatur mengenai pelat flat-slab ada beberapa hal yang dapat saya hipotesa, antara lain: Lendutan yang terjadi pada pelat flat-slab lebih besar dibandingkan dengan lendutan yang terjadi pada pelat balok. Dan besarnya nilai lendutan tergantung pada dimensi dari pelat tersebut. sementara itu, momen yang terjadi pada kedua jenis pelat tersebut sama besarnya apabila beban yang diberikan pada kedua jenis pelat tersebut sama besar.

I.2. PERMASALAHAN

Permasalahan yang terjadi pada pelat sangat luas dan rumit. Kasus-kasus seperti lendutan, momen lentur, momen puntir, gaya geser, analisa tegangan dan regangan, torsi, dan lain sebagainya. Hal ini belum termasuk permasalahan yang terjadi akibat bentuk pelat yang beragam dan kondisi perletakan yang berbeda pada pelat. Oleh karena itu, dibutuhkan waktu yang lama untuk dapat mempelajari dan mengatasi semua masalah yang terjadi pada kasus pelat.

kasus pelat flat-slab ini karena tepi pelat tidak ditumpu oleh balok sehingga menyebabkan terjadi lendutan pada tepi pelat. Sementara pada kasus pelat balok karena tepi dari pelat tersebut menggunakan balok sehingga lendutan hanya terjadi di tengah pelat sementara lendutan yang terjadi pada tepi pelat ini hampir tidak ada. Inilah perbedaan yang khas dari kedua jenis pelat ini dan inilah yang mendasari penulisan tugas akhir ini yaitu untuk mengetahui seberapa besar perbedaan gaya dalam dari kedua pelat ini dari segi perhitungan mekanika teknik.

(sumber : Theory of plates and shells, S. Timoshenko) Gambar.1.4. Lendutan pada Flat Beam

Reaksi (R) yang terjadi pada gambar lendutan pelat diatas dapat dicari dengan menggunakan rumus

( )

=

( )

− _ _ =

dxdy w d v D M

R xy

2 1

2 2

(sumber : Theory of plates and shells, S. Timoshenko)

I.3. TUJUAN PENULISAN

I.4. PEMBATASAN MASALAH

Karena luasnya permasalahan yang terjadi dalam pembahasan mengenai pelat dan akibat dari keterbatasan literatur serta waktu yang kurang mencukupi, sehingga dalam penulisan tugas akhir ini hanya akan membahas mengenai perhitungan mekanika teknik dari pelat yang dibandingkan saja. Dengan kata lain, hal-hal diluar perhitungan mekanika teknik, seperti perhitungan bahan, jenis bahan dan lain sebagainya tidak akan dibahas dalam tugas akhir ini.

I.5. METODOLOGI PENULISAN

BAB II

TINJAUAN PUSTAKA

II.1. Teori Dasar Elastisitas

Teori Elastisitas merupakan cabang yang sangat penting dari fisis matematis, yang mengkaji hubungan antara gaya, perpindahan, tegangan dan regangan dalam sebuah benda elastis. Bila suatu benda dibebani oleh gaya luar, benda tersebut akan mengalami deformasi sehingga timbul tegangan dan regangan. Perubahan bentuk ini tergantung pada konfigurasi geometris dari benda tersebut dan pada sifat mekanis bahannya. Dalam teori elastisitas kita batasi pembahasan hanya pada bahan yang elastis linier, yaitu keadaan dimana hubungan antara regangan dan tegangan bersifat linier dan perubahan bentuk serta tegangan akan hilang bila gaya luar dihilangkan.Selain hal tersebut, teori elastisitas menganggap bahan bersifat homogen dan isotropik, dengan demikian sifat mekanis bahan sama dalam segala arah.

II.1.1. Komponen Tegangan

Tegangan didefinisikan sebagai intensitas gaya yang bekerja pada tiap satuan luas bahan. Untuk menjelaskan ini, maka akan ditinjau sebuah benda yang dalam keadaan setimbang seperti terlihat pada Gambar.2.1. Akibat kerja gaya luar P1, P2, P3, P4, P5, P6, dan P7, maka akan terjadi gaya dalam di antara benda. Untuk mempelajari besar gaya ini pada titik sembarang O, maka benda diandaikan dibagi menjadi dua bagian A dan B oleh penampang mm yang melalui titik O.

(sumber : Theory of elasticity, S. Timoshenko)

Kemudian tinjaulah salah satu bagian ini, misalnya A. Bagian ini dapat dinyatakan dalam keadaan setimbang akibat gaya luar P1, P2, P3, P4, P5, P6, P7 dan gaya dalam terbagi di sepanjang penampang mm yang merupakan kerja bahan. Oleh karena intensitas distribusi ini, tegangan dapat diperoleh dengan membagi gaya tarik total P dengan luas potongan penampang A.

x

y

z

P1

P2

P3

P4

P5

P6

P7

Gambar.2.1.Benda Tampang Sembarang yang Dibebani oleh Gaya-Gaya Luar m

m

O

B

Untuk memperoleh besar gaya yang bekerja pada luasan kecil δA, misalnya dari potongan penampang mm pada titik O, dapat diamati bahwa gaya yang bekerja pada elemen luas ini diakibatkan oleh kerja bahan bagian B terhadap bahan bagian A yang dapat diubah menjadi sebuah resultante δP. Apabila tekanan terus diberikan pada luas elemen δA, harga batas δP/δA akan menghasilkan besar tegangan yang bekerja pada potongan penampang mm pada titik O. arah batas resultante δP adalah arah tegangan.

Umumnya, arah tegangan ini miring terhadap luas δA tempat gaya bekerja sehingga dapat diuraikan menjadi dua komponen tegangan yaitu tegangan normal yang tegak lurus terhadap luas dan tegangan geser yang bekerja pada

bidang luas δA.

(sumber : Theory of elasticity, S. Timoshenko)

Untuk menjelaskan tegangan yang bekerja pada keenam sisi elemen ini diperluka n tiga simbol σx, σy, σz untuk tegangan normal dan enam simbol τxy, τyx,

τxz, τzx, τyz, τzy untuk tegangan geser. Dengan meninjau kesetimbangan elemen

secara sederhana, maka jumlah simbol tegangan geser dapat dikurangi menjadi tiga.

Gambar.2.2.Komponen-Komponen Tegangan yang Bekerja Pada Potongan Kubus Kecil x

y

z

σx

τxy

τxz

τzx

σy

τyz

τzy

τyx

σz

σz

τzx

τzy

τyz

σy

τyx

τxz

τxy

σx

(sumber : Theory of elasticity, S. Timoshenko)

Apabila momen gaya yang bekerja pada elemen terhadap garis yang melalui titik tengah C dan sejajar sumbu x, maka hanya tegangan permukaan yang diperlihatkan pada Gambar.2.3 yang perlu ditinjau. Gaya benda, seperti berat elemen, dapat diabaikan karena semakin kecil ukuran elemen, maka gaya benda yang bekerja padanya berkurang sebesar ukuran linier pangkat tiga. Sedangkan gaya permukaan berkurang sebesar ukuran linier kuadrat. Oleh karena itu, untuk elemen yang sangat kecil, besar gaya benda sangat kecil jika dibandingkan dengan gaya permukaan sehingga dapat dihilangkan ketika menghitung momen.

Dengan cara yang sama, orde momen akibat ketidak-merataan distribusi gaya normal lebih tinggi dibandingkan dengan orde momen akibat gaya geser dan menjadi nol dalam limit. Juga gaya pada masing-masing sisi dapat ditinjau sebagai luas sisi kali tegangan di tengah. Jika ukuran elemen kecil pada Gambar.2.3 adalah dx, dy, dz, maka momen gaya terhadap P, maka persamaan kesetimbangan elemen ini adalah :

τxz dx dy dz = τzx dx dy dz (2.1)

z

x C

P

τZX

τXZ

τZX τXZ

Dua persamaan lain dapat diperoleh dengan cara yang sama sehingga didapatkan :

τxy = τyx τzx = τxz τzy = τyz (2.2)

Dengan demikian enam besaran σx, σy, σz, τxy = τyx, τzx = τxz, τzy = τyz

cukup untuk menjelaskan tegangan yang bekerja pada koordinat bidang melalui sebuah titik. Besaran-besaran ini disebut komponen tegangan pada suatu titik.

Jika kubus pada Gambar 2.3 diberikan suatu komponen gaya per satuan volume sebesar X, Y, Z pada masing-masing sumbu x, y, dan z maka gambar komponen tegangan dalam Gambar.2.3 akan menjadi seperti pada Gambar.2.4 di bawah ini dan persamaan kesetimbangan akan dapat diperoleh dengan menjumlahkan semua gaya pada elemen dalam arah x yaitu :

(sumber : Theory of elasticity, S. Timoshenko)

Sesudah dibagi dengan jx, jy, jz, dan seterusnya hingga batas penyusutan elemen hingga titik x, y, z maka akan didapatkan :

0 = + ∂ ∂ + ∂ ∂ + ∂ ∂

X

z zx y

yx x

x τ τ

σ

0 = + ∂ ∂ + ∂ ∂ + ∂ ∂

Y

z zy x

xy y

y τ τ

σ

(2.3)

0 = + ∂ ∂ + ∂ ∂ + ∂ ∂

Z

y yz x

xz z

z τ τ

σ

Persamaan (2.3) ini harus dipenuhi di semua titik di seluruh volume benda. Tegangan berubah di seluruh volume benda, dan apabila sampai pada permukaan, tegangan-tegangan ini harus sedemikian rupa sehingga setimbang dengan gaya luar yang bekerja pada permukaan benda.

Gambar.2.4.Komponen-Komponen Tegangan yang Bekerja Pada Potongan Kubus Kecil Dimana Gaya Luar Per Satuan Volume X, Y, Z Bekerja

x

y

z

σx+ σx

τxy + τxy

τzx

τzy

σz

τyz

σy

τyx

τxz

τxy

σx P

τxz + τxz

σz+ σz

τzx + τzx

τzy + τzy

σy+ σy

τyx + τyx

II.1.2. Komponen Regangan

Regangan didefinisikan sebagai suatu perbandingan antara perubahan dimensi suatu bahan dengan dimensi awalnya. Karena merupakan rasio antara dua panjang, maka regangan ini merupakan besaran tak berdimensi, artinya regangan tidak mempunyai satuan. Dengan demikian, regangan dinyatakan hanya dengan suatu bilangan, tidak bergantung pada sistem satuan apapun. Harga numerik dari regangan biasanya sangat kecil karena batang yang terbuat dari bahan struktural hanya mengalami perubahan panjang yang kecil apabila dibebani.

Dalam membahas perubahan bentuk benda elastis, selalu dianggap bahwa benda terkekang sepenuhnya sehingga tidak bisa bergerak sebagai benda kaku sehingga tidak mungkin ada perpindahan partikel benda tanpa perubahan bentuk benda tersebut.

Pada pembahasan ini yang ditinjau hanya perubahan bentuk yang kecil yang biasa terjadi pada struktur teknik. Perpindahan kecil pertikel yang berubah bentuk ini diuraikan ke dalam komponen u, v, w berturut-turut sejajar dengan sumbu koordinat. Besar komponen ini dianggap sangat kecil dan bervariasi di seluruh volume benda.

x

y

z O

dx

dy dz

A C

B P

Tinjau elemen kecil dx dy dz dari sebuah benda elastis seperti terlihat pada Gambar.2.5. Apabila benda mengalami perubahan bentuk dan u, v, w merupakan komponen perpindahan titik P, perpindahan titik di dekatnya , A, dalam arah x pada sumbu x adalah orde pertama dalam dx, yaitu u + (ju/jx) dx akibat pertambahan fungsi u sebesar (ju/jx) dx sesuai dengan pertambahan panjang elemen PA akibat perubahan bentuk adalah (ju/jx) dx. Sedangkan satuan perpanjangan (unit elongation) pada titik P dalam arah x adalah (ju/jx). Dengan

cara yang sama, maka diperoleh satuan perpanjangan dalam arah y dan z adalah (jv/jy) dan (jw/jz).

(sumber : Theory of elasticity, S. Timoshenko)

[image:30.595.184.337.372.508.2]

Sekarang tinjaulah pelentingan sudut antara elemen PA dan PB dalam Gambar.2.6. Apabila u dan v adalah perpindahan titik P dalam arah x dan y, perpindahan titik A dalam arah y dan titik B dalam arah x berturut-turut adalah v + (jv/jx) dx dan u + (ju/jy) dy. Akibat perpindahan ini, maka P’A’ merupakan arah baru elemen PA yang letaknya miring terhadap arah awal dengan sudut kecil yang ditunjukkan pada gambar, yaitu sama dengan (jv/jx). Dengan cara yang

O

y

x

dx

dy

v u

P'

A'

B'

v v +_xdx

u u +_ydy

B

A P

sama arah P’B’ miring terhadap PB dengan sudut kecil (ju/jy). Dari sini dapat dilihat bahwa sudut awal APB yaitu sudut antara kedua elemen PA dan PB berkurang sebesar (jv/jx) + (ju/jy). Sudut ini adalah regangan geser (shearing strain) antara bidang xz dan yz. Regangan geser antara bidang xy dan xz dan

bidang yx dan yz dapat diperoleh dengan cara yang sama.

Selanjutnya kita menggunakan huruf Є untuk satuan perpanjangan dan huruf γ untuk regangan geser. Untuk menunjukkan arah regangan digunakan subskrip yang sama terhadap huruf ini sama seperti untuk komponen tegangan. Kemudian diperoleh dari pembahasan di atas beberapa besaran berikut :

x u

x

∂ ∂ = ∈

y v

y

∂ ∂ = ∈

z w

z

∂ ∂ = ∈

x v y u

yx xy

∂ ∂ + ∂ ∂ = =γ γ

x w z u

zx xz

∂ ∂ + ∂ ∂ = =γ γ

y w z v

zy yz

∂ ∂ + ∂ ∂ = =γ

γ (2.4)

Keenam besaran ini disebut sebagai komponen regangan geser.

II.1.3. Hubungan Tegangan dan Regangan (Hukum Hooke)

Hubungan linier antara komponen tegangan dan komponen regangan umumnya dikenal sebagai hukum Hooke. Satuan perpanjangan elemen hingga batas proporsional diberikan oleh

E

x x

σ

=

∈ (2.5)

kecil. Perpanjangan elemen dalam arah x ini akan diikuti dengan pengecilan pada komponen melintang yaitu

E

x y

σ ϑ

− = ∈

E

x z

σ ϑ

− =

∈ (2.6)

dimana adalah suatu konstanta yang disebut dengan ratio Poisson (Poisson’s Ratio). Untuk sebagian besar bahan, ratio poisson dapat diambil sama dengan

0,25. Untuk baja struktur biasanya diambil sama dengan 0,3.

Apabila elemen di atas mengalami kerja tegangan normal σx, σy, σz secara

serempak, terbagi rata di sepanjang sisinya, komponen resultante regangan dapat diperoleh dari persamaan (2.5) dan (2.6) yaitu :

(

)

[

x y z

]

x

E σ −ϑσ +σ =

∈ 1

(

)

[

y x z

]

y

E σ −ϑ σ +σ =

∈ 1

(2.7)

(

)

[

z x y

]

z

E σ −ϑσ +σ =

∈ 1

(sumber : Theory of elasticity, S. Timoshenko)

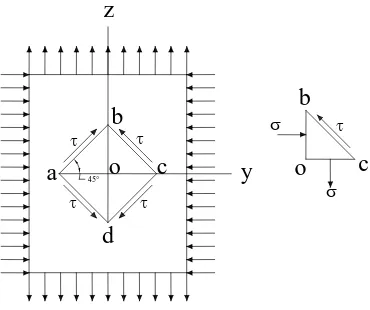
Tinjaulah kasus khusus yaitu perubahan bentuk segi empat paralelogram di mana σz = σ, σy = –σ , dan σx = 0. Potonglah sebuah elemen abcd dengan

[image:33.595.195.380.124.279.2]

bidang yang sejajar dengan sumbu x dan terletak 45˚ terhadap sumbu y dan z (Gambar.2.9). Dengan menjumlah gaya sepanjang dan tegak lurus bc, bahwa tegangan normal pada sisi elemen ini nol dan tegangan geser pada sisi adalah :

τ

= ½ (σz – σy) = σ (2.8)

Kondisi tegangan seperti itu disebut geser murni (pure shear). Pertambahan panjang elemen tegak Ob sama dengan berkurangnya panjang elemen mendatar Oa dan Oc, dan dengan mengabaikan besaran kecil dari orde kedua, kita bisa

menyimpulkan bahwa panjang elemen ab dan bc tidak berubah selama terjadinya perubahan bentuk. Sudut antara sisi ab dan bc berubah dan besar regangan geser yang bersangkutan γ bisa diperoleh dari segi tiga Obc. Sedudah perbuahan bentuk akan didapatkan :

b

y z

d a 45° o c

b c o σ

σ τ τ

τ τ

τ

z y y Ob Oc ∈ + ∈ + =       − = 1 1 2 4 tan π

Untuk γ yang kecil, tan (γ/2) ≈γ/2, maka :

z y y y y y y Ob Oc ∈ + ∈ + = + − = + − =       − = 1 1 2 1 2 1 2 tan 4 tan 1 2 tan 4 tan 2 4 tan π π π

Maka diperoleh :

2 y

y=−

∈ dan 2 y

z=

∈

Sedangkan jika nilai-nilai σz = σ, σy = –σ , dan σx = 0 disubstitusikan ke dalam

persamaan (2.7) maka akan diperoleh :

(

)

2 1 ) ( 1 y E E

y =−

+ − = − − = ∈ σ ϑσ ϑ σ

( )

[

]

(

1

)

₂

1 y E E z = + − = − − − = ∈ σ ϑ σ ϑ σ

Maka diperoleh hubungan antara regangan dengan regangan geser :

2 y

∈=

(2.9)

Hubungan antara regangan dan tegangan geser didefinisikan oleh konstanta E dan v yaitu :

(

)

(

)

E E τ ϑ σ ϑ

γ = 21+ =21+ (2.10)

Jika digunakan notasi :

(

+ϑ

)

= 1 2 E G (2.11)

G τ

γ = (2.12)

dimana konstanta G didenisikan oleh (2.11), dan disebut modulus elastisitas dalam geser (modulus of elasticity in shear) atau modulus kekakuan (modulus of

rigidity).

Apabila tegangan geser bekerja ke semua sisi elemen, seperti terlihat pada Gambar.2.5, pelentingan sudut antara dua sisi yang berpotongan hanya tergantung kepada komponen tegangan geser yang bersangkutan dan diperoleh :

G

xy xy

τ γ =

G

yz yz

τ γ =

G

xz xz

τ γ =

II.2. Analisa Pelat Lentur

Pelat dan shell pada mulanya adalah suatu elemen struktur bidang rata maupun lengkung dimana ketebalannya lebih kecil dibandingkan dimensi lainnya, Ketebalan suatu pelat biasanya diukur pada arah normal sumbu (garis berat) pelat. Dilihat dari segi ketebalannya, pelat dapat dikategorikan menjadi 3 jenis, yaitu:

1. Pelat tipis dengan lendutan kecil (thin plate with small deflection) 2. Pelat tipis dengan lendutan besar (thin plate with large deflection) 3. Pelat tebal (thick plate)

penyederhanaan yang konsisten dengan besarnya lendutan yang biasanya ditemukan pada struktur pelat.

Asumsi yang mendasar di dalam teori lendutan kecil pada pelat terlentur atau disebut teori klasik untuk material isotropik, homogen dan elastis didasarkan pada geometri lendutan (deformasi), antara lain:

1. Lendutan di tengah bentang pelat lebih kecil disbanding ketebalan pelat itu sendiri dan kemiringan lengkungan pelat sangat kecil sehingga dapat diabaikan.

2. Penampang pada bidang system pelat tidak berubah pada saat lenturan. 3. Bdang tegak lurus pada bidang system pelat akan tetap tegak lurus setelah

pelenturan sehingga regangan geser vertical γxzdan γyz dapat diabaikan. 4. Tegangan normal pada bentang σz sangat kecil dibandingkan komponen

lainnya sehingga dapat diabaikan. Pada pelat tebal, regangan geser sangat penting seperti blok pada umumnya.

II.2.1 Hubungan Regangan – Kelengkungan

Beranjak dari anggapan tersebut di atas, hubungan regangan – perpindahan dapat digambarkan sebagai berikut :

x u

x

∂ ∂ =

ε =0

∂ ∂ =

z w

z

ε

y u

y ∂

∂ =

ε =0

∂ ∂ + ∂ ∂ =

z u x w

xz

γ (2.13)

x v y u

xy

∂ ∂ + ∂ ∂ =

γ =0

∂ ∂ + ∂ ∂ =

z v y w

xz

Melalui Persamaan : 0 = ∂ ∂ + ∂ ∂ = z u x w xz γ z u x w ∂ ∂ − = ∂ ∂ _x z u w ∂ ∂ ∂ − = ∂ ) , ( 0 x y

u x w z u + ∂ ∂ −

= dan v(x,y)

y w z v + ∂ ∂ − =

akan didapat fungsi w dalam parameter x,y atau w = (x,y), dengan kata lain perpindahan lateral tidak dipengaruhi fungsi komponen z (tebal pelat). Dengan asumsi kedua di atas didapatkan harga u0 (x,y) = 0 dan v0 (x,y) = 0

sehingga didapat: x w z u ∂ ∂ − = dan y w z v ∂ ∂ − = (2.14)

subtitusi persamaan (2.14) ke persamaan (2.13) menghasilkan:

2 2 ) ( x w z x w z x x ∂ ∂ − = ∂ ∂ − ∂∂ = ε 2 2 y w z y ∂ ∂ − = ε y x w z xy ∂ ∂∂ −

= 2 2

γ (2.15)

Persamaan ini memberikan nilai regangan di setiap titik. Kelengkungan dari pelat lentur didefenisikan sebagai laju perubahan kemiringan sudut sepanjang pelat. Dengan asumsi pertama dan persamaan mewakili kelengkungan pelat.

Sehingga kelengkungan k (kappa) pada tengah bentang yang paralel dengan bidang xz, yz, dan xy dapat digambarkan sebagai berikut :

x x k x w x

r ∂ =

∂ ∂∂ = ( ) 1 x y k x w x

r ∂ =

∂ ∂∂

= ( )

1

xy xy

k y w x

r ∂ =

∂ ∂∂

= ( )

1

Sehingga hubungan regangan dan kelengkungan adalah superposisi persamaan dan sebagai :

x x =−zk

ε εy =−zky εxy =−2zkxy (2.17)

II.2.2 Tegangan dan Resultan Tegangan

Pada kasus tegangan dan regangan tiga dimensi yang mengikuti hukum hook untuk benda isotropis, homogen dan elastis, hubungan tegangan dan regangan adalah sebagai berikut :

)] (

[ 1

z y x

x v

E σ σ σ

ε = − +

G r_xy =τxy

)] (

[ 1

z x y

y v

E σ σ σ

ε = − +

G rxz xz

τ

= (2.18)

)] (

[ 1

y x z

z v

E σ σ σ

ε = − +

G r_yz =τyz

dimana :

E = Modulus Elastisitas Bahan v = Poisson Ratio

G = Modulus Geser ] ) 1 ( 2 [

v E G

+ =

Notasi untuk tegangan normal digunakan lambang σ (sigma) dan tegangan

Tegangan normal bernilai positif bila tegangan tersebut menghasilkan tegangan tarik dan sebaliknya. Arah positif tegangan geser pada sisi seberang dari elemen kubus diambil sebagai arah positif sumbu koordinat, apabila tegangan tarik pada sisi yang sama mempunyai arah positif dari sumbu yang bersangkutan. Apabila arah tegangan tarik berlawanan dengan arah positif maka arah positif komponen tegangan geser dibalik.

Dengan memasukkan :

εx = γyz = γxz = 0 diperoleh :

) (

1 2 x y

x v v E ε ε σ + − = ) (

1 2 y x

y v v E ε ε σ + − = (2.19) xy xy Gγ

τ =

Untuk pelat lengkung persamaan menjadi :

Dari persamaan-persamaan di atas dapat diketahui bahwa tegangan tidak terjadi pada sumbu pelat dan akan berubah secara linier sepanjang tebal pelat. Tegangan terdistribusi sepanjang tebal pelat yang diakibatkan oleh momen lentur Mx, My dan Mxy.

Dengan mengambil integral :

dy M dz z dy dz dy z x t t x t t

x =

∫

=

∫

₋ − 2 / 2 / 2 / 2 / . . . . .

.σ σ (2.21)

Dengan cara yang sama tegangan yang lain akan diperoleh dan dibuat dalam bentuk matriks hubungan momen lentur dan tegangan :

∫

−           =       

 /2

2 / . . t t xy y x dz z Mxy My Mx τ σ σ (2.22)

dimana : Mxy = Myx

Hubungan gaya geser dan tegangan geser adalah :

∫

−      =     

 /2

2 / . t t yz xz dz Qy Qx τ τ (2.23)

Melalui persamaan (2.22) diselesaikan seperti :

∫

−

= /2 2 / . . t t

x zdz

Mx σ

( )

zdz

( )

−

∫

   ∂ ∂ + ∂ ∂ − −

= /2

2 / 2 2 2 2 2

2 . . .

1 t t dz z y w x w v E Mx

( )

− ∂∂ + ∂∂  − = 2 2 2 2 2 3 . 1 12 . y w x w v t E Mx (2.24) Faktor

( )

2 3 1 12 . v t E −

− disebut faktor kekakuan lentur pelat

Dari persamaan tersebut di atas diperoleh :

3 . . 12 t z M_x x σ 3 . . 12 t z M_y y = σ 3 . . 12 t z M_xy xy = τ (2.25)

Untuk menentukan komponen-komponen tegangan arah z yaitu : σz, τxz, dan τyz digunakan persamaan differensial kesetimbangan untuk elemen pelat dalam suatu bentuk tegangan umum :

0 = ∂ ∂ + ∂ ∂ + ∂ ∂ z y x xz xy

x τ τ

σ 0 = ∂ ∂ + ∂ ∂ + ∂ ∂ z x y yz xy

y τ τ

σ (2.26) 0 = ∂ ∂ + ∂ ∂ + ∂ ∂ z x z yz xz

z τ τ

σ

Dari persamaan (2.26) diperoleh :

    ∂ ∂ + ∂ ∂ − = ∂ ∂ y x z xz x

xz σ τ

dz y x w v z E y y w v x w v z E x t z xz . 1 . 1 . 2 / 2 2 2 2 2 2

∫

_                 ∂ ∂∂ + − ∂∂ +           ∂ ∂ + ∂ ∂ − − ∂∂ − = τ

( )

( )

dz

y x w v z E y w v x w v z E t z xz . . 1 . 1 . 2 / 2 3 3 3 3 3 2

∫

            ∂ ∂ ∂ + +       ∂ ∂ + ∂ ∂ − = τ

( )

( )

( )

dz

y x w v z E y x w v v z E x w v z E t z xz . . 1 . . 1 . . 1 . 2 / 2 3 2 3 2 3 3 2

∫

      ∂ ∂∂ + + ∂ ∂∂ + + ∂ ∂ − = τ

( )

( )

( )

dz

v v v y x w z E x w v z E t z xz . 1 1 1 . . 1 . 2 / 2 2 3 3 3 2

∫

            + + + ∂ ∂∂ + ∂ ∂ − = τ

( )

dz

y w x w x v z E t z xz . 1 . 2 / 2 2 2 2 2

∫

_    ∂ ∂ + ∂ ∂ ∂∂ − = τ

( )

         ∂ ∂ + ∂ ∂ ∂∂       − + = 2 2 2 2 2 2 2 4 1 2 y w x w x z t v E xz

τ (2.27)

Dengan cara yang sama diperoleh :

( )

         ∂ ∂ + ∂ ∂ ∂∂       − − = 2 2 2 2 2 2 2 4 1 2 y w x w y z t v E yz

τ (2.28)

Melalui persamaan di atas dapat dilihat distribusi komponen tegangan τxz dan τyz

sepanjang ketebalan pelat merupakan persamaan parabola. Sedangkan komponen

tegangan normal σz dapat ditentukan melalui persamaan ketiga pada persamaan (2.26) dengan mendistribusikan komponen tegangan yang telah diperoleh pada persamaan (2.27) dan (2.28) sebagai berikut :

( )

( )

dz y w x w y z t v E y y w x w x z t v E x t z . . 4 1 2 . 4 1 2 2 2 2 2 2 2 2 2 / 2 2 2 2 2 2 2 2           ∂ ∂ + ∂ ∂ ∂∂       − − ∂∂ +           ∂ ∂ + ∂ ∂ ∂∂       − − ∂∂ − =

∫

σ

( )

( )

dz

y w x w y z t v E y w x w x z t v E t z . . 4 1 2 . 4 1 2 2 2 2 2 2 2 2 2 2 2 / 2 2 2 2 2 2 2 2 2 2           ∂ ∂ + ∂ ∂ ∂∂       − − +           ∂ ∂ + ∂ ∂ ∂∂       − − − =

∫

σ

( )

dz

y w x w y x z t v E t z . . 4 1 2 2 / 2 2 2 2 2 2 2 2 2 2 2 2

∫

          ∂ ∂ + ∂ ∂     ∂∂ + ∂∂       − − − = σ

( )

          ∂ ∂ + ∂ ∂     ∂ ∂ + ∂ ∂       _{− +} − − = 2 2 2 2 2 2 2 2 3 2 3 2 2 . 3 4 12 1 2 y w x w y x z z t t v E σ (2.29)

Komponen tegangan arah z selalu kecil dibandingkan dengan tegangan-tegangan pada arah lain (plane stress) dan ini sesuai dengan asumsi ke empat di atas, dimana tegangan arah z pada bidang tengah pelat sangat kecil dan dapat diabaikan.

II.2.3 Variasi Tegangan di dalam Pelat

Perhatikan suatu elemen pelat kecil dx dy yang memikul beban terbagi merata per satuan luas p. Untuk penyederhanaan, diasumsikan gaya dan momen yang bekerja pada sisi penampang terdistribusi merata sepanjang sisi elemen.

Dengan adanya perubahan tempat misalnya dari sudut kiri atas ke sudut kanan bawah elemen pelat, maka salah satu komponen gaya misalkan Mx yang bereaksi pada sisi elemen negatif akan berubah relatif terhadap permukaan elemen positif.

Turunan parsial dipergunakan karena Mx adalah fungsi dari x dan y. dari gambar, pelat dalam kondisi setimbang bila mana jumlah gaya yang bekerja pada arah z sama dengan nol.

0 . . .

. . . . .

= +

∂ ∂ + ∂

∂ _{dxdy pdxdy}

y Qy dy

dx x Qx

sehingga diperoleh :

0 .

.

= + ∂ ∂ + ∂

∂ _p

y Qy x

Qx

(2.30)

Kesetimbangan momen pada sumbu x :

0 . . .

. . . . .

= −

∂ ∂ + ∂

∂ _{dxdy Qydxdy}

y My dy

dx x Mxy

sehingga diperoleh :

0 .

.

= − ∂ ∂ + ∂

∂ _Qy

y My x

Mxy

(2.31)

begitu juga untuk kesetimbangan momen pada sumbu y :

0 .

.

= − ∂ ∂ + ∂

∂ _Qx

x Mx y

Mxy

(2.32)

p y My dy x Mxy x Mx − = ∂ ∂ + ∂ ∂ + ∂ ∂ 2 2 2 2 2 . 2 (2.33)

Persamaan (2.33) merupakan persamaan differensial kesetimbangan pelat tipis. Gaya geser vertikal jika dinyatakan dalam fungsi x dan y adalah turunan pertama dari persamaan kesetimbangan momen pada persamaan (2.23) menjadi :

( )

w

x D y w x w x D

Qx ₂ 2

2 2 2 ∇ ∂∂ − =     ∂ ∂ + ∂ ∂ ∂∂ − = (2.34)

( )

w

x D y w x w x D

Qy ₂ 2

2 2 2 ∇ ∂∂ − =     ∂ ∂ + ∂ ∂ ∂∂ − =

dimana : ₂

2 2 2 2 y x ∂ ∂ + ∂ ∂ = ∇

II.2.4 Persamaan Lendutan Pelat

Persamaan differensial dasar lendutan pelat diambil dari persamaan (2.24) dan (2.33) menjadi :

D p y Ky y x Kxy x Kx = ∂ ∂ + ∂ ∂ ∂ + ∂ ∂ 2 2 2 2 2 . 2

dengan mengganti persamaan kelengkungan di atas menjadi persamaan lendutan dengan memasukkan persamaan (2.16) diperoleh :

D p y w y x w x w = ∂ ∂ + ∂ ∂∂ + ∂ ∂ 4 4 2 2 4 4 4 .

Persamaan ini merupakan persamaan differensial lendutan pelat yang dibebani merata sebesar p. Persamaan lendutan w di dapat dengan mengintegrasi persamaan tersebut pada syarat batas yang ada. Jika persamaan (2.34) dan (2.35) dimasukkan ke dalam persamaan tegangan pada (2.27), (2.28) dan (2.29) akan diperoleh :

    

  

      − =

2 2 1 2 3

t z t

Qx xy

τ

    

  

      − =

2 2 1 2 3

t z t

Q_y

yz

τ

    

  

      + − −

=

3 2 3 1 2 3 2 4 3

t z t

z p

z

σ

(2.36)

II.2.5 Beberapa Syarat Batas

Distribusi tegangan yang terjadi pada pelat tidak terlepas dari syarat batas (Boundary Condition), antara lain gaya dan perpindahan. Pada persamaan differensial kesetimbangan pelat dibutuhkan dua syarat batas utama pada masing-masing tepi yaitu lendutan dan rotasi atau gaya dan momen atau kombinasi diantaranya. Perbedaan yang mendasar antara syarat batas pelat dan balok adalah momen puntir (torsi) di sepanjang tepi pelat.

Beberapa kondisi batas untuk suatu pelat persegi panjang, dimana sumbu x dan y diambil sejajar dengan sisi-sisi pelat, yaitu :

a. Tepi terjepit

( )

w _x=a =0 ;  =0      ∂ ∂ =a x x w

b. Pelat yang ditumpu sederhana

Jika pada pelat x = a ditumpu sederhana, maka lendutan sepanjang tepi ini adalah nol. Namun tepi ini dapat berputar bebas terhadap garis tepi, sehingga tidak terdapat momen lentur Mx sepanjang tepi ini.

( )

w _x=a =0 ;

( )

₂ 0 2 2 2 =     ∂ ∂ + ∂ ∂ − = = = a x a x y w v x w D Mx

c. Tepi Bebas

Jika tepi pelat bebas pada x = a, maka pada tepi ini tidak terdapat momen lentur Mx dan momen puntir Mxy dan gaya geser Qx, Sehingga :

( )

₂ 0

2 2 2 =     ∂ ∂ + ∂ ∂ − = = = a x a x y w v x w D Mx

( )

( )

0

. 1 2 =     ∂ ∂∂ − − = = = a x a x y x w v D Mxy

( )

₂ 0

2 2 2 =     ∂ ∂ + ∂ ∂ ∂∂ − = = = a x a x y w x w x D Qx

(

)

_      ∂ ∂∂ − + ∂ ∂ − = ∂ ∂ + = y x w v y w D x M Q

Vy y xy 2

3

3 3

2

= a dapat dijadikan dengan dua buah gaya vertikal sebesar Mxy dan terpisah dengan jarak sebesar dy.

Dari gambar terlihat bahwa :

a x

y Mxy x

Q

=

  

 ∂ ∂ − =

′ .

Oleh karena persyaratan gabungan antara momen puntir Mxy dan gaya geser Qx sepanjang tepi batas x = a menjadi :

(

)

=0

  



∂ ∂ − = ′ + =

=a x

y Mxy Qx

x Q Qx Vx

atau :

(

2

)

₂ 0 3

3 3

=   



∂ ∂∂ − + ∂ ∂ − =

=a x

y x

w v x

w D Vx

Dengan mentransformasikan momen puntir seperti yang terlihat pada gambar selain diperoleh gaya sebesar Q’x sepanjang tepi x = a, juga diperoleh dua buah gaya terpusat pada sudut tepi tersebut. Dengan cara yang sama, transformasi momen puntir Myx sepanjang tepi y = b juga akan menghasilkan gaya geser sepanjang tepi dan gaya terpusat pada sudutnya. Sehingga besarnya reaksi pada sudut R untuk x = a dan y = b ialah :

( )

( )

b y a x b

y a x

y x

w v D Mxy

R

= = =

= = − _∂∂ _∂ 

=

, 2

, 2 1

BAB III

METODOLOGI PENELITIAN

III.1. ANALISA FLAT SLAB III.1.1. Lendutan

Pelat rata yang dibebani dengan beban merata akan mengalami lendutan. Karena ukuran pelat relatif besar dibandingkan jarak antar kolom ( paling tidak ada tiga bentang menerus ), maka lendutan pada semua panel tidak terletak pada batas panel ( panel dalam ) dianggap sama dan ditinjau sebagai lendutan panel dengan sisi a dan b yang dibebani secara merata.

(sumber : Theory of plates and shells, S. Timoshenko) Gambar 3.1. Lendutan pelat rata

Panel ditumpu pada sudut-sudutnya,sehingga lendutan pada sudut adalah nol. Dengan memakai metode Navier.

w=w1+w2 dimana:

w1 = lendutan lajur yang sejajar terhadap sumbu y dan dibebani dengan beban merata q

w2 = lendutan dengan fungsi deret trigonometri Navier

=

∑

∞

=

+

,.. 4 , 2

0 .cos( )

m a

x m Ym

A π

Lendutan w1 diperoleh dengan menggunakan persamaan :

D q w =

∇ 1

karena lendutan lajur w1 merupakan fungsi y maka persamaan tersebut dapat disederhanakan menjadi :

D q y w = ∂ ∂ 4 4

Dengan mengintegrasi persamaan ini terhadap y dan menggunakan syarat-syarat batas sebagai berikut :

( )

w_{1 y=±b/2} =0

2 / 1 b y y w ± =     ∂ ∂

Diperoleh persamaan w1 : 2

2 2 4

1 1 4

384     − = b y D qb w (3.1)

Navier memberikan persamaan w2 dalam deret trigonometri, yaitu :

∑

∞ = + = ,.. 4 , 2 0

2 .cos( )

m a x m Ym A w π

fungsi Ym yang hanya merupakan fungsi y saja harus sedemikian rupa sehingga setiap suku deret ini memenuhi persamaan homogen berikut :

0 2 4 2 4 2 2 2 4 4 2 4 = ∂ ∂ + ∂∂ + ∂ ∂ y w y x w x w

Dengan memasukkan w2 ke dalam persamaan di atas maka diperoleh : 0 cos . 2 ,.. 4 , 2 4 4 4 2 2 2 =     _{− +}

∑

∞ = a x m Ym a m Ym a m Ym m II

IV π π π

atau 0 2 ₄ 4 4 2 2 2 = + − Ym a m Ym a m

YmIV π II π

Penyelesaian umum persamaan ini adalah :

      _{+ + +} = a y m a y m Dm a y m Cm a y m a y m Bm a y m Am

Ym .cosh π π sinh π .sinh π π cosh π

dipertahankan dan mengambil konstanta-konstanta integrasi Cm = Dm = 0, sehingga :       ₊ = a y m a y m Bm a y m Am

Ym .cosh π π sinh π

dan karena lendutan w2 simetris terhadap sumbu y, maka semua suku ganjil dapat dihilangkan.

∑

∞ =      + = ,.. 4 , 2 0

2 .cosh

m a x m Ym A w π

dengan memasukkan Ym ke dalam persamaan ini diperoleh :

            ₊ + =

∑

∞ = a x m a y m a y m Bm a y m Am A w m . cos . sinh . . cosh . ,.. 4 , 2 0 2 π π π π _(3.2)

Persamaan lendutan total menjadi :

            ₊ + +     − =

∑

∞ = a x m a y m a y m Bm a y m Am A b y D qb w m . cos . sinh . . cosh . 4 1

384 0 _2,4,..

2

2 2

4 π π π π

(3.3) Konstanta Am, Bm dan A0 diturunkan dengan syarat batas sepanjang tepi, yaitu : a. Kemiringan tegak lurus batas tepi adalah nol

b. Gaya geser sepanjang batas tepi adalah nol c. Lendutan pada sudut adalah nol

Dengan memasukkan y = b/2 diperoleh 1 =0 ∂ ∂ y w             ₊ + ∂∂ = ∂ ∂

∑

∞

=2,4,.. 0 2 cos . sinh cosh . m a x m a y m a y m Bm a y m Am A y y

w π π π π

a y m a y m a y m Bm a y m a m Bm a y m y

Am. . sinh π . π sinh π π .cosh π .cos π

2           ₊ +      −

Dengan memasukkan y= b/2 diperoleh 2 =0 ∂ ∂ y w seperti : a x m a b m a b m Bm a b m a m Bm a b m b Am y w b y 2 cos . 2 cosh 4 2 sinh 2 sinh 2 / . 2 2 /

2 π π π π π π

          ₊ +      − =     ∂ ∂ = (3.5)

Sehingga dari persamaan 0

2 / 2 1 =     ∂ ∂ + ∂ ∂ = ∂ ∂ =b y y w y w y w Diperoleh : a b m a b m a b m Am Bm 2 tanh 2 2 tanh . π π π + − = (3.6) Pada gambar terlihat bahwa potongan n-n yang mendekati batas y=b/2, gaya geser Qy ternyata nol pada semua titik kecuali pada titik kolom. Dengan menyatakan Qy dalam bentuk deret trigonometris dan berdasarkan sifat simetris, diperoleh :

∑

∞ = + = ,.. 4 , 2

0 .cos.

m a x m Cm C Qy π (3.7) dimana : Qy = 0 untuk 0 < x < a/2-c

dan 4 . . . 2 / 2 / b a q dy Q a c a

y =−

∫

₋

2 .

2 /2

2 / qb dx Qy a Co a c a − = =

∫

− 2 / 2 / 2 / ) 1 .( . . cos . 4 m a c a qb dx a x m Qy a

Cm=

∫

=− −

− π sehingga : 2 / 2 3 3 3 2 / . ) ( b y b y y x w y w D Qy = = =− ∂_∂ +_∂∂ _∂  2 . . cos . ) 1 ( . ) ( ,.. 4 , 2 2 / 2 / b q a x m b q Qy m m b y −     ₋ − =

∑

∞ =

= π (3.8)

Karena =0 ∂ ∂ x y

, maka suku kedua dalam tanda kurung hilang, sehingga diperoleh :

∑

∞ = = − − =     ∂ ∂ − ,.. 4 , 2 2 / 2 / 3 3 . cos . ) 1 ( . m m b y a x m pb y w

D π (3.9)

Dengan memasukkan persamaan persamaan (3.2) ke dalam persamaan (3.9) seperti :                   ₊ + ∂∂ − = ∂ ∂ −

∑

∞ = a x m a y m a y m Bm a y m Am A y D y w D m . cos . . sinh . . cosh . ,.. 4 , 2 0 3 3 3

3 π π π π

(

)

[

]

/2

3 3 3 ) 1 .( . cosh . . sinh .

3Bm m Bm m m qb m

Am a

m

D π + α + α α = − (3.10)

dimana : a b m m 2 . π α =

Dengan menyelesaikan persamaan (3.6) dan (3.10):

            + − +           + −

+ m m

m m m Am m m m m Am Am a m

D α α

α

α α

α α

α α

π _{. .cosh}

tanh tanh sinh . tanh tanh 3 3 3 3 2 / ) 1 .( .b m

q − = 2 / 3 3 3 ) 1 ( . . tanh tanh . cosh tanh tanh . sinh 3 sinh m D m b qa m m m m m m m m m m

Am = −

    + − + − π α α α α α α α α α α 2 / 3 3 3 ) 1 ( . . tanh tanh . cosh tanh tanh . sinh 2 tanh sinh . m D m b qa m m m m m m m m m m m m m

Am = −

2 / 3 3 3 ) 1 .( tanh tanh . sinh 2 m D m qa m m m m

Am = −

    + α π α α α

( )

m _m m_m D m b qa Am m α α α α

π sinh .tanh

tanh . 1 2 2 / 3 3 3 + − − = sedangkan m m m Am Bm α α tanhα

tanh + − = m m m m m m m D m b qa Bm m α α α α α α α π tanh tanh tanh . sinh tanh . ) 1 ( 2 2 / 3 3 3 +      _{− −} + − =

( )

m D m b qa Bm m α π sinh 1 . 1 2 2 / 3 3 3 − =

Sehingga Am dan Bm yang diperoleh dimasukkan ke dalam persamaan (3.3) menjadi :

( )

( )

a x m a y m m m a y m m m m m m D b qa A y D qb w m m m . cos . . sin 1 . 1 . cosh tanh sinh tanh 1 2 2 4 1 384 3 2 / ,.. 4 , 2 3 2 / 3 3 0 2 2 4 π π α π α α α α π       − + ₊ − + +     − =

∑

∞ =

sehingga lendutan pelat adalah :

( )

    _{− +} − + +     − =

∑

∞ = a y m m m a y m a y m m m m a x m m D b qa A b y D qb w m m . cosh ) tanh ( . sinh . tanh tanh . sinh / cos 1 2 4 1

384 2,4,..

3 2 / 3 3 0 2 2 2 4 π α α π π α α α π

π _(3.11)

Konstanta A0 dapat ditetapkan dengan syarat batas tidak terjadi lendutan pada sudut panel, yaitu :

( )

w _x=a/2,y=b/2 =0 sehingga didapat :

∑

∞ =      ₋ + − = ,.. 4 , 2 2 3 3 3 0 tanh tanh 1

2 m m

m m m m D b qa A αα α α π

( )

( )

∑

∑

∞ = ∞ =













−

+

−

−









−

+

+

−

+







 −

=

,.. 4 , 2 2 3 3 3 ,.. 4 , 2 3 2 / 3 3 2 2 2 4

tanh

tanh

1

2

.

cosh

)

tanh

(

.

sinh

.

tanh

tanh

.

sinh

/

cos

1

2

4

1

384

m m m

m

m

m

m

m

D

b

qa

a

y

m

m

m

a

y

m

a

y

m

m

m

m

a

x

m

m

D

b

qa

b

y

D

qb

w

α

α

α

α

π

π

α

α

π

π

α

α

α

π

π

(3.12) persamaan (3.12) merupakan persamaan lendutan pada setiap titik pada pelat. Lendutan maksimum pelat terjadi pada pusat panel dan dapat diperoleh dengan memasukkan nilai x = 0 dan y = 0 sehingga diperoleh :

(

)

∑

( )

∑

∞ = ∞ = = = = − − + −  − +  ,.... 6 , 4 , 2 2 3 3 3 ,.... 6 , 4 , 2 3 2 / 3 3 4 0 , 0 tanh tanh 1 2 tanh . sinh tanh 1 2 384 max m m m m m

m m m

m m m y x m D b qa m D b qa D qb W αα α α π α α α α π (3.13)

III.1.2. Momen Lentur

Dari persamaan (2.24) pada Bab II terdapat hubungan momen dan lendutan pada pelat persegi sebagai berikut :

    ∂ ∂ + ∂ ∂ − = 2 2 2 2 y w v x w D Mx     ∂ ∂ + ∂ ∂ − = 2 2 2 2 x w v y w D My

Dengan menurunkan persamaan (3.12) dan memasukkannya ke dalam persamaan (2.24) tersebut akan diperoleh :

( )

(

)

( )

( )

( )

_   _{− − − + +} − −     ₋ =

∑

∞ = a y m m v a y m m v a y m a y m m v m m m a x m b a q b y b q My m m . cosh tanh 1 . cosh . 1 . sinh . . tanh . 1 tanh . sinh . 2 / . cos 1 . . 2 24 1 . ,.. 4 , 2 2 / 2 2 2 π α π α π π α α α π π ………(3.15) Sedangkan Momen torsi pelat diturunkan dari persamaan pada bab II :

( )

_xw_y v D Mxy ∂ ∂∂ − −

= 1 2

( )

(

)

(1 )

tanh tanh 1 ] / cosh tanh . sinh . tanh tanh . sinh / . cos 1 2 4 1 384 2 3 ,.. 4 , 2 3 2 / 3 3 2 2 2 4 v D m m m m m a y m m m a y m a y m m m m a x m m D b qa b y D qb y x m m −           ₋ + − +                   − +     − − ∂ ∂ ∂ − =

∑

∞ = αα α α π α α π π α α α π π

( )

(

)

(

)

m_a

a m m m a y m y a m a y m a m m m m a x m a m m b qa v m m π π α α π π π π α α α π π π sinh tanh / . cosh . . sinh tanh tanh sinh / . sin 1 2 ) 1 ( ,.. 4 , 2 2 2 2 3 2 / 3 3 + −           ₊ − − − =

∑

∞ = ……….. (3.16)

Syarat batas untuk panel persegi dalam (interior) sepanjang tepi sumbu x adalah : 0 = ∂ ∂ x w 0 2 2 2 2 =     ∂ ∂ + ∂ ∂ ∂∂ − = y w x w x D

Qx pada ( x= +/- a/2 )

(sumber : Theory of plates and shells, S. Timoshenko) Gambar 3.2. Pelat di atas kolom ruang

Qy = 0 ( 0 < x < a/2 - c )

∫

/₋2 =−

2 / 0 4 . . . a c a b a p dx Qy

Gaya geser Qy dapat dibuat dalam bentuk deret sebagai berikut :

∑

∞ = + = ,.. 4 , 2 0 . cos . m a x m Cm