Penaksiran Parameter Persamaan Simultan Dengan Metode Kuadrat Terkecil Dua Tahap

PENAKSIRAN PARAMETER PERSAMAAN SIMULTAN

DENGAN METODE KUADRAT TERKECIL DUA TAHAP

SKRIPSI

ANDRIAN SURYA

070823019

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

PENAKSIRAN PARAMETER PERSAMAAN SIMULTAN DENGAN METODE KUADRAT TERKECIL DUA TAHAP

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains

ANDRIAN SURYA 070823019

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

PERSETUJUAN

Judul : PENAKSIRAN PARAMETER PADA PERSAMAAN SIMULTAN DENGAN METODE KUADRAT TERKECIL DUA TAHAP

Kategori : SKRIPSI

Nama : ANDRIAN SURYA Nomor Induk Mahasiswa : 070823019

Program Studi : SARJANA (S1) MATEMATIKA

Departemen : MATEMATIKA

Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN

ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA

Diluluskan di Medan, Komisi Pembimbing :

Pembimbing 2 Pembimbing 1

Drs. Marwan Harahap, M. Eng Drs. H. Haluddin Panjaitan

Diketahui/Disetujui oleh

Departemen Matematika FMIPA USU

Ketua,

PERNYATAAN

PENAKSIRAN PARAMETER PERSAMAAN SIMULTAN DENGAN METODE KUADRAT TERKECIL DUA TAHAP

SKRIPSI

Saya mengakui bahwa tugas skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing – masing disebutkan sumbernya.

Medan, Agustus 2011

ABSTRAK

Model persamaan simultan adalah model dimana terdapat interdenpedensi atau saling ketergantungan antar variabel. Bukan hanya variabel yang bisa mempengaruhi variabel tetapi juga variabel bisa mempengaruhi variabel sehingga dalam model tersebut terjadi hubungan dua arah.

Metode kuadrat terkecil dua tahap digunakan untuk menaksir parameter persamaan simultan, dimana persamaan dalam persamaan persamaan simultan bersifat linier dan terlalu teridentifikasi (overidentified).

ESTIMATION OF EQUATION PARAMETERS SIMULTANEOUSLY WITH TWO STAGE LEAST SQUARES METHOD

ABSTRACT

Simultaneous equations model is a model where there are interdependence between variables. Not only the X variables that could affect the Y variables but also Y variables that can affect the X variables in the model occurred two-way relationship. Two-stage least squares method used to estimate the parameters of simultaneous equations, where equations of simultaneous equations in the equation is linear and too identified (over-identified)

DAFTAR ISI

Halaman

Persetujuan ii

Pernyataan iii Penghargaan iv Abstrak v Abstract vi

Daftar Isi vii

Daftar Tabel viii

Bab 1 Pendahuluan 1

1.1 Latar Belakang 1

1.2 Perumusan Masalah 3

1.3 Tujuan Penelitian 3

1.4 Kontribusi Penelitian 3

1.5 Tinjauan Pustaka 3

1.6 Metode Penelitian 6

Bab 2 Landasan Teori 7

2.1 Analisis Regresi 7

2.1.1 Regresi Linear 7

2.1.2 Metode Kuadrat Terkecil 9

2.1.3 Regresi Kuadrat Terkecil 11

2.2 Determinan Matriks 12

2.2.1 Menghitung Determinan dengan Reduksi Baris 13

2.2.2 Sifat-sifat fungsi Determinan 15

2.2.3 Ekspansi Kofaktor dengan Kaidah Cramer 15

2.3 Multiple Regresi 17

2.3.1 Taksiran atau Pendugaan pada Koefisien Multiple Regresi 19

Bab 3 Pembahasan dan Hasil 22

3.1 Kuadrat Terkecil Dua Tahap 22

3.1.1 Syarat ordo untuk pengidentifikasian 22 3.1.2 Syarat rank untuk pengidentifikasian 23 3.2 Menaksir dengan Metode Kuadrat Terkecil 24

Bab 4 Kesimpulan dan Saran 34

4.1 Kesimpulan 34

DAFTAR TABEL

Halaman Tabel 3.1 Pendapatan, jumlah uang beredar, investasi dan pengeluaran 25

ABSTRAK

Model persamaan simultan adalah model dimana terdapat interdenpedensi atau saling ketergantungan antar variabel. Bukan hanya variabel yang bisa mempengaruhi variabel tetapi juga variabel bisa mempengaruhi variabel sehingga dalam model tersebut terjadi hubungan dua arah.

Metode kuadrat terkecil dua tahap digunakan untuk menaksir parameter persamaan simultan, dimana persamaan dalam persamaan persamaan simultan bersifat linier dan terlalu teridentifikasi (overidentified).

ESTIMATION OF EQUATION PARAMETERS SIMULTANEOUSLY WITH TWO STAGE LEAST SQUARES METHOD

ABSTRACT

Simultaneous equations model is a model where there are interdependence between variables. Not only the X variables that could affect the Y variables but also Y variables that can affect the X variables in the model occurred two-way relationship. Two-stage least squares method used to estimate the parameters of simultaneous equations, where equations of simultaneous equations in the equation is linear and too identified (over-identified)

BAB 1

PENDAHULUAN

1.1Latar Belakang

Perkembangan statistik sebagai alat bantu untuk mengambil keputusan yang lebih baik telah mempengaruhi hampir seluruh aspek kehidupan. Setiap orang, baik sadar maupun tidak sadar sering menggunakan statistik sebagai bahan pertimbangan untuk mengambil sebuah keputusan. Statistik dapat diartikan sebagai sekumpulan cara maupun aturan-aturan yang berkaitan dengan pengumpulan, pengolahan (analisis), penarikan kesimpulan atas data-data kuantitatif maupun kualitatif. Dengan demikian, keputusan yang diambil berdasarkan statistik berarti keputusan yang berdasarkan analisis dan interpretasi data kuantitatif maupun kualitatif .

Terdapat beberapa metode yang dapat digunakan untuk memperoleh nilai taksiran dari parameter model persamaan tunggal. Salah satunya adalah metode Kuadrat Terkecil (Ordinary Least Squares – OLS).

Masalah yang kemudian muncul adalah pendugaan dengan menggunakan metode OLS menjadi tidak berarti, apabila model yang dibuat merupakan suatu persamaan simultan dimana pada model ini berlaku hubungan dua arah yang membuat variabel bebas dan variabel tak bebas menjadi tidak jelas atau dengan kata lain menjadi meragukan yang mana sebenarnya variabel bebas dan variabel tak bebasnya. Hal ini terjadi karena model persamaan simultan memiliki beberapa persamaan. Pada persamaan yang satu suatu variabel dapat bertindak sebagai variabel yang bebas dan pada persamaan yang lainnya variabel tersebut dapat juga bertindak sebagai variabel yang tak bebas. Oleh karena itu, pemberian nama variabel bebas dan variabel tak bebas di dalam sistem persamaan simultan sudah tidak tepat lagi. Sehingga untuk selanjutnya dalam persamaan simultan akan ada yang namanya variabel endogen dan variabel eksogen.

1.2Perumusan Masalah

Pada persamaan simultan perlu metode khusus untuk memperoleh penaksir parameter-parameter yang bersifat tidak bias dan juga konsisten. Metode OLS tidak dapat memberikan penaksiran yang tak bias dan konsisten jika diterapkan pada persamaan simultan.

Salah satu metode yang dapat digunakan untuk menaksir parameter persamaan simultan adalah dengan menggunakan metode Kuadrat Terkecil Dua Tahap (Two Stage Least Square – 2SLS) dimana persamaan dalam sistem persamaan simultan bersifat linear dan terlalu teridentifikasi (overidentified).

1.3Tujuan Penelitian

Tujuan penelitian ini adalah menguraikan cara mendapatkan penaksiran parameter persamaan simultan dengan metode Kuadrat Terkecil Dua Tahap (Two Stage Least Square – 2SLS).

1.4Kontribusi Penelitian

Dengan diketahuinya parameter dari persamaan simultan tersebut diharapkan sebagai dasar pembuatan keputusan/pemecahan persoalan ataupun untuk dasar penelitian lebih lanjut.

1.5Tinjauan Pustaka

…(1.1)

 

Dengan :

= variabel endogen = variabel eksogen = kesalahan pengganggu

= observasi

= koefisien variabel endogen = koefisien variabel eksogen

Untuk menaksir parameter persamaan simultan dengan menggunakan metode Kuadrat Terkecil Dua Tahap, salah satu model ekonomi yang memiliki persamaan simultan adalah fungsi pendapatan dan penawaran uang. Pada persamaan simultan ini, fungsi pendapatan dipengaruhi oleh besarnya uang beredar, investasi, dan juga pengeluaran konsumsi pemerintah Sedangkan fungsi penawaran atau uang beredar dipengaruhi oleh pendapatan.

Fungsi pendapatan : …(1.2)

Fungsi penawaran uang : …(1.3)

dengan :

= pendapatan = jumlah uang beredar = investasi pemerintah

Tahap 1 (Stage 1)

Untuk membuat agar tidak berkorelasi dengan , buatlah regresi terhadap semua variabel eksogen yang berada dalam seluruh sistem persamaan (model), tidak hanya yang terdapat pada persamaannya sendiri. Dalam hal ini regresi terhadap dan sebagai berikut :

…(1.4)

Dengan merupakan pengganti dari konstanta karena telah diregresikan terhadap dan dan merupakan kesalahan penggangu.

sehingga dari persamaan (1.4) diperoleh persamaan regresi sebagai berikut:

…(1.5)

Dari persamaan (1.5), persamaan (1.2) dapat ditulis sebagai berikut :

…(1.6)

Tahap 2 (Stage 2)

Persamaan penawaran uang yang over identified sekarang ditulis sebagai berikut :

…(1.7)

Selanjutnya metode OLS dapat dipergunakan untuk menghasilkan perkiraan parameter untuk fungsi tersebut.

Untuk persamaan (1.6) perkiraan standart error nya adalah :

Dengan :

= standard error = variabel endogen = taksiran untuk

= taksiran koefisien variabel endogen = banyak sampel

1.6Metode Penelitian

Metode penelitian dalam analisis data pada penelitian ini adalah sebagai berikut: 1. Mengidentifikasi persamaan yang over-identified sehingga ditentukan persamaan

mana yang akan dipakai untuk mengestimasi.

BAB 2

LANDASAN TEORI

2.1Analisis Regresi

Dalam beberapa masalah terdapat dua atau lebih variabel yang hubungannya tidak dapat dipisahkan, dan hal tersebut biasanya diselidiki sifat hubungannya. Analisis regresi adalah sebuah teknik statistika untuk memeriksa dan memodelkan hubungan diantara variabel-variabel. Tahapan regresi terdiri dari 2 yaitu regresi sederhana dan multiple regresi. Penerapannya dapat dijumpai secara luas di banyak bidang seperti teknik, ekonomi, manajemen, ilmu-ilmu biologi, ilmu-ilmu sosial, dan ilmu-ilmu pertanian. Analisis regresi berguna dalam menelaah hubungan dua variabel atau lebih, dan terutama untuk menelusuri pola hubungan yang modelnya belum diketahui dengan sempurna, sehingga dalam penerapannya lebih bersifat eksploratif.

2.1.1 Regresi Linier

; untuk

dengan : = variabel terikat ke = variabel bebas ke

= intersep (titik potong kurva terhadap sumbu ) = kemiringan (slope) kurva linier.

kesalahan (error)

Analisis regresi setidak-tidaknya memiliki 3 kegunaan, yaitu untuk tujuan deskripsi dari fenomena data atau kasus yang sedang diteliti, untuk tujuan kontrol, serta untuk tujuan prediksi. Regresi mampu mendeskripsikan fenomena data melalui terbentuknya suatu model hubungan yang bersifatnya numerik. Regresi juga dapat digunakan untuk melakukan pengendalian (kontrol)terhadap suatu kasus atau hal-hal yang sedang diamati melalui penggunaan model regresi yang diperoleh. Selain itu, model regresi juga dapat dimanfaatkan untuk melakukan prediksi untukvariabel terikat. Namun yang perlu diingat, prediksi di dalam konsep regresi hanya boleh dilakukan didalam rentang data dari variabel-variabel bebas yang digunakan untuk membentuk model regresi tersebut. Misal, suatu model regresi diperoleh dengan mempergunakan data variabel bebas yang memiliki rentang antara 5 s.d. 25, maka prediksi hanya boleh dilakukan bila suatu nilai yang digunakan sebagai input untuk variabel berada di dalam rentang tersebut. Konsep ini disebut sebagai interpolasi.

Koefisien regresi dapat dibedakan menjadi 2 macam, yaitu:

1. Intersep (intercept)

Intersep, definisi secara metematis adalah suatu titik perpotongan antara suatu garis dengan sumbu pada diagram/sumbu kartesius saat nilai . Sedangkan definisi secara statistika adalah nilai rata-rata pada variabel apabila nilai pada variabel

bernilai 0. Dengan kata lain, apabila X tidak memberikan kontribusi, maka secara rata-rata, variabel akan bernilai sebesar intersep. Perlu diingat, intersep hanyalah suatu konstanta yang memungkinkan munculnya koefisien lain di dalam model regresi. Intersep tidak selalu dapat atau perlu untuk diinterpretasikan. Apabila data pengamatan pada variabel X tidak mencakup nilai 0 atau mendekati 0, maka intersep tidak memiliki makna yang berarti, sehingga tidak perlu diinterpretasikan.

2. Slope

Secara matematis, slope merupakan ukuran kemiringan dari suatu garis. Slope adalah koefisien regresi untuk variabel (variabel bebas). Dalam konsep statistika, slope merupakan suatu nilai yang menunjukkan seberapa besar kontribusi (sumbangan) yang diberikan suatu variabel terhadap variabel . Nilai slope dapat pula diartikan sebagai rata-rata pertambahan (atau pengurangan) yang terjadi pada variabel untuk setiap peningkatan satu satuan variabel

2.1.2 Metode Kuadrat Terkecil (Ordinary Least Square – OLS)

;

Jadi metode kuadrat terkecil adalah metode untuk menghitung dan sedemikian

rupa sehingga terkecil (minimum). Caranya ialah dengan membuat turunan

parsial (partial differential) dari mula-mula terhadap kemudian terhadap dan menyamakannya dengan nol.

… (2.1)

… (2.2)

Persamaan (2.1) dibagi dengan

Sehingga

Sehingga

2.1.3 Regresi Kuadrat Terkecil

Metode ini didasarkan pada pemilihan ₀ dan ₁ sehingga meminimalkan jumlah kuadrat deviasi titik-titik data dari garis yang dicocokkan.

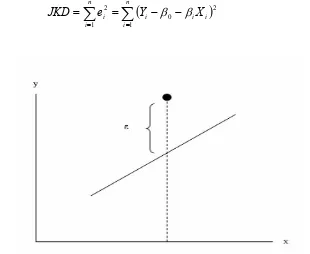
Jumlah dari kuadrat deviasi (JKD) dari garis adalah:

...

(2.3)



 

_  _    n

i

n

i

i i i

i Y X

e JKD

1 1

2 0

[image:21.595.134.444.293.547.2]

2  



Gambar 2.3 Suatu pengamatan (data) yang tidak tepat pada garis regresi







i i



n i i n i i i X Y X SSD X Y SSD 1 0 1 1 1 1 0 0 2 2                  





  ... (2.4) Dan karenanya ... (2.5)









0

0 1 0 1 1 1 0      





  i i n i i n i i i X Y X X Y    

dari persamaan (2.5), diperoleh

... (2.6)











         n i n i i i i n i i i n i n i i i Y X X X Y X n 1 1 2 1 0 1 1 1 0    

persamaan (2.6) disebut dengan persamaan normal. Dari persamaan (2.6) diperoleh,



 















   n X X n Y X Y X i i i i i i 2 2 1 ˆ 

dan ˆ₀ Y ˆ₁X, dimana Y dan X adalah n Y n

i i



1 dan X n

n i i



1 . dan yang diperoleh dengan cara ini disebut taksiran kuadrat terkecil masing-masing dari

0 ˆ

 ˆ1

0

 dan ₁. Dengan demikian, taksiran persamaan regresi dapat ditulis sebagai,

, yang disebut persamaan prediksi kuadrat terkecil. X

Yˆ ˆ₀ ˆ₁

Defenisi 1. Determinan dari suatu matriks bujur sangkar A, dinotasikan dengan |A| atau det(A) adalah fungsi skalar yang didefinisikan sedemikian rupa sehingga merupakan jumlah hasil kali unsur- unsur yang sejajar diagonal utama dikurangi jumlah unsur- unsur yang sejajar diagonal lain.

Contoh 2.1

(i) _ ; maka 

 

  

22 21

12 11

a a

a a A

(ii) ; maka

  

 

  

  

33 32 31

23 22 21

13 12 11

a a a

a a a

a a a

A

2.2.1Menghitung Determinan dengan Reduksi Baris

Di bagian ini akan diperlihatkan bahwa determinan sebuah matriks dapat dihitung dengan mereduksi matriks tersebut kepada bentuk eselon baris. Metode ini penting karena metode ini menghindari perhitungan yang panjang yang terlibat di dalam pemakaian definisi determinan secara langsung.

Mula-mula ditinjau dua golongan matriks yang determinannya dapat dihitung dengan mudah, tak perduli berapapun besarnya ukuran matriks tersebut.

Teorema 1. Jika A adalah sebarang matriks kuadrat yang mengandung sebarisan bilangan nol, maka det(A) = 0.

Sebuah matriks kuadrat dinamakan segitiga atas (upper triangular) jika semua entri di bawah diagonal utama adalah segitiga bawah (lower triangular) jika semua entri di atas diagonal utama adalah nol. Sebuah matriks baik yang merupakan segitiga bawah dinamakan segitiga (triangular).

Contoh 2.2

             44 34 33 24 23 22 14 13 12 11 0 0 0 0 0 0 a a a a a a a a a a A

Sebuah matriks segitiga bawah 4 x 4 yang umum mempunyai bentuk

             44 43 42 41 33 32 31 22 21 11 0 0 0 0 0 0 a a a a a a a a a a A

Teorema 2. Jika A adalah sebuah matriks segitiga yang berukuran n x n, maka det(A) adalah hasil perkalian entri-entri pada diagonal utama yakni det

 

A a₁₁a₂₂a_nn . Contoh 2.3                    4 0 0 0 0 8 9 0 0 0 6 7 6 0 0 1 5 7 3 0 3 8 3 7 2 A maka 1296 ) 4 )( 9 )( 6 )( 3 )( 2 ( 4 0 0 0 0 8 9 0 0 0 6 7 6 0 0 1 5 7 3 0 3 8 3 7 2        A

Teorema 3. Anggap A adalah sebarang matriks n x n.

(b) Jika A

 

A 

adalah matriks yang dihasilkan bila dua baris dari A dipertukarkan, maka

 

A

det

det 

(c) Jika A adalah matriks yang dihasilkan bila sebuah kelipatan dari satu baris dari A ditambahkan kepada baris lain, maka det

 

A det

 

A

2.2.2. Sifat-sifat Fungsi Determinan

Jika A adalah sebarang matriks m x n, maka transposisi dari A (transpose of A) dinyatakan oleh dan didefinisikan sebagai matriks n x m yang kolom pertamanya adalah baris pertama dari A, yang kolom keduanya adalah baris kedua dari A, yang kolom ketiganya adalah baris ketiga dari A, dan seterusnya.

t

A

Sifat-sifat Operasi Transposisi

 





 

kA kA dimana k adalah sebarang skalar

iii B A B A ii A A i t t t t t t t ; ) ( ) ( ) (     

2.2.3. Ekspansi Kofaktor dengan Kaidah Cramer

Definisi 2. Jika A adalah sebuah matriks kuadrat, maka minor entri dinyatakan oleh dan didefinisikan sebagai determinan dari submatriks yang tinggal setelah baris ke i dan kolom ke j dicoret dari A. Bilangan

ij

a

ij

M

 

ij j i

M 

1 dinyatakan oleh

dinamakan kofaktor entri .

ij K ij a Contoh 2.4 Andaikan             8 4 1 6 5 2 4 1 3 A

Minor entri a₁₁ adalah

16

8 4

6 5

11  

M

 

1 11 11 16

1 1

11    



M M K

Definisi 3. Jika A adalah sebarang matriks n x n dan adalah kofaktor , maka matriks

ij

K a_ij

              nn n n n n K K K K K K K K K       2 1 2 22 21 1 12 11

dinamakan matriks kofaktor dari A. Transposisi matriks ini dinamakan adjoin dari A dan dinyatakan dengan adj(A).

Teorema 4. Jika A adalah sebuah matriks yang dapat dibalik, maka

   

adj A A A det 1 1  

Bukti. Mula-mula akan diperlihatkan bahwa Aadj

 

A det

 

A I

 

                                   nn jn n n n j n j nn n n in i i n n K K K K K K K K K K K K a a a a a a a a a a a a A adj A                     2 1 2 2 22 12 1 1 21 11 2 1 2 1 2 22 21 1 12 11

Entri di dalam baris ke i dan kolom ke j dari A adj (A) adalah

a_i1K_j1a_i2K_j2 a_inK_jn ...

(2.7)

Jika i = j, maka (2.7) adalah ekspansi kofaktor dari det(A) sepanjang baris ke i dari A. Sebaliknya, jika i j, maka koefisien-koefisien dan kofaktor-kofaktor berasal dari baris-baris A yang berbeda, sehingga nilai dari (2.7) sama dengan nol. Maka

 

 

 

 

 

A I A A A A adj A det det 0 0 0 det 0 0 0 det                     ... (2.8)

Karena A dapat dibalik, maka det

 

A 0, maka persamaan (2.8) dapat dituliskan kembali sebagai

 



Aadj

 

A



I

A 

det 1

atau

   

adj A I A A      det 1

Dengan mengalikan kedua ruas dari kiri dengan A1 maka akan menghasilkan

   

adj A A A det 1 1   _... (2.9)

2.3 Multiple Regresi

Multiple regresi adalah analisis regresi yang meramalkan pengaruh dua variabel bebas atau lebih terhadap satu variabel terikat . Dapat juga digunakan untuk membuktikan ada atau tidaknya hubungan fungsional antara dua buah variabel bebas atau lebih dengan sebuah variabel terikat .

Bentuk persamaan umum multiple regresi adalah



_    n i i iX Y 1

0  



i ki ki i

i X X

X

Y ₀ _{1 1} _{2 2} ... 

…(2.10)

Apabila dinyatakan dalam bentuk matriks, akan diperoleh rumus berikut

   X Y

                                                                                    kn n n ki i i k ki k i k i n i X X X X X X X X X X X X X Y Y Y Y Y 2 1 2 1 2 22 12 21 11 2 1 1 0 2 1 1 1 1 1                         

Koefisien  harus diestimasi berdasarkan data hasil penelitian sampel acak. Prosedur estimasi tergantung pada asumsi mengenai variabel X dan kesalahan pengganggu ε. Beberapa asumsi yang penting adalah sebagai berikut:

1. nilai harapan setiap kesalahan pengganggu sama dengan nol E(_i)0, untuk semua i. 0                                           0 0 0 0 ) ( ) ( ) ( ) ( 2 1     n i E E E E    

2. Kesalahan pengganggu yang satu (εi) tidak berkorelasi (bebas) terhadap kesalahan

pengganggu lainnya (εj), akan tetapi mempunyai varians yang sama.

untuk semua i. 2 2 ) ( , , 0 )

(_i_j  i j E _i  E

'

 _{= transpos dari vektor kolom ε, atau dengan kata lain, ' merupakan vektor baris}

'

 = ( ε ... ε ... ε ... ε ) . I = matriks identitas, karena setiap kesalahan pengganggu mempunyai varians yang sama.

1 2 i n

3. X1i, X2i, ... , Xki merupakan bilangan real, tanpa mengandung kesalahan. Dengan

perkataan lain, matriks merupakan himpunan angka-angka konstan (fixed numbers).

4. Matriks X mempunyai rank k n _(ada k kolom dari matriks X yang bebas linear). Jumlah observasi n harus lebih banyak dari jumlah variabel, atau lebih banyak dari koefisien regresi linear yang akan diestimasi.

... (2.11)

k kX

X X

Yˆ ˆ0 ˆ1 1ˆ2 2 ...ˆ

Apabila ˆ0, ˆ1, ˆ2, ... , ˆk sudah dihitung sebagai penduga parameter 1,2 , ... ,

k

 , berdasarkan data dari sampel, maka Yˆ dapat digunakan untuk meramalkan , setelah X1, X2, ... , Xk diketahui nilainya.

2.3.1 Taksiran atau Pendugaan pada Koefisien Multiple Regresi

Misalkanˆ sebagai penduga  merupakan vektor kolom dengan k baris sebagai berikut:

     

 

    

 



k

   

ˆ ˆ ˆ

ˆ 2

1

 Y 

ˆ

X Xˆ

                                  ˆ ˆ ˆ ˆ ˆ 1 1 1 1 2 1 0 2 1 2 1 2 22 12 1 21 11 2 1 2 1 _                                                                                    k kn n n ki i i k k n i e n i X X X X X X X X X X X X X Y Y Y Y Y e e e e





 

            2 2 2 1 1 0 2 2 2 1 1 0 ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ki k i i i i ki k i i i i X X X Y e X X X Y e           ... (2.12)

Estimasi vektor  dengan menggunakan kuadrat terkecil, ialah vektor _sedemikian rupa sehingga jumlah kuadrat kesalahan pengganggu, e

ˆ

’

e =



e_i2minimum. Caranya

ialah dengan melakukan penurunan parsial



e_i2terhadap setiap komponen vektor dan menyamakannya dengan 0.

ˆ





 



ˆ ˆ ˆ ˆ







0

2 ˆ 0 1 ˆ ˆ ˆ ˆ 2 ˆ 1 2 2 1 1 0 1 2 2 2 1 1 0 0 2                  













i ki k i i i i ki k i i i i X X X X Y e X X X Y e          











ˆ ˆ ˆ ˆ







0

2 ˆ 0 ˆ ˆ ˆ ˆ 2 ˆ 2 2 1 1 0 2 2 2 2 1 1 0 2 2                    













ki ki k i i i k i i ki k i i i i X X X X Y e X X X X Y e                

... (2.13)







































                    i ki ki k ki i ki i ki i i ki i k i i i i i i ki i k i i i i i ki k i i Y X X X X X X X Y X X X X X X X Y X X X X X X X Y X X X n 2 2 2 1 1 0 2 2 2 2 2 2 1 1 2 0 1 1 2 1 2 2 1 1 1 0 2 2 1 1 0 ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ                          ... (2.14)

Persamaan di atas disebut persamaan normal.

Dengan meminimumkan e'e



Y Xˆ



 YXˆ



maka dihasilkan :







     ˆ ˆ ˆ 2 ˆ ˆ ' 1 2 X X Y X Y Y X Y X Y e e e n i i             



_

dengan turunan parsial dari persamaan 0

ˆ      e e

, maka didapatkan :

atau ...(2.15) ...(2.16) 0 ˆ 2

2    

 X Y X X



XX



XY  1

ˆ 

 

BAB 3

PEMBAHASAN DAN HASIL

Seperti disebutkan sebelumnya, bahwa secara umum pendekatan yang dapat

digunakan untuk menaksir parameter pada model persamaan simultan ada dua, yaitu

metode persamaan tunggal (Single Equation Methods) atau dikenal juga dengan

metode informasi terbatas (Limited Information Methods) contohnya adalah 2SLS dan

LIML, dan metode sistem (System Methods of Estimation) atau metode informasi

penuh (Full Information Methods) contohnya adalah 3SLS dan FIML. Akan tetapi

dalam penulisan skripsi ini hanya dibatasi pada penaksiran dengan pendekatan

persamaan tunggal, yaitu metode Kuadrat Terkecil Dua Tahap (Two Stage Least

Squares – 2SLS) dan metode Informasi Terbatas Kemungkinan Terbesar (Limited

Information Maximum Likelihood-LIML).

3.1Kuadrat Terkecil Dua Tahap (Two Stage Least Square – 2SLS)

Kuadrat Terkecil Dua Tahap pada dasarnya perhitungannya sama dengan Kuadrat

Terkecil (Ordinary Least Square – OLS), hanya saja pada Kuadrat Terkecil Dua

Tahap proses estimasinya berisi 2 kali langkah aplikasi metode OLS

3.1.1 Syarat Ordo untuk Pengidentifikasian

Dalam suatu model dengan persamaan simultan, agar suatu persamaan

persamaan tertentu harus lebih besar atau sama dengan banyaknya variebel endogen

yang ada pada persamaan tertentu dikurangi satu.

3.1.2 Syarat Rank untuk Pengidentifikasian

Ada beberapa kemungkinan mengenai identifikasi yaitu :

a. , dan rank matriks A adalah maka persamaan itu terlalu

diidentifikasi (overidentified)

b. , rank matriks A adalah , maka tepat diidentifikasi

(exactly identified)

c. , persamaan itu tidak diidentifikasi.

Untuk melihat kondisi identifikasi pada persamaan simultan telah

dikembangkan oleh Maddala (1992). Misalkan pada persamaan simultan tertentu yang

terdiri dari 3 persamaan didapatkan variabel endogen sebanyak 3 yaitu dan

variabel eksogen . Selanjutnya, untuk melihat kondisi identifikasi maka perlu

dibuat tabel identifikasi sebagai berikut :

Persamaan 1 0 0

Persamaan 2 0 0 0

Persamaan 3 0 0

Tanda 0 berarti variabel pada kolom tidak terdapat pada persamaan baris

sedangkan tanda berarti variabel pada kolom dimiliki pada persamaan baris.

Sebuah persamaan dikatakan terlalu diidentifikasi bila banyaknya tanda 0 lebih

besar dari , tepat diidentifikasi bila banyaknya tanda 0 sama dengan ,

dan kurang diidentifikasi bila banyaknya tanda 0 kurang dari

Pada contoh diatas sama dengan 2. Tanda 0 sebanyak 2 pada

persamaan 3 persamaaan 3.Maka persamaan 1 dan 3 tepat diidentifikasi sedangkan

3.2Menaksir dengan Metode Kuadrat Terkecil Dua Tahap.

Salah satu model ekonomi yang memiliki persamaan simultan adalah fungsi

pendapatan dan penawaran uang. Pada persamaan simultan ini, fungsi pendapatan

dipengaruhi oleh besarnya uang beredar, investasi dan juga pengeluaran konsumsi

pemerintah. Sedangkan fungsi penawaran atau uang beredar dipengaruhi oleh

pendapatan. Oleh karena itu, variabel pendapatan dan uang beredar merupakan

variabel endogen dan variabel investasi dan pengeluaran konsumsi pemerintah adalah

variabel eksogen.

Fungsi pendapatan :

Fungsi penawaran uang :

dengan :

= pendapatan

= jumlah uang beredar

= investasi pemerintah

= pengeluaran konsumsi pemerintah

Untuk menaksir parameter pada persamaan diatas maka terlebih dulu

dilakukan pengidentifikasian pada persamaan tersebut. Pengidentifikasian secara

praktis dapat dilakukan seperti yang dikembangkan oleh Maddala (1977) adalah

sebagai berikut:

Fungsi pendapatan

Fungsi penawaran uang 0 0

Pada persamaan diatas, banyaknya G adalah 2 maka suatu persamaan terlalu

diidentifikasi bila banyaknya tanda 0 lebih dari G-1 atau dengan kata lain lebih dari 1

dan tepat diidentifikasi bila banyaknya tanda 0 sama dengan 1. Fungsi pendapatan

tidak memiliki tanda 0 maka fungsi tersebut tidak diidentifikasikan sedangkan fungsi

Sebagai gambaran dari bentuk persamaan di atas dapat dilihat dari contoh

sebagai berikut yang memuat data pendapatan, jumlah uang beredar, investasi dan

pengeluaran pemerintah suatu negara X.

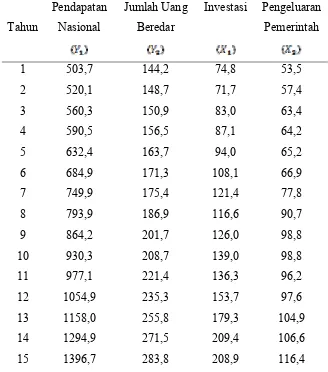
Tabel 1.1 Pendapatan, jumlah uang beredar, investasi dan pengeluaran

pemerintah suatu negara X.

Tahun

Pendapatan

Nasional

Jumlah Uang

Beredar

Investasi Pengeluaran

Pemerintah

1 503,7 144,2 74,8 53,5

2 520,1 148,7 71,7 57,4

3 560,3 150,9 83,0 63,4

4 590,5 156,5 87,1 64,2

5 632,4 163,7 94,0 65,2

6 684,9 171,3 108,1 66,9

7 749,9 175,4 121,4 77,8

8 793,9 186,9 116,6 90,7

9 864,2 201,7 126,0 98,8

10 930,3 208,7 139,0 98,8

11 977,1 221,4 136,3 96,2

12 1054,9 235,3 153,7 97,6

13 1158,0 255,8 179,3 104,9

14 1294,9 271,5 209,4 106,6

15 1396,7 283,8 208,9 116,4

Sumber data : J. Supranto, Ekonometrika, hal 281.

Apabila dinyatakan dalam bentuk matriks, maka dan adalah matriks.

[image:35.595.151.479.210.582.2]

Tahap 1 (Stage 1)

Untuk membuat agar (kolom 1 pada matriks tidak berkorelasi dengan ,

buatlah regresi terhadap semua variabel eksogen yang berada dalam seluruh sistem

persamaan (model), tidak hanya yang terdapat pada persamaannya sendiri. Dalam hal

ini regresi terhadap dan sebagai berikut :

dimana adalah kesalahan pengganggu

Dengan metode ekspansi kofaktor sepanjang kolom pertama dari A, maka diperoleh

determinan A yaitu

Selanjutnya dihitung kofaktor-kofaktor dari matriks A sebagai berikut :

Untuk memperoleh nilsi koefisien , maka

=

ersamaan multiple regresi adalah P

aka persamaan multiple regresinya adalah : M

ehingga diperoleh taksiran untuk

ahap 2 (Stage 2)

ran uang yang over identified sekarang ditulis sebagai berikut : T

Persamaan penawa

Selanjutnya kofaktor dari matriks adalah sebagai berikut :

adalah

Sehingga

leh nilai koefisien

Untuk mempero , maka

 

Untuk mendapatkan standard error dari persamaan diatas adalah :

       

144,2

60,44948 0,1627 492,77 3,5909576 12,89

148,7

60,44948 0,1627 489,78 8,5783954 73,59

22

- 3

1

1

-150,9

60,44948 0,1627 564,42 -1,364355 1,86

156,5

60,44948 0,1627 587,17 0,5359299 0,29

163,7

60,44948 0,1627 624,35 1,6871694 2,85

171,3

60,44948 0,1627 699,25 -2,89722 8,39

175,4

60,44948 0,1627 799,21 -15,05712 6,72

186,9

60,44948 0,1627 816,20 6,320551 9,95

201,7

60,44948 0,1627 888,09 -3,215684 10,34

208,7

60,44948 0,1627 952,21 -6,645836 44,17

221,4

60,44948 0,1627 930,70 9,5535944 91,27

235,3

60,44948 0,1627 020,93 8,775378 77,01

255,8

60,44948 0,1627 170,21 4,9928767 24,93

271,5

60,44948 0,1627 1324,02 4,328623 18,74

283,8

60,44948 0,1627 1352,45 3,3475187 11,21

644,20

etode tersebut memperlihatkan bahwa besarnya pendapatan dari suatu negara

taupun masyarakat berpengaruh positif terhadap jumlah uang yang beredar didalam M

negara tersebut. Semakin besar pendapatan maka semakin besar juga jumlah uang

yang beredar. Sesuai dengan teori moneter yang telah dikemukakan oleh Keynes

bahwa salah satu faktor yang menentukan permintaan uang adalah pendapatan

nasional yaitu semakin tinggi pendapatan nasional semakin tinggi permintaan uang

untuk transaksi dan investasi (cadangan uang). Jumlah uang beredar merupakan

besarnya penawaran uang yang ada pada masyarakat. Dalam keadaan seimbang,

penawaran uang sama dengan permintaan uang yang terdiri dari permintaan uang

BAB 4

KESIMPULAN DAN SARAN

4.1 Kesimpulan

diambil dari penelitian dan penganalisaan data yang telah

ilakukan dapat diambil kesimpulan sebagai berikut: Kesimpulan yang dapat

d

1. Metode kuadrat terkecil dua tahap dapat dilakukan bila hubungan antara

variabel dan variabel terjadi hubungan dua arah.

2. Fungsi penawaran uang yang overidentified :

diperoleh hasil

Dengan standard error adalah7,038

3. Metode kuadrat terkecil akan menghasilkan nilai yang bias bila digunakan

4.1 Saran

metode kuadrat terkecil biasa pada persamaan simultan tidak

dianjurkan karena akan menghasilkan nilai estimasi yang bias.

etode Kuadrat

1. Penggunaan

2. Penelitian ini dapat dikembangkan dengan membandingkan Metode Kuadrat

Terkecil Dua Tahap (Two Stage Least Square – 2SLS) dan M

Terkecil Tiga Tahap (Three Stage Least Squares - 3SLS), Informasi Terbatas

Kemungkinan Terbesar (Limited Information Maximum Likelihood – LIML),

Informasi Penuh Kemungkinan Terbesar (Full Information Maximum

DAFTAR PUSTAKA

1. Davidson, Russell and MacKinnon, Jam Econometric Theory and

2. Dougherty, Christoper. 2007.Introduction to Econometrics, 3th ed., USA Oxford

3. Gujarati, Damodar N. 2004. Basic Economteric, 4th ed., New York: The

McGraw-4. Jaeger, David. A and Parys Juliane. 2009. On the Sensitivity of Return to

5. Johnston, J. 1972. Econometric Methods. Second Edition. Japan: McGraw-Hill.

6. Maddala, G. S. 1992. Introduction to Econometrics, 2nd ed., New York :

7. Sarwoko. 2005. Dasar-Dasar Ekonometrika. Jakarta: Penerbit Andi Yogyakarta.

8. Supranto, J. 2004. Ekonometri. Jakarta : Penerbit Ghalia Indonesia.

es G. 1999.

Methods. USA .Oxford University Press.

Oxford University Press.

Hill Companies.

Schooling Estimates to Estimation Methods, Model Specification, and

Influential Outliers If Identification Is Weak. Discussion Paper Series No.

3961. Forschungsinstitut zur Zukunft der Arbeit Institute for the Study of

Labor.

9. Ullah Aman and Nagar A. L. 1974. The Exact Mean Of The Two-Stage Least

Squares Estimator Of The Structural Parameters In An Equation Having