DAFTAR PUSTAKA
Nico. Iryanto. Tarigan, Gim. 2014. “Aplikasi Metode Cutting Plane Dalam Optimisasi Jumlah Produksi Tahunan Pada PT. XYZ”. J. Saintia Matematika. Volume 2, No. 2, pp. 127-136
Kusumadewi, S., Purnomo, H. 2010. Aplikasi Logika Fuzzy untuk Pendukung Keputusan Edisi 2. Graha Ilmu. Yogyakarta.
Purba, R. 2012. Penerapan Logika Fuzzy Pada Program Linier. Di dalam: Seminar Nasional Matematika dan Pendidikan Matematika FMIPA UNY, Yogyakarta, 10 November 2012.
Siagian, P. 2006. Penelitian Operasional: Teori dan Praktek. Penerbit Universitas
Indonesia. Jakarta.
Sitorus, P.1997.Program Linier. Universitas Trisakti. Jakarta. Siswanto. 2006. Operations Research. Erlangga, Jakarta.
Suantio, H., Rambe, A.J.M. dan Siregar, I. 2013. Aplikasi Fuzzy Linear Programming untuk Produksi Bola Lampu di PT XYZ. Jurnal TeknikIndustri. 2:4.
Taha, H.A. 1996. Riset Operasi, Jilid I. Ed ke-5. Editor: Dr. Lyndon Saputra. Binarupa Aksara. Jakarta.
Thie, Paul R.1938. An Introduction to linear programing and Game Theory. Departmen of mathematics Boston College. Singapore.
LAMPIRAN
Lampiran 1. Penyelesaian dengan menggunakan Software POM – QM.
BAB 3
HASIL DAN PEMBAHASAN
3.1. Program Linier Fuzzy
Program linier merupakan salah satu model yang dapat digunakan untuk menyelesaikan masalah optimasi. Pada program linier, permasalahan dimodelkan secara tetap denga menggunakan parameter-parameter yang umum digunakan. Pada program linier, keberadaan data dan formulasi yang digunakan juga sudah bersifat tertentu, pasti dan tidak menimbulkan ambiguitas (Kusumadewi & Purnomo, 2010).
Salah satu contoh model program linier klasik (Zimmermann) adalah: Maksimumkan:
=
Dengan batasan:
0
Dengan , ∈ , ∈ , ∈ (3.1)
Atau
Minimumkan: =
0
Dengan , ∈ , ∈ , ∈ (3.2)
, dan adalah bilangan-bilangan crisp (tegas), tanda pada kasus maksimasi dan tanda pada kasus minimasi juga bermakna crisp (tegas), demikian juga perintah “maksimumkan” atau “minimumka” merupakan bentuk imperatif tegas.
Jika diasumsikan bahwa keputusan program linier akan dibuat pada lingkungan fuzzy, maka bentuk (3.1) dan (3.2) akan mengalami sedikit perubahan, yaitu:
1. Bentuk imperatif pada fungsi objektif tidak lagi benar-benar “maksimum” atau “minimum”, karena adanya beberapa hal yang perlu mendapat pertimbangan dalam suatu sistem.
2. Tanda (pada batasan) dalam kasus maksimasi dan tanda (pada batasan) dalam kasus minimasi tidak lagi bermakna crisp secara matematis, namun sedikit mengalami pelanggaran makna. Hal ini juga disebabkan karena adanya beberapa yang perlu dipertimbangkan dalam sistem yang mengakibatkan batasan tidak dapat didekati secara tegas.
Program linier fuzzy adalah program linier yang dinyatakan dengan fungsi objektif dan fungsi kendala yang memiliki parameter fuzzy dan ketidaksamaan fuzzy. Tujuan dari program linier fuzzy adalah mencari solusi yang dapat diterima berdasarkan kriteria yang dinyatakan dalam fungsi objektif dan kendala. Solusi tersebut berbentuk himpunan fuzzy yang memiliki derajat kebenaran tertentu pada selang [0,1].
Pada program linier fuzzy, akan dicari suatu nilai yang merupakan nilai yang merupakan fungsi objektif yang akan dioptimasikan sedemikian hingga tunduk pada batasan-batasan yang dimodelkan dengan menggunakan himpunan fuzzy. Sehingga untuk kasus maksimasi (3.1) akan diperoleh:
Tentukan sedemikian hingga:
0 (3.3) Dan untuk kasus minimasi (3.2) akan diperoleh:
�
0 (3.4)
Yang dapat dibawa menjadi suatu bentuk seperti dibawah:
0 (3.5)
Tiap-tiap baris/batasan (0,,1,2,…, m) akan dipresentasikan dengan sebuah himpunan fuzzy, dengan fungsi keanggotaan pada himpunan ke-i adalah ( ). Fungsi keanggotaan untuk model keputusan himpunan fuzzy dapat dinyatakan sebagai:
� = min [ ] (3.6)
= 0,1,2,…,
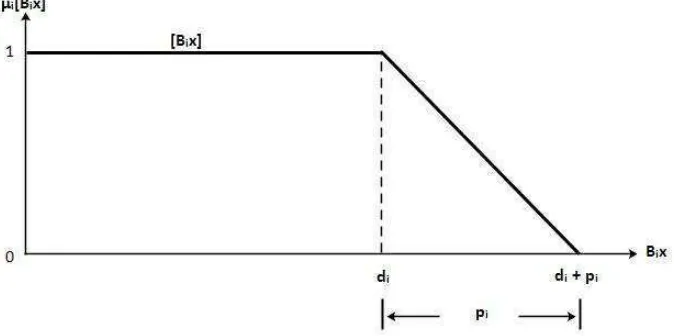
Gambar 3.1. menunjukkan fungsi keanggotaan tersebut
Gambar 3.1. Fungsi Keanggotaan
[ ] =
1; 1− − ;
0;
< +
> +
(3.9)
= 0,1,2,…,
Dengan adalah toleransi interval yang diperbolehkan untuk melakukan pelanggaran dengan baik pada fungsi objektif maupun batasan. Dengan mensubstitusikan akan diperoleh:
max 0 = max 0min 1− − (3.10)
Dari gambar dapat dilihat bahwa, semakin besar nilai domain, akan memiliki nilai keanggotaan yang cenderung semakin kecil. Sehingga untuk mencari nilai − dapat dihitung sebagai = 1− , dengan:
+ = − (3.11)
Maksimumkan :
Dengan batasan : + + ; = 0,1,2,…,
0 (3.12)
3.2 Penggunaan Metode Cutting Plane
Metode cutting plane digunakan untuk permasalahan yang variabel keputusannya harus bernilai bilangan bulat. Program linear tidak efektif untuk menyelesaikan permasalahan tersebut sehingga dikembangkan metode cutting plane yang lebih efektif dan memberikan hasil yang lebih baik. Langkah-langkah penyelesaian program bilangan bulgat dengan metode cutting plane diringkas sebagai berikut: 1. Selesaikan masalah program bilangan bulat dengan menggunakan metode
simpleks. Jika masalah sederhana, kendala gomory dapat diselesaikan dengan pendekatan grafik, sehingga pendekatan kendala gomory kurang efisien. 2. Periksa solusi optimum. Jika semua variabel basis memiliki nilai bilangan
bulat, solusi optimum yang berupa bilangan bulat telah diperoleh dan proses solusi telah berakhir. Jika satu atau lebih variabel basis masih memiliki nilai pecahan, lanjutkan ke tahap 3.
3. Buatlah suatu kendala gomory dan cari solusi optimum melalui prosedur dual simpleks. Kembali ke tahap 2 (Taha, 1996).
Tabel 3. 1 Solusi Optimum Masalah Program Linear
− ... ... ... ... ... ... ... ...
di mana: = variabel basis = variabel nonbasis
Perhatikan persamaan ke di mana variabel diasumsikan bernilai tidak bilangan bulat sebagai berikut:
= sumber daya yang tersedia dalam fungsi kendala yang berupa noninteger
Kemudian pisahkan dan menjadi bagian yang bulat dan bagian pecah non
7
sehingga adapun kendala gomory yang diinginkan sebagai berikut: −
Pada umumnya, persamaan kendala yang berhubungan dengan solusi pecah dipilih untuk menghasilkan suatu kendala gomory. Namun, sebagai aturan biasanya dipilih persamaan yang memiliki maksimum. Adapun tabel baru setelah penambahan kendala gomory disajikan pada Tabel 2.3 sebagai berikut:
Tabel 3. 3 Penambahan Kendala Gomory
1 2 ... ... ... ... ... ...
digunakan kembali untuk mengatasi ketidaklayakan. Jika pada setiap iterasi metode dual simpleks menunjukkan bahwa tidak ada solusi layak, berarti masalah itu tidak memiliki solusi integer yang layak.
3.3 Ilustrasi Numerik Pembulatan Program Linear Fuzzy dengan Menggunakan Metode Cutting Plane
Sebuah perusahaan X memproduksi 4 jenis produk yang berbeda yang masing-masing membutuhkan 3 macam bahan baku, yaitu A, B, dan C. Produk tersebut dikerjakan melalui 2 proses pengerjaan manual, yaitu proses I dan proses II. Setiap unit produk I membutuhkan 10 ons bahan baku A, 6 ons bahan baku B dan 12 ons bahan baku C. Setiap unit produk II membutuhkan 8 ons bahan baku A, 10 ons bahan baku B dan 12 ons bahan baku C. Setiap unit produk III membutuhkan 12 ons bahan baku A, 8 ons bahan baku B, dan 15 ons bahan baku C. Setiap unit produk IV membutuhkan 14 ons bahan baku A, 12 ons bahan baku B, dan 13 ons bahan baku C. Akibat keterbatasan gudang bahan baku dan dana yang ada, bahan baku yang disediakan tiap minggu adalah sebesar 240 kg bahan baku A, 18 kg bahan baku B, dan 25 kg bahan baku C. Namun demikian pihak perusahaan masih memungkinkan adanya penambahan bahan baku A hingga 60 kg, bahan baku B hingga 20 kg dan bahan baku C hingga 50 kg, asalkan dengan penambahan sedikit saja, keuntungan yang diperoleh perusahaan akan bertambah.
Setiap unit produk I membutuhkan waktu 4 jam pada proses I, dan 2 jam pada proses II. Setiap unit produk II membutuhkan waktu 3 jam pada proses I dan 4 jam pada proses II. Setiap unit produk III membutuhkan waktu 5 jam pada proses I dan 3 jam pada proses II. Setiap unit produk IV membutuhkan 6 jam pada proses I dan 5 jam pada proses II. Jumlah karyawan pada proses I sebanyak 18 orang, sedangkan pada proses II sebanyak 20 orang. Perusahaan bekerja dengan 1 shift, mulai pukul 08.00 sampai pukul 16.00 dengan istirahat selama 1 jam mulai pukul 12.00 hingga 13.00, selama 6 hari kerja dalam 1 minggu.
Rp 7.000,00. Informasi bagian pemasaran menyatakan bahwa berapa pun jumlah produk yang dibuat perusahaan akan terserap seluruhnya oleh pasar. Berdasarkan kondisi tersebut, berapakah keuntungan maksimum yang bisa diperoleh oleh perusahaan ?
Penyelesaian: Langkah 1
Menyelesaikan persoalan menggunakan program linear biasa.
Dalam penyelesaian kasus ini, selanjutnya satuan bahan baku dinyatakan dalam ons. Jam kerja karyawan per minggu dapat dihitung:
Pada proses I ditetapkan karyawan sejumlah 18 orang, dengan jam kerja selama 7 jam selama 6 hari per minggu. Maka jam kerja per minggu pada proses I adalah : 18 7 6 = 756 .
Pada proses II ditetapkan karyawan sejumlah 20 orang, dengan jam kerja selama 7 jam selama 6 hari minggu. Maka jam kerja per minggu pada proses II adalah : 20 7 6 = 840 .
Penambahan bahan baku yang diperbolehkan (toleransi) pada setiap bahan baku:
Pada bahan baku I penambahan bahan baku yang diperbolehkan maksimal 60 kg = 600 ons.
Pada bahan baku II penambahan bahan baku yang diperbolehkan maksimal 20 kg = 200 ons.
Pada bahan baku III penambahan bahan baku yang diperbolehkan maksimal 50 kg = 500 ons.
Kasus ini dapat ditabulasikan sebagai berikut:
Tabel 3.4. Bentuk Tabulasi Permasalahan
Sumber Produk Kapasitas ( ons)
I II III IV Maksimum Toleransi
Bahan Baku A 10 8 11 12 2400 600
Bahan Baku C 12 9 13 9 2500 500
Jam Proses I 4 3 5 4 756 0
Jam Proses II 2 4 3 5 840 0
Keuntungan/unit 4000 6000 5500 7000
Untuk menyelesaikan permasalahan di atas, langkah yang dilakukan adalah merumuskan karakteristik pada program linear biasa, yaitu:
1. Menentukan variabel keputusan
1 : Produk I,
2 : Produk II,
3 : Produk III,
4 : Produk IV,
2. Merumuskan fungsi tujuan
Fungsi tujuan dari permasalahan ini adalah memaksimalkan keuntungan dari tiap produk yang akan diproduksi, yakni produk I, produk II, produk III dan produk IV sehingga dapat dirumuskan menjadi:
= 4000 1+ 6000 2+ 5500 3+ 7000 4
3. Merumuskan fungsi kendala
Fungsi kendala pada bahan baku A
10 1+ 8 2+ 11 3+ 12 4 2400 + 600
Fungsi kendala pada bahan baku B
6 1+ 10 2+ 8 3+ 10 4 1800 + 200
Fungsi kendala pada bahan baku C
12 1+ 9 2+ 15 3+ 9 4 2500 + 500
Fungsi kendala berdasarkan jam kerja karyawan per minggu pada proses II 2 1+ 4 2+ 3 3+ 5 4 840
Sehingga permasalahan di atas dapat dituliskan sebagai berikut: Maksimumkan:
= 4000 1+ 6000 2+ 5500 3+ 7000 4
Kendala:
10 1+ 8 2+ 11 3+ 12 4 2400 + 600
6 1+ 10 2+ 8 3+ 10 4 1800 + 200 12 1+ 9 2+ 13 3+ 9 4 2500 + 500
4 1+ 3 2 + 5 3 + 4 4 756
2 1+ 4 2 + 3 3 + 5 4 840
1, 2, 3 0
Untuk = 0, maka bentuk di atas menjadi:
Maksimumkan: 4000 1+ 6000 2 + 5500 3+ 7000 4 Kendala :
10 1+ 8 2+ 11 3 + 12 4 2400
6 1+ 10 2+ 8 3+ 10 4 1800
12 1+ 9 2+ 13 3 + 9 4 2500
4 1+ 3 2+ 5 3+ 4 4 756 2 1+ 4 2 + 3 3 + 5 4 840
1, 2, 3 0
Variabel masuk : 2 Variabel keluar : 2
Tabel 3.8. Iterasi 3 untuk = 0
Karena baris � − 0, maka persoalan di atas telah optimal dengan = 1230857 untuk 1 = 0, 2 = 25,7143, 3 = 17,012 dan 4 = 126,8571.
Untuk = 1 , maka bentuk diatas menjadi:
Maksimumkan: 4000 1+ 6000 2 + 5500 3+ 7000 4 Kendala : 10 1+ 8 2+ 11 3+ 12 4 3000
6 1+ 10 2+ 8 3+ 10 4 2000
12 1+ 9 2+ 13 3 + 9 4 3500
4 1+ 3 2 + 5 3 + 4 4 756
2 + 4 + 3 + 5 840
4 7000 -0,1538 0,8462 0 1 0 0 0 -0,2308 0,3846 148,6154
Zj 4000 5500 5500 7000 0 0 0 500 1000 1218000
� − 0 -500 0 0 0 0 0 500 1000 1218000
Basis 4000 6000 5500 7000 0 0 0 0 0
1 2 3 4 1 2 3 4 5
1 0 1,7857 0 0 0 1 0,6071 0 -1,9036 -2,0714 394,8571 2 6000 0,0714 1 0 0 0 0,4643 0 -0,3571 -0,6429 25,7143 3 0 1,2143 0 0 0 0 -1,1071 1 -2,0714 2,0714 681,1429 3 5500 0,9286 0 1 0 0 0,0357 0 0,3571 -0,3571 17,012 4 7000 -0,2143 0 0 1 0 -0,3929 0 0,0714 0,9286 126,8571
1, 2, 3 0
Dapat diselesaikan menggunakan metode simpleks sebagai berikut: Tabel 3.9. Iterasi 0 untuk = 1
Basis 4000 6000 5500 7000 0 0 0 0 0
1 2 3 4 1 2 3 4 5
1 0 10 8 11 12 1 0 0 0 0 3000
2 0 6 10 8 10 0 1 0 0 0 2000
3 0 12 9 13 9 0 0 1 0 0 3500
4 0 4 3 5 4 0 0 0 1 0 756
5 0 2 4 3 5 0 0 0 0 1 840
� 0 0 0 0 0 0 0 0 0 0
� − -4000 -6000 -5500 -7000 0 0 0 0 0 0
Variabel masuk : 4 Variabel keluar : 5
Tabel 3.10. Iterasi 1 untuk = 1
Variabel masuk : 3
Basis 4000 6000 5500 7000 0 0 0 0 0
1 2 3 4 1 2 3 4 5
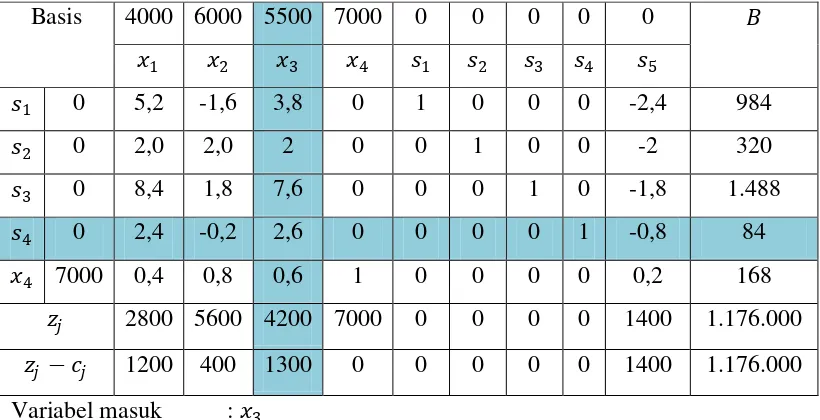
1 0 5,2 -1,6 3,8 0 1 0 0 0 -2,4 984
2 0 2,0 2,0 2 0 0 1 0 0 -2 320
3 0 8,4 1,8 7,6 0 0 0 1 0 -1,8 1.488 4 0 2,4 -0,2 2,6 0 0 0 0 1 -0,8 84 4 7000 0,4 0,8 0,6 1 0 0 0 0 0,2 168
Variabel keluar : 4
Tabel 3.11. Iterasi 2 untuk = 1
Basis 4000 6000 5500 7000 0 0 0 0 0
1 2 3 4 1 2 3 4 5
1 0 1,6923 -1,3077 0 0 1 0 0 -1,4615 -1,2308 861,2308
2 0 0,1538 2,1538 0 0 0 1 0 -0,7692 -1,3846 255,3846
3 0 1,3846 2,3846 0 0 0 0 1 -2,9231 0,5385 1.242,4615
3 5500 0,9231 -0,0769 1 0 0 0 0 0,3846 -0,3077 32,3077
4 7000 -0,1538 0,8462 0 1 0 0 0 -0,2308 0,3846 148,6154
� 4000 5500 5500 7000 0 0 0 500 1000 1.218.000
� − 0 -500 0 0 0 0 0 500 1000 0
Variabel masuk : 2 Variabel keluar : 2
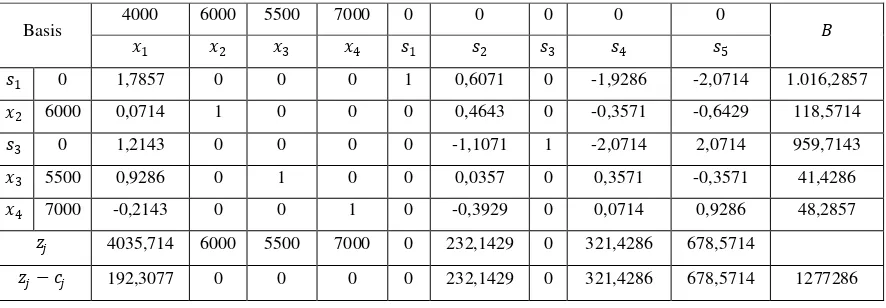
Tabel 3.12. Iterasi 3 untuk = 1
Basis 4000 6000 5500 7000 0 0 0 0 0
1 2 3 4 1 2 3 4 5
1 0 1,7857 0 0 0 1 0,6071 0 -1,9286 -2,0714 1.016,2857 2 6000 0,0714 1 0 0 0 0,4643 0 -0,3571 -0,6429 118,5714
3 0 1,2143 0 0 0 0 -1,1071 1 -2,0714 2,0714 959,7143
3 5500 0,9286 0 1 0 0 0,0357 0 0,3571 -0,3571 41,4286 4 7000 -0,2143 0 0 1 0 -0,3929 0 0,0714 0,9286 48,2857
� 4035,714 6000 5500 7000 0 232,1429 0 321,4286 678,5714
Karena baris � − 0, maka persoalan di atas telah optimal dengan = 1277286 untuk 1 = 0, 2 = 118,5714, 3 = 41,4286 dan 4 = 48,2857.
Langkah 2.
Menyelesaikan persoalan dengan mengubah model menjadi program linear fuzzy. Dari kedua hasil untuk = 0 dan = 1, dapat ditentukan nilai 0, yaitu hasil pengurangan dari nilai pada saat = 1 dengan pada saat = 0.
Maka = 1277286−1230857 = 46429
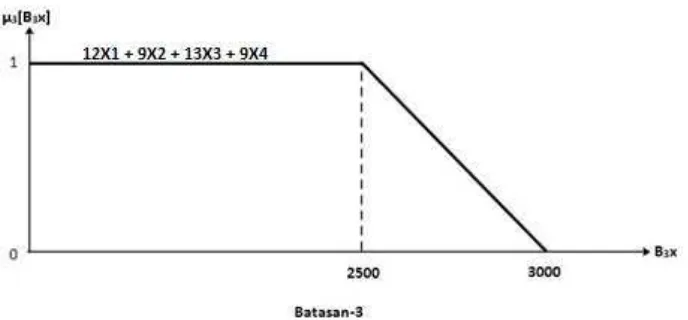
Fungsi keanggotaan tiap-tiap persamaan terlihat pada gambar
Gambar 3.3. Fungsi Keanggotaan dari Batasan-1
Gambar 3.4. Fungsi Keanggotaan dari Batasan-2
Untuk menghitung nilai λ −cut berdasarkan bentuk (3.12) yaitu dengan
mengambil nilai λ= 1−t, akhirnya dapat dibentuk model program linear fuzzy sebagai berikut:
46429 − 4000 1+ 6000 2+ 5500 3+ 7000 4 46429−1277286 =−1230857
600 + 10 1+ 8 2+ 11 3+ 12 4 600 + 2400
200 + 6 1+ 10 2+ 8 3+ 10 4 200 + 1800
500 + 12 1+ 9 2+ 13 3+ 9 4 500 + 2500
4 1+ 3 2+ 5 3+ 4 4 756
2 1+ 4 2+ 3 3+ 5 4 840
λ, x1, x2, x3, x4 0
Sehingga bentuk program linearnya menjadi: Maksimumkan: λ
Kendala: − 46429 + 4000 1+ 6000 2 + 5500 3+ 7000 4 1230857 600 + 10 1+ 8 2+ 11 3+ 12 4 3000
200 + 6 1+ 10 2+ 8 3+ 10 4 2000
500 + 12 1+ 9 2+ 13 3+ 9 4 3000
4 1+ 3 2 + 5 3 + 4 4 756
2 1+ 4 2+ 3 3+ 5 4 840
, 1, 2, 3, 4 0
Didapatkan solusi = 0,5; 1 = 0; 2 = 72,1429; 3 = 37,8572, 4 = 87,5714 dengan nilai = 1254071
Nilai untuk setiap batasan:
Batasan 1
10 1+ 8 2+ 11 3+ 12 4, disubstitusi dengan hasil yang diperoleh 1 = 0; 2 = 72,1429; 3 = 37,8572, 4 = 87,5714
10 0 + 8 72,1429 + 11 37,8572 + 12 87,5714 =2044,429
Batasan 2
6 1+ 10 2+ 8 3+ 10 4, disubstitusi dengan hasil yang diperoleh 1 = 0; 2 = 72,1429; 3 = 37,8572, 4 = 87,5714
6 0 + 10 72,1429 + 8 37,8572 + 10 87,5714 = 1900
Batasan 3
12 1+ 9 2+ 13 3+ 9 4, disubstitusi dengan hasil yang diperoleh 1 = 0; 2 = 72,1429; 3 = 37,8572, dan 4 = 87,5714
12 0 + 9 72,1429 + 13 37,8572 + 9 87,5714 = 1929,5723
Batasan 4
4 1+ 3 2+ 5 3+ 4 4, disubstitusi dengan hasil yang diperoleh 1 = 0; 2 = 72,1429; 3 = 37,8572, dan 4 = 87,5714
4 0 + 3 72,1429 + 5 37,8572 + 4 87,5714 = 756
Batasan 5
2 1+ 4 2+ 3 3+ 5 4, , disubstitusi dengan hasil yang diperoleh 1 = 0; 2 = 72,1429; 3 = 37,8572, 4 = 87,5714
Derajat keanggotaan untuk setiap batasan:
Batasan 1 : 1 1� = 1 (karena 2044,4292 < 2400)
Batasan 2 : 2 2� = 2000−1900
200 = 0,5000
Batasan 3 : 3 3� = 1 (karena 1929,5723 < 2500)
Dengan menggunakan program linear biasa ( = 0), keuntungan maksimum akan diperoleh jika produk II diproduksi sebanyak 25,7143 unit, produk III diproduksi sebanyak 17,012 unit, produk IV 126,8571 dan tidak memproduksi produk I dengan keuntungan yang diperoleh sebesar Rp 1.230.857,-.
Dengan kondisi di atas diperoleh dari kendala berdasarkan bahan baku bahwa:
Pada bahan baku A dibutuhkan sebanyak
10 1+ 8 2+ 11 3+ 12 4 dengan 1 = 0, 2 = 25,7143, 3 = 17,012 dan 4 = 126,8571.
10 0 + 8 25,7143 + 11 17,012 + 12 17,012 = 1915,1316 ons.
Pada bahan baku B dibutuhkan sebanyak
6 1+ 10 2+ 8 3+ 10 4 dengan 1 = 0, 2 = 25,7143, 3 = 17,012 dan 4 = 126,8571.
6 0 + 10 25,7143 + 8 17,012 + 10 126,8571 = 1661,8100 ons.
Pada bahan baku C dibutuhkan sebanyak
12 1+ 9 2+ 13 3+ 9 4 dengan 1 = 0, 2 = 25,7143, 3 = 17,012 dan 4 = 126,8571.
12 0 + 9 25,7143 + 13 17,012 + 13 126,8571 = 1594,2986 ons
Lama waktu pada proses I selama
4 1+ 3 2+ 5 3+ 4 4 dengan 1 = 0, 2 = 25,7143, 3 = 17,012 dan 4 = 126,8571.
4 0 + 3 25,7143 + 5 17,012 + 126,85710 = 669,6313 menit.
Lama waktu pada proses I selama
2 1+ 4 2+ 3 3+ 5 4 dengan 1 = 0, 2 = 25,7143, 3 = 17,012 dan 4 = 126,8571.
2 0 + 4 25,7143 + 3 17,012 + 5 126,8571 = 788,1787 menit.
Apabila digunakan program linear fuzzy ( = 0,5000) keuntungan maksimum akan diperoleh jika produk II diproduksi sebanyak 72,1429 unit, produk III diproduksi sebanyak 37,8572 unit, produk IV diproduksi sebanyak 87,5714 dan tidak memproduksi produk I dengan keuntungan yang diperoleh sebesar Rp 1.254.072,00 lebih banyak Rp 23.215,00 dibandingkan dengan program linear biasa.
Dengan kondisi di atas diperoleh dari kendala berdasarkan bahan baku yaitu:
Pada bahan baku A dibutuhkan sebanyak
10 1+ 8 2+ 12 3+ 14 4 dengan 1 = 0; 2 = 72,1429; 3 = 37,8572 dan 4 = 87,571.
10 0 + 8 72,1429 + 11 37,8572 + 12 87,571 = 2044,4244 ons.
Pada bahan baku B dibutuhkan sebanyak 6 1+ 10 2+ 8 3+ 10 4 dengan
1 = 0; 2 = 72,1429; 3 = 37,8572 dan 4 = 87,571.
6 0 + 10 72,1429 + 8 37,8572 + 10 87,5710 = 1900 ons.
12 1+ 9 2+ 13 3+ 9 4 dengan 1 = 0; 2 = 72,1429; 3 = 37,8572 dan 4 = 87,571.
12 0 + 9 72,1429 + 13 37,8572 + 9 87,571 = 1.929,5687 ons
Dengan kondisi di atas diperoleh dari kendala berdasarkan jam proses bahwa:
Lama waktu pada proses I selama
4 1+ 3 2+ 5 3+ 4 4
dengan 1 = 0; 2 = 72,1429; 3 = 37,8572 dan 4 = 87,571. 4 0 + 3 72,1429 + 5 37,8572 + 4 87,5710 = 756menit.
Lama waktu pada proses II selama
2 1+ 4 2+ 3 3+ 5 4
dengan 1 = 0; 2 = 72,1429; 3 = 37,8572 dan 4 = 87,571. 2 0 + 4 72,1429 + 3 37,8572 + 5 87,5710 =840menit.
Nilai = 0,5 mengandung pengertian bahwa − untuk setiap himpunan yang digunakan untuk mengimplementasikan setiap batasan sebesar 0,500. Dengan kata lain, skala terbesar = 1−0,500 = 0,500 digunakan untuk menentukan besarnya penambahan terbesar dari setiap batasan yang diizinkan seperti di bawah ini:
Pada batasan 1, penambahan bahan baku A diizinkan hingga 600 ons, pada kenyataannya penambahan yang dibutuhkan maksimal hanya sebesar 0,5 600 = 300 ons.
Pada batasan 2, penambahan bahan baku B diizinkan hingga 200 ons, pada kenyataannya penambahan yang dibutuhkan maksimal hanya sebesar 0,5 200 = 100 ons.
Langkah 3.
Membulatkan hasil yang diperoleh menggunakan metode cutting plane.
Setelah diperoleh hasil pengerjaan program linear fuzzy langkah selanjutnya adalah membulatkan nilai produk yang optimal dari hasil yang diperoleh karena tidak mungkin produk yang akan diproduksi bernilai pecahan. Metode pembulatan yang digunakan adalah metode cutting plane. Dapat dilihat bahwa hasil optimal yang diperoleh adalah 1 = 0; 2 = 72,1429; 3 = 37,8572 dan 4 = 87,571.dengan nilai = 1254071. Batasan ditambahkan sesuai dengan batasan
maksimal yang telah diperoleh dari penyelesaian program linear fuzzy, yaitu:
Batasan 1
Tabel 3.13. Iterasi ke-4 hasil optimal dengan program linear fuzzy
Pada tabel di atas dipilih 3 sebagai batasan gomory pertama ( 1) karena nilai desimal pada 3 lebih besar, maka:
0,9286 1+ 3 + 0,0357 2 + 0,357 4– 0,3571 5 = 37,8571
0,9286 1+ 3 + 0,0357 2 + 0,357 4 – 0,3571 5 = (37 + 0,8571) ; koefisien bernilai integer dan desimal di pisahkan
Koefisien bernilai integer dihilangkan, koefisien bernilai pecahan dimasukkan dalam persamaan sebagai berikut:
– =−
=1
1 - (0,9286 1 + 0,0357 2 + 0,357 4 – 0,3571 5) = -0,8571 1 - 0,9286 1 - 0,0357 2 - 0,357 4 + 0,3571 5 = -0,8571
Batasan gomory tersebut dimasukkan kembali kedalam tabel 3.13 kemudian diselesaikan dengan cara yang sama yaitu dengan metode simpleks.
Basis 4000 6000 5500 7000 0 0 0 0 0
1 2 3 4 1 2 3 4 5
Tabel 3.14. Penambahan kendala gomory pertama pada Tabel 3.13.
Variabel masuk : 1
Variabel keluar : 1
Tabel 3.15. Iterasi ke -1 penambahan kendala gomory pertama
Pada tabel di atas dipilih 1 sebagai batasan gomory kedua ( 2) karena nilai desimal pada 3 lebih besar, maka:
-1,077 1 + 1 + 0,038 2 + 0,385 4 - 0,385 5 = 0,923
(-2 + 0,923) 1 + 1 + 0,038 2 + 0,385 4 - 0,385 5 = 0,923 ; koefisien bernilai integer dan desimal di pisahkan
-2 1 + 0,923 1 + 1 + 0,038 2 + 0,385 4 - 0,385 5 = 0,923
Koefisien bernilai integer dihilangkan, koefisien bernilai pecahan dimasukkan dalam persamaan sebagai berikut:
– =−
=1
2−(0,923 1 + 0,038 2 + 0,385 4 - 0,385 5 ) = - 0,923 2−0,923 1 - 0,038 2 - 0,385 4 + 0,385 5 = - 0,923
Batasan gomory tersebut di masukkan kembali kedalam tabel 3.14 kemudian diselesaikan dengan cara yang sama yaitu dengan metode simpleks,
Tabel 3.16. Penambahan kendala gomory ke-2 pada Tabel 3.15
Variabel masuk : 4 Variabel keluar : 2
Tabel 3.17. Iterasi ke- 1 penambahan kendala gomory kedua
Karena baris � − 0, maka persoalan di atas telah optimal dengan =
1254000 untuk 1 = 2, 2 = 72, 3 = 36 dan 4 = 88, Karena semua nilai dari variabel x sudah memenuhi seperti yang diinginkan yaitu bernilai integer maka proses pembentukan kendala gomory dihentikan.
Dari perhitungan diatas dapat dilihat bahwa hasil yang diperoleh menggunakan program linear biasa sangat berbeda jika dibandingkan dengan hasil yang diperoleh menggunakan program linear fuzzy. Solusi program linear pada kasus non-fuzzy dan fuzzy terlihat pada Tabel 3.18.
Basis 0 0 4000 6000 5500 7000 0 0 0 0 0
2 1 1 2 3 4 1 2 3 4 5
1 0 2,082 0 0 0 0 0 1 0,459 0 -3,417 -0,583 652
2 6000 0,083 0 0 1 0 0 0 0,459 0 -0,417 -0,583 72
3 0 1,417 0 0 0 0 0 0 -1,208 1 -3,084 3,084 818
3 5500 1,083 0 0 0 1 0 0 -0,041 0 -0,417 0,417 36
4 7000 -0,250 0 0 0 0 1 0 -0,375 0 0,250 0,750 88
1 4000 -1,167 0 1 0 0 0 0 0,082 0 0,834 -0,834 2
Telah didapatkan solusi yang optimal menggunakan logika fuzzy diatas. Namun, dapat terlihat bahwa hasil yang diperoleh bernilai desimal sementara satuan yang ditetapkan adalah satuan unit. Hal ini tentu tidak relevan karena nilai satuan unit tidak mungkin bernilai desimal. Tidak mungkin perusahaan tersebut memproduksi produk dengan nilai pecahan. Apabila dilakukan pembulatan biasa atau pembulatan terdekat dapat menggangu nilai dari batasan yang diberikan sehingga hal tersebut tidak efisien.
Untuk mengatasi hal ini dilakukan pembulatan menggunakan metode cutting plane yaitu metode pembulatan dengan penambahan kendala gomory yang bertujuan menyingkirkan beberapa ruang penyelesaian yang tidak berisi titik bilangan bulat yang layak, tetapi tidak pernah menyingkirkan satupun titik bilangan bulat yang layak, sehingga diperoleh hasil yang integer dan optimal serta tidak mengganggu batasan yang telah ditentukan.
Tabel 3.19. Perbandingan Solusi Sebelum dan Sesudah Pembulatan Solusi Sebelum Pembulatan Solusi Sesudah Pembulatan
1 = 0 1 = 2
2 = 72,1429 2 = 72
3 = 37,8572 3 = 36
4 = 87,5714 4 = 88
= 1254071 = 1254000
BAB 4
KESIMPULAN DAN SARAN
4.1. Kesimpulan
Dari kajian dan analisis yang dilakukan dapat disimpulkan bahwa:
1. Metode pembulatan dengan cutting plane memberikan hasil yang integer namun tetap optimal.
2. Proses penambahan kendala gomory berhenti ketika nilai yang diinginkan sudah terpenuhi yaitu bernilai integer.
3. Pada program linear fuzzy, nilai − sangat berperan dalam menentukan besarnya penambahan maksimum dari setiap batasan yang diizinkan.
4.2. Saran
1. Dapat dikembangkan program aplikasi untuk menyelesaikan permasalahan program linear fuzzy menggunakan metode cutting plane.
BAB 2
LANDASAN TEORI
2.1 Program Linier
Program linier merupakan model matematik untuk mendapatkan alternatif penggunaan terbaik atas sumber-sumber organisasi. Kata sifat linier digunakan untuk menunjukkan fungsi-fungsi matematik yang digunakan dalam bentuk linier dalam arti hubungan langsung dan persis proporsional. Program menyatakan penggunaan teknik matematika tertentu. Jadi program linier adalah suatu teknik perencanaan yang bersifat analitis menggunakan model matematis dengan tujuan menemukan beberapa kombinasi alternatif pemecahan optimum terhadap persoalan (Aminuddin, 2005).
Program linier adalah suatu teknik penyelesaian optimal atas suatu problema keputusan dengan cara menentukan terlebih dahulu fungsi tujuan (memaksimalkan atau meminimalkan) dan kendala-kendala yang ada ke dalam model matematik persamaan linier. Program linier sering digunakan dalam penyelesaian problema-problema alokasi sumber daya, seperti dalam bidang manufacturing, pemasaran, keuangan, personalia, administrasi, dan lain sebagainya (Sitorus, 1997).
2.1.1 Persyaratan Penyelesaian Program Linier
Syarat-syarat yang harus dipenuhi dalam merumuskan suatu problema keputusan ke dalam model matematik persamaan linier adalah sebagai berikut (Sitorus, 1997):
Apa yang menjadi tujuan permasalahan yang dihadapi yang ingin dipecahkan dan dicari jalan keluarnya. Tujuan ini harus jelas dan tegas yang disebut fungsi tujuan.
2. Alternatif Perbandingan
Harus ada sesuatu atau berbagai alternatif yang ingin diperbandingkan, misalnya antara kombinasi waktu tercepat dan biaya tertinggi dengan waktu terlambat dan biaya terendah.
3. Sumber Daya
Sumber daya yang dianalisis harus berada dalam keadaan yang terbatas. 4. Perumusan Kuantitatif
Fungsi tujuan dan kendala harus dapat dirumuskan secara kuantitatif sesuai dengan yang disebut dalam model matematika.
5. Keterkaitan Peubah
Peubah-peubah yang membentuk fungsi tujuan dan kendala tersebut harus memiliki hubungan fungsional atau hubungan keterkaitan.
2.1.2 Model Umum Matematik Program Linier
11 1+ 12 2+ + 1 = 1
21 1+ 22 2+ + 2 = 2
1 1+ 2 2+ + =
Sehingga untuk bentuk umum dari kendala program linier adalah:
=1 atau untuk = 1, 2, 3,…,
0 untuk = 1, 2, 3,…,
Keterangan:
= Fungsi tujuan = Variabel keputusan
= Nilai kontribusi dari variabel keputusan
= Koefisien teknologi dari variabel keputusan dalam kendala = Sumber daya yang tersedia dalam kendala
ke-2.1.3 Karakteristik Program Linier
Karakteristik-karakteristik dalam program linier yang biasa digunakan untuk memodelkan suatu masalah dan memformulasikannya secara matematik, yaitu (Siswanto, 2006):
1. Variabel Keputusan
Variabel keputusan adalah variabel yang secara lengkap menguraikan keputusan-keputusan yang akan dibuat.
2. Fungsi Tujuan
Fungsi tujuan merupakan suatu hubungan linier dari variabel keputusan yang berupa fungsi maksimum atau minimum.
3. Fungsi Kendala
pertidaksamaan yang juga merupakan hubungan linier dari variabel keputusan yang mencerminkan keterbatasan sumber daya dalam suatu masalah.
2.1.4 Metode Simpleks
Cara yang paling sederhana unrtuk menyelesaikan permasalahan program linier adalah dengan pendekatan grafikal. Namun cara tersebut hanya bisa diterapkan untuk program linier dengan dua variabel keputusan. Pada kenyataannya sebagian besar permasalahan program linier mempunyai lebih dari dua variabel keputusan. Hal ini tentu sulit untuk menerapkan pendekatan grafikal untuk memperoleh penyelesaian dari permasalahan tersebut.
Oleh karena itu, pada tahun 1947 George Dantzig mengajukan suatu metode yang tepat untuk menyelesaikan permasalahan program linier yang disebut metode simpleks. Metode simpleks merupakan prosedur aljabar yang bersifat iteratif yang bergerak selangkah demi selangkah, dimulai dari titik ekstrim pada daerah feasible (ruang solusi) menuju titik ekstrim yang optimum.
Berikut langkah-langkah dalam menyelesaikan permasalahan program linier dengan metode simpleks (Handayani, 2014):
1. Konversikan formulasi persoalan ke dalam bentuk standar.
Agar persamaan garis batasan memenuhi persyaratan penyelesaian daerah kelayakan (feasible) maka semua pertidaksamaan diubah menjadi persamaan dengan cara menambahkan variabel slack, surplus dan variabel buatan (artifisial variabel) pada tiap batasan (constraint) serta memberi harga nol pada setiap koefisien tujuannya. Batasan dapat dimodifikasi sebagai berikut:
a. Untuk batasan bernotasi diubah ke dalam bentuk persamaan dengan menambahkan variabel slack.
dapat diatasi dengan membuat suatu bilangan penalty M (M bilangan positif yang sangan besar) sebagai harga dari variabel buatan tersebut dalam fungsi tujuan. Untuk kasus maksimasi maka dibuat –M sebagai harga dari variabel buatan dan untuk kasus minimasi dibuat +M sebagai harga dari variabel buatan. Cara pendekatan ini dikenal dengan metode M besar (Big M method).
2. Susun persamaan-persamaan ke dalam tabel simpleks
Tabel 2.1. Bentuk Tabel Simpleks − yang paling positif untuk kasus minimasi atau yang memiliki nilai − yang paling negatif untuk kasus maksimasi.
4. Pilih baris kunci yang memiliki nilai indeks terkecil. Nilai indeks adalah perbandingan nilai kanan dengan kolom kunci,
5. Tentukan nilai elemen cell, yaitu nilai perpotongan antara kolom kunci dan baris kunci.
6. Lakukan iterasi dengan menentukan baris kunci baru, baris Z baru, dan baris variabel-variabel slack baru.
a. Baris kunci baru ditentukan dengan membagi baris kunci lama dengan elemen cell.
Baris lama – (nilai kolom kunci baris yang sesuai × baris kunci baru) c. Letakkan nilai-nilai baris yang baru diperoleh ke dalam tabel.
7. Lakukan uji optimalisasi. Jika semua koefisien pada baris − sudah tidak ada lagi yang bernilai positif (untuk kasus minimasi) atau sudah tidak ada lagi yang bernilai negatif (untuk kasus maksimasi) berarti sudah optimal. Jika kriteria belum terpenuhi, diulangi dari langkah 3.
2.2 Program Bilangan Bulat
Program bilangan bulat ialah persoalan program linier di mana pemecahan optimalnya harus me nghasilkan bilangan bulat. Dengan kata lain dari antara berbagai bilangan bulat diharuskan mencari nilai-nilai variabel yang fisibel dan membuat fungsi tujuan optimum. Ada beberapa persoalan program linier yang solusinya tidak masuk akal jika solusi yang dihasilkan berupa bilangan pecahan. Diadalam persoalan ekonomi sering kali djumpai variabel-variabel yang nilainya harus positif misalnya produksi mobil, produksi kapal terbang, jumlah jembatan, jumlah gedung, kebutuhan tenaga kerja, jumlah penganggur, jumlah ternak, dan lain sebagainya. Dalam persoalan ini bilangan-bilangan pecahan tidak mempunyai arti (Supranto, 1983).
1 = 7,4 jet, maka pembulatan dapat mempengaruhi keuntungan bermiliar-miliar
dolar. Dalam hal ini maka program bilangan bulat hadir menyelesaikan permasalahan sedemikian rupa sehingga suatu solusi bilangan bulat optimal dijamin tercapai (Taylor, 2001).
Program bilangan bulat memiliki model matematika yang sama dengan model program linier pada umumnya hanya saja ditambah batasan bahwa variabelnya harus bilangan bulat sebagai berikut (Syahputra, 2012):
maks/min: Z =
= Nilai kontribusi dari variabel keputusan
= Koefisien teknologi dari variabel keputusan dalam kendala = Sumber daya yang tersedia dalam kendala
ke-Berdasarkan jenis keputusan yang akan diperoleh persoalan integer programming dapat dibedakan atas tiga jenis, yaitu (Ritonga, 2015):
1. Pemrograman bilangan bulat murni (pure integer programming), yaitu merupakan pemrograman bilangan bulat di mana semua nilai variabel keputusan haruslah bilangan bulat.
2. Pemrograman bilangan bulat campuran (mixed integer programming), yaitu merupakan pemrograman bilangan bulat di mana nilai variabel keputusannya bernilai bilangan bulat dan variabel yang lainya bernilai bilangan desimal atau pecahan.
pengambilan keputusan, di mana jika solusi yang didapat berupa angka 1 berarti menyatakan “ya” atau angka 0 berarti menyatakan “tidak”.
2. 2. 1 Metode Pembulatan (Rounding Method)
Metode ini sangat sederhana dan cepat dalam menyelesaikan program bilangan bulat. Sebelum metode ini diterapkan, maka terlebih dahulu dicari penyelesaian dari problema dengan menggunakan metode program linier biasa, yaitu metode grafik. Selanjutnya, metode ini diterapkan dengan cara melakukan pembulatan hasil nilai variabel keputusan (bilangan pecahan) yang diperoleh dari metode grafik tersebut (Sitorus, 1997).
Kelemahan utama metode ini ialah bahwa hasil pembulatan yang dilakukan dapat menyimpang jauh dari penyelesaian optimal bilangan bulat sesungguhnya dalam penyelesaiannya dianggap tidak layak apabila hasilnya lebih besar daripada penyelesaaian optimal bilangan bulat atau penyelesaian optimal pecahan (metode grafik). Hasil penyelesaian optimal metode pembulatan tidak akan pernah nilai optimalnya lebih besar daripada hasil yang diperoleh dari metode grafik biasa (pecahan). Hal ini disebabkan bahwa adanya persyaratan pembulatan yang tidak boleh keluar dari daerah kelayakan (metode pembulatan) dan tambahan kendala (metode pembulatan), yang kesemuanya mengakibatkan luas daerah kelayakan bertambah kecil (Sitorus, 1997).
2. 2. 2. Metode Branch and Bound
Metode ini sering digunakan untuk menyelesaikan masalah program bilangan bulat karena hasil yang diperoleh dalam penyelsaian optimal lebih teliti dan lebih baik dari kedua metode lainnya. Kelemahan pokok metode ini adalah prosedur untuk mencapai hasil yang optimal sangat panjang (Sitorus, 1997).
Prosedur penyelesaian problema megoptimalkan proram linier bilangan bulat dengan metode ini adalah sebagai berikut (Sitorus, 1997):
Masalah yang dihadapi diselesaikan lebih dahulu menggunkan metode simpleks atau menggunakan metode grafik sampai diperoleh hasil yang optimal.
Langkah 2: Pemeriksaan Penyelesaian Optimal
Hasil optimal pada langkah 1 diperiksa apakah variabel keputusan yang diperoleh bernilai integer atau pecahan. Apabila semua nilai variabel keputusan yang dihasilkan telah bernilai integer maka solusi optimal telah tercapai. Apabila tidak maka proses iterasi dilanjutkan.
Langkah 3: Penyusunan Subproblema (Branching)
Apabila penyelesaian optimal belum tercapai, maka problema tersebut dimodifikasi ke dalam dua subproblema dengan memasukkan kendala baru ke masing-masing subproblema tersebut.
Langkah 4: Penentuan Nilai Batas (Bounding)
Hasil optimal yang diperoleh dengan metode program linier biasa merupakan nilai batas atas bagi setiap subproblema. Sedangkan hasil optimal dengan penyelesaian integer merupakan nilai batas bawah bagi masing-masing subproblema. Selanjutnya apabila subproblema yang memiliki batas atas yang lebih rendah dari batas bawah yang berlaku, maka subproblema tersebut tidak perlu dianalisis lagi. Apabila dalam penyelesaian integer menghasilkan hasil yang sama atau lebih baik daripada nilai batas atas dari setiap problema, maka penyelesaian optimal integer telah tercapai. Apabila tidak, maka subproblema yang memiliki nilai batas atas yang terbaik dipilih selanjutnya menjadi subproblema baru. Proses iterasi kembali pada langkah 2 sehingga demikian seterusnya.
perjalanan yang terdapat pada persoalan pedagang keliling atau Travelling Salesman Problem (TSP) (Simarmata, 2015).
2.2.3. Metode Cutting Plane
Metode cutting plane merupakan metode yang digunakan untuk menyelesaikan program linear bilangan bulat, baik bilangan bulat murni maupun campuran dengan penambahan kendala baru yang disebut gomory. Kendala gomory diberikan jika nilai dari variabel keputusan belum bulat (bernilai pecahan). Kendala-kendala tersebut secara efektif akan menyingkirkan beberapa ruang penyelesaian yang tidak berisi titik bilangan bulat yang layak, tetapi tidak pernah menyingkirkan satupun titik bilangan bulat yang layak (Taha, 1996).
Metode cutting plane dikembangkan untuk menemukan solusi optimum bagi program bilangan bulat. Metode ini dilakukan dengan menambahkan suatu kendala yang dinamakan kendala gomory. Penambahan kendala gomory dilakukan pada tabel optimal sehingga dapat mempersingkat perhitungan (Siagian, 2006).
2.3. Fuzzy
Istilah fuzzy lahir dari gagasan seorang guru besar pada University of California, Berkeley, Amerika Serikat, Prof. Lotfi Asker Zadeh. Sejak tahun 1960 Zadeh telah merasa bahwa sistem analisis matematika tradisional yang dikenal sampai saat itu bersifat terlalu eksak sehingga tidak dapat berfungsi dalam banyak masalah dunia nyata yang seringkali amat kompleks. Pada akhirnya di tahun 1965 Zadeh mempublikasikan karangan ilmiahnya berjudul “Fuzzy Set”. Terobosan baru yang deperkenalkan oleh Zadeh ini telah memperluas konsep himpunan klasik menjadi himpunan fuzzy yang dapat mempresentasikan nilai-nilai ketidakpastian yang ditemui dalam kehidupan nyata (Handayani, 2014).
oleh sebuah fungsi keanggotaan yang memberikan tiap obyek sebuah nilai keanggotaan yang rentang nilainya antara 0 dan 1. Pada teori himpunan fuzzy, peranan derajat keanggotaan sebagai penentu keberadaan elemen dalam suatu himpunan sangatlah penting. Nilai keanggotaan atau derajat keanggotaan atau membership function menjadi cirri utama dari penalaran dengan logika fuzzy tersebut (Kusumadewi & Purnomo, 2010).
2.3.1. Alasan Penggunaan Logika Fuzzy
Menurut Cox (1994), ada beberapa alasan mengapa orang menggunakan logika fuzzy, antara lain (Kusumadewi & Purnomo, 2010):
1. Konsep logika fuzzy mudah dimengert. Karena logika fuzzy menggunakan dasar teori himpunan, maka konsep matematis yang mendasari penalaran fuzzy tersebut cukup mudah dimengerti.
2. Logika fuzzy sangat fleksibel, artinya mampu beradaptasi dengan perubahan-perubahan, dan ketidakpastian yang menyertai permasalahan.
3. Logika fuzzy memiliki toleransi terhadap data yang tidak tepat. Jika diberikan sekelompok data yang cukup homogen, dan kemudian ada beberapa data
yang “eksklusif”, maka logika fuzzy memiliki kemampuan untuk menangani data eksklusif tersebut.
4. Logika fuzzy mampu memodelkan fungsi-fungsi nonlinier yang sangat kompleks.
5. Logika fuzzy dapat membangun dan mengaplikasikan pengalaman-pengalaman para pakar secara langsung tanpa harus melalui proses pelatihan. Dalam hal ini, sering dikenal dengan nama Fuzzy Expert Systems menjadi bagian terpenting.
7. Logika fuzzy didasarkan pada bahasa alami. Logika fuzzy menggunakan bahasa sehari-hari sehingga mudah dimengerti.
2.3.2 Himpunan Fuzzy
Nol (0), yang berarti bahwa suatu item tidak menjadi anggota dalam suatu himpunan.
Himpunan fuzzy memiliki 2 atribut, yaitu (Kusumadewi & Purnomo, 2010): a. Linguistik, yaitu penamaan suatu grup yang mewakili suatu keadaan atau
kondisi tertentu dengan menggunakan bahasa alami, seperti: muda, parobaya, tua.
b. Numeris, yaitu suatu nilai (angka) yang menunjukkan ukuran dari suatu variabel seperti: 40, 25, 50, dsb.
Misalkan diketahui klasifikasi sabagai berikut:
MUDA < 35
SETENGAH BAYA 35 55
TUA > 55
diterapkan pada hal-hal yang bersifat kontinu, seperti umur. Selain itu, untuk menunjukkan suatu nilai kebenaran 0 dan 1, dapat digunakan nilai pecahan, dan menunjuk 1 atau nilai yang dekat dengan 1 untuk umur 45 tahun, kemudian perlahan menurun menuju 0 untuk umur di bawah 35 tahun dan di atas 55 tahun (Sihotang, 2011).
Ada beberapa hal yang perlu diketahui dalam memahami sistem fuzzy, yaitu (Kusumadewi & Purnomo, 2010):
a. Variabel fuzzy
Variabel fuzzy merupakan variabel yang hendak dibahas dalam suatu sistem fuzzy. Contoh: umur, temperature, permintaan, dsb.
b. Himpunan fuzzy
Himpunan fuzzy merupakan suatu grup yang mewakili suatu kondisi atau keadaan tertentu dalam suatu variabel fuzzy.
c. Semesta pembicaraan
Semesta pembicaraan adalah keseluruhan nilai yang diperbolehkan untuk dioperasikan dalam suatu variabel fuzzy. Semesta pembicaraan merupakan himpunan bilangan ril yang senantiasa naik (bertambah) secara monoton dari kiri ke kanan. Nilai semesta pembicaraan dapat berupa bilangan positif maupun negatif.
d. Domain
Domain himpunan fuzzy adalah keseluruhan nilai yang diizinkan dalam semesta pembicaraan dan boleh dioperasikan dalam sutu himpunan fuzzy. Seperti semesta pembicaraan, domain merupakan himpunan bilangan ril yang senantiasa naik (bertambah) secara monoton dari kiri ke kanan. Nilai domain dapat berupa bilangan positif maupun negatif.
2.3.3 Fungsi Keanggotaan
keanggotaan) yang memiliki interval antara 0 sampai 1. Salah satu cara yang dapat digunakan untuk mendapatkan nilai keanggotaan adalah dengan melalui pendekatan fungsi.
2.3.3.1 Representasi Linier
Pada representasi linier, pemetaan input ke dearajat keanggotaannya digambarkan sebagai suatu garis lurus. Bentuk ini paling sederhana dan menjadi pilihan yang baik untuk mendekati suatu konsep yang kurang jelas. Ada dua keadaan himpunan fuzzy yang linier. Pertama, kenaikan himpunan dimulai pada nilai kodomain yang memiliki derajat keanggotaan nol (0) bergerak ke kanan menuju nilai domain yang memiliki derajat keanggotaan lebih tinggi (Kusumadewi & Purnomo, 2010).
Representasi Linier Naik
Gambar 2.1 Representasi Linier Naik Fungsi keanggotaan:
=
0;
( − )/( − )
1;
Representasi Linier Turun
Gambar 2.2 Representasi Linier Turun Fungsi Keanggotaan:
= ( − )/( − );
0;
2.3.3.2 Representasi Kurva Segitiga
Gambar 2.3. Representasi Kurva Segitiga
Fungsi keanggotaan:
=
0;
( − )/( − ); ( − )/( − );
2.3.3.3 Representasi Kurva Trapesium
Kurva trapesium pada dasarnya seperti bentuk segitiga, hanya saja ada beberapa
titik yang memiliki nilai keanggotaan 1.
Gambar 2.4. Representasi Kurva Trapesium Fungsi keanggotaan:
� =
0;
( − )/( − ); 1;
BAB 1 PENDAHULUAN
1.1. Latar Belakang
Program linier merupakan metode matematika dalam mengalokasikan sumber daya yang terbatas untuk mencapai suatu tujuan, seperti memaksimumkan keuntungan dan meminimumkan biaya. Program linier banyak diterapkan dalam masalah ekonomi, militer dan sosial. Program linier berkaitan dengan penjelasan suatu kasus dalam dunia nyata sebagai suatu model matematika yang terdiri dari sebuah fungsi tujuan linier dengan beberapa kendala linier.
Program linier merupakan instrumen pengambilan keputusan yang berkaitan dengan pengalokasian sumber daya dalam mencapai tujuan tertentu. Sumber daya berupa uang, tenaga kerja, material, mesin, fasilitas, ilmu pengetahuan, teknologi, keahlian, waktu dan ruang. Sumber daya ini sifatnya terbatas. Dengan demikian, program linier berperan sebagai alat untuk membantu dalam pengambilan keputusan manajemen dengan cara mengidentifikasi kombinasi sumber daya yang tersedia sehingga tujuan yang diinginkan dapat tercapai dengan optimal.
Apabila suatu masalah program linier hanya mengandung dua kegiatan (variabel keputusan) saja, maka dapat diselesaikan dengan metode grafik. Bila terdapat lebih dari dua variabel maka metode grafik tidak dapat digunakan lagi, sehingga diperlukan metode simpleks. Metode ini lazim dipakai untuk menentukan kombinasi dari tiga variabel atau lebih. Kedua metode ini sampai sekarang masih sangat popular dan masih mengalami perkembangan, salah satunya menggunakan logika fuzzy.
yang pertama kali diperkenalkan oleh Prof. Lotfi A. Zadeh dari Universitas California di Berckeley pada tahun 1965. Teori ini dapat digunakan untuk menangani ketidakpastian dalam masalah dunia nyata. Teori ini memperkenalkan yang keanggotaannya dinyatakan dengan derajat keanggotaan tertentu dalam selang tertutup antara 0 dan 1. Program linier fuzzy adalah program linier yang dinyatakan dengan fungsi objektif dan fungsi kendala yang memiliki parameter fuzzy dan ketidaksamaan fuzzy. Tujuan dari program linier fuzzy adalah mencari solusi yang dapat diterima berdasarkan kriteria yang dinyatakan dalam fungsi objektif dan kendala. Solusi tersebut berbentuk himpunan fuzzy yang memiliki derajat kebenaran tertentu pada selang [0,1] (Purba, 2012).
Hasil yang diperoleh dari penyelesaian yang menggunakan program linier fuzzy sering kali menghasilkan nilai yang berbentuk pecahan sementara satuan yang ditetapkan misalkan adalah satuan unit dalam suatu perancangan produksi. Hal ini tentu tidak relevan karena satuan unit tidak mungkin bernilai pecahan. Oleh karena itu, diperlukan suatu metode pembulatan untuk menghasilkan nilai yang integer dari hasil perolehan program linier fuzzy tersebut. Metode pembulatan yang akan digunakan penulis adalah metode pembulatan cutting plane. Berdasarkan latar belakang tersebut maka penulis memilih judul tugas akhir
“Penerapan Metode Cutting Plane pada Pembulatan Hasil Program Linier Fuzzy”.
1.2. Perumusan Masalah
1.3. Batasan Masalah
Untuk menghindari meluasnya masalah dalam tulisan ini, maka permasalahan dibatasi sebagai berikut:
1. Penelitian ini terfokus pada masalah program bilangan integer.
2. Penelitian ini terfokus pada pembulatan hasil yang berbentuk desimal.
1.4.Tujuan Penelitian
Penelitian ini bertujuan untuk mendapatkan hasil bilangan yang integer dan tetap optimal dengan cutting plane
1.5. Kontribusi Penelitian
Manfaat dari penelitian ini adalah sebagai berikut:
1. Untuk menambah wawasan dan memperkaya literatur dalam bidang operasi riset yang berhubungan dengan program linier fuzzy bagi penulis dan pembaca.
2. Sebagai bahan pertimbangan untuk penulis dan pembaca agar dapat mempelajari dan mengembangkan ilmu matematika dalam berbagai permasalahan serta aplikasinya.
1.6. Tinjauan Pustaka
Sebagai sumber pendukung teori dalam tulisan ini, penulis mengambil beberapa pustaka yang memberikan kontribusi dalam penyelesaian tulisan ini.
baik untuk mendekati suatau konsep yang kurang jelas. Ada dua keadaan himpunan fuzzy yang linier. Pertama, kenaikan himpunan dimulai pada nilai kodomain yang memiliki derajat keanggotaan nol (0) bergerak kekanan menuju nilai domaini yang memiliki derajat keanggotaan lebih tinggi ( Kusumadewi & Purnomo, 2010).
Fuzzy linaearr programming menggabungkan antara model pemrograman linier biasa dan konsep logika fuzzy sebagai salah satu cara pengambilan keputusan dalam menentukan jumlah produk yang optimal dengan mempertimbangkan keterbatasan sumber daya produksi (Suantio, Rambe & Siregar, 2013).
Fuzzy Linier Programming merupakan modifikasi dari teori Linier Programming digabung dengan Fuzzy Logic di mana hasilnya akan lebih kecil jika dibandingkan dengan hasil pada metode Linier Programming. Dengan menerapkan Fuzzy Linier Programming dalam menentukan tingkat produksi maksimum dianggap dapat membantu untuk memetakan suatu input ke dalam suatu output tanpa mengabaikan faktor-faktor yang ada. Dengan metode ini diharapkan nantinya dapat membantu dalam proses pengambilan keputusan yang tepat yang mana Fuzzy Logic dapat digunakan dalam pemecahan masalah program linier tersebut. Hal ini merupakan syarat mutlak untuk dapat digunakan dalam Fuzzy Linier Programming (Wanayumini, 2012).
Penyelesaian program linier secara klasik dianggap kurang tepat lagi, hal ini disebabkan penyelesaian program linier secara klasik tidak melibatkan asumsi-asumsi yang ada padahal model yang terbentuk dalam dunia nyata selalu terbentuk dengan asumsi-asumsi yang ada. Penyelesaian program linier secara logika fuzzy akan memberikan hasil yang lebih baik jika dibandingkan dengan penyelesaian program linier secara klasik (Purba, 2012).
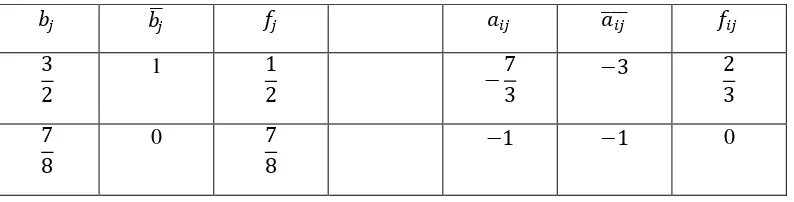
Metode Cutting Plane membahas masalah pemrograman linier yang dipecahkan, yaitu dengan mengabaikan kondisi integer. Misalnya, tabel optimal terakhir untuk program linier diketahui. Pilih sembarang baris tabel optimal simpleks yang dalam kolom bi memuat pecahan. Misalkan baris ke-i adalah baris
yang terpilih, kemudian pisahkan bi dan aijmenjadi bagian yang bulat dan bagian
− =− =1
Keterangan : adalah variabel slack cutting plane ke n; fi adalah bagian
pecahan dari bi, fij adalah koefisien variabel non basis,wj adalah variabel non
basis.
Ide dari metode cutting plane adalah kendala terhadap masalah pada saat tertentu sehingga diperoleh masalah program linier dengan sebuah solusi yang optimal dengan hasil bilangan integer. Hal pertama yang dilakukan pada metode ini adalah dengan menyelesaikan persamaan dengan program linier biasa, apabila diperoleh penyelesaian bilangan integer dan merupakan hasil yang optimal maka proses dihentikan. Jika tidak maka akan ditambahakan sebuah kendala kedalam masalah dan diselesaikan kembali dengan program linier biasa, apabila belum menghasilkan solusi yang integer, maka dilakukan lagi penambahan kendala sampai hasil yang diperoleh adalah bilangan integer (Paul R Thie, 1938).
1.7. Metodologi Penelitian
Langkah-langkah yang akan dilakukan dalam menyelesaikan penelitian ini adalah :
1. Mencari literatur dari beberapa buku, jurnal, situs dan karya tulis lainnya yang berhubungan dengan program linier fuzzy dan metode cutting plane. 2. Membahas definisi program linier, program bilangan bulat dan
menjelaskan fuzzy.
3. Membahas program linier fuzzy serta pembulatannya menggunakan metode cutting plane.
PENERAPAN METODE CUTTING PLANE PADA PEMBULATAN HASIL PROGRAM LINIER FUZZY
ABSTRAK
Program linear fuzzy merupakan program linear dengan fungsi objektif yang akan dioptimisasikan sehingga tunduk pada batasan-batasan yang dimodelkan dengan menggunakan himpunan fuzzy. Tujuan dari program linear fuzzy adalah mencari solusi yang optimal berdasarkan kriteria yang dinyatakan dalam fungsi objektif dan kendala. Parogram linear fuzzy dapat diaplikasikan pada pengoptimalan produksi barang tertentu. Namun sering kali hasil yang diperoleh berupa nilai yang berbentuk desimal padahal satuan unit tidak mungkin berupa pecahan, untuk mengatasi masalah tersebut, penulis memilih metode cutting plane untuk membulatkan hasil yang berupa desimal tersebut. Meode cutting plane merupakan suatu metode yang digunakan untuk menyelesaikanprogram linear bilangan bulat dengan penambahan kendala baru yang disebut gomory. Solusi yang dihasilkan setelah pembulatan lebih kecil dibandingkan dengan solusi sebelum dilakukan pembulatan.
APPLICATION OF CUTTING PLANE METHOD ON INTEGERING THE RESULT OF FUZZY LINIER PROGRAMMING
ABSTRACT
Fuzzy linear programming is a linear programming with objective function that will be optimizationed so that submit on constraints witch modeled using by fuzzy set. The purpose of fuzzy linear programming is to find the solution that can be accepted with criteria that expressed on objective function and constraint. Fuzzy linear programming can be applicated on optimizing of certain goods. But the decimal obtained solution is often however decimal unit is not possible, to solve the problem, the writer use the cutting plane method to integering the obtained decimal solution. Cutting plane method is a method that used to solve the integer linear programming with the addition of new constraint called gomory. The integering obtained solution is less than before integering obtained solution.
LINIER FUZZY
SKRIPSI
SAHATA SIANTURI
120803054
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
PEMBULATAN HASIL PROGRAM
LINIER FUZZY
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar
Sarjana Sains
SAHATA SIANTURI
120803054
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
PERSETUJUAN
Judul : Penerapan Metode Cutting Plane Pada Pembulatan Hasil Program Linier Fuzzy.
Kategori : Skripsi
Nama : Sahata Sianturi
Nomor Induk Mahasiswa : 120803054
Program Studi : Sarjana (S1) Matematika Departemen : Matematika
Fakultas : Matematika Dan Ilmu Pengetahuan Alam (FMIPA) Universitas Sumatera Utara
Diluluskan di Medan, Juli 2016
Komisi Pembimbing:
Pembimbing 2, Pembimbing 1,
Drs. Gim Tarigan, M.Si Drs. Pengarapen Bangun, M.Si NIP. 19550202 198601 1 001 NIP. 19560815 198503 1 005
Disetujui oleh:
Departemen Matematika FMIPA USU Ketua,
Prof. Dr. Tulus, M.Si.
PERNYATAAN
PENERAPAN METODE CUTTING PLANE PADA PEMBULATAN HASIL PROGRAM LINIER FUZZY
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil karya saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, Juli 2016
PENGHARGAAN
Puji dan syukur penulis panjatkan kepada Tuhan Yesus Kristus dengan kasih dan berkatNya penulis dapat menyelesaikan penyusunan skripsi ini dengan judul Penerapan Metode Cutting Plane Pada Pembulatan hasil Program Linier Fuzzy.
Terima kasih juga penulisa sampaikan kepada :
1. Bapak Drs. Pengarapen Bangun, M.Si selaku pembimbing 1 dan Bapak Drs. Gim Tarigan, M.Si selaku pembimbing 2 yang telah membimbing penulis selama penulisan skripsi ini.
2. Bapak Dr. Syahriol Sitorus, M.IT dan Drs. Marihat Situmorang, M. Kom selaku dosen penguji yang telah memberikan kritik dan saran yang membangun dalam penyempurnaan skripsi ini.
3. Bapak Prof. Dr. Tulus, M.Si. Ph.D dan Ibu Dr. Mardiningsih, M.Si selaku Ketua dan Sekretaris Departemen Matematika FMIPA-USU Medan.
4. Bapak Dr. Kerista Sebayang, M. S selaku Dekan FMIPA USU serta seluruh civitas akademika di lingkungan FMIPA USU.
5. Ayahanda Manangkap Sianturi dan Ibunda Selly Sihombing serta abang dan kaka saya yang selama ini memberikan bantuan dan dorongan kepada penulis.
6. Teman-teman grup “Sama Wisuda” yaitu Mega, Agustina, Goklim, Oka, Willy, Daniel, Purnomo, Artha, Ayen, Fransiskus, Desi, dan Yosephin atas motivasi, nasehat, semangat dan bantuannya kepada penulis.
PENERAPAN METODE CUTTING PLANE PADA PEMBULATAN HASIL PROGRAM LINIER FUZZY
ABSTRAK
Program linear fuzzy merupakan program linear dengan fungsi objektif yang akan dioptimisasikan sehingga tunduk pada batasan-batasan yang dimodelkan dengan menggunakan himpunan fuzzy. Tujuan dari program linear fuzzy adalah mencari solusi yang optimal berdasarkan kriteria yang dinyatakan dalam fungsi objektif dan kendala. Parogram linear fuzzy dapat diaplikasikan pada pengoptimalan produksi barang tertentu. Namun sering kali hasil yang diperoleh berupa nilai yang berbentuk desimal padahal satuan unit tidak mungkin berupa pecahan, untuk mengatasi masalah tersebut, penulis memilih metode cutting plane untuk membulatkan hasil yang berupa desimal tersebut. Meode cutting plane merupakan suatu metode yang digunakan untuk menyelesaikanprogram linear bilangan bulat dengan penambahan kendala baru yang disebut gomory. Solusi yang dihasilkan setelah pembulatan lebih kecil dibandingkan dengan solusi sebelum dilakukan pembulatan.
APPLICATION OF CUTTING PLANE METHOD ON INTEGERING THE RESULT OF FUZZY LINIER PROGRAMMING
ABSTRACT
Fuzzy linear programming is a linear programming with objective function that will be optimizationed so that submit on constraints witch modeled using by fuzzy set. The purpose of fuzzy linear programming is to find the solution that can be accepted with criteria that expressed on objective function and constraint. Fuzzy linear programming can be applicated on optimizing of certain goods. But the decimal obtained solution is often however decimal unit is not possible, to solve the problem, the writer use the cutting plane method to integering the obtained decimal solution. Cutting plane method is a method that used to solve the integer linear programming with the addition of new constraint called gomory. The integering obtained solution is less than before integering obtained solution.
DAFTAR ISI
1. 5 Kontribusi Penelitian 3
1. 6 Tinjauan Pustaka 3
1. 7 Metodologi Penelitian 5
BAB 2 LANDASAN TEORI 7
2. 1 Program Linier 7
2. 1. 1 Persyaratan Penyelesaian Program Linier 7 2. 1. 2 Model Umum Matematik Program Linier 8 2. 1. 3 Karakteristik Program Linier 10
2. 1. 4 Metode Simpleks 11
2. 2 Program Bilangan Bulat 13
2.2.1. Metode Pembulatan (Rounding Method) 15 2.2.2 Metode Branch and Bound 15
2.2.3 Metode Cutting Plane 17
2.3 Fuzzy 17
2.3.1 Alasan Penggunaan Logika Fuzzy 18
2.3.2 Himpunan Fuzzy 19
2.3.3 Fungsi Keanggotaan 20
BAB 3 HASIL DAN PEMBAHASAN 24
3.1 Program Linier Fuzzy 24
3.2 Penggunaan Metode Cutting Plane 28 3.3 Ilustrasi Numerik Pembulatan Program Linear Fuzzy
dengan Menggunakan Metode Cutting Plane
31
BAB 4 KESIMPULAN DAN SARAN 51
4. 1 Kesimpulan 51
4. 2 Saran 51
DAFTAR PUSTAKA 52
DAFTAR TABEL
Nomor Judul Halaman
Tabel
Tabel 2.1 Bentuk Tabel Simpleks 11
Tabel 3.1 Solusi Optimum Masalah Program Linear 27 Tabel 3.2 Bentuk integer dan noninteger 28
Tabel 3.3 Penambahan Kendala Gomory 29
Tabel 3.4 Bentuk Tabulasi Permasalahan 31
Tabel 3.5 Iterasi 0 untuk ݐ = 0 34
Tabel 3.6 Iterasi 1 untuk ݐ = 0 34
Tabel 3.7 Iterasi 2 untuk ݐ = 0 34
Tabel 3.8 Iterasi 3 untuk ݐ = 0 35
Tabel 3.9 Iterasi 0 untuk ݐ = 1 36
Tabel 3.10 Iterasi 1 untuk ݐ = 1 36
Tabel 3.11 Iterasi 2 untuk ݐ = 1 37
Tabel 3.12 Iterasi 3 untuk ݐ = 1 37
DAFTAR GAMBAR
Nomor Judul Halaman
Gambar
Gambar 2.1 Representasi Linier Naik 20 Gambar 2.2 Representasi Linier Turun 21
Gambar 2.3 Representasi Kurva Segitiga 21
Gambar 2.4 Representasi Kurva Trapesium 22
Gambar 3.1 Fungsi Keanggotaan 26
DAFTAR LAMPIRAN
No Lampiran Judul Lampiran Halaman