Model Matematika Penyebaran DBD Tipe SIR dan Simulasinya

MODEL MATEMATIKA PENYEBARAN DBD TIPE

SIR

DAN SIMULASINYA

ASMAIDI

SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR

PERNYATAAN MENGENAI TESIS DAN

SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA*

Dengan ini saya menyatakan bahwa tesis berjudul Model Matematika Penyebaran DBD Tipe SIR dan Simulasinya adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apapun kepada perguruan tinggi manapun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.

Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.

Bogor, September 2014

Asmaidi

RINGKASAN

ASMAIDI. Model Matematika Penyebaran DBD Tipe SIR dan Simulasinya. Dibimbing oleh PAIAN SIANTURI dan ENDAR HASAFAH NUGRAHANI.

Pada tulisan ini dikembangkan model matematika penyebaran demam berdarah dengue (DBD) tipe SIR, di mana SIR merupakan singkatan dari

susceptible (S), infected (I) dan recovered (R). Model matematika tersebut dikontruksi dari model yang dikembangkan oleh Massad et al. (2011) dan Amaku

et al. (2013). Pada kedua model tersebut terdapat tiga asumsi, yaitu laju perpindahan nyamuk laten menjadi nyamuk terinfeksi, produksi telur nyamuk dan faktor suhu yang digunakan dalam penetasan telur nyamuk. Berdasarkan asumsi yang terdapat pada kedua model tersebut, maka model matematika tipe SIR

dimodifikasi dengan mengasumsikan laju perpindahan nyamuk laten menjadi nyamuk terinfeksi tidak melibatkan waktu tunda. Dalam hal produksi telur nyamuk, telur nyamuk sehat diproduksi oleh nyamuk rentan dan nyamuk terinfeksi, sedangkan telur nyamuk terifeksi hanya diproduksi oleh nyamuk terinfeksi. Selain itu, dalam memproduksi nyamuk rentan dan nyamuk terinfeksi dari telur-telurnya digunakan faktor suhu konstan.

Pada model matematika tipe SIR modifikasi, ditentukan titik tetap. Selanjutnya dilakukan analisis kestabilan masing-masing titik tetap dengan mempertimbangkan bilangan reproduksi dasar ℛ0 . Bilangan reproduksi dasar merupakan nilai harapan banyaknya infeksi setiap satuan waktu. Jika ℛ0 < 1, maka rata-rata setiap individu terinfeksi akan menginfeksi kurang dari satu individu baru, sehingga penyakit tidak akan menyebar. Jika ℛ0 > 1, maka rata-rata setiap individu terinfeksi akan menginfeksi lebih dari satu individu baru, sehingga penyakit akan menyebar. Untuk menunjukkan perilaku populasi pada kondisi ℛ0< 1 dan ℛ0 > 1, maka dilakukan simulasi. Selain itu, simulasi juga dilakukan untuk melihat pengaruh laju kematian nyamuk terhadap penyebaran penyakit.

populasi telur nyamuk terinfeksi, pada awal simulasi berkurang, akan tetapi pada akhir simulasi jumlahnya sama.

SUMMARY

ASMAIDI. Mathematical Model of Dengue Transmission of SIR Type and Its Simulation. Supervised by PAIAN SIANTURI and ENDAR HASAFAH NUGRAHANI.

This paper presents a mathematical model of transmission of dengue hemorrhagic fever (DHF) of SIR type, where SIR is an abbreviation of susceptible (S), infected (I) and recovered (R). The presented mathematical model is a modification based on the models developed by Massad et al. (2011) and Amaku

et al. (2013). There are three assumptions were considered, the rate of displacement of latent mosquitoes become infected, mosquito eggs production and temperature factor in mosquito eggs hatching. The modified assumptions is: the rate of displacement of latent mosquitoes to become infected mosquitoes does not involve a time delay. In the case of mosquito eggs production, non-infected eggs are produced by infected mosquitoes and susceptible mosquitoes, while the infected eggs are only produced by infected mosquitoes. Moreover, a constant temperature factor is assumed in egg production of susceptible and infected mosquitoes.

This research aims to analyze the modified mathematical model. First step is to obtain the fixed points, then analyze the stability of each fixed point by considering the basic reproduction number ℛ0 . The basic reproduction number is the expected value of infections per unit of time. The number is considered as a benchmark of disease transmission in the population. If ℛ0 < 1, then on average each infected individual will be infecting less than one newly individual, so that the disease will disappear. If ℛ0 < 1, then on average each infected individual will generate more than one newly infected individuals, so that the disease will spread. To demonstrate the behavior of each population on the condition ℛ0 < 1 and ℛ0 > 1, a simulation study is performed. In addition, the simulation is also conducted to see the effect of mosquito mortality rate against the spread of disease.

population, at the beginning of the simulation was decreased, but at the end of the simulation the population level is same.

© Hak Cipta Milik IPB, Tahun 2014

Hak Cipta Dilindungi Undang-Undang

Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumbernya. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik, atau tinjauan suatu masalah; dan pengutipan tersebut tidak merugikan kepentingan IPB

Tesis

sebagai salah satu syarat untuk memperoleh gelar Magister Sains

pada

Program Studi Matematika Terapan

MODEL MATEMATIKA PENYEBARAN DBD TIPE

SIR

DAN SIMULASINYA

SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR

Judul Tesis : Model Matematika Penyebaran DBD Tipe SIR dan Simulasinya Nama : Asmaidi

NIM : G551120111

Disetujui oleh Komisi Pembimbing

Dr Paian Sianturi Ketua

Dr Ir Endar H Nugrahani, MS Anggota

Diketahui oleh

Ketua Program Studi Matematika Terapan

Dr Jaharuddin, MS

Dekan Sekolah Pascasarjana

Dr Ir Dahrul Syah, MScAgr

PRAKATA

Puji dan syukur penulis panjatkan kepada Allah subhanahu wa ta’ala atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Tema yang dipilih dalam penelitian yang dilaksanakan sejak bulan Februari 2014 ini ialah pemodelan matematika, dengan judul Model Matematika Penyebaran DBD Tipe

SIR dan Simulasinya.

Penulisan tesis ini merupakan salah satu syarat memperoleh gelar Magister Sains pada Program Studi Matematika Terapan Sekolah Pascasarjana Institut Pertanian Bogor. Penulis menyadari bahwa bantuan-bantuan dan arahan-arahan dari kedua pembimbing sangat membantu dalam menyelesaikan karya tulis ini. Terima kasih penulis ucapkan kepada Bapak Dr Paian Sianturi selaku ketua pembimbing dan Ibu Dr Ir Endar H Nugrahani, MS selaku anggota pembimbing.

Penulis juga menyampaikan terima kasih kepada:

1. Prof Dr Ir Herry Suhardiyanto, MSc selaku Rektor Institut Pertanian Bogor. 2. Dr Ir Dahrul Syah, MscAgr selaku Dekan Sekolah Pascasarjana Institut

Pertanian Bogor.

3. Dr Jaharuddin, MS selaku Ketua Program Studi Matematika Terapan dan selaku penguji luar komisi pembimbing.

4. Seluruh dosen dan staf pegawai tata usaha Departemen Matematika Institut Pertanian Bogor.

5. Direktorat Jenderal Pendidikan Tinggi (DIKTI) sebagai sponsor Beasiswa Unggulan.

6. Ayah, ibu (Alm), seluruh keluarga dan Silvi Prisha Bahri terima kasih atas segala doa dan kasih sayangnya sehingga penulis berhasil menyelesaikan studi di Program Studi Matematika Terapan Institut Pertanian Bogor.

7. Sanusi, M. Usman, Zulfiqar Busra, Rinancy Tumilaar dan Sri Lestari M terima kasih atas doa, saran dan bantuan yang telah diberikan kepada penulis dalam menyelesaikan karya ilmiah ini.

8. Seluruh mahasiswa Program Studi S2 Matematika Terapan Institut Pertanian Bogor khususnya angkatan tahun 2012.

Semoga segala bantuan, bimbingan, dan motivasi yang telah diberikan kepada penulis senantiasa mendapat balasan dari Allah subhanahu wa ta’ala.

Semoga karya ilmiah ini bermanfaat.

Bogor, September 2014

DAFTAR ISI

Titik Tetap dan Kestabilan Titik Tetap Kriteria Routh-Hurwitz

Bilangan Reproduksi Dasar ℛ0

3 MODEL MATEMATIKA PENYEBARAN PENYAKIT DEMAM

DAFTAR TABEL

1 Parameter pada diagram kompartemen Massad et al. (2011) dan Amaku et al. (2013)

2 Sifat kestabilan titik tetap

3 Nilai parameter pada model modifikasi

4 Nilai ℛ0 dengan parameter �_� ditingkatkan dan parameter lain tetap

DAFTAR GAMBAR

1 Diagram kompartemen Massad et al. (2011) 2 Diagram kompartemen Amaku et al. (2013) 3 Diagram kompartemen Modifikasi

4 Perilaku populasi manusia ketika ℛ0 < 1

10 Populasi manusia dengan parameter �_� ditingkatkan 11 Populasi nyamuk dengan parameter �_� ditingkatkan 12 Populasi telur nyamuk dengan parameter �_� ditingkatkan

DAFTAR LAMPIRAN

1 Penentuan titik tetap

1

PENDAHULUAN

Latar Belakang

Berdasarkan kasus demam berdarah dengue (DBD) yang terjadi, muncul berbagai solusi untuk pencegahan dan penanggulangan penyebaran DBD, salah satunya adalah membuat suatu model matematika. Pada tahun 1911, dikembangkan model matematika penyebaran penyakit malaria yang dikenal dengan model Ross, kemudian model Ross dikembangkan oleh MacDonald pada tahun 1957 yang dikenal dengan model Ross-MacDonald (Ngwa dan Shu 2000).

Pada akhir abad ke-20 pemodelan matematika menjadi meluas. Sebagai contoh, pemodelan matematika tentang penyebaran penyakit menular, seperti malaria dan demam berdarah. Pemodelan matematika tersebut dibuat dengan berbagai pertimbangan, salah satunya adalah model matematika penyebaran DBD yang mempertimbangkan faktor suhu.

Model matematika penyebaran DBD yang mempertimbangkan faktor suhu pernah dilakukan oleh Massad et al. (2011) dan Amaku et al. (2013), dengan mengembangkan model SIR manusia-nyamuk-telur nyamuk. SIR merupakan singkatan dari susceptible (S), infected (I) dan recovered (R). Pada model SIR

manusia-nyamuk-telur nyamuk, populasi manusia terdiri atas tiga populasi, yaitu manusia rentan, manusia terinfeksi dan manusia sembuh. Populasi nyamuk terdiri atas tiga populasi, yaitu nyamuk rentan, nyamuk laten dan nyamuk terinfeksi. Populasi telur nyamuk terdiri atas dua populasi, yaitu telur nyamuk sehat dan telur nyamuk terifeksi.

Pada model yang dirumuskan oleh Massad et al. (2011), diasumsikan laju perpindahan nyamuk laten menjadi nyamuk terinfeksi melibatkan waktu tunda sebagai periode masa inkubasi pada nyamuk. Selain itu, Massad et al. (2011) mengasumsikan telur nyamuk sehat diproduksi oleh nyamuk rentan dan nyamuk terinfeksi, sedangkan telur nyamuk terifeksi hanya diproduksi oleh nyamuk terinfeksi. Faktor suhu yang digunakan dalam penetasan telur-telur nyamuk tidak konstan.

Berbeda dengan model Amaku et al. (2013), di mana laju perpindahan nyamuk laten menjadi nyamuk terinfeksi tidak melibatkan waktu tunda dan telur nyamuk sehat diproduksi oleh ketiga kompartemen nyamuk, sedangkan telur nyamuk terifeksi diproduksi oleh nyamuk laten dan nyamuk terinfeksi. Faktor suhu yang digunakan dalam penetasan telur-telur nyamuk adalah konstan.

2

Tujuan Penelitian

Penelitian ini bertujuan untuk,

1. Memodifikasi model matematika penyebaran penyakit demam berdarah. 2. Menentukan titik tetap dan kestabilan titik tetap model modifikasi. 3. Menentukan bilangan reproduksi dasar ℛ₀ model modifikasi.

4. Melakukan simulasi pada model modifikasi untuk melihat perilaku populasi manusia, nyamuk dan telur nyamuk.

5. Melakukan simulasi pengaruh laju kematian nyamuk terhadap penyebaran penyakit pada populasi.

2

TINJAUAN PUSTAKA

Persamaan Diferensial Linear

Definisi 1 [Persamaan Diferensial Linear Orde-1]

Bentuk umum persamaan diferensial linear orde-1 adalah:

+ = , (2.1) dengan ( ) dan ( ) adalah fungsi sembarang. Persamaan (2.1) dikatakan linear, jika ruas kiri merupakan fungsi linear dari x dan . Jika ( ) = 0, maka diperoleh persamaan diferensial linear homogen orde-1, jika ( )≠0 diperoleh persamaan diferensial linear tak homogen orde-1.

Definisi 2 [Persamaan Diferensial Linear Orde-2 dengan Koefisien Konstan] Bentuk umum persamaan diferensial linear orde-2 dengan koefisien konstan adalah:

+ 1 + 2 = , (2.2) dengan ₁ dan ₂ konstan. Jika = 0, maka diperoleh persamaan diferensial homogen orde-2. Jika ≠0, maka diperoleh persamaan diferensial tak homogen orde-2.

Sistem Persamaan Diferensial

Definisi 1 [Sistem Persamaan Diferensial Orde-1]

Sistem persamaan diferensial orde-1 terdiri atas n persamaan dan n fungsi dari � ( = 1, 2,…, ) dapat ditulis

1 = 1( , 1, 2,… , )

2 = 2( , 1, 2,… , ) (2.3)

3 Sistem persamaan diferensial (2.3) dapat ditulis dalam notasi vektor, yaitu � =� �,� ,� ∈ ℝ�, (2.4) dengan

Definisi 2 [Sistem Persamaan Diferensial Homogen Orde-1]

Sistem persamaan diferensial homogen orde-1 terdiri atas n persamaan dan

n fungsi dari � ( = 1, 2,…, ) dapat ditulis

Matriks A _{disebut sebagai matriks koefisien.}

Definisi 3 [Sistem Persamaan Diferensial Tak Homogen Orde-1] Sistem persamaan diferensial tak homogen orde-1 dinyatakan:

� � = �� � +�, (2.6) dengan � adalah vektor konstan tak nol dengan ukuran × 1.

Definisi 4 [Sistem Persamaan Diferensial Mandiri Orde-1] Diketahui sistem persamaan diferensial mandiri orde-1, yaitu

� =� � ,� ∈ ℝ�, (2.7) dengan adalah suatu fungsi kontinu bernilai real dari x_{. Sistem persamaan}

diferensial (2.7) disebut sistem persamaan diferensial mandiri (autonomous) orde-1, karena tidak mengandung nilai t secara eksplisit di dalamnya (Tu 1994).

Nilai Eigen dan Vektor Eigen

Sistem persamaan diferensial dapat ditulis dalam bentuk:

4

di mana A _{merupakan matriks segi yang berukuran × , maka vektor taknol di} ℝ� _{disebut vektor eigen dari �, jika untuk suatu skalar , yang disebut nilai eigen} dari A_{, berlaku:}

Diketahui sistem persamaan diferensial taklinear seperti (2.7), dengan menggunakan ekspansi deret Taylor di sekitar titik tetap � diperoleh:

� = �+�(�), (2.12) hasil pelinearan dari persamaan (2.7).

Titik Tetap dan Kestabilan Titik Tetap

Titik Tetap

Misalkan diketahui sistem persamaan diferensial mandiri orde-1 seperti (2.7), maka titik � disebut titik tetap atau titik kesetimbangan, jika � = 0.

5 Kestabilan Titik Tetap

Misalkan sistem persamaan diferensial (2.7) memiliki titik tetap � . Kestabilan titik tetap tersebut dapat dilihat dari nilai-nilai eigennya, yaitu dengan = 1, 2, 3,…, yang diperoleh dari � − = 0.

Secara umum titik tetap mempunyai sifat sebagai berikut: 1. Stabil, jika

a. Setiap nilai eigen real adalah negatif: < 0 untuk setiap i, atau b. Nilai eigen kompleks bagian Re( ) < 0 untuk setiap i.

2. Takstabil, jika

a. Terdapat paling sedikit satu nilai eigen real positif: > 0.

b. Terdapat paling sedikit satu nilai eigen kompleks dengan Re( ) > 0.

(Edelstein-Keshet 2005)

Kriteria Routh-Hurwitz

Misalkan diberikan persamaan karakteristik: + ₁ −1₊

2 −2+ + = 0 (2.14)

Didefinisikan matriks sebagai berikut:

= 1 , = 1

dengan syarat setiap unsur (l,m) pada matrik adalah:

6

Bilangan reproduksi dasar merupakan nilai harapan banyaknya infeksi setiap satuan waktu. Menurut van den Driessche dan Watmough (2002) bilangan reproduksi dasar didefinisikan nilai harapan banyaknya populasi rentan yang menjadi terinfeksi selama masa infeksi. Selain itu, menurut van den Driessche dan Watmough (2002) kondisi yang memungkinkan untuk ℛ₀ adalah

1. Jika ℛ₀ < 1, maka rata-rata setiap individu terinfeksi akan menginfeksi kurang dari satu individu baru, sehingga penyakit tidak akan menyebar.

2. Jika ℛ₀ > 1, maka rata-rata setiap individu terinfeksi akan menginfeksi lebih dari satu individu baru, sehingga penyakit akan menyebar.

Bilangan reproduksi dasar dalam tulisan ini ditentukan dengan menggunakan the next generation matrix . The next generation matrix perpindahan individu yang dievaluasi pada titik tetap � . Menurut Jones (2007),

ℛ0 merupakan nilai eigen dominan dari matriks = �− .

3

MODEL MATEMATIKA PENYEBARAN PENYAKIT

DEMAM BERDARAH

Penyebaran Virus DBD

DBD merupakan penyakit berbahaya yang disebabkan oleh virus dengue yang hidup di dalam tubuh nyamuk Aedes aegypti. Nyamuk Aedes aegypti adalah vektor utama penyakit demam berdarah dengue dan berkembang biak pada awal dan akhir musim penghujan. Perkembangbiakan nyamuk Aedes aegypti

7 Proses penularan virus dengue dibedakan menjadi dua macam. Pertama, penularan vertikal dalam tubuh nyamuk. Menurut Malavige et al. (2004), virus dengue dapat ditularkan oleh nyamuk betina pada telur-telurnya. Selain itu dapat ditularkan melalui kontak seksual dari nyamuk jantan ke nyamuk betina yang disebut penularan secara vertikal. Kedua, penularan melalui gigitan nyamuk terhadap manusia.

Penelitian Terdahulu

Berdasarkan diagram kompartemen yang dirumuskan oleh Massad et al.

(2011) dan Amaku et al. (2013), maka dikembangkan diagram kompartemen penyebaran penyakit demam berdarah baru. Diagram kompartemen yang dikembangkan menggunakan asumsi dari kedua diagram kompartemen tersebut. Adapun diagram kompartemen Massad et al. (2011) dan Amaku et al. (2013) dijelaskan sebagai berikut.

Diagram Kompartemen Massad et al. ₍₂₀₁₁₎

Diagram kompartemen Massad et al. (2011), menggambarkan penyebaran dengue dalam tiga populasi, yaitu manusia, nyamuk dan telur nyamuk. Populasi diagram kompartemen Massad et al. (2011), digambarkan pada Gambar 1.

8

Berdasarkan diagram kompartemen pada Gambar 1, diperoleh sistem persamaan diferensial untuk masing-masing kompartemen, yaitu

= 1− − +

Keterangan parameter dapat dilihat pada Tabel 1.

Laju infeksi dari nyamuk terinfeksi ke manusia rentan adalah = , di mana rasio total populasi nyamuk terhadap total populasi manusia, sehingga laju perpindahan manusia rentan menjadi manusia terinfeksi menjadi

= = = . (3.2)

Laju infeksi dari manusia terinfeksi ke nyamuk rentan adalah = , sehingga laju perpindahan nyamuk rentan menjadi nyamuk laten menjadi

= = . (3.3)

Laju perpindahan nyamuk laten menjadi nyamuk terinfeksi, yaitu

− � = − � −� _−� − � , (3.4)

9 Dalam penetasan telur nyamuk dipengaruhi oleh suhu, di mana faktor suhu dibedakan atas dua kelompok, yaitu suhu yang digunakan dalam penetasan telur nyamuk sehat dinyatakan dengan , sedangkan suhu yang digunakan dalam penetasan telur nyamuk terinfeksi dinyatakan dengan . Faktor suhu ditulis

= − 2� +� � − 2� +� ; = , . (3.5)

Persamaan ke tujuh dan delapan pada persamaan (3.1) masing-masing menjelaskan tentang populasi telur nyamuk sehat dan telur nyamuk terinfeksi. Telur nyamuk sehat diproduksi oleh nyamuk rentan dan nyamuk terinfeksi, sedangkan telur nyamuk terinfeksi hanya diproduksi oleh nyamuk terinfeksi.

Pada penelitian yang dilakukan Massad et al. (2011), analisis kestabilan dilakukan dengan menggunakan definisi bilangan reproduksi dasar, yaitu

ℛ0= Diagram Kompartemen Amaku et al. ₍₂₀₁₃₎

Diagram kompartemen Amaku et al. (2013), yaitu diagram kompartemen

SIR manusia-nyamuk-telur nyamuk. Adapun diagram kompartemen tersebut dapat dilihat pada Gambar 2.

Berdasarkan diagram kompartemen pada Gambar 2, diperoleh sistem persamaan diferensial untuk masing-masing kompartemen, yaitu

= 1− − +

10

Keterangan parameter dapat dilihat pada Tabel 1.

Laju infeksi dari nyamuk terinfeksi maupun manusia terinfeksi mengikuti persamaan (3.2) dan (3.3). Laju perpindahan nyamuk laten menjadi nyamuk terinfeksi tidak melibatkan waktu tunda, dilambangkan dengan _. Selain itu, faktor suhu yang digunakan dalam penetasan telur nyamuk adalah konstan, yaitu

� = � = 0.07. (3.8)

Pada diagram kompartemen Amaku et al. (2013), telur nyamuk sehat diproduksi oleh ketiga kompartemen nyamuk, sedangkan telur nyamuk terinfeksi selain diproduksi oleh nyamuk terinfeksi juga diproduksi oleh nyamuk laten.

Berdasarkan diagram kompartemen Massad et al. (2011) dan Amaku et al.

(2013) terdapat tiga asumsi berbeda yang menjadi pengamatan dan kontribusi penulis untuk melakukan modifikasi, sehingga diperoleh diagram kompartemen baru.

Asumsi pertama, pada diagram kompartemen Massad et al. (2011), laju perpindahan nyamuk laten menjadi nyamuk terinfeksi melibatkan waktu tunda sebagai periode masa inkubasi pada nyamuk yang disimbolkan �, sehingga sistem yang diperoleh berbentuk sistem persamaan diferensial tunda (SPDT). Secara matematika, SPDT sulit untuk ditentukan penyelesaiannya. Oleh karena itu, dilakukan modifikasi, dengan mengasumsikan laju perpindahan nyamuk laten menjadi nyamuk terinfeksi tidak melibatkan waktu tunda, (Amaku et al 2013).

Asumsi kedua, laju penetasan telur nyamuk, baik telur nyamuk sehat maupun telur nyamuk terinfeksi. Penetasan telur nyamuk dipengaruhi oleh suhu, di mana Massad et al. (2011) menggunakan faktor suhu tidak konstan (persamaan 3.5), sedangkan Amaku et al. (2013) menggunakan faktor suhu konstan (persamaan 3.8). Dalam hal ini, penulis mengasumsikan faktor suhu yang digunakan dalam penetasan telur nyamuk konstan.

11 nyamuk terinfeksi, telur nyamuk terinfeksi hanya diproduksi oleh nyamuk terinfeksi, sedangkan Amaku et al. (2013), mengasumsikan telur nyamuk sehat diproduksi oleh ketiga kompartemen nyamuk, telur nyamuk terinfeksi diproduksi oleh nyamuk laten dan nyamuk terinfeksi. Dalam diagram kompartemen yang dikembangkan ini, laju produksi telur nyamuk merujuk pada diagram kompartemen Massad et al. (2011). Hal ini, sesuai penelitian bahwa nyamuk betina terinfeksi dapat menurunkan virus kepada telur-telurnya (Malavige et al

2004).

Adapun parameter yang terdapat pada diagram kompartemen Massad et al.

(2011) dan Amaku et al. (2013) dapat dilihat pada Tabel 1.

Tabel 1 Parameter pada diagram kompartemen Massad et al. (2011) dan Amaku et al. (2013)

Parameter Keterangan Satuan

Peluang transmisi virus dengue dari nyamuk ke manusia pergigitan

tanpa satuan Peluang transmisi virus dengue dari manusia

ke nyamuk pergigitan

tanpa satuan Laju kematian manusia disebabkan penyakit waktu-1

Laju pemulihan manusia waktu-1

Laju perpindahan nyamuk laten menjadi nyamuk terinfeksi

waktu-1 Laju kematian manusia secara alami waktu-1 Laju kematian nyamuk secara alami waktu-1 Laju kematian telur nyamuk secara alami waktu-1

Laju kelahiran manusia waktu-1

Daya dukung lingkungan pada populasi manusia

tanpa satuan Rata-rata gigitan nyamuk per hari waktu-1

� Laju penetasan telur sehat waktu-1

� Laju penetasan telur terinfeksi waktu-1

� Faktor koreksi suhu tanpa satuan

Proporsi telur nyamuk terinfeksi tanpa satuan

Laju nyamuk bertelur waktu-1

Daya dukung lingkungan pada populasi telur nyamuk

tanpa satuan

Faktor modulasi musim tanpa satuan

Faktor modulasi musim tanpa satuan

� Periode masa inkubasi pada nyamuk Waktu

Frekuensi dalam siklus musiman waktu-1

� Fase sinusoida tanpa satuan

12

Diagram KompartemenModifikasi

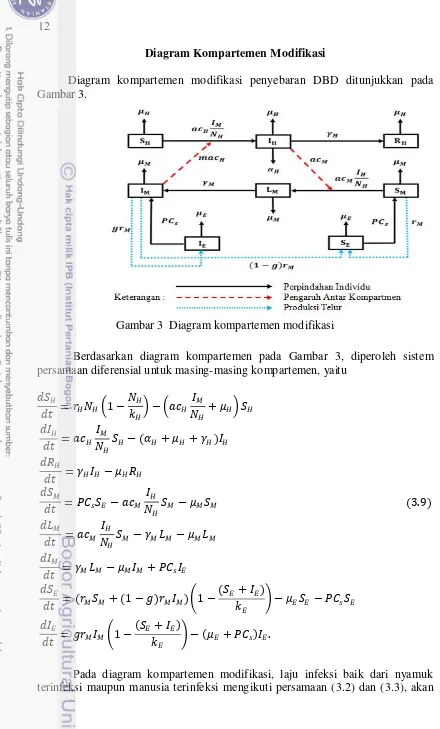
Diagram kompartemen modifikasi penyebaran DBD ditunjukkan pada Gambar 3.

Berdasarkan diagram kompartemen pada Gambar 3, diperoleh sistem persamaan diferensial untuk masing-masing kompartemen, yaitu

= 1− − +

= − + +

= −

=�� − − (3.9)

= − −

= − +��

= + 1− 1− + − − ��

= 1− + − +�� .

Pada diagram kompartemen modifikasi, laju infeksi baik dari nyamuk terinfeksi maupun manusia terinfeksi mengikuti persamaan (3.2) dan (3.3), akan

13 tetapi simbol peluang infeksi dari manusia terinfeksi dan nyamuk terinfeksi dilambangkan dengan dan .

Untuk mempermudah analisis pada persamaan (3.9), dilakukan penyederhanaan dengan membuat perbandingan masing-masing populasi terhadap total populasi, yaitu

= ; = ; = ; = ; = ; = ; = ; = ,

(3.10) Kemudian sistem (3.10) disubtitusikan ke sistem (3.9) sehingga diperoleh sistem persamaan diferensial, yaitu nyamuk. Dengan mengambil kelima persamaan tersebut (3.11), maka titik tetap, bilangan reproduksi dasar, kestabilan titik tetap dan perilaku populasi dari diagram kompartemen modifikasi dapat diamati.

4

HASIL DAN PEMBAHASAN

Titik Tetap

Persamaan yang digunakan untuk menentukan titik tetap adalah persamaan (3.11). Menentukan titik tetap sistem persamaan diferensial dari diagram kompartemen modifikasi dilakukan dengan cara,

14

Menggunakan software mathematica diperoleh titik tetap tanpa penyakit (disease-free equilibrium) dan titik tetap endemik (endemic equilibrium). Titik

Keterangan dapat dilihat pada Lampiran 1.

Selanjutnya dilakukan analisis kestabilan untuk masing-masing titik tetap. Dalam melakukan analisis kestabilan diperlukan bilangan reproduksi dasar ℛ₀ . Oleh karena itu, terlebih dahulu ditentukan bilangan reproduksi dasarnya.

Bilangan Reproduksi Dasar

Bilangan reproduksi dasar merupakan nilai harapan banyaknya populasi rentan menjadi terinfeksi selama masa infeksi. Menurut Jones (2007), bilangan reproduksi dasar dapat ditentukan dengan menggunakan persamaan yang hanya mengandung infeksi. Pendekatan yang digunakan untuk menentukan bilangan reproduksi dasar mengikuti Jones (2007), yaitu menggunakan the next generation matrix G _{yang didefinisikan}

15 diperoleh matriks ,yaitu

=

Selanjutnya ditentukan nilai eigen dari matriks . Berdasarkan analisis yang dilakukan diperoleh nilai eigen dominan dari matrik , yaitu

ℛ₀ = −

( + + ) ( + ) (4.5)

Tahap berikutnya dilakukan analisis kestabilan titik tetap tanpa penyakit dan titik tetap endemik.

Kestabilan Titik Tetap

Kestabilan Titik Tetap Tanpa Penyakit

Misalkan sistem persamaan (3.11) ditulis dalam bentuk,

1 , , , , = 1− − +

2 , , , , = − + +

3 , , , , = 1− − − + (4.6)

4 , , , , = − +��

5 , , , , = 1− − +��

Untuk menentukan kestabilan di sekitar titik tetap tanpa penyakit

16

sehingga diperoleh matriks Jacobi, berikutnya titik tetap � disubtitusikan ke dalam matriks Jacobi, hasil subtitusi diperoleh matriks

_� =

Selanjutnya ditentukan nilai eigen dengan cara,

_� − = 0 (4.9)

Berdasarkan analisis yang dilakukan diperoleh lima nilai eigen. Nilai eigen pertama − dan empat nilai eigen berikutnya merupakan akar-akar dari persamaan karakteristik

0 4+ 1 3+ 2 2 + 3 + 4 = 0, (4.11)

di mana ₀, ₁, ₂, ₃ dan ₄ dapat dilihat pada Lampiran 3.

Menurut kriteria Routh-Hurwitz untuk persamaan karakteristik berderajat 4, kondisi kestabilan harus memenuhi sifat,

17 Dengan mensubtitusikan nilai parameter yang terdapat pada model, maka diperoleh nilai ₁, ₂, ₃ dan ₄ memenuhi kriteria Routh-Hurwitz yaitu ₁ > 0, 3 > 0, 4 > 0 dan 1 2 3 > 32+ 12 4, di mana nilai ℛ0 = 0.31. Berdasarkan hasil tersebut, dapat disimpulkan sistem (3.11) stabil di sekitar titik tetap tanpa penyakit.

KestabilanTitik Tetap Endemik

Kestabilan titik tetap endemik ditentukan dengan melakukan pelinearan terhadap persamaan (4.6), sehingga diperoleh matriks Jacobi yang dapat dilihat pada Lampiran 3. Titik tetap endemik � yang diperoleh terlalu komplek, sehingga sulit untuk dilakukan analisis. Berdasarkan hal itu, maka nilai parameter yang terdapat pada model disubtitusikan ke dalam titik tetap endemik, kemudian titik tetap tersebut disubtitusikan ke dalam matriks Jacobi yang merupakan hasil pelinearan dari sistem (4.6). Dengan menggunakan software mathematica

diperoleh lima nilai eigen, yaitu empat di antaranya nilai eigen bilangan kompleks di mana bagian realnya negatif dan satu nilai eigen real negatif, dengan nilai

ℛ0 = 7.93. Menurut (Edelstein-Keshet 2005) dapat disimpulkan sistem (3.11) stabil di sekitar titik tetap endemik.

Keterangan dapat dilihat pada Lampiran 3.

Sifat kestabilan sistem (3.11) di sekitar titik tetap tanpa penyakit dan titik tetap endemik dirangkum pada Tabel 2.

Tabel 2 Sifat kestabilan titik tetap

Kondisi Titik tetap tanpa penyakit � Titik tetap endemik �

ℛ0 < 1 Stabil Tidak Stabil

ℛ0 > 1 Tidak Stabil Stabil

18

Tabel 3 Nilai parameter pada model modifikasi

Parameter Nilai Parameter Sumber

0.6 Burattini et al. (2007)

Perilaku Populasi untuk Kondisi � < 1

Pada saat simulasi untuk kondisi ℛ₀ < 1, total masing-masing populasi = 10, = 20, = 70 dan parameter lain terdapat pada Tabel 3. Sistem (3.11) mempunyai titik tetap tanpa penyakit untuk kondisi ℛ₀ < 1 yang dapat ditunjukkan dengan simulasi menggunakan software mathematica, dengan nilai

ℛ0 = 0.31. Adapun titik tetap tanpa penyakit, yaitu

� , , , , = 0.685697, 0 , 0 , 0 , 0 .

Keterangan dapat dilihat pada Lampiran 4.

Dalam melakukan simulasi digunakan nilai parameter rata-rata gigitan nyamuk adalah 0.146, Amaku et al. (2013). Adapun nilai awal yang digunakan pada saat simulasi adalah = 0.85, = 0.15, = 0.2, = 0.1 dan = 0. Perilaku populasi untuk kondisi ℛ0 < 1 ditunjukkan pada Gambar 4, 5 dan 6.

19 Populasi manusia rentan menurun dari nilai awal, kemudian stabil di sekitar = 0.685697. Populasi manusia terinfeksi menurun dari nilai awal, kemudian stabil di sekitar = 0, sedangkan populsi manusia sembuh meningkat dari nilai awal, kemudian stabil di sekitar = 1− − = 0.314303.

Gambar 5 Perilaku populasi nyamuk ketika ℛ₀ < 1

Populasi nyamuk laten menurun dari nilai awal, kemudian stabil di sekitar = 0, populasi nyamuk terinfeksi menurun dari nilai awal, kemudian stabil di sekitar = 0, sedangkan populasi nyamuk rentan meningkat dari nilai awal, kemudian stabil di sekitar = 1− − = 1.

Gambar 6 Perilaku populasi telur nyamuk ketika ℛ₀ < 1

Populasi telur nyamuk terinfeksi meningkat dari nilai awal, kemudian menurun dan akhirnya stabil di sekitar = 0, sedangkan populasi telur nyamuk sehat menurun dari nilai awal, kemudian meningkat dan akhirnya stabil di sekitar = 1− = 1.

Berdasarkan simulasi yang dilakukan dapat disimpulkan bahwa tiap populasi menuju titik tetap tanpa penyakit atau dengan kata lain populasi manusia, nyamuk dan telur nyamuk stabil di sekitar titik tetap 0.685697, 0 , 0 , 0 , 0 .

20

Perilaku Populasi untuk Kondisi � > 1

Sistem (3.11) mempunyai titik tetap endemik untuk kondisi ℛ₀ > 1 yang dapat ditunjukkan dengan simulasi menggunakan software mathematica. Titik tetap diperoleh menggunakan nilai parameter yang terdapat pada Tabel 3 dengan nilai ℛ₀ = 7.93 dan titik tetap endemik, yaitu

� ∗_, ∗_, ∗ _, ∗_, ∗ _{= 0.006656, 0.000165 , 0.000901 , 0.000804 , 0.002250 .}

Keterangan dapat dilihat pada Lampiran 4.

Nilai parameter rata-rata gigitan nyamuk yang digunakan adalah 3.7, Massad et al. (2011). Berdasarkan simulasi yang dilakukan dapat diamati perilaku masing-masing populasi ketika ℛ₀ > 1, seperti pada Gambar 7, 8 dan 9.

Gambar 7 Perilaku populasi manusia ketika ℛ₀ > 1

Populasi manusia rentan menurun dari nilai awal, kemudian stabil di sekitar = 0.006656, populasi manusia terinfeksi meningkat dari nilai awal, kemudian menurun dan akhirnya stabil di sekitar = 0.000165, sedangkan populasi manusia sembuh meningkat dari nilai awal, kemudian stabil di sekitar = 1− − = 0.993179.

21 Populasi nyamuk laten meningkat dari nilai awal, kemudian menurun dan akhirnya stabil di sekitar = 0.000901, populasi nyamuk terinfeksi meningkat dari nilai awal, kemudian menurun dan akhirnya stabil di sekitar

= 0.000804, sedangkan populasi nyamuk rentan menurun dari nilai awal, kemudian meningkat dan akhirnya stabil di sekitar = 1− − = dapat disimpulkan bahwa tiap populasi stabil di sekitar titik tetap endemik, yaitu

0.006656, 0.000165 , 0.000901 , 0.000804 , 0.002250

Tahap selanjutnya dilakukan simulasi pengaruh laju kematian nyamuk terhadap penyebaran penyakit dalam populasi. Pada simulasi ini, parameter diambil pada interval [0.163, 0.563] dengan langkah 0.1 yang masih memenuhi kondisi ℛ₀ < 1.

Simulasi Laju Kematian Nyamuk

Simulasi ini diperlukan untuk melihat pengaruh laju kematian nyamuk terhadap penyebaran penyakit dalam populasi. Selain itu, akan ditunjukkan bahwa peningkatan laju kematian nyamuk dapat menurunkan nilai bilangan reproduksi dasar (ℛ₀) yang didefinisikan pada persamaan (4.5). Terdapat 4 nilai yang diambil pada interval [0.263 , 0.563] dengan langkah 0.1. Nilai parameter rata-rata gigitan nyamuk yang digunakan 0.146, sedangkan parameter lain tetap. Nilai

22

Tabel 4 Nilai ℛ₀ dengan parameter ditingkatkan dan parameter lain tetap Nilai ℛ₀

0.146 0.263 0.31

0.146 0.363 0.23

0.146 0.463 0.19

0.146 0.563 0.16

Berdasarkan Tabel 4 dapat diperhatikan bahwa nilai ℛ₀ masih kurang dari 1. Meningkatnya parameter menyebabkan ℛ₀ turun, sehingga membantu menekan laju penyebaran penyakit.

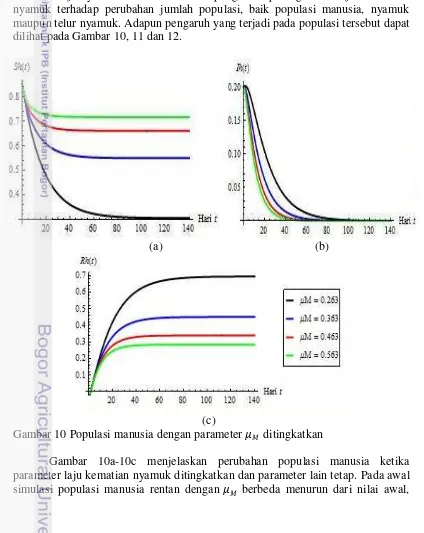
Selanjutnya dilakukan simulasi pengaruh peningkatan laju kematian nyamuk terhadap perubahan jumlah populasi, baik populasi manusia, nyamuk maupun telur nyamuk. Adapun pengaruh yang terjadi pada populasi tersebut dapat dilihat pada Gambar 10, 11 dan 12.

(a) (b)

(c)

Gambar 10 Populasi manusia dengan parameter ditingkatkan

23 akan tetapi pada akhir simulasi populasi tersebut dengan terbesar jumlahnya lebih banyak. Populasi manusia terinfeksi pada awal simulasi dengan berbeda menurun dari nilai awal, akan tetapi pada akhir simulasi populasi tersebut jumlahnya sama. Untuk populasi manusia sembuh, pada awal simulasi populasi tersebut dengan berbeda meningkat dari nilai awal, akan tetapi pada akhir simulasi populasi tersebut dengan terbesar jumlahnya lebih sedikit.

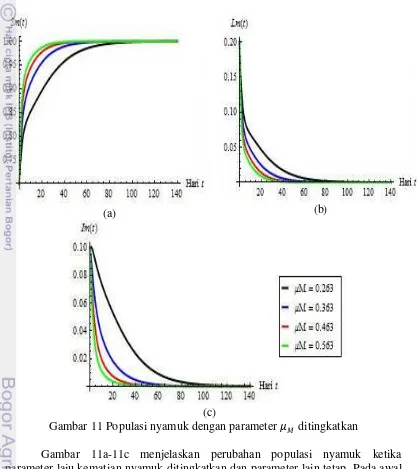
Pengaruh yang terjadi pada populasi nyamuk jika laju kematian nyamuk ditingkatkan dapat dilihat pada Gambar 11.

(a) (b)

(c)

Gambar 11 Populasi nyamuk dengan parameter ditingkatkan

24

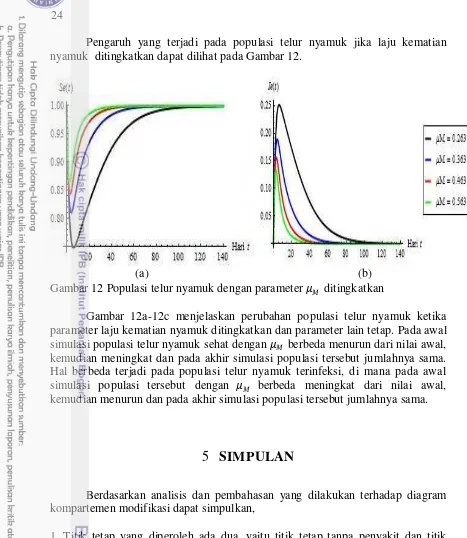
Pengaruh yang terjadi pada populasi telur nyamuk jika laju kematian nyamuk ditingkatkan dapat dilihat pada Gambar 12.

(a) (b)

Gambar 12 Populasi telur nyamuk dengan parameter ditingkatkan

Gambar 12a-12c menjelaskan perubahan populasi telur nyamuk ketika parameter laju kematian nyamuk ditingkatkan dan parameter lain tetap. Pada awal simulasi populasi telur nyamuk sehat dengan berbeda menurun dari nilai awal, kemudian meningkat dan pada akhir simulasi populasi tersebut jumlahnya sama. Hal berbeda terjadi pada populasi telur nyamuk terinfeksi, di mana pada awal simulasi populasi tersebut dengan berbeda meningkat dari nilai awal, kemudian menurun dan pada akhir simulasi populasi tersebut jumlahnya sama.

5

SIMPULAN

Berdasarkan analisis dan pembahasan yang dilakukan terhadap diagram kompartemen modifikasi dapat simpulkan,

1. Titik tetap yang diperoleh ada dua, yaitu titik tetap tanpa penyakit dan titik tetap endemik.

2. Titik tetap tanpa penyakit stabil untuk kondisi ℛ₀ < 1, sedangkan titik tetap endemik stabil untuk kondisi ℛ₀ > 1.

3. Hasil simulasi menunjukkan bahwa meningkatnya laju kematian nyamuk menyebabkan ℛ₀ turun, sehingga membantu menekan laju penyebaran penyakit.

4. Hasil simulasi juga menunjukkan bahwa meningkatnya laju kematian nyamuk

memberi pengaruh terhadap populasi manusia, nyamuk dan telur nyamuk, yaitu

25 simulasi populasi tersebut berkurang, akan tetapi pada akhir simulasi jumlahnya sama.

b. Pada awal simulasi populasi nyamuk rentan meningkat, akan tetapi pada akhir simulasi populasi tersebut jumlahnya sama. Untuk populasi nyamuk laten dan nyamuk terinfeksi, pada awal simulasi berkurang, akan tetapi pada akhir simulasi jumlah masing-masing populasi tersebut sama.

c. Populasi telur nyamuk sehat meningkat pada awal simulasi, akan tetapi pada akhir simulasi jumlah populasi tersebut sama. Untuk populasi telur nyamuk terinfeksi, pada awal simulasi berkurang, akan tetapi pada akhir simulasi jumlahnya sama.

DAFTAR PUSTAKA

Amaku M, Coutinho FAB, Raimundo SM, Lopez LF, Burattini MN, Massad E. 2013. A comparative analysis of the relative efficacy of vector-control strategies against dengue fever. Bull Math Biol. 1-21. doi: 10.1007/s11538-014-9939-5.

Burattini MN, Chen M, Chow A, Coutinho FAB, Goh KT, Lopez LF, MA S, Massad E. 2007. Modelling the control strategies against dengue in Singapore.Epidemiol Infect. doi: 10.1017/S0950268807008667.

Edelstein-Keshet L. 2005. Mathematical Models in Biology. New York: Random House.

Jones JH. 2007. Note on ℛ₀. California: Department of Anthropological Sciences Stanford University.

Jumadi. 2007. Model matematika penyebaran penyakit demam berdarah dengue. Tesis S2. Program Studi Matematika Terapan: Institut Pertanian Bogor. Malavige GN, Fernando S, Fernando DJ, Seneviratne SL. 2004. Dengue viral

infections. Postgrad Med Journal. 80: 588-601.

Massad E, Coutinho FAB, Lopez LF, da Silva DR. 2011. Modeling the impact of global warming on vector-borne infections. ScienceDirect. 8:169-199. doi: 10.1016/j.plrev.2011.01.001.

Ngwa GA, Shu WS. 2000. A mathematical model for endemic malaria with variable human and mosquito populations. Math. Comput. Modelling. 32:747-763. PII: SO8957177(00)69169-2.

Solihin G. 2004. Ekologi vektor demam berdarah dengue. Warta Kesehatan TNI-AL. 14(1).31-38.

Tu PNV. 1994. Dynamical System: An Introduction with Applications in Economics and Biology. New York: Springer-Verlag.

26

28

31 Lampiran 3 Kestabilan titik tetap

34

36

39 Lampiran 5 Simulasi laju kematian nyamuk dan perhitungan ℛ0

40

41

RIWAYAT HIDUP