Penyelesaian Masalah Desain Network Takberkapasitas Dengan Dekomposisi Benders dan Metode Branch-Andbound

PENYELESAIAN MASALAH DESAIN NETWORK TAKBERKAPASITAS

DENGAN DEKOMPOSISI BENDERS DAN METODE

BRANCH-AND-BOUND

PUTI PARAMITA ROSLIYANTI

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

PENYELESAIAN MASALAH DESAIN NETWORK TAKBERKAPASITAS

DENGAN DEKOMPOSISI BENDERS DAN METODE

BRANCH-AND-BOUND

PUTI PARAMITA ROSLIYANTI

G54103008

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

ABSTRACT

PUTI PARAMITA ROSLIYANTI. Solving the Uncapacitated Network Design Problem by Benders Decomposition and Branch-and-Bound Method. Under the direction of FARIDA HANUM and AGAH DRAJAT GARNADI.

Design network problem is a multicommodity minimum cost network flow problem. Its applications appear in many fields, include planning in telecommunication network, transportation network, water resource, computer networking, vehicle fleet, and product distribution. This problem is generally divided into capacitated and uncapacitated network design problems.

The main purpose of uncapacitated network design problem is to design or improve a network configuration by choosing certain arcs to be included in the network, in order to reach minimum value of total cost, with assumption that the number of commodity flow which can be sended along those arcs is unrestricted (uncapacitated). There are several methods have been developed to find a solution of this model, two of them are Benders decomposition and branch-and-bound. The basic concept of Benders decomposition is to solve a primal linear programming (LP) problem by considering one of its variable vectors has a fixed value, so that for any iteration of this algorithm, the problems that contain one of these variable vectors can be solved. The basic principle of branch-and-bound method is to split a feasible region of LP-relaxation by constructing subproblems.

ABSTRAK

PUTI PARAMITA ROSLIYANTI. Penyelesaian Masalah Desain Network Takberkapasitas dengan Dekomposisi Benders dan Metode Branch-and-Bound. Dibimbing oleh FARIDA HANUM dan AGAH DRAJAT GARNADI.

Masalah desain network merupakan suatu masalah aliran network (network flow) biaya minimum untuk lebih dari satu komoditas. Aplikasinya banyak muncul dalam perencanaan jaringan telekomunikasi, transportasi, sumberdaya air, komunikasi komputer (computer networking), maupun perencanaan armada kendaraan dan distribusi barang. Secara garis besar, masalah ini dapat dikelompokkan ke dalam dua jenis, yakni masalah desain network berkapasitas dan takberkapasitas.

Permasalahan pokok dari masalah desain network takberkapasitas adalah mendesain atau menyempurnakan suatu konfigurasi network dengan memilih sisi-sisi berarah tertentu untuk berada di dalamnya sedemikian sehingga biaya totalnya menjadi minimum, dengan asumsi bahwa banyaknya flow komoditas yang dapat melewati sisi-sisi berarah tersebut tidak dibatasi (takberkapasitas). Ada beberapa metode yang dikembangkan untuk mencari solusi model masalah ini, dua di antaranya adalah dekomposisi Benders dan metode branch-and-bound. Konsep dasar dekomposisi Benders adalah menyelesaikan masalah pemrograman linear primal dengan menganggap salah satu vektor variabelnya bernilai tetap sedemikian sehingga untuk sembarang iterasi dari algoritme ini nantinya masalah-masalah yang memuat salah satu vektor variabel, namun tidak seluruhnya, dapat diselesaikan. Prinsip dasar metode branch-and-bound adalah memecah daerah fisibel suatu masalah pemrograman linear relaksasi dengan membuat subproblem-subproblem.

PENYELESAIAN MASALAH DESAIN NETWORK TAKBERKAPASITAS

DENGAN DEKOMPOSISI BENDERS DAN METODE

BRANCH-AND-BOUND

Skripsi

sebagai salah satu syarat untuk memperoleh gelar

Sarjana Sains pada

Departemen Matematika

PUTI PARAMITA ROSLIYANTI

G54103008

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

Judul

: Penyelesaian Masalah Desain

Network

Takberkapasitas dengan

Dekomposisi Benders dan Metode

Branch-and-Bound

Nama : Puti Paramita Rosliyanti

NIM :

G54103008

Menyetujui,

Pembimbing I

Dra. Farida Hanum, M.Si.

NIP 131 956 709

Pembimbing II

Drs. Agah D. Garnadi, Grad. Dipl. Sc.

NIP 131 804 648

Mengetahui,

Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Prof. Dr. Ir. Yonny Koesmaryono, MS.

NIP. 131 473 999

KATA PENGANTAR

Puji dan syukur penulis panjatkan ke hadirat Allah SWT atas segala nikmat, karunia, izin, dan pertolongan-Nya sehingga penulisan skripsi ini berhasil diselesaikan. Tema yang dipilih adalah Riset Operasi dengan judul Penyelesaian Masalah Desain Network Takberkapasitas dengan Dekomposisi Benders dan Metode Branch-and-Bound. Skripsi ini merupakan syarat untuk menyelesaikan studi pada Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor.

Terima kasih penulis ucapkan kepada :

1. Ibu Dra. Farida Hanum M.Si dan Bapak Drs. Agah D. Garnadi, Grad. Dipl. Sc. selaku dosen pembimbing, atas segala kesabaran dan masukannya selama membimbing penulis; tak lupa kepada Bapak Dr. Toni Bakhtiar selaku penguji;

2. ibu kandungku tercinta, (alm.) Puti Rosmeiliza B. S., yang telah melahirkan, mendidik, dan membesarkan penulis hingga usia 17 tahun; bapak dan bundaku tercinta, Sumaryanto dan Anggraini Sukmawati, atas segala dukungan, motivasi, pembelajaran, masukan, dan segala kasih sayang yang diberikan kepada penulis; juga adik-adikku tersayang, Arif dan Ajeng, atas segala kasih sayang dan keceriaannya;

3. keluarga besar Zagloel Dt. Moeroen, terutama Mama Ade dan Ibu Riri; keluarga besar (alm.) Atmosoekarto, terutama Bulik Nuning dan Bulik Kris; keluarga besar H. Munawar, terutama eyang putri;

4. sahabat-sahabatku tersayang, Nay dan Dara, atas segala tawa dan tangis, manis dan pahit, suka dan duka dalam empat tahun persahabatan kita; sahabatku-sahabatku, Baidhuri dan Ilma, atas doa-doa dan dukungannya;

5. teman-teman mahasiswa matematika angkatan 40: Septi, Ifni, Tiwi, Indah, Icha, Vina, Ami, Achie, Mika, Uli, Mayang, Metha, Elis, Marlin, Sri, Ulfa, Nchie, Yuda, Dwi, Nisa, Walidah, Agatha, Herni, Rama, Yudi, Abdillah, Ari, Jayu, Prima, Mufti, Azis, Berri, Abay, Dimas, Kafi, Rusli, Sawa, Aam, Lili, Putra, Yusuf, Manto, Ali, Demi, Anton, Febri, atas segenap dukungan, suka-duka dan keceriaan selama penulis menempuh studi di Departemen Matematika IPB;

6. kakak-kakak mahasiswa matematika angkatan 39, terutama kak Arie Wijayanto, atas segala bantuannya; adik-adik mahasiswa matematika angkatan 41, terutama Dian dan Diah yang telah bersedia menjadi pembahas; adik-adik mahasiswa matematika angkatan 42; seluruh pengajar, pegawai, dan staf Departemen Matematika IPB;

7. keluarga besar BEM FMIPA IPB angkatan 2005-2006: kakakku Fajri Ma’rifatullah (atas segala doa, dukungan, motivasi, dan masukan bagi penulis dalam berbagai hal), Uli, Ari, kak Riana Safaat, Cheri, Fariz, Rina, Ajeng, Tresna, Jayadin, Marwan, Pras, Tiwi, Agita, Achie, Maul, Dyna, Lewe, Rizal, Awit, Asih, Great, Haristinah, Astrid, Yuyun, Arul, Ihsan, Putri, Halida, Haris, Lia, Isran, Ayu, Nenny, Agung Seno, Deny Kurniawan, Bayu, Chandra, Lutfi, Utami Rahayu, dan (alm.) Rachma Ruly Maharatri, atas segenap dukungan, doa, dorongan semangat, dan warna-warni dalam setahun kebersamaan kita; 8. keluarga besar pengurus GUMATIKA IPB periode 2004-2005; pengurus BEM FMIPA

2004-2005, terutama Mbak Henny Yulanda, yang telah memberikan banyak inspirasi; pengurus BEM FMIPA IPB 2006-2007;

9. staf dan pengajar Lembaga Pendidikan Primagama Cimanggu dan Sukasari, terutama Mas Mulyadi, Mas Wildan, dan Mbak Ari;

10. teman-teman penghuni Lorong 10 Gedung A2 Asrama TPB IPB 2003-2004, terutama Silvi, Rahma, Lita, Puji, Pujay, Tila, Natalia; Fajar Faizal dan Dwi Budi H, atas doa dan bantuannya; Aried Ardhina dan Bian Adiantoro, atas dukungan dan dorongan semangat selama penyusunan skripsi ini; Novan A. Pratama dan kru Centium, atas bantuannya dalam hal print dan perbanyakan draft skripsi; juga pihak-pihak lain yang telah membantu penyusunan skripsi ini, yang tidak dapat disebutkan satu persatu.

Penulis menyadari bahwa dalam tulisan ini masih terdapat kekurangan dan jauh dari kesempurnaan, oleh karena itu dibutuhkan kritik dan saran yang membangun dari pembaca. Semoga tulisan ini dapat bermanfaat.

Bogor, Oktober 2007

RIWAYAT HIDUP

Penulis dilahirkan di Bandung pada tanggal 20 Oktober 1985 dari pasangan Ir. Sumaryanto, MS dan (alm) Ir. Puti Rosmeiliza Budi Savitri. Penulis merupakan anak pertama dari tiga bersaudara.

Pada tahun 2003 penulis lulus dari SMU Negeri 1 Bogor dan pada tahun yang sama lulus seleksi masuk IPB melalui jalur Undangan Seleksi Masuk IPB. Penulis memilih Program Studi Matematika, Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.

vii

DAFTAR ISI

Halaman

DAFTAR TABEL ... viii

DAFTAR GAMBAR ... viii

DAFTAR LAMPIRAN ... viii

1 PENDAHULUAN Latar Belakang ... 1

Tujuan ... 2

2 LANDASAN TEORI Fungsi Linear dan Pertidaksamaan Linear ... 2

Pemrograman Linear ... 2

Dualitas Pemrograman Linear ... 4

Integer Programming ... 5

Pemrograman Linear Relaksasi ... 6

Graf... 6

Network Flow... 8

Metode Branch-and-Bound ... 9

3 DEKOMPOSISI BENDERS... 12

4 DESKRIPSI DAN FORMULASI MASALAH DESAIN NETWORK TAKBERKAPASITAS ... 14

5 PENYELESAIAN MASALAH DESAIN NETWORK TAKBERKAPASITAS DENGAN DEKOMPOSISI BENDERS... 15

6 PENYELESAIAN MASALAH DESAIN NETWORK TAKBERKAPASITAS DENGAN METODE BRANCH-AND-BOUND ... 18

7 SIMPULAN DAN SARAN Simpulan ... 20

Saran ... 20

DAFTAR PUSTAKA ... 21

viii

DAFTAR TABEL

Halaman 1 Hubungan antara variabel-variabel dan kendala-kendala pada masalah

primal dan masalah dual ... 5

2 Sisi-sisi berarah yang digunakan dalam network ... 19

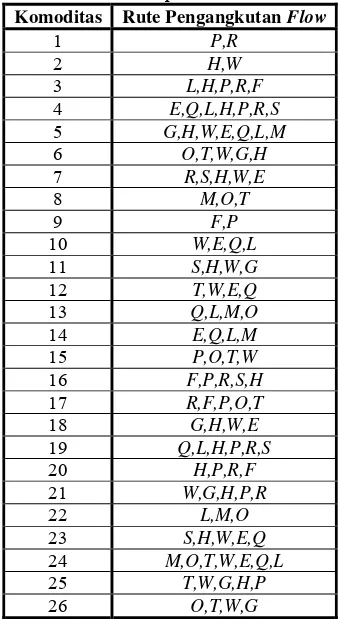
3 Rute pengangkutan flow optimal untuk setiap komoditas ... 19

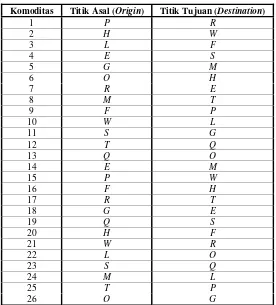
4 Data titik asal dan titik tujuan untuk setiap komoditas ... 30

5 Biaya tetap (fij) untuk setiap sisi berarah ( , )i j ... 31

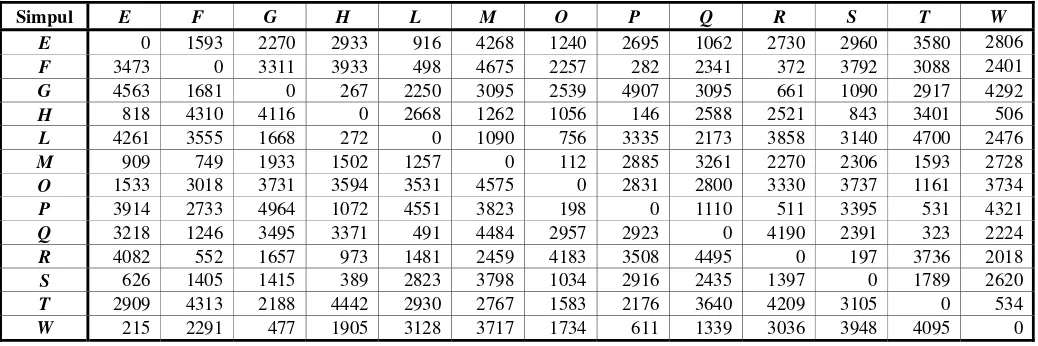
6 Biaya pengangkutan ( k) ij c untuk setiap komoditas k pada sisi berarah ( , )i j ... 32

DAFTAR GAMBAR

Halaman 1 Ilustrasi himpunan konveks dan yang bukan himpunan konveks ... 4

2 Graf G=( , )V E ... 6

3 Graf 'G =( , )V A ... 6

4 Sisi berarah menjauhi atau mendekati, suksesor, dan predesesor ... 7

5 Graf berbobot 'G =( , )V A ... 7

6 Network, source, dan sink... 7

7 Flow dan kapasitas sisi berarah ... 8

8 Daerah fisibel untuk PL-relaksasi dari IP (2.10) ... 10

9 Daerah fisibel untuk subproblem 2 dan subproblem 3 dari IP (2.10) ... 10

10 Seluruh pencabangan pada metode branch-and-bound untuk menyelesaikan IP (2.10) ... 11

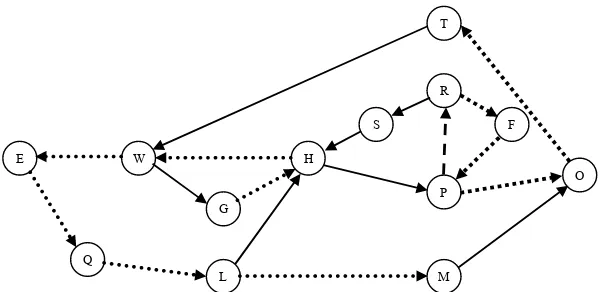
11 Ilustrasi network optimal yang dihasilkan berdasarkan Tabel 2 dan Tabel 3 ... 20

DAFTAR LAMPIRAN

Halaman 1 Bukti-Bukti Teorema dan Akibat pada Titik Ekstrem dan Dualitas Pemrograman Linear ... 23

2 Syntax Program LINDO 6.1 untuk Menyelesaikan Masalah Pemrograman Linear dengan Metode Branch-and-Bound Beserta Hasil yang Diperoleh ... 25

3 Syntax Program LINDO 6.1 untuk Menyelesaikan Masalah Pemrograman Linear dengan Metode Dekomposisi Benders Beserta Hasil yang Diperoleh ... 27

4 Pembangkitan Data-data Biaya Pengangkutan dan Biaya Tetap dengan Mathematica 5.2 Beserta Syntax Inputnya ... 29

5 Data-data Hipotetik untuk Implementasi Penyelesaian Masalah Desain Network Takberkapasitas dengan Metode Branch-and-Bound ... 30

6 Syntax Program LINGO 8.0 untuk Masalah Desain Network Takberkapasitas ... 36

PENYELESAIAN MASALAH DESAIN NETWORK TAKBERKAPASITAS

DENGAN DEKOMPOSISI BENDERS DAN METODE

BRANCH-AND-BOUND

PUTI PARAMITA ROSLIYANTI

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

PENYELESAIAN MASALAH DESAIN NETWORK TAKBERKAPASITAS

DENGAN DEKOMPOSISI BENDERS DAN METODE

BRANCH-AND-BOUND

PUTI PARAMITA ROSLIYANTI

G54103008

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

ABSTRACT

PUTI PARAMITA ROSLIYANTI. Solving the Uncapacitated Network Design Problem by Benders Decomposition and Branch-and-Bound Method. Under the direction of FARIDA HANUM and AGAH DRAJAT GARNADI.

Design network problem is a multicommodity minimum cost network flow problem. Its applications appear in many fields, include planning in telecommunication network, transportation network, water resource, computer networking, vehicle fleet, and product distribution. This problem is generally divided into capacitated and uncapacitated network design problems.

The main purpose of uncapacitated network design problem is to design or improve a network configuration by choosing certain arcs to be included in the network, in order to reach minimum value of total cost, with assumption that the number of commodity flow which can be sended along those arcs is unrestricted (uncapacitated). There are several methods have been developed to find a solution of this model, two of them are Benders decomposition and branch-and-bound. The basic concept of Benders decomposition is to solve a primal linear programming (LP) problem by considering one of its variable vectors has a fixed value, so that for any iteration of this algorithm, the problems that contain one of these variable vectors can be solved. The basic principle of branch-and-bound method is to split a feasible region of LP-relaxation by constructing subproblems.

ABSTRAK

PUTI PARAMITA ROSLIYANTI. Penyelesaian Masalah Desain Network Takberkapasitas dengan Dekomposisi Benders dan Metode Branch-and-Bound. Dibimbing oleh FARIDA HANUM dan AGAH DRAJAT GARNADI.

Masalah desain network merupakan suatu masalah aliran network (network flow) biaya minimum untuk lebih dari satu komoditas. Aplikasinya banyak muncul dalam perencanaan jaringan telekomunikasi, transportasi, sumberdaya air, komunikasi komputer (computer networking), maupun perencanaan armada kendaraan dan distribusi barang. Secara garis besar, masalah ini dapat dikelompokkan ke dalam dua jenis, yakni masalah desain network berkapasitas dan takberkapasitas.

Permasalahan pokok dari masalah desain network takberkapasitas adalah mendesain atau menyempurnakan suatu konfigurasi network dengan memilih sisi-sisi berarah tertentu untuk berada di dalamnya sedemikian sehingga biaya totalnya menjadi minimum, dengan asumsi bahwa banyaknya flow komoditas yang dapat melewati sisi-sisi berarah tersebut tidak dibatasi (takberkapasitas). Ada beberapa metode yang dikembangkan untuk mencari solusi model masalah ini, dua di antaranya adalah dekomposisi Benders dan metode branch-and-bound. Konsep dasar dekomposisi Benders adalah menyelesaikan masalah pemrograman linear primal dengan menganggap salah satu vektor variabelnya bernilai tetap sedemikian sehingga untuk sembarang iterasi dari algoritme ini nantinya masalah-masalah yang memuat salah satu vektor variabel, namun tidak seluruhnya, dapat diselesaikan. Prinsip dasar metode branch-and-bound adalah memecah daerah fisibel suatu masalah pemrograman linear relaksasi dengan membuat subproblem-subproblem.

PENYELESAIAN MASALAH DESAIN NETWORK TAKBERKAPASITAS

DENGAN DEKOMPOSISI BENDERS DAN METODE

BRANCH-AND-BOUND

Skripsi

sebagai salah satu syarat untuk memperoleh gelar

Sarjana Sains pada

Departemen Matematika

PUTI PARAMITA ROSLIYANTI

G54103008

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

Judul

: Penyelesaian Masalah Desain

Network

Takberkapasitas dengan

Dekomposisi Benders dan Metode

Branch-and-Bound

Nama : Puti Paramita Rosliyanti

NIM :

G54103008

Menyetujui,

Pembimbing I

Dra. Farida Hanum, M.Si.

NIP 131 956 709

Pembimbing II

Drs. Agah D. Garnadi, Grad. Dipl. Sc.

NIP 131 804 648

Mengetahui,

Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Prof. Dr. Ir. Yonny Koesmaryono, MS.

NIP. 131 473 999

KATA PENGANTAR

Puji dan syukur penulis panjatkan ke hadirat Allah SWT atas segala nikmat, karunia, izin, dan pertolongan-Nya sehingga penulisan skripsi ini berhasil diselesaikan. Tema yang dipilih adalah Riset Operasi dengan judul Penyelesaian Masalah Desain Network Takberkapasitas dengan Dekomposisi Benders dan Metode Branch-and-Bound. Skripsi ini merupakan syarat untuk menyelesaikan studi pada Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor.

Terima kasih penulis ucapkan kepada :

1. Ibu Dra. Farida Hanum M.Si dan Bapak Drs. Agah D. Garnadi, Grad. Dipl. Sc. selaku dosen pembimbing, atas segala kesabaran dan masukannya selama membimbing penulis; tak lupa kepada Bapak Dr. Toni Bakhtiar selaku penguji;

2. ibu kandungku tercinta, (alm.) Puti Rosmeiliza B. S., yang telah melahirkan, mendidik, dan membesarkan penulis hingga usia 17 tahun; bapak dan bundaku tercinta, Sumaryanto dan Anggraini Sukmawati, atas segala dukungan, motivasi, pembelajaran, masukan, dan segala kasih sayang yang diberikan kepada penulis; juga adik-adikku tersayang, Arif dan Ajeng, atas segala kasih sayang dan keceriaannya;

3. keluarga besar Zagloel Dt. Moeroen, terutama Mama Ade dan Ibu Riri; keluarga besar (alm.) Atmosoekarto, terutama Bulik Nuning dan Bulik Kris; keluarga besar H. Munawar, terutama eyang putri;

4. sahabat-sahabatku tersayang, Nay dan Dara, atas segala tawa dan tangis, manis dan pahit, suka dan duka dalam empat tahun persahabatan kita; sahabatku-sahabatku, Baidhuri dan Ilma, atas doa-doa dan dukungannya;

5. teman-teman mahasiswa matematika angkatan 40: Septi, Ifni, Tiwi, Indah, Icha, Vina, Ami, Achie, Mika, Uli, Mayang, Metha, Elis, Marlin, Sri, Ulfa, Nchie, Yuda, Dwi, Nisa, Walidah, Agatha, Herni, Rama, Yudi, Abdillah, Ari, Jayu, Prima, Mufti, Azis, Berri, Abay, Dimas, Kafi, Rusli, Sawa, Aam, Lili, Putra, Yusuf, Manto, Ali, Demi, Anton, Febri, atas segenap dukungan, suka-duka dan keceriaan selama penulis menempuh studi di Departemen Matematika IPB;

6. kakak-kakak mahasiswa matematika angkatan 39, terutama kak Arie Wijayanto, atas segala bantuannya; adik-adik mahasiswa matematika angkatan 41, terutama Dian dan Diah yang telah bersedia menjadi pembahas; adik-adik mahasiswa matematika angkatan 42; seluruh pengajar, pegawai, dan staf Departemen Matematika IPB;

7. keluarga besar BEM FMIPA IPB angkatan 2005-2006: kakakku Fajri Ma’rifatullah (atas segala doa, dukungan, motivasi, dan masukan bagi penulis dalam berbagai hal), Uli, Ari, kak Riana Safaat, Cheri, Fariz, Rina, Ajeng, Tresna, Jayadin, Marwan, Pras, Tiwi, Agita, Achie, Maul, Dyna, Lewe, Rizal, Awit, Asih, Great, Haristinah, Astrid, Yuyun, Arul, Ihsan, Putri, Halida, Haris, Lia, Isran, Ayu, Nenny, Agung Seno, Deny Kurniawan, Bayu, Chandra, Lutfi, Utami Rahayu, dan (alm.) Rachma Ruly Maharatri, atas segenap dukungan, doa, dorongan semangat, dan warna-warni dalam setahun kebersamaan kita; 8. keluarga besar pengurus GUMATIKA IPB periode 2004-2005; pengurus BEM FMIPA

2004-2005, terutama Mbak Henny Yulanda, yang telah memberikan banyak inspirasi; pengurus BEM FMIPA IPB 2006-2007;

9. staf dan pengajar Lembaga Pendidikan Primagama Cimanggu dan Sukasari, terutama Mas Mulyadi, Mas Wildan, dan Mbak Ari;

10. teman-teman penghuni Lorong 10 Gedung A2 Asrama TPB IPB 2003-2004, terutama Silvi, Rahma, Lita, Puji, Pujay, Tila, Natalia; Fajar Faizal dan Dwi Budi H, atas doa dan bantuannya; Aried Ardhina dan Bian Adiantoro, atas dukungan dan dorongan semangat selama penyusunan skripsi ini; Novan A. Pratama dan kru Centium, atas bantuannya dalam hal print dan perbanyakan draft skripsi; juga pihak-pihak lain yang telah membantu penyusunan skripsi ini, yang tidak dapat disebutkan satu persatu.

Penulis menyadari bahwa dalam tulisan ini masih terdapat kekurangan dan jauh dari kesempurnaan, oleh karena itu dibutuhkan kritik dan saran yang membangun dari pembaca. Semoga tulisan ini dapat bermanfaat.

Bogor, Oktober 2007

RIWAYAT HIDUP

Penulis dilahirkan di Bandung pada tanggal 20 Oktober 1985 dari pasangan Ir. Sumaryanto, MS dan (alm) Ir. Puti Rosmeiliza Budi Savitri. Penulis merupakan anak pertama dari tiga bersaudara.

Pada tahun 2003 penulis lulus dari SMU Negeri 1 Bogor dan pada tahun yang sama lulus seleksi masuk IPB melalui jalur Undangan Seleksi Masuk IPB. Penulis memilih Program Studi Matematika, Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.

vii

DAFTAR ISI

Halaman

DAFTAR TABEL ... viii

DAFTAR GAMBAR ... viii

DAFTAR LAMPIRAN ... viii

1 PENDAHULUAN Latar Belakang ... 1

Tujuan ... 2

2 LANDASAN TEORI Fungsi Linear dan Pertidaksamaan Linear ... 2

Pemrograman Linear ... 2

Dualitas Pemrograman Linear ... 4

Integer Programming ... 5

Pemrograman Linear Relaksasi ... 6

Graf... 6

Network Flow... 8

Metode Branch-and-Bound ... 9

3 DEKOMPOSISI BENDERS... 12

4 DESKRIPSI DAN FORMULASI MASALAH DESAIN NETWORK TAKBERKAPASITAS ... 14

5 PENYELESAIAN MASALAH DESAIN NETWORK TAKBERKAPASITAS DENGAN DEKOMPOSISI BENDERS... 15

6 PENYELESAIAN MASALAH DESAIN NETWORK TAKBERKAPASITAS DENGAN METODE BRANCH-AND-BOUND ... 18

7 SIMPULAN DAN SARAN Simpulan ... 20

Saran ... 20

DAFTAR PUSTAKA ... 21

viii

DAFTAR TABEL

Halaman 1 Hubungan antara variabel-variabel dan kendala-kendala pada masalah

primal dan masalah dual ... 5

2 Sisi-sisi berarah yang digunakan dalam network ... 19

3 Rute pengangkutan flow optimal untuk setiap komoditas ... 19

4 Data titik asal dan titik tujuan untuk setiap komoditas ... 30

5 Biaya tetap (fij) untuk setiap sisi berarah ( , )i j ... 31

6 Biaya pengangkutan ( k) ij c untuk setiap komoditas k pada sisi berarah ( , )i j ... 32

DAFTAR GAMBAR

Halaman 1 Ilustrasi himpunan konveks dan yang bukan himpunan konveks ... 4

2 Graf G=( , )V E ... 6

3 Graf 'G =( , )V A ... 6

4 Sisi berarah menjauhi atau mendekati, suksesor, dan predesesor ... 7

5 Graf berbobot 'G =( , )V A ... 7

6 Network, source, dan sink... 7

7 Flow dan kapasitas sisi berarah ... 8

8 Daerah fisibel untuk PL-relaksasi dari IP (2.10) ... 10

9 Daerah fisibel untuk subproblem 2 dan subproblem 3 dari IP (2.10) ... 10

10 Seluruh pencabangan pada metode branch-and-bound untuk menyelesaikan IP (2.10) ... 11

11 Ilustrasi network optimal yang dihasilkan berdasarkan Tabel 2 dan Tabel 3 ... 20

DAFTAR LAMPIRAN

Halaman 1 Bukti-Bukti Teorema dan Akibat pada Titik Ekstrem dan Dualitas Pemrograman Linear ... 23

2 Syntax Program LINDO 6.1 untuk Menyelesaikan Masalah Pemrograman Linear dengan Metode Branch-and-Bound Beserta Hasil yang Diperoleh ... 25

3 Syntax Program LINDO 6.1 untuk Menyelesaikan Masalah Pemrograman Linear dengan Metode Dekomposisi Benders Beserta Hasil yang Diperoleh ... 27

4 Pembangkitan Data-data Biaya Pengangkutan dan Biaya Tetap dengan Mathematica 5.2 Beserta Syntax Inputnya ... 29

5 Data-data Hipotetik untuk Implementasi Penyelesaian Masalah Desain Network Takberkapasitas dengan Metode Branch-and-Bound ... 30

6 Syntax Program LINGO 8.0 untuk Masalah Desain Network Takberkapasitas ... 36

1

I PENDAHULUAN

1.1 Latar Belakang

Berbagai permasalahan dalam dunia nyata terkait dengan jaringan, misalnya jaringan telekomunikasi, lalu lintas, transportasi, maupun distribusi produk. Dalam matematika, permasalahan-permasalahan tersebut dapat dirumuskan ke dalam suatu model optimisasi

yang disebut model optimisasi network, yang

menggunakan representasi graf. Model ini bermacam-macam, salah satunya adalah

model masalah desain network.

Masalah desain network merupakan suatu

masalah aliran network (network flow) biaya

minimum untuk lebih dari satu komoditas (multicommodity) dengan biaya tetap pada sisi berarahnya. Masalah ini tergolong ke dalam

pemrograman integer campuran (mixed

integer programming). Aplikasi masalah ini amat beragam, di antaranya adalah konstruksi jalan-jalan baru dalam suatu jaringan lalu lintas, konstruksi sambungan-sambungan (links) baru dalam jaringan transportasi, desain topologi jaringan komunikasi komputer, desain jaringan telekomunikasi, maupun perencanaan armada kendaraan yang terkait dengan keputusan dalam hal pelayanan dan berbagai bidang lainnya yang menyangkut perencanaan distribusi dan transportasi. Istilah

komoditas dalam masalah desain network

misalnya dapat berupa barang-barang dalam jaringan transportasi atau sinyal-sinyal data dalam jaringan komputer.

Secara garis besar, masalah desain network

dapat dikelompokkan ke dalam dua bagian,

yakni masalah desain network berkapasitas

(capacitated network design problem) dan

masalah desain network takberkapasitas

(uncapacitated network design problem). Yang membedakan keduanya adalah ada atau tidaknya batasan komoditas yang dapat

melalui suatu sisi berarah (arc) dalam

network, yang disebut kapasitas sisi berarah. Seringkali dalam persoalan nyata kapasitas

sisi berarah dalam suatu network sangat besar,

sehingga kapasitas tersebut dapat diabaikan atau dianggap takberkapasitas. Hal ini misalnya muncul dalam penggunaan serat optik pada jaringan telekomunikasi.

Fokus desain network takberkapasitas pada

dasarnya adalah pemilihan sisi berarah yang dikehendaki untuk berada di dalam suatu

konfigurasi network yang meminimumkan

biaya total pada network tersebut. Yang

dimaksud dengan konfigurasi suatu network

adalah wujud atau bentuk dari network

tersebut terkait dengan simpul-simpul maupun

sisi-sisi berarah yang terdapat di dalamnya. Kasus khusus dalam masalah ini meliputi

masalah network biaya tetap (fixed charge

network problem) yang hanya melibatkan satu

komoditas, simple plant location problem

(SPLP), travelling salesman problem (TSP),

dan masalah Steiner Tree. Secara spesifik,

penerapan masalah ini mencakup masalah-masalah dalam perencanaan komunikasi, transportasi, dan sumber daya air, serta representasi keputusan yang menyangkut lokasi fasilitas, misalnya penempatan gudang pabrik, fasilitas darurat, maupun jaringan

komputer (computer networking).

Ada beberapa metode yang telah dikembangkan untuk mencari solusi model optimisasi ini, di antaranya adalah metode

dekomposisi Benders (Magnanti et al., 1986),

metode dual ascent (Balakrishnan et al.,

1989), dekomposisi dan relaksasi Lagrange dengan pertidaksamaan valid (Holmberg &

Migdalas, 1991), metode branch-and-bound

berbasis pemrograman linear standar, metode simpleks yang dimodifikasi, dekomposisi silang, yang dikembangkan oleh Van Roy pada tahun 1983 dan diaplikasikan pada masalah ini oleh Holmberg pada tahun 1990,

mean value cross decomposition (Holmberg, 1992), serta heuristik Lagrange (Holmberg & Hellstrand, 1998).

Dalam karya ilmiah ini akan dibahas metode dekomposisi Benders, suatu metode solusi yang dikembangkan oleh J.F. Benders pada tahun 1962. Metode ini telah digunakan pada masalah dengan variabel-variabel

kontinu berjumlah besar, variabel integer

relatif sedikit, dan kendala-kendalanya

memiliki struktur khusus (Magnanti et al.,

1986). Metode ini terbukti sangat berguna untuk beberapa konteks masalah yang meliputi desain sistem distribusi (Geoffrion &

Graves, 1974), aircraft routing (Richardson,

1976), dan penjadwalan mesin kereta api (Florian et al., 1976).

Dekomposisi Benders dalam karya ilmiah ini digunakan untuk mencari suatu batas bawah nilai fungsi objektif optimal dan

menyelesaikan masalah desain network

takberkapasitas. Selain itu akan ditunjukkan pula penyelesaian masalah ini dengan

menggunakan metode branch-and-bound

dengan bantuan software LINGO 8.0.

Untuk menyederhanakan model ini digunakan asumsi bahwa asal dan tujuan

tunggal (single origin and destination) untuk

2

1.2 Tujuan

Tujuan dari karya ilmiah ini meliputi:

1. mempelajari model masalah desain

network takberkapasitas dengan asal (origin) dan tujuan (destination) tunggal untuk setiap komoditas;

2. mencari batas bawah nilai optimal fungsi

objektif dan menyelesaikan masalah

desain network takberkapasitas dengan

menggunakan dekomposisi Benders;

3. menyelesaikan masalah desain network

takberkapasitas dengan menggunakan

metode branch-and-bound.

II LANDASAN TEORI

Untuk memahami masalah desain network

takberkapasitas dan teknik-teknik pemecahan yang digunakan dalam karya tulis ini diperlukan pengertian beberapa konsep berikut ini.

Fungsi Linear dan Pertidaksamaan Linear

Fungsi linear dan pertidaksamaan linear merupakan salah satu konsep dasar yang harus dipahami terkait dengan konsep pemrograman linear.

Definisi 1 (Fungsi Linear)

Misalkan f(x1,x2,...,xn) menyatakan

suatu fungsi dalam variabel-variabel

n x x

x1, 2,..., . Fungsi f(x1,x2,...,xn) dikatakan

linear jika dan hanya jika untuk suatu

himpunan konstanta c1,c2,...,cn,

. ... )

,..., ,

(x1 x2 xn c1x1 c2x2 cnxn

f = + + +

(Winston, 2004)

Sebagai gambaran, f(x1,x2)=2x1+x2

merupakan fungsi linear, sementara

2 2 1 2 1, )

(x x x x

f = bukan fungsi linear.

Misalkan b sembarang bilangan, suatu

persamaan f(x1,x2,...,xn)=b merupakan

persamaan linear.

Definisi 2 (Pertidaksamaan Linear)

Untuk sembarang fungsi linear )

,..., ,

(x1 x2 xn

f dan sembarang bilangan ,b

pertidaksamaan f(x1,x2,...,xn)≤b dan

b x x x

f( 1, 2,..., n)≥ adalah pertidaksamaan

linear.

(Winston, 2004)

Pemrograman Linear

Menurut Winston (2004), pemrograman

linear (PL) atau linear programming adalah

suatu masalah optimisasi yang memenuhi ketentuan-ketentuan sebagai berikut.

a) Tujuan masalah tersebut adalah

memaksimumkan atau meminimumkan suatu fungsi linear dari sejumlah variabel

keputusan. Fungsi yang akan dimaksimumkan atau diminimumkan ini

disebut fungsi objektif.

b) Nilai variabel-variabel keputusannya harus

memenuhi suatu himpunan kendala. Setiap kendala harus berupa persamaan linear atau pertidaksamaan linear.

c) Ada pembatasan tanda untuk setiap

variabel dalam masalah ini. Untuk

sembarang variabel xi, pembatasan tanda

menentukan xi harus taknegatif (xi ≥0)

atau tidak dibatasi tandanya (unrestricted

in sign).

Suatu PL mempunyai bentuk standar seperti yang didefinisikan sebagai berikut.

Definisi 3 (Bentuk Standar PL)

Pemrograman linear min terhadap z= = ≥ T c x Ax b x 0 (2.1)

dikatakan PL dalam bentuk standar, dengan x

dan c vektor-vektor berukuran n, vektor b

berukuran m, dan A matriks berukuran m × n

yang disebut sebagai matriks kendala, dengan

m≤n.

(Nash & Sofer, 1996)

Sebagai catatan, yang dimaksud dengan

vektor berukuran n adalah vektor yang

memiliki dimensi (ukuran) n × 1.

Solusi Pemrograman Linear

3

Pada masalah PL (2.1), vektor x yang

memenuhi kendala Ax=b disebut solusi PL

(2.1). Misalkan matriks A dapat dinyatakan

sebagai A=

(

B N

)

, dengan B adalah

matriks berukuran m × m yang elemennya

berupa koefisien variabel basis dan N

merupakan matriks berukuran m× −(n m)

yang elemen-elemennya berupa koefisien variabel nonbasis pada matriks kendala.

Dalam hal ini matriks B disebut matriks basis

untuk PL (2.1).

Definisi 4 (Matriks Basis)

Matriks B disebut matriks basis untuk PL

(2.1) jika B adalah matriks taksingular, yaitu

matriks yang determinannya tidak sama dengan nol.

(Garfinkel & Nemhauser, 1972)

Misalkan x dapat dinyatakan sebagai

vektor = ⎜ ⎟⎛ ⎞

⎝ ⎠ B N x x

x , dengan xB adalah vektor

variabel basis dan xN adalah vektor variabel

nonbasis, maka Ax=b dapat dinyatakan

sebagai =

(

)

⎛_⎜ ⎞_⎟

⎝ ⎠ B N x Ax B N

x

.

=Bx + NxB N =b (2.2)

Karena matriks B adalah matriks taksingular,

maka B memiliki invers, sehingga dari (2.2)

B

x dapat dinyatakan sebagai:

- .

= -1 -1

B N

x B b B Nx (2.3)

Definisi 5 (Solusi Basis)

Solusi dari suatu PL disebut solusi basis jika memenuhi syarat berikut:

i. solusi tersebut memenuhi kendala pada

PL;

ii. kolom-kolom dari matriks kendala yang

berpadanan dengan komponen taknol dari solusi tersebut adalah bebas linear.

(Nash & Sofer, 1996)

Menurut Garfinkel & Nemhauser (1972), solusi dari suatu PL disebut solusi basis jika

memenuhi xB =B b-1 , xN =0.

Definisi 6 (Solusi Basis Fisibel)

Vektor x disebut solusi basis fisibel jika x

merupakan solusi basis dan x≥0.

(Nash & Sofer, 1996)

Ilustrasi solusi basis dan solusi basis fisibel diberikan dalam Contoh 1.

Contoh 1

Misalkan diberikan PL (2.4) berikut:

1 2

1 2 3

1 2 4

1 5

1 2 3 4 5

min 2 3

terhadap 2 4

2 11

5

, , , , 0,

z x x

x x x

x x x

x x x x x x x = − − − + + = − + + = + = ≥ (2.4)

dari PL (2.4) diperoleh:

2 1 1 0 0 4

1 2 0 1 0 , 11

1 0 0 0 1 5

− ⎛ ⎞ ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ = −_{⎜ ⎟} =_{⎜ ⎟} ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠

A b .

Misalkan dipilih

(

x3 x4 x5

)

dan ,

(

x1 x2

)

= T = T

B N

x x

maka matriks basisnya adalah

1 0 0

0 1 0

0 0 1

⎛ ⎞ ⎜ ⎟ = ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ B .

Dengan menggunakan matriks basis di atas didapatkan

(

0 0

)

, 4 11 5−

(

)

.

= T = 1 = T

N B

x x B b (2.5)

Solusi (2.5) merupakan solusi basis, karena memenuhi kendala pada PL (2.4) dan kolom-kolom pada matriks kendala yang berpadanan dengan komponen taknol dari

(2.5), yaitu B bebas linear (kolom yang satu

bukan merupakan kelipatan dari kolom yang lain). Solusi (2.5) juga merupakan solusi basis fisibel, karena nilai-nilai variabelnya lebih dari atau sama dengan nol.

PL (2.1) dapat dinyatakan dalam bentuk

B

x dan xN sebagai berikut

min terhadap

,

z= +

+ =

≥

T T

B B N N

B N

c x c x

Bx Nx b

x 0

(2.6)

dengan cB vektor koefisien variabel basis

pada fungsi objektif dan cN vektor koefisien

variabel nonbasis pada fungsi objektif. Jika persamaan (2.3) disubstitusikan ke dalam fungsi objektif PL (2.6) maka akan didapat

( )

( ) .

z − −

− −

= − +

= + −

T 1 1 T

B N N N

T 1 T T 1

B N B N

c B b B Nx c x c B b c c B N x

Definisi 7 (Vektor Pengali Simpleks)

Jika didefinisikan B

T T 1 T

BB B c

c

y=( −) = − ,

maka z dapat ditulis sebagai

. ) ( N T T N T x N y c b

y + −

=

z (2.7)

Vektor y disebut vektor pengali simpleks.

4

Untuk suatu solusi basis xN =0 dan

,

ˆ _{B b}

b

x 1

B

− =

= maka ˆ cTB 1b,

B

− =

z dengan zˆ

menyatakan nilai optimal untuk z.

Definisi 8 (Reduced Cost)

Misalkan cˆ menyatakan elemen vektor j

) (

ˆ c c B N

c T 1

B T N T N − −

≡ yang bersesuaian dengan

variabel xj, koefisien cˆ disebut j reduced cost

dari xj. Reduced cost adalah penambahan

nilai fungsi objektif jika suatu variabel nonbasis dijadikan variabel basis (artinya menjadi solusi taknol) pada suatu PL.

(Nash & Sofer, 1996)

Hal yang juga penting dalam konsep pemrograman linear adalah daerah fisibel, solusi optimal, himpunan konveks, dan titik ekstrem, yang didefinisikan sebagai berikut.

Definisi 9 (Daerah Fisibel)

Daerah fisibel suatu PL adalah himpunan semua titik yang memenuhi semua kendala dan pembatasan tanda pada PL tersebut.

(Winston, 2004)

Definisi 10 (Solusi Optimal)

Untuk masalah maksimisasi, solusi optimal suatu PL adalah suatu titik dalam daerah fisibel dengan nilai fungsi objektif terbesar. Untuk masalah minimisasi, solusi optimal suatu PL adalah suatu titik dalam daerah fisibel dengan nilai fungsi objektif terkecil.

(Winston, 2004)

Definisi 11 (Himpunan Konveks)

Misalkan S menyatakan himpunan titik. S

adalah himpunan konveks jika segmen garis yang menghubungkan sembarang titik-titik

dalam S seluruhnya termuat dalam S.

(Winston, 2004)

Ilustrasi himpunan konveks dan yang bukan himpunan konveks diberikan pada gambar di bawah ini.

Gambar 1 Ilustrasi himpunan konveks dan yang bukan himpunan konveks.

Pada Gambar 1, lingkaran (i) dan persegi panjang (ii) merupakan himpunan konveks, sedangkan bidang (iii) dan cincin (iv) bukan himpunan konveks.

Definisi 12 (Titik Ekstrem)

Untuk sembarang himpunan konveks S,

titik P anggota S dikatakan sebagai suatu titik

ekstrem jika untuk setiap segmen garis yang

seluruhnya terletak dalam S dan memuat titik

P, titik P merupakan titik ujung dari segmen

garis tersebut.

(Winston, 2004)

Menurut Nash & Sofer (1996), suatu titik

S

x∈ disebut titik ekstrem dari suatu

himpunan konveks S jika titik tersebut tidak

dapat dinyatakan dalam bentuk , ) 1

( z

y x=α + −α

dengan ,y,z∈S 0<α<1 dan y,z≠x.

Berdasarkan Gambar 1, seluruh titik yang berada pada keliling lingkaran (i) merupakan titik ekstrem, demikian pula titik-titik ujung (sudut) persegi panjang (ii).

Optimalitas titik ekstrem pada suatu masalah pemrograman linear ditunjukkan pada terorema berikut ini.

Teorema 1 (Optimalitas Titik Ekstrem)

Solusi optimal suatu masalah PL dicapai pada suatu titik ekstrem atau himpunan titik-titik ekstrem.

Bukti teorema ini dapat dilihat pada Lampiran 1.

(Hazell & Norton, 1986)

Dualitas Pemrograman Linear

Menurut Nemhauser & Wolsey (1999), dualitas pemrograman linear berkaitan dengan sepasang masalah PL dan hubungan antarsolusi keduanya. Salah satu dari sepasang masalah PL ini disebut masalah primal dan lainnya disebut masalah dual.

Masalah dual dan primal berkaitan sangat erat sedemikian sehingga solusi optimal dari salah satu masalah akan secara otomatis menghasilkan solusi optimal bagi masalah lainnya. Masalah dual adalah sebuah masalah PL yang diturunkan dari sebuah masalah PL primal dengan mengikuti kaidah-kaidah berikut:

1. untuk setiap kendala masalah primal

terdapat suatu variabel masalah dual;

2. untuk setiap variabel masalah primal

terdapat suatu kendala masalah dual;

(i) (ii)

5

3. koefisien dari sebuah variabel pada

kendala masalah primal membentuk koefisien yang terdapat pada ruas kiri kendala masalah dual yang bersesuaian dan koefisien fungsi objektif dari variabel terkait menjadi ruas kanan kendala masalah dual.

(Taha, 1996)

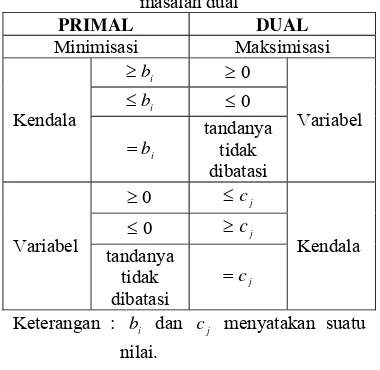
Secara ringkas, hubungan antara variabel-variabel kendala pada masalah primal dan masalah dual diberikan dalam tabel berikut

Tabel 1 Hubungan antara variabel-variabel dan kendala-kendala pada masalah primal dan

masalah dual

PRIMAL DUAL

Minimisasi Maksimisasi

i b

≥ ≥0

i b

≤ ≤0

Kendala

i b

= tandanya tidak

dibatasi

Variabel

0

≥ ≤cj

0

≤ ≥cj

Variabel _tandanya

tidak dibatasi j c = Kendala

Keterangan : bi dan cj menyatakan suatu

nilai.

Misalkan suatu masalah PL primal dinyatakan sebagai berikut

min terhadap , z= ≥ ≥ T c x Ax b x 0 (P)

maka dual dari masalah di atas adalah max terhadap , w= ≤ ≥ T T b y A y c

y 0

(D)

dengan c dan x vektor-vektor berukuran n, b

dan y vektor-vektor berukuran m, dan A

matriks berukuran m×n.

Keterkaitan antara solusi masalah primal dan solusi masalah dual dijabarkan dalam teorema-teorema berikut ini.

Teorema 2 (Dualitas Lemah)

Misalkan x adalah solusi fisibel masalah

primal (P) dan y adalah solusi fisibel masalah

dual (D), maka

.

z= T ≥ T =w c x b y

Bukti teorema ini dapat dilihat pada Lampiran 1.

(Nash & Sofer, 1996)

Teorema 2 ini berlaku untuk masalah primal yang berbentuk minimisasi dan dualnya, sementara untuk masalah primal berupa maksimisasi dan dualnya, nilai fungsi

objektif masalah primal ≤ nilai fungsi objektif

masalah dual. Hal mendasar dari dualitas pemrograman linear adalah bahwa jika kedua masalah primal dan dual ini fisibel maka nilai-nilai optimalnya sama, yang diperjelas oleh teorema berikut.

Teorema 3 (Dualitas Kuat)

Misalkan diberikan sepasang masalah PL primal dan dual. Jika salah satu masalah memiliki solusi optimal demikian pula yang lain dan nilai objektif kedua masalah ini sama. Bukti teorema ini dapat dilihat pada Lampiran 1.

(Nash & Sofer, 1996)

Contoh dualitas pemrograman linear diberikan sebagai berikut.

Contoh 2 (Dualitas Pemrograman Linear)

Misalkan masalah primal (P)

1 2

1 2

1 2

1 2

1 2

min 7 2

terhadap 2 4

5 20

2 2 7

, 0,

z x x

x x x x x x x x = + − + ≥ + ≥ − − ≥ − ≥ (P)

maka dual dari masalah di atas adalah

1 2 3

1 2 3

1 2 3

1 2 3

max 4 20 7

terhadap 5 2 7

2 2 2

, , 0.

w y y y

y y y

y y y

y y y

= + −

− + − ≤

+ − ≤

≥

(D)

Integer Programming (Pemrograman Integer)

Integer programming (IP) atau

pemrograman integer adalah suatu model

pemrograman linear dengan variabel yang

digunakan berupa bilangan bulat (integer).

Jika semua variabel harus berupa integer,

maka masalah tersebut dinamakan pure

integer programming. Jika hanya sebagian

yang harus berupa integer, maka disebut

mixed integer programming. IP dengan semua variabelnya harus bernilai 0 atau 1 disebut 0-1 IP.

6

Pemrograman Linear Relaksasi

Konsep pemrograman linear relaksasi atau PL-relaksasi diberikan dalam definisi berikut ini.

Definisi 13 (Pemrograman Linear Relaksasi)

Pemrograman linear relaksasi atau sering disebut PL-relaksasi merupakan suatu pemrograman linear yang diperoleh dari suatu

IP dengan menghilangkan kendala integer

atau kendala 0-1 pada setiap variabelnya. Untuk masalah maksimisasi, nilai optimal fungsi objektif PL-relaksasi lebih besar atau sama dengan nilai optimal fungsi objektif IP, sedangkan untuk masalah minimisasi, nilai optimal fungsi objektif PL-relaksasi lebih kecil atau sama dengan nilai optimal fungsi objektif IP.

(Winston, 1995)

Graf

Konsep graf yang digunakan dalam karya ilmiah ini meliputi definisi-definisi berikut ini.

Definisi 14 (Graf)

Suatu graf G adalah pasangan terurut

( , ),V E dengan V himpunan takkosong dan

berhingga dan E adalah himpunan takterurut

yang menghubungkan elemen-elemen di V,

dinotasikan dengan G=( , ).V E Elemen V

dinamakan simpul (vertex/node) dan elemen E

dinamakan sisi (edge), dinotasikan dengan

{ , }i j , yakni sisi yang menghubungkan simpul

i dengan simpul j, dengan ,i j∈V.

(Foulds, 1992)

Graf seperti disebutkan pada definisi di atas disebut juga graf takberarah. Ilustrasi graf takberarah dapat dilihat pada Gambar 2 berikut

Gambar 2 Graf G=( , ).V E

Pada Gambar 2 di atas diperlihatkan bahwa {1, 2,3, 4, 5}

V= dan

{{1, 2},{1, 3},{1, 4},{2, 3},{3, 4},{3, 5}}.

E=

Definisi 15 (Graf Berarah)

Graf berarah (directed graph/digraph) G'

adalah pasangan terurut ( , )V A dengan V

himpunan takkosong dan berhingga, dan A

adalah himpungan pasangan terurut yang

menghubungkan elemen-elemen di V,

dinotasikan dengan G'=( , ).V A

Elemen-elemen dari A disebut arc (sisi berarah) dan

dituliskan sebagai

( )

i j, , dengan ,i j∈V. (Foulds, 1992)

Ilustrasi graf berarah dapat dilihat pada gambar berikut

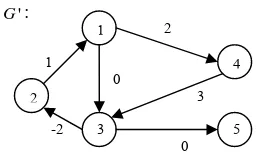
Gambar 3 Graf G'=( , ).V A

Pada Gambar 3 diperlihatkan bahwa {1, 2, 3, 4, 5}

V= dan

{(1, 2), (1, 3), (1, 4), (2,1), (3, 2), (3, 5), (4, 3)}. A=

Definisi 16(Walk)

Suatu walk pada graf G=( , )V E adalah

suatu barisan simpul dan sisi dari G dengan

bentuk:

{

} {

} {

}

1, 1, 2 , 2, 2, 3 ,..., n1, n , n ,

v v v v v v v− v v

atau ditulis dengan ringkas :

1, 2,..., n

v v v atau v v1, 2,...,vn.

Walk tersebut menghubungkan simpul v1

dengan simpul vn.

(Foulds, 1992)

Definisi 17 (Path)

Path pada suatu graf G adalah suatu walk

dengan semua simpulnya berbeda.

(Foulds, 1992)

Ilustrasi walk dan path diberikan sebagai

berikut. Pada graf G yang terdapat dalam

Gambar 2, salah satu contoh walk adalah

1, 2, 3, 4, 3, 5 , sedangkan 1, 2, 3, 5 adalah

salah satu contoh path.

Definisi 18 (Walk Berarah)

Walk berarah pada suatu graf berarah

' ( , )

G = V A adalah suatu barisan terurut

2

1

3

4

5

G:

'

G :

2

1

3

4

7

simpul dan sisi pada G' yang berbentuk

, , ,..., ,

, 1 1

0 a v an vn

v dengan setiap sisi

berarah a_i menghubungkan simpul-simpul

1

−

i

v dan v_i secara berurutan.

(Foulds, 1992)

Definisi 19 (Path Berarah)

Path berarah pada graf berarah G'

adalah suatu walk berarah yang semua

simpulnya berbeda.

(Foulds, 1992)

Ilustrasi walk dan path berarah diberikan

sebagai berikut. Pada graf berarah G' yang

terdapat dalam Gambar 3, contoh walk

berarah adalah 1, 3, 2,1, 4, 3, 5 . Contoh path

berarah adalah 2,1, 4, 3, 5 , sementara

1, 2, 3, 5 bukan path berarah, karena tidak

ada sisi berarah dari simpul 2 ke simpul 3.

Definisi 20 (Sisi Berarah Menjauhi atau Mendekati, Suksesor, dan Predesesor)

Misalkan diberikan graf berarah

' ( , )

G = V A . Jika a=( ,v vi j)∈A maka sisi

berarah ini dikatakan menjauhi vi dan

mendekati vj. Simpul vi disebut predesesor

bagi simpul vj, dan simpul vj disebut

suksesor bagi simpul vi.

(Foulds, 1992)

Ilustrasinya diberikan dalam gambar berikut.

Gambar 4 Sisi berarah menjauhi atau mendekati, suksesor, dan predesesor.

Definisi 21 (Graf Berbobot)

Suatu graf G=( , )V E atau graf berarah

' ( , )

G = V A dikatakan berbobot jika terdapat

fungsi :w E→ ℜ atau :A A→ ℜ (dengan

ℜ himpunan bilangan real) yang memberikan

bobot pada setiap elemen E atau A.

(Foulds, 1992)

Ilustrasi graf berbobot diberikan dalam Gambar 5.

Gambar 5 Graf berbobot G'=( , ).V A

Misalkan diberikan :A A→ ℜ untuk graf

berbobot G'=( , )V A pada Gambar 5, maka

((4, 3))

A = 3 atau dapat pula ditulis

4,3 2,1 1,3 3,5 3,2

1,4

3; 1; 0; 2;

2.

= = = = = −

=

A A A A A

A

Terdapat kasus khusus dari graf berbobot,

yaitu network. Untuk memahami konsep

network diperlukan definisi-definisi source

dan sink berikut ini.

Definisi 22 (Source)

Source adalah suatu simpul dengan tidak ada sisi berarah yang mendekati simpul tersebut.

(Foulds, 1992)

Definisi 23 (Sink)

Sink adalah suatu simpul sehingga tidak

ada sisi berarah yang menjauhi simpul tersebut.

(Foulds, 1992)

Definisi 24 (Network)

Network adalah suatu graf berarah yang

mempunyai tepat satu source dan satu sink.

(Foulds, 1992)

Ilustrasi network, source, dan sink

diberikan dalam Gambar 6.

Gambar 6 Network, source, dan sink.

Pada Gambar 6, graf berarah G merupakan

network dengan simpul 1 sebagai source dan

simpul 5 sebagai sink.

Pengertian network yang lebih sederhana

diberikan oleh Ahuja et al. (1993),

1

2

-2 0

3

0 2

1

3

4

5

' G :

2

1

3

4

5

G:

i

8

Balakrishnan (1997), dan Bertsimas &

Tsitsiklis (1997), yakni bahwa network adalah

suatu graf yang simpul-simpul dan sisi-sisi berarahnya memiliki informasi numerik (suatu

nilai). Ada kalanya suatu network memiliki

lebih dari satu source maupun sink,

sebagaimana yang akan digunakan dalam karya ilmiah ini.

Network Flow

Terkait dengan bahasan network flow,

terlebih dahulu perlu dipahami konsep flow

dalam suatu network yang diberikan pada

definisi berikut ini.

Definisi 25 (Flow)

Suatu flow, misalnya dinotasikan dengan f,

adalah suatu fungsi bernilai integer yang

didefinisikan pada himpunan sisi berarah pada

suatu network sedemikian sehingga

0≤ f e( )≤c e( ) untuk setiap sisi berarah e,

dengan c e( )=c i j( , ) menyatakan kapasitas

sisi berarah, bernilai taknegatif, dan ( )f e

suatu integer yang menyatakan flow sepanjang

sisi berarah e.

(Balakrishnan, 1997)

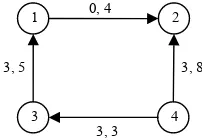
Ilustrasi flow pada suatu network diberikan

pada Gambar 7 berikut

Gambar 7 Flow dan kapasitas sisi berarah.

Berdasarkan Gambar 7 di atas, pada setiap sisi

berarah terdapat dua buah integer yang

dipisahkan oleh tanda koma. Integer pertama

menyatakan flow sepanjang sisi berarah yang

terkait dan integer kedua menyatakan

kapasitas sisi berarah tersebut.

Network flow merupakan suatu kasus dalam PL yang memiliki struktur khusus dan menggunakan representasi graf. Bentuk dasar

suatu masalah network flow dikenal dengan

sebutan masalah network flow biaya minimum

(minimum cost network flow problem). Pada masalah ini, fungsi objektifnya berupa minimisasi biaya yang terkait dengan suatu sisi berarah dengan kendala-kendala yang

meliputi kendala konservasi flow dan kendala

pembatasan flow.

Misalkan biaya pengangkutan (shipping)

setiap unit flow komoditas pada sisi berarah

( , )i j ∈A dinyatakan dengan cij, banyaknya

unit flow komoditas yang melalui sisi berarah

( , )i j untuk setiap ( , )i j ∈A dinotasikan

dengan xij, batas bawah dan batas atas

banyaknya flow komoditas yang diangkut

melalui sisi berarah ( , )i j untuk setiap

( , )i j ∈A berturut-turut dinyatakan dengan lij

dan uij, dan bi menyatakan supply/demand

pada simpul i∈N. Formulasi umum suatu

masalah network flow diberikan sebagai

berikut: ( , ) :( , ) :( , ) min terhadap (2.8)

( , ) , (2.9)

ij ij i j A

ij ji i

j i j A j i j A ij ij ij c x

x x b i N

l x u i j A

∈ ∈ ∈ − = ∀ ∈ ≤ ≤ ∀ ∈

∑

∑

∑

dengan N menyatakan himpunan simpul

dalam suatu network dan A menyatakan

himpunan sisi berarah dalam network tersebut.

Jika bi >0, bi disebut supply pada simpul i

dan simpul i disebut simpul supply. Jika

0

i

b < , bi disebut demand pada simpul i dan

simpul i disebut simpul demand. Jika bi =0,

simpul i disebut simpul transshipment. Batas

atas, uij, disebut juga kapasitas sisi berarah

( , )i j . Persamaan (2.8) menyatakan kendala

konservasi flow dan pertidaksamaan (2.9)

menyatakan kendala pembatasan flow.

Kendala konservasi flow merupakan suatu

kendala yang menjaga keseimbangan flow

pada suatu simpul, yang menyatakan bahwa

banyaknya flow yang masuk ke suatu simpul

harus sama dengan banyaknya flow yang

keluar dari simpul tersebut. Kendala

pembatasan flow merupakan suatu kendala

yang membatasi banyaknya flow yang dapat

melewati suatu sisi berarah.

(Ahuja et al., 1993)

Masalah Path Terpendek (The Shortest Path Problem)

Masalah path terpendek merupakan kasus

khusus dalam masalah network flow biaya

minimum. Didefinisikan panjang untuk

sembarang path berarah dalam suatu network

sebagai jumlah biaya semua sisi berarah

dalam path tersebut. Dalam masalah ini akan

dicari suatu path terpendek, yakni path

berarah dari suatu simpul asal ke simpul

tujuan dengan panjangterkecil.

1

3

2

4 0, 4

3, 5 3, 8

9

Metode Branch-and-Bound

Pemecahan masalah pemrograman integer

dapat dilakukan dengan metode

branch-and-bound. Prinsip dasar metode ini adalah memecah daerah fisibel suatu masalah PL-relaksasi dengan membuat subproblem-subproblem. Ada dua konsep dasar dalam

algoritme branch-and-bound.

• Cabang (Branch)

Membuat partisi daerah solusi dari masalah utama (PL-relaksasi) dengan membentuk subproblem-subproblem, tujuannya untuk menghapus daerah solusi yang tidak fisibel. Hal ini dicapai dengan menentukan kendala yang penting untuk menghasilkan solusi IP,

secara tidak langsung titik integer yang tidak

fisibel terhapus. Dengan kata lain, hasil pengumpulan lengkap dari subproblem-subproblem ini menunjukkan setiap titik

integer yang fisibel dalam masalah asli. Karena sifat partisi tersebut, maka prosedur

ini dinamakan pencabangan (branching).

• Batas (Bound)

Misalkan masalah utamanya berupa masalah maksimisasi, nilai objektif yang optimal untuk setiap subproblem dibuat dengan membatasi pencabangan dengan batas atas dari nilai objektif yang dihubungkan dengan sembarang

nilai integer yang fisibel. Hal ini sangat

penting untuk mengatur dan menempatkan solusi optimal. Operasi pembatasan ini

dinamakan pembatasan (bounding).

(Taha, 1975)

Metode branch-and-bound diawali dari

menyelesaikan PL-relaksasi dari suatu integer

programming. Jika semua nilai variabel keputusan solusi optimal sudah berupa

integer, maka solusi tersebut merupakan solusi optimal IP. Jika tidak, dilakukan pencabangan dan penambahan batasan pada PL-relaksasinya kemudian diselesaikan.

Winston (2004) menyebutkan bahwa nilai

fungsi objektif optimal untuk IP ≤ nilai

fungsi objektif optimal untuk PL-relaksasi (masalah maksimisasi), sehingga nilai fungsi objektif optimal PL-relaksasi merupakan batas atas bagi nilai fungsi objektif optimal untuk masalah IP. Diungkapkan pula oleh Winston (2004) bahwa nilai fungsi objektif optimal untuk suatu kandidat solusi merupakan batas bawah nilai fungsi objektif optimal untuk masalah IP asalnya. Suatu kandidat solusi diperoleh jika solusi dari suatu subproblem

sudah memenuhi kendala integer pada

masalah IP, artinya fungsi objektif dan semua

variabelnya sudah bernilai integer.

Berikut ini adalah langkah-langkah penyelesaian suatu masalah maksimisasi

dengan metode branch-and-bound.

• Langkah 0

Didefinisikan z sebagai batas bawah dari nilai

fungsi objektif (solusi) IP yang optimal. Pada

awalnya ditetapkan z=−∞ dan i=0.

• Langkah 1

Subproblem LP( )i dipilih sebagai bagian

masalah berikutnya untuk diteliti. Subproblem

( )i

LP diselesaikan dan diukur dengan kondisi

yang sesuai.

a) Jika LP( )i terukur, batas bawah z

diperbarui jika solusi IP yang lebih baik ditemukan. Jika tidak, bagian masalah

(subproblem) baru i dipilih dan langkah 1

diulangi. Jika semua subproblem telah diteliti, maka proses dihentikan.

b) Jika LP( )i tidak terukur, proses

dilanjutkan ke langkah 2 untuk

melakukan pencabangan LP( )i .

Menurut Winston (2004), suatu subproblem

dikatakan terukur (fathomed) jika terdapat

situasi sebagai berikut.

1. Subproblem tersebut takfisibel, sehingga

tidak dapat menghasilkan solusi optimal untuk IP.

2. Subproblem tersebut menghasilkan suatu

solusi optimal dengan semua variabelnya

bernilai integer. Jika solusi optimal ini

mempunyai nilai fungsi objektif yang lebih baik daripada solusi fisibel yang diperoleh sebelumnya, maka solusi ini menjadi kandidat solusi optimal dan nilai fungsi objektifnya menjadi batas bawah nilai fungsi objektif optimal bagi masalah IP pada saat itu. Bisa jadi subproblem ini menghasilkan solusi optimal untuk masalah IP.

3. Nilai fungsi objektif optimal untuk

subproblem tersebut tidak melebihi (untuk masalah maksimisasi) batas bawah saat itu, maka subproblem ini dapat dieliminasi.

• Langkah 2

Dipilih salah satu variabel xj yang nilai

optimalnya adalah x*_j yang tidak memenuhi

batasan integer dalam solusi LP_i. Bidang

1 ] [ ]

[x*_j <x_j < x*_j + disingkirkan dengan

membuat dua subproblem PL yang berkaitan menjadi dua subproblem yang tidak dapat dipenuhi secara bersamaan, yaitu

] [ *j

j x

10

dengan [x*_j] didefinisikan sebagai integer

terbesar yang kurang dari atau sama dengan .

* j

x Kembali ke langkah 1.

(Taha, 1996)

Untuk memudahkan pemahaman metode

branch-and-bound diberikan contoh sebagai berikut.

Contoh 3 (Metode Branch-and-Bound)

Misalkan diberikan pemrograman integer

(IP) berikut

max z=5x1+4x2 terhadap x1+x2≤5

10x1+6x2≤45 (2.10) x x1, 2≥0

x x1, 2 integer.

Solusi optimal PL-relaksasi dari masalah

IP (2.10) adalah x1=3.75, x2 =1.25, dan

23.75

z= (lihat pada Lampiran 2). Batas atas

nilai optimal fungsi objektif masalah ini

adalah z=23.75. Daerah fisibel masalah

(2.10) ditunjukkan pada Gambar 8.

Gambar 8 Daerah fisibel untuk PL-relaksasi dari IP (2.10).

Keterangan :

= solusi optimal PL-relaksasi IP (2.10) = titik-titik fisibel bagi IP (2.10)

Langkah berikutnya adalah memartisi daerah fisibel PL-relaksasi menjadi dua bagian berdasarkan variabel yang berbentuk

pecahan (non-integer). Karena nilai dari kedua

variabel yang diperoleh bukan integer, maka

dipilih salah satu variabel untuk dasar

pencabangan. Misalkan dipilih x1 sebagai

dasar pencabangan. Jika masalah PL-relaksasi diberi nama subproblem 1, maka pencabangan tersebut menghasilkan 2 subproblem, yaitu:

• subproblem 2: subproblem 1 ditambah

kendala x1≥4;

• subproblem 3: subproblem 1 ditambah

kendala x1≤3.

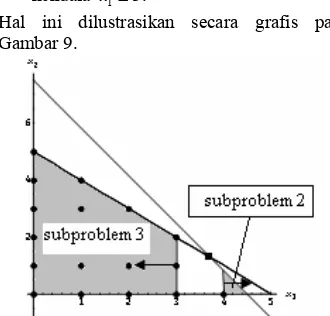
Hal ini dilustrasikan secara grafis pada Gambar 9.

Gambar 9 Daerah fisibel untuk subproblem 2 dan subproblem 3 dari IP (2.10).

Setiap titik (solusi) fisibel dari IP (2.10) termuat dalam daerah fisibel subproblem 2 atau subproblem 3. Setiap subproblem ini saling lepas. Subproblem 2 dan subproblem 3

dikatakan dicabangkan oleh x1.

Sekarang dipilih subproblem yang belum diselesaikan. Misalkan dipilih subproblem 2, kemudian diselesaikan. Solusi optimal untuk

subproblem 2 ini adalah x1=4, x2=0.83,

dan z=23.33 (lihat Lampiran 2). Karena

nilai fungsi objektif yang diperoleh dari subproblem 1 lebih baik (lebih besar) dari pada nilai fungsi objektif yang diperoleh dari subproblem 2, maka batas atas bagi masalah

ini adalah z=23.75.

Karena solusi optimal yang dihasilkan

subproblem 2 bukan solusi integer, maka

dipilih pencabangan pada subproblem 2 atas

2,

x sehingga diperoleh dua subproblem lagi,

yakni:

• subproblem 4: subproblem 2 ditambah

kendala x2≥1;

• subproblem 5: subproblem 2 ditambah

kendala x2≤0.

Saat ini subproblem yang belum diselesaikan adalah subproblem 3, 4, dan 5. Salah satu subproblem dipilih, misalnya

dengan aturan LIFO (Last In First Out).

[image:30.612.331.496.126.284.2]

11

Karena aturan LIFO, dipilih subproblem 5, yang kemudian menghasilkan solusi optimal

1 4.5,

x = x2=0, dan z=22.5 (lihat pada

Lampiran 2). Batas atas bagi masalah ini

adalah z=23.75, karena nilai ini lebih baik

daripada nilai objektif yang diperoleh dari subproblem 5.

Karena x1=4.5 bukan integer, maka

dilakukan kembali pencabangan atas x1,

sehingga diperoleh:

• subproblem 6: subproblem 5 ditambah

kendala x1≥5;

• subproblem 7: subproblem 5 ditambah

kendala x1≤4.

Misalkan dipilih subproblem 6. Ternyata subproblem ini juga takfisibel (lihat pada Lampiran 2), sehingga tidak dapat menghasilkan solusi optimal. Dengan demikian subproblem-subproblem yang belum diselesaikan adalah subproblem 3 dan subproblem 7. Karena aturan LIFO, dipilih subproblem 7. Subproblem ini kemudian

menghasilkan solusi optimal x₁=4, 0,x₂=

dan z=20 (lihat pada Lampiran 2). Dapat

dilihat bahwa solusi optimal subproblem ini

semuanya berupa integer, sehingga

merupakan kandidat solusi untuk IP (2.10).

Nilai z pada kandidat solusi ini merupakan

batas bawah bagi nilai optimal IP. Penyelesaian subproblem 3 menghasilkan

solusi optimal x1=3, 2,x2= dan z=23

(lihat pada Lampiran 2). Batas bawah yang ditetapkan dari solusi optimal subproblem 7 terlalu lemah dan tidak lebih baik dari nilai solusi optimal yang dihasilkan oleh subproblem 3. Dengan demikian, nilai solusi

optimal subproblem 3, yakni z=23 menjadi

batas bawah yang baru. Semua solusi optimal

telah berupa integer dan tidak perlu lagi

dilakukan pencabangan, sehingga solusi optimal dari subproblem 3 merupakan solusi

optimal IP (2.10), yakni x₁=3, x2=2, dan

23.

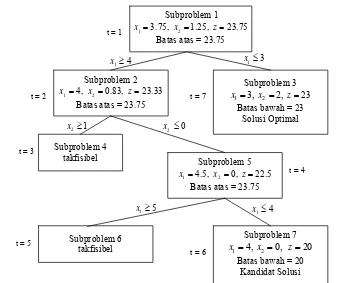
z= Pohon pencabangan yang

[image:31.612.160.516.353.636.2]

menunjukkan penyelesaian masalah IP (2.10) secara keseluruhan ditunjukkan pada Gambar 10.

Gambar 10 Seluruh pencabangan pada metode branch-and-bound untuk

menyelesaikan IP (2.10). Subproblem 1

1 3.75,

x = x2=1.25, z=23.75

Batas atas = 23.75

Subproblem 2

1 4,

x = x2=0.83, z=23.33

Batas atas = 23.75

Subproblem 3

1 3, 2,2

x = x = z=23 Batas bawah = 23

Solusi Optimal

Subproblem 7

1 4, 0, 2 20

x = x = z=

Batas bawah = 20 Kandidat Solusi Subproblem 5

1 4.5,

x = x2 =0,z=22.5 Batas atas = 23.75

Subproblem 6 takfisibel Subproblem 4

takfisibel

t = 1

t = 7

t = 4

t = 6 t = 2

t = 5 t = 3

1 4

x ≥ x1≤3

2 1

x ≥ x₂≤0

1 5

12

III DEKOMPOSISI BENDERS

Dekomposisi Benders (Benders, 1962) merupakan metode yang digunakan pada masalah yang memiliki variabel-variabel

kontinu dalam jumlah besar, variabel integer

relatif sedikit, dan struktur khusus pada kendala-kendalanya.

Prosedur Dekomposisi Benders

Prosedur metode dekomposisi Benders menyelesaikan masalah pemrograman linear primal (P) berikut dengan menganggap salah satu vektor variabel pada masalah tersebut,

dalam hal ini Y, bernilai tetap sedemikian

sehingga untuk sembarang iterasi dari algoritme ini nantinya masalah-masalah yang memuat salah satu vektor variabel, namun tidak keduanya, dapat diselesaikan.

Misalkan diberikan masalah primal

max

terhadap

z= +

+ ≤ ≥ ≥ CX DY AX EY b

X 0 Y 0

(P)

dengan X dan Y vektor-vektor berukuran n, C

dan D vektor-vektor 1 ×n, A dan E

matriks-matriks m×n, dan b vektor m× 1.

Misalkan vektor Y dianggaptetap pada suatu

nilai yang diberikan, dengan Y ≥ 0, maka

masalah (P) di atas dapat direduksi menjadi bentuk berikut

max terhadap .

v= + ≤ − ≥ CX DY AX b EY

X 0

(PX)

Misalkan u adalah vektor dual, maka dual

dari masalah (PX) adalah

min ( )

terhadap .

w= −

≥ ≥ u b EY uA C

u 0

(D1)

Taha (1975) menyebutkan bahwa masalah (D1) di atas memiliki dua sifat penting, yakni:

i) daerah solusi fisibelnya adalah

{ , }

R= u uA≥C u≥0 yang bebas dari

pemilihan Y;