EKSPONEN TITIK DARI SEBUAH KELAS DIGRAPH DWIWARNA DENGAN SATU LOOP
SKRIPSI
SITI SAHARA 090803001
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
EKSPONEN TITIK MASUK DARI SEBUAH KELAS DIGRAF DWI-WARNA
DENGAN N-TITIK GANJIL
SKRIPSI
Diajukan untuk melengkapi tugas akhir dan memenuhi syarat mencapai gelar
Sarjana Sains
SITI SAHARA 090803001
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
i
PERSETUJUAN
Judul : EKSPONEN TITIK MASUK DARI SEBUAH KELAS
DIGRAF DWIWARNA DENGAN N-TITIK GANJIL
Kategori : SKRIPSI
Nama : KARTIKA DEWI PUTRI
Nomor Induk Mahasiswa : 090803072
Program Studi : SARJANA (S1) MATEMATIKA
Departemen : MATEMATIKA
Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN ALAM
(FMIPA) UNIVERSITAS SUMATERA UTARA
Medan, November 2013
Komisi Pembimbing :
Pembimbing 2 Pembimbing 1
Dr. Mardiningsih, M.Si Prof. Dr. Saib Suwilo, M.Sc
NIP.19630405 198811 2 001 NIP.19640109 198803 1 004
Diketahui oleh :
Departemen Matematika FMIPA USU Ketua,
PERNYATAAN
EKSPONEN TITIK MASUK DARI SEBUAH KELAS DIGRAF DWIWARNA DENGAN N-TITIK GANJIL
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa ku-tipan dan ringkasan penting yang masing-masing disebutkan sumbernya.
Medan, November 2013
iii
PENGHARGAAN
Segala puji dan syukur bagi Tuhan semesta alam, Allah SWT yang melimpahkan rahmat dan ridho-Nya sehingga penulis dapat menyelesaikan skripsi yang berjudul
”EKSPONEN TITIK MASUK DARI SEBUAH KELAS DIGRAF
DWI-WARNA DENGAN N-TITIK GANJIL” ini dengan baik. Shalawat beriring
salam kepada Nabi Muhammad SAW beserta keluarga dan para sahabat.
Terima kasih penulis ucapkan kepada semua pihak yang telah membantu, mem-otivasi, dan mendo’akan penulis dari awal penulisan hingga selesai penulisan skripsi ini, yaitu kepada
1. Bapak Prof. Dr. Tulus, M.Si, dan Ibu Dr. Mardiningsih, M.Si, selaku Ketua dan Sekretaris Departemen Matematika FMIPA USU Medan.
2. Bapak Prof. Dr. Saib Suwilo, M.Sc, selaku Dosen Pembimbing I dan Ibu Dr. Mardiningsih, M.Si, selaku Dosen Pembimbing II, yang telah banyak membantu penulis dan memberikan dukungan baik berupa nasihat, motivasi maupun ilmu pengetahuan kepada penulis dalam menyelesaikan penelitian ini.
3. Bapak Prof. Dr. Tulus, M.Si, selaku Dosen Pembanding I, dan Bapak Drs. Suwarno Ariswoyo, M.Si, selaku Dosen Pembimbing II, yang telah memberikan nasehat, kritik dan saran yang membangun selama penelitian.
4. Seluruh staf pengajar dan staf administrasi Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Sumatera Utara, Medan.
Penulis juga mengucapkan terima kasih kepada Ibunda Rahmawati dan Ayahanda Zainal Arifin yang begitu sabar membimbing, mendo’akan dan memberikan dukun-gan moril maupun materil serta motivasi kepada penulis untuk segera menyelesaikan skripsi ini. Kepada Kakanda Ayu Wardhani, yang senantiasa menyemangati penulis. Mardhatillah dan Siti Sahara yang senantiasa saling memotivasi, saling mendo’akan dan saling membantu dalam menyelesaikan skripsi ini.
Penulis juga mengucapkan terima kasih kepada Kak Laras, Kak Linda, Kak Nurul, Jundi, Bakti, Lukas, Panca, Fitri, Izzati, Vela, Ade, Mantari, Matematika 2009, IM3 dan rekan-rekan lainnya. Semoga Allah SWT memberi balasan atas ban-tuan yang telah diberikan kepada penulis.
Penulis menyadari masih banyak kekurangan dalam penulisan ini, untuk itu saran dan kritik yang membangun dari pembaca sangat diperlukan. Akhir kata penulis mengucapkan terima kasih atas perhatiannya, semoga tulisan ini bermanfaat.
ABSTRAK
Sebuah digraf dwiwarna D(2) adalah primitif jika terdapat bilangan bulat tak negatif s dan t sehingga untuk setiap pasang titik u dan v di D(2) terdapat (s, t)-walk dari u ke v. Bilangan bulat positif s+t terkecil dari semua bilangan bulat tak negatif s dan t yang demikian disebut eksponen dari digraf dwi-warna D(2) dan dinotasikan dengan exp(D(2)). Misalkan v adalah sebarang titik di D(2). Eksponen titik masuk dari titikv padaD(2) adalah bilangan bulat positif terkecils+tsehingga untuk setiap titikudiD(2) terdapat (s, t)-walk dari titikuke titikv, dinotasikan dengan expin(v). Tulisan ini mendiskusikan eksponen titik masuk dari sebuah kelas digraf dwi-warna primitifD(2) atasn ≥5 titik yang terdiri dari n-cyclev1→v2 →v3 → · · · →vn→v1 dan n−1
2
-cycle v1 → v2 → v3 → · · · → vn+1 2
→ v1 dengan tiga arc biru, vn → v1 , vn+1
2
→vn+3 2 andv
n+1 2
→v1. Diperlihatkan bahwa eksponen titik masuk dari sebarang titik vk diD(2) adalah expin(vk) = 1
2(n2−n+ 2k−2) for k= 1,2,· · ·, n
v
INNER VERTEX EXPONENTS OF A CLASS TWO-COLORED DIGRAPH ON ODD VERTICES
ABSTRACT
A two-colored digraph D(2) is primitive provided there are nonnegative integers and t such that for each pair of verticesuand v there exsist a (s, t)-walk from vertex uto vertex v. The smallest positive integers+t taken over all such nonnegative integers s and t is the exponent of a two-colored digraph D(2), denoted by exp(D(2)). Let v be a vertex of D(2). The inner vertex exponent v is the smallest positive integers+t such that for every vertex u in D(2) there is an (s, t)-walk from u to v, denoted by expin(v). This paper discuss inner vertex exponent of primitive two colored-digraph D(2) on n ≥5 vertices consisting n-cyclev1 → v2 →v3 → · · · →vn→ v1 and
n−1 2
-cycle v1 → v2 → v3 → · · · → vn+1
2 with three blue arcs, vn → v1 , v
n+1 2 → v
n+3 2 and vn+1
2
→v1. The inner vertex exponent of vk inD(2) isexpin(vk) = 1 2(n
2−n+ 2k−2) for k = 1,2,· · ·, n
DAFTAR ISI
Halaman
PERSETUJUAN i
PERNYATAAN ii
PENGHARGAAN iii
ABSTRAK iv
ABSTRACT v
DAFTAR ISI vi
DAFTAR GAMBAR vii
BAB 1 PENDAHULUAN
1.1 Latar Belakang Penelitian 1
1.2 Perumusan Masalah 3
1.3 Tujuan Penelitian 3
1.4 Manfaat Penelitian 3
BAB 2 DIGRAF DWI-WARNA PRIMITIF
2.1 Definisi 4
2.2 Matriks Adjacency 6
2.3 Primitifitas 9
2.4 Matriks Tak Negatif dan Eksponen Digraf Dwi-warna 11 2.5 Eksponen Titik Masuk Digraf dan Digraf Dwi-warna 18
2.6 Sistem Persamaan Diophantine 21
2.7 Formula Eksponen Titik Masuk Digraf Dwi-warna 22
BAB 3 METODOLOGI PENELITIAN
3.1 Komputasi Nilai Eksponen Titik Masuk 26
3.1 Pembuktian Nilai Eksponen Titik Masuk 26
BAB 4 EKSPONEN TITIK MASUK DIGRAF DWI-WARNA PRIMITIF 28
BAB 5 KESIMPULAN DAN SARAN
5.1 Kesimpulan 34
5.2 Saran 35
vii
DAFTAR GAMBAR
Gambar Halaman
1.1 Digraf Dwi-warna Primitif 3
2.1 Digraf 5
2.2 Digraf Dwi-warna 6
2.3 Digraf dengan 6 titik dan 8 arc 7
2.4 Digraf dwi-warna dengan 6 titik 8 arc 8
ABSTRAK
Sebuah digraf dwiwarna D(2) adalah primitif jika terdapat bilangan bulat tak negatif s dan t sehingga untuk setiap pasang titik u dan v di D(2) terdapat (s, t)-walk dari u ke v. Bilangan bulat positif s+t terkecil dari semua bilangan bulat tak negatif s dan t yang demikian disebut eksponen dari digraf dwi-warna D(2) dan dinotasikan dengan exp(D(2)). Misalkan v adalah sebarang titik di D(2). Eksponen titik masuk dari titikv padaD(2) adalah bilangan bulat positif terkecils+tsehingga untuk setiap titikudiD(2) terdapat (s, t)-walk dari titikuke titikv, dinotasikan dengan expin(v). Tulisan ini mendiskusikan eksponen titik masuk dari sebuah kelas digraf dwi-warna primitifD(2) atasn ≥5 titik yang terdiri dari n-cyclev1→v2 →v3 → · · · →vn→v1 dan n−1
2
-cycle v1 → v2 → v3 → · · · → vn+1 2
→ v1 dengan tiga arc biru, vn → v1 , vn+1
2
→vn+3 2 andv
n+1 2
→v1. Diperlihatkan bahwa eksponen titik masuk dari sebarang titik vk diD(2) adalah expin(vk) = 1
2(n2−n+ 2k−2) for k= 1,2,· · ·, n
v
INNER VERTEX EXPONENTS OF A CLASS TWO-COLORED DIGRAPH ON ODD VERTICES
ABSTRACT
A two-colored digraph D(2) is primitive provided there are nonnegative integers and t such that for each pair of verticesuand v there exsist a (s, t)-walk from vertex uto vertex v. The smallest positive integers+t taken over all such nonnegative integers s and t is the exponent of a two-colored digraph D(2), denoted by exp(D(2)). Let v be a vertex of D(2). The inner vertex exponent v is the smallest positive integers+t such that for every vertex u in D(2) there is an (s, t)-walk from u to v, denoted by expin(v). This paper discuss inner vertex exponent of primitive two colored-digraph D(2) on n ≥5 vertices consisting n-cyclev1 → v2 →v3 → · · · →vn→ v1 and
n−1 2
-cycle v1 → v2 → v3 → · · · → vn+1
2 with three blue arcs, vn → v1 , v
n+1 2 → v
n+3 2 and vn+1
2
→v1. The inner vertex exponent of vk inD(2) isexpin(vk) = 1 2(n
2−n+ 2k−2) for k = 1,2,· · ·, n
PENDAHULUAN
1.1 Latar Belakang Penelitian
Salah satu bentuk penerapan matriks primitif telah dilakukan olehGoogle Search Engineuntuk proses merankingwebsite. Parameter yang digunakan adalah vektor eigen dari matriks H. Matriks H adalah matriks yang tiap barisnya merupakan normalisasi hyperlink dengan Hij = Pi1, dengan Pi adalah banyak link dari
hala-man web, atau yang direpresentasikan sebagai titik, dariidan 0 jika tidak terdapat link. Parameter lain yang mendukung adalah eksponen dari digraf primitif yang bersesuaian (Langville dan Meyer, 2006).
MisalkanAadalah matriksn×n tak negatif, yaitu setiap unsur diA berni-lai tak negatif. A dikatakan primitif jika dan hanya jika terdapat bilangan bulat positifk sedemikian hingga setiap unsur diAk adalah positif. Nilai terkecil darik
yang demikian disebut eksponen dari A, dinotasikan dengan exp(A).
Studi tentang eksponen dari matriks tak negatif A biasanya dilakukan melalui digraf D yang bersesuaian dengan A. Digraf D adalah digraf dengan n-titik sehingga terdapat arc vi → vj di D jika dan hanya jika aij > 0, aij ∈ A.
Sebuah digrafDterhubung kuat jika untuk setiap pasang titik (vi, vj) diD
terda-pat walk berarah (directed walk) dari vi ke vj dan dari vj kevi. Digraf D primitif
jika dan hanya jika terdapat bilangan bulat positif m dimana ada sebuah walk dengan panjang m dari setiap pasang titik di D. Minimum m adalah eksponen dari D, dinotasikan dengan exp(D). Jika terdapat walk dengan panjang l yang menghubungkan titikvi ke setiap titik di D, maka nilai terkecill disebut sebagai
eksponen titik keluar dariD, dinotasikan dengan expoutD(vi). Jika terdapat walk
dengan panjang l yang menghubungkan setiap titik di D ke titik vi, maka nilai
2
Digraf denganarcyang diwarnai dengan merah atau biru, namun tidak ke-duanya pada satuarcsekaligus disebut digraf dwi-warna, dinotasikan sebagai D(2) (Fornasini dan Valcher, 1997). Digraf dwi-warna adalah primitif dengan syarat terdapat bilangan bulat tak negatifs dan t sehingga untuk setiap pasangan yang tidak harus berbeda titik vi dan vj terdapat sebuah walk (s, t) di D(2) dari vi ke
vj, dengan masing-masing sdan tadalah panjang walk berwarna merah dan biru.
Eksponen dari digraf dwi-warna primitifD(2) adalah bilangan bulat positif terkecil dari s+t dari semua jumlahan yang mungkin dari bilangan bulat tak negatif s dant. Eksponen titik keluar dari digraf dwi-warna primitif adalah bilangan bulat positif terkecilp+q sedemikian hingga terdapat walk (p, q) dari titikvi ke setiap
titik diD(2) , dinotasikan dengan expoutD(2)(vi). Eksponen titik masuk dari digraf
dwi-warna primitif adalah bilangan bulat positif terkecilm+nsedemikian hingga terdapat walk (m, n) dari setiap titik di D(2) ke titik vi di D(2) , dinotasikan
den-gan expinD(2)(vi).
Penelitian mengenai eksponen dari digraf dwi-warna dimulai oleh Shader dan Suwilo (2003). Sejak saat itu, penelitian yang berkaitan dengan eksponen digraf dwi-warna mengalami perkembangan. Salah satunya penelitian mengenai eksponen dari sebuah kelas digraf dwi-warna yang dilakukan oleh Bai dan Shao (2007). Diperlihatkan batasan eksponen digraf pada sebuah digraf dengan n-titik ganjil yang memuat cycle v1 → v2 → v3 → ... → vn → v1 dan memuat arc vn →vn+1
2 . Eksponen titik mulai diperkenalkan oleh Gao dan Shao (2009).
Diper-lihatkan eksponen titik keluar dari setiap titik pada digraf dwi-warna Wielandt, yaitu digraf dengan n ≥ 3 titik yang memuat cycle vn → vn−1 → ... → v2 →
v1 → vn dan memuat arc v1 → vn−1. Penelitian mengenai eksponen titik keluar
pada sebuah kelas digraf Hamilton dwi-warna juga telah dilakukan oleh Syah-marani dan Suwilo (2012). Diperlihatkan batasan dari eksponen titik keluar dari digraf Hamilton dwi-warna primitif L(2)n dengan n ≥ 5 titik yang memuat cycle
v1 →vn→vn−1 →...→ v2 →v1 dan memuat arc v1 →vn−1.
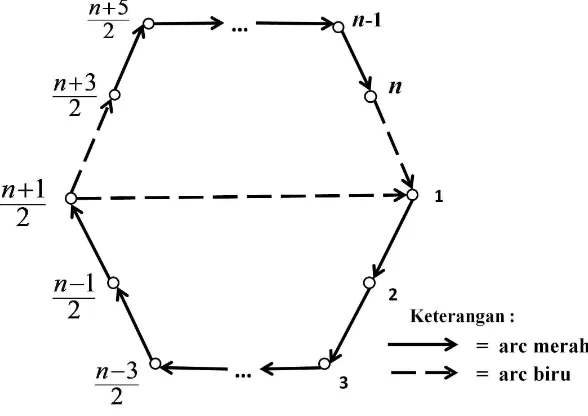
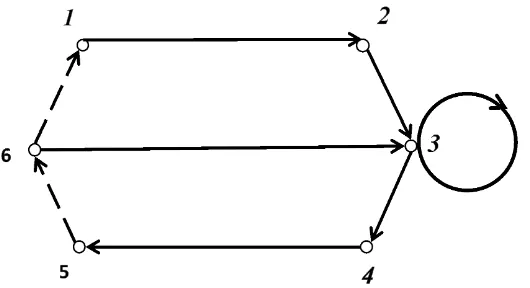
Andaikan D(2) adalah digraf dwi-warna yang terdiri dari n-titik ganjil dimana n ≥ 5, dengan 3 arc biru pada arc vn → v1, vn+1
2 → v1, v n+1
2 → v
n+3
2 dan arc
lainnya berwarna merah, serta memuatcycle dengan panjang ndan n+1
2 . Masalah dari penelitian ini adalah siapa eksponen titik masuk dari digraf dwi-warna seperti pada Gambar 1.1 berikut.
Gambar 1.1 Digraf Dwi-warna Primitif
1.3 Tujuan Penelitian
Tujuan penelitian ini adalah untuk mendapatkan pola dari eksponen titik ma-suk digraf dwi-warna dengan n-titik ganjil seperti pada Gambar 1.1.
1.4 Manfaat Penelitian
BAB 2
DIGRAF DWI-WARNA PRIMITIF
Pada Bab ini akan dijelaskan beberapa konsep dasar seperti definisi dan teorema yang dijadikan landasan dalam penelitian ini. konsep dasar yang dimaksud adalah yang berkaitan dengan permasalahan dalam penelitian ini seperti keterhubungan, primitifitas, eksponen dan eksponen titik masuk dari digraf dan digraf dwi-warna.
2.1 Definisi
Pada subbab ini akan diberikan definisi tentang digraf dan digraf dwi-warna serta notasi-notasi yang akan dipergunakan dalam pembahasan selanjutnya.
2.1.1 Digraf
Graf adalah himpunan tak kosong dari titik-titik yang dihubungkan oleh garis. Jika garis yang menghubungkan titik-titik tersebut diberikan arah, maka disebut sebagai digraf, dan dinotasikan sebagai D. Dengan kata lain, sebuah digraf D terdiri dari dua himpunan, yaitu :
1. Himpunan titik yang dinotasikan dengan V = {v1, v2, v3,· · · , vn} dengan i
adalah bilangan bulat positif danvi adalah elemen dari himpunanV,n(V)6=
0.
2. Himpunan E yang merupakan himpunan pasangan berurut V ×V yang tak harus berbeda dari semua titik, elemen dari E disebut arcdari digrafD.
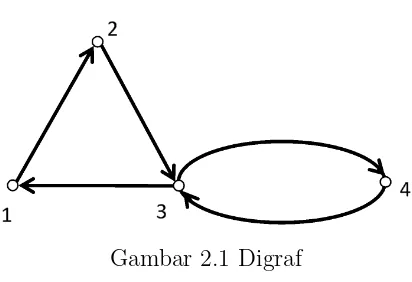
Jika diberikan notasi E = (v1, v3) berarti terdapat sebuah arc dari titik v1 ke v3 atau dapat dituliskan dengan notasi v1 →v3.
Gambar 2.1 Digraf
Andaikan suatu digrafD dengan ntitik, denganu danv adalah titik diD. Suatu walk dengan panjangm dariu danv adalah suatu barisanarcdiDdalam bentuk v0 → v1 → v2 → · · · → vm dengan m ≥ 0, v0 = u dan vm = v. Jika u = v
maka walk tersebut dikatakan walk tertutup dan jika u 6= v maka walk tersebut dikatakanwalk terbuka. Suatupath adalahwalk dengan titik yang tidak berulang, tetapi titik awal dan titik akhir boleh berulang yang disebutpath tertutup. Suatu path tertutup u → v disebut dengan cycle dan cycle dengan panjang 1 disebut loop.
Berikut penjelasan berdasarkan Gambar 2.1
1. Barisan arcv1 →v2 →v3 →v1 →v2 →v3 →v4 disebut walk dari v1 ke v4
2. Barisan arcv1 →v2 →v3 →v4 disebut pathdari v1 kev4
3. Barisan arcv1 →v2 →v3 →v1 disebut path tertutupatau cycle
2.1.2 Digraf Dwi-warna
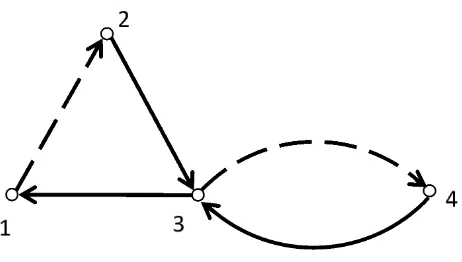
Digraf dengan arc yang diwarnai dengan merah atau biru, namun tidak kedu-anya pada satu arc sekaligus disebut digraf dwi-warna, dinotasikan dengan D(2) (Fornasini dan Valcher, 1997). Sebuaharcmerah dari titikuke titikv akan dino-tasikan denganu→r vdanarcbiru dari titikuke titikvdinotasikan denganu→b v.
6
Gambar 2.2 Digraf Dwi-warna
Sebuah (s, t)-walkpada digraf dwi-warna D(2)adalah sebuah walkyang terdiri dari s buah arc merah dan t buah arc biru. Andaikan sebuah walk w, dengan r(w) danb(w) masing-masing adalah banyakarcmerah danarcbiru padawalk w, maka dapat dinotasikan sebagai l(w) =r(w) +b(w) atau dapat direpresentasikan
dalam bentuk vektor, yaitu
"
r(w) b(w)
#
.
Suatupathadalah walkdengan titik yang tidak berulang, tetapi titik awal dan titik akhir boleh berulang yang disebutpath tertutup. Suatupath tertutupu →v disebut dengan cycle dan cycle dengan panjang 1 disebutloop, dengan komposisi
"
Berikut adalah penjelasan berdasarkan Gambar 2.2.
1. v1
→v1 adalah path tertutupataucycledengan komposisi
"
2 1
#
.
yaitu matriks yang elemennya adalah 0 atau 1, yang disebut sebagai matriks ad-jacency.
2.2.1 Matriks Adjacency Digraf
Sebuah matriks adjacency dari digraf dengan n-titik adalah matriks berordo n A(D) = [aij] dengan
aij =
1 jikaterdapatarcdarivikevj,
0 sebaliknya.
Contoh 2.2.1Berikut ini adalah representasi digraf yang terdiri dari 6 titik dan 8arc. Dari digraf berikut dapat dibentuk sebuah matriksadjacencydengan mem-perhatikanarc yang menghubungkan titik-titik pada digraf tersebut.
Gambar 2.3 Digraf dengan 6 titik dan 8arc
Matriksadjacency dari digraf di atas adalah sebagai berikut.
A(D) =
0 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 1 0 1 0 0 0
2.2.2 Matriks Adjacency Digraf Dwi-warna
8
dua, yaitu matriks adjacency berorde n untuk arc merah R = [rij] dan matriks
adjacency untukarcbiru B = [bij] dengan ketentuan sebagai berikut.
R= [rij] =
1, jikaterdapatarcmerahdarivikevj
0, jikasebaliknya.
1, jikaterdapatarcbirudarivikevj
0, jikasebaliknya.
Contoh 2.2.2Berikut adalah digraf dwi-warna yang terdiri dari 6 titik dengan 6 arcmerah dan 2arc biru.
Gambar 2.4 Digraf dwi-warna dengan 6 titik dan 8arc
Matriksadjacency dari digraf dwi-warna di atas adalah sebagai berikut.
2.3 Primitifitas
Pada subbab ini akan dibahas mengenai digraf dan digraf dwi-warna terhubung kuat dan primitifitasnya.
2.3.1 Digraf Primitif
Sebuah digrafDterhubung kuat jika untuk setiap pasang titik (vi, vj) diD
terda-pat walkberarah (directed walk) dari vi kevj dan dari vj ke vi . Digraf D primitif
jika dan hanya jika terdapat bilangan bulat positif m dimana ada sebuah walk dengan panjang m dari setiap pasang titik di D.
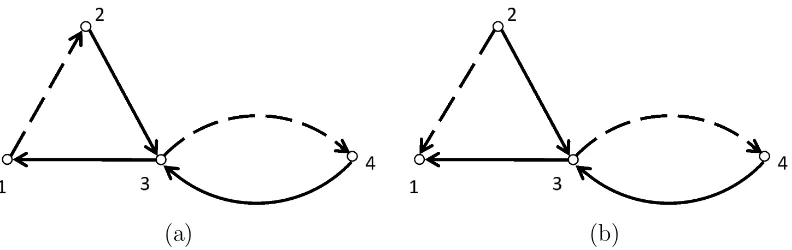
Contoh 2.3.1Berikut adalah contoh digraf terhubung kuat dan tidak terhubung kuat.
(a) (b)
Gambar 2.5 Digraf terhubung kuat dan tidak terhubung kuat
Gambar 2.5(a) menunjukkan digraf terhubung kuat karena terdapat walk dari tiap pasang titik di digraf D, dan Gambar 2.5(b) menunjukkan digraf tidak ter-hubung kuat, karena tidak terdapatwalk dari v3 ke v4.
Digraf D yang terhubung kuat dikatakan primitif, jika terdapat suatu bilangan bulat positif m sedemikian hingga untuk setiap pasang titik u dan v di D terdapat suatu walk dengan panjang m.
Lemma 2.3.1Andaikan D adalah digraf terhubung kuat, maka setiap titik v di D terletak pada cycle.
10
titik di D, maka setiap titik v di Dpasti terletak pada suatu cycle.
2.3.2 Digraf Dwi-warna Primitif
Sebuah digraf dwi-warna D(2) adalah terhubung kuat jika untuk setiap pasang titik u dan v di D(2) terdapat walk dari titik u ke titik v dan walk dari titik v ke titikutanpa memperhatikan warna setiaparcyang dilalui. Berikut adalah contoh digraf dwi-warnaD(2) terhubung kuat dan digraf dwi-warnaD(2) tidak terhubung kuat.
Contoh 2.3.2 Representasi dari digraf dwi-warna terhubung kuat
(a) (b)
Gambar 2.6 Digraf dwi-warna terhubung kuat dan tidak terhubung kuat
Gambar 2.6 memperlihatkan bahwa (a) adalah digraf dwi-warna D(2) terhubung kuat karena terdapat walk dari satu titik ke titik yang lain dan (b) adalah digraf dwi-warnaD(2) yang tidak terhubung kuat karena tidak terdapatwalkdariv1 kev2.
Sebuah digraf dwi-warna terhubung kuat D(2) disebut primitif jika ter-dapat bilangan tak negatif s dan t sehingga untuk setiap pasang titik u dan v di D(2) terdapat (s, t)-walk dari u ke v. Andaikan C = {C1, C2, ..., Ct} adalah
himpunan semuacycleyang terdapat di D(2) dan didefinisikanM sebagai matriks cycle dari D(2) orde 2×t dengan setiap kolom ke-i dari M merupakan komposisi dari cycle-cycle Ci, i= 1,2, ..., t seperti berikut
M =
"
r(C1) r(C2) · · · r(Ct)
b(C1) b(C2) · · · b(Ct)
#
.
perseku-Valcher, 1997).
Lemma 2.3.2 Andaikan D(2) adalah digraf dwi-warna terhubung kuat dengan paling sedikit satu arc setiap warna. Misalkan M adalah matriks cycle dari D(2). DigrafD(2) adalah primitif jika dan hanya jika content dari matriks M adalah 1.
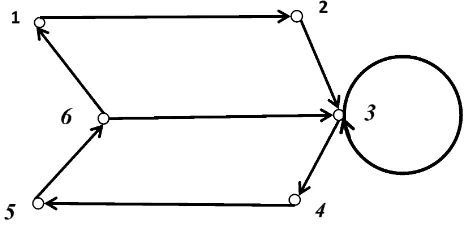
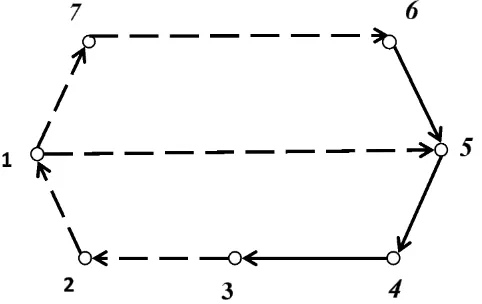
Contoh 2.3.3Representasi digraf dwi-warna terhubung kuat dan primitif
Gambar 2.7 Digraf dwi-warna terhubung kuat dan primitif.
Digraf dwi-warna D(2) pada Gambar 2.7 adalah terhubung kuat yang terdiri dari
cycle v1
b
→ v7
b
→ v6
r
→ v5
r
→ v4
r
→ v3
b
→ v2
b
→ v1 dengan komposisi
"
3 4
#
, dan
cycle v1 →b v5 →r v4 →r v3 →b v2 →b v1 dengan komposisi
"
2 3
#
dan maka matriks
cycle dari D(2) adalah M =
"
3 2 4 3
#
dengan det (M) = 1. Oleh karena det (M)
= 1, maka digraf dwi-warna terhubung kuatD(2) adalah primitif.
2.4 Matriks Tak Negatif dan Eksponen Digraf Dwi-warna
Berikut ini akan dibahas pengertian matriks tak negatif dan hubungannya dengan Digraf dwi-warna D(2).
2.4.1 Matriks Tak Negatif
Matriks tak negatifAmerupakan sebuah matriks yang setiap entriaijdariAadalah
12
bilangan bulat positif maka matriks tersebut disebut matriks positif. Perhatikan dua buah matriks berikut ini.
A=
0 1 1 2 0 3 5 7 0
, matriks tak negatif; B =
9 3 1 5 7 2 6 1 1
, matriks positif.
2.4.2 Eksponen Digraf
Eksponen dari sebuah digraf D merupakan bilangan bulat positif terkecil k se-hingga untuk setiap pasang titik u dan v di D terdapat walk dari u ke v dengan panjangk dan dinotasikan dengan exp(D).
Proposisi 2.4.2 A adalah suatu matriks adjacency dari digraf D. Entri ak ij dari
Ak menyatakan banyak walk dari v
i ke vj dengan panjang k di digraf D.
Bukti. Andaikan A adalah suatu matriks adjacency dari digraf D, maka setiap entri (i, j) dariAmenyatakanarcdari titikvi kevj di digrafD. Ini mengakibatkan jikak= 1, maka setiap entria1ij dariA1 menyatakanwalkdari titikvi kevj dengan panjang 1.
Andaikan setiap entri a(ijk) dari Ak menyatakan banyaknya walk dari titik v i ke
vj yang panjangnya k diD, untuk k ≥1. Selanjutnya akan diperlihatkan bahwa
a(ijk+1)adalah banyaknyawalkdarivi kevj dengan panjangk+1 diDdengank ≥1.
Perhatikan setiap walk dari titik vi ke vj diD dengan panjang k+ 1 yang
terdiri dari walk vi ke vl dengan panjang k untuk l = 1,2, ..., n, dan dilanjutkan
dengan arc dari titik vi ke vj, sehingga a(ilk) aij menyatakan walk dengan panjang
k+ 1 dari titikvi ke vj di D untuk k = 1,2, ..., n. Jika tidak terdapat walk yang
panjangnya k dari titik vi ke vj di D, maka ail(k) = 0 sehingga a(ilk) aij = 0. Hal
ini berakibat tidak terdapatwalk yang panjangnyak+ 1 dari titikvi kevj melalui
titikvl di D sehingga diperoleh banyaknyawalk yang panjangnyak+ 1 dari titik
vi kevj di D adalah
ai(k1)a1j+ai(2k)a2j +...+a(ink)anj = n
X
karena
Sehingga a(ijk+1) adalah benar menyatakan banyaknyawalk dari titikvi ke titikvj
yang panjangnyak+ 1 di D. Berikut adalah contoh menentukan eksponen suatu digraf dengan menggunakan proposisi 2.1.
Contoh 2.4.2 Perhatikan Gambar 2.5(a). Matriks adjacency dari digraf pada Gambar 2.5(a) adalah sebagai berikut
A=
Berdasarkan Proposisi 2.4.2, banyaknyawalkdari titikvike titikvjdengan
pan-jangk dinyatakan oleh entriak
ij dari matriksAk yang semuanya positif. Eksponen
dari digraf D adalah bilangan positif terkecilk yang mengakibatkan matriks Ak
positif. Perhatikan matriks berikut.
a. Untuk k= 1; diperoleh A1 =
Bukan eksponen dari digraf pada contoh 2.4.2, karena tidak terdapat walk dengan panjang 1 dari titik 1 ke titik 4, titik 2 ke titik 3, titik 3 ke titik 2, titik 4 ke titik 3 dan titik 3 ke titik 4.
14
dengan panjang 2 dari titik 1 ke titik 2, titik 1 ke titik 3, titik 2 ke titik 3, titik 2 ke titik 4 , titik 3 ke titik 4, dan titik 4 ke titik 1.
Bukan eksponen dari digraf pada contoh 2.4.2, karena tidak terdapat walk dengan panjang 3 dari titik 1 ke titik 4, titik 2 ke titik 4, titik 3 ke titik 1, titik 3 ke titik 2, titik 4 ke titik 2 dan titik 4 ke titik 3.
Bukan eksponen dari digraf pada contoh 2.4.2, karena tidak terdapat walk dengan panjang 4 dari titik 2 ke titik 3, dan titik 3 ke titik 4.
e. Untuk k= 5; diperoleh A5 =
Bukan eksponen dari digraf pada contoh 2.4.2, karena tidak terdapat walk dengan panjang 5 dari titik 2 ke titik 4.
f. Untuk k= 6; diperoleh A6 =
Karena terdapat walk dengan panjang 6 dari tiap pasang titik yang ada diD, maka eksponen dari digraf pada contoh 2.4.2 adalah exp(D) = 6.
2.4.3 Eksponen Digraf Dwi-warna
bu-sehingga untuk setiap pasang titikudan v diD(2) terdapat sebuah (s, t)-walkdari u ke v yang terdiri dari s-arc merah dan t-arc biru. Eksponen dari digraf dwi-warna D(2) dinotasikan oleh exp(D(2)).
Andaikan A dan B adalah matiks tak negatif orde m. Untuk bilan-gan tak negatif s dan t, didefinisikan (s, t)-Hurwitz product, (A, B)(s,t) dari A dan B adalah jumlah keseluruhan matriks dari hasil perkalian A sebanyak s kali dan B sebanyak t kali. Sebagai contoh, (A, B)(1,0) = A, (A, B)(0,1) = B, (A, B)(1,1)=AB+BAdan (A, B)(2,2)=A2B2+ABAB+AB2A+BABA+B2A2.
Lemma 2.4.3 Jika (R,B) adalah matriks adjacency dari digraf dwi-warna D(2), maka entri (i, j)dari (R, B)(s,t) adalah jumlah (s, t)-walk dari titik u ke v di D(2).
Bukti. Akan dibuktikan dengan induksi pada (s+t) dan (s+t+1), jikas = 0 maka t= 1 atau jika s= 1 maka t = 0. Jika s= 0 maka entri (i,j) dari (R, B)(0,1) =B
adalah walk dengan komposisi
"
0 1
#
di D(2). Dengan cara yang sama, jika s = 1
dan t = 0 maka (R, B)(1,0) = R adalah walk dengan entri (i, j) menyatakan walk
dengan komposisi
"
1 0
#
di D(2).
Anggap Lemma 2.4.3 benar untuk semua bilangan bulat tak negatifs′ dan t′ dengan s′ +t′ ≤ s+t, akan diperlihatkan untuk s+t+ 1 juga benar dengan catatan sebagai berikut
(R, B)(s+1,t)=R(R, B)(s,t)+B(R, B)(s+1,t−1)
dengan induksi matematika entri (i, j) pada R(R, B)(s,t) adalah walk dari v
i kevj
yang dimulai denganarcmerah diikuti oleh sebuah (s, t)-walkdan entri (i, j) pada B(R, B)(s+1,t−1) adalah jumlahwalk dari v
i kevj yang dimulai dengan sebuah arc
biru dan diikuti oleh sebuah (s+ 1, t−1)-walk sedemikian hingga entri (i, j) dari (R, B)(s+1,t) adalah jumlah (s+ 1, t)-walk dari ike j. Perhatikan contoh berikut.
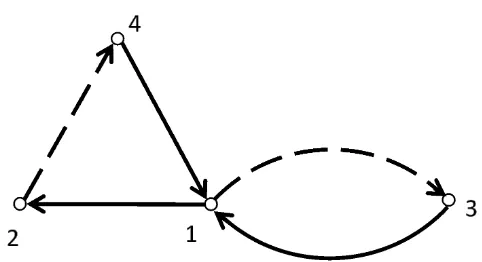
16
Gambar 2.8 Digraf dwi-warna dengan 4 titik dan 5arc
Matriksadjacency merah dan biru dari Gambar 2.8 adalah
R=
Berdasarkan Lemma 2.4.3, banyaknya walk dari titik i ke titik j dengan panjang s +t adalah entri (i, j) dari (R, B)(s,t) yang semuanya bernilai positif, dan (s+t) terkecil dari yang demikian adalah eksponen dari matriks (R, B)(s,t). Perhatikan matriks (R, B)(s,t) berikut
2. (R, B)(0,2) =B2 =
18
6. (R, B)(7,5) =R(R, B)(6,5)+B(R, B)(7,4) =
10 5 4 6 6 4 1 3 5 1 6 4 5 1 6 4
Karena terdapat walk dengan panjang 12 dari tiap pasang titik pada di-graf dwi-warnaD(2), maka eksponen dari digraf dwi-warna D(2) pada Gambar 2.8
adalah exp(D2) = 12, dengan komposisi
"
7 5
#
yang terdiri 7 arcmerah dan 5 arc
biru.
2.5 Eksponen Titik Masuk Digraf dan Digraf Dwi-warna
Pada subbab ini akan dibahas mengenai definisi eksponen titik masuk digraf D dan eksponen titik masuk digraf dwi-warna D(2) serta contoh bagaimana menen-tukan eksponen titik masuk dari digrafD dan digraf dwi-warna D(2).
2.5.1 Eksponen Titik Masuk Digraf
MisalkanDadalah sebuah digraf primitif atasntitikv1, v2, ..., vn. Untuk sebarang
vi diD, i= 1,2, ..., n,eksponen titik vi yang dinotasikan dengan expinD(vi) adalah
bilangan bulat positif terkecilk sedemikian hingga terdapatwalk dengan panjang k dari setiap titik di ke titikvi diD, dan himpunan eksponenexpD(X) adalah
bi-langan bulat positif terkecilpsehingga untuk setiap titikvj di Dterdapat sebuah
walk dari paling sedikit satu titik di X ke vj dengan panjang p.
Andaikan D adalah digraf primitif orde n. Jika titik-titik di D adalah (v1, v2, ..., vn) sedemikian hingga
expD(v1)≤expD(v2)≤ · · · ≤expD(vn)
maka expD(vk) adalah tipe pertama generalisasi eksponen ke-kdariD, dinotasikan
expD(vk) (Brualdi dan Liu, 1990).
Matriksadjacency dari digraf pada Gambar 2.5(a) adalah sebagai berikut
Berdasarkan Proposisi 2.4, eksponen titik dari Ddiperoleh dengan melihat entriaij dari Ak, dengan entri pada kolom ke-i harus bernilai positif. Perhatikan
matriks Ak berikut
a. Untuk k= 4; diperoleh A4 =
Karena kolom pertama bernilai positif, maka expinD(v1) = 4
b. Untuk k= 5; diperoleh A5 =
Kolom keempat bernilai postif, maka expinD(v4) = 6.
Dengan demikian eksponen titik digraf pada Gambar 2.5(a), expinD(v1) = 4, expinD(v2) = expinD(v3) = 5, dan expinD(v4) = 6.
2.5.2 Eksponen Titik Masuk Digraf Dwi-warna
Misalkan D(2) adalah digraf dwi-warna dengan V(D(2)) adalah himpunan semua titik di D(2), yaitu V(D(2) = {v
1, v2,· · ·, vn}. Untuk sebarang titik vk ∈ V(D(2),
maka eksponen titik vk di D(2) yang dinotasikan sebagai expinD(2)(vk) adalah
20
dari setiap titik diD(2) ke titikvk.
Andaikan D(2) adalah digraf dwi-warna primitif orde n. Jika titik-titik di D(2) adalah (v1, v2, ..., vn) sedemikian hingga
expinD(2)(v1)≤expinD(2)(v2)≤ · · · ≤expinD(2)(vk)
maka expD(2)(vk) adalah tipe pertama generalisasi eksponen titik ke-k dari digraf
dwi-warna D(2) (Gao dan Shao, 2009).
Untuk mencari eksponen titik digraf dwi-warna primitif D(2), dapat di-lakukan dengan operasi (s, t)-matriksHurwitz ProductRdanByang dapat didefin-isikan secara rekurensif. Untuk bilangan bulat tak negatif terkecils dan t, jika k adalah adalah titik diD(2), maka semua entri pada kolom ke-k dari matriks terse-but bernilai positif.
Contoh 2.5.2 Perhatikan kembali digraf dwi-warna primitif pada Contoh 2.4.3. Berikut akan dicari eksponen titik masuk dari masing-masing titik pada digraf dwi-warna D(2) pada Gambar 2.8 dengan melihat entri (i, j) dari (R, B)(s,t) pada kolom ke-i bernilai positif. Menggunakan Contoh 2.4.3 telah diperoleh matriks-matriks (R, B)(s,t), maka
a. Untuks+t= 5 dengan (R, B)(3,2) =R(R, B)(2,2)+B(R, B)(3,1)=
2 1 0 1 1 1 0 0 1 0 1 1 1 0 1 1
Karena semua entri pada kolom pertama dengan (R, B)(3,2) bernilai positif, maka expin(v1) = 5 yang terdiri dari 3-arcmerah dan 2-arcbiru.
b. Untuks+t= 6 dengan (R, B)(4,2) =R(R, B)(3,2)+B(R, B)(4,1)=
1 2 0 0 0 1 0 0 2 1 0 1 2 1 0 1
c. Untuks+t= 6 dengan (R, B)(3,3) =R(R, B)(2,3)+B(R, B)(3,2)=
1 0 2 1 1 0 1 1 0 0 1 0 0 0 1 0
Karena semua entri pada kolom ketiga dengan (R, B)(3,3) bernilai positif, maka expin(v3) = 6 yang terdiri dari 3-arcmerah dan 3-arcbiru.
d. Untuks+t= 7 dengan (R, B)(4,3) =R(R, B)(4,3)+B(R, B)(4,2)=
3 1 1 2 2 1 0 1 1 0 2 1 1 0 2 1
Karena semua entri pada kolom keempat dengan (R, B)(4,3) bernilai positif, maka expin(v4) = 7 yang terdiri dari 4-arcmerah dan 3-arcbiru.
2.6 Sistem Persamaan Diophantine
Persamaan diophantine adalah suatu persamaan dalam bentuk
a1x1 +a2x2+· · ·+anxn=b (1)
dengan solusi dari persamaan tersebut adalah bilangan bulat untuk semua bilan-gan bulata1,a2 ,..., an ,b. Andaikan bahwan≥1 dan koefisien-koefisiena1 ,a2 ,...,an tak semuanya nol.
Teorema 2.6.1 Persamaan (1) adalah punya solusi bulat jika dan hanya jika gcd(a1, a2, ..., an) membagi b.
Sistem persamaan diophantine adalah himpunan dari m persamaan dio-phantine dalam n variabel yang sama dengan m dan n adalah bilangan bulat positif seperti berikut
a11x1 +a12x2+· · ·+a1nxn=b1 a21x1 +a22x2+· · ·+a2nxn=b2
...
am1x1+am2x2+· · ·+amnxn=bm
22
Sistem persamaan diophantine pada persamaan (2) dapat juga dituliskan sebagai sebuah persamaan matriks Ax = b, dimana
A=
Kolom-kolom dari matriksA adalah koefisien-koefisien dari variabel x1,x2, ...,xn
pada persamaan (2).
Teorema 2.6.2Sistem persamaan diophantineAx = bdari persamaan (2) memi-liki solusi bilangan bulat jika dan hanya jika pembagi persekutuan terbesar dari determinan submatriks 2×2 dari A adalah ±1.
2.7 Formula Eksponen Titik Masuk Digraf Dwi-warna
Pada bagian akan dibahas cara menentukan batas bawah dan batas atas ekspo-nen titik digraf dwi-warna primitif yang memuat dua cycle sebagaimana yang ditawarkan oleh Suwilo (2011). Terlebih dahulu akan dibahas mengenai teknik untuk menentukan batas bawah eksponen titik digraf dwi-warna primitif.
Lemma 2.7.1Andaikan D(2) adalah digraf dwi-warna primitif yang memuat dua
cycle dengan matriks cycleM =
"
r(C1) b(C2) b(C1) r(C2)
#
. Misalkanvk adalah sembarang
titik di D(2) dan terdapat sebuah (s, t)-walk dari setiap titik v
j di D(2) ke titik vk
untuk sembarang
bi-langan bulat tak negatif g, h, dan untuk suatu pathp(j,k) dari vj ke vk.
Bukti Untuk sembarang 1 ≤ j ≤ n, misalkan pjk adalah path dari titik vj ke
titik vk. D(2) memuat dua cycle sehingga setiap walk di D(2) dapat dituliskan
"
dengan x1, x2 ≥ 0. Karena D(2) primitif, maka M invertible. Menggunakan
"
dan persamaan (3) diperoleh persamaan berikut
M
dan Lemma (2.7.1) terbukti.
Dari pembuktian Lemma 2.7.1 , maka diperoleh teorema berikut.
Teorema 2.7.1AndaikanD(2) adalah digraf dwi-warna primitif yang terdiri dari cycle C1 dan C2. Misalkan vk adalah titik di D(2). Untuk sembarang titik vi dan
Bukti. Andaikan bahwa eksponen titik masuk vk dicapai oleh (s, t)-walk
den-gan
dan diperoleh persamaan berikut
24
0, maka didefinisikan
gk =b(C2)r(pj,k)−r(C2)b(pj,k)≥0 (5)
dan jika untuk sembarang titikvi, dimanai= 1,2, ..., ndiperoleh nilair(C1)b(pi,k)
−b(C1)r(pi,k)≥0, maka didefinisikan
hk =r(C1)b(pi,k)−b(C1)r(pi,k)≥0 (6)
sehingga g ≥gk dan h≥hk. Oleh Lemma (2.6.1) diperoleh
"
s
t
#
=M
"
g
h
#
≥M
"
gk
hk
#
(7)
sehingga expin(vk) = s+t ≥ (r(C1) +b(C1))gk+ (r(C2) +b(C2))hk = l(C1)gk+
l(C2)hk.
Proposisi berikut dapat digunakan untuk menentukan batas bawah ekspo-nen titik masuk digraf dwi-warna primitif dari sebuah titik yang ditentukan, mis-alkan titikv. Didefinisikan bahwa d(vk, v) adalah panjang walk terpendek dari vk
kev.
Proposisi 2.7.1 Asumsikan D(2) adalah digraf dwi-warna primitif atas n titik. Mi-salkan v adalah sebuah titik di D(2) dengan expin(v). Untuk sembarang titik vk, k = 1,2, ..., n di D(2), expin(vk)≤expin(v) +d(vk, v).
Bukti. Untuk setiap k = 1,2, ..., n misalkan pv,k adalah (r(pv,k), b(pv,k))-path
dari v ke titik vk dengan panjang d(v, vk). Karena eksponen titik masuk v adalah
expin(v), maka terdapat (s, t)-walk dengan panjang expin(v) = s+t dari setiap titik vj, j = 1,2, ..., n ke titik v. Ini menunjukkan bahwa setiap titik vk di D(2)
terdapat suatu (s+r(pv,k), t+b(pv,k))-walk dari setiap titik v ke setiap titik vk.
Walk tersebut ber-awal dari v menuju vk melalui (r(pv,k), b(pv,k))-path dan
kemu-dian menuju vj melalui suatu (s, t)-walk dari vj ke v. Oleh karena itu diperoleh
masuk digraf dwi-warna yang memuat duacycle.
Proposisi 2.7.2 Andaikan D(2) adalah digraf dwi-warna yang terdiri atas cycle
C1 danC2. Misalkan vk adalah titik diD(2) yang terdapat pada cycleC1 dan cycle
C2. Jika untuk setiap i = 1,2, ..., n dan sembarang bilangan bulat positif s dan t, terdapat path pi,k dari vi ke vk sehingga sistem persamaan
Mx +
"
r(pi,k)
b(pi,k)
#
=
"
s
t
#
(8)
punya solusi bilangan bulat tak negatif, makaexpin(vk)≤s+t.
Bukti. Misalkan bahwa solusi dari sistem persamaan (8) adalah x = (x1, x2)T. Karena D(2) primitif, maka matrikscycle M invertible, sehingga x1 dan x2 tidak dapat nol kedua-duanya. Karenax1, x2 6= 0 dan kedua cycle C1 dan C2 memuat titikvk, maka terdapat tiga kemungkinan berikut.
Jika x1 > 0 dan x2 > 0, maka walk dari titik vi ke titik vk akan bergerak
sebanyak x1 kali mengelilingicycle C1 dan bergerak sebanyakx2 kali mengelilingi cycle C2 dan kembali lagi ke titik vi, kemudian terus bergerak menuju titik vk di
sepanjang pathpi,k adalah sebuah (s, t)-walkdari vi kevk. Jikax1 = 0 danx2 >0, maka walk dari titik vi ke titik vk akan bergerak sebanyak x2 kali mengelilingi cycle C2 dan kembali lagi ke titik vi, kemudian terus bergerak menuju titik vk di
sepanjang pathpi,k adalah sebuah (s, t)-walkdari vi kevk. Jikax1 >0 danx2 = 0, maka walk dari titik vi ke titik vk akan bergerak sebanyak x1 kali mengelilingi cycle C1 dan kembali lagi ke titik vi, kemudian terus bergerak menuju titik vk
di sepanjang path pi,k adalah sebuah (s, t)-walk dari vi ke vk. Dengan demikian,
untuk setiap titikvi,i= 1,2, ..., nterdapat sebuah (s, t)-walkdarivikevk, sehingga
BAB 3
METODE PENELITIAN
Untuk menentukan eksponen titik masuk dari sebuah kelas digraf dwi-warna D(2) dengann-titik, akan dilaukan dalam 2 langkah pendekatan, yaitu sebagai berikut.
3.1 Komputasi Nilai Eksponen Titik Masuk
Dengan menggunakan kode program yang ditulis dengan MATLAB akan diperoleh bilangan bulat tak negatif s dan t sehingga
expin(vk) =s+t
Hal ini dilakukan dengan menghitung hasil kali (s, t)-Hurwitz dari matriks adja-cency A dan B secara rekursif.
Berikut adalah algoritma yang digunakan untuk menghitung eksponen titik masuk dari sebuah kelas digraf dwi-warnaD(2)dengann-titik ganjil, dimanan≥5.
1. Mengecek primitifitas digraf dwi-warna D(2)
2. Menotasikan digraf dwi-warnaD(2) dalam bentuk matriks adjacency, matriks A untukarc berwarna merah dan matriks B untukarc berwarna biru.
3. Menghitung hasil kali (s, t)-Hurwitz dari matriks adjacency A dan B secara rekursif, dengan (A, B)(s,t)=A(A, B)(s−1,t)+B(A, B)(s,t−1)
4. Apabila seluruh entri matriks dari hasil kali (s, t)-Hurwitz dari matriks A dan B bernilai positif maka expin(vk) =s+t.
3.2 Pembuktian Nilai Eksponen Titik Masuk
mem-negatif gk dan hk sedemikian hingga
"
s
t
#
≥ M
"
gk
hk
#
sehingga expin(vk) = s+t ≥ l(C1)gk+l(C2)hk, dengan M adalah matriks cycle
dari digraf dwi-warna D(2), l(C1) adalah panjang dari cycle C
1 dan l(C2) adalah panjang dari cycleC2.
Langkah berikutnya adalah memperlihatkan bahwa expin(vk) ≤ s +t.
Karena digraf dwi-warna D(2) primitif, maka determinan dari matriks cycle M adalah ±1 dan setiap walk pada digraf dwi-warna D(2) dapat didekomposisi men-jadi suatu path dari titik vi ke titik vk dan beberapa buah cycle, sehingga untuk
memperlihatkan expin(vk)≤ s+t, cukup diperlihatkan bahwa sistem persamaan
diophantine
M
"
x1
x2
#
+
"
r(pi,k)
b(pi,k)
#
=
"
s
t
#
, dengan i= 1,2,· · · , n
punya solusi bulat tak negatif x1, x2 ≥0 untuk semua titik vi dan beberapa path
pi,k dari titikvi ke titik vk.
Dengan memperlihatkan expin(vk) ≥ s+t dan expin(vk) ≤ s+t, maka
BAB 4
EKSPONEN TITIK MASUK DIGRAF DWI-WARNA PRIMITIF
Pada bab ini akan diperlihatkan hasil dari penelitian ini, yaitu pola eksponen titik masuk dari digraf dwi-warna dengann-titik ganjil yang memuat tigaarcberwarna biru dan duacycle.
4.1 Eksponen Titik Masuk Digraf Dwi-warna Primitif
Andaikan D(2) adalah sebuah digraf dwi-warna dengan n-titik ganjil dan n ≥ 5. D(2) memuat dua cycle, yaitu n-cycle v1 →v2 →v3→ · · · →vn−1 →vn→v1 dan
2 → v1. Representasi digrafD
(2) dapat dilihat seperti pada Gambar 1.1.
Eksponen titik masuk digraf D(2) akan diperlihatkan pada teorema berikut.
Teorema 4.1 Andaikan digraf dwi-warna primitif D(2) dengan n-titik ganjil, dan
n ≥ 5, D(2) memuat dua cycle, yaitu n-cycle dan n+1 2
-cycle serta tiga arc berwarna biru pada vn → v1, vn+1
bar 1.1. Maka, eksponen titik masuk dari D(2) adalah expin(vk) = (s+t) dimana
"
BuktiBerikut ini akan diperlihatkan bahwa eksponen titik masuk dari digraf dwi-warna primitif D(2) adalah expin(v
k) = n
2−n+2k−2
2 untuk semua k = 1,2,· · · , n. Untuk itu akan dipilih (n−3
nakanpathpx∗,k dari titikx∗ke titikvkuntuk menentukan nilaigkpada persamaan (5) dan path py∗,k dari titik y∗ ke titik vk untuk menentukan nilai hk pada per-samaan (6) pada Bab 2. Pembuktian akan dibedakan dalam dua kasus berikut.
1. Untuk kasus 1≤k≤ n+1 2
Akan diperlihatkan batas atas dari eksponen titik masuk digraf dwi-warna primitif D(2) adalah expin(v Dengan menggunakan persamaan (5) maka diperoleh
gk = b(C2)r(px∗,k)−r(C2)b(px∗,k) (9) Oleh persamaan (6) maka diperoleh
hk = r(C1)b(py∗,k)−b(C1)r(py∗,k) (11)
Oleh Teorema(2.7.1), diperoleh
30
tidak memiliki solusi bulat tak negatif, yaitu
"
Karena xharus memiliki solusi tak negatif, berdasarkan penjelasan diatas dapat
dilihat bahwa dari titikv1ke titikv1tidak adawalkdengan komposisi
"n2
Oleh karena itu, komposisiwalkyang memungkinkan adalah dengan menam-bahkan satu kali mengelilingicycle pertama satu kali, yaitu
"n2
Akan diperlihatkan batas atas dari eksponen titik masuk digraf dwi-warna primitif D(2) adalah expin(vk) ≥ n 0. Dengan menggunakan persamaan (5) diperoleh
persamaan (6) diperoleh
Oleh Teorema 2.7.1, diperoleh
"
Perhatikan untukwalk dari vn ke vn, sistem persamaan
Mx=
tidak memiliki solusi bulat tak negatif, yaitu
"
Berdasarkan penjelasan di atas, dapat dilihat bahwa tidak ada walk dari titik vn
ke titikvn dengan komposisi
"n2
32
kali mengelilingicycle pertama, yaitu
"n2
Langkah berikutnya adalah memperlihatkan bahwa batas atas dari eksponen titik masuk digraf dwi-warna primitifD(2) expin≤ n2
−n+2k−2
2 untukk = 1,2,· · ·n. Akan diperlihatkan bahwa expin(v1) = n2
−n
2 dan dengan menggunakan Proposisi 2.7.1 akan ditentukan batas atas eksponen titik untuk setiap titikvkdiD(2). Oleh
persamaan (16) diketahui bahwa untuk k = 1, expin(v1) ≥ n2−n
2 . Maka akan diperlihatkan bahwa expin(v1)≤ n2−n
2 . Kemudian akan diperlihatkan untuk setiap titikvi,i= 1,2,· · · , n terdapatpathpi,1 dari titik vi ke titikv1 sedemikian hingga
memiliki solusi bulat tak negatif, yaitux1, x2 ≥0.
KarenaD(2)primitif maka matrikscycleMinvertible, denganM−1 =
"
Determinan dari matrikscycle M adalah 1, Teorema 2.6.2 menjamin bahwa per-samaan (25) memiliki solusi bulat. Pembuktian akan diperlihatkan dalam dua kasus berikut.
1. Untuk 1≤i≤ n+1 2
Misalkan pi,1 adalah path dari titik vi ke titik v1, yaitu r(pi,1) = n+12 − i dan
b(pi,n) = 1, dari persamaan (25) diperoleh
x1, x2 ≥ 0. Sehingga dapat disimpulkan bahwa untuk setiap vi, 1 ≤ i ≤ n+12
terdapat path dari titik vi ke titik v1 yang mengakibatkan sistem persamaan (26) memiliki solusi bulat tak negatif. Karena titik v1 berada pada cycle C1 dan C2, oleh Proposisi 2.7.1 menjamin bahwa expin(v1)≤ n2−n
2 .
2. Untuk n+3
2 ≤i≤n
Misalkanpi,1adalahpathdari titikvike titikv1, yaitur(pi,1) =n−idanb(pi,1) = 1, dari persamaan (25) diperoleh
"
Untuk sembarang titikvi, n+32 ≤i ≤n terdapatpathpi,nyang mengakibatkan
x1, x2 ≥ 0. Sehingga dapat disimpulkan bahwa untuk setiap vi, n+32 ≤ i ≤ n
terdapat path dari titik vi ke titik v1 yang mengakibatkan sistem persamaan (27) memiliki solusi bulat tak negatif. Karena titik v1 berada pada cycle C1 dan C2, oleh Proposisi 2.7.1 menjamin bahwa expin(v1)≤ n2−n
2 .
Dari persamaan (16), (24), dan (28) dapat disimpulkan bahwa eksponen titik masuk dari digraf dwi-warna perimitifD(2) adalah expin(vk) = n
2
−n+2k−2
2 dengan komposisiarc merah danarc biru sebagai berikut.
BAB 5
KESIMPULAN DAN SARAN
5.1 Kesimpulan
Andaikan D(2) adalah digraf dwi-warna primitif yang terdiri dari n-titik ganjil, dan n ≥5 dengan 3 arc biru pada arc vn →v1, vn+1
2 →v1, v n+1
2 → v n+3
2 dan arc
lainnya berwarna merah, serta memuatcycle dengan panjang n dan n+1
2 . Berikut adalah komposisi arc merah dan arc biru dari eksponen titik masuk dari sebuah titikvk di D(2).
"
s
t
#
=
n2 −3n+2k
2
n−1
, untuk1≤ k≤ n+12
n2−3n+2k−2 2
n
, untukn+32 ≤k ≤n
dimana expin(vk) =s+t.
5.2 Saran
[1] Bai, Z. dan Shao, Y. 2007. Exponents of A Class of Two-colored Digraphs. J ournal of Shanxi U niversity, 30, 19-23.
[2] Brualdi, R. A dan Ryser, H. J. 1991. Combinatorial Matrix Theory. Cam-bridge: Cambridge University Press.
[3] Fornasini, E. dan Valcher, M. E. Directed Graphs, 2D State Models, and Cha-racteristic Polynomials of Irreducible Matrix Pair. Linear Algebra Appl., 263 (1997): 275 - 310.
[4] Gao, Y dan Shao, Y. Generalized Exponents of Primitif Two-colored Di-graphs. Linear Algebra Appl. 430 (2009): 1550-1565.
[5] Langville, A. N dan Meyer, C. D. Deeper Inside PageRank. Internet Math-ematics. Vol.I, No. 3 (2004) : 335-380.
[6] Shader, B. L dan Suwilo, S. Exponent of Nonnegative Pairs. Linear Algebra Appl,. 363 ( 2003): 275 - 293.
[7] Suwilo, S. Vertex Exponents of Two-colored Primitive Extremal Ministrong Digraph. Global Journal of Technology and Optimization. Vol.2, No.2 (2011):166-174.
[8] Suwilo, S dan Syafrianty, A. Vertex Exponents of A Class of Two Colored Di-graphs with Even Number of Vertices. East-West J. of Mathematics. Special volume (2012): 1-15.