SITTI SAHRIMAN
SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR
BOGOR 2014
MODEL
STATISTICAL DOWNSCALING
DENGAN
TIME LAG
DATA
PERNYATAAN MENGENAI TESIS DAN
SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA*
Dengan ini saya menyatakan bahwa tesis berjudul Model Statistical Downscaling dengan Time Lag Data Global Circulation Model untuk Peramalan Curah Hujan adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.
Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.
Bogor, September 2014
Sitti Sahriman
RINGKASAN
SITTI SAHRIMAN. Model Statistical Downscaling dengan Time Lag Data
Global Circulation Model untuk Peramalan Curah Hujan. Dibimbing oleh ANIK DJURAIDAH dan AJI HAMIM WIGENA.
Sebagai negara kepulauan, Indonesia rentan terhadap dampak perubahan iklim. Perubahan iklim menjadi ancaman serius pada berbagai bidang, khususnya pada bidang pertanian. Naiknya suhu permukaan bumi menyebabkan terjadinya perubahan pola musim yang berdampak pada menurunnya produktivitas pertanian. Curah hujan merupakan unsur iklim dengan keragaman cukup besar di Indonesia. Oleh karena itu, pendugaan curah hujan memberikan kontribusi positif bagi bidang pertanian.
Statistical downscaling merupakan model statistik yang digunakan untuk menduga data curah hujan (berskala lokal) dengan memanfaatkan informasi global berupa data presipitasi (berskala global) dari luaran global circulation model climate model intercomparison project (GCM CMIP5). Namun umumnya, data luaran GCM berdimensi besar sehingga memungkinkan terjadinya multikolineritas pada data presipitasi. Oleh karena itu, model statistical downscaling yang dapat mengatasi masalah tersebut adalah regresi kuadrat terkecil parsial (RKTP) dan regresi komponen utama (RKU).
Umumnya, korelasi antara data curah hujan dengan data presipitasi GCM harus kuat untuk menjelaskan dengan baik keragaman iklim lokal. Penentuan pergeseran waktu (time lag) dibutuhkan terhadap data presipitasi GCM untuk menghasilkan korelasi yang kuat antara kedua peubah. Time lag ditentukan berdasarkan korelasi silang tertinggi antara data curah hujan dengan data presipitasi GCM. Korelasi silang dihitung menggunakan fungsi korelasi silang (CCF). Tujuan dari penelitian ini adalah menentukan time lag data presipitasi GCM dan membangun model statistical downscaling menggunakan metode RKTP dan RKU dengan time lag data presipitasi GCM. Data Curah hujan di Kabupaten Indramayu digunakan sebagai peubah respon dan data presipitasi GCM digunakan sebagai peubah predictor pada periode 1979-2008. Data periode 1979-2007 digunakan untuk membangun model dan data periode 2008 digunakan untuk validasi model.
Pemodelan dengan menggunakan metode RKTP pada data GCM-lag (GCM dengan time lag)memberikan nilai R2 sekitar 71.7% dan nilai RMSE (root mean square error) sekitar 57.93. Berdasarkan pendugaan data curah hujan periode 2008, model RKTP menghasilkan nilai korelasi sekitar 0.93 dengan nilai root mean square error of prediction (RMSEP) sekitar 75.26. Selain itu, metode RKTP menunjukkan 5 kelompok data curah hujan berdasarkan plot antara skor dan skor . Pengelompokan ini digunakan sebagai peubah boneka dalam model RKU. Model RKU mampu memberikan R2 berkisar 62%−63% dan nilai RMSE berkisar
sekitar 8.78% dengan nilai RMSE, korelasi, dan RMSEP yang relatif sama dengan model RKU. Akan tetapi, sisaan model RKUB masih heterogen. Masalah ini diatasi dengan menambahkan peubah boneka ke dalam model RKU (RKUK). Hasilnya menunjukkan bahwa model RKU dengan peubah boneka memberikan nilai R2 (berkisar 92.9%−93.4%) dan korelasi (0.99) yang lebih tinggi daripada model RKU, RKTP, dan RKUB. Nilai RMSE berkisar 28.06−29.09 dan RMSEP berkisar 28.48−31.04. Model RKU dengan bobot dan peubah boneka (RKUBK) memberikan hasil yang sama dengan model RKUK. Penambahan peubah boneka ke dalam model RKUB mampu meningkatkan nilai R2 sekitar 30.1% dan menurunkan nilai RMSE sekitar 37.83. Penambahan peubah boneka ke dalam model RKU maupun RKUB mampu menghasilkan model dengan sisaan yang lebih homogen. Secara umum, model RKUK menunjukkan performa yang lebih baik daripada model RKU, RKTP, RKUB, maupun RKUBK. Dengan nilai R2 dan korelasi yang relatif sama dengan model RKUBK, model RKUK lebih sederhana. Model RKUK dengan satu komponen merupakan model statistical downscaling
terbaik. Model tersebut memiliki nilai RMSEP (28.48) yang lebih kecil dan nilai korelasi (0.99) yang tinggi serta ragam sisaan yang lebih homogen daripada model lainnya. Analisis juga dilakukan terhadap data presipitasi GCM tanpa time lag. Model statistical downscaling dengan prediktor GCM-lag mempunyai nilai R2 yang lebih tinggi dan RMSEP yang lebih rendah daripada model statistical downscaling dengan GCM tanpa time lag.
Kata kunci: fungsi korelasi silang, global circulation model, peubah boneka, regresi kuadrat terkecil parsial, regresi komponen utama, statistical downscaling
SUMMARY
SITTI SAHRIMAN. Statistical Downscaling Model with Time Lag of Global Circulation Model to Forecast Rainfall. Supervised by ANIK DJURAIDAH and AJI HAMIM WIGENA.
As an archipelago country, Indonesia is more vulnerable to the climate change impacts. Climate change can be a serious threat to many fields, especially agriculture. Rising temperatures on the earth surface may alter the weather patterns thus cause declining in agricultural productivity. Rainfall is one of fundamental element of climate which has large variability. Therefore, the estimation of rainfall give an essential contribution to the agriculture development.
Statistical downscaling is a statistical model used to estimate rainfall data (local-scale) by using global information such as the precipitation data (global-scale) from global circulation model climate model intercomparison project (GCM CMIP5). However, the GCM produces large dimensions of data output that enables multicollinearity in the precipitation data. Therefore, the statistical downscaling model which can solve this problem is partial least squares regression (PLSR) and principal component regression (PCR).
In general, the correlation between rainfall and precipitation data of GCM should be strong enough to explain the local climate variability. Time shift (time lag) determination was needed on the GCM precipitation data to produce strong correlation between these two varibles. Time lag was determined based on the highest cross-correlation between rainfall and GCM precipitation data. Cross-correlation was calculated using the cross-Cross-correlation function (CCF). The objectives of the research were to determine the time lag of precipitation GCM data and build SD model using PCR method with time lag of the GCM precipitation data. Rainfall data in Indramayu were used as response variable and the GCM precipitation were used as predictor variables from 1979 to 2008. Data from 1979 to 2008 were used to construct the model and data period 2008 were used for model validation.
(ranged from 92.9% to 93.4%) and correlation (0.99) than PCR, PLSR, and PCRW models. The RMSE ranged from 28.06 to 29.09 and RMSEP ranged from 28.48 to 31.04. The PCR models with weights and dummy variables (PCRWD) gave similar results to PCRD. The addition of dummy variables in the PCRW models can increase the R2 into 30.1% and decrease the RMSE become 37.83. The
addition of dummy variables in the PCR and PCRW models produced a model with more homogeneous error. Generally, the PCRD models produce better performance than PCR, PLSR, PCRW, and PCRWD models. As the R2 and the
correlation were relatively similar with the PCRWD models, PCRD were considered as simpler models. In this study, the PCRD model with one component was concluded as the best statistical downscaling model. The model had the smallest RMSEP (28.48), highest correlation (0.99), and the error variance was more homogeneous than the other models. Analyses were also conducted on the GCM precipitation without the time lag. The statistical downscaling model with lag-GCM predictors had higher R2, correlation, and lower RMSEP than statistical
downscaling with GCM without time lag.
© Hak Cipta Milik IPB, Tahun 2014
Hak Cipta Dilindungi Undang-Undang
Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumbernya. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik, atau tinjauan suatu masalah; dan pengutipan tersebut tidak merugikan kepentingan IPB
Tesis
sebagai salah satu syarat untuk memperoleh gelar Magister Sains
pada
Program Studi Statistika
MODEL
STATISTICAL DOWNSCALING
DENGAN
TIME LAG
DATA
GLOBAL CIRCULATION MODEL
UNTUK PERAMALAN CURAH
HUJAN
SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR
BOGOR 2014
Judul Tesis : Model Statistical Downscaling dengan Time Lag Data Global Circulation Model untuk Peramalan Curah Hujan
Nama : Sitti Sahriman
NIM : G152120231
Disetujui oleh Komisi Pembimbing
Dr Ir Anik Djuraidah, MS Ketua
Dr Ir Aji Hamim Wigena, MSc Anggota
Diketahui oleh
Ketua Program Studi Statistika Terapan
Dr Ir Indahwati, MSi
Dekan Sekolah Pascasarjana
Dr Ir Dahrul Syah, MScAgr
Sitti Sahriman
PRAKATA
Bismillahirrohmanirrohim.
Puji dan syukur dipanjatkan kehadirat Allah subhanahu wa ta’ala atas limpahan rahmat dan karunia-Nya sehingga penulis dapat menyelesaikan karya ilmiah ini. Shalawat serta salam semoga tetap tercurah kepada junjungan kita Nabi
besar Muhammad Shalallahu ‘Alaihi Wassallam beserta keluarga Beliau, para
Shahabat, para tabi’in, tabi’ut tabi’in dan para penerus perjuangan Beliau hingga akhir zaman. Karya ilmiah ini berjudul “Model Statistical Downscaling dengan
Time Lag Data Global Circulation Global untuk Peramalan Curah Hujan”.
Keberhasilan penulisan karya ilmiah ini tidak lepas dari bantuan, bimbingan, dan petunjuk dari berbagai pihak. Oleh karena itu, penulis menyampaikan penghargaan dan ucapan terima kasih yang sebesar-besarnya khususnya kepada:
1. Ibu Dr Ir Anik Djuraidah, MS selaku pembimbing I dan Bapak Dr Ir Aji Hamim Wigena, MSc selaku pembimbing II yang dengan penuh kesabaran telah memberikan bimbingan, arahan, saran dan motivasi kepada penulis selama penyusunan karya ilmiah ini.
2. Bapak Dr Ir Muhammad Nur Aidi, MS selaku penguji luar komisi yang telah banyak memberikan kritikan, masukan, dan arahan yang sangat membangun dalam penyusunan karya ilmiah ini.
3. Seluruh staf pengajar pascasarjana Departemen Statistika IPB yang telah banyak memberikan ilmu dan arahan selama perkuliahan sampai dengan penyusunan karya ilmiah ini.
4. Teman-teman statistika angkatan 2012 atas kebersamaan, kekompakannya, bantuan dan masukannya selama bersama-sama menempuh kuliah.
5. Teman-teman seperjuangan, Wirnancy Julia sari, Sitti Masyitah, dan Ade Ayu Putrigati yang selalu menemani disaat senang maupun susah, terima kasih atas perhatian, bantuan dan kerjasama, dan kekompakannya.
6. Tante Sitti Fatima dan Om Madisaeni yang dengan sabar dan ikhlas merawat penulis, khususnya pada saat penulis beberapa kali mengalami sakit.
7. Kedua orangtua, Ayahanda H La Hamidi dan Ibunda Hj Wa Raeda, yang telah banyak memberikan dukungan moril, materi, doa, dan kasih sayang yang tulus kepada penulis.
8. Kakekku tersayang H ABD Salam, kakakku tercinta Sitti Darahlina, adikku tercinta Sahmudin, dan seluruh keluarga besar atas dukungan semangatnya serta doa yang tak henti-hentinya dipanjatkan buat penulis.
9. Seluruh pihak yang namanya tidak dapat disebutkan satu per satu, terima kasih atas bantuannya.
Atas segala bantuan yang diberikan, penulis hanya bisa berdoa dengan harapan semoga semua kebaikan yang penuh keikhlasan tersebut dicatat sebagai amal ibadah dan mendapatkan balasan berupa pahala di sisi Allah Subhanahu wa ta’ala, Aamiin Ya Rabbal Alamin. Penulis menyadari bahwa masih banyak terdapat kekurangan dalam penulisan karya ilmiah ini. Namun, penulis berharap karya ilmiah ini dapat bermanfaat bagi berbagai pihak yang membutuhkan.
Wassalam.
DAFTAR ISI
DAFTAR TABEL vi
DAFTAR GAMBAR vi
DAFTAR LAMPIRAN vi
1 PENDAHULUAN 1
Latar Belakang 1
Tujuan Penelitian 2
2 TINJAUAN PUSTAKA 2
Statistical Downscaling 2
Regresi Kuadrat Terkecil Parsial 4
Regresi Komponen Utama 5
3 METODE PENELITIAN 9
Data 9
Metode Analisis 9
4 HASIL DAN PEMBAHASAN 11
Eksplorasi Data 11
Time Lag Data Presipitasi GCM 11
Variance Inflation Factors 11
Model Statistical Downscaling 12
Regresi Kuadrat Terkecil Parsial 12
Regresi Komponen Utama 14
RKU Terboboti 15
RKU dengan Peubah Boneka 17
RKU Terboboti dan Peubah Boneka 18
Peramalan Data Curah Hujan dan Pemilihan Model Terbaik 19
5 SIMPULAN 22
DAFTAR PUSTAKA 22
LAMPIRAN 25
DAFTAR TABEL
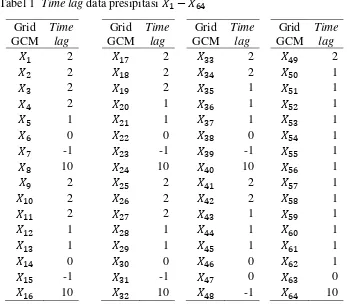
1 Time lag data presipitasi − 12 2 Komponen terekstrak pada model RKTP 13 3 Nilai akar ciri dan proporsi keragaman 5 KU pada data GCM-lag 15 4 Nilai R2 dan RMSE model awal RKU 15
5 Nilai R2 dan RMSE model RKUB 16
6 Nilai R2 dan RMSE model RKUK 17
7 Nilai R2 dan RMSE model RKUBK 18
8 Nilai korelasi dan RMSEP setiap model pada data GCM-lag dan GCM 20
DAFTAR GAMBAR
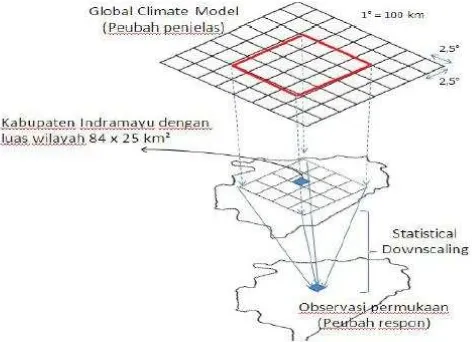
1 Statistical downscaling 3
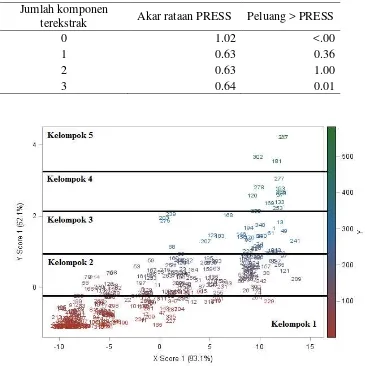
2 Plot skor dan skor 13
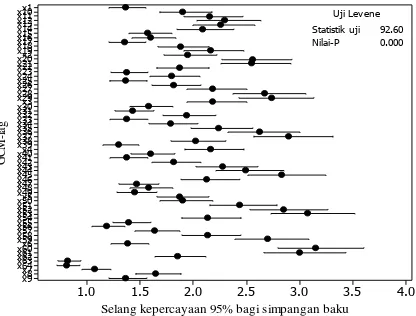
3 Uji kehomogenan ragam data presipitasi GCM-lag 14
4 Plot sisaan model R1KU 15
5 Uji kehomogenan ragam kelompok bulan untuk data presipitasi GCM-lag 16
6 Plot sisaan model R1KUB 16
7 Plot sisaan model R1KUK 17
8 Plot sisaan model R4KUBK 18
9 Plot nilai curah hujan aktual dan curah hujan dugaan model RKTP dan RKU periode 2008 dengan data GCM-lag 21 10 Plot nilai curah hujan aktual dan curah hujan dugaan model RKUB
periode 2008 dengan data GCM-lag 21 11 Plot nilai curah hujan aktual dan curah hujan dugaan model RKUK
periode 2008 dengan data GCM-lag 21 12 Plot nilai curah hujan aktual dan curah hujan dugaan model RKUBK
periode 2008 dengan data GCM-lag 22
DAFTAR LAMPIRAN
1 Tabulasi data curah hujan dan presipitasi GCM
periode 1979-2008 26
2 Diagram alir analisis data 27
3 Penentuan time lag data presipitasi , , dan 28 4 Korelasi antara curah hujan dengan presipitasi GCM dan GCM-lag 30 5 Nilai variance inflation factors data presipitasi GCM-lag 31 6 Koefisien regresi model RKU, RKUB, RKUK, dan RKUBK 32
7 Diagnostik sisaan model awal RKU 33
8 Uji kesamaan ragam tiap kelompok bulan data curah hujan 34 9 Diagnostik sisaan model RKUB 35
10 Diagnostik sisaan model RKUK 36
11 Diagnostik sisaan model RKUBK 37
1
1 PENDAHULUAN
Latar Belakang
Indonesia terletak pada 6°LU−11°LS dan beriklim tropis dengan curah hujan tinggi pada setiap tahun. Indonesia juga merupakan negara kepulauan terbesar di dunia dengan lebih dari 17000 pulau dan 80.000 km garis pantai. Posisi geografis Indonesia rentan terhadap dampak perubahan iklim. Umumnya perubahan iklim yang terjadi di Indonesia ditandai dengan adanya perubahan temperatur rata-rata harian, pola curah hujan, tinggi permukaan laut, dan variabilitas iklim (misalnya el-nino, la-nina, indian dipole). Perubahan ini memberi dampak serius terhadap berbagai sektor, misalnya kesehatan, pertanian, perekonomian (Supangat 2013).
Provinsi Jawa Barat adalah salah satu sentra produksi padi yang memberikan kontribusi terbesar terhadap produksi beras nasional, yakni sebesar 17.6%. Dinas Pertanian Provinsi Jawa Barat mengharapkan Jawa Barat tetap menjadi pemasok tertinggi untuk beras nasional. Namun, upaya pemerintah untuk mempertahankan swasembada beras yang telah dicapai semakin sulit disebabkan oleh dampak perubahan iklim (Raharjo 2011). Naiknya suhu permukaan bumi menyebabkan terjadinya perubahan pola musim, yakni musim kemarau lebih panjang dan musim hujan yang lebih intensif namun lebih pendek, meningkatnya siklus anomali musim kering dan musim hujan, serta berkurangnya kelembaban tanah. Hal ini berdampak pada menurunnya produktivitas pertanian. Pada skala yang ekstrim, perubahan iklim berakibat pada kegagalan panen berkepanjangan sehingga dapat mengancam ketahanan pangan nasional (Eduzon 2011).
Iklim mempunyai dua unsur utama, yakni suhu dan curah hujan. Indonesia sebagai daerah tropis mempunyai keragaman suhu yang kecil, sementara keragaman curah hujan cukup besar. Oleh karena itu, curah hujan merupakan unsur iklim yang penting untuk diamati terkait dengan dampak perubahan iklim (Hermawan 2010). Berkaitan dengan iklim di Indonesia, proses pembentukan hujan di kawasan tropis merupakan proses yang paling sukar disimulasikan. Hingga saat ini belum ada satu model iklim yang mampu mensimulasikan pola curah hujan di Indonesia dengan baik. Topografi dan interaksi laut, darat, dan atmosfir yang sangat kompleks menambah kerumitan simulasi dan prediksi curah hujan di wilayah Indonesia. Oleh karena itu, model-model iklim resolusi tinggi perlu dikembangkan dalam skala lokal dengan mempertimbangkan informasi dari sirkulasi atmosfir global, seperti presipitasi yang dapat diperoleh dari global circulation model (Notodiputro et al. 2005).
2
menghubungkan peubah iklim luaran GCM yang berskala global (presipitasi) dengan peubah iklim yang berskala lokal (curah hujan) (Fernandez 2005).
Data GCM umumnya berdimensi besar dan memiliki korelasi yang tinggi antar gridnya. Oleh karena itu, metode yang sering digunakan dalam statistical downscaling adalah regresi komponen utama (RKU) (Notodiputro et al. 2005). Serupa dengan RKU, regresi kuadrat terkecil parsial (RKTP) juga dapat digunakan untuk mengatasi korelasi yang tinggi antar peubah prediktor. Metode ini telah digunakan oleh Bergant dan Kajfez-Bogataj (Wigena 2011). RKU berdasarkan pada analisis komponen utama (AKU), sedangkan RKTP berdasarkan pada kuadrat terkecil parsial (KTP). AKU berfokus pada keragaman dalam peubah prediktor, sedangkan KTP berfokus pada keragaman antara peubah prediktor dengan peubah respon (Sutikno et al. 2010).
Model statistical dowscaling membutuhkan korelasi yang kuat antara data GCM dengan curah hujan untuk menjelaskan keragaman iklim lokal dengan baik (Busuioc et al. 2001). Korelasi yang kuat menghasilkan pola yang sama antara kedua peubah. Oleh karena itu, terlebih dahulu perlu dilakukan pemeriksaan kemungkinan adanya pergeseran waktu (time lag) pada data presipitasi GCM yang dapat mengakibatkan perbedaan pola dengan data curah hujan. Time lag
dapat ditentukan melalui korelasi silang tertinggi antara data curah hujan dengan data GCM menggunakan fungsi korelasi silang (CCF).
Wigena (2011) menggunakan metode RKTP multi respon untuk statistical dowscaling pada peramalan curah hujan di kabupaten Indramayu. Estiningtyas dan Wigena (2011) menggunakan RKU dan RKTP untuk memprediksi curah hujan pada kondisi el-nino, la-nina, dan normal di kabupaten Indramayu. Warawati (2013) membandingkan antara metode RKTP, Regresi Kuadrat Terkecil Terboboti (RKTT), dan RKU dalam peramalan curah hujan di stasiun Sukadana dengan teknik statistical downscaling berdasarkan data satelit tropical rainfall measuring mission.
Penelitian sebelumnya belum menentukan time lag data GCM. Oleh karena itu, penelitian ini menggunakan CCF dalam menentukkan time lag data luaran GCM. Metode yang digunakan dalam model SD adalah RKTP dan RKU.
Tujuan Penelitian Tujuan dari penelitian ini adalah untuk: 1. Menentukan time lag data GCM.
2. Memodelkan statistical downscaling menggunakan metode RKTP dan RKU dengan time lag data presipitasi luaran GCM.
2 TINJAUAN PUSTAKA
Statistical Downscaling
3 global, GCM tidak dapat melakukan simulasi dengan baik untuk peubah iklim yang berskala lokal (Huth dan Keysely 2000). Oleh karena itu, GCM tidak dapat langsung digunakan untuk merepresentasikan keadaan iklim yang berskala lokal (Zorita dan Storch 1999). Bergant et al. (2002) menyatakan bahwa statistical downscaling (SD) dapat digunakan untuk mengatasi masalah perbedaan skala antara peubah prediktor dan peubah respon.
SD merupakan suatu fungsi transfer yang menggambarkan hubungan fungsional sirkulasi atmosfir global (luaran GCM) dengan unsur-unsur iklim lokal. Ide dasar dari SD adalah mencari hubungan antara parameter iklim skala global dengan parameter iklim skala lokal dan menggunakan hubungan ini untuk proyeksi hasil simulasi GCM pada iklim masa lalu, sekarang, atau masa depan yang berskala lokal. SD menggunakan model statistik dalam menggambarkan hubungan antara data pada grid berskala global (prediktor) dengan data pada grid berskala lokal (respon) untuk menterjemahkan anomali-anomali skala global menjadi anomali dari beberapa peubah iklim lokal (Zorita dan Storch 1999). Pendekatan ini mencari informasi skala lokal berdasarkan pada informasi skala global melalui hubungan fungsional antara kedua skala tersebut. Namun, keadaan skala lokal tersebut bisa beragam atau adanya regionalisasi untuk kondisi skala global yang sama. Dengan kata lain, keadaan skala lokalnya bisa beragam untuk keadaan skala global yang sama.
Persamaan umum SD adalah sebagai berikut (Sailor et al. 2000; Trigo dan Palutikof 2001 dalam Wigena 2006):
= (2.1) dengan �× adalah peubah-peubah iklim lokal (misalnya: curah hujan), �×� adalah peubah-peubah luaran GCM (misalnya: presipitasi), adalah banyaknya waktu (misalnya: harian atau bulanan), adalah banyaknya grid domain GCM. SD diilustrasikan dalam Gambar 1 yang menghubungkan data GCM berskala global dengan data hasil observasi di permukaan bumi yang berskala lokal.
Model SD akan memberikan hasil yang baik jika memenuhi tiga syarat utama, yakni hubungan antara respon dengan prediktor harus kuat untuk menjelaskan keragaman iklim lokal dengan baik, peubah prediktor harus disimulasikan dengan baik oleh GCM, dan hubungan antara respon dengan
4
prediktor tidak berubah dengan adanya perubahan waktu dan tetap sama meskipun ada perubahan iklim di masa depan (Busuioc et al. 2001). Oleh karena itu, penentuan time lag pada data presipitasi GCM membantu dalam meningkatkan keeratan hubungan antara kedua peubah. Selain itu, pemilihan peubah-peubah prediktor dan penentuan domain (lokasi dan jumlah grid) perlu dilakukan karena kedua hal tersebut juga merupakan faktor kritis yang dapat mempengaruhi kestabilan peramalan (Wilby dan Wigley 1997 dalam Wigena 2006). Dengan demikian, pemilihan peubah prediktor (data GCM) sebaiknya berdasarkan pada korelasi yang kuat antara peubah tersebut dengan curah hujan (Wigena 2006).
Metode yang umum digunakan dalam pemodelan SD untuk mengatasi masalah dimensi data atau multikolinieritas antar peubah prediktor adalah RKU yang berdasarkan AKU. Serupa dengan RKU, metode lain yang sering digunakan adalah RKTP (Estiningtyas dan Wigena 2011; Huth dan Keysely 2000).
Regresi Kuadrat Terkecil Parsial
RKTP merupakan salah satu metode yang dapat digunakan untuk mengatasi masalah multikolinearitas pada peubah prediktor. Metode RKTP mengkombinasikan antara AKU dengan regresi linier. Hal ini dilakukan dengan tujuan untuk memprediksi suatu gugus peubah respon berdasarkan gugus peubah prediktor (Wigena 2011). Metode RKTP dapat diterapkan pada pendugaan satu respon maupun multi respon.
Metode RKTP memproyeksikan data ke sejumlah faktor utama dan kemudian memodelkan faktor-faktor tersebut dengan regresi linier (Djuraidah 2003). Faktor tersebut disebut sebagai skor. Skor dalam RKTP dihitung berdasarkan kriteria memaksimalkan peragam antara peubah dan . Perhitungan nilai skor dalam RKTP menggunakan metode kuadrat terkecil (MKT) dan dilakukan secara parsial (Ismah etal. 2009).
Misalkan berukuran × , dengan adalah banyaknya pengamatan dan adalah banyaknya peubah prediktor, terdiri dari vektor , = , , … , , dan berukuran × , dengan adalah banyaknya peubah respon, terdiri dari vektor , = , , … , . Metode RKTP menghasilkan sejumlah komponen baru yang akan memodelkan terhadap sehingga diperoleh hubungan antara dan . Komponen-komponen baru tersebut disebut sebagai skor dan dapat dituliskan sebagai � dengan = , , … , �. Setiap skor � yang dihasilkan saling orthogonal sehingga RKTP dapat mengatasi masalah multikolinieritas pada peubah prediktor. Skor merupakan kombinasi linier peubah-peubah asal dengan koefisien pembobot �. Proses tersebut dapat diformulasikan sebagai (Wold et al. 2001):
�= ∑ � , = , , … ,
= (2.2) Skor ( �) digunakan sebagai prediktor untuk respon dan model dari . Skor tersebut mempunyai sifat-sifat sebagai berikut:
1. Skor dikalikan dengan loading � sehingga sisaannya kecil.
= ∑� � � + ⟹ = �′+
Pada kondisi > , skor ( ) dikalikan dengan pembobot � sehingga sisaannya ( ) kecil.
5 2. Skor adalah prediktor bagi , yakni:
= ∑� � �+ ⟹ = ′+ (2.4) Sisaan ( ) merupakan simpangan antara respon pengamatan dengan respon dugaan. Berdasarkan persamaan (2.2) dan persamaan (2.4) dapat dituliskan sebagai model regresi ganda dengan formula sebagai berikut:
= ∑� � ∑ � + = ∑ +
= ′+ = +
Koefisien model RKTP, , adalah sebagai berikut:
= ∑� � � ⟹ = ′
Prediksi bagi data pengamatan yang baru dapat diperoleh berdasarkan data dan matriks koefisien .
Regresi Komponen Utama
Peubah-peubah data GCM umumnya memiliki dimensi yang besar sehingga memungkinkan adanya multikolinieritas atau korelasi yang tinggi antar grid GCM. Selain RKTP, metode lain yang dapat digunakan untuk mengatasi masalah multikolinieritas adalah RKU. Metode RKU diawali dengan AKU untuk mereduksi dimensi data atau mengatasi multikolinieritas.
AKU adalah suatu prosedur untuk mereduksi dimensi data dengan mentransformasi peubah-peubah asal yang saling berkorelasi menjadi sekumpulan peubah baru yang tidak berkorelasi dengan tetap mempertahankan sebanyak mungkin keragaman data yang mampu dijelaskan. Peubah-peubah baru itu dikenal sebagai komponen utama (KU) (Johnson dan Wichern 2007).
KU dapat diperoleh dari pasangan nilai akar ciri dan vektor ciri matriks ragam-peragam atau matriks korelasi. Matrik ragam-peragam dari peubah digunakan apabila tidak terdapat perbedaan satuan antar peubah prediktor. Sebaliknya, matriks korelasi dari peubah digunakan pada saat terdapat perbedaan satuan antar peubah prediktor. Selain itu, matriks korelasi juga digunakan jika terdapat keragaman yang besar dalam matriks peubah predictor. Standardisasi data dilakukan terlebih dahulu jika menggunakan matriks korelasi. Standardisasi data perlu dilakukan supaya dominansi satu atau lebih peubah prediktor dalam KU dapat dihindari.
Jika ′ = [ , , … , �] mempunyai matriks ragam-peragam � dengan nilai akar ciri � ≥ � ≥ ≥ �� ≥ , maka diperoleh yang merupakan kombinasi linier peubah asal (Johnson dan Wichern2007), yakni:
= � ′ = + + +
� �
= � ′ = + + +
� �
6
dari � , � , … , �� sedemikian rupa sehingga ( ) = � ′� � maksimum dengan fungsi kendala � ′� = .
KU pertama adalah kombinasi linear � ′ yang memaksimumkan � ′ dengan fungsi kendala � ′� = .
KU kedua adalah kombinasi linear � ′ yang memaksimumkan � ′ dengan fungsi kendala � ′� = dan � ′ , � ′ = � ′� � = .
KU ke-j adalah kombinasi linear �′ yang memaksimumkan � ′ dengan fungsi kendala �′� = dan (�′ , �′′ ) = � ′� �′= untuk
′ < .
KU mempunyai ragam yang sama dengan nilai akar ciri dari matriks � sehingga untuk persamaan KU ke-j,
= � ′ = + + +
� � (2.6) mempunyai nilai ( ) = � ′� � = � = , , … ,
( , ′) = � ′� �′= ≠ ′ = , , … , Matriks ragam-peragam dari dapat dituliskan sebagai berikut:
� = [
� �
⋱
… ��
]
Dengan demikian, total keragaman peubah asal sama dengan total keragaman yang dijelaskan oleh KU dan dapat dituliskan sebagai berikut:
� + � + + �� = � + � + + ��
∑�= ( ) = � = ∑�= ( ) (2.7) Jika total keragaman populasi adalah � + � + + �� = � + � + + ��, maka kontribusi keragaman relatif yang mampu dijelaskan oleh KU ke-j adalah:
� +� + +�� = + + + � (2.8) Jika KU yang diambil sebanyak r komponen, dengan < , maka besarnya keragaman kumulatif untuk r buah KU adalah sebagai berikut:
∑�=
∑�= × % (2.9) Selain menggunakan matriks ragam-peragam, KU juga dapat dibentuk menggunakan matriks korelasi. Matriks korelasi digunakan ketika peubah-peubah prediktor yang diamati memiliki perbedaan satuan atau memiliki keragaman yang besar dalam matriks peubah prediktor. Penurunan KU menggunakan matriks korelasi terlebih dahulu dilakukan dengan mentransformasi peubah asal menjadi bentuk baku dengan formula sebagai berikut:
=(� − )
7 Notasi matriksnya dapat dituliskan sebagai
= ( / )− − � (2.11) dengan
/ = √� , √� , … , √��
=
adalah matriks peubah asal yang telah dibakukan. Keragaman dapat dituliskan sebagai berikut:
= ( / )− �( / )− = � (2.12) dengan � adalah matriks korelasi peubah asal . KU ke-j, yang dibentuk berdasarkan peubah-peubah yang dibakukan ′ = [ , , … , �], dapat ditentukan dari vektor ciri yang diperoleh melalui matriks korelasi peubah asal dengan formula KU sebagai berikut:
= � ′ = + + +
� �
Proporsi total keragaman yang dapat dijelaskan oleh KU ke-j dari adalah: ragam yang dapat dijelaskan oleh KU ke-j =
� (2.13) dengan � adalah nilai akar ciri dari matriks �. Teras matriks korelasi sama dengan p.
Metode yang digunakan untuk menentukan jumlah KU yang akan digunakan dalam analisis RKU adalah sebagai berikut (Fekedulegn et al. 2002):
Membuang komponen yang memiliki nilai akar ciri terkecil. Alasannya adalah bahwa KU dengan nilai akar ciri terkecil mengandung sedikit informasi. Dengan menggunakan prosedur ini, KU dieliminasi sampai komponen yang tersisa menjelaskan beberapa persentase keragaman (yang dipilih sebelumnya) dari total keragaman (misalnya 80% atau lebih).
Beberapa peneliti menggunakan aturan memilih KU yang memiliki nilai akar ciri lebih besar dari satu.
Setelah dilakukan AKU, langkah selanjutnya adalah meregresikan KU yang terpilih terhadap peubah respon menggunakan RKU. Terdapat dua cara untuk menentukan KU dalam RKU sehingga terdapat dua bentuk pendugaan koefisien regresi, yakni berdasarkan matriks ragam-peragam dan matriks korelasi.
Misalkan mariks � adalah matriks ortogonal berisi vektor ciri dari � peubah asal yang memenuhi persamaan �′� = ��′ = �. Proses pembentukan RKU dari regresi linier berganda dengan = � dan = �′ adalah (Jollife 2002):
= + �
8
= + � (2.14)
yang mengganti peubah prediktor dengan KU pada model regresi. Model RKU hasil reduksi menjadi r komponen adalah sebagai berikut:
= � + � �+ � (2.15)
dengan �~� , � � merupakan vektor sisaan berukuran × , merupakan matriks peubah prediktor berukuran × + , merupakan vektor peubah respon berukuran × , � adalah intersep, adalah vektor bernilai satu berukuran × , � adalah matriks KU berukuran × , dan � adalah vektor berisi koefisien KU berukuran × .
Persamaan RKU yang dibentuk berdasarkan matriks korelasi hampir sama dengan yang dibentuk berdasarkan matriks ragam-peragam, yakni cukup dengan mengganti peubah-peubah , , … , � menjadi peubah-peubah baku
, , … , �. Model RKU yang dibangun berdasarkan matriks korelasi sama dengan persamaan (2.15) dengan = �.
Pendugaan koefisien regresi pada RKU menggunakan metode kemungkinan maksimum dengan koefisien �̂ , �̂ , … , �̂� merupakan penduga bagi koefisien
Jika diambil contoh acak sebanyak , maka fungsi kepekatan peluang bersamanya dapat dirumuskan sebagai, dengan fungsi kemungkinan dapat dirumuskan seperti pada persamaan (2.18).
9 sehingga diperoleh,
̂ = ′ − ′ (2.19) Hasil yang sama dengan persamaan (2.19) juga dapat diperoleh dengan menggunakan MKT. Jika ̂� = [�̂ , �̂ , … , �̂�] adalah penduga bagi koefisien RKU dengan r komponen, maka persamaan (2.19) menjadi,
̂� = �′ � − �′ (2.20) dengan � = �� jika menggunakan matriks ragam peragam peubah dan � = ��jika menggunakan matriks korelasi peubah . �� adalah matriks berukuran × yang elemen-elemennya merupakan vektor ciri, dan � , � , … , �� merupakan vektor ciri yang masing-masing berukuran × .
3 METODE PENELITIAN
Data
Data yang digunakan dalam penelitian ini adalah data presipitasi GCM
climate model intercomparison project (CMIP5) dalam satuan mm/bulan dan data curah hujan di Kabupaten Indramayu pada periode 1979-2008. Tabulasi data disajikan dalam Lampiran 1. Data curah hujan yang digunakan dalam penelitian ini merupakan rata-rata curah hujan pada 15 stasiun di Kabupaten Indramayu (Bangkir, Bulak, Cidempet, Cikedung, Losarang, Sukadana, Sumurwatu, Tugu, Ujunggaris, Lohbener, Sudimampir, Juntinyuat, Kedokan Bunder, Krangkeng, dan Bondan). Data GCM CMIP5 diperoleh dari situs web http://www.climatexp.knmi.nl/ yang dikeluarkan oleh KNMI Belanda. Data presipitasi luaran GCM yang berskala global digunakan sebagai peubah prediktor dan data curah hujan stasiun di Kabupaten Indramayu digunakan sebagai peubah respon. Musim hujan di Indonesia terjadi pada bulan Oktober hingga Maret dan musim kemarau terjadi pada bulan April hingga September.
Domain GCM yang digunakan dalam penelitian ini adalah sejumah grid berbentuk persegi berukuran 8×8 grid (2.5°×2.5° untuk setiap grid) pada 98.75°BT s.d 116.25°BT dan −16.25°LS s.d 1.25°LU di atas sekitar wilayah Indramayu. Penggunaan ukuran domain 8×8 grid di atas wilayah Indramayu memberikan hasil yang lebih stabil atau konsisten serta tidak sensitif terhadap data pencilan (Wigena 2006).
Metode Analisis
10
Tahapan analisis yang dilakukan dalam penelitian ini disajikan dalam bentuk diagram alir pada Lampiran 2 dengan rincian sebagai berikut:
1. Menentukan time lag data GCM menggunakan CCF yang dapat dirumuskan 2007) dan data validasi (periode 2008).
3. Mengidentifikasi multikolinearitas pada data presipitasi menggunakan variance inflation factors (VIF).
4. Menerapkan teknik SD menggunakan metode RKTP dan RKU.
Algoritma pendugaan parameter RKTP yang digunakan dalam penelitian ini adalah non-linear iterative partial least squares (NIPALS) dengan tahapan sebagai berikut (Wold et al. 2001):
a) Mendapatkan nilai vektor awal . Pada umumnya nilai vektor awal diperoleh dari nilai vektor tunggal , yakni = dengan merupakan vektor peubah respon yang telah diskalakan.
b) Menghitung pembobot− ( ) menggunakan formula = ′ ⁄ ′ dan mengortonormalkan vektor dengan formula = ⁄√ ′ sehingga
‖ ‖ = . merupakan matriks peubah prediktor yang telah diskalakan c) Menghitung skor− , = . validasi silang mengindikasikan tidak ada lagi informasi yang nyata dari terhadap .
h) Menduga vektor koefisien regresi pada analisis RKTP dengan formula sebagai berikut:
= ′
Tahapan analisis metode RKU yang dilakukan dalam penelitian ini adalah sebagai berikut (Mattjik dan Sumertajaya 2011):
a) Menguji kehomogenan ragam data presipitasi luaran GCM.
b) Jika ragam data presipitasi homogen, maka matriks ragam-peragam peubah digunakan dalam AKU. Akan tetapi, jika ragam data presipitasi heterogen, maka peubah prediktor ditransformasi terlebih dahulu menjadi bentuk baku . Selanjutnya, matriks ragam-peragam peubah (matriks korelasi peubah ) digunakan dalam AKU.
c) Menghitung nilai akar ciri � dan vektor ciri � , serta skor KU ( ). d) Meregresikan dengan yang terpilih.
e) Mentransformasi persamaan regresi dari ke (jika menggunakan matriks korelasi).
11 5. Pemeriksaan asumsi kehomogenan ragam sisaan menggunakan plot antara nilai sisaan dengan curah hujan dugaan. Jika plot sisaan membentuk pola tertentu maka mengindikasikan terjadi pelanggaran asumsi kehomogenan ragam sisaan. 6. Validasi model pada data periode 2008. Alat validasi model yang digunakan
adalah nilai korelasi dan root mean squared error of prediction (RMSEP).
4 HASIL DAN PEMBAHASAN
Eksplorasi Data
Time Lag Data Presipitasi GCM
Time lag data presipitasi luaran GCM ditentukan berdasarkan nilai korelasi silang tertinggi antara data presipitasi dengan data curah hujan. Nilai korelasi tersebut dihitung dengan menggunakan CCF. Berdasarkan Lampiran 3(a), plot curah hujan di Kabupaten Indramayu menunjukkan bahwa curah hujan tertinggi rata-rata terjadi pada bulan Januari dan Februari. Serupa dengan Lampiran 3(a), plot presipitasi juga menunjukkan presipitasi tertinggi rata-rata terjadi pada bulan Januari dan Februari (Lampiran 3(f)). Hal ini berarti bahwa tidak terjadi pergeseran waktu pada data presipitasi . Sebaliknya, terjadi pergeseran waktu pada data presipitasi dan . Lampiran 3(c) dan 3(h) menunjukkan bahwa presipitasi tertinggi rata-rata terjadi pada bulan Maret untuk presipitasi dan bulan Desember untuk presipitasi . Hal ini mengakibatkan korelasi yang rendah antara data curah hujan dengan data presipitasi dan . Oleh karena itu, CCF digunakan untuk menentukan time lag data presipitasi.
Hasil pada Lampiran 3(b), 3(e), dan 3(g) menunjukkan bahwa presipitasi
, , dan memiliki korelasi silang tertinggi (time lag) dengan curah hujan berturut-turut pada time lag ke-2, ke-0, dan ke-(-1). Curah hujan bulan Januari terjadi di bulan Maret pada data presipitasi dan terjadi di bulan Desember pada data presipitasi . Oleh karena itu, data presipitasi dilakukan penundaan 2 bulan, sedangkan data presipitasi dilakukan pergeseran 1 bulan ke depan. Presipitasi tidak dilakukan penundaan maupun pergeseran karena mempunyai korelasi silang tertinggi pada time lag ke-0. Pola tebaran data presipitasi dan dengan penundaan mengikuti pola curah hujan (Lampiran 3(d) dan 3(i)). Pergeseran terjauh data presipitasi terjadi pada time lag ke-10. Namun, time lag
data presipitasi umumnya terjadi pada time lag ke-1 (Tabel 1).
Hasil perhitungan pada Lampiran 4 menunjukkan bahwa presipitasi GCM dengan penundaan mempunyai korelasi yang lebih tinggi daripada presipitasi GCM tanpa penundaan. Jumlah grid GCM dengan penundaan (GCM-lag) yang memiliki korelasi lebih dari 0.7 dengan data curah hujan adalah sebanyak 73%. Sementara itu, korelasi antara data curah hujan dengan data presipitasi tanpa penundaan (GCM) yang lebih dari 0.7 hanya mencapai 9%.
Variance Inflation Factors
12
Model Statistical Downscaling Regresi Kuadrat Terkecil Parsial
RKTP merupakan salah satu pendekatan dalam model SD untuk mengatasi masalah multikolinearitas pada data luaran GCM. Metode RKTP menghasilkan sejumlah komponen baru yang memodelkan terhadap . Jumlah komponen yang digunakan dalam RKTP ditentukan berdasarkan nilai statistik prediction residual sum of squares (PRESS). PRESS merupakan suatu pendekatan yang dipertimbangkan untuk prosedur kestabilan penduga koefisien regresi. Nilai PRESS yang minimum memberikan kestabilan pendugaan yang lebih tinggi terhadap model jika ada data baru. Berdasarkan Tabel 2, nilai PRESS memperlihatkan bahwa cukup menggunakan satu komponen dalam model RKTP meskipun terdapat dua komponen yang memiliki nilai akar rataan PRESS terkecil (komponen yang memiliki nilai peluang>0.05). Satu komponen terekstrak dapat menjelaskan sebesar 83.1% keragaman data presipitasi GCM-lag dan sebesar 62.1% keragaman data curah hujan (Gambar 2). Hasil perhitungan menunjukkan bahwa metode RKTP dengan nilai R2 sebesar 71.7% cukup baik dalam menjelaskan keragaman data dengan nilai root mean square error (RMSE) yang dihasilkan sebesar 57.93.
13 amatan dengan curah hujan tertinggi. Amatan ke-25 merupakan curah hujan bulan Januari 1981 dengan nilai sebesar 582.6 mm/bulan. Gambar 2 juga menggambarkan kondisi sisaan dari model RKTP. Semakin tinggi nilai skor , maka nilai sisaan semakin besar yang mengindikasikan sisaan model RKTP tidak homogen (membentuk pola divergen).
Gambar 2 menunjukkan 5 kelompok data curah hujan berdasarkan kelompok warna dominan pada data curah hujan yang bersesuaian dengan nilai skor . Kelompok 1 umumnya terjadi pada bulan Mei hingga Oktober dengan intensitas 0−110.53 mm/bulan, kelompok 2 umumnya terjadi pada bulan Maret, April, dan November dengan intensitas 110.54−235.07 mm/bulan, kelompok 3 umumnya terjadi pada bulan Desember dengan intensitas 235.08 − 353.73 mm/bulan, kelompok 4 umumnya terjadi pada bulan Februari dengan intensitas 353.74−454.73 mm/bulan, dan kelompok 5 umumnya terjadi pada bulan Januari dengan intensitas lebih dari 454.73 mm/bulan. Pengelompokan ini dilakukan secara subjektif dengan mempertimbangkan warna dominan yang terbentuk. Jika menggunakan analisis diskriminan, maka diperoleh persentase ketepatan pengelompokan sebesar 94.8%.
Tabel 2 Komponen terekstrak pada model RKTP Jumlah komponen
terekstrak Akar rataan PRESS Peluang > PRESS
0 1.02 <.00
1 0.63 0.36
2 0.63 1.00
3 0.64 0.01
14
Regresi Komponen Utama
Pemodelan pada metode RKU diawali dengan AKU untuk mereduksi dimensi atau mengatasi masalah multikolinieritas dalam data. Penentuan matriks yang digunakan untuk mereduksi dimensi data dipilih berdasarkan hasil uji kehomogenen ragam data GCM-lag yang menggunakan uji Levene. Pemeriksaan kehomogenan ragam menggunakan statistik uji Levene dengan hipotesis:
H0: ragam data GCM-lag homogen
H1: ragam data GCM-lag tidak homogen
Berdasarkan Gambar 3, nilai peluang yang dihasilkan oleh uji Levene lebih kecil dari taraf 5% yang digunakan. Hal ini berarti bahwa data presipitasi − dari GCM-lag secara nyata memiliki ragam yang heterogen. Oleh karena itu, AKU dibentuk berdasarkan matriks korelasi untuk mereduksi dimensi data.
Jumlah KU yang digunakan untuk membangun model RKU ditentukan berdasarkan proporsi kumulatif keragaman total berkisar 80%−95%. Tabel 3 menunjukkan bahwa 4 KU pertama (KU1-KU4) dapat menjelaskan keragaman data presipitasi GCM-lag sebesar 95%. Dengan demikian, terdapat 4 model awal RKU berdasarkan jumlah KU yang digunakan.
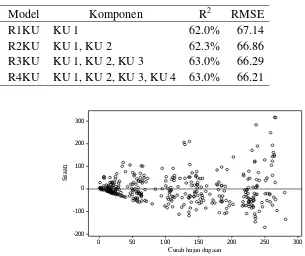
Model awal RKU dibangun dengan meregresikan KU terpilih dengan data curah hujan. Hasilnya menunjukkan bahwa model awal RKU kurang baik dalam menjelaskan keragaman data dibandingkan model RKTP. Nilai R2 yang dihasilkan berkisar 62%−63% dengan RMSE yang cukup besar, yakni berkisar 66.21−67.14 (Tabel 4). Hal ini berarti bahwa model awal RKU hanya mampu menjelaskan keragaman data sekitar 62.58%. Nilai dugaan koefisien regresi disajikan dalam Lampiran 8. Hasil pada Lampiran 6 menunjukkan bahwa peningkatan nilai koefisien regresi model RKU (R1KU, R2KU, R3KU, dan R4KU) tidak berbeda nyata sehingga mengakibatkan nilai R2 model-model RKU
juga tidak berbeda jauh.
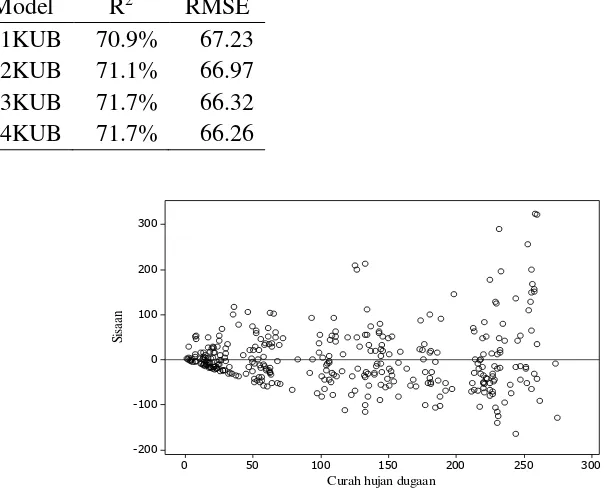
Diagnosis sisaan dilakukan terhadap keempat model RKU. Model R1KU menunjukkan kondisi ragam sisaan yang tidak homogen (Gambar 4). Tebaran sisaan model R1KU membentuk pola divergen. Tebaran sisaan pada curah hujan tinggi lebih beragam dibandingkan dengan curah hujan rendah. Serupa dengan itu, tebaran sisaan model R2KU, R3KU, dan R4KU juga menunjukkan kondisi yang tidak homogen (Lampiran 7). Oleh karena itu, analisis dilanjutkan dengan mengalikan pembobot dalam model RKU. Pembobot ditentukan berdasarkan keragaman setiap bulan.
Selang kepercayaan 95% bagi simpangan baku Statistik uji 92.60 Nilai-P 0.000
Uji Lev ene
15
RKU Terboboti
Perkalian bobot ke dalam model RKU (RKUB) bertujuan untuk menangani masalah keheterogenan sisaan. Pembobotan ditentukan berdasarkan keragaman setiap bulan. Hal ini dilakukan dengan mengelompokkan data curah hujan ke dalam kelompok bulan. Selanjutnya, bulan yang memiliki ragam yang sama dikelompokkan ke dalam satu kelompok. Simpangan baku dihitung pada setiap kelompok yang terbentuk. Nilai pembobotnya adalah satu per nilai simpangan baku masing-masing kelompok.
Gambar 5 memperlihatkan bahwa data curah hujan dalam kelompok bulan memiliki lebar selang kepercayaan yang berbeda. Hal ini mengindikasikan bahwa ragam data curah hujan dalam kelompok bulan tidak homogen. Oleh karena itu, pengelompokan dilakukan terhadap data curah hujan yang memiliki ragam sama. Hasil uji kesamaan ragam menunjukkan bahwa terdapat 3 kelompok yang memiliki ragam yang homogen (Lampiran 8). Kelompok 1 yang terdiri dari bulan Agustus dan September mempunyai bobot 0.0515, kelompok 2 yang terdiri dari bulan Maret, April, Mei, Juni, Juli, Oktober, dan Desember mempunyai bobot 0.0131, dan kelompok 3 yang terdiri dari bulan November, Januari, dan Februari mempunyai bobot 0.0081.
Tabel 3 Nilai akar ciri dan proporsi keragaman 5 KU pada data GCM-lag
16
Selang kepercayaan 95% bagi simpangan baku
Gambar 5 Uji kehomogenan ragam kelompok bulan data untuk presipitasi GCM-lag
Tabel 5 memberikan informasi bahwa model RKUB memberikan hasil yang lebih baik daripada model awal RKU, namun relatif sama dengan model RKTP. Perkalian bobot ke dalam model RKU menghasilkan nilai R2 berkisar 70.9%−71.7% dan nilai RMSE berkisar 66.26−67.23. Hal ini berarti bahwa nilai R2 meningkat sekitar 8.78% dari model RKU dengan nilai RMSE yang relatif sama. Nilai R2 model RKUB (R1KUB, R2KUB, R3KUB, dan R4KUB) dalam
17
Penambahan peubah boneka pada model awal RKU (RKUK) juga dilakukan dengan tujuan untuk menangani masalah keheterogenan sisaan. Peubah boneka ditentukan berdasarkan hasil pengelompokan model RKTP (Gambar 2). Plot antara skor dengan skor memperlihatkan 5 kelompok data curah hujan berdasarkan kelompok warna dominan sehingga terdapat 4 peubah boneka yang ditambahkan ke dalam model RKU.
Hasil pada Tabel 6 memberikan informasi bahwa model RKUK mampu menghasilkan model yang lebih baik daripada model RKU, RKUB, maupun RKTP. Nilai RMSE yang dihasilkan relatif kecil, yakni berkisar 28.06−29.09. Penambahan peubah boneka mampu menangani keragaman sisaan dengan menurunkan nilai RMSE sekitar 38.01. Selain itu, nilai R2 yang diperoleh berkisar 92.9%−93.4. Hal ini berarti bahwa model RKUK lebih baik dalam menjelaskan keragaman data. Penambahan peubah boneka mampu meningkatkan nilai R2 sekitar 30.53%. Ketepatan dalam mengelompokkan data curah hujan
menghasilkan model yang lebih memadai dan akurat berdasarkan nilai R2 dan RMSE yang dihasilkan. Selain itu, jumlah KU yang digunakan dalam model RKUK tidak mempengaruhi nilai R2 model karena nilai R2 yang diperoleh tidak
jauh berbeda. Hal ini disebabkan karena nilai koefisien regresi setelah penambahan KU dalam model RKUK hanya sedikit (Lampiran 6).
18
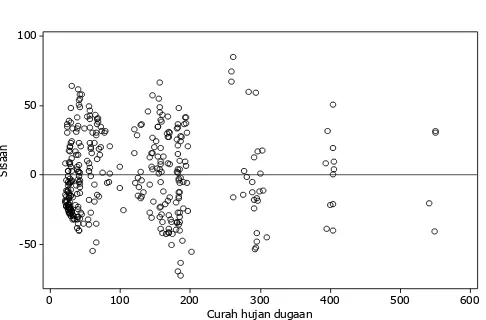
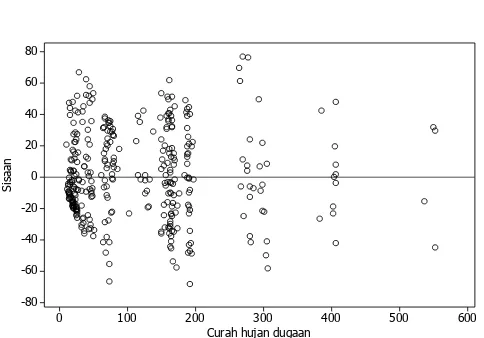
pola tebaran sisaan masing-masing kelompok pada Gambar 7 dan Lampiran 10 lebih homogen daripada pola tebaran sisaan model awal RKU, RKUB, dan RKTP. Penambahan peubah boneka pada model RKU mampu menghasilkan model dengan tebaran sisaan yang lebih homogen. Analisis selanjutnya adalah dengan menambahkan peubah boneka ke dalam model RKUB.
RKU Terboboti dan Peubah Boneka
Penambahan peubah boneka ke dalam model RKU terboboti (RKUBK) dilakukan untuk mengatasi masalah heteroskedastisitas. Hasilnya menunjukkan bahwa model RKUBK mampu menghasilkan nilai R2 berkisar 92.4%−92.9%
(Tabel 7). Nilai R2 model RKUBK yang menggunakan satu atau lebih KU tidak berbeda jauh karena penambahan jumlah KU hanya meningkatkan nilai koefisien regresi sekitar 1−4 satuan (Lampiran 6). Penambahan peubah boneka ke dalam model RKUB dapat meningkatkan nilai R2 sekitar 30.1%. Selain itu, nilai RMSE
yang dihasilkan berkisar 28.16−29.38. Penambahan peubah boneka ke dalam model RKUB menurunkan nilai RMSE sekitar 37.83.
Diagnostik dilakukan terhadap sisaan model RKUBK. Gambar 8 memperlihatkan 5 kelompok sisaan pada model R4KUBK. Plot sisaan untuk model R1KUBK, R2KUBK, dan R3KUBK tercantum pada Lampiran 11. Plot sisaan pada Lampiran 11 juga memperlihatkan 5 kelompok sisaan. Namun, pola tebaran sisaan masing-masing kelompok pada Gambar 8 dan Lampiran 11 relatif lebih homogen daripada pola tebaran sisaan model awal RKU, RKUB, maupun RKTP. Hal ini berarti bahwa penambahan peubah boneka ke dalam model RKUB juga mampu menghasilkan model dengan sisaan yang lebih homogen.
Tabel 7 Nilai R2 dan RMSE model RKUBK
19 Peramalan Data Curah Hujan dan Pemilihan Model Terbaik
Hasil pemodelan data curah hujan menunjukkan bahwa metode RKTP, RKU, dan RKUB tidak dapat mengatasi masalah keheterogenan ragam sisaan. Akan tetapi, metode RKUK dan RKUBK dapat mengatasi masalah tersebut. Selain itu, keragaman data yang mampu dijelaskan oleh model RKUK dan RKUBK cukup baik daripada model RKTP, RKU, dan RKUB. Namun, model RKUK lebih baik daripada model RKUBK karena lebih sederhana dengan nilai R2 dan RMSE yang relatif sama. Model RKUK juga konsisten pada hasil validasi model sebagai model terbaik. Peramalan data curah hujan untuk validasi model menggunakan data curah hujan periode 2008. Tahap validasi model menghitung RMSEP dan korelasi antara curah hujan aktual dengan curah hujan dugaan. Nilai korelasi menggambarkan kesesuaian antara model dugaan dengan data baru dan RMSEP menggambarkan keakuratan model dalam menduga data baru.
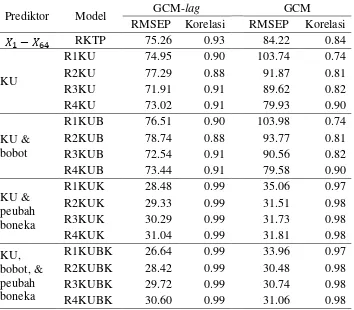
Tabel 8 menyajikan nilai korelasi dan RMSEP hasil dugaan data curah hujan yang menggunakan data presipitasi GCM-lag dan GCM. Hasil dugaan data curah hujan yang menggunakan data GCM-lag lebih unggul daripada menggunakan data GCM. Model RKTP pada data GCM-lag menghasilkan dugaan curah hujan dengan nilai korelasi (0.93) yang lebih tinggi dan nilai RMSEP (75.26) yang lebih rendah daripada korelasi (0.84) dan RMSEP (84.22) dari model RKTP pada data GCM. Lebih lanjut, pendugaan data curah hujan yang menggunakan model RKU dan RKUB pada data GCM-lag (RMSEP berkisar 71.91−77.29 dan korelasi berkisar 0.88−0.91) lebih baik daripada model RKU dan RKUB pada data GCM (RMSEP berkisar 79.58−103.98 dan korelasi berkisar 0.74−0.90). Selain itu, model RKUK dan RKUBK mampu memberikan hasil dugaan dengan nilai RMSEP berkisar 26.64−31.04 pada data GCM-lag dan RMSEP berkisar 30.48−35.06 pada data GCM, sedangkan nilai korelasinya berturut-turut berkisar 0.99 dan 0.97−0.98. Secara umum, model RKUK pada data GCM-lag mampu melakukan pendugaan data curah hujan yang lebih akurat dibandingkan model lainnya dengan model yang lebih sederhana. Model RKUK yang melibatkan KU1 merupakan model yang memberikan hasil dugaan terbaik berdasarkan nilai RMSEP (28.48) terkecil dan korelasi (0.99) lebih tinggi.
20
Model RKUK dan RKUBK pada data GCM-lag menghasilkan pola curah hujan dugaan yang relatif sama (Gambar 11 dan Gambar 12). Model RKUK dan RKUBK mampu melakukan pendugaan curah hujan yang mengikuti pola curah hujan aktual dibandingkan model RKU, RKTP, dan RKUB. Selain itu, jarak antara curah hujan aktual dengan curah hujan dugaan yang dihasilkan lebih dekat daripada jarak yang dihasilkan model RKU, RKTP, maupun RKUB. Serupa dengan model RKUK dan RKUBK pada data GCM-lag, pola curah hujan dugaan hasil dari model RKUK dan RKUBK pada data GCM juga menunjukkan pola yang sama dengan curah hujan aktual (Lampiran 12(c) dan 12(d)). Jarak antara curah hujan aktual dengan curah hujan dugaan model RKUK dan RKUBK pada data GCM yang ditunjukkan relatif dekat. Namun secara rata-rata, model RKUK dan RKUBK pada data GCM-lag menunjukkan performa yang lebih baik dibandingkan dengan model RKUK dan RKUBK pada data GCM. Nilai dugaan curah hujan dari model RKUK dan RKUBK pada data GCM-lag lebih mendekati dan mengikuti pola curah hujan aktual (RMSEP berkisar 26.64−31.04 dan korelasi sebesar 0.99) dibandingkan dengan hasil dugaan model RKUK dan RKUBK pada data GCM (RMSEP berkisar 30.48−35.06 dan korelasi berkisar 0.97−0.98). Secara umum, model RKU yang melibatkan komponen pertama dengan penambahan peubah boneka (R1KUK) pada data GCM-lag merupakan model terbaik karena dapat menghasilkan dugaan curah hujan yang lebih akurat (RMSEP sebesar 28.49 dan korelasi sebesar 0.99) dengan model yang lebih sederhana daripada model lainnya pada musim kemarau maupun pada musim hujan. Hal ini mengindikasikan bahwa penambahan peubah boneka ke dalam model RKU dapat memperbaiki dugaan data curah hujan.
Tabel 8 Nilai korelasi dan RMSEP setiap model pada data GCM-lag dan GCM
21
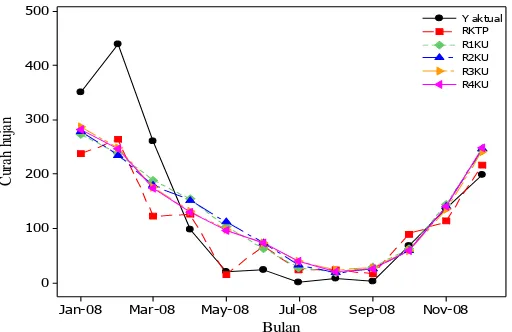
Gambar 9 Plot nilai curah hujan aktual dan curah hujan dugaan model RKTP dan RKU periode 2008 dengan data GCM-lag
Gambar 10 Plot nilai curah hujan aktual dan curah hujan dugaan model RKUB periode 2008 dengan data GCM-lag
22
5 SIMPULAN
Korelasi silang antara data curah hujan dan presipitasi luaran GCM berperan penting dalam pemodelan statistical downscaling. Korelasi silang tertinggi menentukan time lag yang dapat mengoptimakan keeratan hubungan antara data curah hujan dan presipitasi luaran GCM sehingga dapat meningkatkan ketepatan pendugaan data curah hujan. Pendugaan data curah hujan yang menggunakan presipitasi GCM dengan time lag memberikan hasil yang lebih akurat daripada menggunakan presipitasi GCM tanpa time lag. Model terbaik adalah hasil pemodelan dari metode RKU yang ditambahkan peubah boneka pada data presipitasi GCM dengan time lag berdasarkan bentuk model yang lebih sederhana dengan nilai R2 yang lebih tinggi dan RMSE yang lebih rendah. Peubah boneka didasarkan pada hasil pengelompokan metode RKTP. Model RKU dengan penambahan peubah boneka mampu memperbaiki hasil dugaan data curah hujan. Model RKU yang hanya melibatkan satu komponen utama dengan penambahan peubah boneka merupakan model terbaik berdasarkan nilai korelasi (0.99) yang tinggi dan RMSEP (28.48) yang dihasilkan. Model statistical downscaling terbaik dapat dituliskan sebagai berikut:
= 503.86 + 3.89 − 441.97 − 354.79 − 246.73 − 145.71 dengan, adalah curah hujan, adalah komponen utama, dan secara berturut-turut , , , merupakan peubah boneka.
DAFTAR PUSTAKA
Bergant K, Kajfez-Bogataj L, Crepinsek Z. 2002. The use of EOF analysis for preparing the phenological and climatological data for statistical downscaling-case study: The beginning of flowering of the dandelion (Taraxacum officinale) in Slovenia. Developments in Statistics. 17:163-174.
23 Busuioc A, Chen D, Hellstrom C. 2001. Performance of statistical downscaling models in GCM validation and regional climate change estimates: application for Swedish precipitation. Int J Climatol. 21:557-578.
Djuraidah A. 2003. Penerapan model nonlinear PLS dengan jaringan syaraf tiruan dalam kalibrasi. Jurnal Matematika, Aplikasi dan Pembelajarannya. 2(1):339-345.
Eduzon. 2011. Dampak perubahan iklim terhadap pertanian. Sosial Ekonomi Pertanian Indonesia [Internet]. [diunduh 2014 Apr 23]. Tersedia pada:
http://sosek-agribisnis.blogspot.com/2011/02/dampak-perubahan-iklim-terhadap.html.
Estiningtyas W, Wigena AH. 2011. Teknik statistical downscaling dengan regresi komponen utama dan regresi kuadrat terkecil parsial untuk prediksi curah hujan pada kondisi el nino, la nina, dan normal. Jurnal Meteorologi dan Geofisika. 12(1):65-72.
Fekedulegn BD, Colbert JJ, Hicks RR Jr, Schuckers ME. 2002. Coping with multicollinearity: An example on application of principal components regression in dendroecology. United States Department of Agriculture. 721:1-43.
Fernandez E. 2005. On the influence of predictors area in statistical downscaling of daily parameters. Norwegia Meteorological Institute. 9:1-21.
Hermawan E. 2010. Pengelompokan pola curah hujan yang terjadi di beberapa kawasan P. Sumatera berbasis hasil analisis teknik spektral. Jurnal Meteorologi dan Geofisika. 11(2): 75-84.
Huth R, Keysely J. 2000. Constructing site-specific sliate change scenarios on a monthly scale using statistical downscaling. Theoretical and Applied Climatolgy.66:13-27.
Ismah, Wigena AH, Djuraidah A. 2009. Pendekatan Regresi Kuadrat Terkecil Parsial Robust Multirespons dalam Model Kalibrasi. Prosiding Seminar Nasional Penelitian, Pendidikan dan Penerapan MIPA. Yogyakarta: UNY. Johnson RA, Wichern DW. 2007. Applied Multivariate Statistical Analysis. New
Jersey (NJ): Pearson Prentice Hall. Ed ke-6.
Jollife IT. 2002. Principal Component Analysis. New York (NY): Springer-Verlag. Ed ke-2.
Mardikyan S, Cetin E. 2008. Efficient choice of biasing constant for ridge regression. Int J Contemp Math Sciences. 3(11):527-536.
Mattjik AA, Sumertajaya IM. 2011. Sidik Peubah Ganda.Bogor (ID): IPB Pr. Notodiputro KA, Wigena AH, Fitriadi. 2005. Pendekatan regresi komponen
utama dan ARIMA untuk statistical downscaling.IPTEK. 11(3):137-142. Raharjo IB. 2011. Sekolah lapangan pengelolaan tanaman terpadu. Balai
Pengkajian Teknologi Pertanian Jawa Barat [Internet]. [diunduh 2013 Nov 28].
Tersedia pada: http://jabar.litbang.deptan.go.id/ind/index.php/program-litbang/slptt/30-slptt.
Supangat A. 2013. Perubahan iklim di Indonesia. DNPI [Internet]. [diunduh 2013 Nov 27]. Tersedia pada: http://sains.kompas.com/read/2013/04/01/11290330/ Perubahan.Iklim.di.Indonesia.
24
Sutikno, Setiawan, Purnomoadi H. 2010. Statistical downscaling output GCM modeling with continuum regression and pre-processing PCA approach.
Journal for Technology and Science. 21(3):109-118.
Warawati AD. 2013. Prakiraan curah hujan stasiun Sukadana dengan teknik statistical downscaling berdasarkan data satelit TRMM [skripsi]. Bogor (ID):Institut Pertanian Bogor.
Wigena AH. 2006. Pemodelan statistical downscaling dengan regresi projection persuit untuk peramalan curah hujan bulanan [disertasi]. Bogor (ID): Institut Pertanian Bogor.
Wigena AH. 2011. Regresi kuadrat terkecil parsial multi respon untuk statistical downscaling. Forum Statistika dan Komputasi. 16(2):12-15.
Wold S, Sjostrom M, Eriksson L. 2001. PLS-regression: a basic tool of chemometrics. Chemometrics and Intelligent Laboratory Systems. 58:109-130. Zorita E, Storch HV. 1999. The analog method as a simple statistical downscaling
25
26
Lampiran 1 Tabulasi data curah hujan dan presipitasi GCM periode 1979-2008 No Waktu
1 Jan-79 301.40 2.09 3.73 5.84 10.69 11.45 10.30 2 Feb-79 182.67 3.55 5.47 7.33 9.27 10.66 9.76 3 Mar-79 200.93 4.48 6.51 7.62 8.72 10.11 9.44 4 Apr-79 125.80 4.34 6.47 7.61 8.17 10.47 10.04 5 Mei-79 114.27 3.61 5.85 7.57 7.84 9.04 8.57 6 Jun-79 53.40 2.18 3.46 5.62 8.01 8.76 7.35 7 Jul-79 4.80 1.69 2.66 4.44 6.56 8.86 8.21 8 Agu-79 6.80 1.31 2.04 3.07 5.36 8.92 8.69 9 Sep-79 66.00 0.81 1.33 2.34 4.86 8.94 10.18 10 Okt-79 68.00 0.73 1.08 1.76 4.71 9.01 10.79 11 Nov-79 128.80 0.60 1.25 2.81 5.65 10.07 10.27 12 Des-79 214.53 0.81 1.59 3.06 8.46 10.85 9.52 13 Jan-80 320.40 1.47 2.99 4.81 10.79 10.94 8.67 14 Feb-80 179.67 3.03 5.16 6.89 10.04 10.19 9.45 15 Mar-80 110.53 4.22 6.39 7.74 8.67 10.23 9.91 16 Apr-80 109.27 4.45 6.93 8.27 8.56 11.07 9.74 17 Mei-80 37.67 3.05 5.15 7.45 9.06 9.99 8.96 18 Jun-80 17.07 2.12 3.28 5.07 7.99 9.12 7.91 19 Jul-80 25.93 1.40 2.47 4.33 7.23 9.31 7.83 20 Agu-80 48.13 1.17 1.64 2.59 6.20 9.45 8.40
27
Data presipitasi GCM Data curah hujan stasiun
di Indramayu
DATA
Data pemodelan Data pengujian
Eksplorasi data
Mereduksi dimensi data presipitasi dengan KTP Mereduksi dimensi data
presipitasi dengan AKU
RKU RKTP
Nilai curah hujan dugaan hasil RKU
Nilai curah hujan dugaan hasil RKTP
Validasi data Validasi data
Perbandingan metode RKU dengan metode RKTP menggunakan RMSEP
dan korelasi
Selesai Mulai
30
Lampiran 4 Korelasi antara curah hujan dengan presipitasi GCM dan GCM-lag
Peubah Curah hujan Peubah Curah hujan
GCM-tunda GCM GCM-tunda GCM
0.76 0.20 0.78 0.31
0.76 0.28 0.76 0.42
0.74 0.36 0.74 0.53
0.70 0.42 0.77 0.61
0.71 0.53 0.77 0.72
0.71 0.71 0.70 0.70
0.63 0.57 0.61 0.47
0.49 -0.06 0.68 0.34
0.76 0.21 0.78 0.40
0.76 0.29 0.75 0.50
0.74 0.38 0.76 0.59
0.72 0.47 0.78 0.65
0.76 0.61 0.75 0.72
0.74 0.74 0.68 0.68
0.61 0.53 0.64 0.64
0.59 0.18 0.68 0.61
0.76 0.22 0.76 0.49
0.76 0.31 0.76 0.57
0.74 0.42 0.78 0.62
0.75 0.53 0.78 0.65
0.78 0.66 0.76 0.68
0.72 0.72 0.72 0.62
0.71 0.54 0.64 0.58
0.69 0.24 0.32 0.39
0.76 0.25 0.77 0.58
0.75 0.34 0.78 0.63
0.73 0.47 0.78 0.66
0.77 0.58 0.79 0.68
0.78 0.70 0.76 0.67
0.72 0.72 0.70 0.59
0.62 0.43 0.60 0.60
31 Lampiran 5 Nilai variance inflation factors data presipitasi GCM-lag
No Prediktor VIF No Prediktor VIF
1 414.34 33 914.33
2 660.06 34 945.79
3 394.59 35 417.10
4 67.05 36 952.68
5 87.77 37 594.49
6 37.25 38 180.29
7 17.49 39 42.25
8 34.22 40 50.12
9 863.10 41 647.95
10 1252.11 42 430.75
11 697.41 43 932.97
12 218.90 44 1109.04
13 235.09 45 755.59
14 162.07 46 160.59
15 60.59 47 33.04
16 85.56 48 23.56
17 1044.13 49 236.24
18 1175.31 50 418.42
19 728.64 51 1055.41
20 613.75 52 1024.86
21 463.53 53 1056.74
22 120.98 54 208.76
23 77.04 55 43.13
24 128.68 56 14.88
25 1058.23 57 139.08
26 985.06 58 646.02
27 412.71 59 922.18
28 847.99 60 834.77
29 526.02 61 590.63
30 121.64 62 148.20
31 90.57 63 5.56
32
Lampiran 6 Koefisien regresi model RKU, RKUB, RKUK, dan RKUBK
Model Koefisien regresi
Konst. KU1 KU2 KU3 KU4 D1 D2 D3 D4
R1KU 122.24 11.78 - - - -
R2KU 122.24 11.78 3.11 - - - -
R3KU 122.24 11.78 3.11 -5.35 - - - - -
R4KU 122.24 11.78 3.11 -5.35 -2.97 - - - -
R1KUB 119.61 11.45 - - - -
R2KUB 120.31 11.35 2.55 - - - -
R3KUB 120.42 11.63 2.82 -5.25 - - - - -
R4KUB 120.59 11.59 2.73 -5.15 -1.93 - - - -
33 Lampiran 7 Diagnostik sisaan model awal RKU
34
Lampiran 8 Uji kesamaan ragam tiap kelompok bulan data curah hujan
(a) Kelompok 1
Okt Mei Mar Jun Jul Des Apr
100 90 80 70 60 50 40 30 20
B
ul
an
Selang kepercayaan 95% bagi simpangan baku
Statistik uji 1.80 Nilai-P 0.100
Uji Lev ene
(b) Kelompok 2
Nov Jan Feb
200 175
150 125
100 75
50
B
ul
an
Selang kepercayaan 95% bagi simpangan baku
Statistik uji 2.50 Nilai-P 0.088
Uji Lev ene
35 Lampiran 9 Diagnostik sisaan model RKUB
36
Lampiran 10 Diagnostik sisaan model RKUK
37 Lampiran 11 Diagnostik sisaan model RKUBK
38
Lampiran 12 Plot nilai curah hujan aktual dan curah hujan dugaan pada periode 2008 dengan data GCM
39 Lampiran 12 Plot nilai curah hujan aktual dan curah hujan dugaan pada
periode 2008 dengan data GCM (Lanjutan)
40