Statistical Downscaling dengan Model Aditif Terampat untuk Pendugaan Curah Hujan Ekstrim

(1)

STATISTICAL DOWNSCALING

DENGAN MODEL ADITIF

TERAMPAT UNTUK PENDUGAAN CURAH HUJAN EKSTRIM

LILIES HANDAYANI

SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR

(2)

(3)

PERNYATAAN MENGENAI TESIS DAN

SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA*

Dengan ini saya menyatakan bahwa tesis berjudul “Statistical Downscaling

dengan Model Aditif Terampat untuk Pendugaan Curah Hujan Ekstrim” adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apapun kepada perguruan tinggi manapun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.

Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.

Bogor, Juni 2014

Lilies Handayani

G151120131

(4)

RINGKASAN

LILIES HANDAYANI. Statistical Downscaling dengan Model Aditif Terampat untuk Pendugaan Curah Hujan Ekstrim. Dibimbing oleh AJI HAMIM WIGENA dan ANIK DJURAIDAH.

Perubahan iklim global dapat meningkatkan kejadian curah hujan ekstrim. Curah hujan ekstrim adalah kondisi curah hujan di atas atau di bawah rata-rata kondisi normalnya. Curah hujan ekstrim, secara garis besar dapat dibedakan menjadi curah hujan ekstrim basah yang berdampak kebanjiran dan curah hujan ekstrim kering yang berdampak kekeringan. Analisis yang mengkaji kejadian-kejadian ekstrim dibutuhkan untuk memperkecil dampak buruk karena adanya kejadian curah hujan ekstrim tersebut.

Model-model dalam menganalisis curah hujan sudah banyak diterapkan di antaranya global circulation model (GCM). Skala spasial yang digunakan dalam GCM masih bersifat global. Data ini tentu saja tidak dapat menjelaskan variabilitas dalam skala lokal yang lebih detail. Teknik untuk menurunkan ukuran skala spasialnya salah satunya dengan menggunakan statistical downscaling (SD). SD merupakan suatu teknik yang menggunakan model statistika untuk mengetahui hubungan antara suatu data yang berskala global dengan data yang berskala lokal.

Karakteristik data GCM yang bersifat nonlinear dan berdimensi besar mengakibatkan kesulitan dalam analisis, terlebih lagi jika peubah penjelasnya semakin banyak. Permasalahan ini dapat diatasi dengan suatu metode alternatif yang lebih fleksibel terhadap asumsi yang disebut metode nonparametrik. Dalam penelitian ini, metode nonparametrik yang digunakan adalah model aditif terampat yang merupakan perluasan dari model aditif dan didasarkan pada model regresi linear dengan memodelkan peubah respon sebagai kombinasi aditif dari hubungan fungsional peubah penjelas yang tidak memerlukan adanya asumsi mengenai distribusi sisaan.

Hasil yang diperoleh menunjukkan bahwa dugaan curah hujan ekstrim di kabupaten Indramayu dengan menggunakan model statistical downscaling

berbasis model aditif terampat yang dihasilkan menunjukkan kecenderungan yang mirip dengan pola data aktualnya dengan nilai RMSE dan RMSEP berturut-turut sebesar 67.676 dan 40.113. Pendugaan curah hujan ekstrim di kabupaten Indramayu tiga tahun ke depan memberikan hasil dugaan terbaik dari semua periode analisis yang digunakan dengan nilai korelasi sebesar 0.787.

(5)

SUMMARY

LILIES HANDAYANI. Statistical Downscaling with Generalized Additive Model for Extreme Rainfall Estimation. Supervised by AJI HAMIM WIGENA and ANIK DJURAIDAH.

Global climate change may also increase the incidence of extreme rainfall. Extreme rainfall is the rainfall that above or below the average normal conditions. Extreme rainfall will be wet extreme rainfall which causes flooded and dry extreme rainfall which causes drought. An analysis examining the extreme events is needed to minimize the adverse impacts due to the extreme rainfall events.

The model used in analyzing rainfall is global circulation model (GCM). Spatial scale used in the GCM is global so these data certainly can not explain the variability in a local scale. Techniques to reduce the size of spatial scale uses statistical downscaling (SD). SD is a statistical technique that uses the model to evaluate the relation between a global scale data with local scale data.

Characteristics of the GCM data are nonlinear and has large dimensions can make difficulty in the analysis, especially if it has many predictor variables. This problem can be overcame by more flexible alternative methods. Nonparametric methods that can properly accommodate the influence of nonlinear without having to know the explicit form is generalized additive model (GAM). GAM is an extension of the additive model based on linear regression model by modeling response as an additive combination of the functional form of predictors that do not require an assumption about the distribution of residual.

The results show that estimation of extreme rainfall in Indramayu district by using SD based on GAM obtained showed a trend similar to the pattern of the actual data with the value of RMSE and RMSEP, respectively for 67.676 and 40.113. Estimation of extreme rainfall in Indramayu district 3 years ahead gives the best estimate result than all periods of analysis used with a correlation value of 0.787.

(6)

© Hak Cipta Milik IPB, Tahun 2014

Hak Cipta Dilindungi Undang-Undang

Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumbernya. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik, atau tinjauan suatu masalah, dan pengutipan tersebut tidak merugikan kepentingan IPB

(7)

Tesis

sebagai salah satu syarat untuk memperoleh gelar Magister Sains pada

Program Studi Statistika

STATISTICAL DOWNSCALING

DENGAN MODEL ADITIF

TERAMPAT UNTUK PENDUGAAN

CURAH HUJAN EKSTRIM

SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR

BOGOR 2014

(8)

(9)

Judul Tesis : Statistical Downscaling dengan Model Aditif Terampat untuk Pendugaan Curah Hujan Ekstrim

Nama : Lilies Handayani NIM : G151120131

Disetujui oleh Komisi Pembimbing

Dr Ir Aji Hamim Wigena, MSc Ketua

Diketahui oleh

Dr Ir Anik Djuraidah, MS Anggota

Ketua Program Studi Statistika

Dekan Sekolah Pascasarjana

Dr Ir Anik Djuraidah, MS Dr Ir Dahrul Syah, MScAgr

(10)

PRAKATA

Puji syukur penulis panjatkan kehadirat Allah SWT atas limpahan rahmat dan ridho-Nya, kesempatan, dan kesehatan yang dikaruniakan-Nya sehingga tesis yang berjudul “Statistical Downscaling dengan Model Aditif Terampat untuk Pendugaan Curah Hujan Ekstrim” ini dapat terselesaikan.

Terima kasih penulis ucapkan kepada Bapak Dr Ir Aji Hamim Wigena, MSc dan Ibu Dr Ir Anik Djuraidah, MS selaku pembimbing, atas kesediaan dan kesabaran untuk membimbing dan membagi ilmunya kepada penulis dalam penyusunan tesis ini. Ucapan terima kasih juga penulis sampaikan sebesar-besarnya kepada seluruh Dosen Departemen Statistika IPB yang telah mengasuh dan mendidik penulis selama di bangku kuliah hingga berhasil menyelesaikan studi, serta seluruh staf Departemen Statistika IPB atas bantuan, pelayanan, dan kerjasamanya selama ini.

Ucapan terima kasih yang tulus dan penghargaan yang tak terhingga juga penulis ucapkan kepada Ayahanda dan Ibunda tercinta H Rosadi Usman, SPd dan Hj Masaat Labalado, MPd yang telah membesarkan dan mendidik penulis dengan penuh kasih sayang demi keberhasilan penulis selama menjalani proses pendidikan, juga adikku tersayang Wahyu Hidayat, SPdn serta keluarga besarku atas doa dan semangatnya.

Terakhir tak lupa penulis juga menyampaikan terima kasih kepada seluruh mahasiswa Pascasarjana Departemen Statistika dan Rumana Sulsel IPB atas segala bantuan dan kebersamaannya selama menghadapi masa-masa terindah maupun tersulit dalam menuntut ilmu, serta semua pihak yang telah banyak membantu dan tak sempat penulis sebutkan satu per satu.

Semoga tesis ini dapat bermanfaat bagi semua pihak yang membutuhkan.

Bogor, Juni 2014

(11)

DAFTAR ISI

DAFTAR TABEL vi

DAFTAR GAMBAR vi

DAFTAR LAMPIRAN vi

1 PENDAHULUAN 1

Latar Belakang 1

Tujuan Penelitian 2

2 TINJAUAN PUSTAKA 3

Curah Hujan 3

Teori Nilai Ekstrim 3

Global Circulation Model (GCM) 4

Statistical Downscaling (SD) 5

Analisis Regresi Nonparametrik 6

3 METODE PENELITIAN 10

Data 10

Metode Analisis 10

4 HASIL DAN PEMBAHASAN 12

Eksplorasi Data 12

Pemodelan 15

Perbandingan Metode GEV dan SD 18

Validasi dan Uji Konsistensi Model 19

5 SIMPULAN DAN SARAN 20

Simpulan 20

Saran 21

DAFTAR PUSTAKA 21

LAMPIRAN 23

(12)

DAFTAR TABEL

1 Deskripsi data curah hujan kabupaten Indramayu tahun 1979-2008 13 2 Curah hujan ekstrim kabupaten Indramayu tahun 1979-2008 14 3 Nilai akar ciri dan proporsi kumulatif analisis komponen utama 15 4 Nilai rata-rata dan simpangan baku dari nilai dugaan parameter GEV

dan nilai return 15

5 Hasil analisis model aditif terampat 17

6 Nilai RMSE, RMSEP, dan korelasi metode GEV dan SD 19 7 Nilai RMSEP dan korelasi di setiap panjang data pendugaan model SD

berbasis GAM 19

8 Nilai korelasi pendugaan model SD berbasis GAM untuk pendugaan

curah hujan ekstrim 3 tahun ke depan 20

DAFTAR GAMBAR

1 Ilustrasi proses statisticaldownscaling (Sutikno 2008) 6

2 Lokasi penelitian (Wigena 2006) 10

3 Pola curah hujan kabupaten Indramayu tahun 1979-2008 13 4 Matriks plot antara data curah hujan ekstrim dengan KU terpilih 16 5 Plot hubungan fungsional masing-masing KU terpilih 18 6 Plot antara curah hujan ekstrim dengan nilai dugaan 18

DAFTAR LAMPIRAN

1 Plot masing-masing variabel data GCM 23

2 Nilai cross correlation function (CCF) tertinggi masing-masing

variabel data GCM 28

3 Plot masing-masing variabel data GCM dengan time lag yang

menghasilkan korelasi paling tinggi 29

4 Uji kehomogenan ragam data GCM 33

5 Nilai dugaan parameter GEV dan nilai return 34 6 Plot data curah hujan ekstrim dengan masing-masing KU terpilih 34 7 Eksplorasi data curah hujan ekstrim dengan masing-masing KU terpilih 35

8 Hasil analisis model aditif terampat 37

9 Plot antara curah hujan ekstrim dengan KU terpilih (KU1, KU2, KU3,

(13)

1 PENDAHULUAN

Latar Belakang

Iklim berperan besar terhadap kehidupan manusia seperti dalam bidang pertanian, transportasi, telekomunikasi, dan pariwisata. Curah hujan sebagai unsur iklim yang paling tinggi keragaman dan fluktuasinya, serta paling dominan mencirikan iklim di Indonesia saat ini juga dipengaruhi oleh perubahan iklim global yang dapat menyebabkan kejadian curah hujan ekstrim. Curah hujan ekstrim adalah kondisi curah hujan di atas atau di bawah rata-rata kondisi normalnya yang secara garis besar dapat dibedakan menjadi curah hujan ekstrim basah yang berdampak kebanjiran dan curah hujan ekstrim kering yang berdampak kekeringan. Analisis yang mengkaji kejadian-kejadian ekstrim dibutuhkan untuk memperkecil dampak buruk karena adanya kejadian curah hujan ekstrim tersebut (Prang 2006).

Penggunaan model sebaran nilai ekstrim terampat (generalized extreme value, GEV) dapat menggambarkan pola kejadian ekstrim curah hujan. Pemodelan dengan GEV sangat bermanfaat untuk melihat karakteristik nilai ekstrim dalam suatu proses lingkungan tertentu dengan memberikan interpretasi mengenai perilaku ekor kanan fungsi peluangnya yang mengandung nilai-nilai ekstrim, walaupu n model GEV tidak menghasilkan dugaan curah hujan ekstrim dengan cukup akurat (Sadik 1999).

Model iklim yang mampu mensimulasi curah hujan di Indonesia dengan baik hingga saat ini belum banyak ditemukan. Topografi dan interaksi laut, darat, dan atmosfir yang sangat kompleks menambah kerumitan simulasi dan prediksi curah hujan di wilayah Indonesia sehingga diperlukan model peramalan curah hujan pada skala lokal dengan mempertimbangkan informasi tentang sirkulasi atmosfer global yang dapat diperoleh dari data global circulation model (GCM). GCM dipandang sebagai data yang paling berpotensi dalam hal menyimulasikan iklim masa lampau, sekarang, dan memprediksi perubahan-perubahan iklim yang mungkin terjadi di masa mendatang (Wilby et al. 2009).

Skala spasial yang digunakan dalam GCM masih bersifat global. Data ini tentu saja tidak dapat menjelaskan variabilitas dalam skala lokal yang lebih detail. Teknik transformasi data dari unit skala besar menjadi data pada unit skala yang lebih kecil menggunakan statistical downscaling (SD) yang memanfaatkan model statistika untuk menentukan hubungan antara suatu data yang berskala global dengan data yang berskala lokal. Perbedaan skala antara peubah penjelas dan respon dapat diatasi menggunakan teknik SD dengan peubah responnya adalah curah hujan skala lokal sedangkan curah hujan skala global sebagai peubah penjelasnya direpresentasikan oleh data GCM (Haryoko 2004).

(14)

2

Analisis yang paling sering digunakan untuk memodelkan hubungan antar peubah penjelas dan respon yang juga dapat diterapkan pada SD adalah analisis regresi linear. Adrianto (2006) mengkaji SD dengan pendekatan regresi linear, dalam hal ini regresi komponen utama dalam pemodelannya. Namun model regresi linear memiliki asumsi-asumsi yang kuat sehingga sering menyulitkan dan dapat mengurangi presisi kesimpulan karena karakteristik dari data GCM yang tidak memenuhi asumsi tersebut. Karakteristik data GCM yang bersifat nonlinear pun dapat bermacam-macam dan akan bertambah sulit dalam analisis jika peubah penjelasnya semakin banyak. Permasalahan ini dapat diatasi dengan suatu metode alternatif yang lebih fleksibel terhadap asumsi yang disebut metode nonparametrik.

Penelitian tentang pemodelan SD dengan pendekatan nonparametrik, antara lain dengan menggunakan metode regresi projection pursuit untuk peramalan curah hujan bulanan (Wigena 2006), regresi splines adaptif berganda untuk peramalan produksi padi (Sutikno 2008), dan Artificial Neural Network (Wilby et al. 2009), namun ketiga penelitian ini belum mengkaji kejadian ekstrim dalam pemodelannya. Mondiana (2012) telah mengkaji pemodelan curah hujan ekstrim secara parametrik tanpa mengakomodasi pengaruh nonlinear pada data GCM.

Metode nonparametrik yang berpotensi untuk pendugaan model SD dalam kajian ekstrim adalah model aditif terampat (generalized additive model, GAM). GAM pertama kali dikembangkan oleh Hastie dan Tibshirani pada tahun 1986. Metode ini dapat mengakomodasi dengan baik adanya pengaruh nonlinear tanpa harus mengetahui bentuk pengaruh tersebut secara eksplisit. Selain itu metode ini juga kekar (robust) terhadap pencilan. GAM merupakan perluasan dari model aditif yang didasarkan pada model regresi linear dengan memodelkan curah hujan lokal

( )

y sebagai kombinasi aditif dari hubungan fungsional peubah penjelas yang tidak memerlukan adanya asumsi mengenai sebaran sisaan. Setiap hubungan fungsional peubah penjelas diduga secara nonparametrik dengan metode pemulusan (Beck & Jackman 1997).

Penelitian ini mengkaji pemodelan SD dengan pendekatan model aditif terampat untuk menggambarkan kejadian curah hujan ekstrim yang terjadi dalam jangka waktu tertentu. Data yang digunakan adalah data curah hujan di kabupaten Indramayu, karena kabupaten Indramayu merupakan penyuplai beras terbesar di Jawa Barat. Areal persawahan di Indramayu saat ini semakin berkurang akibat dampak perubahan iklim yang ekstrim dan pemanasan global.

Tujuan Penelitian

Tujuan dari penelitian ini, antara lain :

1. Membandingkan hasil dugaan curah hujan ekstrim menggunakan sebaran nilai ekstrim dengan model statistical downscaling dengan pendekatan parametrik dan nonparametrik (model aditif terampat).

(15)

3

2 TINJAUAN PUSTAKA

Curah Hujan

Kehidupan manusia dan makhluk hidup lainnya di muka bumi ini tidak lepas dari pengaruh cuaca dan iklim. Unsur cuaca dan iklim yang sangat bervariasi adalah curah hujan. Di Indonesia yang mayoritas penduduknya adalah petani, curah hujan merupakan faktor utama yang mempengaruhi hasil produksi pertanian yang optimal.

Curah hujan adalah ketinggian air hujan yang terkumpul dalam tempat yang datar, tidak menguap, tidak meresap, dan tidak mengalir. Satuan curah hujan diukur dalam milimeter (mm) atau inci. Curah hujan 1 (satu) milimeter artinya dalam luasan satu meter persegi pada tempat yang datar tertampung air setinggi satu milimeter atau tertampung air sebanyak satu liter. Curah hujan yang jatuh di wilayah Indonesia dipengaruhi oleh beberapa faktor antara lain bentuk medan/topografi, arah lereng medan, arah angin yang sejajar garis pantai dan jarak perjalan angin di atas medan. Cuaca ekstrim adalah keadaan atau fenomena kondisi cuaca di atas normal yang terjadi pada suatu wilayah tertentu berskala jangka pendek (Hidayat 2008).

Identifikasi tentang curah hujan ekstrim dapat menggunakan metode block maxima, yaitu dengan membuat blok periode waktu yaitu periode tahunan. Blok yang terbentuk selanjutnya dianalisis untuk menentukan nilai pengamatan yang maksimum dan pengamatan-pengamatan tersebut dianggap sebagai pengamatan yang ekstrim (Gilli & Kellezi 2003).

Teori Nilai Ekstrim

Teori nilai ekstrim (extreme value theory, EVT) adalah salah satu teori yang membahas kejadian-kejadian ekstrim. EVT memberi perhatian pada informasi kejadian-kejadian ekstrim yang diperoleh untuk membentuk fungsi sebaran dari nilai-nilai tersebut. Analisis terhadap nilai-nilai ekstrim fenomena curah hujan sangatlah penting, terutama bagi pemerintah dan kementerian terkait untuk pengambilan suatu kebijakan (Sadik 1999).

Analisis tentang kejadian ekstrim memungkinkan kita untuk menduga terjadinya kejadian ekstrim tersebut. Misalkan Y1,Y2,,Yn adalah peubah acak

yang bebas dan identik, maka Y_{( )}_n =max

(

Y₁,Y₂,,Y_n

)

konvergen pada sebaran kumulatif:

( )

  

  

 

= 

  

 

   



 −

− −

≠ 

   

  

   



 ₊ −

− =

−

0 , exp

exp

0 , 1

exp

1

, ,

ξ σ

µ

ξ σ

µ

ξ ξ

ξ σ µ

y y

y F

(16)

4 ( )

( )

        =            ₋ − −      ₋ − ≠               − + −       − + = − − − 0 , exp exp exp 1 0 , 1 exp 1 1 1 1 1 , , ξ σ µ σ µ σ ξ σ µ ξ σ µ ξ σ ξ ξ ξ σ µ y y y y y f

dengan µ adalah parameter lokasi,

σ

adalah parameter skala, dan ξ adalah parameter bentuk. Pendugaan parameter-parameter tersebut dilakukan dengan metode kemungkinan maksimum (Chaves 2001).

Besaran/kuantitas yang menjadi perhatian bukan hanya tertuju pada pendugaan parameter itu sendiri, tetapi pada kuantil yang juga disebut sebagai tingkat pengembalian (return level) dari penduga GEV. Nilai dugaan tingkat pengembalian, sebagai berikut:

       =             − − − ≠         −             − − + = − 0 ˆ , 1 1 log log ˆ ˆ 0 ˆ , 1 1 1 ln ˆ ˆ ˆ ˆ ˆ ξ σ µ ξ ξ σ µ ξ k k Rk p

dengan k adalah jangka waktu dan p adalah periode. Nilai dugaan tingkat pengembalian curah hujan maksimum yang diperoleh akan dipakai untuk validasi pada data curah hujan. Nilai tingkat pengembalian merupakan nilai maksimum yang diharapkan akan dilampaui satu kali dalam jangka waktu k dengan periode p, atau dengan kata lain dalam k jangka waktu, curah hujan akan mencapai nilai maksimum R (Gilli & Kellezi 2003).

Global Circulation Model

Global circulation model (GCM) merupakan alat terpenting dalam memahami sistem iklim karena mampu memberikan informasi tentang pergeseran iklim di masa yang akan datang. GCM menghasilkan data dalam bentuk grid atau petak wilayah dengan resolusi rendah (2,5o atau ± 300 km) yang merepresentasikan keadaan iklim global tetapi tidak dalam skala regional atau lokal. Data GCM dalam bentuk grid-grid menunjukkan bahwa GCM merupakan salah satu contoh bentuk data spasial, yaitu data yang berkaitan dengan keruangan. GCM merupakan penggambaran matematis dari sejumlah besar interaksi fisika, kimia, dan dinamika atmosfer bumi. Model ini menduga perubahan unsur-unsur cuaca dalam bentuk luaran grid-grid menurut lintang dan bujur. Model ini dapat di-run untuk menduga kepekaan iklim terhadap kondisi yang berbeda seperti perubahan gas rumah kaca. GCM seringkali digunakan untuk menyimulasi iklim pada kondisi dua kali CO2. Penelitian dengan menggunakan GCM

seringkali terkendala pada pemilihan luas, metode, dan domainnya, ini tentu saja dapat menyulitkan untuk melanjutkan analisis. Pendekatan yang dapat dilakukan untuk menyelesaikan masalah tersebut adalah dengan penentuan domain menggunakan statistical downscaling (SD).

SD menghubungkan peubah iklim global dan lokal sebagai proyeksi output

(17)

5 dalam penggunaan metode statistika untuk downscaling adalah data GCM yang digunakan berupa data deret waktu dengan jumlah yang banyak dan tidak saling bebas sehingga tidak dapat langsung digunakan dalam model statistik, sehingga pemodelan SD dilakukan terlebih dahulu dengan jalan pra-pemrosesan reduksi dimensi domain grid untuk mengatasi kasus multikolinearitas. Metode reduksi dimensi yang sering digunakan adalah analisis komponen utama (AKU), namun kinerja AKU sendiri hanyalah sebatas memapatkan dimensi grid skala besar menjadi kecil belum pada bagaimana mendapatkan validasi model terbaik.

Ide awal dari AKU adalah menyusutkan dimensi dari sekumpulan data yang berisi sejumlah peubah penjelas yang saling berhubungan, dengan tetap mempertahankan sebanyak mungkin keragaman yang dapat dijelaskan. Pereduksian dimensi dilakukan dengan cara mentransformasi peubah-peubah asli yang berkorelasi menjadi satu set peubah baru yang tidak berkorelasi. Peubah-peubah baru ini disebut sebagai komponen utama (KU) yang merupakan ringkasan/susutan dari peubah asal dengan tetap mampu menjelaskan semaksimal mungkin peubah asalnya (Johnson & Wichern 2002).

KU adalah kombinasi linear dari p peubah asal yang merupakan koordinat baru dari rotasi peubah asal sebagai sumbu koordinat. Sumbu baru ini mampu menjelaskan keragaman maksimum dan menghasilkan penjelasan yang lebih sederhana. Syarat membentuk KU agar mempunyai keragaman yang besar dengan memilih e_i'=

[

e₁ e₂  e_p

]

sedemikian hingga var

(

e_i'X

)

maksimum, dengan

1

=

i i'e

e dan cov

(

e_i'X,e_i_''X

)

=0, untuk i'<i; i=1,2,p; i'=1,2,p

KU dapat diperoleh dari pasangan nilai akar ciri ( )

λ

i matriks ragam

peragam atau matriks korelasi. Presentase keragaman total yang dapat dijelaskan oleh KU ke-i adalah sebagai berikut:

p i

i

λ λ

λ

λ + + + =



2 1

-ke ragam Proporsi

dengan p adalah banyaknya peubah asal. Jumlah KU yang dipilih mampu memberikan kumulatif persen keragaman antara 80-90% dari total keragaman (Jolliffe 1986).

Statistical Downscaling

Downscaling adalah suatu cara menginterpolasi peubah-peubah penjelas atmosfir berskala besar terhadap peubah-peubah berskala lebih kecil. Proses

downscaling umumnya dibutuhkan ketika dampak dari berbagai variasi dan perubahan peubah-peubah iklim tidak dapat diduga dari prediksi resolusi global GCM, oleh karena dampak tersebut sangat sensitif terhadap iklim skala lokal. Teknik downscaling telah banyak dikembangkan dengan maksud meningkatkan manfaat informasi regional yang dihasilkan GCM serta menyediakan informasi iklim resolusi tinggi.

(18)

6

respon tidak berubah dengan perubahan waktu dan tetap sama meskipun ada perubahan iklim (Busuioc et al. 2001).

Metode SD didasarkan pada asumsi bahwa iklim lokal dikendalikan oleh dua faktor, yaitu kondisi iklim skala besar (resolusi rendah) dan kondisi/karakteristik fisiografik regional/lokal. Informasi iklim regional atau lokal dapat diperoleh dengan langkah awal menentukan suatu model statistik yang menghubungkan peubah iklim skala besar (X) dengan peubah-peubah regional dan lokal (y). Luaran skala besar dari simulasi GCM dimasukkan sebagai input bagi model statistik tersebut untuk memperkirakan karakteristik iklim lokal atau regional yang bersangkutan. Bentuk umum model SD, yaitu:

( )t = f

(

X( )t×g

)

y

dengan, ( )t

y : peubah iklim lokal (curah hujan) ( )t×g

X : peubah luaran GCM (presipitation) t : banyaknya waktu (bulanan)

g : banyaknya grid domain GCM

Gambar 1 Ilustrasi proses statistical downscaling (Sutikno 2008)

Teknik SD yang digunakan beragam berdasarkan region/spasial, temporal, peubah respon/prediktan, peubah penjelas, dan metode statistik yang digunakan membangun model hubungan skala besar dan skala lokal/regional. Teknik SD yang sering digunakan adalah regresi, korelasi kanonik, dan dekomposisi nilai singular (Uvo et al. 2001).

Analisis Regresi Nonparametrik

Analisis regresi adalah analisis yang digunakan untuk melihat hubungan antar peubah respon dan penjelas. Pendekatan pendugaan yang paling sering digunakan adalah pendekatan parametrik. Asumsi yang mendasari pendekatan ini

Global Circulation Model (peubah penjelas)

Statistical Downscaling Observasi Permukaan

(peubah respon) Kabupaten Indramayu

(luas wilayah 84 x 25 km2)

1o = 100 km

(19)

7 adalah kurva regresi dapat diwakili oleh suatu model parametrik (Hardle 1994). Bentuk umum dari model regresi linear, yaitu:

ε β

β β

β + + + + +

= x x _px_p

y ₀ ₁ ₁ ₂ ₂ 

dengan y adalah peubah respon, x_i

(

i =1,2,p

)

adalah peubah penjelas,

(

j p

)

j =0,1,

β adalah parameter pada model, ε adalah galat acak, dan p adalah banyaknya peubah penjelas.

Metode pendugaan parameter model tersebut dapat dilakukan dengan berbagai cara. Metode yang paling popular adalah metode kuadrat terkecil (MKT). Permasalahan-permasalahan yang terjadi pun banyak ditemukan karena persyaratan yang harus dipenuhi pada asumsi-asumsi yang mendasari MKT seringkali menyulitkan, namun tentunya ada solusi untuk permasalahan tersebut. MKT terboboti dapat digunakan untuk mengatasi ketidakhomogenan ragam, masalah multikolinearitas pada regresi linear berganda dapat diatasi regresi komponen utama dan regresi gulud.

Metode-metode di atas dikenal sebagai metode regresi parametrik. Dalam perkembangannya metode tersebut juga belum dapat menjawab semua permasalahan yang ada. Kesulitan dalam menentukan bentuk model yang tepat jika tidak ada informasi awal mengenai bentuk hubungan peubah respon dan penjelasnya merupakan masalah yang sering terjadi. Diagnostik terhadap perilaku sisaan sebenarnya dapat dijadikan alat untuk melihat bentuk hubungan tersebut, namun langkah ini membutuhkan proses yang panjang dan pengalaman yang cukup untuk menduga bentuk hubungan yang tepat. Permasalahan tersebut dapat diselesaikan dengan berkembangnya suatu metode regresi nonparametrik yang tidak memerlukan asumsi sebaran data sehingga metode ini menjadi lebih kekar (Draper & Smith 1981).

Regresi nonparametrik digunakan untuk memodelkan hubungan antar peubah tanpa penetapan bentuk khusus tentang fungsi regresinya. Hubungan antara respon y dengan peubah penjelas x dinyatakan dalam model berikut:

( )

i i

i f x

y = +

ε

, untuk i=1,2,,n

dengan f

()

. menyatakan bentuk hubungan fungsional nonparametrik dan

ε

_i adalah galat acak.

Fungsi Pemulusan Spline

(20)

8

Fungsi spline berorde ke-m dengan satu peubah penjelas adalah sembarang fungsi yang secara umum dapat disajikan dalam bentuk:

( )

∑

(

)

= − + + − = − + + = s k m k k r m r r

rX β x K

β β x f 1 1 1 1 0

dengan fungsi sepenggal (truncated) sebagai berikut:

(

)

(

)

    ≥ ≥ − = − − + − + k k m k m k K x ; K x ; K x K x 0 1 1 k

K adalah matriks yang berisi knot ke-k dari vektor peubah penjelas x; s

k =1,2,, ; dan s adalah banyaknya knot. Knot diartikan sebagai suatu titik fokus dalam fungsi spline sehingga kurva yang dibentuk tersegmen pada titik tersebut. Selanjutnya, f

( )

x_i pada model nonparametrik diperoleh dengan meminimumkan fungsi jumlah kuadrat terpenalti (penalized least square), yaitu:

( )

[

]

[

( )

]

              b a n i i

i f x λ f'' x dx

y

J =

∑

− +

∫

= 1 0 2 1 2 ˆ

dengan a merupakan jumlah kuadrat sisaan atau fungsi jarak antara data dan dugaan, b merupakan penalti kekasaran (ukuran kemulusan kurva dalam memetakan data), dan λ≥0 adalah parameter pemulus. Minimisasi J pada nilai

λ tertentu akan memberikan kompromi antara kebaikan pengepasan dengan kemulusan kurva (penalty). Nilai λ yang besar akan memberikan bobot penalti (kemulusan) yang besar dan mempunyai ragam yang kecil. Setelah ditentukan turunan pertama terhadap f maka diperoleh fungsi pemulus linier, yaitu:

(

1 K

)

y Sy

fˆ= +λ −1 =

dengan K adalah matriks penalti yang mempunyai struktur spesifik, yaitu: D

C D K= T −1 (n−2)×n

D adalah matriks upper triagonal yang memiliki struktur sebagai berikut:

(

)

(

)

(

)

             + − + − + − − − − − − − − − − − − − − − − − 1 1 1 1 1 2 1 2 1 3 1 3 1 2 1 2 1 2 1 2 1 1 1 1 0 0 0 0 0 n n n

n λ λ λ

λ λ λ λ λ λ λ λ λ          

dan C₍_n₋₂_{) (}_×_n₋₂₎ adalah matriks symmetric tridiagonal yang memiliki struktur sebagai berikut:

(

)

(

)

(

)

           + + + − − − − 1 2 2 2 3 2 2 2 2 1 2 0 2 0 2 n n n n λ λ λ λ λ λ λ λ λ λ       

Pemilihan Parameter Pemulus Optimal

(21)

9

( )

[

]

∑

= − = n i i i f x

y n 1 2 ˆ 1 MSE

Metode pemilihan parameter pemulus lainnya adalah menggunakan metode validasi silang terampat (generalized cross validation, GCV), yaitu:

( )

[

]

( ) ( )

[

]

1

[

(

)

]

2

2 1 2 MSE 1 ˆ 1 GCV H I H I − = − − =

∑

= ₋ tr n tr tr n x f y n n i i i

dengan H=X

(

XTX

)

−1XT dan I adalah matriks identitas.

Pemilihan faktor pemulus optimal dalam regresi nonparametrik dapat dilakukan melalui derajat bebas efektif yang diperoleh dari fungsi berikut:

( )

S

tr

Df =

S merupakan matriks pemulus dengan S=

(

1+λK

)

−1 (Eubank 1988).

Model Aditif Terampat

Model nonparametrik kemudian diperluas untuk peubah penjelas lebih dari satu dan dikenal dengan model aditif yang didefinisikan sebagai berikut:

( )

X ε

y= +

∑

+

= p j j j f f 1 0

dengan ε bebas stokastik terhadap peubah penjelas X, dan memenuhi E

( )

ε =0

dan cov

( )

ε =

σ

2I, sedangkan f_j adalah bentuk fungsional antara respon dengan peubah penjelas X_j.

Perluasan model aditif untuk sebaran keluarga eksponensial menjadi model aditif terampat (generalized additive model selanjutnya disingkat GAM). Bentuk umum model GAM adalah sebagai berikut:

(

)

[

]

∑

( )

= + = = p j ij j

p f f x

x x x y E g 1 0 2

1, ,,

η , untuk i =1,2,,n

dengan g adalah fungsi penghubung dan f_j adalah bentuk hubungan fungsional antara peubah respon dan penjelas yang dimodelkan secara nonparametrik dengan suatu fungsi pemulus (Hastie & Tibshirani 1990).

Metode pendugaan GAM menggunakan algoritma backfitting. Pendugaan fungsi mulus f₀, f₁

() ()

., f₂ .,, f_p

()

. pada model aditif, dengan E

(

f_j

( )

X_j

)

=0 menggunakan galat partial

∑

( )

≠ − − = p j k k k

j y f f X

R ₀ sehingga E

(

R_j X_j

)

= f_j

( )

X_j

dengan meminimumkan

( )

2 1 0       − −

∑

= p k k k f f

E y X , maka penduga f_j akan

diperoleh secara iteratif jika diberikan penduga f_i untuk i ≠ j (Hastie & Tibshirani 1990).

(22)

10

matriks prediksiXp yang berisi nilai-nilai peubah penjelas baru. Matriks prediksi diperoleh dari persamaan μˆ Xpβˆ

p = , dengan β

(

X X λS

)

X y

T

T 1

ˆ ₌ ₊ − _(Wood

2006).

3 METODE PENELITIAN

Data

Data GCM yang digunakan adalah data curah hujan bulanan Climate Model Intercomparison Project (CMIP5) yang dikeluarkan oleh Belanda dari situs web tahun 1979 sampai dengan 2008 dengan posisi wilayah 16.25oLU – 1.25oLS dan 98.75oBB – 116.25oBT . Luasan daerah berbentuk persegi berukuran 8 x 8 grid, sehingga terdapat 64 peubah X.

Gambar 2 Lokasi penelitian (Wigena 2006)

Data curah hujan lokal yang digunakan adalah data rata-rata curah hujan dari stasiun klimatologi kabupaten Indramayu. Data curah hujan dari stasiun ini berada pada rentang waktu 1979 sampai dengan 2008 (panjang data 30 tahun) dengan total 360 data.

Metode Analisis

Eksplorasi Data

1. Data curah hujan kabupaten Indramayu

a. Statistika deskriptif sebagai informasi awal untuk melihat keragaman dari data amatan

b. Mengidentifikasi data curah hujan ekstrim dengan metode block maxima, yaitu dengan membagi data dalam blok periode tahunan lalu menentukan data curah hujan maksimum di setiap tahun

c. Membagi data curah hujan ekstrim atas dua bagian, yaitu data training

untuk menyusun model (tahun 1979-2005) dan data testing untuk validasi model (tahun 2006-2008)

2. Data GCM

(23)

11 a. Membuat plot masing-masing peubah data GCM

b. Mengevaluasi hubungan curah hujan dengan setiap peubah data GCM menggunakan cross correlation function (CCF)

c. Memeriksa kehomogenan ragam peubah-peubah data GCM menggunakan uji Bartlett

d. Mereduksi dimensi peubah penjelas (data GCM) yang bersesuaian dengan curah hujan ekstrim menggunakan analisis komponen utama (AKU), dengan langkah-langkah berikut:

• Anggap sekumpulan observasi x_i, dengan i=1,2,,p pada input data

n

R

• Membuat matriks ragam peragam atau matriks korelasi, misalnya A

• Menentukan nilai akar ciri (eigen value) dengan menggunakan persamaan A−λI =0

• Menentukan jumlah komponen utama berdasarkan ukuran keragaman lebih dari 90% dan nilai akar ciri lebih besar dari satu

(

λ

_i >1

)

• Menghitung skor komponen utama (KU) dari model y_i =a_i'X, dengan

i

a adalah vektor ciri (eigen vector)

Pemodelan

1. Sebaran nilai ekstrim GEV

a. Menentukan nilai dugaan parameter (µˆ,σˆ, dan ξˆ ) menggunakan metode kemungkinan maksimum

b. Menentukan nilai tingkat pengembalian curah hujan yang akan memberikan gambaran curah hujan maksimum yang diharapkan dapat dilampaui satu kali dalam jangka waktu tertentu

2. Statistical downscaling (SD) berbasis komponen utama (KU)

a. Pembentukan model dengan menggunakan metode kuadrat terkecil (MKT) b. Pemeriksaan multikolinearitas berdasarkan nilai variance inflation Factor

(VIF) menggunakan formula

( )

₂ 1

1

i i

R VIF

−

= dengan R_i2 adalah koefisien determinasi dari peubah penjelas KUi yang diregresikan terhadap peubah

penjelas lainnya. Jika nilai VIF <10, maka tidak ada indikasi multikolinear 3. Statistical downscaling (SD) berbasis model aditif terampat

a. Membuat plot peubah curah hujan ekstrim dengan masing-masing KU terpilih untuk melihat indikasi awal adanya pengaruh nonlinear pada data b. Menentukan derajat pemulus dan banyaknya knot pemulus pada peubah

penjelas yang mempunyai hubungan nonlinear c. Menduga fungsi f_j pada model

∑

( )

= +

= p

j

ij j x

f f

1 0

η , untuk i=1,2,,n

menggunakan algoritma backfitting, dengan langkah-langkah berikut: • Nilai awal: f0 =E

( )

y ,

( ) ( ) ( )

0 0 0

2 0

1 = f = = fp =

f  , m=0

(24)

12

- untuk j=1 sampai p:

( )

∑

≠ − − = p j k k m k

j y f f X

R ₀ , ( )m

(

_j _j

)

j E

f = R X

• Ulangi tahap iterasi sampai ( )

( )

2 1 0       − − =

∑

= p k k m k f f

JKG y X tidak turun

d. Membuat plot hubungan fungsional dari model yang dibentuk untuk melihat bentuk ketergantungan peubah curah hujan ekstrim dengan masing-masing KU terpilih

Validasi dan Uji Konsistensi Model

1. Menghitung nilai root mean square error of prediction (RMSEP)

menggunakan formula

∑

(

)

= − = n i i i y y n 1 2 ˆ 1

RMSEP . Semakin kecil nilai

RMSEP, maka semakin kecil perbedaan antara nilai dugaan dengan nilai aktual, yang berarti model yang dibentuk semakin akurat dalam menghasilkan nilai dugaan

2. Menghitung nilai korelasi antara curah hujan ekstrim dengan nilai dugaan

menggunakan formula               −               −             − =

∑

= = = = = = = 2 1 1 2 2 1 1 2 1 1 1 ˆ ˆ ˆ ˆ n i i n i i n i i n i i n i i n i i n i i i y y n y y n y y y y n

r untuk

menunjukkan keeratan hubungan antara nilai dugaan dengan nilai aktualnya. Semakin besar (dan positif) nilai korelasi maka semakin kuat hubungan antara nilai dugaan dan nilai aktualnya, yang berarti pola nilai dugaan semakin mendekati pola data aktualnya

4 HASIL DAN PEMBAHASAN

Eksplorasi Data

Data Curah Hujan Kabupaten Indramayu

Deskripsi data curah hujan untuk untuk Kabupaten Indramayu perlu dilakukan sebagai informasi awal untuk mengetahui karakteristik dan pola curah hujan yang digunakan untuk analisis berikutnya. Hasil yang diperoleh menunjukkan bahwa di kabupaten Indramayu dari tahun 1979 sampai 2008 memiliki rata-rata curah hujan sebesar 123 mm. Nilai curah hujan terendah sebesar 0 mm dan nilai curah hujan tertinggi sebesar 583 mm, sedangkan nilai simpangan baku yang digunakan untuk menyatakan keragaman curah hujan di kabupaten Indramayu sebesar 110 mm.

(25)

13 tepatnya pada bulan Januari karena rata-rata curah hujannya paling tinggi diantara bulan-bulan lainnya. Gambar 3 juga dapat memperlihatkan periode musim hujan dan musim kemarau yaitu musim hujan yang umumnya terjadi antara bulan Oktober sampai Maret dan musim kemarau terjadi antara bulan April sampai September.

Gambar 3 Pola curah hujan kabupaten Indramayu tahun 1979-2008

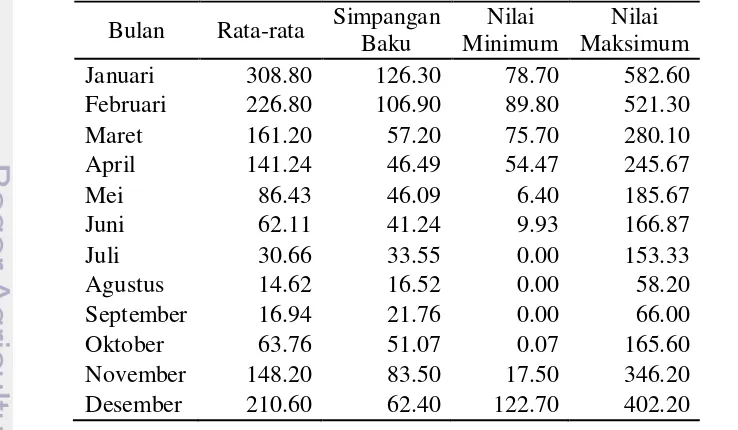
Tabel 1 menunjukkan bahwa pada bulan-bulan yang masuk dalam musim hujan rata-rata curah hujan bulanannya relatif tinggi sedangkan pada bulan-bulan di musim kemarau, curah hujannya relatif rendah. Simpangan baku terbesar berada pada bulan Januari yaitu 126.30 mm yang menunjukkan bahwa curah hujan pada bulan Januari 1979-2008 sangat beragam.

Tabel 1Deskripsi data curah hujan kabupaten Indramayu tahun 1979-2008 Bulan Rata-rata Simpangan

Baku

Nilai Minimum

Nilai Maksimum Januari 308.80 126.30 78.70 582.60 Februari 226.80 106.90 89.80 521.30

Maret 161.20 57.20 75.70 280.10

April 141.24 46.49 54.47 245.67

Mei 86.43 46.09 6.40 185.67

Juni 62.11 41.24 9.93 166.87

Juli 30.66 33.55 0.00 153.33

Agustus 14.62 16.52 0.00 58.20

September 16.94 21.76 0.00 66.00

Oktober 63.76 51.07 0.07 165.60

November 148.20 83.50 17.50 346.20 Desember 210.60 62.40 122.70 402.20

Identifikasi curah hujan ekstrim pada kabupaten Indramayu dilakukan dengan menggunakan metode block maxima, yaitu dengan membuat blok periode

cura

h

hu

ja

n

(

m

)

(26)

14

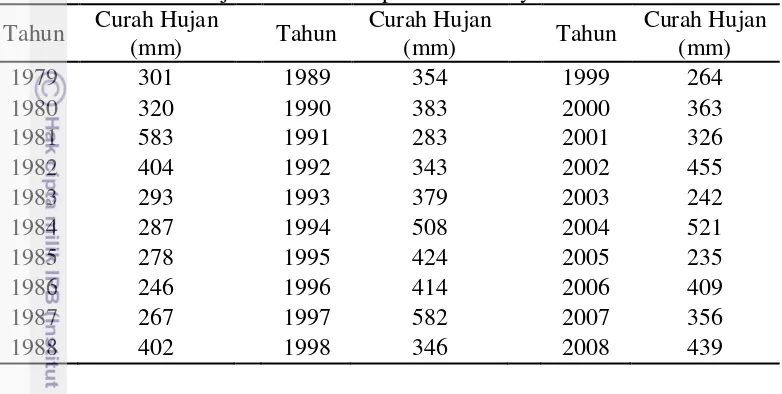
waktu yaitu periode tahunan sehingga terdapat 30 blok (dari tahun 1979 sampai 2008). Setelah blok terbentuk selanjutnya ditentukan nilai curah hujan tertinggi di setiap blok dan curah hujan tersebut dianggap sebagai curah hujan ekstrim seperti yang tertera pada Tabel 2.

Tabel 2Curah hujan ekstrim kabupaten Indramayu tahun 1979-2008 Tahun Curah Hujan

(mm) Tahun

Curah Hujan

(mm) Tahun

Curah Hujan (mm)

1979 301 1989 354 1999 264

1980 320 1990 383 2000 363

1981 583 1991 283 2001 326

1982 404 1992 343 2002 455

1983 293 1993 379 2003 242

1984 287 1994 508 2004 521

1985 278 1995 424 2005 235

1986 246 1996 414 2006 409

1987 267 1997 582 2007 356

1988 402 1998 346 2008 439

Data GCM

Eksplorasi dilakukan dengan membuat plot masing-masing peubah data GCM (Lampiran 1), lalu mengevaluasi hubungan curah hujan dengan setiap peubah data GCM menggunakan cross correlation function (CCF), sehingga diperoleh peubah-peubah data GCM dengan time lag yang menghasilkan korelasi paling tinggi dengan data curah hujan yang disajikan pada Lampiran 2. Pemodelan selanjutnya dilakukan dengan menggunakan peubah data curah hujan dan peubah data GCM sesuai dengan time lag yang terpilih.

Pemeriksaan kehomogenan ragam data GCM menggunakan test Bartlett atau Levene untuk acuan dalam penentuan matriks yang akan digunakan pada pereduksian dimensi GCM, dengan hipotesis berikut :

H0 : ragam data GCM homogen

H1 : ragam data GCM tidak homogen

Berdasarkan hasil uji kehomogenan ragam (Lampiran 4), diperoleh nilai

05 . 0

= < − p α

nilai sehingga H0 ditolak, berarti ragam dari data GCM tidak

homogen. Karena ragam data GCM tidak homogen, maka matriks yang digunakan dalam reduksi dimensi data GCM adalah matriks korelasi.

Data GCM yang digunakan adalah data pengamatan yang bersesuaian dengan data curah hujan ekstrim. Data GCM merupakan data bulanan dengan luasan daerah berbentuk persegi berukuran 8 x 8 grid, sehingga terdapat 64 peubah X. Dimensi ini dianggap cukup besar untuk dianalisis, sehingga perlu dilakukan pereduksian dimensi dari komponen peubah asal menjadi dimensi komponen utama (KU), KU yang dihasilkan merupakan ringkasan dari peubah asal dengan tetap mampu menjelaskan semaksimal mungkin peubah asalnya.

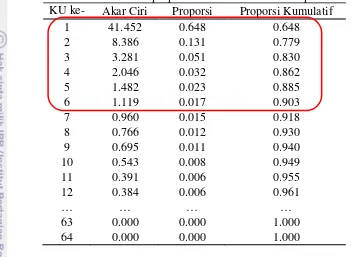
Tabel 3 menunjukkan bahwa jumlah komponen utama yang memiliki nilai akar ciri yang lebih besar daripada satu

(

λ

i >1

)

adalah sebanyak enam komponen

(27)

15 asalnya. Analisis selanjutnya peubah respon (y) dalam hal ini adalah curah hujan ekstrim di kabupaten Indramayu akan dimodelkan dengan enam peubah penjelas (peubah data GCM yang direduksi menggunakan AKU) yang merupakan skor komponen utama

(

KU₁,KU₂,KU₃,KU₄,KU₅,KU₆

)

.

Tabel 3 Nilai akar ciri dan proporsi kumulatif analisis komponen utama KU ke- Akar Ciri Proporsi Proporsi Kumulatif

1 41.452 0.648 0.648

2 8.386 0.131 0.779

3 3.281 0.051 0.830

4 2.046 0.032 0.862

5 1.482 0.023 0.885

6 1.119 0.017 0.903

7 0.960 0.015 0.918

8 0.766 0.012 0.930

9 0.695 0.011 0.940

10 0.543 0.008 0.949

11 0.391 0.006 0.955

12 0.384 0.006 0.961

… … … …

63 0.000 0.000 1.000

64 0.000 0.000 1.000

Pemodelan

Sebaran Nilai Ekstrim GEV

Teori nilai ekstrim bertujuan untuk mengkaji perilaku stokastik suatu proses pada suatu nilai ambang tertentu. Analisis ini juga memungkinkan untuk menduga suatu kejadian ekstrim (yang diinterpretasikan oleh nilai return) dengan menggunakan distribusi GEV. Hasil dugaan parameter-parameter GEV dan nilai return disajikan secara lengkap pada Lampiran 5.

Tabel 4 menunjukkan bahwa penduga parameter lokasi µ, parameter skala

σ

, dan parameter bentuk ξ tiap tahun memberikan hasil yang tidak terlalu jauh berbeda. Hal ini ditunjukkan oleh nilai simpangan baku berturut-turut 5.549, 3.148, dan 0.094. Nilai ini menunjukkan tingkat keragaman yang relatif kecil. Tabel 4 Nilai rata-rata dan simpangan baku dari nilai dugaan parameter GEV dan

nilai return

Statistik µˆ

σ

_ˆ ξ_ˆ _R_ˆ12 Rata-rata 68.893 68.667 0.191 284 Simpangan Baku 5.549 3.148 0.094 14.793

(28)

16

bahwa distribusi GEV belum cukup baik dalam menghasilkan nilai dugaan curah hujan ekstrim di kabupaten Indramayu.

SD Berbasis Komponen Utama

Data curah hujan ekstrim di kabupaten Indramayu selanjutnya akan dianalisis menggunakan regresi komponen utama (RKU) dan pendugaan parameter-parameternya menggunakan metode kuadrat terkecil (MKT). Data peubah penjelas (KU) yang dipilih adalah data yang bersesuian dengan data curah hujan ekstrim di kabupaten Indramayu, sehingga kemungkinan akan mengalami perubahan karakteristik pada peubah tersebut, namun setelah dilakukan pengujian, nilai-nilai VIF semuanya lebih kecil dari 10 sehingga asumsi tidak adanya multikolinearitas tetap terpenuhi pada peubah penjelas tersebut. Model RKU yang dihasilkan yaitu :

6 70 . 13 5 70 . 7 4 40 . 15 3 00 . 4 2 71 . 4 1 22 . 4

302 KU KU KU KU KU KU

y = + − − − + −

Nilai R2 =16.3% menunjukkan bahwa pada model dengan MKT, data GCM hanya dapat menjelaskan sebesar 16.3% keragaman dari data curah hujan ekstrim kabupaten Indramayu. Hasil dugaan dari RKU memberikan nilai RMSE sebesar 101.433, RMSEP sebesar 70.839, dan nilai korelasi sebesar 0.404. Nilai-nilai tersebut menunjukkan bahwa SD berbasis KU belum menghasilkan model pendugaan yang baik.

SD Berbasis Model Aditif Terampat

Langkah selanjutnya dilakukan eksplorasi terhadap data. Eksplorasi dilakukan dengan membuat matriks plot data untuk melihat indikasi awal apakah ada pengaruh nonlinear atau tidak. Gambar 4 memperlihatkan bahwa hubungan parsial antara peubah respon dengan masing-masing peubah penjelas ada yang tidak linear. Hal ini jelas terlihat dengan sebaran data yang menyebar mengikuti suatu sebaran nonlinear tertentu.

cura

h

hu

ja

n

eks

tr

im

cura

h

hu

ja

n

eks

tr

im

Skor komponen utama

(29)

17 Gambar 4 Matriks plot antara data curah hujan ekstrim dengan KU terpilih

Hasil plot di atas menunjukkan bahwa sudah selayaknya dalam penentuan model, pengaruh nonlinear diakomodasi karena jika ini tidak dilakukan, maka model yang dihasilkan tidak cukup baik. Eksplorasi lebih lengkap disajikan pada Lampiran 6 dan Lampiran 7 yang menunjukkan plot curah hujan ekstrim dengan masing-masing KU terpilih. Plot tersebut dibentuk dari model dengan derajat bebas terbaik atau dengan kata lain memiliki nilai GCV (generalized cross validation) terkecil jika dibandingkan model dengan derajat bebas yang lain. Derajat bebas terpilih untuk masing-masing hubungan fungsional antara curah hujan ekstrim dengan KU akan dijadikan acuan dalam pemodelan GAM.

Model aditif terampat (GAM) merupakan model alternatif yang selanjutnya digunakan untuk mengakomodasi pengaruh nonlinear dari peubah penjelas melalui pendekatan regresi nonparametrik. Pemodelan regresi nonparametrik memiliki kelenturan terutama dalam penentuan bentuk kurva yang tidak perlu ditentukan secara a priori, tetapi kurva dibentuk sesuai dengan datanya (data driven). Analisis GAM dilakukan dengan memodelkan curah hujan ekstrim sebagai kombinasi aditif dari hubungan fungsional peubah KU terpilih. Hasil analisis GAM disajikan secara lengkap pada Lampiran 8 dan Lampiran 9.

Berdasarkan hasil yang diperoleh pada Lampiran 8, terlihat bahwa peubah penjelas KU2, KU3, dan KU5 memberikan pengaruh yang tidak nyata terhadap peubah respon (curah hujan ekstrim), hal ini diakibatkan karena sebaran data pada plot parsial yang ditunjukkan pada Lampiran 9 menyebar di daerah rataan yang mengindikasikan bahwa tidak ada kontribusi dari peubah penjelas KU2, KU3, dan KU5 terhadap peubah curah hujan ekstrim. Sehingga pemodelan dengan GAM dilakukan hanya dengan melibatkan peubah penjelas KU1, KU4, dan KU6. Model GAM yang diperoleh, yaitu: y= f

(

KU1

) (

+ f KU4

) (

+ f KU6

)

Tabel 5 Hasil analisis model aditif terampat Hubungan

Fungsional

Derajat

Bebas F Nilai p

λ

f(KU1) 8.517 4.047 0.001 1.499

f(KU4) 1.000 6.171 0.017 0.362

f(KU6) 3.655 2.164 0.080 1.500

Berdasarkan metode GAM diperoleh nilai

λ

optimum yang menggambarkan tingkat kemulusan kurva dari masing-masing peubah penjelas. Selain itu, juga diperoleh plot hubungan fungsional peubah penjelas pada Gambar 5 yang mempertegas hasil sebelumnya, dimana hubungan antara peubah respon dengan beberapa peubah penjelas bersifat nonlinear.

(30)

18

menunjukkan bahwa model SD berbasis GAM cukup baik dalam menghasilkan nilai dugaan curah hujan ekstrim di kabupaten Indramayu.

Gambar 5 Plot hubungan fungsional masing-masing KU terpilih

Perbandingan Metode GEV dan SD

[image:30.595.109.433.121.344.2]

Hasil analisis curah hujan ekstrim dari ketiga metode di atas disajikan pada Gambar 6 yang memberikan informasi bahwa metode SD berbasis GAM memiliki pola paling mirip dengan data curah hujan ekstrim. Ini berarti bahwa hasil dugaan dengan metode SD berbasis GAM mendekati nilai data curah hujan ekstrim aktual di kabupaten Indramayu.

Gambar 6 Plot antara curah hujan ekstrim dengan nilai dugaan

2010 2005

2000 1995

1990 1985

1980 600

500

400

300

200

tahun

c

u

ra

h

u

ja

n

e

k

s

tr

im

[image:30.595.92.471.473.723.2]

(31)

19

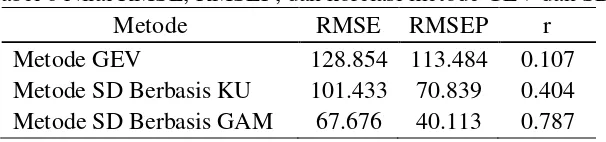
[image:31.595.162.465.178.249.2]

Hasil tersebut juga dipertegas dengan nilai RMSE, RMSEP, dan nilai korelasi dari ketiga metode yang ditunjukkan pada Tabel 6. Metode SD berbasis GAM memberikan nilai RMSE dan RMSEP terkecil, sekaligus memiliki nilai korelasi terbesar dari ketiga metode.

Tabel 6 Nilai RMSE, RMSEP, dan korelasi metode GEV dan SD

Metode RMSE RMSEP r

Metode GEV 128.854 113.484 0.107 Metode SD Berbasis KU 101.433 70.839 0.404 Metode SD Berbasis GAM 67.676 40.113 0.787

Berdasarkan model SD berbasis GAM yang terbentuk diperoleh nilai korelasi yang signifikan antara nilai dugaan dengan nilai aktual curah hujan ekstrim, yaitu sebesar 0.787. Nilai ini menunjukkan bahwa terdapat hubungan yang kuat (dan positif) antara nilai dugaan dan nilai aktual, yang berarti pola nilai dugaan semakin mendekati pola data curah hujan ekstrim di kabupaten Indramayu. Selain itu, juga diperoleh nilai RMSEP sebesar 40.113. Nilai ini menunjukkan bahwa terdapat perbedaan yang kecil antara nilai dugaan dengan nilai aktual, yang berarti bahwa model yang dibentuk semakin akurat dalam menghasilkan nilai dugaan curah hujan ekstrim di kabupaten Indramayu.

Validasi dan Uji Konsistensi Model

Validasi Model

Informasi mengenai dugaan curah hujan ekstrim menjadi cukup berarti sebagai upaya guna meminimumkan resiko yang dapat terjadi, sehingga perlu dilakukan pengecekan terhadap keakuratan dugaannya. Validasi adalah tahapan untuk memperoleh gambaran tentang keakuratan dugaan model tersebut.

Berdasarkan Tabel 7 terlihat bahwa semakin panjang data yang akan diduga maka nilai RMSEP akan relatif semakin besar, sedangkan nilai korelasi relatif semakin kecil. Model SD berbasis GAM memberikan nilai RMSEP terkecil, yaitu pada pendugaan data curah hujan ekstrim 3 tahun ke depan.

Tabel 7 Nilai RMSEP di setiap panjang data pendugaan model SD berbasis GAM

Data Historis Data Dugaan RMSEP

λ

(32)

20

Indramayu untuk 3 tahun ke depan. Berdasarkan nilai

λ

optimum yang diperoleh untuk masing-masing hubungan fungsional pada peubah penjelas terlihat bahwa nilainya konsisten pada berbagai panjang waktu pendugaan dengan nilai simpangan baku yang kecil untuk KU1, KU4, dan KU6 masing-masing sebesar 0.287, 0.0905, dan 0.295. Namun, perlu diperhitungkan lagi apakah model yang dihasilkan tersebut juga memiliki nilai korelasi yang konsisten untuk setiap waktu pendugaan yang berbeda.

Uji Konsistensi Model

Konsistensi model SD berbasis GAM dapat diketahui dari hasil pendugaan yang konsisten pada berbagai waktu pendugaan. Model SD akan memberikan hasil yang baik jika hubungan antara peubah respon dengan peubah penjelas tidak berubah dengan perubahan waktu dan tetap sama meskipun ada perubahan iklim, atau model SD tetap konsisten dalam pendugaannya pada waktu-waktu yang berbeda (Wigena 2006). Nilai korelasi untuk setiap data historis yang tercantum pada Tabel 8 tidak memiliki perbedaan yang terlalu jauh.

Tabel 8 Nilai korelasi pendugaan model SD berbasis GAM untuk pendugaan curah hujan ekstrim 3 tahun ke depan

Data Historis Data Dugaan r 1979-2005 2006-2008 0.787 1979-2004 2005-2007 0.780 1979-2003 2004-2006 0.766 1979-2002 2003-2005 0.654 1979-2001 2002-2004 0.565

Berdasarkan hasil yang diperoleh nilai simpangan baku dari nilai korelasi pada setiap waktu pendugaan yang sangat kecil yaitu sebesar 0.098 yang menunjukkan bahwa model yang dihasilkan dapat dikatakan cukup konsisten dalam menghasilkan nilai dugaan 3 tahun ke depan.

5 SIMPULAN DAN SARAN

Simpulan

Berdasarkan hasil analisis curah hujan ekstrim di kabupaten Indramayu, dapat disimpulkan bahwa :

1. Dugaan curah hujan ekstrim di kabupaten Indramayu dengan menggunakan

(33)

21 2. Pendugaan curah hujan ekstrim di kabupaten Indramayu 3 tahun ke depan

menggunakan statistical downscaling berbasis model aditif terampat memberikan hasil dugaan terbaik dari semua periode analisis yang digunakan. Hasil pendugaan yang diperoleh juga konsisten pada berbagai waktu pendugaan, sehingga dapat disimpulkan bahwa model ini relevan untuk digunakan di lapangan.

Saran

Pada penelitian ini, model aditif terampat (GAM) yang digunakan merupakan model umum, sehingga disarankan untuk mengkaji penerapan model aditif terampat yang lebih khusus seperti vektor model aditif terampat (VGAM) yang dapat digunakan bukan hanya untuk data numerik, tetapi juga untuk kasus yang datanya bersifat kategorik.

Penelitian lanjutan terkait juga dapat diterapkan di daerah lain (di luar Jawa Barat) untuk mengkaji kejadian curah hujan ekstrim dan diharapkan dapat menanggulangi dampak buruk yang akan terjadi. Penelitian tentang statistical downscaling disarankan dapat dikaji lagi bukan hanya untuk peubah curah hujan, tetapi juga terhadap peubah-peubah iklim lain, seperti tekanan udara, kelembaban, suhu di atas permukaan, dan lain sebagainya yang mungkin dapat menyebabkan kondisi ekstrim kering maupun basah.

DAFTAR PUSTAKA

Beck N, Jackman S. 1997. Getting The Mean Right is a Good Thing: GAMs. San Diego: University of California.

Busuioc A, Chen D, Hellstrom C. 2001. Performance of statistical downscaling models in GCM validation and regional climate change estimates (Application for Swedish precipitation). International Journal of Climate

21: 557-578.

Chaves DV. 2001. Extreme Data Mining. Approximity Papers.

Draper NR, Smith H. 1981. Applied Regression Analysis, 2nd. John Wiley and Sons, Inc.

Eubank R. 1988. Spline Smoothing and Nonparametric Regression. New York: Marcel Dekker.

Gilli M, Kellezi E. 2003. An Application of Extreme Value Theory for Measuring Risk. Departement of Econometrics, University of Geneva, Switzerland. Hardle W. 1994. Applied Nonparametric Regression. New York: Cambridge

University Press.

Haryoko U. 2004. Pendekatan Reduksi Dimensi Luaran GCM untuk Penyusunan Model SD [Tesis]. Bogor: Institut Pertanian Bogor.

Hastie T, Tibshirani R. 1990. Generalized Additive Models. London: Chapman and Hall.

Hidayat S. 2008. Iklim Lokal. Pusat Pengembangan Bahan Ajar Universitas Mercubuana.

(34)

22

Jolliffe IT. 1986. Principal Component Analysis, 2nd. New York: Springer Verlag. Mondiana YQ. 2012. Pemodelan Statistical Downscaling dengan Regresi Kuantil

untuk Pendugaan Curah Hujan Ekstrim [Tesis]. Bogor: Institut Pertanian Bogor.

Prang JD. 2006. Sebaran Nilai Ekstrim Terampat dalam Fenomena Curah Hujan [Tesis]. Bogor: Institut Pertanian Bogor.

Sadik K. 1999. Pemodelan Nilai Ekstrim Terampat untuk Proses Lingkungan (Studi Kasus pada Curah Hujan Harian) [Tesis]. Bogor: Institut Pertanian Bogor.

Uvo CB, Olsson J, Morita O, Jinno K, Kawamura A, Nishiyama K, Koreeda N, Nakashima T. 2001. Statistical atmospheric downscaling for rainfall estimation in Kyushu Island Japan. Hydrology and Earth System Sciences 5: 259-271.

Wigena AH. 2006. Pemodelan Statistical Downscaling dengan Regresi Projection Pursuit untuk Peramalan Curah Hujan Bulanan (Kasus Curah Hujan Bulanan di Indramayu) [Disertasi]. Bogor: Institut Pertanian Bogor.

Wilby RL, Charles SP, Zorita E, Timbal B, Whetton P, Mearns LO. 2009. A review of climate risk information for adaptation and development planning.

Journal of Climatology 29: 1193-1215.

(35)

23

Lampiran 1 Plot masing-masing variabel data GCM

2 4 6 8 10 12

1

2

3

4

5

plot presipitasi gcm grid 1

waktu

P

resi

pi

tasi

2 4 6 8 10 12

1 2 3 4 5 6 7

plot presipitasi gcm grid 2

waktu

P

resi

pi

tasi

2 4 6 8 10 12

2 3 4 5 6 7 8 9

waktu

P

resi

pi

tasi

2 4 6 8 10 12

4

6

8

10

waktu

P

resi

pi

tasi

2 4 6 8 10 12

4

6

8

10

12

waktu

P

resi

pi

tasi

2 4 6 8 10 12

5 6 7 8 9 10 11

plot presipitasi gcm grid 6

waktu

P

resi

pi

tasi

2 4 6 8 10 12

6

7

8

9

10

waktu

P

resi

pi

tasi

2 4 6 8 10 12

6 7 8 9 10 11 12

waktu

P

resi

pi

tasi

2 4 6 8 10 12

1

2

3

4

5

waktu

P

resi

pi

tasi

2 4 6 8 10 12

1 2 3 4 5 6 7

waktu

P

resi

pi

tasi

2 4 6 8 10 12

2 3 4 5 6 7 8

plot presipitasi gcm grid 11

waktu

P

resi

pi

tasi

2 4 6 8 10 12

2

4

6

8

10

waktu

P

resi

pi

(36)

24

2 4 6 8 10 12

4

6

8

10

12

waktu

P

resi

pi

tasi

2 4 6 8 10 12

6

8

10

12

waktu

P

resi

pi

tasi

2 4 6 8 10 12

6 7 8 9 10 11 12

waktu

P

resi

pi

tasi

2 4 6 8 10 12

6 7 8 9 10 11 12

waktu

P

resi

pi

tasi

2 4 6 8 10 12

1

2

3

4

5

plot presipitasi gcm grid 17

waktu

pr

esi

pi

tasi

2 4 6 8 10 12

1 2 3 4 5 6 7

waktu

pr

esi

pi

tasi

2 4 6 8 10 12

1 2 3 4 5 6 7 8

waktu

pr

esi

pi

tasi

2 4 6 8 10 12

2

4

6

8

10

waktu

pr

esi

pi

tasi

2 4 6 8 10 12

4

6

8

10

12

waktu

pr

esi

pi

tasi

2 4 6 8 10 12

5 6 7 8 9 10 11

plot presipitasi gcm grid 22

waktu

pr

esi

pi

tasi

2 4 6 8 10 12

6 7 8 9 10 11

waktu

pr

esi

pi

tasi

2 4 6 8 10 12

6 7 8 9 10 11 12

waktu

pr

esi

pi

tasi

2 4 6 8 10 12

1

2

3

4

5

waktu

pr

esi

pi

tasi

2 4 6 8 10 12

1 2 3 4 5 6

waktu

pr

esi

pi

tasi

2 4 6 8 10 12

1 2 3 4 5 6 7 8

plot presipitasi gcm grid 27

waktu

pr

esi

pi

(37)

25

2 4 6 8 10 12

2

4

6

8

10

waktu

pr

esi

pi

tasi

2 4 6 8 10 12

4

6

8

10

12

waktu

pr

esi

pi

tasi

2 4 6 8 10 12

5 6 7 8 9 10

waktu

pr

esi

pi

tasi

2 4 6 8 10 12

6

8

10

waktu

pr

esi

pi

tasi

2 4 6 8 10 12

4

6

8

10

12

waktu

pr

esi

pi

tasi

2 4 6 8 10 12

1

2

3

4

5

plot presipitasi gcm grid 33

Waktu

P

resi

pi

tasi

2 4 6 8 10 12

1 2 3 4 5 6

Waktu

P

resi

pi

tasi

2 4 6 8 10 12

2

4

6

8

Waktu

P

resi

pi

tasi

2 4 6 8 10 12

2

4

6

8

10

Waktu

P

resi

pi

tasi

2 4 6 8 10 12

4

6

8

10

12

Waktu

P

resi

pi

tasi

2 4 6 8 10 12

4

6

8

10

12

plot presipitasi gcm grid 38

Waktu

P

resi

pi

tasi

2 4 6 8 10 12

5 6 7 8 9 10 11 12

Waktu

P

resi

pi

tasi

2 4 6 8 10 12

6 7 8 9 10 11 12

Waktu

P

resi

pi

tasi

2 4 6 8 10 12

1

2

3

4

5

Waktu

P

resi

pi

tasi

2 4 6 8 10 12

1 2 3 4 5 6 7

Waktu

P

resi

pi

(38)

26

2 4 6 8 10 12

2

4

6

8

Waktu

P

resi

pi

tasi

2 4 6 8 10 12

2

4

6

8

10

plot presipitasi gcm grid 44

Waktu

P

resi

pi

tasi

2 4 6 8 10 12

4

6

8

10

12

Waktu

P

resi

pi

tasi

2 4 6 8 10 12

4

6

8

10

12

Waktu

P

resi

pi

tasi

2 4 6 8 10 12

6 7 8 9 10 11

Waktu

P

resi

pi

tasi

2 4 6 8 10 12

6 7 8 9 10 11 12

Waktu

P

resi

pi

tasi

2 4 6 8 10 12

0 1 2 3 4 5

Plot Presipitasi gcm gr

Waktu

P

resi

pi

tasi

2 4 6 8 10 12

1 2 3 4 5 6 7

Plot Presipitasi gcm gr

Waktu

P

resi

pi

tasi

2 4 6 8 10 12

2

4

6

8

Waktu

P

resi

pi

tasi

2 4 6 8 10 12

2

4

6

8

10

Waktu

P

resi

pi

tasi

2 4 6 8 10 12

4

6

8

10

12

Waktu

P

resi

pi

tasi

2 4 6 8 10 12

4

6

8

10

Waktu

P

resi

pi

tasi

2 4 6 8 10 12

6 7 8 9 10 11

Plot Presipitasi gcm gr

Waktu

P

resi

pi

tasi

2 4 6 8 10 12

6 7 8 9 10 11

Waktu

P

resi

pi

tasi

2 4 6 8 10 12

0 1 2 3 4 5 6

Waktu

P

resi

pi

(39)

27

2 4 6 8 10 12

0

2

4

6

8

Waktu

P

resi

pi

tasi

2 4 6 8 10 12

2

4

6

8

Waktu

P

resi

pi

tasi

2 4 6 8 10 12

2

4

6

8

10

12

Waktu

P

resi

pi

tasi

2 4 6 8 10 12

2

4

6

8

10

12

Plot Presipitasi gcm gr

Waktu

P

resi

pi

tasi

2 4 6 8 10 12

4

6

8

10

Waktu

P

resi

pi

tasi

2 4 6 8 10 12

8

9

10

11

12

Waktu

P

resi

pi

tasi

2 4 6 8 10 12

8

9

10

11

Waktu

P

resi

pi