Nurpaidah Tuti alawiah
Misrukiani Resa safitri Nurul Wahyuni
Kamaruddin Muh.surya
Kelompok
VII
D3 farmasi
Stikes Pelamonia Kesdam VII Wirabuana Tahun Ajaran
2016/2017
Matematika
Konsep Turunan
KATA PENGATAR
Pujisyukur kami panjatkan kehadirat Allah Subhanahuwata΄ala, karena berkat dan Rahmat-Nya kami dapat menyelesaikan makalah yang berjudul. “Konsep Turunan”.Makalah ini diajukan guna memenuhi tugas mata kuliah “MATEMATIKA”. Kami mengucapkan terimakasih kepada semua pihak yang telah membantu sehingga makalah ini dapat diselesaikan sesuai dengan waktunya. Makalah ini masih jauh dari sempurna, oleh karena itu kami mengharapkan masukan dan saran yang bersifat membangun demi kesempurnaan makalah ini.
Semoga makalah ini memberikan informasi bagi mahasiswa khususnya,dan masyarakat umumnya dan bermanfaat untuk pengembangun ilmu pengetahuan bagi kita semua.
Makassar, September 2016
DAFTAR ISI
KATA PENGANTAR...i DAFTAR ISI ... ii BAB I PENDAHULUAN
A. Latar Belakang... 1 B. Rumusan Masalah... 1 C. Tujuan Masalah... 1
BAB II PEMBAHASAN
A. Konsep Turunan Untuk Mencari Garis Singgung... 2 B. Mendeteksi Terjadinya Nilai Ekstrim Suatu Fungsi... 7 C. Contoh Penggunaan Konsep Turunan Dalam Kehidupan
Sehari-hari... 9
BAB III PENUTUP
A. Kesimpulan...13 B. Saran...13
Daftar Pustaka
Salah satu penerapan atau penggunaan turunan dalam matematika adalah menentukan kemiringan garis singgung menggunakan konsep turunan. Pada mata kuliah kali ini kita akan mempelajari cara Menentukan Kemiringan Garis Singgung Menggunakan Konsep Turunan. Untuk memudahkan dalam mempelajari materi Persamaan Garis Singgung pada Kurva Menggunakan Turunan, sebaiknya juga baca materi "definisi turunan" , "turunan fungsi aljabar" dan "turunan fungsi trigonometri".
B. Rumusan Masalah
1. Bagaimana cara mencari kemiringan garis singgung menggunakan konsep turunan
2. Bagaimana cara mendeteksi nilai ekstrim suatu fungsi
3. Apa contoh penerapan konsep turunan dalam kehidupan sehari-hari C. Tujuan Penulisan
1. Mengetahui cara mencari kemiringan garis singgung menggunakan konsep turunan
2. Mengetahui cara mendeteksi nilai ekstrim suatu fungsi
3. Mengetahui contoh penerapan konsep turunan dalam kehidupan sehari-hari
BAB II PEMBAHASAN
A. Konsep Turunan Untuk Mencari Kemiringan Garis Singgung 1. Menentukan Gradien garis singgung
Perhatikan gambar berikut !
A.
Titik P(x,y) adalah sembarang titik pada kurva y=f(x), sehingga koordinat titik P dapat dituliskan sebagai (x,f(x)). Absis titik Q adalah (x+h) sehingga koordinat titik Q adalah {(x+h),(f(x+h)}. Jika h → 0, maka S akan menjadi garis singgung pada kurva di titik P yaitu PS. Dengan demikian gradien garis singgung pada kurva di titik P adalah sebagai berikut.
m=tanQPR=limh→0f(x+h)−f(x)h=f′(x)
Artinya gradien garis singgung di titik A(a,f(a)) adalah m=f′(a) .
2. Langkah-langkah menentukan gradien di titik A(a,f(a)) pada kurva y=f(x) :
3. Menentukan Persamaan Garis Singgung pada Kurva
Secara umum persamaan garis di titik A(x1,y1) pada kurva y=f(x)
dapat ditentukan dengan rumus :
Persamaan garis lurus : y−y1=m(x−x1)
dengan gradiennya : m=f′(x1) .
Contoh :
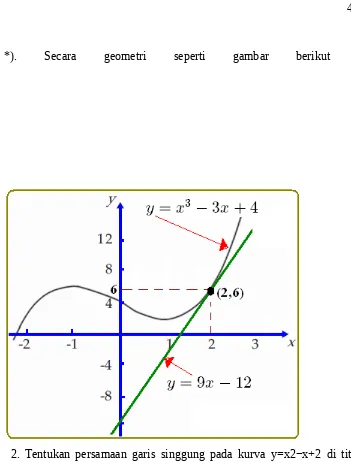
1). Tentukan persamaan garis singgung di titik (2,6) pada kurva y=x3−3x+4 ?
Penyelesaian
a. Menentukan turunan fungsinya : y=x3−3x+4→f′(x)=3x2−3 b. Menentukan gradien di titik (2,6) : m=f′(2)→m=3.22−3=9
*). Menyusun persamaan garis singgung (PGS) di titik (2,6) dan m=9 y−y1y−6y−6y=m(x−x1)=9(x−2)=9x−18=9x−12
Jadi, PGS nya adalah y=9x−12 .
*). Secara geometri seperti gambar berikut :
2. Tentukan persamaan garis singgung pada kurva y=x2−x+2 di titik dengan absis 1, dan tentukan titik potong garis singgungnya terhadap sumbu X dan Sumbu Y ?
Penyelesaian
*). Menentukan titik singgung (x1,y1) dengan substitusi absis x=1 ke persamaan kurvanya,
x=1→y=x2−x+2=12−1+2=2
Sehingga titik singgungnya (x1,y1)=(1,2)
*). Menentukan turunan fungsi, y=x2−x+2→f′(x)=2x−1
*). Menentukan gradiennya di titik (1,2) m=f′(1)→m=2.1−1=1
*). Menyusun persamaan garis singgung (PGS) di titik (1,2) dan m=1
y−y1y−2y−2y=m(x−x1)=1(x−1)=x−1=x+1 Jadi, PGS nya adalah y=x+1 .
*). Menentukan titik potong pada sumbu-sumbu : Titik potong sumbu X, substitusi y=0
y=0→y=x+1→0=x+1→x=−1 .
Sehingga titik potong sumbu X di titik (−1,0). Titik potong sumbu Y, substitusi x=0
x=0→y=x+1→y=0+1→y=1 .
Sehingga titik potong sumbu Y di titik (0,1).
3. . Garis y=x+1 memotong parabola y=x2+2x+1 di titik A dan B. Tentukan persamaan garis singgung parabola itu di titik A dan B. Jika titik potong kedua garis singgung adalah (a,b), maka nilai a+b=.... ?
Penyelesaian :
*). Menentukan titik potong kedua kedua persamaan yaitu titik A dan B
y1x2+2x+1x2+xx(x+1)x=0∨x=y2=x+1=0=0=−1 Substitusi x=0 dan x=−1 ke salah satu persamaan : untuk x=0→y=x+1=0+1=1
Sehingga titik potong pertamanya A(0,1), untuk x=−1→y=x+1=−1+1=0
Sehingga titik potong keduanya B(−1,0),
Diperoleh titik potongnya di A(0,1) dan B(−1,0)
*). Menentukan persamaan garis singgung di titik A dan B pada parabola,
Turunan fungsi : y=x2+2x+1→f′(x)=2x+2 Titik A(0,1),
gradien : m=f′(0)=2.0+2=2
PGS : y−y1=m(x−x2)→y−1=2(x−0)→y=2x+1
Titik B(−1,0),
gradien : m=f′(−1)=2.(−1)+2=0
PGS : y−y1=m(x−x2)→y−0=0(x−(−1))→y=0
Diperoleh persamaan garis singgung di titik A adalah y=2x+1 dan di titik B adalah y=0 .
*). Menentukan titik potong kedua garis singgung : garis singgungnya : y=0 dan y=2x+1
substitusi pers(i) ke pers(ii) : y=0→y02xx=2x+1=2x+1=−1=−12
Diperoleh titik potong kedua garis singgungnya (−12,0) ,
pada soal juga dikatakan titik potong kedua garis singgung adalah (a,b) ,
aritnya (a,b)=(−12,0)
Sehingga nilai a+b=−12+0=−12 Jadi, nilai a+b=−12
B. Cara Mendeteksi Nilai Ekstrim Suatu Fungsi 1. Misalkan f terdefenisi pada selang I yang memuat
a. f(c) merupakan nilai minimum f pada I jika f(c) ≤ f(x) untuk semua x dalam I.
b. f(c) merupakan nilai maksimum f pada I jika f(c) ≥ f(x) untuk semua x dalam I.
2. Nilai minimum dan maksimumsuatu fungsi pada selang tertentu disebut sebagai nilai ekstrim suatu fungsi pada selang tersebut. Nilai minimum dan maksimum suatu fungsi pada selang tertentu juga disebut sebagai nilai minimum mutlak dan nilai maksimum mutlak pada selang tersebut. Nilai ekstrim suatu fungsi dapat terjadi pada ujung selang. Nilai ekstrim yang terjadi pada ujung selang disebut nilai ekstrim ujung .
Suatu fungsi tidak harus memiliki nilai minimum atau maksimum pada selang tertentu. Sebagai contoh, pada gambar (1) dan (2) di atas, kita dapat melihat bahwa fungsif(x) = x² + 1 memiliki minimum dan maksimum pada selang tutup [–1, 2], tetapi tidak memiliki maksimum pada selang buka (– 1, 2). Selain itu, pada gambar (3), kita dapat melihat bahwa kekontinuan dapat mempengaruhi keberadaan nilai ekstrim pada suatu selang. Hal ini menghasilkan teorema berikut.
Teorema 1 Teorema Nilai Ekstrim
Jika f kontinu pada selang tutup [a, b], maka f memiliki nilai minimum dan maksimum pada selang tersebut.
Teorema Nilai Ekstrim di atas dapat disebut sebagai teorema keberadaan karena teorema tersebut hanya menyebutkan keberadaan nilai minimum dan maksimum, tetapi tidak menunjukkan bagaimana menentukan nilai-nilai tersebut.
Nilai Ekstrim Lokal danNilai Kritis
Pada gambar di bawah ini, grafikf(x) = x³ – 3x² memiliki maksimum local pada titik (0, 0) dan minimum local pada titik (2, –4). Secara tidak formal, untuk suatu fungsi kontinu, kita dapat berpikir bahwa maksimum local nya berada pada “bukit” grafik, dan minimum local nya terletak pada “lembah” grafik. Bukit dan lembah seperti itu dapat terjadi dalam dua cara. Ketika bukit atau lembah tersebut halus, grafik fungsi yang memuat bukit atau lembah tersebut memiliki garis singgung horizontal pada puncak bukit atau lembah tersebut. Ketika bukit atau lembah tersebut tajam, grafik fungsi yang memuat nya tidak akan memiliki turunan pada puncak bukit atau lembah tersebut.
C. Contoh Penerapan Konsep Turunan Dalam Kehidupan Sehari – Hari 1. Sebuah kembang api diluncurkan ke udara. Ketinggian kembang api h = f
(t) (dalam meter) pada t sekon dimodelkan dengan f (t) = 16t2 + 200 t + 4.
Tentukan kecepatan luncur kembang api saat t = 3 sekon. Penyelesaian:
Jadi, kecepatan luncur kembang api saat t = 3 sekon adalah 296 m/s. 2. Sebuah perusahaan memproduksi x unit barang per hari dengan biaya x3 –
600x2 + 112.500xrupiah. Berapa unit barang yang harus diproduksi setiap
harinya supaya biaya produksi menjadi minimal? Penyelesaian:
Oleh karena p′′(x)=6x−1.200 dan p′′(250)=6(250)−1.200=300>0, maka jumlah barang yang harus diproduksi tiap harinya agar biaya minimum adalah 250 unit.
3. Sebuah bola tenis ditembakkan ke atas. Jika tinggi bola tenis (cm) dari permukaan tanah setelah t detik dirumuskan dengan h(t)=120t−5t2, maka tentukan tinggi maksimum yang dapat dicapai bola tenis tersebut.
Penyelesaian:
Bola tenis akan mencapai ketinggian maksimum dari permukaan tanah untuk t yang memenuhi h′(t)=0 dan h”(t)<0
h′(t)=0
Oleh karena h “ (x) = -10 < 0, maka bola tenis akan mencapai ketinggian
maksimum dari permukaan tanah.
Selanjutnya, dengan mensubtitusikan t=12 ke h(t) diperoleh: h(12)=120(12)−5(12)2=720.
Dengan demikian, tinggi maksimum yang dapat dicapai bola tenis adalah 720 cm.
4. Sebuah perusahaan peralatan dapur memproduksi x unit barang dengan biaya (x2−70x+250) ribu rupah. Jika pendapatan setelah semua barang habis terjual adalah 100x ribu rupiah, maka hitung keuntungan maksimum yang dapat diperoleh perusahaan tersebut.
Penyelesaian:
Misalkan keuntungan perusahaan adalah f(x), sehingga:
f(x)= pendapatan – biaya produksi
f(x)=100x−(x2−70x+250)
⇔
f(x)=−x2+170x−250
⇔
Keuntungan maksimum akan diperoleh untuk nilai x yang memenuhi f′ (x)=0 dan f”(x)<0
f′(x)=0 −2x+170=0
⇔
2x=170
⇔
x=85
⇔
Oleh karena f “ (x) = -2 < 0, maka keuntungan yang diperoleh adalah maksimum.
Besar keuntungan pada saat x=85 adalah f(85)=−852−70(85)+250=175. Jadi, keuntungan maksimum perusahaan adalah 175.000 rupiah
4. Langkah-langkah menentukan gradien di titik A(a,f(a)) pada kurva y=f(x) :
i). Tentukan turunan fungsinya (f′(x)) ii). Substitusi nilai x=a atau absis titik A(a,f(a)) iii). Gradiennya (m) adalah m=f′(a)
5. Menentukan Persamaan Garis Singgung pada Kurva
Secara umum persamaan garis di titik A(x1,y1) pada kurva y=f(x)
dapat ditentukan dengan rumus :
Persamaan garis lurus : y−y1=m(x−x1)
dengan gradiennya : m=f′(x1) . dengan gradiennya : m=f′(x1) .
*). Menyusun persamaan garis singgung (PGS) di titik (2,6) dan m=9
y−y1y−6y−6y=m(x−x1)=9(x−2)=9x−18=9x−12 Jadi, PGS nya adalah y=9x−12 .
BAB III PENUTUP A. KESIMPULAN
Salah satu penerapan atau penggunaan turunan dalam matematika adalah mencari kemiringan garis singgung menggunakan konsep turunan pada titik tertentu. Pada mata kuliah kali ini kita telah mempelajari cara mencari kemiringan garis singgung menggunakan konsep turunan beserta contoh – contohnya.
B. SARAN
Setelah mempelajari materi ini mahasiswa dapat :
1. Mencari kemiringan garis singgung menggunakan konsep turunan 2. Mengetahui nilai ekstrim
3. Mengetahui contoh penerapan konsep turunan dalam kehidupan sehari-hari
DAFTAR PUSTAKA
http//mtk%20dasar/persamaan-garis-singgung-pada-kurva-menggunakan-turunan.html
mtk%20dasar/PenerapanTurunaNilaiEkstrim%20Fungsi%20pada %20Suatu%20SelangPendidikan%20Matematika.html