Studi Transformasi Bentuk Fuzzy Linear Programming Ke Bentuk Linear Programming

PROGRAMMING

KE BENTUK

LINEAR PROGRAMMING

SKRIPSI

JOSEPHINE

050803006

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains

JOSEPHINE

050803006

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

PERSETUJUAN

Judul

: STUDI TRANSFORMASI BENTUK

FUZZY LINEAR

PROGRAMMING KE BENTUK

LINEAR

PROGRAMMING

Kategori

: SKRIPSI

Nama

: JOSEPHINE

Nomor Induk Mahasiswa

: 050803006

Program Studi

: SARJANA (S1) MATEMATIKA

Departemen

: MATEMATIKA

Fakultas

: MATEMATIKA DAN ILMU PENGETAHUAN

ALAM (FMIPA) UNIVERSITAS SUMATERA

UTARA

Diluluskan di

Medan, Juni 2011

Komisi

Pembimbing

:

Pembimbing II,

Pembimbing I,

Prof. Dr. Iryanto, M.Si. Prof. Dr. Herman Mawengkang

NIP. 19460404 197107 1 001 NIP. 19461128 197403 1 001

Diketahui/ Disetujui oleh

Departemen Matematika FMIPA USU

Ketua,

Prof. Dr. Tulus, M.Si.

PERNYATAAN

STUDI TRANSFORMASI BENTUK

FUZZY LINEAR PROGRAMMING KE BENTUK

LINEAR PROGRAMMING

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan

dan ringkasan yang masing – masing disebutkan sumbernya.

Medan, Juni 2011

PENGHARGAAN

Puji dan syukur penulis panjatkan kepada Tuhan Yang Maha Pemurah dan Maha

Penyayang, dengan limpah karunia-Nya sehingga penulis dapat menyelesaikan skripsi ini

guna melengkapi syarat memperoleh gelar sarjana Matematika pada Fakultas Matematika

dan Ilmu Pengetahuan Alam di Universitas Sumatera Utara.

ABSTRAK

THE STUDY OF TRANSFORMATION FROM FUZZY LINEAR

PROGRAMMING TO LINEAR PROGRAMMING

ABSTRACT

DAFTAR ISI

Halaman

Persetujuan

ii

Pernyataan

iii

Penghargaan iv

Abstrak

v

Abstract

vi

Daftar Isi

vii

Bab 1 Pendahuluan

1.1 Latar Belakang

1

1.1.1 Linear Programming

2

1.1.2 Fuzzy Linear Programming

2

1.2 Perumusan Masalah

3

1.3 Pembatasan Masalah

3

1.4 Tujuan Penulisan

3

1.5 Manfaat Penulisan

3

1.6 Metodologi Penulisan

4

1.7 Tinjauan Pustaka

4

Bab 2 Landasan Teori

2.1

Himpunan

Fuzzy

6

2.2 Fungsi Keanggotaan

pada Himpunan Fuzzy

6

2.3

Bilangan

Fuzzy

8

2.4 Aritmatika pada Bilangan Fuzzy Triangular

10

2.5 Matriks Non Negatif dan Vektor Fuzzy Non Negatif

11

2.6 Sistem Persamaan Linear Fuzzy

11

2.7 Metode Penyelesaian Program Linear

20

Bab 3 Pembahasan

23

Bab 4 Kesimpulan dan Saran

4.1

Kesimpulan

29

4.2

Saran

29

ABSTRAK

THE STUDY OF TRANSFORMATION FROM FUZZY LINEAR

PROGRAMMING TO LINEAR PROGRAMMING

ABSTRACT

PENDAHULUAN

1.1 Latar Belakang

Teori himpunan fuzzy banyak diterapkan dalam berbagai disiplin ilmu seperti teori

kontrol dan manajemen sains, pemodelan matematika dan berbagai aplikasi dalam

bidang perindustrian. Karena dalam praktek kenyataanasumsi kepastian tentang

nilai-nilai parameter pada masalah pengambilan keputusan yang dimodelkan dengan

program linear sering sulit dipenuhi, maka sering terjadi kekurangakuratan dalam

masalah pengambilan keputusan. Untuk memecahkan dan mengakomodasi

ketidakpastian tersebut, akan didekati dengan teori himpunan fuzzy. Fuzzy Linear

Programming memiliki peranan penting dalam pemodelan fuzzy yang dapat

merumuskan ketidakpastian ke dalam lingkungan nyata.

Banyak jenis permasalahan Fuzzy Linear Programming yang pernah

dikemukakan oleh para ahli dan juga telah diusulkan beberapa pendekatan untuk

memecahkan masalah ini. Secara khusus, metode yang paling sesuai adalah

didasarkan pada konsep perbandingan bilangan fuzzy dengan menggunakanranking

function. Biasanya dalam metode tersebut, didefinisikan sebuah crisp model yang

disetarakan dengan masalahFuzzy Linear Programming dan kemudian menggunakan

solusi yang optimal dari model tersebut sebagai solusi yang optimal dariFuzzy Linear

Programming. Selain itu, dengan menggunakan ranking function linear umum,

diperkenalkan algoritma dual simplex untuk menyelesaikan masalah pemograman

linear dengan variabel fuzzy dandualnya.

Asumsikan bahwa dalam sebuah permasalahan program linear terdapat

masalah Fuzzy Linear Programming. Mungkin saja beberapa koefisien dari

permasalahan tersebut, misalnya pada fungsi tujuan, koefisien teknis, koefisien ruas

kanan ataupun variabel pengambilan keputusan itu merupakan bilangan fuzzy.

1.1.1 Linear Programming

Untuk mendefinisikan masalah Fuzzy Linear Programming, sebelumnya

diperkenalkan permasalahan program linear. Program linear adalah sebuah metode

matematika yang digunakan untuk mencari hasil paling optimal (seperti keuntungan

maksimal atau biaya terendah) dalam suatu model matematika dengan beberapa daftar

kendala yang direpresentasikan dalam persamaan linier. Sebuah permasalahan

program linear dapat didefinisikan sebagai berikut:

Maks : z = cx

s.t : Ax b

x ≥0

di mana :

x =(x1, , xn)T, c = (c1, , cn),b = (b1, , bm)T, danA = [aij]m×n

cj, bi, dan aij merupakan bilangan – bilangan crisp. Tetapi bagaimanapun, dalam

masalah pengambilan keputusan di dunia nyata, adalah hal biasa jika estimasi

koefisienLinear Programming yang digunakan itu tidak tepat. Selain itu, pengambil

keputusan juga mungkin mengizinkan beberapa pelanggaran dalam pencapaian

kendala. Dalam kasus ini,Fuzzy Linear Programming memberikan fleksibilitas.

1.1.2 Fuzzy Linear Programming

Pandang masalahLinear Programming berikut:

Maks : ~z = c x~

s.t :

  

≥ =

0 ~

~ ~

x b x A

di mana matriks koefisienA = [aij]m×n dan vektor c = (c1, , cn) adalah matrikscrisp

non negatif sehingga ~x_j,b~_i ∈F(R) untuk semua 1≤ j≤ n , 1≤i ≤ m , disebut

sebagai masalahFuzzy Linear Programming.

Dalam tulisan ini akan dijelaskan cara menyelesaikan Fuzzy Linear

Programming dengan mentransformasikan bentuk Fuzzy Linear Programming ke

bentukLinear Programmingterlebih dahulu.

1.2 Perumusan Masalah

Masalah yang akan dibahas adalah bagaimana cara mentransformasikan bentukFuzzy

Linear Programming menjadi permasalahan program linear klasik yang

penyelesaiannya lebih familiar dan sederhana.

1.3 Pembatasan Masalah

Dalam tulisan ini, masalah yang dibahas adalah penyelesaian persoalan Fuzzy Linear

Programming dengan bilangan fuzzy triangular. Sebuah bilangan fuzzy

triangular A~ sebarang ditunjukkan oleh A~=(mA,αA,βA) dengan F(R) adalah

himpunan dari bilangan fuzzy triangular.

1.4 Tujuan Penulisan

Tujuan yang ingin dicapai adalah untuk mengetahui cara menyelesaikan masalah

Fuzzy Linear Programming dengan bilangan fuzzy triangular dengan

mentransformasikannya terlebih dahulu ke bentuk masalahLinear Programming.

1.5 Manfaat Penulisan

Penulisan ini dapat dimanfaatkan untuk mempermudah di dalam menyelesaikan

permasalahan Fuzzy Linear Programming dan berguna di dalam studi/ pembelajaran

1.6 Metodologi Penulisan

Metodologi penulisan ini bersifat literatur atau kepustakaan dengan langkah - langkah

sebagai berikut :

1. Memaparkan beberapa definisi serta teorema yang mendukung dalam

memperoleh hasil utama penulisan ini.

2. Memaparkan langkah – langkah penyelesaian permasalahan Fuzzy Linear

Programming dengan tahapan sebagai berikut:

a. Memaparkan tentang bilangan fuzzy, yaitu dalam hal ini dengan

menjelaskan tentang bilangan fuzzy triangular dan aritmatika pada

bilangan fuzzy triangular.

b. Memaparkan tentang metode yang digunakan untuk menyelesaikan

masalahFuzzy Linear Programming dan disertai dengan ilustrasi.

1.7 Tinjauan Pustaka

L.A. Zadeh (1965, hal: 338) menyatakan bahwa suatu himpunan fuzzy merupakan

sebuah kelas dari objek – objek dengan suatu rangkaian kesatuan dari nilai

keanggotaan. Demikian sebuah himpunan digolongkan oleh sebuah fungsi

(karakteristik) keanggotaan yang memberikan setiap objek sebuah nilai keanggotaan

yang berkisar antara 0 dan 1.

H.J. Zimmermann (1975, hal: 209) menyatakan bahwa pada Fuzzy Linear

Programming, fungsi objektif dan kendala – kendalanya ditunjukkan dengan fungsi

keanggotaannya. Zimmermann mendefinisikan fungsi keanggotaan untuk fungsi

objektif dan untuk kendala – kendala pada permasalahanFuzzy Linear Programming.

Sri Kusumadewi dan Hari Purnomo (2004, hal: 376) menyatakan bahwa pada

Fuzzy Linear Programming, akan dicari suatu nilaiz yang merupakan fungsi objektif

yang akan dioptimasikan sehingga memenuhi batasan – batasan yang dimodelkan

sebuah himpunan fuzzy dan menentukan fungsi keanggotaan untuk himpunan fuzzy

tersebut.

S.H. Nasseri (2008, hal: 2473) menyatakan bahwaFuzzy Linear Programming

adalah sebuah aplikasi dari teori himpunan fuzzy pada masalah proses pengambilan

keputusan linear, di mana sebagian besar dari masalah tersebut terkait dengan

LANDASAN TEORI

2.1 Himpunan Fuzzy

Tidak semua himpunan yang dijumpai dalam kehidupan sehari-hari terdefinisi secara

jelas, misalnya himpunan orang miskin, himpunan orang pandai, himpunan orang

tinggi, dan sebagainya. Misalnya, pada himpunan orang tinggi, tidak dapat ditentukan

secara tegas apakah seseorang adalah tinggi atau tidak tinggi. Anggap bahwa definisi

“orang tinggi” adalah orang yang tingginya lebih besar atau sama dengan 1.75 meter,

maka orang yang tingginya 1.74 meter menurut definisi tersebut termasuk orang yang

tidak tinggi. Sulit diterima bahwa orang yang tingginya 1.74 meter itu tidak termasuk

orang tinggi. Hal ini menunjukkan bahwa batas antara kelompok orang tinggi dan

kelompok orang yang tidak tinggi tidak dapat ditentukan secara tegas.

Untuk mengatasi permasalahan himpunan dengan batas yang tidak tegas itu,

L.A. Zadeh mengaitkan himpunan tersebut dengan suatu fungsi yang menyatakan nilai

keanggotaan pada suatu himpunan tak kosong sebarang dengan mengaitkan pada

interval [0,1]. Himpunan tersebut disebut himpunan fuzzy dan fungsi ini disebut

fungsi keanggotaan (membership function) dan nilai fungsi itu disebut derajat

keanggotaan.

2.2 Fungsi Keanggotaan pada Himpunan Fuzzy

KetikaA adalah sebuah himpunan tegas (crisp), fungsi keanggotaannya hanya terdapat

2 nilai kemungkinan, yaitu 0 dan 1, dengan f_A(x) = 1 atau 0 tergantung pada x

menjadi anggota dalam suatu himpunan. Nol (0) berarti suatu item tidak menjadi

anggota dalam suatu himpunan.

Sebuah himpunan fuzzy A pada X ditandai oleh fungsi keanggotaan fA(x)

yang berhubungan dengan setiap titik di X, sebuah bilangan real pada interval

[ ]

0,1

dengan nilai dari f_A(x) pada x mewakili derajat keanggotaan x pada A. Maka,

semakin dekat nilai f_A(x) ke semesta pembicaraan, semakin tinggi derajat

keanggotaanx padaA.

Semesta pembicaraan adalah keseluruhan nilai yang diperbolehkan untuk

dioperasikan dalam suatu variabel fuzzy. Semesta pembicaraan merupakan himpunan

bilanganreal yang senantiasa naik (bertambah) secara monoton dari kiri ke kanan dan

nilai semesta pembicaraan dapat berupa bilangan positif atau negatif.

Domain himpunan fuzzy adalah keseluruhan nilai yang diizinkan dalam

semesta pembicaraan dan boleh dioperasikan dalam suatu himpunan fuzzy. Fungsi

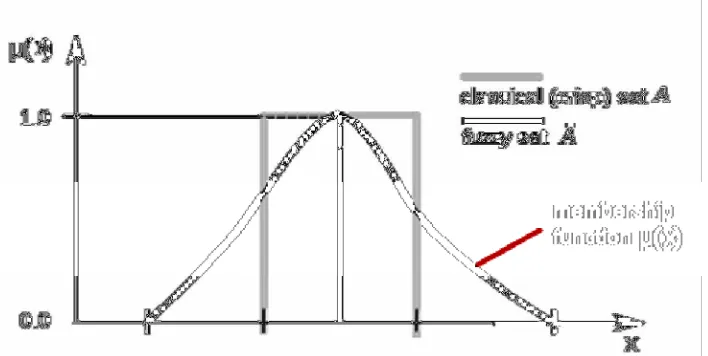
keanggotaan (membership function) adalah suatu kurva yang menunjukkan pemetaan

titik – titik input data ke dalam nilai keanggotaan yang mempunyai interval antara 0

[image:17.612.165.519.472.650.2]

sampai 1.

Keterangan gambar:

Classical (crisp) set A= himpunan tegasA

Fuzzy set A~ = himpunan fuzzy A~

membership function = fungsi keanggotaan µ(x)

Definisi 2.1: X adalah sebuah himpunan tak kosong. Sebuah himpunan fuzzy A

padaX ditandai oleh fungsi keanggotaannya:

[ ]

0,1

:X →

A

danA(x) diinterpretasikan sebagai derajat keanggotaan dari elemenx

pada himpunan fuzzyA untuk setiap x∈X .

Nilai 0 digunakan untuk mewakili bukan anggota, nilai 1 digunakan untuk

mewakili keanggotaan penuh, dan nilai – nilai di antaranya digunakan untuk mewakili

derajat keanggotaan menengah. PemetaanA juga disebut sebagai fungsi keanggotaan

dari himpunan fuzzyA.

Definisi 2.2: Sebuah himpunan fuzzy adalah kosong jika dan hanya jika fungsi

keanggotaannya sama dengan 0 padaX.

Definisi 2.3: Dua himpunan fuzzy A dan B adalah sama, ditulis A = B, jika dan

hanya jika f_A(x)= f_B(x)untuk semuax padaX.

2.3 Bilangan Fuzzy

Sebuah bilangan fuzzy merupakan perluasan dari bilangan biasa, dalam arti bahwa hal

itu tidak mengacu pada suatu nilai tunggal melainkan pada suatu himpunan nilai –

nilai yang mungkin berhubungan, dimana setiap nilai kemungkinan memiliki bobot

sendiri antara 0 dan 1. Bobot ini disebut sebagai fungsi keanggotaan. Dengan

demikian, sebuah bilangan fuzzy adalah sebuah kasus khusus dari himpunan fuzzy

konveks. Sama seperti Logika Fuzzy yang merupakan perluasan dari Logika Boolean

fuzzy merupakan perluasan dari bilangan real. Perhitungan dengan menggunakan

bilangan fuzzy memungkinkan penggabungan ketidakpastian parameter, sifat,

geometri, kondisi awal, dan sebagainya.

Sebelum menjelaskan tentang bilangan fuzzy, berikut beberapa hal dan definisi

yang penting dalam teori himpunan fuzzy: (Hadi Nasseri, 2008, hal: 1778)

1. Sebuah himpunan fuzzyA padaR (barisan bilanganreal) didefinisikan sebagai

himpunan pasangan terurut A=

{

(x,µ_A(x))|x∈R

}

, di mana ~(x)

A

µ disebut

sebagai fungsi keanggotaan untuk himpunan fuzzy.

2. Sebuah himpunan fuzzyA disebut normal jika terdapat paling sedikit satu titik

R

x∈ dengan ~(x)=1

A

µ .

3. Sebuah himpunan fuzzy A pada R adalah konveks jika untuk setiap x,y∈R

setiap λ∈[0,1] sehingga µ_A(λx+(1−λ)y≥min

{

µ_A(x),µ_A(y)

}

.

4. Sebuah bilangan fuzzy adalah sebuah himpunan fuzzy pada barisan bilangan

real yang memenuhi kondisi normalitas dan konveksitas.

Definisi 2.4: Bilangan fuzzyA~ adalah sebuah normalisasi himpunan fuzzy konveks

pada barisan bilanganRsehingga:

1. Terdapat paling sedikit satu x_o∈R dengan ~(x₀)=1

A

µ .

2. ~(x)

A

µ setidaknya kontinu sebagian.

Diasumsikan fungsi keanggotaan dari sebarang bilangan fuzzy A~ adalah

sebagai berikut:

  

   

 

+ ≤ ≤ −

−

≤ ≤ − −

−

=

lainnya yang

untuk m x m m x

m x m

x m

x _A A A A

A

A A

A A A

A

, 0

, 1

, 1

) (

~ β

β

α α

µ

di mana mA adalah nilai rata – rata dari A~ dan αAdan βA adalah penyebaran kiri

bilangan fuzzy triangular ditunjukkan dengan A~=(mA,αA,βA) dan F(R) adalah himpunan dari bilangan fuzzy triangular.

Definisi 2.5: Sebuah bilangan fuzzy A~=

{

(

x,µ~_A(x)

)

x∈R

}

adalah non negatif jika

dan hanya jika ~(x)=0

A

µ untuk semua x<0. Jadi sebuah bilangan

fuzzy triangular A~=(mA,αA,βA) adalah non negatif jika

0

≥ − A A

m α .

Definisi 2.6: Dua buah bilangan fuzzy triangular A~=(mA,αA,βA) dan

) , , (

~ B B B

m

B= α β dikatakan sama jika dan hanya jika mA =mB ,

B A _α

α = , dan β =A βB_.

Definisi 2.7: Sebuah bilangan fuzzy A~=(mA,αA,βA) dikatakan simetris jika

A A _β α = .

2.4 Aritmatika pada Bilangan Fuzzy Triangular

Asumsikan _A~=(_mA,αA,βA)_{dan B}~=_(mB_,αB_,βB_{)adalah dua buah bilangan fuzzy}

triangular, aritmatika pada pada kedua bilangan fuzzy tersebut adalah sebagai berikut:

(S.H. Nasseri, 2008, hal: 2475)

a. Penjumlahan : A~+B~ = (mA+mB,αA+αB,βA +βB)

b. Perkalian skalar: λA~ =

  

≤ ≥ =

0 ),

, , (

0 ),

, , ( ) , , (

λ λα

λβ λ

λ λβ

λα λ β

α λ

jika m

jika m

m _{A A A}

A A A A

A A

2.5 Matriks Non Negatif dan Vektor Fuzzy Non Negatif

Definisi 2.8: Sebuah matriksA disebut non negatif dan dinotasikanA≥0 jika setiap

elemen dariA adalah bilangan non negatif.

Definisi 2.9: Sebuah vektor fuzzy b~=(b~i)m_×1 disebut non negatif dan dinotasikan

0 ~

≥

b jika setiap elemen dari b~adalah fuzzy non negatif, dengan kata

lain b~_i ≥0.

2.6 Sistem Persamaan Linear Fuzzy

Sistem persamaan linearn variabel dann persamaan ditulis dalam bentuk matriks:

y

Ax= (1)

denganA matriks persegi yang entri-entrinya merupakan bilangan real danx, y adalah

vektor – vektor di dalam Rn.

Diberikan u₁,u₂,L ,u_n,v₁,v₂,L ,v_n∈F _{dan a R} j

i, ∈ untuk1≤i, j≤n, maka

sistem persamaan linear fuzzy:

n n n n n n n n n n v u a u a u a v u a u a u a v u a u a u a = + + + = + + + = + + + , 2 2 , 1 1 , 2 , 2 2 2 , 2 1 1 , 2 1 , 1 2 2 , 1 1 1 , 1 L M M M M L L (2)

Sistem persamaan (2) dapat ditulis dalam bentuk matriks AU =V dengan

            = n n n n n n a a a a a a a a a A , 2 , 1 , , 2 2 , 2 1 , 2 , 1 2 , 1 1 , 1 L M O M M L L

, 2 ,

1             = n u u u U

M dan

Model sistem persamaan linear (2) mempunyai solusi fuzzy jika terdapat vektor             = n x x x X M 2 1

di dalam Fn sedemikian hingga _{jk j} j

n k v x a =

∑

=1 ,

dan _{jk j j}

n k v x a =

∑

=1 ,

,

untuk setiap j=1,2,L ,n_.

MengingatDefinisi 2.6 dan aritmatika pada bilangan fuzzy, fungsi-fungsi vj

dan v_j dapat ditulis sebagai kombinasi linear dari xj dan x_j. Sistem persamaan (2)

diubah ke bentuk 2 variabel dann 2 persamaan menjadi:n

∗ ∗ _=V

BX (3)

dengan             = n n n n n n b b b b b b b b b B 2 , 2 2 , 2 1 , 2 2 , 2 2 , 2 1 , 2 2 , 1 2 , 1 1 , 1 L M O M M L L

, X∗ =

[

x₁,L ,x_n,−x1,L ,−xn

]

T dan

[

]

T

n n v v

v v

V∗ = ₁,L , ,− 1,L ,− .

Entri-entri b_i,j ditentukan sebagai berikut:

1. jika a_i,j ≥ 0, maka b_i,j = a_i,j danb_i+n,j+n =a_i,j

2. jika a_i,j < 0, maka b_i,j+n =−a_i,j dan b_i+n,j =−a_i,j

3. b_i,j = 0, untuk yang lainnya.

Persamaan (3) bukan sistem persamaan linear fuzzy. Persamaan (3) merupakan

persamaan linear biasa yang nilai variabelnya berada dalam ruang fungsi. Dengan

menggunakan persamaan (3), dimungkinkan sistem persamaan linear fuzzy dapat

diselesaikan melalui penyelesaian sistem persamaan linear biasa. Lebih lanjut, matriks

B pada persamaan (3) dapat ditulis dalam bentuk matriks blok _

     = 1 2 2 1 B B B B B ,

Contoh 1:

Diberikan sistem persamaan linear fuzzy:

2 2 1 1 2 1 v x x v x x = + = −

Matriks A seperti dalam persamaan (2) adalah _

     − 1 1 1 1

. Oleh karena itu, diperoleh

matriksB dengan persamaan (3) adalah

            = 1 1 0 0 0 1 1 0 0 0 1 1 1 0 0 1 B .

Contoh 2 :

Diberikan sistem persamaan linear fuzzy:

2 2 1 1 2 1

3x v

x v x x = + = −

Jika sistem persamaan ini diubah menjadi persamaan (3), maka:

2 2 1 1 1 2 2 2 1 1 2 1 ) ( 3 ) ( ) ( 3 ) ( v x x v x x v x x v x x − = − + − − = − + = + = − +

Teorema 2.1:Diberikan _

     = 1 2 2 1 B B B B

B adalah matriks koefesien pada persamaan (3).

Matriks B non singular jika dan hanya jika matriks-matriks A=B₁−B₂

dan B₁+B₂ keduanya non singular.

Bukti :

(⇒) Dengan menggunakan operasi elementer baris/ kolom pada matriks

      = 1 2 2 1 B B B B

B , didapat matriks _

     + + = 1 2 2 1 2 1 B B B B B B

C . Jika matriks C dikenai

operasi elementer jumlahan dua kolom, didapat _

     − + = 2 1 2 2 1 0 B B B B B

adalah matriks yang dihasilkan dari operasi elementer jumlahan dua baris/ kolom dari

matriks B. Sedangkan matriks D adalah matriks yang dihasilkan dari operasi

elementer jumlahan dua baris/ kolom dari matriksC.

Hal ini berakibat:

det(B) = det(C) = det(D),

sehingga det(B) = det(D)

= det(B1 + B2) · det(B1 B2)

KarenaB non singular maka det(B)≠ 0 dan det(B1 + B2) · det(B1 B2) = det(B)≠ 0.

Hal ini mengakibatkan det(B1 + B2)≠ 0 dan det (B1 B2)≠ 0. Jadi matriks A=B1−B2

dan B₁+B₂ keduanya non singular.

(⇐) Diketahui matriks A=B₁−B₂ dan B₁+B₂ keduanya non singular. Jadi det(B1 + B2)≠ 0 dan det(B1 B2)≠ 0.

Dengan cara yang sama seperti pada bagian sebelumnya, didapat:

det(B) = det(C) = det(D)

dengan _

  



 + +

=

1 2

2 1 2 1

B B

B B B B

C dan _

  

 

− +

=

2 1 2

2

1 0

B B B

B B

D .

Hal ini berakibat:

det(B)= det(D)

= det(B1 + B2) · det(B1 B2)≠ 0

Karena nilai det(B1 + B2)≠ 0 dan nilai det(B1 B2)≠ 0. SehinggaBadalah matriks non

singular.

Teorema 2.2:Diberikan _

  

  =

1 2

2 1

B B

B B

B adalah matriks koefisien pada persamaan (3).

Jika invers matriksB ada, maka inversnya berbentuk _

  

  =

−

M N

N M B 1

.

Bukti :

Misalkan b_i,j dan b∗i,j berturut-turut menyatakan entri matriksB dan B−1 pada baris

ke-i dan kolom ke-j. Karena ( )

) det(

1

1 _{adj B}

B

j i

b∗, =

) det( ) det( ) 1 ( _, B B_ji

j i+ −

(4)

dengan B_j,i sub matriks yang diperoleh dengan cara mengeliminasi baris ke-j dan

kolom ke-i dari matriks B.

Perhatikan sub matriks B_j+n,i dan B_j,i+n . Matriks B_j+n,i dapat diperoleh

melalui operasi elementer pertukaran baris dan kolom dari B_j,i+n sebanyak p kali,

denganp bilangan genap. Oleh karenanya, det(B_j+n,i) = (-1)p det(B_j,i+n) = det(B_j,i+n).

Dari persamaan (4) dan mengingat det(B_j+n,i) = det(B_j,i+n), maka:

j n i

b∗+ , =

) det( ) det( ) 1 ( _, B B_{ji n}

j n i + + + − = ) det( ) det( ) 1 ( _, B B_{j ni}

j n i + + + −

= b∗i,j+n

untuk setiap1≤i,j≤n. Sampai di sini, didapat _

     ∗ ∗ = − N N B 1

Perhatikan juga sub matriks B_j,i dan B_j+n,i+n , untuk 1≤i,j≤n . Karena

      = 1 2 2 1 B B B B

B maka B_j+n,i+n dapat diperoleh menggunakan operasi elementer

pertukaran baris dan kolom dari B_j,i sebanyakq kali, denganq bilangan genap. Oleh karenanya,

det(B_j,i) = (-1)q det(B_j+n,i+n)

= det(B_j+n,i+n). Hal ini berakibat:

j i b∗, =

) det( ) det( ) 1 ( _, B B_ji

j i+ − = ) det( ) det( ) 1 ( ) 1

( 2 _,

B

B_{j ni n}

= ) det( ) det( ) 1 ( ( ) ( ) _, B

B_{j ni n}

n j n i + + + + + −

= b∗i+n,j+n

untuk setiap1≤i,j≤n.

Terbukti bahwa _

     = − M N N M

B 1 .

Persamaan (3) merupakan perubahan bentuk dari sistem persamaan linear

fuzzy. Walaupun persamaan (3) mempunyai solusi tunggal, tidak berarti sistem

persamaan linear fuzzy langsung diperoleh solusinya. JikaB dalam (3) non singular,

tidak ada jaminan bahwa X =B−1V∈F_{, untuk setiapV}∈_F.

Contoh berikut memperlihatkan bahwa persamaan (3) mempunyai solusi

tunggal tetapi permasalahan sistem persamaan linear fuzzy tidak mempunyai solusi

tunggal.

Contoh 3:

Diberikan permasalahan sistem persamaan linear fuzzy:

) 2 , ( 3 2

1 x x r r

x + − = −

) 3 , 2 (

2 _{2 3}

1 x x r

x − + = +

) 1 , 2 ( 3

2x₁+x₂+ x₃ = − − −r

Jika diubah dalam bentuk persamaan (3), maka diperoleh matriks-matriks :

       

 

       

 

=

3 1 2 0 0 0

1 0 1 0 2 0

0 1 1 1 0 0

0 0 0 3 1 2

0 2 0 1 0 1

1 0 0 0 1 1

B mempunyai invers, sehingga solusi persamaan (3) adalah:

T r r

r r

r r

X =[−2.31+3.62 ,−0.62−0.77 ,1.08−2.15 ,−4.69+3.38 ,1.62−0.32 ,2.92−1.85 ]

Misalkan: x₁=

[

−2.31+3.62r,4.69−3.38r

]

T,

[

]

T

r r

x₂ = −0.62−0.77 ,−1.62+0.23

[

]

3 1.08 2.15 , 2.92 1.85

T

x = − r − + r

Vektor

(

x₁,x₂,x₃

)

bukan solusi sistem persamaan linear fuzzy ini, karena x₁ dan x₂

bukan bilangan fuzzy.

Teorema berikut memperlihatkan syarat cukup dan syarat perlu agar solusi

persamaan (3) juga menjadi solusi untuk sistem persamaan linear fuzzy semula.

Sebelumnya, didefinisikan pengertian sifat non negatif yang dimiliki suatu matriks.

Matriks Q=

[ ]

q_i,j dikatakan non negatif jika untuk setiapi dan setiapj berlaku

0

,j ≥ i

q . Sebagai contoh, matriks koefisien pada persamaan (3) di atas adalah matriks

non negatif.

Teorema 2.3:Diberikan sistem persamaan linear fuzzy AU =V dengan n variabel

dan n persamaan. Persamaan BX∗ =V∗ seperti persamaan (3), dengan

B non singular. Solusi BX∗ =V∗ menjadi solusi sistem persamaan

linear fuzzy AU =V jika dan hanya jika matriks B−1 non negatif.

Bukti :

(⇒) Misalkan −1

B = [b∗i,j] dan

[

]

T n n x x x

x

− = ∗

=

∑

ij i

n

j

i b v

x , 1 i n j i n j v b∗ + =

∑

, 1 (5) − = − ∗+ =

∑

i nj i

n

j

i b v

x , 1 i n j n i n j v b∗+ + =

∑

,

1

(6)

untuk1≤i,j≤n.

Selanjutnya karena _

     = − M N N M

B 1 _{maka persamaan (6) menjadi:}

− =

− ∗ +

=

∑

ij n i

n

j

i b v

x , 1 i j i n j v b , 1 ∗ =

∑

, sehingga xi = ij i

n j v b , 1 ∗ =

∑

ij n i

n

j

v b∗ + =

∑

− , 1

(7)

Jika persamaan (7) dikurangi dengan persamaan (5), maka diperoleh:

= − i i x

x ( ij i n j v b , 1 ∗ =

∑

ij n i

n

j

v b∗ + =

∑

− , 1 )− ( ∗ − =

∑

ij i

n j v b , 1 i n j i n j v b∗ + =

∑

,

1

)

= ( ij i

n j v b , 1 ∗ =

∑

− ∗ − =

∑

ij i

n

j

v b , 1

) + ( ij n i

n

j

v b∗ + =

∑

, 1 i n j i n j v b∗ + =

∑

− , 1 ) = ( , ( ) 1 i i j i n j v v

b∗ −

=

∑

+ , ( ) 1 i i n j i n j v v b∗ + − =

∑

) (8)

Diketahui V∈Fn maka v v₁, ₂,L ,v_n∈F _{, sehingga ( )}

i i v

v − ≥ 0 untuk setiap

n i≤ ≤

1 .

Diketahui pula bahwa xi −x_i ≥ 0. Hal ini berakibat b∗i,j≥ 0 untuk setiapi dan

j. Dengan kata lain matriks B−1 = [b∗i,j] non negatif.

(⇐) Misalkan _B−1 _{= [}

j i

b∗, ] matriks non negatif. Jadi b∗i,j≥ 0 untuk setiap i dan j.

Dengan cara yang sama seperti pada bagian sebelumnya, didapat persamaan (8):

= − i i x

x ( , ( )

1 i i j i n j v v

b∗ −

=

∑

+ , ( ) 1 i i n j i n j v v b∗ + − =

∑

).

Selain itu, diketahui pula V∗ =

[

v₁,L ,v_n,−v1,L ,−vn

]

T solusi persamaan (3)

dan v v₁, ₂,L ,v_n∈F_{, maka ( )}

i i v

= − i i x

x ( , ( )

1

i i j i n

j

v v

b∗ −

=

∑

+ , ( )

1

i i n j i n

j

v v b∗ + − =

∑

) ≥ 0, untuk 1≤i≤n sehingga

1, 2, , n

x x L x ∈F _atau

1 2

[ ,x x ,L ,x_n]∈Fn_{. Dengan demikian, solusi ini menjadi solusi}

sistem persamaan linear fuzzy.

Dalam Contoh 3, matriks B adalah matriks non negatif. Tetapi invers matriks B,

yakni B−1 adalah:

2.7692 -0.8462 -0.4615 2.2308 -1.1538 -0.5385

-0.4615 0.3077 0.0769 -0.5385 0.6923 -0.0769

-1.6923 0.4615 0.6154 -1.3077 0.5385 0.3846

2.2308 -1.1538 -0.5385 2.7692 -0.8462 -0.4615

-0.5385 0.6923 -0.0769 -0.4615 0.3077 0.0769

-1.3077 0.5385 0.3846 -1.6923 0.4615 0.6154

 

 

 

 

 

 

 

 

 

jelas bukan matriks non-negatif. Sebab terdapat entri matriks B−1 yang bernilai negatif.

Mengingat Teorema 2.3, solusi persamaan linearnya tidak langsung menjadi solusi

persamaan linear fuzzy.

Sebuah sistem persamaan linear fuzzy dapat diubah menjadi bentuk sistem persamaan

linear biasa. Dari sistem n variabel dan n persamaan diubah menjadi sistem 2n

variabel dan 2n persamaan. Solusi sistem persamaan baru tidak secara langsung

menjadi solusi sistem persamaan semula. Contoh 3 memperlihatkan bahwa solusi

sistem persamaan baru tidak menjadi sistem persamaan semula. Jika matriks koefisien

dari sistem persamaan bersifat non negatif, maka solusinya menjadi sistem persamaan

semula. Hal ini ditulis dalamTeorema 2.2.

Definisi 2.10:Tinjau sistem persamaan linear m×n sebagai berikut:

b x

A~= ~ (9)

di mana A adalah sebuah matriks crisp non negatif dan ~x =(~x_j),

) ~ ( ~

i

b

b = adalah vektor – vektor fuzzy non negatif dan ~x_j,b~_i∈F(R)

untuk semua 1≤ j≤n , 1≤i≤m , disebut sebagai sebuah sistem

Definisi 2.11:Sebuah vektor fuzzy non negatif x~ merupakan solusi dari Ax~=b~ jika

x

~ memenuhi sistem persamaan tersebut, di manaA dan b~ seperti yang didefinisikan pada (9).

Adapun karena ~x∈Fn(R) dan b~∈Fm(R) , dapat diasumsikan

) , , (

~ _{x x}α _xβ

x = m dan b~=(bm,bα,bβ) di mana xm,xα,xβ ∈Rn dan bm,bα,bβ ∈Rm. Maka, sistem Ax~=b~ dapat ditulis sebagai berikut:

0 ),

, , ( ) , ,

(x xα xβ = b bα bβ x −xα ≥

A m m m (10)

Di samping itu, b~ dan x~ adalah dua buah vektor fuzzy non negatif, maka dengan

menggunakanDefinisi 2.6dan aritmatika pada bilangan fuzzy triangular non negatif,

dapat diselesaikan sistemcrisp berikut:

m m

b

Ax = , Axα =bα, Axβ =bβ (11)

Ingat bahwa jika menggunakan bilangan fuzzy triangular yang simetris (Definisi 2.7),

maka sistem Axβ =bβ tidak perlu diselesaikan karena sama dengan sistem Axα =bα.

2.7 Metode Penyelesaian Program Linear

Dalam tulisan ini, setelah permasalahan dalam bentuk Fuzzy Linear Programming

ditransformasi ke bentuk Linear Programming, akan dicari solusi yang optimal dari

model tersebut dan solusi itu juga digunakan sebagai solusi yang optimal dari Fuzzy

Linear Programming.

Linear Programming adalah sebuah metode matematika yang digunakan untuk

mencari hasil paling optimal (seperti keuntungan maksimal atau biaya terendah)

dalam suatu model matematika dengan beberapa daftar kendala yang

direpresentasikan dalam persamaan linear. Sebuah permasalahanLinear Programming

dapat didefinisikan sebagai berikut:

Maks : z = cx

s.t : Ax b

di mana :

x =(x1, , xn)T, c = (c1, , cn),b = (b1, , bm)T, danA = [aij]m×n.

Ada beberapa cara untuk menyelesaikan persoalan Linear Programming,

diantaranya dengan menggunakan metode grafik dan metode simplex. Metode grafik

tidak dapat digunakan menyelesaikan persoalan program linear yang memiliki

variabel keputusan yang cukup besar atau lebih dari dua, jadi untuk menyelesaikannya

digunakan metodesimplex.

Langkah – langkah penyelesaian program linear dengan metode grafik:

1. Bentuk model matematika dari persoalan untuk:

a. Fungsi tujuan (objective function)

b. Fungsi kendala (constraint)

2. Ubah bentuk pertidaksamaan pada kendala menjadi persamaan.

3. Gambarkan grafik pada langkah ke -2 dan tentukan daerah layak.

4. Uji titik – titik ekstrim yang diperoleh dengan mensubstitusikan nilai titik ke

fungsi tujuan.

Langkah – langkah penyelesaian program linear dengan metodesimplex:

1. Formulasikan dan standarisasikan persoalan ke model linear.

2. Tambahkan variabelslack pada masing – masing constraint (pembatas) untuk

memperoleh bentuk standar. Model ini digunakan untuk identifikasi solusi

feasible awal dari pembatas bernilai lebih kecil atau sama dengan.

3. Buat tabelsimplex awal.

4. Pilih kolom kunci, yaitu kolom yang memiliki nilai (cj-zj) yang paling positif

untuk kasus maksimasi atau yang memiliki nilai (cj - zj) yang paling negatif

untuk kasus minimasi.

5. Pilih baris kunci yang memiliki nilai indeks terkecil. Nilai indeks adalah

perbandingan nilai kanan dengan kolom kunci.

6. Menentukan nilai elemencell, yaitu nilai perpotongan antara kolom kunci dan

baris kunci.

7. Lakukan iterasi dengan menentukan baris kunci baru, baris z baru, dan baris

a. Baris kunci baru ditentukan dengan membagi baris kunci lama dengan

elemencell.

b. Baris z baru dan baris – baris lainnya ditentukan dengan cara:

Baris lama – (nilai kolom kunci baris yang sesuai × baris kunci baru)

c. Letakkan nilai – nilai baris yang baru diperoleh ke dalam tabel

8. Lakukan uji optimalitas. Jika semua koefisien pada baris (cj - zj) sudah tidak

ada lagi yang bernilai positif (untuk kasus maksimasi) atau sudah tidak ada

lagi bernilai negatif (untuk kasus minimasi) berarti sudah optimal. Jika kriteria

PEMBAHASAN

Adapun yang menjadi pembahasan adalah cara mentransformasikan persoalan dalam

bentukFuzzy Linear Programmingdengan bilangan fuzzy triangular ke bentukLinear

Programming dan kemudian akan dicari solusi yang optimal. Dalam kasus ini, akan

didefinisikan sebuah model crisp yang disetarakan dengan masalah Fuzzy Linear

Programming dan kemudian menggunakan solusi yang optimal dari model tersebut

sebagai solusi yang optimal dariFuzzy Linear Programming.

Berikut beberapa definisi penting yang digunakan dalam menyelesaikan

permasalahan: (S.H. Nasseri, 2008, hal 2476 – 2477)

Definisi 3.1: Pandang masalahLinear Programming berikut:

Maks : ~z = c x~

s.t :

  

≥ =

0 ~

~ ~

x b x A

(1)

di mana matriks koefisien A = [aij]m×n dan vektor c = (c1, , cn)

adalah matriks crisp non negatif dan vektor berturut – turut dan

) ~ ( ~

j

x

x = , b~ =(b~_i) adalah vektor fuzzy non negatif sehingga

) ( ~ ,

~ _{b F R}

x_{j i} ∈ untuk semua 1≤ j≤ n , 1≤i ≤m , disebut sebagai

masalahFuzzy Linear Programming.

Definisi 3.2: Sebuah vektor fuzzy ~ adalah solusi yang layak (x feasible) dari

b x

A~=~, ~x ≥0di mana A dan b~ seperti yang didefinisikan pada (1),

Adapun karena ~x∈Fn(R) dan b~∈Fm(R) , dapat diasumsikan

) , , (

~ _{x x}α _xβ

x = m _{dan b}~=_(bm_,bα_,bβ_{) di mana x}m_,xα_,xβ ∈_Rn _{dan b}m_,bα_,bβ ∈_Rm_.

Maka, sistem A~x=b~ dapat ditulis sebagai berikut: ) , , ( ) , ,

(x xα xβ b bα bβ

A m = m (2)

Di samping itu, b~ dan x~ adalah dua buah vektor fuzzy non negatif, maka

dengan menggunakan Definisi 2.6 dan aritmatika pada bilangan fuzzy triangular non

negatif, itu adalah setara dengan sistemcrisp berikut:

m m

b

Ax = , Axα =bα, Axβ =bβ , xm−xα ≥0 (3)

Sekarang ditetapkan operator ”max” atau maksimum untuk sebuah fungsi

linear fuzzy yang didefinisikan sebagai berikut:

n n n j j j

n c x cx c x x

x f

z (~, ~ ) ~ ~ ~ ~

1 1 1

1 = = ⊕ ⊕

=

∑

=

K

K _,

di mana c_j, j=1,K ,n _{merupakan bilanganreal dan x F R j n}

j ( ), 1, ,

~ _{∈ = K .}

Definisi 3.3: Anggap x~=(~x₁,K ,~x_n)T _dan T

m

b b

b~=(~₁,K ~ ) _{adalah dua buah vektor}

fuzzy non negatif, di mana ~x_j =(x_j,x_j,x_j)dan b~_j =(b_i,b_i,b_i)∈F(R).

Sebuah vektor fuzzy x~ memaksimumkan fungsi linear

) ~ , , ~ ( ~

1 xn

x f

z = K sehingga:

0 ~ ~ ~ ≥ = x b x A

, (4)

di mana x~_j =(x_j,x_j,x_j), j=1,K ,n _dan

j j j x x

x , , , j=1,K ,n _adalah

bilangan real non negatif jika dan hanya jika

n n n

n x x R

x x x x x x x x 3 2 2 2 1 1

1, , , , , , , , , )

( ∈

= K _{memaksimumkan fungsi}

real berikut:

∑

∑

< > − + + − + = 0 0 )) ( 2 1 ( )) ( 2 1 ( j j c j j j j j j c j

j x x x c x x x

c

Sehingga: 0 , , , 0 , , , = = − ≥ ≥

=b Ax b Ax b x x x x x

Ax (6)

Contoh:

Sebuah perusahaan membuat 2 produk, yaitu P1 dan P2. Laba per unit P1 adalah Rp

4.000,00 dan P2 adalah Rp 3000,00. Setiap unit P1 memerlukan waktu kerja 2 kali

lebih banyak dari pada P2. Total waktu kerja yang ada sekurang-kurangnya 500 jam

per hari dan dapat berubah karena bekerja lembur. Persediaan bahan baku mencapai

hampir 400 unit untuk kedua produk, P1 dan P2 per hari, tetapi berdasarkan

pengalaman masa lalu, bahan baku masih bisa ditambah lagi. Berapa unit P1 dan P2

yang dapat diproduksi per hari untuk memaksimumkan laba total ? (S.H. Nasseri,

2008, hal: 2477)

Solusi:

Misalkan ~x₁ dan ~x₂ menyatakan jumlah produk P1 dan P2 yang diproduksi per hari, maka persoalan di atas dapat dirumuskan seperti program linear berikut dengan

menggunakan variabel – variabel fuzzy triangular.

Maks: ~z =4.000~x₁⊕3.000~x₂

Kendala:      ≥ ≤ ⊕ ≤ ⊕ 0 ~ , ~ 500 ~ ~ 2 400 ~ ~ 2 1 2 1 2 1 x x x x x x (7)

Bahan baku yang tersedia adalah mendekati 400 unit dan lama waktu kerja adalah

mendekati 500 jam, maka dapat dimodelkan menjadi (400,5,5) dan (500,7,7) berturut

– turut. Saat ini, model fuzzy linear programming dapat ditulis dalam bentuk standar

seperti berikut ini:

Maks: ~z =4.000~x₁⊕3.000~x₂

di mana ~x₃ dan ~x₄ merupakan dua buah variabelslack.

Maka, persoalan Fuzzy Linear Programming tersebut ekivalen dengan:

Maks: ~z =4.000(x1,x1,x1)⊕3.000(x2,x2,x2)

Kendala:       ≥ = ⊕ ⊕ = ⊕ ⊕ 0 ) , , ( ), , , ( ), , , ( ), , , ( ) 7 , 7 , 500 ( ) , , ( ) , , ( ) , , ( 2 ) 5 , 5 , 400 ( ) , , ( ) , , ( ) , , ( 4 4 4 3 3 3 2 2 2 1 1 1 4 4 4 2 2 2 1 1 1 3 3 3 2 2 2 1 1 1 x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x

Karena bilangan – bilangan fuzzy tersebut simetris, maka cukup untuk menyelesaikan

persoalanfuzzy linear programming berikut:

Maks: z=4.000x₁⊕3.000x₂

Kendala:       ≥ = ⊕ ⊕ = ⊕ ⊕ 0 ) , , ( ), , , ( ), , , ( ), , , ( ) 7 , 7 , 500 ( ) , , ( ) , , ( ) , , ( 2 ) 5 , 5 , 400 ( ) , , ( ) , , ( ) , , ( 4 4 4 3 3 3 2 2 2 1 1 1 4 4 4 2 2 2 1 1 1 3 3 3 2 2 2 1 1 1 x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x

Sekarang kita dapat memperoleh solusi optimal untuk persoalan fuzzy (7) dengan

menyelesaikan program linear berikut:

Maks: z=4.000x₁+3.000x₂

Kendala:          = ≥ ≥ ≥ − = + + = + + = + + = + + 4 , 1 , 0 , 0 , 0 7 2 5 500 2 400 4 2 1 3 2 1 4 2 1 3 2 1 K i x x x x x x x x x x x x x x x x i i i i

Program linear tersebut dapat diselesaikan dengan menggunakan metode simplex

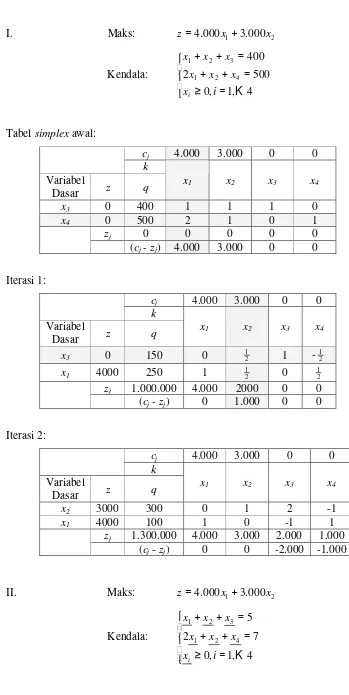
I. Maks: z=4.000x₁+3.000x₂ Kendala:      = ≥ = + + = + + 4 , 1 , 0 500 2 400 4 2 1 3 2 1 K i x x x x x x x i

Tabelsimplex awal:

Iterasi 1:

Iterasi 2:

II. Maks: z=4.000x₁+3.000x₂

Kendala:       = ≥ = + + = + + 4 , 1 , 0 7 2 5 4 2 1 3 2 1 K i x x x x x x x i

cj 4.000 3.000 0 0

k

Variabel

Dasar z q

x1 x2 x3 x4

x3 0 400 1 1 1 0

x4 0 500 2 1 0 1

zj 0 0 0 0 0

(cj-zj) 4.000 3.000 0 0

cj 4.000 3.000 0 0

k

Variabel

Dasar z q

x1 x2 x3 x4

x3 0 150 0 2

1 ₁

-2 1

x1 4000 250 1 2

1

0 2

1

zj 1.000.000 4.000 2000 0 0

(cj-zj) 0 1.000 0 0

cj 4.000 3.000 0 0

k

Variabel

Dasar z q

x1 x2 x3 x4

x2 3000 300 0 1 2 -1

x1 4000 100 1 0 -1 1

zj 1.300.000 4.000 3.000 2.000 1.000

[image:37.612.121.470.54.749.2]

Tabelsimplex awal:

Iterasi 1:

Iterasi 2:

Solusi yang optimal untuk persoalanLinear Programming di atas adalah:

0 , 0 , 3 , 2 , 0 , 0 , 300 ,

100 _{2 3 4 1 2 3 4}

1 = x = x = x = x = x = x = x =

x .

Sehingga diperoleh solusi fuzzy yang optimal untuk persoalan (7) adalah:

) 0 , 0 , 0 ( ~ ), 0 , 0 , 0 ( ~ ), 3 , 3 , 300 ( ~ ), 2 , 2 , 100 ( ~ 4 3 2

1 = = = =

∗ ∗ ∗ ∗ x x x x .

Sedangkan solusi fuzzy yang optimal untuk fungsi tujuan adalah:

000 . 0 ~ 30 . 1 ) 000 . 17 , 000 . 17 , 000 . 300 . 1 ( ~ 000 . 3 ~ 000 . 4 ~ 2

1 ⊕ = =

= ∗ ∗

∗ _{x x}

z

cj 4.000 3.000 0 0

k

Variabel

Dasar z q

1

x x₂ x₃ x₄

3

x 0 5 1 1 1 0

4

x 0 7 2 1 0 1

zj 0 0 0 0 0

(cj-zj) 4.000 3.000 0 0

cj 4.000 3.000 0 0

k

Variabel

Dasar z q

1

x x₂ x₃ x₄

3

x 0 1.5 0 2

1 ₁

-2 1

1

x 4000 3.5 1 ₂1 ₀

2 1

zj 14.000 4.000 2000 0 0

(cj-zj) 0 1.000 0 0

cj 4.000 3.000 0 0

k

Variabel

Dasar z q

1

x x₂ x₃ x₄

2

x 3000 3 0 1 2 -1

1

x 4000 2 1 0 -1 1

zj 17.000 4.000 3.000 2.000 1.000

[image:38.612.121.465.80.548.2]

KESIMPULAN DAN SARAN

4.1 Kesimpulan

Dalam tulisan ini, diusulkan sebuah metode penyelesaian permasalahan Fuzzy Linear

Programming dengan cara mentransformasikan bentuk Fuzzy Linear Programming

dengan bilangan fuzzy triangular ke bentuk Linear Programming terlebih dahulu.

Perlakuan terhadap fungsi tujuan yang ditransformasi adalah sama dengan perlakuan

terhadap kendala-kendala, yaitu dengan mendefinisikan sebuah sistem crisp yang

disetarakan dengan masalah Fuzzy Linear Programming dan kemudian dicari solusi

yang optimal. Solusi yang optimal dari sistem tersebut digunakan sebagai solusi yang

optimal dariFuzzy Linear Programming.

4.2 Saran

Saran dalam penelitian ini adalah untuk tidak membatasi persoalan hanya

dengan menggunakan bilangan fuzzy triangular. Penulis berharap ada penelitian lebih

lanjut tentang cara menyelesaikan permasalahan Fuzzy Linear Programming yang

Henrik, L.L. 15 Januari 2011.Fuzzy Number Arithmetic. http://aaue.dk/~legind

/FL_E2006/FL-14/FL14b%20fuzzy%20arithmetics.pdf.

Kusumadewi, Sri dan Hari Purnomo. 2004. Aplikasi Logika Fuzzy Untuk

Pendukung Keputusan. Yogyakarta : Graha Ilmu.

Nasseri, Hadi. 2008. ”Fuzzy Numbers: Positive and Nonnegative”.

International Mathematical Forum 3(36): hal. 1.777 – 1780.

Nasseri, S.H. 2008. “A New Method for Solving Fuzzy Linear Programming

by Solving Linear Programming”. Journal of Applied Mathematical Sciences 2(50):

hal. 2473 – 2480.

Zadeh, L.A. 1965. “Fuzzy Sets”.Information and Control 8: hal. 338 – 353

Zimmermann, H.J. 1975. “Description and Optimization of Fuzzy Systems”.