POISSON PERIODIK DENGAN TREN FUNGSI PANGKAT
DONI FERNANDO PUTRA
SEKOLAH PASCASARJANA
INSTITUT PERTANIAN BOGOR
Dengan ini saya menyatakan bahwa tesis Kekonsistenan Penduga dari Fungsi Sebaran dan Fungsi Kepekatan Waktu Tunggu dari Proses Poisson Periodik dengan Tren Fungsi Pangkat adalah karya saya sendiri dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apapun kepada perguruan tinggi manapun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam daftar pustaka dibagian akhir tesis ini.
Bogor, Januari 2012
Function and the Density of Waiting Time of a Periodic Poisson Process with Power Function Trend. Supervised by I WAYAN MANGKU and RETNO BUDIARTI.
This thesis is concerned with estimation of distribution and density functions of waiting time of a periodic Poisson process with power function trend. The intensity function is assumed to consist of two components, namely, a periodic component and a power function trend component. It is also assumed that the Poisson process is observed in interval . Let denotes the waiting time of -th event since the beginning of observation of the Poisson process discussed. Estimators of the distribution function and the density function of have been constructed and their consistency as the length of observation interval of the process goes to infinity have been proved. Finally some numerical results are also presented.
Fungsi Kepekatan Waktu Tunggu dari Proses Poisson Periodik dengan Tren Fungsi Pangkat. Dibimbing oleh I WAYAN MANGKU dan RETNO BUDIARTI.
Terdapat banyak hal dalam kehidupan sehari-hari yang dapat dijelaskan dengan suatu proses stokastik. Misalnya, proses kedatangan pelanggan pada suatu antrian di pusat servis, banyaknya orang yang menggunakan suatu line telepon, banyaknya orang yang memerlukan penanganan kesehatan pada rumah sakit dan banyaknya kendaraan yang melewati suatu ruas jalan raya akan berbeda untuk setiap waktu tertentu. Fenomena tersebut dapat dimodelkan dengan suatu proses stokastik, yaitu model yang menggunakan aturan-aturan peluang untuk menggambarkan perilaku suatu sistem yang tidak diketahui dengan pasti di periode waktu yang akan datang.
Proses stokastik dibedakan menjadi dua, yaitu proses stokastik dengan waktu diskret dan proses stokastik dengan waktu kontinu. Salah satu bentuk khusus dari proses stokastik dengan waktu kontinu adalah proses Poisson dengan fungsi intensitas berupa fungsi periodik. Proses tersebut antara lain dapat digunakan untuk memodelkan suatu proses kedatangan pasien yang memerlukan pelayanan kesehatan segera setelah terjadi suatu bencana, kecelakaan, dan lain sebagainya dengan periode satu hari, atau memodelkan fenomena-fenomena serupa. Jika laju kedatangan pasien tersebut meningkat berdasarkan suatu fungsi pangkat terhadap waktu maka model yang lebih tepat untuk digunakan adalah proses Poisson periodik dengan suatu komponen tren berbentuk fungsi pangkat.
Berdasarkan alasan sebelumnya, model fungsi intensitas untuk kasus ini dapat dirumuskan sebagai berikut
diasumsikan bahwa periode diketahui, tetapi koefisien dan fungsi pada titik
tidak diketahui, dengan adalah suatu fungsi periodik, dan
adalah komponen tren dengan . Kajian ini dibatasi hanya untuk kasus
.
dengan
dan
dimana adalah bilangan bulat terbesar yang lebih kecil atau sama dengan ,
yaitu , , adalah suatu kernel dan adalah barisan
bilangan nyata positif yang konvergen ke nol, yaitu untuk .
Dari hasil pengkajian yang dilakukan, disimpulkan bahwa :
a) Jika fungsi intensitas dan terintegralkan lokal, maka
untuk setiap bilangan nyata dan untuk setiap bilangan bulat positif
diperoleh
bulat positif , diperoleh
untuk asalkan merupakan titik Lebesgue dari .
c) Berdasarkan hasil simulasi diperoleh bahwa kualitas penduga dari fungsi
sebaran waktu tunggu pertama lebih baik dari waktu tunggu kedua untuk
ukuran yang sama, artinya diperlukan nilai yang lebih besar untuk waktu
tunggu kedua dibandingkan waktu tunggu pertama. Diperoleh pola penduga
yang lebih dekat ke pola sebarannya untuk pangkat 0,25 dibandingkan
© Hak Cipta milik IPB, tahun 2012
Hak Cipta dilindungi Undang-Undang
Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumbernya. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik, atau tinjauan suatu masalah; dan pengutipan tersebut tidak merugikan kepentingan yang wajar IPB.
POISSON PERIODIK DENGAN TREN FUNGSI PANGKAT
DONI FERNANDO PUTRA
Tesis
Sebagai salah satu syarat untuk memperoleh gelar Magister Sains pada
Program Studi Matematika Terapan
SEKOLAH PASCASARJANA
INSTITUT PERTANIAN BOGOR
Nama : Doni Fernando Putra
NRP : G551090441
Disetujui Komisi Pembimbing
Dr. Ir. I Wayan Mangku, M.Sc.
Ketua Anggota
Ir. Retno Budiarti, MS
Diketahui
Ketua Program Studi Dekan Sekolah Pascasarjana
Matematika Terapan
Dr. Ir. Endar H. Nugrahani, MS. Dr.Ir. Dahrul Syah, M.Sc.Agr
karunia-Nya sehingga penulis dapat menyelesaikan tesis yang berjudul “Kekonsistenan Penduga dari Fungsi Sebaran dan Fungsi Kepekatan Waktu Tunggu dari Proses Poisson Periodik dengan Tren Fungsi Pangkat”. Tesis ini disusun sebagai salah satu syarat untuk memperoleh gelar Magister Sains pada program studi Matematika Terapan.
Penulis mengucapkan terima kasih kepada :
1. Dr. Ir. I Wayan Mangku, M.Sc sebagai ketua komisi pembimbing dan Ir. Retno Budiarti, MS selaku anggota komisi pembimbing yang telah memberikan bimbingan dan arahan dalam penyusunan tesis ini serta Dr. Ir. Hadi Sumarno, MS selaku penguji yang telah banyak memberikan saran. 2. Ibunda tercinta, Surisdiyanti Sukandar atas doa, cinta dan dukungannya. 3. Saudara-saudara dan sahabat-sahabatku, atas doa dan dukungan semangatnya. 4. Semua pihak yang tidak dapat penulis sebutkan satu persatu, yang telah
membantu dalam penyusunan tesis ini.
Penulis menyadari bahwa masih banyak kekurangan dalam penyusunan tesis ini. Oleh karena itu kritik, saran, dan masukan sangat penulis harapkan demi penyempurnaan dan perbaikan tulisan ini. Semoga karya ilmiah ini bermanfaat untuk semua pembaca. Amin.
Bogor, Januari 2012
Ayah Ibnu Hajar dan ibu Surisdiyanti Sukandar. Penulis merupakan putra pertama dari 3 bersaudara.
Tahun 2005 Penulis lulus dari SMA Negeri 4 Curup dan pada tahun yang sama lulus seleksi masuk Universitas Sriwijaya, Palembang, melalui jalur Seleksi Penerimaan Mahasiswa Baru. Penulis diterima pada jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.
BAB I PENDAHULUAN ………..…. 1
1.1 Latar Belakang ………..……..……... 1
1.2 Tujuan Penelitian ………..………..………..…..…... 2
BAB II TINJAUAN PUSTAKA ………..….... 3 2.1 Proses Poisson Periodik …………...………...…….….. 3 2.2 Pendugaan Fungsi Intensitas Proses Poisson Periodik ….….…... 5 2.3 Penduga Konsisten dari Fungsi Sebaran dan Fungsi
Kepekatan Waktu Tunggu dari Proses Poisson
Periodik dengan Tren Linear ………...…... 7
BAB III REVIEW PENDUGAAN FUNGSI INTENSITAS LOKAL DAN GLOBAL DARI PROSES POISSON PERIODIK
DENGAN TREN FUNGSI PANGKAT ………....………...….. 9 3.1 Pendugaan Fungsi Intensitas Lokal dari Proses Poisson
dengan Tren Fungsi Pangkat ……….…... 9 3.1.1 Pendugaan ………..…....10
3.1.2 Pendugaan ….………... 14
3.2 Pendugaan Fungsi Intensitas Global dari Proses Poisson
dengan Tren Fungsi Pangkat ……… 19
BAB IV KEKONSISTENAN PENDUGA DARI FUNGSI SEBARAN DAN FUNGSI KEPEKATAN WAKTU TUNGGU DARI PROSES POISSON PERIODIK DENGAN TREN FUNGSI
PANGKAT ………... 29
4.1 Perumusan Penduga ………. 29
4.2 Beberapa Lema Teknis ………..………... 32
4.3 Kekonsistenan Penduga dari Fungsi Sebaran Waktu Tunggu dari Proses Poisson Periodik dengan Tren Fungsi Pangkat ……. 49 4.4 Kekonsistenan Penduga dari Fungsi Kepekatan Waktu
Tunggu dari Proses Poisson Periodik dengan Tren Fungsi
Pangkat ………... 54
4.5 Hasil Simulasi .………... 56
BAB V KESIMPULAN ………..……... 61
DAFTAR PUSTAKA ………..…....… 63
1. Ruang Contoh, Kejadian dan Peluang ………….………. 67
2. Peubah Acak dan Fungsi Sebaran ……….... 68
3. Kekonvergenan ………..69
4. Nilai Harapan, Ragam dan Momen ………...70
5. Beberapa Definisi dan Lema Teknis ……….72
6. Program Penentuan Fungsi Sebaran dan Penduganya
Untuk Waktu Tunggu Kejadian Pertama dengan Pangkat 0.25 ………74
7. Program Penentuan Fungsi Sebaran dan Penduganya
Untuk Waktu Tunggu Kejadian Kedua dengan Pangkat 0.25 …...…………75
8. Program Penentuan Fungsi Sebaran dan Penduganya
Untuk Waktu Tunggu Kejadian Pertama dengan Pangkat 0.75 ………77
9. Program Penentuan Fungsi Sebaran dan Penduganya
BAB 1
PENDAHULUAN
1.1Latar Belakang
Terdapat banyak hal dalam kehidupan sehari-hari yang dapat dijelaskan
dengan suatu proses stokastik. Misalnya, proses kedatangan pelanggan pada suatu
antrian di pusat servis, banyaknya orang yang menggunakan suatu line telepon,
banyaknya orang yang memerlukan penanganan kesehatan pada rumah sakit dan
banyaknya kendaraan yang melewati suatu ruas jalan raya akan berbeda untuk
setiap waktu tertentu. Fenomena tersebut dapat dimodelkan dengan suatu proses
stokastik, yaitu model yang menggunakan aturan-aturan peluang untuk
menggambarkan perilaku suatu sistem yang tidak diketahui dengan pasti di
periode waktu yang akan datang.
Proses stokastik dibedakan menjadi dua, yaitu proses stokastik dengan
waktu diskret dan proses stokastik dengan waktu kontinu. Salah satu bentuk
khusus dari proses stokastik dengan waktu kontinu adalah proses Poisson dengan
fungsi intensitas berupa fungsi periodik. Proses tersebut antara lain dapat
digunakan untuk memodelkan suatu proses kedatangan pasien yang memerlukan
pelayanan kesehatan segera setelah terjadi suatu bencana, kecelakaan, dan lain
sebagainya dengan periode satu hari, atau memodelkan fenomena-fenomena
serupa. Jika laju kedatangan pasien tersebut meningkat berdasarkan suatu fungsi
pangkat terhadap waktu maka model yang lebih tepat untuk digunakan adalah
proses Poisson periodik dengan suatu komponen tren berbentuk fungsi pangkat.
Berdasarkan alasan sebelumnya, model fungsi intensitas untuk kasus ini
dapat dirumuskan sebagai berikut
diasumsikan bahwa periode diketahui, tetapi koefisien dan fungsi pada titik
tidak diketahui, dengan adalah suatu fungsi periodik, dan
adalah komponen tren dengan . Kajian ini dibatasi hanya untuk kasus
Pendugaan terhadap fungsi sebaran dan fungsi kepekatan dari waktu tunggu
bermanfaat dalam peramalan perilaku sistem atau fenomena. Pasien yang datang
pada suatu rumah sakit harus mendapatkan pelayanan sesegera mungkin, hal ini
mengindikasikan seberapa jauh kesiagaan tim medis dalam mengambil tindakan
dan merekapun perlu mempertimbangkan kapan waktu berikutnya peristiwa
serupa terulang kembali. Berdasarkan contoh fenomena tersebut, pada tulisan ini
dikaji penduga-penduga konsisten dari fungsi sebaran waktu tunggu dan fungsi
kepekatan waktu tunggu dari proses Poisson periodik dengan tren fungsi pangkat.
1.2Tujuan Penelitian
Tujuan penulisan karya ilmiah ini adalah untuk :
1. Merumuskan penduga dari fungsi sebaran waktu tunggu proses Poisson
periodik dengan komponen tren berbentuk fungsi pangkat dan membuktikan
kekonsistenannya.
2. Merumuskan penduga dari fungsi kepekatan waktu tunggu proses Poisson
periodik dengan komponen tren berbentuk fungsi pangkat dan membuktikan
kekonsistenannya.
3. Melakukan simulasi komputer untuk mempelajari perilaku penduga fungsi
sebaran bagi waktu tunggu kejadian pertama dan kejadian kedua untuk
ukuran sampel terbatas, serta mempelajari pola dugaan fungsi sebaran waktu
BAB 2
TINJAUAN PUSTAKA
2.1 Proses Poisson Periodik Definisi 2.1 (Proses stokastik)
Proses stokastik adalah suatu himpunan dari peubah acak yang
memetakan suatu ruang contoh ke suatu ruang state .
(Ross, 1996)
Jika merupakan himpunan tercacah, maka suatu proses stokastik
disebut proses stokastik dengan waktu diskret, sedangkan disebut proses
stokastik dengan waktu kontinu jika merupakan suatu interval.
Definisi 2.2 (Inkremen bebas)
Suatu proses stokastik dengan waktu kontinu disebut memiliki
inkremen bebas jika untuk semua , peubah acak
adalah bebas.
(Ross, 1996)
Diartikan pula, suatu proses stokastik dengan waktu kontinu disebut
memiliki inkremen bebas jika proses berubahnya nilai pada interval waktu yang
tidak tumpang tindih (overlaping) adalah bebas.
Definisi 2.3 (Inkremen stasioner)
Suatu proses stokastik dengan waktu kontinu disebut memiliki
inkremen stasioner jika memiliki sebaran yang sama untuk
semua nilai .
(Ross, 1996)
Definisi 2.4 (Proses pencacahan)
Suatu proses stokastik disebut proses pencacahan jika
Suatu proses pencacahan harus memenuhi syarat-syarat berikut :
(i) untuk semua
(ii) Nilai adalah integer.
(iii) Jika maka
(iv) Untuk maka sama dengan banyaknya kejadian yang
terjadi pada interval .
(Ross, 1996)
Definisi 2.5 (Proses Poisson)
Suatu proses pencacahan disebut proses Poisson dengan laju ,
, jika dipenuhi tiga syarat berikut :
(i)
(ii) Proses tersebut memiliki inkremen bebas.
(iii) Banyaknya kejadian pada sebarang interval waktu dengan panjang ,
memiliki sebaran Poisson dengan nilai harapan .
Jadi untuk semua
(Ross, 1996)
Definisi 2.6 (Fungsi periodik) Suatu fungsi disebut periodik jika :
untuk semua dan Konstanta terkecil yang memenuhi persamaan di
atas disebut periode dari fungsi tersebut.
(Browder, 1996)
Definisi 2.7 (Proses Poisson periodik)
Proses Poisson periodik adalah suatu proses Poisson tak homogen yang fungsi
intensitasnya adalah fungsi periodik.
2.2 Pendugaan Fungsi Intenitas Proses Poisson Periodik
Fungsi intensitas suatu proses Poisson periodik merupakan laju dari proses
Poisson tersebut. Fungsi intensitas terbagi atas dua, yaitu fungsi intensitas lokal
dan fungsi intensitas global. Fungsi intensitas lokal merupakan laju dari proses
Poisson dititik tertentu, sedangkan fungsi intensitas global merupakan rata-rata
laju dari proses Poisson pada interval dengan panjang menuju tak hingga.
Pendekatan yang digunakan pada pendugaan fungsi intensitas lokal dari
suatu proses Poisson di titik adalah dengan menaksir nilai rata-rata dari
banyaknya kejadian di sekitar titik . Secara matematis, misalkan
dan menyatakan banyaknya kejadian yang terjadi pada maka
fungsi intensitas lokal di titik dapat didekati dengan .
Sedangkan pendekatan yang digunakan pada pendugaan fungsi intensitas global
dari suatu proses Poisson adalah dengan menaksir nilai rata-rata dari banyaknya
kejadian dalam interval . Secara matematis, penduga bagi fungsi intensitas
global pada dapat dinyatakan dengan .
Pada proses Poisson periodik, terdapat beberapa metode nonparametrik
untuk menduga fungsi intensitas pada suatu titik yang diberikan, diantaranya
adalah metode penduga tipe kernel dan metode penduga titik terdekat (nearest
neighbor estimation). Dua metode tersebut telah digunakan untuk menduga secara
konsisten fungsi intensitas lokal dengan periode (diketahui) (Helmers dan
Mangku 2000). Selain itu, pendugaan fungsi intensitas lokal menggunakan
metode titik terdekat serta pembuktian kekonsistenan lemah dan kuat dari
penduga yang telah dikaji pada Mangku (1999). Ada metode lain, yaitu dengan
meniru bentuk umum metode maximum likelihood untuk menduga laju proses
Poisson homogen yang dapat diterapkan untuk menduga laju proses Poisson
homogen yang dapat diterapkan untuk menduga fungsi intensitas global pada
Poisson periodik (Helmers dan Mangku 2000).
Fungsi intensitas proses Poisson telah digunakan pada pemodelan laju
dirumuskan suatu algoritma untuk menduga fungsi intensitas suatu proses Poisson
dengan tren eksponensial kuadratik dan periodik (Helmers dan Zitikis 1999).
Pendugaan fungsi intensitas ini dapat dibedakan berdasarkan periodenya,
yaitu jika periodenya tidak diketahui dan jika periodenya diketahui. Untuk periode
yang tidak diketahui, pendugaan fungsi intensitas lebih rumit dibandingkan proses
dengan periodenya diketahui. Meskipun demikian kekonsistenan penduga tipe
kernel dari fungsi intensitas suatu proses Poisson periodik untuk kasus periode
tidak diketahui telah dikaji pada Helmers et al. (2003). Untuk periode yang
diketahui telah dilakukan kajian perumusan penduga tipe kernel serta pembuktian
dari kekonvergenan lemah dan kuat dari penduga yang diperoleh (Mangku 2006a)
dan pembuktian kenormalan asimtotik dari penduga yang diperoleh (Mangku
2006b).
Pemodelan suatu fenomena dengan proses Poisson periodik berkembang
dengan menyertakan suatu komponen tren linear (Helmers dan Mangku 2009),
maupun menggunakan periode ganda dalam fungsi intensitasnya (Helmers et al.
2007). Adapun pendugaan untuk fungsi intensitas globalnya telah dilakukan pada
Mangku (2005).
Selain itu, pendugaan fungsi intensitas suatu proses Poisson periodik yang
menyertakan suatu komponen tren berbentuk fungsi pangkat telah dilakukan
kajiannya. Tentang kekonsistenan dari penduga yang diperoleh dengan
menggunakan fungsi kernel seragam telah dikaji pada Rahayu (2008), sifat-sifat
statistik penduga yang diperoleh dengan menggunakan fungsi kernel seragam
telah dikaji pada Rachmawati (2008), pendugaan fungsi intensitas global dari
komponen periodiknya telah dikaji pada Yuliawati (2008), serta sifat-sifat statistik
penduga yang diperoleh dengan menggunakan fungsi kernel umum telah dikaji
pada Farida (2008), dan pendugaan fungsi intensitas dengan dua kasus, yaitu tren
fungsi pangkat dengan kemiringan dari tren yang diketahui dan tidak diketahui,
selain itu telah dikaji kekonvergenan sebaran asimtotik bagi fungsi periodik untuk
2.3 Penduga Konsisten dari Fungsi Sebaran dan Fungsi Kepekatan Waktu Tunggu dari Proses Poisson Periodik dengan Tren Linear.
Diasumsikan fungsi intensitas dari suatu proses Poisson nonhomogen yang
diamati pada interval terbatas adalah terintegralkan lokal. Dirumuskan fungsi
sebaran dan fungsi kepekatan waktu tunggu, serta penduga dari fungsi-fungsi
tersebut. Untuk suatu bilangan bulat positif diperoleh bahwa penduga fungsi
sebaran waktu tunggu konvergen dalam peluang terhadap fungsi sebaran waktu
tunggunya, dan diperoleh juga bahwa penduga fungsi kepekatan waktu tunggu
konvergen dalam peluang terhadap fungsi kepekatan waktu tunggunya, asalkan
interval yang diamati merupakan titik Lebesgue dari fungsi intensitas, seperti yang
BAB 3
REVIEW
PENDUGAAN FUNGSI INTENSITAS LOKAL DAN
GLOBAL DARI PROSES POISSON PERIODIK
DENGAN TREN FUNGSI PANGKAT
Misalkan adalah proses Poisson nonhomogen pada interval
dengan fungsi intensitas yang tidak diketahui. Fungsi diasumsikan
terintegralkan lokal dan terdiri dari dua komponen, yaitu suatu komponen periodik
(siklik) dengan periode (diketahui) dan suatu komponen tren yang berupa
fungsi pangkat. Dengan kata lain untuk sebarang titik , fungsi intensitas
dapat dituliskan sebagai berikut :
dengan adalah fungsi periodik dengan periode , menyatakan kemiringan
tren dimana dan (diketahui) merupakan bilangan nyata sebarang dimana
. Kita tidak mengasumsikan suatu bentuk parametrik dari kecuali
bahwa adalah fungsi periodik, sehingga untuk semua titik dan seluruh
, dengan adalah himpunan bilangan bulat, dapat dituliskan sebagai berikut
3.1 Pendugaan Fungsi Intensitas Lokal dari Proses Poisson dengan Tren Fungsi Pangkat
Berdasarkan Rachmawati (2010), misalkan untuk suatu , hanya
terdapat sebuah realisasi dari proses Poisson yang terdefinisi pada suatu
ruang peluang dengan fungsi intensitas seperti pada yang diamati
pada interval terbatas . Karena adalah fungsi periodik dengan
periode , maka masalah menduga pada titik dengan dapat
Diasumsikan fungsi intensitas global bagi merupakan nilai rata-rata dari
pada yaitu .
Misalkan adalah barisan bilangan nyata positif yang konvergen ke nol,
yaitu
untuk dan misalkan pula adalah suatu fungsi bernilai real,
disebut kernel, jika memenuhi sifat-sifat berikut :
(K.1) merupakan fungsi kepekatan peluang.
(K.2) terbatas.
(K.3) memiliki daerah definisi pada .
3.1.1 Pendugaan
Berdasarkan modifikasi penduga pada Rachmawati (2010), diperoleh
penduga untuk seperti berikut :
untuk .
Untuk mendapatkan penduga , cukup diperlihatkan bahwa
Karena memenuhi , maka ruas kanan persamaan di atas dapat ditulis
Perhatikan suku pertama , dengan menggunakan asumsi adalah fungsi
adalah . Langkah berikutnya, mengga nti
dengan padanan stokastiknya yaitu maka diperoleh
Jika kedua ruas dikalikan dengan diperoleh
sehingga
Perhatikan bahwa konvergen ke 0 jika dan , sehingga
. Persamaan di atas dapat dituliskan sebagai
maka diperoleh penduga dari , yaitu seperti pada .
Lema 3.1
Misalkan fungsi intensitas seperti dan terintegralkan lokal, maka
untuk , dengan Dengan kata lain, merupakan
penduga yang konsisten bagi , dengan Mean Square Error-nya adalah
untuk .
Bukti :
untuk . Ruas kanan adalah
Karena fungsi intensitas seperti , maka
untuk
Perhatikan bahwa konvergen ke 0 jika dan .
Sehingga . Persamaan diatas dapat dituliskan sebagai
untuk
Dengan mensubstitusikan ke , diperoleh seperti pada .
Ragam dari diperoleh dengan cara serupa, yaitu :
Karena adalah proses Poisson, maka sehingga persamaan di
Karena fungsi intensitas seperti , maka
untuk
Perhatikan bahwa konvergen ke 0 jika , dan . Sehingga
untuk
Dengan mensubstitusikan pada , maka diperoleh seperti
pada .
Didefinisikan berikut :
dimana .
Berikutnya, substitusikan dan pada , maka diperoleh
untuk
Langkah selanjutnya, dengan menjumlahkan dan menyederhanakan hasil
pada maka diperoleh seperti pada .
Telah dibuktikan dan , sehingga Lema 3.1 terbukti.
Teorema 3.1 (Kekonsistenan )
untuk .
Bukti :
Untuk membuktikan , berdasarkan definisi akan ditunjukkan bahwa
untuk . Berdasarkan ketaksamaan segitiga, diperoleh
Berdasarkan Lema 3.1 diperoleh , berarti , ada sehingga
Sehingga . Jadi untuk membuktikan
bahwa , digunakan ketaksamaan Chebychev, sehingga
diperoleh
Berdasarkan Lema 3.1, diperoleh untuk sehingga diperoleh
. Berdasarkan langkah-langka h di atas, Teorema 3.1 terbukti.
3.1.2 Pendugaan
Berdasarkan Farida (2008) dan Rachmawati (2010), diperoleh modifikasi
penduga dari pada titik sebagai berikut :
dengan , , adalah suatu kernel dan adalah barisan
bilangan nyata positif yang konvergen menuju nol, yaitu untuk ,
serta adalah penduga bagi seperti .
Lema 3.2
Jika fungsi intensitas seperti dan terintegralkan lokal, serta kernel
untuk , asalkan adalah titik Lebesgue dari . Jika kernel memenuhi
kondisi (K.1), (K.2), (K.3), dan , untuk , maka
untuk .
Bukti :
Berdasarkan , dapat dihitung sebagai berikut :
Dari dapat dimisalkan
maka dapat dinyatakan sebagai
Suku pertama pada ruas kanan diperoleh sebagai berikut
untuk
(Lihat Farida 2008 & Rachmawati 2010).
Dengan menggunakan pada persamaan di atas, maka diperoleh
untuk . Dengan mensubstitusikan dan pada , maka
diperoleh persamaan seperti .
Ragam dari diperoleh dengan menggunakan sehingga
Dengan memisalkan seperti maka persamaan di atas dapat ditulis
untuk (Lihat Farida 2008 & Rachmawati 2010). Nilai suku kedua dari ruas
kanan dapat ditentukan sebagai berikut
Dengan menggunakan pada persamaan di atas, maka diperoleh
untuk . Dari dan , dengan menggunakan ketaksamaan
untuk . Karena dan untuk maka untuk
sehingga persamaan di atas dapat dituliskan menjadi
untuk . Kemudian, dengan mensubstitusikan hasil dan
pada maka diperoleh seperti pada .
Teorema 3.2 (Kekonsistenan )
Jika fungsi intensitas seperti dan terintegralkan lokal, serta kernel
memenuhi kondisi (K.1), (K.2), (K.3), dan maka
untuk , asalkan adalah titik Lebesgue dari .
Bukti :
Untuk setiap berlaku
jika .
Menggunakan ketaksamaan segitiga, ruas kiri persamaan di atas dapat ditulis
sebagai berikut :
Berdasarkan , diperoleh
kemudian untuk setiap , ada sehingga
dengan menggunakan ketaksamaan Chebychev pada persamaan di atas, diperoleh
Menggunakan hasil pada , maka dapat dituliskan sebagai berikut
untuk . Melihat hubungan antara persamaan di atas dan , maka
terbukti bahwa jika .
Berdasarkan langkah-langka h di atas, Teorema 3.2 terbukti.
3.2 Pendugaan Fungsi Intensitas Global dari Proses Poisson dengan Tren Fungsi Pangkat
Fungsi intensitas global merupakan rata-rata laju dari proses Poisson pada
interval dengan panjang menuju tak hingga. Pendekatan yang digunakan pada
pendugaan fungsi intensitas global dari suatu proses Poisson adalah dengan
menaksir nilai rata-rata dari banyaknya kejadian dalam interval . Secara
matematis, penduga bagi fungsi intensitas global pada dapat dinyatakan
dengan .
Memodifikasi hasil pada Yuliawati (2008), kita asumsikan bahwa periode
diketahui, tetapi fungsi pada tidak ketahui, didefinisikan penduga untuk
sebagai berikut
dengan adalah bilangan bulat terbesar yang lebih kecil atau sama dengan ,
yaitu dan seperti .
Teorema 3.3 (Kekonsistenan )
Jika fungsi intensitas memenuhi dan terintegralkan lokal, maka
Bukti : Teorema 3.3 akan dibuktikan setelah bukti Teorema 3.4 dan Teorema 3.5.
Teorema 3.4 (Pendekatan Asimtotik untuk Bias dari )
Jika fungsi intensitas memenuhi dan terintegralkan lokal, maka
untuk .
Bukti :
Pertama, akan dibuktikan sebagai nilai harapan dari yaitu
Perhatikan, suku pertama pada ruas kanan , yaitu
dengan perubahan batas integral, maka persamaan diatas menjadi
Jika fungsi intensitas memenuhi dan terintegralkan lokal, maka persamaan
Berdasarkan , suku pertama ruas kanan menjadi
Diketahui bahwa
jika (Lihat Titchmarsh 1960).
Langkah selanjutnya, dengan mensubstitusikan pada , maka
diperoleh
jika
Perhatikan salah satu komponen berikut,
jika
Dengan mensubstitusikan pada , diperoleh
Selanjutnya, dengan menggabungkan dan , maka diperoleh
ruas kanan pada seperti berikut :
jika
Berikutnya, perhatikan suku kedua ruas kanan yaitu
Dengan menggunakan maka kuantitas di atas menjadi
untuk .
Selanjutnya, dengan mensubstitusikan hasil yang diperoleh dari
dan ke , maka diperoleh seperti pada .
Bedasarkan langkah-langkah di atas, Teorema 3.4 terbukti.
Teorema 3.5 (Pendekatan Asimtotik untuk Ragam dari )
Jika fungsi intensitas memenuhi dan terintegralkan lokal, maka
untuk
untuk
jika
Bukti :
Akan dibuktikan dan . Catatan, untuk setiap dimana
j,k = 1,2,…, maka dan tidak saling
tumpang tindih (tidak overlap). Sehingga dan
adalah bebas, untuk .
Telah didefinisikan penduga bagi yaitu pada sehingga
dapat dihitung sebagai
dengan memisalkan
Perhatikan suku pertama ruas kanan dari Berdasarkan kuantitas
yang diperlukan, dapat dibedakan dalam tiga kasus, yaitu
dan .
Untuk kasus diperoleh
jika .
Untuk kasus diperoleh
Untuk kasus diperoleh
jika .
(Lihat Yuliawati, 2008).
Berikutnya untuk suku kedua ruas kanan sehingga dapat
diperoleh sebagai berikut
Langkah berikutnya, dengan mensubstitusikan pada persamaan di
atas, diperoleh persamaan berikut
untuk .
Selanjutnya, dengan menggunakan ketaksamaan Chaucy Schwarz pada
suku ketiga ruas kanan diperoleh sebagai berikut
Berdasarkan kuantitas yang diperlukan, ekspresi di atas dapat dibedakan dalam
tiga kasus, yaitu dan .
untuk
Berdasarkan hasil yang tunjukkan pada langkah-langkah sebelumnya, diperoleh
, untuk .
Dengan cara yang sama dilakukan untuk kedua kasus berikutnya, yaitu
untuk kasus dan kasus . Diperoleh dan
, untuk , akibatnya dan ,
sehingga , untuk .
Dengan menggabungkan hasil yang diperoleh dari langkah-langkah di atas
ke sehingga diperoleh yang dibedakan menjadi tiga kasus
berikut, yaitu
Untuk kasus
untuk . Dengan kata lain diperoleh seperti pada .
untuk . Dengan kata lain diperoleh seperti pada .
Untuk kasus
untuk . Dengan kata lain diperoleh seperti pada .
Berdasarkan langkah-langka h di atas, Teorema 3.5 terbukti.
Bukti Teorema 3.3 :
Berdasarkan diperoleh
atau dapat ditulis sebagai
jika
Sedangkan dari dan diperoleh
atau dapat ditulis juga sebagai
jika
Selanjutnya, akan dibuktikan bahwa adalah penduga konsisten bagi ,
yaitu bahwa untuk setiap berlaku
jika .
Dengan menggunakan ketaksamaan segitiga, maka menjadi
Berdasarkan , ada sehingga
untuk setiap .
Dengan mensubstitusikan ke , diperoleh
Kemudian dengan melihat hubungan antara dan diperoleh
Berdasarkan hasil yang diperoleh dari pertaksamaan di atas, dengan
menggunakan pertaksamaan Chebyshev, diperoleh
Perhatikan, dengan menggunakan pada dapat ditunjukkan
hubungan bahwa jika .
BAB 4
KEKONSISTENAN PENDUGA DARI FUNGSI SEBARAN DAN
FUNGSI KEPEKATAN WAKTU TUNGGU DARI PROSES
POISSON PERIODIK DENGAN TREN FUNGSI PANGKAT
4.1 Perumusan Penduga
Misalkan adalah proses Poisson nonhomogen pada interval dengan
fungsi intensitas yang tidak diketahui. Fungsi diasumsikan terintegralkan lokal
dan terdiri dari dua komponen, yaitu suatu komponen periodik (siklik) dengan
periode (diketahui) dan suatu komponen tren yang berupa fungsi pangkat.
Dengan kata lain untuk sebarang titik , fungsi intensitas dapat
dituliskan sebagai berikut :
dengan adalah fungsi periodik dengan periode , menyatakan kemiringan
tren dimana dan (diketahui) merupakan bilangan nyata sebarang dimana
. Kita tidak mengasumsikan suatu bentuk parametrik dari kecuali
bahwa adalah fungsi periodik, sehingga untuk semua titik dan seluruh
, dengan adalah himpunan bilangan bulat, dapat dituliskan sebagai berikut
Misalkan untuk suatu , kita hanya memiliki sebuah realisasi
dari proses Poisson yang terdefinisi pada suatu ruang peluang dengan
fungsi intensitas seperti pada yang diamati pada interval terbatas
. Untuk setiap bilangan nyata dan untuk suatu bilangan bulat
positif , diperoleh fungsi sebaran dari waktu tunggu
dimana Karena memenuhi maka
diperoleh
Misalkan dimana untuk setiap bilangan nyata , maka
menunjukkan bilangan bulat terbesar yang kurang dari atau sama dengan . Maka
untuk setiap didapatkan dengan . Dimisalkan
merupakan intensitas global dari . Maka untuk setiap
dapat ditulis sebagai berikut
Untuk setiap bilangan nyata dan untuk setiap bilangan bulat positif ,
Berdasarkan dan , diperoleh penduga fungsi sebaran dan fungsi
kepekatan waktu tunggu secara berturut-turut dengan menggunakan data amatan
, yaitu suatu proses Poisson yang diamati pada diberikan
sebagai berikut
dengan
dengan penduga seperti pada sebagai berikut :
dengan adalah bilangan bulat terbesar yang lebih kecil atau sama dengan ,
yaitu , penduga seperti pada sebagai berikut :
dimana adalah barisan bilangan nyata positif yang konvergen menuju nol,
yaitu untuk . Berikutnya, diformulasikan penduga sebagai
berikut :
dengan .
4.2 Beberapa Lema Teknis
Berikut ini disajikan beberapa lema teknis. Prinsip-prinsip yang diperoleh
melalui keempat lema berikut ini digunakan sebagai salah satu alat untuk
membuktikan kekonsistenan penduga dari fungsi sebaran dan fungsi kepekatan
waktu tunggu.
Lema 4.1
Misalkan dan adalah barisan-barisan peubah acak, serta dan
adalah konstanta bilangan nyata. Jika dan untuk , maka
untuk
Bukti :
Misalkan dan untuk , dengan menggunakan Definisi L.12
dan misalkan diberikan, maka
sehingga
Dengan kata lain, terbukti bahwa untuk
Lema 4.2
Misalkan dan adalah barisan-barisan peubah acak, serta dan
adalah konstanta bilangan nyata. Jika dan untuk , maka
untuk
Bukti :
Misalkan dan untuk , dengan menggunakan Definisi L.12
dan misalkan diberikan, maka
Berdasarkan Definisi L.12, diperoleh
sehingga
Lema 4.3
Misalkan dan adalah barisan-barisan peubah acak, serta dan
adalah konstanta bilangan nyata. Jika dan untuk , maka
, untuk .
Bukti :
Diasumsikan bahwa dan untuk , dengan menggunakan
Definisi L.12 dan misalkan diberikan, maka
Perhatikan ruas kanan dari .
Berdasarkan diperoleh , sehingga
artinya
Berikutnya, berdasarkan diperoleh , sehingga
artinya
Berikutnya, dengan mensubstitusikan hasil yang diperoleh dari ke
Kemudian, untuk , diperoleh sebagai berikut :
Berdasarkan hasil yang diperoleh pada , diperoleh sebagai berikut
artinya terbukti bahwa , untuk .
Lema 4.4
Misalkan adalah barisan-barisan peubah acak, dan adalah konstanta
bilangan nyata. Jika dan adalah fungsi kontinu, maka ,
untuk .
Bukti :
Diasumsikan , artinya untuk
Akan dibuktikan bahwa , untuk . Artinya,
Perhatikan, karena adalah fungsi kontinu, diberikan , ada , sehingga
,
sehingga
Berdasarkan , diperoleh sebagai berikut :
Corollary 4.1
Jika fungsi intensitas memenuhi dan terintegralkan lokal, maka untuk
setiap bilangan nyata , diperoleh
untuk .
Bukti :
Perhatikan bahwa, dapat pula dinyatakan seperti berikut
Dengan kata lain, akan dibuktikan bahwa merupakan penduga konsisten
dari .
Berdasarkan dan , diperoleh hubungan berikut :
untuk .
Berikutnya, untuk membuktikan , dapat ditunjukkan dengan
membuktikan Lema 4.5, serta menggunakan prinsip Lema 4.1, Teorema 3.1 dan
Teorema 3.3 sebagai berikut :
Lema 4.5
Jika fungsi intensitas memenuhi dan terintegralkan lokal, maka untuk
setiap bilangan nyata , diperoleh
untuk .
Bukti :
Melalui Lema 4.5, akan dibuktikan bahwa merupakan penduga
konsisten dari , untuk .
Langkah pertama, dengan menggunakan , diperoleh nilai harapannya
Untuk persamaan pertama dari ruas kanan kita dapat mengganti batas
integral sebagai berikut
Karena fungsi intensitas memenuhi dan terintegralkan lokal, sehingga
persamaan di atas dapat dituliskan sebagai berikut
Perhatikan komponen pertama dengan menggunakan diperoleh
untuk .
Langkah berikutnya, dengan mensubstitusikan persamaan di atas dan
pada diperoleh
untuk .
Perhatikan kembali persamaan kedua dari ruas kanan , kemudian
dengan menggunakan diperoleh sebagai berikut
untuk .
Selanjutnya, dengan mensubstitusikan dan pada
maka diperoleh
untuk
Langkah berikutnya, dengan memisalkan diperoleh
dengan
Perhatikan,
Karena merupakan proses Poisson, maka sehingga persamaan
di atas ditulis menjadi
Karena fungsi intensitas memenuhi dan terintegralkan lokal, jadi
Berdasarkan , diperoleh komponen pertama sebagai berikut
Berdasarkan kuantitas yang diperlukan, sehingga dapat dibedakan
dalam tiga kasus berikut :
Untuk kasus
jika .
jika .
Untuk
jika .
Berikutnya, untuk komponen kedua diperoleh
Perhatikan salah satu komponen ruas kanan pada , dengan menggunakan
ekspansi Taylor, diperoleh bahwa
Karena untuk , maka perilaku sama dengan . Persamaan di atas
Selanjutnya, dengan mensubstitusikan ke , diperoleh
hubungan berikut
Berdasarkan kuantitas yang diperlukan, maka dapat dibedakan
dalam tiga kasus berikut :
Untuk kasus
jika .
jika .
Untuk kasus
jika .
Berdasarkan hasil yang didapatkan dari langkah-langkah sebelumnya,
diperoleh ruas kanan sebagai berikut :
Untuk kasus
jika .
Untuk kasus
Untuk kasus
jika .
Kemudian, kita lanjutkan untuk memperoleh nilai ragam dari sebagai
berikut,
Berdasarkan persamaan di atas dapat dituliskan menjadi
jika .
Selanjutnya, dengan menggunakan ketaksamaan Chaucy Schwarz, maka
diperoleh sebagai berikut
berdasarkan kuantitas yang diperlukan, maka dibedakan dalam tiga kasus, yaitu :
Pertama, kasus Untuk , karena dan
berakibat dan , sehingga
Kedua, kasus Untuk , karena dan
berakibat dan , sehingga
.
Ketiga, kasus Untuk , karena dan
berakibat dan , sehingga
.
Berdasarkan dan , diperoleh
jika .
Selanjutnya, dengan menggabungkan hasil yang diperoleh dari
dan ke diperoleh
yang dibedakan menjadi tiga kasus berikut, yaitu :
Untuk kasus
jika .
jika .
Untuk kasus
jika .
Langkah berikutnya, untuk membuktikan Lema 4.5, dengan menggunakan
diperoleh
Berdasarkan dan diperoleh
Selanjutnya, akan dibuktikan bahwa adalah penduga konsisten
bagi , yaitu bahwa untuk setiap berlaku
jika .
Ruas kiri persamaan di atas dapat ditulis sebagai berikut
Berdasarkan ketaksamaan segitiga, maka menjadi
Selanjutnya, berdasarkan , maka ada sehingga
untuk setiap .
Berikutnya, dengan melihat hubungan antara dan diperoleh
Berdasarkan pertaksamaan Chebyshev, diperoleh
Perhatikan, dengan melihat hubungan dan diperoleh bahwa
jika . Artinya, Lema 4.5 terbukti.
Perhatikan, dengan menggunakan Lema 4.5, Teorema 3.1, Teorema 3.3
dan prinsip Lema 4.1 untuk membuktikan Corollary 4.1, sehingga diperoleh
untuk . Terbukti bahwa merupakan penduga konsisten dari ,
jika .
4.3 Kekonsistenan Penduga dari Fungsi Sebaran Waktu Tunggu dari Proses Poisson Periodik dengan Tren Fungsi Pangkat
Pada teorema berikut dibuktikan kekonsistenan penduga dari fungsi
sebaran waktu tunggu, jika panjang interval pengamatan menuju tak hingga.
Pengkajian terhadap teorema ini penting dilakukan untuk menjawab salah satu
masalah utama dalam penelitian ini.
Teorema 4.1
Jika fungsi intensitas memenuhi dan terintegralkan lokal, maka untuk
setiap bilangan nyata dan untuk setiap bilangan bulat positif diperoleh
Bukti :
Perhatikan, salah satu komponen pertama ruas kanan dari berikut :
Berdasarkan Corollary 4.1, diperoleh
, untuk .
Selanjutnya, dengan menggunakan prinsip Lema 4.4, diperoleh
untuk ,
karena merupakan fungsi kontinu.
Kemudian, dengan menggunakan prinsip Lema 4.3 dan melihat hubungan yang
ditunjukkan pada langkah di atas, diperoleh
untuk .
Berikutnya, perhatikan salah satu komponen kedua ruas kanan dari
berikut :
Berdasarkan langkah yang diperoleh melalui Induksi Matematika pada
untuk semua , ditunjukkan bahwa
.
Langkah pertama, basis induksi :
(berdasarkan Corollary 4.1).
Langkah kedua, hipotesis induksi :
Diasumsikan benar bahwa .
Langkah ketiga, langkah induksi :
Akan ditunjukkan bahwa
Perhatikan,
dengan menggunakan hasil yang diperoleh dari langkah pertama dan langkah
kedua, maka persamaan di atas menjadi
Karena langkah pertama sampai langkah ketiga diperlihatkan benar, sehingga
terbukti bahwa untuk semua
Selanjutnya, dengan mensubstitusikan pada , diperoleh
hubungan berikut :
Berdasarkan hubungan yang diperoleh dari dan ditunjukkan
bahwa , dengan kata lain Teorema 4.1 terbukti.
4.4 Kekonsistenan Penduga dari Fungsi Kepekatan Waktu Tunggu dari Proses Poisson Periodik dengan Tren Fungsi Pangkat
Pada teorema berikut dibuktikan kekonsistenan penduga dari fungsi
kepekatan waktu tunggu, jika panjang interval pengamatan menuju tak hingga.
Pengkajian terhadap teorema ini penting dilakukan untuk menjawab salah satu
masalah utama dalam penelitian ini.
Teorema 4.2
Jika fungsi intensitas memenuhi dan terintegralkan lokal, serta
maka untuk setiap bilangan nyata dan bilangan bulat positif , diperoleh
untuk asalkan merupakan titik Lebesgue dari .
Bukti :
untuk , dapat pula dinyatakan sebagai
Berdasarkan dan pada persamaan di atas, diperoleh
Telah ditunjukkan dari langkah sebelumnya, bahwa
untuk dan untuk .
Berdasarkan langkah-langkah yang diperoleh sebelumnya, dapat
ditunjukkan sebagai berikut
Menurut Teorema 3.2, diperoleh bahwa
untuk .
Menurut Teorema 3.1, diperoleh bahwa
untuk .
Selanjutnya, dengan menggunakan prinsip Lema 4.4 terhadap Corollary 4.1,
diperoleh hasil seperti berikut :
, untuk , maka , untuk , karena
merupakan fungsi kontinu.
Berdasarkan hasil yang diperoleh seperti pada , dimana diperoleh
hubungan , dibuktikan bahwa
untuk (proses pembuktian dapat ditunjukkan dengan menggunakan
induksi matematika, seperti pembuktian sebelumnya).
Berikutnya, dengan menggunakan prinsip Lema 4.1, diperoleh bahwa
Selanjutnya, dengan menggunakan prinsip Lema 4.3 terhadap hasil yang
diperoleh dari langkah-langkah di atas, maka
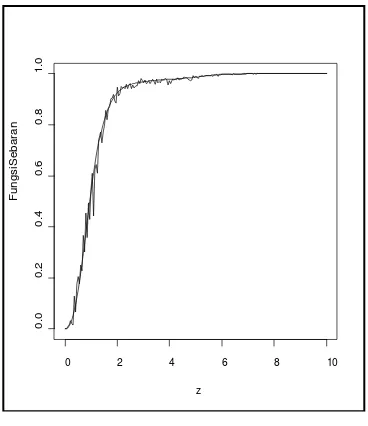
4.5 Hasil Simulasi
Di sini diperlihatkan cara menentukan penduga untuk fungsi sebaran
waktu tunggu kejadian pertama dan kejadian kedua dengan menggunakan data
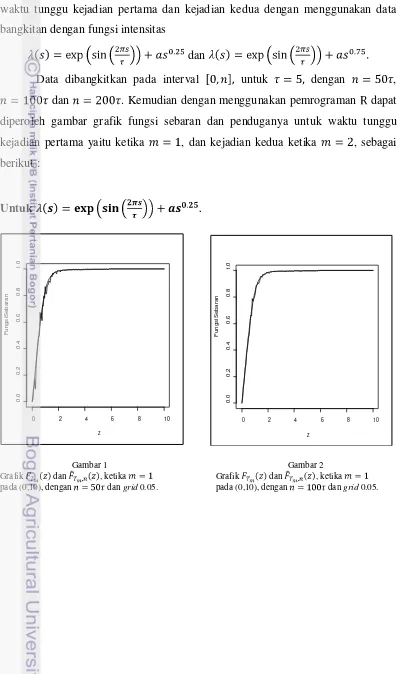
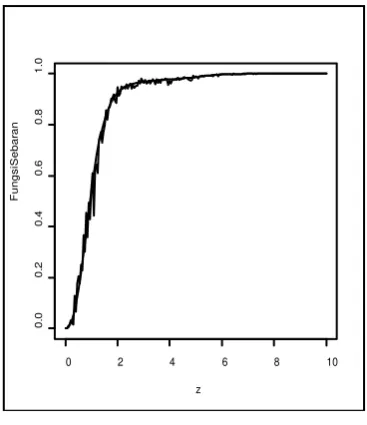
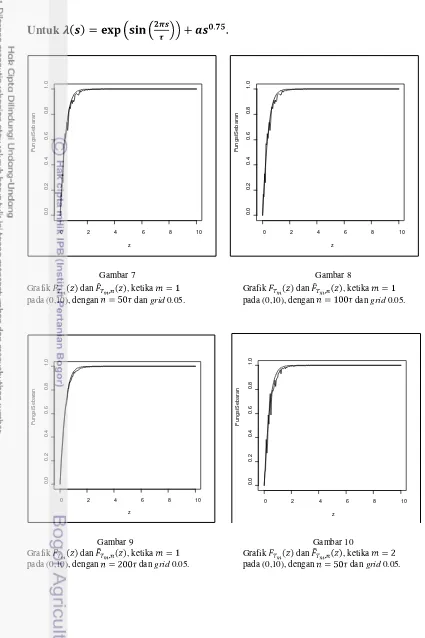
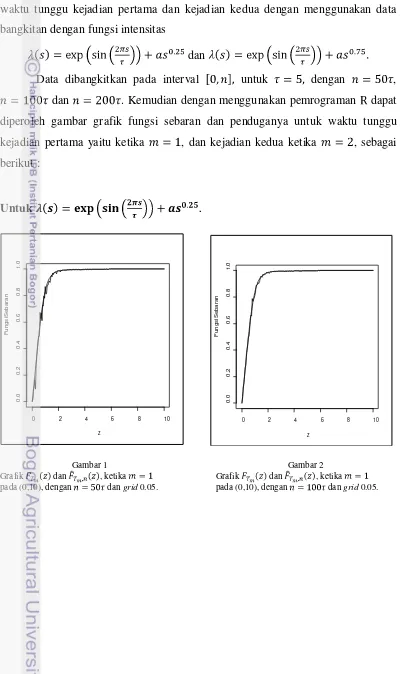
bangkitan dengan fungsi intensitas
dan
Data dibangkitkan pada interval untuk dengan ,
dan . Kemudian dengan menggunakan pemrograman dapat
diperoleh gambar grafik fungsi sebaran dan penduganya untuk waktu tunggu
kejadian pertama yaitu ketika , dan kejadian kedua ketika , sebagai
Gambar 11 Gambar 12
Grafik dan , ketika Grafik dan , ketika
pada (0,10), dengan dan grid 0.05. pada (0,10), dengan dan grid 0.05.
Berdasarkan gambar di atas, terlihat bahwa suatu penduga bagi fungsi
sebaran kejadian pertama dan kejadian kedua akan mendekati sebaran yang
sebenarnya jika semakin besar panjang interval pengamatan . Hal ini sesuai
dengan Teorema 4.1, yaitu akan konvergen ke jika .
Untuk pangkat diperoleh pola dugaan yang lebih dekat terhadap pola
fungsi sebarannya dibandingkan pangkat .
BAB 5
KESIMPULAN
Pada tulisan ini dikaji suatu metode untuk menduga fungsi sebaran dan
fungsi kepekatan waktu tunggu dari proses Poisson periodik dengan tren fungsi
pangkat. Diformulasikan fungsi intensitas dengan komponen tren fungsi pangkat
sebagai berikut :
diasumsikan bahwa periode diketahui, tetapi koefisien dan fungsi pada titik
tidak diketahui.
Pada situasi ini kita gunakan penduga fungsi sebaran waktu tunggu dan
penduga fungsi kepekatan waktu tunggu berturut-turut sebagai berikut :
dengan
dimana adalah bilangan bulat terbesar yang lebih kecil atau sama dengan ,
yaitu , , adalah suatu kernel dan adalah barisan
bilangan nyata positif yang konvergen ke nol, yaitu untuk .
Dari hasil pengkajian yang dilakukan, disimpulkan bahwa :
a) Jika fungsi intensitas dan terintegralkan lokal, maka
untuk setiap bilangan nyata dan untuk setiap bilangan bulat positif
diperoleh
untuk
b) Jika fungsi intensitas dan terintegralkan lokal, serta
maka untuk setiap bilangan nyata dan untuk setiap bilangan
bulat positif , diperoleh
untuk asalkan merupakan titik Lebesgue dari .
c) Berdasarkan hasil simulasi diperoleh bahwa kualitas penduga dari fungsi
sebaran waktu tunggu pertama lebih baik dari waktu tunggu kedua untuk
ukuran yang sama, artinya diperlukan nilai yang lebih besar untuk waktu
tunggu kedua dibandingkan waktu tunggu pertama. Diperoleh pola penduga
yang lebih dekat ke pola sebarannya untuk pangkat 0,25 dibandingkan pangkat
DAFTAR PUSTAKA
Browder A. 1996. Mathematical Analysis : An Introduction. Springer, New York.
Casella G, Berger RL. 2002. Statistical Inference. 2nd
Dudley RM. 1989. Real Analysis and Probability. Wadsworth & Brooks. California.
Ed. Wadsworth & Brooks/Cole, Pasific Grove, California.
Farida T. 2008. Penduga Komponen Periodik dari Fungsi Intensitas Proses Poisson Periodik dengan Tren Fungsi Pangkat [tesis]. Bogor: Program Pascasarjana, Institut Pertanian Bogor.
Ghahramani S. 2005. Fundamental of Probability. 3rd
Grimmet GR, Stirzaker DR. 1992. Probability and Random Processes. 2
Ed. Prentice Hall. New York.
nd
Helmers R. 1995. On Estimating the Intensity of Oil Polution in the North Sea.
CWI Note BS-N9501.
Ed. Clarendon Press. Oxford.
Helmers R, Zitikis R. 1999. On Estimation of Poisson Intensity Function. Ann.
Ins. Math, 51 (2) 265-280.
Helmers R, Mangku IW. 2000. Statistical Estimation of Poisson Intensity Function. Proceedings of the SEAM-GMU International Conference on
Mathematics and Its Applications, Yogyakarta, July 26-29, 1999, p. 9-21.
Helmers R, Mangku IW. 2009. Estimating the Intensity of a Cyclic Poisson Process in the Precense of Linear Trend. Ann. Inst. Stat. Math, 61 (3), 559-628.
Helmers R, Mangku IW, Zitikis R. 2003. Consistent Estimation of the Intensity Function of a Cyclic Poisson Process. Journal of Multivariate Analysis, 84, 19-39.
Helmers R, Mangku IW, Zitikis R. 2007. A Non-parametric Estimator for thr Doubly Periodic Poisson Intensity Function. Statistical Methodology, 4, 481-492.
Hogg et al. 2005. Introduction to Mathematical Statistics. 5th
Mangku IW. 1999. Nearest Neighbor Estimation of the Intensity Function of a Cyclic Poisson Process. CWI Report PNA-R9914.
Ed. Prentice Hall, Engelwood Cliffs. New Jersey.
Mangku IW. 2001. Estimating the Intensity of a Cyclic Poisson Process.
Mangku IW. 2005. A Note on Estimation of the Global Intensity of a Cyclic Poisson Process in the Presence of Linear Trend. Journal of Mathematics and
Its Aplications, Vol. 4, No:2.
Mangku IW. 2006a. Weak and Strong Convergence of a Kernel-type Estimator for the Intensity of a Periodic Poisson Process. Journal of Mathematics and Its
Aplications, Vol. 5, No:1.
Mangku IW. 2006b. Asymtotic Normality of a Kernel-type Estimator for the Intensity of a Periodic Poisson Process. Journal of Mathematics and Its
Aplications, Vol. 5, No:2.
Mangku IW. 2010.Consistent Estimation of the Distribution Function and the Density of Waiting Time of a Cyclic Poisson Process with Linear Trend. Far
East Journal of Theoretical Statistics, 33 (1), 81-91.
Purcell EJ, Varberg D. 1998. Kalkulus dan Geometri Analisis. Jilid 2. Ed. ke-5. Penerbit Erlangga. Jakarta.
Rachmawati, RN. 2008. Sifat-sifat Statistika Penduga Fungsi IntensitasPoisson Periodik dengan Tren Fungsi Pangkat [skripsi]. Bogor: Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor.
Rachmawati, RN. 2010. Sebaran Asimtotik Penduga Komponen Periode Fungsi Intensitas Proses Poisson Periodik dengan Tren Fungsi Pangkat [tesis]. Bogor: Program Pascasarjana, Institut Pertanian Bogor.
Rahayu M. 2008. Kekonsistenan Penduga Fungsi Intensitas Proses Poisson Periodik dengan Tren Fungsi Pangkat [skripsi]. Bogor: Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor.
Ross SM. 1996. Stochastic Processes. 2nd
Stewart J. 1999. Kalkulus. Jilid 1. Ed. ke-4. Penerbit Erlangga. Jakarta.
Ed. John Wiley & Sons. New York.
Titchmarsh, E. C. 1960. The Theory of Functions. Oxford University Press. London.
Wheeden RL, Zygmund A. 1997. Measure and Integral : An Introduction to Real
Analysis. Marcell Dekker. New York.
Lampiran 1. Ruang Contoh, Kejadian dan Peluang
Definisi L.1 (Ruang contoh dan kejadian)
Himpunan dari semua peristiwa yang mungkin muncul sebagai akibat atau hasil
dari suatu percobaan disebut ruang contoh, misalkan dinotasikan dengan S.
Himpunan bagian dari ruang contoh, termasuk ruang contoh itu sendiri dan
himpunan kosong disebut kejadian.
(Cassela dan Berger, 2002)
Definisi L.2 (Medan- )
Suatu himpunan yang anggotanya terdiri atas himpunan bagian dari disebut
medan- jika memenuhi syarat sebagai berikut :
(i)
(ii) Jika maka
(iii) Jika maka
(Grimmet dan Stirzaker, 1992)
Medan- terkecil yang mengandung semua selang berbentuk ,
disebut medan Borel, dinotasikan dan anggota dari medan Borel disebut
himpunan Borel.
Definisi L.3 (Ukuran peluang)
Ukuran peluang P pada adalah fungsi P : yang memenuhi :
(i) P P .
(ii) Jika adalah himpunan disjoin yang merupakan anggota dari , yaitu
(Grimmet dan Stirzaker, 1992)
Tripel disebut sebagai ruang peluang.
Definisi L.4 (Kejadian saling bebas)
Kejadian dan dikatakan saling bebas jika P . Secara
umum, himpunan kejadian dikatakan saling bebas jika,
untuk setiap himpunan bagian J dari I.
(Grimmet dan Stirzaker, 1992)
Lampiran 2. Peubah Acak dan Fungsi Sebaran
Definisi L.5 (Peubah acak)
Peubah acak X adalah suatu fungsi dari ruang contoh S ke himpunan bilangan
nyata .
(Cassela dan Berger, 2002)
Definisi L.6 (Fungsi sebaran kumulatif)
Fungsi sebaran kumulatif dari suatu peubah acak X, dinotasikan sebagai ,
adalah didefinisikan sebagai :
, untuk semua .
(Cassela dan Berger, 2002)
Definisi L.7 (Peubah acak diskret)
Peubah acak X dikatakan diskret jika semua nilai dari peubah acak
tersebut merupakan himpunan tercacah.
Untuk peubah acak diskret fungsi massa peluang didefinisikan sebagai
berikut :
Definisi L.8 (Fungsi massa peluang)
Fungsi massa peluang dari suatu peubah acak diskret X adalah fungsi
yang diberikan oleh .
(Grimmet dan Stirzaker, 1992)
Definisi L.9 (Peubah acak Poisson)
Peubah acak X disebut peubah acak Poisson dengan parameter , jika fungsi
massa peluangnya dinyatakan oleh
(Ghahramani, 2005)
Lampiran 3. Kekonvergenan
Definisi L.10 (Kekonvergenan barisan bilangan nyata)
Barisan disebut mempunyai limit dan dituliskan atau
jika , apabila untuk setiap terdapat sebuah bilangan
sedemikian sehingga jika maka . Jika ada,
dikatakan barisan tersebut konvergen. Jika tidak, barisan tersebut dikatakan
divergen.
(Stewart, 1999)
Lema L.1 (Deret- )
Deret (disebut juga deret- ) konvergen jika , dan divergen jika
.
Definisi L.11 (Kekonsistenan)
Misalkan merupakan penduga konsisten bagi , untuk , atau dapat
dinyatakan sebagai
untuk . Jika untuk , untuk .
Definisi L.12 (Kekonvergenan dalam peluang)
Misalkan adalah peubah acak dalam ruang peluang .
Barisan peubah acak dikatakan konvergen dalam peluang ke , dinotasikan
, jika untuk setiap
atau
untuk . Dengan kata lain, jika untuk , maka
atau .
(Hogg et al. 2005)
Lampiran 4. Nilai Harapan, Ragam dan Momen
Definisi L.13 (Nilai harapan)
Misalkan adalah peubah acak diskret dengan fungsi massa peluang
. Nilai harapan dari dinotasikan , adalah
jika jumlah di atas konvergen mutlak.
(Hogg et al. 2005)
Lema L.2
Jika adalah peubah acak dan adalah konstanta
sebarang, maka
Definisi L.14 (Ragam)
Misalkan adalah peubah acak diskret dengan fungsi massa peluang dan
nilai harapan ragam dari dinotasikan dengan atau , adalah
(Hogg et al. 2005)
Lema L.3
Jika adalah peubah acak maka untuk sebarang konstanta dan berlaku
(Ghahramani, 2005) Bukti :
Dari definisi dapat dituliskan bahwa
Dengan demikian Lema L.3 terbukti.
Definisi L.15 (Covarian)
Jika dan adalah peubah acak yang saling bebas, maka
(Ghahramani, 2005) Bukti :
Dengan demikian Lema L.4 terbukti.
Definisi L.16 (Momen pusat ke- )
Jika adalah bilangan bulat positif, maka momen pusat ke- atau dari peubah
acak adalah
(Hogg et al. 2005) Nilai harapan peubah acak merupakan momen pertama dari . Nilai harapan dari kuadrat perbedaan jarak antara peubah acak dengan nilai harapannya disebut ragam dari . Ragam merupakan momen pusat ke-2 dari peubah acak .
Lampiran 5. Beberapa Definisi dan Lema Teknis
Definisi L.17 (Terintegralkan lokal)
Fungsi intensitas disebut terintegralkan lokal, jika untuk sembarang himpunan
Borel terbatas diperoleh
(Dudley, 1989)
Definisi L.18 (Titik Lebesgue)
Suatu titik disebut titik Lebesgue dari suatu fungsi , jika
Definisi L.19 ( (1) dan (1) )
(i) Suatu barisan bilangan nyata disebut terbatas dan ditulis (1)
untuk , jika ada bilangan terhingga dan sehingga
untuk semua bilangan asli .
(ii) Suatu barisan yang konvergen ke nol untuk , dapat ditulis
(1) untuk .
(Purcell dan Varberg, 1998)
Lema L.5 (Formula Young dari Teorema Taylor)
Misalkan mempunyai nilai turunan ke- yang terhingga pada suatu titik , maka
untuk .
Bukti : Lihat Serfling (1980).
Lema L.6 (Ketaksamaan Markov)
Jika adalah peubah acak, maka untuk suatu
(Ghahramani, 2005)
Bukti :
Misalkan , maka , dengan adalah fungsi indikator dari
. Jika ditentukan nilai harapannya, maka diperoleh
Lema L.7 (Ketaksamaan Chebyshev)
Jika adalah peubah acak dengan nilai harapan dan ragam , maka untuk
setiap
(Ghahramani, 2005)
Bukti :
Karena menggunakan ketaksamaan Markov, maka ketaksamaan
Chebyshev diperoleh
Oleh karena adalah ekuivalen , dengan demikian
Lema L.7 terbukti.
Lampiran 6. Program Penentuan Fungsi Sebaran dan Penduganya Untuk Waktu Tunggu Kejadian Pertama dengan Pangkat 0.25
Fzduga=function(tau,n,z)
x=s[s>i*tau-(tau/2)&s< i*tau+(tau/2)] sum1=sum1+(length(x)*(1/(tau*i^(0.25)))) }
tetaduga=((1-0.25)/(ntau^(1-0.25)))*sum1-((1-0.25)*aduga*(tau^0.25)*(ntau^0.25)) zr=z-(tau*floor(z/tau))
for(j in 1:ntau)
Lampiran 7. Program Penentuan Fungsi Sebaran dan Penduganya Untuk Waktu Tunggu Kejadian Kedua dengan Pangkat 0.25
P=lambda/maxlambda
Lampiran 8. Program Penentuan Fungsi Sebaran dan Penduganya Untuk Waktu Tunggu Kejadian Pertama dengan Pangkat 0.75
Fzduga=function(tau,n,z)
analitik=seq(1:length(z))
Lampiran 9. Program Penentuan Fungsi Sebaran dan Penduganya Untuk Waktu Tunggu Kejadian Pertama dengan Pangkat 0.75
Fzduga=function(tau,n,z)
Function and the Density of Waiting Time of a Periodic Poisson Process with Power Function Trend. Supervised by I WAYAN MANGKU and RETNO BUDIARTI.
This thesis is concerned with estimation of distribution and density functions of waiting time of a periodic Poisson process with power function trend. The intensity function is assumed to consist of two components, namely, a periodic component and a power function trend component. It is also assumed that the Poisson process is observed in interval . Let denotes the waiting time of -th event since the beginning of observation of the Poisson process discussed. Estimators of the distribution function and the density function of have been constructed and their consistency as the length of observation interval of the process goes to infinity have been proved. Finally some numerical results are also presented.
BAB 1
PENDAHULUAN
1.1Latar Belakang
Terdapat banyak hal dalam kehidupan sehari-hari yang dapat dijelaskan
dengan suatu proses stokastik. Misalnya, proses kedatangan pelanggan pada suatu
antrian di pusat servis, banyaknya orang yang menggunakan suatu line telepon,
banyaknya orang yang memerlukan penanganan kesehatan pada rumah sakit dan
banyaknya kendaraan yang melewati suatu ruas jalan raya akan berbeda untuk
setiap waktu tertentu. Fenomena tersebut dapat dimodelkan dengan suatu proses
stokastik, yaitu model yang menggunakan aturan-aturan peluang untuk
menggambarkan perilaku suatu sistem yang tidak diketahui dengan pasti di
periode waktu yang akan datang.
Proses stokastik dibedakan menjadi dua, yaitu proses stokastik dengan
waktu diskret dan proses stokastik dengan waktu kontinu. Salah satu bentuk
khusus dari proses stokastik dengan waktu kontinu adalah proses Poisson dengan
fungsi intensitas berupa fungsi periodik. Proses tersebut antara lain dapat
digunakan untuk memodelkan suatu proses kedatangan pasien yang memerlukan
pelayanan kesehatan segera setelah terjadi suatu bencana, kecelakaan, dan lain
sebagainya dengan periode satu hari, atau memodelkan fenomena-fenomena
serupa. Jika laju kedatangan pasien tersebut meningkat berdasarkan suatu fungsi
pangkat terhadap waktu maka model yang lebih tepat untuk digunakan adalah
proses Poisson periodik dengan suatu komponen tren berbentuk fungsi pangkat.
Berdasarkan alasan sebelumnya, model fungsi intensitas untuk kasus ini
dapat dirumuskan sebagai berikut
diasumsikan bahwa periode diketahui, tetapi koefisien dan fungsi pada titik
tidak diketahui, dengan adalah suatu fungsi periodik, dan
adalah komponen tren dengan . Kajian ini dibatasi hanya untuk kasus
Pendugaan terhadap fungsi sebaran dan fungsi kepekatan dari waktu tunggu
bermanfaat dalam peramalan perilaku sistem atau fenomena. Pasien yang datang
pada suatu rumah sakit harus mendapatkan pelayanan sesegera mungkin, hal ini
mengindikasikan seberapa jauh kesiagaan tim medis dalam mengambil tindakan
dan merekapun perlu mempertimbangkan kapan waktu berikutnya peristiwa
serupa terulang kembali. Berdasarkan contoh fenomena tersebut, pada tulisan ini
dikaji penduga-penduga konsisten dari fungsi sebaran waktu tunggu dan fungsi
kepekatan waktu tunggu dari proses Poisson periodik dengan tren fungsi pangkat.
1.2Tujuan Penelitian
Tujuan penulisan karya ilmiah ini adalah untuk :
1. Merumuskan penduga dari fungsi sebaran waktu tunggu proses Poisson
periodik dengan komponen tren berbentuk fungsi pangkat dan membuktikan
kekonsistenannya.
2. Merumuskan penduga dari fungsi kepekatan waktu tunggu proses Poisson
periodik dengan komponen tren berbentuk fungsi pangkat dan membuktikan
kekonsistenannya.
3. Melakukan simulasi komputer untuk mempelajari perilaku penduga fungsi
sebaran bagi waktu tunggu kejadian pertama dan kejadian kedua untuk
ukuran sampel terbatas, serta mempelajari pola dugaan fungsi sebaran waktu
BAB 2
TINJAUAN PUSTAKA
2.1 Proses Poisson Periodik Definisi 2.1 (Proses stokastik)
Proses stokastik adalah suatu himpunan dari peubah acak yang
memetakan suatu ruang contoh ke suatu ruang state .
(Ross, 1996)
Jika merupakan himpunan tercacah, maka suatu proses stokastik
disebut proses stokastik dengan waktu diskret, sedangkan disebut proses
stokastik dengan waktu kontinu jika merupakan suatu interval.
Definisi 2.2 (Inkremen bebas)
Suatu proses stokastik dengan waktu kontinu disebut memiliki
inkremen bebas jika untuk semua , peubah acak
adalah bebas.
(Ross, 1996)
Diartikan pula, suatu proses stokastik dengan waktu kontinu disebut
memiliki inkremen bebas jika proses berubahnya nilai pada interval waktu yang
tidak tumpang tindih (overlaping) adalah bebas.
Definisi 2.3 (Inkremen stasioner)
Suatu proses stokastik dengan waktu kontinu disebut memiliki
inkremen stasioner jika memiliki sebaran yang sama untuk
semua nilai .
(Ross, 1996)
Definisi 2.4 (Proses pencacahan)
Suatu proses stokastik disebut proses pencacahan jika