Kekonsistenan Kuat Dan Sebaran Asimtotik Penduga Intensitas Berupa Fungsi Periodik Kali Tren Fungsi Pangkat Proses Poisson Nonhomogen

(1)

KEKONSISTENAN KUAT DAN SEBARAN ASIMTOTIK

PENDUGA INTENSITAS BERUPA FUNGSI PERIODIK

KALI TREN FUNGSI PANGKAT PROSES POISSON

NONHOMOGEN

IKHSAN MAULIDI

SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR

(2)

(3)

PERNYATAAN MENGENAI TESIS DAN

SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA

Dengan ini saya menyatakan bahwa tesis berjudul Kekonsistenan Kuat dan Sebaran Asimtotik Penduga Intensitas Berupa Fungsi Periodik Kali Tren Fungsi Pangkat Proses Poisson Nonhomogen adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.

Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.

Bogor, Juni 2015

Ikhsan Maulidi

(4)

RINGKASAN

IKHSAN MAULIDI. Kekonsistenan Kuat dan Sebaran Asimtotik Penduga Intensitas Berupa Fungsi Periodik Kali Tren Fungsi Pangkat Proses Poisson Nonhomogen. Dibimbing oleh I WAYAN MANGKU dan HADI SUMARNO.

Banyak fenomena nyata dalam kehidupan sehari-hari yang dapat dimodelkan dengan proses stokastik, seperti pada proses kedatangan pelanggan ke suatu pusat pelayanan. Berdasarkan waktu, proses stokastik dapat dibedakan menjadi dua, yaitu proses stokastik diskret dan proses stokastik kontinu. Proses pencacahan merupakan proses stokastik kontinu yang menghitung banyaknya kejadian pada suatu selang waktu. Proses Poisson merupakan salah satu kasus khusus proses pencacahan dimana banyaknya kejadian pada suatu selang waktu diasumsikan menyebar Poisson. Proses Poisson dapat dibedakan menjadi proses Poisson homogen dan proses Poisson nonhomogen. Pada proses Poisson homogen, fungsi intensitas merupakan fungsi yang konstan (tidak bergantung pada waktu), sedangkan pada proses Poisson non homogen, fungsi intensitas merupakan fungsi yang bergantung pada waktu. Dalam penelitian ini proses Poisson yang dikaji adalah proses Poisson nonhomogen dimana fungsi intensitasnya berupa fungsi periodik kali tren fungsi pangkat.

Misalkan adalah proses Poisson nonhomogen pada interval dengan fungsi intensitas yang tidak diketahui dan diasumsikan fungsi intensitas tersebut terintegralkan lokal. Diasumsikan pula bahwa fungsi intensitas ini merupakan perkalian antara komponen periodik dan komponen tren berbentuk fungsi pangkat dengan diketahui, sehingga untuk setiap fungsi

Dalam karya ilmiah ini telah dibuktikan kekonsistenan kuat penduga intensitas berupa fungsi periodik kali tren fungsi pangkat pada proses Poisson nonhomogen yang telah dirumuskan. Pembuktian kekonsistenan kuat menggunakan pendekatan asimtotik bias dan ragam serta Lema Borel Cantelli.

(5)

Penduga yang dikaji menggunakan fungsi kernel umum yang memenuhi kondisi (K1) adalah fungsi kepekatan peluang, (K2) terbatas, (K3) terdefinisi pada selang , selain itu diasumsikan memiliki turunan kedua yang terbatas di sekitar . Analisis matematika yang telah dilakukan untuk menentukan sebaran asimtotik dibedakan menjadi tiga kasus, yakni dan Dari simulasi yang telah dilakukan diperoleh hasil bahwa jika nilai semakin besar, maka dibutuhkan selang pengamatan yang lebih panjang untuk memperoleh kekonvergenan penduga.

(6)

SUMMARY

IKHSAN MAULIDI. Strong Consistency and Asymptotic Normality of a Kernel-Type Estimator for the Intensity Obtained as the Product of a Periodic Function with the Power Function Trend of a Nonhomogeneous Poisson Process. Supervised by I WAYAN MANGKU and HADI SUMARNO.

Many real phenomenon can be modeled by using stochastic processes, such as the customer arrival process to the service center. Base on the time, the stochastic processes can be classified into discrete stochastic process and continuous stochastic process. The counting process is a continuous stochastic process which counts the number of events on an interval of time. The Poisson process is a counting process where the number of arrivals is assumed to follow a Poisson distribution. The Poisson process can be classified into homogeneous and nonhomogeneous Poisson process. In homogeneous Poisson process, the intensity is constant (not dependent to the time), however in nonhomogeneous Poisson process, the intensity dependent to the time. In this paper, the Poisson process that have been studied is nonhomogeneous Poisson process which have intensity function obtained as the product of a periodic function with the power function.

Let be a nonhomogeneous Poisson process on having (unknown) locally integrable intensity function . We assume the intensity function to be a product of a periodic function with the power function trend. That is, the equation

( nonhomogeneous Poisson process was proved. The proof was constructed by using bias and variance approach and also Borel Cantelli’s Lemma.

(7)

The estimators use general kernel which satisfies (K1) is a density function, (K2) is bounded function, (K3) has closed support and also is assumed to have a bounded second derivative around The mathematical analysis have been done to show asymptotic normality of the estimator consider three different cases, namely and The result of computer simulation shows that the larger the value of , it is needed the longer the observation interval to get the convergent of the estimator.

(8)

© Hak Cipta Milik IPB, Tahun 2015

Hak Cipta Dilindungi Undang-Undang

Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumbernya. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik, atau tinjauan suatu masalah; dan pengutipan tersebut tidak merugikan kepentingan IPB

(9)

Tesis

sebagai salah satu syarat untuk memperoleh gelar Magister Sains

pada

Program Studi Matematika Terapan

KEKONSISTENAN KUAT DAN SEBARAN ASIMTOTIK

PENDUGA INTENSITAS BERUPA FUNGSI PERIODIK

KALI TREN FUNGSI PANGKAT PROSES POISSON

NONHOMOGEN

SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR

BOGOR 2015

(10)

(11)

Judul Tesis : Kekonsistenan Kuat dan Sebaran Asimtotik Penduga Intensitas Berupa Fungsi Periodik Kali Tren Fungsi Pangkat Proses Poisson Nonhomogen

Nama : Ikhsan Maulidi

NIM : G551140546

Disetujui oleh Komisi Pembimbing

Prof Dr Ir I Wayan Mangku, MSc Ketua

Dr Ir Hadi Sumarno, MS Anggota

Diketahui oleh

Ketua Program Studi Matematika Terapan

Dr Jaharuddin, MS

Dekan Sekolah Pascasarjana

Dr Ir Dahrul Syah, MScAgr

(12)

PRAKATA

Puji dan syukur penulis panjatkan kepada Allah subhanahu wa ta’ala atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Tema yang dipilih dalam penelitian yang dilaksanakan sejak bulan November 2014 ini ialah kekonsistenan kuat dan sebaran asimtotik penduga, dengan judul Kekonsistenan Kuat dan Sebaran Asimtotik Penduga Intensitas Berupa Fungsi Periodik Kali Tren Fungsi Pangkat Proses Poisson Nonhomogen.

Terima kasih penulis ucapkan kepada Bapak Prof Dr Ir I Wayan Mangku, MSc dan Bapak Dr Hadi Sumarno, MS, serta Bapak Dr Ir I Gusti Putu Purnaba, DEA yang telah banyak memberi saran. Di samping itu, ungkapan terima kasih juga disampaikan kepada ayah, ibu, seluruh keluarga, teman-teman atas segala doa dan kasih sayangnya.

Semoga karya ilmiah ini bermanfaat.

Bogor, Juni 2015

(13)

DAFTAR ISI

DAFTAR TABEL v

DAFTAR GAMBAR vi DAFTAR LAMPIRAN vi

1 PENDAHULUAN 1

Latar Belakang 1

Perumusan Masalah 2

Tujuan Penelitian 2

2 TINJAUAN PUSTAKA 3

Proses Stokastik 3

Proses Poisson 3

Proses Poisson Periodik 4

Pendugaan Fungsi Intensitas Proses Poisson Periodik 4

3 METODE PENELITIAN 5

4 REVIEW PERUMUSAN PENDUGA 5

5 HASIL DAN PEMBAHASAN 6

Kekonsistenan Kuat Penduga 6

Sebaran Asimtotik Penduga 12

Simulasi Numerik 31

6 SIMPULAN 34

DAFTAR PUSTAKA 34

LAMPIRAN 36

RIWAYAT HIDUP 49

DAFTAR TABEL

1 Hasil simulasi dari penduga yang dibangkitkan dan hasil teori untuk

31

32

(14)

DAFTAR GAMBAR

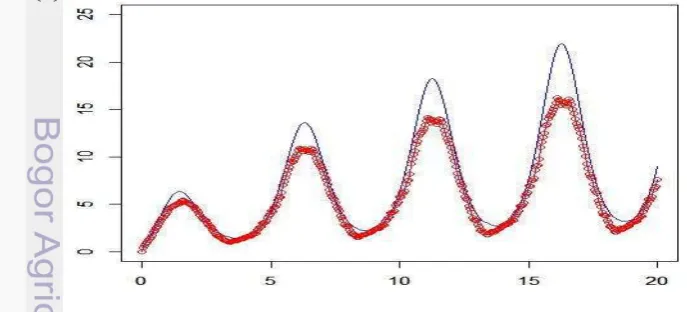
1 Grafik fungsi intensitas beserta nilai dugaannya ( o ) dengan interval pengamatan [0,100] untuk dengan menggunakan

fungsi kernel seragam 32

2 Grafik fungsi intensitas beserta nilai dugaannya ( o ) dengan interval pengamatan [0,100] untuk dengan menggunakan fungsi

kernel seragam 33

3 Grafik fungsi intensitas beserta nilai dugaannya ( o ) dengan interval pengamatan [0,100] untuk dengan menggunakan fungsi

kernel seragam 33

DAFTAR LAMPIRAN

1 Beberapa Konsep Dasar 36

2 Bukti Lema 2 (Kekonvergenan Ragam dan Aproksimasi Asimtotik

Bagi Ragam) 39

3 Bukti Deret ∑ merupakan deret yang konvergen jika 44

4 Formula Young dari Teorema Taylor 44

(15)

1 PENDAHULUAN

Latar Belakang

Banyak fenomena nyata dalam kehidupan sehari-hari yang dapat dimodelkan dengan proses stokastik. Model semacam ini menggunakan aturan-aturan peluang yang menggambarkan perilaku suatu sistem yang tidak diketahui secara pasti di masa yang akan datang. Misalnya proses kedatangan pelanggan ke suatu pusat servis (bank, kantor pos, supermarket, dan sebagainya). Berdasarkan waktu, proses stokastik dibedakan menjadi dua, yaitu proses stokastik dengan waktu diskret dan proses stokastik dengan waktu kontinu. Salah satu proses stokastik dengan waktu kontinu adalah proses Poisson. Proses Poisson merupakan proses pencacahan (counting process) dimana banyaknya kejadian pada interval waktu menyebar dengan peubah acak Poisson.

Proses Poisson dibedakan menjadi dua, yaitu proses Poisson homogen dan proses Poisson nonhomogen. Pada proses Poisson homogen fungsi intensitas (fungsi nilai harapan) merupakan fungsi yang konstan (tidak bergantung pada waktu), sedangkan pada proses Poisson nonhomogen fungsi intensitas bergantung pada waktu. Proses Poisson periodik adalah suatu proses Poisson nonhomogen yang fungsi intensitasnya berupa fungsi periodik. Proses ini merupakan salah satu bentuk khusus dari proses stokastik dengan waktu kontinu yang memiliki banyak manfaat dalam memodelkan berbagai macam fenomena nyata yang berkaitan dengan aturan peluang. Fenomena yang dapat dimodelkan dengan proses Poisson periodik di antaranya dalam bidang komunikasi, hidrologi, meteorologi, asuransi, dan seismologi (Helmers et al. 2003). Dalam suatu proses Poisson periodik, bentuk fungsi intensitas pada periode sebelumnya dengan sesudahnya memiliki pola yang serupa. Oleh sebab itu, dalam kehidupan sehari-hari proses Poisson periodik berguna untuk memprediksi suatu kejadian pada periode berikutnya.

(16)

2

ditentukan sebaran asimtotik dari penduga tipe kernel umum yang dirumuskan pada Erliana (2014).

Perumusan Masalah

Misalkan adalah proses Poisson nonhomogen pada interval dengan fungsi intensitas yang tidak diketahui dan diasumsikan fungsi intensitas tersebut terintegralkan lokal. Diasumsikan pula bahwa fungsi intensitas ini merupakan perkalian antara komponen periodik dan komponen tren berbentuk fungsi pangkat dengan diketahui, sehingga untuk setiap fungsi

Pada Erliana (2014) telah dibuktikan kekonsistenan lemah dan telah ditentukan aproksimasi bias, ragam, dan MSE bagi penduga yang dikaji. Pada penelitian ini telah dibuktikan kekonsistenan kuat dan ditentukan sebaran asimtotik penduga komponen periodik fungsi intensitas yang dikaji.

Tujuan Penelitian

Tujuan dari penelitian ini adalah sebagai berikut:

1 Membuktikan kekonsistenan kuat penduga komponen periodik fungsi intensitas berupa fungsi periodik kali tren fungsi pangkat pada proses Poisson nonhomogen.

2 Menentukan sebaran asimtotik penduga komponen periodik dari fungsi intensitas tersebut.

(17)

3

Suatu proses stokastik disebut proses stokastik dengan waktu kontinu jika berupa suatu interval (Ross 2010). Proses stokastik dengan waktu kontinu

3. Banyaknya kejadian pada sebarang interval waktu dengan panjang , memiliki sebaran (distribusi) Poisson dengan nilai harapan Jadi untuk semua

(18)

4

Proses Poisson Periodik

Proses Poisson periodik adalah suatu proses Poisson nonhomogen yang fungsi intensitasnya berupa fungsi periodik. Suatu fungsi disebut periodik jika untuk semua dan . Konstanta terkecil yang memenuhi persamaan merupakan periode dari fungsi tersebut. Berdasarkan sifat keperiodikan dari fungsi intensitas , dapat disusun penduga konsisten pada sebarang titik yang diberikan dengan hanya menggunakan realisasi tunggal. Hal ini dikarenakan dalam pendugaan pada sebarang titik , tidak hanya dapat menggunakan informasi di sekitar saja, tetapi juga dapat menggunakan informasi di sekitar untuk sebarang , asalkan (Mangku 2001).

Pendugaan Fungsi Intensitas Proses Poisson Periodik

Fungsi intensitas suatu proses Poisson periodik merupakan laju dari proses Poisson tersebut. Terdapat dua jenis fungsi intensitas, yaitu fungsi intensitas lokal dan fungsi intensitas global. Perbedaan antara dua fungsi intensitas tersebut adalah fungsi intensitas lokal merupakan laju dari proses Poisson di titik tertentu, sedangkan fungsi intensitas global merupakan rata-rata laju dari proses Poisson pada interval dengan panjang menuju tak hingga.

Pendugaan fungsi intensitas lokal pada suatu proses Poisson periodik di suatu titik dapat dihampiri dengan rata-rata banyaknya kejadian proses Poisson tersebut di sekitar titik sedangkan pendugaan fungsi intensitas global diduga dengan memperkirakan rata-rata banyaknya kejadian proses Poisson dalam interval waktu

Secara matematis, pendugaan fungsi intensitas lokal di sekitar titik s dapat dituliskan sebagai

(19)

5

3 METODE PENELITIAN

Penelitian ini merupakan kajian teoritis tentang bukti kekonsistenan kuat penduga dan sebaran asimtotik penduga komponen periodik pada fungsi intensitas dengan tren fungsi pangkat pada proses Poisson nonhomogen. Misalkan

adalah suatu fungsi bernilai real. Fungsi disebut kernel jika memenuhi sifat-sifat, yaitu: (K1) merupakan fungsi kepekatan peluang, (K2) terbatas, dan (K3) memiliki daerah definisi pada (Helmers et al. 2003).

Metode yang akan digunakan untuk membuktikan kekonvergenan kuat penduga komponen periodik adalah menggunakan konsep kekonvergenan lengkap dan Lema Borel Cantelli. Sementara metode yang digunakan untuk merumuskan sebaran asimtotik dari penduga adalah menggunakan konsep Teorema Limit Pusat dari barisan peubah acak bebas tetapi tidak identik.

Adapun langkah – langkah dalam penelitian ini adalah :

1 Membuktikan kekonvergenan kuat penduga komponen periodik dari fungsi intensitas periodik kali tren fungsi pangkat.

2 Menentukan sebaran asimtotik penduga fungsi intensitas. 3 Melakukan simulasi pembangkitan penduga.

4 REVIEW PERUMUSAN PENDUGA

Misalkan adalah suatu fungsi kernel yang memenuhi sifat – sifat (K1), (K2), (K3), serta adalah barisan bilangan real positif yang konvergen ke nol, yaitu Penyusunan penduga pada persamaan (6) mengikuti proses penyusunan penduga tipe kernel yang telah dikerjakan Mangku (2011). Karena hanya terdapat realisasi tunggal dari suatu proses Poisson , maka untuk menduga pada sembarang

Berdasarkan persamaan (3), persamaan (7) dapat ditulis menjadi

∑

(20)

6

Nilai fungsi dapat didekati dengan rata-rata nilai fungsi pada interval sehingga persamaan (8) menjadi

∑ ∫

∑ ∑ ∑ Dengan demikian, penduga bagi adalah

̂ ∑

Penduga pada persamaan (10) memberikan bobot yang sama pada setiap data dalam menentukan rata-rata banyaknya kejadian pada interval [ ], sehingga persamaan (10) dapat ditulis menjadi

̂ ∑ ∫

Dengan mengganti fungsi dengan kernel umum yang memenuhi (K1), (K2), dan (K3), maka diperoleh penduga bagi seperti pada persamaan (6), yaitu

̂ _∑ ∫

5 HASIL DAN PEMBAHASAN

Kekonsistenan Kuat Penduga ̂

Kekonsistenan kuat penduga adalah implikasi dari kekonvergenan lengkap. Oleh karena itu untuk membuktikan kekonsistenan kuat, terlebih dahulu harus dibuktikan kekonvergenan lengkap penduga. Berikut adalah Teorema 1 tentang kekonvergenan lengkap penduga dan Beberapa Lema yang dapat membantu untuk membuktikan Teorema 1.

Teorema 1 (Kekonvergenan Lengkap Penduga)

Misalkan fungsi memenuhi persamaan (3) dan terintegralkan lokal. Jika kernel

K memenuhi sifat (K1), (K2), (K3) dan dengan serta maka

̂

(21)

7 Lema 1 (Ketakbiasan Asimtotik)

Misalkan fungsi intensitas memenuhi (3) dan terintegralkan lokal, , fungsi kernel K memenuhi (K1), (K2), dan (K3), maka

̂ untuk

Bukti :

Dari persamaan (6) kita ketahui bahwa

̂ _∑ ∫

Maka

̂ (_∑ ∫

_∑ ∫

∑ ∫ . (11) Misalkan atau , maka persamaan (11) menjadi ∑ ∫ (12) Karena memenuhi persamaan (3) dan memenuhi maka persamaan (12) menjadi

̂ _∑ ∫ (

∑ ∫ (

∫ ∑ .

Karena ∑

untuk

(Lampiran 1) maka

(22)

8

∫ (13) Suku pertama dari persamaan (13) dapat dijabarkan menjadi

∫ ( ∫ ( (

∫ ( ∫ (14) Karena memenuhi (K2) dan (K3), serta merupakan titik Lebesgue maka suku pertama persamaan (14) menjadi

∫ ( ( ∫ (

( ∫ | |

. (15) Dari suku kedua persamaan (14), karena memenuhi (K1) diperoleh

∫ ∫ (16) Dari persamaan (15) dan persamaan (16) maka suku pertama persamaan (13) menjadi . Suku kedua persamaan (13) merupakan Jadi terbukti

̂ untuk

Lema 2 (Kekonvergenan Ragam dan Aproksimasi Asimtotik bagi Ragam)

Misalkan fungsi intensitas memenuhi persamaan (3) dan terintegralkan lokal. Jika kernel K memenuhi (K1), (K2), dan (K3), dan merupakan titik Lebesguebagi , serta memenuhi kasus berikut:

 _untuk



untuk

 untuk . maka

̂ (17)

Ada pun aproksimasi bagi ragam penduga adalah: (1) ̂

(23)

9 (2) ̂ ∫ jika (19) (3) ̂ ∫ , dengan

∑ , jika

(20)

Lema ini telah dibuktikan pada Erliana (2014) (Lampiran 2). Bukti Teorema 1:

Berdasarkan definisi kekonvergenan lengkap, untuk membuktikan ̂ adalah penduga yang konvergen lengkap ke berarti akan dibuktikan

bahwa

∑ (| ̂ | (21)

Komponen | | dapat dituliskan (| ̂ |

(| ̂ ̂ ̂ | (22)

Berdasarkan ketaksamaan segitiga dan Teorema dalam teori peluang maka persamaan (21) menjadi

(| ̂ |

(| ̂ ̂ | | ̂ |

(| ̂ ̂ | | ̂ | (23)

Berdasarkan Lema 1, jika ̂ maka | ̂ | , sehingga persamaan (23) menjadi

(| ̂ | | ̂ ̂ | .

Dengan menggunakan ketaksamaan Chebishev, dapat diperoleh | ̂ ̂ | ̂ ,

atau

∑ | ̂ ̂ | _∑

̂

(24)

(25)

11

Dari ketiga kasus di atas maka Teorema 1 terbukti.

Akibat 1 (Kekonsistenan Kuat bagi ̂ )

(26)

12

Bukti Akibat 1:

Berdasarkan definisi konvergen hampir pasti, untuk membuktikan ̂ adalah penduga konsisten kuat bagi , maka setara dengan

membuktikan bahwa

| ̂ |

atau

| ̂ |

Dari Teorema 1, diketahui ∑ (| ̂ | Berdasarkan Lema Borel-Cantelli bagian (i), jika ∑ (| ̂ | maka kejadian {| ̂ | } hanya terjadi sebanyak terhingga yang berimplikasi bahwa

| ̂ |

Jadi Akibat 1 terbukti.

Sebaran Asimtotik Penduga ̂

Teorema 2 (Sebaran Normal Asimtotik ̂ untuk )

Misalkan fungsi intensitas seperti persamaan (1) dan terintegralkan lokal. Misalkan kernel memenuhi kondisi (K1), (K2), (K3), dan terbatas di sekitar _, _untuk_dan _memiliki

turunan kedua yang terbatas di sekitar . (i). Jika maka

( _{( ̂}

untuk dengan

∫

(ii). Jika maka ( _{( ̂}

untuk dengan ∫ dan

∫

Teorema 3 (Sebaran Normal Asimtotik ̂ untuk )

(27)

13 untuk dan memiliki turunan kedua yang terbatas di sekitar .

(i). Jika

maka

( ̂

untuk dengan ∫ (ii). Jika

maka

( ̂

untuk dengan ∫ dan ∫ Teorema 4 (Sebaran Normal Asimtotik ̂ untuk )

Misalkan fungsi intensitas seperti persamaan (1) dan terintegralkan lokal. Misalkan kernel memenuhi kondisi (K1), (K2), (K3), dan terbatas di sekitar untuk dan memiliki turunan kedua yang terbatas di sekitar .

(i). Jika maka

( ̂

untuk dengan ∫ dan (∑

(ii). Jika maka

( ̂

untuk dengan ∫ ∫ dan (∑

Bukti Teorema 2, Teorema 3, dan Teorema 4

Untuk membuktikan Teorema 2, Teorema 3, dan Teorema 4, terlebih dahulu ruas kiri (25), (27), (29) dapat ditulis berturut-turut sebagai berikut

( _{( ̂}

( _̂

̂ ( ( ̂

(28)

14

̂ ̂ ( ̂

( ̂

̂ ̂ ( ̂

sehingga untuk membuktikan Teorema 2, cukup dibuktikan

( _̂

̂

dengan seperti pada (25) untuk , dan jika ( maka ( _{( ̂}

untuk Jika ( maka (

∫ untuk

Untuk membuktikan Teorema 3, cukup dibuktikan

̂ ̂

dengan seperti pada (27) untuk , dan jika

maka

( ̂

untuk Jika

maka

( ̂

∫ untuk

Untuk membuktikan Teorema 4, cukup dibuktikan

( ̂ ̂

dengan seperti pada (29) untuk , dan jika maka

( ( ̂

untuk Jika maka ( ( ̂

(29)

15 untuk

Pertama dibuktikan bentuk (31), (34), dan (37). Ruas kiri persamaan (31), (34), dan (37) berturut-turut dapat ditulis sebagai berikut

( _{√ ̂}

(

̂ ̂

√ ̂ ₎

√ ̂ (

̂ ̂

√ ̂ ₎

( √ ̂

(

̂ ̂

√ ̂ ₎

Untuk membuktikan (40), (41), dan (42) konvergen ke ruas kanan (31), (34), dan (37) dapat diterapkan Teorema Limit Pusat pada Lema 6 (Lampiran 5).

Pemisalan dan Nilai Harapan

Misalkan

∫

maka

∫

Misalkan , sehingga persamaan (43) menjadi

∫ ( (

(30)

16

∫ ( ( (

Karena merupakan fungsi yang periodik, maka persamaan (45) menjadi

∫ ( (

∫ ( ∫ (

Suku pertama persamaan (46) adalah

∫ ( (

∫ ( (47) Dengan menggunakan formula Young dari deret Taylor (Lampiran 4) diperoleh

(

sehingga persamaan (47) menjadi

∫ ∫ (48) Karena terbatas ( memenuhi K2), maka terdapat sedemikian sehingga persamaan (48) menjadi

(31)

17 Selanjutnya karena merupakan titik Lebesgue, maka diperoleh suku pertama persamaan (46) sebagai berikut:

∫ (

(49)

Ada pun untuk suku kedua persamaan (46) dapat dijabarkan sebagai berikut

∫ ( (

∫ ( ∫ ∫

∫ (50) Misalkan , maka persamaan (50) menjadi

∫

Karena fungsi kernel memenuhi K1 maka persamaan (51) menjadi

Dari persamaan (49) dan persamaan (52) maka

Penentuan Ragam

Dengan menggunakan pada pemisalan sebelumnya, maka

∫

untuk nilai yang besar dan interval dan tidak overlap sehingga untuk semua

(32)

18

∫

Karena menyebar Poisson maka , maka persamaan (35) menjadi ∫

Misalkan , , maka persamaan (54) menjadi

∫ Karena memenuhi persamaan (3) dan periodik, maka

∫ ∫

(55) Dengan menggunakan formula Young dari Teorema Taylor (Serfling 1980), diperoleh bahwa

(

( ₍

₍

Karena untuk , maka perilaku dari sama dengan Oleh sebab itu, persamaan di atas dapat ditulis menjadi

(

sehingga persamaan (55) menjadi ∫ _[

]

∫

(33)

19 Dengan penggantian peubah, misalkan dan karena kernel memenuhi (K3) maka persamaan (56)

∫

∫ Karena terbatas di sekitar , maka suku kedua persamaan (57)

∫

Dengan demikian

∫

Misalkan (∑ , sehingga diperoleh

∑ ∫

∫ ∑

∑

Dalam lampiran 2 telah dibuktikan bahwa untuk

∑

Untuk ∑

Untuk

∑

(34)

20

dengan (∑ Dengan demikian untuk setiap kasus nilai diperoleh nilai sebagai berikut :



kasus

∫ (

∑

∫ ∑ ∫

∫ ∫

karena untuk dan maka

∫ ∫ ∫

∫ ∫



Kasus

∫

∫ ∫

∫

(35)

21 karena untuk , maka

∫

(

∫ ∫



Kasus

∫

∫ ∫ ∫ dengan

∑

sehingga diperoleh

∫

(

∫

(

Jelas untuk dan sehingga ∫

∫

(36)

22

∫ ∫

∫

Selanjutnya dengan pemisalan seperti pada persamaan sebelumnya, yaitu ∑ ∑ ∫

∫

∑ ∫ ∫ Karena merupakan proses Poisson maka akibatnya

∑ ∑ [ ∫

∫ ]

∑ ∫

∑ ∫ (58) Sebelumnya telah diperoleh bahwa

∫

Karena terbatas, maka

(37)

23

∫

Karena terbatas, maka persamaan (58) menjadi ∑ ∫

∑ ∫

Dengan menyubstitusikan persamaan (41) ke persamaan (42) maka diperoleh:

∑

∑ ∑ (

Misalkan selanjutnya suku pertama ruas kanan persamaan (61) dapat diuraikan sebagai berikut :

∑ ∑ ∫

∑ ∫

∑

∫ ∑ ∑ Karena

maka

∑ ∫ ∑

∑ (62)

Perhatikan bahwa

∑

Akibatnya persamaan (62) menjadi

∑ ∫

(38)

24

∫

₍₆₃₎

Karena untuk , maka persamaan (63) menjadi ∫

(

Selanjutnya suku kedua persamaan (61) dapat diuraikan sebagai berikut : ∑ (

∑ ∫

(65)

dengan Selanjutnya karena

maka persamaan (65) menjadi

∑ ∫

∑ [ ∫ ]

∫ ∑

∑

∫ (

∑

(39)

25 ∫

∫

(40)

26

∑

∫ [ ∫ ]



kasus

∑

∑ ∑ (

∫

∫ (69) Karena dan ketika , maka persamaan (69) menjadi

∑

∫

[ ∫ ]

Dengan demikian barisan merupakan barisan peubah acak bebas dengan nilai harapan dan ragam yang nilainya terhingga dan tak nol untuk sembarang sehingga penduga ̂ merupakan jumlah dari peubah acak bebas yang dikalikan suatu konstanta, yaitu

̂ _∑ ∫

∑

(41)

(42)

28

_{√ ̂}

√_∫

untuk .

Untuk membuktikan (32) dan (33) dapat digunakan Lema 1 sehingga diperoleh _{( ̂}

_∫

(71)

Karena untuk maka persamaan (71) menjadi ∫

untuk sehingga persamaan (32) terbukti.

Kemudian karena untuk maka persamaan (71) menjadi

( _∫

∫

untuk sehingga persamaan (33) terbukti. Dengan demikan Teorema 2 terbukti.

Dengan cara yang sama, untuk membuktikan (34), cukup membuktikan √ ̂ √ ∫

Dengan menggunakan Lema 2 maka ruas kiri persamaan (72) menjadi

√

(43)

29

√ ∫

Dengan menggunakan deret Taylor seperti sebelumnya diperoleh (72).

Selanjutnya untuk membuktikan (35) dan (36) dapat menggunakan Lema 1 sehingga diperoleh

( ̂

∫

(

∫

Karena

untuk maka persamaan (73) menjadi

( _∫

untuk sehingga persamaan (35) terbukti. Karena

untuk maka persamaan (73) menjadi

( _∫

∫

untuk sehingga persamaan (36) terbukti. Dengan demikan Teorema 3 terbukti.

(44)

30

√ ̂ √ ∫ (74)

Dengan menggunakan Lema 2 maka ruas kiri persamaan (74) menjadi √ ∫

√ ( ∫

(

√ _∫

Dengan menggunakan deret Taylor seperti sebelumnya diperoleh (74). Selanjutnya, untuk membuktikan (38) dan (39) dapat menggunakan Lema 1, sehingga diperoleh

( ̂

∫

_∫

( _∫

Karena untuk maka persamaan (75) menjadi ( _∫

untuk sehingga persamaan (38) terbukti.

Karena untuk maka persamaan (75) menjadi ( _∫

∫

(45)

31

Simulasi Numerik

Simulasi dilakukan dengan membangkitkan penduga intensitas lokal pada interval dengan Metode yang digunakan adalah metode Monte Carlo. Tujuan dari simulasi ini adalah melihat bagaimana laju kekonvergenan ragam dan bias dari penduga.

Fungsi intensitas yang digunakan dalam simulasi ini adalah ( program R (Lampiran 5). Algoritma simulasi yang dilakukan adalah sebagai berikut :



Bangkitkan realisasi proses Poisson periodik pada interval pengamatan dan periode .



Bangkitkan penduga di suatu titik dengan bandwidth dan kernel seragam.



Tentukan mean dugaan, mean teori, ragam dugaan, ragam teori, bias, dan selisih nilai ragam penduga dengan ragam teori.

(46)

32 ragam hasil simulasi. Terlihat bahwa bias di Tabel 1 lebih cepat konvergen ke nol dibandingkan dengan bias yang ditampilkan Tabel 2 dan Tabel 3. Sehingga untuk nilai yang lebih besar membutuhkan selang pengamatan yang besar untuk menentukan kekonvergenan penduga tersebut.

Berbeda halnya dengan bias, nilai ragam yang ditampilkan Tabel 1 lebih lambat konvergen ke nol bila dibandingkan dengan Tabel 2 dan Tabel 3. Sehingga semakin besar nilai , ragam yang dihasilkan penduga semakin kecil.

(47)

33

Gambar 2 Grafik fungsi intensitas beserta nilai dugaannya ( o ) dengan interval pengamatan [0,100] untuk dengan menggunakan fungsi kernel seragam

Gambar 3 Grafik fungsi intensitas beserta nilai dugaannya ( o ) dengan interval pengamatan [0,100] untuk dengan menggunakan fungsi kernel seragam

Gambar 1, Gambar 2, dan Gambar 3 memperlihat plot dugaan penduga dan fungsi intensitas yang sebenarnya. Dari Gambar terlihat bahwa semakin besar nilai maka bias yang dalam hal ini merupakan selisih antara titik berwarna merah dengan garis grafik intensitas adalah semakin besar untuk interval pengamatan

(48)

34

6 SIMPULAN

Berdasarkan penelitian yang telah dilakukan, diperoleh simpulan sebagai berikut:

1. Telah terbukti sifat kekonsistenan kuat penduga intensitas berupa fungsi periodik kali tren fungsi pangkat pada proses Poisson nonhomogen, bukti disajikan dalam Teorema kekonvergenan lengkap penduga dan Akibat dari Teorema ini yaitu terbuktinya sifat konsisten kuat penduga, sehingga penduga yang telah dirumuskan merupakan penduga yang konsisten kuat.

2. Sebaran asimtotik untuk penduga komponen periodik dengan berbagai kasus nilai pangkat telah dirumuskan dalam Teorema sebaran normal asimtotik penduga.

Erliana W. 2014. Pendugaan tipe kernel umum untuk intensitas berupa fungsi periodik kali tren fungsi pangkat proses Poisson nonhomogen [Tesis]. Bogor (ID): Institut Pertanian Bogor.

Ghahramani S. 2005. Fundamental of Probability with Stochastics Processes. Third Edition. New Jersey: Pearson Prentice Hall.

Grimmett GR, Stirzaker DR. 2001. Probability and Random Processes. Third Edition. New York: Oxford University Press, Inc.

Helmers R, Mangku IW. 2009. Estimating the intensity of a cyclic Poisson

Helms, LL. 1996. Introductory to probability teory: With contemporary application. W. H. Freeman & Company. New York.

Hogg RV, Craig AT, Mc Kean JW. 2005. Introduction to Mathematical Statistics. Six Edition. New Jersey: Prentice Hall, Upper Saddle River.

(49)

35 Ismayulia W. 2011. Pendugaan komponen periodik fungsi intensitas berbentuk fungsi periodik kali tren linear suatu proses Poisson non-homogen [skripsi]. Bogor (ID): Institut Pertanian Bogor.

Mangku IW. 1999. Nearest neighbor estimation of the intensity function of a cyclic Poisson Process. CWI report PNA-R9914.

Mangku IW. 2001. Estimating the intensity of a cyclic Poisson process [Ph.D.Thesis]. Amsterdam (NL): University of Amsterdam.

Mangku IW. 2011. Estimating the intensity obtained as the product of a periodic function with the linear tren of a non-homogeneous Poisson process. Far East Journal of Mathematical Science (FJMS). 51:141-150.

Ramdani P. 2011. Pendugaan komponen periodik fungsi intensitas berbentuk fungsi periodik kali tren kuadratik suatu proses Poisson non-homogen [skripsi]. Bogor (ID): Institut Pertanian Bogor.

Ross SM. 1996. Stochastics Processes. Second Edition. New York: John Wiley & Sons.

Ross SM. 2010. Introduction to Probability Models. Tenth Edition. UK: Elsevier, Inc.

Serfling RJ. 1980. Approximation Theorems of Mathematical Statistics.

NewYork (US): J Wiley.

Stewart J. 1999. Kalkulus. Jilid 2. Ed ke-4. Jakarta (ID): Erlangga.

Taslim. 2011. Kekonsistenan penduga komponen periodik fungsi intensitas berbentuk perkalian fungsi periodik dengan tren kuadratik pada proses Poisson non homogen [tesis]. Bogor (ID): Institut Pertanian Bogor.

(50)

36

LAMPIRAN

Lampiran 1 Beberapa Konsep Dasar

Peluang

Ruang contoh dan kejadian

Suatu percobaan yang dapat diulang dalam kondisi yang sama, yang hasilnya tidak bisa diprediksi secara tepat tetapi kita bisa mengetahui semua kemungkinan hasil yang muncul disebut peubah acak. Himpunan semua hasil yang mungkin dari suatu percobaan acak disebut ruang contoh dan dinotasikan dengan Ω. Suatu kejadian adalah himpunan bagian dari ruang contoh (Ross 2010).

Ukuran peluang

Suatu ukuran pada adalah suatu fungsi yang memenuhi syarat-syarat berikut:

dan

Jika adalah himpunan-himpunan yang saling lepas, yaitu untuk setiap pasangan dengan maka ⋃

∑ (Grimmet dan Stirzaker 1992). Peubah acak

Peubah acak X adalah fungsi bernilai real yang terdefinisi dalam ruang contoh Ω (Ross 2010). Peubah acak terdiri dari peubah acak diskret dan peubah acak kontinu. Peubah acak dikatakan kontinu jika terdapat fungsi tak negatif yang terdefinisi untuk yaitu fungsi kepekatan peluang sehingga ∫ untuk setiap himpunan B. Jika maka ∫ (Ross 2010). Peubah acak disebut peubah acak diskret jika himpunan semua kemungkinan dari peubah acak adalah himpunan tercacah (Ghahramani 2005). Peubah acak diskret memiliki fungsi massa peluang yaitu fungsi dari ke yang memenuhi syarat berikut (Ghahramani 2005).

a. jika { }

b. dan c. ∑

Salah satu contoh peubah acak diskret adalah peubah acak Poisson. Peubah acak Poisson adalah peubah acak diskret X yang memunyai nilai kemungkinan 0,1,2,3,... disebut peubah acak Poisson dengan parameter λ, λ jika

(51)

37 Nilai harapan dari peubah acak diskret dengan himpunan kemungkinan nilai dan fungsi massa peluang didefinisikan sebagai ∑ (Ghahramani 2005). Misalkan , maka dan Var( ) disebut simpangan baku dan ragam dari didefinisikan sebagai √ .

Kekonvergenan

Kekonvergenan Barisan Bilangan Real

Barisan {_an} disebut memunyai limit L dan ditulis atau jika apabila untuk setiap terdapat sebuah bilangan M

sedemikian rupa sehingga jika maka | | . Jika ada, maka barisan tersebut dikatakan konvergen. Jika tidak, maka barisan tersebut divergen (Steward 1999).

Konvergen dalam Peluang

Misalkan adalah barisan peubah acak pada suatu ruang peluang . Barisan peubah acak dikatakan konvergen dalam peluang ke , dinotasikan jika untuk setiap berlaku | | untuk (Serfling 1980).

Konvergen Hampir Pasti

Misalkan adalah barisan peubah acak pada suatu ruang peluang . Barisan peubah acak dikatakan konvergen hampir pasti ke peubah acak ditulis → jika

Dengan kata lain

konvergen hampir pasti adalah konvergen dengan peluang satu (Grimmet dan Stirzaker 1992).

Konvergen Lengkap

Misalkan adalah barisan peubah acak pada suatu ruang peluang . Barisan peubah acak dikatakan konvergen lengkap ke peubah acak , jika untuk setiap , berlaku ∑ | | (Grimmet dan Stirzaker 1992).

Konvergen dalam Sebaran

(52)

38

Kekonsistenan Penduga

Misalkan adalah n peubah acak yang merupakan contoh dari sebaran peubah acak X yang memiliki fungsi kepekatan peluang atau fungsi massa peluang di mana Suatu fungsi dari contoh tersebut disebut statistik. T merupakan penduga tak bias dari jika Jika maka merupakan penduga bias dari (Hogg 5 et al. 2005 ). T merupakan penduga konsisten jika T konvergen dalam peluang ke (Hogg et al. 2014).

Beberapa Lema dan Definisi

Definisi 1 (Big-O dan Litle-o)

Simbol dan adalah cara untuk membandingkan besarnya dua fungsi dan dengan menuju suatu limit L.

(i) Notasi menyatakan bahwa |

| terbatas, untuk

(ii) Notasi ( menyatakan bahwa |

| , untuk

(Serfling 1980).

Definisi 2 (Fungsi Indikator)

Fungsi indikator dari suatu himpunan A, sering ditulis , didefinisikan sebagai {

(Casella dan Berger 1990).

Lema 3 (Ketaksamaan Chebyshev)

Jika adalah peubah acak dengan nilai harapan dan ragam maka | | , untuk setiap (Ghahramani 2005).

Lema 4 (Ketaksamaan Markov)

Jika adalah peubah acak, maka untuk suatu , | | | | (Ghahramani 2005).

Lema 5 (Lema Borel-Cantelli)

(i) Misalkan adalah sebarang kejadian, jika ∑ maka .

(53)

39 Definisi 3 (Terintegralkan lokal)

Fungsi intensitas disebut terintegralkan lokal, jika untuk sebarang himpunan Borel terbatas B kita peroleh ∫ (Dudley 1989).

Lampiran 2 Bukti Lema 2 (Kekonvergenan Ragam dan Aproksimasi Asimtotik Bagi Ragam)

(54)

40

(55)

(56)

42

(57)

43 Akibatnya, suku pertama pada ruas kanan dari persamaan (1.18) menjadi

(58)

44 Dengan uji integral dan metode pengintegralan parsial diperoleh

∫

Dengan menggunakan formula Young dari Teorema Taylor, maka diperoleh

(59)

45

"Program Membangkitkan Penduga di Suatu Titik (Kernel Seragam)"

duga<-function(data,wsize,titik,band,tau) {

(60)

46

"Contoh Simulasi untuk b<1 dengan Menggunakan Kernel Seragam"

"Contoh Simulasi untuk b=1 dengan Menggunakan Kernel Seragam"

(61)

47

“Contoh Simulasi untuk b>1 dengan Menggunakan

Kernel Seragam" s<-3

(62)

48

lambda<-2*exp(sin(2*pi*s/5))*s^b

lambdaturunan2<- 2*(b-1)*b*exp(sin(2*pi*s/5))*s^(-

2+b)+8/5*b*exp(sin(2*pi*s/5))*pi*s^(b-1)*cos(2*pi*s/5)+8/25*exp(sin(2*pi*s/5))*pi^2*s^b*cos((

2*pi*s/5)^2)-8/25*exp(sin(2*pi*s/5))*pi^2*s^b*sin(2*pi*s/5)

band <-

((9*lambda*(n/5)^(1-b)*0.5*n^-2)/(lambdaturunan2^2))^(1/5)

dugaanku<-penduga1(n,s,band,5,500) lambda

mean(dugaanku)

varteori <-(0.5*lambda*(n/5)^(1-b))/(n^2*band) varteori

var(dugaanku)

bias <- mean(dugaanku)-lambda bias

var(dugaanku)-varteori

"Program Menampilkan Grafik Fungsi Intensitas

Beserta Penduga"

Gambar<-function(a,b,tau,g) {

x<-seq(a,b,0.05)

ytrue<-2*exp(sin((2*pi*x)/tau))*(x^g)

plot(x,ytrue,xlim=c(0,20),ylim=c(0,25),type="l",col =4)

par(new=T)

plot(x,lambdaduga1,xlim=c(0,20),ylim=c(0,25),type=" o",col=2)

}

"Contoh program untuk membuat grafik selang [0,20]" b<-0.5

n<-100

data <- Random(n,5) band <- 0.35

(63)

49 RIWAYAT HIDUP

Penulis dilahirkan di Langsa pada tanggal 02 Oktober 1992 sebagai anak keempat dari pasangan Muhammad dan Mardhiah. Tahun 2010 penulis melanjutkan studi S1 Matematika di Institut Pertanian Bogor melalui jalur Beasiswa Utusan Daerah (BUD) pemerintah provinsi Aceh. Tahun 2013 penulis mengikuti perkuliahan program Pasca Sarjana IPB melalui jalur Fast Track

(Program Sinergi). Pada tahun 2014 penulis lulus program program studi S1 dengan predikat Cum Laude.