BAB I PENDAHULUAN
1.1 Latar Belakang
Belakangan ini, ilmu matematika telah berkembang pesat. Bukan hanya sebatas hitung menghitung menggunakan skala statistik, nilai, angka-angka real, kalkulus dan peluang. Akan tetapi, perkembangan ilmu matematika juga terjadi didasarkan pada penalaran – penalaran yang logis atas sistem matematis.
Penalaran yang dilakukan oleh para ahli matematik diperoleh atas realita kehidupan yang nyata yang dirasakan oleh manusia. Perkembangan dan aplikasi dan bagian matematik ini sangat dirasakan oleh manusia di berbagai kehidupan. Penalaran inilah dalam bahasa matematika sering disebut logika.
Logika merupakan suatu aktivitas manusia yang berkaitan dengan penggunaan akal dan pikiran sehingga menghasilkan suatu penalaran dengan kebenaran – kebenaran yang dapat dibuktikan secara matematis. Meskipun tanpa perhitungan melalui angka-angka atau dengan statistik, tetapi dapat diuji dan masuk akal akan kebenarannya.
Berbagai macam peralatan elektronik yang ada di sekitar kita, merupakan contoh nyata dari kemampuan manusia dalam menerapkan disiplin ilmu logika matematika di berbagai bidang kehidupan. Diantaranya seperti listrik, komputer, televisi dan radio dikembangkan atas dasar dan aturan logika matematika sederhana yang dibentuk dalam sebuah rangkaian elektronik yaitu menggunakan rangkaian benar yang biasanya dinyatakan dengan on dan off.
1.2 Rumusan Masalah
Adapun masalah yang akan di bahas dalam makalah ini adalah 1. Apa yang dimaksud tautologi ?
2. Tabel kebenaran tautologi ? 3. Apa yang dimaksud kontradiksi ? 4. Tabel kebenaran kontradiksi ?
1.3 Tujuan Penulisan
BAB II PEMBAHASAN
2.1 Tautologi
Tautologi adalah pernyataan majemuk yang selalu benar untuk semua kemungkinan nilai kebenaran dari pernyataan-pernyataan komponennya.
Untuk membuktikan apakah suatu pernyataan Tautologi, maka ada dua cara yang digunakan. Caranya dengan menggunakan tabel kebenaran, yaitu jika semua pilihan bernilai B (benar) maka disebut Tautologi.
Tabel kebenaran dari ( p q ) ˄ ⟹q berikut ini : p q ( p q )˄ ( p q) ˄ ⟹ q
B B B B
B S S B
S B S B
S S S B
Selalu bernilai Benar (Termasuk TAUTOLOGI) Contoh 1 :
Lihat pada argumen berikut :
Jika Tono pergi kuliah, maka Tini juga pergi kuliah. Jika Siska tidur, maka Tini pergi kuliah. Dengan demikian, jika Tono pergi kuliah atau Siska tidur, maka Tini pergi kuliah.
Diubah ke variabel proposional:
Diubah lagi menjadi ekspresi logika yang terdiri dari premis-premis dan kesimpulan.
Dari tabel kebenaran diatas menunjukkan bahwa pernyataan majemuk : ((A → B) ʌ (C → B)) → ((A V C) → B adalah semua benar (Tautologi).
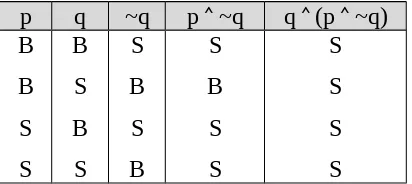
1. (p ʌ ~q) p Pembahasan :
Ini adalah tabel kebenaran yang menunjukkan Tautologi dengan alasan yaitu semua pernyataannya bersifat benar atau True (T). maka dengan perkataan lain pernyataan majemuk (p ʌ ~q) p selalu benar.
2. [(p q) ʌ p] p q Pembahasan :
(1) (2) (3) (4) (5)
Berdasarkan tabel diatas pada kolom 5, nilai kebenaran pernyataan majemuk itu adalah BBBB. Dengan perkataan lain, pernyataan majemuk [(p q) ʌ p] p q selalu benar
:
a. (p ʌ q) q Penyelesaian:
(p ʌ q) q ~(p ʌ q) v q ~p v ~q v q ~p v T T ...(Tautologi)
Dari pembuktian diatas telah nampaklah bahwa pernyataan majemuk dari (p ʌ q) q adalah tautologi karena hasilnya T (true) atau benar.
Pembuktian dengan menggunakan tabel kebenaran dari pernyataan majemuk (p ʌ q) q yaitu:
Pada tabel diatas nampaklah bahwa kalimat majemuk (p ʌ q) q merupakan Tautologi.
b. q (p v q) penyelesaian:
q (p v q) ~q v (p v q) ~q v (q v p) T v p T ...(Tautologi)
c. Tunjukkan bahwa pernyataan majemuk [(p ⟹ q) ~p] ˄ ⟹ ~p adalah sebuah tautologi. Jawab :
P q (p ʌ q) (p ʌ q) q B
B S S
B S B S
B S S S
Perhatikan tabel kebenaran berikut ini :
p Q ~p (p ⟹ q) (p ⟹ q) ~p˄ [(p ⟹ q) ~p] ˄ ⟹ ~p
B B S B S B
B S S S S B
S B B B B B
S S B B B B
Jadi pernyataan majemuk [(p ⟹ q) ~p] ˄ ⟹ ~p adalah sebuah Tautologi.
2.2 Tautologi dan Rumus Rumus
Di dalam logika kalimat semesta pembicaraannya adalah himpunan fakta-fakta (peristiwa, situasi) yang merupakan unsur-unsur di luar bahasa. Agar kita dapat membicarakan suatu peristiwa (fakta) tertentu dari semestanya kita memerlukan suatu lambang. Lambang ini disebut kalimat konstan/konstanta yang ditulis dengan "A", "B" dan sebagainya.
Contoh 2.2.1 Jika "Tono mahasiswa dengan IPK 3,5" mempunyai simbol "A" dan "Tono berasal dari luar Jawa" mempunyai simbol "B", maka kalimat
1. "Tono mahasiswa dengan IPK 3,5 dan berasal dari luar Jawa" mempunyai simbol "A B".
2. "Jika Tono berasal dari luar kota, maka Tono mahasiswa dengan IPK 3,5" mempunyai simbol "B⇒ A"
Dalam hal ini simbol "A", "B", "A B" dan "B⇒ A" merupakan konstanta kalimat atau kalimat konstan.
Definisi 2.2.2 Simbol yang melambangkan sebarang fakta (peristiwa) disebut vari- abel kalimat, yang ditulis dengan "p", "q", "r" dan sebagainya.
Contoh 2.2.3 Misalkan diberikan bentuk-bentuk 1. "p q"
2. "(p r)⇒ q"
dan jika variabel "p", "q" dan "r" diganti dengan kalimat-kalimat konstan akan berubah menjadi suatu pernyataan. Sebagai contoh pada kalimat ke-1,
1. Jika "p" disubstitusi dengan kalimat "Kuadrat bilangan real selalu non negatif" "q" disubstitusi dengan kalimat "Ada bilangan asli yang lebih kecil daripada 1"
Maka diperoleh pernyataan:
"Kuadrat bilangan real selalu non negatif dan ada bilangan asli yang lebih kecil daripada 1", yang bernilai salah.
2. Jika "p" disubtitusi dengan kalimat "Kuadrat bilangan real selalu non negatif" "q" disubstitusi dengan kalimat "Tidak ada bilangan asli yang lebih kecil dari- pada 1"
Maka diperoleh pernyataan:
"Kuadrat bilangan real selalu non negatif dan tidak ada bilangan asli yang lebih kecil daripada 1", yang bernilai benar.
Definisi 2.2.4 Bentuk-bentuk yang memuat variabel kalimat dan yang menya- jikan hukum-hukum logika kalimat disebut tautologi.
Di dalam tautologi setiap penggantian dari semua variabel di dalamnya dengan konstanta-konstanta kalimat akan menghasilkan suatu pernyataan yang bernilai benar. Tentu saja dalam suatu penggantian, untuk masing-masing variabel (sim- bol) yang sama harus digantikan dengan konstanta kalimat yang sama.
Untuk melihat apakah suatu bentuk kalimat merupakan suatu tautologi atau bukan dapat dilakukan dengan membuat tabel nilai kebenaran dari bentuk tersebut dengan mendaftar semua kemungkinan (kombinasi "p" dan "q") dari setiap nilai kebenaran variabelnya.
Selanjutnya, untuk membuktikan suatu bentuk kalimat merupakan tautologi selain menggunakan tabel kebenaran dapat juga dilakukan dari luar tabel dengan mengamati hasil dari tabel. Sebagai contoh akan dibuktikan
1. p =⇒ (p q), dan
Penyelesaian:
1. Bentuk ini merupakan implikasi, sehingga akan bernilai benar jika anteseden
bernilai salah atau konsekuen benar. Satu-satunya kemungkinkan yang dapat membuat kalimat bernilai salah adalah anteseden yaitu "p" bernilai benar. Tetapi jika "p" bernilai benar, maka sesuai nilai kebenaran dari disjungsi, bentuk "p q" pasti bernilai benar apapun "q". Akibatnya "p =⇒ (p q)" juga bernilai benar.
2. Bentuk kalimat ini merupakan biimplikasi, sehingga akan bernilai salah hanya jika keduanya mempunyai nilai kebenaran yang berbeda.
Karena "p' dan "q" merupakan variabel kalimat, maka hanya cukup dibuk- tikan salah satu sisi saja. Misalkan sisi sebelah kiri bernilai benar, maka "p" bernilai salah atau "q =⇒ r" bernilai benar. Jika "p" bernilai salah, maka apapun "r", implikasi "p =⇒ r" pasti bernilai benar, sehingga
"q =⇒ (p =⇒ r))"
pasti bernilai benar. Sedangkan jika "q =⇒ r" bernilai benar, maka "q" bernilai salah atau "r bernilai benar, sehingga bentuk
"q =⇒ (p =⇒ r))" pasti bernilai benar.
Rumus-rumus tautologi
Berikut ini diberikan rumus-rumus tautologi. Semua rumus dapat dibuktikan dengan menggunakan metode tabel nilai.
Rumus 2.1 (Komutatif) 1. p q⇐⇒ q p 2. p q⇐⇒ q p
Bukti:
p q . p q q p
Rumus 2.2 (Distributif)
1 . p (q r)⇐⇒ (p q) (p r) (Identitas, negasi rangkap dan idempoten)
1. p⇐⇒ p
1. (p⇐⇒ q)⇐⇒ ((p =⇒ q) (q =⇒ p))
2. ((p =⇒ q) (q =⇒ r))⇐⇒ (p =⇒ r). (Sifat Transitif) Metode Pembuktian
Di dalam bidang matematika ada tiga hukum penting tautologi yang digunakan sebagai metode pembuktian yaitu:
1. Modus Ponens 2. Hukum Kontraposisi 3. Reductio ad absurdum.
Modus ponens termasuk dalam bukti secara langsung. Sedangkan kontraposisi dan reductio ad absurdum dipandang sebagai bukti tidak langsung. Pembuktian suatu teori lebih diutamakan menggunakan bukti secara langsung.
Modus Ponens
Rumus : (p (p =⇒ q)) =⇒ q.
Hukum ini dapat disajikan dengan skema sebagai berikut :
=> .
Jika implikasi " =⇒ " merupakan fakta (hukum) yang benar dan fakta "" terjadi, maka dapat disimpulkan fakta "" pasti terjadi.
Contoh 2.4.1 Buktikan, bahwa salah satu titik potong grafik fungsi dengan per- samaan y = f(x) = 3x 3 3x 2 1 terhadap sumbu X berada di interval [1, 2]. Penyelesaian: Di dalam kalkulus berlaku sifat (implikasi) jika f kontinu pada interval [a, b], dan berlaku f(a) dan f(b) berbeda tanda, maka dapat ditemukan c [a, b] yang memenuhi f(c) = 0. Jadi implikasi ini bernilai benar.
3
f (x 0) = 3x 0 3x 02 1 = 0
Jadi salah satu titik potong grafik fungsi f terhadap sumbu X berada di interval [1, 2].
2.4.2 Hukum Kontraposisi
Seringkali kita mengalami kesulitan untuk membuktikan bahwa peristiwa "" terjadi dari diketahuinya fakta "". Untuk itu kita bisa menggunakan hukum kontraposisi
Rumus 2.14 (p =⇒ q)⇐⇒ (¯ q = ⇒ p¯).
Dengan kata lain, jika dari fakta " ¯" dapat dipastikan terjadinya "¯", maka da- pat ditarik kesimpulan, bahwa dengan berlakunya fakta "" dapat dipastikan ""
terjadi. Sebaliknya jika implikasi " =⇒ " merupakan fakta yang benar, maka dengan diketahuinya " ¯" terjadi, dapat ditarik kesimpulan "¯" pasti terjadi, seperti skema berikut ini:
=> ¯.
¯
Contoh Buktikan, bahwa jika 1 + (1) n= 0, maka̸ n genap.
Penyelesaian: Ingkaran n genap adalah n ganjil. Akibatnya (1) n =1, se- hingga 1 + (1) n = 0 yang merupakan ingkaran dari 1 + (1) n= 0. Jadi kon- ̸
traposisinya dapat dibuktikan, sehingga kalimat aslinya secara tidak langsung juga terbukti.
2.4.3 Reductio ad absurdum
Misalkan kita akan membuktikan pernyataan "". Untuk itu diandaikan yang berlaku adalah ingkaran dari "", yaitu "¯". Dari pengandaian tersebut dengan penalaran yang sahih diturunkan suatu kontradiksi. Hal ini hanya mungkin terjadi kalau terjadi kesalahan pada pengandaian, sehingga pengandaian harus diingkar, yaitu "¯
".
Rumus 2.15 p =⇒ (q q¯)) =⇒ p.p.Ā
Misalkan akan dibuktikan penyataan "". Diandaikan "". Jika dari kalimat "" dapat diturunkan " ", maka dapat disimpulkan "" terjadi.
=⇒ ( ) =⇒ Benar : Tautologi =⇒ ( ) Diturunkan dari ""
T : Modus Ponens
2.5 Kontradiksi
Kontradiksi adalah kebalikan dari tautologi yaitu suatu bentuk pernyataan yang hanya mempunyai contoh substansi yang salah, atau sebuah pernyataan majemuk yang salah dalam segala hal tanpa memandang nilai kebenaran dari komponen-komponennya. Untuk membuktikan apakah suatu pernyataan tersebut kontradiksi, maka ada dua cara yang digunakan. Cara pertama dengan menggunakan tabel kebenaran, yaitu jika semua pilihan bernilai F atau salah maka disebut kontradiksi,
Tabel kebenaran dari [( p ⟹ q ) p] ~q berikut ini :˄ ˄
Selalu bernilai Salah (Termasuk KONTRADIKSI)
Contoh dari Kontradiksi: 1. (A ʌ ~A)
Pembahasan: p q ~q ( p ⟹
q ) [ ( p ⟹ q ) p ] ˄
[ ( p ⟹ q ) ) p] ~q˄ ˄
B B S B B S
B S B S S S
S B S B S S
A ~A (A ʌ ~A) B
S
S B
S S
Dari tabel kebenaran diatas dapatlah disimpulkan bahwa pernyataan majemuk (A ʌ ~A) selalu salah.
2. P ʌ (~p ʌ q) Pembahasan:
p Q ~p (~p ʌ q) P ʌ (~p ʌ q)
B B S S
B S B S
S S B B
S S B S
S S S S
Ini adalah tabel kebenaran yang menunjukkan kontradiksi dengan alasan yaitu semua pernyataan bernilai salah (F).
Contoh: 3. Perhatikan tabel kebenaran dari [( p ⟹ q ) p] ~q berikut ini :˄ ˄
Selalu bernilai Salah (Termasuk KONTRADIKSI)
p q ~q ( p ⟹ q ) [ ( p ⟹ q ) p ]˄ [ ( p ⟹ q ) ) p] ~q˄ ˄
B B S B B S
B S B S S S
S B S B S S
Contoh: 4. Tunjukkan bahwa pernyataan majemuk q (p ~q) merupakan suatu ˄ ˄ kontradiksi.
Tabel kebenaran dari q (p ~q) adalah sebagai berikut :˄ ˄
p q ~q p ~q˄ q (p ~q)˄ ˄ B
B S S
B S B S
S B S B
S B S S
S S S S
Pada kolom yang paling kanan dari tabel di atas, tampak bahwa q ( p ~q ) selalu ˄ ˄ berniat salah untuk setiap nilai kebenaran dari komponennya. Oleh karena itu, pernyataan q (p ~q) adalah suatu “kontradiksi”.˄ ˄
BAB III PENUTUP
3.1 Kesimpulan
3.2 Saran
Dengan penyusunan makalah ini, kami berharap pengetahuan mengenai logika matematika dapat diaplikasikan dalam kehidupan atau dapat digunakan dalam banyak aspek kehidupan. Melalui logika, kita dapat mengetahui apakah suatu pernyataan bernilai benar atau salah. Hal terpenting yang akan didapatkan setelah mempelajari logika matematika adalah kemampuan atau keahlian mengambil kesimpulan dengan benar atau sah.
DAFTAR PUSTAKA
Sumber internet :
https:// id . wikipedia .org/ wiki / Tautologi (diakses tanggal 15 maret 2016)
https:// id . wikipedia .org/ wiki / Kontradiksi (diakses tanggal 15 maret 2016)
Sumber buku :
![Tabel kebenaran dari [( p ⟹ q ) p] ~q berikut ini :˄ ˄](https://thumb-ap.123doks.com/thumbv2/123dok/3240072.1741023/14.612.86.427.407.516/tabel-kebenaran-dari-p-q-p-berikut-ini.webp)