KAJIAN TELBS PADA REGRESI LINIER DENGAN KASUS PENCILAN

(1)

Prosiding SEMNAS Pendidikan Matematika 2017 ISBN. 978-602-50629-0-2 237 ©Program Studi Pendidikan Matematika FKIP-UNIKU

KAJIAN TELBS PADA REGRESI LINIER DENGAN KASUS PENCILAN Nurul Gusriani1), Firdaniza2), Novi Octavianti3)

1,2,3)

Departemen Matematika FMIPA Universitas Padjadjaran, Jalan Raya Bandung-Sumedang Km. 21 Jatinangor 45363

Email: 1nurul.gusriani@unpad.ac.id,2firdaniza@unpad.ac.id,3novioctaa@gmail.com

Abstrak

Masalah pencilan pada analisis regresi linier akan menyebabkan asumsi Gaussian tidak terpenuhi, sehingga jika digunakan metode kuadrat terkecil akan menghasilkan model yang tidak baik. Salah satu metode yang digunakan untuk memodelkan regresi lindier berganda pada data yang mengandung pencilan adalah metode TELBS. Metode ini menghasilkan model yang dapat mewakili sebagian besar data. Paper ini mengkaji metode TELBS dan mengaplikasikannya pada data simulasi dengan membangkitkan data error berdistribusi normal (0,1). Dengan menghitung koefisien determinasi berdasarkan metode kuadrat terkecil dan metode TELBS diperoleh hasil bahwa metode TELBS adalah metode yang tepat digunakan untuk menaksir parameter regresi linier ketika data terkontaminasi oleh pencilan.

Kata Kunci :data pencilan, koefisiendeterminasi, metode TELBS,

A. PENDAHULUAN

Data pencilan adalah salah satu masalah dalam analisis regresi linier. Adanya pencilan dalam data akan menyebabkan garis regresi berdasarkan Metode Kuadrat Terkecil (MKT) akan tertarik ke arah pencilan tersebut. Hal ini akan menyebabkan error yang dihasilan menjadi besar sehingga asumsi Gaussian tentang kenormalan bisa jadi tidak terpenuhi.

Untuk mengatasi hal tersebut, digunakan metode robust sebagai aternatif dari MKT. Prosedur robust ditujukan untuk mengakomodasi

adanya keanehan data, sekaligus meniadakan identifikasi adanya data outlier dan juga bersifat otomatis dalam menanggulangi data outlier (Cahyawati, D., 2009).

Sampai saat ini banyak penelitian yang mengkaji metode penaksiran parameter regresi yang robust terhadap pencilan. Masing-masing metode pada umumnya mempunyai kelebihan dan kekurangannya, sehingga, seiring dengan waktu, satu metode menjadi popular pada masanya dan kemudian dipatahkan oleh metode lain yang punya kelebihan. Beberapa metode

(2)

robust terhadap pencilan diantaranya yaitu: penaksir M yang dikemukakan Huber pada tahun 1973, Least Median Square (LMS) dan Least Trimmed Square (LTS) yang dikemukakan oleh Rousseeuw pada tahun 1984 (Hubert, Mia et al., 2008). Birch memperkenalkan metode pembobotan robust yang merupakan generalisasi dari penaksir M (Birch, J.B., 1992). Metode ini dinamakan penaksir Bounded-Influence (penaksir B-I). Selanjutnya, regresi Minimum Covariance Determinant (MCD) dikemukakan oleh Rousseeuw pada tahun 2004 dan lebih lanjut oleh Hubert (Hubert, Mia et al., 2008). Metode ini dapat mendeteksi adanya pencilan dalam data (Rousseeuw, 2004).

Metode terbaru adalah metode TELBS (Tabatabai, M.A. et al., 2012). Metode ini sekaligus dapat menangani masalah pencilan baik dalam ruang X ataupun ruang Y. Paper ini mengkaji metode TELBS dan memperlihatkan keunggulan metode TELBS dalam menaksir parameter regresi ketika pencilan terjadi di ruang X atau Y, dengan menggunakan data simulasi yang dibangkitkan dari distribusi normal (0,1). Koefisiem determinasi

menjadi dasar penentuan model terbaik.

B. TINJAUAN PUSTAKA

AnalisisRegresi

Analisis regresi merupakan aplikasi statistika yang dapat membantu memodelkan hubungan antara variabel bebas (X) dengan varibel tak bebas (Y). Model yang terbentuk dapat berupa hubungan linier atau non linier.

Model sampel regresi linier dapat dinyatakan dalam persamaan:

dimana i = 1, 2, …, n dan j =1, 2, …, p dengan yi dan xij berturut-turut merupakan pengamatan ke-i untuk variabel tak bebas dan variabel bebas ke-j. Metode yang umum digunakan untuk menaksir parameter adalah Metode Kuadrat Terkecil (MKT). Metode MKT merupakan metode yang paling mudah dilakukan dengan asumsi-asumsi tertentu yang disebut asumsi Gaussian (Myers, R.H, 1990). Jika semua asumsi Gaussian dipenuhi maka adalah parameter taksiran yang memenuhi sifat linier, tidak berbias dan memiliki varians minimum.

(3)

Persamaan (1) jika dinyatakan dalam bentuk matriks, akan menghasilkan:

Dengan menggunakan Metode Kuadrat Terkecil (MKT), komponen ditaksir dengan prinsip meminimumkan jumlah kuadrat residual sehingga menghasilkan taksiran sebagai berikut:

Koefisien Determinasi

Nilai koefisien determinasi R2 mencerminkan seberapa besar variasi dari variabel tak bebas (Y) dapat dijelaskan oleh variabel bebas (X). Nilai R2 bernilai antara 0 sampai 1, jika nilai R2 mendekati 1 menunjukkan tingkat ketepatan model yang semakin baik dalam menerangkan variasi data (Sembiring, R.K, 2003). Koefisien determinasi dinyatakan dalam rumus berikut:

Pencilan

Pencilan adalah pengamatan yang jauh dari pusat data yang mungkin berpengaruh besar terhadap koefisien regresi (Sembiring, R.K, 2003). Keberadaan pencilan dapat menyebabkan error dan variansi data menjadi besar. Akibatnya interval taksiran parameternya menjadi besar.

Pencilan baru ditolak jika setelah ditelusuri ternyata mengakibatkan kesalahan-kesalahan pada ukuran atau analisis, ketidaktepatan pencatatan data, dan terjadi kerusakan alat pengukuran. Bila ternyata bukan akibat dari kesalahan-kesalahan semacam itu, penyelidikan yang seksama harus dilakukan (Chandraningtyas, S., dkk., 2013). Penyelidikan atau diagnosa dalam analisis regresi adalah salah satu cara untuk memantau masalah yang timbul baik yang berkaitan dengan data ataupun model.

Salah satu cara diagnosa yang berkaitan dengan data yaitu pencilan adalah dengan menggunakan matriks hat (Myers, R.H, 1990) yang didefinisikan sebagai berikut:

(4)

Matriks hat pada dasarnya mentransformasikan vektor nilai pengamatan y ke vektor nilai y taksiran. Diagonal utama dari matriks hat yaitu hii akan menunjukkan nilai yang lebih besar dari 2p/n jika data merupakan pencilan.

Metode TELBS

Salah satu metode regresi untuk mengestimasi parameter regresi ketika terdapat pencilan adalah metode TELBS. Estimasi TELBS bekerja lebih baik jika dibandingkan dengan metode kuadrat terkecil, penaksir M dan MM (Tabatabai, M.A. et al., 2012).

Menurut Tabatabai et al. (2012), regresi robust estimasi TELBS dilakukan dengan meminimumkan fungsi objektif

dimana:

(7) dan

Nilai estimator dapat diperoleh dari persamaan sebagai berikut:

(10)

Pemilihan konstanta 1,1926 membuat merupakan suatu estimasi yang mendekati tak bias dari sampel yang terbatas (Rousseeuw, P.J and Croux, 1993). adalah bilangan real positif yang disebut sebagai konstanta kesesuaian (tunning constant) yang bernilai 0.628.

Untuk meminimumkan persamaan (6), turunan dari terhadap 0 dan j disamakan dengan nol, sehingga menghasilkan persamaan:

(11)

dimana

.

Didefinisikan fungsi pembobot wii (Tabatabai, M.A. et al., 2012) adalah:

(12)

(5)

maka persamaan (11) dapat ditulis menjadi:

(13) Persamaan (13) jika diturunkan terhadap 0 dan j akan menghasilan bentuk matriks sebagai berikut :

sehingga diperoleh penaksir metode TELBS yaitu:

(14)

dimana W adalah matriks bujursangkar degan elemen diagonalnya adalah wii pada persamaan (12) dan entri matriks

Pada metode TELBS nilai taksiran diperoleh dengan melakukan iterasi pada matriks W. Iterasi berhenti jika kekonvergenan tercapai.

Koefisien determinasi pada analisis regresi robust dengan metode estimasi TELBS didefinisikan sebagai berikut (Tabatabai, M.A. et al., 2012):

(15)

DATA

Data yang digunakan adalah data simulasi yang diperoleh dengan membangkitkan distribusi normal (0,1) sebanyak n=30. Simulasi dilakukan untuk melihat pola yang dihasilkan dengan kondisi data yang disesuaikan. Pada paper ini dilakukan simulasi dua kali dengan mengkondisikan terjadi pencilan masing-masing di ruang X dan ruang Y. Dengan dua kondisi pencilan di ruang yang berbeda kemudian dilakukan analisis untuk memperlihatkan keunggulan metode TELBS yang dapat menangani pencilan baik di ruang X maupun di ruang Y.

Prosedur untuk simulasi diberikan sebagai berikut:

1. Membangkitkan 30 data error yang mengikuti distribusi normal (0,1).

2. Menentukan data secara sembarang untuk dijadikan variabel bebas.

3. Membentuk variabel tak bebas dengan menggunakan persamaan (2) dengan koefisien

(6)

intersep dan koefisien regresi yang ditentukan terlebih dahulu. 4. Setelah terbentuk variabel bebas dan variabel tak bebas, beberapa data diubah menjadi data ekstrim sebagai pencilan. 5. Set data kemudian diolah

berdasarkan MKT dan metode TELBS.

C. HASIL DAN PEMBAHASAN

Simulasi dilakukan untuk membuktikan ketepatan metode pada data yang sudah dipersiapkan sebelumnya dengan mengkondisikan adanya pencilan di beberapa titik. Hasil data hasil simulasi dengan pencilan di ruang X dan ruang Y disajikan pada Tabel 1 dan Tabel 2 sebagai berikut:

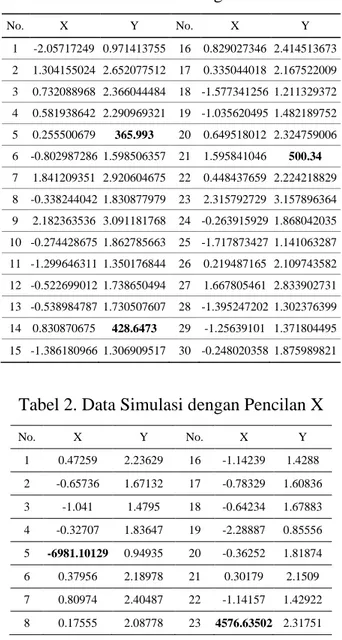
Tabel 1. Data Simulasi dengan Pencilan Y

No. X Y No. X Y 1 -2.05717249 0.971413755 16 0.829027346 2.414513673 2 1.304155024 2.652077512 17 0.335044018 2.167522009 3 0.732088968 2.366044484 18 -1.5773412561.211329372 4 0.581938642 2.290969321 19 -1.0356204951.482189752 5 0.255500679 365.993 20 0.649518012 2.324759006 6 -0.8029872861.598506357 21 1.595841046 500.34 7 1.841209351 2.920604675 22 0.448437659 2.224218829 8 -0.3382440421.830877979 23 2.315792729 3.157896364 9 2.182363536 3.091181768 24 -0.2639159291.868042035 10 -0.2744286751.862785663 25 -1.7178734271.141063287 11 -1.2996463111.350176844 26 0.219487165 2.109743582 12 -0.5226990121.738650494 27 1.667805461 2.833902731 13 -0.5389847871.730507607 28 -1.3952472021.302376399 14 0.830870675 428.6473 29 -1.25639101 1.371804495 15 -1.3861809661.306909517 30 -0.2480203581.875989821

Tabel 2. Data Simulasi dengan Pencilan X

No. X Y No. X Y 1 0.47259 2.23629 16 -1.14239 1.4288 2 -0.65736 1.67132 17 -0.78329 1.60836 3 -1.041 1.4795 18 -0.64234 1.67883 4 -0.32707 1.83647 19 -2.28887 0.85556 5 -6981.10129 0.94935 20 -0.36252 1.81874 6 0.37956 2.18978 21 0.30179 2.1509 7 0.80974 2.40487 22 -1.14157 1.42922 8 0.17555 2.08778 23 4576.63502 2.31751

(7)

9 -0.29233 1.85383 24 -0.02679 1.98661 10 -0.00213 1.99894 25 0.22662 2.11331 11 -3345.20931 1.89534 26 -1.22583 1.38708 12 0.38426 2.19213 27 -0.69885 1.65058 13 0.41239 2.2062 28 -1.82963 1.08518 14 0.1836 2.0918 29 0.11924 2.05962 15 0.30538 2.15269 30 1.03969 2.51985

Pada Tabel 1 diberikan pencilan di ruang Y pada data ke-5,14, dan 21, kemudian dianalisis dengan menggunakan MKT dan metode TELBS sebagai berikut:

Tabel 3. Hasil Data Simulasi dengan MKT dan Metode TELBS

Komponen MKT TELBS

0 43.9265 1.9999 1 28.2803 0.4999

R2 0.0678 0.9999

Pada Tabel 3 dapat dilihat bahwa hasil taksiran dengan menggunakan metode TELBS memperlihatkan nilai koefisien determinasi yang dihasilkan hampir sempurna.

Untuk data hasil simulasi dengan pencilan di ruang X pada Tabel 2, terdapat tiga buah pencilan di ruang X, yaitu pada data ke-5,11, dan 23. Data ini kemudian dianalisis dengan menggunakan MKT dan metode TELBS seperti pada Tabel 4. Tabel 4. Hasil Data Simulasi dengan MKT

dan Metode TELBS

Komponen MKT TELBS 0 1.83751237 4 2.00000098 8 1 3.67673E-05 0.50000148 3 R2 0.021933811 0.99999999

Sejalan dengan hasil pada data pencilan di ruang Y, koefisien determinasi hasil metode TELBS kembali menunjukkan

hasil yang hampir sempurna. Dengan demikian dapat dikatakan bahwa model

(8)

yang diperoleh adalah model yang terbaik.

D. SIMPULAN DAN SARAN

Metode TELBS dapat menghasilkan taksiran parameter regresi ketika terdapat data pencilan baik di ruang X maupun di ruang Y. Model yang diperoleh dengan menggunakan metode TELBS menjadi model yang mewakili sebagian besar data dengan ditandai oleh nilai koefisien determinasi yang tinggi.

Paper ini hanya membahas pembentukan model regresi linier ketika pencilan terdeteksi, disarankan untuk penelitian selanjutnya dilakukan pengujian koefisien regresi.

UCAPAN TERIMA KASIH

Ucapan terima kasih kepada pihak Universitas Padjadjaran yang telah mendanai penelitian dalam skema Hibah Internal Universitas Padjadjaran.

DAFTAR PUSTAKA

Birch, J.B. (1992). Estimation and Inference in Multiple Regression Using Robust Weight: A Unifield Approach, Technical Report 92-2. Departemen of Statistics Virginia Polytechnic Institute and State University. Blackburg Virginia. Cahyawati, D. (2009). Efektifitas

Metode Regresi Robust Penduga Welsch dalam Mengatasi Pencilan pada Pemodelan Regresi Linear Berganda, Jurnal Penelitian Sains, Vol.12, no.1(A). Unsri, Sumatera Selatan.

Chandraningtyas, S., dkk. (2013). Regresi Robust MM-Estimator untuk Penanganan Pencilan pada

Regresi Linier Berganda, Jurnal Gaussian, Vol. 2, no.4, 395-404. Undip, Semarang.

Gujarati, D.N. (1988). Basic Econometrica, 2 nd Edition. New York, McGraw-Hill Inc.

Gusriani, N., Firdaniza, Ardelina, D. (2011). Kajian Penaksir Bounded-Influence dan Metode Minimum Covariance Determinant pada Analisis Regresi Linier Berganda untuk Kasus Pencilan, Laporan Penelitian. Jurusan Matematika FMIPA Unpad, Bandung.

Hubert, Mia et al. (2008). High-Breakdown Robust Multivariate Methods. Statistical Science, Vol.

23 No.1 (online:

http://arxiv.org/pdf/0808.0657).

Myers, R.H. (1990). Classical and Modern Regression With Applications. 2 nd edition. Boston, PSW-KENT Publishing Company. Rousseeuw, P.J and Croux. (1993).

Alternative to the Median Absolute Deviation. American Statistical Association. 1993, Vol. 88, No. 424, 1993.

Rousseeuw, P.J, et al. (2004) Robust Multivariat Regression,

Technometrics (online), Vol. 46. No. 3

(ftp://ftp.win.ua.ac.bc/pub/preprint

s/04/Robmul04.pdf)

Sembiring, R.K. (2003). Analisis Regresi, Edisi 2. Bandung: ITB. Tabatabai, M.A. et al., (2012). TELBS

Robust Linear Regression Method, Open Acces Medical Statistics, USA, Dove Medical Press.