Vol. 13, No. 2 (2017), pp. 115–121. doi:10.24198/jmi.v13.n2.11891.115-121
Bilangan Kromatik Lokasi
n
Amalgamasi Bintang
yang dihubungkan oleh suatu Lintasan
Asmiati
Jurusan Matematika, Fakultas MIPA, Universitas Lampung Jl. Brodjonegoro No. 1 Gd. Meneng, Bandar Lampung
[email protected], [email protected]
Abstrak
Bilangan kromatik lokasi graf diperkenalkan oleh Chartrand et al. pada tahun 2002. Konsep ini merupakan perpaduan dari konsep dimensi partisi dan pewarnaan graf. Penentuan bilangan kromatik lokasi suatu graf dilakukan dengan mengkonstruksi batas atasnya dan penentuan batas bawahnya. Dalam paper ini, kami mengkaji tentang bilangan kromatik lokasi amalgamasi bintang tertentu, yang dinotasikan dengannSk,m. Bilangan kromatik lokasi nSk,m untuk k, m≥2, k ≤m, dengan
n, k, mbilangan asli adalah (m+1), jika 1≤n≤
m k−1
dan(m+2), untukn≤
m k−1
Kata kunci: amalgamasi bintang, bilangan kromatik lokasi graf, pewarnaan graf.
Abstract
The locating chromatic number of a graph was introduced by Chartrand et al in 2002. This concept is combined from the graph partition dimen-sion and graph coloring. Determining the locating chromatic number of graph with construct the upper bound and the lower bound of the graph. In this paper, we determine the locating chromatic number for certain amalgamation of stars, denoted by nSk,m. We prove that the locating chromatic number,nSk,mfor,k, m≥2, k≤m, natural numbersn, k, m is(m+ 1), if1≤n≤
m k−1
and(m+ 2), forn≤
m k−1
.
Keywords: amalgamation of stars, locating-chromatic number of graph, graph col-oring
1. Pendahuluan
Bilangan kromatik lokasi pada suatu graf merupakan pengembangan konsep dimensi partisi (Chartrand, et al, [6]) dan pewarnaan suatu graf. Berikut ini diberikan definisi bilangan kromatik lokasi graf yang diambil dari Chartrand, et al, [7]. Misalkancsuatu pewarnaan titik pada grafGdengan warna titikutidak sama dengan warna titikv(c(u)6= (v)) untukudanv
yang bertetangga diG. MisalkanCi himpunan titiktitik yang diberi warnai, yang selanjutnya disebut kelas warna dan Π =C1, C2, , Ck adalah himpunan yang terdiri dari kelas kelas warna dari V(G). Kode warna cΠ(v) dari v adalah k-pasang terurut (d(v, C1), d(v, C2), , d(v, Ck)) dengan d(v, Ci) = min{d(v, x)x∈ Ci} untuk 1≤ i ≤k. Selanjutnya, k-pasang terurut dari kode warna tersebut, kita nyatakan dengan komponen ke-1,, komponen ke-k. Jika setiap titik di V(G) mempunyai kode warna yang berbeda, maka cdisebut pewarnaan lokasi dari grafG.
2000 Mathematics Subject Classification: 05C12, 05C15. Received: 2017-04-18; accepted: 2017-11-01
Banyaknya warna minimum yang digunakan untuk pewarnaan lokasi tersebut disebut bilangan kromatik lokasi dariG, dan dinotasikan denganχL(G).
Teorema 1.1. (Chartrand, et al, [7]) MisalkanGgraf terhubung dancsuatu pewarnaan lokasi
padaG. Jikas dant adalah dua titik berbeda diGsedemikian sehinggad(s, u) =d(t, u)untuk setiapu∈V(G)\{s, t}, makac(s)6=c(t). Dalam hal khusus, jikasdantadalah titik-titik yang tidak bertetangga di Gsedemikian sehingga N(s) =N(t), makac(s)6=c(t).
Bukti. Misalkancadalah suatu pewarnaan lokasi pada graf terhubungGdan misalkan
Π = {C1, C2, , Ck} adalah himpunan kelas-kelas warna dariV(G). Untuk titik s, t ∈ V(G), andaikan c(s) = c(t) sedemikian sehingga titik s, t ∈V(G), andaikanc(s) = c(t) sedemikian sehingga titik s dan t berada dalam kelas warna yang sama, misal Ci dari Π. Akibat-nya, d(s, Ci) = d(t, Ci) = 0. Karena d(s, u) = d(t, u) untuk setiap u ∈ V(G)\{s, t} maka d(s, Ci) =d(t, Cj) untuk setiapj /∈i,1≤j ≤≤k. Akibatnya,cΠ(s) =cΠ(t) sehinggac bukan
pewarnaan lokasi. Jadic(s)6=c(t) ✷
Akibat 1.2. (Chartrand, et al, [7]) JikaGadalah suatu graf terhubung dan terdapat titik yang
bertetangga dengan k daun diG, maka χL(G)≥k+ 1.
Kajian bilangan kromatik lokasi pada suatu graf merupakan hal yang menarik hingga saat ini, karena belum adanya teorema yang dapat digunakan untuk menentukan bilangan kromatik lokasi graf secara umum. Pada graf pohon, Chartrand et al. [7] telah mendapatkan bilangan kromatik lokasi pada graf lintasan, graf bintang, graf bintang ganda, graf ulat, dan graf pohon berorden≥5, yang memiliki bilangan kromatik lokasi 3,4, , nkecualin−1. Selanjutnya Asmiati et al. [1],[2] telah mendapatkan bilangan kromatik lokasi pada graf amalgamasi bintang homogen dan graf kembang api; Des Welyyanti [8] untuk graf pohon n-ary lengkap, dan Asmiati [4] pada graf amalgamasi bintang tak homogen.
Beberapa kajian tentang karakterisasi graf amalgamasi pohon dengan bilangan kromatik lokasi tertentu juga telah dilakukan diantaranya adalah: Chartrand et al. [7] telah mendap-atkan karakterisasi graf berbilangan kromatik lokasi (n−1) atau (n−2); Asmiati et al. [3] untuk karakterisasi graf memuat siklus berbilangan kromatik lokasi tiga; Baskoro et al. [5] telah mendapatkan karakterisasi semua pohon berbilangan kromatik lokasi tiga.
Berdasarkan hasil-hasil yang sudah didapatkan oleh Asmiati et al [1] dan Asmiati [4], maka pada paper ini didiskusikan tentang bilangan kromatik lokasi amalgamasi bintang ter-tentu, yaitu n buah amalgamasi bintang homogen yang dihubungkan oleh sebuah lintasan.
2. Hasil dan Pembahasan
Misalkan Sm+2, adalah graf bintang dengan (m+ 2) titik. Amalgamasi bintang, Sk,m dengank, m≥2 adalah graf yang diperoleh dari (k−1) buah graf bintangSm+2, dengan cara
menyatukan sebuah daun dari setiap grafSm+2 . Titik penyatuan tersebut disebut titik pusat
Sk,m . GrafnSk,m adalah graf yang diperoleh dari nkopi graf Sk,m, yang mana setiap titik pusatSk,m, xi, , i= 1,2, , ndihubungkan oleh suatu lintasan dan (n−1) titik baru, dinotasikan yi, i= 1,2, , n−1 merupakan titik-titik subdivisi pada sisixixi+1, i= 1,2, , n−1. Selanjutnya,
pada graf nSk,m , titik pusat untuk setiap Sm+2, , dinotasikan denganlij, i = 1,2,3, , n dan j = 1,2,3, , k−1, sedangkan daun ke- t yang menempel pada titik li
j, dinotasikan dengan ljti, t= 1,2,3, , m.
Pada bagian ini akan didiskusikan bilangan kromatik lokasinSk,m untukk≤mdengan n, k, mbilangan asli.
Teorema 2.1. Misalkan nSk,m adalah graf amalgamasi bintang tertentu untuk ,k, m ≥ 2,
k≤m, dengann, k, mbilangan asli
χL(nSk,m) =
(
m+ 1; 1≤n≤j m k−1
k
Bukti. Pertama-tama akan ditentukan batas bawah dan batas atas dari χL(nSk,m)
untuk 1 ≤ n ≤ 1 ≤ n ≤ j m k−1
k
1 ≤ n ≤ 1 ≤ n ≤ j m k−1
k
. Karena setiap titik li j untuk i = 1,2,3, , n dan j = 1,2,3, , k−1 bertetangga dengan m daun, maka berdasarkan Akibat 1.1, χL(nSk,m)≥m+ 1. Selanjutnya akan ditentukan batas atas dariχL(nSk,m) untuk 1≤ n≤1≤n≤j m
k−1 k
. Misalkancadalah suatu pewarnaan dariV(nSk,m) menggunakan (m+ 1) warna, yaitu
• c(xi) = 1, untuki= 1,2,3, , n
• c(yi) = 2, untukiganjil dan c(yi) = 3, untukigenap,i= 1,2,3, , n−1 • {c(li
j)}= 2,3, , m+ 1, untuki= 1,2,3, , ndanj= 1,2,3, , k−1
• {c(ljti)} = 1,2,3, , m+ 1\{c(lij)}, untuk i = 1,2,3, , n dan j = 1,2,3, , k −1 dan t= 1,2,3, , m
Akibatnya pewarnaan c akan membangun suatu partisi Π = {C1, C2, C3, , Cm+1} pada
V(nSk,m) , denganCiadalah himpunan dari semua titik yang bewarnaiuntuki= 1,2,3, , m+ 1.
Selanjutnya akan ditunjukkan bahwa kode warna untuk setiap titik diV(nSk,m)berbeda. Misalkanu, v ∈V(nSk,m) danc(u) =c(v) maka pandang kasus-kasus berikut ini:
• Jika u=xi, v=xk untuk suatui, kdani6=k, makacΠ(u)6=cΠ(v) karenad(u, Ci)6= d(v, Ci).
• Jikau=xi, v=ljti untuk suatui, j, t, maka cΠ(u)6=cΠ(v), karena pada cΠ(u) , titik
yang diberi warna (m+ 1) terdapat sekurang-kurangnya dua komponen bernilai satu, sedangkan padacΠ(v), titik yang diberi warna (m+ 1) memuat tepat satu komponen
yang bernilai 1.
• Jika u=xi, v=ljth untuk suatui, h, j, tdani6=h, makacΠ(u)6=cΠ(v), karena pada
cΠ(u) , titik yang diberi warna (m+ 1) terdapat sekurang-kurangnya dua komponen
bernilai satu, sedangkan pada cΠ(v), titik yang diberi warna (m+ 1) memuat tepat
tepat satu komponen yang bernilai 1.
• Jikau= yi, v = lij, untuk suatu i, j maka cΠ(u) 6= cΠ(v). karena pada cΠ(u) , titik
yang diberi warna (m+ 1) terdapat tepat dua komponen yang bernilai 1, sedangkan padac(v), titik yang diberi warna (m+1) terdapat sekurang-kurangnya dua komponen bernilai satu.
• Jika u =yi, v = lkj, untuk suatu i, k, j dan i 6= k maka cΠ(u) 6= cΠ(v) karena pada
cΠ(u) , titik yang diberi warna (m+ 1) terdapat tepat dua komponen yang bernilai
1, sedangkan padac(v), titik yang diberi warna (m+ 1) terdapat sekurang-kurangnya dua komponen bernilai satu.
• Jika u=yi, v=ljti untuk suatu i, j, t maka cΠ(u)6=cΠ(v). karena padacΠ(u), titik
yang diberi warna (m+ 1) terdapat tepat dua komponen yang bernilai 1, sedangkan padac(v), titik yang diberi warna (m+ 1) terdapat tepat satu komponen yang bernilai satu.
• Jika u=yi, v =ljtk untuk suatu i, k, j, tdan i6=k maka cΠ(u)6=cΠ(v) karena pada
cΠ(u) , titik yang diberi warna (m+ 1) terdapat tepat dua komponen yang bernilai 1,
sedangkan pada c(v), titik yang diberi warna (m+ 1) terdapat tepat satu komponen yang bernilai satu.
• Jikau=li
j, v=ljtimaka untuk suatui, j, tmakacΠ(u)6=cΠ(v)karena padacΠ(u), titik
yang diberi warna (m+ 1) terdapat sekurang-kurangnya dua komponen bernilai satu, sedangkan pada c(v), titik yang diberi warna (m+ 1) terdapat tepat satu komponen yang bernilai satu.
• Jikau=li
j, v=lhtk, maka untuk suatui, j, k, h, tdani6=k, j=6 hmakacΠ(u)6=cΠ(v)
karena pada cΠ(u), titik yang diberi warna (m+ 1) terdapat sekurang-kurangnya dua
• Jika u=ljti, v =lhti, maka untuk suatu i, j, h, t, j 6= hmaka cΠ(u) 6=cΠ(v) karena
Dapat dilihat bahwa kode warna dari semua titik diV(nSk,m)untukn≤
j
m k−1
k
adalah berbeda, makacmerupakan pewarnaan lokasi. JadiχL(nSk,m)≤m+ 1 . Akibatnya diperoleh χL(nSk,m) =m+ 1 .
Selanjutnya akan ditentukan batas bawah dan batas atas untukn >j m k−1
. Akan ditunjukkan bahwa (m+ 1) tidaklah cukup untuk mewarnai nSk,m. Untuk suatu kontradiksi, andaikan terdapat pewarnaan lokasi c pada nSk,m menggunakan (m+ 1) warna. Karena n >
j
m k−1
k
, maka terdapat suatu i,j,k dengan i 6= k sedemikian hingga {c(li
j)} = {c(ljk)} = {1,2,3, , m+ 1}.
Misalkancadalah pewarnaannSk,mmenggunakan (m+2) warna untukn >
j
m k−1
k
. Beri warna titik titik di nSk,msebagai berikut:
• c(xi) = 1, untuki= 1,2,3, , n
Pewarnaanc akan membangun suatu partisi Π = V(nSk,m). Akan ditunjukkan bahwa kode warna semua titik di nSk,mberbeda.
cΠ(x1) =
0; komponenke−1
1;komponen ke−2danke−k
0;komponenke−1 2; komponen ke−2 1;komponen ke−(m+ 1)
cΠ(y1) =
1;komponenke−1 0;komponen ke−2
cΠ(l11t) =
2;komponen ke−1 1;komponen ke−2 0;komponen ke−(t+ 1) 2;komponen ke−(m+ 1) 2; lainnya
cΠ(l11m) =
2; komponen ke−1 1; komponen ke−2 0;komponen ke−(m+ 1) 2; lainnya
cΠ(l1(k−1)m) =
2;komponen ke−1 1;komponen ke−(k−1) 0;komponen ke−(m+ 1) 4;lainnya
)
Untuki≥2, j= 1,2,3, , k−1, t= 1,2,3, , m
cΠ(ljmi ) =
0; komponen ke−t
1;komponen ke−(j+ 1)
i+ 5; lainnya
Karena kode warna semua titik di V(nSk,m) berbeda, maka c merupakan pewarnaan lokasi padanSk,m. JadiχL(nSk,m)≤m+2 untukn >
j
m k−1
k
. Akibatnya,χL(nSk,m) =m+2. ✷
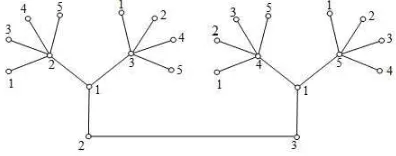
Sebagai ilustrasi, diberikan pewarnaan lokasinS3,4 untuk 1≤n≤2 yang dapat dilihat
pada gambar berikut:
Gambar 1. Pewarnaan lokasi minimum pada graf 2S3,4
Sebagai ilustrasi, diberikan pewarnaan lokasinS3,4untukn >2 yang dapat dilihat pada
gambar berikut:
3. Simpulan
Bilangan kromatik lokasi pada grafnSk,muntukk, m≥2, k≤m, dengann, k, mbilangan asli adalah (m+ 1), jika 1≤n≤1≤n≤j m
k−1 k
dan (m+ 2), untuk n >j m k−1
k
. Penelitian ini dapat dilanjutkan untukk > m.
Daftar Pustaka
[1] Asmiati, H. Assiyatun, E.T. Baskoro, 2011, Locating- chromatic number of amalgamation of stars, ITB J.Sci., 43A, 1-8.
[2] Asmiati, H. Assiyatun, E.T. Baskoro, D. Suprijanto, R. Simanjuntak, S. Uttunggadewa, 2012, Locating-chromatic number of firecracker graphs, Far East J. Math.Sci., 63(1), 11-23.
[3] Asmiati, E.T. Baskoro, 2012, Characterizing of graphs containing cycle with locating-chromatic number three, AIP Conf. Proc., 1450, 351-357.
[4] Asmiati, Locating-chromatic number of non homogeneous amalgamation of stars, 2014, Far East J. Math. Sci., 93(1), 89-96.
[5] E. T. Baskoro, Asmiati, 2013, Characterizing all trees with locating-chromatic number 3, Elec. J. Graph Theory Appl. 1(2), 109-117.
[6] G. Chartrand, E. Salehi, dan P. Zhang, 1998, On the partition dimension of graph, Congr. Numer., 130, 157-168.
[7] G. Chartrand, D. Erwin, M.A. Henning, P.J. Slater, dan P. Zhang, 2003, Graph of order n with locating-chromatic number n-1, Discrete Math., 269, 65-79.