MATEMATIKA TEKNIK I Belajar Matematika T

Supriono

suprionomuda@yahoo.com

Bismillahirrahmanirrahim.

Segala puji Bagi Allah, Tuhan seru sekalian alam yang telah membimbing penulis untuk

memperbaiki buku pegangan Matematika Teknik bagi mahasiswa Teknik Jurusan Teknik Elektro.

Buku ini disusun selain sebagai bekal untuk mempelajari mata kuliah tingkat lanjut juga untuk

memberikan gambaran bagi mahasiswa Teknik Elektro tentang permasalahan dibidang Teknik Elektro.

Agar tujuan dari buku ini dapat tercapai maka disarankan bagi pengguna untuk menggunakan Scilab,

yang dapat didownload di “www.scilab.org”.

Pilihan penulis untuk menggunakan Scilab karena aplikasi ini dapat didownload secara gratis

serta memiliki banyak fungsi untuk bidang Engineering. Selain itu, Scilab memiliki beberapa toolbox,

didalam Scial disebut ATOM, dapat kita pilih sesuai dengan kebutuhan kita. Toolbox di Scilab sangat

lengkap dan Powerfull untuk bidang Teknik Elektro. Penulis menyarankan agar para pembaca tidak

hanya menginstall Scilab saja tetapi juga harus melengkapi dengan ATOM (toolbox).

Penulis menyadari banyak dari pembaca belum mengetahui tentang Scilab maka penulis

melampirkan tentang Scilab diakhir buku ini sebagai lampiran. Pada lampiran pertama sangat berguna

bagi pembaca yang sama sekali tidak mengetahui tentang Scila. Lampiran pertama tersebut karangan

Mirza Nur Hidayat. Agar pembaca memiliki pengetahuan yang lebih tentang grafik, maka penulis pada

lampiran kedua menulis khusus tentang Grafik yang berjudul “Grafik Dua Dimensi”. Karena buku ini

ditujukan bagi mahasiswa Elektro maka pada lampiran akhir, penulis melampirkan bagaimana

menghubungkan Scilab dengan Arduino. Lampiran tersebut berjudul “SCILAB untuk Elektronika dan

Instrumentasi Dasar” yang ditulis oleh Mirza Nur Hidayat.

Walaupun buku ini telah diterapkan semenjak tahun 2002 tetapi masih banyak kekurangan

ataupun kesalahan karena rendahnya ilmu yang penulis miliki. Menyadari semua kekurangan dan

kelemahan pada diri penulis maka sangat diharapkan kritik dan saran serta masukan dari semua pihak

untuk perbaikan buku ini. Disisi lain buku ini boleh dicopy, diperbanyak, didistribusikan kepada orang

lain dan mengambil keuntungan dari buku ini tampa ada pelanggaran hak cipta karena buku ini bersifat

Open Content atau lebih dikenal dengan nama Copy Left. Aturan mainnya hanyalah anda tetap wajib mencantumkan nama penulis.

Kiranya buku ini dapat menjadi salah satu bagian dari untaian mutiara ilmu yang sedang dirajut

Halaman

Sampul Dalam ...i

Kata Pengantar ...ii

DAFTAR ISI ...iii

BAB I PERSAMAAN DIFERENSIAL ORDE SATU 1. Pendahuluan ...1.

2. Penyelesaian Persamaan Dierensial Orde Satu ...2.

3. Orthogonal Trayektori ...15.

4. Penerapan Persamaan diferensial Orde Satu ...18.

BAB II PERSAMAAN DIFERENSIAL ORDE DUA 1. Pendahuluan ...30.

2.Persamaan Diferensial Orde Dua dengan Koefisien Konstan – Penyelesaian Umum ....32.

3. Persamaan Diferensial dalam Sistem Linier ...38.

4. Aplikasi Persamaan Diferensial Linier Orde Dua ...…51.

5. Persamaan Diferensial Euler - Cauchy ...65.

BAB III PEMETAAN LAPLACE 1. Pendahuluan ...68.

2. Penerapan Pemetaan Laplace pada Persamaan Diferensial ...74.

3. Uraian Atas Pecahan Parsial ...80.

4. Fungsi Unit Step, Pergeseran pada Salib Sumbu-s dan Pergeseran pada salib sumbu-t ...83.

5. Fungsi Fungsi Periodik ...89.

1. Pendahuluan ...105.

2. Representasi Fungsi Fungsi Periodik dalam Deret Fourier ...106.

3. Fungsi Genap dan Fungsi Ganjil ...110.

4. Pemetaan Cosinus Fourier dan Pemetaan Sinus Fourier ...123.

5. Pemetaan Fourier ...127.

BAB V KALKULUS DIFERENSIAL VEKTOR 1. Pendahuluan. ...134.

2. Tangen, Panjang Busur dari Kurva ...136.

3. Kecepatan dan percepatan ...140.

4. Divergensi dan Curl ...142.

BAB VI DERET 1. Pendahuluan ...145.

2. Deret Mac Laurin dan Deret Taylor ...149.

3. Penyelesaian Persamaan Diferensial dengan Deret ...151.

4. Persamaan Diferensial Orde Dua dengan Koefisien Berubah ...159.

5. Persamaan Legendre ...162.

BAB 7 MATRIK DAN DETERMINAN 1. Definisi ...165.

2. Sistem Persamaan Linier ...171.

3. Eigen Value dan Eigen Vector ...173.

4. Penyelesaian Persamaan Diferensial dengan Metode Matrik ...177.

5. Penerapan dalam Bidang Teknik ...185.

BAB I

PERSAMAAN DIFERENSIAL ORDE SATU

1. Pendahuluan

Persamaan diferensial menyatakan hubungan dinamik antara variabel bebas dan variabel tak bebas, maksudnya hubungan tersebut memuat besaran besaran yang berubah, dan karena itu persamaan persamaan diferensial sering muncul dalam persoalan persoalan teknik .

Orde suatu persamaan diferensial ditentukan oleh turunan tertinggi yang terdapat dalam persamaan diferensial tersebut.

Contoh.

Orde satu : 3tdy dt−4y

2₌

0

Orde dua : 5tyd 2

y dt2−6

dy

dtysint=0 Orde tiga : d

3 y

dt3−5y2=0 dst.

Setelah mempelajari persamaan diferensial orde satu maka diharapkan dapat :

1. Dapat menyelesaikan persamaan diferensial orde satu dengan bermacam macam metode.

2 Penyelesaian Persamaan Diferensial Orde Satu 2.1 Metode Integrasi Langsung.

Jika persamaan differensial dapat disusun dalam bentuk : dy_dt=ft _{, maka} persamaan dapat diselesaikan dengan metode integrasi sederhana.

Contoh 1. 2tdy

dt−2t

2₋

8=0 … … … …. … … … (1)

⇒dy

dt=t 4

t ⇒∫dy=∫



t 4

t



dt

⇒y=1

2t

2_

4 lntC _{… … … .(2)} Persamaan (2) disebut penyeselaian umum bagi persamaan diferensial (1). Jika harga y diketahui pada harga t tertentu maka harga C dapat ditentukan dan penyeselaiannya disebut penyelesaian khusus.

Contoh 2. etdy

dt4e

2t₋

5=0 _{pada t = 0 , y = 0 … … … ... ...(3)}

⇒dy

dt=−4e t_

5e−t _{… … … … …. … … … (4)} ⇒

∫

dy=

∫

(

−4et+5e−t

)

dt

⇒y=−4et−5e−t+C _{… … … … …. … … … …(5)}

dengan memasukkan harga t dan y kedalam persamaan (4) maka Harga C diperoleh ⇒y=−4et−5e−t+9 … … … …. … … … …(6) Persamaan (5) adalah penyelesaian khusus dari persamaan diferensial (3).

Penyelesaian mempergunakan komputer dengan program Scilab.

dy

dt

=

f

(

t , y

)

dengan

y

(

t

0

)=

y

0

Sehingga persamaan (3) kita rubah menjadi bentuk persamaan (4). Program komputer dengan Scilab ditulis sebagai berikut :

function ydot=f(t, y)

ydot = (-4*exp(t)) + (5*exp(-t)); //persamaan (4) endfunction

y0=0; t0=0;

//respons dinamis(perubahan thd waktu) diamati dari t = 0 sampai t = pi

t=0:0.1:%pi;

y = ode(y0,t0,t,f); plot2d(t,y);

xgrid(5);

1. etdy

dt−sin(3t)+4t 3

.e3t+5=0

2. cos(2t)dy

dt +5sin(2t)−5t 3₌₀

3. 5tdy dt−5t

2dy dt +5=0

Supplemen Integral

1.

∫

1 f xdx=

1

f 'xlnfx

2. Menghitung Integral dengan menggunakan Scilab.

Ada dua fungsi dalam menghitung integral dengan menggunakan Scilab yaitu fungsi y = integ(a, b, “f”) dan fungsi y = integrate(“f(t)”, “t”, a, b).

integral yang dimaksud adalah berbentuk :

y

=

∫

a b

f

(

t

)

. dt

Contoh .

Hitunglah integral :

∫

0 3

3_t2+2_{t dt}

a. Menggunakan fungsi y = intg(a, b, “f”) function y=f(t)

y = (3*t^2) + (2*t)

endfunction

y = intg(0, 3, f);

disp(y);

b. Menggunakan fungsi y = integrate(“f(t)”, “t”, a, b)

2.2 Metode Pemisahan Variabel.

Metode Integrasi langsung akan gagal jika diterapkan pada persamaan diferensial

yang berbentuk dy

dt=f(t , y) , variabel y yang berada pada ruas kanan mengakibatkan integrasi langsung tidak dapat diterapkan.

Penyelesaian persamaan diferensial berbentuk dy

dt=f (t , y) adalah dengan memisahkan variabel t dan variabel y sehingga persamaan dapat berbentuk

dy

dt=f(t).F(y) yaitu suatu persamaan yang ruas kanannya dapat dinyatakan sebagai perkalian fungsi t dan fungsi y.

Contoh 3. dy

dt=1+t+2y+2yt .. … … … …. …(6)

⇒dy

dt=(1+t)(1+2y) ⇒

(

dy

1+2y

)

=(1+t)dt ⇒

∫

(

1

1+2y

)

dy=

∫

(1+t)dt

⇒1

2ln(2y+1)=t+ 1 2t

2_+C

… … … (7)

Contoh 4. dy dt=

3t2

2y dengan t = 0, y = 4 … … … (8) ⇒2y.dy=3t2.dt ⇒

∫

2y.dy=

∫

3t2dt

y2=t3+C dengan memasukkan harga t dan y diperoleh harga C ∴y2=t3+16

Untuk menguji jawaban sudah benar atau tidak maka perlu dicocokkan dengan metode komputer yaitu dengan fungsi ode pada Scilab.

Script program tersebut adalah :

function ydot=f(t, y)

ydot = (3/2)*((t^2)/y);

endfunction

y0=4; t0=0;

//respons dinamis(perubahan thd waktu) diamati dari t = 0 sampai t = pi

t= linspace(0, 3, 500);

ys = ode(y0,t0,t,f); // ys = y dengan Scilab

ym = sqrt((t.^3)+16 ); //ym = y dengan Matematis atau persamaan (9)

subplot(2,1,1), plot2d(t, ys);

xgrid();

xtitle("Hasil dengan menggunakan fungsi ODE");

subplot(2,1,2), plot2d(t, ym);

xgrid();

Contoh 5. dy dt=

1+y

2+t … … … … … … … …(10)

⇒

∫

(

1

1+y

)

dy=

∫

(

1

2+t

)

dt ⇒ln(1+y)=ln(2+t)+lnC

∴y=C(2+t)−1 … .. … … … (11)

Sebagai bahan latihan selesaikanlah persamaan diferensial dibawah ini, kemudian verifikasilah jawaban dengan menggunakan Komputer

1. 2y2+tdy

dt =(4+2y).cos(2t) y(0) = 2;

2. dy

dt= 1

t+sin(5t) y(0) = 7.

Tips. Untuk menghindari tak terhingga maka 1

t diubah menjadi

1 t+1._d−7

3. dy

dt=yt+y+2t+2 y(0) = 5;

4. dy_dt= 1

t2y−y y(0) = 3;

5. sin(t) 1+y

dy

dt =2 cos(t) y(0) = 0; Tips sin(t) diubah menjadi sin(t)+1.d-7

6. 2y2tan(t)dy

dt=

(

4+2y 2

₎

sec2(t) Pengerjaan untuk no.6.

Rubahlah bentuknya menjadi : dy

dt=

2.3 Metode Persamaan Homogen – dengan Substitusi y = vt

Jika suatu persamaan diferensial tidak dapat dipisahkan antara faktor y disebelah kiri dan faktor t disebelah kanan maka dapat dilakukan dengan cara substitusi (y = vt). Kunci utama untuk menggunakan metode substitusi y = vt adalah persamaan diferensial tersebut haruslah homogen. Persamaan diferensial dikatakan homogen jika pangkat t dan pangkat y yang terlibat dalam masing masing suku sama derajatnya.

Contoh 6. dy dt=

3t+y

t … … … (12) dengan menggunakan substitusi y = vt kedalam persamaan (12)

y = vt ⇒dy dt=t

dv dt+v

dt dt

∴

dy

dt

=

t

dv

dt

+

v

… … … (13) persamaan (12) dapat ditulis menjadi

⇒t dv dt+v=

3t+vt

t ⇒t dv

dt=3+v−v ⇒ dv dt=

3

t

v

=

3

C

ln

(

t

)

v

=

C

ln

(

t

)

3 … … … …. …. … …. … … …. … … … …(14)

karena v=y

t maka persamaan (14) menjadi

y

=

C

.

t

ln

(

t

)

3 … … … … … … …. … … … (15) Contoh 7.

Selesaikanlah persamaan diferensial derajat dua dibawah ini dy

dt=− yt+y2

t2+yt … … … .. (16)

⇒v+tdv dt=−

(v.t)t+(v.t)2

t2+(v.t)t ⇒v+ tdv

dt=−

⇒t dv

dt=−2v ⇒ln(v)=Cln

(

1 t2

)

∴v=C

t2 … … … …. … (17)

dengan memasukkan harga v=y

t kepersamaan (17) maka penyelesaian pers. (16) y = C/t … … … …. …. …. … … …. …. … …. … … …. (18)

Sebagai bahan latihan selesaikanlah persamaan diferensial berikut : 1. (y−t)dy

dt=t+2y

2. 3t2dy dt=t

2₊₃ y2

3.

(

2t2+yt

)

dy

dt=yt−y 2

4.

(

4t3+y3

)

dy dt=ty

2

2.4 Persamaan Diferensial Exact.

Suatu persamaan diferensial berbentuk : M(x, y)dx + N(x, y)dy = 0

Exact jika memenuhi persyaratan : ∂_∂M y =

∂N ∂x

Dikatakan Exact karena ruas kiri merupakan total atau dierensial Exact : du=∂u

∴ a. ∂u ∂x =M

b. ∂u ∂y =N

Jika persamaan persamaan Exact, maka penyelesaiannya : u=

∫

M.dx + k(y) .

Harga k(y) diperoleh dari ∂u

∂y untuk memperoleh dk

dy , kemudian mengintegralkan.

Atau : u=

∫

N.dy +l(x) .

Harga l(x) diperoleh dari ∂_∂u

x untuk memperoleh dl

dx , kemudian mengintegralkan.

Contoh.

selesaikanlah :

2x.Sin(3y).dx + (3x2_{.Cos(3y) + 2y).dy = 0}

Jawab.

M = 2x.Sin(3y) N = (3x2_{.Cos(3y) + 2y)}

∂M

∂y =6x.Cos(3y)

∂N

∂x=6x.Cos(3y) ∂M

∂y = ∂N

∂x ⇒ Exact

maka :

u=

∫

M.dx+k(y) u=

∫

2x.Sin(3y).dx +k(y)

d

dy.k(y)=2y ⇒ k(y)=y 2

+C

maka penyelesaiaannya : u = x2

.Sin(3y) + y2

+ C

Sebagai bahan latihan dirumah, jika persamaan diferensial berikut Exact, selesaikanlah : 1. 2.Sin(2x).Sinh(y).dx = Cos(2x).Cosh(y).dy.

2. 4x.dx + 9y.dy = 0 y(3) = 0.

3. (y + 3)dx + (x-2)dy = 0 y(1) = -7

2.5 Metode Faktor Integral – Persamaan diferensial linear.

Persamaan diferensial yang berbentuk : dy

dt +Py=Q … … … ... (19) dengan P dan Q adalah fungsi dari t atau merupakan suatu konstanta.

Persamaan (19) disebut persamaan diferensial linear orde satu. Penyelesaian persamaan (19) adalah dengan menggunakan faktor integral yaitu mengalikan kedua ruas persamaan (19) dengan faktor integral. Faktor Integral persamaan (19) adalah berbentuk _e∫P.dx Contoh 8.

dy

dt−2y=t … … … …. …. … … …. … … … .. .. (20) dengan membandingkan persamaan (19) dan persamaan (20) maka didapat :

P = -2 dan Q = t

Faktor integral : _e∫−2dt =e−2t

Kedua ruas persamaan (20) dikalikan dengan faktor integral =e−2t ⇒e−2t dy

dt−2y.e

−2t_=t.e−2t

y.e−2t=

∫

t.e−2tdt … … … (21) ruas kanan persamaan (21) dihitung dengan menggunakan integral perbagian.

⇒y.e−2t=−e

−2t 2

(

t+

1 2

)

+C

∴y=1 2

(

t+

1

2

)

+C.e 2t

… … … …. … (22)

Penyederhanaan berikut akan sangat menolong dalam menyelesaikan persamaan diferensial dengan metode faktor integral

Misal y=elnT lny=lnT ∴y=T

ini menunjukkan bahwa eln(fungsi) _{= fungsi}

maka : eln(x) _{= x}

eln(sin(x)) _{= sin(x)}

eln(x2) =x2

e2 ln(sin(x))=eln(sin2(x))

=sin2

(x)

Contoh 9. 2t2dy

dt+2yt=t 3

… … … (23) ⇒dy

dt+ y t =

t

2 _{… … … …. … … …. … … … (24)}

Faktor integral _e∫ 1

tdt ⇒eln(t) ∴t

Kedua ruas persamaan (24) dikalikan dengan faktor integral t ⇒t dy

dt+y= t2

2 ⇒ d dt(yt)=

t2

2 ⇒yt=

∫

t2

∴y=1 6t

2₊C

t … … … …. … … … (25)

sebagai bahan latihan kerjakanlah persamaan diferensial berikut

1. dy

dt+3t y=3e 5t

2. 5tdy

dt+5y=t 2

sin(5t)

3. cos(2t)dy

dt +sin(2t)y=5 cos(2t)

4. (2t−3)dy

dt−y=(2t−3) 3

2.6 Metode Persamaan Bernoulli.

Ide dasar metode persamaan Bernoulli diambil dari metode Faktor Integrasi. Bentuk

umum persamaan Bernoulli : dy

dt+Py=Qy n

dengan P dan Q sama seperti pada metode Faktor Integrasi yaitu dapat berupa konstanta atau fungsi t.

Penyelesaian persamaan Bernoulli adalah dengan mengubahnya menjadi bentuk

metode Faktor Integrasi yaitu dy

dt+Py=Q . Langkah langkah yang diambil untuk untuk mengubah Persamaan Bernoulli menjadi bentuk Faktor Integrasi adalah :

1. Membagi kedua ruas persamaan Bernoulli dengan yn _{, sehingga menghasilkan :}

y−ndy dt+Py

1−n_=Q

… … … .. (26)

2. Substitusi persamaan (26) dengan z = y1-n _sehingga dz

dt=(1−n)y

(1−n)y−ndy Faktor integral dari persamaan (29)

∴y= 1 −2t2+Ct3

Kerjakanlah persamaan diferensial berikut sebagai bahan latihan. 1. 2t2y−t3dy

dt=4y 3_sin(

2t)

2. dy

dt +4y=y 4

e3t

3. 2y−t dy

dt=2t(t+4)y 2

4. dy

dt −2ysin(t)=2y 3

sin2(t)

5. dy

dt +y=y 3

3. Orthogonal Trayektori

Jika suatu kurva (f) telah diketahui, maka terkadang diperlukan untuk mengetahui lintasan kurva lain (y) yang memotong kurva f secara tegak lurus. Kurva f(x, y, c) = 0 disajikan dalam bentuk persamaan diferensial y' = f(x, y).

Lintasan orthogonal kurva y pada kurva f : y

.

=− 1

f (x , y)

Contoh 11.

Tentukanlah trayektori orthogonal dari kurva y = cx2_.

Jawab.

orthogonal trayektori :

y

.

=− 1

2y x

⇒ dy dx=−

x

2y ⇒2y.dy=−x.dx

y2=1 2x

2_+c

y2+1 2 x

2_{+c=0 ⇒}

ellipse

Skript program dengan scilab :

t = linspace (-6, 6, 500);

//memplot _y=



_0.5x2_C dengan c = 4 dan c = 0

y1 = sqrt(0.5*(t.^2) + 4); y2 =sqrt(0.5*(t.^2)); //memplot x2 _{+ y}2 _{= 36;}

y3 = sqrt(36 -(t.^2));

Contoh 12.

Sebuah konduktor sepanjang sumbu-y menghasilkan medan magnet x2 _{+ y}2 _{= c. Silinder}

concentris yang terbentuk menunjukkan medan magnet dengan permukaan eqipotensial yang sama. Tentukanlah gaya pada medan magnet (Gaya listrik merupakan trayektori orthogonal).

Jawab.

Medan magnet x2 _{+ y}2 _{= c. ( merupakan linkaran concentris atau eqipotensial)}

2x + 2yy' = 0

y' = - x/y

orthogal trayektori atau gaya listrik pada medan magnet y' = y/x.

dy dx=

y

x ⇒

dy y =

dx x

y = kx

-1 -0.5 0

0.5 1 -1

0 1 2 -5 0 5

sumbu x sumbu y

s

u

m

b

u

z

konduktor

Latihan

Tentukanlah orthigonal trayektori dari kurva berikut. 1. x2+2y2=c

2. y = cex

4. Penerapan Persamaan Diferensial Orde Satu

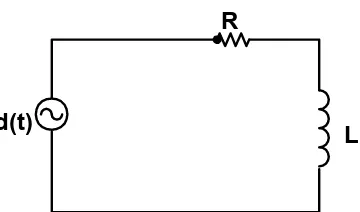
Rangkaian RL Contoh 11.

Pada rangkaian Gambar 1 Switch S menutup pada t = 0, arus pada induktor pada saat switch menutup adalah nol. Tentukanalah arus yang mengalir pada induktor dan plotlah arus Vs waktu.

Dik. E = 12 V, R = 1,2 ohm, L = 250mH.

Penyelesaian

Persamaan tegangan pada rangkaian gambar 1. E=Ri+Ldi

dt … … … …. … … … …. …. …. … … (31)

S _R

L E

+

Faktor Integral persamaan (32) pada saat t = 0 (switch terbuka) arus sama dengan nol, maka persamaan (34) menjadi

∴i=E R

(1−

e

−R

Lt

)

_{… … … …. …. … .. … ... .(35)}

dengan memasukkan harga untuk E, R dan L maka persamaan (35) menjadi i=10

(

1−e−4,8t

)

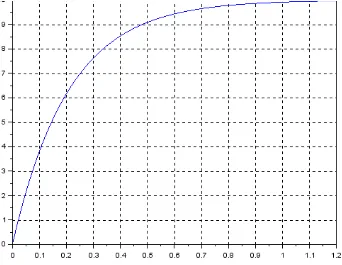
Skript program dengan Scilab. t = linspace(0, 1.2, 400);

i = 10*(1 - exp(-4.8*t));

plot2d(t, i);

xgrid();

Penyelesaian dengan menggunakan fungsi ode, dari persamaan (32) dirubah menjadi

Contoh 12.

Gambar 3 memperlihatkan rangkaian RL, pada saat t = 0 switch pada posisi 1 dengan arus yang mengalir pada t = 0 adalah nol. Pada saat t = 0,25 detik switch dipindahkan ke posisi 2. tentukanlah arus yang mengalir melalui induktor dan plotlah arus Vs Waktu dari t = 0 detik sampai t = 1,2 detik.

Dik. E = 12 V, R1 = 1,2 ohm, R2 = 1,0 ohm, L = 250 mH.

S

R1

L E

+

- R2

1

2

Penyelesaian

a. Pada saat t = 0 detik sampai t = 0,25 detik (switch pada posisi 1) Arus yang mengalir :

i(t)= E R1

(1−

e

−R1

L t

)

_{… … … …. … … … (36)}

dengan memasukkan harga E, R1 dan L kedalam persamaan (36) i(t)=10

(

1−e−4,8t

)

b. Pada saat t = 0,25 detik sampai t = 1,2 detik. 0=Ldi

dt+Ri dengan R = R1 + R2 ⇒ di dt=−

R Li

di i =−

R Ldt

i(t)=Ce

−R

Lt … … … …. … …. … … … … …. … … (37) Pada saat switch dipindahkan keposisi 2 arus yang mengalir pada induktor sebesar :

i(t)=10(1−e−4,8 .(0,25)

)=6

,99A

6,99=Ce−8,8 .(0 , 25) ⇒C=63,0848

dengan memasukkan R = R1 + R2 = 2,2 ohm, L = 250 mH dan konstanta C = 63,0848 i(t)=63,0848e−8,8t … … … …. … … … …. … .. … (38) Grafik arus Vs waktu mulai t = 0 detik sampai t = 1, 2 detik diperlihatkan gambar 4. Skript program dengan Scilab

t1 = linspace(0, 0.25, 500); t2 = linspace(0.25, 1, 500); i1 = 10*(1 - exp(-4.8*t1)); i2 = 63.0848*exp(-8.8*t2); subplot(1,2,1), plot(t1,i1); title("Saat switch Menutup"); xlabel("detik");

ylabel("A") xgrid();

subplot(1,2,2), plot(t2,i2); title("Saat switch Membuka"); xlabel("detik");

xgrid();

Penyelesaian contoh 12 dengan menggunakan fungsi ode

1. pada saat switch berada pada posisi 1, persamaan differensial adalah :

di dt=

E L−

R1

L .i dengan i(0) = 0

2. pada saat switch berada pada posisi 2, persamaan diferensial menjadi :

⇒di_dt=−R_Li dengan R = R1 + R2 dan i(0) = 6,99A

Script program

//Persamaan Differensial pada saat switch pada posisi 1

function idot1=f1(t, i)

R = 1.2; L = 250.d-3; E = 12; idot1 = (E/L)- ((R/L)*i);

endfunction

//Persamaan Differensial pada saat switch pada posisi 2

function idot2=f2(t, i)

R = 1.2 + 1; L = 250.d-3; idot2 = -(R/L)*i

endfunction

y0=0;

i1a = ode(y0,t0,0.25,f1); // 0,25 = waktu switch berpindah, i1a = i1 akhir

disp("Arus pada saat switch berpindah", i1a);

//memplot arus dari t = 0 sampai t = 0,25 detik

i1 = ode(y0, t0, t1, f1);

subplot(1,2,1); plot2d(t1, i1);

xtitle("Ketika Switch pada posisi 1")

xgrid(5);

t2 = linspace(0, 0.8, 500 );

i2 = ode(i1a, 0, t2, f2);

subplot(1,2,2), plot2d(t2+0.25, i2);

xtitle("Ketika Switch berada pada posisi 2");

xgrid(5);

Contoh 13.

Pada rangkaian Gambar 5 Switch S menutup pada t = 0, arus pada induktor pada saat switch menutup adalah nol. Tentukanlah arus yang mengalir pada induktor dan plotlah arus Vs waktu.

Penyelesaian E=Ri+Ldi

dt

⇒di dt+

R L=

A

LSin(2πft) … … … .(39)

d

(

i.e R Lt

)=

A

L.e R Lt

.Sin(2π ft)

i.e R

Lt₌ A.e R Lt

(2π fL)2+R2

(

RSin(2π ft)−2π fLCos(2π ft)

)

+C

i.(t)= A. (2π fL)2

+R2

(

RSin(2π ft)−2π fLCos(2π ft)

)

+C.e

−R L t

… … … (40) dengan memasukkan harga harga pada persamaan 40.

i(t)=0,0023 .Sin(2π50t)−0,1528.Cos(2π50t)+Ce−4,8 t … … … (41) Pada saat t = 0, arus yang mengalir nol ( I = 0).

i(t)=0,0023 .Sin(2π50t)−0,1528.Cos(2π50t)+0,1528e−4,8t … … … … (42)

S

R

L E(t)

Skript program dengan Scilab

t = linspace(0, 0.3, 500);

i = (0.0023*sin(2*%pi*50*t)) - (0.1528*cos(2*%pi*50*t)) + (0.1528*exp(-4.88*t));

plot(t,i); xgrid();

xlabel("detik"); ylabel("A")

Skript program dengan fungsi ode

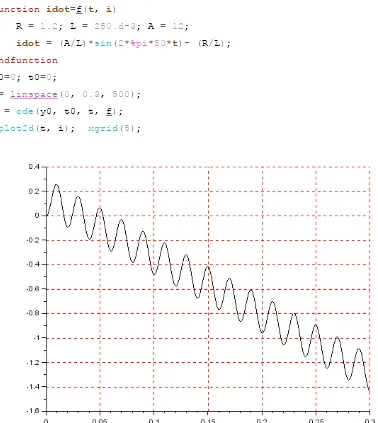
function idot=f(t, i)

R = 1.2; L = 250.d-3; A = 12;

idot = (A/L)*sin(2*%pi*50*t)- (R/L);

endfunction

y0=0; t0=0;

t= linspace(0, 0.3, 500);

i = ode(y0, t0, t, f);

plot2d(t, i); xgrid(5);

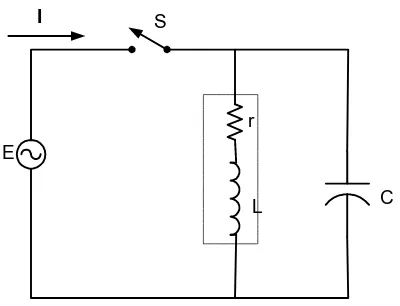
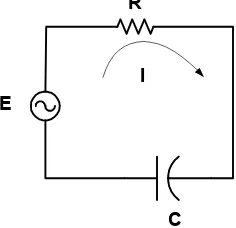
Rangkaian RC. Contoh 14.

Switch S pada gambar 7 menutup pada t = 0, keadaan awal kapasitor Vc = 0, tentukanlah tegangan pada kapasitor dan plotlah tegangan terhadap waktu.

E = 12 volt, R = 22 ohm, C = 220F .

Penyelesaian.

Pada saat switch S menutup persamaan tegangan : E=Ri+1

C

∫

i.dt … … … …. … … … … …. … (43)

karena i=dq

dt maka persamaan (43) menjadi E=Rdq

dt + q

C … … … …. … … … …(44)

⇒E

R= dq dt

q

R.C ⇒q.e t RC₌E

R

∫

e t RC

dt

⇒q=CE+ke− t

RC dengan k = konstanta

Karena pada keadaan awal muatan kapasitor adalah nol

S _R

C E

+

∴q=CE

(1−

e

− t

RC

)

… … … .. … … .(45)

arus yang mangalir pada kapasitor i=dq

dt= E Re

− t

RC _{… … … ... ...(46)} tegangan pada kapasitor

v_c=1

C

∫

i.dt=−E.e

− t

RC_{+k dengan k = konstanta, karena keadaan awal V}

c = 0

v_c=E(1−e

− t

RC

)

… … … …. … … … … ... ... ... ..(47)

Skript program Scilab

E = 12; R = 22; C = 220e-6; t = linspace(0, 0.025, 500); v = E*(1 - exp(-t/(R*C))); plot(t,v);

xgrid();

xlabel("detik"); ylabel("volt");

title("Kenaikan Tegangan capacitor pada rangkaian RC");

Contoh 15.

Switch S berada posisi 1 ketika t = 0 dan dipindahkan keposisi 2 pada t = 0,1 detik. Jika muatan awal pada kapasitor nol dan R1 = 100 ohm, R2 = 20 ohm, C = 470 F dan catu daya DC sebesar 15 volt, tentukanlah tegangan pada kapasitor dan plotlah tegangan terhadap waktu

Penyelesaian.

Pada t = 0 sampai t = 0,1 detik E=R₁dq

dt + q

C … … … …. … … … …. … … … ... ... ... (48) Persamaan (48) memberikan

∴q=CE

(1−e

− t

R₁C

)

_{… … … …. … … .. .. … …. … ….. …. … … .. … … ...(49)}

v_c=E

(

1−e

− t

R₁C

)

_{… … … .. … … … … …. …. … … ... ... ... ...(50)} Pada t = 0,1 detik Switch pada posisi 2, persamaan tegangan diperlihatkan pada (50).

0=R₂dq dt+

q

C … … … … .. … …. …. … …. …. … …. … …. … …. ... ... ... ..(50) persamaan (50) memberikan

S R1

C E

+

-R2 1

2

Pada saat S pada posisi 2 kapasitor telah terisi muatan yang diberikan oleh persamaan (49) yang merupakan keadaan awal pada posisi 2

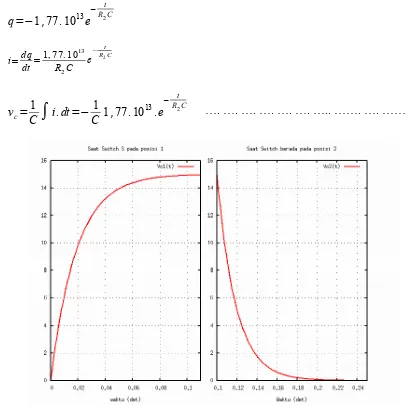
q=−1,77 . 1013e

− t

R₂C

i=dq

dt=

1, 77. 1013

R₂C e

− t

R2C

v_c=1

C

∫

i.dt=− 1

C1,77 . 10 13

.e

− t

R₂C

…. …. …. …. …. …. ….. ……. …. …….(52)

BAB II

PERSAMAAN DIFERENSIAL LINIER ORDE DUA

1. Pendahuluan

Setelah mempelajari persamaan diferensial orde dua maka diharapkan :

1. Dapat menyelesaikan persamaan diferensial orde dua.

2. Dapat menyelesaikan suatu Sistem Linier dengan menggunakan metode Eliminasi atau

dengan menggunakan metode Matrik.

3. Dapat menyelesaikan suatu rangkaian yang mengandung R, L dan C.

4. Dapat membuat model matematis suatu rangkaian Listrik yang mengandung multiple

loop.

1. Persamaan diferensial linier adalah tiap suku dalam persamaan diferensial,

variable-variable y, y’, y’’, …, y(n) _{berderajat satu atau nol.}

Contoh 1.

1. tdy

dt−2y=t

3

linier tak homogen orde satu

2. d

2

y dt2 +2

dy

dt+3y=cos(t) linier tak homogen orde dua

3. y(4)−y=0 linier tak homogen orde empat.

2. Suatu kumpulan n fungsi f1, f2, f3, …, fn, masing masing terdefinisi dan kontinu,

dikatakan linier dependent jika kontanta konstanta a1, a2, a3, …, an, tidak semuanya

secara bersama-sama sama dengan nol, sehingga :

f₁(t)=3t+12

5 ; f2(t)=5t+4

⇒a₁

(

3t+12

5

)

+a2(5t+4)=0 … … … …. … … … …. … … … … …. ... .(1)

persamaan (1) menghasilkan a1= 5, a2 = -3.

3. Suatu kumpulan n fungsi f1, f2, f3, …, fn, masing masing terdefinisi dan kontinu,

dikatakan linier independent jika kontanta konstanta a1, a2, a3, …, an, semuanya

secara bersama-sama sama dengan nol, sehingga :

a₁f₁+a₂ f₂+a₃ f₃+. . .+a_n f_n=0 _{menghasilkan a1 = a2 = a3 = … = an = 0}

Contoh 3

f₁(t)=t f₂(t)=t2 _∴y=Cln(t)4

a₁(t)+a₂

(

t2

)

=0 … … … ... ... (2)

persamaan (2) menghasilkan a1 = a2 = 0

Teorema :

Jika y1, y2. y3, … , yn merupakan n buah persamaan diferensial, misalkan bahwa fungsi fungsi

tersebut linier independent dikatakan bahwa fungsi fungsi tersebut membentuk himpunan

fundamental (sistem fundamental) penyelesaian persamaan diferensial tersebut.

Akibat.

Jika y1, y2. y3, … , yn membentuk himpunan fundamental penyelesaian persamaan diferensial.

Maka pernyataan :

y=c1y1+c2y2+c3y3+. . .+cnyn

dengan ci adalah konstanta konstanta sembarang, merupakan penyelesaian umum persamaan

diferensial.

y'''−6y''+11y'−6y=0 … … … ... (3)

Jawab.

Persamaan diferensial pada persamaan (3) memiliki persamaan karakteristik :

m3−6m2+11m−6=0 (m−1)(m−2)(m−3)

himpunan fundamental persamaan (3) adalah :

y₁=C₁et , y₂=C₂e2t , y3=C3e 3t

Penyelesaian umum persamaan (3) adalah :

y=C₁et+C₂e2t+C₃e3t … … … .. … … … …(4)

1. Persamaan Diferensial Orde Dua dengan Koefisien konstant – Penyelesaiaan Umum

Bentuk umum persamaan diferensial orde dua :

ad

2

y dt2 +b

dy

dt+cy=f (t) … … … …. (5)

Untuk memudahkan pemahaman maka kita tinjau dahulu persamaan diferensial (5) dengan

f(t) = 0. Bentuk persamaan (5) menjadi persamaan (6)

ad

2

y dt2 +b

dy

dt+cy=0 … … … (6)

Penyelesaian persamaan (6) adalah :

y=Aem1t₊

Bem2t _{… … … ...(7)}

Dengan A dan B adalah konstanta sembarang, m1, m2 adalah akar akar persamaan

karakteristik : am2+bm+c=0

d2y dt2 +3

dy

dt+2y=0 … … … ..(8)

dengan y(0) = 4 dan y’(0) = 0

Jawab.

m2+3m+2=0 ⇒(m+1)(m+2)=0

m = -1, dan m = -2

y=Ae−t+Be−2 t … … … …(9a)

y

.

=−Ae−t−2Be−2t … … … …(9b)

dengan memasukkan harga awal kedalam persamaan (9a) dan (9b) maka didapat :

y=

8

e

−t

−

4

e

−2t … … … …(9c)

Menyelesaikan dengan Scilab

Menyelesaikan persamaan differensial orde dua dengan menggunakan komputer

mempergunakan metode reduksi order. Persamaan differensial order dua kita ubah menjadi

order pertama. Kita tulis kembali persamaan (8)

d2y dt2 +3

dy

dt+2y=0 dengan y(0) = 4 dan y’(0) = 0

misalkan :

x1(t) = y(t)

x2(t) = y’(t)

masing masing diturunkan terhadap t

x₁

.

(t)=y

.

(t) ⇒x₁

.

=x₂(t) … … … …(9d)

x₂

.

(t)=y

..

(t) x₂

.

(t)=−3y

.

−2y

x₂

.

(t)=−3x₂(t)−2x₁(t) … … … …(9e)

sehingga persamaan (8) dapat ditulis menjadi :

⇒x1

.

=x2(t)

x₂

.

kemudian keadaan awal dirubah dalam bentuk x1dan x2

x1(0) = 4 dan x2(0) = 0

Penulisan persamaan (8) dengan memasukkan keadaan awal menjadi :

⇒x₁

.

=x₂(t) dengan x1(0) = 4 … … … (9f)

x₂

.

(t)=−3x₂(t)−2x₁(t) dengan x2(0) = 0… … … (9g) Script program dalam Scilab.

function dx=f(t, x)

dx_{(1) =} x_{(2); //persamaan (9f)}

dx_{(2) = -3*}x_{(2) - 2*}x_{(1); //persamaan (9g)} endfunction

y = ode([4, 0], 0, 1, f); disp("solusinya : ", y)

Solusinya : 2.4016944 -1.8603532

Contoh 6.

d2y dt2 +

dy

dt−12y=0

⇒m2+m−12=0 ⇒(m−3)(m+4)=0

y=Ae−4 t+Be3t

Macam macam akar karakteristik persamaan diferensial orde dua

Persamaan diferensial orde dua dalam bentuk :

ad

2

y dt2 +b

dy

dt+cy=0 … … … ...(10)

dengan persamaan karakteristik : am2+bm+c=0

Memiliki kemungkinan akar karakteristik sebagai berikut :

y=eαt(A+Bt)

c) Kedua akar kompleks m1 =  + j dan m2 =  - j

y=eαt

(

A.Cos(βt)+B.Sin(βt)

)

Contoh 7.

Tentukanlah penyelesaian umum persamaan diferensial (11)

d2y dt2 +4

dy

dt+4y=0 … … … ... ...(11)

⇒m2+4m+4=0 m1 = m2 = -2

y=e−2t(A+Bt)

Contoh 8.

d2y dt2 −2

dy

dt+10y=0

⇒m2−2m+10=0

m1 = 1 + j3, m2 = 1 – j3

y=et

(

A.Cos(3t)+B.Sin(3t)

)

Contoh 9.

d2y

dt2 +16y=0 … … … …(12)

⇒m2+16=0 m1 = j4, m2 = -j4

y=A.Cos(4t)+B.Sin(4t)

Contoh 10.

d2y

dt2 −25y=0 … … … (13)

y=Ae5 t+Be−5t

Sampai saat ini kita hanya menbahas persamaan diferensial dalam bentuk

ad

2

y dt2 +b

dy

dt+cy=f (t) … … … …(14)

dengan f(t) = 0.

Penyelesaian persamaan (14) terdiri dari :

y=Aem1t₊

Bem2t _{disebut juga fungsi komplementer dan}

y = f(t) fungsi t disebut juga integral khusus.

Penyelesaian persamaan (14) berbentuk :

Jawab lengkap = fungsi komplementer + integral khusus

Integral khusus diperoleh dengan menggunakan bentuk umum dari fungsi diruas kanan

persamaan yang diberikan, yaitu dengan mensubstitusikan bentuk umum tersebut kedalam

persamaanya dan kemudian menyamakan koefisien koefisiennya.

Contoh 11.

d

2

y dt2 −5

dy

dt+6y=t

2

… … … ..(15)

fungsi komplementer :

⇒m2−5m+6=0 m1 = 2, m2 = 3

⇒y=Ae2 t+Be3 t … … … ….. .. (16)

Integral Khusus

y=Ct2+Dt+E … … … .(17)

dy

dt=2Ct+D … … … …(18)

d2y

dt2 =2C … … … ….. (19)

dengan menyamakan koefisien dari t yang berpangkat sama :

(t2_{) 6C = 1 C}=1 6

(t) 6D – 10C = 0 D= 5 18

2C – 5D + 6E = 0 E=19 108

Persamaan (17) integral khusus

y=1 6t

2₊ 5

18t+ 19

108 … … … (21)

Jawab lengkap persamaan (15)

⇒y=Ae2 t+Be3 t+1 6t

2₊ 5

18 t+ 19

108 … … … ... ..(22)

Bentuk berikut akan sangat berguna dalam mencari integral khusus

1. f(t) = k y = C

2. f(t) = kt y = Ct + D

3. f(t) = kt2 _{y = Ct}2 _{+ Dt + E}

4. f(t) = k.Sin(t) atau k.Cos(t) y = C.Cos(t) + D.sin(t)

5. f(t) = k.Sinh(t) atau k.Cosh(t) y = C.Cosh(t) + D.sinh(t)

6. f(t) = ekt _{y = C.e}kt

Sebagai bahan latihan anda kerjakanlah persamaan diferensial berikut.

1. d

2

y dt2 −

dy

dt−2y=10e

3t

2. d

2

y dt2 +4

dy

dt−2y=5t

2₊

t _{; y = 1 dan y’ = -2 pada t = 0}

3. 2d

2

y dt2 −7

dy

4. d

2

y

dt2 −2y=e

3t

5. 2d

2

y

dt2 +12y=Sin(3t)

6. d

2

y dt2 +3

dy

dt+2y=3 .Sin(t) pada t = 0, y = 0,9 dan y’ = -0,7

2. Persamaan Diferensial Dalam Sistem Linier

Sampai saat ini kita hanya menyelesaikan persamaan diferensial dengan satu fungsi yang

tak diketahui. Penerapan persamaan diferensial dalam Teknik, banyak mengandung n

persamaan diferensial dengan n buah fungsi yang tidak diketahui. Pusat perhatian kita pada

penerapan persamaan diferensial yaitu dalam sistem linier.

Untuk memudahkan penulisan kita menggantikan y dengan x, yaitu fungsi y(t) dengan x(t).

x1 .₌

a₁₁x₁+a₁₂x₂+. . .+a_1nx_n+f₁(t)

x₂.=a₂₁x₁+a₂₂x₂+.. .+a_2nx_n+f₂(t)

… … … .. … … … (23)

………

x_n.=a_n1x₁+a_n2x₂+.. .+a_nnx_n+f_n(t)

Teorema

Setiap kombinasi linier dari penyelesaian penyelesaian (23) juga merupakan suatu

penyelesaian persamaan diferensial (23)

Contoh.

x₁

.

=x₂

x₂

.

=−2x₁+3x₂

… … … … …. … … … …. … … …..(24)

[

x₁ x₂

]

=

[

et

et

]

… … … .. … … .. … … … ... (25)

[

x₁ x₂

]

=

[

e2t

2e2t

]

… … … …. … … .. … … … (26)

Persamaan (25) dan persamaan (26) adalah penyelesaian persamaan (24), karena

persamaan (25) dan (26) linier independent maka kombinasi linier dari persamaan (24) dan

persamaan (25) juga merupakan penyelesaian persamaan diferensial (24)

[

x₁

x₂

]

=C1

[

et

et

]

+C2

[

e2t

2e2t

]

… … … …. … … … …. … .. …. …. … … … (27)

Catatan

Jika determinant penyelesaian-penyelesaian persamaan diferensial tidak nol, maka kombinasi

linier dari penyelesaian-penyelesaian tersebut adalah linier independent

Dalam contoh diatas

[

e t

e2t et e2t

]

=2e

3t₋

e3t=e3t≠0

Dalam menyelesaikan persamaan diferensial linier dengan n persamaan dan n variable

kita dapat mempergunakan metode eliminasi atau metode matrik. Metode eliminasi akan sangat

bermamfaat jika hanya mengandung dua persamaan diferensial. Jika sistem linier tersebut

mengandung lebih dari dua persamaan diferensial maka akan sangat bermamfaat jika

dipergunakan metode matrik.

2.1 Metode Eliminasi

Contoh 12.

x₁

.

=x₂+t

x₂

.

=−2x₁+3x₂+1

x1(0)=3

x2(0)=5 … …. … … …. … … … (28)

x₁

..

=x₂

.

+1 … … … ...(29)

Subtitusikan bagian bawah persamaan (28) kedalam persamaan (29)

x₁

..

=−2x₁+3x₂+2 … … .. … ….. …. ….. … … …. … … … … …. … …. …. ...(30)

dari persamaan (28) diketahui bahwa _x 2=x1

.

₋

t , maka persamaan (30) menjadi

x₁

..

=−2x₁+3x₁

.

−3t+2 … … … .. … … … …. … .. … …. … … … … ..(31)

x₁

..

−3x₁

.

−2x₁=3t−2 … … … …. … ... … …. … … … … .(32)

fungsi komplementer dari persamaan (32)

x₁=C₁et+C₂e2t … … … .. … … … …. … .. … …. … … … … ..(33)

Integral khusus dari persamaan (32)

x₁=At+B _{, x}

1

.

₌

A , x2

..

₌ 0

0−3A−2At+2B=3t−2 … … … …. … … … … ... (34)

dari persamaan (34) diperoleh :

A=−3

2 dan B=− 5 4

jadi integral khusus : x1=−

3 2t−

5 4

sehingga penyelesaian lengkap persamaan diferensial (32)

x₁=C₁et+C₂e2t−3 2t−

5

4 … … … …. … … … … ... (35)

Persamaan (35) kita substitusiakan kedalam persamaan (28) sehingga diperoleh

x₂=C₁et+2C₂e2t−t−3

C1 + 2C2 = 6,5

diperoleh harga C1 dan C2, yaitu :

C1 = 2 dan C2 = 2,25

Sehingga persamaan (35) dan persamaan (36) ditulis menjadi :

x₁=2et+2,25e2t−3 2t−

5

4 … … … …. … … … … ... (35a)

x₂=2et+2,25e2t−t−3

2 … … … …. … … … … ... .. (36a)

Penyelesaian dengan mempergunakan Scilab.

function dx=f(t, x)

dx(1)= x(2) + t;

dx(2) = -2*x(1) + 3*x(2) + 1;

endfunction

// Uji untuk t = 1

y = ode([3, 5], 0, 1, f);

disp(y);

19.311947 36.18733

2.2 Metode Matrik.

Contoh 13.

x₁

.

=2x₁+x₂

x₂

.

=−3x₁+6x₂

…. … … … …(37)

Penyelesaian

Penyelesaian persamaan (37) adalah berbentuk

[

x₁ x₂

]

=

[

A₁eλt

 adalah akar persamaan karakteristik

kita bentuk determinant dengan koefisien koefisien dari persamaan (37) dengan diagonal

utamanya dikurangi 

[

2−λ 1

−3 6−λ

]

=0 , λ

2

−8λ+15=0

1 = 3 dan 2 = 5

Jika  = 1 = 3 maka konstanta A1 dan A2

[

2−3 1 −3 6−3

]

.

[

A₁

A₂

]

=0 … … … .. … … … …. … .. … …. … … … … ..(39)

-A1 + A2 = 0

-3A1 + 3A2 = 0 A1 = A2

Dengan mengambil A1 = A2 = 1 kita peroleh persamaan (38) menjadi

[

x₁ x₂

]

=

[

e3t

e3t

]

… … … .. … … … …. … .. … …. … … … (40)

Jika  = 2 = 5 maka konstanta A1 dan A2

|

2−5 1 −3 6−5

|

.

[

A₁

A₂

]

=0 … … … .. … … … …. … .. … …. … … … ….. (41)

-3A1 + A2 = 0

-3A1 + A2 = 0 A2 = 3A1

Dengan mengambil A1 = 1, maka A2 = 3, kita peroleh persamaan (38) menjadi

[

x₁ x₂

]

=

[

e5t

3e5t

]

… … … .. … … … …. … .. … …. … … … ... .(42)

[

x₁

x₂

]

=C1

[

e3t e3t

]

+C2

[

e5t

3e5t

]

… … … .. … … … …. … .. … …. … … … … ..(43)

Contoh 14.

x₁

.

=2x₁−x₂

x₂

.

=9x₁+2x₂

Penyelesaian persamaan (44) adalah berbentuk

[

x₁ x₂

]

=

[

A₁eλt A₂eλt

]

 adalah akar persamaan karakteristik

kita bentuk determinant dengan koefisien koefisien dari persamaan (44) dengan diagonal

utamanya dikurangi 

,

[

2−λ −1

9 2−λ

]

=0 λ

2

−4λ+13=0

1 = 2 + 3i dan 2 = 2 – 3i

Jika  = 1 = 2 + 3i maka konstanta A1 dan A2

[

2−2+3i 1 −3 6−2+3i

]

[

A₁

A₂

]

=0 … … … .. … … … …. … .. … …. … …(45)

-3iA1 - A2 = 0

9A1 – 3iA2 = 0 A2 = -3iA1

Dengan mengambil A1 = 1 maka A2 =-3i

[

x₁ x₂

]

=

[

e(2+3i)t

−3ie(2+3i)t

]

… … .. … … … …. … .. … …. … … … …… … … ...(46)

dari deret Euler ea+bi=ea

(

Cos(b)+iSin(b)

)

sehingga persamaan (46) menjadi

[

x₁ x₂

]

=

[

e2(Cos3t+iSin3t)

−3ie2(Cos3t+isin 3t)

]

… … .. … … … …. … .. … …. … … … ...(47)

Jika  = 2 = 2 - 3i maka konstanta A1 dan A2

[

2−2−3i 1 −3 6−2−3i

]

[

A₁ A₂

]

=0

3iA1 – A2 = 0

9A1 +3iA2 = 0 A2 = 3iA1

[

x₁ x₂

]

=

[

e(2−3i)t 3ie(2−3 i)t

]

[

x₁ x₂

]

=

[

e2t(Cos3t−iSin3t)

−3ie2t(Cos3t−isin 3t)

]

… .. … … … …. … .. … …. … … … ...(48)

sehingga penyelesaian persamaan (44)

[

x₁ x₂

]

=

[

C₁e2tCos3t+C₂e2tSin3t

3C₁ie2 tSin3t−3C₂e2tCos3t

]

… .. … … … …. … .. … …. … … .(49)

Contoh 15.

x₁

.

=x₂

x₂

.

=−x₁+2x₂

… … … ..(50)

Penyelesaian persamaan diferensial pada persamaan (50) berbentuk :

[

x₁ x₂

]

=

[

A₁eλt

A₂eλt

]

… … … ... .(51)

persamaan akar akar karakteristik persamaan (50)

[

0−λ 1

−1 2−λ

]

=0 ⇒λ

2

−2λ+1=0

1 = 2 = 1 untuk  = 1 = 1

[

−1 1 −1 1

]

[

A₁

A₂

]

=0 A1 = A2

dengan mengambil A1 = 1 maka A2 = 1

maka persamaan (51) menjadi :

[

x₁ x

]

=

[

et

Karena akar karakteristik sama maka penyelesaian persamaan (50) berbentuk :

[

x₁ x₂

]

=

[

(

a₁t+b1)et

(

a₂t+b2)et

]

… … … ... .(53)

penyelesaian persamaan (50) adalah persamaan (52) dan persamaan (53) dan harus linier

independent. Konstanta a1, a2, b1, b2 pada persamaan (53) ditentukan dengan cara :

Substitusikan persamaan (53) kedalam persamaan (50)

a₁et+

(

a₁t+b₁

)

et=

(

a₂t+b₂

)

et

a₂et+

(

a₂t+b2)et=−

(

a₁t+b1)et+2

(

a₂t+b2)et _{… … … ..(54)}

dengan membagi dengan et_{dan menyamakan koefisien t dari persamaaan (54)}

a1 + b1 = b2 a1 = a2

a2 + b2 = -b1 + 2b2 a2 = -a1 + 2a2

dengan mengambil a1 = 1 maka a2 = 1

a1 + b1 = b2 ; jika b1 = 0 maka b2 = 1

maka persamaan (53) menjadi :

[

x₁ x₂

]

=

[

tet

(t+1)et

]

… … … ... ..(55)

Jika persamaan (52) dan persamaan (55) adalah penyelesaian persamaan (50), maka haruslah

linier independent. Untuk itu kita uji persamaan (52) dan persamaan (55) apakah linier

indpendent atau tidak.

[

et tet et (t+1)et

]

=e

2t

linier independent

maka penyelesaian persamaan (50) :

[

x₁

x₂

]

=C1

[

et

et

]

+C2

[

tet

(t+1)et

]

… … … ...(56)

x₁

.

=x₂−x₃+x₄

x₂

.

=−x₂+x₄

x₃

.

=x₃−x₄

x₄

.

=2x₄

dengan

¿

x₁(0)=2 x2(0)=2

x₃(0)=4 x4(0)=6

¿

… … … ….(57)

penyelesaiaan persamaan (57) berbentuk :

[

x₁ x₂ x₃ x₄

]

=

[

A₁eλt

A₂eλt

A₃eλt

A₄eλt

]

… … … ... ... ... .(58)

persamaan akar karakteristik dari persamaan diferensial (57)

[

−λ 1 −1 1

0 −1−λ 0 1

0 0 1−λ −1

0 0 0 2−λ

]

=0

-(-1 - )(1 - )(2 - ) = 0

1 = 0; 2 = -1; 3 = 1; 4 = 2

Jika  = 1 = 0

[

0 1 −1 1

0 −1 0 1

0 0 1 −1

0 0 0 2

]

[

A₁ A₂ A₃ A₄

]

=0

A2 + A3 + A4 = 0 -A2 + A4 = 0

A3 – A4 = 0 A2 = A3 = A4 = 0 2A4 = 0

[

x₁ x₂ x₃ x₄

]

=

[

1 0 0 0

]

… … … ... ... ... ...(59)

Jika  = 2 = -1

[

1 1 −1 1

0 0 0 1

0 0 2 −1

0 0 0 3

]

[

A₁ A₂ A₃ A₄

]

=0

A1 + A2 – A3 + A4 = 0 A1 + A2 = 0 A4 = 0

2A3 – A4 = 0 A3 = A4 = 0

3A4 = 0

Jika A1 = 1 maka A2 = -1

Maka penyelesaian persamaan (57)

[

x₁ x₂ x₃ x₄

]

=

[

e−t −e−t

0 0

]

… … … ... (60)

Jika  = 3 = 1

[

−1 1 −1 1

0 −2 0 1

0 0 0 −1

0 0 0 1

]

[

A₁ A₂ A₃ A₄

]

=0

-A1 + A2 – A3 + A4 = 0

-2A2 + A4 = 0 A2 = A4 = 0

-A4 = 0 A1 = -A3

A4 = 0 jika A1 = 1, maka A3 = -1

[

x₁

maka penyelesaian persamaan (57)

[

x₁

maka penyelesaian umum persamaan (57)

[

x₁

[

2

ditulis dalam bentuk matrik menjadi:

[

1 1 1 −7

sehingga persamaan (63) ditulis menjadi persamaan (63a) :

[

Penyelesaian persamaan (57) dengan mempergunakan fungsi ode.

function dx_=f(t_, x₎

//Pengujian pada titik t = 1

y = ode([2, 2, 4, 6], 0, 1, f);

disp(y)

Sistem Linier tak Homogen – Metode Variasi Parameter.

Penyelesaian umum persamaan diferensial homogen dari persamaan (64)

[

x_1h

Penyelesaian khusus system linier tidak homogen dari persamaan (64)

[

x_1p

Substitusikan persamaan (66) kedalam persamaan (64)

u₁

.

(t)e3t+u₂

.

(t)e5t=f (t)

u₁

.

(t)e3t+3u₂

.

(t)e5t=g(t)

Dengan menggunakan aturan Cramer

[

x_1p x_2p

]

=

t 2

[

e3t e3t

]

−

1 4e

−2t

[

e5t

3e5t

]

Penyelesaian umum persamaan diferensial dari persamaan (64)

[

x₁

x₂

]

=C1

[

e3t

e3t

]

+C2

[

e5t 3e5t

]

+

t 2

[

e3t e3t

]

−

1 4e

−2t

[

e5t

3e5t

]

3. Aplikasi Persamaan Diferensial Linier Orde Dua.

Contoh. 18.

Switch S mentup pada t = 0, muatan pada kapasitor pada t = 0 adalah nol dan arus pada keadaan

awal nol. Tentukanlah tegangan Vc(t) pada gambar 1 pada saat Switch S menutup. Diketehui R

= 0,1, L = 0,25H, C = 220F, E = 120 volt.

Penyelesaian.

E=R.i+Ldi dt+

1

C

∫

i.dt … … … (67)

karena i=dq

dt persamaan (67) menjadi

E=Rdq dt +L

d2q dt2 +

q

C … … … .(68)

S _R

C E

+

-L

Vc(t)

d2q dt2 +

R L

dq dt+

q LC=

E

L ⇒ d2q

dt2 +0,4 dq

dt +1 .82 .10

4_q=480

penyelesaian homogen (fungsi komplementer)

⇒d

2

q dt2 +0,4

dq

dt +1 .82 .10

4

q=0 _{… … … ... .(69)}

m2 _{+ 0,4m + 1,82.10}4 _{= 0}

m1 = -0,2 + j134,91, m2 = -0,2 – j134,91

q=e−0,2t₍

A.Cos(134,91t)+B.Sin(134,92t)) … … … .(70)

Integral Khusus

q = C. q’ _{= 0 q}” _{= 0}

1,82.104_{C = 480 C = 0.026}

Jawab Lengkap.

q=e−0,2t

(

A.Cos(134,92t)+B.Sin(134,92t)

)

+0,026 … … … ... .(71)

arus yang mengalir pada rangkaian tertutup gambar 1.

i(t)=dq dt

i(t)=−0,2e−0,2t

(

A.Cos(134,92t)+B.Sin(134,92t)

)

+

e−0,2t

(

−134,92A.Sin(134,91t)+134,92B.Cos(134,92t)

)

… … … …(72)

karena keadaan awal rangkaian yaitu arus nol dan tegangan kapasitor Vc = nol., maka dari

persamaan (71) dan persamaan (72)

0 = A + 0 + 0,026 A = -0,026

dan

0 = -0,2(A + 0) + (0 + 134,92B) B = -3,854.10-5

tegangan pada kapasitor

v_c(t)=1 C

∫

idt

v_c(t)=4,546. 103

[

e−0,2t

(

−0,0026 .Cos(134,91t)−3,854. 10−5.Sin(134,92t)

)

+0,026

]

… (73)

Skript program dengan Scilab :

t = linspace(0, 19, 400);

v = 4.546e3 *(exp(-0.2*t).*(-0.0026*cos(134.91*t) - 3.854e-5*sin(134.91*t)) + 0.026);

plot(t, v); xgrid(3);

Contoh 19.

S

C E

+

-L

Vc(t)