SKRIPSI
Diajukan Untuk Melengkapi Tugas-Tugas dan Memenuhi Syarat-Syarat Guna Memperoleh Gelar Sarjana Pendidikan (S.Pd)
Dalam Ilmu Matematika
Oleh Puji Hayati NPM : 1311050054
Jurusan: Pendidikan Matematika
FAKULTAS TARBIYAH DAN KEGURUAN UNIVERSITAS ISLAM NEGERI RADEN INTAN
(Studi Kasus pada Siswa SMP Negeri 4 Bandar Lampung TP. 2016/2017)
Skripsi
Diajukan Untuk Melengkapi Tugas-tugas dan Memenuhi Syarat-syarat Guna Mendapatkan Gelar Sarjana Pendidikan (S.Pd.)
dalam Ilmu Tarbiyah dan Keguruan
Oleh : Puji Hayati NPM: 1311050054
Jurusan : Pendidikan Matematika
Pembimbing I : Mujib, M.Pd.
Pembimbing II : Rany Widyastuti, M.Pd.
FAKULTAS TARBIYAH DAN KEGURUAN UNIVERSITAS ISLAM NEGERI RADEN INTAN
ii ABSTRAK
ANALISIS TINGKAT KETERAMPILAN GEOMETRI BERDASARKAN TAHAP BERPIKIR VAN HIELE
DITINJAU DARI KECERDASAN SPASIAL SISWA KELAS IX SMP NEGERI 4
BANDAR LAMPUNG Oleh
Puji Hayati
Berdasarkan hasil pra-survey diketahui bahwa di SMP Negeri 4 Bandar Lampung, geometri menempati peringkat terendah dalam Ujian Nasional SMP/MTs tahun 2016. Fakta lain ditemukan bahwa siswa masih kebingungan dalam memahami bangun geometri. Salah satu faktor penyebabnya adalah kemampuan dan kecerdasan keruangan siswa yang berbeda-beda. Dalam membantu terciptanya pemahaman konsep geometri diperlukan keterampilan geometri yang menurut Hoffer ada 5, yaitu: visual, verbal, menggambar, logika, dan terapan. Menurut Van Hiele seseorang akan melalui 5 tahap berpikir dalam belajar geometri, yaitu tingkat 0: visualisasi, tingkat 1: analisis, tingkat 2: abstraksi, tingkat 3: deduksi formal, dan tingkat 4: rigor. Kecerdasan spasial yaitu kemampuan memahami bangun dalam tiga dimensi secara tepat dan akurat walaupun dari sudut pandang berbeda.Tujuan penelitian ini adalah untuk mendeskripsikan tingkat keterampilan geometri berdasarkan tahap berpikir Van Hiele ditinjau dari kecerdasan spasial siswa kelas IX SMP Negeri 4 Bandar Lampung.
Penelitian ini merupakan penelitian kualitatif. Penelitian ini dilakukan di SMP Negeri 4 Bandar Lampung. Subjek penelitian diambil dengan purposive sampling yaitu 6 siswa kelas IX I yang terdiri dari masing-masing 2 siswa dengan kecerdasan spasial tinggi, sedang, dan rendah. Subjek dipilih dengan dasar telah mendapat materi tentang bangun ruang sisi datar dan telah mengikuti tes kecerdasan spasial. Teknik pengumpulan data yang dilakukan adalah tes kecerdasan spasial, tes tertulis geometri, dan wawancara. Validitas data menggunakan triangulasi waktu. Teknik analisis data menggunakan reduksi data, penyajian data, dan penarikan kesimpulan.
Hasil penelitian ini menunjukkan bahwa: (1) Subjek dengan kecerdasan spasial tinggi memiliki tingkat keterampilan geometri sebagai berikut: visual tingkat 2, verbal tingkat 2, menggambar tingkat 2, logika tingkat 2, dan terapan tingkat 1. (2) Subjek dengan kecerdasan spasial sedang memiliki tingkat keterampilan geometri sebagai berikut: visual tingkat 1, verbal tingkat 1, menggambar tingkat 2, logika tingkat 1, dan terapan tingkat 1. (3) Subjek dengan kecerdasan spasial rendah memiliki tingkat keterampilan geometri sebagai berikut: visual tingkat 1, verbal tingkat 1, menggambar tingkat 1, logika tingkat 0, dan terapan tingkat 0.
iv MOTTO
َﻻ َ ﱠ ٱ ﱠنِإ ِ ﱠ ٱ ِﺮْﻣَأ ْﻦِﻣ ۥُﮫَﻧﻮُﻈَﻔْﺤَﯾ ۦِﮫِﻔْﻠَﺧ ْﻦِﻣَو ِﮫْﯾَﺪَﯾ ِﻦْﯿَﺑ ۢﻦﱢﻣ ٌﺖَٰﺒﱢﻘَﻌُﻣ ۥُﮫَﻟ
َﻘِﺑ ﺎَﻣ ُﺮﱢﯿَﻐُﯾ
َﻼَﻓ اًءٓﻮُﺳ ٍمْﻮَﻘِﺑ ُ ﱠ ٱ َداَرَأ ٓاَذِإَو ْﻢِﮭِﺴُﻔﻧَﺄِﺑ ﺎَﻣ ۟اوُﺮﱢﯿَﻐُﯾ ٰﻰﱠﺘَﺣ ٍمْﻮ
ٍلاَو ﻦِﻣ ۦِﮫِﻧوُد ﻦﱢﻣ ﻢُﮭَﻟ ﺎَﻣَو ۥُﮫَﻟ ﱠدَﺮَﻣ
v
PERSEMBAHAN
Segala puji bagi Allah SWT yang telah memberikan nikmat kepada semua mahluk ciptaannya. Shalawat teriring salam senantiasa tercurahkan kepada Baginda Nabi Agung Muhammad SAW.
Alhamdulillahirobbil’alamin, ribuan rasa syukur penulis sujudkan kepada Sang pemilik semesta alam atas tugas akhir skripsi ini dapat terselesaikan dengan baik sesuai dengan yang diharapkan. Dengan segala kerendahan hati, ketulusan jiwa, dan keagungan kuasa Illahi penulis persembahkan karya ini kepada:
1. Kedua orang tuaku tercinta, Bapak Awi dan Ibu Nursyamsiah yang telah membesarkanku, mendidikku dan mengajarkan nilai-nilai kehidupan yang baik untuk bekal kesuksesanku. Terimakasih pak, mak, aku sayang bapak mamak.
2. Adik-adikku (Dewi Intan Nur’aini, Rifqi Ahmad Sholeh, dan Ahmad Ardian Akbar), yang selalu menjadi adik dan sahabat terkasih bagiku yang tak pernah letih memberi dukungan dan motivasi kepadaku serta mampu mengembalikan asaku. Aku sayang kalian.
vi
RIWAYAT HIDUP
Puji Hayati, dilahirkan tanggal 24 September 1995 di desa Gajah Timur 3, kecamatan Kotagajah, Kabupaten Lampung Tengah. Anak pertama dari empat bersaudara putri dari pasangan Bapak Awi dan Ibu Nur Syamsiah.
vii
KATA PENGANTAR
Puji syukur kepada Allah SWT sang Maha Pemilik, Maha Mengetahui, dan Maha Penyayang atas segala rahmat dan hidayah-Nya sehingga penulis dapat menyelesaikan skripsi yang berjudul “Analisis Tingkat Keterampilan Geometri Berdasarkan Tahap Berpikir Van Hiele ditinjau dari Kecerdasan Spasial Siswa Kelas IX SMP Negeri 4 Bandar Lampung”. Sholawat teriring salam semoga tetap tecurah kepada uswatun hasanah Nabi Agung Muhammad SAW, Nabi yang telah membawa cahaya Islam kepada seluruh alam.
Tujuan penulisan skripsi ini adalah sebagai salah satu syarat dalam menyelesaikan program Strata Satu (S1) di Fakultas Tarbiyah dan Keguruan Jurusan Pendidikan Matematika Universitas Islam Negeri (UIN) Raden Intan Lampung. Penulis menyadari dalam penulisan skripsi ini tidak mungkin dapat terselesaikan tanpa adanya bantuan, bimbingan dan saran dari berbagai pihak. Oleh karena itu, dalam kesempatan ini penulis mengucapkan terima kasih kepada:
1. Dr. H. Chairul Anwar, M.Pd. selaku Dekan Fakultas Tarbiyah dan Keguruan UIN Raden Intan Lampung.
viii
3. Bapak Mujib, M.Pd. selaku pembimbing I dan Ibu Rany Widyastuti, M.Pd. selaku pembimbing II yang telah dengan sabar dan ikhlas memberikan bimbingan dan pengarahannya selama ini.
4. Seluruh dosen Fakultas Tarbiyah dan Keguruan khususnya Jurusan Pendidikan Matematika yang telah mendidik dan memberikan ilmu pengetahuan yang teramat berharga kepada penulis selama menempuh pendidikan.
5. Bapak Sartijan, S.Pd selaku Kepala SMP Negeri 4 Bandar Lampun yang telah memberikan izin kepada penulis untuk melakukan penelitian.
6. Ibu Meri Yudiarti, S.Pd selaku guru matematika di kelas IX SMP Negeri 4 Bandar Lampung yang telah memberikan kesempatan serta arahan selama penulis melakukan penelitian.
7. Bapak dan Ibu guru SMP Negeri 4 Bandar Lampung yang telah banyak mendukung dan membantu penulis selama melakukan penelitian.
ix
9. Rekan mahasiswa, khususnya rekan-rekan pendidikan matematika kelas A angkatan 2013 yang selalu memberikan semangat, dukungan, bantuan, kritik dan saran dalam penyelesaian skripsi.
10. Semua pihak yang tidak dapat penulis sebutkan satu persatu yang telah membantu dan mendoakan dalam penyelesaian skripsi ini.
Semoga Allah SWT membalas amal baik semua pihak yang telah membantu dalam menyelesaikan skripsi ini. Penulis menyadari sepenuhnya bahwa masih banyak kekurangan dalam skripsi ini. Penulis berharap semoga skripsi ini dapat bermanfaat bagi diri penulis khususnya dan pembaca pada umumnya.
Bandar Lampung, Juni 2017
x DAFTAR ISI
Halaman
HALAMAN JUDUL ... i
ABSTRAK ... ii
PERSETUJUAN ... iii
PENGESAHAN... iv
MOTTO ... v
PERSEMBAHAN ... vi
RIWAYAT HIDUP ... vii
KATA PENGANTAR ... viii
DAFTAR ISI ... xi
DAFTAR TABEL ... xiii
DAFTAR BAGAN ... xiv
DAFTAR LAMPIRAN ... xv
BAB I PENDAHULUAN ... 1
A. ... La tar Belakang Masalah ... 1
B. ... Id entifikasi Masalah ... 12
C. ... Pe mbatasan Masalah ... 13
D. ... R umusan Masalah ... 13
xi
BAB II TINJAUAN PUSTAKA ... 15 A. ... K
ajian Teori ... 15 1. ... A
nalisis Tingkat Keterampilan Geometri ... 15 2. ... Ta
hap Berpikir Van Hiele ... 19 3. ... In
dikator Keterampilan Geometri Berdasarkan Tingkat
Berpikir Van Hiele ... 32
xii
F... V aliditas Data ... 70 G. ... Te
knik Analisis Data ... 71
BAB IV HASIL PENELITIAN DAN PEMBAHASAN ... 73 A. ... H
asil Penelitian ... 73 1. ... Pe
ngumpulan Data Penelitian ... 73 2. ... H
asil Pengembangan Instrumen... 76 3. ... D
eskripsi Hasil Tugas Berbasis Wawancara ... 80 4. ... V
aliditas Data ... 161 5. ... A
nalisis Data ... 175 B. ... Pe
mbahasan ... 201
BAB V KESIMPULAN DAN SARAN ... 209 A. ... K
esimpulan ... 209 B. ... Sa
ran ... 210
xiii
DAFTAR TABEL
Halaman Tabel 1.1 Presentase Penguasaan Materi Soal Matematika UN SMP/ MTs
Tahun Pelajaran 2015/2016 di SMP Negeri 4 Bandar Lampung ... 4
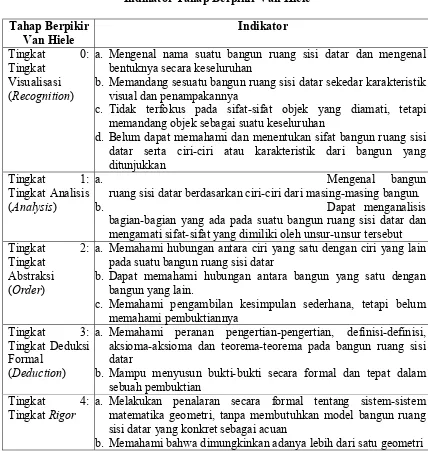
Tabel 2.1 Indikator Keterampilan Geometri ... 32
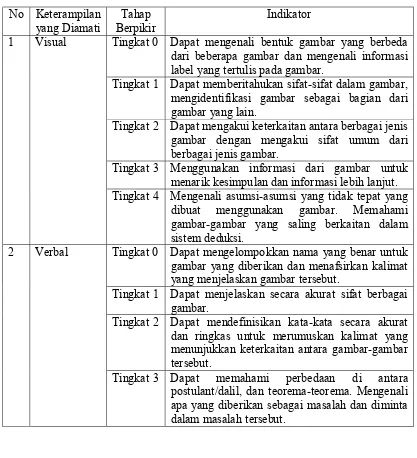
Tabel 2.2 Indikator Tahap Berpikir Van Hiele ... 34
Tabel 2.3 Indikator Keterampilan Geometri dalam Memecahkan Masalah Geometri berdasarkan Tingkat Berpikir Van Hiele ... 35
Tabel 2.4 Indikator Keterampilan Geometri Berdasarkan Tahap Berpikir Van Hiele ... 37
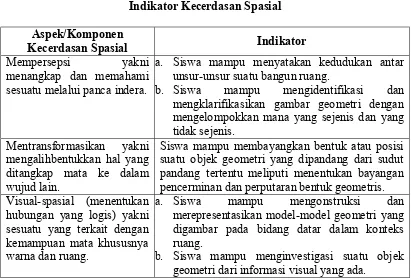
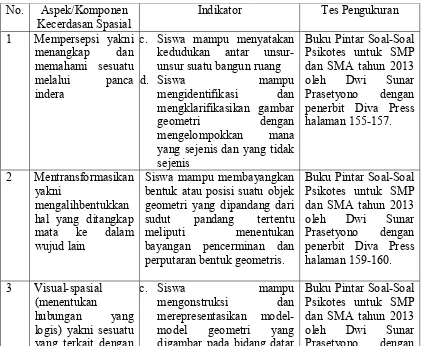
Tabel 2.5 Indikator Kecerdasan Spasial ... 47
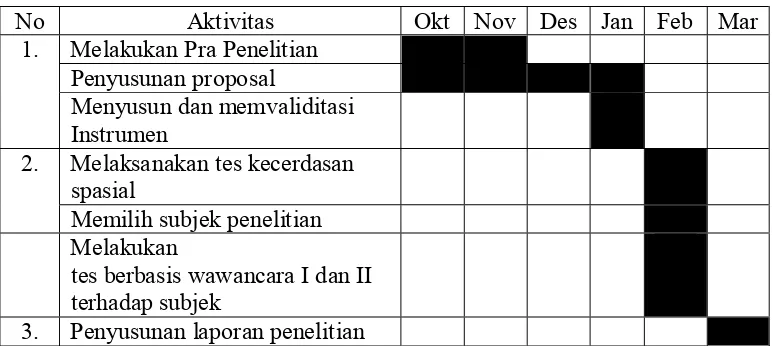
Tabel 3.1 Jadwal Rancangan Penelitian ... 55
Tabel 3.2 Penentuan Kategori Kecerdasam Spasial Siswa ... 58
Tabel 3.3 Sumber Tes Pengukuran Kecerdasan Spasial ... 61
Tabel 4.1 Pengelompokkan Kecerdasan Spasial ... 74
Tabel 4.2 Daftar Nama Kode Subjek Penelitian ... 75
Tabel 4.3 Hasil Uji Coba Tes Tertulis Geometri ... 78
Tabel 4.4 Validitas Data Tugas Berbasis Wawancara ST ... 161
Tabel 4.5 Validitas Data Tugas Berbasis Wawancara SS ... 166
Tabel 4.6 Validitas Data Tugas Berbasis Wawancara SR ... 171
Tabel 4.7 Kesimpulan Tingkat Keterampilan Geometri Subjek ... 200
xiv
DAFTAR BAGAN
xv
DAFTAR LAMPIRAN
Halaman
Lampiran 1: Kisi-kisi Uji Coba Tes Tertulis Geometri ... 212
Lampiran 2: Kisi-kisi Indikator Uji Coba Tes Tertulis Geometri ... 213
Lampiran 3: Pedoman Penskoran Uji Coba Tes Tertulis Geometri ... 215
Lampiran 4: Soal Uji Coba Tes Tertulis Geometri ... 217
Lampiran 5: Kunci Jawaban Uji Coba Tes Tertulis Geometri ... 219
Lampiran 6: Soal Tes Tertulis Geometri Tipe A ... 226
Lampiran 7: Soal Tes Tertulis Geometri Tipe B ... 227
Lampiran 8: Lembar Validasi Tes Tertulis Geometri ... 228
Lampiran 9: Instrumen Pedoman Wawancara ... 230
Lampiran 10: Lembar Validasi Instrumen Pedoman Wawancara ... 233
Lampiran 11: Indikator Kecerdasan Spasial ... 235
Lampiran 12: Kisi-kisi Indikator Kecerdasan Spasial ... 236
Lampiran 13: Pedoman Penskoran Tes Kecerdasan Spasial ... 237
Lampiran 14: Petunjuk Pelaksanaan Tes Kecerdasan Spasial ... 238
Lampiran 15: Tes Kecerdasan Spasial ... 240
Lampiran 16: Kunci Jawaban Instrumen Tes Kecerdasan Spasial ... 248
Lampiran 17: Daftar Nama Peserta Didik ... 252
Lampiran 18: Hasil Uji Coba Tes Tertulis Geometri ... 253
Lampiran 19: Perhitungan Manual Uji Validitas Tes Tertulis Geometri... 254
Lampiran 20: Perhitungan Manual Uji Reliabilitas Tes Tertulis Geometri ... 257
Lampiran 21: Hasil Tes Kecerdasan Spasial ... 261
Lampiran 22: Ketentuan Kelompok Siswa ... 262
Lampiran 23: Perhitungan Manual Hasil Tes Kecerdasan Spasial ... 263
Lampiran 24: Transkip Wawancara Siswa... 266
xvi
BAB I PENDAHULUAN
A. Latar Belakang Masalah
Matematika adalah suatu alat untuk mengembangkan cara berpikir. Matematika merupakan suatu ilmu yang berhubungan dengan menelaah bentuk-bentuk atau struktur-struktur yang abstrak. Matematika timbul karena pikiran-pikiran manusia yang berhubungan dengan ide, proses dan penalaran. Matematika sangat diperlukan baik untuk kehidupan sehari-hari maupun dalam menghadapi kemajuan IPTEK sehingga matematika perlu dibekalkan kepada setiap peserta didik sejak SD, bahkan sejak TK.1
Mengingat pentingnya ilmu matematika dalam kehidupan, Al-Quran telah memberikan contoh aspek matematika diantaranya seperti dalam QS. Al. Isra ayat 12.
hapuskan tanda malam dan Kami jadikan tanda siang itu terang, agar kamu mencari kurnia dari Tuhanmu, dan supaya kamu mengetahui
bilangan tahun-tahun dan perhitungan. Dan segala sesuatu telah Kami terangkan dengan jelas.” (QS Al-Isra17:12)
Matematika adalah ilmu dasar tentang berhitung. Dalam kehidupan sehari-hari, kita tentu akan menjumpai berbagai persoalan yang berkaitan dengan perhitungan. Mulai dari waktu, pekerjaan, dan uang, semuanya memerlukan perhitungan. Ayat tersebut menunjukan bahwa pentingnya ilmu matematika untuk dipelajari dan diterapkan dalam kehidupan sehari–hari yang berguna sebagai alat bantu menyelesaikan persoalan yang memerlukan perhitungan.
dalam TIMSS ada dua yaitu : domain isi dan domain kognitif, domain isi matematika terdiri dari : Bilangan, Aljabar, Geometri dan Peluang. Sedangkan domain kognitif yang diukur dari TIMSS adalah Pengetahuan, Penerapan dan Penalaran.2
SMP Negeri 4 Bandar Lampung adalah salah satu lembaga pendidikan menengah pertama yang ada di Bandar Lampung. Berdasarkan observasi yang dilakukan penulis di SMP Negeri 4 Bandar Lampung, tahap berpikir siswa yang benar dalam matematika sering diremehkan siswa itu sendiri. Hal ini dapat dilihat dari pengerjaan tugas yang diberikan guru kepada siswa. Terkadang dalam menyelesaikan masalah matematika, tidak sedikit siswa yang hanya berorientasi pada jawaban akhir tanpa disertai proses pengerjaan yang benar. Padahal proses untuk menuju ke jawaban akhir itu yang lebih dipentingkan dalam pembelajaran matematika. Tahap berpikir siswa terbentuk dari tahapan-tahapan siswa dalam belajar, dimana setiap belajar matematika dimulai dari berpikir sederhana lalu berkembang ke taraf berpikir kompleks. Seorang guru hendaknya lebih memahami tahap pola pikir siswanya sehingga penyampaian materi dapat berjalan lebih efektif.
Geometri merupakan materi yang paling dekat dalam kehidupan sehari-hari. Bangun geometri selalu dapat dikaitkan dalam benda sehari-hari. Geometri merupakan salah satu materi matematika yang memperoleh porsi cukup besar untuk dipelajari siswa di sekolah. Materi geometri di SMP yang harus dikuasai siswa sesuai standar kompetensi dan kompetensi dasar meliputi hubungan antar garis, sudut,
2 TIMSS and PIRLS, “TIMSS Advanced 2015 Assessment Frameworks” (On-line), tersedia
segitiga, segiempat, teorema Pythagoras, lingkaran, bangun ruang sisi datar, kesebangunan dan kekongruenan, dan bangun ruang sisi lengkung.
Pada kenyataan di lapangan, geometri menjadi materi pokok yang belum memuaskan penguasaannya. Menurut Puspendik siswa Indonesia menguasai soal-soal yang bersifat rutin, komputasi sederhana, serta mengukur pengetahuan akan fakta yang berkonteks keseharian. Siswa Indonesia perlu penguatan kemampuan mengintegrasikan informasi, menarik kesimpulan, serta menggeneralisir pengetahuan yang dimiliki ke hal-hal yang lain. Kesalahan konsep sering menjadi penyebab lemahnya penguasaan geometri. Di SMP Negeri 4 Bandar Lampung, geometri menempati peringkat terendah dalam Ujian Nasional SMP/MTs tahun 2016. Hal ini berdasarkan dari hasil perhitungan Pusat Pendidikan.3
Tabel 1.1
Persentase Penguasaan Materi Soal Matematika Ujian Nasional SMP/MTs Tahun Pelajaran 2015/2016 di SMP Negeri 4 Bandar Lampung
No.
Urut Kemampuan Yang Diuji Nilai Rata-Rata
1 Geometri dan Pengukuran 75,50
2 Aljabar 80,43
3 Bilangan 81,58
4 Statistika dan Peluang 85,61
Sumber Data: Laporan Hasil Ujian Nasional Tahun Pelajaran 2015/2016
Ujian nasional SMP/MTs tahun pelajaran 2015/2016 di provinsi Lampung diikuti oleh 134.442 siswa, dengan jumlah siswa yang mengikuti ujian nasional di kota Bandar Lampung sebanyak 16.642 siswa, dan di SMP Negeri 4 Bandar Lampung sendiri, diikuti oleh 301 siswa. Dari Tabel 1.1 dapat diketahui bahwa persentase penguasaan materi soal matematika ujian nasional SMP/MTs tahun pelajaran 2015/2016 di SMP Negeri 4 Bandar Lampung. Untuk nilai rata-rata pokok bahasan Geometri dan Pengukuran memperoleh nilai sebesar 75,50, untuk nilai rata-rata pokok bahasan Aljabar memperoleh nilai sebesar 80,43, kemudian untuk nilai rata-rata pokok bahasan Bilangan memperoleh nilai sebesar 81,58, sedangkan untuk nilai rata-rata pokok bahasan Statistika dan Peluang memperoleh nilai sebesar 85,61. Jadi dapat disimpulkan bahwa nilai rata-rata daya serap terendah untuk ujian nasional SMP/MTs tahun 2016, di SMP Negeri 4 Bandar Lampung, adalah pada pokok bahasan Geometri.
dapat memahami maksud dari soal yang diberikan. Hal inilah yang secara tidak langsung membuat siswa harus berpikir lebih tinggi dalam menyelesaikan permasalahan geometri.
Kesulitan siswa dalam memecahkan masalah geometri perlu dibenahi. Pembenahan ini dimulai dari guru sebagai penyalur ilmu, hingga ke siswa itu sendiri. Orang tua siswa hanya mengerti bahwa anak mereka belajar di sekolah. Hal lain seperti tingkat berpikir siswa, hanya guru yang lebih mengerti. Maka dari itu diperlukan pembenahan dalam transfer ilmu seperti yang selama ini dilakukan. Pembenahan tersebut dapat dimulai dari mengetahui tingkat berpikir siswa sehingga transfer ilmu yang dilakukan guru dapat lebih efektif diterima siswa.
Menurut Ruseffendi (dalam Nur’aini dkk), objek yang terkait langsung dengan aktifitas belajar matematika meliputi fakta, keterampilan, konsep, dan aturan/prinsip. Keempat objek langsung ini dapat dibedakan antara satu dengan lainnya secara jelas karena masing-masing objek langsung tersebut dapat didefinisi secara jelas.4 Dari penjelasan tersebut terlihat bahwa di dalam belajar matematika tidak hanya konsep dan prinsip yang dibutuhkan, tetapi juga skill (keterampilan). Pada permasalahan geometri, keterampilan geometri siswa dapat mempengaruhi keberhasilan pelaksanaan belajar siswa. Keterampilan geometri yang dimaksud adalah keterampilan siswa dalam belajar geometri yang menurut Hoffer (dalam Nur’aini dkk) terdiri dari 5 keterampilan, yaitu: (1) keterampilan visual (visual skill), (2)
keterampilan verbal (descriptive skill), (3) keterampilan menggambar (drawing skill), (4) keterampilan logika (logical skill), dan (5) keterampilan terapan (applied skill).5 Dalam menyelesaikan permasalahan siswa dituntut untuk memiliki keterampilan-keterampilan geometri tersebut. Tetapi kenyataannya dengan melihat bukti-bukti yang ada, keterampilan geometri siswa masih belum optimal dalam menyelesaikan permasalahan geometri.
Dalam mempelajari geometri, siswa memerlukan konsep yang matang sehingga siswa mampu menerapkan keterampilan geometri yang dimiliki. Selain itu, dalam memecahkan masalah geometri siswa membutuhkan pola berpikir dalam menerapkan konsep dan keterampilan memecahkan masalah tersebut. Secara umum siswa belum memiliki kemampuan yang baik mengenai sifat-sifat yang dimiliki oleh setiap jenis bangun ruang dan bangun datar sehingga belum bisa mengklasifikasikan suatu objek. Siswa memang telah diajarkan sifat-sifat setiap objek pada awal memasuki materi bangun ruang dan bangun datar. Tetapi tidak semua siswa dapat memahami secara keseluruhan konsep sifat-sifat tersebut, apalagi jika dihadapkan pada masalah geometri yang agak rumit. Walaupun sebenarnya contoh soal yang hampir sama proses penyelesaiannya telah diberikan oleh guru. Hal tersebut dapat terjadi karena faktor dari pengajaran guru, maupun faktor dari tingkat berpikir siswa. Berdasarkan hal itu diperlukan perhatian tentang keterampilan geometri siswa dalam menyelesaikan masalah geometri.
Berdasarkan penelitian yang dilakukan oleh Van Hiele seseorang akan melalui lima tahap perkembangan berpikir dalam belajar geometri. Kelima tahap perkembangan berpikir Van Hiele yaitu:
1. Tingkat 0: Tingkat Visualisasi (Recognition) 2. Tingkat 1: Tingkat Analisis (Analysis) 3. Tingkat 2: Tingkat Abstraksi (Order)
4. Tingkat 3: Tingkat Deduksi Formal (Deduction) 5. Tingkat 4: Tingkat Rigor6
Van Hiele adalah seorang pengajar matematika Belanda yang telah mengadakan penelitian di lapangan, melalui observasi dan tanya jawab, kemudian hasil penelitiannya ditulis dalam disertasinya pada tahun 1954. Penelitian yang dilakukan Van Hiele melahirkan beberapa kesimpulan mengenai tahap-tahap perkembangan kognitif anak dalam memahami geometri.7 Teori Van Hiele adalah suatu teori tentang tingkat berpikir siswa dalam mempelajari geometri. Di mana siswa tidak dapat naik ke tingkat yang lebih tinggi tanpa melewati tingkat yang lebih rendah. Kecepatan perpindahan dari suatu tingkat ke tinggal selanjutnya lebih bergantung pada isi dan metode pembelajaran dari pada umur ataupun kematangan. Dengan demikian, guru harus menyediakan pengalaman belajar yang cocok dengan tahap berpikir siswa, sehingga kegiatan belajar peserta didik harus disesuaikan dengan tahap berpikirnya.
6 Ardhi Prabowo, Eri Ristiani, Op.Cit. h. 76.
Beberapa penelitian yang dilakukan, menunjukkan bahwa siswa pada sekolah menengah awal baru sampai pada level 0 sampai 2 pada teori Van Hiele. Penelitian yang dilakukan Burger dan Shaughnessy (dalam Aisia dan Mega) menyatakan bahwa level berpikir siswa SMP pada belajar geometri tertinggi pada level 2 (deduksi Informal) dan sebagian besar pada level 0 (visualisasi). Pernyataan ini juga didukung oleh pendapat Van De Walle (dalam Aisia dan Mega) yang menyatakan bahwa sebagian besar siswa SMP/MTs berada di antara level 0 (visualisasi) sampai level 2 (deduksi informal). Aisia U. Sofyana dan Mega T. Budiarto juga mengatakan bahwa untuk memberikan model dan media pembelajaran yang tepat bagi siswa mengenai profil keterampilan geometri siswa SMP dalam memecahkan masalah geometri berdasarkan perkembangan berpikir Van Hiele pada level 0, level 1, dan level 2.8 Hal serupa diungkapkan oleh Nur’aini bahwa siswa SMP baru sampai pada tingkat 0-2 pada teori Van Hiele. Hasil penelitiannya menunjukkan bahwa siswa dalam tiap tingkat berpikir Van Hiele mempunyai karakteristik keterampilan geometri yang berbeda-beda. Siswa membutuhkan keterampilan-keterampilan geometri yang digunakan untuk memecahkan masalah geometri.9
8 Aisia U. Sofyana, Mega T. Budiarto, “Profil Keterampilan Geometri Siswa SMP dalam Memecahkan Masalah Geometri Berdasarkan Level Perkembangan Berpikir Van Hiele”. Jurnal Elektronik Matematika, Vol.2 No.1 (2013), h. 3.
dalam pembuktian, keterampilan membuat lukisan dasar geometri dan mempunyai pandang ruang yang memadai.10
Kemampuan keruangan sangat dibutuhkan dalam kehidupan sehari-hari maupun dalam profesionalisme pekerjaan seseorang. Selain itu, tahap berpikir siswa dalam pembelajaran geometri dapat dipengaruhi oleh kecerdasan majemuk (multiple intelegence), salah satunya adalah kecerdasan spasial. Kecerdasan spasial berguna untuk menggambarkan dan mencerna informasi dalam suatu permasalahan sehingga dapat menentukan jawaban akhir atau penyelesaian masalah.
Berdasarkan keterangan dari bapak Sahala Sitompul selaku guru mata pelajaran matematika SMP N 4 Bandar Lampung, menyatakan bahwa siswa masih kebingungan dalam memahami bangun geometri. Saat siswa dihadapkan pada soal penggabungan beberapa bangun datar misalnya, siswa cenderung sulit mengidentifikasi jenis bangun datar yang ada. Contoh lain dalam soal aplikasi geometri dalam kehidupan, siswa juga masih kesulitan. Daya khayal siswa dan kemampuan menuangkannya dalam bentuk gambar sangat diperlukan agar tercapai penyelesaian yang akurat. Padahal siswa telah dibekali materi bangun datar sebelumnya. Salah satu faktor penyebabnya adalah kemampuan dan kecerdasan keruangan siswa yang berbeda-beda.
Guna mencapai penguasaan konsep dan keterampilan penerapan konsep matematika diperlukan informasi tentang kecerdasan siswa. Kecerdasan spasial dibutuhkan siswa untuk membentuk pemahaman keruangan. Kecerdasan ini melibatkan kepekaan terhadap warna, garis, bentuk, ruang, dan hubungan-hubungan yang ada di antara unsur-unsur itu. Geometri merupakan materi yang berhubungan dengan garis, sudut, serta berbagai bentuk bangun datar ataupun ruang. Kecerdasan spasial yang dimiliki tiap siswa berbeda-beda, begitu pula kemampuan dalam menyelesaikan setiap permasalahan geometri.
Dari hal-hal yang telah diuraikan di atas muncul pemikiran penulis untuk mengetahui tahap-tahap berpikir siswa SMP dalam mengerjakan soal matematika khususnya di pokok bahasan geometri dengan melakukan penelitian berjudul “Analisis Tingkat Keterampilan Geometri Berdasarkan Tahap Berpikir Van Hiele Ditinjau dari Kecerdasan Spasial Siswa Kelas IX SMP Negeri 4 Bandar Lampung”
B. Identifikasi Masalah
Berdasarkan uraian latar belakang masalah di atas, maka penulis mengidentifikasikan masalah sebagai berikut:
1. Hasil survey TIMSS (Trends in Mathematics and Science Study) untuk Indonesia menempati peringkat yang belum memuaskan.
2. Nilai terendah ujian nasional SMP/MTs tahun 2016 di SMP Negeri 4 Bandar Lampung ditempati oleh pokok bahasan Geometri.
4. Banyak guru yang tidak memahami tahap pola pikir siswanya sehingga penyampaian materi berjalan kurang efektif.
C. Pembatasan Masalah
Mengingat keterbatasan penulis, baik dari segi kemampuan, waktu, tenaga, serta biaya yang ada maka masalah di atas dibatasi dengan materi soal dan tahap berpikir yang digunakan dalam menganalisis tingkat keterampilan geometri siswa. Soal yang digunakan yaitu mengenai materi Bangun Ruang Sisi Datar dan hasil jawaban siswa kemudian digolongkan pada tingkat keterampilan geometri berdasarkan tahap berpikir Van Hiele pada level 0, level 1, dan level 2 ditinjau dari kecerdasan Spasial.
D. Rumusan Masalah
Berdasarkan latar belakang yang telah diuraikan di atas, maka rumusan masalah dalam penelitian ini adalah : Bagaimanakah tingkat keterampilan geometri siswa berdasarkan tahap berpikir Van Hiele ditinjau dari kecerdasan spasial siswa kelas IX SMP Negeri 4 Bandar Lampung?
E. Tujuan Dan Manfaat Penelitian 1. Tujuan dari penelitian ini adalah:
2. Manfaat Penelitian
a. Manfaat Teoritis
Hasil penelitian diharapkan dapat dijadikan suatu hasil temuan baru terkait dengan teori keterampilan geometri dan menjadi bahan referensi untuk melakukan penelitian terkait keterampilan geometri pada subjek yang memiliki karkteristik yang berbeda.
b. Manfaat Praktis 1) Bagi peserta didik
Memberikan informasi kepada siswa mengenai karakteristik kemampuan yang dimilikinya, sehingga mampu memberikan arahan diri dalam meningkatkan pemahaman materi dalam pembelajaran.
2) Bagi guru
Memberikan informasi kepada guru mengenai kemampuan yang dimiliki siswanya sehingga dapat dijadikan bahan pertimbangan dalam proses pembelajaran yang lebih efektif.
3) Bagi sekolah
BAB II
TINJAUAN PUSTAKA
A. Kajian Teori
1. Analisis Tingkat Keterampilan Geometri a. Definisi Analisis
Menurut Kamus Besar Bahasa Indonesia (KBBI), analisis adalah penyelidikan terhadap suatu peristiwa (karangan, perbuatan, dan sebagainya) untuk mengetahui keadaan yang sebenarnya (sebab-musabab, duduk perkaranya, dan sebagainya).1 Menurut Djam’an Satori dan Aan Komariah, analisis adalah suatu usaha untuk mengurai suatu masalah atau fokus kajian menjadi bagian-bagian (decomposition) sehingga susunan/tataan bentuk sesuatu yang diurai itu tampak dengan jelas dan karenanya bisa secara lebih terang ditangkap maknanya atau lebih jernih dimengerti duduk perkaranya.2
Nasution (dalam Sugiyono) mengungkapkan bahwa:
“Melakukan analisis adalah pekerjaan yang sulit, memerlukan kerja keras. Analisis memerlukan daya kreatif serta kemampuan intelektual yang tinggi. Tidak ada cara tertentu yang dapat diikuti untuk mengadakan analisis, sehingga setiap peneliti harus mencari sendiri metode yang dirasakan cocok dengan sifat penelitiannya. Bahan yang sama bisa diklasifikasikan lain oleh peneliti yang berbeda.” 3
1 KBBI, “Analisis”(On-line), tersedia di: http://kbbi.wed.id (24 September 2016)
2 Djam’an Satori, Aan Komariah, Metodologi Penelitian Kualitatif (Bandung:Alfabeta, 2014), h.200 .
Spradly (dalam Sugiyono) menyatakan bahwa:
“Analisis dalam penelitian jenis apapun, adalah merupakan cara berpikir. Hal itu berkaitan dengan pengujian secara sistematis terhadap sesuatu untuk menentukan bagian, dan hubungannya dengan keseluruhan. Analisis adalah untuk mencari pola.” 4
Berdasarkan pendapat-pendapat di atas, disimpulkan bahwa analisis adalah suatu usaha penyelidikan, dan penguraian suatu peristiwa atau masalah dengan cara berpikir secara kreatif dan intelektual yang tinggi. Kegiatan ini dilakukan secara sistematis. Susunan/tataan yang dibuat dengan jelas, sehingga dimengerti duduk perkaranya.
b. Macam-macam Keterampilan Geometri
Menurut National Council of Teachers of Mathematics (NCTM) (dalam Nur’aini dkk) menyatakan bahwa secara umum kemampuan geometri yang harus dimiliki siswa adalah: 1) Mampu menganalisis karakter dan sifat dari bentuk geometri baik 2D dan 3D; dan mampu membangun argumen-argumen matematika mengenai hubungan geometri dengan yang lainnya; 2) Mampu menentukan kedudukan suatu titik dengan lebih spesifik dan gambaran hubungan spasial dengan sistem yang lain; 3) Aplikasi transformasi dan menggunakannya secara simetris untuk menganalisis situasi matematika; 4) Menggunakan visualisasi, penalaran spasial, dan model geometri untuk memecahkan permasalahan. Untuk itu tujuan pembelajaran geometri secara umum adalah agar siswa memperoleh rasa percaya diri mengenai kemampuan
(keterampilan) matematikanya, menjadi pemecah masalah yang baik, dapat berkomunikasi secara matematis, dan dapat bernalar secara matematis.5
Hoffer (dalam Aisia dan Mega) mengemukakan lima keterampilan dasar dalam belajar geometri. Kelima keterampilan dasar tersebut dapat dijabarkan sebagai berikut: 6
1) Keterampilan Visual (Visual skill)
Keterampilan visual menurut Hoffer, meliputi kemampuan untuk mengenal bermacam-macam bangun datar dan ruang, mengamati bagian-bagian dari sebuah-bangun dan keterkaitan bagian satu dengan bagian yang lain, menunjukkan pusat simetri, sumbu simetri, dan bidang simetri dari sebuah gambar bangun, mengklasifikasikan bangun-bangun geometri menurut ciri-ciri yang teramati, menyimpulkan informasi lanjut berdasarkan pengamatan visual, dan memvisualisasikan model geometri, atau contoh-contoh penangkal yang dinyatakan secara implisit oleh data dalam suatu sistem matematika deduktif.
2) Keterampilan Verbal (Descriptive skill)
Keterampilan verbal menurut Hoffer, meliputi kemampuan untuk menunjukkan bermacam bangun geometri menurut namanya, memvisualisasikan bangun geometri menurut deskripsi verbalnya, mengungkapkan bangun geometri dan sifat-sifatnya, merumuskan definisi dengan tepat dan benar, mengungkapkan hubungan antar
5 Nur’aini Muhassanah, Imam Sujadi, dan Riyadi, “Analisis Keterampilan Geometri Siswa dalam Memecahkan Masalah Geometri Berdasarkan Tingkat Berpikir Van Hiele”. Jurnal Elektronik Pembelajaran Matematika, Vol.2 No.1 (Maret 2014), h. 55-56.
bangun, mengenali struktur logis dari masalah verbal, dan merumuskan pernyataan generalisasi dan abstraksi.
3) Keterampilan Menggambar (Drawing skill)
Keterampilan menggambar menurut Hoffer, meliputi kemampuan untuk mensketsa gambar bangun dan melabel titik tertentu, mensketsa gambar bangun menurut deskripsi verbalnya, menggambar atau mengkonstruksi gambar bangun berdasarkan sifat-sifat yang diberikan, mengkonstruksi gambar bangun yang mempunyai kaitan tertentu dengan gambar-gambar yang telah diberikan, mensketsa bagian-bagian bidang dan interaksi gambar-gambar bangun yang diberikan, menambahkan unsur-unsur tambahan yang berguna pada sebuah gambar bangun, mengenal peranan (keterbatasan) sketsa dan gambar bangun yang terkonstruksi, dan mensketsa atau mengkonstruksi model geometri atau contoh penyangkal.
4) Keterampilan Logika (Logical skill)
5) Keterampilan Terapan (Applied Skill)
Keterampilan terapan menurut Hoffer, meliputi kemampuan untuk mengenal model fisik dari bangun geometri. Mensketsa atau mengkonstruksi model geometri berdasarkan objek fisiknya, menerapkan sifat dari model geometri pada sifat-sifat dari objek fisik, mengembangkan model-model geometri untuk fenomena alam, dan menerapkan model-model geometri dalam pemecahan masalah.
Jadi keterampilan geometri menurut Hoffer ada 5, yaitu keterampilan visual (visual skill), keterampilan verbal (descriptive skill), keterampilan menggambar (drawing skill), keterampilan logika (logical skill), dan keterampilan terapan (applied skill). Masing-masing keterampilan mengacu pada tahap berpikir menurut Van Hiele. Keterampilan-keterampilan tersebut berkaitan dengan pembelajaran geometri. Siswa dalam pembelajaran geometri yang menekankan keterampilan-keterampian tersebut, akan membantu terciptanya pemahaman konsep geometri dengan baik.
2. Tahap Berpikir Van Hiele
a. Definisi Bepikir
Menurut Kamus Besar Bahasa Indonesia (KBBI), berpikir adalah menggunakan akal budi untuk mempertimbangkan dan memutuskan sesuatu; menimbang-nimbang dalam ingatan.7 Menurut Ruggiero (dalam Tatag) mengartikan berpikir adalah suatu aktivitas mental untuk membantu memformulasikan atau memecahkan suatu masalah,
membuat keputusan dan memenuhi hasrat keinginan (fulfit a destre to understand). Pendapat ini menunjukkan bahwa ketika seseorang merumuskan suatu masalah maka ia melakukan suatu aktivitas berpikir. Sedangkan menurut Tatag berpikir adalah merupakan suatu kegiatan mental yang dialami seseorang bila mereka dihadapkan pada suatu masalah atau situasi yang harus dipecahkan.8
Berdasarkan pendapat-pendapat di atas, dapat disimpulkan bahwa berpikir adalah suatu aktivitas mental yang dialami oleh seseorang dengan menggunakan akal budi untuk mempertimbangkan dan memutuskan sesuatu dalam menghadapi masalah yang harus dipecahkan. Dalam berpikir, seseorang memerlukan berbagai pertimbangan-pertimbangan untuk memutuskan masalah. Aktivitas berpikir ini bertujuan untuk memecahkan masalah-masalah dengan akal yang dimilikinya.
b. Sejarah Teori Van Hiele
Van Hiele adalah seorang pengajar matematika Belanda yang telah mengadakan penelitian di lapangan, melalui observasi dan tanya jawab, kemudian hasil penelitiannya ditulis dalam disertasinya pada tahun 1954. Penelitian yang dilakukan Van Hiele melahirkan beberapa kesimpulan mengenai tahap-tahap perkembangan kognitif anak dalam memahami geometri. Van Hiele (dalam Nyimas dkk)
menyatakan bahwa terdapat 5 tahap pemahaman geometri yaitu: Tahap pengenalan, analisis, pengurutan, duduksi, dan keakuratan.9
Teori tentang tahap berpikir kognitif dalam mempelajari geometri dikembangkan oleh Pierre Van Hiele dan istrinya, Dian Van Hiele-Geldof, yang dirumuskan pada tahun 1957 sampai 1959. Model Van Hiele mengidentifikasi lima tingkat berpikir di dalam ilmu geometri. Menurut model ini, pelajar yang dibantu oleh intruksi yang sesuai, melalui tingkatan-tingkatan ini, yaitu mulai dengan pengenalan bentuk-bentuk secara keseluruhan, melangkah maju kepada penemuan sifat-sifat dari figur-figur dan penalaran informal tentang figur-figur dan sifat-sifat mereka, dan memuncak di suatu studi yang ketat dari ilmu geometri yang secara aksioma.10
Selain mengemukakan mengenai tahap-tahap perkembangan kognitif dalam memahami geometri, Van Hiele juga mengemukakan beberapa teori berkaitan dengan pembelajaran geometri. Teori yang dikemukakan Van Hiele (dalam Nyimas dkk) antara lain adalah sebagai berikut:11
1) Tiga unsur yang utama pembelajaran geometri yaitu waktu, materi pembelajaran dan metode penyusun yang apabila dikelola secara terpadu dapat mengakibatkan meningkatnya kemampuan berpikir anak kepada tahap yang lebih tinggi dari tahap yang sebelumnya.
9 Nyimas Aisyah, et. al. Pengembangan Pembelajaran Matematika SD. (Jakarta: Dirjen Dikti Depdiknas, 2007), h. 4.1.
10 Natodi, “Deskripsi Kemampuan Siswa SMP N 1 Kapahiang tentang Konsep dan Prinsip pada Operasi Hitung Pecahan Campuran Ditinjau Berdasarkan Teori Van Hiele”. (Tesis UB, 2013), h.36.
2) Menurut Van Hiele seorang anak yang berada pada tingkat yang lebih rendah tidak mungkin dapat mengerti atau memahami materi yang berada pada tingkat yang lebih tinggi dari anak tersebut. Kalaupun anak itu dipaksakan untuk memahaminya, anak itu baru bisa memahami melalui hafalan saja bukan melalui pengertian.
3) Untuk mendapatkan hasil yang diinginkan yaitu anak memahami geometri dengan pengertian, kegiatan belajar anak harus disesuaikan dengan tingkat perkembangan anak atau disesuaikan dengan taraf berpikirnya. Dengan demikian anak dapat memperkaya pengalaman dan berpikirnya, selain itu sebagai persiapan untuk meningkatkan tahap berpikirnya kepada tahap yang lebih tinggi dari tahap sebelumnya.
c. Tingkat Berpikir Menurut Teori Van Hiele
Menurut teori Van Hiele (dalam Ardhi dan Eri), seseorang akan melalui lima tahap perkembangan berpikir dalam belajar geometri. Kelima tahap perkembangan berpikir Van Hiele adalah tahap 0 (visualisasi), tahap 1 (analisis), tahap 2 (deduksi formal), tahap 3 (deduksi), dan tahap 4 (rigor). Tahap perkembangan berpikir Van Hiele dapat dijelaskan sebagai berikut :12
1) Tingkat 0: Tingkat Visualisasi (Recognition)
Tingkat ini juga dikenal dengan tahap dasar, tahap rekognisi, tahap holistik, tahap visual, dan disebut juga tingkat pengenalan. Pada tingkat ini, siswa baru mengenal nama suatu bangun dan mengenal bentuknya secara keseluruhan. Sebagai contoh adalah persegi dan persegi panjang tampak berbeda. “The student can learn names of figures and recognizes a shape as a whole. The example is squares and
rectangles seem to be different”.
Ciri-ciri tahap visual ini adalah siswa mampu mengidentifikasi, memberi nama, membandingkan, dan mengoperasikan gambar-gambar geometri seperti segitiga, sudut, dan perpotongan garis berdasarkan penampakannya. Siswa memandang sesuatu bangun geometri sekedar karakteristik visual dan penampakannya. Siswa secara eksplisit tidak terfokus pada sifat-sifat objek yang diamati, tetapi memandang objek sebagai suatu keseluruhan (wholistic). Pada tingkat ini siswa belum memperhatikan komponen-komponen dari masing-masing bangun. Dengan demikian,
meskipun pada tingkat ini siswa sudah mengenal nama suatu bangun, siswa belum dapat memahami dan menentukan sifat geometri serta ciri-ciri atau karakteristik dari bangun yang ditunjukkan. Contoh lain pada tingkat ini adalah siswa tahu bahwa suatu bangun bernama kubus, tetapi ia belum menyadari ciri-ciri dari bangun yang bernama kubus tersebut.
2) Tingkat 1: Tingkat Analisis (Analysis)
Tingkat ini sering disebut juga tingkat deskriptif. Pada tingkat ini, siswa dapat menyebutkan sifat-sifat yang dimiliki suatu bangun. Sebagai contoh adalah suatu persegi panjang memilki empat sudut siku-siku. “The student can identify properties of figures. The example is rectangles have four right angles”.
Jadi pada tingkat ini, siswa sudah mengenal bangun-bangun geometri berdasarkan ciri-ciri dari masing-masing bangun. Dengan kata lain, pada tingkat ini siswa sudah bisa menganalisis bagian-bagian yang ada pada suatu bangun dan mengamati sifat-sifat yang dimiliki oleh unsur-unsur tersebut. Contoh lain pada tingkat ini adalah siswa sudah bisa mengatakan bahwa suatu bangun merupakan kubus karena bangun itu memiliki enam sisi persegi yang sama.
3) Tingkat 2: Tingkat Abstraksi (Order)
pembuktiannya. “The student can logically order figures and relationships, but does not operate within a mathematical system”.
Contoh lainnya adalah, pada tingkat ini siswa sudah bisa mengatakan bahwa jika pada suatu segiempat, sisi-sisi yang berhadapan sejajar, maka sisi-sisi yang berhadapan itu sama panjang. Di samping itu pada tingkat ini siswa sudah memahami perlunya definisi untuk tiap-tiap bangun. Pada tingkat ini siswa juga sudah bisa memahami hubungan antara bangun yang satu dengan bangun yang lain. Misalnya pada tingkat ini siswa sudah bisa memahami bahwa setiap persegi adalah persegi panjang, karena persegi juga memiliki ciri-ciri persegi panjang.
4) Tingkat 3: Tingkat Deduksi Formal (Deduction)
Pada tingkat ini siswa sudah memahami peranan pengertian-pengertian, definisi-definisi, aksioma-aksioma dan teorema-teorema pada geometri. Pada tingkat ini siswa sudah mulai mampu menyusun bukti-bukti secara formal. “The student understands the significance of deduction and the roles of postulates, theorems, and proof. Proofs
can be written with understanding”.
jajar genjang, kemudian setelah itu ditunjukkan semua sudutnya membentuk sudut
satu putaran penuh, namun belum tentu tepat. Seperti diketahui bahwa pengukuran itu
pada dasarnya mencari nilai yang paling dekat dengan ukuran sebenarnya. Jadi,
mungkin saja dapat keliru dalam mengukur sudut-sudut dalam jajargenjang tersebut.
Untuk itu, pembuktian secara deduktif merupakan cara yang tepat dalam pembuktian
dalam matematika.
5)Tingkat 4: Tingkat Rigor
Tingkat ini disebut juga tingkat metamatematis. Pada tingkat ini, siswa mampu
melakukan penalaran secara formal tentang sistem-sistem matematika (termasuk
sistem-sistem geometri), tanpa membutuhkan model-model yang konkret sebagai
acuan. Pada tingkat ini, siswa memahami bahwa dimungkinkan adanya lebih dari satu
geometri. Sebagai contoh, pada tingkat ini siswa menyadari bahwa jika salah satu
aksioma pada suatu sistem geometri diubah, maka seluruh geometri tersebut juga
akan berubah. Sehingga pada tingkat ini siswa sudah bisa memahami adanya
geometri-geometri yang lain di samping geometri Euclides. “Contohnya adalah
geometri non-Euclides”.
Temuan baru dalam penelitian yang dilakukan Jackson mengungkapkan bahwa
adanya transisi dari tingkat satu ke tingkat yang lebih tinggi. Lebih lanjut dalam
penelitiannya ia menunjukkan, ada 26 dari 36 siswa (72,2%) dengan tingkat 0 yang
mulai menggunakan sifat-sifat dari bangun tertentu (karakteristik tingkat 1), tetapi
sifat-sifat yang digunakannya tidak sesuai. Selain itu, ada 6 dari 36 siswa (16,7%)
pemahamannya masih dipengaruhi oleh karakteristik visual bangun tersebut
(karakteristik tingkat 0). Ini berarti siswa-siswa tersebut masih ada di tingkat 0, tetapi
mereka mulai berpikir di tingkat 1 walaupun belum lengkap. Dengan kata lain,
siswa-siswa tersebut berada pada transisi dari tingkat 0 ke 1, atau dengan kata lain tingkat 1
yang belum sempurna/maksimal, yaitu pra-analisis.13
Lebih rinci, Kaswamati Abdullah menunjukkan dalam penelitiannya bahwa
peserta didik kemampuan tinggi sekitrar 6,67% berada pada tingkat pra deduksi
formal dan pra abstraksi, peserta didik kemampuan sedang sekitar 20% berada pada
tingkat pra abstraksi dan pra analisis, serta untuk peserta didik kemampuan rendah
sekitar 73,33% berada pada tingkat pra analisis dan pra visualisasi. Sama seperti yang
dikatakan oleh Van Hiele, tingkatan dalam berpikir geometri itu akan dilalui oleh
peserta didik secara berurutan. Peserta didik akan memasuki tingkatan berpikir yang
berikutnya apabila peserta didik tersebut sudah bisa melewati tingkatan yang
sebelumnya. Jika materi yang diajarkan kepada peserta didik yang berada diatas
tingkatan mereka, maka akan direduksi oleh pengadaan tingkatan tersebut. Setiap
peserta didik pun melalui tahapan-tahapan yang berbeda dalam melewati dari satu
tingkat ketingkat berikutnya.14
13 Jackson Pasini Mairing, “Tingkat Berpikir Geometri Siswa Kelas VII SMP Berdasarkan Teori Van Hiele”. Jurnal Pendidikan Matematika, Vol. 5 No. 1 (1 Maret 2016), h. 36.
Penemuan-penemuan tersebut didukung dengan pendapat Nor Khoiriyah dalam
penelitiannya bahwa terjadinya ketidakkonsistenan terhadap karakteristik tingkat
berpikir siswa dalam memahami konsep dipengaruhi beberapa alasan. Pertama,
adanya miskonsepsi yang dialami subjek terhadap beberapa konsep yang terlibat
dalam penyelesaian permasalahan. Kedua, dipengaruhi keterampilan visual yang
hifatnya juga hierarkis. Ketiga, meskipun subjek tidak dapat menguasai suatu tingkat
berpikir, namun jawaban-jawaban subjek secara verbal menunjukkan jawaban yang
logis dan terurut. Keempat, adanya materi penelitian yang melibatkan keterampilan
visual, verbal, logical, drawing, dan applied yang kompleks dan bersifat hierarkis
sebagaimana rumusan Hoffer.15
Berdasarkan hal tersebut tahap berpikir siswa dalam teori Van Hiele dapat
berkembang lebih luas yaitu dengan adanya transisi antar tingkat berpikir, sehingga
bukan tidak mungkin jika seorang siswa berapa pada salah satu tingkat berpikir Van
Hiele tetapi belum sempurna penguasaannya. Namun demikian, menurut Van Hiele
semua anak mempelajari geometri dengan melalui 5 tahap tersebut, dengan urutan
yang sama, dan tidak dimungkinkan adanya tingkat yang diloncati. Akan tetapi,
kapan seseorang siswa mulai memasuki suatu tingkat yang baru tidak selalu sama
antara siswa yang satu dengan siswa yang lain. Seseorang harus melewati
tahapan-tahapan yang ada untuk bisa menuju tahap yang lebih tinggi.
d. Karakteristik Teori Van Hiele
Menurut teori Pierre dan Dina Van Hiele (dalam Nyimas dkk) tingkat-tingkat
pemikiran geometrik dan fase pembelajaran siswa berkembang atau maju menurut
tingkat-tingkat sebagai berikut: dari tingkat visual Gestalt-like melalui tingkat-tingkat
sophisticated dari deskripsi, analisis, abstraksi dan bukti. Teori ini mempunyai
karakteristik sebagai berikut:16
1) Belajar adalah suatu proses yang diskontinu, yaitu ada loncatan-loncatan dalam
kurva belajar yang menyatakan adanya tingkat-tingkat pemikiran yang diskrit dan
berbeda secara kualitatif.
2) Tingkat-tingkat itu berurutan dan berhirarki. Supaya siswa dapat berperan dengan
baik pada suatu tingkat yang lanjut dalam hirarki van Hiele, ia harus menguasai
sebagian besar dari tingkat yang lebih rendah. Kenaikan dari tingkat yang satu ke
tingkat yang berikutnya lebih banyak tergantung dari pembelajaran daripada umur
atau kedewasaan biologis. Seorang guru dapat mengurangi materi pelajaran ke
tingkat yang lebih rendah, dapat membimbing untuk mengingat-ingat hafalan,
tetapi seorang siswa tidak dapat mengambil jalan pintas ke tingkat tinggi dan
berhasil mencapai mencapai pengertian, sebab menghafal bukan ciri yang penting
dari tingkat manapun. Untuk mencapai pengertian dibutuhkan kegiatan tertentu
dari fase-fase pembelajaran.
3) Konsep-konsep yang secara implisit dipahami pada suatu tingkat menjadi
dipahami secara eksplisit pada tingkat berikutnya. Pada setiap tingkat muncul
secara ekstrinsik dari sesuatu yang intrinsik pada tingkat sebelumnya. Pada
tingkat dasar, gambar-gambar sebenarnya juga tertentu oleh sifat-sifatnya, tetapi
seseorang yang berpikiran pada tingkat ini tidak sadar atau tidak tahu akan
sifat-sifat itu.
4) Setiap tingkat mempunyai bahasanya sendiri, mempunyai simbol linguistiknya
sendiri dan sistem relasinya sendiri yang menghubungkan simbol-simbol itu.
Suatu relasi yang benar pada suatu tingkat, ternyata akan tidak benar pada tingkat
yang lain. Misalnya pemikiran tentang persegi dan persegi panjang. Dua orang
yang berpikir pada tingkat yang berlainan tidak dapat saling mengerti, dan yang
satu tidak dapat mengikuti yang lain. Struktur bahasa adalah suatu faktor yang
kritis dalam perpindahan tingkat-tingkat ini.
Adapun sifat-sifat model Van Hiele menurut Chowley (dalam Natodi), adalah
sebagai berikut:17
1) Urutan, tingkat-tingkat kemampuan berpikir yang ada bersifat hirarkis
(berurutan), dan siswa melangkah maju melalui tingkatan yang satu ke tingkatan
tertentu dengan hasil memuaskan, siswa perlu mendapatkan penyiapan yang tepat
pada tingkatan yang mendahului.
2) Kemajuan-kemajuan atau peningkatan dari tingkat satu ke tingkat berikutnya
lebih tergantung pada isi dan metode pembelajaran yang memungkinkan siswa
untuk melompati suatu tingkatan.
3) Intrinsik dan ekstrinsik. Objek-objek yang dipelajari secara lebih cermat pada
tingkat berikutnya sebagai contoh, pada tingkat 0 bentuk gambar-gambar baru
dipahami secara keseluruhan (secara global), tidak seperti pada tingkat
komponen-komponen dan sifat-sifatnya.
4) Linguistik (ilmu bahasa). Tiap tingkat mempunyai simbol bahasa sendiri dan
sistem realisasi sendiri yang berkaitan dengan simbol-simbol tersebut, yang
mungkin belum dimengerti pada tingkat sebelumnya, sebagai contoh, siswa pada
tingkat 2 (abstraksi) lebih dari satu nama, misalnya persegi yang disebut persegi
panjang yang khusus (karena persegi merupakan kejadian khusus dari
jajargenjang). Siswa pada tingkat 1 tidak mempunyai pengertian bahwa nama
yang berbeda-beda itu dapat digunakan untuk menyebutkan sebuah bangun.
5) Kekeliruan pemasangan. Jika siswa berada pada suatu tingkatan-tingkatan
pembelajaran dan kemajuan mungkin tidak berada, maka hasrat belajar dan
kemajuan mungkin tidak terjadi. Ini terjadi apabila strategi pembelajaran yang
digunakan guru, materi pembelajaran yang digunakan guru, materi pembelajaran,
isi, kosa dan sebagainya berada pada tingkat yang lebih tinggi atau lebih rendah
Jadi Teori Van Hiele memiliki karakteristik yaitu belajar adalah proses yang
tidak kontinu, berurutan atau hirarki, peningkatan, intrinsik dan ekstrinsik, linguistik,
serta kekeliruan pemasangan. Kelima karakteristik tersebut harus ada ketika seorang
guru menerapkan Teori Van Hiele dalam proses pembelajaran. Dengan adanya
kelima karakteristik tersebut, pembelajaran dengan Teori Van Hiele diharapkan dapat
memberikan kemudahan bagi siswa untuk memahami materi geometri sehingga
berdampak pada meningkatnya hasil belajar siswa.
3. Indikator Keterampilan Geometri Berdasarkan Tingkat Berpikir Van Hiele Berdasarkan penjelasan mengenai macam-macam keterampilan geometri, maka
indikator setiap keterampilan geometri dalam materi bangun ruang sisi datar adalah
sebagai berikut: 18
Tabel 2.1
Indikator Keterampilan Geometri Keterampilan
Geometri Indikator
Visual (Visual skill) a. Mengenal bermacam-macam bangun ruang sisi datar b. Mengamati bagian-bagian dari sebuah bangun ruang
sisi datar
c. Mengklasifikasikan bangun ruang sisi datar menurut sifat dan ciri-cirinya
d. Menyimpulkan informasi lanjut berdasarkan pengamatan visual
e. Memvisualisasikan model geometri Verbal (Descriptive
skill) a. Menunjukkan bermacam bangun ruang sisi datar menurut namanya
b. Memvisualisasikan bangun ruang sisi datar menurut deskripsi verbalnya
c. Mengungkapkan bangun ruang sisi datar dan sifat-sifatnya
d. merumuskan definisi bangun ruang sisi datar dengan tepat dan benar
e. Mengungkapkan hubungan antar bangun Menggambar (Drawing
skill) a. Mensketsa gambar bangun ruang sisi datar dan melabel titik tertentu b. Mensketsa gambar bangun ruang sisi datar menurut
deskripsi verbalnya
c. Menggambar bangun ruang sisi datar berdasarkan sifat-sifat yang diberikan
d. Mengkonstruksi gambar bangun yang mempunyai kaitan tertentu dengan gambar-gambar yang telah diberikan
e. Mensketsa atau mengkonstruksi model geometri dan contoh penyangkalnya.
Logika (Logical skill) a. Mengenal perbedaan dan persamaaan antar bangun b. Mengenal bangun ruang sisi datar yang dapat
diklasifikasikan menurut sifat-sifatnya c. Menerapkan sifat-sifat penting dari definisi
d. Menujukkan akibat-akibat logis dari data-data yang diberikan serta mengembangkan bukti-bukti yang logis e. Mengenal peranan dan keterbatasan bangun ruang sisi
datar dari sifatnya
Terapan (Applied Skill) a. Mengenal model fisik dari bangun ruang sisi datar b. Mensketsa atau mengkonstruksi model geometri
berdasarkan objek fisiknya
c. Menerapkan sifat-sifat dari model bangun ruang sisi datar pada sifat-sifat dari objek fisik
d. Mengembangkan model-model bangun ruang sisi datar untuk fenomena alam
e. Menerapkan model-model geometri dalam pemecahan masalah.
Berdasarkan penjelasan mengenai tahap berpikir Van Hiele, maka disusun pula
indikator tahap berpikir menurut Van Hiele dalam materi bangun ruang sisi datar
sebagai berikut:19
Tabel 2.2
b. Memandang sesuatu bangun ruang sisi datar sekedar karakteristik visual dan penampakannya
c. Tidak terfokus pada sifat-sifat objek yang diamati, tetapi memandang objek sebagai suatu keseluruhan
d. Belum dapat memahami dan menentukan sifat bangun ruang sisi datar serta ciri-ciri atau karakteristik dari bangun yang ditunjukkan
Tingkat 1: Tingkat Analisis (Analysis)
a. Mengenal bangun
ruang sisi datar berdasarkan ciri-ciri dari masing-masing bangun.
b. Dapat menganalisis
bagian-bagian yang ada pada suatu bangun ruang sisi datar dan mengamati sifat-sifat yang dimiliki oleh unsur-unsur tersebut Tingkat 2:
Tingkat Abstraksi (Order)
a. Memahami hubungan antara ciri yang satu dengan ciri yang lain pada suatu bangun ruang sisi datar
b. Dapat memahami hubungan antara bangun yang satu dengan bangun yang lain.
c. Memahami pengambilan kesimpulan sederhana, tetapi belum memahami pembuktiannya
Tingkat 3: Tingkat Deduksi Formal
(Deduction)
a. Memahami peranan pengertian-pengertian, definisi-definisi, aksioma-aksioma dan teorema-teorema pada bangun ruang sisi datar
b. Mampu menyusun bukti-bukti secara formal dan tepat dalam sebuah pembuktian
Tingkat 4:
Tingkat Rigor a. Melakukan penalaran secara formal tentang sistem-sistem matematika geometri, tanpa membutuhkan model bangun ruang sisi datar yang konkret sebagai acuan
b. Memahami bahwa dimungkinkan adanya lebih dari satu geometri
Kedua jenis indikator di atas kemudian diklasifikasi untuk memperoleh indikator
mengenai tingkat keterampilan geometri berdasarkan tahap berpikir Van Hiele.
masalah geometri menurut tingkat berpikir Van Hiele pada indikator dalam tabel
berikut: 20
Tabel 2.3
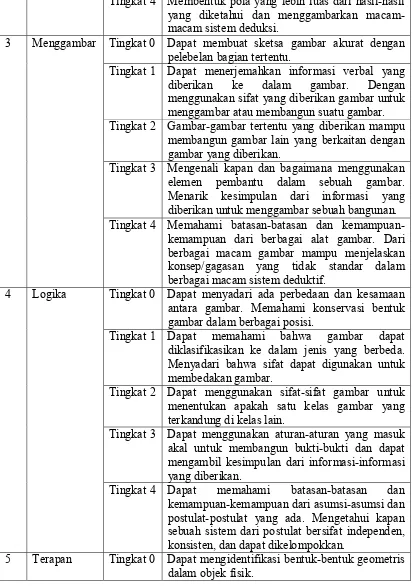
Indikator Keterampilan Geometri dalam Memecahkan Masalah Geometri berdasarkan Tingkat Berpikir Van Hiele
No Keterampilan
yang Diamati Berpikir Tahap Indikator
1 Visual Tingkat 0 Dapat mengenali bentuk gambar yang berbeda dari beberapa gambar dan mengenali informasi label yang tertulis pada gambar.
Tingkat 1 Dapat memberitahukan sifat-sifat dalam gambar, mengidentifikasi gambar sebagai bagian dari gambar yang lain.
Tingkat 2 Dapat mengakui keterkaitan antara berbagai jenis gambar dengan mengakui sifat umum dari berbagai jenis gambar.
Tingkat 3 Menggunakan informasi dari gambar untuk menarik kesimpulan dan informasi lebih lanjut. Tingkat 4 Mengenali asumsi-asumsi yang tidak tepat yang
dibuat menggunakan gambar. Memahami gambar-gambar yang saling berkaitan dalam sistem deduksi.
2 Verbal Tingkat 0 Dapat mengelompokkan nama yang benar untuk gambar yang diberikan dan menafsirkan kalimat yang menjelaskan gambar tersebut.
Tingkat 1 Dapat menjelaskan secara akurat sifat berbagai gambar.
Tingkat 2 Dapat mendefinisikan kata-kata secara akurat dan ringkas untuk merumuskan kalimat yang menunjukkan keterkaitan antara gambar-gambar tersebut.
Tingkat 3 Dapat memahami perbedaan di antara postulant/dalil, dan teorema-teorema. Mengenali apa yang diberikan sebagai masalah dan diminta dalam masalah tersebut.
Tingkat 4 Membentuk pola yang lebih luas dari hasil-hasil yang diketahui dan menggambarkan macam-macam sistem deduksi.
3 Menggambar Tingkat 0 Dapat membuat sketsa gambar akurat dengan pelebelan bagian tertentu.
Tingkat 1 Dapat menerjemahkan informasi verbal yang diberikan ke dalam gambar. Dengan menggunakan sifat yang diberikan gambar untuk menggambar atau membangun suatu gambar. Tingkat 2 Gambar-gambar tertentu yang diberikan mampu
membangun gambar lain yang berkaitan dengan gambar yang diberikan.
Tingkat 3 Mengenali kapan dan bagaimana menggunakan elemen pembantu dalam sebuah gambar. Menarik kesimpulan dari informasi yang diberikan untuk menggambar sebuah bangunan. Tingkat 4 Memahami batasan-batasan dan
kemampuan-kemampuan dari berbagai alat gambar. Dari berbagai macam gambar mampu menjelaskan konsep/gagasan yang tidak standar dalam berbagai macam sistem deduktif.
4 Logika Tingkat 0 Dapat menyadari ada perbedaan dan kesamaan antara gambar. Memahami konservasi bentuk gambar dalam berbagai posisi.
Tingkat 1 Dapat memahami bahwa gambar dapat diklasifikasikan ke dalam jenis yang berbeda. Menyadari bahwa sifat dapat digunakan untuk membedakan gambar.
Tingkat 2 Dapat menggunakan sifat-sifat gambar untuk menentukan apakah satu kelas gambar yang terkandung di kelas lain.
Tingkat 3 Dapat menggunakan aturan-aturan yang masuk akal untuk membangun bukti-bukti dan dapat mengambil kesimpulan dari informasi-informasi yang diberikan.
Tingkat 4 Dapat memahami batasan-batasan dan kemampuan-kemampuan dari asumsi-asumsi dan postulat-postulat yang ada. Mengetahui kapan sebuah sistem dari postulat bersifat independen, konsisten, dan dapat dikelompokkan.
Tingkat 1 Dapat menjelaskan sifat geometris dari benda-benda fisik dan mengubah fenomena fisik tersebut di atas kertas atau model. Dapat menggunakan model geometri tersebut dalam pemecahan masalah.
Tingkat 2 Dapat memahami konsep model matematika yang mewakili hubungan antara objek.
Tingkat 3 Dapat menarik kesimpulan tentang sifat-sifat objek dari informasi yang diberikan dan dapat menyelesaikan masalah yang berkaitan dengan masalah-masalah objek tersebut.
Tingkat 4 Dapat menggunakan model-model matematika untuk menjelaskan sistem yang bersifat abstrak dan menggambar sifat-sifat fisik, sosial, dan fenomena alam.
Menurut Sri Rejeki kriteria tingkat keterampilan dasar geometri berdasarkan
tingkat berpikir Van Hiele adalah sebagai berikut:21
Tabel 2.4
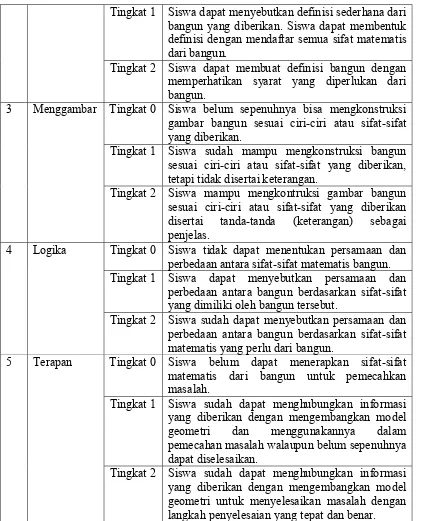
Indikator Keterampilan Geometri Berdasarkan Tahap Berpikir Van Hiele
No Keterampilan
yang Diamati Berpikir Tahap Indikator
1 Visual Tingkat 0 Siswa dapat mengenal bentuk bangun tanpa mengetahui sifat-sifat yang dimiliki oleh bangun. Tingkat 1 Siswa dapat mengelompokkan bangun
berdasarkan sifat-sifat matematis yang sama dari beberapa bangun.
Tingkat 2 Siswa dapat mengelompokkan bangun berdasarkan hubungan diantara beberapa bentuk bangun.
2 Verbal Tingkat 0 Siswa tidak dapat menyebutkan definisi bangun yang disediakan. Siswa hanya membentuk definisi yang berkaitan dengan deskripsi sifat-sifat fisik dari bangun.
Tingkat 1 Siswa dapat menyebutkan definisi sederhana dari bangun yang diberikan. Siswa dapat membentuk definisi dengan mendaftar semua sifat matematis dari bangun.
Tingkat 2 Siswa dapat membuat definisi bangun dengan memperhatikan syarat yang diperlukan dari bangun.
3 Menggambar Tingkat 0 Siswa belum sepenuhnya bisa mengkonstruksi gambar bangun sesuai ciri-ciri atau sifat-sifat yang diberikan.
Tingkat 1 Siswa sudah mampu mengkonstruksi bangun sesuai ciri-ciri atau sifat-sifat yang diberikan, tetapi tidak disertai keterangan.
Tingkat 2 Siswa mampu mengkontruksi gambar bangun sesuai ciri-ciri atau sifat-sifat yang diberikan disertai tanda-tanda (keterangan) sebagai penjelas.
4 Logika Tingkat 0 Siswa tidak dapat menentukan persamaan dan perbedaan antara sifat-sifat matematis bangun. Tingkat 1 Siswa dapat menyebutkan persamaan dan
perbedaan antara bangun berdasarkan sifat-sifat yang dimiliki oleh bangun tersebut.
Tingkat 2 Siswa sudah dapat menyebutkan persamaan dan perbedaan antara bangun berdasarkan sifat-sifat matematis yang perlu dari bangun.
5 Terapan Tingkat 0 Siswa belum dapat menerapkan sifat-sifat matematis dari bangun untuk pemecahkan masalah.
Tingkat 1 Siswa sudah dapat menghubungkan informasi yang diberikan dengan mengembangkan model geometri dan menggunakannya dalam pemecahan masalah walaupun belum sepenuhnya dapat diselesaikan.
Berdasarkan indikator-indikator yang telah disebutkan di atas dan mengacu pada
latar belakang masalah serta pembatasan masalah pada Bab 1, maka keterampilan
geometri yang digunakan yaitu 5 keterampilan geometri meliputi keterampilan visual,
verbal, menggambar, logika, dan terapan dan tahap berpikir Van Hiele yang
digunakan yaitu pada tingkat 0, tingkat 1, dan tingkat 2. Adapun indikator yang
digunakan dalam penelitian ini adalah indikator menurut Sri Rejeki pada Tabel 2.4.
4. Kecerdasan Spasial
a. Definisi kecerdasan Spasial
Teori Multiple Intelligences diperkenalkan pada tahun 1983 oleh Dr. Howard Gardner, guru besar di bidang Psikologi dan Pendidikan dari Harvard University. Dr.
Gardner menyebutkan bahwa inteligensi bukanlah suatu kesatuan tunggal yang bisa
diukur secara sederhana dengan tes IQ. Inteligensi dapat ditingkatkan dan
berkembang sepanjang sejarah hidup seseorang. Dr. Gardner mendefinisikan
inteligensi sebagai suatu kapasitas untuk memecahkan permasalahan atau membentuk
produk yang bernilai dalam satu atau lebih latar budaya.22
Temuan kecerdasan menurut paradigma Multiple Intelligences, telah mengalami pekembangan sejak pertama kali ditemukan. Pada buku nya Frame of The Mind Howard Gardner pada awalnya menemukan tujuh kecerdasan. Setelah itu Gardner
menemukan kecerdasan yang ke-8 dan ke-9. Menurut Gardner kecerdasan dalam
Multiple Intelligences meliputi kecerdasan verbal-linguistik (cerdas kata), kecerdasan logos-matematis (cerdas angka), keccerdasan visual-spasial (cerdas gambar-warna),
kecerdasan musikal (cerdas musik-lagu), kecerdasan kinestetik (cerdas gerak),
kecerdasan interpersonal (cerdas sosial), kecerdasan intrapersonal (cerdas diri),
kecerdasan naturalis (cerdas alam), kecerdasan eksistensial (cerdas hakikat).23
Menurut Howard Gardner (dalam Julia), kecerdasan spasial yang kadang-kadang
disebut kecerdasan visual atau visual-spasial, adalah kemampuan untuk membentuk
membentuk dan menggunakan model mental. Orang yang memiliki kecerdasan ini
cenderung berpikir dalam atau dengan gambar dan cenderung mudah belajar melalui
sajian-sajian visual seperti film, gambar, video, dan peragaan yang menggunakan
model dan slide. Mereka gemar menggambar, melukis atau mengukir gagasan-gagasan yang ada di kepala dan sering menyajikan perasaan hatinya melalui seni.24
Menurut Baharuddin orang yang memiliki kecerdasan spasial mudah
membayangkan benda dalam ruang berdimensi tiga. Mereka mudah mengenal relasi
benda-benda dalam ruang secara tepat. Mereka juga memiliki persepsi yang tepat
tentang suatu benda dengan ruang disekitarnya, dan dapat memandang dari segala
sudut.25 Menurut Armstrong (dalam Tadkiroatun), kecerdasan spasial atau
visual-spasial atau kecerdasan gambar atau kecerdasan pandang-ruang didefinisikan sebagai
kemampuan mempersepsi dunia visual-spasial secara akurat serta
23 Tadkiroatun Musfiroh, Pengembangan Kecerdasan Majemuk (Jakarta: Universitas Terbuka, 2010), h.1.12.
24 Julia Jasmine, Metode Mengajar Multiple Intelligences,terjemahan Purwanto (Bandung: Nuansa: 2016, h. 21-22.
mentransformasikan persepsi visual-spasial tersebut dalam berbagai bentuk.
Kemampuan berpikir visual-spasial merupakan kemampuan berpikir dalam bentuk
visualisasi, gambar, dan bentuk tiga dimensi.26
Berdasarkan uraian di atas, dapat disimpulkan bahwa kecerdasan spasial adalah
kecerdasan gambar atau kecerdasan pandang ruang yaitu kemampuan memahami
bangun dalam tiga dimensi atau ruang secara tepat dan akurat. Mereka dapat
mengenali objek walaupun dari sudut pandang yang berbeda.
b. Komponen Kecerdasan Spasial
Komponen inti dari kecerdasan visual-spasial adalah kepekaan pada garis, warna,
bentuk, ruang, keseimbanganbayangan, harmoni, pola, dan hubungan antar unsur
tersebut. Komponen lainnya adalah kemampuan membayangkan, mempresentasikan
ide secara visual dan spasial, dan mengorientasikan diri secara tepat. Komponen inti
dari kecerdasan visual-spasial benar-benar bertumpu pada ketajaman melihat dan
ketelitian pengamatan27
Kecerdasan Visual-Spasial adalah kapasita untuk mengenali dan melakukan
penggambaran atas objek atau pola yang diterima otak. Jika anda memiliki
kecerdasan visual-spasial yang berkembang dengan baik maka anda mempunyai
kapasitas mengelola gambar, bentuk, dan ruang tiga dimensi dengan aktivitas utama