STRATEGI PEMENANGAN PERMAINAN CONGKLAK SKRIPSI. Diajukan Untuk Memenuhi salah satu syarat. memperoleh gelar sarjana pendidikan

SKRIPSI

Diajukan Untuk Memenuhi salah satu syarat

memperoleh gelar sarjana pendidikan

program studi pendidikan matematika

Disusun oleh :

Agty Devina Puspitasari

161414096

PROGRAM STUDI PENDIDIKAN MATEMATIKA

JURUSAN PENDIDIKAN MATEMATIKA DANILMU PENGETAHUAN ALAM

FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN

UNIVERSITAS SANATA DHARMA

YOGYAKARTA

ii

A THESIS

Submitted as the Partial Fulfillment of the Requirements

to Obtain a Bachelor of Education Degree

on Mathematics Education Study Program

Written by :

Agty Devina Puspitasari

Student ID :161414096

MATHEMATICS EDUCATION STUDY PROGRAM

DEPARTEMENT OF MATHEMATICS AND SCIENCE EDUCATION

FACULTY OF TEACHER TRAINING AND EDUCATION

SANATA DHARMA UNIVERSITY

YOGYAKARTA

v

The only person responsible for your future is yourself

and only you

Dengan tulus karya ini ku persembahkan kepada

Tuhan Yesus yang senantiasa membimbing dan Menyertaiku.

Ayahku Clement Andreas Agus Priantono dan Mamahku Maria Endang

Sutyasasih.

Adikku Paulina Agty Sekaringtyas.

Teman-teman seperjuanganku di Pendidikan Matematika,

Dan Almamaterku Universitas Sanata Dharma.

viii

Agty Devina Puspitasari. 2020. STRATEGI PEMENANGAN PERMAINAN

CONGKLAK. Program Studi Pendidikan Matematika, Jurusan Pendidikan

Matematika dan Ilmu Pengetahuan Alam, Fakultas Keguruan dan Ilmu

Pendidikan, Universitas Sanata Dharma.

Congklak merupakan nama salah satu permainan tradisional di

Indonesia.Permainan congklak adalah sebuah permainan yang berbentuk papan

yang memiliki 14 dan 16 lubang.Pada papan permainan congklak terdiri atas 12

atau 14 lubang kecil dan 2 lubang besar atau lubang induk. Permainan congklak

dimainkan secara berpasangan, untuk memulai permainan congklak harus

ditentukan terlebih dahulu siapa yang akan bermain terlebih dahulu. Pada saat

bermain congklak apabila biji terakhir jatuh pada lubang kecil miliknya sendiri

atau lubang kecil milik lawan dan tidak ada minimal satu biji congklak yang

mendiami lubang tersebut, maka pemain tersebut harus berhenti dan berganti

giliran main dengan pemain lainnya.

Penelitian ini bertujuan untuk menemukan pola langkah yang tepat untuk

memenangkan permainan congklak dengan mengkaji hubungan matematis antara

congklak dengan sirkuit Hamilton.sirkuit Hamilton adalah sirkuit yang melalui

tiap verteks di dalam graf tepat satu kali, kecuali verteks asal yang sekaligus

merupakan verteks akhir yang dilalui dua kali. Dalam sirkuit Hamilton titik yang

menjadi titik awal akan menjadi titik akhir, dalam permainan congklak hal

tersebut justru harus dihindari karena akan mengakibatkan berhentinya giliran

main pemain tersebut. Berdasarkan kasus tersebut peneliti ingin mengkaji lebih

lanjut mengenai pola langkah yang sebaiknya digunakan oleh pemain agar dapat

memenangkan permainan tersebut.

Metode yang digunakan dalam penelitian ini adalah deskriptif kualitatif

dengan objek penelitian congklak.Peneliti mengkaji tentang pola langkah serta

sirkuit Hamilton yang terbentuk pada pemain yang mendapatkan giliran pertama

untuk bermain.Hasil dari penelitian ini adalah pemain dapat memenangkan

permainan pada saat jumlah biji congklak mencapai 37 biji yang terdapat pada

lubang induk pemain. Namun apabila diteruskan permainannya akan

menghasilkan jumlah biji maksimal pada lubang induk sebanyak 55 di iterasi

88,89, dan 90.

ix

Education Study Program, Departement of Mathematics and Science

Education, Faculty of Teacher Training and Education, Sanata Dharma

University.

Congklak is one of the Indonesian traditional games. Congklak game can

be found in some regions in Indonesia e.g. Java, Lampung, Sulawesi, and some

Malayan regions e.g. Riau and South Sumatera. Although congklak is an

Indonesian traditional game, it can be found in some neighboring countries like

Malaysia, Singapore, and Brunei Darussalam. Congklak is shaped as a board

with 14 and 16 holes. Congklak is usually made from woods or plastics. The used

counters were usually small cowrie shells or plant seeds, but as time goes by, the

commonly used congklak counters are plastic seeds. On the congklak board, there

are 12 or 14 small holes and 2 bigger holes as the main holes. The game is played

in pairs and turn. Firstly, the one who will start the game should be decided. It

can be done by doing a scissors-paper-rock game. In one turn, if the last seed

drops to a small empty hole that belongs to either the player or the opponent, the

player should stop and switch to the other player.

This research aims to find the correct movement pattern for winning the

congklak game by studying the mathematical relationship between the congklak

game and the Hamilton circuit. Hamilton circuit is a circuit that passes through

every vertex of a graph exactly once, except for the original vertex (which is also

the final vertex), it is passed twice. In the Hamilton circuit, the starting point will

be the endpoint. In the congklak game, that condition should be avoided for the

cause of losing the chance in continuing the playing turn. According to that case,

the researcher wanted to do a further study of the movement pattern that should

be used by players to win the game.

This research used descriptive qualitative method and the object research

is congklak.Research examine the pattern of step and the Hamilton circuit that is

formed on the player who gets the first turn to play.The result of this research are

the player can win when the congklak seeds in the hole is 37. However, if it

continues it can produce a maximum number of seeds 55on the iteration 88, 89,

and 90.

x

Puji dan syukur penulis ucapkan kepada Tuhan Yang Maha Esa karena

atas berkat dan rahmatNya penulis dapat menyelesaikan skripsi dengan judul

“Cara Memenangkan Permainan Congklak dengan Menemukan Pola Langkah

yang Tepat”dengan baik. Skripsi ini disusun sebagai salah satu syarat memperoleh

gelar sarjana pendidikan pada Program Studi Pendidikan Matematika, Jurusan

Pendidikan Matematika dan Ilmu Pengetahuan Alam, Fakultas Keguruan dan

Ilmu Pendidikan, Universitas Sanata Dharma.

Berbagai hambatan dan rintangan telah penulis hadapi selama penulisan

skripsi ini, namun berkat bantuan doa, dukungan, serta motivasi semua pihak

peneliti dapat menyelesaikan skripsi ini. Oleh karena itu peneliti ingin

mengucapkan terimakasih kepada :

1. Bapak Dr. Yohanes Harsoyo, S.Pd., M.Si., selaku Dekan Fakultas Keguruan

dan Ilmu Pendidikan, Universitas Sanata Dharma.

2. Bapak Dr. Marcellinus Andy Rudhito, S.Pd., selaku Ketua Jurusan Pendidikan

Matematika dan Ilmu Pengetahuan Alam.

3. Bapak Beni Utomo, M.Sc., selaku Ketua Program Studi Pendidikan

Matematika, Universitas Sanata Dharma.

4. Bapak Dominikus Arif Budi Prasetyo, M.Si., selaku Dosen Pembimbing

Skripsi yang dengan sabar membimbing peneliti dalam mengerjakan skripsi.

5. Bapak Yosep Dwi Kristanto, M.Pd., selaku Dosen Pembimbing Akademik.

xi

memberikan ilmu pengetahuan dan bekal ketrampilan.

7. Orang tua saya Drs. Clement Andreas Agus Priantono dan Maria Endang

Sutyasasih yang selalu memberikan doa dan motivasi.

8. Mateas Handy Wicaksono, S.Pd., selaku kakak tingkat sekaligus alumni

Program Studi Pendidikan Matematika Universitas Sanata Dharma yang telah

membimbing dan memotivasi penulis dalam menyelesaikan skripsi ini.

9. Seluruh teman-teman pendidikan matematika angkatan 2016 yang telah

berjuang bersama-sama untuk menyelesaikan studi di Universitas Sanata

Dharma.

10. Serta semua pihak yang tidak dapat disebutkan satu-persatu.

Penulis mengharapkan kritik dan saran yang membangun agar dapat

bermanfaat bagi penulis dalam penulisan karya ilmiah dikemudian

hari.Penulis berharap agar kiranya skripsi ini dapat bermanfaat bagi banyak

pihak.

Yogyakarta, 27 Juli 2020

Penulis

xii

HALAMAN PERSETUJUAN PEMBIMBING ... iii

LEMBAR PENGESAHAN ... iv

HALAMAN PERSEMBAHAN ... v

PERNYATAAN KEASLIAN KARYA ... vi

LEMBAR PERNYATAAN PERSETUJUAN ... vii

PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS ... vii

ABSTRAK ... viii

ABSTRACT ... ix

KATA PENGANTAR ... x

DAFTAR ISI ... xii

DAFTAR GAMBAR ... xiv

DAFTAR TABEL ... xv

BAB I PENDAHULUAN ... 1

A. Latar Belakang ... 1

B. Rumusan Masalah ... 3

C. Tujuan Penelitian ... 3

D. Pembatasan Masalah ... 3

E. Manfaat Penelitian ... 4

F. Penulisan ... 4

BAB II KAJIAN PUSTAKA ... 6

A. Permainan Congklak ... 6

B. Dasar-Dasar Graf ... 8

BAB IIILintasan Hamilton, Sirkuit Hamilton, Graf Hamilton ... 15

Graf semi Hamilton, Aturan Permainan Congklak

BAB IV OPTIMASI PEMENANGAN CONGKLAK ... 20

xiii

C. Kriteria Penentuan Pola Langkah yang Dipilih Sebagai Solusi

Terbaik ... 42

BAB V PENUTUP ... 43

A. Kesimpulan ... 43

B. Saran ... 44

DAFTAR PUSTAKA ... 45

LAMPIRAN ... 46

xiv

Gambar 2.2 ... 12

Gambar 2.3 ... 13

Gambar 2.4 ... 14

Gambar 2.5 ... 15

Gambar 2.6 ... 15

Gambar 2.7 ... 15

Gambar 2.8 ... 16

Gambar 2.9 ... 17

Gambar 2.10 ... 19

Gambar 3.1 Lintasan Hamilton ... 20

Gambar 3.2 Sirkuit Hamilton ... 21

Gambar 3.3 Graf semi Hamilton ... 22

Gambar 3.4 ... 23

xv

Tabel 4.2 Untuk Lubang 𝐴

1

... 27

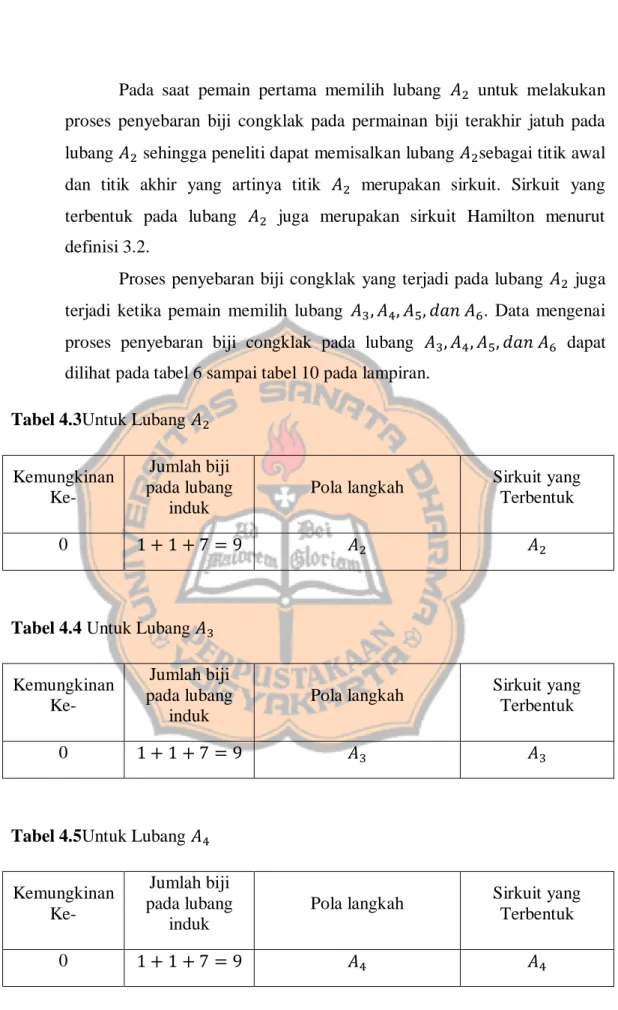
Tabel 4.3 Untuk Lubang 𝐴

₂

... 28

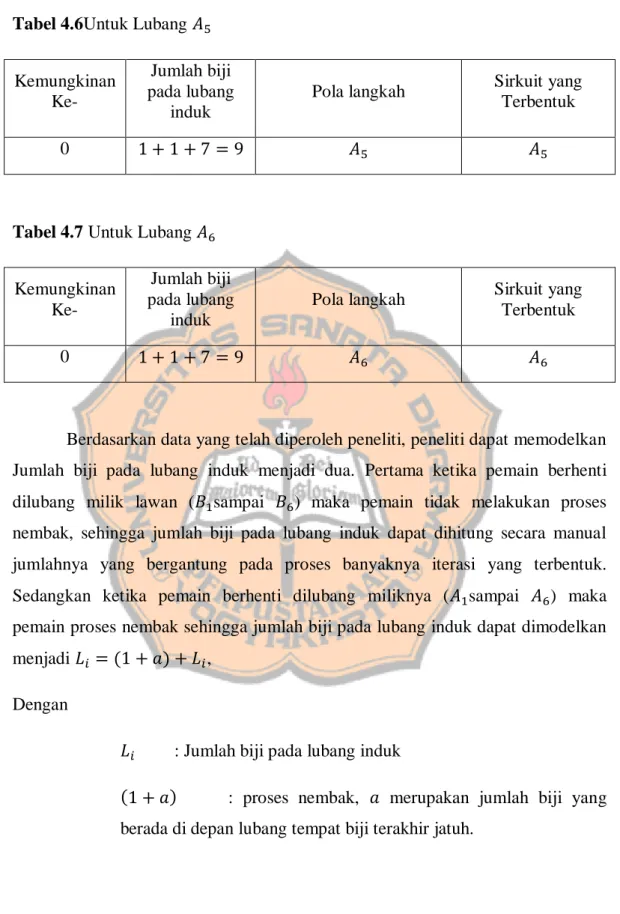
Tabel 4.4 Untuk Lubang 𝐴

3

... 30

Tabel 4.5 Untuk Lubang 𝐴

₄

... 48

Tabel 4.6 Untuk Lubang 𝐴

₅

... 48

Tabel 4.7 Untuk Lubang 𝐴

₆

... 49

Tabel 4.8 Untuk Lubang 𝐴

6

... 49

Tabel 4.9 Untuk Lubang 𝐴

₆

... 49

Tabel 4.10 Untuk Lubang 𝐴

₆

... 49

Tabel 5 lubang 𝐴

₁

... 54

Tabel 5.1 Kemungkinan 1 ... 54

Tabel 5.2 Kemungkinan 2 ... 54

Tabel 5.3 Kemungkinan 3 ... 54

Tabel 5.4 Kemungkinan 4 ... 55

Tabel 5.5 Kemungkinan 5 ... 55

Tabel 5.6 Kemungkinan 6 ... 55

Tabel 5.7 Kemungkinan 7 ... 56

Tabel 5.8 Kemungkinan 8 ... 56

Tabel 5.9 Kemungkinan 9 ... 56

Tabel 5.10 Kemungkinan 10 ... 57

Tabel 5.1 1Kemungkinan 11 ... 57

Tabel 5.12 Kemungkinan 12 ... 58

Tabel 5.13 Kemungkinan 13 ... 59

xvi

Tabel 5.16 Kemungkinan 16 ... 62

Tabel 5.17 Kemungkinan 17 ... 63

Tabel 5.18 Kemungkinan 18 ... 64

Tabel 5.19 Kemungkinan 19 ... 65

Tabel 5.20 Kemungkinan 20 ... 66

Tabel 5.21 Kemungkinan 21 ... 68

Tabel 5.22 Kemungkinan 22 ... 69

Tabel 5.23 Kemungkinan 23 ... 71

Tabel 5.24 Kemungkinan 24 ... 73

Tabel 5.25 Kemungkinan 25 ... 74

Tabel 5.26 Kemungkinan 26 ... 76

Tabel 5.27 Kemungkinan 27 ... 77

Tabel 5.28 Kemungkinan 28 ... 79

Tabel 5.29 Kemungkinan 29 ... 80

Tabel 5.30 Kemungkinan 30 ... 82

Tabel 5.31 Kemungkinan 31 ... 84

Tabel 5.32 Kemungkinan 32 ... 85

Tabel 5.33 Kemungkinan 33 ... 87

Tabel 5.34 Kemungkinan 34 ... 89

Tabel 5.35 Kemungkinan 35 ... 90

Tabel 5.36 Kemungkinan 36 ... 92

Tabel 5.37 Kemungkinan 37 ... 93

Tabel 5.38 Kemungkinan 38 ... 95

xvii

Tabel 5.41 Kemungkinan 41 ... 100

Tabel 5.42 Kemungkinan 42 ... 101

Tabel 5.43 Kemungkinan 43 ... 103

Tabel 5.44 Kemungkinan 44 ... 105

Tabel 5.45 Kemungkinan 45 ... 106

Tabel 5.46 Kemungkinan 46 ... 108

Tabel 5.47 Kemungkinan 47 ... 109

Tabel 5.48 Kemungkinan 48 ... 111

Tabel 5.49 Kemungkinan 49 ... 113

Tabel 5.50 Kemungkinan 50 ... 115

Tabel 5.51 Kemungkinan 51 ... 116

Tabel 5.52 Kemungkinan 52 ... 118

Tabel 5.53 Kemungkinan 53 ... 120

Tabel 5.54 Kemungkinan 54 ... 122

Tabel 5.55 Kemungkinan 55 ... 123

Tabel 5.56 Kemungkinan 56 ... 125

Tabel 5.57 Kemungkinan 57 ... 127

Tabel 5.58 Kemungkinan 58 ... 129

Tabel 5.59 Kemungkinan 59 ... 132

Tabel 5.60 Kemungkinan 60 ... 134

Tabel 5.61 Kemungkinan 61 ... 136

Tabel 5.62 Kemungkinan 62 ... 138

Tabel 5.63 Kemungkinan 63 ... 140

xviii

Tabel 5.66 Kemungkinan 66 ... 148

Tabel 5.67 Kemungkinan 67 ... 150

Tabel 5.68 Kemungkinan 68 ... 153

Tabel 5.69 Kemungkinan 69 ... 155

Tabel 5.70 Kemungkinan 70 ... 158

Tabel 5.71 Kemungkinan 71 ... 160

Tabel 5.72 Kemungkinan 72 ... 162

Tabel 5.73 Kemungkinan 73 ... 164

Tabel 5.74 Kemungkinan 74 ... 167

Tabel 5.75 Kemungkinan 75 ... 169

Tabel 5.76 Kemungkinan 76 ... 171

Tabel 5.77 Kemungkinan 77 ... 173

Tabel 5.78 Kemungkinan 78 ... 176

Tabel 5.79 Kemungkinan 79 ... 178

Tabel 5.80 Kemungkinan 80 ... 180

Tabel 5.81 Kemungkinan 81 ... 182

Tabel 5.82 Kemungkinan 82 ... 184

Tabel 5.83 Kemungkinan 83 ... 187

Tabel 5.84 Kemungkinan 84 ... 189

Tabel 5.85 Kemungkinan 85 ... 191

Tabel 5.86 Kemungkinan 86 ... 194

Tabel 5.87 Kemungkinan 87 ... 196

Tabel 5.88 Kemungkinan 88 ... 198

xix

Tabel 6 Lubang 𝐴

2

... 206

Tabel 7 Lubang 𝐴

₃

... 206

Tabel 8 Lubang 𝐴

₄

... 206

Tabel 9 Lubang 𝐴

5

... 206

Tabel 10 Lubang 𝐴

₆

... 20

1

PENDAHULUAN

A. Latar Belakang

Indonesia memiliki banyak ragam kebudayaan. Menurut KBBI,

Kebudayaan memiliki pengertian hasil kegiatan dan penciptaan batin (akal

budi) manusia seperti kepercayaan, kesenian, dan adat istiadat. Disetiap

negara pasti memiliki kebudayaannya masing – masing. Di Indonesia,

kebudayaan dibagi menjadi dua sub yaitu warisan budaya benda dan

warisan budaya tak benda. Warisan budaya benda meliputi 2319 cagar

budaya dan 435 museum, sedangkan warisan budaya tak benda terdiri dari

kesenian, sejarah, kepercayaan dan tradisi (Kemendikbud : 2019).

Indonesia memiliki 735 bahasa daerah, 1351 peralatan kesenian, 1087

jenis makanan tradisional, dan 261 kain tradisional. Budaya di Indonesia

tidak hanya sebatas yang disebutkan, namun juga termasuk permainan

tradisional yang tersebar di berbagai daerah di Indonesia.Permainan

tradisional di Indonesia sendiri berjumlah 766 permainan tradisional

(Kemendikbud, 2018).Sejarah permainan tradisional berasal dari hasil

kebudayaan dari masyarakat setempat, bukan bawaan bangsa asing yang

sering dikira sebagian pihak.

Congklak merupakan nama salah satu permainan tradisional di

Indonesia. Permainan congklak dimainkan secara berpasangan.Permainan

congklak dapat ditemukan di beberapa daerah di Indonesia seperti Jawa,

Lampung, Sulawesi, dan beberapa daerah Melayu seperti Riau dan

Sumatra Selatan.Meskipun congklak merupakan permainan tradisional

Indonesia, permainan ini dapat ditemukan di beberapa Negara tetangga

seperti Malaysia, Singapura, dan Brunei Darussalam.Permainan congklak

memiliki sebutannya masing-masing pada setiap daerah contohnya dakon,

dhakon, dhakonan, dentuman lamban, makaotan, dan dalam bahasa Inggris

disebut mancala. (Utomo, 2017:1)

terbuat dari kayu atau plastidan biji congklak biasanya mengunakan

cangkang kerang yang berbentuk kecil atau biji-bijian, namun seiring

perkembangan jaman biji congklak kini terbuat dari biji-biji plastik.Pada

papan permainan congklak terdiri atas 12 atau 14 lubang kecil dan 2

lubang besar atau lubang induk.

Pada permainan congklak terdapat beberapa istilah berlaku antara

lain satu jalan, dua jalan, dan iterasi. Istilah satu jalan artinya pemain

mengambil seluruh biji pada suatu lubang kecil miliknya dan disebarkan

ke semua lubang yang lain kecuali lubang induk milik lawan. (Utomo,

2017:1). Proses ini hanya dilakukan satu kali sampai pemain tersebut tidak

dapat melakukan penyebaran biji lagi. Hal tersebut dikarenakan biji

congklak terakhir yang diambilnya jatuh pada lubang kosong yang tidak

terisi minimal satu biji congklak yang mendiami lubang tersebut.Apabila

biji terakhir jatuh pada lubang kecil miliknya dan terdapat biji congklak

pada lubang kecil milik lawan yang berada tepat didepan lubang tempat

biji terakhir itu jatuh, maka pemain tersebut dapat mengambil semua biji

congklak di lubang yang bersangkutan dan biji congklak pada lubang

milik lawan yang berada didepannya untuk ditaruh pada lubang besar

milik pemain tersebut. Hal ini disebut sebagai nembak.Apabila biji

terakhir jatuh pada lubang kecil miliknya sendiri atau lubang kecil milik

lawan dan tidak ada minimal satu biji congklak yang mendiami lubang

tersebut, maka pemain tersebut harus berhenti dan berganti giliran main

dengan pemain lainnya.

Apabila biji terakhir jatuh pada lubang besar, maka pemainyang

bersangkutan masih dapat melanjutkan giliran bermainnya dengan

memilih lubang manapun miliknya.Setelah memilih lubang, pemain

tersebut mengambil semua biji yang terdapat pada lubang tersebut dan

melakukan penyebaran biji sepertiyang telah dijelaskan sebelumnya.

miliknya dan melakukan penyebaran biji lagi. Proses penyebaran biji ini

disebut dengan satu iterasi. Proses satu iterasi ini dapat dikembangkan

istilah serupa dua iterasi, tiga iterasi dan lainnya.

Semua proses penyebaran biji congklak dilakukan searah jarum

jam. Pemenang dari permainan congklak ini ditentukan dari banyaknya

biji congklak yang terkumpul pada lubang induk miliknya.Pemain yang

mengumpulkan biji paling banyak dianggap sebagai pemenang.

Peneliti menduga adanya hubungan matematis antara congklak

dengan sirkuit Hamilton pada saat biji terakhir jatuh pada lubang kecil

miliknya sendiri atau lubang kecil milik lawan dan tidak ada minimal satu

biji congklak yang mendiami lubang tersebut, maka pemain tersebut harus

berhenti.Lintasan Hamilton adalah lintasan yang melalui tiap verteks

didalam graf tepat satu kali. Bila lintasan itu kembali ke verteks asal

membentuk lintasan tertutup (sirkuit), maka lintasan itu dinamakan sirkuit

Hamilton. Dengan kata lain sirkuit Hamilton adalah sirkuit yang melalui

tiap verteks di dalam graf tepat satu kali, kecuali verteks asal yang

sekaligus merupakan verteks akhir yang dilalui dua kali.

Dalam sirkuit Hamilton titik yang menjadi titik awal akan menjadi

titik akhir, dalam permainan congklak hal tersebut justru harus dihindari

karena akan mengakibatkan berhentinya giliran main pemain tersebut.

Berdasarkan kasus tersebut peneliti ingin mengkaji lebih lanjut mengenai

pola langkah yang sebaiknya digunakan oleh pemain agar dapat

memenangkan permainan tersebut.

B. Rumusan Masalah :

1. Bagaimanakah pola langkah yang dapat terbentuk pada permainan

congklak?

C. Tujuan Penelitian :

1. Mengetahui pola langkah yang dapat terbentuk pada permainan

congklak.

2. Mengetahui pola langkah yang tepat untuk memenangkan permainan

congklak.

D. Pembatasan Masalah

Agar penelitian ini lebih terarah dan mencegah terjadinya

penafsiran yang kurang tepat, serta supaya tujuan penelitian ini tercapai

peneliti membatasi masalah hanya pada bagaimana cara menemukan

langkah yang tepat yang dilakukan oleh pemain pertama dalam bermain

congklak dengan menghindari kemungkinan terjadinya sirkuit Hamilton

pada langkah pertama yang dilakukan oleh pemai pertama, congklak yang

digunakan adalah congklak dengan 14 lubang. 14 lubang tersebut

merupakan 12 lubang kecil dan 2 lubang induk. Dalam permainan

congklak terdapat aturan mikul dan nembak namun dalam penelitian ini

aturan yang digunakan hanya aturan nambak saja.

E. Manfaat Penelitian

1. Manfaat Teoritis

Hasil dari penelitian ini dapat dijadikan sumber referensi bagi

peneliti selanjutnya yang akan melakukan penelitian serupa.

2. Manfaat Praktis

Hasil penelitian ini dapat menunjukan contok penerapan

matematika dalam kehidupan sehari-hari terlebih untuk memenangkan

permainan congklak.

F. Metode Penelitian

Metode yang digunakan dalam penelitian ini adalah deskriptif

kualitatif dengan objek penelitian congklak.Peneliti akan mengkaji tentang

pola langkah serta sirkuit Hamilton yang terbentuk pada pemain yang

mendapatkan giliran pertama untuk bermain congklak. Setelah peneliti

menemukan beberapa pola langkah peneliti memilih polah langkah yang

paling tepat untuk memenangkan permainan congkak.Data diperoleh

melalui dokumen-dokumen dan observasi (percobaan empiris).Dalam

melakukan observasi, peneliti mengamati percobaan empiris yang

dilakukan oleh pemain congklak. Setelah melakukan kegiatan studi

dokumen dan observasi peneliti menganalisis data yang diperoleh

menggunakan teknis analisis data menurut Miles dan Huberman (1992:

16),terdapat 4 tahap yaitu (1) pengumpulan data; (2) reduksi data; (3)

penyajian data; (4) pengambilan keputusan dan verifikasi.

Tahapan Penelitian

Dalam melakukan penelitian inipeneliti melakukan beberapa tahapan.

Tahapan penelitian tersebut diantaranya yaitu :

1. Melakukan kegiatan studi dokumen berupa penelitian-penelitian yang

relevan terkait permainan congklak dan sirkuit Hamilton.

2. Peneliti melakukan percobaan untuk menentukan kemungkinan serta pola

langkah yang terjadi pada saat memainkan permainan congklak.

3. Peneliti mencatat kemungkinan-kemungkinan tersebut serta pola

langkahnya.

Setelah melakukan kegiatan studi dokumen dan observasi peneliti

menganalisis data yang diperoleh menggunakan teknis analisis data menurut

Miles dan Huberman (1992: 16). Teknik analisis data tersebut ada 4 tahapan,

yaitu :

3. Penyajian data

4. Pengambilan keputusan dan verifikasi

G. Sistematika Penulisan

Untuk mempermudah penulis maupun pembaca dalam mengkaji skripsi

ini, skripsi ini dibagi menjadi 5 bagian, yaitu :

BAB 1

Pada bab ini dipaparkan mengenai latar belakang masalah,

rumusan masalah, batasan masalah, tujuan penelitian, manfaat penelitian,

metode penelitian serta sistematika penulisan.

BAB II

Pada bab ini dipaparkan mengenai definisi etnomatematika, graf

dan sirkuit.

BAB III

Padabab ini dipaparkan mengenai lintasan Hamilton, sirkuit

hamilton, graf hamilton, dan graf semi hamilton, serta aturan permainan

congklak.

BAB IV

Pada bab ini dipaparkan hasil penelitian dan pembahasan dalam

beberapa subbab. Pertama disajikan data mengenai flowchart permainan

congklak serta penjelasan singkat terkait flowchart tersebut. Kedua akan

dijelaskan mengenai syarat pemilihan pola langkah yang dipilih sebagai

solusi terbaik.Ketiga mengenai Pola langkah serta sirkuit Hamilton yang

terbentuk berdasarkan data dari hasil percobaan yang telah dilakukan.

BAB V PENUTUP

memenangkan permainan congklak dan dipaparkan juga saran-saran yang

berkaitan dengan pembahasan

8

KAJIAN PUSTAKA

A. Permainan Congklak

Congklak merupakan salah satu permainan yang ada di Indonesia.

Permainan congklak dimainkan oleh dua orang yang berhadapan

(Indonesia, 2019). Dalam bermain congklak menggunakan papan congklak

yang berisi 14 lubang, dimana 12 lubang merupakan lubang kecil yang

saling berhadapan dan 2 lubang merupakan lumbung atau lubang induk

milik masing-masing pemain. Pada congklak 14 lubang masing-masing

lubang kecil pada papan congklak berisi 6 buah biji congklak.

Pada awal permainan setiap lubang kecil diisi dengan 6 buah biji.

Dua orang pemain yang saling berhadapan melakukan suit untuk

menentukan siapa yang akan bermain terlebih dahulu. Pemain pertama

memulai permainan dengan memilih salah satu lubang (𝐴

₁

𝑠𝑎𝑚𝑝𝑎𝑖 𝐴

₆

)

yang akan diambil bijinya pada lubang tersebut untuk melakukan

penyebaran biji congklak pada setiap lubangnya. Proses penyebaran biji

dilakukan searah dengan putaran jarum jam. Pada saat melakukan

penyebaran biji setiap lubang congklak diisi dengan satu buah biji

congklak disetiap lubangnya. Bila biji congklak terakhir jatuh pada lubang

kecil yang masih berisi biji lainnya pemain tersebut dapat mengambil

biji-biji yang ada kemudian melanjutkan proses penyebaran biji-biji. Apabila biji-biji

terakhir jatuh padalubang indukk atau lumbung miliknya maka pemain

tersebut bisa memilih kembali lubang kecil miliknya yang berisi sejumlah

biji congklak kemudian melakukan proses penyebaran biji congklak lagi.

Apabila biji congklak terakhir jatuh pada lubang miliknya yang tidak

terdapat minimal 1 biji congklak maka proses penyebaran biji berhenti dan

bergantian dengan pemain kedua sama halnya ketika biji congklak terakhir

jatuh pada lubang kecil milik lawan yang tidak terdapat minimal 1 buah

biji congklak.

jatuh pada lubang kecil milik pemain yang sedang melakukan proses

penyebaran biji congklak, pemain tersebut berhak mengambil seluruh biji

congklak yang ada diseberang lubang tempat biji terakhir jatuh.

Sedangkan mikul adalah suatu proses pengambilan biji congklak yang ada

di kanan dan dikiri tempat biji terakhir jatuh ketika biji terakhir jatuh pada

lubang kecil milik lawan. (Style, 2019).

Permainan congklak dianggap selesai ketika sudah tidak ada biji

congklak lagi yang dapat diambil baik dilubang milik pemain pertama

maupun pemain kedua. Pemenang dari permainan ini ditentukan dari

pemain mana yang memiliki jumlah biji congklak paling banyak dilubang

induk atau lumbung miliknya (Kumparan, 2019).

B. Dasar-Dasar Graf dan Subgraf

Definisi 2.1 (Ronsen, Kenneth H., 2019:673)

Diberikan himpunan tak kosong titik

𝑉 = {𝑣

₁

, 𝑣

₂

, … , 𝑣

_𝑛

} dan himpunan

sisi

𝐸 = {𝑒

₁

, 𝑒

₂

, … , 𝑒

_𝑛

}. Suatu himpunan G yang terdiri dari V dan E

disebut graf yang dinotasikan dengan 𝐺 = (𝑉, 𝐸).

Berikut diberikan contoh mengenai suatu graf.

Contoh 2.1

Diberikan

𝑉 = {𝑣

₁

, 𝑣

₂

, 𝑣

₃

} dan 𝐸 = {𝑒

₁

, 𝑒

₂

, 𝑒

₃

, 𝑒

₄

}. Graf tersebut dapat

digambarkan sebagai berikut :

Gambar 2.1 Graf G

Pada gambar 2.1 dapat dilihat bahwa gambar tersebut memiliki tiga

simpul yaitu

𝑣

₁

, 𝑣

₂

, 𝑣

₃

yang artinya memiliki himpunan tak kosong

simpul dengan jumlah yang berhingga dan terdapat pula empat sisi yaitu

𝑒

₁

, 𝑒

₂

, 𝑒

₃

, 𝑒

₄

yang artinya memiliki himpunan sisi yang jumlahnya

berhingga. Setiap sisi tersebut menghubungkan pasangan simpul-simpul.

Sisi 𝑒

₁

menghubungkan simpul 𝑣

₁

dan 𝑣

₂

. Sisi 𝑒

₂

menghubungkan simpul

𝑣

₁

dan

𝑣

₃

. Simpul 𝑒

₃

menghubungkan simpul

𝑣

₁

dan

𝑣

₃

. Serta sisi

𝑒

₄

menghubungkan simpul

𝑣

₂

dan

𝑣

₃

. Oleh karena itu gambar 2.1 sesuai

dengan definisi 2.1 merupakan sebuah graf.

Definisi 2.2 (Wilson, Robin J., 2009:12)

Sebuah simpul

𝑣 adalah jumlah sisi yang menghubungkan simpul 𝑣.

Derajat simpul 𝑣 dapat dituliskan sebagai deg(𝑣).

Berikut merupakan contoh derajat.

Contoh 2.2 :

Pada gambar 2.1 dapat diketahui bahwa

𝑑𝑒𝑔(𝑣

1

) = 𝑑𝑒𝑔(𝑣

3

) = 3 dan

deg(𝑣

₂

) = 2

.

Definisi 2.3 (Marsudi, 2016:5)

Contoh 2.3

Dapat dilihat pada gambar 2.1 banyaknya sisi pada graf tersebut adalah 4

yaitu

𝑒

₁

, 𝑒

₂

, 𝑒

₃

, 𝑒

₄

sehingga menurut definisi 2.3 ukuran graf tersebut

adalah 4.

Definisi 2.4 (Marsudi, 2016:5)

Order dari suatu graf G adalah banyaknya simpul dalam graf G.

Berikut ini akan diberikan contoh dari order.

Contoh 2.4

Dapat dilihat pada gambar 2.1 banyaknya simpul pada graf tersebut

adalah 3 yaitu

𝑣

₁

, 𝑣

₂

, 𝑣

₃

sehingga menurut definisi 2.4 order dari graf

tersebut adalah 3.

Berikut diberikan definisi graf sederhana. Untuk menjelaskan definisi

graf sederhana dan graf lengkap akan dijelaskan terlebih dahulu mengenai

sisi berganda dan gelang (loop).

Definisi 2.5 (Siang, J. J, 2009:219)

Dua garis yang berbeda𝑒

_𝑖

𝑑𝑎𝑛 𝑒

_𝑗

, dengan

𝑖 ≠ 𝑗 yang terkait dengan titik

ujung yang sama disebut garis sejajar (parallel).

Contoh 2.5

Pada gambar 2.1 yang merepresentasikan sebagai sebuah graf terlihat

bahwa sisi

𝑒

₂

dan

𝑒

₃

menghubungkan dua titik yang sama yaitu titik

Definisi 2.6 (Siang, J. J, 2011:268)

Garis yang hanya berhubungan dengan satu titik ujung disebut Loop.

Berikut diberikan contoh suatu gelang(loop)

Contoh 2.6

Gambar 2.2

Pada gambar 2.2 yang merepresentasikan sebuah graf dapat dilihat bahwa

𝑒

₁

menghubungkan simpul

𝑣

₁

dengan dirinya sendiri, sehingga

berdasarkan definisi 2.4 𝑒

1

merupakan loop.

Definisi 2.7 (Wilson, Robin. J, 2009:8)

Sebuah graf yang tidak memiliki gelang (loop) dan sisi parelel disebut

graf sederhana.

Berikut ini akan dijelaskan mengenai contoh graf sederhana.

Contoh 2.7

Gambarlah semua graf sederhana yang dapat dibentuk dari 4 titik

{a,b,c,d} dan 2 garis.

maka ada

(

4

2

) =

4!

2!₂!

= 6. Garis yang mungkin dibuat yaitu garis-garis

yang titik-titik ujungnya adalah {a,b},{a,c}, {a,d}, {b,c}, {b,d}, dan

{c,d}.

Dari keenam garis tersebut selanjutnya dipilih 2 diantaranya.Sehingga

(

4

2

) =

4!

2!₄!

= 15 buah graf yang mungkin dibentuk.

Gambar 2.3

Berikut diberikan definisi graf lengkap. Untuk menjelaskan definisi graf

lengkap akan dijelaskan terlebih dahulu mengenai definisi bertetangga

dan bersisian.

kemudian dikatakan bersisian (incident) dengan sisi tersebut.

Dua buah sisi pada sebuah graf disebut bertetangga (adjacent) jika

terdapat sebuah simpul yang sama diantara keduanya.

Berikut ini akan dijelaskan mengenai contoh dua buah simpul dan dua

buah sisi yang saling bertetangga.

Contoh 2.8

Pada gambar 2.2 dapat dilihat bahwa :

a) simpul

𝑣

1

bertetangga dengan simpul

𝑣

2

dan keduanya bersisian

dengan dengan sisi 𝑒

₂

.

b) simpul

𝑣

₂

bertetangga dengan simpul

𝑣

₃

dan keduanya bersisian

dengan dengan sisi 𝑒

3

.

c) simpul

𝑣

₁

bertetangga dengan simpul

𝑣

₃

dan keduanya bersisian

dengan dengan sisi 𝑒

₄

.

Definisi 2.9(Wilson, Robin. J, 2009:19)

Sebuah graf sederhana dimana setiap simpul yang berbeda saling

bertetangga disebut graf lengkap (complete graph). Graf lengkap dengan

n simpul dapat dinotasikan sebagai (𝐾

_𝑛

).

Gambar 2.4

Pada gambar 2.4 graf tersebut merupakan graf sedethana yang

masing-masing simpulnya saling bertetangga, yaitu :

a) Simpul 𝑣

₁

bertetangga dengan simpul 𝑣

₂

, 𝑣

_3,

dan 𝑣

₄

.

b) Simpul 𝑣

₂

bertetangga dengan simpul 𝑣

₂

, 𝑣

₃

, dan 𝑣

₄

c) Simpul 𝑣

₃

bertetangga dengan simpul 𝑣

₁

, 𝑣

₂

, dan 𝑣

₄

d) Simpul 𝑣

₄

bertetangga dengan simpul 𝑣

₁

, 𝑣

₂

, dan 𝑣

₃

Sehingga berdasarkan definisi 2.6 graf yang ada pada gambar 2.4

merupakan graf lengkap dengan banyaknya simpul adalah 4 dan dapat

dinotasikan dengan 𝐾

4

.

Definisi 2.10 (Siang, J. J, 2009:229)

Suatu graf G disebut graf bipartite apabila V(G) merupakan gabungan

dari 2 himpunan tak kosong

𝑉

₁

dan

𝑉

₂

dan setiap garis dalam G

menghubungkan suatu titik dalam 𝑉

₁

dengan titik dalam 𝑉

_2.

Apabila dalam graf Bipartite setiap titik dalam

𝑉

₁

berhubungan dengan

setiap titik pada 𝑉

₂

, maka grafnya disebut graf bipartite lengkap.

Jika

𝑉

₁

terdiri dari m titik dan dan

𝑉

₂

terdiri dari n titik, maka graf

bipartite lengkapnya diberi symbol 𝐾

_𝑚,𝑛.

Gambar 2.5

Gambar 2.6

Gambar 2.7

a. Gambar 2.5 merupakan graf bipartisi lengkap. Terlihat bahwa titik-titik

grafnya terbagi menjadi dua bagian, yaitu

𝑉

₁

= {𝑣

₁

, 𝑣

₂

, 𝑣

₃

} dan 𝑉

₂

=

{𝑣

4

, 𝑣

5

}. Setiap titik dalam 𝑉

1

dihubungkan dengan semua titik dalam

𝑉

2

sehingga grafnya merupakan 𝐾

3,2

b. Gambar 2.6 merupakan graf bipartite saja karena titik-titik dalam graf

tersebut terbagi menjadi dua bagian yaitu 𝑉

₁

= {𝑣

₁

, 𝑣

₃

} dan 𝑉

₂

= {𝑣

₂

, 𝑣

₄

}.

Akan tetapi tidak semua titik dalam 𝑉

₁

dihubungkan dengan 𝑉

_2.

c. Gambar 2.7 Dengan pengaturan letak titik-titiknya, maka graf tersebut

dapat digambarkan sebagai berikut :

Gambar 2.8

Dari gambar 2.7 tampak bahwa titik-titiknya terbagi menjadi dua yaitu

𝑉

₁

= {𝑣

₁

, 𝑣

₃

, 𝑣

₅

} dan 𝑉

₂

= {𝑣

₂

, 𝑣

₄

, 𝑣

₆

}. Setiap garis menghubungkan

setiap titik dalam

𝑉

₁

dengan sebuah titik pada

𝑉

₂

sehingga grafnya

merupakan graf bipartite.

Konsep pada subgraf sama dengan konsep himpunan bagian.

Dalam teori himpunan, himpunan A dinyatakan himpunan bagian B jika

dan hanya jika setiap anggota A merupakan anggota B. Karena graf

merupakan himpunan yang terdiri dari titik dan garis maka H dikatakan

subgraf G jika semua titik dan garis H juga merupakan titik dan garis

dalam G.

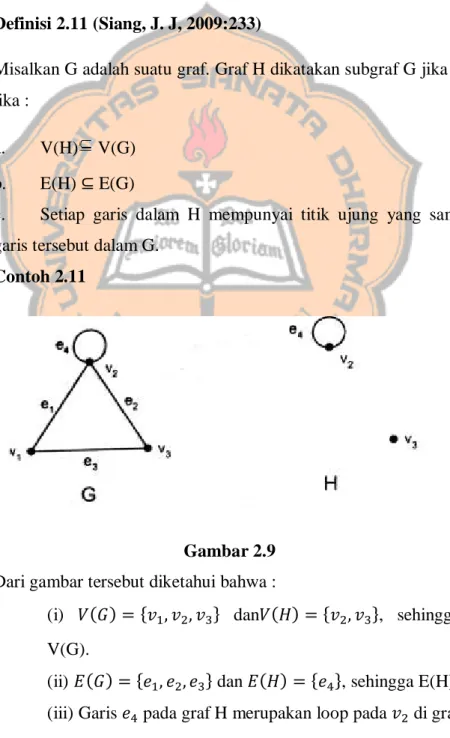
Definisi 2.11 (Siang, J. J, 2009:233)

Misalkan G adalah suatu graf. Graf H dikatakan subgraf G jika dan hanya

jika :

a.

V(H) V(G)

b.

E(H) ⊆ E(G)

c.

Setiap garis dalam H mempunyai titik ujung yang sama dengan

garis tersebut dalam G.

Contoh 2.11

Gambar 2.9

Dari gambar tersebut diketahui bahwa :

(i)

𝑉(𝐺) = {𝑣

₁

, 𝑣

₂

, 𝑣

₃

} dan𝑉(𝐻) = {𝑣

₂

, 𝑣

₃

}, sehingga V(H)

V(G).

(ii) 𝐸(𝐺) = {𝑒

1

, 𝑒

2

, 𝑒

3

} dan 𝐸(𝐻) = {𝑒

4

}, sehingga E(H) ⊆ E(G).

(iii) Garis 𝑒

₄

pada graf H merupakan loop pada 𝑣

₂

di graf G.

Selanjutnya akan dijelaskan mengenai jalan (walk), lintasan (path), dan sirkuit

(cycle)

Definisi 2.12 (Marsudi, 2016:11-12)

Jalan(walk) 𝑢 − 𝑣 dalam graf G adalah barisan simpul-simpul dalam graf G yang

dimulai dari simpul u dan berakhir di simpul v sedemikian sehingga

simpul-simpul yang berurutan dalam barisan adalah bersisian (adjacent), dapat ditulis

𝑤: 𝑢 = 𝑣

₀

→ 𝑣

₁

→ 𝑣

₂

→ ⋯ → 𝑣

_𝑘

= 𝑣. Dimana 𝑘 ≥ 0; 𝑣

_𝑖

dan 𝑣

_𝑖+1

adjacent untuk

𝑖 = 0, 1, 2, … , 𝑘 − 1.

Jika 𝑢 = 𝑣, maka 𝑊 adalah jalan tertutup. Sedangkan jika 𝑢 ≠ 𝑤 maka 𝑊 adalah

jalan terbuka. Banyaknya sisi yang muncul dalam satu jalan (termasuk sisi yang

muncul lebih dari satu) disebut panjang jalan.

Berikut ini merupakan contoh dari walk.

Contoh 2.12

Gambar 2.10

Pada gambar 2.8 dapat dilihat bahwa barisan simpul-simpul 𝑣

₁

− 𝑣

₆

∶ 𝑣

₁

→ 𝑣

₂

→

𝑣

3

→ 𝑣

5

→ 𝑣

4

→ 𝑣

3

→ 𝑣

2

→ 𝑣

8

adalah jalan terbuka denga panjang jalan 7.

lintasan tertutup. Banyaknya sisi yang muncul dalam lintasan disebutpanjang

lintasan. Panjang lintasan terpendek dari

𝑢 ke 𝑣 disebut jarak dari 𝑢 ke 𝑣 dengan

notasi 𝑑(𝑢, 𝑣).

Berikut ini akan dijelaskan mengenai contoh suatu lintasan(path).

Contoh 2.13

Lihatlah gambar 2.10, jalan 𝑣

₁

− 𝑣

₈

adalah 𝑃: 𝑣

₁

→ 𝑣

₂

→ 𝑣

₆

→ 𝑣

₇

→ 𝑣

₈

merupakan sebuah lintasan menurut definisi 2.10 karena simpul-simpulnya

berlainan dengan panjang lintasan 4.

Definisi 2.14 (Rinaldi, 2005)

Siklus(cycle) adalah lintasan tertutup (closed path), yaitu lintasan yang memiliki

titik awal dan titik akhir yang sama.

Contoh 2.14

Lihatlah

gambar

2.10.

Pada

gambar

tersebut

dapat

dilihat

bahwa

𝐶: 𝑣

₂

, 𝑣

₃

, 𝑣

₅

, 𝑣

₆

, 𝑣

₂

merupakan siklus karena setiap sisinya berlainan dan setiap

simpulnya tidak muncul lebih dari satu kali kecuali

𝑣

2

yang merupakan simpul

awal dan simpul akhir.

21

Lintasan Hamilton, Sirkuit Hamilton, Graf Hamilton, dan Graf semi

Hamilton, Aturan Permainan Congklak

Definisi 3.1 (Rinaldi, 2005)

Lintasan Hamilton adalah lintasan yang melalui tiap simpul di dalam suatu Graf

tepat satu kali.

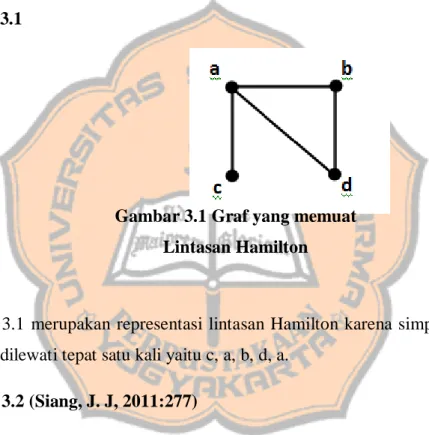
Contoh 3.1

Gambar 3.1 merupakan representasi lintasan Hamilton karena simpul dalam graf

tersebut dilewati tepat satu kali yaitu c, a, b, d, a.

Definisi 3.2 (Siang, J. J, 2011:277)

Suatu graf terhubung G disebut sirkuit Hamilton bila ada sirkuit yang

mengunjungi setiap titiknya tepat satu kali (kecuali titik awal yang sama dengan

titik akhirnya).

Dalam sirkuit Hamilton semua titik harus dikunjungi tepat satu kali dan

tidak harus melalui semua garisnya.Dalam sirkuit Hamilton yang paling

diperhatikan dan penting adalah kunjungan pada setiap titiknya.

Jika G merupakan sirkuit Hamilton, maka G memiliki subgraf H dengan sifat-sifat

berikut :

Gambar 3.1 Graf yang memuat

Lintasan Hamilton

3) H memiliki jumlah garis yang sama dengan jumlah titiknya

Syarat (1) dan (2) jelas menurut definisi sirkuit Hamilton, yang mengharuskan

mengunjungi semua titik dalam G. Oleh karena dalam sirkuit Hamilton, setiap dua

titik dihubungankan dengan tepat satu garis, maka jumlah garisnya sama dengan

jumlah titiknya. Hal itu dinyatakan dalam syarat (3).

Contoh 3.2

Gambar 3.2 Graf yang memuat

sirkuit Hamilton

Gambar 3.2 merupakan representasi dari graf yang memuat sirkuit Hamilton yaitu

a, b, d, c.

Pengertian Graf Hamilton(Rinaldi, 2005)

Jika graf G memuat sirkuit Hamilton maka graf G disebut Graf Hamilton

Contoh 3.3

Gambar 3.2 merupakan graf Hamilton karena memuat sirkuit Hamilton yaitu a, b,

c. d, a

Graf G yang hanya memuat lintasan Hamilton disebut Graf semi Hamilton.

Contoh 3.4

Gambar 3.3

Gambar 3.3 merupakan graf semi Hamilton karena memuat lintasan Hamilton

yaitu b, a, c, d.

Teorema 3.1

Setiap Graf lengkap adalah graf Hamilton.

Aturan Permainan Congklak

1. Permainan congklak dimainkan oleh dua pemain, dari dua pemain tersebut

ditentukan siapa yang akan bermain pertama.

2. Pemain pertama memilih salah satu lubang kecil yang ada dihadapannya.

3. Pemain tersebut mengambil semua biji yang ada pada lubang kecil yang

dia pilih.

4. Pemain menyebar biji conglak satu persatu kelubang berikutnya searah

jarum jam.

5. Dalam menyebarkan biji congklak apabila pemain akan melewati lubang

induk atau lumbung milik lawan pemain tidak boleh mengisi lumbung

milik lawan.

6. Proses penyebaran biji terus berlangsung sampai biji congklak terakhir

jatuh pada lubang milik lawan yang tidak terdapat biji congklak.

penyebaran biji lagi.

8. Apabila biji congklak jatuh pada lubang kecil miliknya pemain dapat

melakukan nembak. Nembak adalah proses pengambilan seluruh biji

congklak milik lawan yang lubang kecilnya tepat berada didepan lubang

kecil milik pemain.

Gambar 3.1

Cara Menentukan Iterasi yang terbentuk dalam permainan congklak :

1. Iterasi pertama dimulai dari pemilihan lubang (𝐴

₁

, 𝐴

₂

, 𝐴

₃

, … 𝐴

₆

)

2. Iterasi kedua dan iterasi selanjutnya dimulai ketika pada iterasi pertama

berhenti di lubang induk.

3. Apabila biji congklak jatuh pada lubang kecil milik pemain tersebut iterasi

berhenti dan dilanjutkan ke proses nembak.

4. Apabila biji congklak jatuh pada lubang kecil milik lawan maka iterasi

tersebut berhenti.

5. Ketika terjadi proses pada point 3 dan 4 akan dilakukan proses penentuan

iterasi baru yang merupakan kelanjutan dari proses iterasi sebelumnya saat

biji congklak jatuh pada lubang induk atau lumbung pemain.

25

Pada bab ini, peneliti meyajikan hasil penelitian dan pembahasan dalam

beberapa subbab. Pertama disajikan data mengenai flowchart permainan congklak

serta penjelasan singkat terkait flowchart tersebut.Kedua akan dijelaskan

mengenai syarat pemilihan pola langkah yang dipilih sebagai solusi terbaik.Ketiga

mengenai Pola langkah serta sirkuit Hamilton yang terbentuk berdasarkan data

dari hasil percobaan yang telah dilakukan.

A. Flowchart Permainan Congklak

Gambar 4.1

Flowchart tersebut dibuat berdasarkan aturan-aturan dalam permainan

congklak.Permainan congklak dimainkan oleh dua pemain, dari dua pemain

tersebut ditentukan siapa yang akan bermain pertama. Setelah ditentukan siapa

1. Pemain pertama memilih salah satu lubang kecil 𝐴

₁

sampai 𝐴

₆

.

2. Pemain tersebut mengambil semua biji yang ada pada lubang kecil

yang dia pilih.

3. Pemain menyebar biji conglak satu persatu kelubang berikutnya

searah jarum jam dengan jumlah biji congklak pada lubang

berikutnya adalah

𝑛 + 1 dan jumlah biji ditangan menjadi 𝑛 −

1.Dalam menyebarkan biji congklak apabila pemain akan melewati

lubang induk atau lumbung milik lawan pemain tidak boleh

mengisi lumbung milik lawan.

4. Ketika jumlah biji ditangan berjumlah

𝑛 = 0, perlu dicek apakah

biji congklak jatuh pada lubang induk atau tidak.

a.

Jika biji congklak jatuh pada lubang induk maka pemain

masih dapat melanjutkan permainan dengan mengulangi

proses pertama.

b.

Jika biji congklak tidak jatuh pada lubang induk perlu dicek

kembali apakah biji terakhir jatuh pada lubang berisi

𝑛 > 1

biji congklak atau tidak.

i.

Jika biji congklak terakhir jatuh pada lubang berisi

𝑛 > 1 biji pemain dapat melanjutkan permainan

dengan mengulangi proses kedua.

ii.

Jika biji congklak terakhir tidak jatuh pada lubang

berisi

𝑛 > 1 biji perlu dicek kembali apakah biji

terakhir jatuh pada lubang miliknya sendiri

(𝐴

₁

sampai

𝐴

₆

) yang berisi

𝑛 < 1 biji congklak atau

tidak.

a.) Jika biji terakhir jatuh pada lubang miliknya

sendiri (𝐴

₁

sampai

𝐴

₆

) yang berisi

𝑛 < 1 biji

b.) Jika biji terakhir tidak jatuh pada lubang

miliknya sendiri (𝐴

₁

sampai 𝐴

₆

) yang berisi 𝑛 <

1 biji congklak maka gilirannya bermain

berhenti.

B. Kriteria Penentuan Pola Langkah yang Dipilih Sebagai Solusi

Terbaik (Wicaksono : 2018) :

1. Langkah yang diambil harus terhindar dari terjadinya sirkuit Hamilton.

2. Biji pada lubang kecil yang dijalankan harus berakhir dilubang induk

atau lumbung.

3. Diperoleh jumlah biji minimal pada lubang induk atau lumbung

pemain sebanyak 𝑛

2

_{+ 1 = 37.}

C. Tabel 4.1Pola langkah yang sudah ditemukan permainan congklak untuk

𝑛 = 1,2,3,4,5,6,7.Dimana 𝑛 merupakan lubang pada papan congklak.

(Wicaksono : 2018) :

𝑛

Jumlah semua biji

2𝑛

2 Jumlah biji pada lubang induk setelah kesempatan pertama Pola Langkah 1 2

𝑛

2

_{= 1}

_𝐴

1 2 8

𝑛

2

_{+ 1 = 5}

_𝐴

2

− 𝐴

1

− 𝐴

2

− 𝐴

1 3 18

𝑛

2

_{= 9}

_𝐴

3

− 𝐴

2

− 𝐴

2

− 𝐴

1

− 𝐴

2

−𝐴

1 4 32

18 ≥ 𝑛

2₊₁

_𝐴

4

− 𝐴

1

− 𝐴

3

− 𝐴

1

− 𝐴

3

− 𝐴

3

− 𝐴

1 5 50

_𝑛

2

_{+ 1 = 26}

𝐴

5

− 𝐴

4

− 𝐴

4

− 𝐴

1

− 𝐴

4

− 𝐴

5

− 𝐴

1

− 𝐴

2

− 𝐴

1

− 𝐴

2

− 𝐴

4

− 𝐴

2

− 𝐴

1 6 64

_𝑛

2

_{+ 1 = 37}

𝐴

6

− 𝐴

2

− 𝐴

3

− 𝐴

1

− 𝐴

3

− 𝐴

2

− 𝐴

4

− 𝐴

5

− 𝐴

6

− 𝐴

4

− 𝐴

4

− 𝐴

1

− 𝐴

₁

D. Pola langkah serta Sirkuit Hamilton yang Terbentuk berdasarkan

Data dari Hasil Percobaan

Berdasarkan data tersebut peneliti akan mengkaji lebih detail untuk

𝑛 = 6 , dengan jumlah biji pada lubang induk atau lumbung adalah

minimal

𝑛

2

_{+ 1 = 37. Peneliti akan mengkaji pada masing-masing lubang mulai}

dari lubang

𝐴

1

sampai

𝐴

6

untuk mengetahui kemungkinan-kemungkinan

terbentuknya pola langkah dan sirkuit Hamilton yang terbentuk

Sebelum permainan dimulai jumlah biji congklak pada

masing-masing lubang kecil adalah 6 biji congklak, keadaan tersebut dinamakan

kondisi awal atau iterasi ke-0

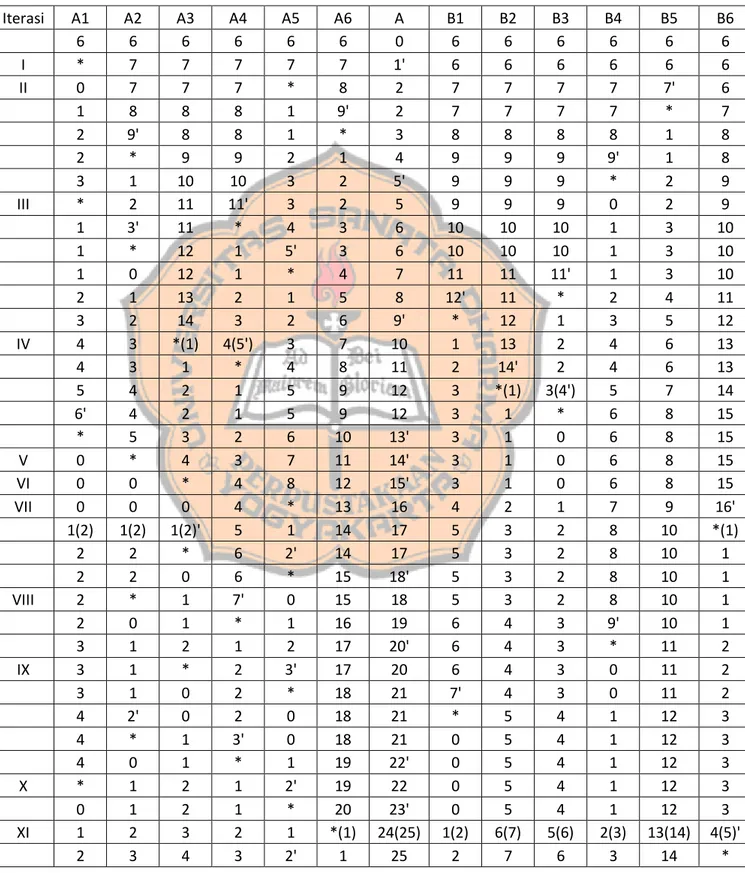
Iterasi A1 A2 A3 A4 A5 A6 A B1 B2 B3 B4 B5 B6

6 6 6 6 6 6 0 6 6 6 6 6 6

Pada saat memulai permainan pemain yang mendapatkan giliran

pertama mendapat kesempatan untuk memilih lubang kecil miliknya yaitu

lubang

𝐴

₁

sampai lubang

𝐴

₆

untuk memulai permainan. Berikut akan

dijelaskan pola langkah yang dilakukan oleh pemain dan banyaknya iterasi

yang terbentuk ketika pemain pertama memilih lubang

𝐴

1

sebagai langkah

awalnya

Untuk Lubang 𝐴

₁

1) Pada kemungkinan ke-1

Ketika pemain pertama memilih lubang

𝐴

₁

sebagai langkah awalnya

peneliti menyebutnya sebagai iterasi pertama. Hasil penyebaran biji

Iterasi A1 A2 A3 A4 A5 A6 A B1 B2 B3 B4 B5 B6 6 6 6 6 6 6 0 6 6 6 6 6 6 I * 7 7 7 7 7 1' 6 6 6 6 6 6 II 0 * 8 8 8 8 2 7 7' 6 6 6 6 1 1 9' 8 8 8 2 7 * 7 7 7 7 1 1 * 9 9 9 3 8 1 8 8 8' 7 2 2 1 10 10 10 4' 8 1 8 8 * 8 III * 3 2' 10 10 10 4 8 1 8 8 0 8 0 3 * 11 11' 10 4 8 1 8 8 0 8 1 4 1' 11 * 11 5 9 2 9 9 1 9

Dengan :

* = proses pengambilan biji congklak yang dipilih

‘ = tempat biji congklak terakhir jatuh

2) Pada iterasi I proses penyebaran biji congklak berhenti pada lubang induk

(lumbung), sehingga pemain tersebut memiliki kesempatan untuk memilih

lubang kecil miliknya untuk melanjutkan proses penyebaran biji congklak

lagi.

3) Pada iterasi II

a) Langkah pertama

Pemain memilih lubang

𝐴

₂

. Ketika pemain melakukan penyebaran

biji congklak tersebut biji terakhir jatuh pada lubang

𝐵

2

, dengan

jumlah biji congklak 7 biji. Jumlah biji congklak pada lubang 𝐵

₂

≠

0 maka pemain tersebut dapat melanjutkan proses penyebaran biji

ke langkah selanjutnya dimulai dari lubang 𝐵

2

.

b) Langkah kedua

Pada langkah kedua pemain melakukan proses penyebaran biji

dengan mengambil biji congklak dilubang

𝐵

2

dan memulai proses

penyebaran biji dari lubang

𝐵

₃

. Proses penyebaran biji congklak

pada langkah kedua ini biji terakhirnya jatuh pada lubang

𝐴

3

dengan jumlah biji congklak 9 biji, sehingga pemain dapat

c) Langkah ketiga

Pada langkah kedua pemain melakukan proses penyebaran biji

dengan mengambil biji congklak dilubang 𝐴

₃

, karena pada langkah

kedua biji terakhir jatuh pada lubang

𝐴

3

. Pada langkah ketiga ini

biji congklak terakhir jatuh pada lubang induk (A) yang artinya

pemain masih dapat melanjutkan permainan dengan memilih

lubang miliknya untuk melakukan proses penyebaran biji lagi

sehingga terbentuk iterasi III.

4) Pada iterasi III

a) Langkah pertama

Pada langkah pertama pemain memilih lubang

𝐴

₁

dengan jumlah

biji congklak 2 biji. Proses penyebaran biji congklak dilangkah

pertama ini dimulai dari lubang

𝐴

₂

dan biji terakhir jatuh pada

lubang

𝐴

₃

dengan jumlah biji congklak 2 biji, karena jumlah biji

congklak dilubang

𝐴

₃

≠ 0 maka pemain dapat melakukan proses

penyebaran biji untuk langkah selanjutnya dimulai dari lubang 𝐴

₃

.

b) Langkah kedua

Pada langkah kedua pemain melakukan proses penyebaran biji

dengan mengambil biji congklak dilubang

𝐴

₃

dan memulai proses

penyebaran biji dari lubang

𝐴

₄

. Biji congklak terakhir jatuh pada

lubang

𝐴

₅

dengan jumlah biji congklak 11 biji, karena jumlah biji

congklak pada lubang

𝐴

₅

≠ 0 maka proses penyebaran biji

congklak dapat dilanjtkan untuk langkah yang ketiga.

c) Langkah ketiga

Pada langkah kedua pemain melakukan proses penyebaran biji

dengan mengambil biji congklak dilubang

𝐴

₃

dan memulai proses

penyebaran biji dari lubang

𝐴

₄

. Pada langkah ketiga ini proses

penyebaran biji congklak berhenti dilubang 𝐴

₃

karena pada lubang

𝐴

₃

tidak terdapat minimal satu biji congklak kecuali biji terakhir

dan titik akhir, sehingga terbentuk sirkuit pada lubang

𝐴

₃

. Sirkuit

yang ada pada lubang

𝐴

3

merupakan sirkuit Hamilton menurut

definisi 3.2.

Sirkuit yang terbentuk yang dituliskan pada tabel 4.2 merupakan sirkuit

yang terbentuk pada langkah yang dilakukan oleh pemain pada setiap

kemungkinannya dan pola langkah yang dituliskan pada tabel 4.2 merupakan

lubang pada langkah pertama setiap iterasinya.

Tabel 4.2

Kemungkinan

Ke-

Jumlah biji

pada lubang

induk

Pola langkah

Sirkuit yang

Terbentuk

1

1 + 5 + 9

= 15

𝐴

1

− 𝐴

2

− 𝐴

1

𝐴

3

2

1 + 5 + 1 = 7

𝐴

₁

− 𝐴

₂

− 𝐴

₂

𝐴

₂

3

1 + 7 + 11

= 19

𝐴

1

− 𝐴

2

− 𝐴

3

𝐴

6

4

1 + 5 + 9

= 15

𝐴

1

− 𝐴

2

− 𝐴

4

𝐴

4

5

1 + 5 + 2 = 8

𝐴

₁

− 𝐴

₂

− 𝐴

₅

𝐴

₅

6

1 + 6 + 10

= 17

𝐴

1

− 𝐴

2

− 𝐴

6

𝐴

3

7

1 + 5 + 3 = 9

𝐴

1

− 𝐴

3

𝐴

4

8

6

𝐴

₁

− 𝐴

₄

𝐵

₁

9

10

𝐴

1

− 𝐴

5

− 𝐴

1

− 𝐴

1

𝐵

1

10

10

𝐴

₁

− 𝐴

₅

− 𝐴

₁

− 𝐴

₂

𝐵

₁

11

17

𝐴

1

− 𝐴

5

− 𝐴

1

− 𝐴

3

− 𝐴

2

− 𝐴

₃

− 𝐴

₄

𝐵

1

− 𝐴

₁

13

1 + 23 + 1

= 25

𝐴

₁

− 𝐴

₅

− 𝐴

₁

− 𝐴

₃

− 𝐴

₂

− 𝐴

₃

− 𝐴

₅

− 𝐴

₂

− 𝐴

₁

𝐴

₄

14

1 + 23 + 6

= 30

𝐴

₁

− 𝐴

₅

− 𝐴

₁

− 𝐴

₃

− 𝐴

₂

− 𝐴

₃

− 𝐴

₅

− 𝐴

₂

− 𝐴

₂

𝐴

₄

15

1 + 26 + 8

= 35

𝐴

₁

− 𝐴

₅

− 𝐴

₁

− 𝐴

₃

− 𝐴

₂

− 𝐴

3

− 𝐴

5

− 𝐴

₂

− 𝐴

₃

− 𝐴

₁

− 𝐴

₂

𝐴

5

16

1 + 23 + 5

= 29

𝐴

₁

− 𝐴

₅

− 𝐴

₁

− 𝐴

₃

− 𝐴

₂

− 𝐴

3

− 𝐴

5

− 𝐴

2

− 𝐴

3

− 𝐴

₁

− 𝐴

₃

𝐴

₅

17

1 + 23 + 5

= 29

𝐴

₁

− 𝐴

₅

− 𝐴

₁

− 𝐴

₃

− 𝐴

₂

− 𝐴

₃

− 𝐴

₅

− 𝐴

₂

− 𝐴

₃

− 𝐴

₁

− 𝐴

₄

𝐴

₅

18

1 + 28 + 15

= 44

𝐴

₁

− 𝐴

₅

− 𝐴

₁

− 𝐴

₃

− 𝐴

₂

− 𝐴

₃

− 𝐴

₅

− 𝐴

₂

− 𝐴

₃

− 𝐴

₁

− 𝐴

₆

− 𝐴

₁

− 𝐴

₁

𝐴

₂

19

37

𝐴

₁

− 𝐴

₅

− 𝐴

₁

− 𝐴

₃

− 𝐴

₂

− 𝐴

₃

− 𝐴

₅

− 𝐴

₂

− 𝐴

₃

− 𝐴

₁

− 𝐴

₆

− 𝐴

1

− 𝐴

3

− 𝐴

₁

− 𝐴

₁

𝐵

3

20

1 + 36 + 2

= 39

𝐴

1

− 𝐴

5

− 𝐴

1

− 𝐴

3

− 𝐴

2

− 𝐴

₃

− 𝐴

₅

− 𝐴

2

− 𝐴

3

− 𝐴

₁

− 𝐴

₆

− 𝐴

₁

− 𝐴

₃

− 𝐴

₁

− 𝐴

₂

𝐴

₂

21

1 + 36 + 6

= 43

− 𝐴

₂

− 𝐴

₃

− 𝐴

₁

− 𝐴

₆

− 𝐴

1

− 𝐴

3

− 𝐴

₁

− 𝐴

₃

𝐴

3

22

38

𝐴

1

− 𝐴

5

− 𝐴

1

− 𝐴

3

− 𝐴

2

− 𝐴

₃

− 𝐴

₅

− 𝐴

2

− 𝐴

3

− 𝐴

₁

− 𝐴

₆

− 𝐴

₁

− 𝐴

₃

− 𝐴

₁

− 𝐴

₄

− 𝐴

₁

𝐵

3

23

1 + 37 + 2

= 40

𝐴

₁

− 𝐴

₅

− 𝐴

₁

− 𝐴

₃

− 𝐴

₂

− 𝐴

₃

− 𝐴

₅

− 𝐴

₂

− 𝐴

₃

− 𝐴

₁

− 𝐴

₆

− 𝐴

₁

− 𝐴

₃

− 𝐴

1

− 𝐴

4

− 𝐴

₂

𝐴

₂

24

1 + 37 + 6

= 44

𝐴

1

− 𝐴

5

− 𝐴

1

− 𝐴

3

− 𝐴

2

− 𝐴

₃

− 𝐴

₅

− 𝐴

2

− 𝐴

3

− 𝐴

₁

− 𝐴

₆

− 𝐴

₁

− 𝐴

₃

− 𝐴

₁

− 𝐴

₄

− 𝐴

₃

𝐴

3

25

1 + 37 + 5

= 43

𝐴

₁

− 𝐴

₅

− 𝐴

₁

− 𝐴

₃

− 𝐴

₂

− 𝐴

₃

− 𝐴

₅

− 𝐴

₂

− 𝐴

₃

− 𝐴

₁

− 𝐴

₆

− 𝐴

₁

− 𝐴

₃

− 𝐴

1

− 𝐴

4

− 𝐴

₅

𝐴

₄

26

1 + 37 + 5 =

𝐴

1

− 𝐴

5

− 𝐴

1

− 𝐴

3

− 𝐴

2

− 𝐴

₃

− 𝐴

₅

− 𝐴

2

− 𝐴

3

− 𝐴

₁

− 𝐴

₆

− 𝐴

₁

− 𝐴

₃

− 𝐴

₁

− 𝐴

₄

− 𝐴

₆

𝐴

4

27

1 + 39 + 8

= 47

− 𝐴

₂

− 𝐴

₃

− 𝐴

₁

− 𝐴

₆

− 𝐴

1

− 𝐴

3

− 𝐴

₁

− 𝐴

₆

− 𝐴

₂

𝐴

₃

28

39

𝐴

₁

− 𝐴

₅

− 𝐴

₁

− 𝐴

₃

− 𝐴

₂

− 𝐴

3

− 𝐴

5

− 𝐴

₂

− 𝐴

₃

− 𝐴

₁

− 𝐴

₆

− 𝐴

₁

− 𝐴

₃

− 𝐴

₂

− 𝐴

₁

− 𝐴

₂

− 𝐴

₃

𝐵

₄

29

1 + 40 + 1

= 42

𝐴

₁

− 𝐴

₅

− 𝐴

₁

− 𝐴

₃

− 𝐴

₂

− 𝐴

₃

− 𝐴

₅

− 𝐴

₂

− 𝐴

₃

− 𝐴

₁

− 𝐴

₆

− 𝐴

1

− 𝐴

3

− 𝐴

₂

− 𝐴

₁

− 𝐴

₂

− 𝐴

₄

𝐴

₂

30

1 + 38 + 3

= 42

𝐴

₁

− 𝐴

₅

− 𝐴

₁

− 𝐴

₃

− 𝐴

₂

− 𝐴

3

− 𝐴

5

− 𝐴

₂

− 𝐴

₃

− 𝐴

₁

− 𝐴

₆

− 𝐴

₁

− 𝐴

₃

− 𝐴

₂

− 𝐴

₁

− 𝐴

₂

− 𝐴

₆

𝐴

₁

31

41

𝐴

₁

− 𝐴

₅

− 𝐴

₁

− 𝐴

₃

− 𝐴

₂

− 𝐴

₃

− 𝐴

₅

− 𝐴

₂

− 𝐴

₃

− 𝐴

₁

− 𝐴

₆

− 𝐴

1

− 𝐴

3

− 𝐴

₂

− 𝐴

₁

− 𝐴

3

𝐵

₆